DBYOLO: Dual-Backbone YOLO Network for Lunar Crater Detection
Abstract
Highlights
- Designed a lightweight dual-backbone network to extract texture and edge features from LROC CCD images and terrain depth features from DTM data.
- Proposed a feature fusion module based on attention mechanisms to dynamically integrate features from multi-source data at different scales.
- mAP50 improved by 3.1% compared to the baseline model.
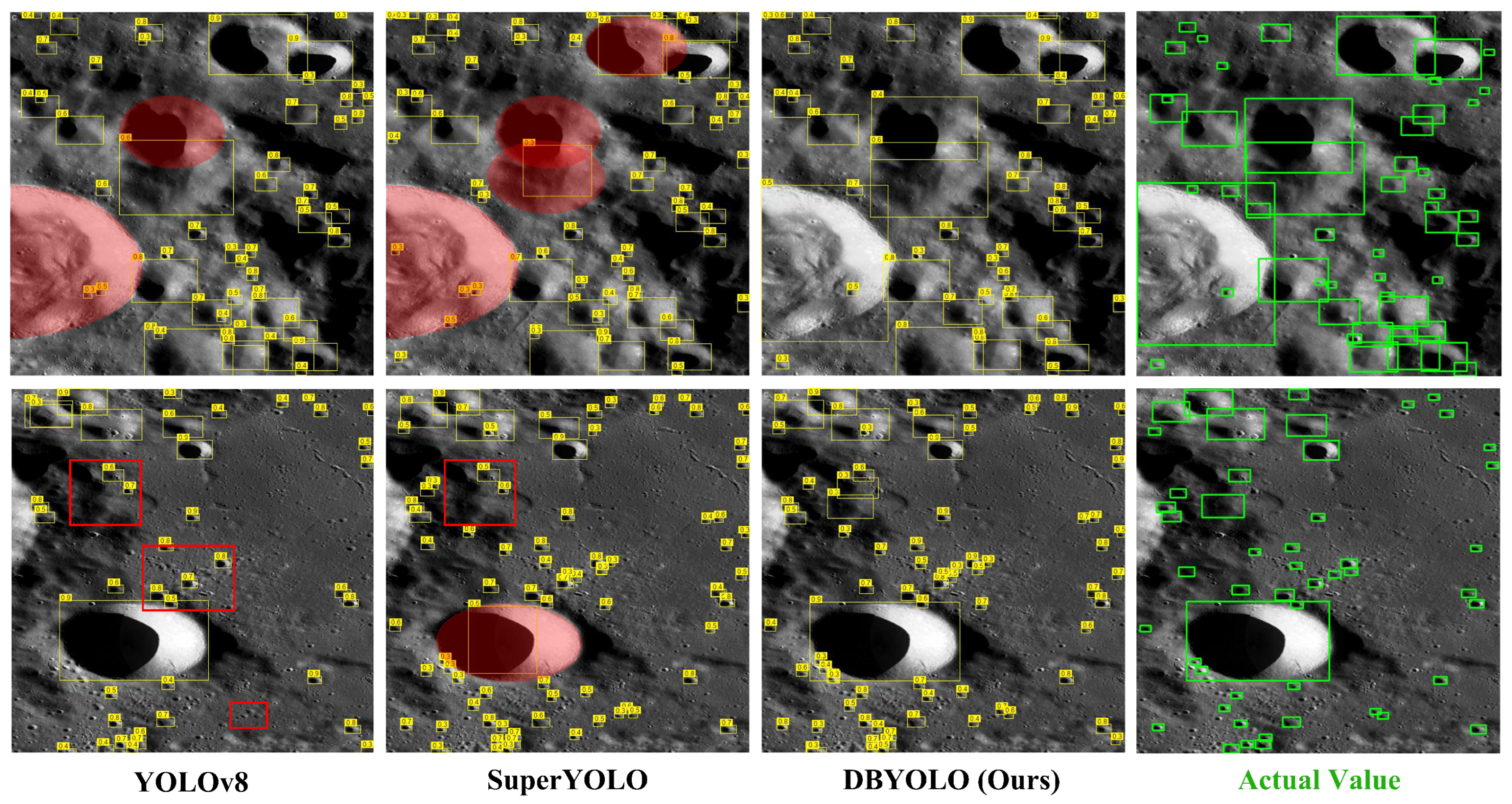
- The model’s prediction plot better fits the ground truth compared to other mainstream models.
Abstract
1. Introduction
2. Related Work
2.1. Manual and Early Automation Methods
2.2. Deep Learning for Crater Detection
2.3. Multi-Source Remote Sensing Image Fusion
2.4. Application of YOLO in Crater Detection
3. Methods
3.1. Data Preparation
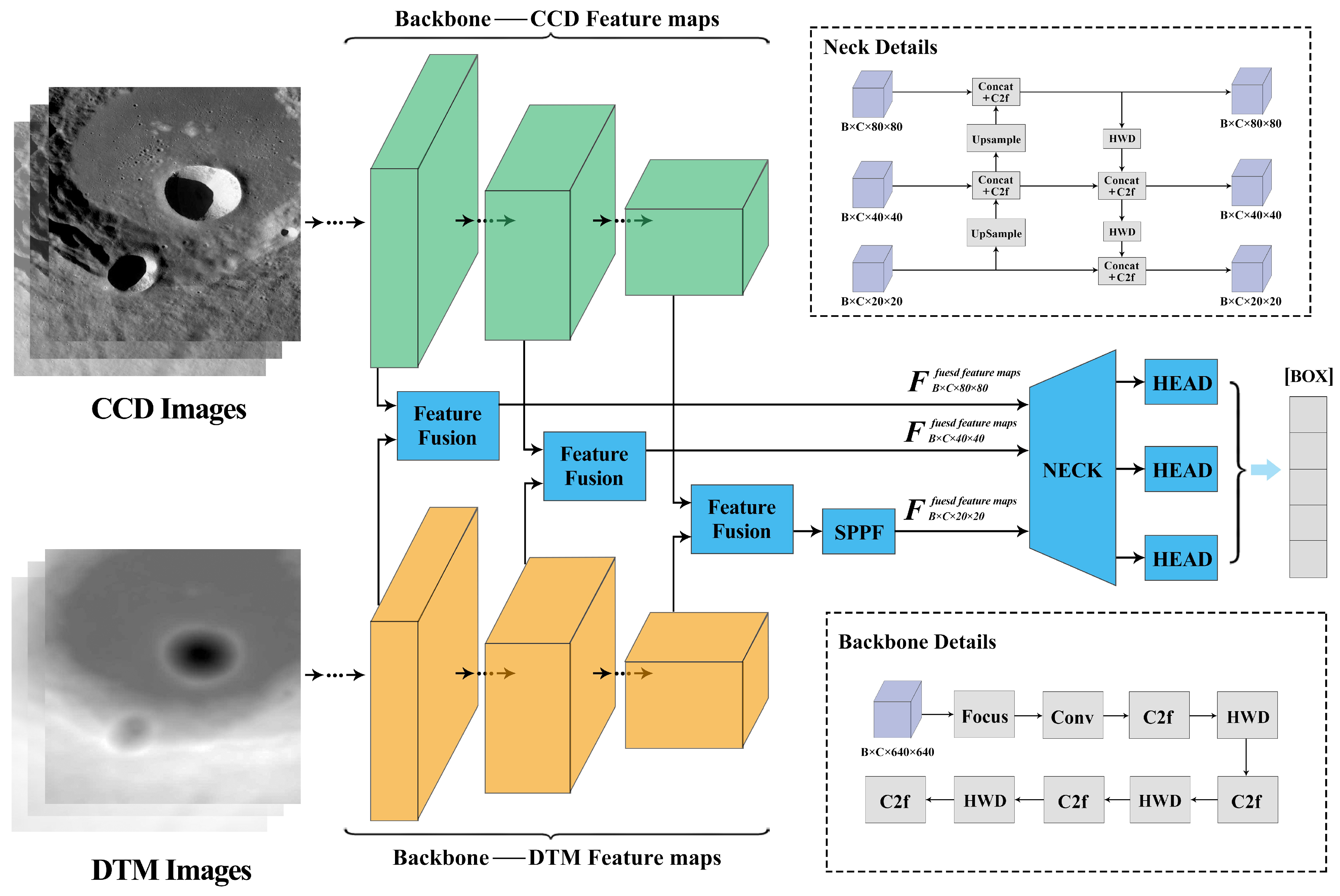
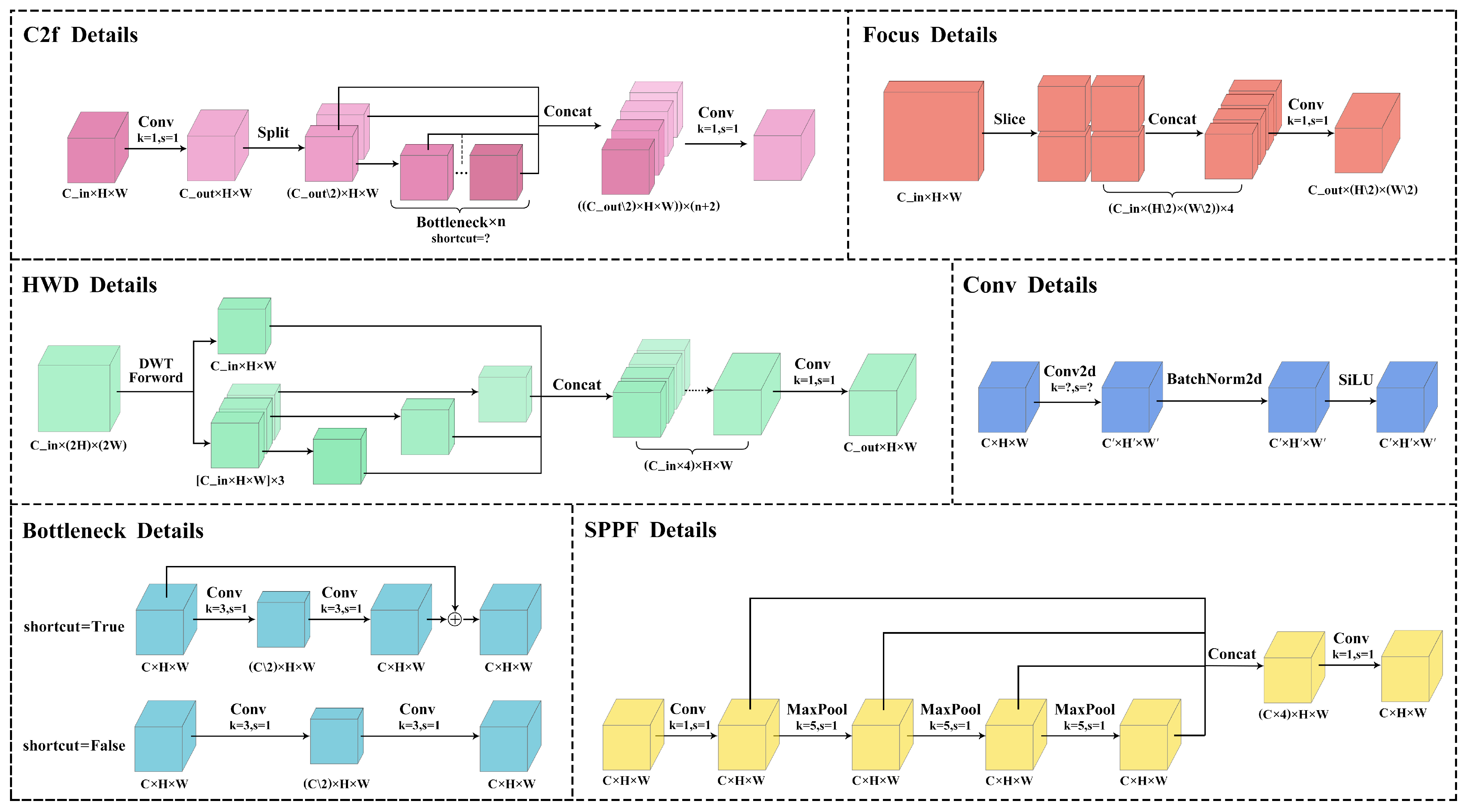
3.2. DBYOLO Architecture
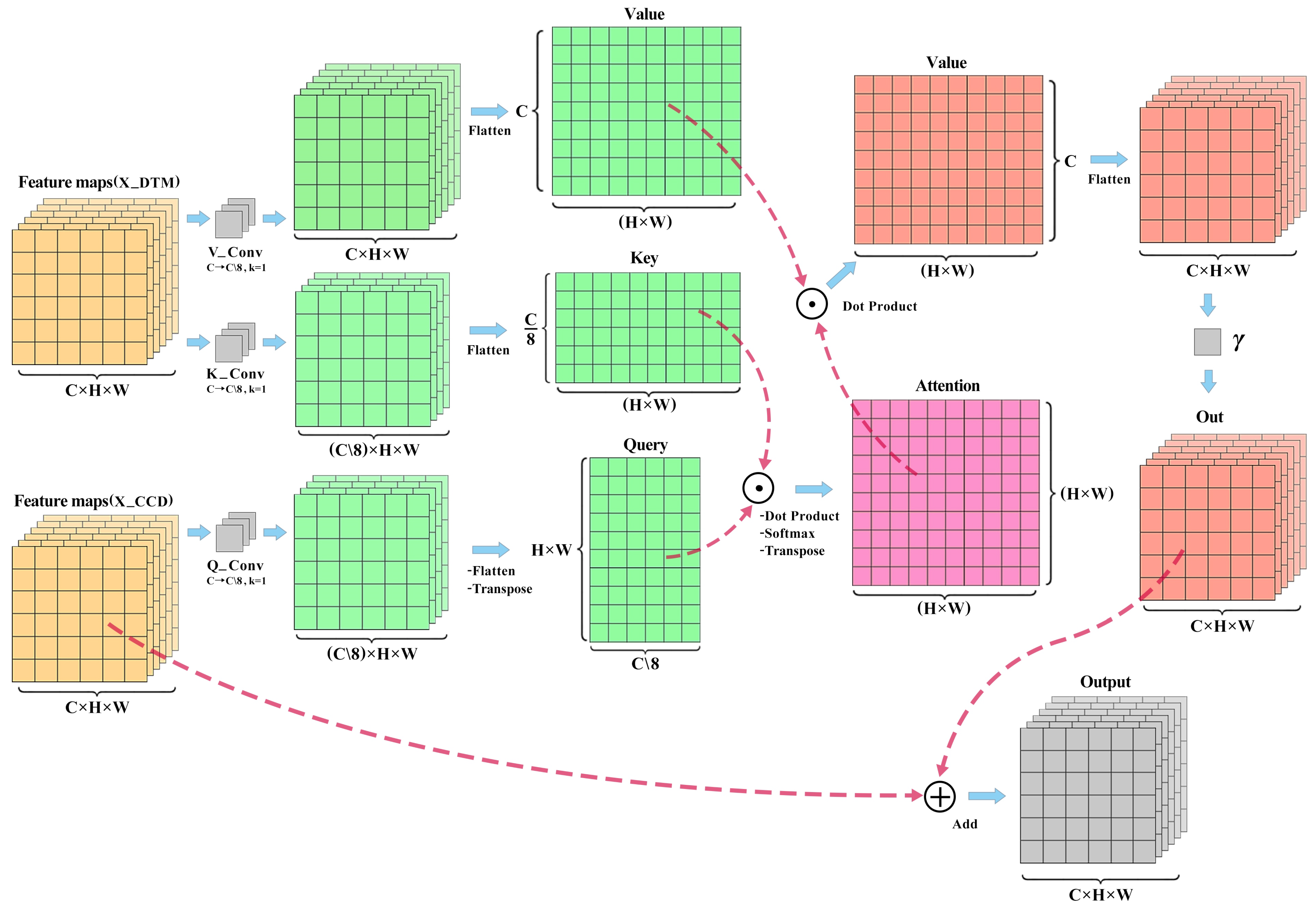
3.3. Attention Feature Fusion Module Architecture
- Feature Dimension Reduction:
- Attention Computation:
- Residual Connection:
- Gradient Calculation of the Loss Function with respect to :
3.4. Evaluation Metrics
4. Experiments
4.1. Experiment Configurations
4.2. Comparison Experiments and Analysis
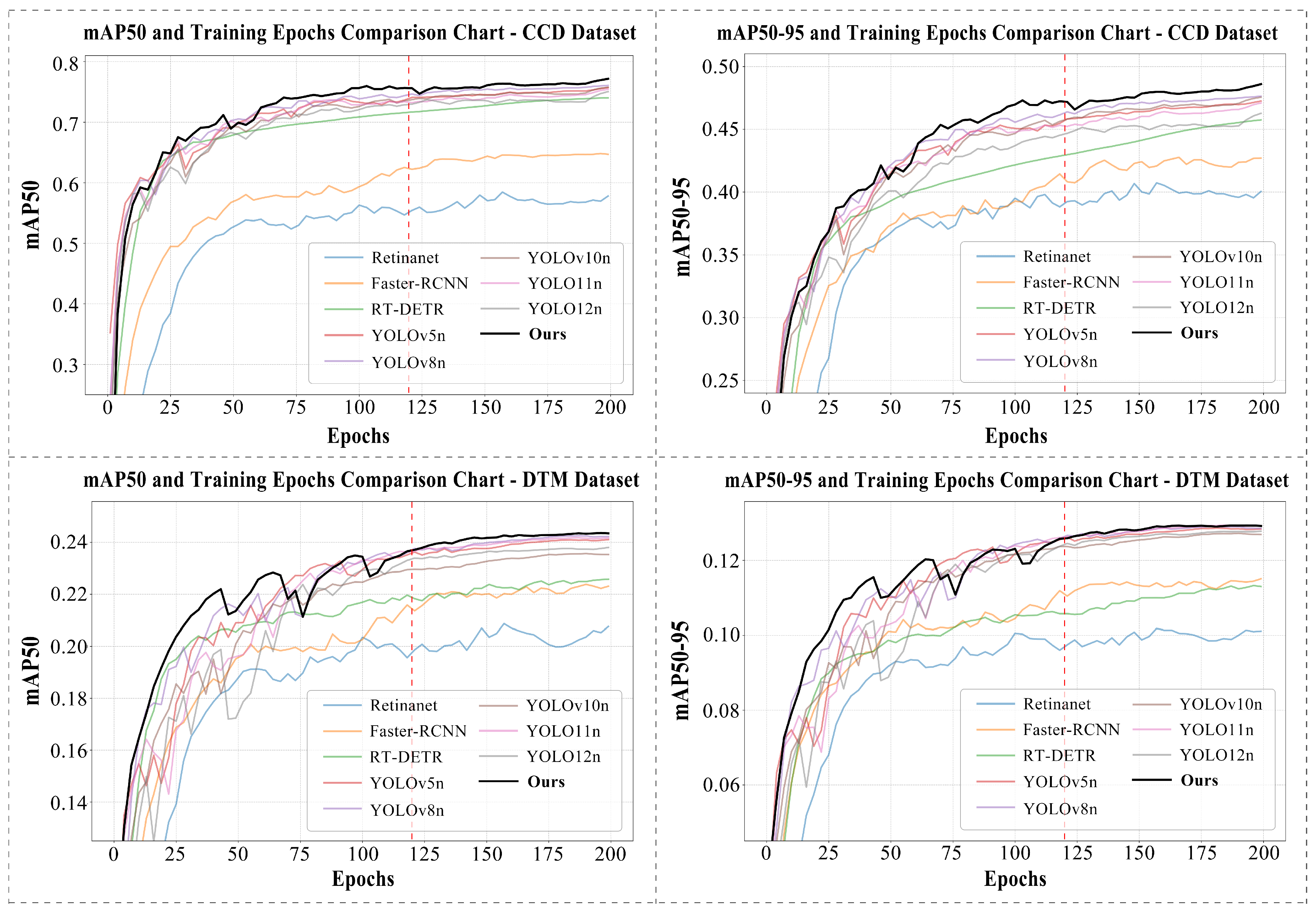
4.2.1. Comparing Mainstream Detection Models Using a Single Dataset
4.2.2. Comparing Mainstream Detection Models Using Multiple Datasets
4.2.3. Experimental Comparison of Mainstream Fusion Modules
4.3. Ablation Experiments and Analysis
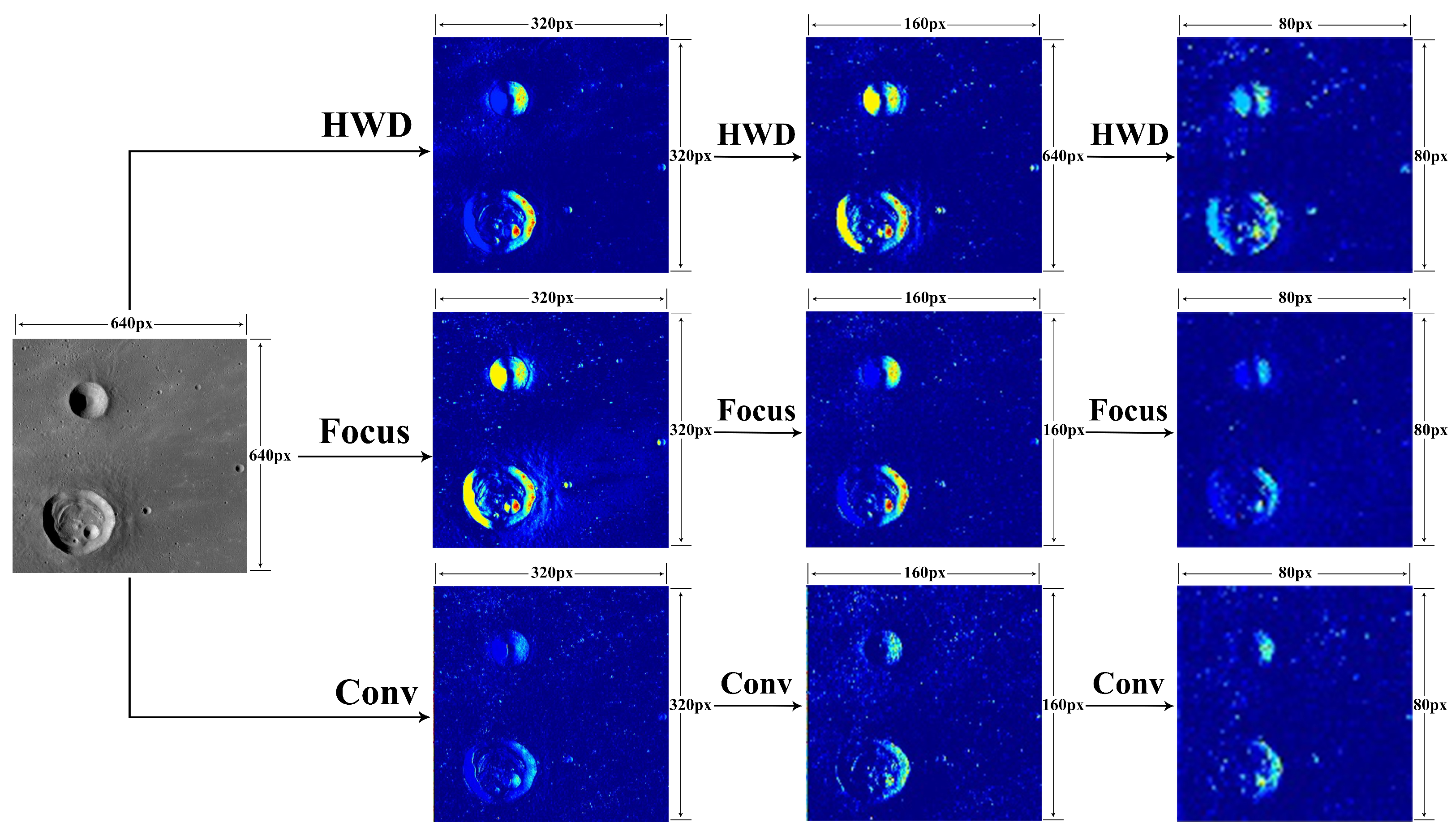
4.3.1. Ablation Experiments on the Backbone
4.3.2. Ablation Experiments on the Fusion Module
5. Conclusions
- Optimization for Small Crater Detection: By incorporating a local feature fusion module, a multi-scale feature fusion framework, and a local attention pyramid module, the feature representation of small targets is enhanced, improving the detection accuracy of small lunar craters [53].
- Model Lightweighting and Efficient Deployment: The current model involves high computational complexity and a large number of parameters. Future work can explore techniques such as model pruning and knowledge distillation to reduce the parameter count and computational overhead, thereby improving inference efficiency on low-power or resource-constrained devices [54,55].
- Expansion of Multimodal Data Sources: This study integrates only CCD imagery and DTM data. In the future, additional modalities such as infrared imagery and spectral data could be incorporated to further enrich feature representations and enhance detection performance [56].
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CCD | Charge-Coupled Device |
| DTM | Digital Terrain Model |
| LROC | Lunar Reconnaissance Orbiter Camera |
| CNN | Convolutional Neural Network |
| YOLO | You Only Look Once |
| HT | Hough Transform |
| DEM | Digital Elevation Map |
| DOM | Digital Orthophoto Map |
| RGB | Red, Green, Blue |
| SAR | Synthetic Aperture Radar |
| LRO | Lunar Reconnaissance Orbiter |
| WAC | Wide Angle Camera |
| SPPF | Spatial Pyramid Pooling-Fast |
| mAP | mean Average Precision |
| IoU | Intersection over Union |
| FN | False Negative |
| TP | True Positive |
| FP | False Positive |
References
- Salih, A.L.; Schulte, P.; Grumpe, A.; Wöhler, C.; Hiesinger, H. Automatic crater detection and age estimation for mare regions on the lunar surface. In Proceedings of the 2017 IEEE 25th European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 August–2 September 2017; pp. 518–522. [Google Scholar]
- Strom, R.G.; Malhotra, R.; Ito, T.; Yoshida, F.; Kring, D.A. The origin of planetary impactors in the inner solar system. Science 2005, 309, 1847–1850. [Google Scholar] [CrossRef] [PubMed]
- Tewari, A.; Prateek, K.; Singh, A.; Khanna, N. Deep learning based systems for crater detection: A review. arXiv 2023, arXiv:2310.07727. [Google Scholar] [CrossRef]
- Weiming, C.; Qiangyi, L.; Jiao, W.; Wenxin, G.; Jianzhong, L. A preliminary study of classification method on lunar topography and landforms. Adv. Earth Sci. 2018, 33, 885. [Google Scholar]
- Richardson, M.; Malagón, A.A.P.; Lebofsky, L.A.; Grier, J.; Gay, P.; Robbins, S.J.; Team, T.C. The CosmoQuest Moon mappers community science project: The effect of incidence angle on the Lunar surface crater distribution. arXiv 2021, arXiv:2110.13404. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1137–1149. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 213–229. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Virtual, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Zhang, J.; Lei, J.; Xie, W.; Fang, Z.; Li, Y.; Du, Q. SuperYOLO: Super resolution assisted object detection in multimodal remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2023, 61, 3258666. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, B.; Guo, X.; Zhu, W.; He, J.; Liu, X.; Yuan, J. DEYOLO: Dual-feature-enhancement YOLO for cross-modality object detection. In Proceedings of the International Conference on Pattern Recognition, Kolkata, India, 1–5 December 2024; Springer: Cham, Switzerland, 2024; pp. 236–252. [Google Scholar]
- Robbins, S.J. A new global database of lunar impact craters > 1–2 km: 1. Crater locations and sizes, comparisons with published databases, and global analysis. J. Geophys. Res. Planets 2019, 124, 871–892. [Google Scholar] [CrossRef]
- Head, J.W., III; Fassett, C.I.; Kadish, S.J.; Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Mazarico, E. Global distribution of large lunar craters: Implications for resurfacing and impactor populations. Science 2010, 329, 1504–1507. [Google Scholar] [CrossRef]
- Michael, G. Coordinate registration by automated crater recognition. Planet. Space Sci. 2003, 51, 563–568. [Google Scholar] [CrossRef]
- Kim, J.R.; Muller, J.P.; van Gasselt, S.; Morley, J.G.; Neukum, G. Automated crater detection, a new tool for Mars cartography and chronology. Photogramm. Eng. Remote Sens. 2005, 71, 1205–1217. [Google Scholar] [CrossRef]
- Galloway, M.J.; Benedix, G.K.; Bland, P.A.; Paxman, J.; Towner, M.C.; Tan, T. Automated crater detection and counting using the Hough transform. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 1579–1583. [Google Scholar]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Hu, Y.; Xiao, J.; Liu, L.; Zhang, L.; Wang, Y. Detection of Small Impact Craters via Semantic Segmenting Lunar Point Clouds Using Deep Learning Network. Remote Sens. 2021, 13, 1826. [Google Scholar] [CrossRef]
- Minaee, S.; Boykov, Y.; Porikli, F.; Plaza, A.; Kehtarnavaz, N.; Terzopoulos, D. Image segmentation using deep learning: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 3523–3542. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Zhu, Z.; Yu, X.; Ji, X.; Luo, T.; Xi, X.; Zhu, M.; Liang, Y. Lunar Crater Detection on Digital Elevation Model: A Complete Workflow Using Deep Learning and Its Application. Remote Sens. 2022, 14, 621. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, P.; Yang, J.; Kang, Z.; Cao, Z.; Yang, Z. Automatic detection for small-scale lunar impact crater using deep learning. Adv. Space Res. 2024, 73, 2175–2187. [Google Scholar] [CrossRef]
- Zang, S.; Mu, L.; Xian, L.; Zhang, W. Semi-Supervised Deep Learning for Lunar Crater Detection Using CE-2 DOM. Remote Sens. 2021, 13, 2819. [Google Scholar] [CrossRef]
- Li, J.; Zheng, K.; Li, Z.; Gao, L.; Jia, X. X-shaped interactive autoencoders with cross-modality mutual learning for unsupervised hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2023, 61, 3300043. [Google Scholar] [CrossRef]
- Li, J.; Zheng, K.; Liu, W.; Li, Z.; Yu, H.; Ni, L. Model-guided coarse-to-fine fusion network for unsupervised hyperspectral image super-resolution. IEEE Geosci. Remote Sens. Lett. 2023, 20, 3309854. [Google Scholar] [CrossRef]
- Tewari, A.; Verma, V.; Srivastava, P.; Jain, V.; Khanna, N. Automated crater detection from co-registered optical images, elevation maps and slope maps using deep learning. Planet. Space Sci. 2022, 218, 105500. [Google Scholar] [CrossRef]
- Yang, C.; Zhao, H.; Bruzzone, L.; Benediktsson, J.A.; Liang, Y.; Liu, B.; Zeng, X.; Guan, R.; Li, C.; Ouyang, Z. Lunar impact crater identification and age estimation with Chang’E data by deep and transfer learning. Nat. Commun. 2020, 11, 6358. [Google Scholar] [CrossRef]
- Mu, L.; Xian, L.; Li, L.; Liu, G.; Chen, M.; Zhang, W. YOLO-crater model for small crater detection. Remote Sens. 2023, 15, 5040. [Google Scholar] [CrossRef]
- Sharma, M.; Dhanaraj, M.; Karnam, S.; Chachlakis, D.G.; Ptucha, R.; Markopoulos, P.P.; Saber, E. YOLOrs: Object detection in multimodal remote sensing imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 1497–1508. [Google Scholar] [CrossRef]
- Tang, J.; Gu, B.; Li, T.; Lu, Y.B. SCCA-YOLO: Spatial Channel Fusion and Context-Aware YOLO for Lunar Crater Detection. Remote Sens. 2025, 17, 2380. [Google Scholar] [CrossRef]
- Zuo, W.; Gao, X.; Wu, D.; Liu, J.; Zeng, X.; Li, C. YOLO-SCNet: A Framework for Enhanced Detection of Small Lunar Craters. Remote Sens. 2025, 17, 1959. [Google Scholar] [CrossRef]
- Speyerer, E.; Robinson, M.; Denevi, B.; LROC Science Team. Lunar Reconnaissance Orbiter Camera global morphological map of the Moon. In Proceedings of the 42nd Annual Lunar and Planetary Science Conference, The Woodlands, TX, USA, 7–11 March 2011; No. 1608. p. 2387. [Google Scholar]
- Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Lemoine, F.G.; Mazarico, E.; Torrence, M.H.; McGarry, J.F.; Rowlands, D.D.; Head, J.W., III; Duxbury, T.H.; et al. Initial observations from the lunar orbiter laser altimeter (LOLA). Geophys. Res. Lett. 2010, 37, L18204. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, B.; Xue, H.; Li, X.; Ma, J. An improved global catalog of lunar impact craters (≥ 1 km) with 3D morphometric information and updates on global crater analysis. J. Geophys. Res. Planets 2021, 126, e2020JE006728. [Google Scholar] [CrossRef]
- Wang, C.Y.; Liao, H.Y.M.; Wu, Y.H.; Chen, P.Y.; Hsieh, J.W.; Yeh, I.H. CSPNet: A new backbone that can enhance learning capability of CNN. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 390–391. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Zhu, X.; Lyu, S.; Wang, X.; Zhao, Q. TPH-YOLOv5: Improved YOLOv5 based on transformer prediction head for object detection on drone-captured scenarios. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Virtual, 11–17 October 2021; pp. 2778–2788. [Google Scholar]
- Xu, G.; Liao, W.; Zhang, X.; Li, C.; He, X.; Wu, X. Haar Wavelet Downsampling: A Simple but Effective Downsampling Module for Semantic Segmentation. Pattern Recognit. 2023, 143, 109819. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition. In Computer Vision—ECCV 2014; Springer International Publishing: Cham, Switzerland, 2014; pp. 346–361. [Google Scholar] [CrossRef]
- Liu, S.; Qi, L.; Qin, H.; Shi, J.; Jia, J. Path aggregation network for instance segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 8759–8768. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Lin, H.; Cheng, X.; Wu, X.; Shen, D. Cat: Cross attention in vision transformer. In Proceedings of the 2022 IEEE International Conference on Multimedia and Expo (ICME), Taipei, Taiwan, 18–22 July 2022; pp. 1–6. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Wang, A.; Chen, H.; Liu, L.; Chen, K.; Lin, Z.; Han, J.; Ding, G. Yolov10: Real-time end-to-end object detection. Adv. Neural Inf. Process. Syst. 2024, 37, 107984–108011. [Google Scholar]
- Khanam, R.; Hussain, M. Yolov11: An overview of the key architectural enhancements. arXiv 2024, arXiv:2410.17725. [Google Scholar] [CrossRef]
- Tian, Y.; Ye, Q.; Doermann, D. Yolov12: Attention-centric real-time object detectors. arXiv 2025, arXiv:2502.12524. [Google Scholar]
- Wang, Z.; Liao, X.; Yuan, J.; Yao, Y.; Li, Z. Cdc-yolofusion: Leveraging cross-scale dynamic convolution fusion for visible-infrared object detection. IEEE Trans. Intell. Veh. 2024, 10, 2080–2093. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, X.; Xiao, P.; He, G. Exchanging dual-encoder–decoder: A new strategy for change detection with semantic guidance and spatial localization. IEEE Trans. Geosci. Remote Sens. 2023, 61, 3327780. [Google Scholar] [CrossRef]
- Chen, P.; Zhang, B.; Hong, D.; Chen, Z.; Yang, X.; Li, B. FCCDN: Feature constraint network for VHR image change detection. ISPRS J. Photogramm. Remote Sens. 2022, 187, 101–119. [Google Scholar] [CrossRef]
- Shao, S.; Xing, L.; Xu, R.; Liu, W.; Wang, Y.J.; Liu, B.D. MDFM: Multi-decision fusing model for few-shot learning. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 5151–5162. [Google Scholar] [CrossRef]
- Tan, M.; Pang, R.; Le, Q.V. Efficientdet: Scalable and efficient object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 10781–10790. [Google Scholar]
- Zheng, X.; Qiu, Y.; Zhang, G.; Lei, T.; Jiang, P. ESL-YOLO: Small object detection with effective feature enhancement and spatial-context-guided fusion network for remote sensing. Remote Sens. 2024, 16, 4374. [Google Scholar] [CrossRef]
- Deng, C.; Jing, D.; Ding, Z.; Han, Y. Sparse channel pruning and assistant distillation for faster aerial object detection. Remote Sens. 2022, 14, 5347. [Google Scholar] [CrossRef]
- Himeur, Y.; Aburaed, N.; Elharrouss, O.; Varlamis, I.; Atalla, S.; Mansoor, W.; Al Ahmad, H. Applications of knowledge distillation in remote sensing: A survey. Inf. Fusion 2024, 115, 102742. [Google Scholar] [CrossRef]
- Sun, L.; Li, Y.; Zheng, M.; Zhong, Z.; Zhang, Y. MCnet: Multiscale visible image and infrared image fusion network. Signal Process. 2023, 208, 108996. [Google Scholar] [CrossRef]


| Experimental Environment | Details |
|---|---|
| GPU | NVIDIA RTX 3060 8G |
| CPU | Intel(R) Core(TM) i7-12700 |
| Operating System | Window 10 Professional |
| Framework | PyTorch 2.3.1 |
| Python Version | 3.10.11 |
| CUDA Version | 11.8 |
| Training Parameters | Details |
|---|---|
| Epochs | 200 |
| Batch Size | 8 |
| Learning Rate | 0.01 |
| Close Mosaic | 80 |
| Image Resolution | |
| Model input Resolution | |
| Weight_decay | 0.0005 |
| Pretrain | False |
| Train datasets | 2769 CCD and DTM |
| Val datasets | 574 CCD and DTM |
| Test datsets | 574 CCD and DTM |
| Model | Parameters | Dataset | Precision | Recall | mAP50 | mAP50-95 |
|---|---|---|---|---|---|---|
| RetinaNet [44] | 36,383,010 | CCD | 0.583 | 0.567 | 0.603 | 0.424 |
| DTM | 0.308 | 0.286 | 0.215 | 0.105 | ||
| Faster-RCNN [6] | 28,328,501 | CCD | 0.615 | 0.603 | 0.654 | 0.431 |
| DTM | 0.320 | 0.292 | 0.225 | 0.116 | ||
| RT-DETR [9] | 20,184,464 | CCD | 0.721 | 0.692 | 0.741 | 0.459 |
| DTM | 0.407 | 0.224 | 0.226 | 0.114 | ||
| YOLOv5n | 2,503,139 | CCD | 0.736 | 0.686 | 0.760 | 0.474 |
| DTM | 0.475 | 0.204 | 0.241 | 0.128 | ||
| YOLOv8n | 3,005,843 | CCD | 0.741 | 0.685 | 0.763 | 0.478 |
| DTM | 0.479 | 0.206 | 0.242 | 0.129 | ||
| YOLOv10n [45] | 2,265,363 | CCD | 0.739 | 0.679 | 0.760 | 0.476 |
| DTM | 0.463 | 0.201 | 0.236 | 0.127 | ||
| YOLO11n [46] | 2,582,347 | CCD | 0.730 | 0.687 | 0.757 | 0.472 |
| DTM | 0.468 | 0.207 | 0.242 | 0.129 | ||
| YOLO12n [47] | 2,556,923 | CCD | 0.735 | 0.680 | 0.756 | 0.466 |
| DTM | 0.455 | 0.205 | 0.238 | 0.127 | ||
| DBYOLO Single-Backbone | 2,693,603 | CCD | 0.750 | 0.695 | 0.776 | 0.489 |
| DTM | 0.480 | 0.209 | 0.244 | 0.130 |
| Models | Parameters | Inference Speed | Train Time (Hours) | Precision | Recall | mAP50 | mAP50-95 |
|---|---|---|---|---|---|---|---|
| YOLOv8n | 3,005,843 | 0.8 ms | 1.116 | 0.741 | 0.685 | 0.763 | 0.478 |
| YOLOv8s | 11,125,971 | 1.3 ms | 1.676 | 0.745 | 0.694 | 0.766 | 0.483 |
| YOLOv8m | 25,840,339 | 2.4 ms | 2.111 | 0.746 | 0.701 | 0.777 | 0.490 |
| YOLOv8l | 43,607,379 | 2.7 ms | 2.602 | 0.757 | 0.704 | 0.787 | 0.498 |
| YOLOv8x | 68,124,531 | 4.0 ms | 3.387 | 0.759 | 0.705 | 0.788 | 0.497 |
| Models | Parameters | Datasets | Precision | Recall | mAP50 | mAP50-95 |
|---|---|---|---|---|---|---|
| YOLOv5n Dual-Backbone | 3,490,726 | CCD_DTM | 0.757 | 0.694 | 0.779 | 0.486 |
| YOLOv8n Dual-Backbone | 4,219,846 | CCD_DTM | 0.757 | 0.696 | 0.780 | 0.489 |
| YOLOv10n Dual-Backbone | 3,584,969 | CCD_DTM | 0.739 | 0.682 | 0.764 | 0.481 |
| YOLO11n Dual-Backbone | 3,654,614 | CCD_DTM | 0.740 | 0.684 | 0.763 | 0.477 |
| YOLO12n Dual-Backbone | 3,280,070 | CCD_DTM | 0.753 | 0.686 | 0.762 | 0.478 |
| DEYOLO [12] | 6,008,143 | CCD_DTM | 0.744 | 0.675 | 0.713 | 0.446 |
| CDC-YOLOFusion [48] | 9,116,115 | CCD_DTM | 0.739 | 0.663 | 0.692 | 0.404 |
| SuperYOLO [11] | 1,932,919 | CCD_DTM | 0.662 | 0.567 | 0.625 | 0.357 |
| DBYOLO (Ours) | 3,689,958 | CCD_DTM | 0.772 | 0.703 | 0.794 | 0.504 |
| Module | Precision | Recall | mAP50 | mAP50-95 |
|---|---|---|---|---|
| TFAM [49] | 0.659 | 0.540 | 0.584 | 0.325 |
| DFM [50] | 0.599 | 0.534 | 0.549 | 0.287 |
| MDFM [51] | 0.679 | 0.598 | 0.655 | 0.371 |
| BiFPN [52] | 0.612 | 0.527 | 0.548 | 0.289 |
| Add and Normalization | 0.568 | 0.481 | 0.485 | 0.244 |
| Concat and PointwiseConv | 0.621 | 0.526 | 0.552 | 0.278 |
| Attention Feature Fusion | 0.772 | 0.703 | 0.794 | 0.504 |
| Focus | HWD | Precision | Recall | mAP50 | mAP50-95 |
|---|---|---|---|---|---|
| - | - | 0.757 | 0.696 | 0.780 | 0.489 |
| ✓ | - | 0.772 | 0.696 | 0.788 | 0.501 |
| - | ✓ | 0.767 | 0.691 | 0.784 | 0.498 |
| ✓ | ✓ | 0.772 | 0.703 | 0.794 | 0.504 |
| Attention | Resnet | Precision | Recall | mAP50 | mAP50-95 | |
|---|---|---|---|---|---|---|
| ✓ | - | - | 0.757 | 0.683 | 0.773 | 0.482 |
| - | ✓ | - | 0.587 | 0.504 | 0.521 | 0.267 |
| - | ✓ | ✓ | 0.603 | 0.505 | 0.528 | 0.273 |
| ✓ | ✓ | - | 0.767 | 0.699 | 0.787 | 0.498 |
| ✓ | ✓ | ✓ | 0.772 | 0.703 | 0.794 | 0.504 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Chen, F.; Qiu, D.; Liu, W.; Yan, J. DBYOLO: Dual-Backbone YOLO Network for Lunar Crater Detection. Remote Sens. 2025, 17, 3377. https://doi.org/10.3390/rs17193377
Liu Y, Chen F, Qiu D, Liu W, Yan J. DBYOLO: Dual-Backbone YOLO Network for Lunar Crater Detection. Remote Sensing. 2025; 17(19):3377. https://doi.org/10.3390/rs17193377
Chicago/Turabian StyleLiu, Yawen, Fukang Chen, Denggao Qiu, Wei Liu, and Jianguo Yan. 2025. "DBYOLO: Dual-Backbone YOLO Network for Lunar Crater Detection" Remote Sensing 17, no. 19: 3377. https://doi.org/10.3390/rs17193377
APA StyleLiu, Y., Chen, F., Qiu, D., Liu, W., & Yan, J. (2025). DBYOLO: Dual-Backbone YOLO Network for Lunar Crater Detection. Remote Sensing, 17(19), 3377. https://doi.org/10.3390/rs17193377






