An Optimal Viewpoint-Guided Visual Indexing Method for UAV Autonomous Localization
Abstract
1. Introduction
- In the viewpoint optimization stage, the method divides the 3D scene surface into geometric primitives (points, lines, polygons) and leverages plane consistency and overlap between adjacent viewpoints to frame it as an overlap optimization problem. The iterative optimization ensures complete scene coverage with minimal redundancy.
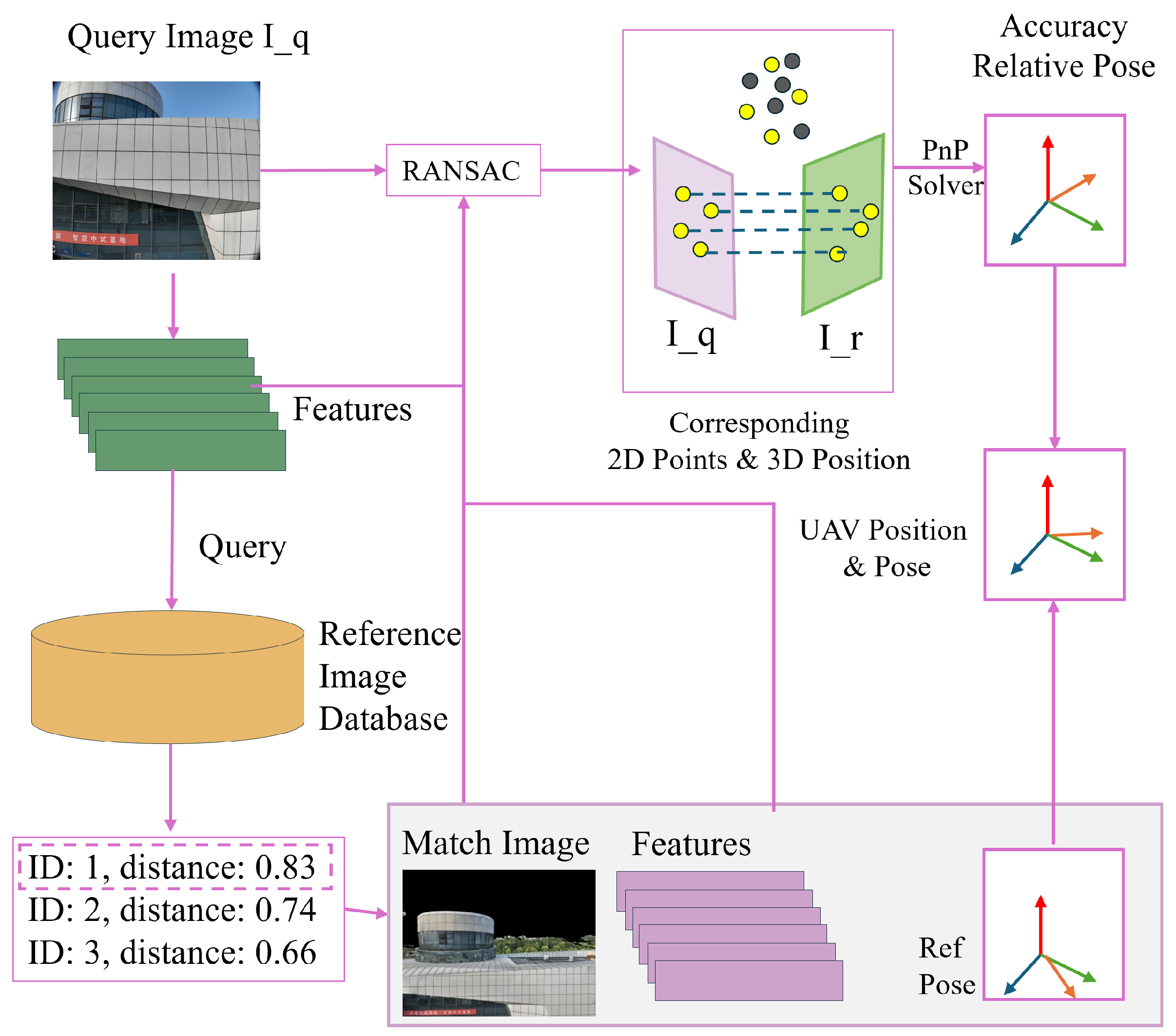
- Inspired by multi-branch tree search [16,17], the method uses a reference image bag-of-words tree to speed up image matching, clustering feature descriptors via K-Means. The tree structure aids in efficient query matching, with Random Sample Consensus (RANSAC) refining matches and the PnP algorithm estimating the drone’s six-DoF pose for fast, GNSS-free localization. The experimental results show the superiority of BoW reference image retrieval pipeline in positioning accuracy and latency.
2. Related Work
2.1. Autonomous Drone Positioning
2.2. Synthesis of Reference Images
2.3. Drone Reference Image to 3D Scene Localization Solving
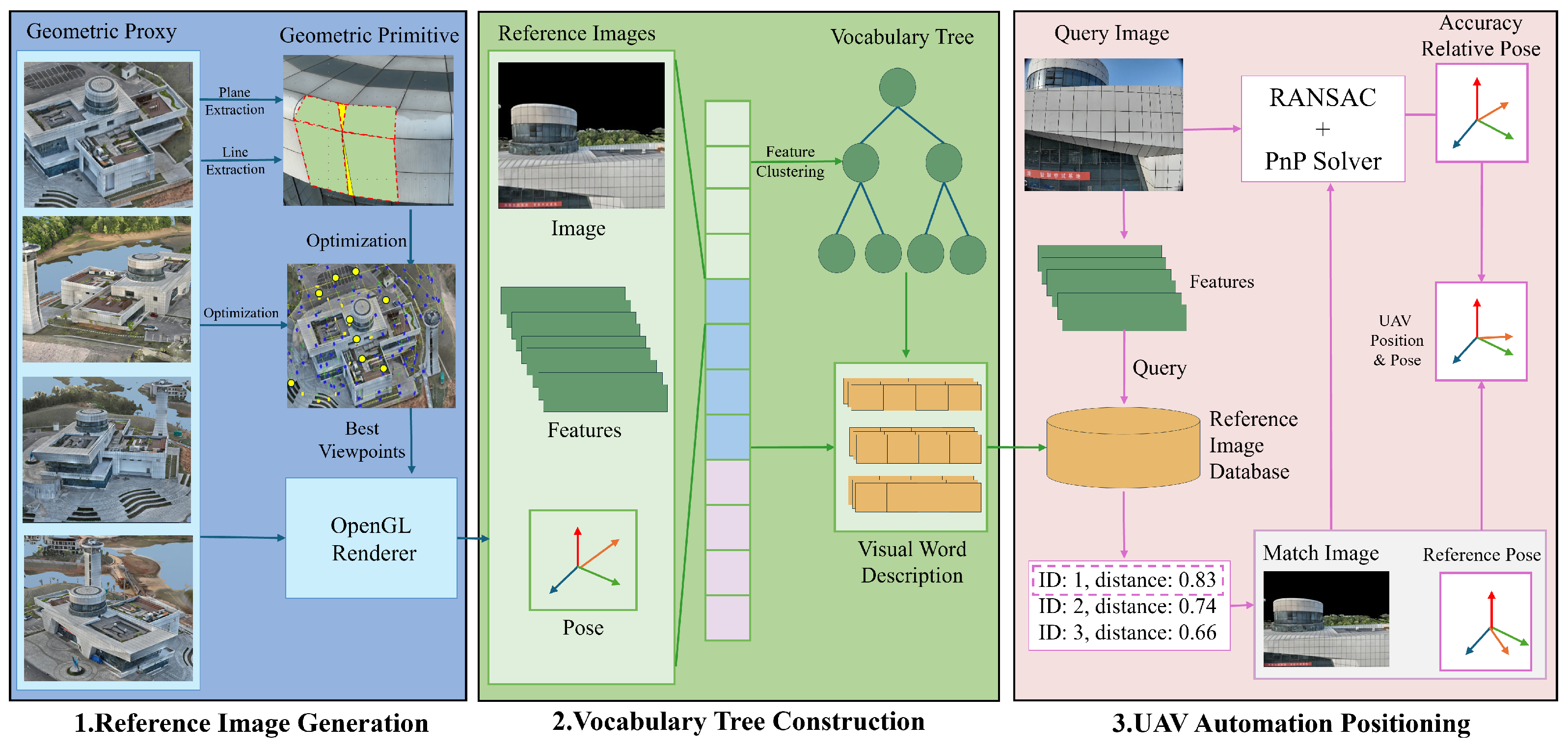
3. Method
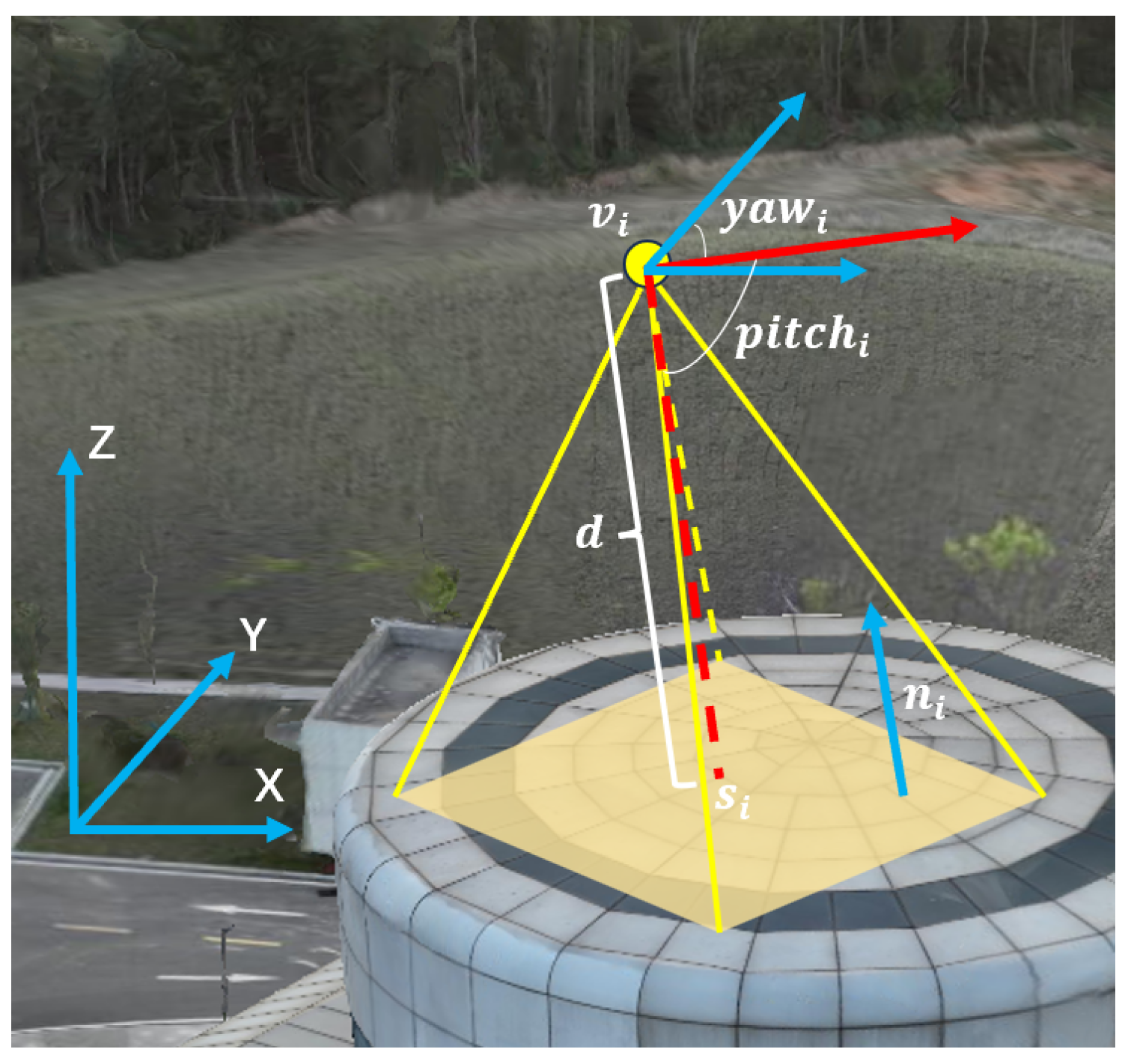
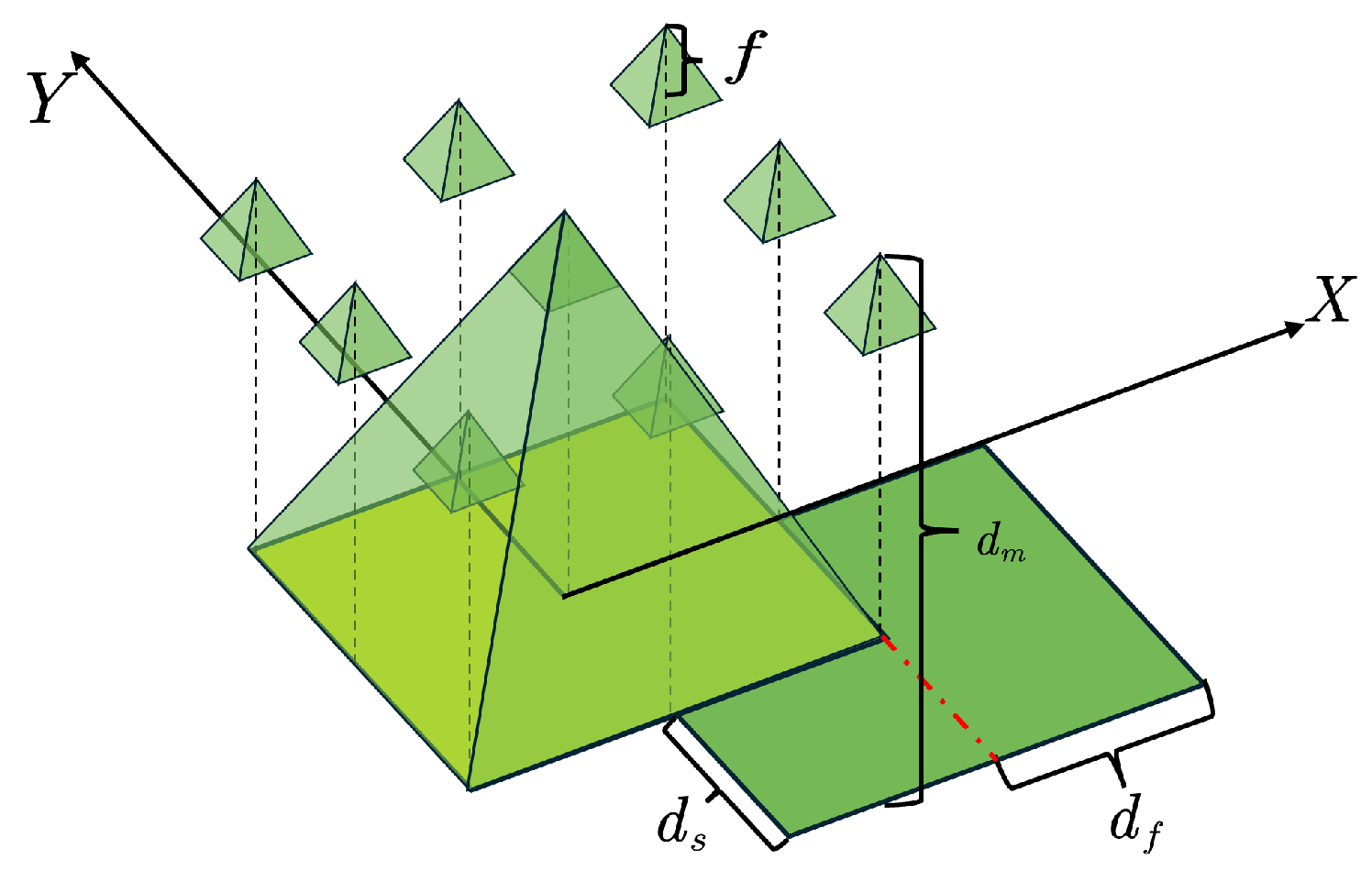
3.1. Heuristic Generation of Optimal Coverage Viewpoints
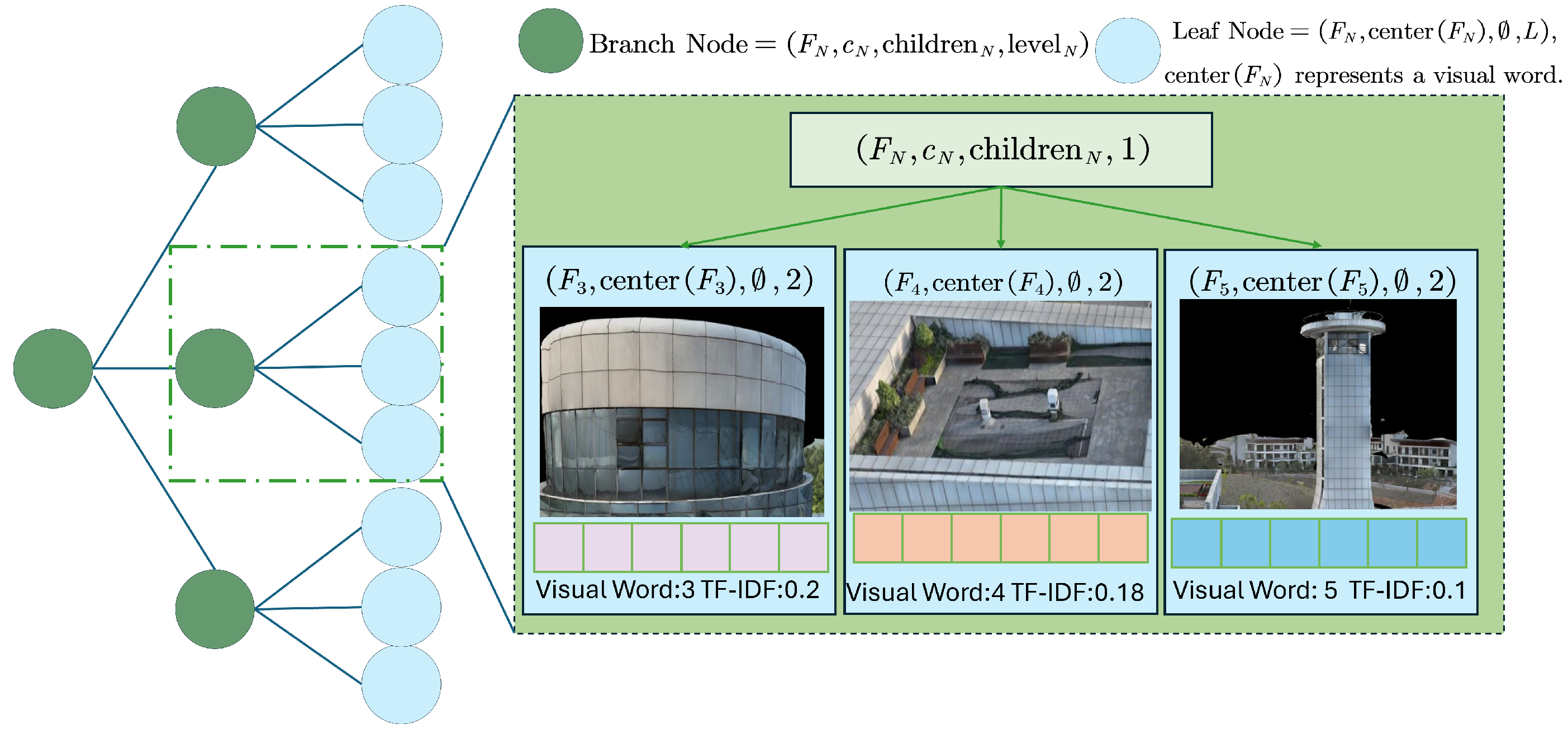
3.2. Bag-of-Words Tree for Reference Images
3.2.1. Generation of Reference Images
3.2.2. Image Feature Extraction and Matching
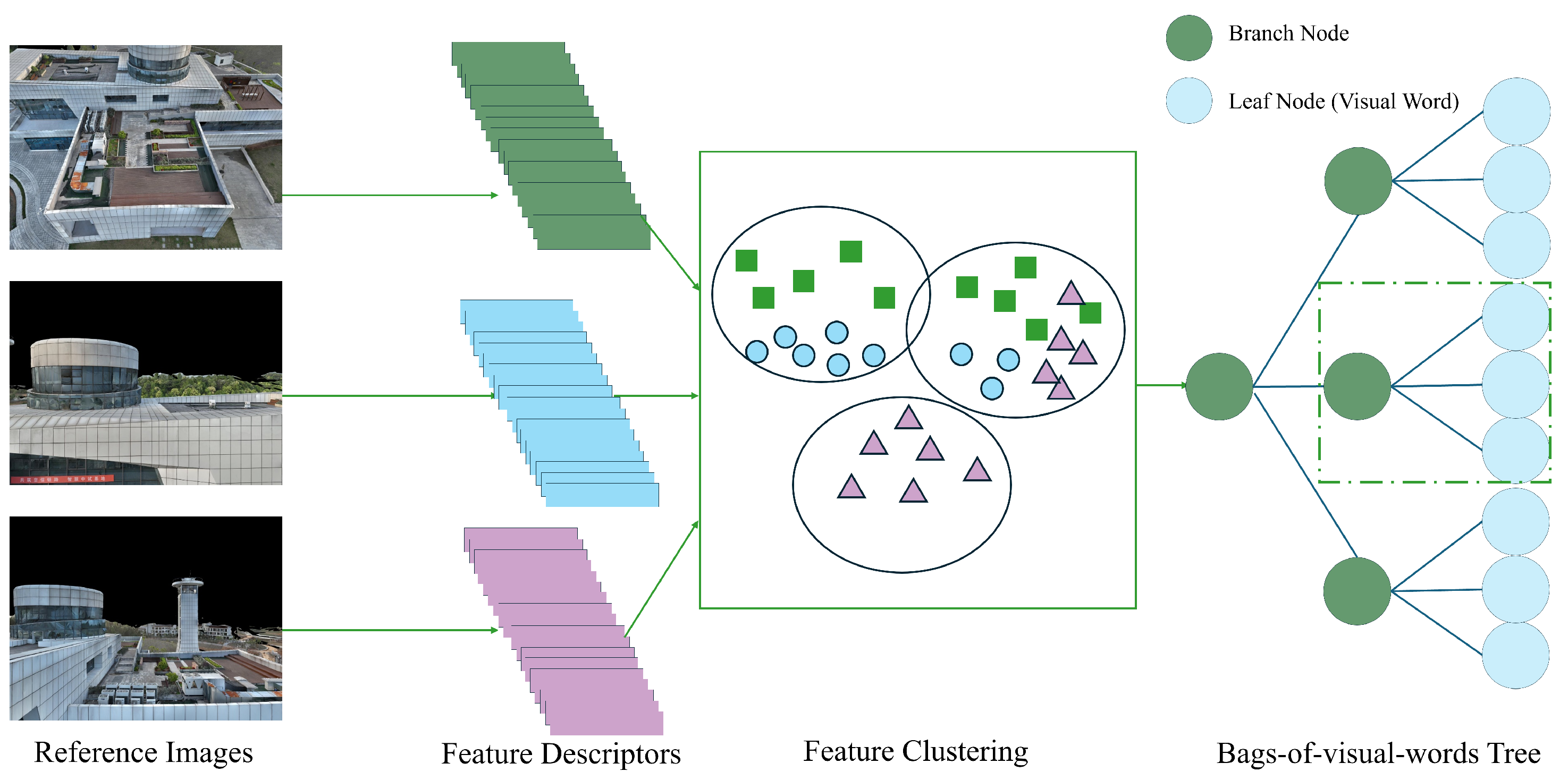
3.2.3. Construction of the Bag-of-Words Tree for Reference Images
3.2.4. Node Weight Assignment
3.3. Autonomous Drone Positioning Based on the Reference Image Bag-of-Words Tree
4. Experimental Results and Discussion
4.1. Experimental Settings
4.2. Experiment Results
4.2.1. Accuracy of the Geometric Model
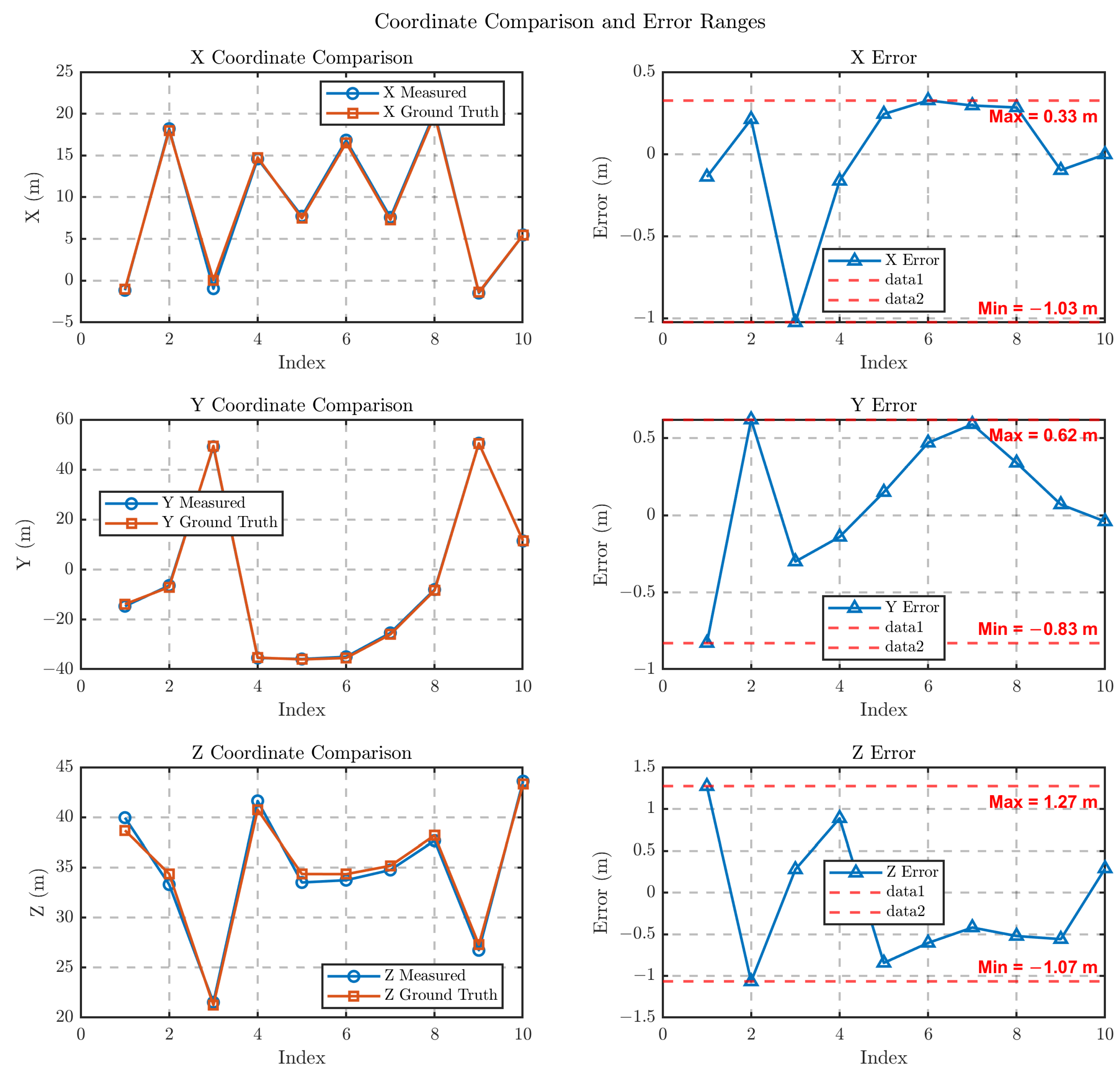
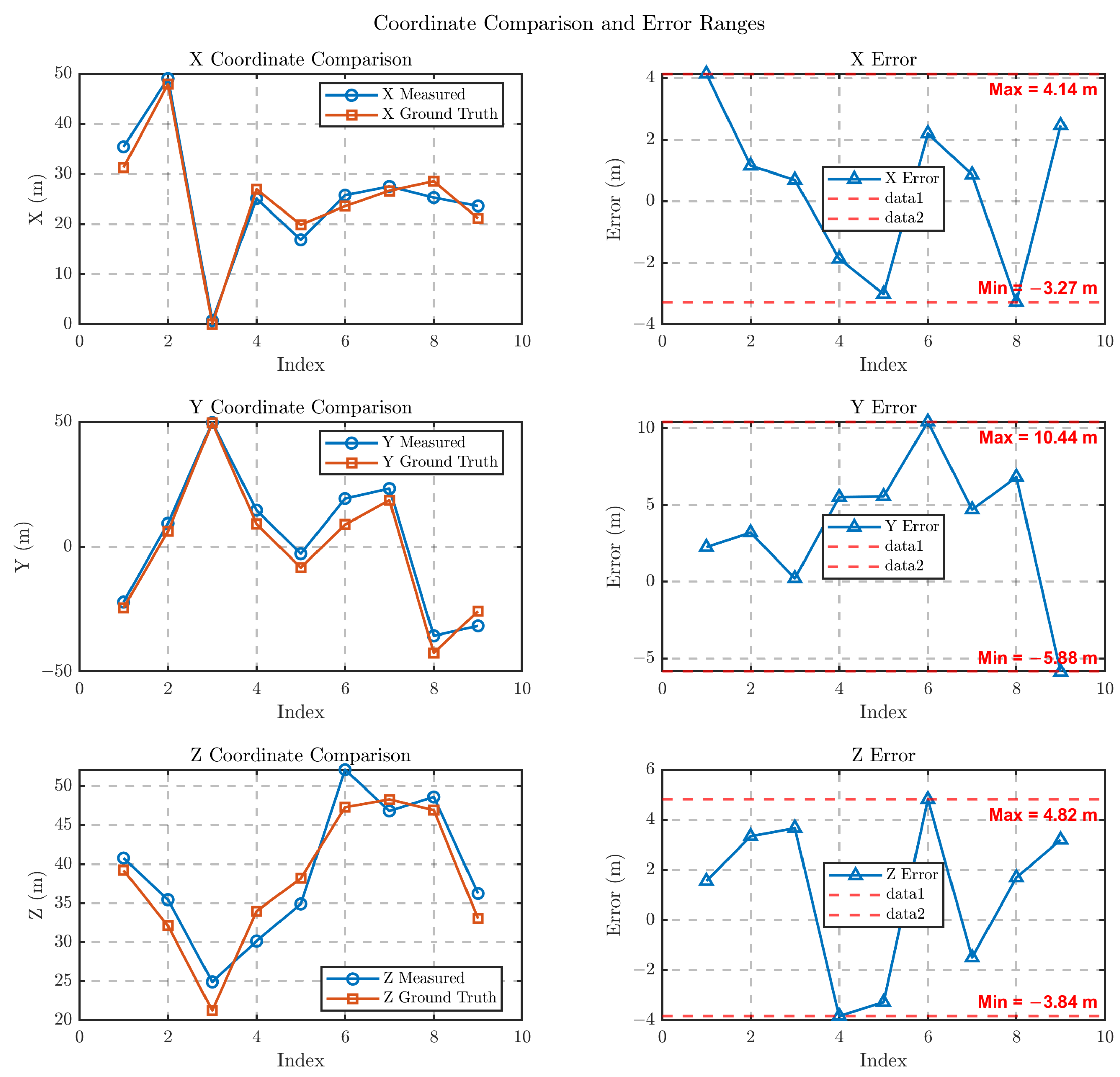
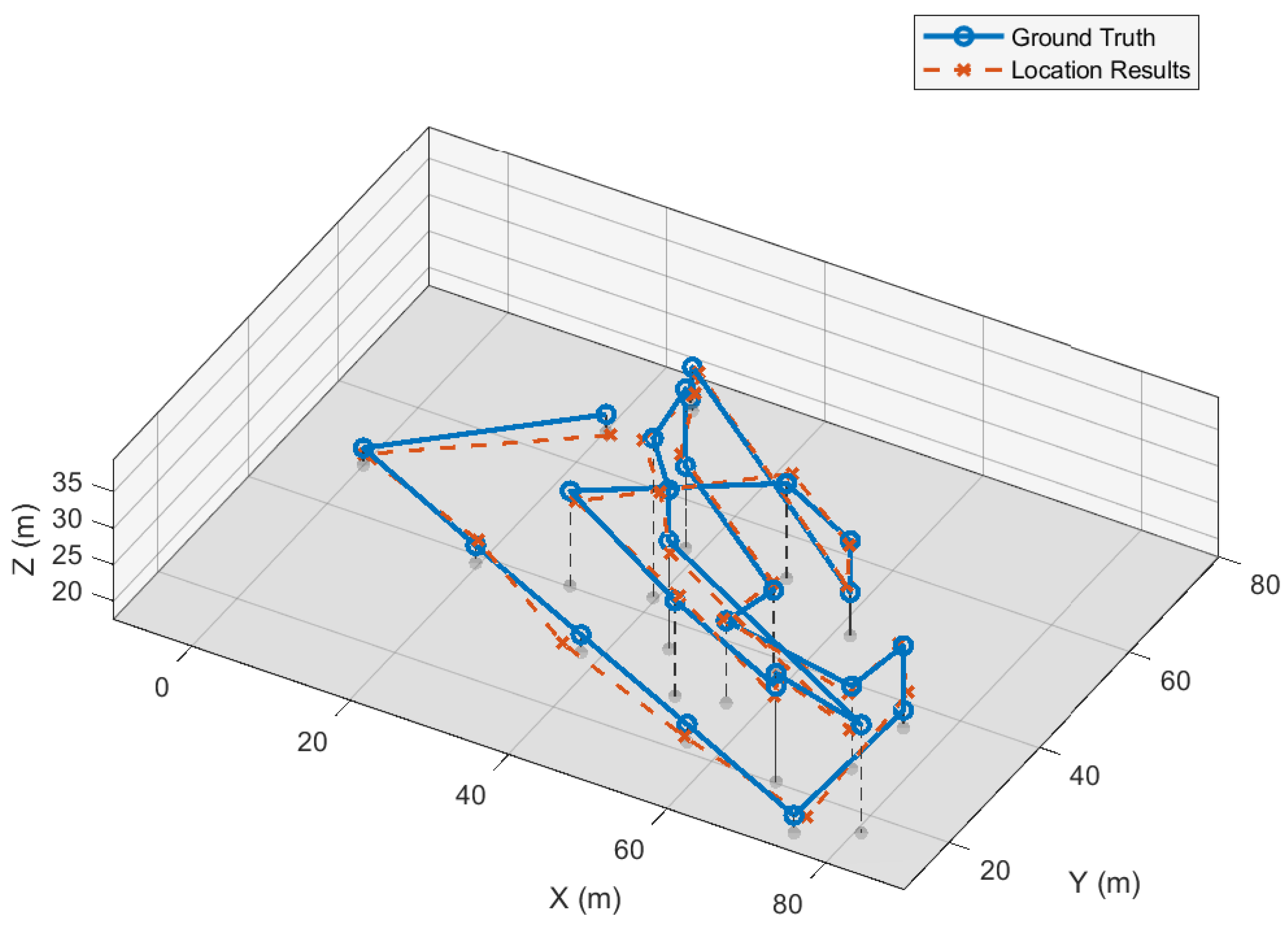
4.2.2. Localization Results in Different Poses and Position
4.2.3. The Effect of Different Feature Matching
4.3. Discussion
4.3.1. Sensitivity Analysis
4.3.2. Comparison with Other Methods
4.3.3. Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Mou, Z.; Gao, F.; Jiang, J.; Ding, R.; Han, Z. UAV-enabled secure communications by multi-agent deep reinforcement learning. IEEE Trans. Veh. Technol. 2020, 69, 11599–11611. [Google Scholar] [CrossRef]
- Mohamed, A.H.; Schwarz, K.P. Adaptive Kalman Filtering for INS/GPS. J. Geod. 1999, 73, 193–203. [Google Scholar] [CrossRef]
- Hussain, A.; Akhtar, F.; Khand, Z.H.; Rajput, A.; Shaukat, Z. Complexity and Limitations of GNSS Signal Reception in Highly Obstructed Enviroments. Eng. Technol. Appl. Sci. Res. 2021, 11, 6864–6868. [Google Scholar] [CrossRef]
- Elamin, A.; Abdelaziz, N.; El-Rabbany, A. A GNSS/INS/LiDAR Integration Scheme for UAV-Based Navigation in GNSS-Challenging Environments. Sensors 2022, 22, 9908. [Google Scholar] [CrossRef]
- Tao, M.; Li, J.; Chen, J.; Liu, Y.; Fan, Y.; Su, J.; Wang, L. Radio frequency interference signature detection in radar remote sensing image using semantic cognition enhancement network. IEEE Trans. Geosci. Remote. Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Chang, Y.; Cheng, Y.; Manzoor, U.; Murray, J. A review of UAV autonomous navigation in GPS-denied environments. Robot. Auton. Syst. 2023, 170, 104533. [Google Scholar] [CrossRef]
- Kinnari, J.; Verdoja, F.; Kyrki, V. GNSS-denied geolocalization of UAVs by visual matching of onboard camera images with orthophotos. In Proceedings of the 2021 20th International Conference on Advanced Robotics (ICAR), Ljubljana, Slovenia, 6–10 December 2021; pp. 555–562. [Google Scholar]
- Jin, S.; Feng, G.P.; Gleason, S. Remote sensing using GNSS signals: Current status and future directions. Adv. Space Res. 2011, 47, 1645–1653. [Google Scholar] [CrossRef]
- Zhu, S.; Yang, T.; Chen, C. Vigor: Cross-view image geo-localization beyond one-to-one retrieval. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 3640–3649. [Google Scholar]
- Zheng, Z.; Wei, Y.; Yang, Y. University-1652: A multi-view multi-source benchmark for drone-based geo-localization. In Proceedings of the 28th ACM international conference on Multimedia, Seattle, WA, USA, 12–16 October 2020; pp. 1395–1403. [Google Scholar]
- Vivanco Cepeda, V.; Nayak, G.K.; Shah, M. Geoclip: Clip-inspired alignment between locations and images for effective worldwide geo-localization. Adv. Neural Inf. Process. Syst. 2023, 36, 8690–8701. [Google Scholar]
- Zhu, R.; Yin, L.; Yang, M.; Wu, F.; Yang, Y.; Hu, W. SUES-200: A multi-height multi-scene cross-view image benchmark across drone and satellite. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 4825–4839. [Google Scholar] [CrossRef]
- Ji, Y.; He, B.; Tan, Z.; Wu, L. Game4Loc: A UAV Geo-Localization Benchmark from Game Data. arXiv 2024, arXiv:2409.16925. [Google Scholar] [CrossRef]
- Xu, W.; Yao, Y.; Cao, J.; Wei, Z.; Liu, C.; Wang, J.; Peng, M. UAV-VisLoc: A Large-scale Dataset for UAV Visual Localization. arXiv 2024, arXiv:2405.11936. [Google Scholar]
- Cui, Y.; Gao, X.; Yu, R.; Chen, X.; Wang, D.; Bai, D. An Autonomous Positioning Method for Drones in GNSS Denial Scenarios Driven by Real-Scene 3D Models. Sensors 2025, 25, 209. [Google Scholar] [CrossRef]
- Nister, D.; Stewenius, H. Scalable recognition with a vocabulary tree. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; Volume 2, pp. 2161–2168. [Google Scholar]
- Sivic; Zisserman. Video Google: A text retrieval approach to object matching in videos. In Proceedings of the Ninth IEEE International Conference on Computer Vision, Nice, France, 13–16 October 2003; Volume 2, pp. 1470–1477. [Google Scholar]
- Liu, Y.; Wu, R.; Yan, S.; Cheng, X.; Zhu, J.; Liu, Y.; Zhang, M. ATLoc: Aerial Thermal Images Localization via View Synthesis. IEEE Trans. Geosci. Remote. Sens. 2024, 62, 1–13. [Google Scholar] [CrossRef]
- Sibbing, D.; Sattler, T.; Leibe, B.; Kobbelt, L. Sift-realistic rendering. In Proceedings of the 2013 International Conference on 3D Vision-3DV 2013, Seattle, WA, USA, 29 June–1 July 2013; pp. 56–63. [Google Scholar]
- Shan, Q.; Wu, C.; Curless, B.; Furukawa, Y.; Hernandez, C.; Seitz, S.M. Accurate geo-registration by ground-to-aerial image matching. In Proceedings of the 2014 2nd International Conference on 3D Vision, Tokyo, Japan, 8–11 December 2014; Volume 1, pp. 525–532. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Aubry, M.; Russell, B.C.; Sivic, J. Painting-to-3D model alignment via discriminative visual elements. ACM Trans. Graph. (ToG) 2014, 33, 1–14. [Google Scholar] [CrossRef]
- Torii, A.; Arandjelovic, R.; Sivic, J.; Okutomi, M.; Pajdla, T. 24/7 place recognition by view synthesis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1808–1817. [Google Scholar]
- Zhang, Z.; Sattler, T.; Scaramuzza, D. Reference pose generation for long-term visual localization via learned features and view synthesis. Int. J. Comput. Vis. 2021, 129, 821–844. [Google Scholar] [CrossRef]
- Liu, Y.; Ji, Z.; Chen, L.; Liu, Y. Linear target change detection from a single image based on three-dimensional real scene. Photogramm. Rec. 2023, 38, 617–635. [Google Scholar] [CrossRef]
- Wang, T.; Li, X.; Tian, L.; Chen, Z.; Li, Z.; Zhang, G.; Li, D.; Shen, X.; Li, X.; JIANG, B. Space remote sensing dynamic monitoring for urban complex. Geomat. Inf. Sci. Wuhan Univ. 2020, 45, 640–650. [Google Scholar]
- Sarlin, P.E.; DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superglue: Learning feature matching with graph neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 4938–4947. [Google Scholar]
- Kim, S.; Min, J.; Cho, M. Transformatcher: Match-to-match attention for semantic correspondence. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 8697–8707. [Google Scholar]
- Lee, J.; Kim, B.; Cho, M. Self-supervised equivariant learning for oriented keypoint detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 4847–4857. [Google Scholar]
- Lee, J.; Kim, B.; Kim, S.; Cho, M. Learning rotation-equivariant features for visual correspondence. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 21887–21897. [Google Scholar]
- He, X.; Sun, J.; Wang, Y.; Huang, D.; Bao, H.; Zhou, X. Onepose++: Keypoint-free one-shot object pose estimation without CAD models. Adv. Neural Inf. Process. Syst. 2022, 35, 35103–35115. [Google Scholar]
- Ding, M.; Wang, Z.; Sun, J.; Shi, J.; Luo, P. CamNet: Coarse-to-fine retrieval for camera re-localization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 2871–2880. [Google Scholar]
- Matteo, B.; Tsesmelis, T.; James, S.; Poiesi, F.; Del Bue, A. 6dgs: 6d pose estimation from a single image and a 3d gaussian splatting model. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2024; pp. 420–436. [Google Scholar]
- Zhou, H.; Ji, Z.; You, X.; Liu, Y.; Chen, L.; Zhao, K.; Lin, S.; Huang, X. Geometric Primitive-Guided UAV Path Planning for High-Quality Image-Based Reconstruction. Remote Sens. 2023, 15, 2632. [Google Scholar] [CrossRef]
- Smith, N.; Moehrle, N.; Goesele, M.; Heidrich, W. Aerial path planning for urban scene reconstruction: A continuous optimization method and benchmark. ACM Trans. Graph. 2018, 37, 6. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van Gool, L. Surf: Speeded up robust features. In Proceedings of the Computer Vision—ECCV 2006: 9th European Conference on Computer Vision, Graz, Austria, 7–13 May 2006. Proceedings, Part I; Springer: Berlin/Heidelberg, Germany, 2006; pp. 404–417. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superpoint: Self-supervised interest point detection and description. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 224–236. [Google Scholar]
- Dusmanu, M.; Rocco, I.; Pajdla, T.; Pollefeys, M.; Sivic, J.; Torii, A.; Sattler, T. D2-net: A trainable cnn for joint description and detection of local features. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 8092–8101. [Google Scholar]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Statistics; University of California Press: Oakland, CA, USA, 1967; Volume 5, pp. 281–298. [Google Scholar]
- Chung, K.L.; Tseng, Y.C.; Chen, H.Y. A Novel and Effective Cooperative RANSAC Image Matching Method Using Geometry Histogram-Based Constructed Reduced Correspondence Set. Remote Sens. 2022, 14, 3256. [Google Scholar] [CrossRef]
- Kneip, L.; Scaramuzza, D.; Siegwart, R. A novel parametrization of the perspective-three-point problem for a direct computation of absolute camera position and orientation. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 2969–2976. [Google Scholar]
- Xu, C.; Zhang, L.; Cheng, L.; Koch, R. Pose estimation from line correspondences: A complete analysis and a series of solutions. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1209–1222. [Google Scholar] [CrossRef] [PubMed]
- Ye, Y.; Teng, X.; Chen, S.; Li, Z.; Liu, L.; Yu, Q.; Tan, T. Exploring the best way for UAV visual localization under Low-altitude Multi-view Observation Condition: A Benchmark. arXiv 2025, arXiv:2503.10692. [Google Scholar]
- Ebrahim, K.; Siva, P.; Mohamed, S. Image matching using SIFT, SURF, BRIEF and ORB: Performance comparison for distorted images. arXiv 2017, arXiv:1710.02726. [Google Scholar]
- Li, X.; Liang, X.; Zhang, F.; Bu, X.; Wan, Y. A 3D Reconstruction Method of Mountain Areas for TomoSAR. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019; pp. 1–4. [Google Scholar]
- Qi, Z.; Zou, Z.; Chen, H.; Shi, Z. 3D Reconstruction of Remote Sensing Mountain Areas with TSDF-Based Neural Networks. Remote Sens. 2022, 14, 4333. [Google Scholar] [CrossRef]



| Focal Length | K1 | K2 | K3 | P1 | P2 |
|---|---|---|---|---|---|
| 33 mm | −0.11153155 | 0.01035897 | −0.02430045 | 0.00011204 | −0.00007903 |
| Metrics | PSNR ↑ | SSIM ↑ | RMSE ↓ |
|---|---|---|---|
| Image Set I | 29.84 | 0.5216 | 0.265 |
| Image Set II | 29.65 | 0.5359 | 0.276 |
| Image Set III | 29.78 | 0.5562 | 0.268 |
| Image Set IV | 29.95 | 0.5087 | 0.258 |
| Image Set V | 29.86 | 0.5179 | 0.263 |
| Average | 29.82 | 0.5281 | 0.266 |
| Position | Error (m) | Rotation Error | Localization Time (ms) |
|---|---|---|---|
| Position I | 1.51 | 0.00060 | 963 |
| Position II | 1.24 | 0.00090 | 901 |
| Position III | 1.22 | 0.00077 | 709 |
| Position IV | 0.91 | 0.00073 | 1291 |
| Position V | 0.89 | 0.00092 | 862 |
| Position VI | 0.83 | 0.00080 | 1028 |
| Position VII | 0.77 | 0.00066 | 1049 |
| Position VIII | 0.69 | 0.00074 | 1023 |
| Position IX | 0.55 | 0.00077 | 835 |
| Position X | 0.29 | 0.00081 | 1023 |
| Metric | SIFT [22] | SURF [37] | ORB [38] |
|---|---|---|---|
| Max Error (m) | 2.422 | 2.498 | 2.437 |
| Min Error (m) | 0.209 | 0.231 | 0.237 |
| Max Rotational Error | 0.004589 | 0.006195 | 0.003686 |
| Min Rotational Error | 0.000301 | 0.000174 | 0.000168 |
| Mean Error (m) | 0.708 | 0.816 | 0.919 |
| Mean Rotational Error | 0.001014 | 0.001013 | 0.000958 |
| Avg. Localization Time (s) | 20 | 35 | 0.75 |
| Parameters | Construction Time (s) | Index Memory (MB) | Average Query Time (ms) | Retrieval Accuracy (%) |
|---|---|---|---|---|
| K = 5, L = 5 | 19.85 | 0.925 | 8.355 | 60 |
| K = 5, L = 8 | 21.02 | 43.495 | 7.177 | 70 |
| K = 5, L = 10 | 19.23 | 68.670 | 7.694 | 74 |
| K = 10, L = 3 | 15.16 | 0.268 | 8.025 | 55 |
| K = 10, L = 5 | 16.70 | 21.683 | 7.898 | 69 |
| K = 10, L = 8 | 21.59 | 68.168 | 7.814 | 72 |
| Method | Accuracy | Latency |
|---|---|---|
| Ours | <1 m (small pose), <5 m (large pose) | 0.7–1.3 s |
| GeoCLIP [11] | N/A (no detailed UAV pose) | N/A |
| SUES-2000 [12] | N/A (no detailed UAV pose) | N/A |
| OnePose++ [31] | N/A (only for household objects) | N/A |
| ATLoc [18] | 5 m, 5° | N/A |
| Based on 3D point cloud [15] | 5 m | 2 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Z.; Zheng, Y.; Ji, Z.; Liu, W. An Optimal Viewpoint-Guided Visual Indexing Method for UAV Autonomous Localization. Remote Sens. 2025, 17, 2194. https://doi.org/10.3390/rs17132194
Ye Z, Zheng Y, Ji Z, Liu W. An Optimal Viewpoint-Guided Visual Indexing Method for UAV Autonomous Localization. Remote Sensing. 2025; 17(13):2194. https://doi.org/10.3390/rs17132194
Chicago/Turabian StyleYe, Zhiyang, Yukun Zheng, Zheng Ji, and Wei Liu. 2025. "An Optimal Viewpoint-Guided Visual Indexing Method for UAV Autonomous Localization" Remote Sensing 17, no. 13: 2194. https://doi.org/10.3390/rs17132194
APA StyleYe, Z., Zheng, Y., Ji, Z., & Liu, W. (2025). An Optimal Viewpoint-Guided Visual Indexing Method for UAV Autonomous Localization. Remote Sensing, 17(13), 2194. https://doi.org/10.3390/rs17132194








