Spaceborne THz-ISAR Imaging of Space Target with Joint Motion Compensation Based on FrFT and GWO
Abstract
1. Introduction
2. Methods
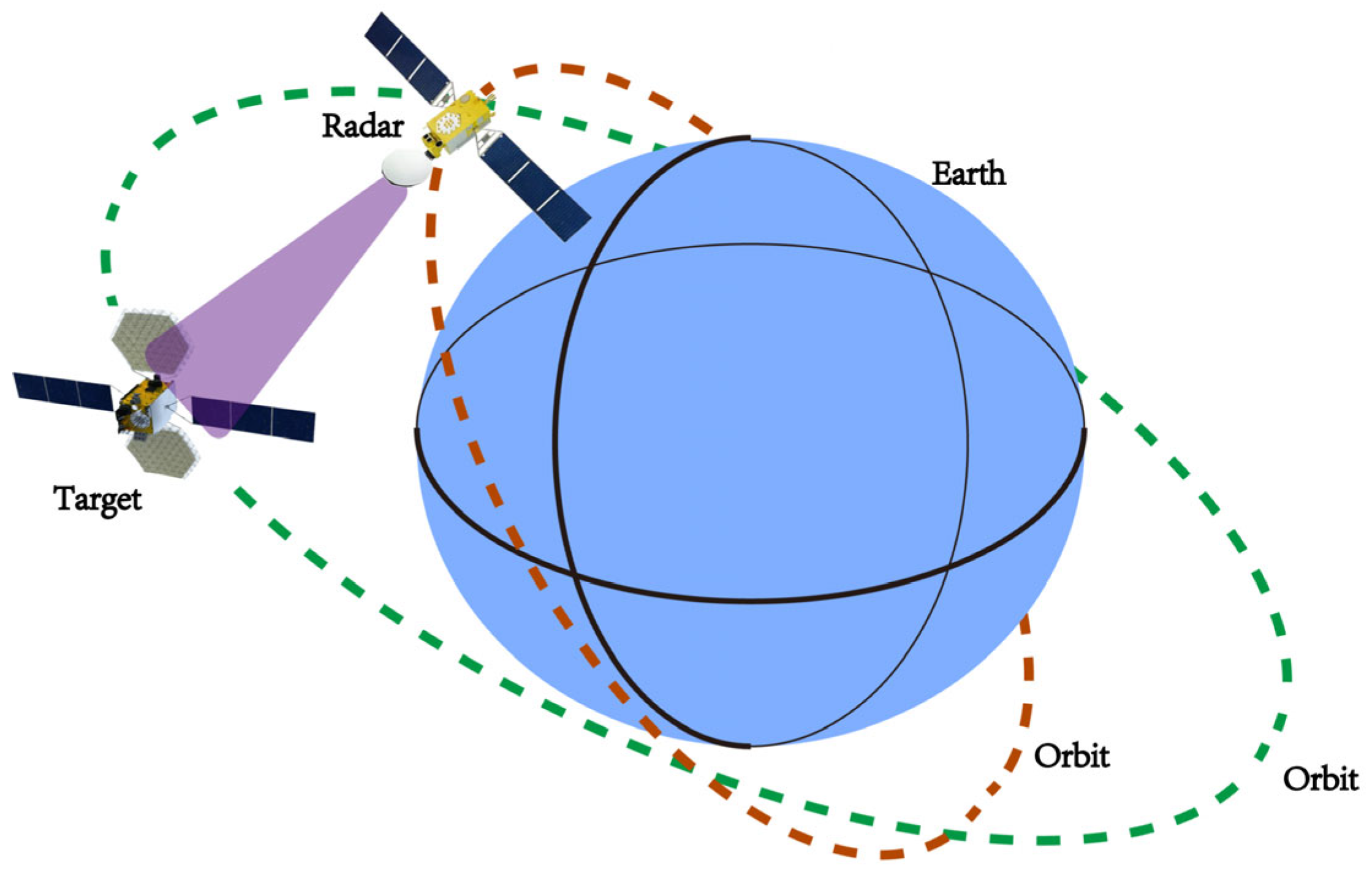
2.1. Spaceborne THz-ISAR Signal Model and Boundary Condition Analysis
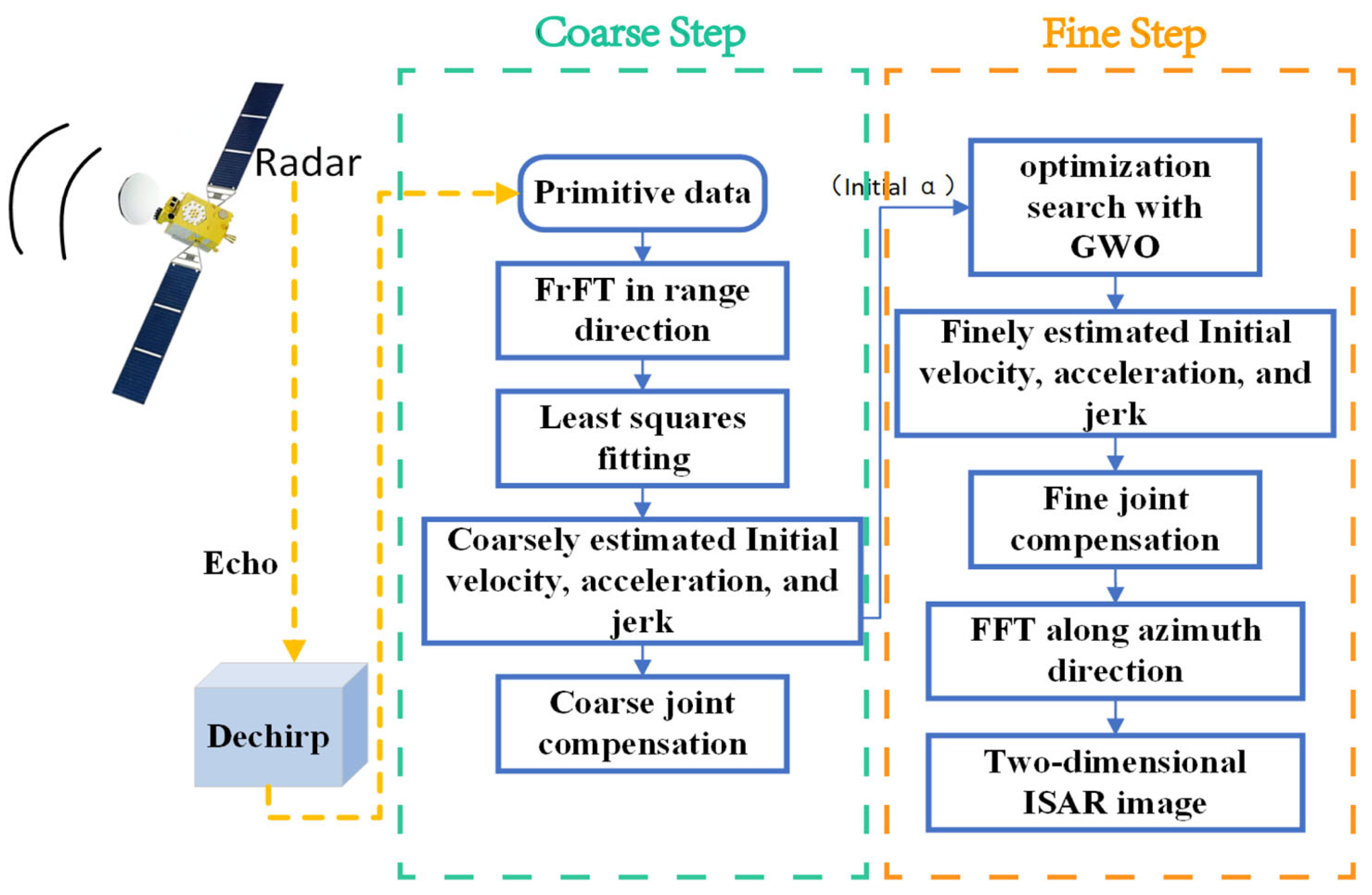
2.2. Spaceborne THz-ISAR Imaging Process and Algorithm
- FrFT is used to coarsely estimate the chirp rate of each pulse;
- Convert the chirp rate obtained in step 1 into velocity, fit the motion parameters using the least squares method, and perform coarse joint compensation;
- Calculate the synthetic waveform entropy (SWE) of the one-dimensional range profile after the coarse joint compensation in step 2.
- Use the SWE of the one-dimensional range profile as the cost function, with its initial value derived from the result in step 3, and the coarsely estimated parameters obtained in step 2 as the wolf in the GWO algorithm, iteratively search for the optimal motion parameter estimates that minimize the SWE.
- Use the estimated parameters in step 4 to perform the precise joint compensation for the echo, and perform Fourier transform along the azimuth direction. A well-focused ISAR image is finally acquired.
2.2.1. FrFT-Based Coarse Joint Compensation Method
- For (Let be an even integer), use FrFT to obtain ;
- To eliminate abrupt error, set empirical value , if or (), then set ;
- For the discrete velocity–time observation sequence , assuming its adherence to a model: , formulate the parameter estimation problem as a least squares optimization: to obtain the estimated parameters;
2.2.2. GWO-Based Fine Joint Compensation Method
- A population of grey wolf individuals is randomly initialized, where each individual’s position represents a candidate solution to the optimization. Define a convergence parameter to control the searching scope;
- Calculate each grey wolf’s fitness value to determine , , and . In this paper, is the coarse estimation result of Section 2.2.1;
- adjusts its movement direction based on the positions of the three leaders, whose positions indicate the current most promising regions;
- The , , and wolves assess their distance to the optimal solution and adaptively adjust their positions. adjusts its positions based on the positions of the three leaders. Re-evaluate the fitness of each grey wolf and update the leaders;
- The algorithm terminates when either the maximum iteration threshold is reached or the obtained solution is good enough and the position of serves as the optimal solution. Otherwise, repeat step 3 and 4.
3. Results
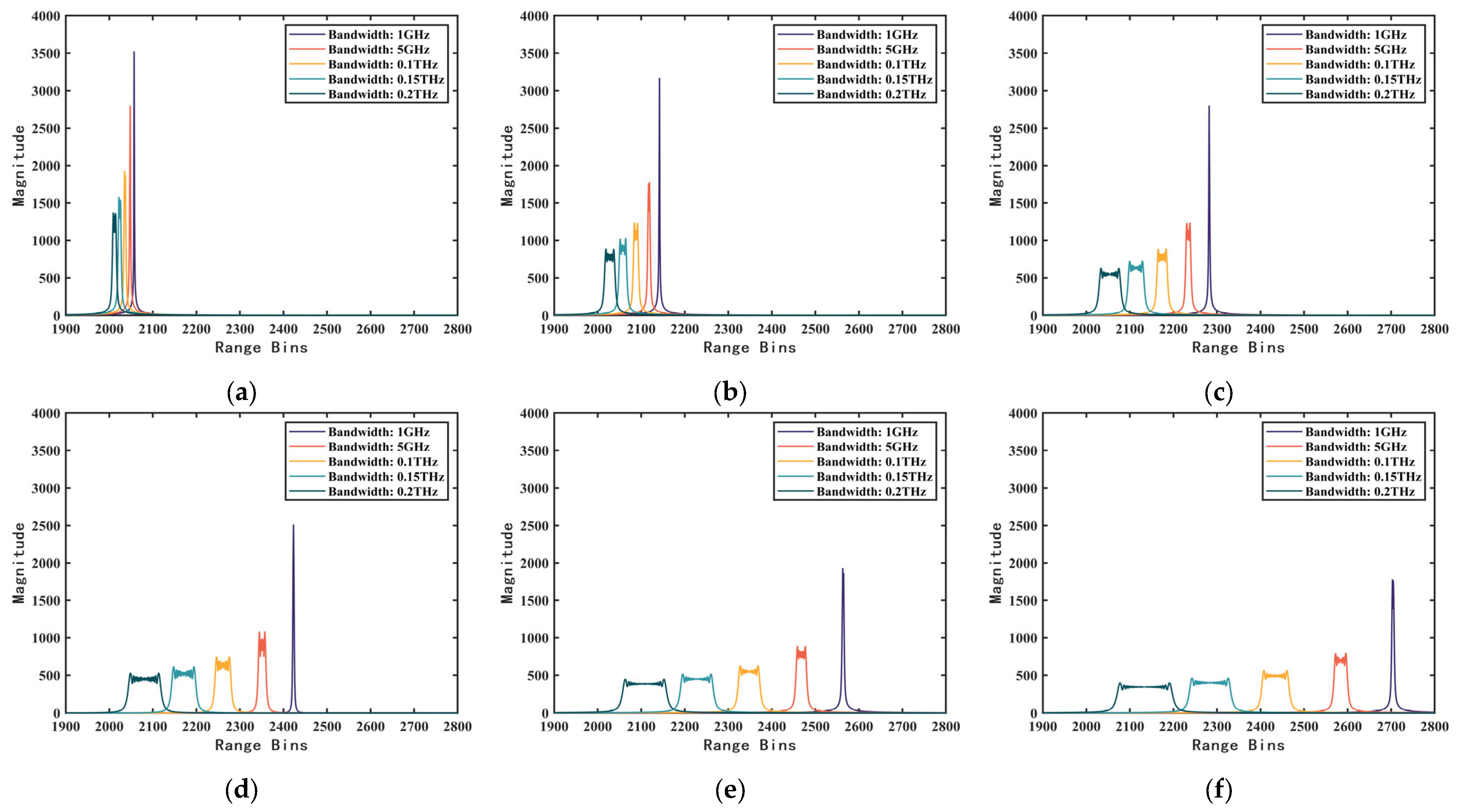
3.1. Simulation Experiments on the Co-Effect of Paramters Based on Single Scattering Point
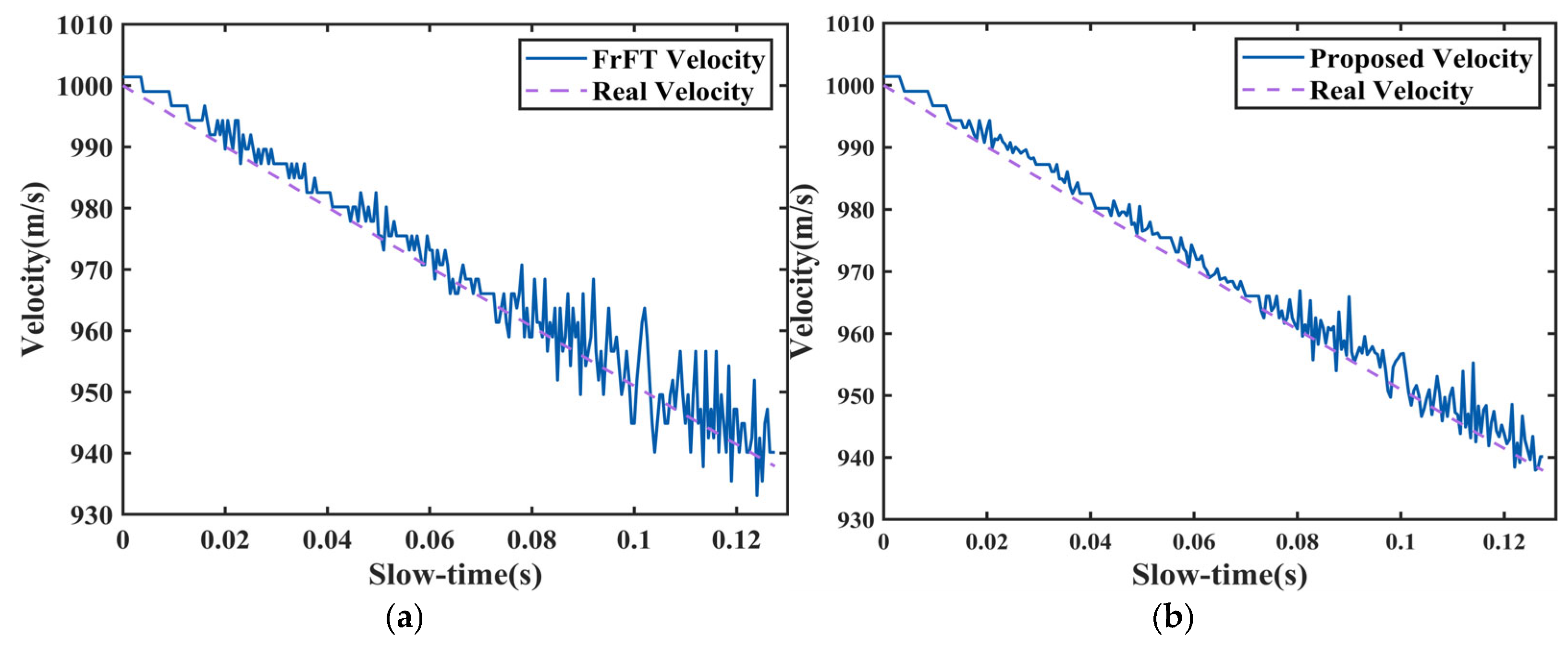
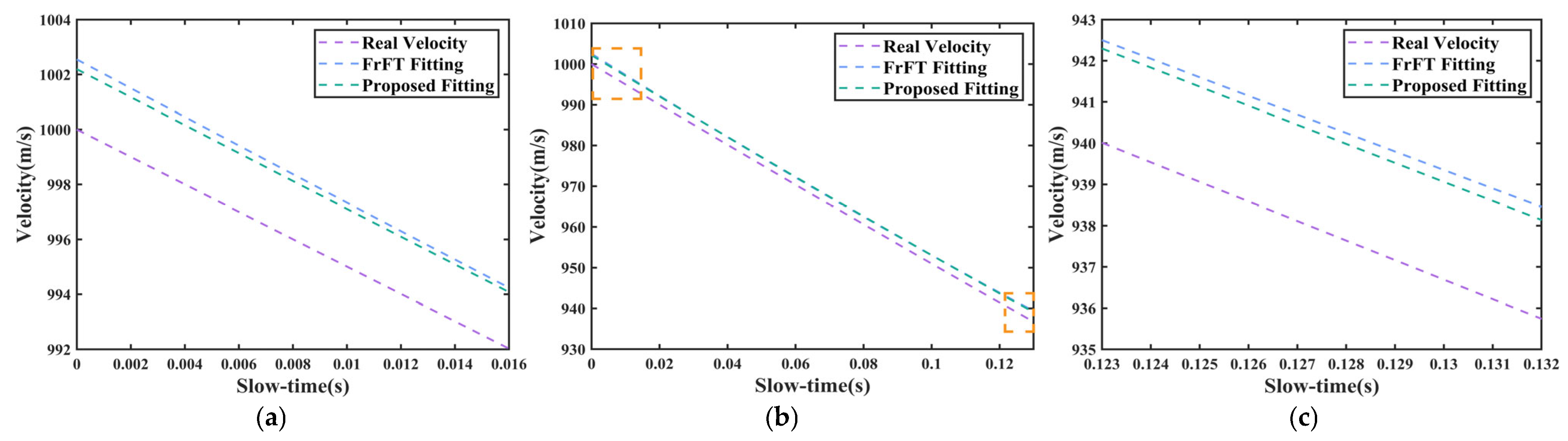
3.2. Simulation Experiment Verifying the FrFT-Based Parameter Estimation Method
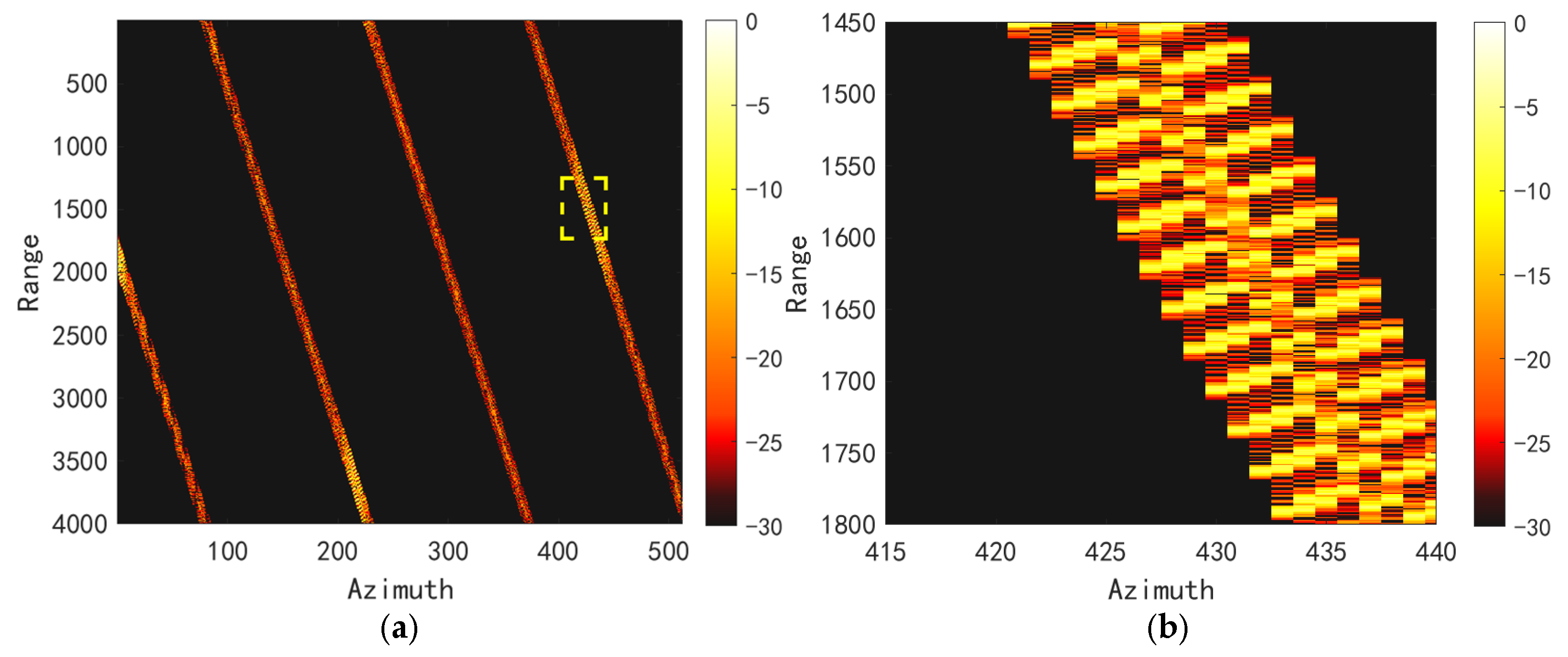
3.3. Satellite Point Cloud Model Simulation Experiments
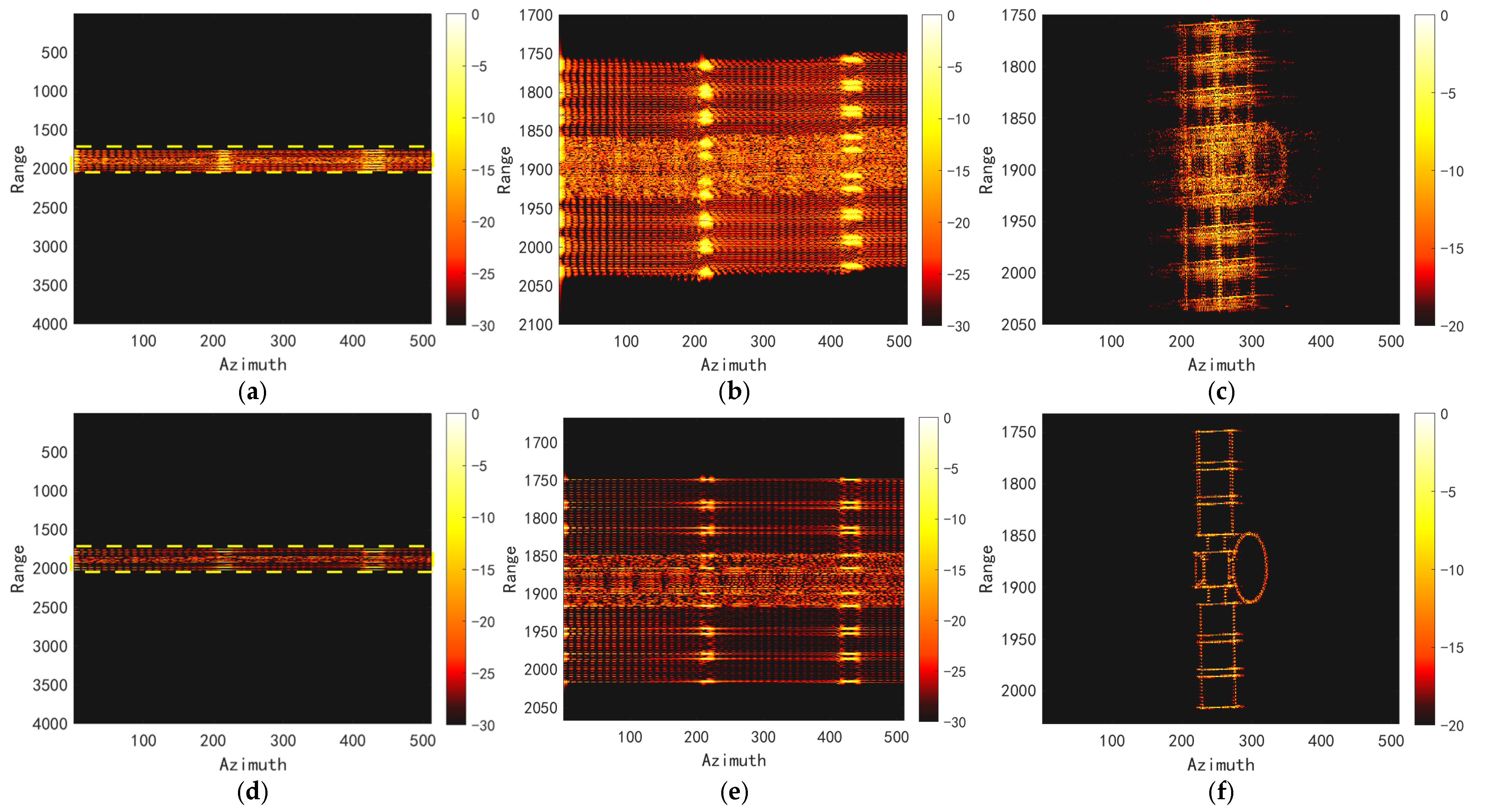
3.4. Satellite Electromagnetic Simulation Experiments
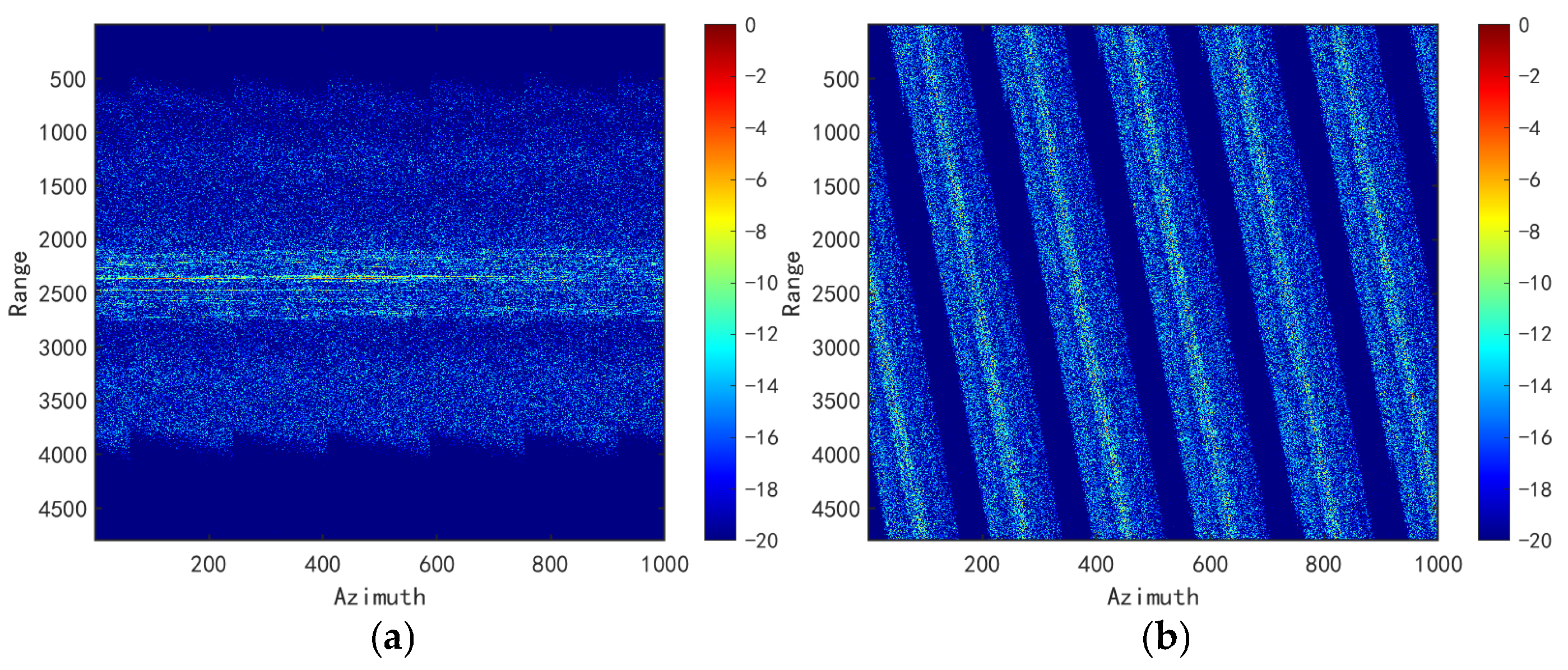
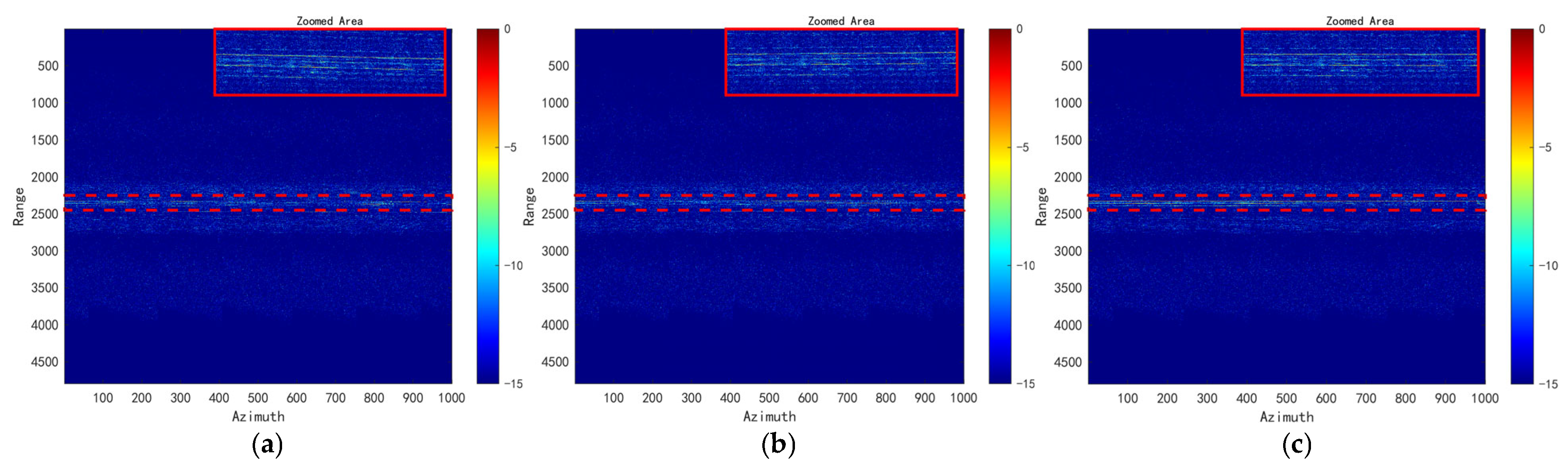
3.5. Field-Measured Data Experiments
4. Discussion
4.1. Discussion of Computational Compexity of PM
4.2. Discussion of the Technical Difficulties of Large Rotation Angle Scenarios
- Decoupling translational and rotational motions;
- Precise estimation of translational/rotational parameters.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Xu, G.; Xing, M.D.; Zhang, L.; Duan, J.; Chen, Q.Q.; Bao, Z. Sparse apertures ISAR imaging and scaling for maneuvering targets. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2942–2956. [Google Scholar] [CrossRef]
- Yang, Q.; Fan, L.; Yi, J.; Wang, H. A Novel High-Precision Terahertz Video SAR Imaging Method. IEEE Geosci. Remote Sens. Lett. 2024, 22, 4002405. [Google Scholar] [CrossRef]
- Yang, L.; Xing, M.; Zhang, L.; Sun, G.C.; Gao, Y.; Zhang, Z.; Bao, Z. Integration of rotation estimation and high-order compensation for ultrahigh-resolution microwave photonic isar imagery. IEEE Trans. Geosci. Remote Sens. 2020, 59, 2095–2115. [Google Scholar] [CrossRef]
- Ma, J.T.; Gao, M.G.; Guo, B.F.; Dong, J.; Xiong, D.; Feng, Q. High resolution inverse synthetic aperture radar imaging of three-axis-stabilized space target by exploiting orbital and sparse priors. Chin. Phys. B 2017, 26, 108401. [Google Scholar] [CrossRef]
- Yuan, H.; Zhang, Y.; Li, H.; Chen, J.; Niu, M. Recognition of Space Target Based on GNN under the Condition of Small Samples for ISAR Image. In Proceedings of the 2021 CIE International Conference on Radar (Radar), Haikou, China, 15–19 December 2021; pp. 1366–1370. [Google Scholar]
- Mostajeran, A.; Naghavi, S.M.; Emadi, M.; Samala, S.; Ginsburg, B.P.; Aseeri, M.; Afshari, E. A High-Resolution 220-GHz Ultra-Wideband Fully Integrated ISAR Imaging System. IEEE Trans. Microw. Theory Tech. 2019, 67, 429–442. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Q.; Deng, B.; Qin, Y.; Wang, H. Experimental Research on Interferometric Inverse Synthetic Aperture Radar Imaging with Multi-Channel Terahertz Radar System. Sensors 2019, 19, 2330. [Google Scholar] [CrossRef] [PubMed]
- Cooper, K.B.; Dengler, R.J.; Llombart, N.; Thomas, B.; Chattopadhyay, G.; Siegel, P.H. THz Imaging Radar for Standoff Personnel Screening. IEEE Trans. Terahertz Sci. Technol. 2011, 1, 169–182. [Google Scholar] [CrossRef]
- Ibraheem, I.; Krumbholz, N.; Mittleman, D.; Koch, M. Low-dispersive dielectric reflectors for future wireless terahertz communication systems. In Proceedings of the 32nd International Conference on Infrared and Millimeter Waves and the 15th International Conference on Terahertz Electronics, Cardiff, UK, 2–9 September 2007; pp. 930–931. [Google Scholar]
- Mcmillan, R.W.; Trussell, C.W.; Bohlander, R.A.; Butterworth, J.C.; Forsythe, R.E. An experimental 225 GHz pulsed coherent radar. IEEE Trans. Microw. Theory Tech. 1991, 39, 555–562. [Google Scholar] [CrossRef]
- Moll, J.; Schops, P.; Krozer, V. Towards three-dimensional millimeter-wave radar with the bistatic fast-factorized back-projection algorithm-potential and limitations. IEEE Trans. Terahertz Sci. Technol. 2012, 2, 432–440. [Google Scholar] [CrossRef]
- Caris, M.; Stanko, S.; Palm, S.; Sommer, R.; Wahlen, A.; Pohl, N. 300 GHz radar for high resolution SAR and ISAR applications. In Proceedings of the 16th International Radar Symposium, Dresden, Germany, 24–26 June 2015; pp. 577–580. [Google Scholar]
- Marchetti, E.; Stove, A.G.; Hoare, E.G.; Cherniakov, M.; Blacknell, D.; Gashinova, M. Space-Based Sub-THz ISAR for Space Situational Awareness—Laboratory Validation. IEEE Trans. Aerosp. Electron. 2022, 58, 4409–4422. [Google Scholar] [CrossRef]
- Marchetti, E.; Stove, A.G.; Hoare, E.G.; Cherniakov, M.; Blacknell, D.; Gashinova, M. Images of satellite elements with a space-borne Sub-THz ISAR system. In Proceedings of the 18th European Radar Conference, London, UK, 5–7 April 2022; pp. 425–428. [Google Scholar]
- Yang, Q.; Fan, L.; Li, R.; Gao, C.; Wang, H. Research on the registration and fusion algorithm of terahertz SAR images. Chin. J. Electron. 2025. accepted. [Google Scholar]
- Ning, Q.; Wang, H.; Yan, Z.; Wang, Z.; Lu, Y. A Fast and Robust Range Alignment Method for ISAR Imaging Based on a Deep Learning Network and Regional Multi-Scale Minimum Entropy Method. Remote Sens. 2024, 16, 3677. [Google Scholar] [CrossRef]
- Tian, B.; Chen, Z.; Xu, S.; Liu, Y. ISAR imaging compensation of high speed targets based on integrated cubic phase function. In MIPPR2013: Multispectral Image Acquisition, Processing, and Analysis; International Society for Optics and Photonics: Bellingham, WA, USA, 2013; Volume 8917, p. 89170B. [Google Scholar]
- Zhang, K.-F.; Feng, Z.-H.; Ma, D.-B. Study on a method of compensation for the range profile of high velocity spatial targets. In Proceedings of the 2010 International Conference on Image Analysis and Signal Processing, Hangzhou, China, 9–11 April 2010; pp. 450–453. [Google Scholar]
- Tian, B.; Lu, Z.; Liu, Y.; Li, X. High velocity motion compensation of IFDS data in ISAR imaging based on adaptive parameter adjustment of matched filter and entropy minimization. IEEE Access 2018, 6, 34272–34278. [Google Scholar] [CrossRef]
- Sheng, J.; Fu, C.; Wang, H.; Liu, Y. High speed motion compensation for terahertz ISAR imaging. In Proceedings of the 2017 International Applied Computational Electromagnetics Society Symposium (ACES), Suzhou, China, 1–4 August 2017; pp. 1–2. [Google Scholar]
- Guo, B.; Li, Z.; Xiao, Y.; Shi, L.; Han, N.; Zhu, X. ISAR Speed Compensation Algorithm for High-speed Moving Target Based on Simulate Anneal. In Proceedings of the 2019 IEEE 19th International Conference on Communication Technology (ICCT), Xi’an, China, 16–19 October 2019; pp. 1595–1599. [Google Scholar]
- Wang, J.; Li, Y.; Song, M.; Huang, P.; Xing, M. Noise Robust High-Speed Motion Compensation for ISAR Imaging Based on Parametric Minimum Entropy Optimization. Remote Sens. 2022, 14, 2178. [Google Scholar] [CrossRef]
- Chen, R.; Jiang, Y.; Ni, H. Optimal Imaging Time Interval Selection Method for Space Target via Time–Frequency Analysis With Spaceborne ISAR. IEEE Geosci. Remote Sens. Lett. 2023, 20, 4012505. [Google Scholar] [CrossRef]
- Feng, T.; He, J.; Luo, Y. ISAR Imaging of High Speed Moving Targets Based-on Radon Transform. In Proceedings of the 5th International Conference on Information Assurance and Security, Xi’an, China, 18–20 August 2009; pp. 597–600. [Google Scholar]
- Chen, C.-C.; Andrews, H.C. Target-Motion-Induced Radar Imaging. IEEE Trans. Aerosp. Electron. Syst. 1980, 16, 2–14. [Google Scholar] [CrossRef]
- Zhao, J.; Liang, Z. CLEAN and FrFT based Cross-range Scaling Method for ISAR Image. In Proceedings of the International Applied Computational Electromagnetics Society Symposium, Xi’an, China, 16–19 August 2024; pp. 1–3. [Google Scholar]
- Jiang, Y.; Zhang, Z.; Du, Y. The ISAR range profile compensation of space target based on Chirplet transform. In Proceedings of the 6th Asia-Pacific Conference on Synthetic Aperture Radar, Xiamen, China, 26–29 November 2019; pp. 1–6. [Google Scholar]
- Zhuang, L.; Lei, W. ISAR echoes coherent processing and imaging using PSO-based adaptive joint time-frequency method. In Proceedings of the 3rd International Asia-Pacific Conference on Synthetic Aperture Radar, Seoul, Republic of Korea, 26–30 September 2011; pp. 1–4. [Google Scholar]
- Nocedal, J.; Wright, S. Numerical Optimization; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Shao, S.; Zhang, L.; Liu, H.; Zhou, Y. Spatial-variant contrast maximization autofocus algorithm for ISAR imaging of maneuvering targets. Sci. China Inf. Sci. 2019, 62, 40303. [Google Scholar] [CrossRef]
- Shao, S.; Zhang, L.; Liu, H.; Zhou, Y. Accelerated translational motion compensation with contrast maximisation optimisation algorithm for inverse synthetic aperture radar imaging. IET Radar Sonar Navig. 2019, 13, 316–325. [Google Scholar] [CrossRef]








| Parameters | Value | Target Parameters | Value |
|---|---|---|---|
| Carrier frequency | 220 GHz | Initial velocity | 1000 m/s |
| Pulse width | 50 μs | Acceleration | −500 m/s2 |
| Bandwidth | 10 GHz | Jerk | 100 m/s3 |
| PRF | 5000 Hz | Slant range | 300 km |
| Parameters | Value | Target Parameters | Value |
|---|---|---|---|
| Carrier frequency | 220 GHz | Initial velocity | 1000 m/s |
| Pulse width | 50 μs | Acceleration | −500 m/s2 |
| Bandwidth | 0.1 THz | Jerk | 100 m/s3 |
| PRF | 5000 Hz | Slant range | 300 km |
| Light velocity | 3 × 108 m/s | Rotation velocity | 0.5 rad/s |
| FrFT | FrFT + PSO | The Proposed Method | |
|---|---|---|---|
| SWE | 8.1633 | 8.1624 | 8.1532 |
| FrFT | FrFT + PSO | PM | |
|---|---|---|---|
| IE | 14.521 | 14.496 | 14.378 |
| IC | 2.9912 | 3.7731 | 6.9954 |
| Time Cost | 608.7932 s | 332.4456 s | 341.3764 s |
| SNR (dB) | IE of FrFT | IE of FrFT + PSO | IE of PM |
|---|---|---|---|
| 5 | 14.521 | 14.496 | 14.378 |
| 0 | 14.589 | 14.573 | 14.542 |
| −5 | 14.629 | 14.622 | 14.61 |
| −10 | 14.641 | 14.636 | 14.628 |
| −15 | 14.652 | 14.651 | 14.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, A.; Yang, Q.; Yuan, Z.; Wang, H.; Yi, J.; Li, S. Spaceborne THz-ISAR Imaging of Space Target with Joint Motion Compensation Based on FrFT and GWO. Remote Sens. 2025, 17, 2152. https://doi.org/10.3390/rs17132152
Zhou A, Yang Q, Yuan Z, Wang H, Yi J, Li S. Spaceborne THz-ISAR Imaging of Space Target with Joint Motion Compensation Based on FrFT and GWO. Remote Sensing. 2025; 17(13):2152. https://doi.org/10.3390/rs17132152
Chicago/Turabian StyleZhou, Ao, Qi Yang, Zhian Yuan, Hongqiang Wang, Jun Yi, and Shuangxun Li. 2025. "Spaceborne THz-ISAR Imaging of Space Target with Joint Motion Compensation Based on FrFT and GWO" Remote Sensing 17, no. 13: 2152. https://doi.org/10.3390/rs17132152
APA StyleZhou, A., Yang, Q., Yuan, Z., Wang, H., Yi, J., & Li, S. (2025). Spaceborne THz-ISAR Imaging of Space Target with Joint Motion Compensation Based on FrFT and GWO. Remote Sensing, 17(13), 2152. https://doi.org/10.3390/rs17132152







