Current Status of Application of Spaceborne GNSS-R Raw Intermediate-Frequency Signal Measurements: Comprehensive Review
Abstract
1. Introduction
2. Current Status of Spaceborne GNSS-R Microsatellites
| Mission | Type of GNSS-R (Receiver Technique) | Frequency Band/Polarization | GNSS System | Is L0-Level Data Publicly Available? | Is L1-Level Data Publicly Available? |
|---|---|---|---|---|---|
| UK-DMC [6] | cGNSS-R | L1/ LHCP | GPS | ✗ | ✗ |
| UK-TDS-1 [31] | cGNSS-R | L1/ LHCP | GPS | ✓ | ✓ |
| CYGNSS [32] | cGNSS-R | L1/ LHCP | GPS | ✓ | ✓ |
| 3Cat-2 [55] | cGNSS-R rGNSS-R iGNSS-R | L1/ LHCP, RHCP | GPS GLONASS Galileo BeiDou | ✗ | ✗ |
| SMAP GNSS-R [56] | cGNSS-R | L2/H, V | GPS | ✗ | ✓ |
| BuFeng-1 A/B [14] | cGNSS-R | L1/ LHCP | GPS BeiDou | ✗ | ✗ |
| Spire [52,57,58,59] | cGNSS-R, GNSS-RO | L1/ LHCP | GPS Galileo | ✗ | ✗ |
| FengYun-3E/3F/3G [33,34] | cGNSS-R, GNSS-RO | L1/ LHCP | GPS Galileo BeiDou | ✗ | ✓ |
| 3Cat-5 A/B (FSSCat) [12] | cGNSS-R | L1/ LHCP | GPS Galileo | ✗ | ✗ |
| 3Cat-4 [60] | cGNSS-R | L1, L2/ LHCP | GPS Galileo | ✗ | ✗ |
| PRETTY [13,61] | iGNSS-R | L1/ LHCP | GPS Galileo | ✗ | ✗ |
| TRITON (FORMOSAT-7R) [62,63] | cGNSS-R | L1/ LHCP | GPS Galileo QZSS | ✗ | ✗ |
| HydroGNSS [19,64] | cGNSS-R | L1, E1/ LHCP, RHCP | GPS Galileo | _ | _ |
| Tianmu-1 [65] | cGNSS-R, GNSS-RO | L1, B1, E1/ LHCP, LHCP + RHCP, H + V | GPS GLONASS Galileo BeiDou QZSS | ✗ | ✗ |
| MuSat Constellation [18] | _ | _ | _ | _ | _ |
3. Coherence Detection and Inland Water Body Monitoring
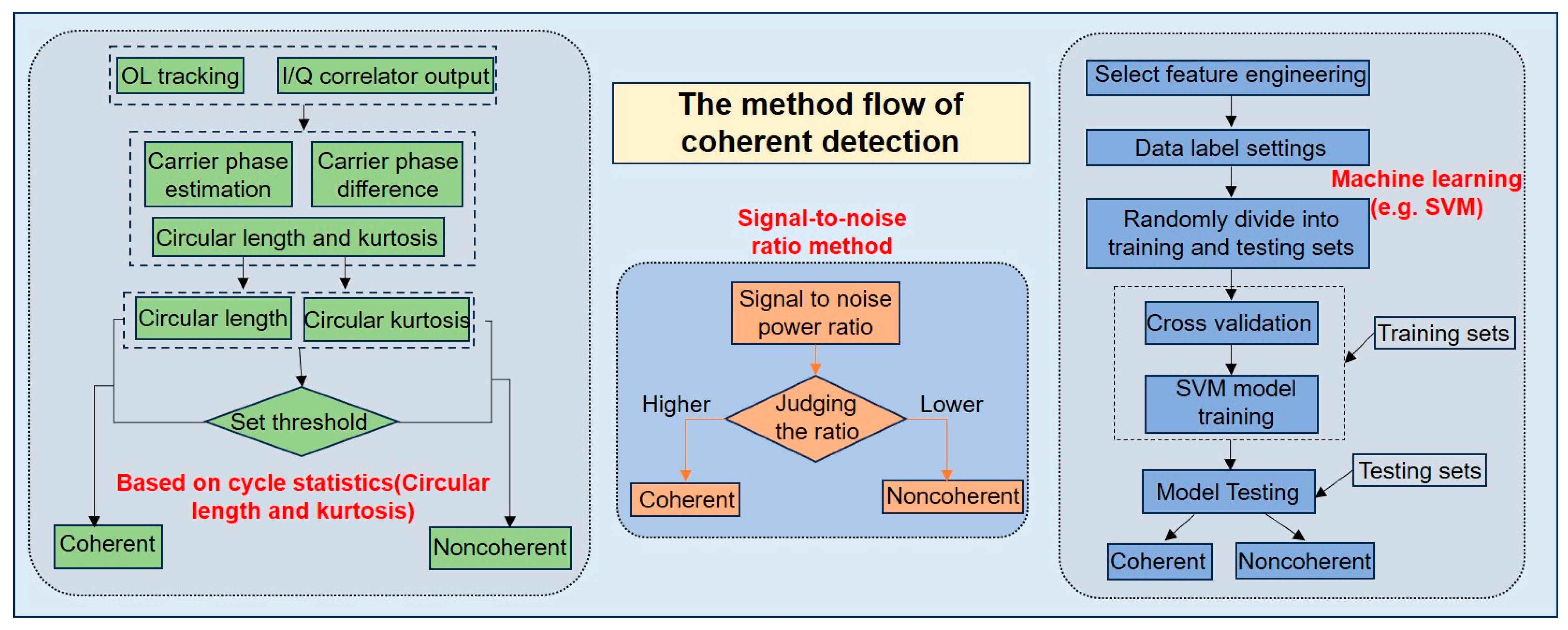
3.1. Coherence Detection
3.2. Inland Water Body Detection
3.3. Retrieval of Inland Water Body (Or Lake Water Body) Surface Height
4. Retrieval of Sea Surface Height
4.1. Code Delay Sea Surface Altimetry
4.2. Retrieval of Sea Surface Height Using Carrier-Phase Measurement
5. Ice Height (Or Ice Sheet Height) Retrieval
6. Ionospheric Total Electron Content and Disturbance Observations
7. Troposphere Monitoring
8. Summary and Future Prospects
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hall, C.D.; Cordey, R.A. Multistatic Scatterometry. In Proceedings of the International Geoscience and Remote Sensing Symposium, Remote Sensing: Moving Toward the 21st Century, Edinburgh, UK, 12–16 September 1988; pp. 561–562. [Google Scholar]
- Martín-Neira, M. A pasive reflectometry and interferometry system (PARIS) application to ocean altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Martin-Neira, M.; Caparrini, M.; Font-Rossello, J.; Lannelongue, S.; Vallmitjana, C.S. The PARIS concept: An experimental demonstration of sea surface altimetry using GPS reflected signals. IEEE Trans. Geosci. Remote Sens. 2001, 39, 142–150. [Google Scholar] [CrossRef]
- Cardellach, E.; Fabra, F.; Nogués-Correig, O.; Oliveras, S.; Ribó, S.; Rius, A. GNSS-R ground-based and airborne campaigns for ocean, land, ice, and snow techniques: Application to the GOLD-RTR data sets. Radio Sci. 2011, 46, 1–16. [Google Scholar] [CrossRef]
- Balasubramaniam, R.; Ruf, C. Characterization of rain impact on L-Band GNSS-R ocean surface measurements. Remote Sens. Environ. 2020, 239, 111607. [Google Scholar] [CrossRef]
- Gleason, S.; Hodgart, S.; Yiping, S.; Gommenginger, C.; Mackin, S.; Adjrad, M.; Unwin, M. Detection and Processing of bistatically reflected GPS signals from low Earth orbit for the purpose of ocean remote sensing. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1229–1241. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, S.; Han, Y.; Yang, S.; Hong, Z.; Ma, D.; Meng, W. Machine Learning Methods for Spaceborne GNSS-R Sea Surface Height Measurement From TDS-1. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1079–1088. [Google Scholar] [CrossRef]
- Alonso-Arroyo, A.; Zavorotny, V.U.; Camps, A. Sea Ice Detection Using U.K. TDS-1 GNSS-R Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4989–5001. [Google Scholar] [CrossRef]
- Rius, A.; Cardellach, E.; Fabra, F.; Li, W.; Ribó, S.; Hernández-Pajares, M. Feasibility of GNSS-R Ice Sheet Altimetry in Greenland Using TDS-1. Remote Sens. 2017, 9, 742. [Google Scholar] [CrossRef]
- Rautiainen, K.; Comite, D.; Cohen, J.; Cardellach, E.; Unwin, M.; Pierdicca, N. Freeze–Thaw Detection Over High-Latitude Regions by Means of GNSS-R Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4302713. [Google Scholar] [CrossRef]
- Ruf, C.; Gleason, S.; Ridley, A.; Rose, R.; Scherrer, J. The nasa cygnss mission: Overview and status update. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 2641–2643. [Google Scholar]
- Camps, A.; Golkar, A.; Gutierrez, A.; Azua, J.A.R.d.; Munoz-Martin, J.F.; Fernandez, L.; Diez, C.; Aguilella, A.; Briatore, S.; Akhtyamov, R.; et al. Fsscat, the 2017 Copernicus Masters’ “Esa Sentinel Small Satellite Challenge” Winner: A Federated Polar and Soil Moisture Tandem Mission Based on 6U Cubesats. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8285–8287. [Google Scholar]
- Dielacher, A.; Fragner, H.; Koudelka, O.; Beck, P.; Wickert, J.; Cardellach, E.; Høeg, P. The ESA Passive Reflectometry and Dosimetry (Pretty) Mission. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 5173–5176. [Google Scholar]
- Jing, C.; Niu, X.; Duan, C.; Lu, F.; Di, G.; Yang, X. Sea Surface Wind Speed Retrieval from the First Chinese GNSS-R Mission: Technique and Preliminary Results. Remote Sens. 2019, 11, 3013. [Google Scholar] [CrossRef]
- Huang, F.; Xia, J.; Yin, C.; Zhai, X.; Xu, N.; Yang, G.; Bai, W.; Sun, Y.; Du, Q.; Liao, M.; et al. Assessment of FY-3E GNOS-II GNSS-R Global Wind Product. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 7899–7912. [Google Scholar] [CrossRef]
- Bu, J.; Wang, Q.; Wang, Z.; Fan, S.; Liu, X.; Zuo, X. Land Remote Sensing Applications Using Spaceborne GNSS Reflectometry: A Comprehensive Overview. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 12811–12841. [Google Scholar] [CrossRef]
- Fu, N.; Li, F. An Introduction of GNSS Reflectometer Remote Sensing Mission From Yunyao Aerospace Technology Co, Ltd. In Proceedings of the 2021 IEEE Specialist Meeting on Reflectometry using GNSS and other Signals of Opportunity (GNSS+R), Beijing, China, 14–17 September 2021; pp. 77–81. [Google Scholar]
- Roberts, M.; Colwell, I.; Chew, C.C.; Masters, D.; Nordstrom, K. The Muon Space GNSS-R Surface Soil Moisture Product. arXiv 2024, arXiv:2412.00072. [Google Scholar]
- Unwin, M.J.; Pierdicca, N.; Cardellach, E.; Rautiainen, K.; Foti, G.; Blunt, P.; Guerriero, L.; Santi, E.; Tossaint, M. An Introduction to the HydroGNSS GNSS Reflectometry Remote Sensing Mission. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 6987–6999. [Google Scholar] [CrossRef]
- Bu, J.; Liu, X.; Wang, Q.; Li, L.; Zuo, X.; Yu, K.; Huang, W. Ocean Remote Sensing Using Spaceborne GNSS-Reflectometry: A Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 13047–13076. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Ribó, S.; Oliveras, S.; Rius, A. Exploration of Multi-Mission Spaceborne GNSS-R Raw IF Data Sets: Processing, Data Products and Potential Applications. Remote Sens. 2022, 14, 1344. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Ribo, S.; Rius, A. Assessment of Spaceborne GNSS-R Ocean Altimetry Performance Using CYGNSS Mission Raw Data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 238–250. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Rius, A.; Ribó, S.; Martín-Neira, M. First spaceborne phase altimetry over sea ice using TechDemoSat-1 GNSS-R signals. Geophys. Res. Lett. 2017, 44, 8369–8376. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Ribó, S.; Rius, A. Lake Level and Surface Topography Measured With Spaceborne GNSS-Reflectometry From CYGNSS Mission: Example for the Lake Qinghai. Geophys. Res. Lett. 2018, 45, 13,332–13,341. [Google Scholar] [CrossRef]
- Mayers, D.; Ruf, C. Measuring Ice Thickness with Cygnss Altimetry. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8535–8538. [Google Scholar]
- Song, M.; He, X.; Wang, X.; Jia, D.; Xiao, R.; Shi, H.; Wu, Y. Study on the Exploration of Spaceborne GNSS-R Raw Data Focusing on Altimetry. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 6142–6154. [Google Scholar] [CrossRef]
- Morton, Y.J.; Wang, Y.; Yang, R. Coherent GNSS Reflection Signal Processing for Precision Altimetry Applications. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 3365–3368. [Google Scholar]
- Wang, Y.; Breitsch, B.; Morton, Y.T.J. A State-Based Method to Simultaneously Reduce Cycle Slips and Noise in Coherent GNSS-R Phase Measurements From Open-Loop Tracking. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8873–8884. [Google Scholar] [CrossRef]
- Peng, J.; Li, W.; Cardellach, E.; Marigold, G.; Clarizia, M.P. Signal Coherence and Water Detection Algorithms for the ESA HydroGNSS Mission. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5801218. [Google Scholar] [CrossRef]
- Xie, J.; Bu, J.; Li, H.; Wang, Q. Spaceborne GNSS Reflectometry for Vegetation and Inland Water Monitoring: Progress, Challenges, Opportunities, and Potential. Remote Sens. 2025, 17, 1199. [Google Scholar] [CrossRef]
- Unwin, M.; Jales, P.; Tye, J.; Gommenginger, C.; Foti, G.; Rosello, J. Spaceborne GNSS-reflectometry on TechDemoSat-1: Early mission operations and exploitation. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 4525–4539. [Google Scholar] [CrossRef]
- Ruf, C.; Chang, P.; Clarizia, M.; Gleason, S.; Jelenak, Z.; Murray, J.; Morris, M.; Musko, S.; Posselt, D.; Provost, D. CYGNSS Handbook Cyclone Global Navigation Satellite System: Deriving Surface Wind Speeds in Tropical Cyclones; National Aeronautics and Space Administration: Ann Arbor, MI, USA, 2016; Volume 154. [Google Scholar]
- Sun, Y.; Wang, X.; Du, Q.; Bai, W.; Xia, J.; Cai, Y.; Wang, D.; Wu, C.; Meng, X.; Tian, Y. The status and progress of Fengyun-3E GNOS II mission for GNSS remote sensing. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 5181–5184. [Google Scholar]
- Sun, Y.; Huang, F.; Xia, J.; Yin, C.; Bai, W.; Du, Q.; Wang, X.; Cai, Y.; Li, W.; Yang, G.; et al. GNOS-II on Fengyun-3 Satellite Series: Exploration of Multi-GNSS Reflection Signals for Operational Applications. Remote Sens. 2023, 15, 5756. [Google Scholar] [CrossRef]
- Jales, P. Spaceborne Receiver Design for Scatterometric GNSS Reflectometry; University of Surrey (UK): Guildford, UK, 2012. [Google Scholar]
- King, L.S.; Unwin, M.; Rawlinson, J.; Guida, R.; Underwood, C. Processing of raw GNSS reflectometry data from TDS-1 in a backscattering configuration. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2916–2924. [Google Scholar] [CrossRef]
- Mashburn, J.; Axelrad, P.; Lowe, S.T.; Larson, K.M. Global Ocean Altimetry With GNSS Reflections From TechDemoSat-1. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4088–4097. [Google Scholar] [CrossRef]
- Ren, X.; Liu, H.; Zhang, J.; Mei, D.; Zhang, X. An Improved Method for Ionospheric TEC Estimation Using the Spaceborne GNSS-R Observations. IEEE Trans. Geosci. Remote Sens. 2022, 60, 3192983. [Google Scholar] [CrossRef]
- Ruf, C.S.; Atlas, R.; Chang, P.S.; Clarizia, M.P.; Garrison, J.L.; Gleason, S.; Katzberg, S.J.; Jelenak, Z.; Johnson, J.T.; Majumdar, S.J. New ocean winds satellite mission to probe hurricanes and tropical convection. Bull. Am. Meteorol. Soc. 2016, 97, 385–395. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Ruf, C.S.; Gleason, S.; Russel, A. A New Multiresolution CYGNSS Data Product for Fully and Partially Coherent Scattering. IEEE Trans. Geosci. Remote Sens. 2023, 61, 3318639. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Ruf, C.; Gleason, S.; Russel, A.; Butler, T. Generation of A New High Resolution Ddm Data Product from Cygnss Raw If Measurements. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 7815–7818. [Google Scholar]
- Zhang, Y.; Yan, Z.; Yang, S.; Meng, W.; Han, Y.; Hong, Z. Feasibility study on Qinghai Lake Boundary detection using CYGNSS raw IF Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 3290680. [Google Scholar] [CrossRef]
- Cardellach, E.; Li, W.; Rius, A.; Semmling, M.; Wickert, J.; Zus, F.; Ruf, C.S.; Buontempo, C. First Precise Spaceborne Sea Surface Altimetry With GNSS Reflected Signals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 102–112. [Google Scholar] [CrossRef]
- Molina, C.; Boudriki Semlali, B.-E.; Park, H.; Camps, A. A preliminary study on ionospheric scintillation anomalies detected using GNSS-R data from NASA CYGNSS mission as possible earthquake precursors. Remote Sens. 2022, 14, 2555. [Google Scholar] [CrossRef]
- Al-Khaldi, M.M.; Johnson, J.T.; Chan, S.K.; Hajj, G. Near-Specular Interferometry With Signals of Opportunity Systems: Potential and Limitations. IEEE Trans. Geosci. Remote Sens. 2025, 63, 3550285. [Google Scholar] [CrossRef]
- Jing, C.; Li, W.; Wan, W.; Lu, F.; Niu, X.; Chen, X.; Rius, A.; Cardellach, E.; Ribó, S.; Liu, B.; et al. A review of the BuFeng-1 GNSS-R mission: Calibration and validation results of sea surface and land surface. Geo-Spat. Inf. Sci. 2024, 27, 638–652. [Google Scholar] [CrossRef]
- Nguyen, V.A.; Nogués-Correig, O.; Yuasa, T.; Masters, D.; Irisov, V. Initial GNSS Phase Altimetry Measurements From the Spire Satellite Constellation. Geophys. Res. Lett. 2020, 47, e2020GL088308. [Google Scholar] [CrossRef]
- Wang, Y.; Morton, Y.J. Evaluation of GNSS-R Retrieved Sea Ice Surface Height Using ICESat-2 Ice Freeboard Measurements. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 7803–7806. [Google Scholar]
- Wang, Y.; Morton, Y.J. Ionospheric total electron content and disturbance observations from space-borne coherent GNSS-R measurements. IEEE Trans. Geosci. Remote Sens. 2021, 60, 3093328. [Google Scholar] [CrossRef]
- Wang, C.; Camps, A.; Hu, X.; Park, H.; Yu, K.; Zhai, X.; Lu, W.; Huang, F.; Liao, M.; Zhang, P.; et al. A Novel Geometry Agnostic Delay and Doppler Tracking Technique for GNSS-Reflectometry: Application to the GNOS-II Payload Onboard the FY-3E. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 8040–8056. [Google Scholar] [CrossRef]
- Wang, Y.; Morton, Y.J. Spaceborne GNSS-R for High Latitude Ionospheric TEC Disturbance Observations. In Proceedings of the 2021 IEEE Specialist Meeting on Reflectometry using GNSS and other Signals of Opportunity (GNSS+R), Beijing, China, 14–17 September 2021; pp. 21–24. [Google Scholar]
- Roesler, C.J.; Morton, Y.J.; Wang, Y.; Nerem, R.S. Coherent GNSS-Reflections Characterization Over Ocean and Sea Ice Based on Spire Global CubeSat Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 3129999. [Google Scholar] [CrossRef]
- Zhang, J.; Morton, Y.J.; Wang, Y.; Roesler, C.J. Mapping Surface Water Extents Using High-Rate Coherent Spaceborne GNSS-R Measurements. IEEE Trans. Geosci. Remote Sens. 2022, 60, 3218254. [Google Scholar] [CrossRef]
- Buendía, R.N.; Tabibi, S.; Talpe, M.; Otosaka, I. Ice sheet height retrievals from Spire grazing angle GNSS-R. Remote Sens. Environ. 2023, 297, 113757. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Camps, A.; Via, P.; Munoz, J.F.; Cortiella, A.; Vidal, D.; Jané, J.; Catarino, N.; Hagenfeldt, M.; Palomo, P. 3Cat-2—An experimental nanosatellite for GNSS-R earth observation: Mission concept and analysis. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 4540–4551. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Lowe, S.; Zuffada, C.; Esterhuizen, S.; Oveisgharan, S. Spaceborne GNSS-R from the SMAP mission: First assessment of polarimetric scatterometry over land and cryosphere. Remote Sens. 2017, 9, 362. [Google Scholar] [CrossRef]
- Masters, D. Design and planning for the first spire GNSS-R missions of 2019. In Proceedings of the IEEE GRSS, Spec. Meeting Reflectometry Using GNSS Other Signals Opportunity, Benevento, Italy, 20–22 May 2019. [Google Scholar]
- Masters, D.; Irisov, V.; Nguyen, V.; Duly, T.; Nogués-Correig, O.; Tan, L.; Yuasa, T.; Ringer, J.; Sikarin, R.; Gorbunov, M. Status and plans for Spire’s growing commercial constellation of GNSS science cubeSats. In Proceedings of the Joint 6th ROM SAF User Workshop and 7th IROWG Workshop, Helsingør, Denmark, 19–25 September 2019; pp. 19–25. [Google Scholar]
- Freeman, V.; Masters, D.; Jales, P.; Esterhuizen, S.; Ebrahimi, E.; Irisov, V.; Ben Khadhra, K. Earth Surface Monitoring with Spire’s New GNSS Reflectometry (GNSS-R) CubeSats. In Proceedings of the EGU General Assembly Conference Abstracts, In Virtual, 4–8 May 2020; p. 13766. [Google Scholar]
- Munoz-Martin, J.F.; Miguelez, N.; Castella, R.; Fernandez, L.; Solanellas, A.; Via, P.; Camps, A. 3Cat-4: Combined GNSS-R, L-Band radiometer with RFI mitigation, and AIS receiver for a I-Unit Cubesat based on software defined radio. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1063–1066. [Google Scholar]
- Dielacher, A.; Fragner, H.; Moritsch, M.; Høeg, P.; Wickert, J.; Cardellach, E.; Koudelka, O.; Beck, P.; Walker, R.; Martin-Neira, M. The passive reflectometer on board of PRETTY. In Proceedings of the ESA ARSIKEO Conference, Noordwijk, The Netherlands, 11–13 November 2019. [Google Scholar]
- Juang, J.-C.; Ma, S.-H.; Lin, C.-T. Study of GNSS-R techniques for FORMOSAT mission. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 4582–4592. [Google Scholar] [CrossRef]
- Wang, H.Y.; Juang, J.C. Retrieval of Ocean Surface Wind Speed Using Reflected BPSK/BOC Signals. Remote Sens. 2020, 12, 2698. [Google Scholar] [CrossRef]
- Peng, J.; Cardellach, E.; Li, W.; Ribó, S.; Rius, A. Toward the Exploitation of HydroGNSS Coherent Channel: High Sampling Rate Products. IEEE Trans. Geosci. Remote Sens. 2025, 63, 3554191. [Google Scholar] [CrossRef]
- Liu, X.; Bu, J.; Zuo, X.; Wang, Z.; Wang, Q.; Wang, Q.; Ji, C.; Zhao, Y.; Yang, H.; He, X. Performance Validation of Sea Surface Wind Speed Retrieval Algorithms and Products From the Chinese Tianmu-1 Constellation GNSS-R: First Results on Comparison With Other Wind Speed Products. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 5189–5203. [Google Scholar] [CrossRef]
- Wang, Y.; Morton, Y.J. Coherent GNSS Reflection Signal Processing for High-Precision and High-Resolution Spaceborne Applications. IEEE Trans. Geosci. Remote Sens. 2021, 59, 831–842. [Google Scholar] [CrossRef]
- Beckmann, P.; Spizzichino, A. The Scattering of Electromagnetic Waves from Rough Surfaces; Artech House, Inc.: Norwood, MA, USA, 1963. [Google Scholar]
- Chen, W.-K. The Electrical Engineering Handbook; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Wang, Y.; Morton, Y.J. Coherent Reflections Using Closed-Loop PLL Processing of CYGNSS IF Data. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 8737–8740. [Google Scholar]
- Wang, Y.; Morton, Y. Coherent components of GNSS-R signal observed from CYGNSS raw IF data. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019; pp. 3319–3326. [Google Scholar]
- Fisher, N.I. Statistical Analysis of Circular Data; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Roesler, C.; Wang, Y.; Morton, Y.J.; Nerem, R.S. Coherent GPS Reflections Over Ocean Surface. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 6218–6221. [Google Scholar]
- Wang, Y.; Liu, Y.; Roesler, C.; Morton, Y.J. Detection of Coherent GNSS-R Measurements Using a Support Vector Machine. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 6210–6213. [Google Scholar]
- Loria, E.; Russo, I.M.; Wang, Y.; Giangregorio, G.; Galdi, C.; Bisceglie, M.d.; Wilson-Downs, B.; Lavalle, M.; O’Brien, A.J.; Morton, Y.J.; et al. Comparison of GNSS-R Coherent Reflection Detection Algorithms Using Simulated and Measured CYGNSS Data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 3277411. [Google Scholar] [CrossRef]
- Chew, C.; Shah, R.; Zuffada, C.; Hajj, G.; Masters, D.; Mannucci, A.J. Demonstrating soil moisture remote sensing with observations from the UK TechDemoSat-1 satellite mission. Geophys. Res. Lett. 2016, 43, 3317–3324. [Google Scholar] [CrossRef]
- Chew, C.C.; Zuffada, C.; Shah, R.; Mannucci, A.J. Mapping sea ice using reflected GNSS signals in a bistatic radar system. In Proceedings of the EGU General Assembly 2016, Vienna, Austria, 17–22 April 2016. [Google Scholar]
- Nghiem, S.V.; Zuffada, C.; Shah, R.; Chew, C.; Lowe, S.T.; Mannucci, A.J.; Cardellach, E.; Brakenridge, G.R.; Geller, G.; Rosenqvist, A. Wetland monitoring with Global Navigation Satellite System reflectometry. Earth Space Sci. 2017, 4, 16–39. [Google Scholar] [CrossRef] [PubMed]
- Yan, Q.; Huang, W. Spaceborne GNSS-R Sea Ice Detection Using Delay-Doppler Maps: First Results From the U.K. TechDemoSat-1 Mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4795–4801. [Google Scholar] [CrossRef]
- Al-Khaldi, M.M.; Johnson, J.T.; Gleason, S.; Chew, C.C.; Gerlein-Safdi, C.; Shah, R.; Zuffada, C. Inland Water Body Mapping Using CYGNSS Coherence Detection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7385–7394. [Google Scholar] [CrossRef]
- Russo, I.M.; Bisceglie, M.d.; Galdi, C.; Lavalle, M.; Zuffada, C. Entropy-Based Coherence Metric for Land Applications of GNSS-R. IEEE Trans. Geosci. Remote Sens. 2022, 60, 3125858. [Google Scholar] [CrossRef]
- Collett, I.; Wang, Y.; Shah, R.; Roesler, C.; Morton, Y.J. GPS Signal Land Reflection Coherence Dependence on Water Extent and Surface Topography using Cygnss Measurements. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 6206–6209. [Google Scholar]
- Collett, I.; Wang, Y.; Shah, R.; Morton, Y.J. Phase Coherence of GPS Signal Land Reflections and its Dependence on Surface Characteristics. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3094407. [Google Scholar] [CrossRef]
- Liu, Q.; Li, W.; Zhang, S.; Nan, Y.; Peng, J.; Ma, Z. Analysis of signal-to-noise ratio retrieved from multi-GNSS satellite data of land surface reflections. GPS Solut. 2023, 27, 151. [Google Scholar] [CrossRef]
- Nan, Y.; Ye, S.; Liu, J.; Guo, B.; Zhang, S.; Li, W. Signal-to-Noise Ratio Analyses of Spaceborne GNSS-Reflectometry from Galileo and BeiDou Satellites. Remote Sens. 2022, 14, 35. [Google Scholar] [CrossRef]
- Zhu, Y.; Guo, F.; Zhang, X. Spaceborne GNSS-R soil moisture retrieval from GPS/BDS-3/Galileo satellites. GPS Solut. 2024, 29, 10. [Google Scholar] [CrossRef]
- Du, H.; Nan, Y.; Li, W.; Cardellach, E.; Ribó, S.; Rius, A. Coherent Combination of GPS III L1 C/A and L1C Signals for GNSS Reflectometry. IEEE Trans. Geosci. Remote Sens. 2024, 62, 3398435. [Google Scholar] [CrossRef]
- Tranvik, L.J.; Downing, J.A.; Cotner, J.B.; Loiselle, S.A.; Striegl, R.G.; Ballatore, T.J.; Dillon, P.; Finlay, K.; Fortino, K.; Knoll, L.B.; et al. Lakes and reservoirs as regulators of carbon cycling and climate. Limnol. Oceanogr. 2009, 54, 2298–2314. [Google Scholar] [CrossRef]
- Pickens, A.H.; Hansen, M.C.; Hancher, M.; Stehman, S.V.; Tyukavina, A.; Potapov, P.; Marroquin, B.; Sherani, Z. Mapping and sampling to characterize global inland water dynamics from 1999 to 2018 with full Landsat time-series. Remote Sens. Environ. 2020, 243, 111792. [Google Scholar] [CrossRef]
- Vanderhoof, M.K.; Alexander, L.; Christensen, J.; Solvik, K.; Nieuwlandt, P.; Sagehorn, M. High-frequency time series comparison of Sentinel-1 and Sentinel-2 satellites for mapping open and vegetated water across the United States (2017–2021). Remote Sens. Environ. 2023, 288, 113498. [Google Scholar] [CrossRef] [PubMed]
- Scott, M.; Chew, C.; Wang, Y.; Roesler, C.; Morton, Y.J. On The Relationship Between The GNSS-R Signal SNR and Coherency With Surface Water: A Case Study Over Lake Okeechobee. In Proceedings of the IGARSS 2023—2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; pp. 3345–3348. [Google Scholar]
- Carreno-Luengo, H.; Ruf, C.S.; Gleason, S.; Russel, A. Detection of inland water bodies under dense biomass by CYGNSS. Remote Sens. Environ. 2024, 301, 113896. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; RibÓ, S.; Rius, A.; Zhou, B. First spaceborne demonstration of BeiDou-3 signals for GNSS reflectometry from CYGNSS constellation. Chin. J. Aeronaut. 2021, 34, 1–10. [Google Scholar] [CrossRef]
- Mei, J.; Yan, S.; Chen, C. Multifeature Water Discrimination Method Based on CYGNSS Intermediate Frequency Data. IEEE Trans. Geosci. Remote Sens. 2025, 63, 3531636. [Google Scholar] [CrossRef]
- Wang, Y.; Morton, Y.J. River Slope Observation From Spaceborne GNSS-R Carrier Phase Measurements: A Case Study. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3127750. [Google Scholar] [CrossRef]
- Wang, Y.; Morton, Y.J. Observation of the Mississippi River Surface Gradients from Spire’s GNSS-R CubeSats. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 4403–4406. [Google Scholar]
- Nielsen, K.; Stenseng, L.; Andersen, O.B.; Villadsen, H.; Knudsen, P. Validation of CryoSat-2 SAR mode based lake levels. Remote Sens. Environ. 2015, 171, 162–170. [Google Scholar] [CrossRef]
- Yanez, C.; Li, W.; Cardellach, E.; Raynal, M.; Picot, N.; Martin-Neira, M.; Borde, F. Lake Water Level Estimation from Grazing GNSS-Reflectometry and Satellite Radar Altimetry over the Great Lakes. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Zhang, J.; Morton, Y.J. Inland Water Body Surface Height Retrievals Using CYGNSS Delay Doppler Maps. IEEE Trans. Geosci. Remote Sens. 2023, 61, 3330410. [Google Scholar] [CrossRef]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Semmling, A.M.; Beckheinrich, J.; Wickert, J.; Beyerle, G.; Schön, S.; Fabra, F.; Pflug, H.; He, K.; Schwabe, J.; Scheinert, M. Sea surface topography retrieved from GNSS reflectometry phase data of the GEOHALO flight mission. Geophys. Res. Lett. 2014, 41, 954–960. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.; Cipollini, P.; Zuffada, C. First spaceborne observation of sea surface height using GPS-Reflectometry. Geophys. Res. Lett. 2016, 43, 767–774. [Google Scholar] [CrossRef]
- Hu, C.; Benson, C.; Rizos, C.; Qiao, L. Single-Pass Sub-Meter Space-Based GNSS-R Ice Altimetry: Results From TDS-1. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3782–3788. [Google Scholar] [CrossRef]
- Li, W.; Rius, A.; Fabra, F.; Cardellach, E.; Ribo, S.; Martin-Neira, M. Revisiting the GNSS-R Waveform Statistics and Its Impact on Altimetric Retrievals. IEEE Trans. Geosci. Remote. Sens. 2018, 56, 2854–2871. [Google Scholar] [CrossRef]
- Mashburn, J.; Axelrad, P.; Zuffada, C.; Loria, E.; O’Brien, A.; Haines, B. Improved GNSS-R Ocean Surface Altimetry With CYGNSS in the Seas of Indonesia. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6071–6087. [Google Scholar] [CrossRef]
- Cardellach, E.; Ao, C.O.; de la Torre Juárez, M.; Hajj, G.A. Carrier phase delay altimetry with GPS-reflection/occultation interferometry from low Earth orbiters. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Semmling, A.M.; Schmidt, T.; Wickert, J.; Schön, S.; Fabra, F.; Cardellach, E.; Rius, A. On the retrieval of the specular reflection in GNSS carrier observations for ocean altimetry. Radio Sci. 2012, 47, 1–13. [Google Scholar] [CrossRef]
- Parrinello, T.; Shepherd, A.; Bouffard, J.; Badessi, S.; Casal, T.; Davidson, M.; Fornari, M.; Maestroni, E.; Scagliola, M. CryoSat: ESA’s ice mission—Eight years in space. Adv. Space Res. 2018, 62, 1178–1190. [Google Scholar] [CrossRef]
- Wang, Y.; Morton, Y.J.; Minear, J.T.; Putnam, A.; Conrad, A.; Axelrad, P.; Nerem, R.S.; Warnock, A.; Ruf, C.; Moreira, D.M.; et al. Measuring river slope using spaceborne GNSS reflectometry: Methodology and first performance assessment. Remote Sens. Environ. 2025, 318, 114597. [Google Scholar]
- Ren, X.; Liu, H.; Mei, D.; Yang, P.; Zhang, Z.; Freeshah, M.; Zhang, X. Leveraging the CYGNSS Spaceborne GNSS-R Observations to Detect Ionospheric Irregularities Over the Oceans: Method and Verification. Space Weather 2022, 20, e2022SW003141. [Google Scholar] [CrossRef]
- Ren, X.; Zhang, J.; Chen, J.; Zhang, X. Global Ionospheric Modeling Using Multi-GNSS and Upcoming LEO Constellations: Two Methods and Comparison. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Molina, C.; Camps, A. First Evidences of Ionospheric Plasma Depletions Observations Using GNSS-R Data from CYGNSS. Remote Sens. 2020, 12, 3782. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Foti, G.; Gommenginger, C. Ionospheric Effects in GNSS-Reflectometry From Space. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5851–5861. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Juan, J.M.; Sanz, J.; Gonzalez-Casado, G.; Barbosa, J.; Fabbro, V.; Lemorton, J.; Orus, R. Ionospheric scintillation monitoring using GNSS-R?, Proceedings of the 38th Annual IEEE International Geoscience and Remote Sensing Symposium, IGARSS 2018, Valencia, Spain, 22–27 July 2018; Institute of Electrical and Electronics Engineers Inc.: Valencia, Spain, 2018; pp. 3339–3342. [Google Scholar]
- Moreno, M.; Semmling, M.; Stienne, G.; Hoque, M.; Wickert, J. Characterizing Ionospheric Effects on GNSS Reflectometry at Grazing Angles from Space. Remote Sens. 2023, 15, 5049. [Google Scholar] [CrossRef]
- Wang, Y.; Morton, Y.J. Polar Ionospheric TEC Enhancement Observation Using GNSS-R. In Proceedings of the 2023 XXXVth General Assembly and Scientific Symposium of the International Union of Radio Science (URSI GASS), Sapporo, Japan, 19–26 August 2023; pp. 1–4. [Google Scholar]
- Priyadarshi, S. A review of ionospheric scintillation models. Surv. Geophys. 2015, 36, 295–324. [Google Scholar] [CrossRef]
- Wu, Y.; Jiang, N.; Xu, Y.; Yeh, T.-K.; Xu, T.; Wang, Y.; Su, W. Improving the capability of water vapor retrieval from Landsat 8 using ensemble machine learning. Int. J. Appl. Earth Obs. Geoinf. 2023, 122, 103407. [Google Scholar] [CrossRef]
- Li, Q.; Böhm, J.; Yuan, L.; Weber, R. Global zenith wet delay modeling with surface meteorological data and machine learning. GPS Solut. 2024, 28, 57. [Google Scholar] [CrossRef]
- Landskron, D.; Böhm, J. VMF3/GPT3: Refined discrete and empirical troposphere mapping functions. J. Geod. 2018, 92, 349–360. [Google Scholar] [CrossRef]
- Li, Q.; Yuan, L.; Jiang, Z. Modeling tropospheric zenith wet delays in the Chinese mainland based on machine learning. GPS Solut. 2023, 27, 171. [Google Scholar] [CrossRef]
- Wang, Y. Troposphere Sensing Using Grazing-Angle GNSS-R Measurement From LEO Satellites. Geophys. Res. Lett. 2023, 50, e2023GL106249. [Google Scholar] [CrossRef]
- Jaberi Shafei, M.; Mashhadi-Hossainali, M. Application of the GNSS-R in tomographic sounding of the Earth atmosphere. Adv. Space Res. 2018, 62, 71–83. [Google Scholar] [CrossRef]
- Scott, M.; Roesler, C.; Wang, Y.; Morton, Y.; Nerem, S. Tropospheric error budget for GNSS-R altimetry at low grazing angles. In Proceedings of the Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), St. Louis, MO, USA, 20–24 September 2021; pp. 4021–4029. [Google Scholar]
- Moreno, M.; Semmling, M.; Stienne, G.; Dalil, W.; Hoque, M.; Wickert, J.; Reboul, S. Airborne Coherent GNSS Reflectometry and Zenith Total Delay Estimation over Coastal Waters. Remote Sens. 2022, 14, 4628. [Google Scholar] [CrossRef]
- Wang, Y. Grazing-angle GNSS-R for the determination of tropospheric delay and water vapor content. In Proceedings of the Proceedings of the 36th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2023); Denver, CO, USA, 11–15 September 2023, pp. 3227–3232.
- Roesler, C.; Morton, Y.J. Retrieving Atmospheric Water Vapor Content from Grazing Angle GNSS Reflectometry Measurements: Methodology and Performance Assessment. TechRxiv 2025. [Google Scholar] [CrossRef]
- Anderson, S.G.; Wang, Y.; Morton, Y.J. Relating GNSS Reflected Signal Coherence to Ice Shelf Surface Deformation and Roughness. IEEE Trans. Geosci. Remote Sens. 2025, 63, 3538558. [Google Scholar] [CrossRef]







| Detector | Introduce | Related Formulas | Explain |
|---|---|---|---|
| Coherence gain detector [74] | This detector utilizes information from the phase and relative amplitude of the received signal. It distinguishes between coherent and noncoherent signals by comparing the increase in correlated power with a threshold. The longer coherent integration time and the nominal integration time are calculated using the correlated power (in decibels). | where is the total signal length and is a sequence of complex samples taken from the DDM after the initial cross-correlation of the measured signal with a local replica. The coherence metric is bounded by [0, 1], where a coherence value of 0 represents a noncoherent signal and a value of 1 represents a fully coherent signal. The typical value of noncoherent reflection is approximately between 0 and 0.2. | |
| In addition, to further reduce noise and compare with other coherent detector algorithms, the normalized integrated power values need to be averaged over a longer period of time, and then these average correlated power ratios are normalized by , which we represent as the quantity “coherence” . | |||
| Phase detector [52] | This detector is based on phase cycle statistics and coherent detection using the carrier phase, using two parameters, circular length (CL) and circular kurtosis, for coherent detection and quantification [71]. Circular length: average unit vector length of the dataset. | where , are uniformly distributed around the unit circle, with values within the range of [0, 1], and is the average value of the dataset. If is uniformly distributed around the unit circle, then , . From the above equation, it can be seen that the closer the value of and is to 1, the more coherent the signal is. | |
| Kurtosis: the measurement of the “peak” of an angle dataset: | |||
| Entropy detector [80] | This detector relies on the generalized eigendecomposition (GED) of the correlation matrix R of complex zero-Doppler delay waveforms. | where is the matrix, whose columns are the N, sequential snapshots of the -length delay waveforms. represents the matrix of normalized eigenvalues, where entropy can effectively represent the dynamic range between eigenvalues related to coherent scattering components and other eigenvalues. In the case of only one strongly coherent component, entropy is 0. On the contrary, only in the case of noncoherent components, the entropy is 1 because there are no major eigenvalues. | |
| To detect coherence in GNSS-R signals, the concept of von Neumann entropy is used to measure the amount of information contained in generalized eigenvalues. |
| Reference | Satellite Data | Detection Area | Method | Result (Accuracy) |
|---|---|---|---|---|
| [91] | CYGNSS L1/L0 | Amazon basin, Pantanal wetlands | Entropy detector | Small water bodies can be detected and imaged under heavy vegetation (i.e., 400 tons/hectare). |
| [42] | CYGNSS L0 | Qinghai Lake | Fusion method of signal–power ratio and effective area delay distance (DLR) | Can achieve higher spatial resolution (0.7 km), with retrieval result error of about 0.5 km. |
| [92] | CYGNSS L0 | Mississippi River | Coherent Coefficient | Proves the feasibility of using the Beidou-3 signal collected by CYGNSS to map flooding inundation. |
| [53] | Spire, CYGNSS L0 | North America, north Eurasia, and near the Gulf of Mexico (Spire data). Southeast USA, Amazon River basin, and Qinghai–Tibet Plateau (CYGNSS data). | Jointly uses carrier phases and signal strength | As for CYGNSS, the difference is mainly less than 0.43 km, with an average of 0.18 km and a standard deviation of 0.16 km. |
| [21] | CYGNSS FM02 L0 | Rousseau Lake, Florida | Coherent Coefficient | An overlay of the mean coherent coefficient in a Google Earth historical image, which clearly shows the consistency between high coherent coefficient pixels and the presence of inland water bodies. |
| [93] | CYGNSS L0 | Amazon River | The threshold, normalized variance, Z-score, variance, and circular correlation (Cir Cor) discriminations | This multi-feature method achieves a high discrimination accuracy (~90%) and provides a high temporal resolution (20 Hz). |
| [94] | CYGNSS L0 | Orinoco River | OL tracking of the reflection signal phase [71] and a novel error correction approach | The retrieved river surface slope ranges from 3.9 to 5.1 cm/km. |
| [95] | Spire | Mississippi River | OL tracking | The retrieved river surface slopes range from 2.2 to 16.6 cm/km, with lower sections being flatter. |
| Retrieval Method | Reference | Satellite (Airborne) Data Used | Reference Surface/Data | Result (Accuracy) |
|---|---|---|---|---|
| Carrier phase | [43] | CYGNSS | DTU18 MSS | The altimetric results show that the measurement system precision is 3/4.1 cm (median/mean) at 20 Hz sampling, cm level at 1 Hz, comparable to dedicated radar altimeters. The combined precision, including systematic errors, is 16/20 cm (median/mean) precision at 50 ms integration (a few cm level at 1 Hz). |
| Code delay | [104] | CYGNSS | DTU10 MSS | Among the three retracing methods, the VZ18DDM method is the most superior. When averaging for 1 s, the VZ18DDM method is based on single-sample and Gaussian smoothing with standard deviations of 5.8 m and 1.9 m, respectively. |
| [37] | TDS-1 | DTU10 MSS | Compared to the mean sea surface topography, the surface height residuals are found to be 6.4 m, 1σ with a 1 s integration time. | |
| [26] | TDS-1 | DTU15 MSS | The results show a good consistency with MSS model. | |
| [103] | SPIR | SPIR, TDS-1 | With airborne data, two different delay estimators, based on the DER method and the FIT method, are assessed. By taking the information of the whole leading edge instead of that at the SP, the altimetry precision obtained with the FIT method is proven to be a factor 1.3–1.5 times better than that of DER. | |
| [22] | CYGNSS | DTU18 MSS | The two-way ranging precision can reach up to 3.9 and 2.5 m with 1 s GPS and Galileo group delay measurement (a factor of ∼2 better for altimetry solution), and its evolution with the signal-to-noise ratio shows good consistency with the theoretical model. |
| Reference | Satellite Data Used | Type of Data Used | Reference Surface/Data | Result (Accuracy) |
|---|---|---|---|---|
| [48] | Spire | L0 | ICESat-2 | Compared with the monthly average ice freeboard measurement values of ICESat-2 L3B, the GNSS-R retrieval results have a certain consistency with the overall trend of ICESat-2 measurement results. |
| [47] | Spire | L0 | Interpolate from the DTU18 mean sea surface model | The comparison between the unsmooth 50 Hz retrieved surface height estimates and the model sea surface shows a good consistency, with an RMS difference of approximately 3.9 cm. |
| [54] | Spire | L0 | DEM | In Greenland and Antarctica, both the RMSE values retrieved by GG-R and the RMSE values of its reference surface model achieve meter-level accuracy. |
| [23] | TDS-1 | L0 | DTU13 MSS | The results show that the RMSD between the measured surface height and the reference one is 4.7 cm with 20 ms phase delay observations (∼140 m along-track sampling distance and ∼400 m spatial resolution). |
| [21] | TDS-1 | L0 | DTU13 MSS | The group delay altimetry results show a much larger error comparing to the carrier-phase ones (0.88 m vs. 0.04 m). |
| Reference | Satellite Data Used | Type of Data | Result (Accuracy) |
|---|---|---|---|
| [112] | TDS-1 | L1 | In low latitudes, open oceans, and low wind speeds, there are coherent scattering components. Under high wind speeds, it is mostly irrelevant. |
| [113] | TDS-1 CYGNSS | L1 | The results show stronger fluctuations in the peak of the DDM associated with ionospheric scintillation events, possibly related to tropical storms. |
| [44] | CYGNSS | L1 | All earthquakes with magnitudes above 4 exhibit a small but detectable positive correlation with ionospheric amplitude scintillation, and the results will improve with increasing magnitudes. |
| [38] | TDS-1 | L1 | The improvement in RMS error during high solar activity is 5.3%, and during low solar activity it is 23.5% (compared to GNSS TEC). |
| [49] | Spire | L0 | The slant global ionospheric TEC maps (TEC) retrieved from GNSS-R measurements and GIM follow similar trends, and the TEC time series based on GNSS-R provides an almost “frozen in time” observation of ionospheric structure. |
| [114] | Spire | L0 | The results during the low solar = activity period show that the total tilted electron content fluctuates up to about 300 TECU, the relative ionospheric delay of GPS L1 frequency is 19 m, the Doppler frequency shift is 2 Hz, and the range of peak electron density height variation is from 215 to 330 km. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Bu, J.; Wang, Y.; Huang, D.; Yang, H.; Zuo, X. Current Status of Application of Spaceborne GNSS-R Raw Intermediate-Frequency Signal Measurements: Comprehensive Review. Remote Sens. 2025, 17, 2144. https://doi.org/10.3390/rs17132144
Wang Q, Bu J, Wang Y, Huang D, Yang H, Zuo X. Current Status of Application of Spaceborne GNSS-R Raw Intermediate-Frequency Signal Measurements: Comprehensive Review. Remote Sensing. 2025; 17(13):2144. https://doi.org/10.3390/rs17132144
Chicago/Turabian StyleWang, Qiulan, Jinwei Bu, Yutong Wang, Donglan Huang, Hui Yang, and Xiaoqing Zuo. 2025. "Current Status of Application of Spaceborne GNSS-R Raw Intermediate-Frequency Signal Measurements: Comprehensive Review" Remote Sensing 17, no. 13: 2144. https://doi.org/10.3390/rs17132144
APA StyleWang, Q., Bu, J., Wang, Y., Huang, D., Yang, H., & Zuo, X. (2025). Current Status of Application of Spaceborne GNSS-R Raw Intermediate-Frequency Signal Measurements: Comprehensive Review. Remote Sensing, 17(13), 2144. https://doi.org/10.3390/rs17132144