Breaking the Cyclic Prefix Barrier: Zero-Padding Correlation Enables Centimeter-Accurate LEO Navigation via 5G NR Signals
Abstract
1. Introduction
- A system architecture for LEO NR opportunity navigation is presented in detail. We design an NR navigation receiver, and the zero-padding correlator (ZPC) is proposed to address the influence of OFDM CP and inter-carrier interference on navigation performance. For the proposed ZPC receiver, all the reference signals in NR can be utilized to provide navigation service.
- A experiment validates that ZPC eliminates the influence caused by CP and inter-carriers and significantly enhances tracking accuracy. Compared with other works, the ZPC receiver achieves higher tracking accuracy. Moreover, the relationship between the tracking accuracy and NR configurations, including bandwidth, spectrum location, and signal components combination, is rigorously investigated.
- We discuss the positioning performance of LEO NR based on an EKF, and simulation results show it can achieve centimeter-level accuracy. Additionally, the clock bias and ionospheric and tropospheric effects on positioning performance are quantitatively analyzed.
2. Related Works
2.1. Non-Cooperative and Cooperative Opportunity Navigation
2.2. OFDM-Based Opportunity Navigation
2.3. LEO Opportunity Navigation
3. Signal Model
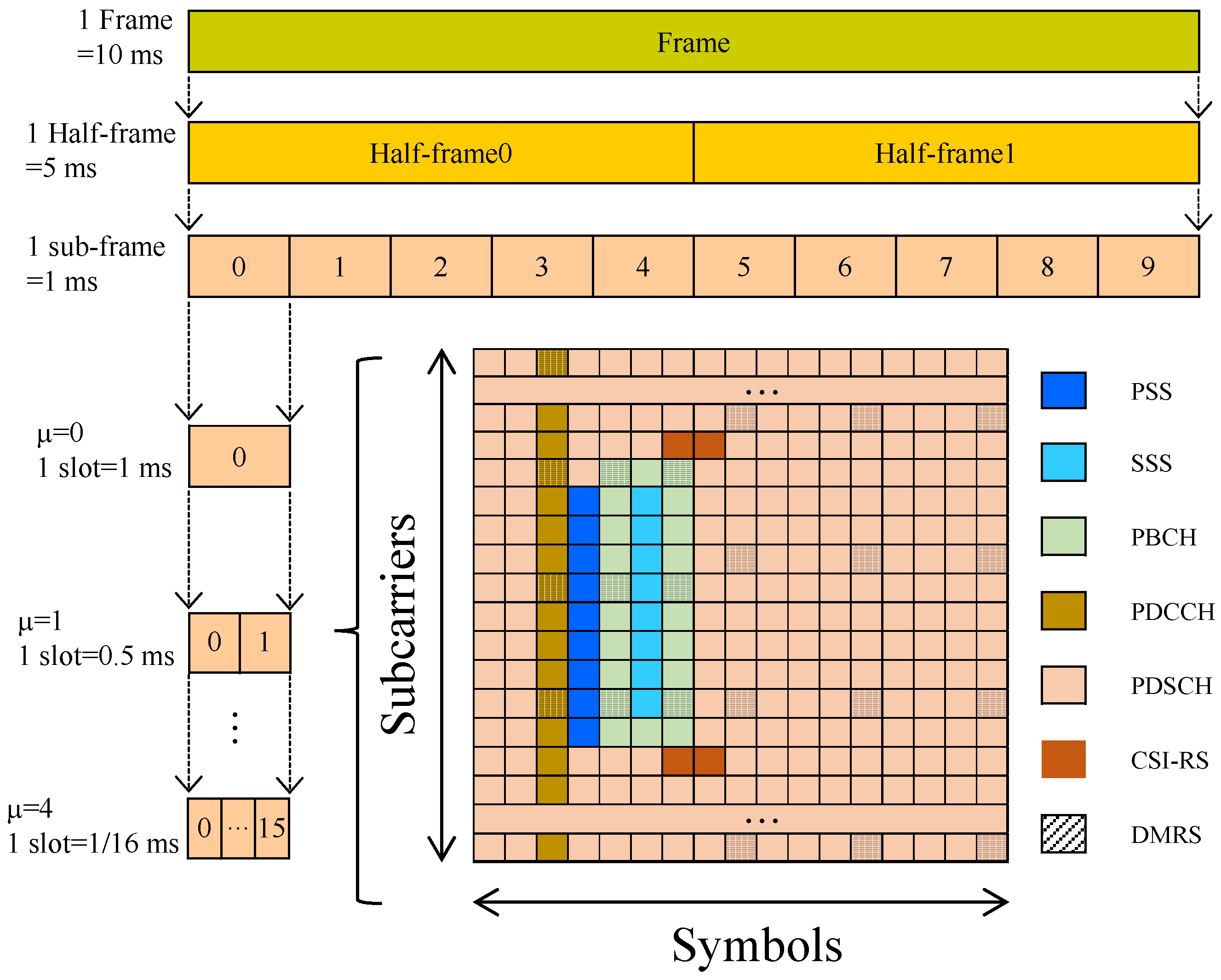
3.1. NR Signal Components
3.2. OFDM Modulation
3.3. PSD of NR Reference Signal
4. NR Navigation System
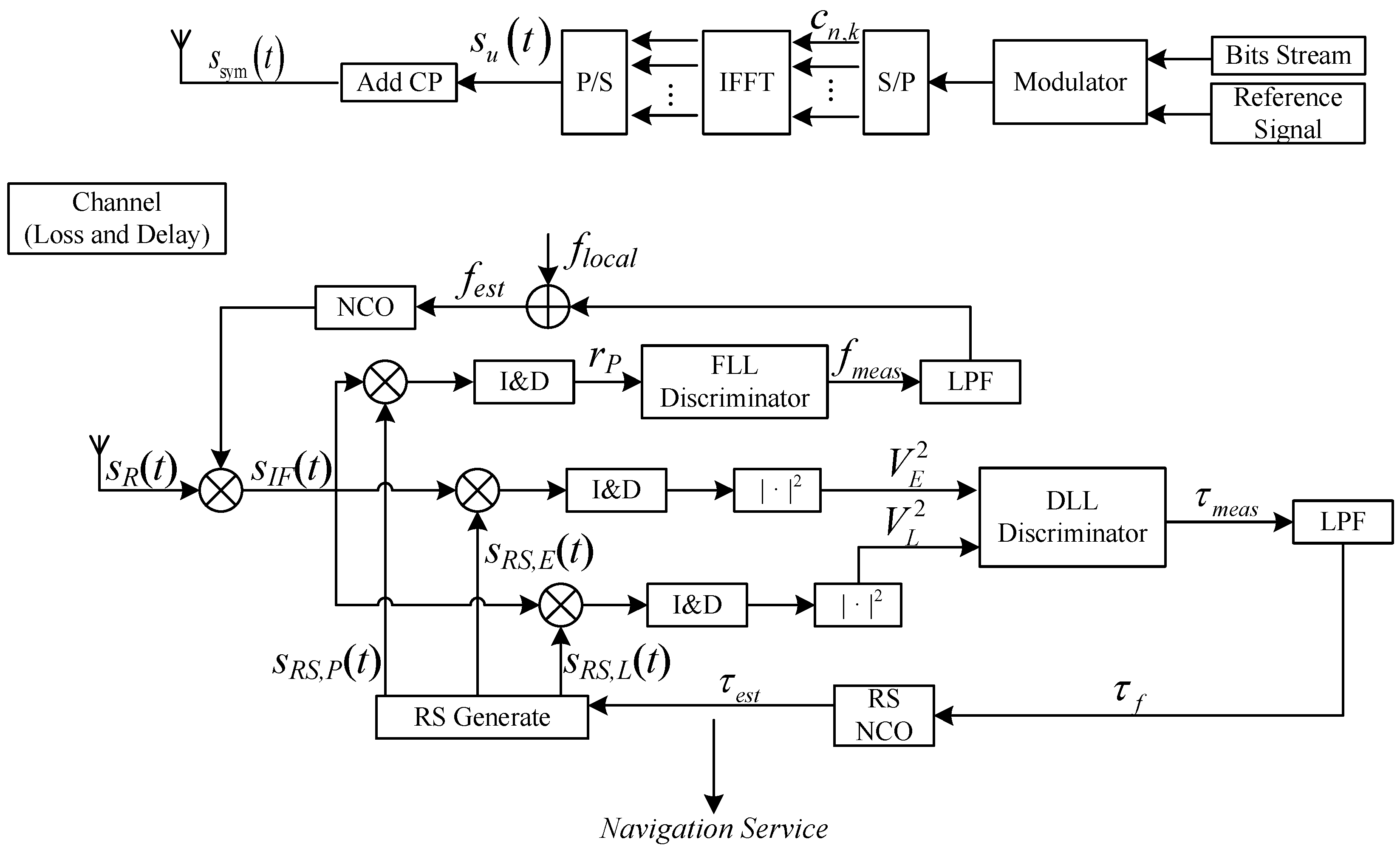
4.1. Transmitting and Reception System Block Diagram
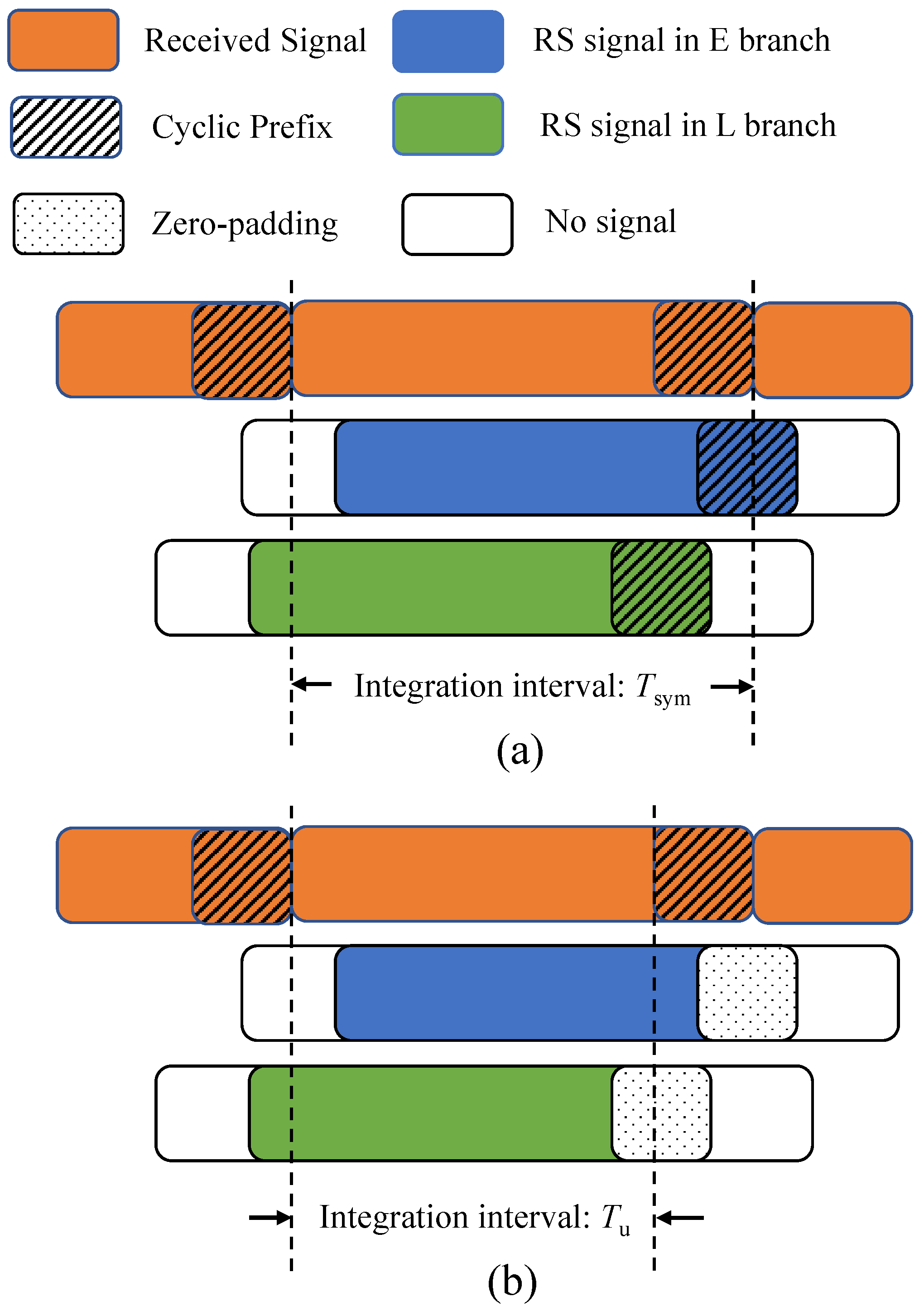
4.2. Interference-Free Correlation: ZPC
4.3. EKF for LEO Navigation
5. Improvement of ZPC Tracking Performance
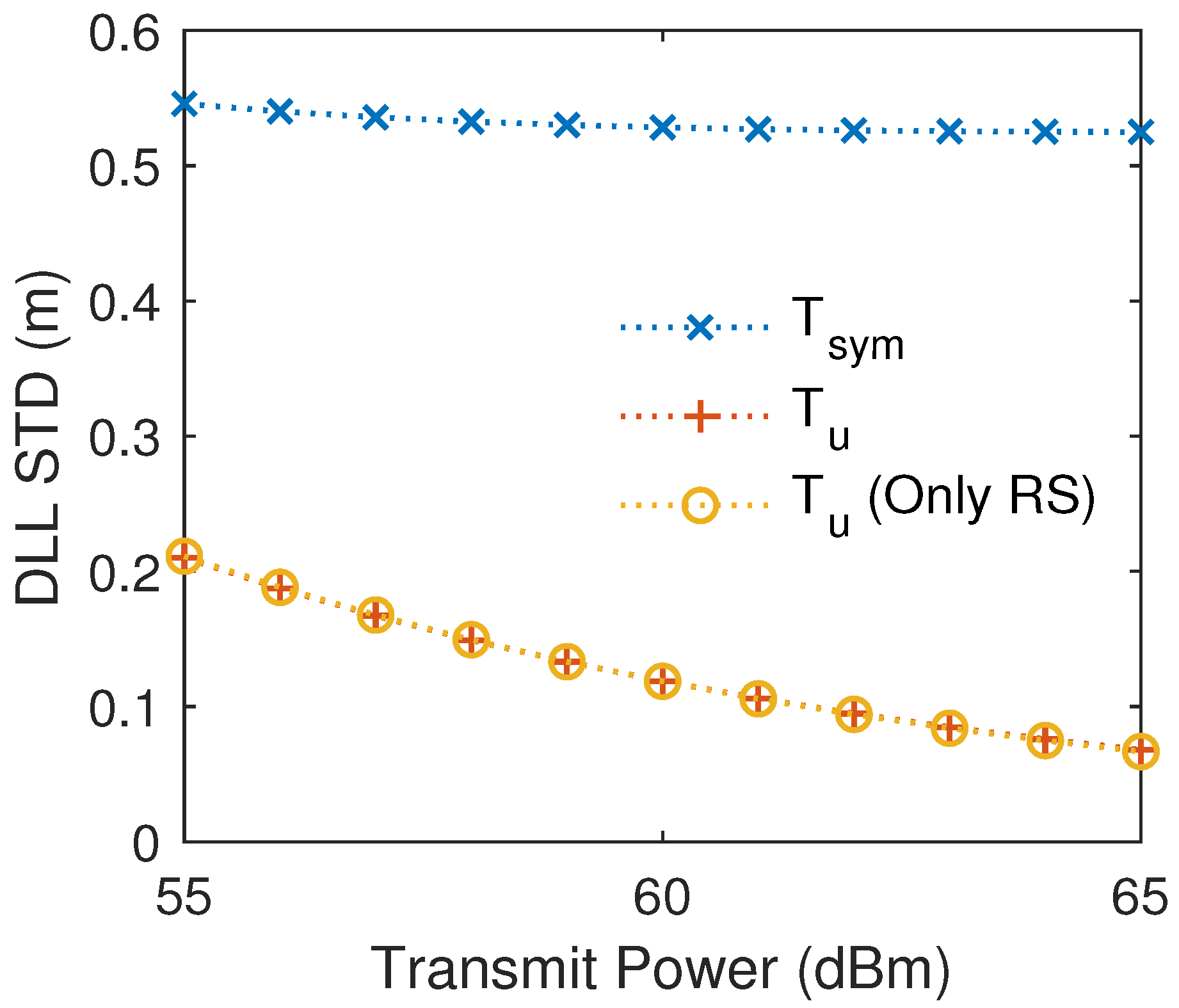
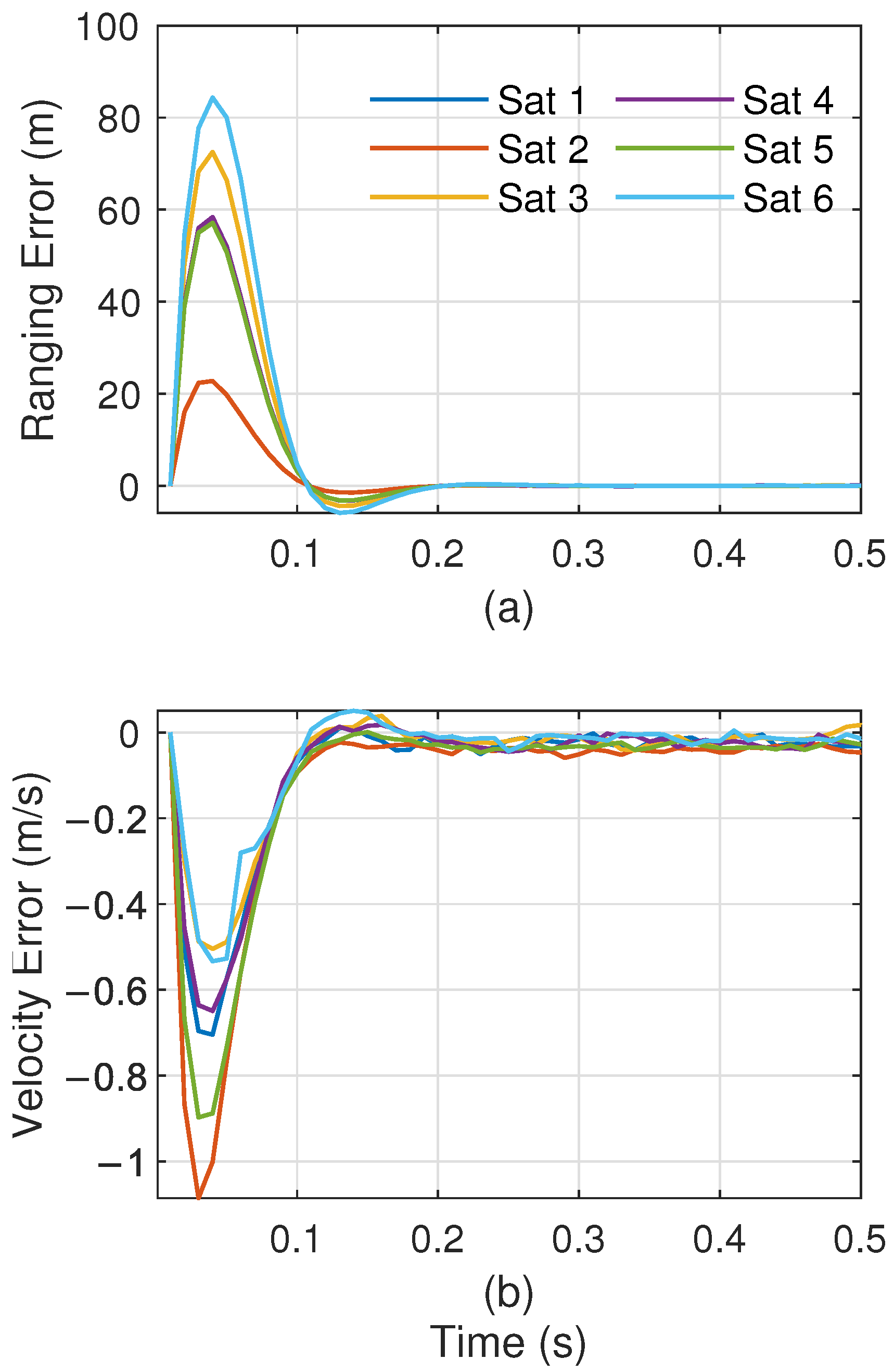
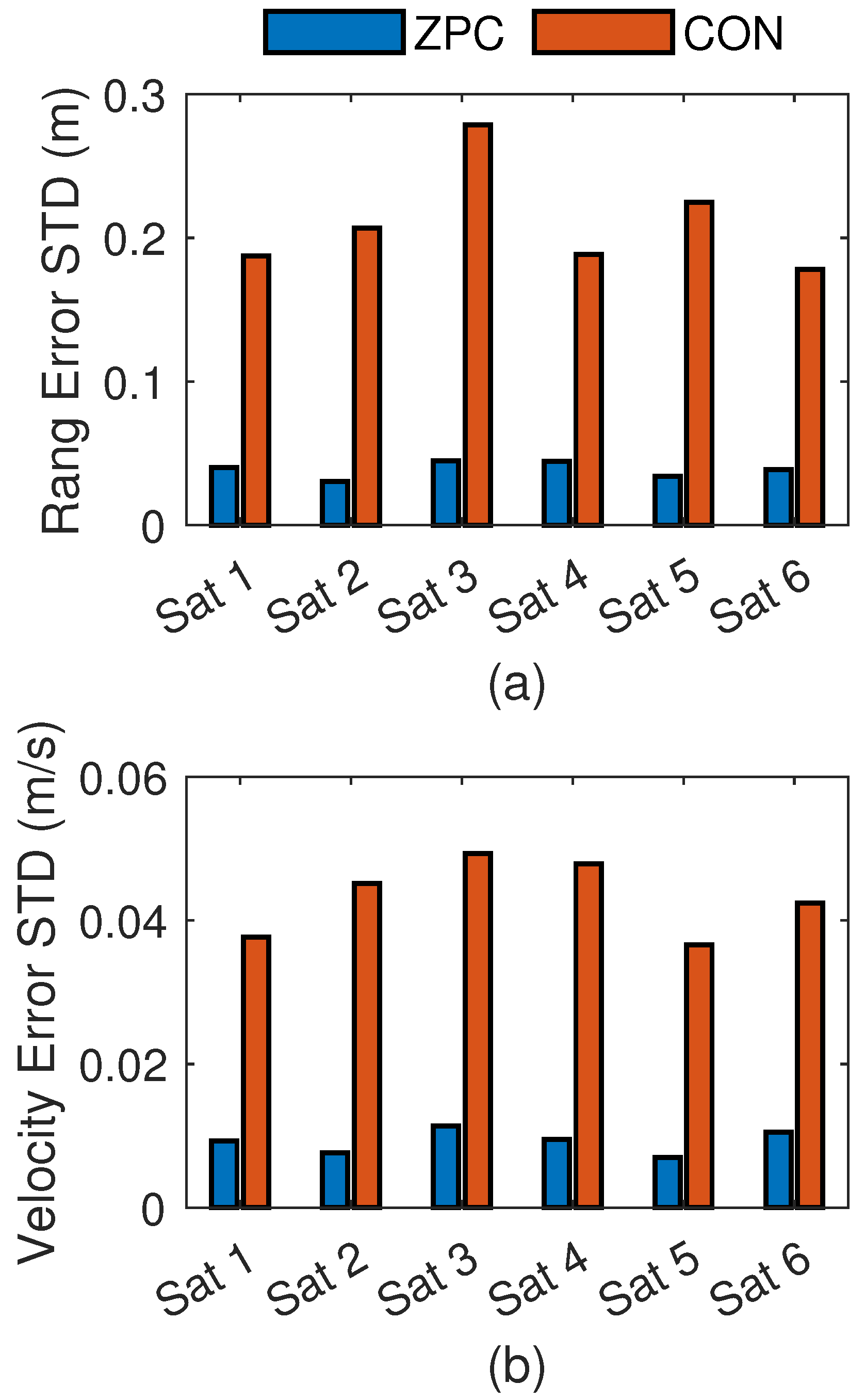
5.1. Validate the ZPC’s Interference-Free Property
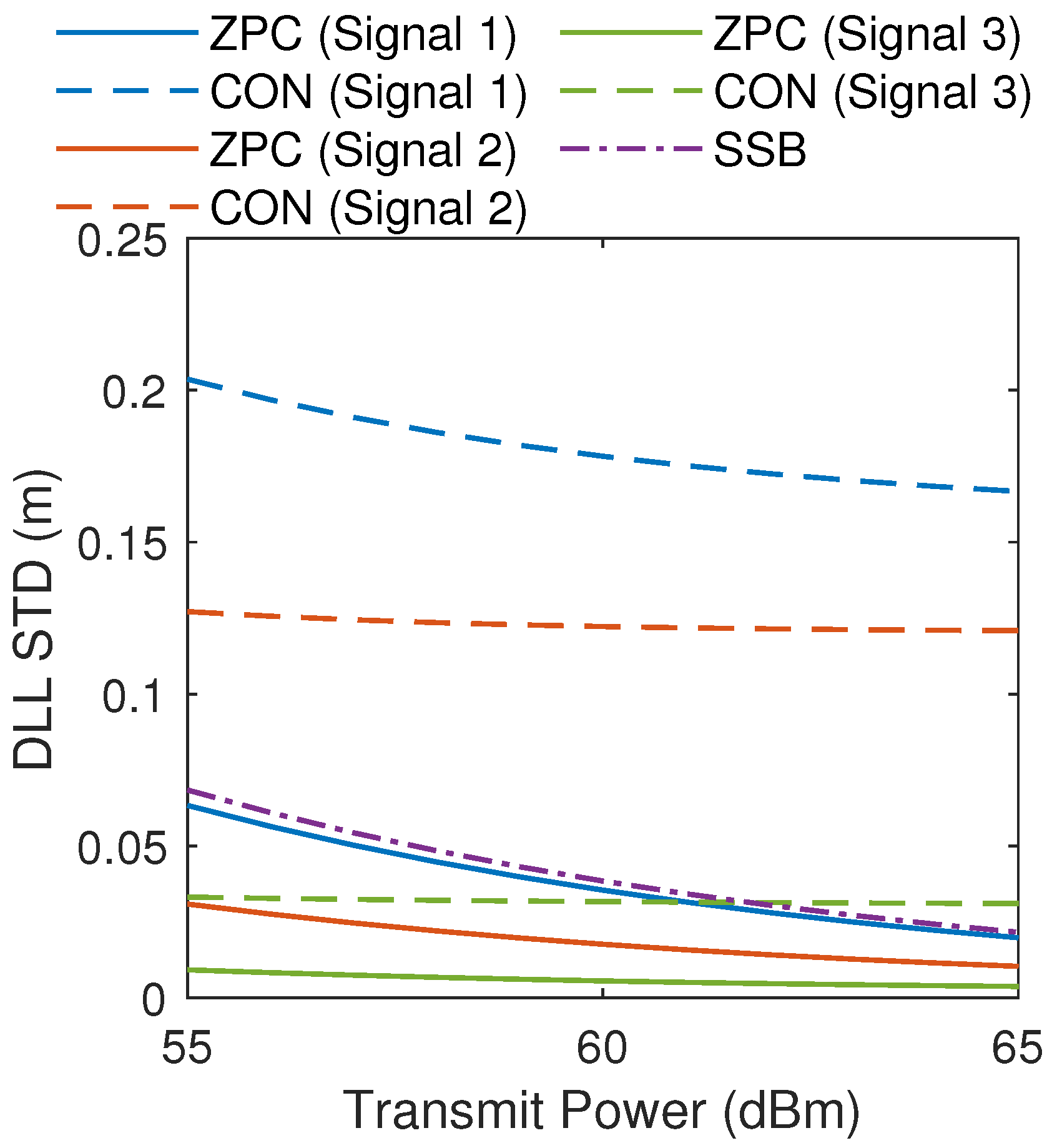
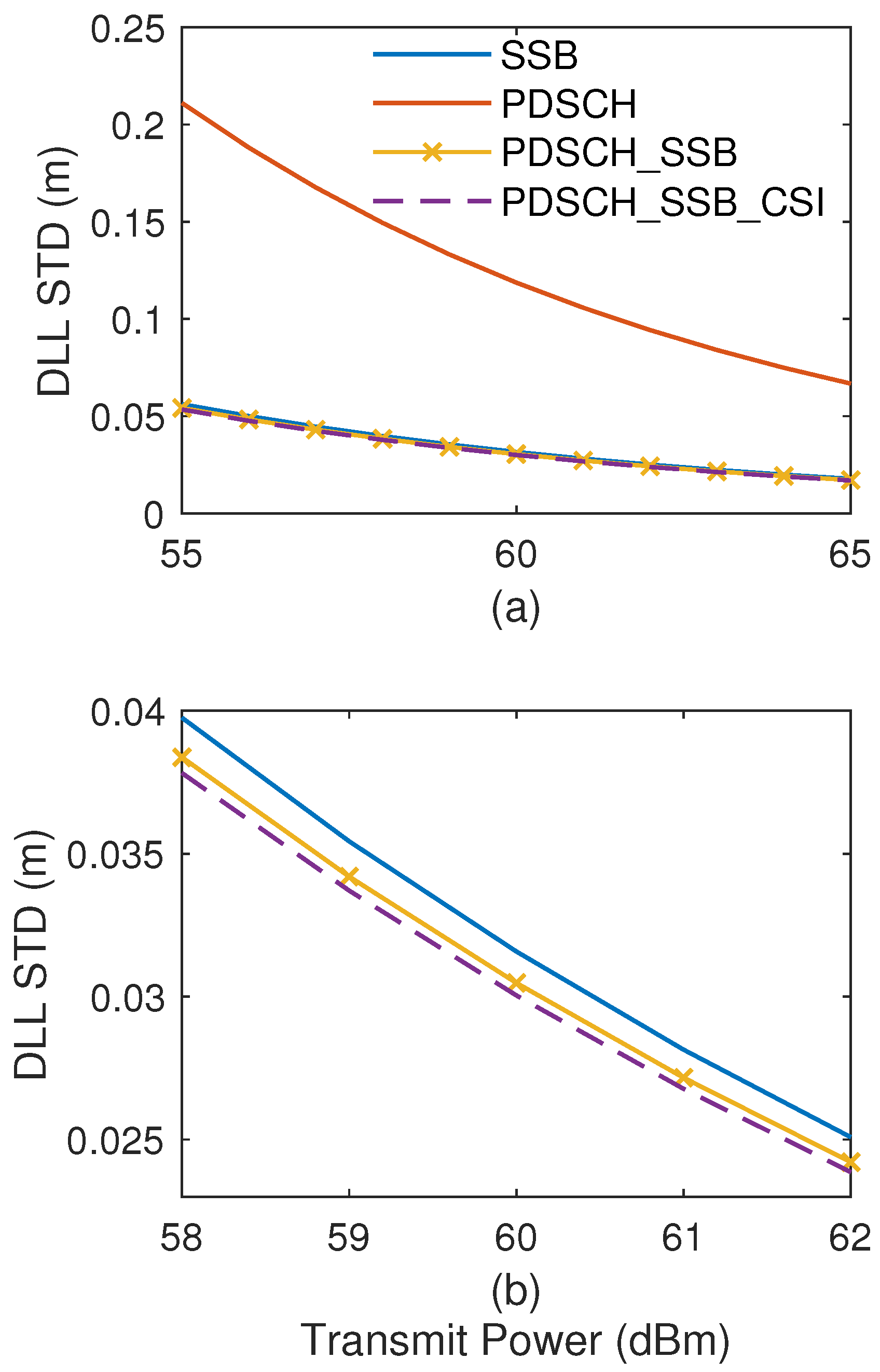
5.2. Tracking Performance Comparison of ZPC Against Other Works
- Signal 1: using default configuration as baseline (see Table 1).
- Signal 2: equivalent bandwidth to Signal 1 with PDSCH spectral center shifted from zero frequency to .
- Signal 3: PDSCH bandwidth expands (1.8 MHz → 10.62 MHz), slot number increase (5 → 9), and DMRS-Additional-Position adjustment (0 → 1). For every NR frame, the resource elements of the reference signal increase from 830 to 6850, leading to an augmentation in the reference signal’s power.
6. NR Tracking Performance Analysis for Different NR and Receiver Configuration
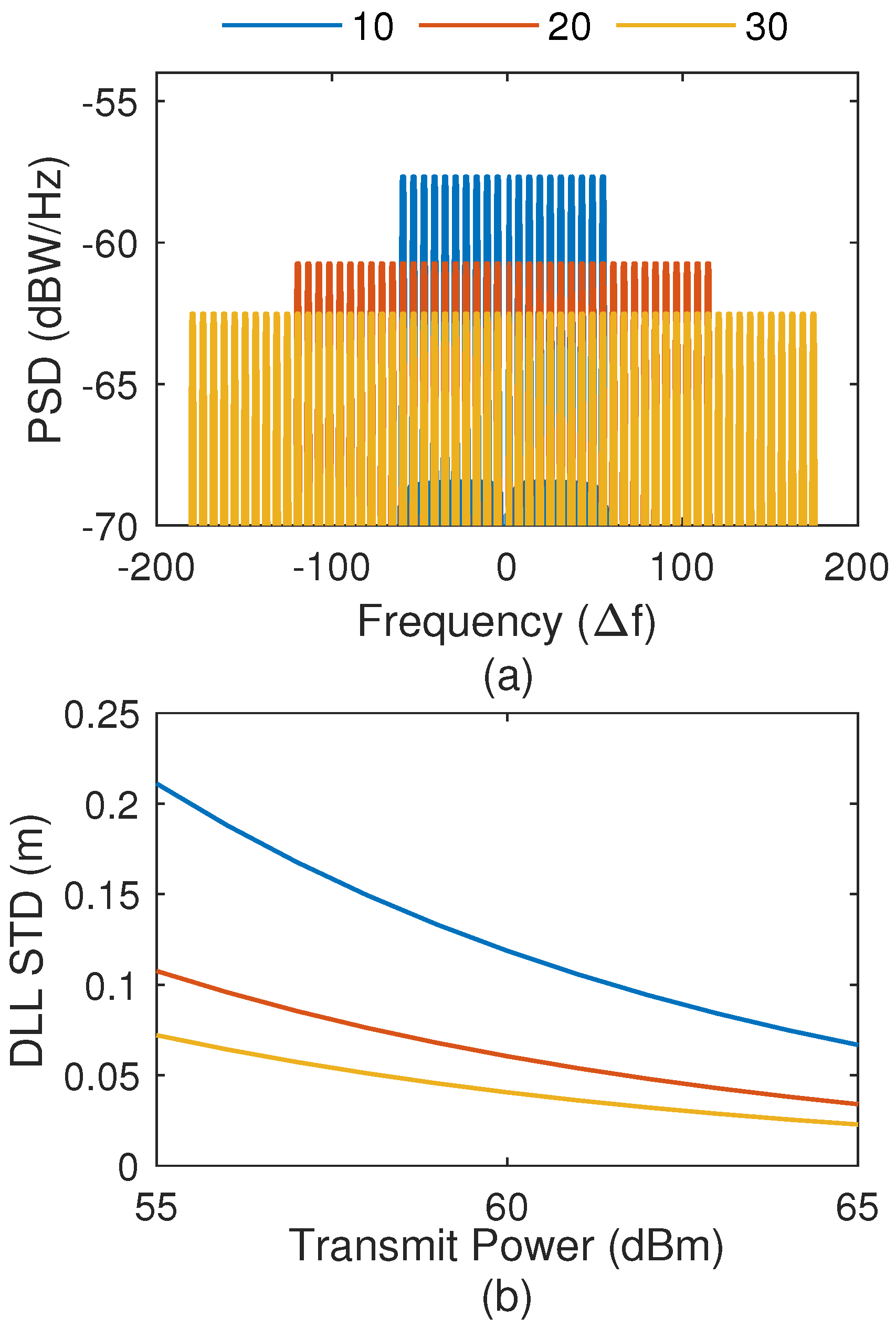
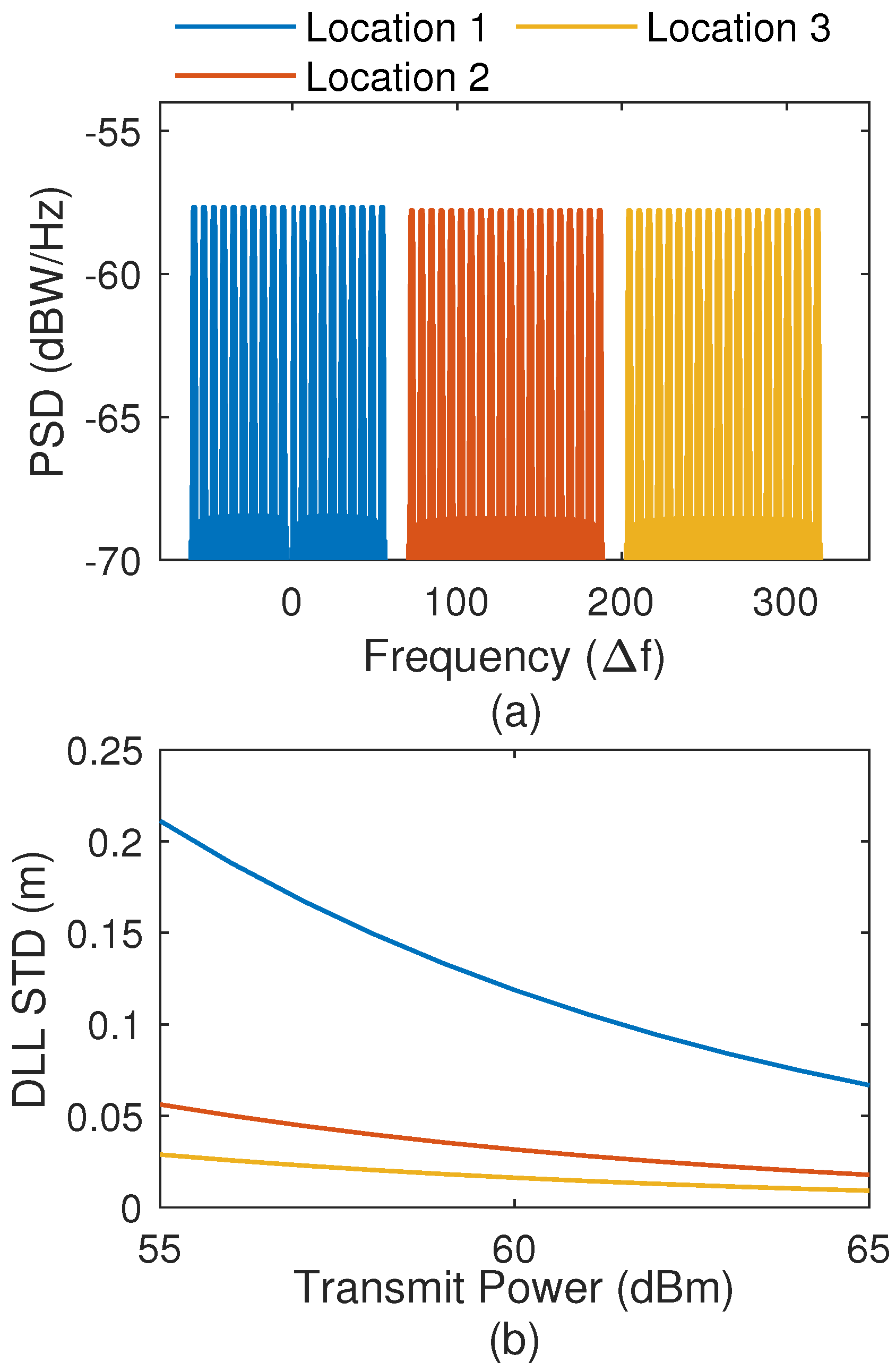
6.1. Impact of NR Signal Configuration on Tracking Accuracy
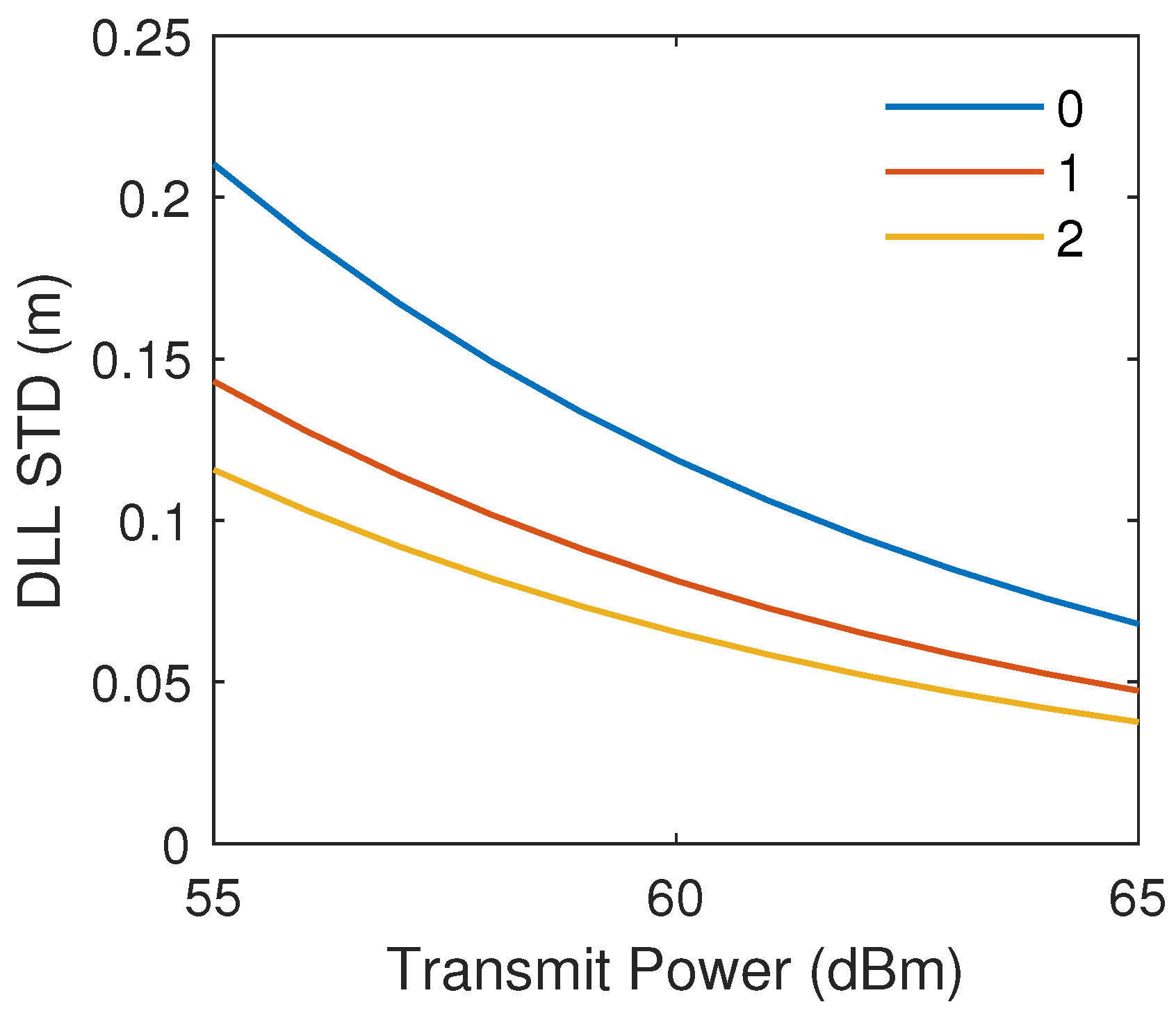
6.2. Impact of Receiver Configuration on Tracking Accuracy
7. Positioning Performance of LEO NR Signal
7.1. LEO Navigation Scenario
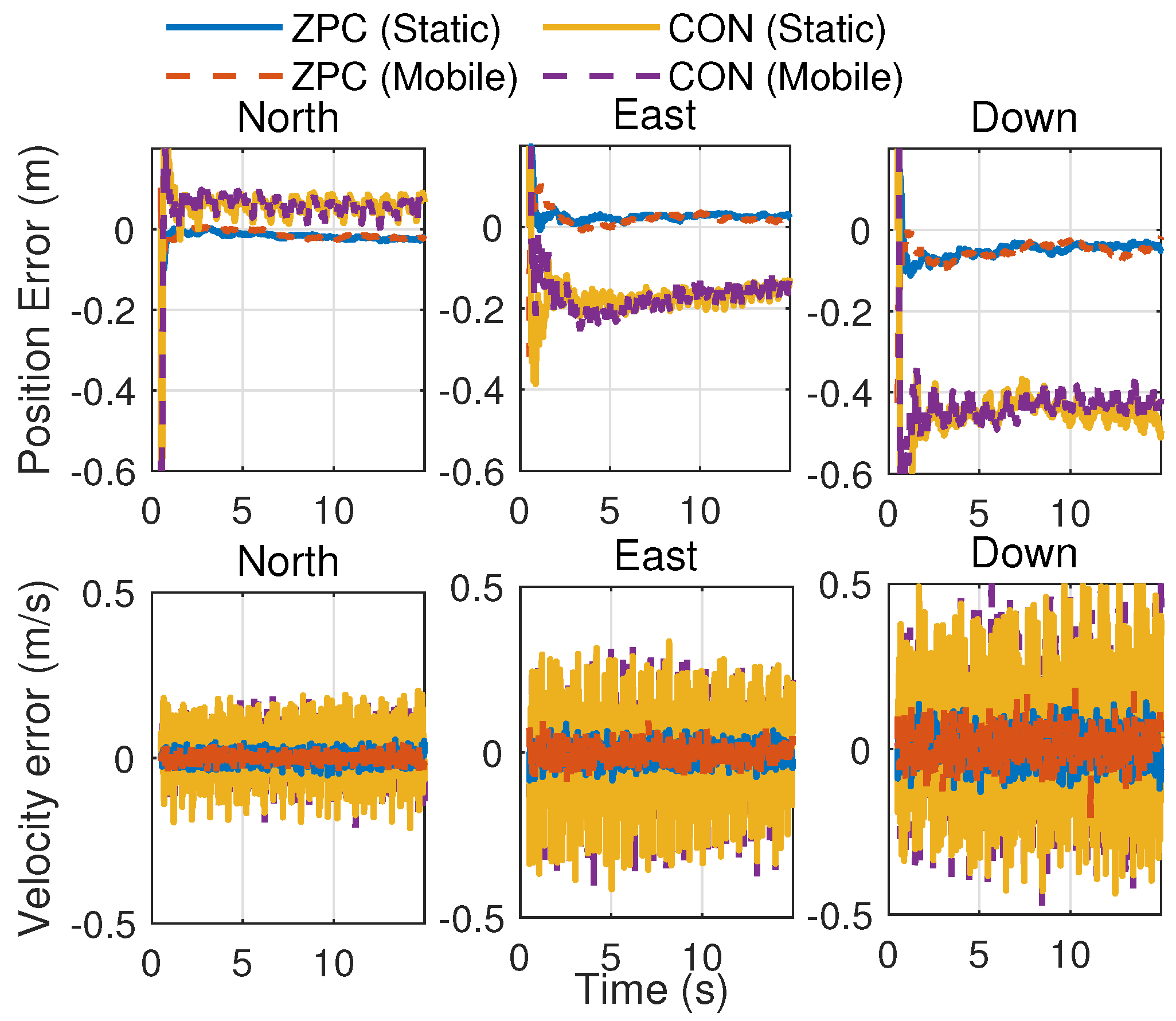
7.2. Positioning Performance
7.3. Positioning Performance with Error Components
- Receiver clock phase offset: 0.1 m;
- Receiver clock frequency drift: 0.01 m/s;
- Satellite clock phase offset STD: 0.5 m;
- Ionospheric error STD: 0.1 m;
- Tropospheric error STD: 0.2 m.
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Carrier-to-Noise Ratio of LEO NR Signal
References
- Langley, R.B.; Teunissen, P.J.G.; Montenbruck, O. Introduction to GNSS. In Springer Handbook of Global Navigation Satellite Systems; Springer International Publishing: Cham, Switzerland, 2017; pp. 3–23. [Google Scholar] [CrossRef]
- Xie, G. Principles of GPS and Receiver Design; Electronic Industry Press: Beijing, China, 2017. [Google Scholar]
- Schmidt, D.; Radke, K.; Camtepe, S.; Foo, E.; Ren, M. A Survey and Analysis of the GNSS Spoofing Threat and Countermeasures. ACM Comput. Surv. 2016, 48, 1–31. [Google Scholar] [CrossRef]
- Reid, T.G.; Neish, A.M.; Walter, T.; Enge, P.K. Broadband LEO Constellations for Navigation. NAVIGATION J. Inst. Navig. 2018, 65, 205–220. [Google Scholar] [CrossRef]
- Reid, T.G.; Neish, A.M.; Walter, T.F.; Enge, P.K. Leveraging commercial broadband leo constellations for navigating. In Proceedings of the 29th International Technical Meeting of the Satellite Division of the Institute of Navigation (Ion Gnss+ 2016), Portland, OR, USA, 12–16 September 2016; Volume 12, p. 2016. [Google Scholar]
- Chen, X.; Wei, Q.; Zhan, Y.; Kuang, L. Performance analysis of the packet-based PNT service in NGSO broadband satellite communication systems. China Commun. 2023, 20, 247–259. [Google Scholar] [CrossRef]
- Yang, Y.; Mao, Y.; Ren, X.; Jia, X.; Sun, B. Demand and key technology for a LEO constellation as augmentation of satellite navigation systems. Satell. Navig. 2024, 5, 11. [Google Scholar] [CrossRef]
- Iannucci, P.A.; Humphreys, T.E. Economical Fused LEO GNSS. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium, PLANS 2020, Portland, OR, USA, 20–23 April 2020; pp. 426–443. [Google Scholar] [CrossRef]
- Reid, T.G.R.; Chan, B.; Goel, A.; Gunning, K.; Manning, B.; Martin, J.; Neish, A.; Perkins, A.; Tarantino, P. Satellite navigation for the age of autonomy. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 342–352. [Google Scholar]
- Lei, W.; Deren, L.; Ruizhi, C.; Wenju, F.; Xin, S.; Hao, J. Low Earth Orbiter (LEO) Navigation Augmentation: Opportunities and Challenges. Chin. J. Eng. Sci. 2020, 22, 144. [Google Scholar] [CrossRef]
- Danchik, R.J. An overview of transit development. Johns Hopkins APL Tech. Dig. 1998, 19, 18–26. [Google Scholar]
- Wang, L.; Chen, R.; Li, D.; Zhang, G.; Shen, X.; Yu, B.; Wu, C.; Xie, S.; Zhang, P.; Li, M.; et al. Initial Assessment of the LEO Based Navigation Signal Augmentation System from Luojia-1A Satellite. Sensors 2018, 18, 3919. [Google Scholar] [CrossRef]
- Li, W.; Yang, Q.; Du, X.; Li, M.; Zhao, Q.; Yang, L.; Qin, Y.; Chang, C.; Wang, Y.; Qin, G. LEO augmented precise point positioning using real observations from two CENTISPACETM experimental satellites. GPS Solut. 2024, 28, 1–13. [Google Scholar] [CrossRef]
- Miller, N.S.; Koza, J.T.; Morgan, S.C.; Martin, S.M.; Neish, A.; Grayson, R.; Reid, T. SNAP: A Xona Space Systems and GPS Software-Defined Receiver. In Proceedings of the 2023 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 24–27 April 2023; pp. 897–904. [Google Scholar] [CrossRef]
- Xiao, L.; Lei, Z. Analysis of iridium-augmented GPS positioning performance. J. Eng. 2019, 2019, 7139–7143. [Google Scholar] [CrossRef]
- Prol, F.S.; Bhuiyan, M.Z.H.; Kaasalainen, S.; Lohan, E.S.; Praks, J.; Celikbilek, K.; Kuusniemi, H. Simulations of Dedicated LEO-PNT Systems for Precise Point Positioning: Methodology, Parameter Analysis, and Accuracy Evaluation. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 6499–6516. [Google Scholar] [CrossRef]
- Stock, W.; Schwarz, R.T.; Hofmann, C.A.; Knopp, A. Survey On Opportunistic PNT With Signals From LEO Communication Satellites. IEEE Commun. Surv. Tutor. 2024, 27, 77–107. [Google Scholar] [CrossRef]
- Wang, L.; Lü, Z.; Tang, X.; Zhang, K.; Wang, F. LEO-augmented GNSS based on communication navigation integrated signal. Sensors 2019, 19, 4700. [Google Scholar] [CrossRef] [PubMed]
- Gutt, G.; Lawrence, D.; Cobb, S.; O’Connor, M. Recent PNT improvements and test results based on low earth orbit satellites. In Proceedings of the Annual Precise Time and Time Interval Systems and Applications Meeting, PTTI, Reston, VA, USA, 28 January–1 February 2018; pp. 72–79. [Google Scholar] [CrossRef]
- Wei, Q.; Chen, X.; Jiang, C.; Huang, Z. Time-of-Arrival Estimation for Integrated Satellite Navigation and Communication Signals. IEEE Trans. Wirel. Commun. 2023, 22, 9867–9880. [Google Scholar] [CrossRef]
- Xue, L.; Li, X.; Wu, W.; Dong, J. Multifunctional Signal Design for Measurement, Navigation and Communication Based on BOC and BPSK Modulation. Remote Sens. 2022, 14, 1653. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, X.; Zhu, X.; Ou, G. MC-BOC: A New Interoperable Modulation and Performance Analysis for BeiDou B1 Signal; Springer: Singapore, 2018. [Google Scholar]
- Li, X.; Rao, Z.; Xue, L. A Channel Compensation Technique Based on Frequency-Hopping Binary Offset Carrier Modulated Signal. Remote Sens. 2023, 15, 1849. [Google Scholar] [CrossRef]
- Li, X.; Zeng, X.; Xue, L. Integrated Communication and Measurement System with BOC-Assisted OFDM. Drones 2022, 7, 14. [Google Scholar] [CrossRef]
- Reid, T.G.R.; Walter, T.; Enge, P.K.; Lawrence, D.; Cobb, H.S.; Gutt, G.; O’Connor, M.; Whelan, D. Navigation from Low Earth Orbit: Part 1: Concept, Current Capability, and Future Promise. In Position, Navigation, and Timing Technologies in the 21st Century; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2020; Chapter 43; pp. 1359–1379. [Google Scholar] [CrossRef]
- Kassas, Z.Z.M. Navigation from Low-Earth Orbit: Part 2: Models, Implementation, and Performance. In Position, Navigation, and Timing Technologies in the 21st Century; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2020; Chapter 43; pp. 1381–1412. [Google Scholar] [CrossRef]
- Singh, U.K.; Shankar, M.R.B.; Ottersten, B. Opportunistic localization using LEO signals. In Proceedings of the 2022 56th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 31 October–2 November 2022; pp. 894–899. [Google Scholar]
- Cho, Y.S. MIMO-OFDM Wireless Communications with MATLAB; Wiley Publishing: Hoboken, NJ, USA, 2010. [Google Scholar]
- Humphreys, T.E.; Iannucci, P.A.; Komodromos, Z.M.; Graff, A.M. Signal Structure of the Starlink Ku-Band Downlink. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 6016–6030. [Google Scholar] [CrossRef]
- Neinavaie, M.; Kassas, Z.M. Unveiling Starlink LEO Satellite OFDM-Like Signal Structure Enabling Precise Positioning. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 2486–2489. [Google Scholar] [CrossRef]
- ETSI. 5G NR Physical Channels and Modulation (3GPP TS 38.211 Version 15.2.0 Release 15). 2018. Available online: https://shop.standards.ie/en-ie/standards/etsi-ts-138-211-v15-2-0-2018-07--1399445_saig_etsi_etsi_3585366/ (accessed on 18 June 2025).
- Tataria, H.; Shafi, M.; Molisch, A.F.; Dohler, M.; Sjoland, H.; Tufvesson, F. 6G Wireless Systems: Vision, Requirements, Challenges, Insights, and Opportunities. Proc. IEEE 2021, 109, 1166–1199. [Google Scholar] [CrossRef]
- Dogra, A.; Jha, R.K.; Jain, S. A Survey on beyond 5G Network with the Advent of 6G: Architecture and Emerging Technologies. IEEE Access 2021, 9, 67512–67547. [Google Scholar] [CrossRef]
- Shahid, H.; Amatetti, C.; Campana, R.; Tong, S.; Panaitopol, D.; Vanelli-Coralli, A.; Mohamed, A.; Zhang, C.; Khalifa, E.; Medeiros, E.; et al. Emerging Advancements in 6G NTN Radio Access Technologies: An Overview. In Proceedings of the 2024 Joint European Conference on Networks and Communications and 6G Summit, EuCNC/6G Summit 2024, Antwerp, Belgium, 3–6 June 2024; pp. 593–598. [Google Scholar] [CrossRef]
- Hu, B.; Li, X.; Xue, L. A Pilot-Based Integration Method of Ranging and LS Channel Estimation for OFDM Systems. Drones 2022, 6, 400. [Google Scholar] [CrossRef]
- Abdallah, A.; Khalife, J.; Kassas, Z.M. Exploiting On-Demand 5G Downlink Signals for Opportunistic Navigation. IEEE Signal Process. Lett. 2023, 30, 389–393. [Google Scholar] [CrossRef]
- Shamaei, K.; Kassas, Z.M. Receiver Design and Time of Arrival Estimation for Opportunistic Localization with 5G Signals. IEEE Trans. Wirel. Commun. 2021, 20, 4716–4731. [Google Scholar] [CrossRef]
- Neinavaie, M.; Kassas, Z.M. Cognitive Sensing and Navigation With Unknown OFDM Signals With Application to Terrestrial 5G and Starlink LEO Satellites. IEEE J. Sel. Areas Commun. 2024, 42, 146–160. [Google Scholar] [CrossRef]
- Kassas, Z.M.; Kozhaya, S.; Kanj, H.; Saroufim, J.; Hayek, S.W.; Neinavaie, M.; Khairallah, N.; Khalife, J. Navigation with Multi-Constellation LEO Satellite Signals of Opportunity: Starlink, OneWeb, Orbcomm, and Iridium. In Proceedings of the 2023 IEEE/ION Position, Location and Navigation Symposium, PLANS 2023, Monterey, CA, USA, 24–27 April 2023; pp. 338–343. [Google Scholar] [CrossRef]
- Neinavaie, M.; Khalife, J.; Kassas, Z.M. Acquisition, Doppler Tracking, and Positioning with Starlink LEO Satellites: First Results. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2606–2610. [Google Scholar] [CrossRef]
- Khalife, J.; Neinavaie, M.; Kassas, Z.Z. The First Carrier Phase Tracking and Positioning Results With Starlink LEO Satellite Signals. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 1487–1491. [Google Scholar] [CrossRef]
- Saroufim, J.; Hayek, S.W.; Kassas, Z.M. Simultaneous LEO satellite tracking and differential LEO-aided IMU navigation. In Proceedings of the 2023 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 24–27 April 2023; pp. 179–188. [Google Scholar]
- McLemore, B.; Psiaki, M.L. Navigation using Doppler shift from LEO constellations and INS data. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 4295–4314. [Google Scholar] [CrossRef]
- Yang, C.; Zang, B.; Gu, B.; Zhang, L.; Dai, C.; Long, L.; Zhang, Z.; Ding, L.; Ji, H. Doppler positioning of dynamic targets with unknown LEO satellite signals. Electronics 2023, 12, 2392. [Google Scholar] [CrossRef]
- Kassas, Z.M. Navigation with cellular signals of opportunity. In Position, Navigation, and Timing Technologies in the 21st Century; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar]
- Kassas, Z.M.; Khairallah, N.; Kozhaya, S. Ad Astra: Simultaneous Tracking and Navigation With Megaconstellation LEO Satellites. IEEE Aerosp. Electron. Syst. Mag. 2024, 39, 46–71. [Google Scholar] [CrossRef]
- Neinavaie, M.; Khalife, J.; Kassas, Z.M. Cognitive Opportunistic Navigation in Private Networks with 5G Signals and beyond. IEEE J. Sel. Top. Signal Process. 2022, 16, 129–143. [Google Scholar] [CrossRef]
- Jardak, N.; Jault, Q. The potential of LEO satellite-based opportunistic navigation for high dynamic applications. Sensors 2022, 22, 2541. [Google Scholar] [CrossRef] [PubMed]
- Khairallah, N.; Kassas, Z.M. Ephemeris Tracking and Error Propagation Analysis of LEO Satellites With Application to Opportunistic Navigation. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 1242–1259. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.; Zhao, S.; He, J.; Shen, Y.; Jiang, X. A Survey on Authentication in Satellite Internet. J. Netw. Netw. Appl. 2022, 2, 183–194. [Google Scholar] [CrossRef]
- Iannucci, P.A.; Humphreys, T.E. Fused Low-Earth-Orbit GNSS. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 3730–3749. [Google Scholar] [CrossRef]
- Shamaei, K.; Kassas, Z.M. A Joint TOA and DOA Acquisition and Tracking Approach for Positioning with LTE Signals. IEEE Trans. Signal Process. 2021, 69, 2689–2705. [Google Scholar] [CrossRef]
- Yang, C.; Arizabaleta-Diez, M.; Weitkemper, P.; Pany, T. An Experimental Analysis of Cyclic and Reference Signals of 4G LTE for TOA Estimation and Positioning in Mobile Fading Environments. IEEE Aerosp. Electron. Syst. Mag. 2022, 37, 16–41. [Google Scholar] [CrossRef]
- Yang, C.; Pany, T.; Weitkemper, P. Effect of Antenna Ports on TOA Estimation with 4G LTE Signals in Urban Mobile Environments. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of the Institute of Navigation, ION GNSS+ 2020, Online, 22–25 September 2020; pp. 2166–2181. [Google Scholar] [CrossRef]
- Wang, P.; Morton, Y.J. Impact Analysis of Intercell Interference in Cellular Networks for Navigation Applications. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 685–694. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, L.; Zhou, X.; Shen, N.; Chen, R. Multipath tracking with LTE signals for accurate TOA estimation in the application of indoor positioning. Geo-Spat. Inf. Sci. 2023, 26, 31–43. [Google Scholar] [CrossRef]
- Wang, P.; Morton, Y.J. Multipath Estimating Delay Lock Loop for LTE Signal TOA Estimation in Indoor and Urban Environments. IEEE Trans. Wirel. Commun. 2020, 19, 5518–5530. [Google Scholar] [CrossRef]
- Abdallah, A.; Kassas, Z. Multipath Mitigation via Synthetic Aperture Beamforming for Indoor and Deep Urban Navigation. IEEE Trans. Veh. Technol. 2021, 70, 8838–8853. [Google Scholar] [CrossRef]
- Whiton, R.; Chen, J.; Johansson, T.; Tufvesson, F. Urban Navigation with LTE using a Large Antenna Array and Machine Learning. In Proceedings of the IEEE Vehicular Technology Conference, Helsinki, Finland, 19–22 June 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Khalife, J.; Kassas, Z.M. Differential Framework for Submeter-Accurate Vehicular Navigation With Cellular Signals. IEEE Trans. Intell. Veh. 2023, 8, 732–744. [Google Scholar] [CrossRef]
- Abdallah, A.A.; Kassas, Z.M. UAV navigation with 5G carrier phase measurements. In Proceedings of the 34th International Technical Meeting of the Satellite Division of the Institute of Navigation, ION GNSS+ 2021, Online, 20–24 September 2021; pp. 3294–3306. [Google Scholar] [CrossRef]
- Xhafa, A.; Del Peral-Rosado, J.A.; López-Salcedo, J.A.; Seco-Granados, G. Evaluation of 5g positioning performance based on utdoa, aoa and base-station selective exclusion. Sensors 2022, 22, 101. [Google Scholar] [CrossRef]
- Koivisto, M.; Talvitie, J.; Rastorgueva-Foi, E.; Lu, Y.; Valkama, M. Channel Parameter Estimation and TX Positioning With Multi-Beam Fusion in 5G mmWave Networks. IEEE Trans. Wirel. Commun. 2022, 21, 3192–3207. [Google Scholar] [CrossRef]
- Lapin, I.; Seco-Granados, G.; Renaudin, O.; Zanier, F.; Ries, L. Joint Delay and Phase Discriminator Based on ESPRIT for 5G NR Positioning. IEEE Access 2021, 9, 126550–126563. [Google Scholar] [CrossRef]
- Wen, F.; Kulmer, J.; Witrisal, K.; Wymeersch, H. 5G Positioning and Mapping with Diffuse Multipath. IEEE Trans. Wirel. Commun. 2021, 20, 1164–1174. [Google Scholar] [CrossRef]
- Gante, J.; Sousa, L.; Falcao, G. Dethroning GPS: Low-Power Accurate 5G Positioning Systems Using Machine Learning. IEEE J. Emerg. Sel. Top. Circuits Syst. 2020, 10, 240–252. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, L.; Zhou, X.; Jiao, Z.; Guo, G.; Chen, R. Machine Learning for Time-of-Arrival Estimation With 5G Signals in Indoor Positioning. IEEE Internet Things J. 2023, 10, 9782–9795. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, L.; Jiao, Z.; Lu, X.; Ruan, Y.; Chen, R. MLLoc: Machine Learning Location System Based on RAIM in Mobile Networks. IEEE Sens. J. 2024, 24, 16953–16960. [Google Scholar] [CrossRef]
- Khalife, J.; Neinavaie, M.; Kassas, Z.M. Navigation with differential carrier phase measurements from megaconstellation LEO satellites. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 1393–1404. [Google Scholar]
- Kozhaya, S.; Kassas, Z.M. On the Fundamental Tracking Performance and Design Considerations of Radio Navigation. IEEE J. Sel. Areas Commun. 2024, 42, 2395–2409. [Google Scholar] [CrossRef]
- Zhao, C.; Qin, H.; Li, Z. Doppler Measurements from Multiconstellations in Opportunistic Navigation. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Cassel, R.S.; Scherer, D.R.; Wilburne, D.R.; Hirschauer, J.E.; Burke, J.H. Impact of improved oscillator stability on LEO-based satellite navigation. In Proceedings of the 2022 International Technical Meeting of the Institute of Navigation, Long Beach, CA, USA, 25–27 January 2022; pp. 893–905. [Google Scholar]
- Zhao, C.; Qin, H.; Wu, N.; Wang, D. Analysis of Baseline Impact on Differential Doppler Positioning and Performance Improvement Method for LEO Opportunistic Navigation. IEEE Trans. Instrum. Meas. 2023, 72, 1–10. [Google Scholar] [CrossRef]
- Yao, Z.; Lu, M. Next-Generation GNSS Signal Design: Theories, Principles and Technologies; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Xie, G. Principles of GNSS: GPS, GLONASS, and Galileo; Publishing House of Electronics Industry: Beijing, China, 2019; p. 443. [Google Scholar]
- Betz, J.W.; Kolodziejski, K.R. Generalized theory of code tracking with an early-late discriminator part II: Noncoherent Processing and Numerical Results. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1538. [Google Scholar] [CrossRef]
- Celestrak. Starlink TLE Data. Available online: https://celestrak.org/NORAD/elements/gp.php?GROUP=starlink (accessed on 5 November 2024).
- Groves, P. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems, 2nd ed.; Artech: London, UK, 2013. [Google Scholar]
- Ippolito, L.J., Jr. Satellite Communications Systems Engineering: Atmospheric Effects, Satellite Link Design and System Performance; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- 3rd Generation Partnership Project; Technical Specification Group Radio Access Network; Study on Narrow-Band Internet of Things (NB-IoT)/enhanced Machine Type Communication (eMTC) support for Non-Terrestrial Networks (NTN) (Release 17). 3GPP Technical Report TR 36.763 V0.2.0, 3rd Generation Partnership Project (3GPP). 2021. Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3747 (accessed on 5 November 2024).





| Parameter | Value | |
|---|---|---|
| NR Basic | FFT Length | 1024 |
| Subcarrier Spacing (kHz) | 15 | |
| Sampling Rate (MHz) | 15.36 | |
| Period (ms) | 10 | |
| Slot Number Per Period | 5 | |
| Symbol Length Per Slot | 8 | |
| Used BandWidth (MHz) | 1.8 | |
| Resource Block Number | 10 | |
| Subcarrier Number | 240 | |
| PDSCH | Modulation | QPSK |
| DMRS Mapping | Type A | |
| DMRS-TypeA-Position | 2 | |
| DMRSLength | 1 | |
| DMRS-Additional-Position | 0 | |
| DMRS-Configuration-Type | 2 | |
| DMRS proportion | 3.50% | |
| Delay-locked loop (DLL) | (Hz) | 20 |
| Damping Coefficient | 0.707 | |
| Integration Time (ms) | 10 | |
| Early–Late Spacing (Sampling Time) | 2 | |
| Transmit Power (W) | 10 | |
| Proportion of Reference Signal in NR signal | 19.44% | |
| Receiver Front-end Bandwidth (MHz) | 15.36 | |
| Sampling Rate (MHz) | 15.36 |
| (ms) | (Hz) | DLL STD (m) | DLL STD Improvement |
|---|---|---|---|
| 5 | 20 | 0.122 | −2.52% |
| 10 | 20 | 0.119 | 0% (baseline) |
| 15 | 20 | 0.116 | 2.52% |
| 10 | 5 | 0.062 | 47.9% |
| 10 | 1 | 0.028 | 76.5% |
| PBCH | CSI | PDSCH DMRS | PDSCH Data | Sum | |
|---|---|---|---|---|---|
| Resource Elements | 830 | 80 | 200 | 4600 | 5710 |
| Resource Proportion (Power Proportion) | 14.54% | 1.40% | 3.50% | 80.56% | 100.00% |
| Parameter | Sat 1 | Sat 2 | Sat 3 | Sat 4 | Sat 5 | Sat 6 |
|---|---|---|---|---|---|---|
| Semi-major Axis a (km) | 7136 | 6980 | 6970 | 7050 | 6820 | 7130 |
| Eccentricity e | 0.0001568 | 0.0001459 | 0.0001603 | 0.0001432 | 0.0001464 | 0.0001406 |
| Inclination i (°) | 53.0531 | 53.2146 | 53.2157 | 43.0039 | 43.0019 | 53.1584 |
| RAAN (°) | 189.0089 | 191.0164 | 305.9367 | 291.2627 | 294.6071 | 192.7046 |
| Argument of Perigee (°) | 63.1495 | 78.6725 | 89.8188 | 270.5086 | 262.0388 | 61.5981 |
| Mean Anomaly M (°) | 82.5489 | 166.1697 | 347.1216 | 212.3624 | 208.9401 | 164.3645 |
| Altitude 1 (km) | 765 | 609 | 599 | 679 | 449 | 759 |
| Mean | Std | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| North | East | Down | 3D | North | East | Down | 3D | ||
| Position error (m) | ZPC (Static) | −0.0184 | 0.0251 | −0.0454 | 0.0561 | 0.0055 | 0.0050 | 0.0096 | 0.0059 |
| ZPC (Mobile) | −0.0152 | 0.0184 | −0.0507 | 0.0585 | 0.0087 | 0.0097 | 0.0139 | 0.0091 | |
| CON (Static) | 0.0585 | −0.1733 | −0.4438 | 0.4807 | 0.0184 | 0.0172 | 0.0249 | 0.0242 | |
| CON (Mobile) | 0.0570 | −0.1765 | −0.4327 | 0.4717 | 0.0199 | 0.0270 | 0.0231 | 0.0288 | |
| Velocity error (m/s) | ZPC (Static) | 0.0005 | −0.0039 | 0.0069 | 0.0487 | 0.0169 | 0.0267 | 0.0459 | 0.0281 |
| ZPC (Mobile) | −0.0012 | −0.0009 | 0.0115 | 0.0484 | 0.0160 | 0.0265 | 0.0465 | 0.0301 | |
| CON (Static) | 0.0189 | −0.0126 | 0.0351 | 0.2157 | 0.0760 | 0.1361 | 0.1876 | 0.1212 | |
| CON (Mobile) | 0.0171 | −0.0099 | 0.0414 | 0.2200 | 0.0762 | −0.1383 | 0.1918 | 0.1240 | |
| Mean | Std | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| North | East | Down | 3D | North | East | Down | 3D | ||
| Position error (m) | Noise | −0.0184 | 0.0252 | −0.0454 | 0.0561 | 0.0055 | 0.0050 | 0.0096 | 0.0059 |
| Noise and clock | −0.0184 | 0.0252 | −0.0454 | 0.0561 | 0.0055 | 0.0050 | 0.0096 | 0.0059 | |
| Noise, clock, and ION 1 | −1.2169 | −0.1098 | 1.8210 | 2.1951 | 0.0135 | 0.0928 | 0.0537 | 0.0445 | |
| Noise, clock, ION, and TRO 2 | −1.7307 | 1.7201 | 5.1643 | 5.7143 | 0.0540 | 0.1142 | 0.1938 | 0.1591 | |
| Velocity error (m/s) | Noise | 0.0005 | −0.0039 | 0.0069 | 0.0487 | 0.0169 | 0.0267 | 0.0459 | 0.0281 |
| Noise and clock | 0.0005 | −0.0039 | 0.0069 | 0.0487 | 0.0169 | 0.0267 | 0.0459 | 0.0281 | |
| Noise, clock, and ION | −0.0184 | −0.0055 | 0.0502 | 0.0696 | 0.0170 | 0.0268 | 0.0460 | 0.0341 | |
| Noise, clock, ION, and TRO | −0.0199 | −0.0279 | 0.0857 | 0.1024 | 0.0172 | 0.0274 | 0.0461 | 0.0347 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, L.; Yang, Y.; Ma, J.; Wu, T.; Qian, X.; Li, H. Breaking the Cyclic Prefix Barrier: Zero-Padding Correlation Enables Centimeter-Accurate LEO Navigation via 5G NR Signals. Remote Sens. 2025, 17, 2116. https://doi.org/10.3390/rs17132116
Deng L, Yang Y, Ma J, Wu T, Qian X, Li H. Breaking the Cyclic Prefix Barrier: Zero-Padding Correlation Enables Centimeter-Accurate LEO Navigation via 5G NR Signals. Remote Sensing. 2025; 17(13):2116. https://doi.org/10.3390/rs17132116
Chicago/Turabian StyleDeng, Lingyu, Yikang Yang, Jiangang Ma, Tao Wu, Xingyou Qian, and Hengnian Li. 2025. "Breaking the Cyclic Prefix Barrier: Zero-Padding Correlation Enables Centimeter-Accurate LEO Navigation via 5G NR Signals" Remote Sensing 17, no. 13: 2116. https://doi.org/10.3390/rs17132116
APA StyleDeng, L., Yang, Y., Ma, J., Wu, T., Qian, X., & Li, H. (2025). Breaking the Cyclic Prefix Barrier: Zero-Padding Correlation Enables Centimeter-Accurate LEO Navigation via 5G NR Signals. Remote Sensing, 17(13), 2116. https://doi.org/10.3390/rs17132116




