Spatial Variation in Coral Diversity and Reef Complexity in the Galápagos: Insights from Underwater Photogrammetry and New Data Extraction Methods
Abstract
1. Introduction
- 1.
- 3D point-annotation for benthic classification: We used an image pair for each annotation point including the best camera view and a synthetic view providing the annotator 3D context (See Section 2.5).
- 2.
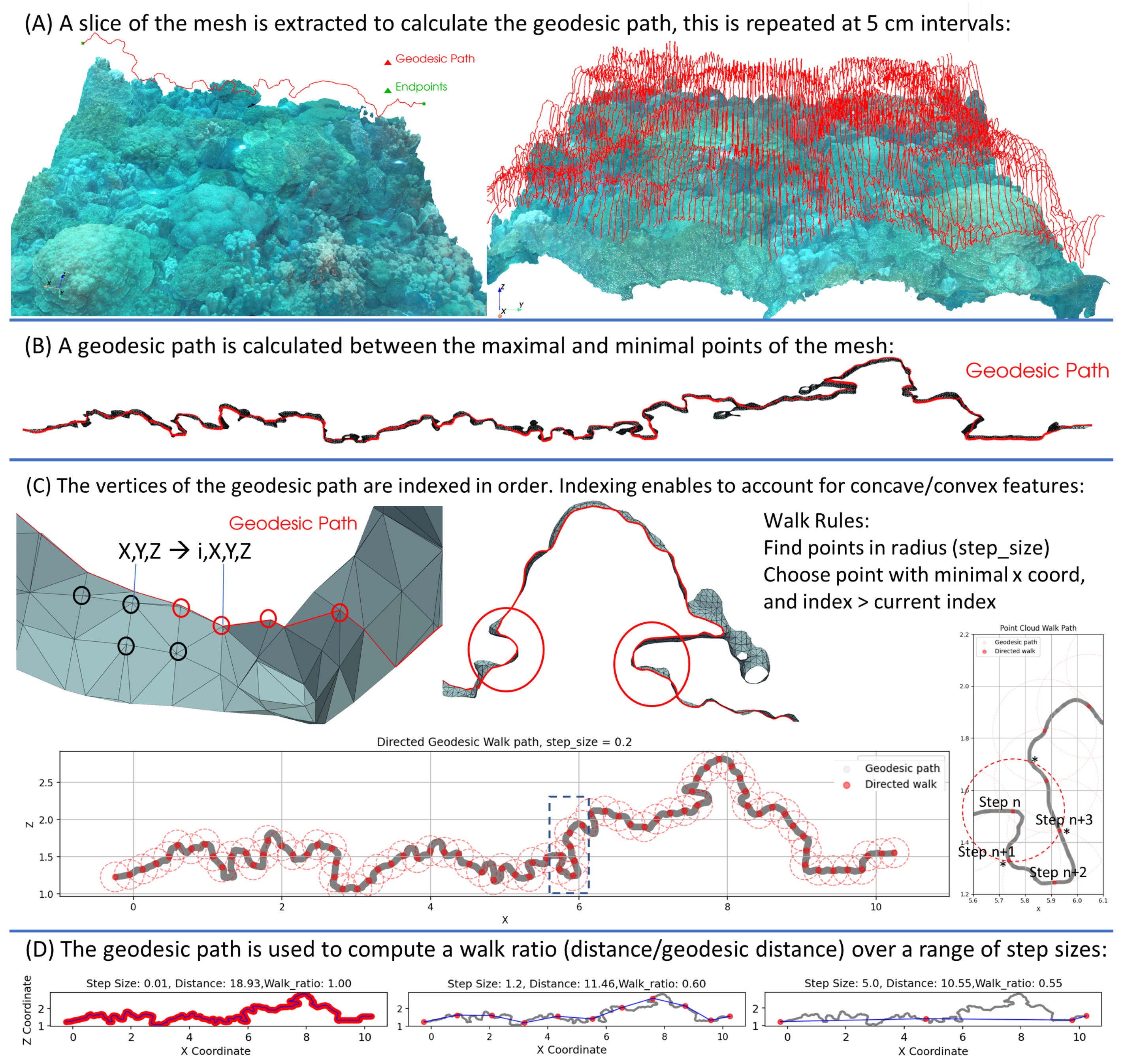
- Fractal dimension calculation using directed geodesic walks: These follow a path along a slice of the 3D model without ignoring overhangs thus accounting for full 3D structure (See Section 2.8.2).
2. Materials and Methods
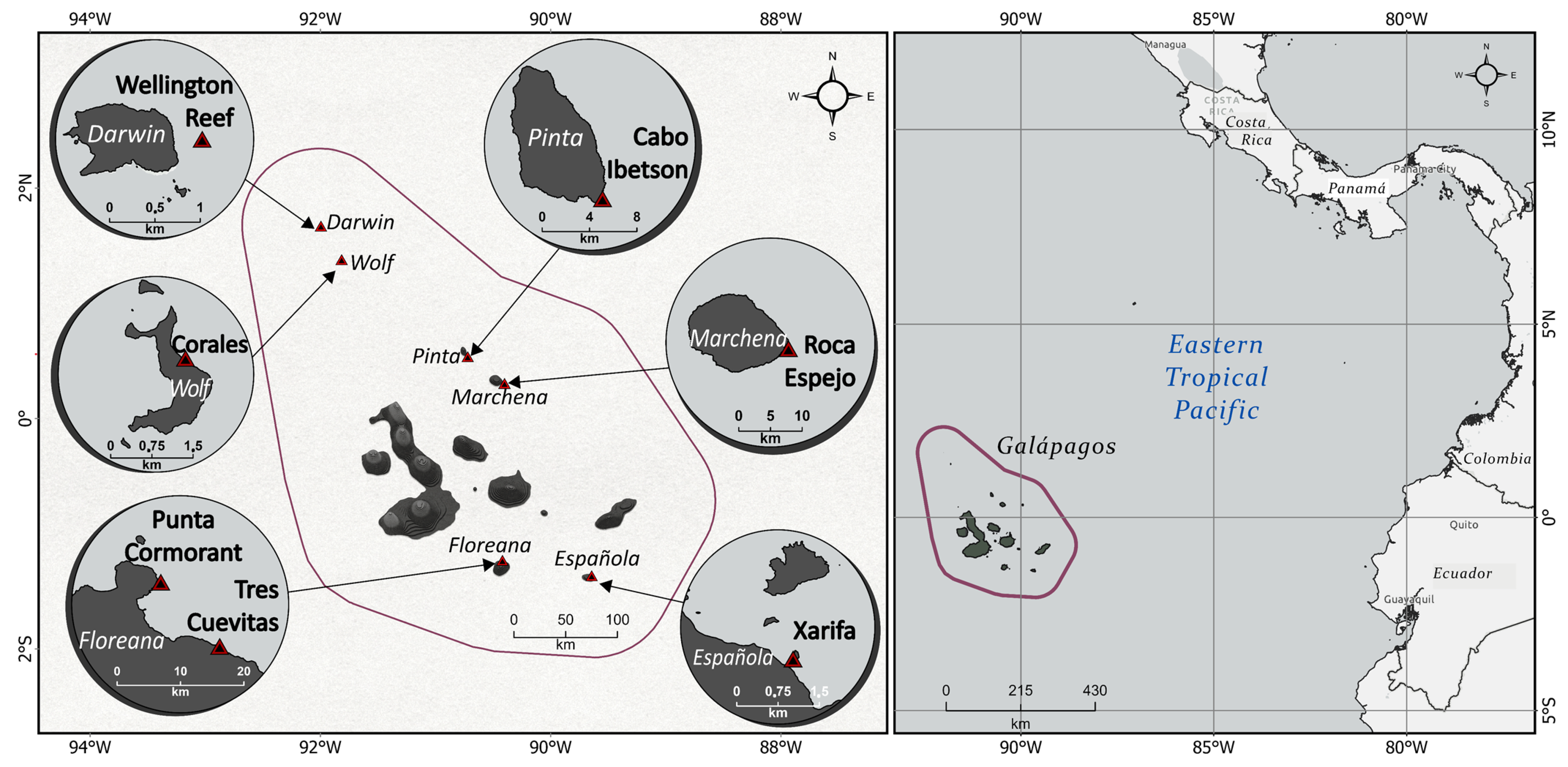
2.1. Study Sites
2.2. Image Acquisition and Scene Set-Up

2.3. 3D Processing
2.4. 3D Model Alignment and Export
2.5. 3D Annotation
2.6. Classification
2.7. Community Metrics
2.8. Structural Complexity Metrics
2.8.1. Fractal Dimension from Cube Counting
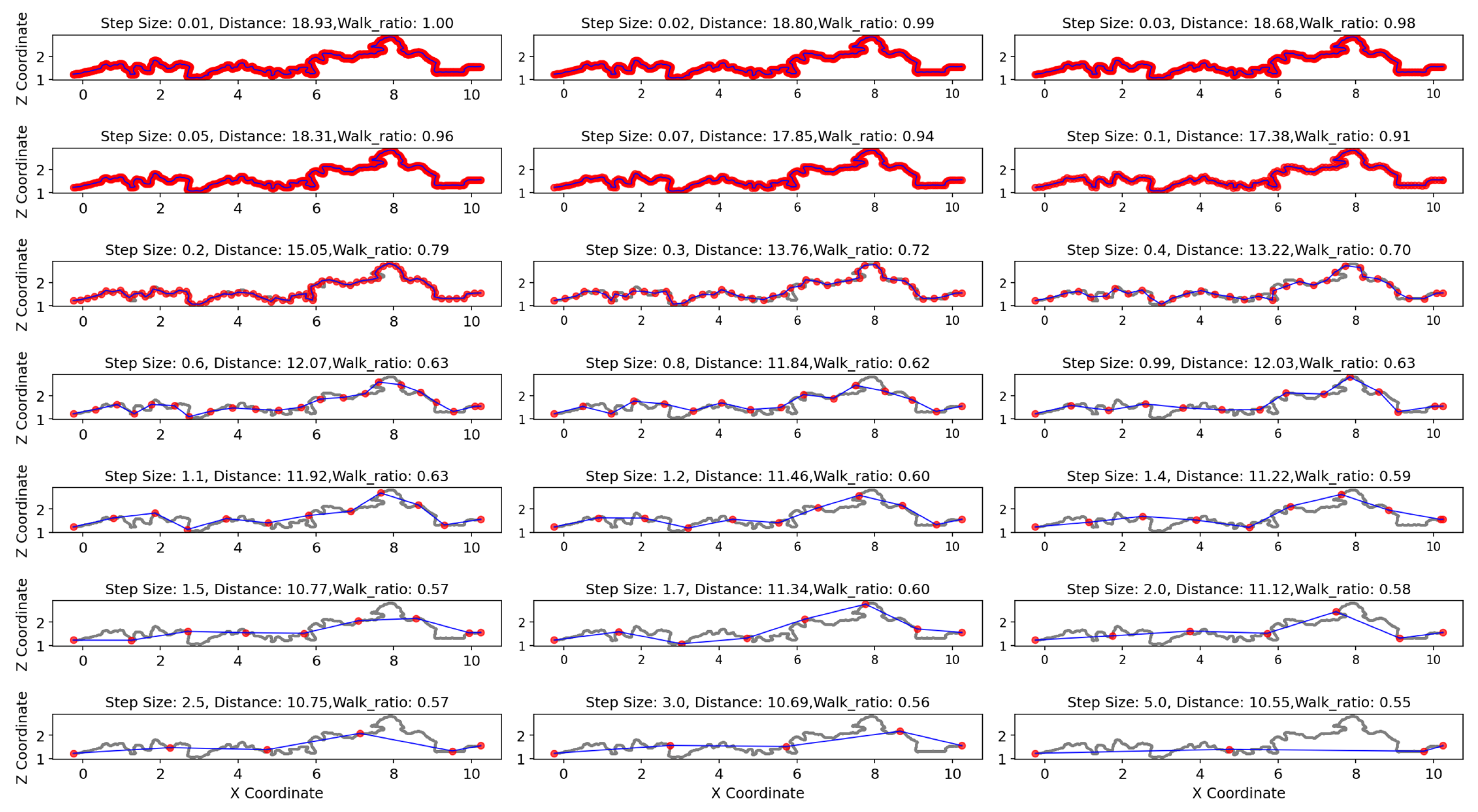
2.8.2. Fractal Dimension from Directed Geodesic Walks
2.9. Estimation of Required Resources
3. Results
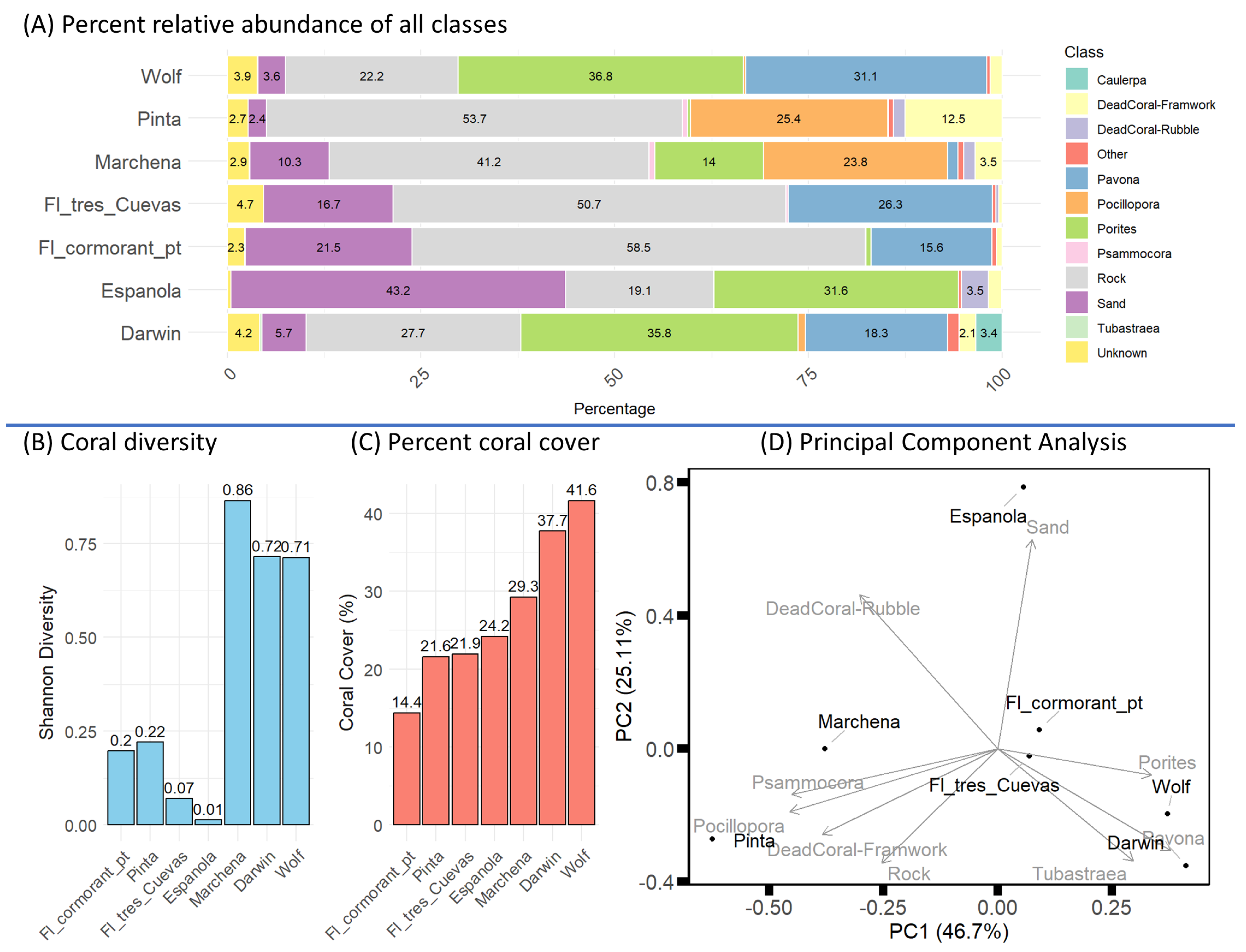
3.1. Community Metrics from 3D Annotations
3.2. Multidimensional Scaling
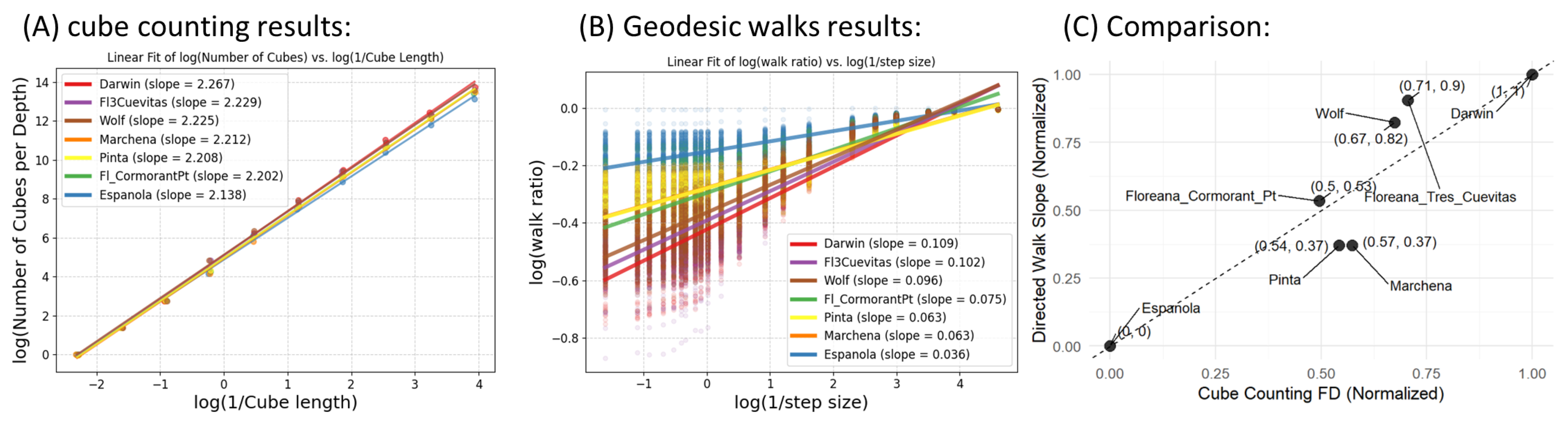
3.3. Structural Complexity from Cube Counting and Walk Ratios
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| PCA | Principal Component Analysis |
| FD | Fractal Dimension |
| DEMs | Digital Elevation Models |
Appendix A. Galápagos_3D Dataset
Appendix A.1. Image Annotations

Appendix A.2. 3D Models

Appendix B. Supporting Tables and Figure
| Darwin-Wellington Reef | Española-Xarifa | Floreana-Tres Cuevitas | Floreana-Punta Cormorant | Marchena-Roca Espejo | Pinta-Cabo Ibetson | Wolf-Corales | |
|---|---|---|---|---|---|---|---|
| Caulerpa | 105 | 1 | 0 | 0 | 0 | 0 | 0 |
| Dead Coral—Framework | 66 | 31 | 11 | 16 | 90 | 332 | 40 |
| Dead Coral—Rubble | 1 | 65 | 12 | 0 | 38 | 39 | 0 |
| Other | 46 | 7 | 12 | 13 | 18 | 18 | 12 |
| Pavona | 566 | 0 | 731 | 351 | 35 | 3 | 812 |
| Pocillopora | 29 | 0 | 1 | 0 | 613 | 674 | 7 |
| Porites | 1108 | 584 | 0 | 16 | 361 | 10 | 961 |
| Rock | 855 | 353 | 1409 | 1317 | 1063 | 1423 | 580 |
| Sand | 177 | 800 | 463 | 485 | 265 | 64 | 93 |
| Tubastraea | 9 | 0 | 1 | 1 | 1 | 0 | 2 |
| Unknown | 129 | 8 | 130 | 51 | 74 | 71 | 101 |
| Psammocora | 0 | 1 | 8 | 1 | 19 | 18 | 0 |
| Cube Counting FD | 2.267 | 2.138 | 2.229 | 2.202 | 2.212 | 2.208 | 2.225 |
| mean∖_slope | 0.108951 | 0.035663 | 0.101956 | 0.074877 | 0.062882 | 0.062978 | 0.096196 |
| lacunarity | 1.495 | 1.626 | 1.998 | 1.615 | 1.458 | 1.536 | 1.684 |
| Surface-Area | 309 | 185 | 225 | 276 | 258 | 265 | 261 |
| Lat | −91.995824 | −89.644622 | −90.408089 | −90.419325 | −90.401241 | −90.720945 | −91.815861 |
| Lon | 1.67824 | −1.357863 | −1.236136 | −1.223949 | 0.312162 | 0.544216 | 1.386624 |
| Depth | 15 | 5 | 10 | 12 | 8 | 8 | 12 |
References
- Izurieta, A.; Delgado, B.; Moity, N.; Calvopina, M.; Cedeno, Y.; Banda-Cruz, G.; Cruz, E.; Aguas, M.; Arroba, F.; Astudillo, I.; et al. A collaboratively derived environmental research agenda for Galápagos. Pac. Conserv. Biol. 2018, 24, 207. [Google Scholar]
- Glynn, P.W.; Wellington, G.M. Corals and Coral Reefs of the Galápagos Islands; University of California Press: Berkeley, CA, USA, 1983. [Google Scholar]
- Riegl, B.; Johnston, M.; Glynn, P.W.; Keith, I.; Rivera, F.; Vera-Zambrano, M.; Banks, S.; Feingold, J.; Glynn, P.J. Some environmental and biological determinants of coral richness, resilience and reef building in Galápagos (Ecuador). Sci. Rep. 2019, 9, 10322. [Google Scholar] [CrossRef] [PubMed]
- Dawson, T.; Henderson, S.; Banks, S. Galapagos coral conservation: Impact mitigation, mapping and monitoring. Galapagos Res. 2009, 66, 65–74. [Google Scholar]
- Foreman, A.D.; Duprey, N.N.; Yuval, M.; Dumestre, M.; Leichliter, J.N.; Rohr, M.C.; Dodwell, R.C.; Dodwell, G.A.; Clua, E.E.; Treibitz, T.; et al. Severe cold-water bleaching of a deep-water reef underscores future challenges for Mesophotic Coral Ecosystems. Sci. Total. Environ. 2024, 951, 175210. [Google Scholar] [CrossRef]
- Hickman, C.P., Jr. Evolutionary responses of marine invertebrates to insular isolation in Galapagos. Galapagos Res. 2009, 66, 32–42. [Google Scholar]
- Edgar, G.J.; Banks, S.A.; Brandt, M.; Bustamante, R.H.; Chiriboga, A.; Earle, S.A.; Garske, L.E.; Glynn, P.W.; Grove, J.S.; Henderson, S.; et al. El Niño, grazers and fisheries interact to greatly elevate extinction risk for Galapagos marine species. Glob. Change Biol. 2010, 16, 2876–2890. [Google Scholar] [CrossRef]
- Glynn, P.W.; Feingold, J.S.; Baker, A.; Banks, S.; Baums, I.B.; Cole, J.; Colgan, M.W.; Fong, P.; Glynn, P.J.; Keith, I.; et al. State of corals and coral reefs of the Galápagos Islands (Ecuador): Past, present and future. Mar. Pollut. Bull. 2018, 133, 717–733. [Google Scholar] [CrossRef]
- Glynn, P.W.; Riegl, B.; Purkis, S.; Kerr, J.M.; Smith, T.B. Coral reef recovery in the Galápagos Islands: The northernmost islands (Darwin and Wenman). Coral Reefs 2015, 34, 421–436. [Google Scholar] [CrossRef]
- Keith, I.; Dawson, T.P.; Collins, K.J.; Campbell, M.L. Marine invasive species: Establishing pathways, their presence and potential threats in the Galapagos Marine Reserve. Pacific Conserv. Biol. 2016, 22, 377–385. [Google Scholar] [CrossRef]
- Feingold, J.S.; Glynn, P.W. Coral research in the Galápagos Islands, Ecuador. In The Galápagos Marine Reserve: A Dynamic Social-Ecological System; Springer: Berlin, Germany, 2013; pp. 3–22. [Google Scholar]
- Glynn, P.W. State of coral reefs in the Galápagos Islands: Natural vs anthropogenic impacts. Mar. Pollut. Bull. 1994, 29, 131–140. [Google Scholar] [CrossRef]
- Banks, S.; Vera, M.; Chiriboga, A. Establishing reference points to assess long-term change in zooxanthellate coral communities of the northern Galápagos coral reefs. Galapagos Res. 2009, 43–66. [Google Scholar]
- Glynn, P.J.; Glynn, P.W.; Riegl, B. El Niño, echinoid bioerosion and recovery potential of an isolated Galápagos coral reef: A modeling perspective. Mar. Biol. 2017, 164, 1–17. [Google Scholar] [CrossRef]
- Rhoades, O.K.; Brandt, M.; Witman, J.D. La Niña-related coral death triggers biodiversity loss of associated communities in the Galápagos. Mar. Ecol. 2023, 44, e12767. [Google Scholar] [CrossRef]
- Peñaherrera-Palma, C.; Harpp, K.; Banks, S. Rapid seafloor mapping of the northern Galapagos Islands, Darwin and Wolf. Galapagos Res. 2016, 68, 2–9. [Google Scholar]
- Burns, J.; Delparte, D.; Gates, R.; Takabayashi, M. Integrating structure-from-motion photogrammetry with geospatial software as a novel technique for quantifying 3D ecological characteristics of coral reefs. PeerJ 2015, 3, e1077. [Google Scholar] [CrossRef]
- Ferrari, R.; Figueira, W.F.; Pratchett, M.S.; Boube, T.; Adam, A.; Kobelkowsky-Vidrio, T.; Doo, S.S.; Atwood, T.B.; Byrne, M. 3D photogrammetry quantifies growth and external erosion of individual coral colonies and skeletons. Sci. Rep. 2017, 7, 16737. [Google Scholar] [CrossRef] [PubMed]
- Yuval, M.; Alonso, I.; Eyal, G.; Tchernov, D.; Loya, Y.; Murillo, A.C.; Treibitz, T. Repeatable semantic reef-mapping through photogrammetry and label-augmentation. Remote Sens. 2021, 13, 659. [Google Scholar] [CrossRef]
- Risk, M.J. Fish diversity on a coral reef in the Virgin Islands. Atoll Res. Bull. 1972, 153, 1–4. [Google Scholar] [CrossRef]
- Loya, Y. Plotless and transect methods. In Coral Reefs: Research Methods; UNESCO: Paris, France, 1978; pp. 197–217. [Google Scholar]
- Hill, J.; Wilkinson, C. Methods for ecological monitoring of coral reefs. Aust. Inst. Mar. Sci. Townsv. 2004, 117, 27. [Google Scholar]
- Laxton, J.; Stablum, W. Sample design for quantitative estimation of sedentary organisms of coral reefs. Biol. J. Linn. Soc. 1974, 6, 1–18. [Google Scholar] [CrossRef]
- Ott, B. Community patterns on a submerged barrier reef at Barbados, West Indies. Int. Rev. Gesamten Hydrobiol. Hydrogr. 1975, 60, 719–736. [Google Scholar] [CrossRef]
- Ferrari, R.; Lachs, L.; Pygas, D.R.; Humanes, A.; Sommer, B.; Figueira, W.F.; Edwards, A.J.; Bythell, J.C.; Guest, J.R. Photogrammetry as a tool to improve ecosystem restoration. Trends Ecol. Evol. 2021, 36, 1093–1101. [Google Scholar] [CrossRef] [PubMed]
- Pavoni, G.; Corsini, M.; Callieri, M.; Palma, M.; Scopigno, R. Semantic segmentation of benthic communities from Ortho-Mosaic maps. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W10, 151–158. [Google Scholar] [CrossRef]
- Miller, S.; Yadav, S.; Madin, J.S. The contribution of corals to reef structural complexity in Kāne ‘ohe Bay. Coral Reefs 2021, 40, 1679–1685. [Google Scholar] [CrossRef]
- Luckhurst, B.; Luckhurst, K. Analysis of the influence of substrate variables on coral reef fish communities. Mar. Biol. 1978, 49, 317–323. [Google Scholar] [CrossRef]
- Rogers, C.S.; Garrison, G.; Grober, R.; Hillis, Z.M.; Franke, M.A. Coral Reef Monitoring Manual for the Caribbean and Western Atlantic; Technical Report; Virgin Islands National Park: St. John, United States Virgin Islands, 1994. [Google Scholar]
- Rogers, C.S.; Miller, J. Coral bleaching, hurricane damage, and benthic cover on coral reefs in St. John, US Virgin Islands: A comparison of surveys with the chain transect method and videography. Bull. Mar. Sci. 2001, 69, 459–470. [Google Scholar]
- Knudby, A.; LeDrew, E. Measuring Structural Complexity on Coral Reefs. In Proceedings of the American Academy of Underwater Sciences 26th Symposium, Dauphin Island, AL, USA, 2007; pp. 181–188. [Google Scholar]
- Bryson, M.; Ferrari, R.; Figueira, W.; Pizarro, O.; Madin, J.; Williams, S.; Byrne, M. Characterization of measurement errors using structure-from-motion and photogrammetry to measure marine habitat structural complexity. Ecol. Evol. 2017, 7, 5669–5681. [Google Scholar] [CrossRef]
- Friedman, A.; Pizarro, O.; Williams, S.B.; Johnson-Roberson, M. Multi-scale measures of rugosity, slope and aspect from benthic stereo image reconstructions. PLoS ONE 2012, 7, e50440. [Google Scholar] [CrossRef]
- Ferrari, R.; McKinnon, D.; He, H.; Smith, R.N.; Corke, P.; González-Rivero, M.; Mumby, P.J.; Upcroft, B. Quantifying multiscale habitat structural complexity: A cost-effective framework for underwater 3D modelling. Remote Sens. 2016, 8, 113. [Google Scholar] [CrossRef]
- González-Rivero, M.; Harborne, A.R.; Herrera-Reveles, A.; Bozec, Y.M.; Rogers, A.; Friedman, A.; Ganase, A.; Hoegh-Guldberg, O. Linking fishes to multiple metrics of coral reef structural complexity using three-dimensional technology. Sci. Rep. 2017, 7, 13965. [Google Scholar] [CrossRef]
- Hylkema, A.; Debrot, A.O.; Osinga, R.; Bron, P.S.; Heesink, D.B.; Izioka, A.K.; Reid, C.B.; Rippen, J.C.; Treibitz, T.; Yuval, M.; et al. Fish assemblages of three common artificial reef designs during early colonization. Ecol. Eng. 2020, 157, 105994. [Google Scholar] [CrossRef]
- Urbina-Barreto, I.; Chiroleu, F.; Pinel, R.; Fréchon, L.; Mahamadaly, V.; Elise, S.; Kulbicki, M.; Quod, J.P.; Dutrieux, E.; Garnier, R.; et al. Quantifying the shelter capacity of coral reefs using photogrammetric 3D modeling: From colonies to reefscapes. Ecol. Indic. 2021, 121, 107151. [Google Scholar] [CrossRef]
- McCarthy, O.S.; Smith, J.E.; Petrovic, V.; Sandin, S.A. Identifying the drivers of structural complexity on Hawaiian coral reefs. Mar. Ecol. Prog. Ser. 2022, 702, 71–86. [Google Scholar] [CrossRef]
- Yuval, M.; Pearl, N.; Tchernov, D.; Martinez, S.; Loya, Y.; Bar-Massada, A.; Treibitz, T. Assessment of storm impact on coral reef structural complexity. Sci. Total Environ. 2023, 891, 164493. [Google Scholar] [CrossRef]
- Aston, E.A.; Duce, S.; Hoey, A.S.; Ferrari, R. A Protocol for Extracting Structural Metrics From 3D Reconstructions of Corals. Front. Mar. Sci. 2022, 9, 854395. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Passoja, D.E.; Paullay, A.J. Fractal character of fracture surfaces of metals. Nature 1984, 308, 721–722. [Google Scholar] [CrossRef]
- Nash, K.L.; Graham, N.A.; Wilson, S.K.; Bellwood, D.R. Cross-scale habitat structure drives fish body size distributions on coral reefs. Ecosystems 2013, 16, 478–490. [Google Scholar] [CrossRef]
- Reichert, J.; Backes, A.R.; Schubert, P.; Wilke, T. The power of 3D fractal dimensions for comparative shape and structural complexity analyses of irregularly shaped organisms. Methods Ecol. Evol. 2017, 8, 1650–1658. [Google Scholar] [CrossRef]
- Fukunaga, A.; Burns, J.H. Metrics of coral reef structural complexity extracted from 3D mesh models and digital elevation models. Remote Sens. 2020, 12, 2676. [Google Scholar] [CrossRef]
- Torres-Pulliza, D.; Dornelas, M.A.; Pizarro, O.; Bewley, M.; Blowes, S.A.; Boutros, N.; Brambilla, V.; Chase, T.J.; Frank, G.; Friedman, A.; et al. A geometric basis for surface habitat complexity and biodiversity. Nat. Ecol. Evol. 2020, 4, 1495–1501. [Google Scholar] [CrossRef]
- Remmers, T.; Grech, A.; Roelfsema, C.; Gordon, S.; Lechene, M.; Ferrari, R. Close-range underwater photogrammetry for coral reef ecology: A systematic literature review. Coral Reefs 2024, 43, 35–52. [Google Scholar] [CrossRef]
- Pavoni, G.; Corsini, M.; Ponchio, F.; Muntoni, A.; Edwards, C.; Pedersen, N.; Sandin, S.; Cignoni, P. TagLab: AI-assisted annotation for the fast and accurate semantic segmentation of coral reef orthoimages. J. Field Robot. 2022, 39, 246–262. [Google Scholar] [CrossRef]
- Remmers, T.; Boutros, N.; Wyatt, M.; Gordon, S.; Toor, M.; Roelfsema, C.; Fabricius, K.; Grech, A.; Lechene, M.; Ferrari, R. RapidBenthos: Automated segmentation and multi-view classification of coral reef communities from photogrammetric reconstruction. Methods Ecol. Evol. 2024, 16, 427–441. [Google Scholar] [CrossRef]
- Kornder, N.A.; Cappelletto, J.; Mueller, B.; Zalm, M.J.; Martinez, S.J.; Vermeij, M.J.; Huisman, J.; de Goeij, J.M. Implications of 2D versus 3D surveys to measure the abundance and composition of benthic coral reef communities. Coral Reefs 2021, 40, 1137–1153. [Google Scholar] [CrossRef]
- Vera, M.; Banks, S. Health status of the coral communities of the northern Galapagos Islands Darwin, Wolf and Marchena. Galapagos Res. 2009, 66, 3–5. [Google Scholar]
- Zhou, Q.Y.; Park, J.; Koltun, V. Open3D: A Modern Library for 3D Data Processing. arXiv 2018, arXiv:1801.09847. [Google Scholar]
- Labelbox, Online. 2025. Available online: https://labelbox.com/ (accessed on 16 May 2025).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Oksanen, J.; Simpson, G.L.; Blanchet, F.G.; Kindt, R.; Legendre, P.; Minchin, P.R.; O’Hara, R.; Solymos, P.; Stevens, M.H.H.; Szoecs, E.; et al. Vegan: Community Ecology Package; R Package Version 2.6-8. 2024. Available online: https://CRAN.R-project.org/package=vegan (accessed on 16 May 2025).
- Schroeder, M. Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise; W.H. Freeman: New York, NY, USA, 1991. [Google Scholar]
- Sullivan, C.B.; Kaszynski, A. PyVista: 3D plotting and mesh analysis through a streamlined interface for the Visualization Toolkit (VTK). J. Open Source Softw. 2019, 4, 1450. [Google Scholar] [CrossRef]
- Edgar, G.; Banks, S.; Fariña, J.; Calvopiña, M.; Martínez, C. Regional biogeography of shallow reef fish and macro-invertebrate communities in the Galapagos archipelago. J. Biogeogr. 2004, 31, 1107–1124. [Google Scholar] [CrossRef]
- Petrovic, V.; Vanoni, D.J.; Richter, A.M.; Levy, T.E.; Kuester, F. Visualizing high resolution three-dimensional and two-dimensional data of cultural heritage sites. Mediterr. Archaeol. Archaeom. 2014, 14, 93–100. [Google Scholar]
- Fox, M.D.; Carter, A.L.; Edwards, C.B.; Takeshita, Y.; Johnson, M.D.; Petrovic, V.; Amir, C.G.; Sala, E.; Sandin, S.A.; Smith, J.E. Limited coral mortality following acute thermal stress and widespread bleaching on Palmyra Atoll, central Pacific. Coral Reefs 2019, 38, 701–712. [Google Scholar] [CrossRef]
- Pavoni, G.; Pierce, J.; Edwards, C.B.; Corsini, M.; Petrovic, V.; Cignoni, P. Integrating Widespread Coral Reef Monitoring Tools for Managing both Area and Point Annotations. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2024, 48, 327–333. [Google Scholar] [CrossRef]
- King, A.; Bhandarkar, S.M.; Hopkinson, B.M. Deep Learning for Semantic Segmentation of Coral Reef Images Using Multi-View Information. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019; pp. 1–10. [Google Scholar]
- Pierce, J.; Butler, M.J., IV; Rzhanov, Y.; Lowell, K.; Dijkstra, J.A. Classifying 3-D models of coral reefs using structure-from-motion and multi-view semantic segmentation. Front. Mar. Sci. 2021, 8, 706674. [Google Scholar] [CrossRef]
- Marlow, J.; Halpin, J.E.; Wilding, T.A. 3D photogrammetry and deep-learning deliver accurate estimates of epibenthic biomass. Methods Ecol. Evol. 2024, 15, 965–977. [Google Scholar] [CrossRef]
- Sauder, J.; Banc-Prandi, G.; Meibom, A.; Tuia, D. Scalable semantic 3D mapping of coral reefs with deep learning. Methods Ecol. Evol. 2024, 15, 916–934. [Google Scholar] [CrossRef]
- Lechene, M.A.; Figueira, W.F.; Murray, N.J.; Aston, E.A.; Gordon, S.E.; Ferrari, R. Evaluating error sources to improve precision in the co-registration of underwater 3D models. Ecol. Inform. 2024, 81, 102632. [Google Scholar] [CrossRef]
- Zhan, Q.; Liang, Y.; Xiao, Y. Color-based segmentation of point clouds. Laser Scanning 2009, 38, 155–161. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuval, M.; Terán, F.; Iñiguez, W.; Bensted-Smith, W.; Keith, I. Spatial Variation in Coral Diversity and Reef Complexity in the Galápagos: Insights from Underwater Photogrammetry and New Data Extraction Methods. Remote Sens. 2025, 17, 1831. https://doi.org/10.3390/rs17111831
Yuval M, Terán F, Iñiguez W, Bensted-Smith W, Keith I. Spatial Variation in Coral Diversity and Reef Complexity in the Galápagos: Insights from Underwater Photogrammetry and New Data Extraction Methods. Remote Sensing. 2025; 17(11):1831. https://doi.org/10.3390/rs17111831
Chicago/Turabian StyleYuval, Matan, Franklin Terán, Wilson Iñiguez, William Bensted-Smith, and Inti Keith. 2025. "Spatial Variation in Coral Diversity and Reef Complexity in the Galápagos: Insights from Underwater Photogrammetry and New Data Extraction Methods" Remote Sensing 17, no. 11: 1831. https://doi.org/10.3390/rs17111831
APA StyleYuval, M., Terán, F., Iñiguez, W., Bensted-Smith, W., & Keith, I. (2025). Spatial Variation in Coral Diversity and Reef Complexity in the Galápagos: Insights from Underwater Photogrammetry and New Data Extraction Methods. Remote Sensing, 17(11), 1831. https://doi.org/10.3390/rs17111831






