Comparative Analysis of Trophic Status Assessment Using Different Sensors and Atmospheric Correction Methods in Greece’s WFD Lake Network
Abstract
1. Introduction
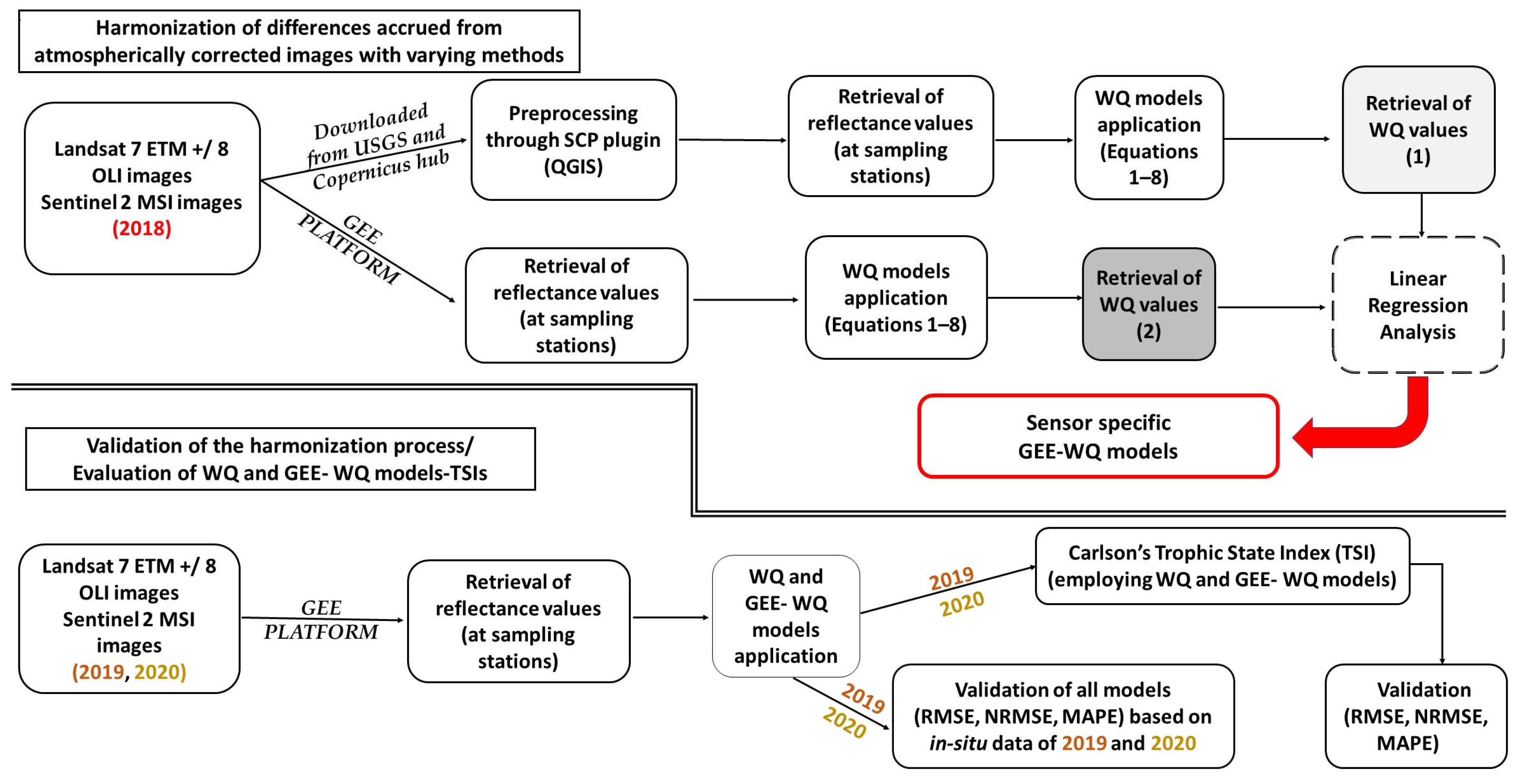
2. Materials and Methods
2.1. In Situ Data
2.2. Satellite Imagery and Pre-Processing
2.3. Harmonization Among SR Products Subjected to Different Atmospheric Correction Methods
- Chl-a models (Equation (1): Chl-ageneral—for all lakes-; Equation (2): Chl-anatural—for natural-only lakes-; Equation (3): Chl-aartificial—for artificial-only lakes-);
- SDD models (Equation (4): Secchigeneral; Equation (5): Secchinatural; Equation (6): Secchiartificial);
- TP models (Equation (7): TPgeneral; Equation (8): TPnatural).
2.4. Carlson’s Trophic State Index (TSI) and Validation
- TSIIN-SITU by employing in situ WQ data;
- TSIMODELLED by applying WQ models, namely Equations (1)–(8);
- TSIGEE-MODELLED by applying the hereby-developed GEE-WQ models ().
3. Results
3.1. Harmonization Among SR Values Subjected to Different AC Methods
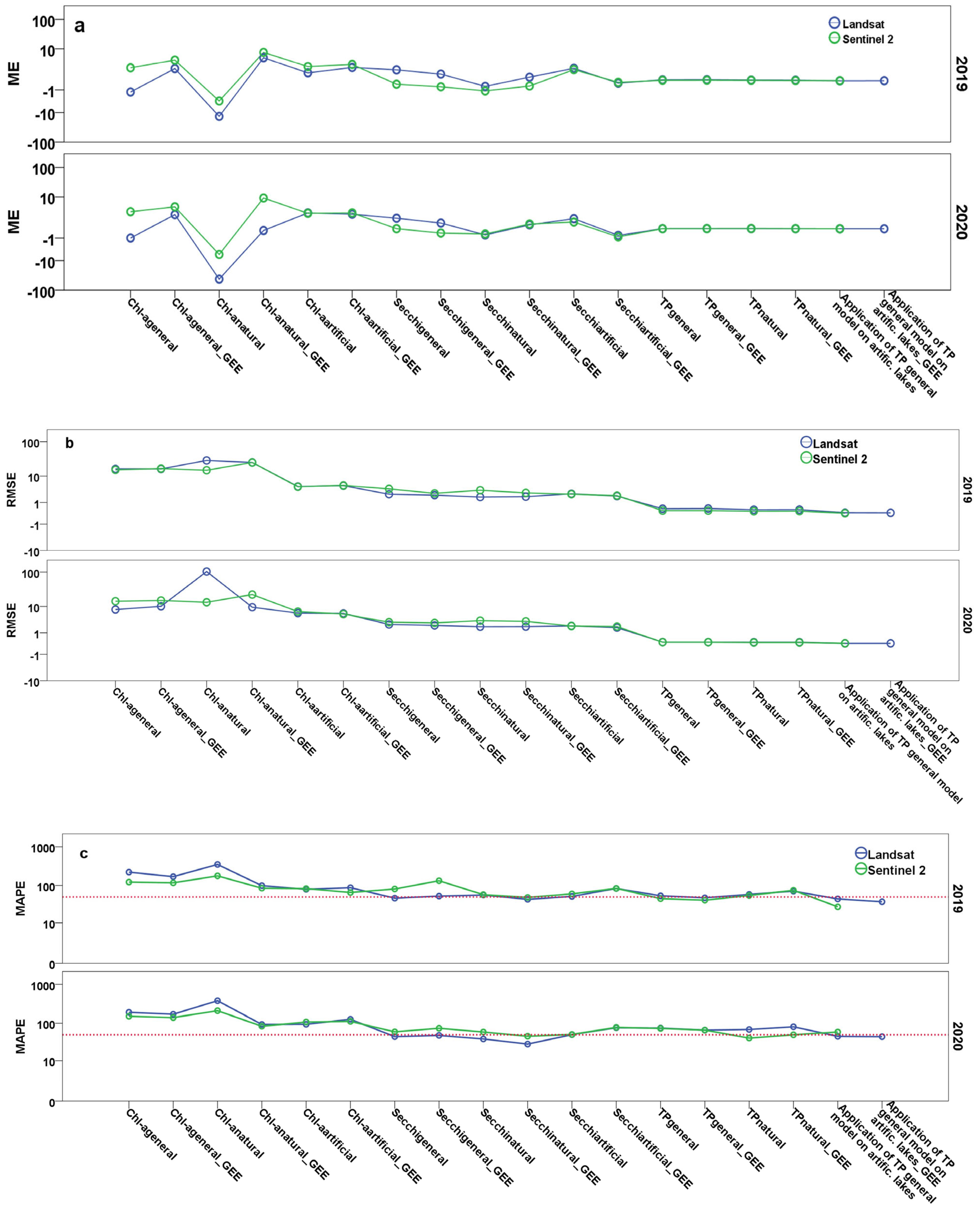
3.2. Validation of Lake WQ Models Employing GEE-Retrieved Reflectance Values
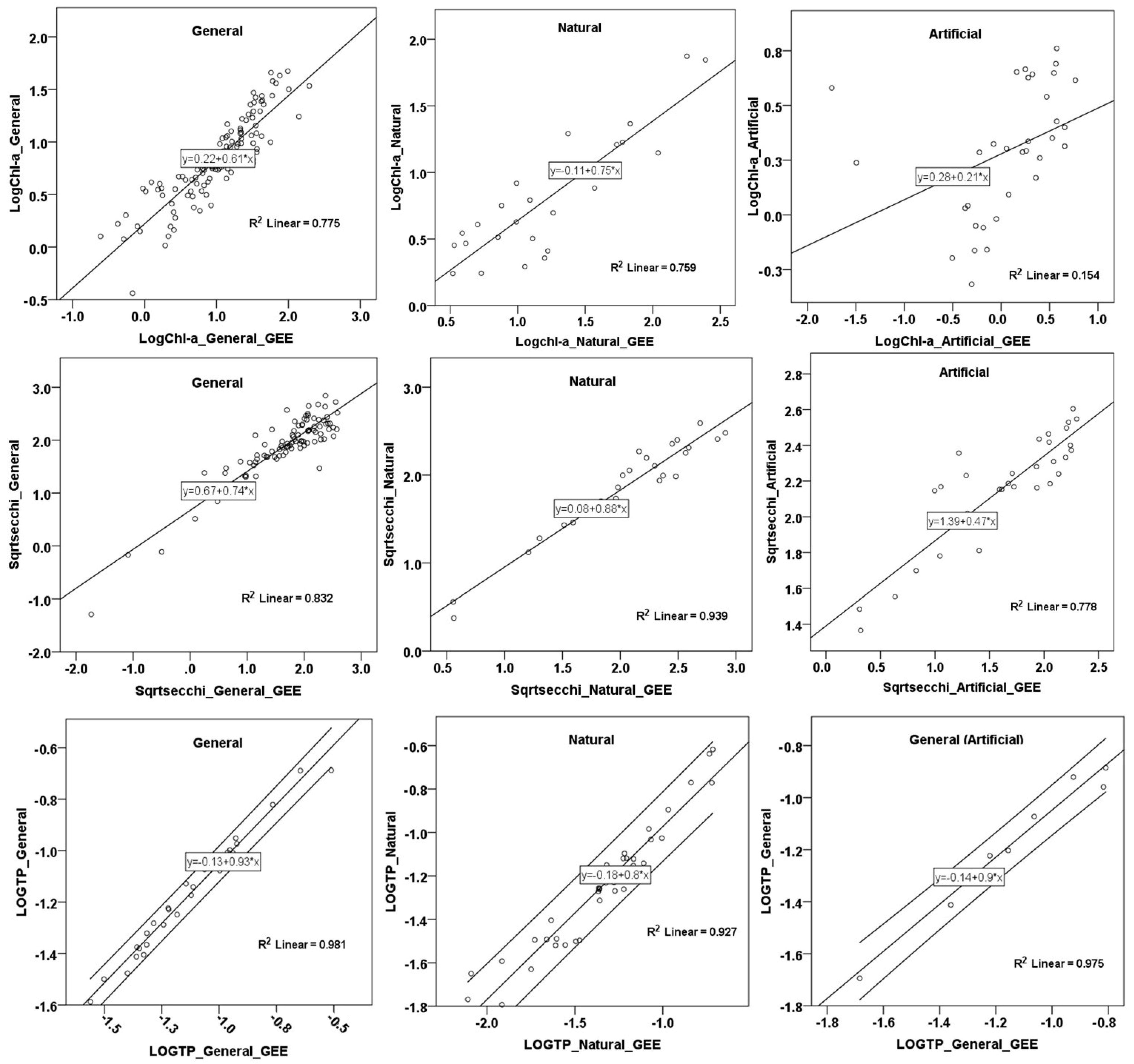
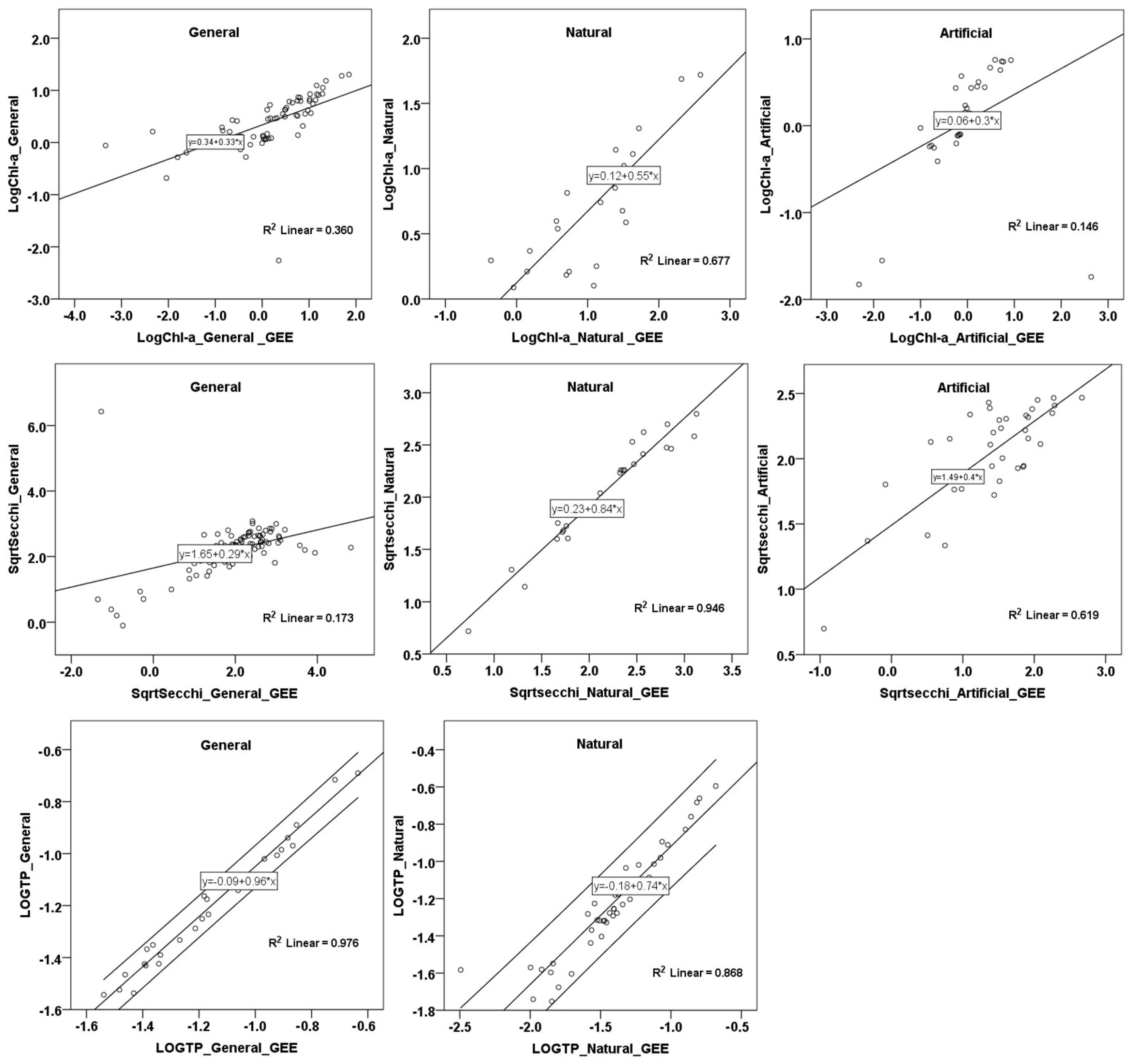
3.2.1. Chl-a Models
3.2.2. SDD Models
3.2.3. TP Models
3.2.4. All WQ Models
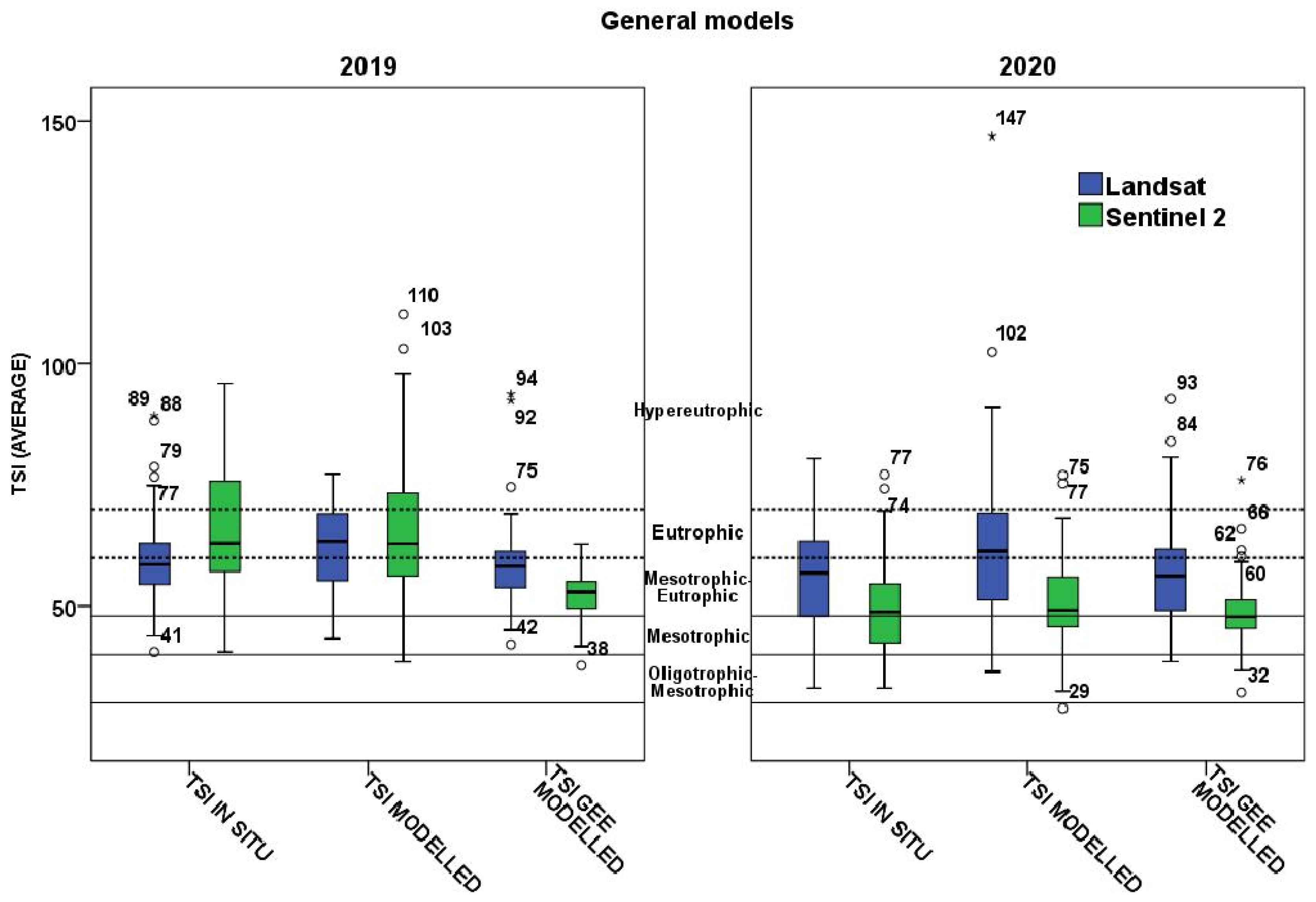
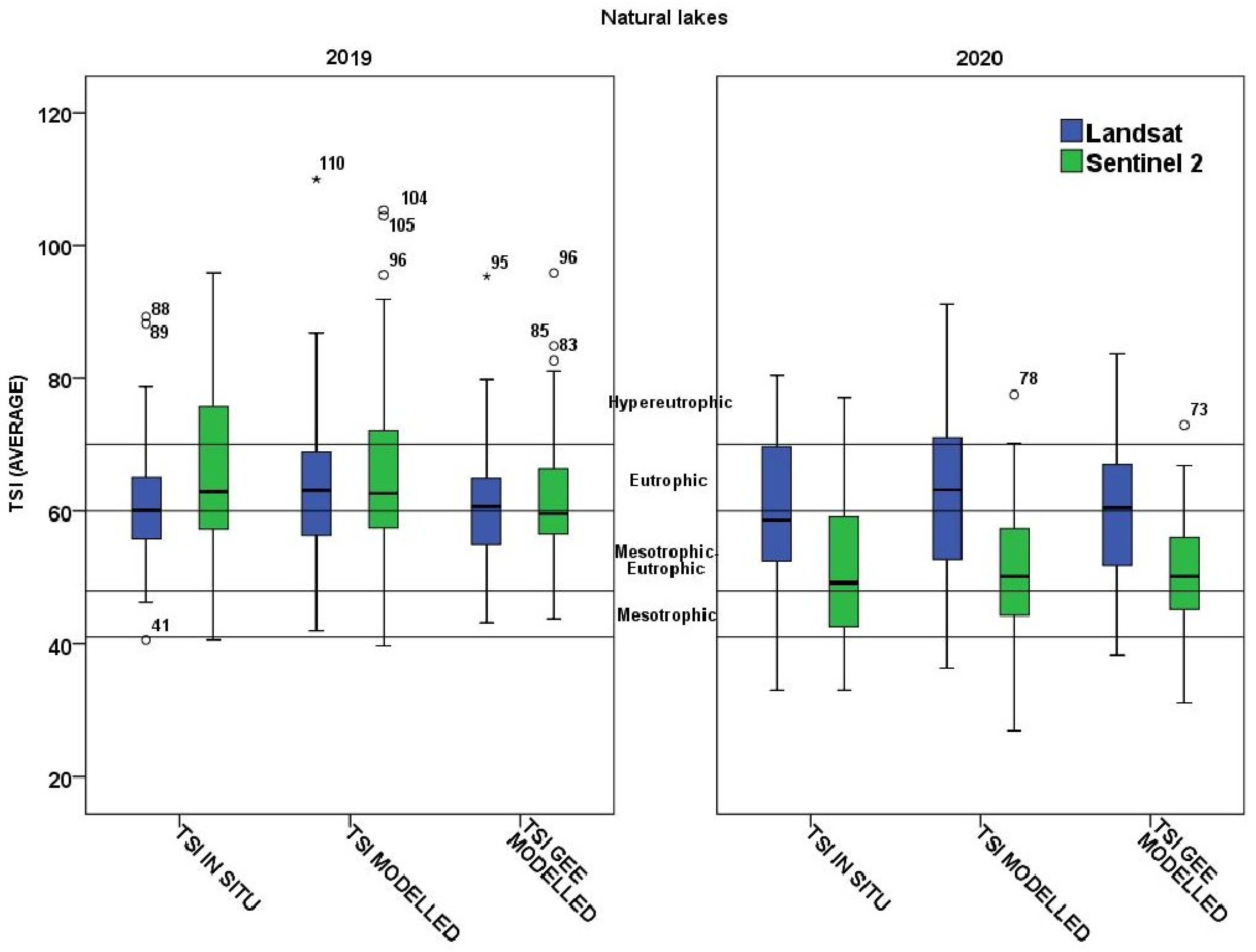
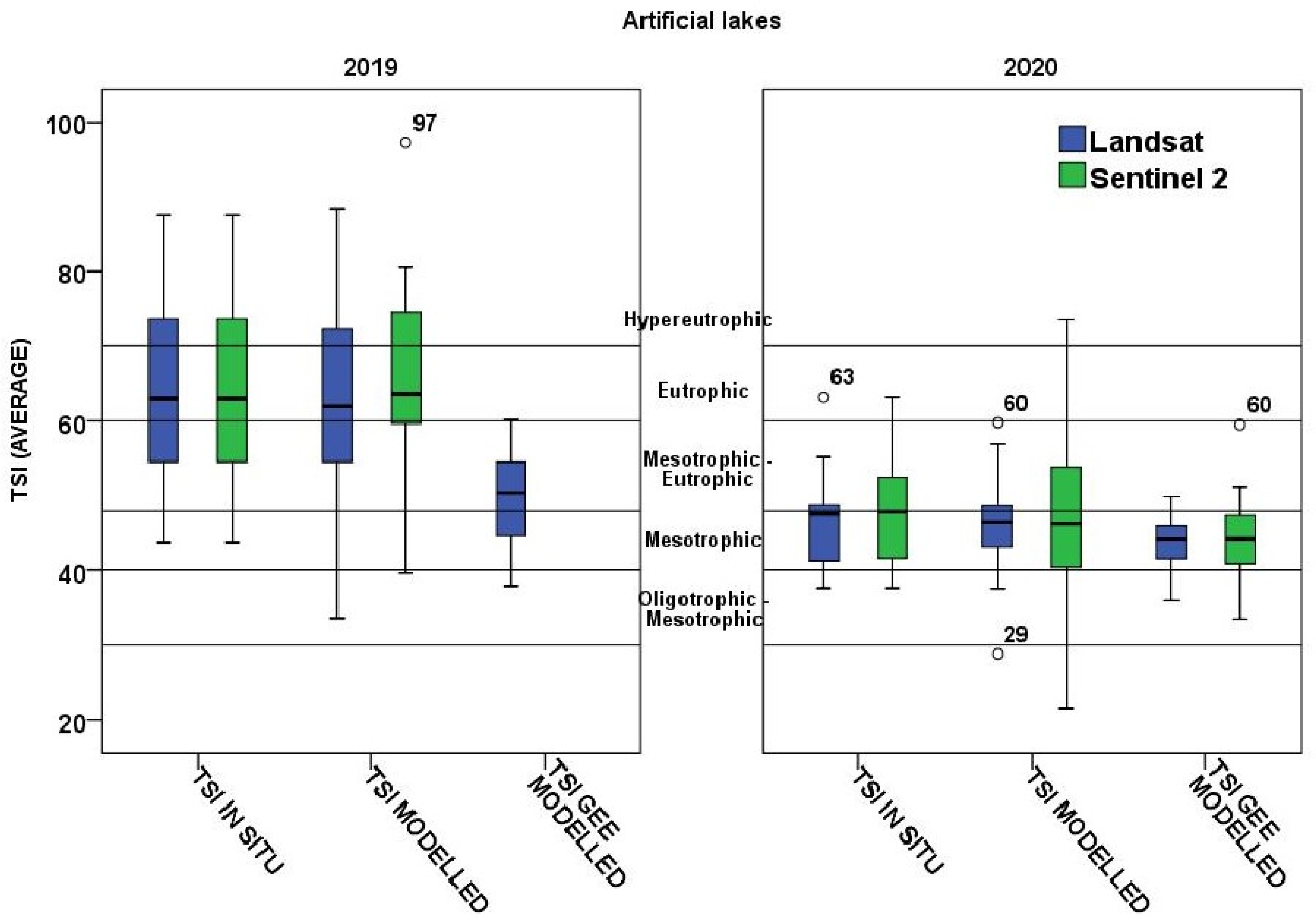
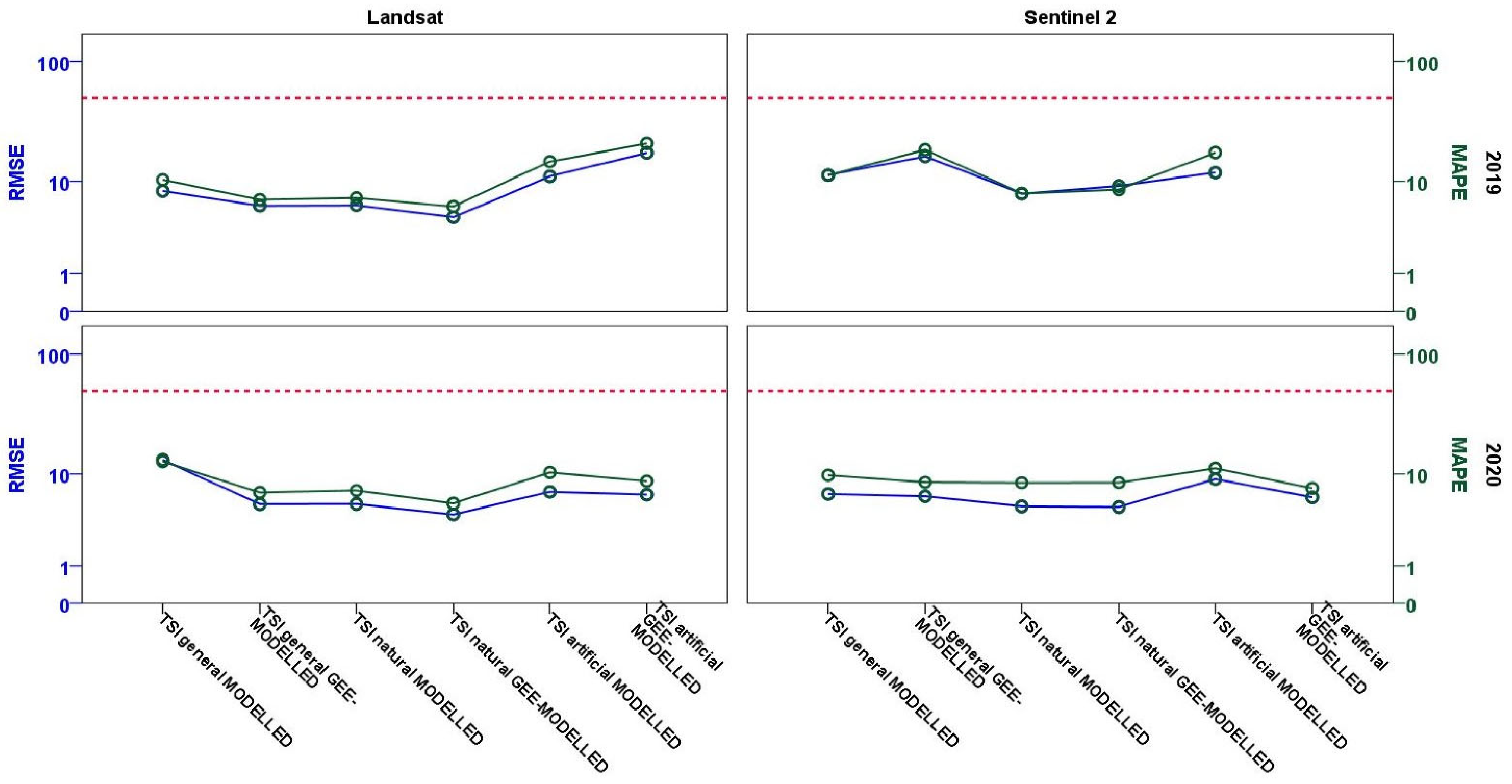
3.3. Satellite-Derived Assessment of Trophic Status of Greek Lakes Based on Carlson’s Trophic State Index (TSI)
4. Discussion
Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pedreros-Guarda, M.; Abarca-del-Río, R.; Escalona, K.; García, I.; Parra, Ó. A Google Earth Engine Application to Retrieve Long-Term Surface Temperature for Small Lakes. Case: San Pedro Lagoons, Chile. Remote Sens. 2021, 13, 4544. [Google Scholar] [CrossRef]
- Fatima, R. Studies on physical, chemical and bacteriological characteristics on quality of spring water in Hajigak iron ore mine, Bamyan province, central Afghanistan. Open J. Geol. 2018, 8, 313–332. [Google Scholar]
- Zhang, D.; Shi, K.; Wang, W.; Wang, X.; Zhang, Y.; Qin, B.; Zhu, M.; Dong, B.; Zhang, Y. An optical mechanism-based deep learning approach for deriving water trophic state of China’s lakes from Landsat images. Water Res. 2024, 252, 121181. [Google Scholar] [CrossRef]
- Carlson, R.E. A trophic state index for lakes. Limnol. Oceanogr 1977, 22, 361–369. [Google Scholar]
- Guan, Q.; Feng, L.; Hou, X.; Schurgers, G.; Zheng, Y.; Tang, J. Eutrophication changes in fifty large lakes on the Yangtze Plain of China derived from MERIS and OLCI observations. Remote Sens. Environ. 2020, 246, 111890. [Google Scholar] [CrossRef]
- Walker, W.W. Use of hypolimnetic oxygen depletion rate as a trophic state index for lakes. Water Resour. Res 1979, 15, 1463–1470. [Google Scholar] [CrossRef]
- Xu, F.-L.; Tao, S.; Dawson, R.; Li, P.-G.; Cao, J. Lake Ecosystem Health Assessment: Indicators and Methods. Water Res. 2001, 35, 3157–3167. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Y.; Shi, K.; Qin, B.; Yao, X.; Zhang, Y. Optical properties and composition changes in chromophoric dissolved organic matter along trophic gradients: Implications for monitoring and assessing lake eutrophication. Water Res. 2018, 131, 255–263. [Google Scholar] [CrossRef]
- Li, J.; Wang, S.; Wu, Y.; Zhang, B.; Chen, X.; Zhang, F.; Shen, Q.; Peng, D.; Tian, L. MODIS observations of water color of the largest 10 lakes in China between 2000 and 2012. Int. J. Digit. Earth 2016, 9, 788–805. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, B.; Li, J.; Shen, Q.; Wu, Y.; Wang, G.; Zou, L.; Wang, S. Validation of a synthetic chlorophyll index for remote estimates of chlorophyll-a in a turbid hypereutrophic lake. Int. J. Remote Sens. 2014, 35, 289–305. [Google Scholar] [CrossRef]
- Brezonik, P.L.; Olmanson, G.L.; Finlay, J.C.; Bauer, M.E. Factors affecting the measurement of CDOM by remote sensing of optically complex inland waters. Remote Sens. Environ. 2015, 157, 199–215. [Google Scholar] [CrossRef]
- Sagan, V.; Peterson, T.K.; Maimaitijiang, M.; Sidike, P.; Sloan, J.; Greeling, A.B.; Samar, M.; Adams, C. Monitoring inland water quality using remote sensing: Potential and limitations of spectral indices, bio-optical simulations, machine learning, and cloud computing. Earth-Sci. Rev. 2020, 205, 103187. [Google Scholar] [CrossRef]
- Markogianni, V.; Kalivas, D.; Petropoulos, G.P.; Dimitriou, E. Estimating Chlorophyll-a of Inland Water Bodies in Greece Based on Landsat Data. Remote Sens. 2020, 12, 2087. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Shi, K.; Zhou, Y.; Li, N. Remote sensing estimation of water clarity for various lakes in China. Water Res. 2021, 192, 116844. [Google Scholar] [CrossRef]
- Song, K.; Wang, Q.; Liu, G.; Jacinthe, P.-A.; Li, S.; Tao, H.; Du, Y.; Wen, Z.; Wang, X.; Guo, W.; et al. A unified model for high resolution mapping of global lake (>1 ha) clarity using landsat imagery data. Sci. Total Environ. 2022, 810, 15118. [Google Scholar] [CrossRef]
- Markogianni, V.; Kalivas, D.; Petropoulos, G.P.; Dimitriou, E. Modelling of Greek Lakes Water Quality Using Earth Observation in the Framework of the Water Framework Directive (WFD). Remote Sens. 2022, 14, 739. [Google Scholar] [CrossRef]
- Gholizadeh, M.; Melesse, A.; Reddi, L. A comprehensive review on water quality parameters estimation using remote sensing techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef]
- Topp, S.; Pavelsky, T.; Jensen, D.; Simard, M.; Ross, M. Research trends in the use of remote sensing for inland water quality science: Moving towards multidisciplinary applications. Water 2020, 12, 169. [Google Scholar] [CrossRef]
- Pizani, F.; Maillard, P. The Determination of Water Quality Parameters by Remote Sensing Technologies: 2000–2020; Universidade Federal de Minas Gerais, [S. l.]: Belo Horizonte, Brazil, 2022; pp. 1–30. [Google Scholar] [CrossRef]
- Kumar, L.; Mutanga, O. Google Earth Engine applications since inception: Usage, trends, and potential. Remote Sens. 2018, 10, 1509. [Google Scholar] [CrossRef]
- Gomes, V.C.F.; Queiroz, G.R.; Ferreira, K.R. An Overview of Platforms for Big Earth Observation Data Management and Analysis. Remote Sens. 2020, 12, 1253. [Google Scholar] [CrossRef]
- Maciel, D.A.; Barbosa, C.C.F.; de Moraes Novo, E.M.L.; Junior, R.F.; Begliomini, F.N. Water clarity in Brazilian water assessed using Sentinel-2 and machine learning methods. ISPRS Int. J. Geoinf. 2021, 182, 134–152. [Google Scholar] [CrossRef]
- Zhao, Q.; Yu, L.; Du, Z.; Peng, D.; Hao, P.; Zhang, Y.; Gong, P. An Overview of the Applications of Earth Observation Satellite Data: Impacts and Future Trends. Remote Sens. 2022, 14, 1863. [Google Scholar] [CrossRef]
- Li, W.; Yang, Q.; Ma, Y.; Yang, Y.; Song, K.; Zhang, J.; Wen, Z.; Liu, G. Remote Sensing Estimation of Long-Term Total Suspended Matter Concentration from Landsat across Lake Qinghai. Water 2022, 14, 2498. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Jia, T.; Zhang, X.; Dong, R. Long-Term Spatial and Temporal Monitoring of Cyanobacteria Blooms Using MODIS on Google Earth Engine: A Case Study in Taihu Lake. Remote Sens. 2019, 11, 2269. [Google Scholar] [CrossRef]
- Zong, J.-M.; Wang, X.-X.; Zhong, Q.-Y.; Xiao, X.-M.; Ma, J.; Zhao, B. Increasing Outbreak of Cyanobacterial Blooms in Large Lakes and Reservoirs under Pressures from Climate Change and Anthropogenic Interferences in the Middle-Lower Yangtze River Basin. Remote Sens. 2019, 11, 1754. [Google Scholar] [CrossRef]
- Maeda, E.E.; Lisboa, F.; Kaikkonen, L.; Kallio, K.; Koponen, S.; Brotas, V.; Kuikka, S. Temporal patterns of phytoplankton phenology across high latitude lakes unveiled by long-term time series of satellite data. Remote Sens. Environ. 2019, 221, 609–620. [Google Scholar] [CrossRef]
- Wang, L.; Xu, M.; Liu, Y.; Liu, H.; Beck, R.; Reif, M.; Emery, E.; Young, J.; Wu, Q. Mapping Freshwater Chlorophyll-a Concentrations at a Regional Scale Integrating Multi-Sensor Satellite Observations with Google Earth Engine. Remote Sens. 2020, 12, 3278. [Google Scholar] [CrossRef]
- Weber, S.J.; Mishra, D.R.; Wilde, S.B.; Kramer, E. Risks for cyanobacterial harmful algal blooms due to land management and climate interactions. Sci. Total Environ. 2020, 703, 134608. [Google Scholar] [CrossRef]
- Lobo, F.d.L.; Nagel, G.W.; Maciel, D.A.; de Carvalho, L.A.S.; Martins, V.S.; Barbosa, C.C.F.; Novo, E.M.L.d.M. AlgaeMAp: Algae Bloom Monitoring Application for Inland Waters in Latin America. Remote Sens. 2021, 13, 2874. [Google Scholar] [CrossRef]
- Somasundaram, D.; Zhang, F.; Ediriweera, S.; Wang, S.; Yin, Z.; Li, J.; Zhang, B. Patterns, Trends and Drivers of Water Transparency in Sri Lanka Using Landsat 8 Observations and Google Earth Engine. Remote Sens. 2021, 13, 2193. [Google Scholar] [CrossRef]
- Bioresita, F.; Hidayatul, U.M.; Wulansari, M.; Putri, N.A. Monitoring seawater quality in the Kali Porong estuary as an area for Lapindo mud disposal leveraging Google Earth Engine. IOP Conference Series: Earth and Environmental Science, Volume 936, Geomatics International Conference 2021 (GEOICON 2021) 27 July 2021, Indonesia (Virtual). IOP Conf. Ser. Earth Environ. Sci. 2021, 936, 012011. [Google Scholar] [CrossRef]
- Vaičiūtė, D.; Bučas, M.; Bresciani, M.; Dabulevičienė, T.; Gintauskas, J.; Mėžinė, J.; Tiškus, E.; Umgiesser, G.; Morkūnas, J.; De Santi, F.; et al. Hot moments and hotspots of cyanobacteria hyperblooms in the Curonian Lagoon (SE Baltic Sea) revealed via remote sensing-based retrospective analysis. Sci. Total Environ. 2021, 769, 145053. [Google Scholar] [CrossRef]
- Kislik, C.; Dronova, I.; Grantham, T.E.; Kelly, M. Mapping algal bloom dynamics in small reservoirs using Sentinel-2 imagery in Google Earth Engine. Ecol. Indic. 2022, 140, 109041. [Google Scholar] [CrossRef]
- Wen, Z.; Wang, Q.; Liu, G.; Jacinthe, P.-A.; Wang, X.; Lyu, L.; Tao, H.; Ma, Y.; Duan, H.; Shang, Y.; et al. Remote sensing of total suspended matter concentration in lakes across China using Landsat images and Google Earth Engine. ISPRS J. Photogramm. Remote Sens. 2022, 187, 61–78. [Google Scholar] [CrossRef]
- Nazeer, M.; Nichol, J.E.; Yung, Y.-K. Evaluation of Atmospheric Correction Models and Landsat Surface Reflectance Product in an Urban Coastal Environment. Int. J. Remote Sens. 2014, 35, 6271–6291. [Google Scholar] [CrossRef]
- Warren, M.; Simis, S.; Martinez-Vicente, V.; Poser, K.; Bresciani, M.; Alikas, K.; Spyrakos, E.; Giardino, C.; Ansper, A. Assessment of atmospheric correction algorithms for the Sentinel-2A MultiSpectral Imager over coastal and inland waters. Remote Sens. Environ. 2019, 225, 267–289. [Google Scholar] [CrossRef]
- Pahlevan, N.; Mangin, A.; Balasubramanian, S.V.; Smith, B.; Alikas, K.; Arai, K.; Barbosa, C.; Bélanger, S.; Binding, C.; Bresciani, M.; et al. ACIX-Aqua: A global assessment of atmospheric correction methods for Landsat-8 and Sentinel-2 over lakes, rivers, and coastal waters. Remote Sens. Environ. 2021, 258, 112366. [Google Scholar] [CrossRef]
- Bresciani, M.; Cazzaniga, I.; Austoni, M.; Sforzi, T.; Buzzi, F.; Morabito, G.; Giardino, C. Mapping phytoplankton blooms in deep subalpine lakes from Sentinel-2A and Landsat-8. Hydrobiologia 2018, 824, 197–214. [Google Scholar] [CrossRef]
- Markogianni, V.; Kalivas, D.; Petropoulos, G.; Dimitriou, E. An appraisal of the potential of Landsat 8 in estimating chlorophyll-a, ammonium concentrations and other water quality indicators. Remote Sens. 2018, 10, 1018. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Schalles, J.; Binding, C.; Cao, Z.; Ma, R.; Alikas, K.; Kangro, K.; Gurlin, D.; Nguyen, H.; et al. Seamless Retrievals of Chlorophyll-A from Sentinel-2 (MSI) and Sentinel-3 (OLCI) in Inland and Coastal Waters: A Machine-learning Approach. Remote Sens. Environ. 2020, 240, 111604. [Google Scholar] [CrossRef]
- Bramich, J.; Bolch, C.J.S.; Fischer, A. Improved red-edge chlorophyll-a detection for Sentinel 2. Ecol. Indic. 2021, 120, 106876. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, H.; He, B.; Yang, X.; Feng, Q.; Kutser, T.; Chen, F.; Zhou, X.; Xiao, F.; Kou, J. Secchi Depth estimation for optically-complex waters based on spectral angle mapping—Derived water classification using Sentinel-2 data. Int. J. Remote Sens. 2021, 42, 3123–3145. [Google Scholar] [CrossRef]
- Mandanici, E.; Bitelli, G. Multi-image and multi-sensor change detection for long-term monitoring of arid environments with Landsat series. Remote Sens. 2015, 7, 14019–14038. [Google Scholar] [CrossRef]
- Tsiaoussi, V.; Kemitzoglou, D.; Mavromati, E. Report on the Application of Phytoplankton Index NMASRP for Reservoirs in Greece; Greek Biotope/Wetland Centre and Special Secretariat for Waters, Ministry of Environment: Thermi, Greece, 2016; 16p. [Google Scholar]
- Tsiaoussi, V.; Mavromati, E.; Kemitzoglou, D. Report on the Development of the National Method for the Assessment of the Ecological Status of Natural Lakes in Greece, Using the Biological Quality Element “Phytoplankton”, 1st ed.; Greek Biotope/Wetland Centre and Special Secretariat for Waters, Ministry of Environment: Thermi, Greece, 2017; p. 17. [Google Scholar]
- Standard Methods Committee of the American Public Health Association, American Water Works Association, and Water Environment Federation. 4500-p phosphorus. In Standard Methods For the Examination of Water and Wastewater; Lipps, W.C., Baxter, T.E., Braun-Howland, E., Eds.; APHA Press: Washington, DC, USA, 2017. [Google Scholar] [CrossRef]
- Mavromati, E.; Kagalou, I.; Kemitzoglou, D.; Apostolakis, A.; Seferlis, M.; Tsiaoussi, V. Relationships among land use patterns, hydromorphological features and physicochemical parameters of surface waters: WFD lake monitoring in Greece. Environ. Process. 2018, 5 (Suppl. S1), 139–151. [Google Scholar] [CrossRef]
- Mandanici, E.; Bitelli, G. Preliminary Comparison of Sentinel-2 and Landsat 8 Imagery for a Combined Use. Remote Sens. 2016, 8, 1014. [Google Scholar] [CrossRef]
- Ermida, S.L.; Soares, P.; Mantas, V.; Göttsche, F.-M.; Trigo, I.F. Google Earth Engine Open-Source Code for Land Surface Temperature Estimation from the Landsat Series. Remote Sens. 2020, 12, 1471. [Google Scholar] [CrossRef]
- Available online: https://documentation.dataspace.copernicus.eu/Data/SentinelMissions/Sentinel2.html (accessed on 10 July 2022).
- Chavez, P.S., Jr. An Improved Dark-Object Subtraction Technique for Atmospheric Scattering Correction of Multispectral data. Remote Sens. Environ. 1988, 24, 459–479. [Google Scholar] [CrossRef]
- El Alem, A.; Lhissou, R.; Chokmani, K.; Oubennaceur, K. Remote Retrieval of Suspended Particulate Matter in Inland Waters: Image-Based or Physical Atmospheric Correction Models? Water 2021, 13, 2149. [Google Scholar] [CrossRef]
- Doña, C.; Sánchez, M.J.; Caselles, V.; Dominguez, J.A.; Camacho, A. Empirical Relationships for Monitoring Water Quality of Lakes and Reservoirs Through Multispectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1632–1641. [Google Scholar] [CrossRef]
- Deutsch, E.S.; Alameddine, I.; El-Fadel, M. Monitoring water quality in a hypereutrophic reservoir using Landsat ETM+ and OLI sensors: How transferable are the water quality algorithms? Environ. Monit. Assess. 2018, 190, 141. [Google Scholar] [CrossRef] [PubMed]
- Lewis, C.D. Industrial and Business Forecasting Methods; Butterworths: London, UK, 1982. [Google Scholar]
- Moreno, J.M.; Pol, A.P.; Abad, A.S.; Blasco, B.C. Using the RMAPE index as a resistant measure of forecast accuracy. Psicothema 2013, 25, 500–506. [Google Scholar] [CrossRef]
- Carlson, R.E.; Simpson, J. A coordinator’s guide to volunteer lake monitoring methods. N. Am. Lake Manag. Soc. 1996, 96, 305. [Google Scholar]
- Devi Prasad, A.G. Carlson’s Trophic State Index for the assessment of trophic status of two lakes in Mandya district. Adv. Appl. Sci. Res. 2012, 3, 2992–2996. [Google Scholar]
- Abdelal, Q.; Assaf, M.N.; Al-Rawabdeh, A.; Arabasi, S.; Rawashdeh, N.A. Assessment of Sentinel-2 and Landsat-8 OLI for Small-Scale Inland Water Quality Modeling and Monitoring Based on Handheld Hyperspectral Ground Truthing. J. Sens. 2022, 2022, 4643924. [Google Scholar] [CrossRef]
- Lin, S.; Novitski, L.N.; Qi, J.; Stevenson, R.J. Landsat TM/ETM+ and machine-learning algorithms for limnological studies and algal bloom management of inland lakes. J. Appl. Remote Sens. 2018, 12, 1. [Google Scholar] [CrossRef]
- Zhao, D.; Huang, J.; Li, Z.; Yu, G.; Shen, H. Dynamic monitoring and analysis of chlorophyll-a concentrations in global lakes using Sentinel-2 images in Google Earth Engine. Sci. Total Environ. 2024, 912, 169152. [Google Scholar] [CrossRef]
- Bonansea, M.; Bazán, R.; Ferrero, S.; Rodríguez, C.; Ledesma, C.; Pinotti, L. Multivariate statistical analysis for estimating surface water quality in reservoirs. Int. J. Hydr. Sci. Technol. 2018, 8, 52–68. [Google Scholar] [CrossRef]
- Zhang, T.; Huang, M.; Wang, Z. Estimation of chlorophyll-a Concentration of lakes based on SVM algorithm and Landsat 8 OLI images. Environ. Sci. Pollut. Res. 2020, 27, 14977–14990. [Google Scholar] [CrossRef]
- IOCCG. Remote Sensing of Inherent Optical Properties: Fundamentals, Tests of Algorithms, and Applications; Lee, Z., Ed.; Reports of the International Ocean-Colour Coordinating Group, No. 5; IOCCG: Dartmouth, NS, Canada, 2006; ISBN 9781896246567. [Google Scholar]
- Allan, M.G.; Hamilton, D.P.; Hicks, B.J.; Brabyn, L. Landsat remote sensing of chlorophyll a concentration in central north island lakes of New Zealand. Int. J. Remote Sens. 2011, 32, 2037–2055. [Google Scholar] [CrossRef]
- Zeng, S.; Lei, S.; Li, Y.; Lyu, H.; Dong, X.; Li, J.; Cai, X. Remote monitoring of total dissolved phosphorus in eutrophic Lake Taihu based on a novel algorithm: Implications for contributing factors and lake management. Environ. Pollut. 2022, 296, 118740. [Google Scholar] [CrossRef] [PubMed]
- Lim, J.; Choi, M. Assessment of water quality based on Landsat 8 operational land imager associated with human activities in Korea. Environ. Monit. Assess. 2015, 187, 384. [Google Scholar] [CrossRef] [PubMed]
- Mukonza, S.S.; Chiang, J.-L. Machine and deep learning-based trophic state classification of national freshwater reservoirs in Taiwan using Sentinel-2 data. Phys. Chem. Earth 2024, 134, 103541. [Google Scholar] [CrossRef]
- Hu, M.; Ma, R.; Xiong, J.; Wang, M.; Cao, Z.; Xue, K. Eutrophication state in the Eastern China based on Landsat 35-year observations. Remote Sens. Environ. 2022, 277, 113057. [Google Scholar] [CrossRef]
- Van der Werff, H.; Van der Meer, F. Sentinel-2A MSI and Landsat 8 OLI provide data continuity for geological remote sensing. Remote Sens. 2016, 8, 883. [Google Scholar] [CrossRef]
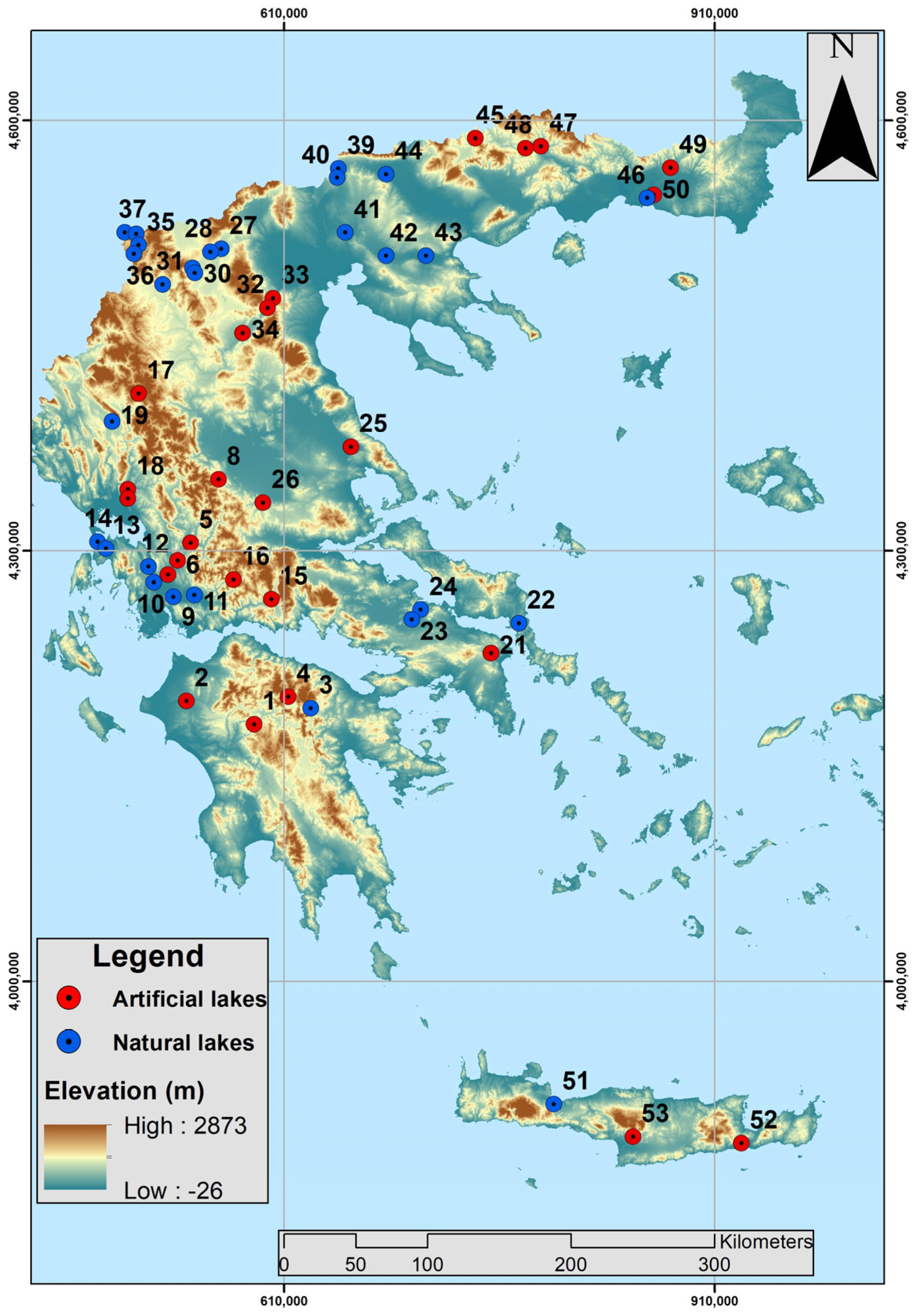
| No | National Name Station | Surface (km2) | (N)atural/ (A)rtificial | Mean Depth (m) | No | National Name Station | Surface (km2) | (N)atural/ (A)rtificial | Mean Depth (m) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Lake Ladona | - | A | - | 28 | Lake Petron | 11.91 | N | 3.1 |
| 2 | Lake Pineiou | 19.64 | A | 15.1 | 29 | Lake Zazari | 2.98 | N | 3.95 |
| 3 | Lake Stymfalia | - | N | 1.31 | 30 | Lake Cheimaditida | 9.82 | N | 1.01 |
| 4 | Lake Feneou | 0.47 | A | 10.5 | 31 | Lake Kastorias | 30.87 | N | 3.7 |
| 5 | Lake Kremaston | 68.43 | A | 47.2 | 32 | Lake Sfikias | 3.96 | A | 23.2 |
| 6 | Lake Kastrakiou | 25.58 | A | 33.2 | 33 | Lake Asomaton | 2.46 | A | 20.8 |
| 7 | Lake Stratou | 7.02 | A | 9.6 | 34 | Lake Polyfytou | 63.49 | A | 22.4 |
| 8 | Lake Tavropou | 21.46 | A | 15.0 | 35 | Lake Mikri Prespa A | - | N | 3.95 |
| 9 | Lake Lysimacheia | 10.87 | N | 3.5 | 36 | Lake Mikri Prespa B | N | - | |
| 10 | Lake Ozeros | 10.57 | N | 3.8 | 37 | Lake Megali Prespa A | - | N | 17 |
| 11 | Lake Trichonida | 93.53 | N | 29.6 | 38 | Lake Megali Prespa B | N | - | |
| 12 | Lake Amvrakia | 13.14 | N | 23.4 | 39 | Lake Doirani 1 | 33.25 | N | 4.6 |
| 13 | Lake Voulkaria | 7.38 | N | 0.96 | 40 | Lake Doirani 2 | N | - | |
| 14 | Lake Saltini | - | N | - | 41 | Lake Pikrolimni | 6.30 | N | 1.2 |
| 15 | Lake Mornou | 17.50 | A | 38.5 | 42 | Lake Koroneia | - | N | 3.8 |
| 16 | Lake Evinou | 2.68 | A | 31.5 | 43 | Lake Volvi | 70.36 | N | 12.3 |
| 17 | Lake Pigon Aoou | 11.44 | A | 20.8 | 44 | Lake Kerkini | - | A | 2.19 |
| 18 | Lake Pournariou | 19.28 | A | 29.8 | 45 | Lake Leukogeion | 0.83 | A | 4.05 |
| 19 | Lake Pamvotida | 21.82 | N | 5.3 | 46 | Lake Ismarida | - | N | 0.9 |
| 20 | Lake Pournariou II | 0.56 | A | 11.7 | 47 | Lake Platanovrysis | 2.99 | A | 26.4 |
| 21 | Lake Marathona | 2.17 | A | 15.8 | 48 | Lake Thisavrou | 13.43 | A | 38.4 |
| 22 | Lake Dystos | - | N | - | 49 | Lake Gratinis | 0.80 | A | 14.2 |
| 23 | Lake Yliki | 19.96 | N | 20.1 | 50 | Lake N. Adrianis | - | A | - |
| 24 | Lake Paralimni | 9.96 | N | 2.99 | 51 | Lake Kourna | - | N | 15 |
| 25 | Lake Karlas | - | A | 0.9 | 52 | Lake Bramianou | - | A | 10.1 |
| 26 | Lake Smokovou | - | A | - | 53 | Lake Faneromenis | 0.33 | A | 9.98 |
| 27 | Lake Vegoritida | 47.67 | N | 26.52 |
| MAPE | Interpretation |
|---|---|
| <10 | Highly accurate forecasting |
| 10–20 | Good forecasting |
| 20–50 | Reasonable forecasting |
| >50 | Inaccurate forecasting |
| TSI Values | Trophic Status | Attributes | No of Class | |
|---|---|---|---|---|
| <40 | <30 | Oligotrophic | Transparent water | 1 |
| 30–40 | Oligotrophic–Mesotrophic | 2 | ||
| 41–50 | 41–48 | Mesotrophic | Higher turbidity, higher algae abundance and macrophytes | 3 |
| 49–50 | Mesotrophic–Eutrophic | 4 | ||
| 51–70 | 51–60 | Mesotrophic–Eutrophic | ||
| 61–70 | Eutrophic | Usually blue-green algae blooms | 5 | |
| >70 | Hypereutrophic | Extreme blue-green algae blooms | 6 | |
| Equations | GEE-WQ Models | N | R | R2 | Sensor |
|---|---|---|---|---|---|
| (10) | LogChl-a_general = 0.221 + 0.61 × (logChl-a_general_GEE) | 115 | 0.88 | 0.78 | Landsat |
| (11) | LogChl-a_natural = −0.109 + (0.747 × logchl-a_natural_GEE) | 26 | 0.87 | 0.76 | |
| (12) | LogChl-a_artificial = 0.279 + (0.209 × logchl-a_artificial_GEE) | 33 | 0.39 | 0.15 | |
| (13) | SQRTSecchi_general = 0.671 + (0.737 × SQRTSecchi_general_GEE) | 95 | 0.91 | 0.83 | |
| (14) | SQRTSecchi_natural = 0.079 + (0.875 × SQRTSecchi_natural_GEE) | 26 | 0.97 | 0.94 | |
| (15) | SQRTSecchi_artificial = 1.391 + (0.475 × SQRTSecchi_artificial_GEE) | 33 | 0.88 | 0.78 | |
| (16) | LogTP_general = −0.127 + (0.925 × LOGTP_general_GEE) | 28 | 0.99 | 0.98 | |
| (17) | LogTP_natural = −0.177 + (0.796 × LOGTP_natural_GEE) | 40 | 0.96 | 0.93 | |
| (18) | LogTP_artificial = −0.143 + (0.905 × LOGTP_artificial_GEE) | 11 | 0.99 | 0.98 |
| Equations | GEE-WQ Models | N | R | R2 | Sensor |
|---|---|---|---|---|---|
| (19) | LogChl-a_general = 0.338 + (0.329 × logchl-a_general_GEE) | 64 | 0.6 | 0.36 | Sentinel 2 |
| (20) | LogChl-a_natural = 0.125 + (0.549 × logchl-a_natural_GEE) | 23 | 0.82 | 0.68 | |
| (21) | LogChl-a_artificial = 0.06 + (0.299 × logchl-a_artificial_GEE) | 33 | 0.38 | 0.15 | |
| (22) | SQRTSecchi_general = 1.646 + (0.291 × SQRTSecchi_general_GEE) | 103 | 0.42 | 0.17 | |
| (23) | SQRTSecchi_natural = 0.233 + (0.841 × SQRTSecchi_natural_GEE) | 24 | 0.97 | 0.95 | |
| (24) | SQRTSecchi_artificial = 1.490 + (0.399 × SQRTSecchi_artificial_GEE) | 36 | 0.79 | 0.62 | |
| (25) | LogTP_general = −0.086 + (0.963 × LOGTP_general_GEE) | 27 | 0.99 | 0.98 | |
| (26) | LogTP_natural = −0.178s + (0.742 × LOGTP_natural_GEE) | 42 | 0.93 | 0.87 |
| Equation | Model | ME | RMSE | NRMSE | MAPE | Sensor |
|---|---|---|---|---|---|---|
| (1) | Chl-a_general | −1.3 | 16.4 | 0.1 | 221.7 | Landsat |
| (10) | Chl-a_general_GEE | 1.5 | 16.4 | 0.1 | 169.5 | |
| (2) | Chl-a_natural | −13.6 | 29.1 | 0.2 | 350.5 | |
| (11) | Chl-a_natural_GEE | 4.6 | 25.4 | 0.2 | 98.9 | |
| (3) | Chl-a_artificial | 0.8 | 4.6 | 0.2 | 79.3 | |
| (12) | Chl-a_artificial_GEE | 1.7 | 4.9 | 0.2 | 87.5 | |
| (1) | Chl-a_general | 1.7 | 15.4 | 0.1 | 122.3 | Sentinel 2 |
| (19) | Chl-a_general_GEE | 3.7 | 16.8 | 0.1 | 116.8 | |
| (2) | Chl-a_natural | −3.6 | 14.9 | 0.1 | 177.7 | |
| (20) | Chl-a_natural_GEE | 7.4 | 25.4 | 0.2 | 84.9 | |
| (3) | Chl-a_artificial | 1.9 | 4.5 | 0.2 | 82.7 | |
| (21) | Chl-a_artificial_GEE | 2.4 | 4.9 | 0.2 | 65.5 |
| Equation | Model | ME | RMSE | NRMSE | MAPE | Sensor |
|---|---|---|---|---|---|---|
| (4) | Secchi_general | 1.27 | 2.4 | 0.19 | 46.5 | Landsat |
| (13) | Secchi_general_GEE | 0.65 | 2.2 | 0.17 | 52.7 | |
| (5) | Secchi_natural | −0.53 | 1.83 | 0.15 | 56.2 | |
| (14) | Secchi_natural_ GEE | 0.31 | 1.9 | 0.16 | 43.3 | |
| (6) | Secchi_artificial | 1.55 | 2.5 | 0.3 | 51.7 | |
| (15) | Secchi_artificial_GEE | −0.2 | 2.01 | 0.24 | 83.2 | |
| (4) | Secchi_general | −0.3 | 3.8 | 0.3 | 80.8 | Sentinel 2 |
| (22) | Secchi_general_GEE | −0.58 | 2.6 | 0.2 | 132.7 | |
| (5) | Secchi_natural | −1.16 | 3.4 | 0.27 | 57.4 | |
| (23) | Secchi_natural_GEE | −0.49 | 2.7 | 0.22 | 48.7 | |
| (6) | Secchi_artificial | 1.31 | 2.4 | 0.29 | 60.2 | |
| (24) | Secchi_artificial_GEE | −0.13 | 2.1 | 0.25 | 83.9 |
| Equation | Model | ME | RMSE | NRMSE | MAPE | Sensor |
|---|---|---|---|---|---|---|
| (7) | TP_general | 0.07 | 0.34 | 0.15 | 53.8 | Landsat |
| (16) | TP_general_GEE | 0.08 | 0.36 | 0.16 | 47.5 | |
| (8) | TP_natural | 0.05 | 0.26 | 0.11 | 58.3 | |
| (17) | TP_natural_GEE | 0.04 | 0.27 | 0.12 | 71.1 | |
| (7) | Application of TP general model on artificial lakes | −0.01 | 0.04 | 0.21 | 44.4 | |
| (16) | Application of TP general model on artificial lakes_GEE | −0.002 | 0.035 | 0.19 | 37.5 | |
| (7) | TP_general | 0.03 | 0.19 | 0.15 | 45.2 | Sentinel 2 |
| (25) | TP_general_GEE | 0.039 | 0.19 | 0.15 | 41.2 | |
| (8) | TP_natural | 0.03 | 0.14 | 0.12 | 54.7 | |
| (26) | TP_natural_ GEE | 0.01 | 0.15 | 0.12 | 74.7 | |
| (7) | Application of TP general model on artificial lakes | 0.002 | 0.01 | 0.37 | 27.5 |
| Class Deviation Between General Models | Landsat | Sentinel 2 | Landsat | Sentinel 2 | Landsat | Sentinel 2 | Landsat | Sentinel 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TSIINSITU TSIMODELLED 2019 | TSIINSITU TSIMODELLED 2020 | TSIINSITU TSIGEE-MODELLED 2019 | TSIINSITU TSIGEE-MODELLED 2020 | |||||||||||||
| Freq. | % | Freq. | % | Freq. | % | Freq. | % | Freq. | % | Freq. | % | Freq. | % | Freq. | % | |
| −2 | 3 | 7.3 | 1 | 1.6 | 1 | 1.5 | 2 | 4.4 | 2 | 4.4 | ||||||
| −1 | 14 | 34.1 | 12 | 18.8 | 31 | 46.3 | 8 | 17.8 | 6 | 14.6 | 14 | 20.9 | 6 | 13.3 | ||
| 0 | 20 | 48.8 | 37 | 57.8 | 28 | 41.8 | 25 | 55.6 | 26 | 63.4 | 17 | 26.6 | 42 | 62.7 | 23 | 51.1 |
| 1 | 4 | 9.8 | 11 | 17.2 | 7 | 10.4 | 8 | 17.8 | 8 | 19.5 | 30 | 46.9 | 11 | 16.4 | 13 | 28.9 |
| 2 | 3 | 4.7 | 2 | 4.4 | 1 | 2.4 | 16 | 25.0 | 1 | 2.2 | ||||||
| 3 | 1 | 1.6 | ||||||||||||||
| Total | 41 | 100 | 64 | 100 | 67 | 100 | 45 | 100 | 41 | 100 | 64 | 100 | 67 | 100 | 45 | 100 |
| Class Deviation Between Natural Lakes | Landsat | Sentinel 2 | Landsat | Sentinel 2 | Landsat | Sentinel 2 | Landsat | Sentinel 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TSIINSITU TSIMODELLED 2019 | TSIINSITU TSIMODELLED 2020 | TSIINSITU TSIGEE-MODELLED 2019 | TSIINSITU TSIGEE-MODELLED 2020 | |||||||||||||
| Freq. | % | Freq. | % | Freq. | % | Freq. | % | Freq. | % | Freq. | % | Freq. | % | Freq. | % | |
| −1 | 9 | 26.5 | 5 | 9.8 | 16 | 32.7 | 4 | 17.4 | 7 | 20.6 | 3 | 5.9 | 9 | 18.4 | 4 | 17.4 |
| 0 | 22 | 64.7 | 34 | 66.7 | 31 | 63.3 | 12 | 52.2 | 21 | 61.8 | 31 | 60.8 | 35 | 71.4 | 12 | 52.2 |
| 1 | 3 | 8.8 | 11 | 21.6 | 1 | 2 | 7 | 30.4 | 6 | 17.6 | 16 | 31.4 | 4 | 8.2 | 7 | 30.4 |
| 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2.0 | ||||||||
| Total | 34 | 100 | 51 | 100 | 49 | 100 | 23 | 100 | 34 | 100 | 51 | 100 | 49 | 100 | 23 | 100 |
| Class Deviation Between Artificial Lakes | Landsat | Sentinel 2 | Landsat | Sentinel 2 | Landsat TSIGEE-MODELLED 2019 | Landsat | Sentinel 2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TSIINSITU TSIMODELLED 2019 | TSIINSITU TSIMODELLED 2020 | TSIINSITU TSIGEE-MODELLED 2020 | ||||||||||||
| Freq. | % | Freq. | % | Freq. | % | Freq. | % | Freq. | % | Freq. | % | Freq. | % | |
| −2 | 1 | 7.7 | 2 | 15.4 | 1 | 5.9 | 1 | 4.5 | ||||||
| −1 | 3 | 23.1 | 3 | 23.1 | 4 | 23.5 | 3 | 17.6 | 1 | 4.5 | ||||
| 0 | 5 | 38.5 | 3 | 23.1 | 8 | 47.1 | 15 | 68.2 | 3 | 23.1 | 10 | 58.8 | 14 | 63.6 |
| 1 | 2 | 15.4 | 5 | 38.5 | 2 | 11.8 | 4 | 18.2 | 5 | 38.5 | 3 | 17.6 | 5 | 22.7 |
| 2 | 2 | 15.4 | 2 | 11.8 | 2 | 9.1 | 3 | 23.1 | 1 | 5.9 | 2 | 9.1 | ||
| 3 | 1 | 7.7 | ||||||||||||
| 4 | 1 | 7.7 | ||||||||||||
| Total | 13 | 100 | 13 | 100 | 17 | 100 | 22 | 100 | 13 | 100 | 17 | 100 | 22 | 100 |
| Models | Landsat | Sentinel 2 | |
|---|---|---|---|
| Chl-a | General | GEE | GEE |
| Natural | DOS1 | DOS1 | |
| Artificial | ALL | DOS1 | |
| Secchi Disk Depth | General | DOS1 | GEE |
| Natural | GEE | DOS1 | |
| Artificial | DOS1 | DOS1 | |
| TP | General | DOS1 | ALL |
| Natural | DOS1 | DOS1 | |
| Artificial | DOS1 | DOS1 |
| 2019 | Chl-a | Secchi | TP | |||||||
| Models | General | Natural | Artificial | General | Natural | Artificial | General | Natural | Artificial | |
| Landsat | X | X | X | X | X | X | ||||
| Sentinel 2 | X | X | X | X | ||||||
| ENHANCEMENT | ||||||||||
| Landsat | NO* | YES | NO | YES | YES | YES* | YES | NO | YES | |
| Sentinel 2 | NO | YES | NO* | YES | YES | YES* | YES | NO | NO MODEL | |
| 2020 | Chl-a | Secchi | TP | |||||||
| Models | General | Natural | Artificial | General | Natural | Artificial | General | Natural | Artificial | |
| Landsat | X | X | X | X | X | X | X | |||
| Sentinel 2 | X | X | X | |||||||
| ENHANCEMENT | ||||||||||
| Landsat | NO | YES | NO | YES* | YES | YES* | YES | NO | YES | |
| Sentinel 2 | NO* | NO* | NO* | NO | YES | NO | YES | NO | NO MODEL | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Markogianni, V.; Kalivas, D.P.; Petropoulos, G.P.; Giovos, R.; Dimitriou, E. Comparative Analysis of Trophic Status Assessment Using Different Sensors and Atmospheric Correction Methods in Greece’s WFD Lake Network. Remote Sens. 2025, 17, 1822. https://doi.org/10.3390/rs17111822
Markogianni V, Kalivas DP, Petropoulos GP, Giovos R, Dimitriou E. Comparative Analysis of Trophic Status Assessment Using Different Sensors and Atmospheric Correction Methods in Greece’s WFD Lake Network. Remote Sensing. 2025; 17(11):1822. https://doi.org/10.3390/rs17111822
Chicago/Turabian StyleMarkogianni, Vassiliki, Dionissios P. Kalivas, George P. Petropoulos, Rigas Giovos, and Elias Dimitriou. 2025. "Comparative Analysis of Trophic Status Assessment Using Different Sensors and Atmospheric Correction Methods in Greece’s WFD Lake Network" Remote Sensing 17, no. 11: 1822. https://doi.org/10.3390/rs17111822
APA StyleMarkogianni, V., Kalivas, D. P., Petropoulos, G. P., Giovos, R., & Dimitriou, E. (2025). Comparative Analysis of Trophic Status Assessment Using Different Sensors and Atmospheric Correction Methods in Greece’s WFD Lake Network. Remote Sensing, 17(11), 1822. https://doi.org/10.3390/rs17111822











