Research on Spaceborne Neural Network Accelerator and Its Fault Tolerance Design
Abstract
1. Introduction
2. Materials and Methods
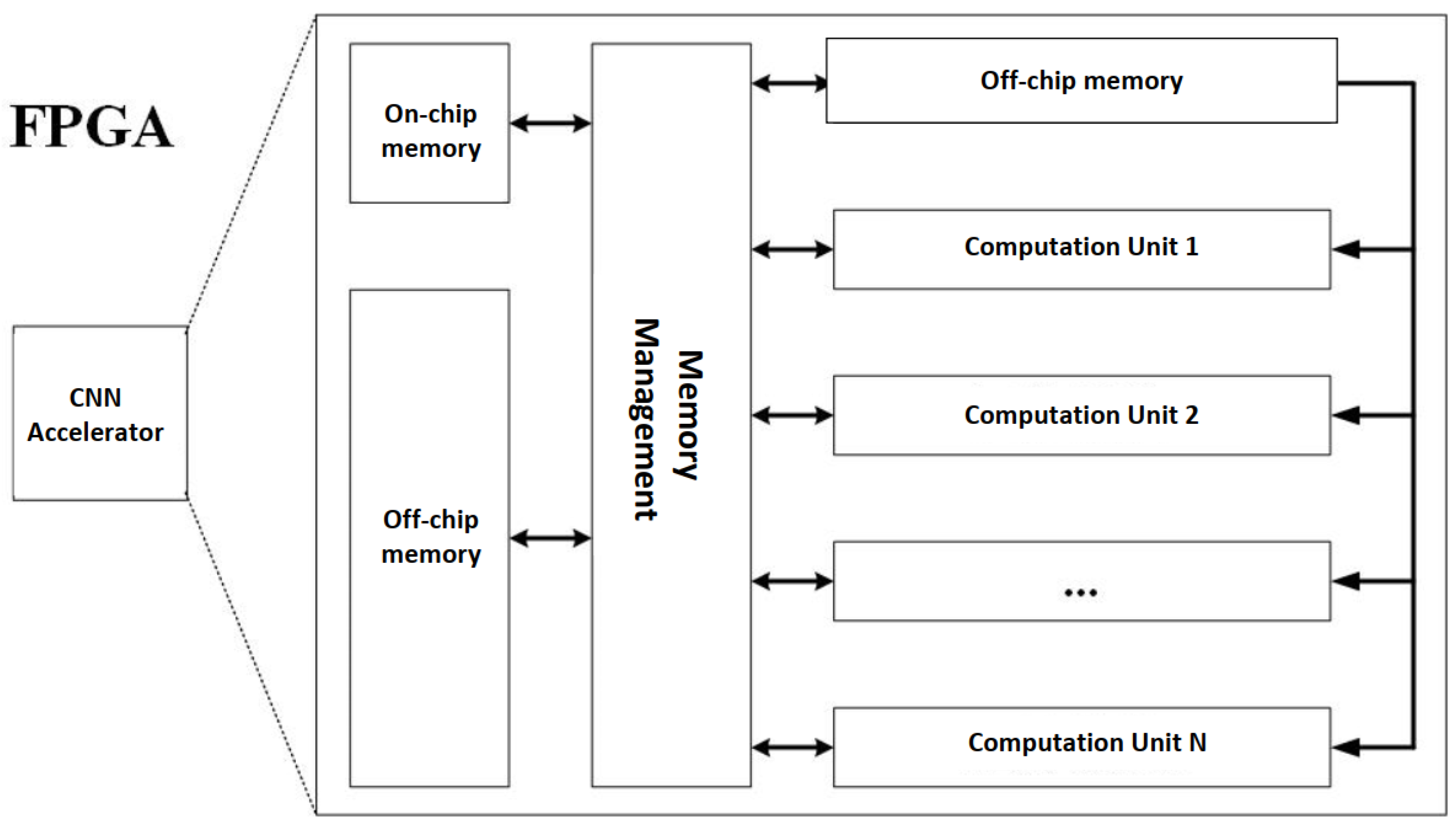
2.1. FPGA Accelerator Research
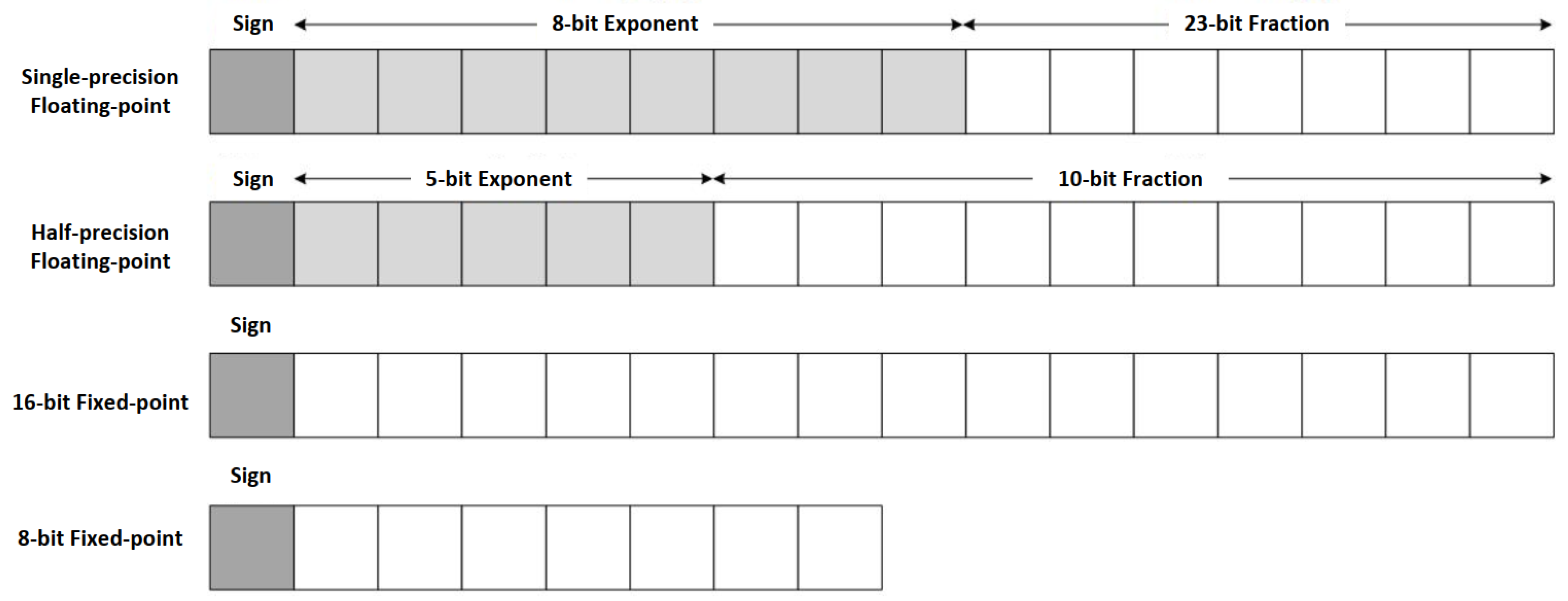
2.2. Analysis of Single-Event Upset (SEU) Impact
2.2.1. Weight Upset
2.2.2. Feature Map Upset
2.2.3. Operation Upset
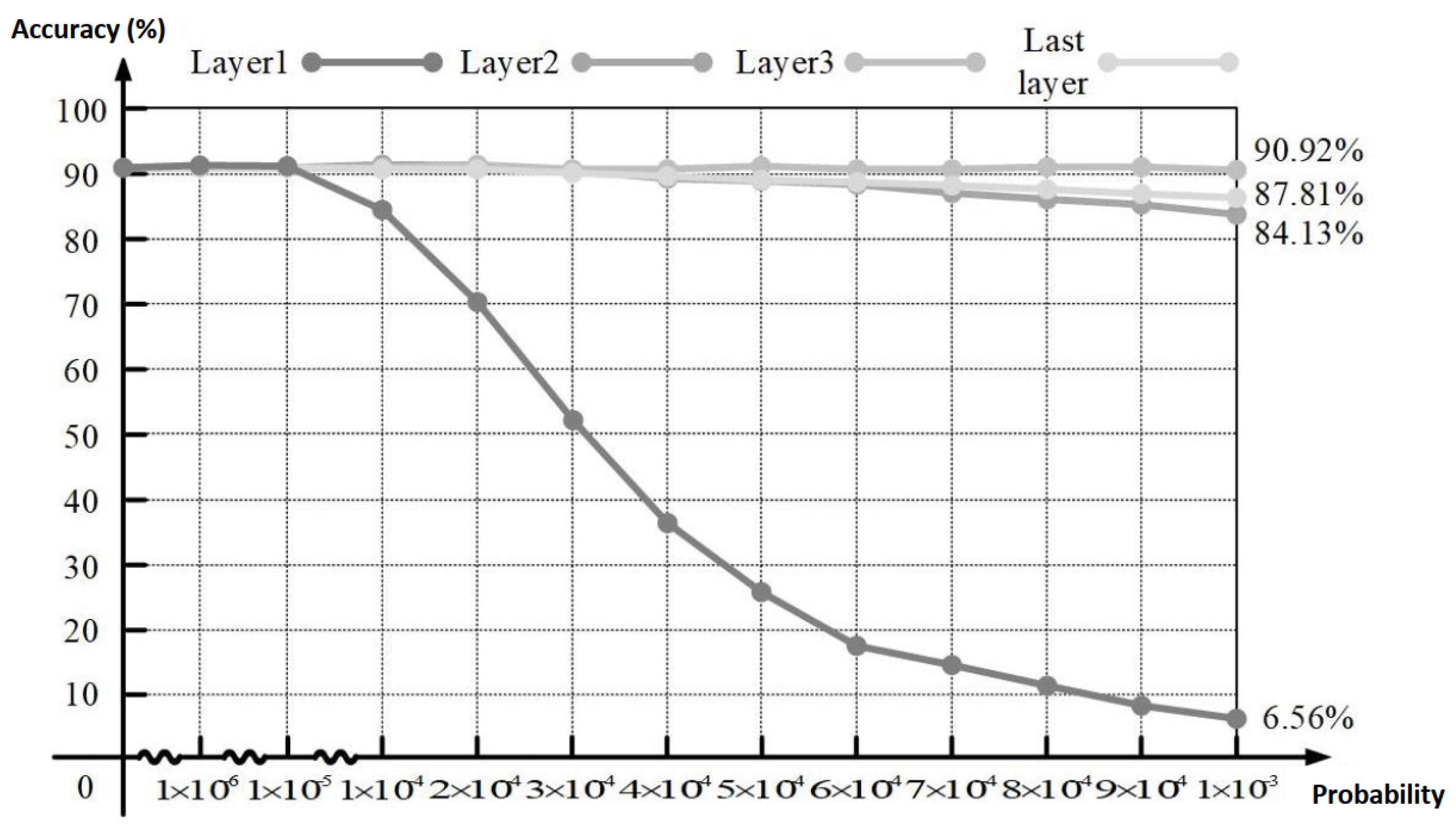
2.3. CNN Fault Tolerance Analysis
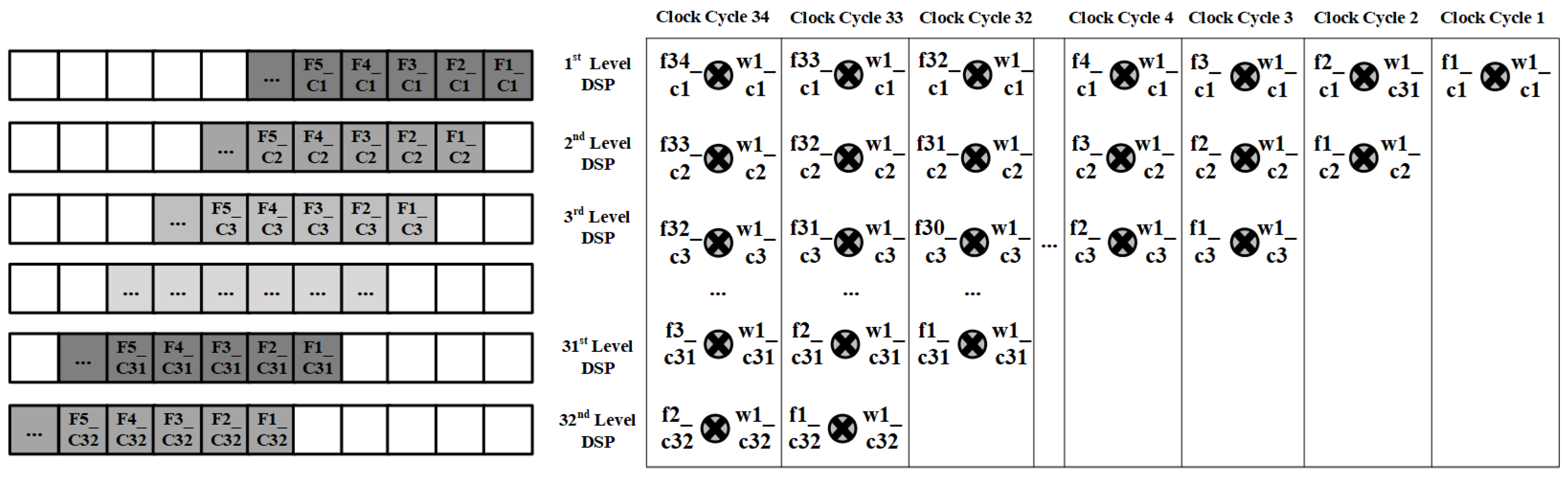
2.4. CNN Accelerator Design
2.4.1. Instruction Encoding Design
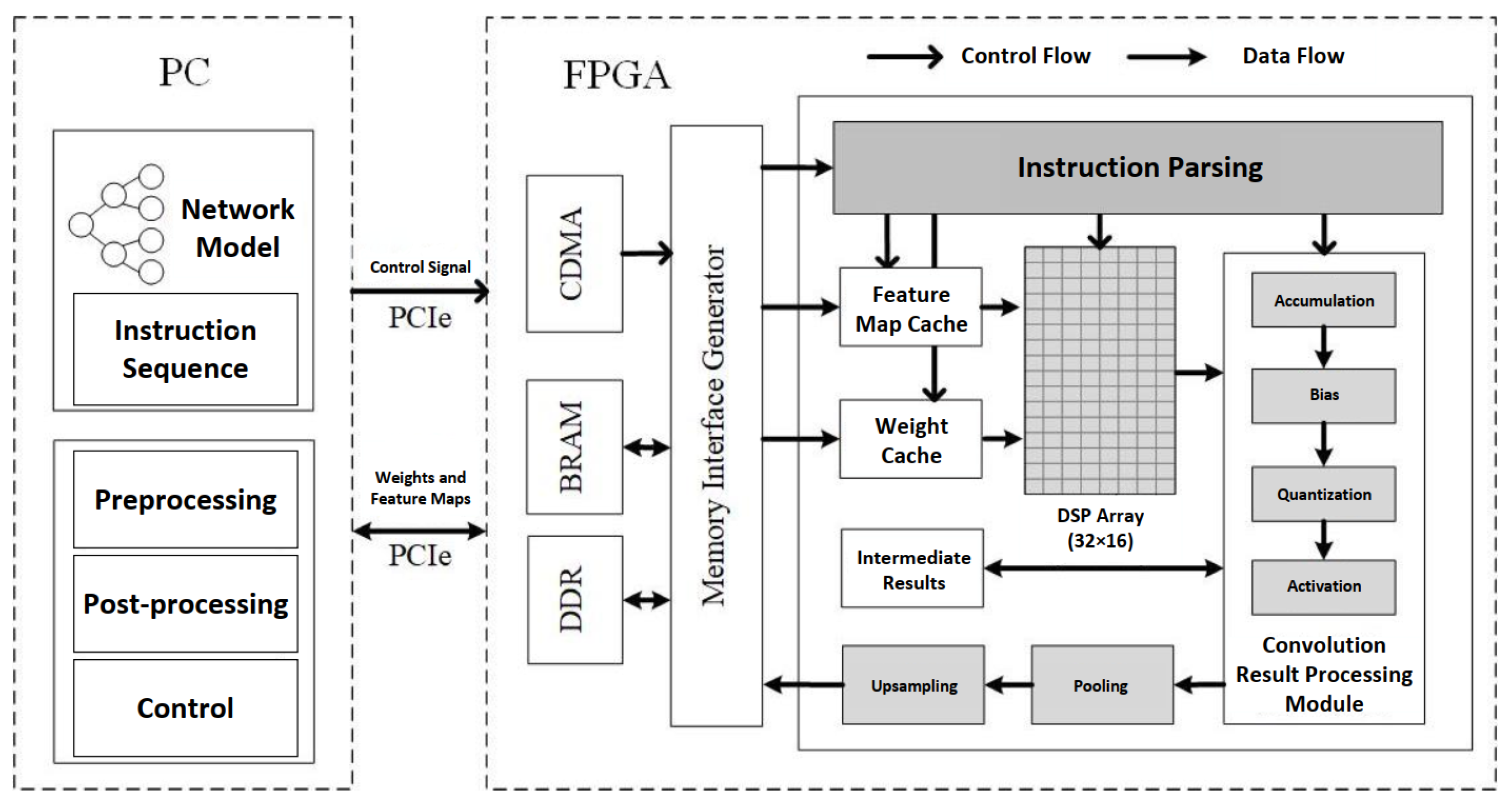
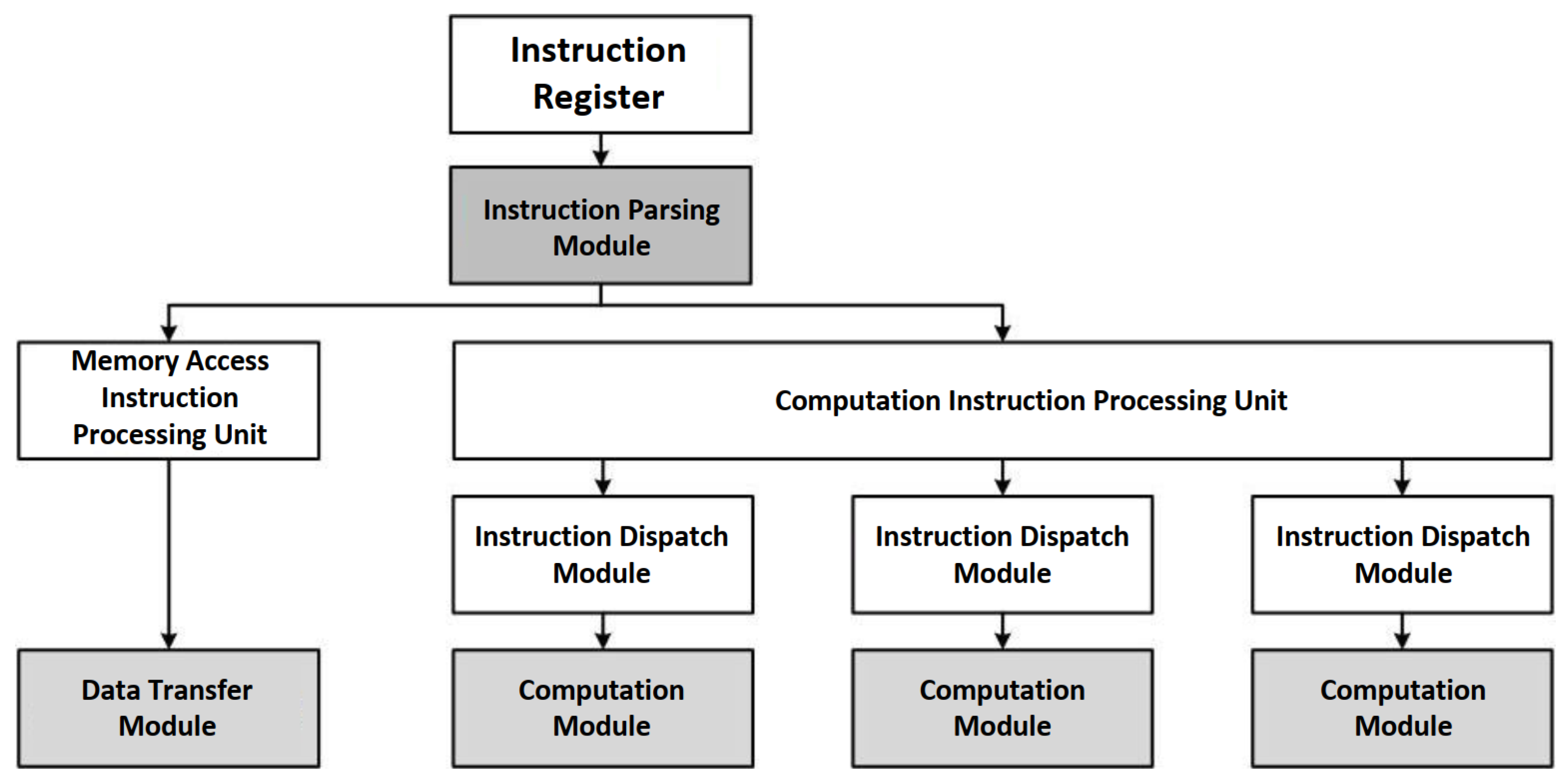
2.4.2. Accelerator Design
Instruction Parsing Module
Convolution Module
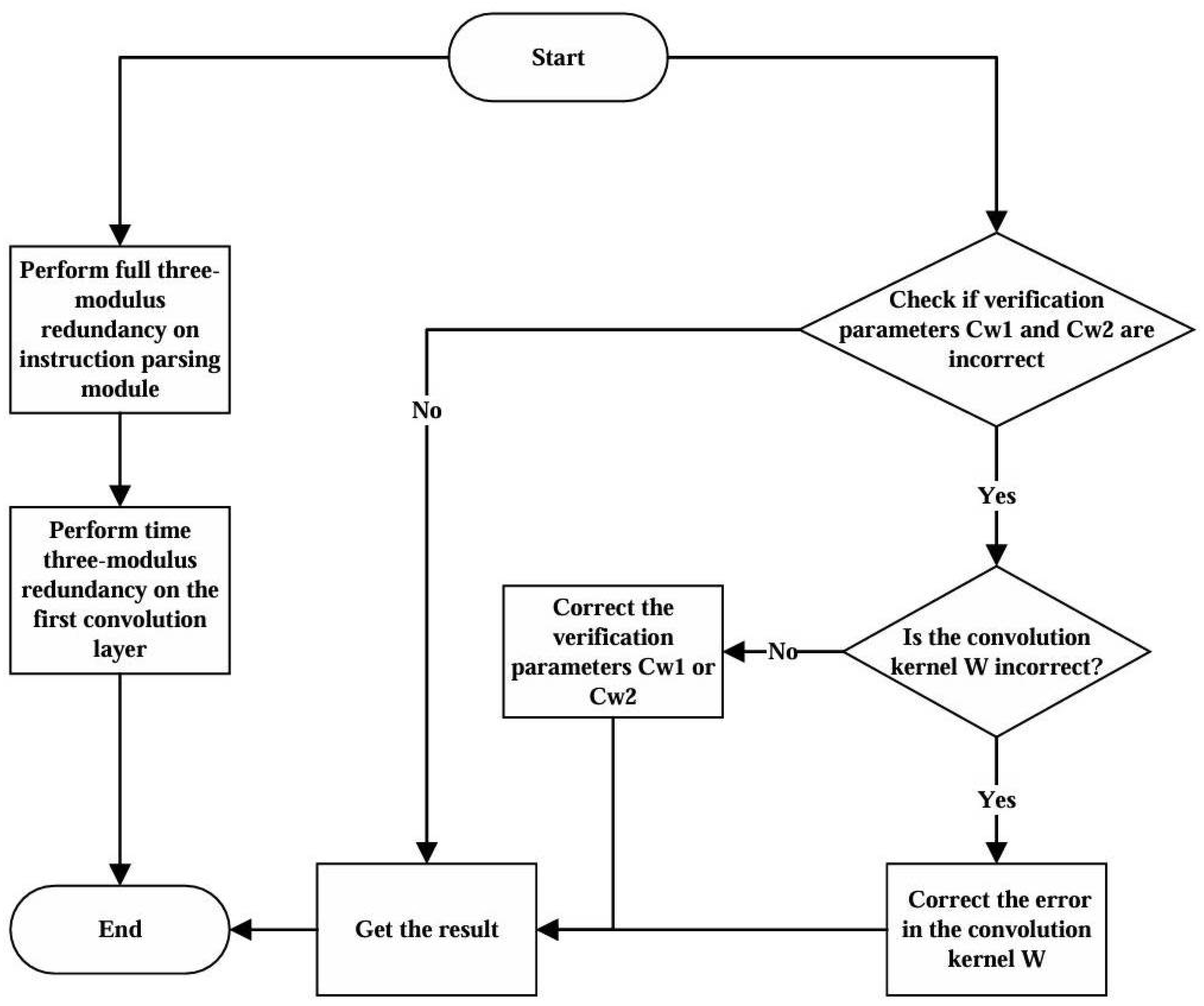
2.5. Fault Tolerance Design
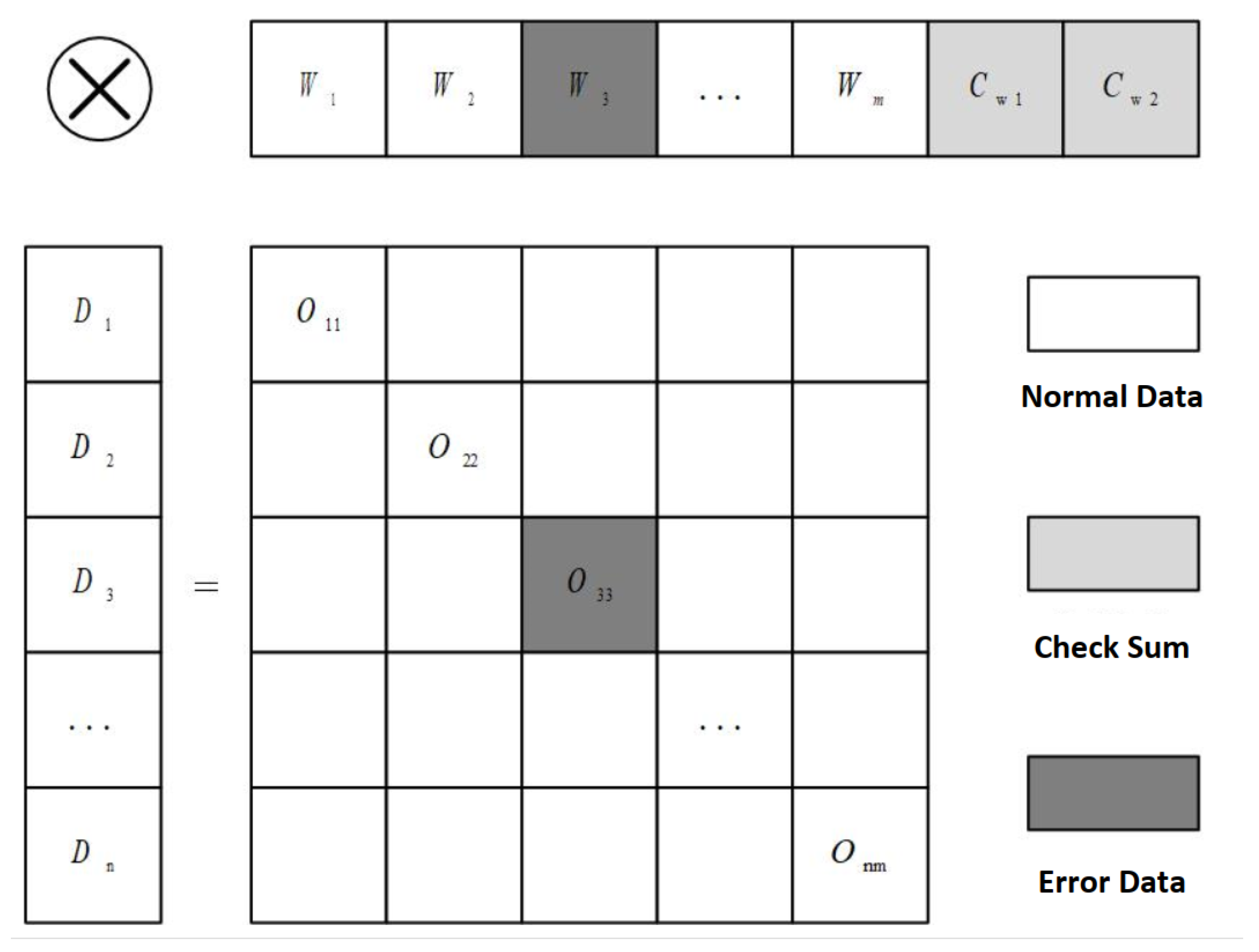
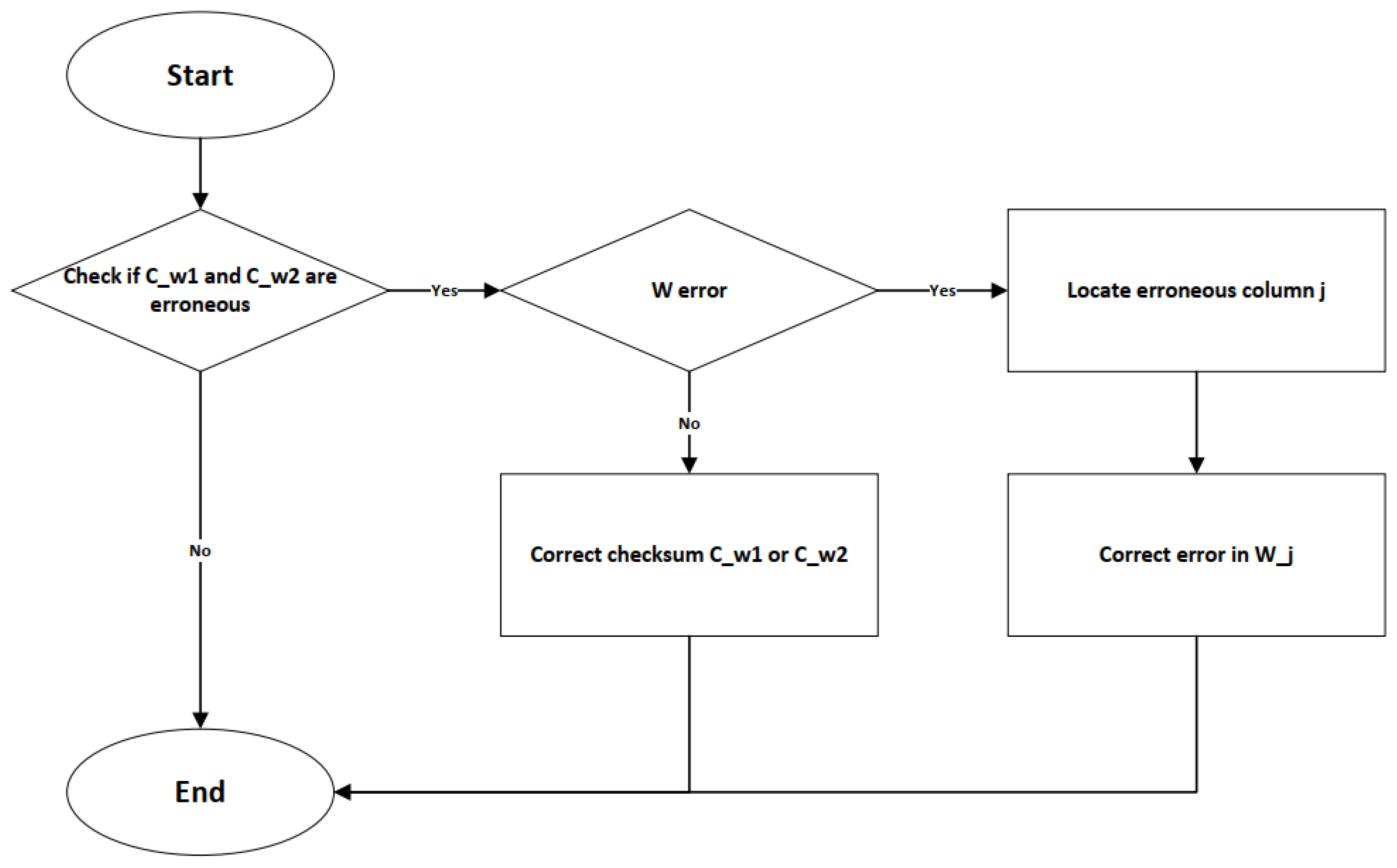
2.5.1. Fault Tolerance Design for Model Parameters
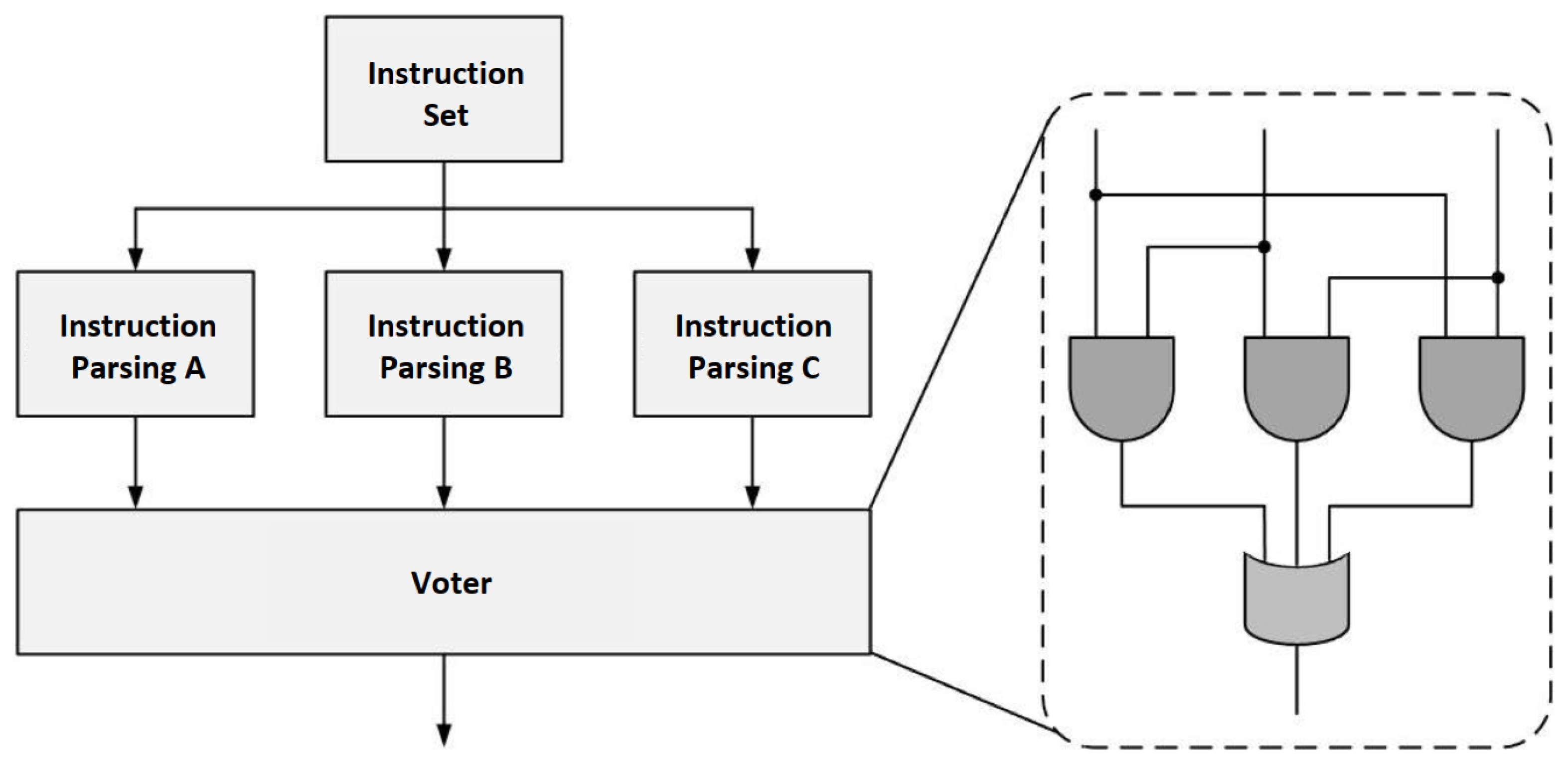
2.5.2. Fault Tolerance Design for Accelerator Control
2.5.3. Fault Tolerance in Computation
3. Results
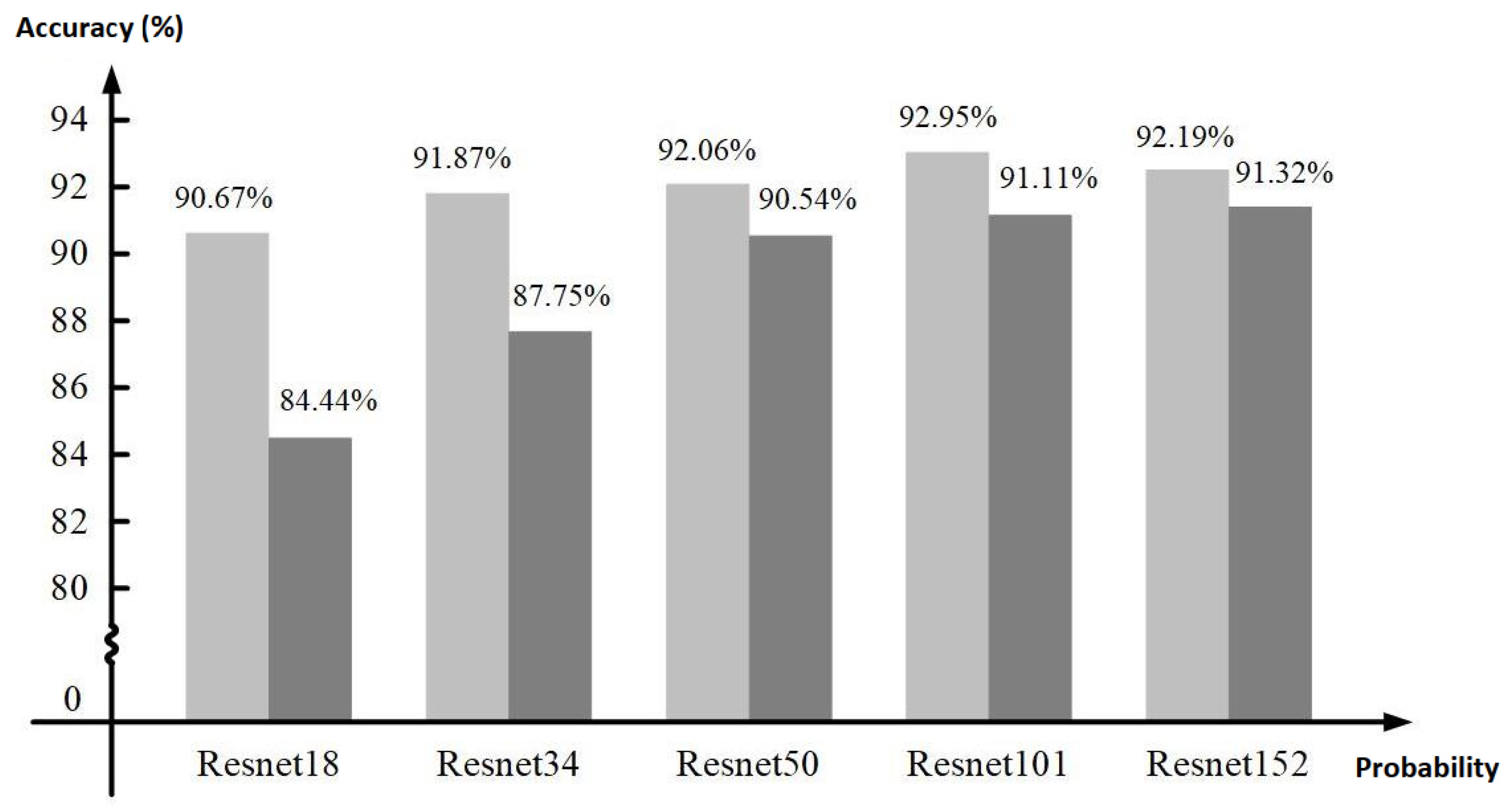
3.1. Hardware Accelerator Performance Comparison
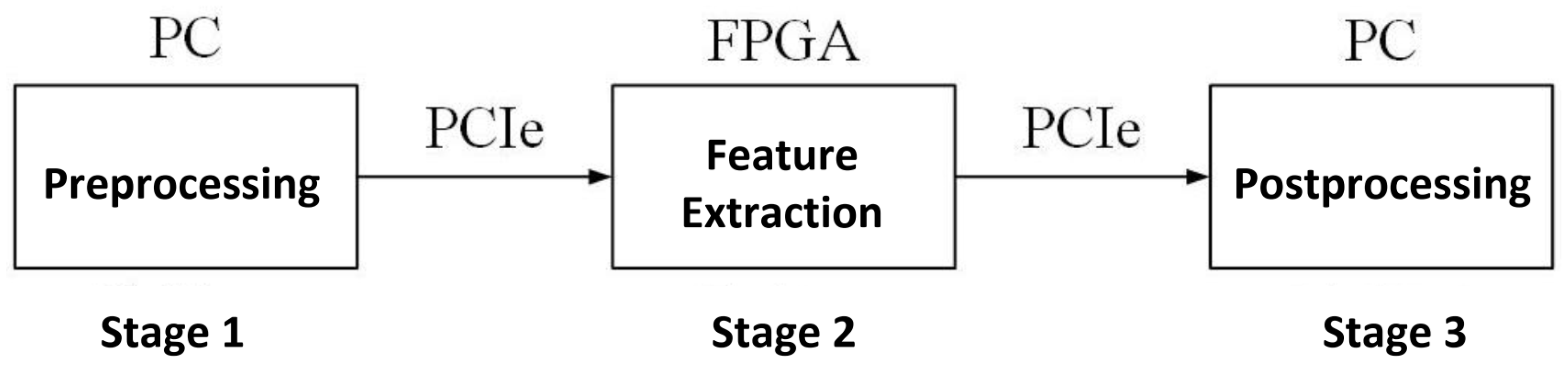
- (a)
- Image Preprocessing: The PC reads the raw image and adjusts its size to through scale transformation. The processed image data are then transferred to the FPGA’s DDR via PCIe.
- (b)
- Image Feature Extraction: The instruction parsing module sequentially reads binary instructions from a fixed address. Based on the parsed results, feature map data and weight data are transferred from DDR to the computational units for processing. Once the computation is completed, the data are written back to DDR.
- (c)
- Image Postprocessing: The feature extraction results are transferred back to the PC via PCIe, where postprocessing is performed. The classification result is printed based on the computed probabilities.
3.2. Fault Tolerance Performance Comparison
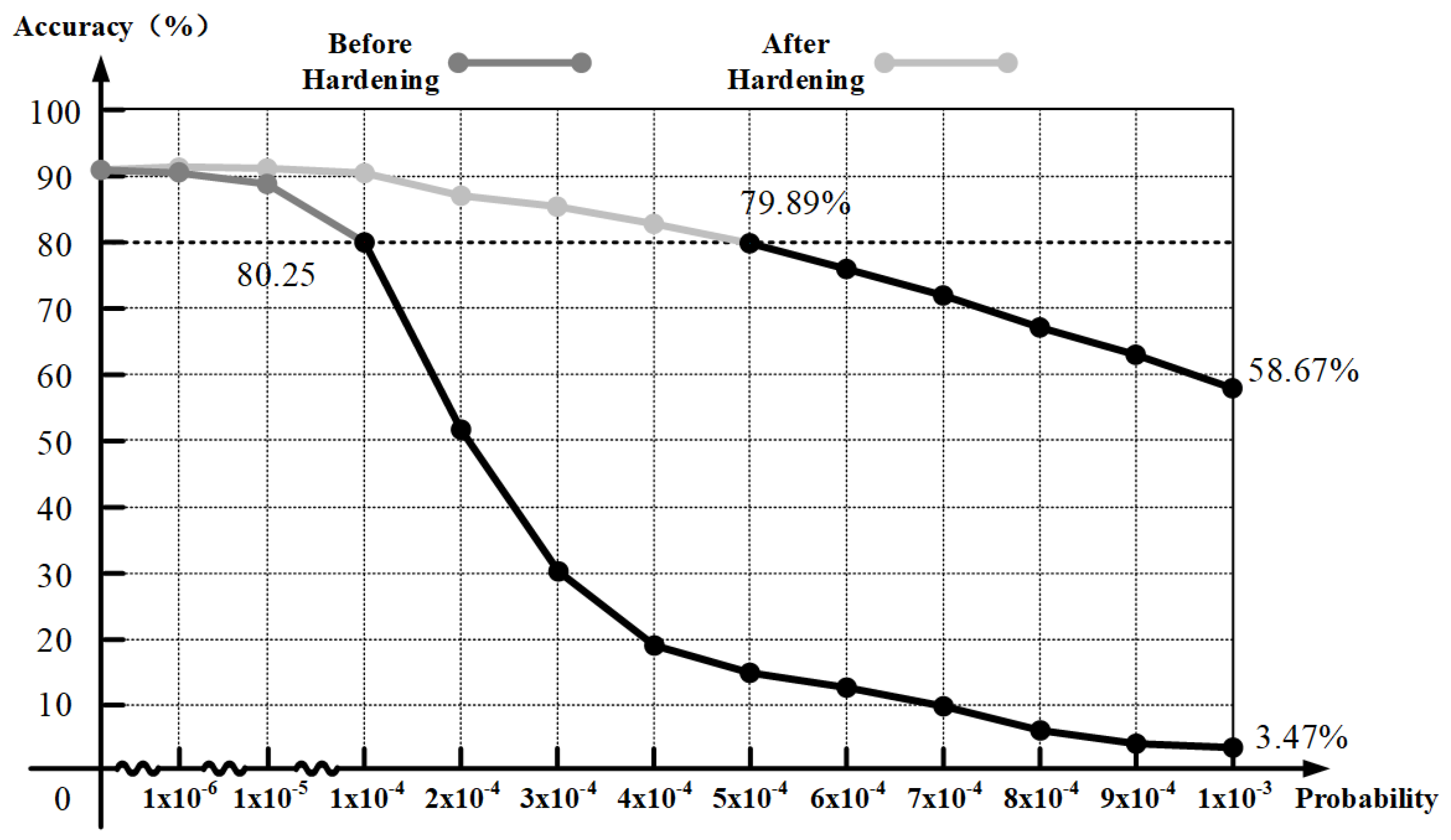
3.2.1. Weight Fault Tolerance Comparative Analysis
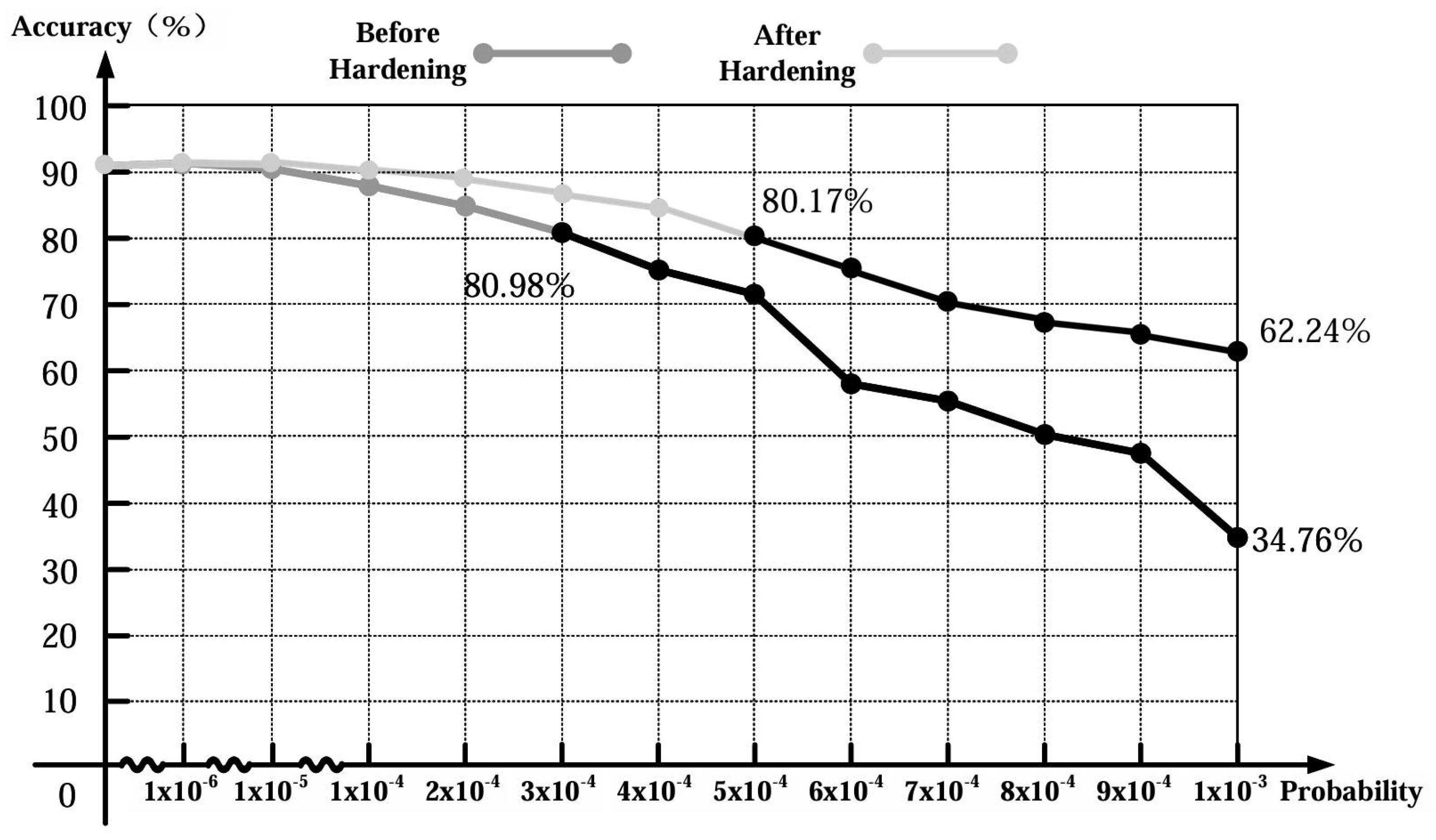
3.2.2. Computation Fault Tolerance Comparative Analysis
3.2.3. Performance Comparison Before and After Fault Tolerance Implementation
4. Discussion
4.1. Performance Evaluation and Comparison
4.2. Fault Tolerance Comparative Analysis
4.3. Summary and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yao, B.; Mao, L.W.Z. Applications of Artificial Intelligence in Space Equipment. Mod. Def. Technol. 2023, 51, 33–42. [Google Scholar] [CrossRef]
- Goodwill, J.; Crum, G.; Mackinnon, J.; Brewer, C.; Monaghan, M.; Wise, T.; Wilson, C. NASA SpaceCube Edge TPU SmallSat Card for Autonomous Operations and Onboard Science-Data Analysis. In Proceedings of the 35th Annual Small Satellite Conference, Virtual, 7–12 August 2021. [Google Scholar]
- Rad, I.O.; Alarcia, R.M.G.; Dengler, S. Preliminary Evaluation of Commercial Off-The-Shelf GPUs for Machine Learning Applications in Space. Master’s Thesis, Technical University of Munich, Munich, Germany, 2023. [Google Scholar]
- Slater, W.S.; Tiwari, N.P.; Lovelly, T.M.; Mee, J.K. Total Ionizing Dose Radiation Testing of NVIDIA Jetson Nano GPUs. In Proceedings of the 2020 IEEE High Performance Extreme Computing Conference (HPEC), Waltham, MA, USA, 22–24 September 2020; pp. 1–3, ISSN 2643-1971. [Google Scholar] [CrossRef]
- Diana, L.; Dini, P. Review on Hardware Devices and Software Techniques Enabling Neural Network Inference Onboard Satellites. Remote Sens. 2024, 16, 3957. [Google Scholar] [CrossRef]
- Hong, H.; Choi, D.; Kim, N.; Lee, H.; Kang, B.; Kang, H.; Kim, H. Survey of convolutional neural network accelerators on field-programmable gate array platforms: Architectures and optimization techniques. J. Real-Time Image Process. 2024, 21, 64. [Google Scholar] [CrossRef]
- Maji, S.; Lee, K.; Gongye, C.; Fei, Y.; Chandrakasan, A.P. An Energy-Efficient Neural Network Accelerator with Improved Resilience Against Fault Attacks. IEEE J. Solid-State Circuits 2024, 59, 3106–3116. [Google Scholar] [CrossRef]
- Liu, F.; Li, H.; Hu, W.; He, Y. Review of neural network model acceleration techniques based on FPGA platforms. Neurocomputing 2024, 610, 128511. [Google Scholar] [CrossRef]
- Cosmas, K.; Kenichi, A. Utilization of FPGA for Onboard Inference of Landmark Localization in CNN-Based Spacecraft Pose Estimation. Aerospace 2020, 7, 159. [Google Scholar] [CrossRef]
- Rapuano, E.; Meoni, G.; Pacini, T.; Dinelli, G.; Furano, G.; Giuffrida, G.; Fanucci, L. An FPGA-Based Hardware Accelerator for CNNs Inference on Board Satellites: Benchmarking with Myriad 2-Based Solution for the CloudScout Case Study. Remote Sens. 2021, 13, 1518. [Google Scholar] [CrossRef]
- Furano, G.; Meoni, G.; Dunne, A.; Moloney, D.; Ferlet-Cavrois, V.; Tavoularis, A.; Byrne, J.; Buckley, L.; Psarakis, M.; Voss, K.O.; et al. Towards the Use of Artificial Intelligence on the Edge in Space Systems: Challenges and Opportunities. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 44–56. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, Y.; Peng, Y.; Zhang, D.; Yan, Z.; Wang, D. A Deep Neural Network Hardware Accelerator System Based on FPGA. Space Control Technol. Appl. 2024, 50, 83–92. [Google Scholar]
- Chen, L.; Li, Y.; Ding, J.; Xu, M.; Zhang, Z.; Zhang, A.; Xie, Y. Hardware Design for Efficient On-Orbit Processing System of Spaceborne SAR Imaging. Signal Process. 2024, 40, 138–151. [Google Scholar]
- Zhang, X.; Wei, X.; Sang, Q.; Chen, H.; Xie, Y. An Efficient FPGA-Based Implementation for Quantized Remote Sensing Image Scene Classification Network. Electronics 2020, 9, 1344. [Google Scholar] [CrossRef]
- Wang, N.; Li, B.; Wei, X.; Wang, Y.; Yan, H. Ship Detection in Spaceborne Infrared Image Based on Lightweight CNN and Multisource Feature Cascade Decision. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4324–4339. [Google Scholar] [CrossRef]
- Yan, T.; Zhang, N.; Li, J.; Liu, W.; Chen, H. Automatic Deployment of Convolutional Neural Networks on FPGA for Spaceborne Remote Sensing Application. Remote Sens. 2022, 14, 3130. [Google Scholar] [CrossRef]
- Yang, G.; Lei, J.; Xie, W.; Fang, Z.; Li, Y.; Wang, J.; Zhang, X. Algorithm/Hardware Codesign for Real-Time On-Satellite CNN-Based Ship Detection in SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Ni, S.; Wei, X.; Zhang, N.; Chen, H. Algorithm–Hardware Co-Optimization and Deployment Method for Field-Programmable Gate-Array-Based Convolutional Neural Network Remote Sensing Image Processing. Remote Sens. 2023, 15, 5784. [Google Scholar] [CrossRef]
- Pitonak, R.; Mucha, J.; Dobis, L.; Javorka, M.; Marusin, M. CloudSatNet-1: FPGA-Based Hardware-Accelerated Quantized CNN for Satellite On-Board Cloud Coverage Classification. Remote Sens. 2022, 14, 3180. [Google Scholar] [CrossRef]
- Guo, Z.; Liu, K.; Liu, W.; Sun, X.; Ding, C.; Li, S. An Overlay Accelerator of DeepLab CNN for Spacecraft Image Segmentation on FPGA. Remote Sens. 2024, 16, 894. [Google Scholar] [CrossRef]
- Wei, X.; Wang, J.W.Y. Research on Detection of SEU Rates of XQR2V3000 FPGA in Orbit. J. Astronaut. 2019, 40, 719–724. [Google Scholar]
- Niranjan, S.; Frenzel, J. A comparison of fault-tolerant state machine architectures for space-borne electronics. IEEE Trans. Reliab. 1996, 45, 109–113. [Google Scholar] [CrossRef]
- Sajjade, F.M.; Goyal, N.; Moogina, R.; Bksvl, V. Soft Error Rate Assessment Studies of Space borne Computer. Int. J. Perform. Eng. 2016, 12, 423. [Google Scholar]
- Wang, D. Design of Reinforced Heterogeneous Redundant Spaceborne Computer Based on COTS Devices. Electron. Meas. Technol. 2020, 43, 1–6. [Google Scholar] [CrossRef]
- Xie, Y.; Zhong, Z.; Li, B.; Xie, Y.; Chen, L.; Chen, H. An ARM-FPGA Hybrid Acceleration and Fault Tolerant Technique for Phase Factor Calculation in Spaceborne Synthetic Aperture Radar Imaging. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 5059–5072. [Google Scholar] [CrossRef]
- Wang, C.; Wang, T. Research Progress on FPGA-Based Machine Learning Hardware Acceleration. Chin. J. Comput. 2020, 43, 1161–1182. [Google Scholar]
- Wu, Y.; Liang, K.L.; Liu, Y.; Cui, H.M. The Progress and Trends of FPGA-Based Accelerators in Deep Learning. Chin. J. Comput. 2019, 42, 2461–2480. [Google Scholar]
- Ye, P.; Huang, J.S.; Sun, Z.Z.; Yang, M.F.; Meng, L.Z. The Process and Experience in the Development of Chinese Lunar Probe. Sci. Sin. Technol. 2014, 44, 543–558. [Google Scholar] [CrossRef]
- Sun, P.; Liu, X.; Mao, E.; Huang, Y.; Zhang, S.; Lou, S. Radiation-Resistant Design Method for Satellite Payload BRAM Using Time-Division Refresh and Location Constraints. J. Natl. Univ. Def. Technol. 2023, 45, 231–236. [Google Scholar]
- Chen, Z.; Zhang, M.Z.J. A Fault-Tolerant Design Method for Onboard Neural Networks. J. Electron. Inf. Technol. 2023, 45, 3234–3243. [Google Scholar]
- Lam, M. Software pipelining: An effective scheduling technique for VLIW machines. SIGPLAN Not. 1988, 23, 318–328. [Google Scholar] [CrossRef]
- Huang, W.; Wu, H.; Chen, Q.; Luo, C.; Zeng, S.; Li, T.; Huang, Y. FPGA-Based High-Throughput CNN Hardware Accelerator With High Computing Resource Utilization Ratio. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 4069–4083. [Google Scholar] [CrossRef]
- Liu, Z.; Dou, Y.; Jiang, J.; Xu, J. Automatic code generation of convolutional neural networks in FPGA implementation. In Proceedings of the 2016 International Conference on Field-Programmable Technology (FPT), Xi’an, China 7–9 December 2016; pp. 61–68. [Google Scholar] [CrossRef]
- Zhang, C.; Sun, G.; Fang, Z.; Zhou, P.; Pan, P.; Cong, J. Caffeine: Toward Uniformed Representation and Acceleration for Deep Convolutional Neural Networks. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2019, 38, 2072–2085. [Google Scholar] [CrossRef]

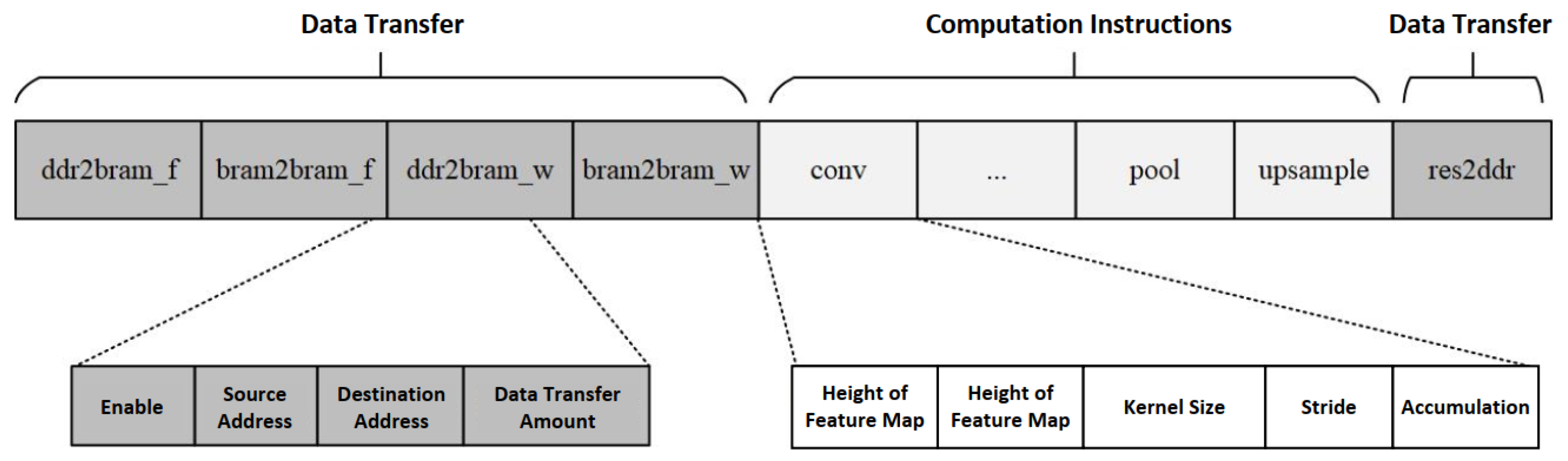



| Instruction Type | Instruction Name | Address | Length | Instruction Function | Parameters | Parameter Functionality |
|---|---|---|---|---|---|---|
| Data Transfer | ddr2bram_f | 0x000 | 105 bit | Transfers feature map data from off-chip DDR memory to on-chip BRAM cache. | .enable | Whether the instruction is executed |
| .srcAddress | The address from which data are sourced | |||||
| .desAddress | The address to which data are directed | |||||
| .length | The quantity of data being loaded | |||||
| bram2bram_f | 0x069 | 70 bit | Transfers feature map data between on-chip BRAM and convolution cache. | .enable | Whether the instruction is executed | |
| .waitma | Whether the instruction awaits the completion of DDR data loading | |||||
| .srcAddress | The address from which data are sourced | |||||
| .length | The quantity of data being loaded | |||||
| ddr2bram_w | 0x0af | 105 bit | Transfers weight data from off-chip DDR memory to on-chip BRAM cache. | .enable | Whether the instruction is executed | |
| .srcAddress | The address from which data are sourced | |||||
| .desAddress | The address to which data are directed | |||||
| .length | The quantity of data being loaded | |||||
| bram2bram_w | 0x118 | 70 bit | Transfers weight data between on-chip BRAM and convolution cache. | .enable | Whether the instruction is executed | |
| .waitma | Whether the instruction awaits the completion of DDR data loading | |||||
| .srcAddress | The address from which data are sourced | |||||
| .length | The quantity of data being loaded | |||||
| Computation Instructions | conv | 0x15e | 33 bit | Convolution control. | .enable | Whether convolution is applied |
| .width | The width of the feature map | |||||
| .high | The height of the feature map | |||||
| .kernel | The size of the convolution kernel | |||||
| .stride | The stride of the convolution operation | |||||
| blockwise | 0x180 | 38 bit | Blockwise convolution merging. | .enable | Whether to merge blockwise convolutions | |
| .merge | Strategy for merging, such as row-wise or column-wise | |||||
| bias | 0x1a7 | 33 bit | Bias control. | .enable | Whether to use bias in the convolution | |
| .width | The width of the feature map | |||||
| .high | The height of the feature map | |||||
| quant | 0x1c6 | 21 bit | Quantization control. | .enable | Whether quantization is applied | |
| .shift | Direction of data shift after quantization | |||||
| .shiftb | Direction of data shift before quantization | |||||
| short | 0x1db | 38 bit | Residual (shortcut) control. | .enable | Whether to use a shortcut connection | |
| .length | Range of the shortcut connection | |||||
| Data Transfer | res2ddr | 0x237 | 69 bit | Transfers computation results to off-chip storage. | .enable | Whether to use an instruction for the operation |
| .address | The address to which data are written | |||||
| .length | The volume of data being written |
| Resource | Total | Original | Triple Modular Redundancy (TMR) | This Paper |
|---|---|---|---|---|
| LUT | 433,200 | 129,771 | 389,313 | 143,865 |
| BRAM | 1470 | 436 | 1308 | 495 |
| DSP | 3600 | 514 | 1542 | 546 |
| Work 1 [32] | Work 2 [33] | Work 3 [34] | This Paper | |||
|---|---|---|---|---|---|---|
| ResNet18 | VGG16 | AlexNet | ||||
| Platform | XC7VX980T | VC709 | VC709 | VC709 | VC709 | VC709 |
| Frequency/MHz | 150 | 100 | 150 | 200 | 200 | 200 |
| DSP | 3395 | 1436 | 2833 | 514 | 514 | 514 |
| TPT/GOPS | 1018.5 | 287.2 | 849.9 | 205.6 | 205.6 | 205.6 |
| APT/GOPS | 1000 | 222.1 | 636 | 189.2 | 193.5 | 182.4 |
| CRE | 98.2% | 77.3% | 74.8% | 92.0% | 94.1% | 88.7% |
| PD | 0.29 | 0.15 | 0.22 | 0.37 | 0.38 | 0.36 |
| Model | VGG16 | AlexNet | VGG16 | ResNet18 | VGG16 | AlexNet |
| Frame Rate (FPS) | — | 21 | 15 | 56 | 7 | 63 |
| Condition | Error Injection Rate | Min Accuracy (%) | Max Accuracy (%) | Mean Accuracy (%) | Std Deviation (%) | Confidence Interval (%) |
|---|---|---|---|---|---|---|
| Before Hardening | 0 | 91.13 | 91.13 | 91.13 | 0.00 | ±0.00 |
| 90.67 | 91.21 | 90.88 | 0.27 | ±0.11 | ||
| 89.50 | 90.08 | 89.72 | 0.42 | ±0.18 | ||
| 87.70 | 88.20 | 87.98 | 0.35 | ±0.15 | ||
| 85.00 | 85.80 | 85.41 | 0.28 | ±0.12 | ||
| 80.20 | 81.00 | 80.62 | 0.40 | ±0.17 | ||
| 75.30 | 75.80 | 75.56 | 0.25 | ±0.11 | ||
| 72.00 | 72.95 | 72.43 | 0.47 | ±0.20 | ||
| 58.77 | 59.98 | 58.93 | 0.60 | ±0.25 | ||
| 55.20 | 55.64 | 55.49 | 0.22 | ±0.09 | ||
| 49.80 | 50.42 | 50.10 | 0.31 | ±0.13 | ||
| 46.80 | 47.44 | 47.29 | 0.33 | ±0.14 | ||
| 35.50 | 35.99 | 35.83 | 0.24 | ±0.10 | ||
| After Hardening | 0 | 91.13 | 91.13 | 91.13 | 0.00 | ±0.00 |
| 90.77 | 91.13 | 90.88 | 0.18 | ±0.08 | ||
| 90.12 | 91.13 | 90.84 | 0.40 | ±0.16 | ||
| 89.20 | 91.13 | 90.84 | 0.96 | ±0.39 | ||
| 88.20 | 90.89 | 90.62 | 1.21 | ±0.49 | ||
| 85.72 | 86.91 | 86.26 | 0.96 | ±0.34 | ||
| 84.93 | 86.04 | 85.57 | 0.28 | ±0.10 | ||
| 79.51 | 81.53 | 80.55 | 1.01 | ±0.40 | ||
| 74.66 | 75.94 | 75.58 | 0.64 | ±0.26 | ||
| 70.43 | 70.96 | 70.61 | 0.26 | ±0.11 | ||
| 68.13 | 68.55 | 68.41 | 0.21 | ±0.09 | ||
| 65.34 | 66.21 | 65.97 | 0.46 | ±0.19 | ||
| 62.18 | 62.27 | 62.23 | 0.06 | ±0.02 |
| Condition | Error Injection Rate | Min Accuracy (%) | Max Accuracy (%) | Mean Accuracy (%) | Std. Deviation (%) | Confidence Interval (%) |
|---|---|---|---|---|---|---|
| Before Hardening | 0 | 91.13 | 91.13 | 91.13 | 0.00 | ±0.00 |
| 90.67 | 91.21 | 90.88 | 0.27 | ±0.11 | ||
| 89.50 | 90.08 | 89.72 | 0.42 | ±0.18 | ||
| 80.43 | 80.01 | 80.24 | 0.35 | ±0.15 | ||
| 51.09 | 52.14 | 51.62 | 0.54 | ±0.23 | ||
| 29.92 | 30.98 | 30.11 | 0.67 | ±0.28 | ||
| 19.34 | 20.08 | 19.97 | 0.45 | ±0.19 | ||
| 15.22 | 15.75 | 15.57 | 0.30 | ±0.13 | ||
| 12.16 | 12.77 | 12.50 | 0.40 | ±0.16 | ||
| 9.97 | 10.14 | 10.06 | 0.10 | ±0.04 | ||
| 6.89 | 8.21 | 7.33 | 0.67 | ±0.28 | ||
| 3.92 | 4.00 | 3.95 | 0.05 | ±0.02 | ||
| 3.40 | 3.55 | 3.47 | 0.08 | ±0.03 | ||
| After Hardening | 0 | 91.13 | 91.13 | 91.13 | 0.00 | ±0.00 |
| 90.99 | 91.13 | 91.04 | 0.07 | ±0.03 | ||
| 90.64 | 91.13 | 91.01 | 0.31 | ±0.13 | ||
| 90.01 | 91.13 | 90.84 | 0.62 | ±0.25 | ||
| 87.13 | 87.94 | 87.46 | 0.40 | ±0.16 | ||
| 85.16 | 86.04 | 85.72 | 0.35 | ±0.14 | ||
| 82.04 | 82.56 | 82.12 | 0.26 | ±0.11 | ||
| 79.65 | 79.89 | 79.84 | 0.13 | ±0.05 | ||
| 76.22 | 76.97 | 76.54 | 0.47 | ±0.19 | ||
| 71.43 | 72.11 | 71.98 | 0.34 | ±0.14 | ||
| 68.24 | 68.55 | 68.43 | 0.21 | ±0.08 | ||
| 62.31 | 62.88 | 62.57 | 0.29 | ±0.12 | ||
| 58.55 | 58.67 | 58.64 | 0.06 | ±0.02 |
| Metric | Baseline | TMR | This Work |
|---|---|---|---|
| Processing Time (s) | 0.0178 | 0.0453 | 0.0194 |
| LUT Utilization | 129,771 | 389,313 | 143,865 |
| BRAM Utilization | 436 | 1308 | 495 |
| DSP Utilization | 514 | 1542 | 546 |
| Power Consumption (W) | 4.877 | 12.680 | 6.047 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, Y.; Wang, J.; Han, X.; Li, Y.; Li, Y.; Tao, Z. Research on Spaceborne Neural Network Accelerator and Its Fault Tolerance Design. Remote Sens. 2025, 17, 69. https://doi.org/10.3390/rs17010069
Shao Y, Wang J, Han X, Li Y, Li Y, Tao Z. Research on Spaceborne Neural Network Accelerator and Its Fault Tolerance Design. Remote Sensing. 2025; 17(1):69. https://doi.org/10.3390/rs17010069
Chicago/Turabian StyleShao, Yingzhao, Junyi Wang, Xiaodong Han, Yunsong Li, Yaolin Li, and Zhanpeng Tao. 2025. "Research on Spaceborne Neural Network Accelerator and Its Fault Tolerance Design" Remote Sensing 17, no. 1: 69. https://doi.org/10.3390/rs17010069
APA StyleShao, Y., Wang, J., Han, X., Li, Y., Li, Y., & Tao, Z. (2025). Research on Spaceborne Neural Network Accelerator and Its Fault Tolerance Design. Remote Sensing, 17(1), 69. https://doi.org/10.3390/rs17010069






