Climate Impact on Evapotranspiration in the Yellow River Basin: Interpretable Forecasting with Advanced Time Series Models and Explainable AI
Abstract
1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data Collection
2.3. Data Preprocessing
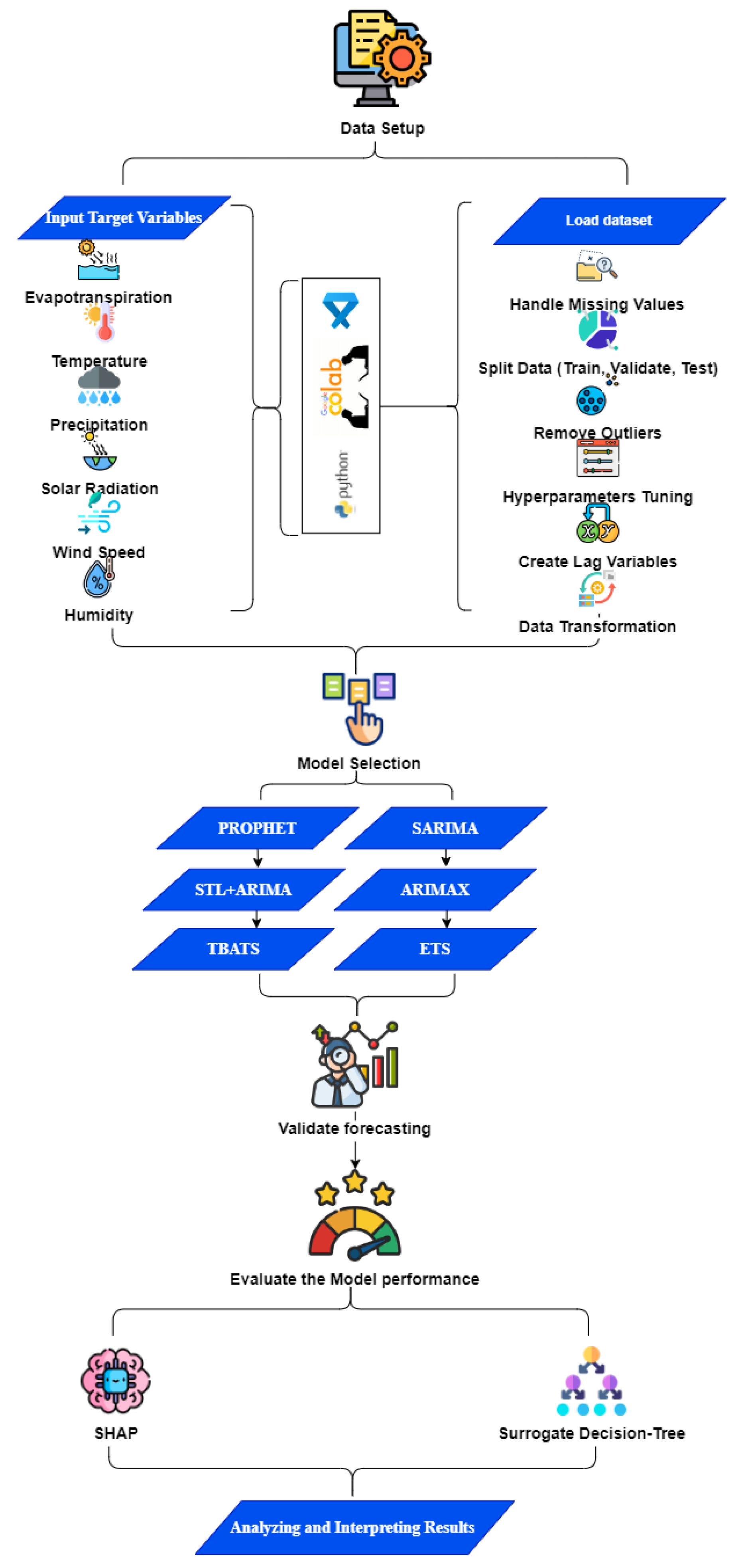
3. Methodology
3.1. Advanced Time Series Models
Evaluation Metrics for Models
3.2. Elucidate the Techniques of XAI
3.3. Algorithms for Time Series Forecasting with XAI Integration
3.3.1. Algorithm 1: XAI-Based Feature Attribution
| Algorithm 1: Explainable Artificial Intelligence (XAI) Time Series Forecasting. |
| Input: Climate dataset (D) |
| Output: Projected ET values for the period 2021–2030, along with corresponding SHAP values. |
| Preprocessing Iterate over each variable Vi in the set D: If Vi represents either ET or temperature: Utilize the Yeo-Johnson transformation. If Vi represents either precipitation or solar radiation: Perform the Box-Cox transformation If Vi represents wind speed, then use Z-score normalization. If Vi represents humidity: Utilize logarithmic and quantile transformation techniques. Perform Savitzky–Golay smoothing on the variable Vi. Apply quantile-based approaches to eliminate outliers from dataset |
| Selection of model Iterate over each model Mi in the set (SARIMA, ETS, Prophet, TBATS, STL + ARIMA, ARIMAX) and do the following steps: Adjust the parameters of Mi to the preprocessed dataset D. |
| Prediction Perform the following steps for each model Mi: Predicted ET levels for the period of 2021–2030. |
| Assessment Perform the following steps for each model Mi: MAE, MSE, and RMSE. Choose the model that has the lowest RMSE. Explainability Utilize the SHAP method on the model that has shown the highest level of performance. Compute the SHAP values for each feature. |
| Return forecasted ET, SHAP values End Algorithm |
3.3.2. Algorithm 2: SHAP-Based Feature Attribution
| Algorithm 2: SHAP-based Feature Attribution |
| Input: (Dataset D), Model (M) |
| Output: SHAP values for vital features |
| Initialized SHAP explainer |
| Determine SHAP values for all records Perform the following for every xi in D’ # Model prediction #Compute SHAP values for xi and save the SHAP_values. Consolidate SHAP values |
End Algorithm |
4. Results
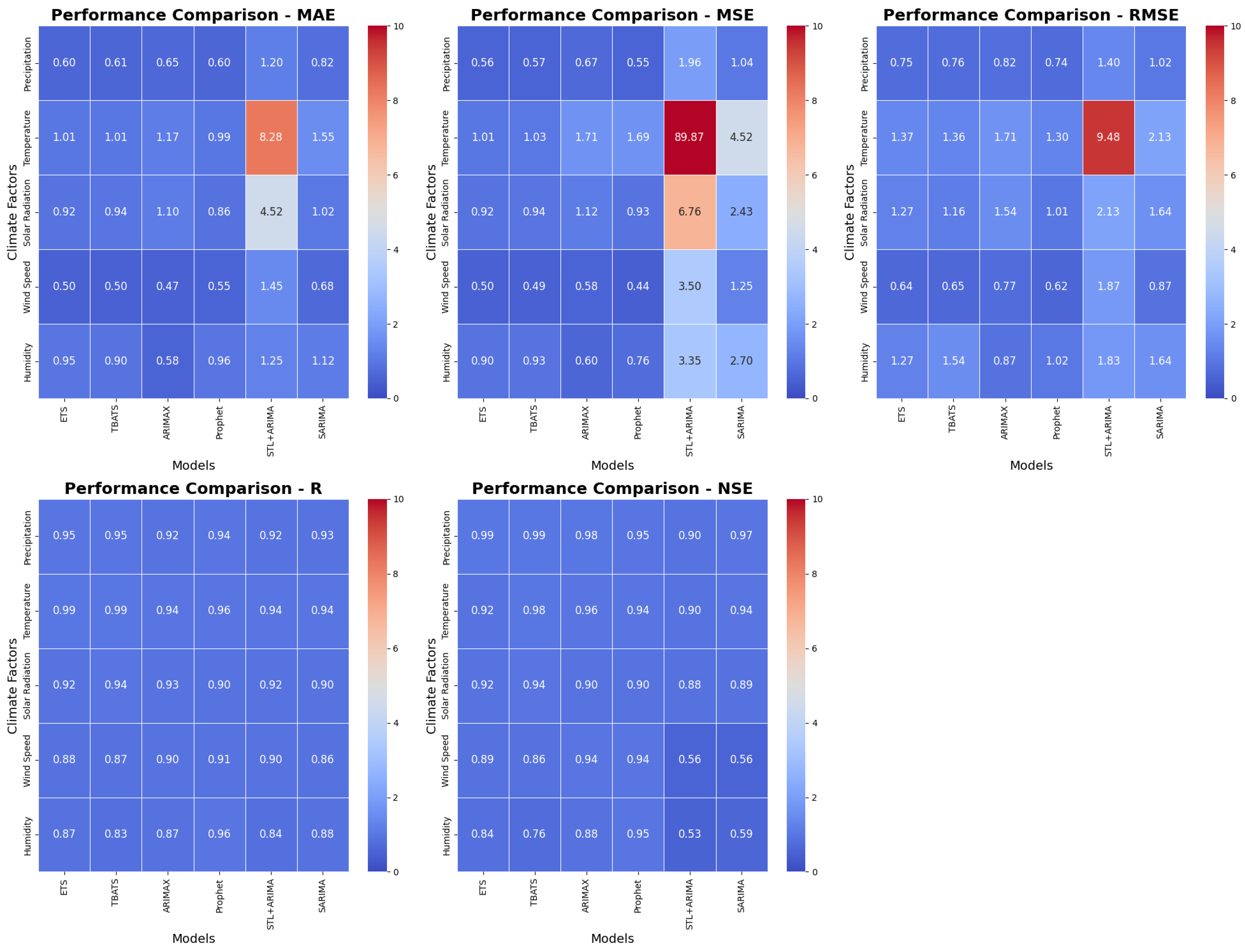
4.1. Overview of Model Performance
4.2. Model-Specific Performance Analysis
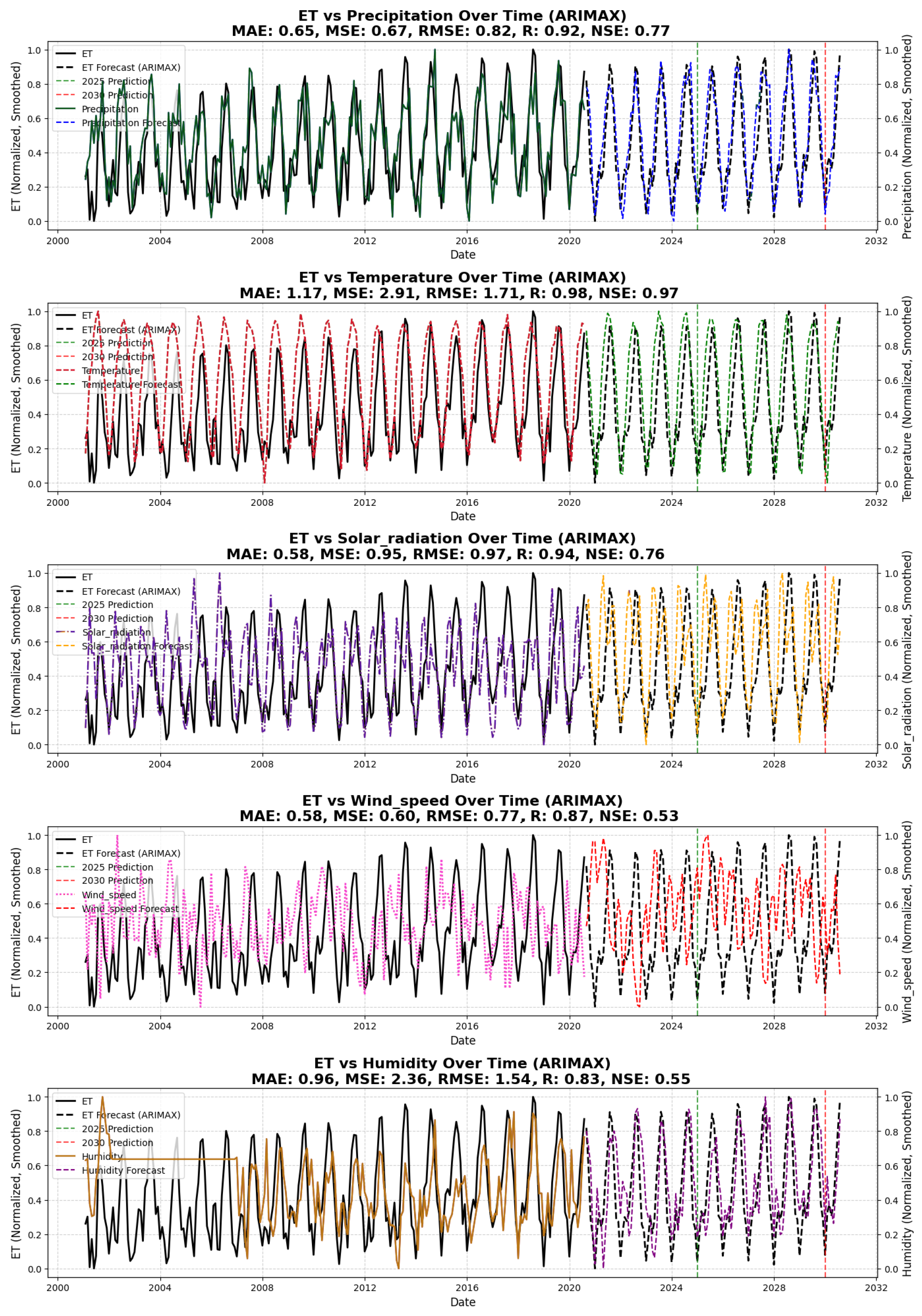
4.2.1. ARIMAX Performance
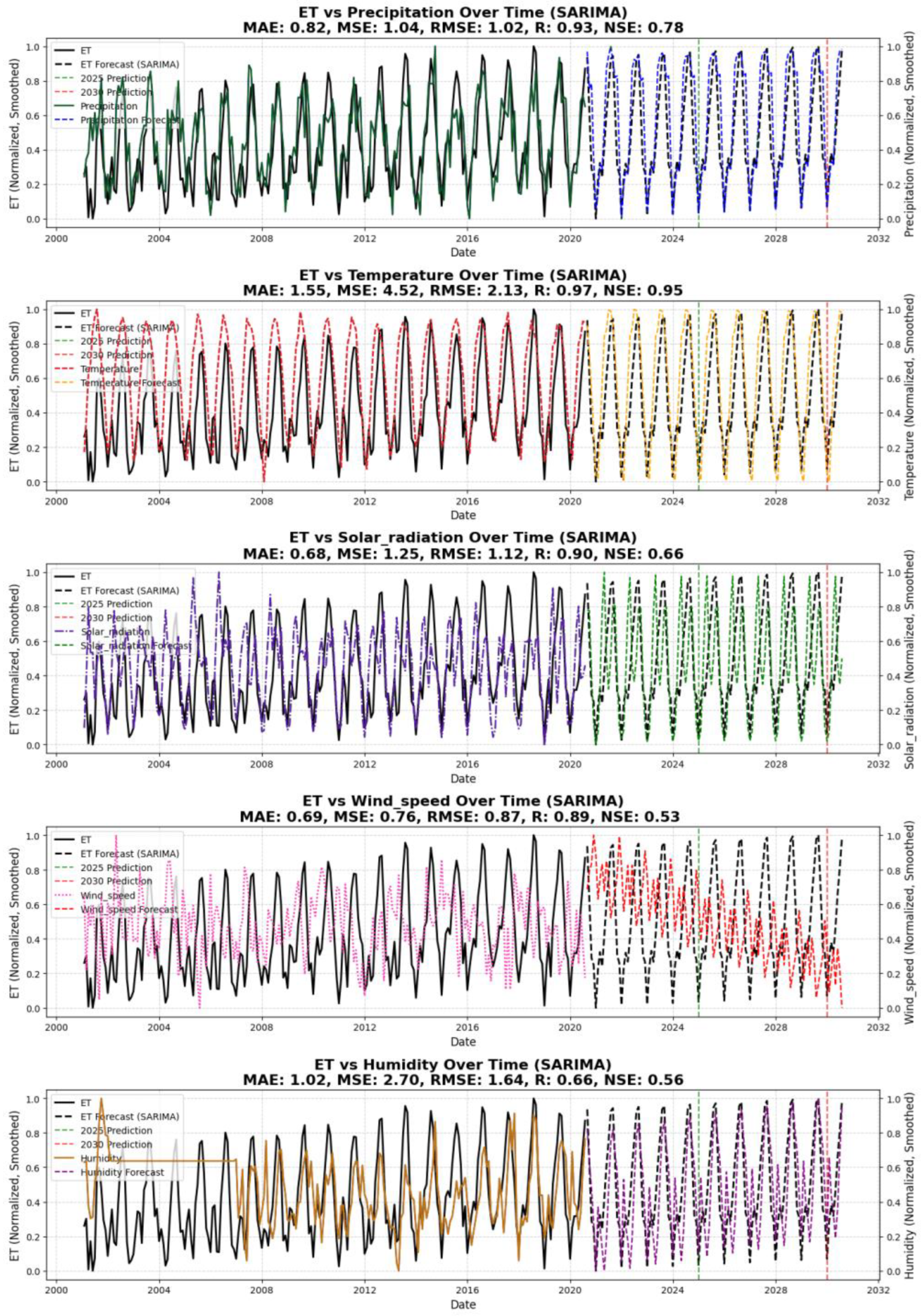
4.2.2. SARIMA Performance
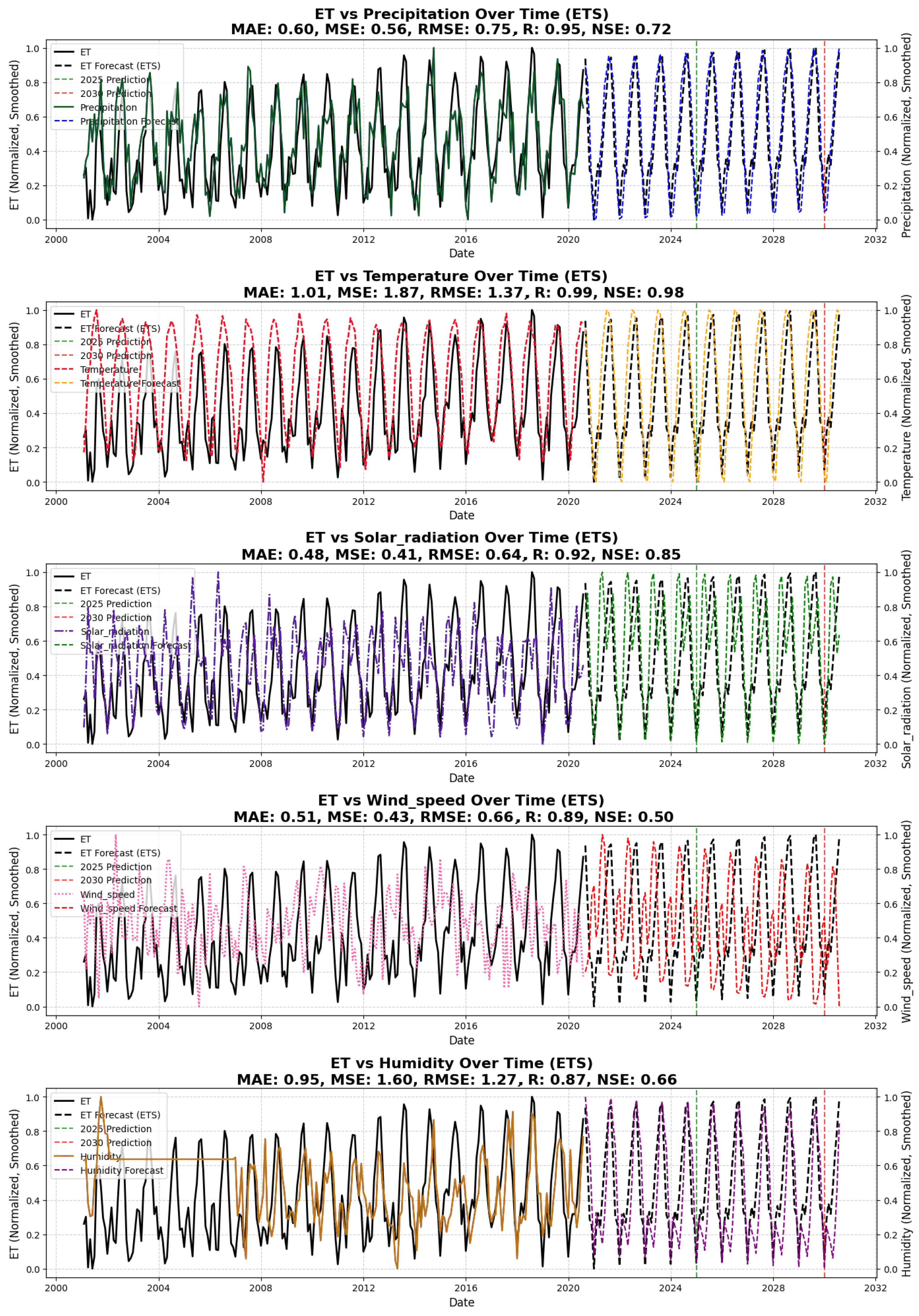
4.2.3. ETS Performance
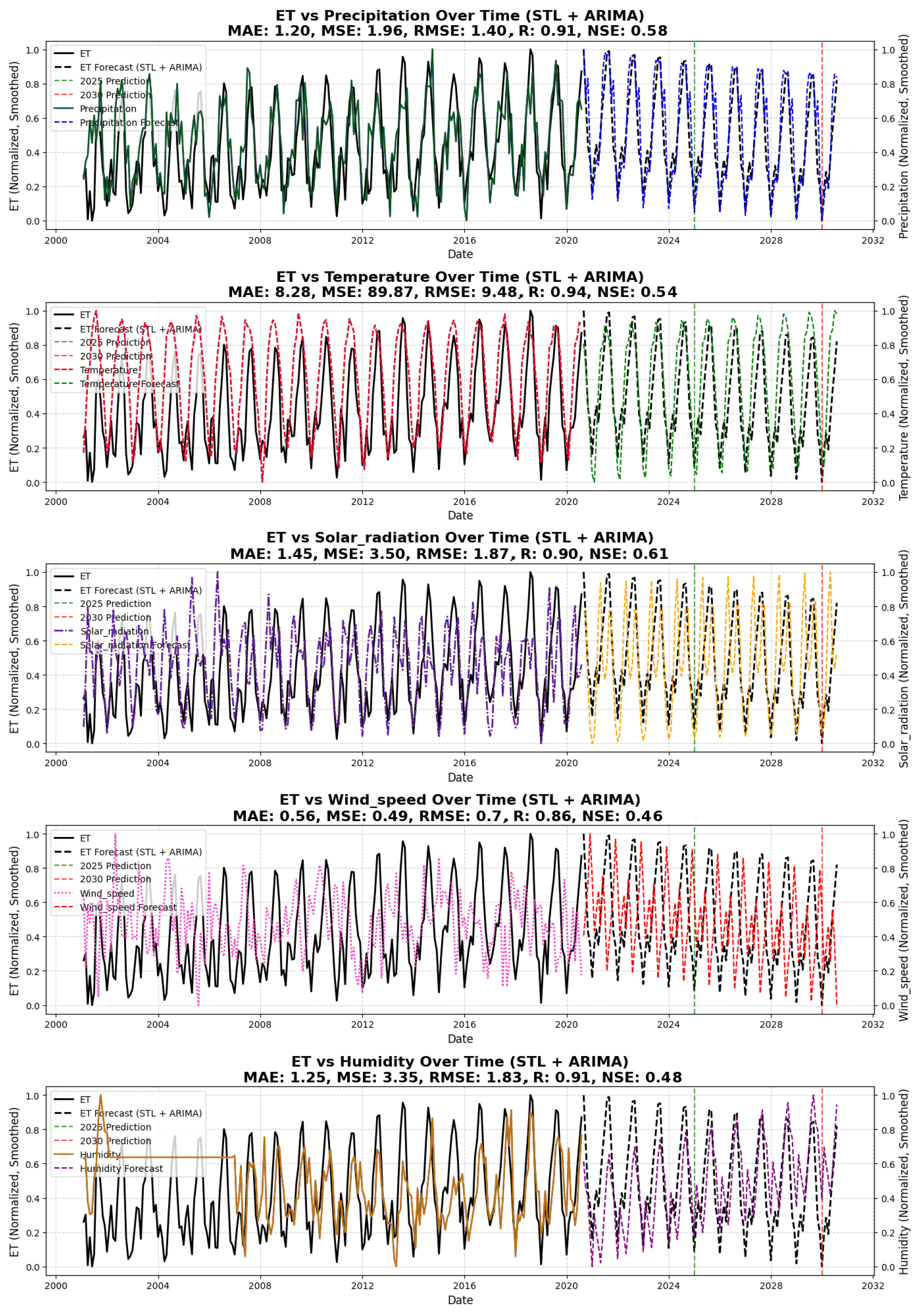
4.2.4. STL + ARIMA Performance
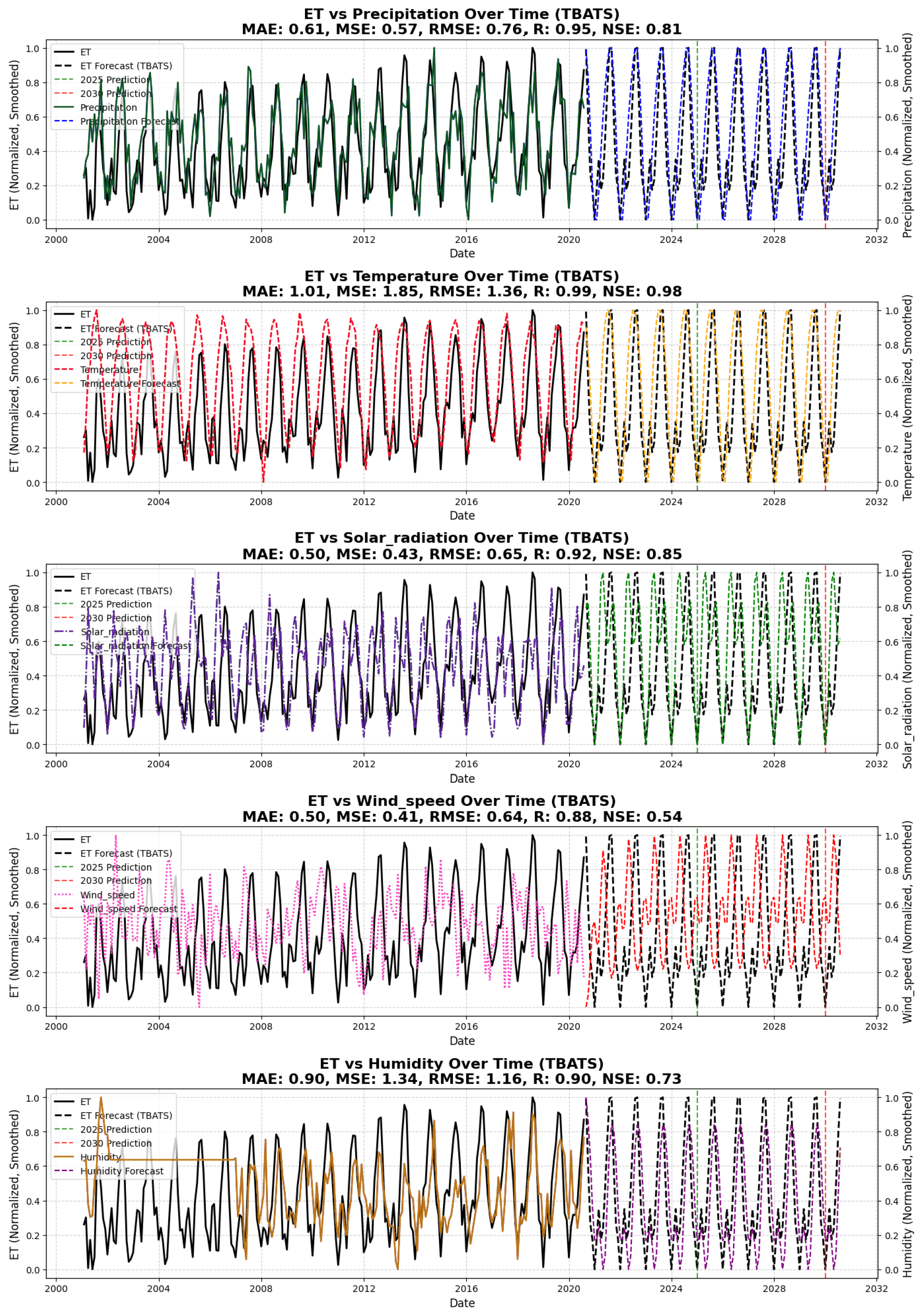
4.2.5. TBATS Performance
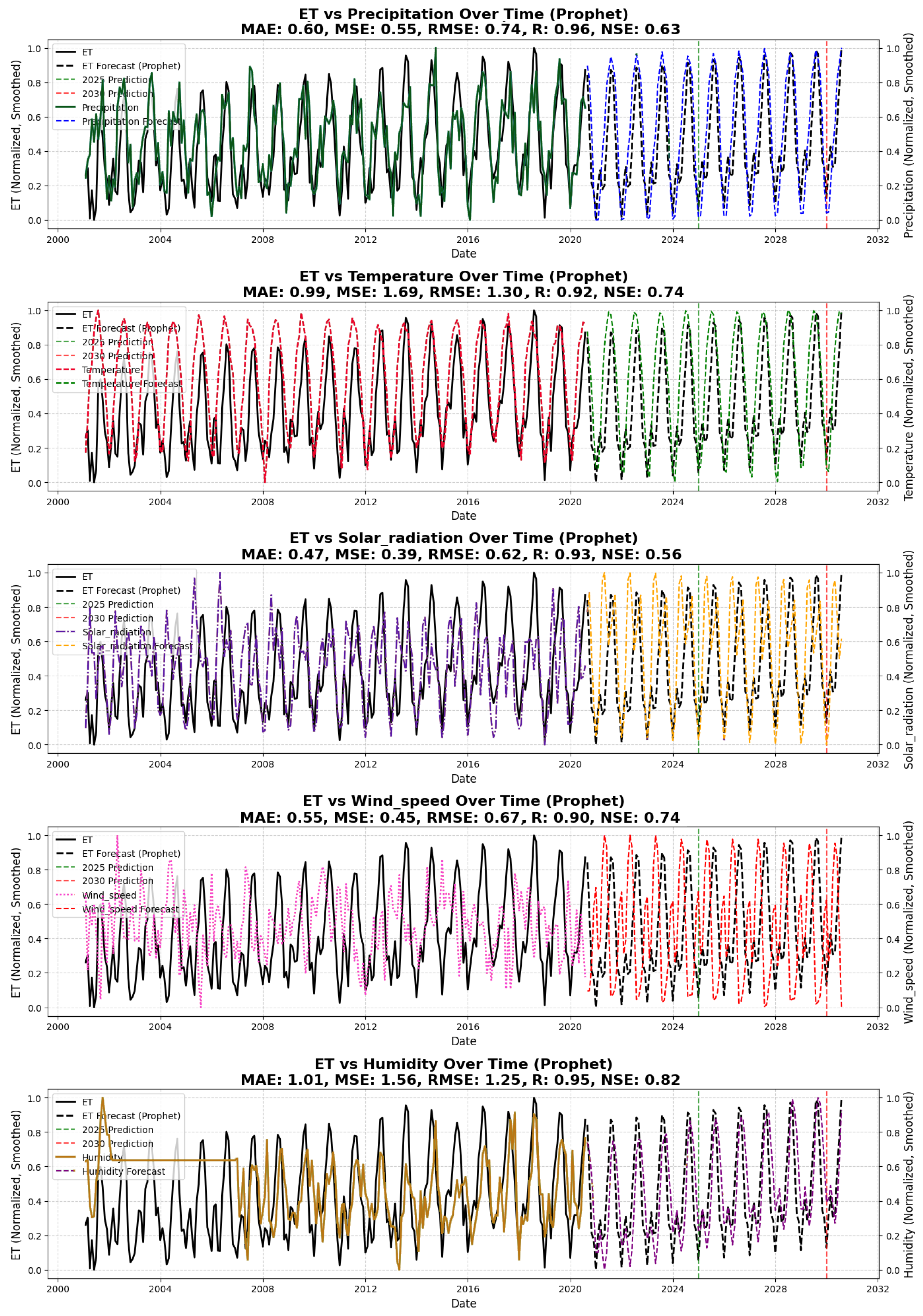
4.2.6. Prophet Performance
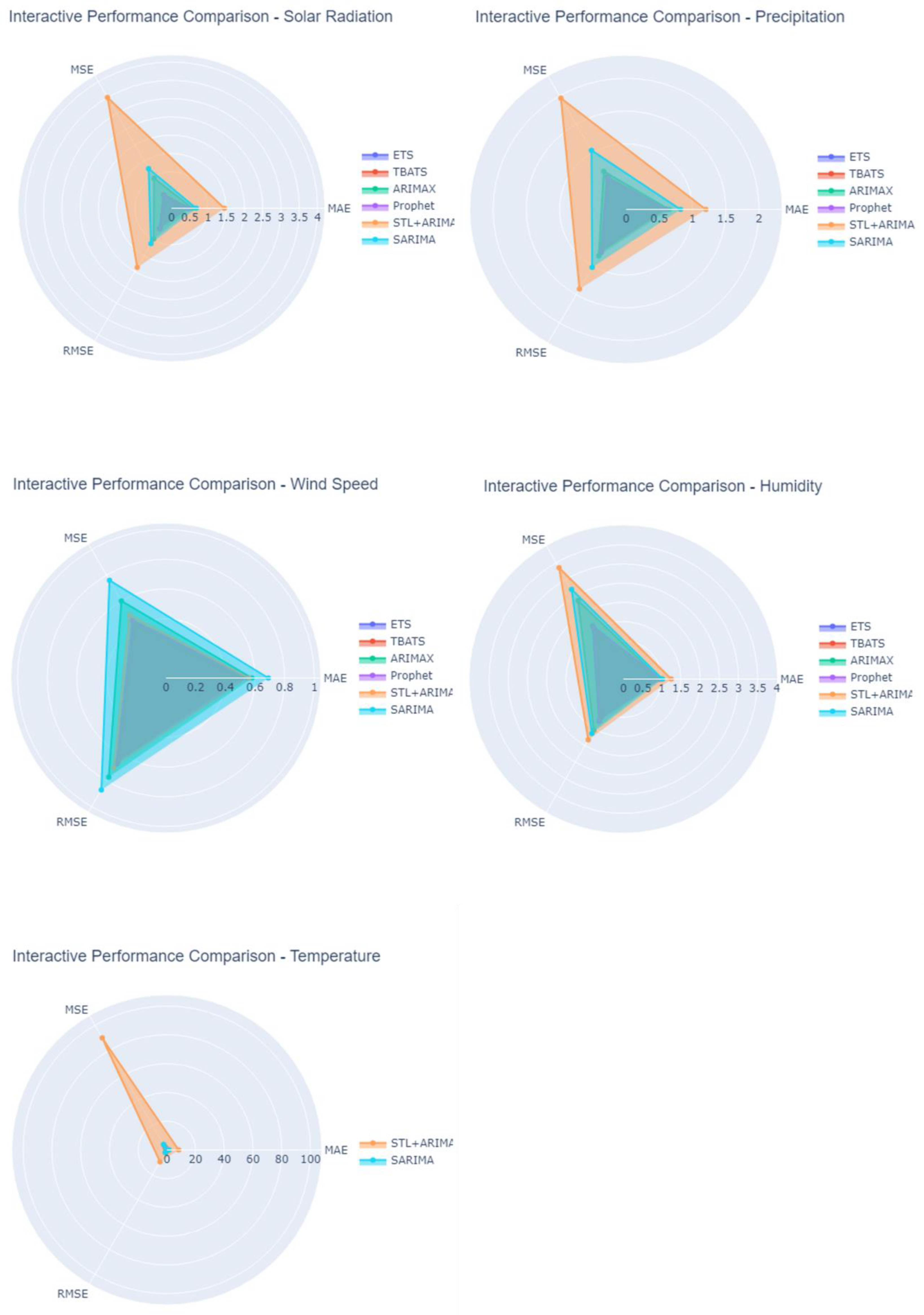
4.3. Model-Interactive Performance Comparison
4.4. XAI and Model Interpretability
4.4.1. Decision Tree Surrogate Model Performance Across Models
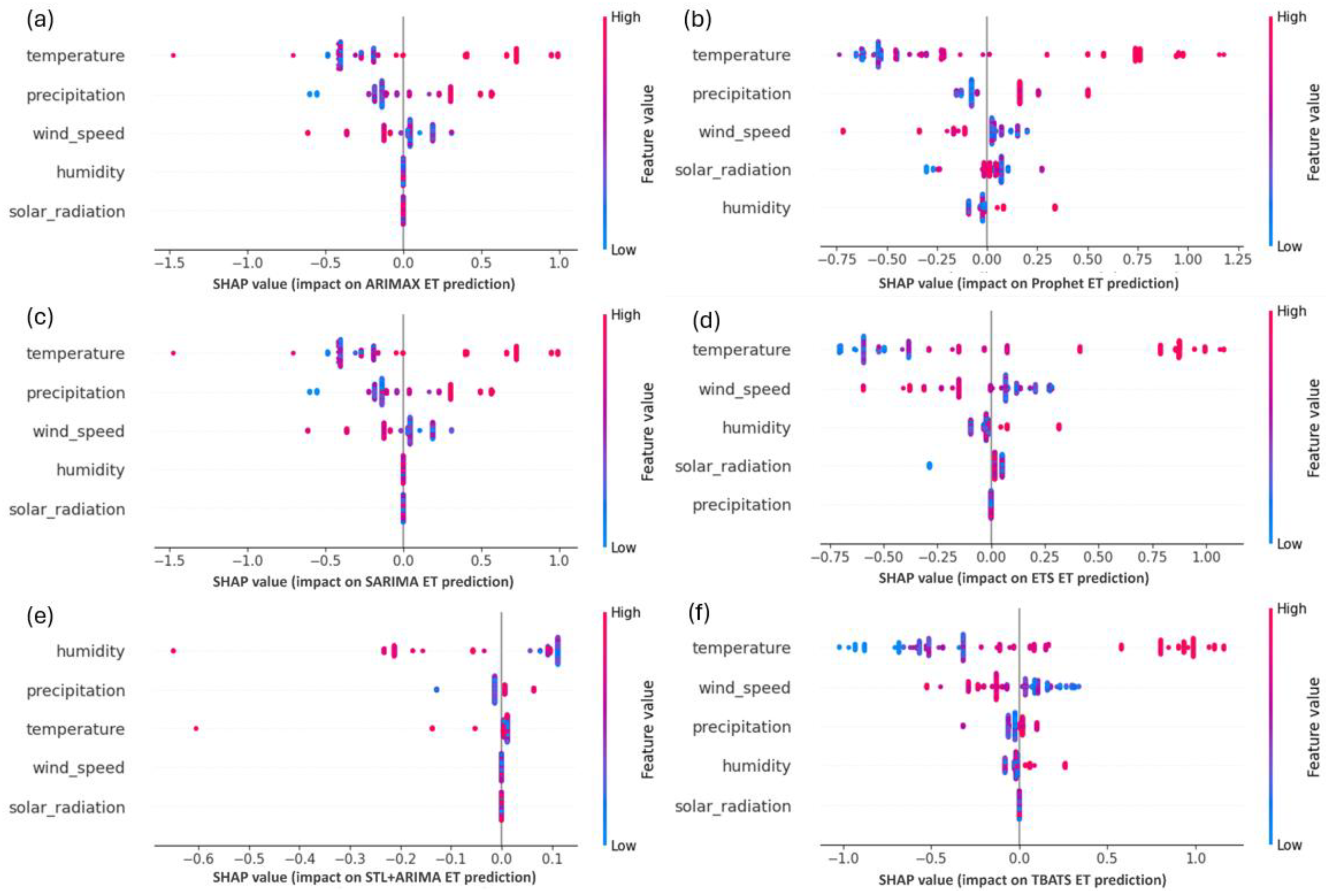
4.4.2. SHAP Value Analysis
4.4.3. Comparison of Model Insights: Decision Trees vs. SHAP Values
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, G.; Tian, P.; Mu, X.; Jiao, J.; Wang, F.; Gao, P. Quantifying the impact of climate variability and human activities on streamflow in the middle reaches of the Yellow River basin, China. J. Hydrol. 2014, 519, 387–398. [Google Scholar] [CrossRef]
- Wang, H.; Xiao, W.; Zhao, Y.; Wang, Y.; Hou, B.; Zhou, Y.; Yang, H.; Zhang, X.; Cui, H.J.W. The spatiotemporal variability of evapotranspiration and its response to climate change and land use/land cover change in the three gorges reservoir. Water 2019, 11, 1739. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Hyndman, R. Forecasting: Principles and Practice; OTexts: Monash University, Australia, 2018. [Google Scholar]
- Taylor, S.J.; Letham, B. Forecasting at scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Doshi-Velez, F.; Kim, B. Towards a rigorous science of interpretable machine learning. arXiv 2017, arXiv:1702.08608. [Google Scholar]
- Lundberg, S. A unified approach to interpreting model predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar]
- Mamalakis, A.; Ebert-Uphoff, I.; Barnes, E.A. Explainable artificial intelligence in meteorology and climate science: Model fine-tuning, calibrating trust and learning new science. In Proceedings of the International Workshop on Extending Explainable AI Beyond Deep Models and Classifiers, Vienna, Austria, 18 July 2020; pp. 315–339. [Google Scholar]
- Chakraborty, D.; Alam, A.; Chaudhuri, S.; Başağaoğlu, H.; Sulbaran, T.; Langar, S. Scenario-based prediction of climate change impacts on building cooling energy consumption with explainable artificial intelligence. Appl. Energy 2021, 291, 116807. [Google Scholar] [CrossRef]
- Peng, J.; Liu, T.; Huang, Y.; Ling, Y.; Li, Z.; Bao, A.; Chen, X.; Kurban, A.; De Maeyer, P. Satellite-based precipitation datasets evaluation using gauge observation and hydrological modeling in a typical arid land watershed of Central Asia. Remote Sens. 2021, 13, 221. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Y.; Tang, Q. Impact assessment of climate change and human activities on streamflow signatures in the Yellow River Basin using the Budyko hypothesis and derived differential equation. J. Hydrol. 2020, 591, 125460. [Google Scholar] [CrossRef]
- Cai, X.; Rosegrant, M.W. Optional water development strategies for the Yellow River Basin: Balancing agricultural and ecological water demands. Water Resour. Res. 2004, 40, W08S04. [Google Scholar] [CrossRef]
- Chen, Y.-p.; Fu, B.-j.; Zhao, Y.; Wang, K.-b.; Zhao, M.M.; Ma, J.-f.; Wu, J.-H.; Xu, C.; Liu, W.-g.; Wang, H. Sustainable development in the Yellow River Basin: Issues and strategies. J. Clean. Prod. 2020, 263, 121223. [Google Scholar] [CrossRef]
- Liu, C.; Xia, J. Water problems and hydrological research in the Yellow River and the Huai and Hai River basins of China. Hydrol. Process. 2004, 18, 2197–2210. [Google Scholar] [CrossRef]
- Milliman, J.D.; Meade, R.H. World-wide delivery of river sediment to the oceans. J. Geol. 1983, 91, 1–21. [Google Scholar] [CrossRef]
- Peng, J.; Chen, S.; Dong, P. Temporal variation of sediment load in the Yellow River basin, China, and its impacts on the lower reaches and the river delta. Catena 2010, 83, 135–147. [Google Scholar] [CrossRef]
- Wei, J.; Lei, Y.; Yao, H.; Ge, J.; Wu, S.; Liu, L. Estimation and influencing factors of agricultural water efficiency in the Yellow River basin, China. J. Clean. Prod. 2021, 308, 127249. [Google Scholar] [CrossRef]
- Wohlfart, C.; Kuenzer, C.; Chen, C.; Liu, G. Social–ecological challenges in the Yellow River basin (China): A review. Environ. Earth Sci. 2016, 75, 1066. [Google Scholar] [CrossRef]
- Zhang, Y.; Xia, J.; She, D. Spatiotemporal variation and statistical characteristic of extreme precipitation in the middle reaches of the Yellow River Basin during 1960–2013. Theor. Appl. Climatol. 2019, 135, 391–408. [Google Scholar] [CrossRef]
- Wang, W.; Shao, Q.; Yang, T.; Peng, S.; Yu, Z.; Taylor, J.; Xing, W.; Zhao, C.; Sun, F. Changes in daily temperature and precipitation extremes in the Yellow River Basin, China. Stoch. Environ. Res. Risk Assess. 2013, 27, 401–421. [Google Scholar] [CrossRef]
- Zhou, K.; Wang, Y.; Chang, J.; Zhou, S.; Guo, A. Spatial and temporal evolution of drought characteristics across the Yellow River basin. Ecol. Indic. 2021, 131, 108207. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the MODIS land-surface temperature/emissivity products. Remote Sens. Environ. 2008, 112, 59–74. [Google Scholar] [CrossRef]
- Raza, A.; Fahmeed, R.; Syed, N.R.; Katipoğlu, O.M.; Zubair, M.; Alshehri, F.; Elbeltagi, A. Performance evaluation of five machine learning algorithms for estimating reference evapotranspiration in an arid climate. Water 2023, 15, 3822. [Google Scholar] [CrossRef]
- Fan, J.; Yue, W.; Wu, L.; Zhang, F.; Cai, H.; Wang, X.; Lu, X.; Xiang, Y. Evaluation of SVM, ELM and four tree-based ensemble models for predicting daily reference evapotranspiration using limited meteorological data in different climates of China. Agric. For. Meteorol. 2018, 263, 225–241. [Google Scholar] [CrossRef]
- Yeo, I.K.; Johnson, R.A. A new family of power transformations to improve normality or symmetry. Biometrika 2000, 87, 954–959. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Box, G.E.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. Ser. B Stat. Methodol. 1964, 26, 211–243. [Google Scholar] [CrossRef]
- Jones, T.A. Skewness and kurtosis as criteria of normality in observed frequency distributions. J. Sediment. Res. 1969, 39, 1622–1627. [Google Scholar] [CrossRef]
- Baik, J.; Liaqat, U.W.; Choi, M. Assessment of satellite-and reanalysis-based evapotranspiration products with two blending approaches over the complex landscapes and climates of Australia. Agric. For. Meteorol. 2018, 263, 388–398. [Google Scholar] [CrossRef]
- Heo, J.-H.; Ahn, H.; Shin, J.-Y.; Kjeldsen, T.R.; Jeong, C. Probability distributions for a quantile mapping technique for a bias correction of precipitation data: A case study to precipitation data under climate change. Water 2019, 11, 1475. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Lee, D.K. Data transformation: A focus on the interpretation. Korean J. Anesthesiol. 2020, 73, 503–508. [Google Scholar] [CrossRef] [PubMed]
- Satrio, C.B.A.; Darmawan, W.; Nadia, B.U.; Hanafiah, N. Time series analysis and forecasting of coronavirus disease in Indonesia using ARIMA model and PROPHET. Procedia Comput. Sci. 2021, 179, 524–532. [Google Scholar] [CrossRef]
- Lem, K.H. The STL-ARIMA approach for seasonal time series forecast: A preliminary study. In Proceedings of the ITM Web of Conferences, Chennai, India, 30–31 December 2024; p. 01008. [Google Scholar]
- Haydier, E.A.; Albarwari, N.H.S.; Ali, T.H. The Comparison Between VAR and ARIMAX Time Series Models in Forecasting. Iraqi J. Stat. Sci. 2023, 20, 249–262. [Google Scholar]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Senthilnathan, S. Usefulness of correlation analysis. Available at SSRN 3416918, Papua New Guinea. 2019. Available online: https://ssrn.com/abstract=3416918 (accessed on 26 December 2024).
- Holzinger, A.; Saranti, A.; Molnar, C.; Biecek, P.; Samek, W. Explainable AI methods-a brief overview. In Proceedings of the International Workshop on Extending Explainable AI Beyond Deep Models and Classifiers. Springer, Vienna, Austria, 18 July 2022; Springer: Cham, Germany; pp. 13–38. [Google Scholar] [CrossRef]
- Tursunalieva, A.; Alexander, D.L.; Dunne, R.; Li, J.; Riera, L.; Zhao, Y. Making Sense of Machine Learning: A Review of Interpretation Techniques and Their Applications. Appl. Sci. 2024, 14, 496. [Google Scholar] [CrossRef]
- Atzmueller, M.; Fürnkranz, J.; Kliegr, T.; Schmid, U. Explainable and interpretable machine learning and data mining. Data Min. Knowl. Discov. 2024, 38, 2571–2595. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should i trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Bhanja, S.N.; Zhang, X.; Wang, J. Estimating long-term groundwater storage and its controlling factors in Alberta, Canada. Hydrol. Earth Syst. Sci. 2018, 22, 6241–6255. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, J.; Peng, J.; Zou, L.; Fan, Y.; Yang, F.; Hu, Z. Alp-valley and elevation effects on the reference evapotranspiration and the dominant climate controls in Red River Basin, China: Insights from geographical differentiation. J. Hydrol. 2023, 620, 129397. [Google Scholar] [CrossRef]
- Goyal, R. Sensitivity of evapotranspiration to global warming: A case study of arid zone of Rajasthan (India). Agric. Water Manag. 2004, 69, 1–11. [Google Scholar] [CrossRef]
- Huntington, T.G. Evidence for intensification of the global water cycle: Review and synthesis. J. Hydrol. 2006, 319, 83–95. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.G.; Lee, S.-I. Consistent individualized feature attribution for tree ensembles. arXiv 2018, arXiv:1802.03888. [Google Scholar]
- Zhao, F.; Ma, S.; Wu, Y.; Qiu, L.; Wang, W.; Lian, Y.; Chen, J.; Sivakumar, B. The role of climate change and vegetation greening on evapotranspiration variation in the Yellow River Basin, China. Agric. For. Meteorol. 2022, 316, 108842. [Google Scholar] [CrossRef]
- Alexandris, S.; Proutsos, N. How significant is the effect of the surface characteristics on the Reference Evapotranspiration estimates? Agric. Water Manag. 2020, 237, 106181. [Google Scholar] [CrossRef]
- Fu, J.; Gong, Y.; Zheng, W.; Zou, J.; Zhang, M.; Zhang, Z.; Qin, J.; Liu, J.; Quan, B. Spatial-temporal variations of terrestrial evapotranspiration across China from 2000 to 2019. Sci. Total Environ. 2022, 825, 153951. [Google Scholar] [CrossRef] [PubMed]
- Drogkoula, M.; Kokkinos, K.; Samaras, N. A comprehensive survey of machine learning methodologies with emphasis in water resources management. Appl. Sci. 2023, 13, 12147. [Google Scholar] [CrossRef]



| Citation | Contribution | Limitation | Foreground | Issues |
|---|---|---|---|---|
| [11] | Examined the spatial and temporal fluctuations in ET by utilizing satellite data, providing a thorough depiction of ET trends in the YRB. | focuses on conducting descriptive analysis and assessing variability, without engaging in predictive modeling or exploring the factors that influence climate patterns. | Provided a comprehensive evaluation of the variability of ET, serving as a foundation for future modeling endeavors. | Did not investigate the use of predictive modeling or advanced time series models for forecasting ET. |
| [12] | Examined the long-term trends in the hydrology of the YRB, specifically focusing on the combined effects of climate change and human activity. | Primarily focused on descriptive research without integrating advanced time series models for prediction. | Emphasized the necessity of utilizing integrated modeling methodologies that consider the effects of both climate and human activities. | Unable to offer predictive insights or investigate the application of modern forecasting models in hydrological research. |
| [6] | Developed the widely used SARIMA and other time series models for climate modeling and other forecasting applications. | The model predictions have limited interpretability and function as a “black box”. | Incorporated SARIMA into the field of time series forecasting for environmental and climate applications. | Does not provide any insight into the causality or significance of various variables in the prediction. |
| [8] | Presented SHAP values as a means of deciphering intricate ML models with applications in several domains, including ET research. | Extremely computationally heavy; could be difficult to scale to massive datasets or complicated models. | Facilitated the utilization of SHAP in several domains, such as environmental science and hydrology. | Computational obstacles encountered while utilizing SHAP in the context of extensive ET forecasting models. |
| [4] | Provided a comprehensive overview of time series forecasting techniques, such as ETS and ARIMA models, commonly employed in climate research. | The main emphasis is on the correctness of the model, without considering its interpretability or transparency | Popularized the Prophet model for large-scale forecasting duties; widely used as a reference for time series forecasting. | Insufficient resources to elucidate model projections and ascertain the primary factors influencing projected results. |
| Climate Variable | Dataset | Dataset Name | Years Covered |
|---|---|---|---|
| ET | ee.ImageCollection (‘MODIS/006/MOD16A2’) | MODIS Global Terrestrial ET | 2001–2020 |
| Precipitation | ee.ImageCollection (“TRMM/3B42”) | TRMM 3B42: TRMM and Other Data Precipitation Estimates | 2001–2020 |
| Solar Radiation | ee.ImageColltion (‘NASA/GLDAS/V021/NOAH/ G025/T3H’) | GLDAS-2.1: Global Land Data Assimilation System | 2001–2020 |
| Temperature | ee.ImageCollection (‘MODIS/006/MOD11A2’) | MODIS Land Surface Temperature/Emissivity 8-Day L3 Global | 2001–2020 |
| Wind Speed | ee.ImageCollection (‘ECMWF/ERA5/DAILY’) | ERA5 Daily Aggregated Data | 2001–2020 |
| Humidity | ee.ImageCollection (‘NASA/GLDAS/V021/ NOAH/G025/T3H’) | GLDAS-2.1: Global Land Data Assimilation System | 2001–2020 |
| Climate Variable | Transformation Applied | Data Smoothing | Outlier Removal |
|---|---|---|---|
| ET | Yeo-Johnson Transformation | Savitzky–Golay Smoothing | None |
| Precipitation | Box-Cox Transformation | None | Removal of extreme outliers |
| Temperature | Yeo-Johnson Transformation (with zeros and negatives) | None | Removal of extreme outliers |
| Solar Radiation | Box-Cox Transformation | None | None |
| Wind Speed | Z-Score Normalization | Exponential Smoothing | Quantile Transformation (with outliers removed) |
| Humidity | Combination of Log and Quantile Transformation | Advanced Smoothing Techniques | Removal of extreme outliers |
| Feature | ARIMAX Model | AIC | BIC |
|---|---|---|---|
| Precipitation | ARIMA (0, 1, 1) (0, 1, 1) 12 | 564.31 | 574.52 |
| Temperature | ARIMA (0, 1, 1) (0, 1, 1) 12 | 828.68 | 838.88 |
| Solar Radiation | ARIMA (0, 1, 1) (0, 1, 1) 12 | 488.31 | 498.52 |
| Wind Speed | ARIMA (0, 1, 1) (0, 1, 1) 12 | 496.68 | 506.89 |
| Humidity | ARIMA (0, 1, 1) (0, 1, 1) 12 | 765.83 | 776.04 |
| Feature | SARIMA Model | AIC | BIC |
|---|---|---|---|
| Precipitation | SARIMA(1, 1, 1)(1, 1, 0, 12) | 578.21 | 591.58 |
| Temperature | SARIMA(1, 1, 1)(1, 1, 0, 12) | 842.71 | 856.08 |
| Solar Radiation | SARIMA(1, 1, 1)(1, 1, 0, 12) | 492.34 | 505.71 |
| Wind Speed | SARIMA(1, 1, 1)(1, 1, 0, 12) | 494.99 | 508.35 |
| Humidity | SARIMA(1, 1, 1)(1, 1, 0, 12) | 722.70 | 736.07 |
| Feature | AIC | BIC |
|---|---|---|
| Precipitation | −1649.94 | −1632.93 |
| Temperature | −1295.70 | −1278.69 |
| Solar Radiation | −1671.21 | −1654.19 |
| Wind Speed | −1545.00 | −1527.99 |
| Humidity | −1255.51 | −1238.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, S.; Wang, H.; Nauman, U.; Dars, R.; Boota, M.W.; Wu, Z. Climate Impact on Evapotranspiration in the Yellow River Basin: Interpretable Forecasting with Advanced Time Series Models and Explainable AI. Remote Sens. 2025, 17, 115. https://doi.org/10.3390/rs17010115
Khan S, Wang H, Nauman U, Dars R, Boota MW, Wu Z. Climate Impact on Evapotranspiration in the Yellow River Basin: Interpretable Forecasting with Advanced Time Series Models and Explainable AI. Remote Sensing. 2025; 17(1):115. https://doi.org/10.3390/rs17010115
Chicago/Turabian StyleKhan, Sheheryar, Huiliang Wang, Umer Nauman, Rabia Dars, Muhammad Waseem Boota, and Zening Wu. 2025. "Climate Impact on Evapotranspiration in the Yellow River Basin: Interpretable Forecasting with Advanced Time Series Models and Explainable AI" Remote Sensing 17, no. 1: 115. https://doi.org/10.3390/rs17010115
APA StyleKhan, S., Wang, H., Nauman, U., Dars, R., Boota, M. W., & Wu, Z. (2025). Climate Impact on Evapotranspiration in the Yellow River Basin: Interpretable Forecasting with Advanced Time Series Models and Explainable AI. Remote Sensing, 17(1), 115. https://doi.org/10.3390/rs17010115












