Research on Azimuth DBF Method of HRWS SPC MAB SAR Imaging Mode with Non-Ideal Antenna Mode
Abstract
1. Introduction
2. Signal Mode of SPC MAB with Reflector Antenna
3. Azimuth DBF Filters Design for SPC MAB Mode
3.1. Traditional Combination Scheme
3.2. Traditional STAP Scheme
3.3. Low-Pass, Band-Limited Signal Spectrum Reconstruction Model
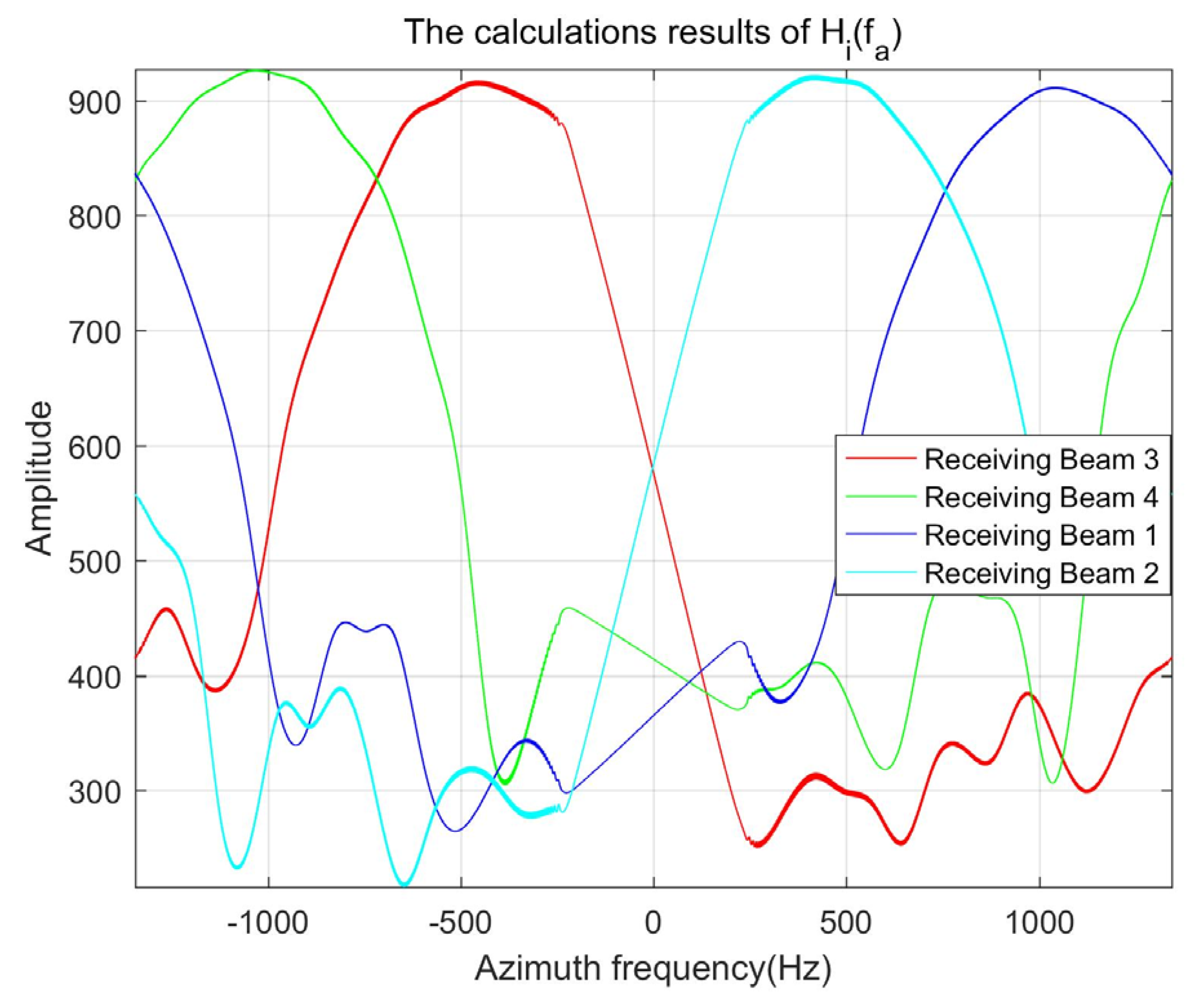
3.3.1. Analysis of Transfer Functions
3.3.2. Design of the DBF Filters
3.3.3. Strategies for Non-Ideal Antenna Patterns Situation
4. Simulations and Results
4.1. Point Target Simulation
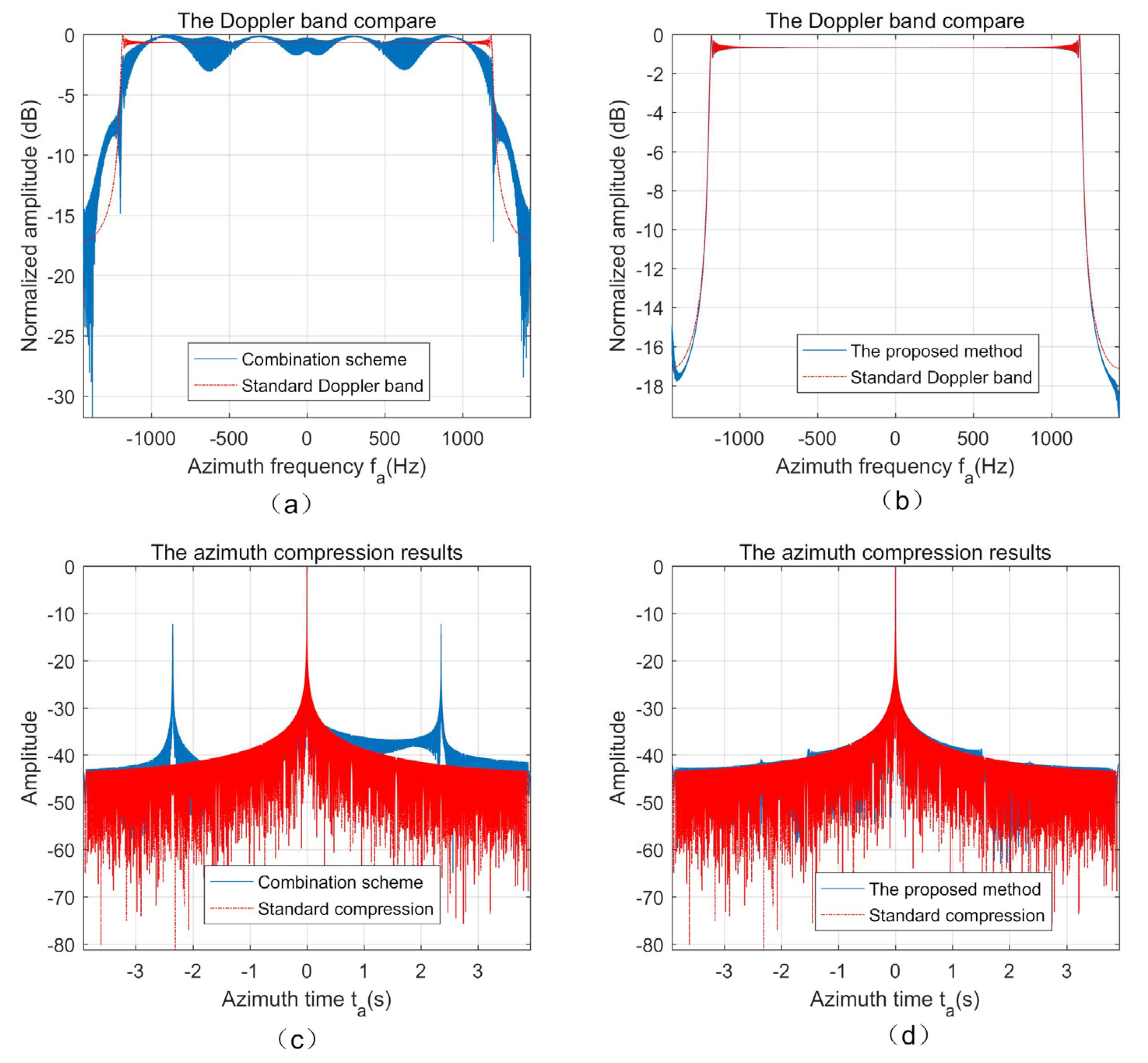
4.1.1. Simulations for Ideal Antenna Mode
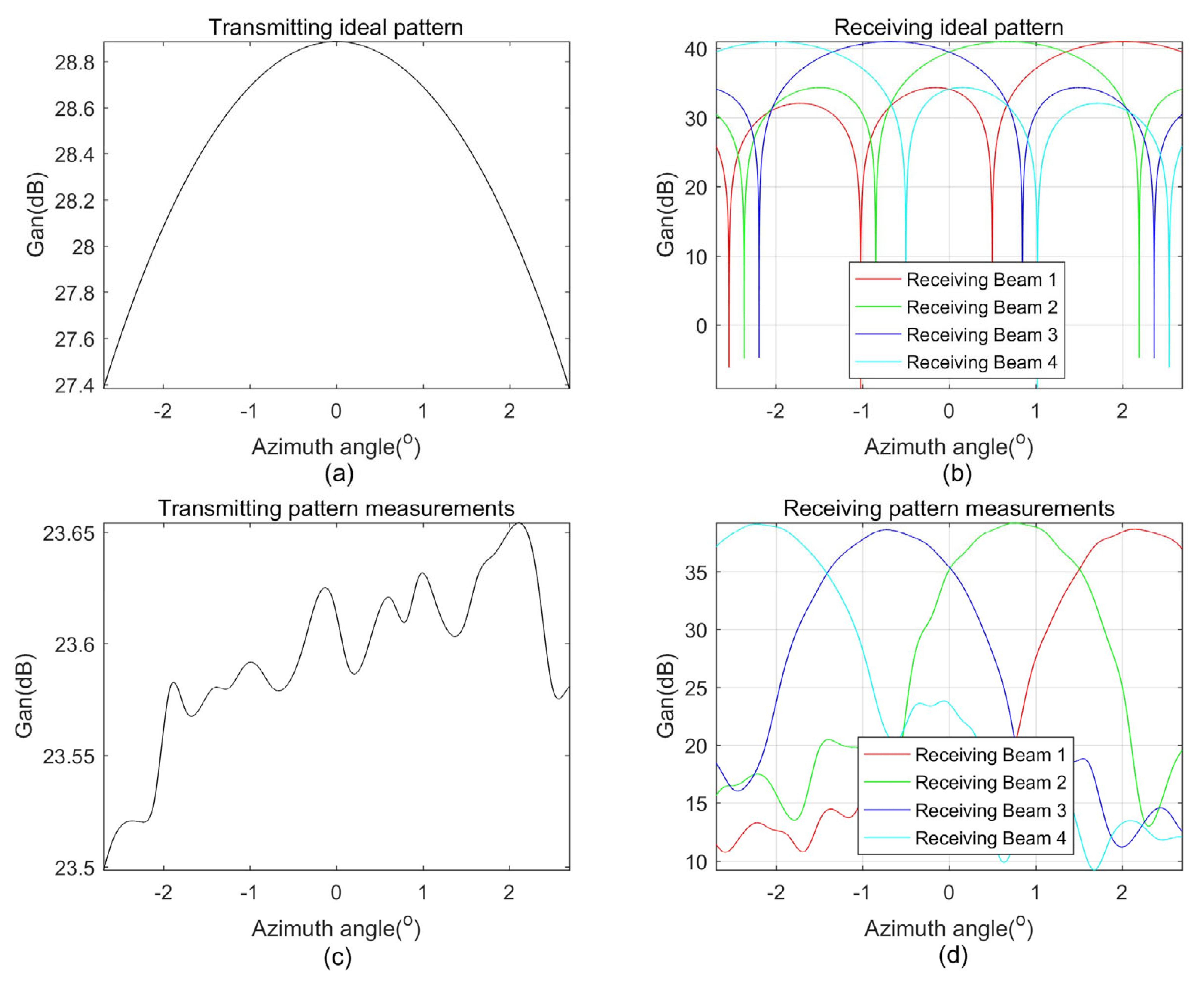
4.1.2. Simulations for Non-Ideal Antenna Mode
4.2. Distributed Targets Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Currie, A.; Brown, M.A. Wide-swath SAR. Radar and Signal Processing. IEE Proc. F 1992, 139, 122–135. [Google Scholar]
- Goodman, N.; Rajakrishna, D.; Stiles, J. Wide swath, high resolution SAR using multiple receive apertures. In Proceedings of the International Geoscience and Remote Sensing Symposium, Hamburg, Germany, 28 June–2 July 1999; pp. 1767–1769. [Google Scholar]
- Suess, M.; Wiesbeck, P. Side-Looking Synthetic Aperture Radar System. European Patent EP1241487, 8 February 2006. [Google Scholar]
- Krieger, G.; Gebert, N.; Moreira, A. Multidimensional waveform encoding: A new digital beamforming technique for synthetic aperture radar remote sensing. IEEE Trans. Geosci. Remote Sens. 2008, 46, 31–46. [Google Scholar] [CrossRef]
- Yu, K.; Zhu, S.; Lan, L.; Yang, B. High-Resolution and Wide-Swath SAR Imaging with Space–Time Coding Array. Remote Sens. 2023, 15, 2465. [Google Scholar] [CrossRef]
- Younis, M.; Fischer, C.; Wiesbeck, W. Digital beamforming in SAR systems. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1735–1739. [Google Scholar] [CrossRef]
- Krieger, G.; Gebert, N.; Younis, M.; Bordoni, F.; Patyuchenko, A.; Moreira, A. Advanced concepts for ultra-wide-swath SAR imaging. In Proceedings of the 7th European Conference on Synthetic Aperture Radar, Friedrichshafen, Germany, 2–5 June 2008; pp. 1–4. [Google Scholar]
- Nicolas, G.; Krieger, G.; Moreira, A. Multichannel Azimuth Processing in ScanSAR and TOPS mode operation. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2994–3008. [Google Scholar]
- Michelangelo, V.; Krieger, G.; Moreira, A. Staggered-SAR: A new concept for high-resolution wide-swath imaging. In Proceedings of the IET International Conference on Radar Systems, Glasgow, UK, 22–25 October 2012; pp. 1–6. [Google Scholar]
- Michelangelo, V.; Krieger, G.; Moreira, A. Staggered SAR: High-Resolution Wide-Swath Imaging by Continuous PRI Variation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4462–4479. [Google Scholar]
- Felipe, Q.A.; Tobias, R.; Gerhard, K. Multichannel Staggered SAR: System Concepts with Reflector and Planar Antennas. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 877–902. [Google Scholar]
- Wang, X.; Ruan, Y.; Zhang, X. Accuracy Improvement of High-Resolution Wide-Swath Spaceborne Synthetic Aperture Radar Imaging with Low Pule Repetition Frequency. Remote Sens. 2023, 15, 3811. [Google Scholar] [CrossRef]
- Ding, C.; Liang, X.; Wang, J.; Chen, L. An novel airborne MIMO-SAR system built in IECAS. In Proceedings of the 2017 International Geoscience and Remote Sensing Symposium, Fort Worth, TX, USA, 23–28 July 2017; pp. 2423–2426. [Google Scholar]
- Jin, G.; Wang, Y.; Zhu, D.; Niu, S.; Yan, H. A Reconfigurable MIMO-SAR Transmission Scheme Based on Inter-Pulse and Intra-Pulse Joint Phase Modulation. IEEE Trans. Signal Process. 2022, 70, 4265–4276. [Google Scholar] [CrossRef]
- Krieger, G.; Gebert, N.; Moreira, A. Unambiguous SAR signal reconstruction from nonuniform displaced phase center sampling. IEEE Trans. Geosci. Remote Sens. 2004, 1, 260–264. [Google Scholar] [CrossRef]
- Li, Z.; Wang, H.; Su, T.; Bao, Z. Generation of wide-swath and high-resolution SAR images from multichannel small spaceborne SAR systems. IEEE Geosci. Remote Sens. Lett. 2005, 2, 82–86. [Google Scholar] [CrossRef]
- Gebert, N.; Almeida, F.Q.; Krieger, G. Airborne Demonstration of Multichannel SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2011, 8, 963–967. [Google Scholar] [CrossRef]
- Sadowy, G.A.; Ghaemi, H.; Hensley, S.C. First Results from an Airborne Ka-band SAR using SweepSAR and Digital Beamforming. In Proceedings of the 9th European Conference on Synthetic Aperture Radar, Nürnberg, Germany, 23–26 April 2012; pp. 23–26. [Google Scholar]
- Wang, H.; Zheng, S.; Dai, S.; Zhao, Y. A New Airborne Ka-band DBF-SAR system and flight test results. In Proceedings of the 12th European Conference on Synthetic Aperture Radar, Aachen, Germany, 5–7 June 2018; pp. 1–5. [Google Scholar]
- Zhou, Y.; Wang, W.; Chen, Z.; Wang, P.; Zhang, H.; Qiu, J.; Zhao, Q.; Deng, Y.; Zhang, Z.; Yu, W.; et al. Digital Beamforming Synthetic Aperture Radar (DBSAR): Experiments and Performance Analysis in Support of 16-Channel Airborne X-Band SAR Data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6784–6798. [Google Scholar] [CrossRef]
- Moreira, A.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.; Younis, M.; Lopez-Dekker, P.; Huber, S.; Villano, M.; Pardini, M.; Eineder, M.; et al. Tandem-L: A Highly Innovative Bistatic SAR Mission for Global Observation of Dynamic Processes on the Earth’s Surface. IEEE Geosci. Remote Sens. Mag. 2015, 3, 9–23. [Google Scholar] [CrossRef]
- Rosen, P.; Hensley, S.; Shaffer, S.; Edelstein, W.; Kim, Y.; Kumar, R.; Misra, T.; Bhan, R.; Sagi, R. The NASA-ISRO SAR (NISAR) mission dual-band radar instrument preliminary design. In Proceedings of the 2017 International Geoscience and Remote Sensing Symposium, Fort Worth, TX, USA, 23–28 July 2017; pp. 23–28. [Google Scholar]
- De, Y.; Yu, W.; Zhang, H.; Wang, W.; Li, D.; Robert, W.A. Forthcoming spaceborne SAR development. J. Radars 2020, 9, 1–33. [Google Scholar]
- Jin, G.; Liu, K.; Liu, D.; Liang, D.; Zhang, H.; Ou, N.; Zhang, Y.; Deng, Y.; Li, C.; Wang, R. An Advanced Phase Synchronization Scheme for LT-1. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1735–1746. [Google Scholar] [CrossRef]
- Xu, Z.; Lu, P.; Cai, Y.; Wu, Y.; Wang, R. Performance Analysis of Channel Imbalance Control and Azimuth Ambiguity Suppression in Azimuth Dual Receiving Antenna Mode of LT-1 Spaceborne SAR System. Remote Sens. 2023, 15, 2765. [Google Scholar] [CrossRef]
- Li, S.Q.; Yang, R.L. Study on Azimuth Signal Processing of Single Phase Center Multiple Beams Synthetic Aperture Radar. J. Electron. Inf. Technol. 2005, 27, 1073–1076. [Google Scholar]
- Song, X.; Yu, W. Reconstruct azimuth signal and suppress interbeam ambiguities of SPCMB SAR with Hybrid filterbank. J. Electron. 2008, 25, 324–329. (In Chinese) [Google Scholar] [CrossRef]
- Huber, S.; Younis, M.; Patyuchenko, A.; Krieger, G.; Moreira, A. Spaceborne Reflector SAR Systems with Digital Beamforming. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3473–3493. [Google Scholar] [CrossRef]
- Papoulis, A. Generalized sampling expansion. IEEE Trans. Circuits Syst. 1977, 24, 652–654. [Google Scholar] [CrossRef]
- Zuo, W. Research on High Resolution Wide Swath SAR Imaging Mode and Algorithm. Ph.D. Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2015. [Google Scholar]
- Lorenz, R.G.; Boyd, S.P. Robust minimum variance beamforming. IEEE Trans. Signal Process. 2005, 53, 1684–1696. [Google Scholar] [CrossRef]
- Reed, I.S.; Mallett, J.D.; Brennan, L.E. Rapid convergence rate in adaptive arrays. IEEE Trans. Aerosp. Electron. Syst. 1974, AES-10, 853–863. [Google Scholar] [CrossRef]




| Parameter | Value | Unit |
| Platform height | 3 | Km |
| Platform velocity | 100 | m/s |
| Reflector diameter | 0.316 | m |
| Carry frequency | 35.0 | GHz |
| Azimuth channel | 4 | - |
| Elevation channel | 4 | - |
| Center looking angle | 70 | º |
| Azimuth resolution | 0.316/4 | m |
| Swath width | 2.4 | Km |
| Pulse duration | 1 | us |
| Signal bandwidth | 120 | MHz |
| PRF | 670 | Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, W.; Li, C.; Zhang, S.; Li, D.; Peng, W.; Li, J.; You, D.; Duan, C. Research on Azimuth DBF Method of HRWS SPC MAB SAR Imaging Mode with Non-Ideal Antenna Mode. Remote Sens. 2024, 16, 1552. https://doi.org/10.3390/rs16091552
Zuo W, Li C, Zhang S, Li D, Peng W, Li J, You D, Duan C. Research on Azimuth DBF Method of HRWS SPC MAB SAR Imaging Mode with Non-Ideal Antenna Mode. Remote Sensing. 2024; 16(9):1552. https://doi.org/10.3390/rs16091552
Chicago/Turabian StyleZuo, Weihua, Caipin Li, Sheng Zhang, Dongtao Li, Wencan Peng, Jinwei Li, Dong You, and Chongdi Duan. 2024. "Research on Azimuth DBF Method of HRWS SPC MAB SAR Imaging Mode with Non-Ideal Antenna Mode" Remote Sensing 16, no. 9: 1552. https://doi.org/10.3390/rs16091552
APA StyleZuo, W., Li, C., Zhang, S., Li, D., Peng, W., Li, J., You, D., & Duan, C. (2024). Research on Azimuth DBF Method of HRWS SPC MAB SAR Imaging Mode with Non-Ideal Antenna Mode. Remote Sensing, 16(9), 1552. https://doi.org/10.3390/rs16091552






