Optimizing Optical Coastal Remote-Sensing Products: Recommendations for Regional Algorithm Calibration
Abstract
1. Introduction
2. Materials and Methods
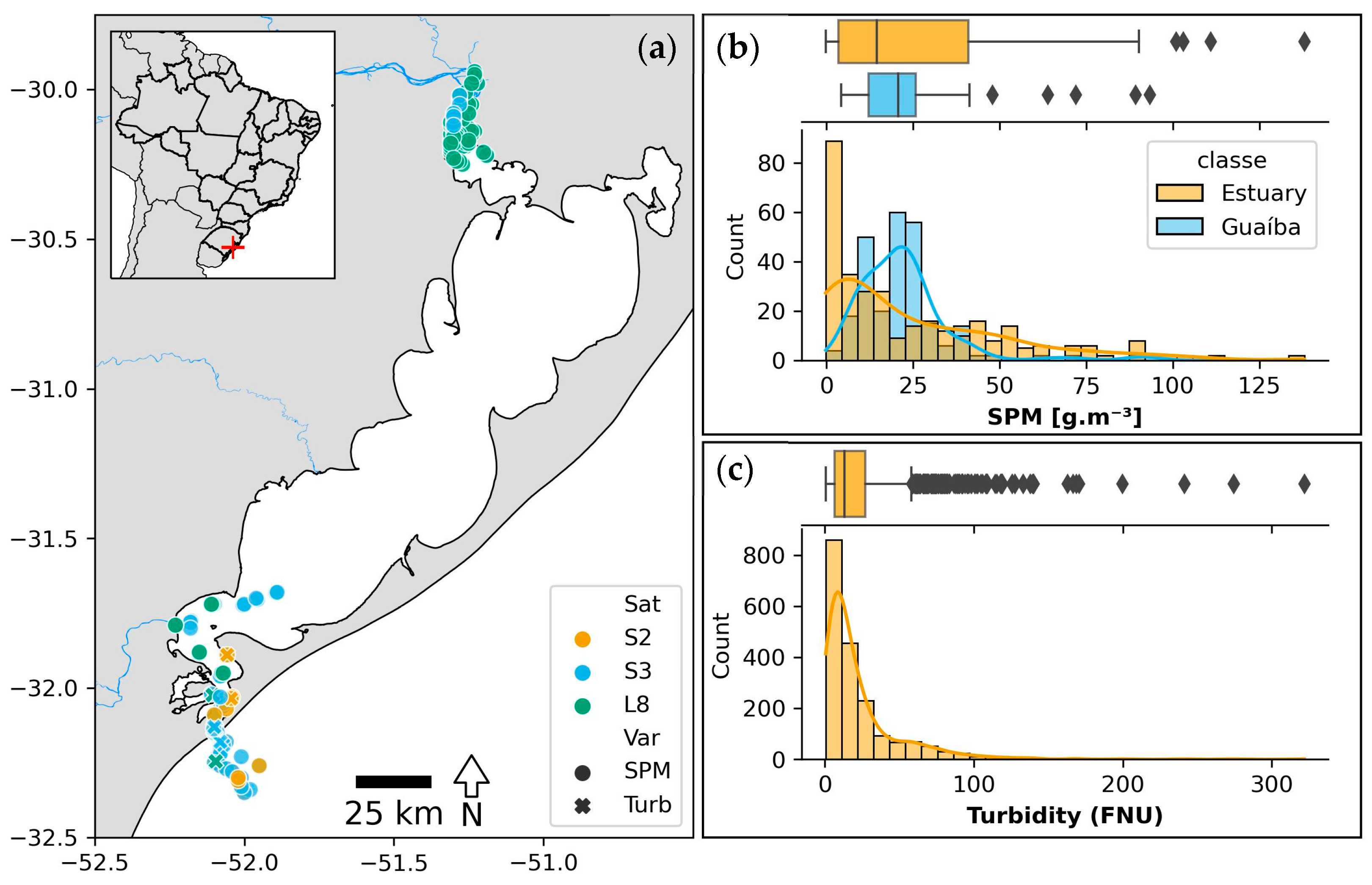
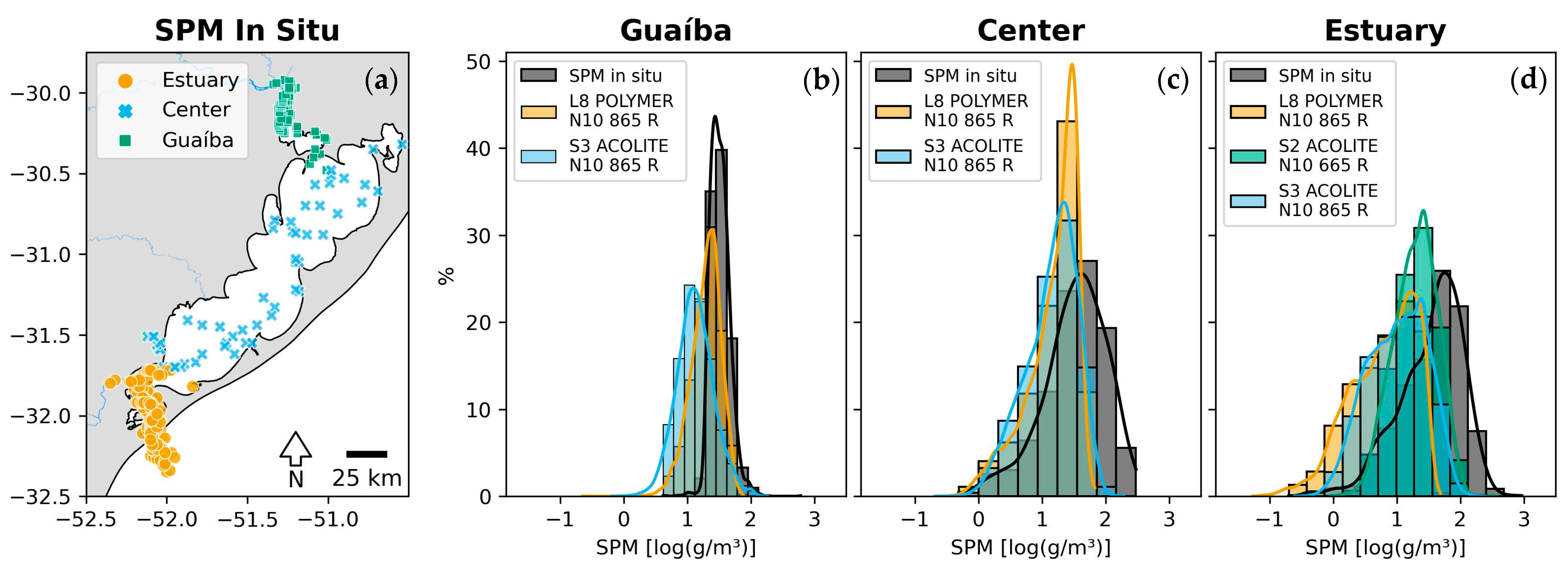
2.1. Study Area
2.2. Data
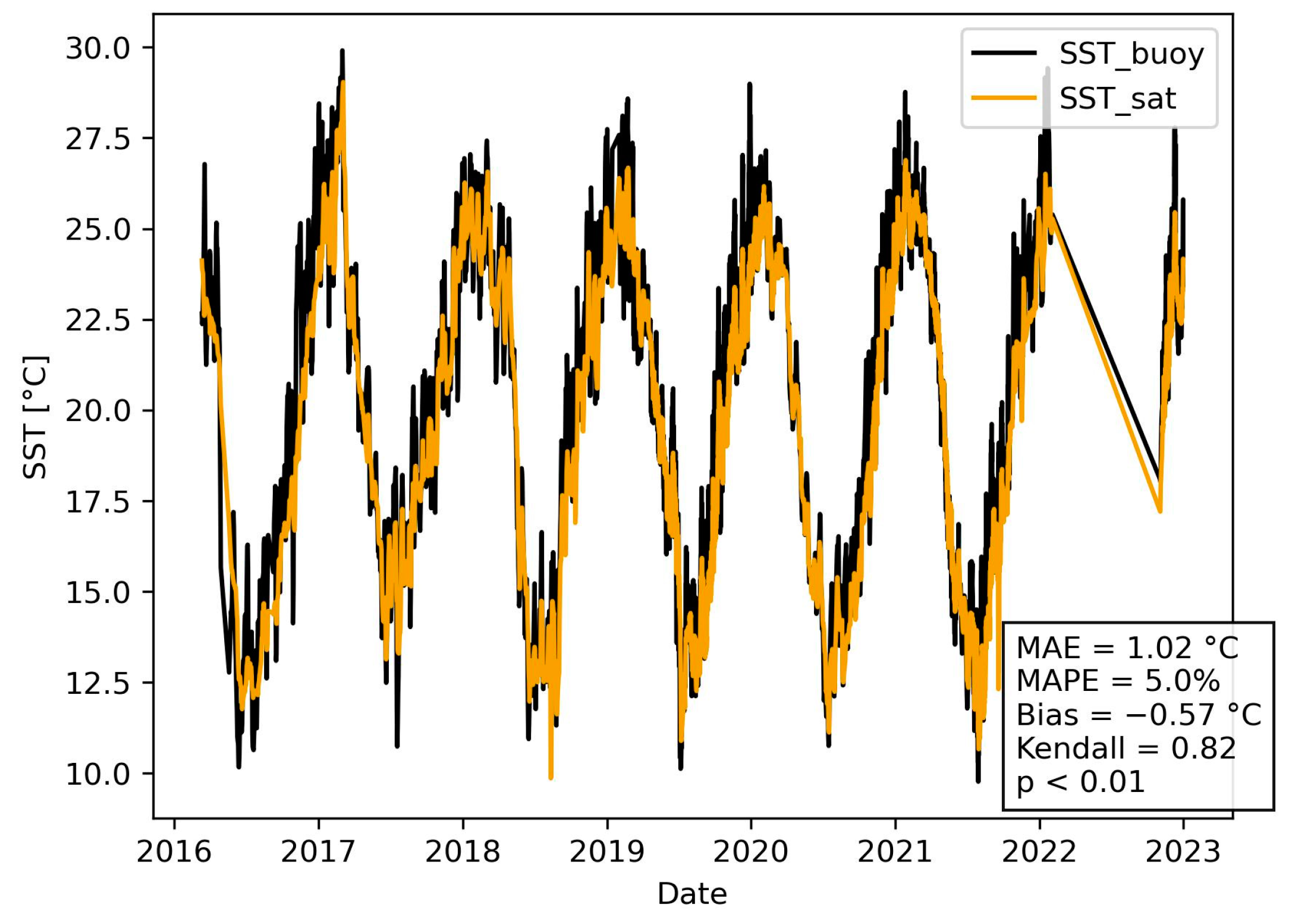
2.2.1. In Situ Data
2.2.2. Remote-Sensing Data
2.3. Methods
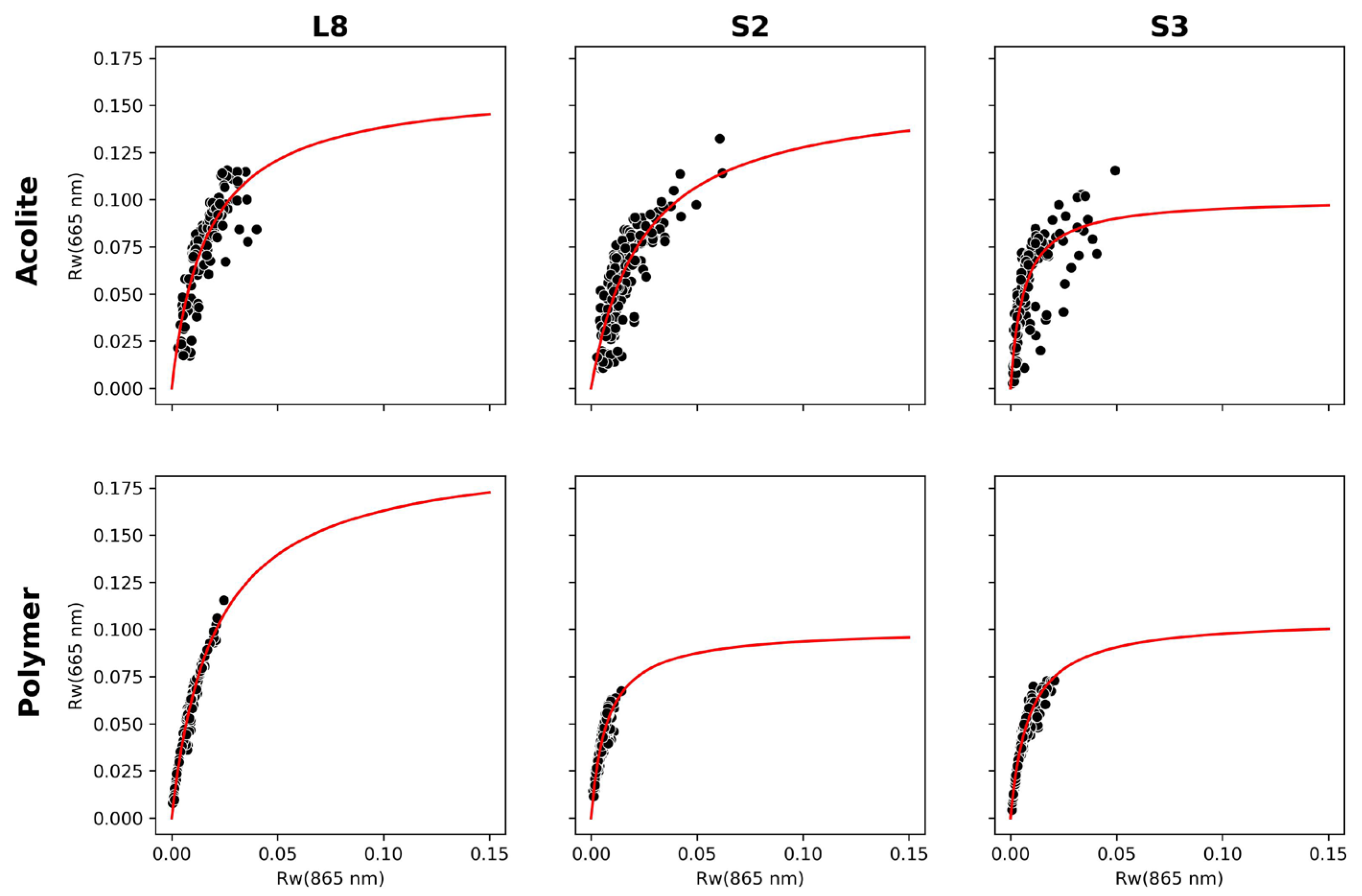
2.3.1. Atmospheric Correction
2.3.2. Matchups
2.3.3. Turbidity and SPM Algorithms
2.3.4. Convolution and Regional Recalibration Methods
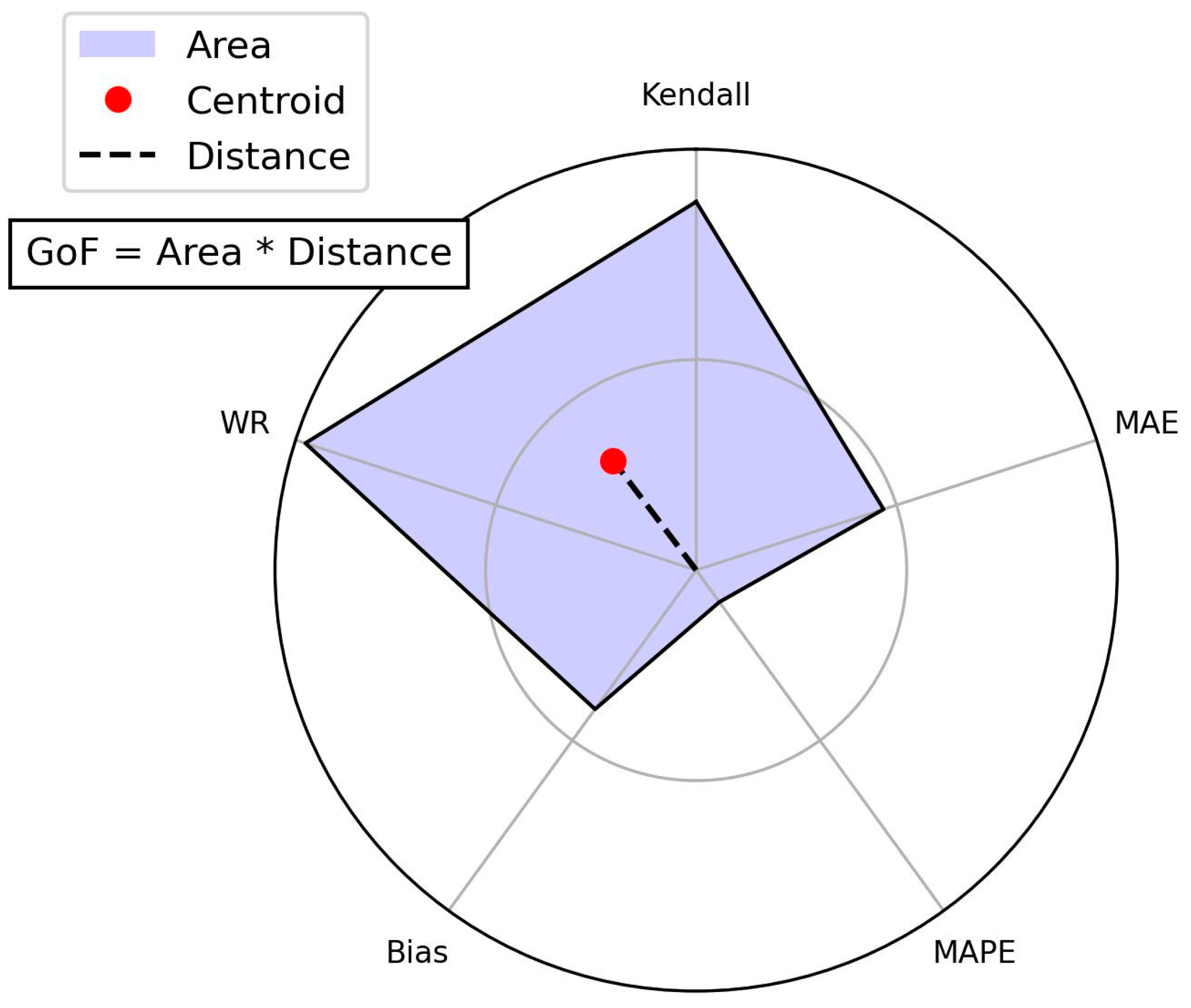
2.3.5. Statistical Parameters
3. Results
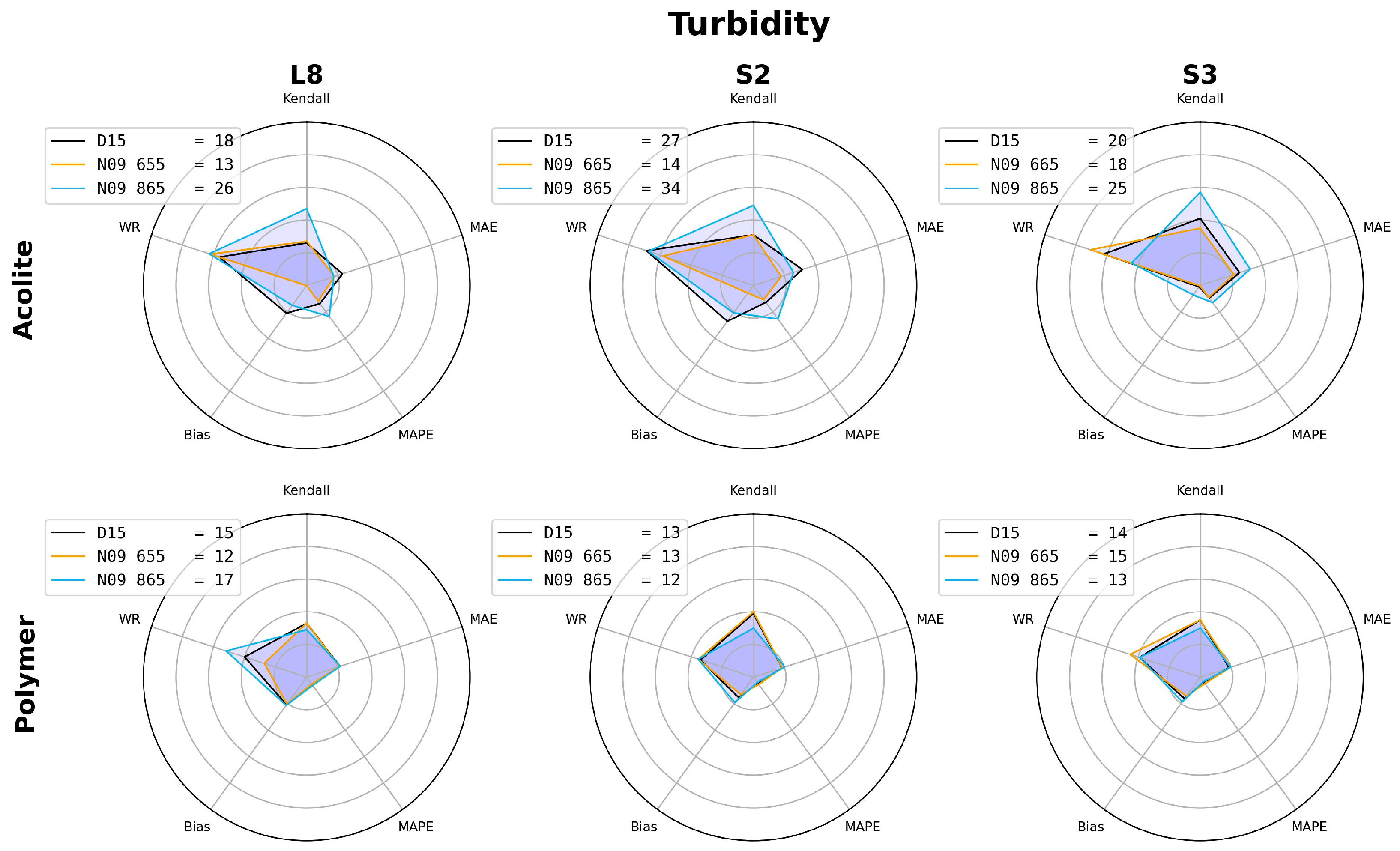
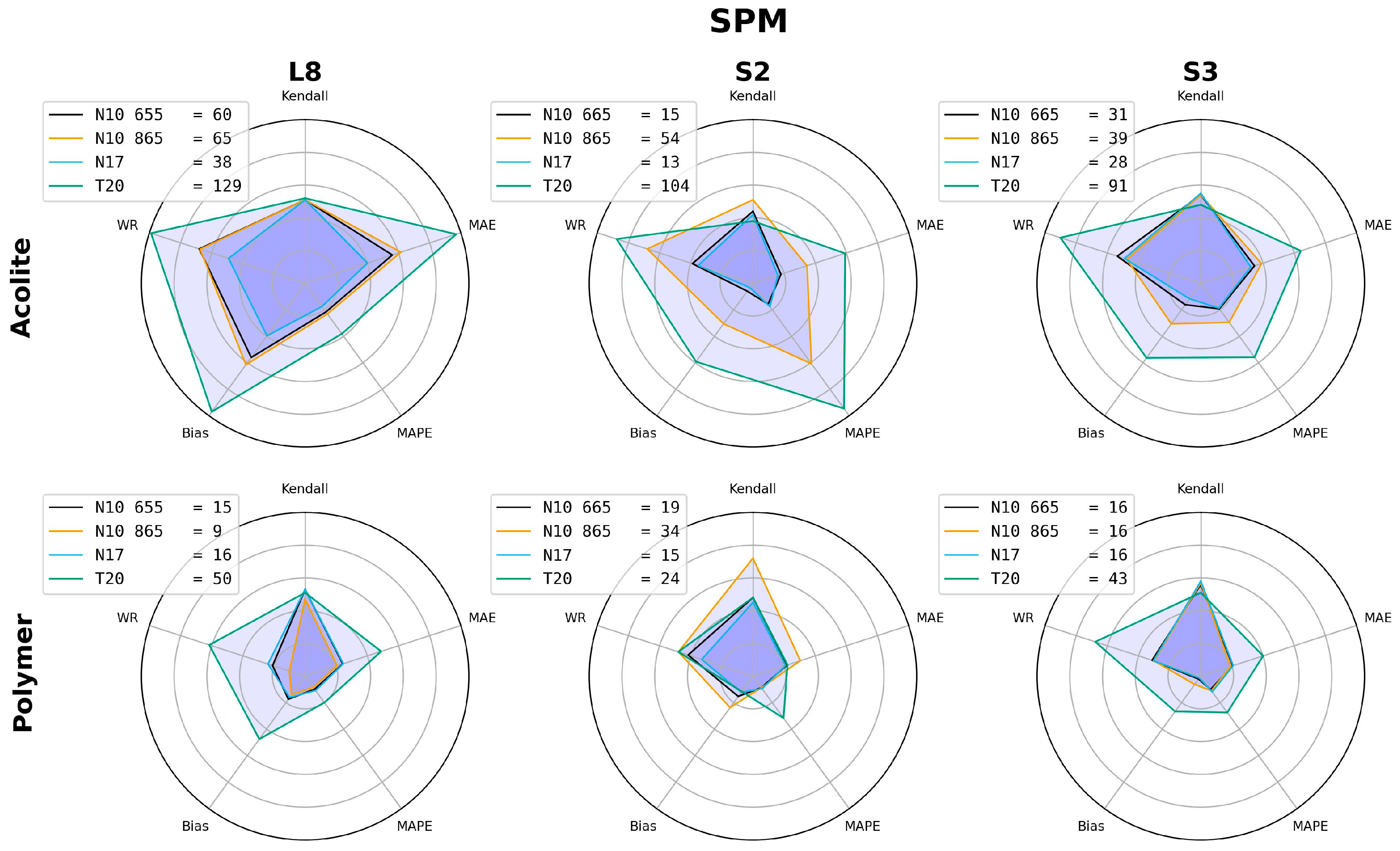
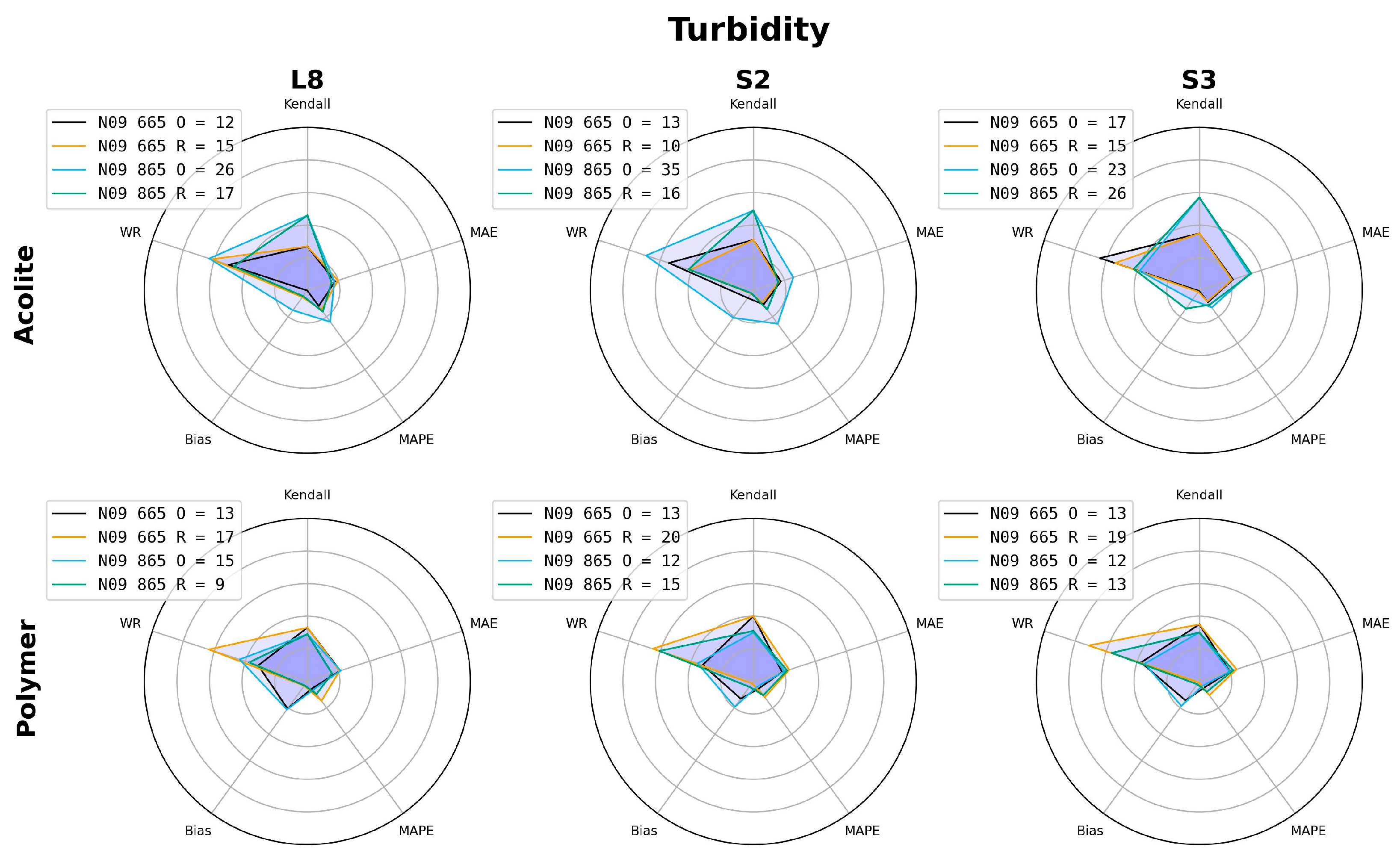
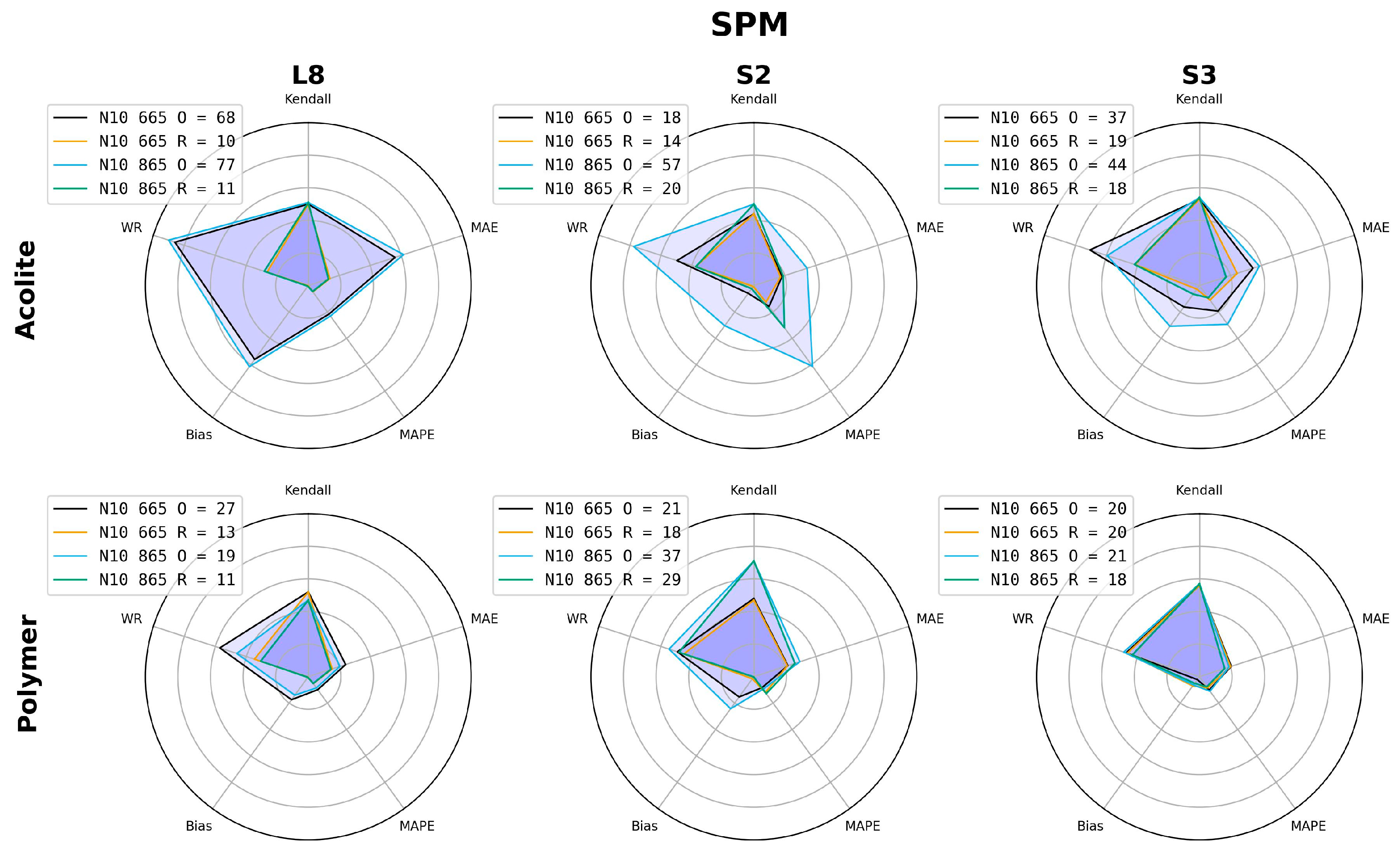
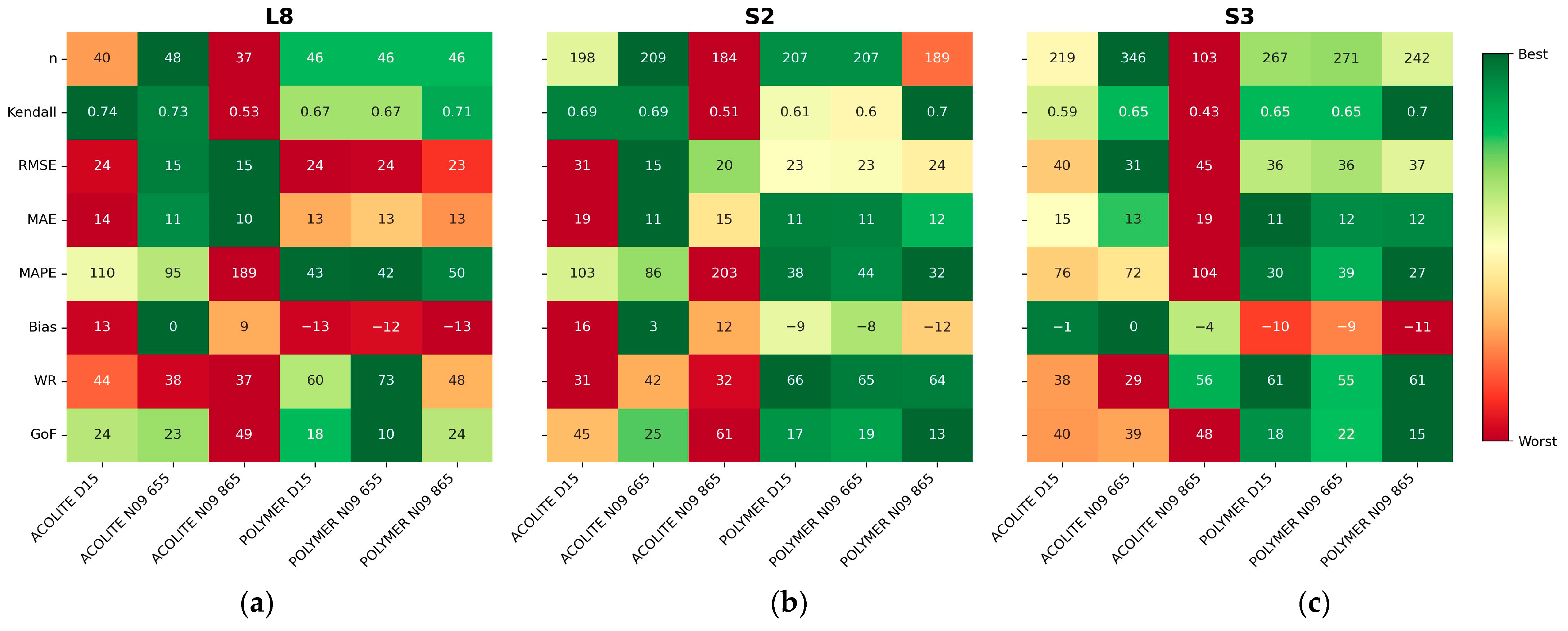
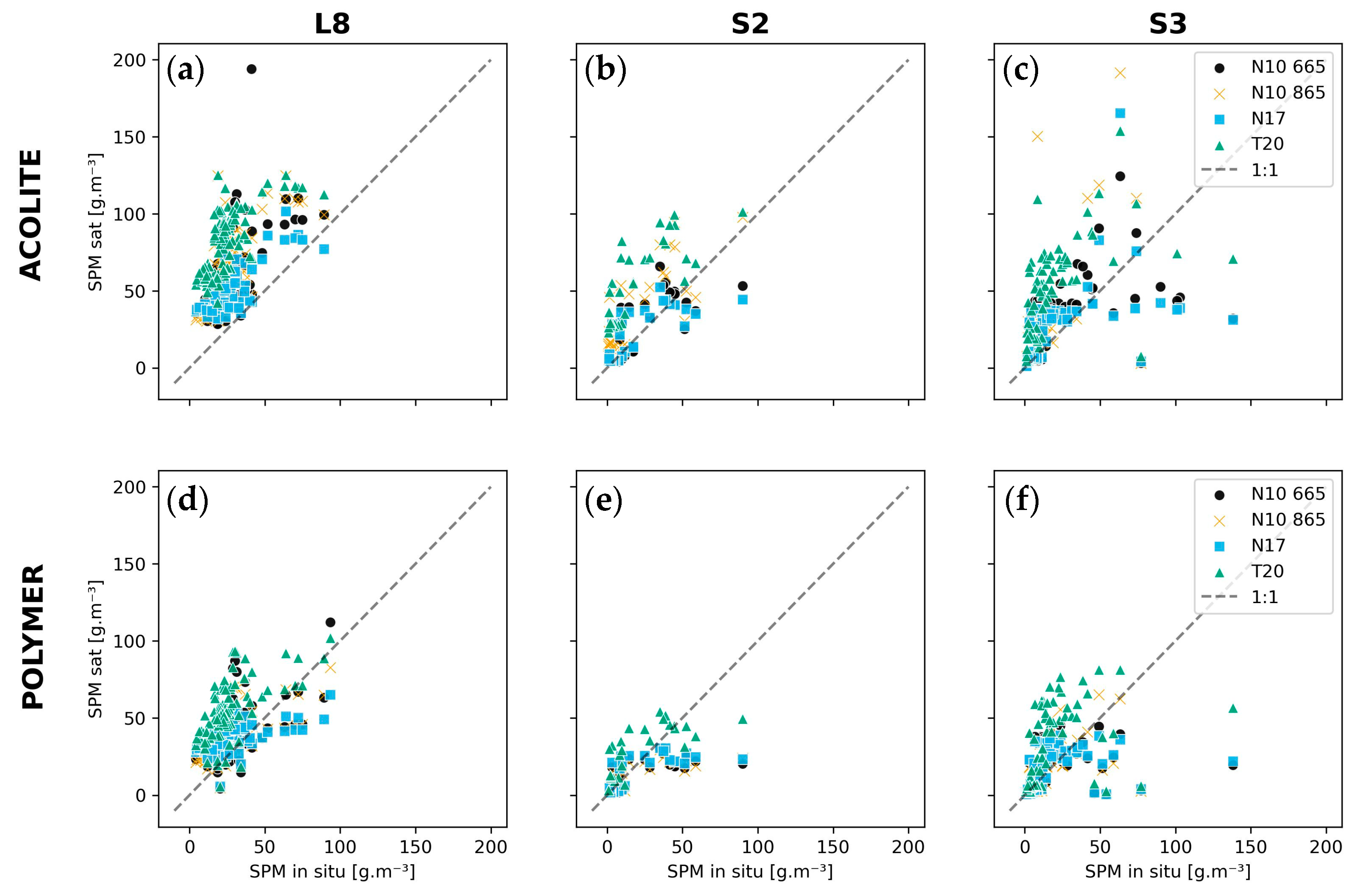
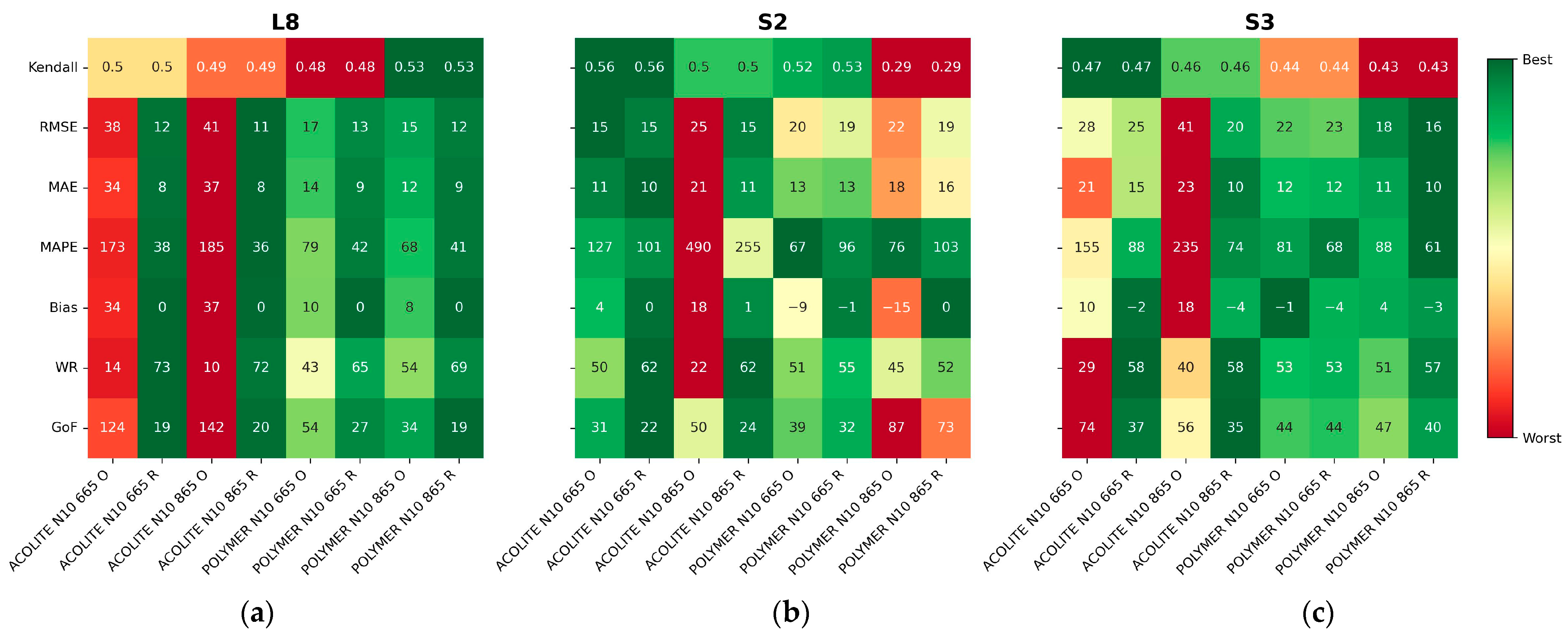
3.1. Performance of the Different Combinations of Atmospheric Corrections and Algorithms
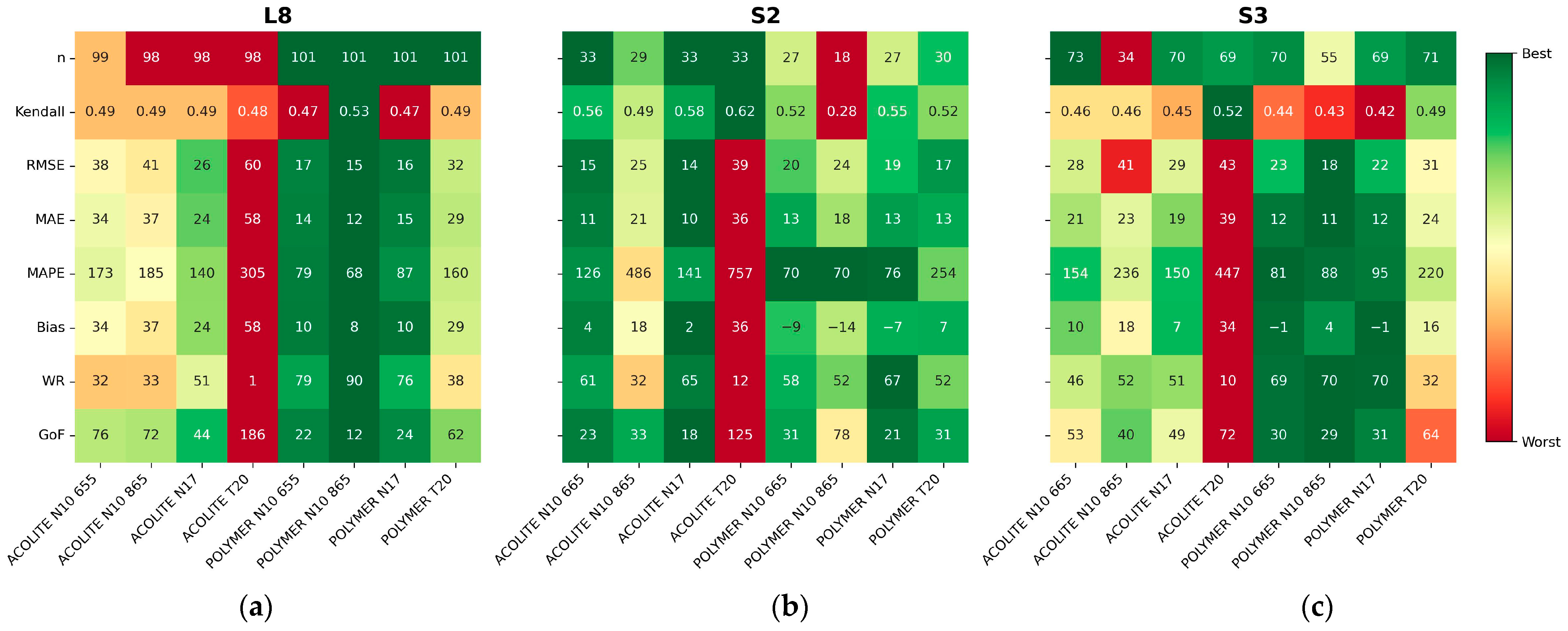
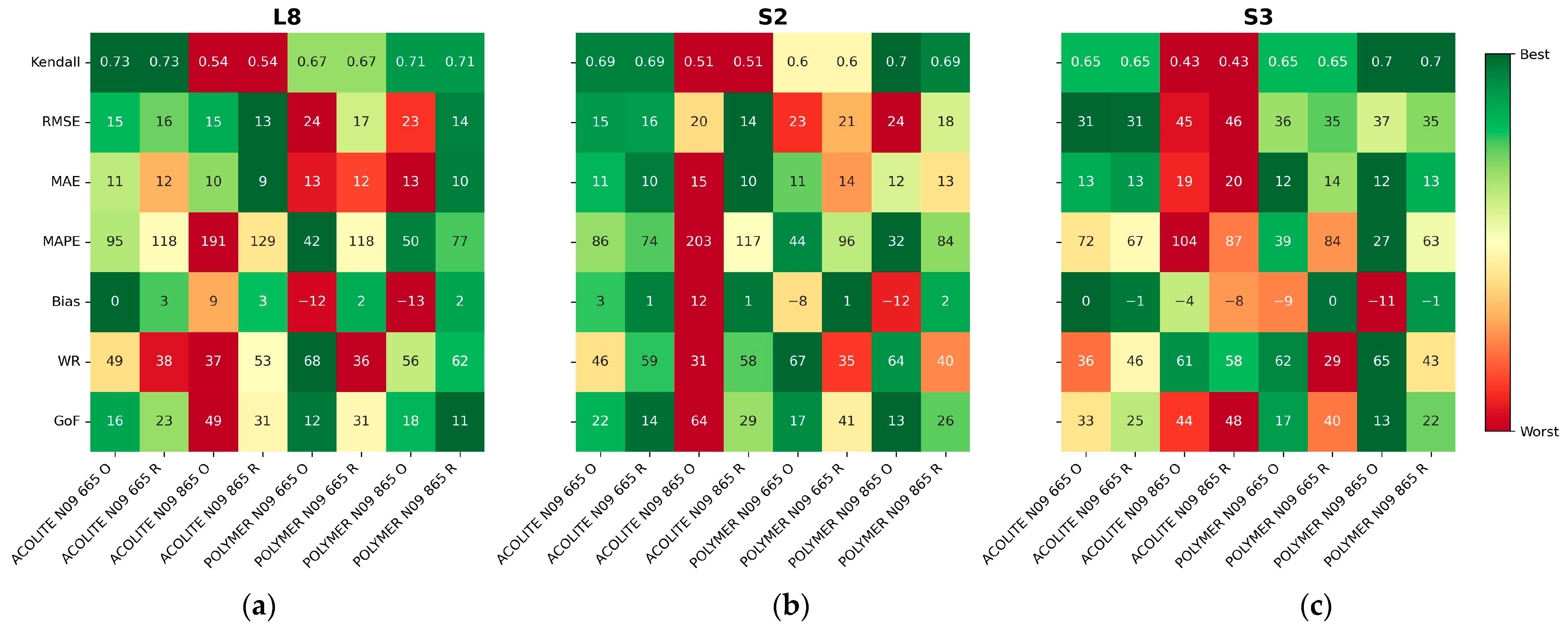
3.2. Regional Recalibration of Coefficients
4. Discussion
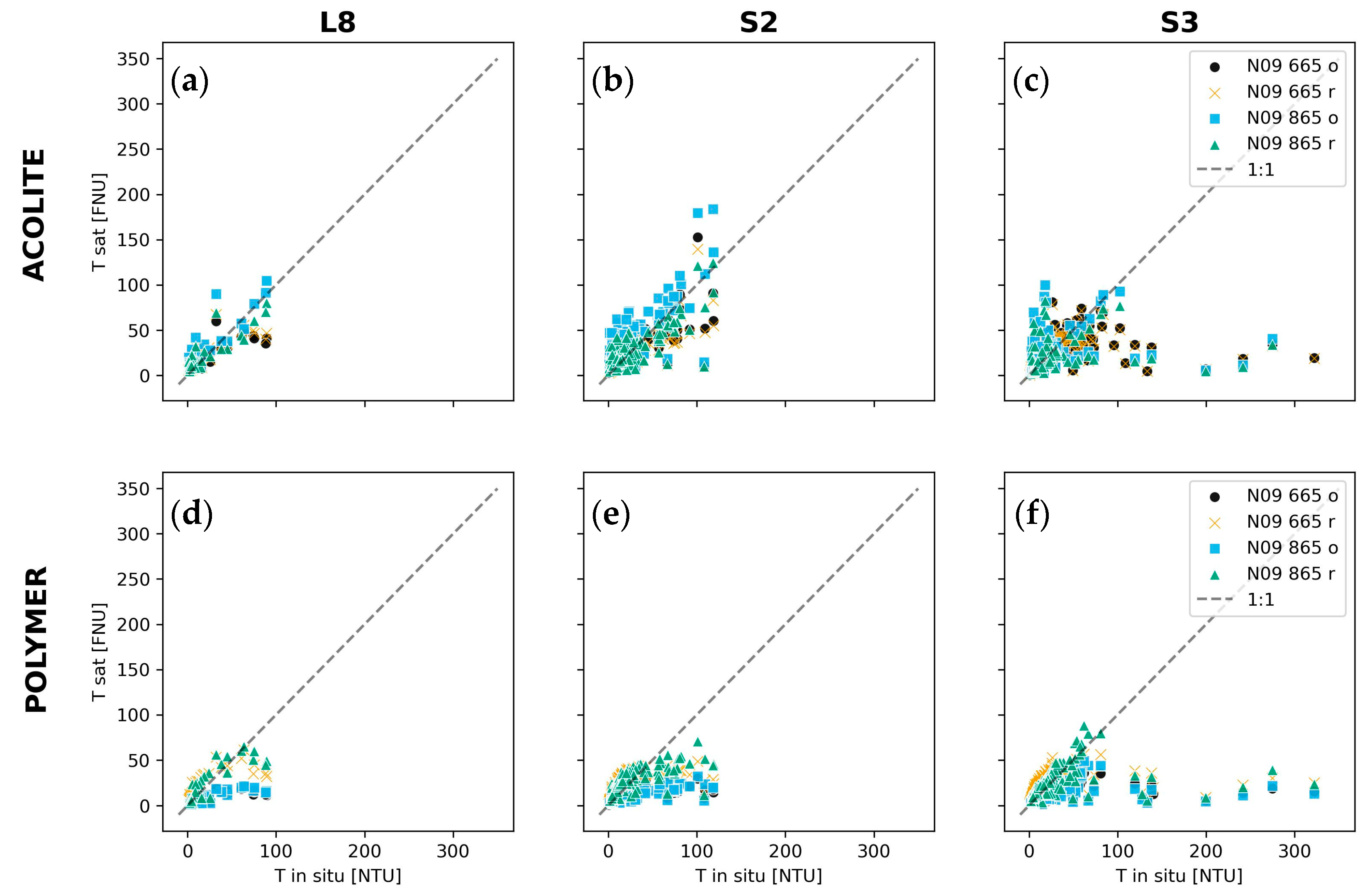
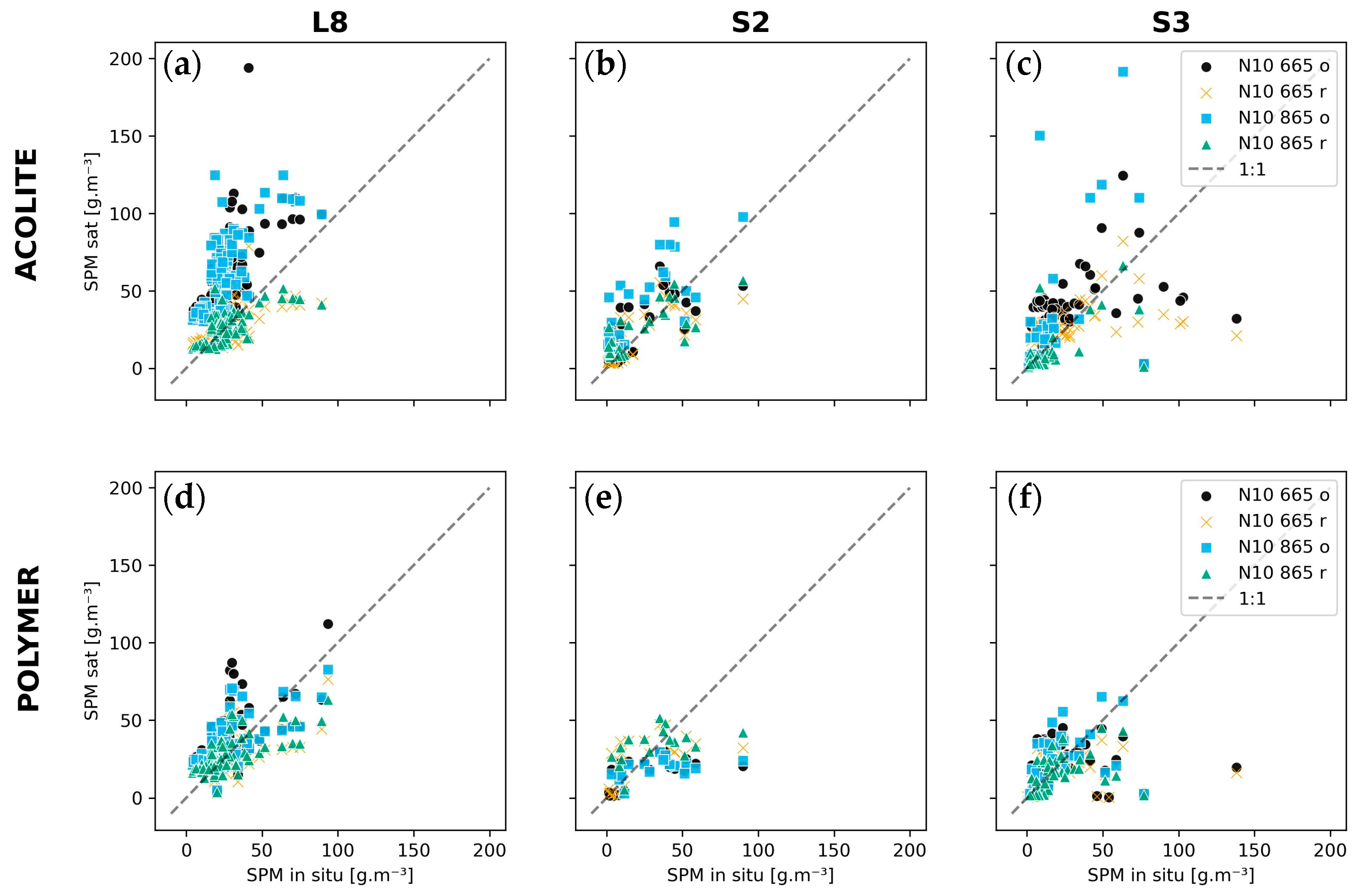
4.1. Previous Studies of Patos Lagoon and Results without Regional Recalibration
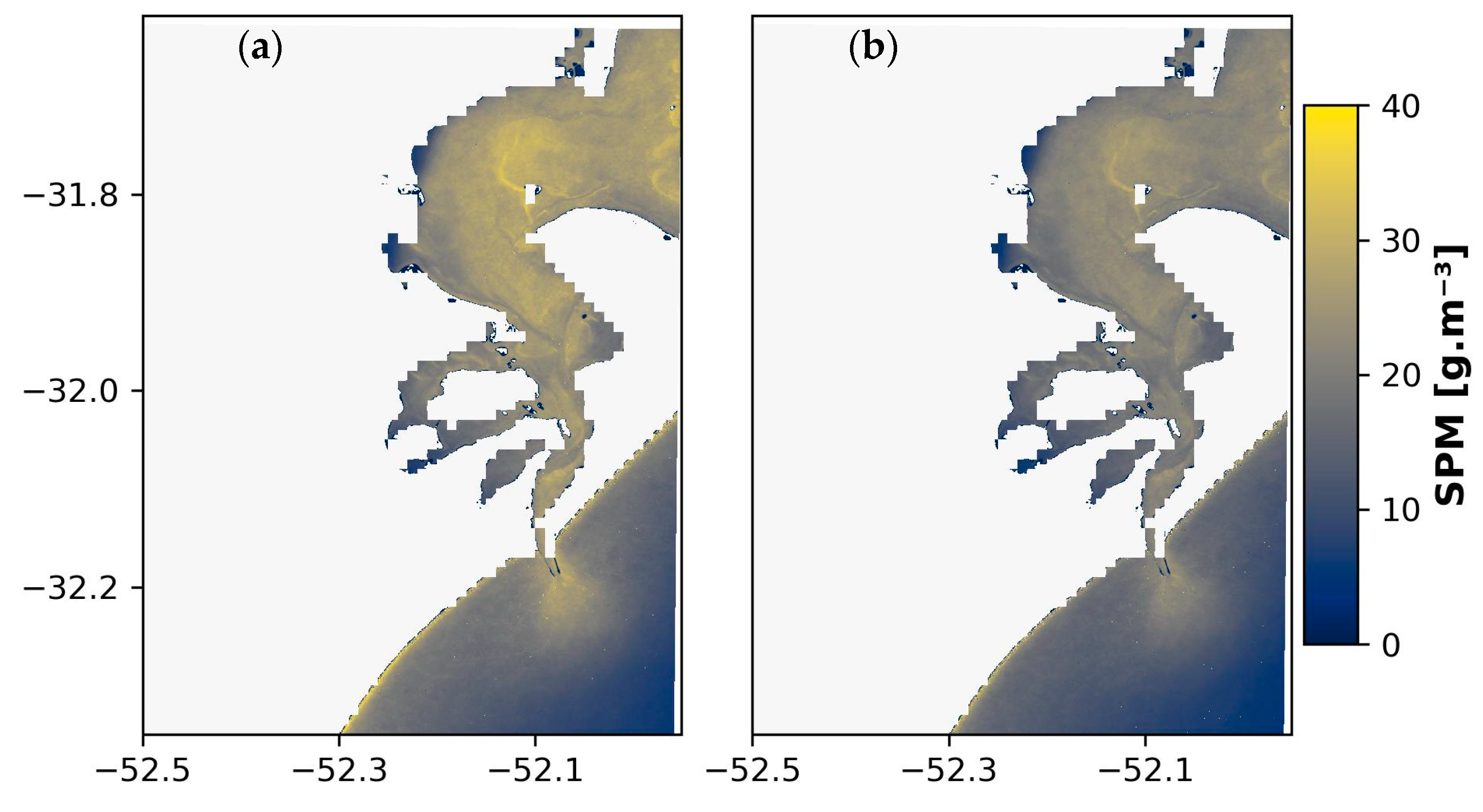
4.2. Regional Recalibration and Sources of Uncertainty
5. Conclusions
- Based on the newly proposed GoF metric, the best algorithm performance was generally linked to POLYMER atmospheric correction, single-band algorithms (N09 and N10), and the NIR band (865 nm), with percentage errors (MAPEs) between 27% and 42% for turbidity and between 68% and 81% for SPM;
- Regional recalibration of the empirical coefficients for N09 and N10 led to a reduction in bias. We recommend the use of recalibrated coefficients for estimating the SPM concentration in Patos Lagoon via remote sensing. For turbidity, the original coefficients yielded a better performance for S2 and S3;
- The method used for recalibrating the coefficients (GeoCalVal) and the metric used to rank the performances (GoF) can be directly applied to other regions and optical remote-sensing products;
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Additional Plots and Tables
| L8 | S2 | S3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AC | ACOLITE | POLYMER | ACOLITE | POLYMER | ACOLITE | POLYMER | ||||||
| Band | 655 | 865 | 655 | 865 | 665 | 865 | 665 | 865 | 665 | 865 | 665 | 865 |
| Turbidity | 283.43 | 1616.89 | 700.11 | 6435.35 | 247.24 | 1418.96 | 440.81 | 4636.58 | 271.42 | 1751.17 | 447.48 | 3826.15 |
| SPM | 136.11 | 1229.06 | 219.57 | 2272.39 | 292.43 | 1724.03 | 551.38 | 5213.88 | 236.63 | 1033.23 | 298.97 | 2062.85 |
References
- Kjerfve, B. Chapter 1 Coastal Lagoons. In Coastal Lagoon Processes; Elsevier Oceanography Series; Elsevier: Amsterdam, The Netherlands, 1994; pp. 1–8. ISBN 978-0-444-88258-5. [Google Scholar]
- Novoa, S.; Doxaran, D.; Ody, A.; Vanhellemont, Q.; Lafon, V.; Lubac, B.; Gernez, P. Atmospheric Corrections and Multi-Conditional Algorithm for Multi-Sensor Remote Sensing of Suspended Particulate Matter in Low-to-High Turbidity Levels Coastal Waters. Remote Sens. 2017, 9, 61. [Google Scholar] [CrossRef]
- Tavora, J.; Fernandes, E.H.L.; Thomas, A.C.; Weatherbee, R.; Schettini, C.A.F. The Influence of River Discharge and Wind on Patos Lagoon, Brazil, Suspended Particulate Matter. Int. J. Remote Sens. 2019, 40, 4506–4525. [Google Scholar] [CrossRef]
- Vantrepotte, V.; Gensac, E.; Loisel, H.; Gardel, A.; Dessailly, D.; Mériaux, X. Satellite Assessment of the Coupling between in Water Suspended Particulate Matter and Mud Banks Dynamics over the French Guiana Coastal Domain. J. S. Am. Earth Sci. 2013, 44, 25–34. [Google Scholar] [CrossRef]
- Bordin, L.H.; Machado, E.D.C.; Mendes, C.R.B.; Fernandes, E.H.L.; Camargo, M.G.; Kerr, R.; Schettini, C.A. Daily Variability of Pelagic Metabolism in a Subtropical Lagoonal Estuary. J. Mar. Syst. 2023, 240, 103861. [Google Scholar] [CrossRef]
- Kitchener, B.G.; Wainwright, J.; Parsons, A.J. A Review of the Principles of Turbidity Measurement. Prog. Phys. Geogr. Earth Environ. 2017, 41, 620–642. [Google Scholar] [CrossRef]
- Hongve, D.; Åkesson, G. Comparison of Nephelometric Turbidity Measurements Using Wavelengths 400–600 and 860 Nm. Water Res. 1998, 32, 3143–3145. [Google Scholar] [CrossRef]
- Neukermans, G.; Ruddick, K.; Loisel, H.; Roose, P. Optimization and Quality Control of Suspended Particulate Matter Concentration Measurement Using Turbidity Measurements: Optimizing [SPM] Measurement. Limnol. Oceanogr. Methods 2012, 10, 1011–1023. [Google Scholar] [CrossRef]
- Nechad, B.; Ruddick, K.G.; Neukermans, G. Calibration and Validation of a Generic Multisensor Algorithm for Mapping of Turbidity in Coastal Waters; Bostater, C.R., Jr., Mertikas, S.P., Neyt, X., Velez-Reyes, M., Eds.; SPIE: Berlin, Germany, 2009; p. 74730H. [Google Scholar]
- Tavora, J.; Jiang, B.; Kiffney, T.; Bourdin, G.; Gray, P.C.; Carvalho, L.S.; Hesketh, G.; Schild, K.M.; Souza, L.F.; Brady, D.C.; et al. Recipes for the Derivation of Water Quality Parameters Using the High-Spatial-Resolution Data from Sensors on Board Sentinel-2A, Sentinel-2B, Landsat-5, Landsat-7, Landsat-8, and Landsat-9 Satellites. J. Remote Sens. 2023, 3, 0049. [Google Scholar] [CrossRef]
- Pahlevan, N.; Mangin, A.; Balasubramanian, S.V.; Smith, B.; Alikas, K.; Arai, K.; Barbosa, C.; Bélanger, S.; Binding, C.; Bresciani, M.; et al. ACIX-Aqua: A Global Assessment of Atmospheric Correction Methods for Landsat-8 and Sentinel-2 over Lakes, Rivers, and Coastal Waters. Remote Sens. Environ. 2021, 258, 112366. [Google Scholar] [CrossRef]
- Luo, Y.; Doxaran, D.; Vanhellemont, Q. Retrieval and Validation of Water Turbidity at Metre-Scale Using Pléiades Satellite Data: A Case Study in the Gironde Estuary. Remote Sens. 2020, 12, 946. [Google Scholar] [CrossRef]
- Gordon, H.R.; Wang, M. Retrieval of Water-Leaving Radiance and Aerosol Optical Thickness over the Oceans with SeaWiFS: A Preliminary Algorithm. Appl. Opt. 1994, 33, 443–452. [Google Scholar] [CrossRef] [PubMed]
- Vanhellemont, Q.; Ruddick, K. Turbid Wakes Associated with Offshore Wind Turbines Observed with Landsat 8. Remote Sens. Environ. 2014, 145, 105–115. [Google Scholar] [CrossRef]
- Bailey, S.W.; Franz, B.A.; Werdell, P.J. Estimation of Near-Infrared Water-Leaving Reflectance for Satellite Ocean Color Data Processing. Opt. Express 2010, 18, 7521–7527. [Google Scholar] [CrossRef] [PubMed]
- Steinmetz, F.; Deschamps, P.-Y.; Ramon, D. Atmospheric Correction in Presence of Sun Glint: Application to MERIS. Opt. Express 2011, 19, 9783–9800. [Google Scholar] [CrossRef] [PubMed]
- Vanhellemont, Q.; Ruddick, K. Atmospheric Correction of Metre-Scale Optical Satellite Data for Inland and Coastal Water Applications. Remote Sens. Environ. 2018, 216, 586–597. [Google Scholar] [CrossRef]
- Salama, M.S.; Radwan, M.; Van Der Velde, R. A Hydro-Optical Model for Deriving Water Quality Variables from Satellite Images (HydroSat): A Case Study of the Nile River Demonstrating the Future Sentinel-2 Capabilities. Phys. Chem. Earth Parts A/B/C 2012, 50–52, 224–232. [Google Scholar] [CrossRef]
- Brockmann, C.; Doerffer, R.; Peters, M.; Stelzer, K.; Embacher, S.; Ruescas, A. Evolution of the C2RCC Neural Network for Sentinel 2 and 3 for the Retrieval of Ocean Colour Products in Normal and Extreme Optically Complex Waters. In Proceedings of the Conference Held Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016. [Google Scholar]
- Hieronymi, M.; Bi, S.; Müller, D.; Schütt, E.M.; Behr, D.; Brockmann, C.; Lebreton, C.; Steinmetz, F.; Stelzer, K.; Vanhellemont, Q. Corrigendum: Ocean Color Atmospheric Correction Methods in View of Usability for Different Optical Water Types. Front. Mar. Sci. 2023, 10, 1307517. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanre, D.; Deuze, J.L.; Herman, M.; Morcette, J.-J. Second Simulation of the Satellite Signal in the Solar Spectrum, 6S: An Overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Vanhellemont, Q.; Ruddick, K. Atmospheric Correction of Sentinel-3/OLCI Data for Mapping of Suspended Particulate Matter and Chlorophyll-a Concentration in Belgian Turbid Coastal Waters. Remote Sens. Environ. 2021, 256, 112284. [Google Scholar] [CrossRef]
- Steinmetz, F.; Ramon, D. Sentinel-2 MSI and Sentinel-3 OLCI Consistent Ocean Colour Products Using POLYMER; Frouin, R.J., Murakami, H., Eds.; SPIE: Honolulu, HI, USA, 2018; p. 10. [Google Scholar]
- Mabit, R.; Araújo, C.A.S.; Singh, R.K.; Bélanger, S. Empirical Remote Sensing Algorithms to Retrieve SPM and CDOM in Québec Coastal Waters. Front. Remote Sens. 2022, 3, 834908. [Google Scholar] [CrossRef]
- Theenathayalan, V.; Sathyendranath, S.; Kulk, G.; Menon, N.; George, G.; Abdulaziz, A.; Selmes, N.; Brewin, R.; Rajendran, A.; Xavier, S.; et al. Regional Satellite Algorithms to Estimate Chlorophyll-a and Total Suspended Matter Concentrations in Vembanad Lake. Remote Sens. 2022, 14, 6404. [Google Scholar] [CrossRef]
- Renosh, P.R.; Doxaran, D.; Keukelaere, L.D.; Gossn, J.I. Evaluation of Atmospheric Correction Algorithms for Sentinel-2-MSI and Sentinel-3-OLCI in Highly Turbid Estuarine Waters. Remote Sens. 2020, 12, 1285. [Google Scholar] [CrossRef]
- Nechad, B.; Ruddick, K.; Park, Y. Calibration and Validation of a Generic Multisensor Algorithm for Mapping of Total Suspended Matter in Turbid Waters. Remote Sens. Environ. 2010, 114, 854–866. [Google Scholar] [CrossRef]
- Yu, X.; Lee, Z.; Shen, F.; Wang, M.; Wei, J.; Jiang, L.; Shang, Z. An Empirical Algorithm to Seamlessly Retrieve the Concentration of Suspended Particulate Matter from Water Color across Ocean to Turbid River Mouths. Remote Sens. Environ. 2019, 235, 111491. [Google Scholar] [CrossRef]
- Távora, J.; Boss, E.; Doxaran, D.; Hill, P. An Algorithm to Estimate Suspended Particulate Matter Concentrations and Associated Uncertainties from Remote Sensing Reflectance in Coastal Environments. Remote Sens. 2020, 12, 2172. [Google Scholar] [CrossRef]
- Salama, M.S.; Verhoef, W. Two-Stream Remote Sensing Model for Water Quality Mapping: 2SeaColor. Remote Sens. Environ. 2015, 157, 111–122. [Google Scholar] [CrossRef]
- Babin, M.; Morel, A.; Fournier-Sicre, V.; Fell, F.; Stramski, D. Light Scattering Properties of Marine Particles in Coastal and Open Ocean Waters Asrelated to the Particle Mass Concentration. Limnol. Oceanogr. 2003, 48, 843–859. [Google Scholar] [CrossRef]
- Luo, Y.; Doxaran, D.; Ruddick, K.; Shen, F.; Gentili, B.; Yan, L.; Huang, H. Saturation of Water Reflectance in Extremely Turbid Media Based on Field Measurements, Satellite Data and Bio-Optical Modelling. Opt. Express 2018, 26, 10435–10451. [Google Scholar] [CrossRef] [PubMed]
- Dogliotti, A.I.; Ruddick, K.G.; Nechad, B.; Doxaran, D.; Knaeps, E. A Single Algorithm to Retrieve Turbidity from Remotely-Sensed Data in All Coastal and Estuarine Waters. Remote Sens. Environ. 2015, 156, 157–168. [Google Scholar] [CrossRef]
- Tavora, J.; Gonçalves, G.A.; Fernandes, E.H.; Salama, M.S.; Van Der Wal, D. Detecting Turbid Plumes from Satellite Remote Sensing: State-of-Art Thresholds and the Novel PLUMES Algorithm. Front. Mar. Sci. 2023, 10, 1215327. [Google Scholar] [CrossRef]
- Vanhellemont, Q. Adaptation of the Dark Spectrum Fitting Atmospheric Correction for Aquatic Applications of the Landsat and Sentinel-2 Archives. Remote Sens. Environ. 2019, 225, 175–192. [Google Scholar] [CrossRef]
- Távora, J.; Fernandes, E.; Bitencourt, L.; Orozco, P. El-Niño Southern Oscillation (ENSO) Effects on the Variability of Patos Lagoon Suspended Particulate Matter. Reg. Stud. Mar. Sci. 2020, 40, 101495. [Google Scholar] [CrossRef]
- Wang, M.; Shi, W. The NIR-SWIR Combined Atmospheric Correction Approach for MODIS Ocean Color Data Processing. Opt. Express 2007, 15, 15722. [Google Scholar] [CrossRef] [PubMed]
- Han, B.; Loisel, H.; Vantrepotte, V.; Mériaux, X.; Bryère, P.; Ouillon, S.; Dessailly, D.; Xing, Q.; Zhu, J. Development of a Semi-Analytical Algorithm for the Retrieval of Suspended Particulate Matter from Remote Sensing over Clear to Very Turbid Waters. Remote Sens. 2016, 8, 211. [Google Scholar] [CrossRef]
- Kjerfve, B. Comparative oceanography of coastal lagoons. In Estuarine Variability; Elsevier: Amsterdam, The Netherlands, 1986; pp. 63–81. ISBN 978-0-12-761890-6. [Google Scholar]
- Fernandes, E.; Mariño-Tapia, I.; Dyer, K.; Möller, O. The Attenuation of Tidal and Subtidal Oscillations in the Patos Lagoon Estuary. Ocean. Dyn. 2004, 54, 348–359. [Google Scholar] [CrossRef]
- Moller, O.; Castaing, P.; Salomon, J.-C.; Lazure, P. The Influence of Local and Non-Local Forcing Effects on the Subtidal Circulation of Patos Lagoon. Estuaries 2001, 24, 297–311. [Google Scholar] [CrossRef]
- Bortolin, E.C.; Távora, J.; Fernandes, E. Long-Term Variability on Suspended Particulate Matter Loads from the Tributaries of the World’s Largest Choked Lagoon. Front. Mar. Sci. 2022, 9, 836739. [Google Scholar] [CrossRef]
- Andrade Neto, J.S.D.; Rigon, L.T.; Toldo, E.E., Jr.; Schettini, C.A.F. Descarga Sólida Em Suspensão Do Sistema Fluvial Do Guaíba, RS, e Sua Variabilidade Temporal. Pesq. Geoc 2012, 39, 161. [Google Scholar] [CrossRef]
- Möller, O.; Távora, J.; Möller, B.; Fernandes, E. Instituto de Oceanografia, Universidade Federal do Rio Grande (FURG), Rio Grande, Rio Grande do Sul, Brazil. 2024; in preparation. [Google Scholar]
- Távora, J.; Fernandes, E.; Möller, O.O. Patos Lagoon, Brazil, Suspended Particulate Matter (SPM) Data Compendium. Geosci. Data J. 2021, 9, 235–255. [Google Scholar] [CrossRef]
- Valente, A.; Sathyendranath, S.; Brotas, V.; Groom, S.; Grant, M.; Taberner, M.; Antoine, D.; Arnone, R.; Balch, W.M.; Barker, K.; et al. A Compilation of Global Bio-Optical in Situ Data for Ocean-Colour Satellite Applications. Earth Syst. Sci. Data 2016, 8, 235–252. [Google Scholar] [CrossRef]
- Park, Y.-J.; Ruddick, K. Model of Remote-Sensing Reflectance Including Bidirectional Effects for Case 1 and Case 2 Waters. Appl. Opt. 2005, 44, 1236. [Google Scholar] [CrossRef] [PubMed]
- Dierssen, H.M.; Vandermeulen, R.A.; Barnes, B.B.; Castagna, A.; Knaeps, E.; Vanhellemont, Q. QWIP: A Quantitative Metric for Quality Control of Aquatic Reflectance Spectral Shape Using the Apparent Visible Wavelength. Front. Remote Sens. 2022, 3, 869611. [Google Scholar] [CrossRef]
- Vandermeulen, R.A.; Mannino, A.; Craig, S.E.; Werdell, P.J. 150 Shades of Green: Using the Full Spectrum of Remote Sensing Reflectance to Elucidate Color Shifts in the Ocean. Remote Sens. Environ. 2020, 247, 111900. [Google Scholar] [CrossRef]
- IOCCG. Uncertainties in Ocean Colour Remote Sensing; IOCCG Report Series; International Ocean Colour Coordinating Group: Dartmouth, NS, Canada, 2019. [Google Scholar]
- Merchant, C.J.; Embury, O.; Bulgin, C.E.; Block, T.; Corlett, G.K.; Fiedler, E.; Good, S.A.; Mittaz, J.; Rayner, N.A.; Berry, D.; et al. Satellite-Based Time-Series of Sea-Surface Temperature since 1981 for Climate Applications. Sci. Data 2019, 6, 223. [Google Scholar] [CrossRef] [PubMed]
- Salama, M.S.; Van Der Velde, R.; Van Der Woerd, H.J.; Kromkamp, J.C.; Philippart, C.J.M.; Joseph, A.T.; O’Neill, P.E.; Lang, R.H.; Gish, T.; Werdell, P.J.; et al. Technical Note: Calibration and Validation of Geophysical Observation Models. Biogeosciences 2012, 9, 2195–2201. [Google Scholar] [CrossRef]
- Seegers, B.N.; Stumpf, R.P.; Schaeffer, B.A.; Loftin, K.A.; Werdell, P.J. Performance Metrics for the Assessment of Satellite Data Products: An Ocean Color Case Study. Opt. Express 2018, 26, 7404. [Google Scholar] [CrossRef] [PubMed]
- Broomell, S.B.; Budescu, D.V.; Por, H.-H. Pair-Wise Comparisons of Multiple Models. Judgm. Decis. Mak. 2011, 6, 821–831. [Google Scholar] [CrossRef]
- Tran, M.D.; Vantrepotte, V.; Loisel, H.; Oliveira, E.N.; Tran, K.T.; Jorge, D.; Mériaux, X.; Paranhos, R. Band Ratios Combination for Estimating Chlorophyll-a from Sentinel-2 and Sentinel-3 in Coastal Waters. Remote Sens. 2023, 15, 1653. [Google Scholar] [CrossRef]
- Ody, A.; Doxaran, D.; Verney, R.; Bourrin, F.; Morin, G.P.; Pairaud, I.; Gangloff, A. Ocean Color Remote Sensing of Suspended Sediments along a Continuum from Rivers to River Plumes: Concentration, Transport, Fluxes and Dynamics. Remote Sens. 2022, 14, 2026. [Google Scholar] [CrossRef]
- Costi, J.; Moraes, B.C.; Marques, W.C. A Regional Algorithm for Investigating the Patos Lagoon Coastal Plume Using Aqua/MODIS and Oceanographic Data. Mar. Syst. Ocean Technol. 2017, 12, 166–177. [Google Scholar] [CrossRef]
- Pagot, M.; Rodríguez, A.; Hillman, G.; Corral, M.; Oroná, C.; Niencheski, L.F. Remote Sensing Assessment of Suspended Matter and Dynamics in Patos Lagoon. J. Coast. Res. 2007, 10047, 116–129. [Google Scholar] [CrossRef]
- Barbosa, F.G.; Lanari, M. Bibliometric Analysis of Peer-Reviewed Literature on the Patos Lagoon, Southern Brazil. An. Acad. Bras. Ciênc. 2022, 94, e20210861. [Google Scholar] [CrossRef] [PubMed]
- Tanre, D.; Herman, M.; Deschamps, P.Y. Influence of the Background Contribution upon Space Measurements of Ground Reflectance. Appl. Opt. 1981, 20, 3676. [Google Scholar] [CrossRef] [PubMed]
- Bulgarelli, B.; Zibordi, G. On the Detectability of Adjacency Effects in Ocean Color Remote Sensing of Mid-Latitude Coastal Environments by SeaWiFS, MODIS-A, MERIS, OLCI, OLI and MSI. Remote Sens. Environ. 2018, 209, 423–438. [Google Scholar] [CrossRef] [PubMed]
- Paulino, R.S.; Martins, V.S.; Novo, E.M.L.M.; Barbosa, C.C.F.; De Carvalho, L.A.S.; Begliomini, F.N. Assessment of Adjacency Correction over Inland Waters Using Sentinel-2 MSI Images. Remote Sens. 2022, 14, 1829. [Google Scholar] [CrossRef]
- Pahlevan, N.; Sarkar, S.; Franz, B.A. Uncertainties in Coastal Ocean Color Products: Impacts of Spatial Sampling. Remote Sens. Environ. 2016, 181, 14–26. [Google Scholar] [CrossRef] [PubMed]
- Dorji, P.; Fearns, P. Impact of the Spatial Resolution of Satellite Remote Sensing Sensors in the Quantification of Total Suspended Sediment Concentration: A Case Study in Turbid Waters of Northern Western Australia. PLoS ONE 2017, 12, e0175042. [Google Scholar] [CrossRef] [PubMed]
- Haraguchi, L.; Carstensen, J.; Abreu, P.C.; Odebrecht, C. Long-Term Changes of the Phytoplankton Community and Biomass in the Subtropical Shallow Patos Lagoon Estuary, Brazil. Estuar. Coast. Shelf Sci. 2015, 162, 76–87. [Google Scholar] [CrossRef]
- Abreu, P.C.; Odebrecht, C.; González, A. Particulate and Dissolved Phytoplankton Production of the Patos Lagoon Estuary, Southern Brazil: Comparison of Methods and Influencing Factors. J. Plankton Res. 1994, 16, 737–753. [Google Scholar] [CrossRef]
- Reynolds, R.A.; Stramski, D.; Neukermans, G. Optical Backscattering by Particles in Arctic Seawater and Relationships to Particle Mass Concentration, Size Distribution, and Bulk Composition. Limnol. Oceanogr. 2016, 61, 1869–1890. [Google Scholar] [CrossRef]
- Willmott, C.; Robeson, S.; Matsuura, K. Climate and Other Models May Be More Accurate Than Reported. EOS 2017, 98, 13–14. [Google Scholar] [CrossRef]
- Cordeiro, C.A.M.M.; Aued, A.W.; Barros, F.; Bastos, A.C.; Bender, M.; Mendes, T.C.; Creed, J.C.; Cruz, I.C.S.; Dias, M.S.; Fernandes, L.D.A.; et al. Long-Term Monitoring Projects of Brazilian Marine and Coastal Ecosystems. PeerJ 2022, 10, e14313. [Google Scholar] [CrossRef] [PubMed]
- Etcheber, H.; Schmidt, S.; Sottolichio, A.; Maneux, E.; Chabaux, G.; Escalier, J.-M.; Wennekes, H.; Derriennic, H.; Schmeltz, M.; Quéméner, L.; et al. Monitoring Water Quality in Estuarine Environments: Lessons from the MAGEST Monitoring Program in the Gironde Fluvial-Estuarine System. Hydrol. Earth Syst. Sci. 2011, 15, 831–840. [Google Scholar] [CrossRef]
- Zibordi, G.; Mélin, F.; Berthon, J.-F.; Holben, B.; Slutsker, I.; Giles, D.; D’Alimonte, D.; Vandemark, D.; Feng, H.; Schuster, G.; et al. AERONET-OC: A Network for the Validation of Ocean Color Primary Products. J. Atmos. Ocean. Technol. 2009, 26, 1634–1651. [Google Scholar] [CrossRef]
- Lehmann, M.K.; Gurlin, D.; Pahlevan, N.; Alikas, K.; Conroy, T.; Anstee, J.; Balasubramanian, S.V.; Barbosa, C.C.F.; Binding, C.; Bracher, A.; et al. GLORIA—A Globally Representative Hyperspectral in Situ Dataset for Optical Sensing of Water Quality. Sci. Data 2023, 10, 100. [Google Scholar] [CrossRef] [PubMed]
- IOCCG. Ocean-Colour Data Merging; IOCCG Report Series; International Ocean Colour Coordinating Group: Dartmouth, NS, Canada, 2007. [Google Scholar]
- Sathyendranath, S.; Brewin, R.; Brockmann, C.; Brotas, V.; Calton, B.; Chuprin, A.; Cipollini, P.; Couto, A.; Dingle, J.; Doerffer, R.; et al. An Ocean-Colour Time Series for Use in Climate Studies: The Experience of the Ocean-Colour Climate Change Initiative (OC-CCI). Sensors 2019, 19, 4285. [Google Scholar] [CrossRef] [PubMed]
- Brocca, L.; Hasenauer, S.; Lacava, T.; Melone, F.; Moramarco, T.; Wagner, W.; Dorigo, W.; Matgen, P.; Martínez-Fernández, J.; Llorens, P.; et al. Soil Moisture Estimation through ASCAT and AMSR-E Sensors: An Intercomparison and Validation Study across Europe. Remote Sens. Environ. 2011, 115, 3390–3408. [Google Scholar] [CrossRef]
- Cloern, J.E.; Abreu, P.C.; Carstensen, J.; Chauvaud, L.; Elmgren, R.; Grall, J.; Greening, H.; Johansson, J.O.R.; Kahru, M.; Sherwood, E.T.; et al. Human Activities and Climate Variability Drive Fast-paced Change across the World’s Estuarine–Coastal Ecosystems. Glob. Chang. Biol. 2016, 22, 513–529. [Google Scholar] [CrossRef] [PubMed]

| Satellite | Algorithm | Wavelength (nm) | A | C |
|---|---|---|---|---|
| L8 | N09 | 655 | 242.27 | 0.1682 |
| 865 | 2108.56 | 0.2115 | ||
| N10 | 655 | 304.30 | 0.1682 | |
| 865 | 2974.41 | 0.2115 | ||
| S2A | N09 | 665 | 268.52 | 0.1725 |
| 865 | 2107.81 | 0.2115 | ||
| N10 | 665 | 347.18 | 0.1725 | |
| 865 | 2974.24 | 0.2115 | ||
| S2B | N09 | 665 | 270.20 | 0.1726 |
| 864 | 2098.48 | 0.2115 | ||
| N10 | 665 | 349.33 | 0.1726 | |
| 864 | 2961.96 | 0.2115 | ||
| S3A | N09 | 665 | 281.95 | 0.1729 |
| 865 | 2116.68 | 0.2115 | ||
| N10 | 665 | 358.57 | 0.1729 | |
| 865 | 2986.40 | 0.2115 | ||
| S3B | N09 | 665 | 281.49 | 0.1729 |
| 865 | 2114.65 | 0.2115 | ||
| N10 | 665 | 357.753 | 0.1729 | |
| 865 | 2983.70 | 0.2115 |
| Sat | Product | AC | Alg | Band | Strengths | Pitfalls |
|---|---|---|---|---|---|---|
| L8 | Turbidity | POLYMER | N09 | 655 | MAPE, WR | RMSE, Bias |
| SPM | POLYMER | N10 | 865 | All | - | |
| S2 | Turbidity | POLYMER | N09 | 865 | Kendall, MAPE | RMSE, Bias |
| SPM | ACOLITE | N17 | All | - | ||
| S3 | Turbidity | POLYMER | N09 | 865 | Kendall, MAPE, WR | RMSE, Bias |
| SPM | POLYMER | N10 | 865 | RMSE, MAE, WR | Kendall |
| Sat | Product | AC | Alg | Band | A | C | Strengths | Pitfalls |
|---|---|---|---|---|---|---|---|---|
| L8 | Turbidity | POLYMER | N09 | 865 | 6435.35 | 0.2115 | All | - |
| SPM | ACOLITE | N10 | 655 | 136.11 | 0.1729 | RMSE, MAE, MAPE, WR | Kendall | |
| POLYMER | N10 | 865 | 2272.39 | 0.2115 | All | - | ||
| S2 | Turbidity | POLYMER | N09 | 865 | 2107.81 (S2A) | 0.2115 | RMSE, Bias | Kendall, MAPE |
| 2098.48 (S2B) | ||||||||
| SPM | ACOLITE | N10 | 665 | 292.43 | 0.1729 | All | - | |
| S3 | Turbidity | POLYMER | N09 | 865 | 2116.68 (S3A) | 0.2115 | Bias, RMSE | Kendall, MAPE, WR |
| 2114.65 (S3B) | ||||||||
| SPM | ACOLITE | N10 | 865 | 1033.23 | 0.2115 | All | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simão, R.; Távora, J.; Salama, M.S.; Fernandes, E. Optimizing Optical Coastal Remote-Sensing Products: Recommendations for Regional Algorithm Calibration. Remote Sens. 2024, 16, 1497. https://doi.org/10.3390/rs16091497
Simão R, Távora J, Salama MS, Fernandes E. Optimizing Optical Coastal Remote-Sensing Products: Recommendations for Regional Algorithm Calibration. Remote Sensing. 2024; 16(9):1497. https://doi.org/10.3390/rs16091497
Chicago/Turabian StyleSimão, Rafael, Juliana Távora, Mhd. Suhyb Salama, and Elisa Fernandes. 2024. "Optimizing Optical Coastal Remote-Sensing Products: Recommendations for Regional Algorithm Calibration" Remote Sensing 16, no. 9: 1497. https://doi.org/10.3390/rs16091497
APA StyleSimão, R., Távora, J., Salama, M. S., & Fernandes, E. (2024). Optimizing Optical Coastal Remote-Sensing Products: Recommendations for Regional Algorithm Calibration. Remote Sensing, 16(9), 1497. https://doi.org/10.3390/rs16091497









