Abstract
The internal waves in the South China Sea are highly correlated with the tidal currents in the Luzon Strait, which makes it possible to establish an internal wave prediction model based on internal wave kinematics. However, the kinematic model requires the input of the exact location and time of the initial internal wave for which the generation mechanism of internal waves in the northern South China Sea must be well understood. By analyzing the internal wave field in the northern South China Sea (SCS) simulated using the MIT General Circulation Model (MITgcm) and observations from satellite synthetic aperture radar (SAR) and mooring temperature–salinity–depth (TSD) chains, the source regions and propagation initiation times of internal waves are identified for three typical tidal phases, i.e., the diurnal-tide-dominated phase (DTP), transition tide phase (TTP), and semidiurnal-tide-dominated phase (STP). The generation procedures of Type A and Type B internal waves are discussed in detail with those data. The present study reveals that Type A and Type B waves are generated at the eastern and western ridges, respectively, and both commence their westward propagation at the peak of the eastward tidal flow. The dynamics of lee waves and the resonance effect with double ridges constitute the generation mechanisms of internal waves in the northern SCS. Combined with varying configurations of tidal conditions, topography, and stratification, the generation procedures of Type A and Type B waves in the DTP, TTP, and STP are elucidated with the generation mechanism in a unified and self-consistent way. In short, during DTP, weaker A waves alternate with weaker B waves each day; during TTP, strong A waves and strong B waves appear alternately every day; and there are two weak A waves per day during the STP. The generation mechanism can help in developing future empirical models for generating internal waves using tidal currents, topography, and stratification without requiring complex fluid dynamics calculations.
1. Introduction
Internal waves occur within the density-stratified interiors of oceans, where the maximum amplitude is found within the ocean itself, and the wave frequency is between the inertial and buoyancy frequencies. Among them, high-frequency internal waves often exist in the form of rank-ordered solitary wave packages or solitary waves and are widely distributed across the continental shelves and marginal seas of the world’s oceans, such as in the South China Sea (SCS) [1,2], Gulf of Mexico [3,4], Gibraltar Strait [5], Strait of Messina [6,7], Sulu Sea [8,9], Andaman Sea [10,11], Arctic Ocean [12], Black Sea [13,14], Lombok Strait [15,16], Georges Bank [17,18], and the Gulf of Maine [19]. They are often generated by the interaction between currents with varying bottom topographies. Nearshore surface waves can also exist in solitary wave forms [20,21,22]. Since the restoring force of internal waves is reduced gravity, which is only one thousandth of the order of gravity of the restoring force of surface waves, internal waves have amplitudes of tens to hundreds of meters, which are much larger than those of surface solitary waves less than ten meters, and a period of ten minutes, which is much longer than the seconds of surface solitary waves. The largest internal wave amplitude that has been observed so far was found in the SCS: 240 m [23]. Therefore, internal solitary waves have the characteristics of meso- to fine-scale structures, large amplitude, and strong local flow velocity. They can cause significant changes in local flow velocity and density in a relatively short time (on the order of tens of minutes), which makes internal solitary waves a major environmental factor threatening the safety of offshore oil drilling platforms [24,25] and underwater vehicles [26,27].
The northern part of the SCS is a well-known active area for internal waves, with the main interval from 20°N to 22°N [1,28,29,30,31,32]. A large number of remote sensing and onsite observations show that the spatiotemporal distribution of internal waves in the SCS is strongly correlated with the tidal phase of the Luzon Strait [33,34,35,36]. This regularity makes it possible to establish an accurate internal wave prediction model and undoubtedly has practical significance for facilities such as offshore oil platforms to deal with threats from internal waves. However, it is hard to directly use a three-dimensional dynamic model to predict internal waves because the width scale of internal solitary waves is on the order of kilometers or hundreds of meters, requiring the horizontal grid to be on the order of hundreds or ten meters, but the propagation range of internal waves reaches the entire northern SCS, which requires a very large horizontal extent of computation domain, for instance, 1210 km × 2035 km, as used in the literature [37]. Such a three-dimensional model is feasible for studying various dynamic mechanisms of internal waves but unfeasible for forecasting due to the requirements of high calculation resources and a short forecasting time. Another idea is to study internal waves as a moving object and calculate the internal wave propagation process based on kinematic principles [31,38]. To obtain high-precision forecast results, it is necessary to align the starting time of the simulated internal wave crest with the real starting time at the generating source. The work of this paper is a preliminary study to achieve this purpose, that is, to determine the location of the source of internal waves in the northern South China Sea and the relationship between the departure time of the internal waves and the local tide phase.
By analyzing the internal wave observation data of the thermistor chain, Ramp et al. [39] discovered, for the first time, that there are two obvious types of internal waves in the northern SCS, which they called Type A and Type B waves. The Type A wave appears in the form of a wave packet composed of multiple waves and arrives at the observation point every 24 h, and the Type B wave appears in the form of a single wave and arrives at the observation point every 25 h. The terms “Type A wave” and “Type B wave” have been widely accepted, being featured in a large number of studies on the generation mechanism of internal waves in the SCS. Many observations have shown that the wave in the deep basin appears as a well-formed single solitary wave, which begins to fission into a solitary wave package at the shoaling continental slope [30,40]. Fission forms depend on the amplitude of the solitary wave [41]. Ramp’s data were obtained along the 350 m isobath situated in the middle of the shoaling continual slope [39]; as a result, both Type A waves that have already undergone fission into solitary wave packets and Type B waves that have not yet undergone fission can exist in the same dataset.
It is now a consensus that internal waves in the northern South China Sea originate from the Luzon Strait and are the result of the interaction between tidal currents and varying topography in stratified water. Numerous studies have indicated that the unique dual-ridge structure of the Luzon Strait plays a key role in the generation of internal waves in the SCS [42,43,44,45,46,47,48]. Discussions regarding the generation of Type A and Type B waves primarily focus on the configuration of tidal components and sea bottom topographical features. However, the specific explanations for the generation mechanisms of these two waves are diverse. The following paragraph lists the views of researchers.
Zhao and Alford [49] posited that Type A waves are generated at the peak of eastward tidal currents while Type B waves originate during the second-strongest phase of eastward currents induced by semidiurnal tidal components. Farmer et al. [44] suggested that nonlinear internal waves exhibit three distinct characteristics: Type A, Type B, and “corner waves”, each determined by the Ostrovsky number of the initial internal tide generated in the Luzon Strait. Zhang et al. [50] proposed that Type A waves form during the strongest phase of eastward tidal currents, whereas Type B waves arise at the peak of westward currents. Vlasenko et al. [51] argued that Type A and Type B waves are produced when semidiurnal tides dominate, and the emergence of Type A or B waves is not directly related to strong or weak currents in the Luzon Strait. Moreover, they noted that Type A waves transform into Type B waves when semidiurnal tides weaken, and vice versa when they strengthen. Chen et al. [52] observed that Type A and Type B waves are generated at the eastern and western ridges, respectively, during peak eastward tides, but they did not indicate how varying tides influence the formation of these waves. They also suggested that Type B waves are solely produced by the western ridge, overlooking the potential significance of the dual-ridge structure in their generation. Li et al. [53] found that diurnal internal tides dominate in the Luzon Strait, while semidiurnal internal tides prevail in the deep basin of the SCS. Zeng et al. [54] posited that Type A and Type B waves originate from disturbances at the eastern ridge, with the western ridge diminishing the amplitude of Type A waves but scarcely affecting their propagation speed, while enhancing the amplitude and reducing the speed of Type B waves. Lai et al. [37] proposed that Type A waves are generated at the western ridge and Type B waves are generated at the eastern ridge, being strongly modified by the resonant process between the two ridges.
It can be seen that there is currently no unified view on the generation mechanism of Type A and Type B waves in the SCS. Most studies focus on specific tidal states, but there are many states of tides. Previous research work was mostly based on onsite observation data, and the data were fixed-point time series temperature profiles. This kind of data is suitable for reflecting the time interval between the occurrence of Type A and Type B waves, that is, the characteristics of internal waves in the time domain, but it cannot express the distribution characteristics of internal waves in space. The information is incomplete for the study of traveling waves.
This paper collects several scenes of wide-swath SAR images of internal waves in the SCS. The distribution of internal waves corresponding to multiple tidal cycles on the propagation path can be seen at the same time. In this way, the internal wave time difference of field observations, the internal wave spatial spacing on SAR images, and the internal wave propagation velocity of numerical simulations can be correlated with each other to jointly describe the generation and propagation phenomena of internal waves. Based on three types of data, we analyzed the generation mechanism of internal waves in the SCS and found a relatively simple and logically closed generation mechanism that can explain the phenomena observed in different tide configuration in a unified way. This is helpful for the establishment of an empirical model for determining the initial streaks of internal waves.
The subsequent parts of the paper are organized as follows: Section 2 defines three principal phases of tidal currents and introduces the data source and configuration of the numerical model. In Section 3, the model is first validated and then the generation time and location of Type A and Type B waves based on the results of the model are outlined. Section 4 discusses the differences and reasons for the formation of Type A and Type B waves and discusses how the double ridge structure of the Luzon Strait affects the generation of internal waves. Section 5 gives conclusions.
2. Data and Methods
2.1. Workflow Description
Figure 1 outlines the overall workflow of this study. Given the predominance of semidiurnal and diurnal tidal components in the Luzon Strait, the tidal currents are categorized into three distinct periods: the diurnal-tide-dominated phase (DTP), the semidiurnal-tide-dominated phase (STP), and the transition tide phase (TTP). For each of these periods, satellite and in situ data are collected, and internal waves are generated using numerical models driven by the tidal current characteristic of these respective periods. This study investigates the generation mechanisms and propagation characteristics of Type A and Type B waves under different tidal regimes, achieved by conducting a comprehensive analysis of satellite data, field data, and simulated internal wave data.
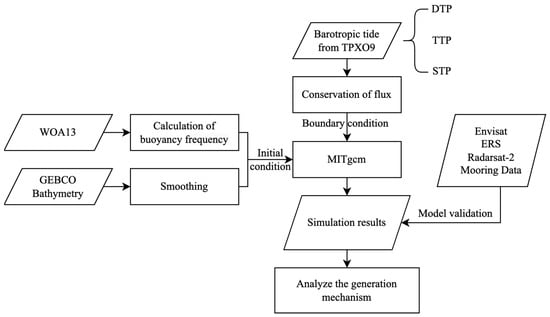
Figure 1.
Workflow of methods. After categorizing the tidal currents into three distinct periods (DTP, TTP, and STP), satellite and in situ data are collected, and internal waves are generated using numerical models driven by the tidal current characteristic of these respective periods. By conducting a comprehensive analysis of satellite data, field data, and simulated internal wave data, the study investigates the generation mechanisms and propagation characteristics of Type A and Type B waves under different tidal regimes.
2.2. Types of Tides
Tides are typically formed by the superposition of constituent tides of different periods. Through harmonic decomposition, these constituents can be extracted and classified according to their periods, such as diurnal and semidiurnal components. In the Luzon Strait’s barotropic tides, the diurnal component is often more pronounced; however, during certain intervals, the semidiurnal component can exceed the diurnal one [55]. The tidal current time series in Figure 2 demonstrates the mixed nature of tidal forcing. During the later part of the spring tide, each day features a single peak in tidal currents during both flood and ebb, a period termed the “diurnal tide”. In contrast, during neap tides, the tidal current more closely resembles a semidiurnal tide [44]. For clarity and differentiation, this paper qualitatively divides the tidal current time series into three distinct phases: (1) the diurnal-tide-dominated phase (DTP), where the diurnal component is significantly stronger, with the semidiurnal component nearly absent; (2) the semidiurnal-tide-dominated phase (STP), where the semidiurnal component is more pronounced while the diurnal component is almost negligible; and (3) the transition tide phase (TTP), where both diurnal and semidiurnal components are strong, often representing a transitional stage between the DTP and STP.
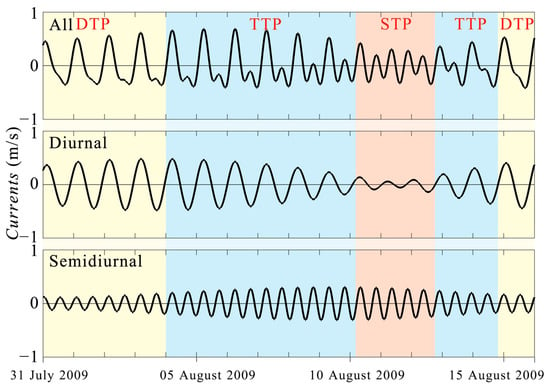
Figure 2.
Three principal phases of tidal currents. Zonal barotropic tidal current speeds (top), diurnal tidal component (middle), and semidiurnal tidal component (bottom) at the predicted location (20.59°N, 121.90°E) using the TPXO model. The shaded areas in the figure represent the DTP (yellow), the TTP (blue), and the STP (red).
2.3. Study Area and Data
In the northern South China Sea (SCS), internal solitary waves are predominantly found in the region stretching from the Luzon Strait to the vicinity of the Dongsha Islands, as shown in Figure 3. It presents a distribution map of internal wave striations in the SCS, extracted from a comprehensive collection of SAR images from satellites such as Envisat ASAR, ERS SAR, Sentinel-A/B SAR, GF3 SAR, and Radarsat-2 SAR. The internal wave crests are represented by red curves. The black solid lines indicate the areas modeled in numerical simulations, which align with the direction of internal wave propagation in the northern SCS. Within the selected modeling area, the C8 (118°E, 21°N) location is derived from the ADCP observations of the SCS Internal Wave Experiment (SIWE) in the northern SCS [56] while the L1 (121.9°E, 20.589°N) location originates from the Asian Seas International Acoustics Experiment (ASIAEX) [57].
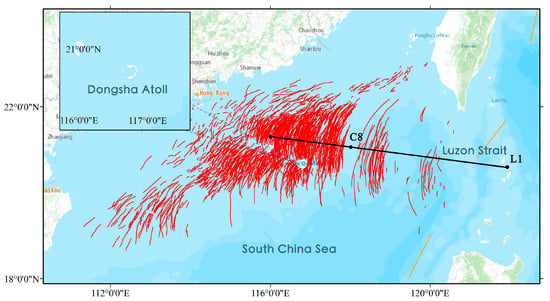
Figure 3.
Distribution map of internal waves in the SCS. The bathymetry for the 2D numerical model uses the cross-section connecting points C8 (21°N, 118°E) and L1 (20.589°N, 121.9°E). The red line represents the internal wave crests in the South China Sea extracted from SAR data collected by various sensors.
Eleven SAR images from the ERS-2, Envisat, and Radarsat-2 satellites were utilized as observational data for internal waves to validate the accuracy of the MITgcm [58]. Of these, eight SAR images from Envisat and Radarsat-2 featured wide swath coverage, allowing for the observation of internal waves corresponding to multiple tidal cycles within a single image. Prior to model validation, these remote sensing images underwent radiometric calibration and range-Doppler terrain correction, followed by the extraction of information pertaining to internal waves [6,30,59,60,61]. Table 1 presents the relevant details of these 11 SAR datasets.

Table 1.
Remote sensing data parameters used in this article.
A transect connecting points C8 (118°E, 21°N) and L1 (121.9°E, 20.589°N) is used for the bathymetry in the 2D numerical model. Previous research [51,62] has demonstrated that using the average bathymetry between 20°N and 21°N for a 2D numerical model is reasonable, and the bathymetry of the transect used in this study in the Luzon Strait area approximates this average depth. The dataset used for constructing the bathymetry is GEBCO_2022, a global topographical model of oceans and land that provides elevation data in meters on a 15 arcsecond interval grid. To adapt to the 2D model and eliminate random errors, data points are uniformly sampled every 460 m along the C8-L1 transect on the GEBCO dataset and smoothed between adjacent points to determine the depth. The highest points of the eastern and western ridges are found to be 608 m and 1759 m, respectively, with a maximum depth of 3629 m. The bathymetry profile is illustrated in Figure 4.
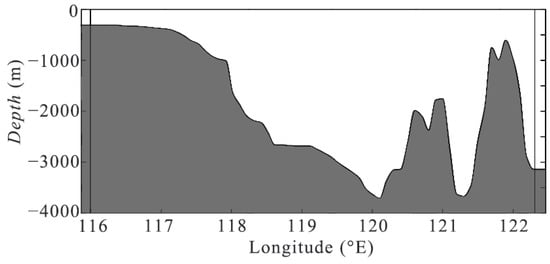
Figure 4.
Bathymetry used in the model.
The model’s initial stratification data are derived from the monthly mean climatology data of World Ocean Atlas 13 (WOA13), which includes temperature and salinity. The buoyancy frequency is calculated along the C8-L1 transect using the following standard formula [63]:
With the stratification conditions deduced from WOA13, a systematic error of approximately two hours is observed in the simulation results of MITgcm due to the relatively shallow main thermocline. To enhance the model’s accuracy, the depth of the top thermocline is artificially shifted downward by 30–50 m for the numerical simulations. The resulting distribution of buoyancy frequency for the model’s stratification conditions is depicted in Figure 5.
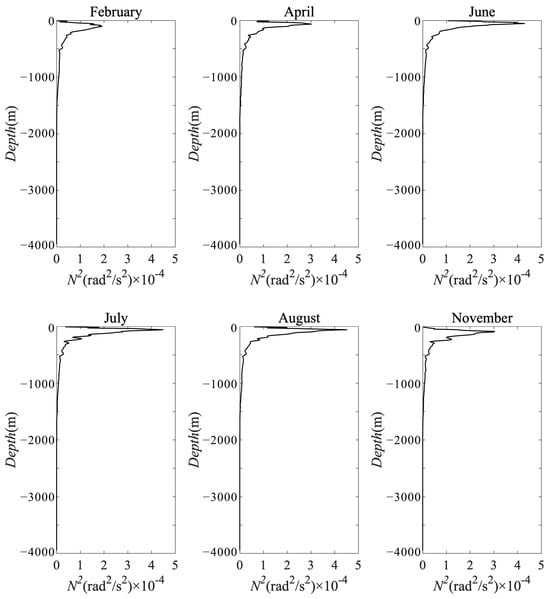
Figure 5.
Stratification conditions used in the model.
The east–west barotropic tidal forcing in the model includes the amplitudes and phases of eight tidal frequencies (M2, S2, N2, K2, K1, O1, P1, and Q1). The amplitudes and phases of these constituents are derived from the Ocean Topography Experiment (TOPEX)/Poseidon 9 (TPXO9) tidal inversion model [64]. Using the TPXO model to obtain barotropic tidal data near the eastern ridge of the Luzon Strait, the barotropic tidal current speed at the model’s eastern boundary is calculated based on the principle of flux conservation. This speed is then used as the boundary condition for the eastern boundary of the model.
2.4. Numerical Simulation
This study applies the Massachusetts Institute of Technology general circulation model (MITgcm) to simulate the generation of internal waves in the SCS and analyze the formation mechanisms of Type A and Type B waves [58]. The choice of MITgcm is informed by its nonhydrostatic formulation, enabling it to simulate fluid phenomena across various scales. Additionally, the adjoint capability of MITgcm allows its application in parameter and state estimation problems, making it suitable for simulating flows in both the atmosphere and oceans. In previous studies, MITgcm has been successfully used to implement internal solitary wave simulation and nonhydrostatic analysis in different regions [35,43]. The model is initialized with bathymetric of C8-L1 transects and stratification conditions of given month, and is driven by the barotropic tidal flow in the eastern boundary. The left boundary is set as natural outflow. To absorb reflected barotropic and baroclinic waves, two sponge areas are added at both western and eastern boundaries, respectively.
The model employs a Cartesian coordinate system (Oxz), with the Oxz plane representing a two-dimensional cross-section of the terrain. The Oz axis is oriented vertically upwards, and the Ox axis extends eastward.
In the horizontal direction, the model comprises 2772 grid points. Within the main computational area, the resolution along the x-axis is set at 250 m [65], a scale that effectively captures all relevant nonhydrostatic effects associated with internal solitary waves [51]. Within the sponge regions, the resolution along the x-axis is increased to 956 m using a hyperbolic tangent function. Vertically, the upper 500 m, which includes the main thermocline, is divided into 50 layers, each with a vertical resolution of 10 m. This is followed by 20 intermediate layers with a resolution of 50 m and, finally, 25 bottom layers with a resolution of 100 m. The model is configured with a Coriolis force parameter of 5.2 × 10−5, a horizontal eddy viscosity of 1 × 10−5, and a vertical eddy viscosity of 1 × 10−3 [51,66]. It operates under nonhydrostatic and implicit free surface conditions. Due to the minor contribution of bottom friction to the total dissipation, the model neglects bottom frictional forces [43].
After obtaining the simulation results from the MITgcm, the accuracy of the model is verified from three perspectives: barotropic tidal components compared with the TPXO9 dataset; internal wave amplitude and arrival times compared with mooring data; and the arrival times and spatial distribution of internal waves compared with remote sensing imagery. Subsequently, Hovmöller diagrams are utilized to preliminarily determine the generation times and locations of these two types of internal waves.
3. Results
In this chapter, we first discuss the validation of the numerical model and then utilize the Hovmöller diagram generated from internal wave simulation results over one month to show the generation times and locations of Type A and Type B waves during different tidal regimes. Subsequently, we present detailed experimental results for each of the three distinct tidal types and examine the specific processes involved in the generation of Type A and Type B waves under these varying conditions.
3.1. Model Validation
In MITgcm, the flow velocity input at the eastern boundary is calculated based on the barotropic tidal current at the eastern ridge of the Luzon Strait, as given by the TPXO model, adhering to the principle of flux conservation. This approach ensures that the flow field obtained at the eastern ridge is consistent with the TPXO tidal model. In Figure 6, the red line represents the input flow field at the eastern boundary, the blue line shows the flow field obtained by the model at the eastern ridge, and the green line indicates the flow velocity at the eastern ridge as forecasted by the TPXO. The results demonstrate that the flow field simulated by the model at the eastern ridge aligns with the barotropic tide as predicted by TPXO.
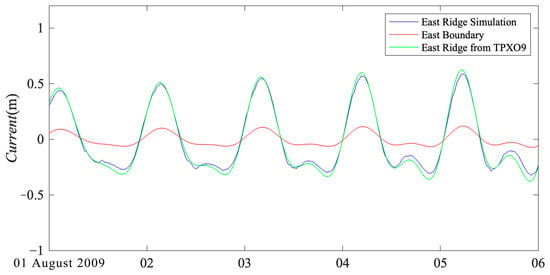
Figure 6.
Barotropic current velocity on the east ridge of the model (blue), barotropic current velocity on the east ridge of the TPXO data set (green), and model east boundary velocity (red).
The temperature–salinity–depth (TSD) chain data used for model validation are sourced from the SCS Internal Wave Experiment (SIWE) in the northern SCS, as referenced in Huang et al.’s work [23,56]. Thermometers, salinometers, and pressure sensors are mounted on the TSD chain between the water levels of −400 m and −50 m approximately. Their sample intervals are 1, 3, and 3 min, respectively. During data processing, the influence of the level fluctuation of the TSD chain itself is removed according to the records of the pressure sensors, so that temperatures can be regards as tracers of water layers corresponding to different calm levels.
Figure 7a shows the temperature profile time series observed with the TSD chain at 21°N, 118°E in early June 2011, in which the temperature contour in bold black represents the water level changes of water layer corresponding to the calm water level of −150 m over time. The typical characteristics of Type A and Type B waves can be recognized from the temperature time series. Figure 7b shows the temperature time series simulated with MITgcm, which are consistent with the TSD chain observations (Figure 7a) and simulation results of Huang [56].
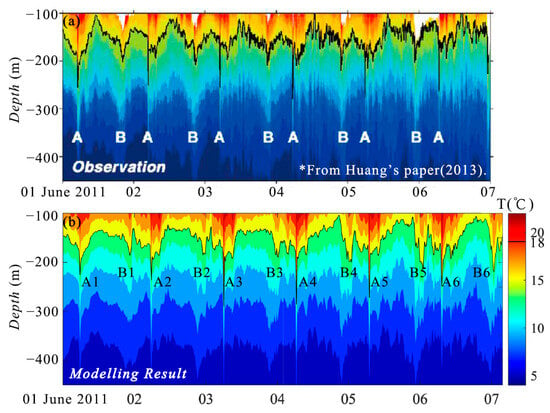
Figure 7.
Comparison between model and mooring data. (a) TSD chain data, where A and B represent the observed Type A and Type B waves, respectively. Adapted with permission from [56], Huang, 2013.; (b) modeling result. Solid black lines indicate the level changes of water layer at the initial depth of 150 m.
The water level fluctuation of water layer corresponding to the calm level of −150 m extracted from observed and simulated time series of temperature profiles, respectively, are overlaid in Figure 8 for comparison. The scatter diagram shown in Figure 9 constitutes the data uniformly sampled from the two curves in Figure 8. Their RMSE and the correlation coefficient are 12.1 m and 0.92, respectively.
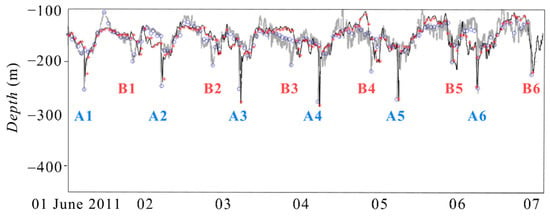
Figure 8.
Comparison of the simulated and field measured water level fluctuations of the water layer at the level of −150 m. The black and gray curves are extracted from the simulated (Figure 7b) and the field measured (Figure 7a) temperature profile time series, respectively. The red asterisks and blue circles mark uniform sampled points of them.
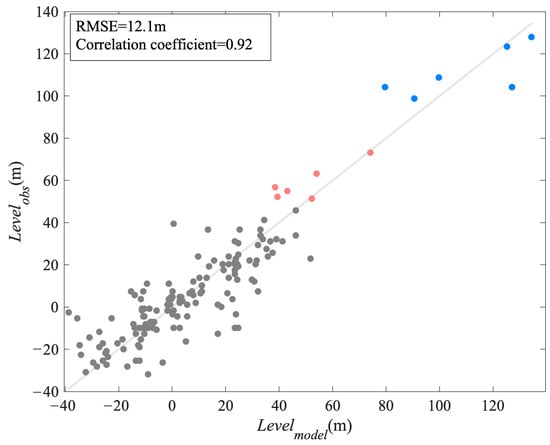
The Type A and Type B waves are identified from both simulated and observed water level fluctuations in Figure 8. Their level displacement and the arrival time difference between simulated and observed waves are listed in Table 2.

Table 2.
The characteristics of internal waves identified from the water layer of −150 m in Figure 7.
Note that TSD chain data only reflect the temporal distribution of Type A and Type B waves at specific locations. In contrast, satellite SAR observations only reveal the spatial distribution of internal waves [33,34,35,36]. For the simulation of traveling internal waves to be considered accurate, it is essential to satisfy both the validation of time series observations (by TSD chains) in a specific location and the validation of large-scale snapshot of internal waves (by space-born SAR) in a specific time.
Table 3 provides the TSD chain data and satellite SAR data used for validation. The first column marks the identifiers for the Type A and Type B internal waves that can be recognized in the data.

Table 3.
Experimental internal wave number details.
Figure 10 shows the internal waves observed in satellite SAR images and the simulated time series of temperature in the cross points of the corresponding internal waves in SAR images and the C8-L1 transect. The internal waves can be found from the time series of temperature, whose time is consistent with the acquisition time of corresponding SAR images with little error.
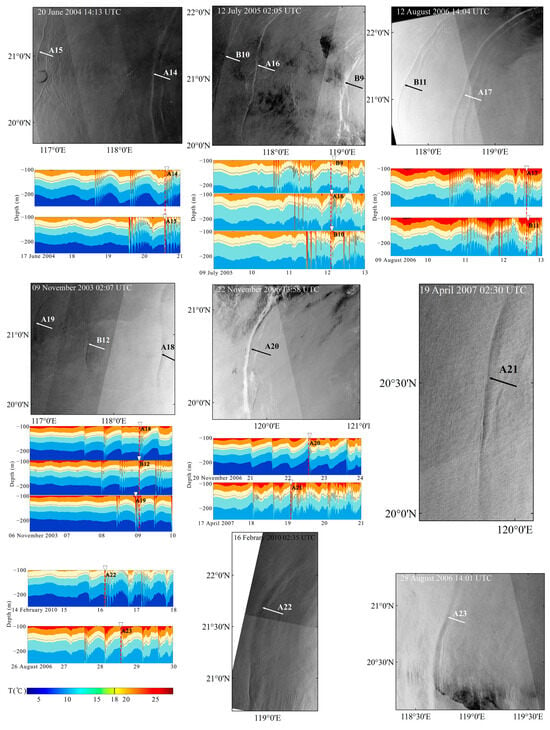
Figure 10.
Comparison of SAR data and model results. All simulated temperature profiles use the same temperature color scale.
For the internal waves observed in SAR images, which are listed in Table 3, we trace back to the Luzon Strait to find the corresponding maximum eastward tidal flow moments. Then, we calculate the arrival times of the corresponding simulated internal waves at the observational sites. This allows us to investigate the errors of the arrival times of the simulated internal waves.
Figure 11 shows the distribution of these errors, with the horizontal axis representing the internal wave ID number. The data in Figure 11 indicate that among the 35 simulated internal waves, 31 (approximately 89% of the total) have a time error within 2 h. Notably, the errors for Type A waves are generally smaller than for Type B waves. The larger errors observed in Type B waves predominantly occur in shallow water areas; this may be attributed to the coarse grid of the model which is unsuitable to simulate the smaller internal solitary wave packages in shallow water.
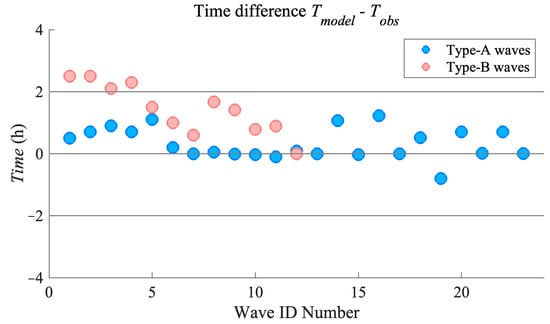
Figure 11.
Error of arrival time of simulated internal waves.
Despite the two-dimensional model used in this study omitting variations in the terrain’s north–south direction and disregarding differences in stratification conditions at various geographic locations, the validation results obtained from the three aforementioned perspectives demonstrate that the simulation still accurately captures the characteristics of generation and propagation of internal waves originating from the Luzon Strait. Consequently, this model serves as an effective tool for investigating the generation mechanisms of Type A and Type B waves.
3.2. Generation Time and Location
When concave large-amplitude internal waves pass through, they cause an increase in temperature in a fixed water level. Consequently, Hovmöller diagrams can be used to intuitively observe the propagation and evolution of internal waves as well as their generation times [56]. The relatively short periods of internal waves are represented as slender, elongated strips in Hovmöller diagrams. Figure 12 presents a Hovmöller diagram drawn from the temperature simulation results at a depth of 105 m in the experiment. To display a longer time series and considering the stability of the stratification in the model, this diagram is constructed by dividing the time interval into several portions, conducting separate experiments for each, and then stitching together the segments after they have stabilized (approximately 2 days each). The right part of Figure 10 shows the tidal conditions at the eastern ridge of the Luzon Strait. By tracing the internal wave signals back to their sources, the temporal relationship between their generation and the tides can be analyzed. The use of tidal data from the eastern ridge to validate the generation times at the western ridge is justified because the maximum time lag in the velocity time series data calculated from the TPXO9 amplitudes and phases extracted from both sides of the double ridges is only about 30 min [43], which is negligible for both semidiurnal and diurnal tidal cycles. The lower part of Figure 12 depicts the bathymetry used in the modeling.
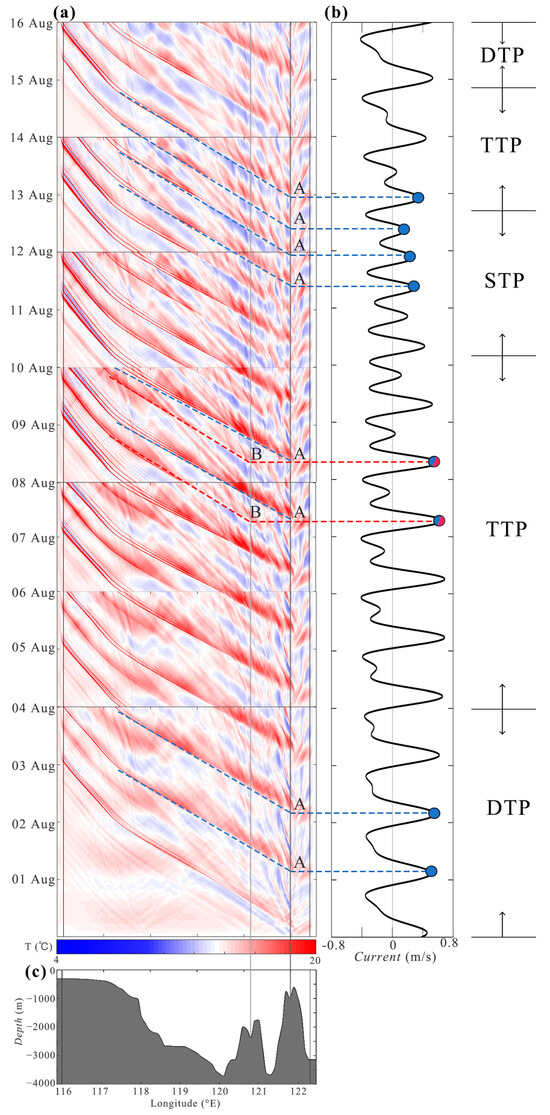
Figure 12.
(a) Hovmöller diagrams show when, where, and how internal waves are generated and propagated. The depth of the drawing is 105 m. The time series is from bottom to top. The color represents the temperature. The relatively short periods of internal waves are represented as slender, elongated strips. By estimating the slope of the line, the speed of internal wave propagation can be obtained. Type A and Type B waves are generated from the east and west ridges of the Luzon Strait, respectively, and then propagate westward. (b) The time series of tidal current. (c) The bathymetry.
The Hovmöller diagram reveals the time and location of internal wave generation. In general, Type A waves are generated at the eastern ridge, while Type B waves originate from the western ridge. Both types begin propagating westward at the peak of the eastward tidal current. Type A waves typically evolve into solitary waves upon reaching the western ridge, whereas Type B waves, being relatively weaker, develop into solitary waves further west. The details of their development vary across different tidal stages. Specifically, during the DTP, there is only one peak in the eastward tidal current each day. At this peak, both Type A and Type B waves are generated, but Type B waves are weaker and only develop into weaker solitary waves west of approximately 119° longitude. In the TTP, Type A and Type B waves appear alternately, and the intensity of Type B waves during this phase is stronger compared to the DTP. During STP, the pattern is characterized by two occurrences of Type A waves each day, corresponding to the twice-daily peaks of the semidiurnal eastward tidal current.
We identified 56 Type A waves and 31 Type B waves using the Hovmöller diagrams derived from several months of simulation results. We calculated the differences between their generation times and the peak times of the eastward tidal currents, as shown in Figure 13. In the figure, a strong correlation is clearly visible between the generation times of these internal waves and the peak of the eastward tidal flow. Through our calculations, we found that the time deviation for Type A waves at the eastern ridge is 5.8 ± 13 min, while for Type B waves, it is 7.2 ± 14 min. These deviations are negligible relative to the semidiurnal tidal cycle. Therefore, these data indicate that Type A and Type B waves are generated, respectively, at the eastern and western ridges, and their initiation of westward propagation coincides with the maximum of the eastward tidal flow.
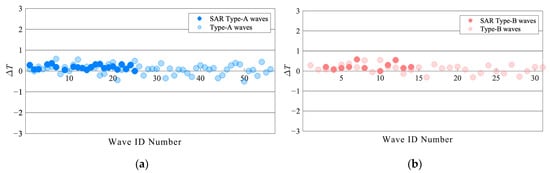
Figure 13.
Distribution of differences between Type A wave (a) and Type B wave; (b) generation time and eastward maximum tidal current time.
3.3. Diurnal-Tide-Dominated Phase (DTP)
Figure 14 shows an Envisat ASAR WSS image acquired on 4 August 2009, during a typical DTP. This SAR image reveals the presence of two Type A waves at 118.34°E 20.96°N (A7) and 116.70°E 21.13°N (A8), as well as a Type B internal wave at 117.50°E 21.05°N (B7). Additionally, in the deeper waters at 119.23°E, there is a faintly detectable Type B wave (indicated by the white dashed box). The Type B wave corresponding to the white dashed box has not yet fully developed into an internal solitary wave. This concave wave has a long wavelength and a weak surface flow gradient, resulting in a faint SAR image signal [59]. Conversely, the Type B wave at location B7, with one day more evolution than the faint one, has fully developed into an internal solitary wave. Its wavelength has shortened, its amplitude has increased, and the surface flow gradient has become more pronounced, leading to a stronger SAR image signal. The right side of Figure 14 displays the results of the model simulation, providing a comparative perspective between observed and modeled wave patterns.
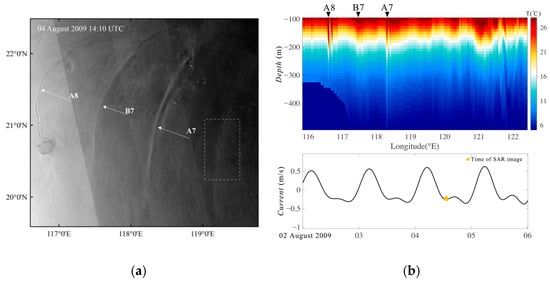
Figure 14.
(a) Envisat image; (b) MITgcm simulation results during the DTP.
3.4. Transition Tide Phase (TTP)
During the TTP, the diurnal and semidiurnal tidal components are of comparable strength. When the peaks of adjacent semidiurnal tides overlap with the peak and trough of the diurnal tide, it results in alternating strong and weak peaks with the semidiurnal cycle. At the times of these strong peaks, when the eastward tidal flow is at its maximum, Type A and Type B waves are generated at the eastern and western ridges, respectively. Although lee waves are also produced at both ridges during the weaker peak periods of eastward flow, these waves are not strong enough to independently form Type A and Type B waves due to the weaker current. However, the lee wave generated at the eastern ridge during a weaker peak, after a period of propagation, arrives at the western ridge precisely at the moment of the next strong peak, thereby enhancing the Type B wave generated at that time of strong peak. Consequently, the B waves during the TTP are stronger than those in the DTP, and they evolve into internal solitary waves earlier than the Type B waves during the DTP, appearing at earlier and more easterly locations. Therefore, during the TTP, internal waves are more distinctly characterized by the alternating appearance of Type A and Type B waves. This pattern aligns with the phenomena observed by Yang et al. (2009).
Figure 15 shows a Radarsat-2 SAR image taken on 24 July 2013, which displays the spatial distribution of three groups of internal wave packages in the SCS, generated consecutively by three semidiurnal tides during the TTP. The image on the right shows the temperature field at the time of SAR imaging as simulated using the MITgcm. These three groups of internal waves are identified in the image as A9 (120.49°E 20.74°N), B8 (119.23°E 20.87°N), and A10 (117.90°E 21.01°N).
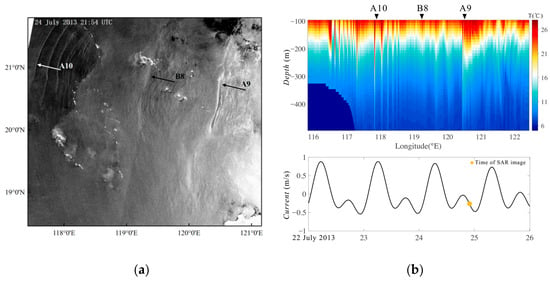
Figure 15.
(a) Radarsat-2 image; (b) MITgcm simulation results during the TTP.
3.5. Semidiurnal-Tide-Dominated Phase (STP)
During the STP, which typically occurs during neap tides, the diurnal tidal component is significantly weaker than the semidiurnal component. At this time, the overall tidal current velocity is relatively low. Due to the weaker barotropic currents and the lower height of the western ridge, Type A waves are only generated at the higher eastern ridge. These Type A waves move slower, but when they reach the western ridge, their amplitude is increased by the resonance effect between the double ridges, thus causing an increase in their speed. Therefore, the internal waves during the STP are characterized by the occurrence of two Type A waves per day. A Radarsat-2 image in Figure 16 shows the typical spatial distribution of internal waves in the SCS during an STP. The image on the right represents the temperature field at the time of SAR imaging as simulated numerically. The SAR image includes three groups of internal waves (counted as leading waves), and their intersections with the C8-L1 transect are located at 118.00°E 21.00°N (A11), 117.11°E 21.09°N (A12), and 116.28°E 21.17°N (A13).
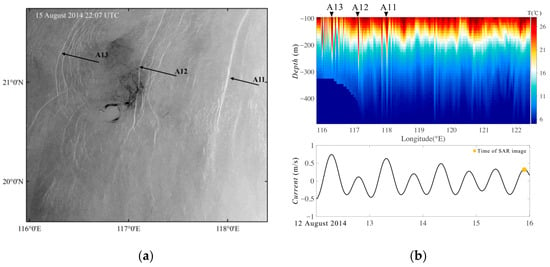
Figure 16.
(a) Radarsat-2 images; (b) MITgcm simulation results during STP.
The Hovmöller diagram reveals noticeable changes in the amplitude and speed of internal waves from their formation to propagation, as illustrated in Figure 17. Initially, when the lee wave forms, it exhibits a bowl-like waveform and then gradually evolves into an internal solitary wave near 120.2°E. During this transition, smaller internal solitary waves can be observed splitting off, as noted by Du et al. [28] through SAR imagery analysis. As the internal solitary waves propagate westward, their amplitude progressively increases due to nonlinear effects. Their speed remains stable until reaching 118.5°E, and it is faster than when they first formed east of 120.2°E. The process of transformation from a lee wave to a typical internal solitary wave can be clearly seen in the right image of Figure 17.
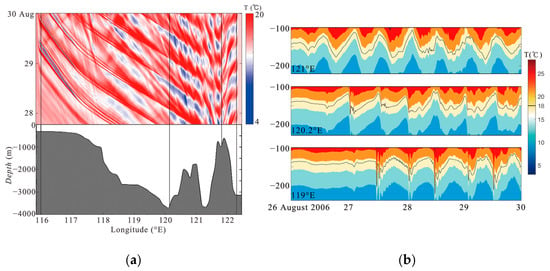
Figure 17.
(a) A Hovmöller diagram during the STP; (b) time series of temperature profile at the longitudes of 121°E, 120.2°E, and 119°E.
4. Discussion
In the previous section, we used Hovmöller diagrams to determine the generation time and location of Type A and Type B waves, and then combined the findings with SAR data to analyze the generation and propagation of solitary waves in the SCS in three stages of DTP, TTP, and STP. In this section, we will discuss the causes of the differences in the generation of Type A and Type B waves in the three stages and provide reasonable explanations.
4.1. Diurnal-Tide-Dominated Phase (DTP)
During the DTP, as the eastward tidal current increases, a concave lee wave forms on the east side of the eastern ridge and begins to propagate westward at the peak of the eastward current. This large concave wave shape steepens at the front due to nonlinear effects, eventually evolving into a solitary wave. This process describes the generation of Type A waves. Brant et al. [6] provide a detailed description of the generation mechanism of such internal solitary waves in the context of the Messina Strait. Similarly, the tidal current interacts with the western ridge to generate Type B waves. However, since the western ridge is relatively lower in height compared to the eastern ridge, the amplitude of the lee wave generated independently by the western ridge is much smaller (as shown in Figure 18), making it difficult to observe Type B waves in the form of internal solitary waves near the Luzon Strait during this phase, as indicated by the dashed box in Figure 14. This observation is consistent with the data reported by Huang [56]. Figure 19 suggests that, due to the effect of decreasing water depth and therefore the increasing nonlinear effect, it is possible for Type B waves to evolve into a solitary wave form near 118°E. This result aligns with the mooring observations of Ramp et al. near to and west of 118°E [39].
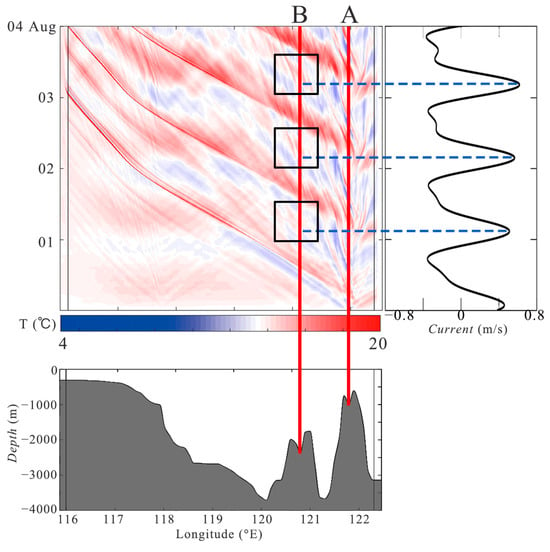
Figure 18.
During the DTP, the interaction between the topography and tidal currents leads to the formation of lee waves at both the eastern and western ridges of the Luzon Strait. These lee waves constitute the sources of Type A and Type B waves. However, the lee waves generated at the western ridge are considerably weaker compared to those at the eastern ridge. It is not until around 118°E that these weaker lee waves from the western ridge evolve into solitary waves.
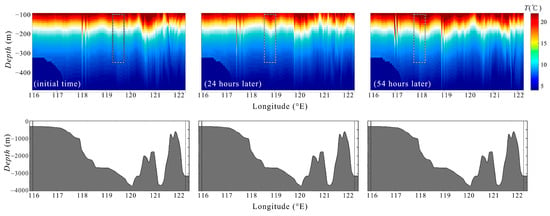
Figure 19.
Type B wave of the DTP propagates to 118°E and becomes steeper, eventually developing into an easily observed internal solitary wave, as shown in the dashed box.
We employ horizontal and vertical velocity fields to intuitively represent the internal water flow within the ocean. Figure 20 displays the simulated instantaneous velocity field and barotropic tide conditions during a typical DTP, where the background colors represent horizontal and vertical velocities, with positive directions being eastward and upward. The barotropic tidal current velocity at that moment is marked in blue circle.
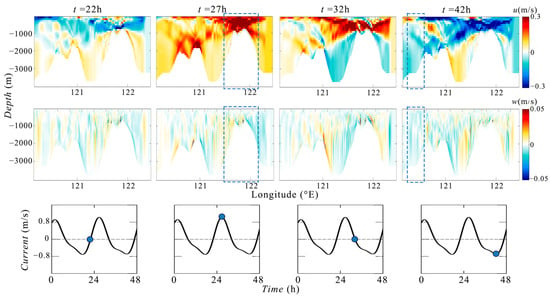
Figure 20.
Evolution of flow field during a period of DTP. From top to bottom are the instantaneous flow field u, w, and barotropic tide current velocity. Positive velocity is eastward or upward. The dashed box at t = 27 marks the flow feature of precursor to lee waves. The dashed box at t = 42 h marks the flow feature of internal solitary wave. The blue circles on the barotropic current velocity charts mark the instantaneous velocities corresponding to 22, 27, 32 and 42 h, respectively.
From t = 22 h to t = 27 h, the eastward barotropic tide gradually strengthens until it reaches its peak. During this period, a flow feature of precursor to lee waves forms with upwards on the west side of the eastern ridge and downwards on the east side. Subsequently, the lee waves begin to propagate westward. Between t = 32 h and t = 42 h, as they cross the western ridge, they evolve into internal solitary waves. This Type A wave can be easily observed in the upper layer of the horizontal velocity field. However, as previously mentioned, within a single diurnal tidal cycle, we cannot directly observe the presence of Type B waves in the Luzon Strait region due to the reasons discussed earlier.
4.2. Transition Tide Phase (TTP)
Using the time evolution graph of the horizontal–vertical velocity field (Figure 21), we can further elucidate the process through which Type B waves at the western ridge are enhanced by the lee waves generated during the preceding semidiurnal tidal cycle (weaker peak). During the TTP, Type A waves are generated at the eastern ridge during stronger peaks of the eastward tidal current. These waves then develop into internal solitary waves as they propagate westward and cross the western ridge. In contrast, Type B waves are generated at the western ridge during stronger peaks of the eastward current, influenced by the combined effects of both ridges across two adjacent tidal cycles. This process is detailed as follows: A waveform propagated by the semidiurnal component during the previous tidal cycle (weaker peak) crosses the western ridge in the subsequent cycle (stronger peak). This crossing results in a downward flow on the east side of the western ridge, thereby enhancing the strength of the lee wave generated by the western ridge at the stronger peak of the eastward flow. This enhanced lee wave then develops into an Type B internal solitary wave.
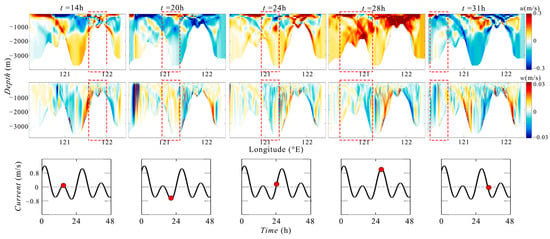
Figure 21.
Evolution of flow field during a period of TTP. From top to bottom are the instantaneous flow field u, w, and barotropic tide. Positive velocity is eastward or upward. The dashed boxes at 14, 20, and 24 h track the westward propagation of a disturbance originating from the eastern ridge. The box at 28 h marks the flow feature of precursor to lee waves with the downward flow on the east side of western ridge enhanced. The red circles on the barotropic current velocity charts mark the instantaneous velocities corresponding to 14, 20, 24, 28, and 31 h, respectively.
As shown in Figure 21, t = 14 h is a weak peak moment, which might either be the local maximum of the eastward tidal current or the minimum of the westward current. In either scenario, there is an upward flow on the west side of the eastern ridge. Subsequently, this upward flow starts to decrease and eventually reverses into a downward flow.
At t = 20 h, when the barotropic tide reaches its maximum westward flow, the downward flow on the west side of the eastern ridge also reaches its maximum. Simultaneously, the upward flow on the east side of the western ridge peaks. This can be interpreted as a wave propagation phenomenon, where the upward flow acts as a wave traveling from the west side of the eastern ridge to the east side of the western ridge.
Around t = 24 h, the westward going wave crosses over the deeper western ridge, which results in a downward flow on the east side of the western ridge. Almost the same time, the barotropic tidal current reverses its direction from west to east.
At t = 28 h, when the tide reaches its maximum eastward flow, following the same mechanism as on the eastern ridge, a relatively weak flow feature of the precursor to a lee wave forms on the western ridge, i.e., the upward flow on west side and downward flow on east side. Note that the crossing over procedure mentioned above has effect of enhancing the downward flow on the east side of the western ridge, and thus also enhancing the lee wave.
At t = 31 h, when the barotropic tidal current shifts from east to west, the enhanced lee wave is released and evolves into a Type B wave during its propagation.
This process highlights the complex dynamics of internal wave formation and the significant role of tidal currents and topography in shaping these phenomena.
4.3. Semidiurnal-Tide-Dominated Phase (STP)
During STP, we use velocity fields combined with internal wave ray theory to explain why relatively strong internal waves can still be generated under conditions of nonstrong barotropic tides. Figure 22 displays the simulated instantaneous velocity field and horizontal flow of the barotropic tide typical for STP.
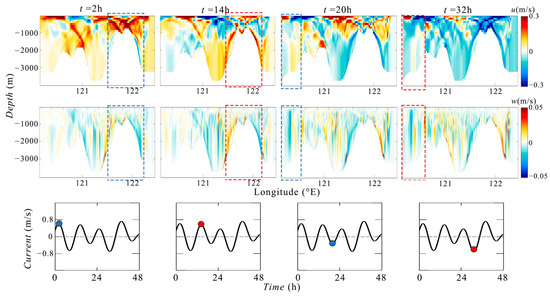
Figure 22.
Evolution of flow field during a period of Flow fields in STP. From top to bottom are the instantaneous flow field u, w, and barotropic tide. Positive velocity is eastward or upward. The blue dashed box at t = 2 h and 20 h mark the generation process of one internal wave. The read box at 14 and 32 h mark the other internal wave. The blue and red circles on the barotropic current velocity charts mark the instantaneous velocities corresponding to 2, 14, 20, and 32 h, respectively.
At t = 2 h, a flow feature of precursor to lee waves emerges at the eastern ridge, caused by the obstruction of the eastward barotropic tide by the ridge.
At t = 14 h, as the flow reaches its second eastward peak of the day, the eastern ridge again exhibits a lee wave precursor feature.
Each lee wave at t = 2 h and 14 h will independently evolve to internal wave. Different colored dashed boxes and circles are used to distinguish two internal wave systems in Figure 22.
The internal wave generated at t = 2 h moves westward and reaches the western ridge when the barotropic tide is approximately at its maximum westward flow. Eventually (at t = 20 h), under the influence of the strong westward flow and the topography of the western ridge, it steepens and transforms into an internal solitary wave, which is then “released” with the westward barotropic tide [67].
At t = 32 h, the lee wave generated at t = 14 h is released following the same process. During this phase, the “resonance” effect of the dual ridges in the Luzon Strait plays a significant role in enhancing the amplitude of Type A waves [42,43]. Observationally, this process results in two occurrences of Type A waves per day during the STP.
Figure 23 illustrates the baroclinic velocities and wave-beam of K1 (a, c) and M2 (b, d) internal waves in the model’s bathymetric cross-section. The simulated horizontal baroclinic velocity field (Figure 23a,b) shows the similar patterns to the internal wave-beams (Figure 23c,d) between the two ridges calculated by Green function method [53]. In the M2 internal wave-beam diagram, many beams originating from the eastern and western ridges roughly overlap [45,68,69,70,71]. This overlap is attributed to the spcific configuration of the dual ridge distance (about 100 km), the semidiurnal internal tide’s first-mode wavelength (147 km) and the depth of two ridges (about 1700 m for western ridge and 600 m for eastern ridge) [72]. It results in a resonance phenomenon of the semidiurnal internal tide between the two ridges, thereby enhancing the generation of semidiurnal internal tides [44,73]. In contrast, the K1 internal tide does not exhibit this feature [53], as the first-mode wavelength of the diurnal internal tide reaches 370 km. Therefore, it is considered that the dual-ridge structure of the Luzon Strait can enhance the intensity of semidiurnal internal tides but not diurnal internal tides [43,46]. Under this mechanism, internal waves during STP, though generated by weaker barotropic tides, may not necessarily have weaker amplitudes.
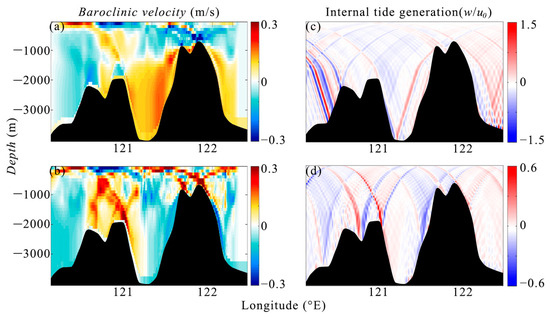
Figure 23.
Horizontal baroclinic velocity field during (a) the DTP and (b) the STP; (c) diurnal and (d) semidiurnal internal tide generation (w/u0) calculated using the Green function method.
5. Conclusions
In this paper, based on a detailed analysis of numerical simulations and SAR data for the diurnal-tide-dominated phase (DTP), transition tide phase (TTP) and semidiurnal-tide-dominated phase (STP), we proposed a relatively simple and unified explanation for internal wave generation suitable for different tidal states. This unified explanation incorporates only two dynamical mechanisms: internal lee waves and resonance of double regime. The specifics are as follows:
- Barotropic tidal currents oscillating relative to submarine ridges generate internal lee waves. These lee waves are always formed on the eastern side of the ridges and start propagating westward at the peak of the eastward tidal current, presenting as a concave surge. The strength of the surge is directly proportional to the intensity of the tidal current and inversely proportional to the depth of water over the ridge’s crest. The lee wave mechanism is effective for both the eastern and western ridges, but their intensities are different. For the same tidal current strength, the lee waves at the eastern ridge are significantly stronger than those at the western ridge. A lee wave must reach a certain intensity to have the potential to evolve into an internal solitary wave. Therefore, during the diurnal tidal peak moments of the DTP, diurnal tidal peak moments of the TTP, and semidiurnal tidal peak moments of the STP, the lee waves generated at the eastern ridge can eventually develop into Type A internal solitary waves.
- Internal tides generated at the eastern ridge can propagate along ray paths and strike the top of the western ridge, with the propagation time coinciding with a semidiurnal tidal cycle. This synchronicity can lead to resonance between the lee waves generated at the western ridge and the rays emanating from the eastern ridge during the previous semidiurnal tidal cycle. Clearly, this resonance effect only occurs when the semidiurnal tidal component is strong. Thus, resonance occurs during the TTP and STP, but not during the DTP.
- During the DTP, in the absence of resonance, even under strong tidal currents, the lee waves at the western ridge remain relatively weak, resulting in weaker Type B internal solitary waves.
- In contrast, during the TTP and STP, the resonance effect strengthens the lee waves at the western ridge. This leads to the development of stronger Type B internal solitary waves during the TTP, and even Type A waves during the STP.
- As a result, during the DTP, weaker Type A and Type B waves alternate daily; during the TTP, stronger daily alternations of Type A and Type B waves occur; and in the STP, two weaker Type A waves are observed each day.
Based on this unified description of internal wave generation in the SCS, it is possible to develop a comprehensive internal wave generation model based on the mechanisms of lee waves and resonance. This model could lay the groundwork for the further development of predictive models for internal waves, enhancing our understanding and forecasting abilities for these complex oceanic phenomena.
Author Contributions
Conceptualization, K.Z.; methodology, K.Z.; software, R.L. and H.L.; validation, R.L. and H.L.; formal analysis, R.L., H.L. and K.Z.; investigation, R.L. and H.L.; data curation, R.S.; writing—original draft preparation, R.L.; writing—review and editing, K.Z.; supervision, T.D. and M.H.; funding acquisition, K.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Qingdao Institute of Collaborative Innovation, grant number LYY-2022-01.
Data Availability Statement
Running scripts for the numerical simulations, as well as simulation results, will be made available upon request from the authors.
Acknowledgments
The ERS-2 and Envisat SAR images used in this paper are provided by Project ID59373 of ESA and NRSCC Dragon Cooperation Programme. The author would like to thank Dr. Xiaodong Huang for providing valuable discussions on in-situ measurements that greatly contributed to this work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Alford, M.H.; Peacock, T.; MacKinnon, J.A.; Nash, J.D.; Buijsman, M.C.; Centurioni, L.R.; Chao, S.-Y.; Chang, M.-H.; Farmer, D.M.; Fringer, O.B.; et al. The Formation and Fate of Internal Waves in the South China Sea. Nature 2015, 521, 65–69. [Google Scholar] [CrossRef]
- Li, Q.; Cao, S.; Luo, Y.; Zhang, K.; Yang, F. Basis Functions for Shallow-Water Temperature Profiles Based on the Internal-Wave Eigenmodes. Acta Oceanol. Sin. 2023, 42, 56–64. [Google Scholar] [CrossRef]
- Fu, L.-L.; Holt, B. Internal Waves in the Gulf of California: Observations from a Spaceborne Radar. J. Geophys. Res. Ocean. 1984, 89, 2053–2060. [Google Scholar] [CrossRef]
- Meunier, T.; Le Boyer, A.; Molodstov, S.; Bower, A.; Furey, H.; Robbins, P. Internal Wave Activity in the Deep Gulf of Mexico. Front. Mar. Sci. 2023, 10, 1285303. [Google Scholar] [CrossRef]
- Roustan, J.; Bordois, L.; Dumas, F.; Auclair, F.; Carton, X. In Situ Observations of the Small-scale Dynamics at Camarinal Sill—Strait of Gibraltar. J. Geophys. Res. Ocean. 2023, 128, e2023JC019738. [Google Scholar] [CrossRef]
- Brandt, P.; Rubino, A.; Alpers, W.; Backhaus, J.O. Internal Waves in the Strait of Messina Studied by a Numerical Model and Synthetic Aperture Radar Images from the ERS 1/2 Satellites. J. Phys. Oceanogr. 1997, 27, 648–663. [Google Scholar] [CrossRef]
- Fourniotis, N.T. Effect of Internal Waves on the Hydrodynamics of a Mediterranean Sea Strait. J. Mar. Sci. Eng. 2024, 12, 532. [Google Scholar] [CrossRef]
- Xie, J.; Du, H.; Gong, Y.; Niu, J.; He, Y.; Chen, Z.; Liu, G.; Liu, L.; Zhang, L.; Cai, S. The Role of Seasonal Circulation in the Variability of Dynamic Parameters of Internal Solitary Waves in the Sulu Sea. Prog. Oceanogr. 2023, 217, 103100. [Google Scholar] [CrossRef]
- Zeng, K.; Alpers, W. Generation of Internal Solitary Waves in the Sulu Sea and Their Refraction by Bottom Topography Studied by ERS SAR Imagery and a Numerical Model. Int. J. Remote Sens. 2004, 25, 1277–1281. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, J.; Meng, J. A Study of the Spatial-Temporal Distribution and Propagation Characteristics of Internal Waves in the Andaman Sea Using MODIS. Acta Oceanol. Sin. 2019, 38, 121–128. [Google Scholar] [CrossRef]
- Osborne, A.; Burch, T. Internal Solitons in the Andaman Sea. Science 1980, 208, 451–460. [Google Scholar] [CrossRef]
- Fer, I.; Koenig, Z.; Kozlov, I.E.; Ostrowski, M.; Rippeth, T.P.; Padman, L.; Bosse, A.; Kolås, E. Tidally Forced Lee Waves Drive Turbulent Mixing along the Arctic Ocean Margins. Geophys. Res. Lett. 2020, 47, e2020GL088083. [Google Scholar] [CrossRef]
- Serebryany, A.; Khimchenko, E.; Popov, O.; Denisov, D.; Kenigsberger, G. Internal Waves Study on a Narrow Steep Shelf of the Black Sea Using the Spatial Antenna of Line Temperature Sensors. J. Mar. Sci. Eng. 2020, 8, 833. [Google Scholar] [CrossRef]
- Silvestrova, K.; Myslenkov, S.; Puzina, O.; Mizyuk, A.; Bykhalova, O. Water Structure in the Utrish Nature Reserve (Black Sea) during 2020–2021 According to Thermistor Chain Data. J. Mar. Sci. Eng. 2023, 11, 887. [Google Scholar] [CrossRef]
- Jackson, C.R. Atlas of Internal Solitary Waves—February 2004. Available online: https://www.internalwaveatlas.com/ (accessed on 18 March 2024).
- Wang, T.; Huang, X.; Zhao, W.; Zheng, S.; Yang, Y.; Tian, J. Internal Solitary Wave Activities near the Indonesian Submarine Wreck Site Inferred from Satellite Images. J. Mar. Sci. Eng. 2022, 10, 197. [Google Scholar] [CrossRef]
- Loder, J.W.; Brickman, D.; Horne, E.P.W. Detailed Structure of Currents and Hydrography on the Northern Side of Georges Bank. J. Geophys. Res. Ocean. 1992, 97, 14331–14351. [Google Scholar] [CrossRef]
- Lamb, K.G. Numerical Experiments of Internal Wave Generation by Strong Tidal Flow across a Finite Amplitude Bank Edge. J. Geophys. Res. Ocean. 1994, 99, 843–864. [Google Scholar] [CrossRef]
- Katavouta, A.; Thompson, K.R.; Lu, Y.; Loder, J.W. Interaction between the Tidal and Seasonal Variability of the Gulf of Maine and Scotian Shelf Region. J. Phys. Oceanogr. 2016, 46, 3279–3298. [Google Scholar] [CrossRef]
- Gao, J.; Ji, C.; Liu, Y.; Gaidai, O.; Ma, X.; Liu, Z. Numerical Study on Transient Harbor Oscillations Induced by Solitary Waves. Ocean Eng. 2016, 126, 467–480. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Dong, G.; Zang, J.; Ma, Y.; Zhou, L. Effects of Offshore Fringing Reefs on the Transient Harbor Resonance Excited by Solitary Waves. Ocean Eng. 2019, 190, 106422. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Chen, H.; Zang, J.; Dong, G. On Hydrodynamic Characteristics of Transient Harbor Resonance Excited by Double Solitary Waves. Ocean Eng. 2021, 219, 108345. [Google Scholar] [CrossRef]
- Huang, X.; Chen, Z.; Zhao, W.; Zhang, Z.; Zhou, C.; Yang, Q.; Tian, J. An Extreme Internal Solitary Wave Event Observed in the Northern South China Sea. Sci. Rep. 2016, 6, 30041. [Google Scholar] [CrossRef] [PubMed]
- Osborne, A.; Burch, T.; Scarlet, R. The Influence of Internal Waves on Deep-Water Drilling. J. Pet. Technol. 1978, 30, 1497–1504. [Google Scholar] [CrossRef]
- Cheng, S.; Yu, Y.; Li, Z.; Huang, Z.; Yang, Z.; Zhang, X.; Cui, Y.; Wu, J.; Liu, X.; Yu, J. The Influence of Internal Solitary Wave on Semi-Submersible Platform System Including Mooring Line Failure. Ocean Eng. 2022, 258, 111604. [Google Scholar] [CrossRef]
- Litter, A.D. Internal Waves: Their Influence Upon Naval Operations; ASW Sonar Technology Report; Defense Technical Information Center: Fort Belvoir, VA, USA, 1996.
- Wang, C.; Wei, D.; Guanghua, L.; Peng, D.; Sen, Z.; Zhuoyue, L.; Xiaopeng, C.; Haibao, H. Numerical Simulation of Influence of Ocean Internal Waves on Hydrodynamic Characteristics of Underwater Vehicles. Chin. Ship Res. 2022, 17, 102–111. [Google Scholar]
- Du, T.; Tseng, Y.; Yan, X. Impacts of Tidal Currents and Kuroshio Intrusion on the Generation of Nonlinear Internal Waves in Luzon Strait. J. Geophys. Res. Ocean. 2008, 113, C08015. [Google Scholar] [CrossRef]
- Hsu, M.-K.; Liu, A.K. Nonlinear Internal Waves in the South China Sea. Can. J. Remote Sens. 2000, 26, 72–81. [Google Scholar] [CrossRef]
- Zhao, Z.; Klemas, V.; Zheng, Q.; Yan, X. Remote Sensing Evidence for Baroclinic Tide Origin of Internal Solitary Waves in the Northeastern South China Sea. Geophys. Res. Lett. 2004, 31, L06302. [Google Scholar] [CrossRef]
- Jackson, C.R. An Empirical Model for Estimating the Geographic Location of Nonlinear Internal Solitary Waves. J. Atmos. Ocean. Technol. 2009, 26, 2243–2255. [Google Scholar] [CrossRef]
- Ebbesmeyer, C.; Coomes, C.A.; Hamilton, R.; Kurrus, K.A.; Sullivan, T.C.; Salem, B.L.; Romea, R.D.; Bauer, R.J. New Observations on Internal Waves (Solitons) in the South China Sea Using an Acoustic Doppler Current Profiler. Mar. Technol. Soc. 91 Proc. 1991, 165–175. [Google Scholar]
- Gong, Q.; Chen, L.; Diao, Y.; Xiong, X.; Sun, J.; Lv, X. On the Identification of Internal Solitary Waves from Moored Observations in the Northern South China Sea. Sci. Rep. 2023, 13, 3133. [Google Scholar] [CrossRef]
- Zang, Z.; Zhang, Y.; Chen, T.; Xie, B.; Zou, X.; Li, Z. A Numerical Simulation of Internal Wave Propagation on a Continental Slope and Its Influence on Sediment Transport. J. Mar. Sci. Eng. 2023, 11, 517. [Google Scholar] [CrossRef]
- Ponte, A.L.; Cornuelle, B.D. Coastal Numerical Modelling of Tides: Sensitivity to Domain Size and Remotely Generated Internal Tide. Ocean Model. 2013, 62, 17–26. [Google Scholar] [CrossRef]
- Simmons, H.; Chang, M.-H.; Chang, Y.-T.; Chao, S.-Y.; Fringer, O.; Jackson, C.R.; Ko, D.S. Modeling and Prediction of Internal Waves in the South China Sea. Oceanography 2011, 24, 88–99. [Google Scholar] [CrossRef]
- Lai, Z.; Jin, G.; Huang, Y.; Chen, H.; Shang, X.; Xiong, X. The Generation of Nonlinear Internal Waves in the South China Sea: A Three-dimensional, Nonhydrostatic Numerical Study. J. Geophys. Res. Ocean. 2019, 124, 8949–8968. [Google Scholar] [CrossRef]
- Zeng, K.; Huang, Z.; He, M. A Propagation Model for Internal Waves in South China Sea Based on Fast Marching Method. Trans. Oceanol. Limnol. 2019, 6, 23–33. [Google Scholar] [CrossRef]
- Ramp, S.R.; Tang, T.Y.; Duda, T.F.; Lynch, J.F.; Liu, A.K.; Chiu, C.-S.; Bahr, F.L.; Kim, H.-R.; Yang, Y.-J. Internal Solitons in the Northeastern South China Sea. Part I: Sources and Deep Water Propagation. IEEE J. Ocean. Eng. 2004, 29, 1157–1181. [Google Scholar] [CrossRef]
- Alford, M.H.; Lien, R.-C.; Simmons, H.; Klymak, J.; Ramp, S.; Yang, Y.J.; Tang, D.; Chang, M.-H. Speed and Evolution of Nonlinear Internal Waves Transiting the South China Sea. J. Phys. Oceanogr. 2010, 40, 1338–1355. [Google Scholar] [CrossRef]
- Sinnett, G.; Ramp, S.R.; Yang, Y.J.; Chang, M.-H.; Jan, S.; Davis, K.A. Large-Amplitude Internal Wave Transformation into Shallow Water. J. Phys. Oceanogr. 2022, 52, 2539–2554. [Google Scholar] [CrossRef]
- Buijsman, M.C.; Klymak, J.M.; Legg, S.; Alford, M.H.; Farmer, D.; MacKinnon, J.A.; Nash, J.D.; Park, J.-H.; Pickering, A.; Simmons, H. Three-Dimensional Double-Ridge Internal Tide Resonance in Luzon Strait. J. Phys. Oceanogr. 2014, 44, 850–869. [Google Scholar] [CrossRef]
- Buijsman, M.C.; Legg, S.; Klymak, J. Double-Ridge Internal Tide Interference and Its Effect on Dissipation in Luzon Strait. J. Phys. Oceanogr. 2012, 42, 1337–1356. [Google Scholar] [CrossRef]
- Farmer, D.; Li, Q.; Park, J. Internal Wave Observations in the South China Sea: The Role of Rotation and Non-linearity. Atmos.-Ocean 2009, 47, 267–280. [Google Scholar] [CrossRef]
- Echeverri, P.; Peacock, T. Internal Tide Generation by Arbitrary Two-Dimensional Topography. J. Fluid Mech. 2010, 659, 247–266. [Google Scholar] [CrossRef]
- Buijsman, M.; McWilliams, J.; Jackson, C. East-west Asymmetry in Nonlinear Internal Waves from Luzon Strait. J. Geophys. Res. Ocean. 2010, 115, C10057. [Google Scholar] [CrossRef]
- Buijsman, M.; Kanarska, Y.; McWilliams, J. On the Generation and Evolution of Nonlinear Internal Waves in the South China Sea. J. Geophys. Res. Ocean. 2010, 115, C02012. [Google Scholar] [CrossRef]
- Shaw, P.; Ko, D.S.; Chao, S. Internal Solitary Waves Induced by Flow over a Ridge: With Applications to the Northern South China Sea. J. Geophys. Res. Ocean. 2009, 114, C02019. [Google Scholar] [CrossRef]
- Zhao, Z.; Alford, M.H. Source and Propagation of Internal Solitary Waves in the Northeastern South China Sea. J. Geophys. Res. Ocean. 2006, 111, C11012. [Google Scholar] [CrossRef]
- Zhang, Z.; Fringer, O.; Ramp, S. Three-dimensional, Nonhydrostatic Numerical Simulation of Nonlinear Internal Wave Generation and Propagation in the South China Sea. J. Geophys. Res. Ocean. 2011, 116, C05022. [Google Scholar] [CrossRef]
- Vlasenko, V.; Guo, C.; Stashchuk, N. On the Mechanism of A-Type and B-Type Internal Solitary Wave Generation in the Northern South China Sea. Deep Sea Res. Part I Oceanogr. Res. Pap. 2012, 69, 100–112. [Google Scholar] [CrossRef]
- Chen, Y.; Shan Ko, D.; Shaw, P. The Generation and Propagation of Internal Solitary Waves in the South China Sea. J. Geophys. Res. Ocean. 2013, 118, 6578–6589. [Google Scholar] [CrossRef]
- Li, Q. Numerical Assessment of Factors Affecting Nonlinear Internal Waves in the South China Sea. Prog. Oceanogr. 2014, 121, 24–43. [Google Scholar] [CrossRef]
- Zeng, Z.; Chen, X.; Yuan, C.; Tang, S.; Chi, L. A Numerical Study of Generation and Propagation of Type-a and Type-b Internal Solitary Waves in the Northern South China Sea. Acta Oceanol. Sin. 2019, 38, 20–30. [Google Scholar] [CrossRef]
- Beardsley, R.C.; Duda, T.F.; Lynch, J.F.; Irish, J.D.; Ramp, S.R.; Chiu, C.-S.; Tang, T.Y.; Yang, Y.-J.; Fang, G. Barotropic Tide in the Northeast South China Sea. IEEE J. Ocean. Eng. 2004, 29, 1075–1086. [Google Scholar] [CrossRef]
- Huang, X. Study on the Spatial Distribution and Time Variation Characteristics of Solitary Waves in the South China Sea; Ocean University of China: Qingdao, China, 2013. [Google Scholar]
- Ramp, S.; Yang, Y.; Bahr, F. Characterizing the Nonlinear Internal Wave Climate in the Northeastern South China Sea. Nonlinear Process. Geophys. 2010, 17, 481–498. [Google Scholar] [CrossRef]
- Marshall, J.; Adcroft, A.; Hill, C.; Perelman, L.; Heisey, C. A Finite-volume, Incompressible Navier Stokes Model for Studies of the Ocean on Parallel Computers. J. Geophys. Res. Ocean. 1997, 102, 5753–5766. [Google Scholar] [CrossRef]
- Alpers, W. Theory of Radar Imaging of Internal Waves. Nature 1985, 314, 245–247. [Google Scholar] [CrossRef]
- Alpers, W.R.; Ross, D.B.; Rufenach, C.L. On the Detectability of Ocean Surface Waves by Real and Synthetic Aperture Radar. J. Geophys. Res. Ocean. 1981, 86, 6481–6498. [Google Scholar] [CrossRef]
- Guo, C.; Vlasenko, V.; Alpers, W.; Stashchuk, N.; Chen, X. Evidence of Short Internal Waves Trailing Strong Internal Solitary Waves in the Northern South China Sea from Synthetic Aperture Radar Observations. Remote Sens. Environ. 2012, 124, 542–550. [Google Scholar] [CrossRef]
- Zheng, Q.; Susanto, R.D.; Ho, C.; Song, Y.T.; Xu, Q. Statistical and Dynamical Analyses of Generation Mechanisms of Solitary Internal Waves in the Northern South China Sea. J. Geophys. Res. Ocean. 2007, 112, C03021. [Google Scholar] [CrossRef]
- Fang, X.; Du, T. Fundamentals of Oceanic Internal Waves and Internal Waves in the China Seas; Ocean University China Press: Qingdao, China, 2005; pp. 71–73. [Google Scholar]
- Egbert, G.D.; Erofeeva, S.Y. Efficient Inverse Modeling of Barotropic Ocean Tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Guo, C.; Chen, X.; Vlasenko, V.; Stashchuk, N. Numerical Investigation of Internal Solitary Waves from the Luzon Strait: Generation Process, Mechanism and Three-Dimensional Effects. Ocean Model. 2011, 38, 203–216. [Google Scholar] [CrossRef]
- Gong, Y.; Chen, X.; Xu, J.; Xie, J.; Chen, Z.; He, Y.; Cai, S. An Internal Solitary Wave Forecasting Model in the Northern South China Sea (ISWFM-NSCS). Geosci. Model Dev. Discuss. 2023, 16, 2851–2871. [Google Scholar] [CrossRef]
- Maxworthy, T. A Note on the Internal Solitary Waves Produced by Tidal Flow over a Three-dimensional Ridge. J. Geophys. Res. Ocean. 1979, 84, 338–346. [Google Scholar] [CrossRef]
- Jan, S.; Lien, R.-C.; Ting, C.-H. Numerical Study of Baroclinic Tides in Luzon Strait. J. Oceanogr. 2008, 64, 789–802. [Google Scholar] [CrossRef]
- Echeverri, P.; Yokossi, T.; Balmforth, N.; Peacock, T. Tidally Generated Internal-Wave Attractors between Double Ridges. J. Fluid Mech. 2011, 669, 354–374. [Google Scholar] [CrossRef]
- Echeverri, P.; Flynn, M.; Winters, K.B.; Peacock, T. Low-Mode Internal Tide Generation by Topography: An Experimental and Numerical Investigation. J. Fluid Mech. 2009, 636, 91–108. [Google Scholar] [CrossRef]
- Jackson, C.R.; Da Silva, J.C.; Jeans, G. The Generation of Nonlinear Internal Waves. Oceanography 2012, 25, 108–123. [Google Scholar] [CrossRef]
- Alford, M.H.; MacKinnon, J.A.; Nash, J.D.; Simmons, H.; Pickering, A.; Klymak, J.M.; Pinkel, R.; Sun, O.; Rainville, L.; Musgrave, R. Energy Flux and Dissipation in Luzon Strait: Two Tales of Two Ridges. J. Phys. Oceanogr. 2011, 41, 2211–2222. [Google Scholar] [CrossRef]
- Garrett, C.; Kunze, E. Internal Tide Generation in the Deep Ocean. Annu. Rev. Fluid Mech. 2007, 39, 57–87. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).