Exploring the Effects of Topography on Leaf Area Index Retrieved from Remote Sensing Data at Various Spatial Scales over Rugged Terrains
Abstract
1. Introduction
2. Materials and Methods
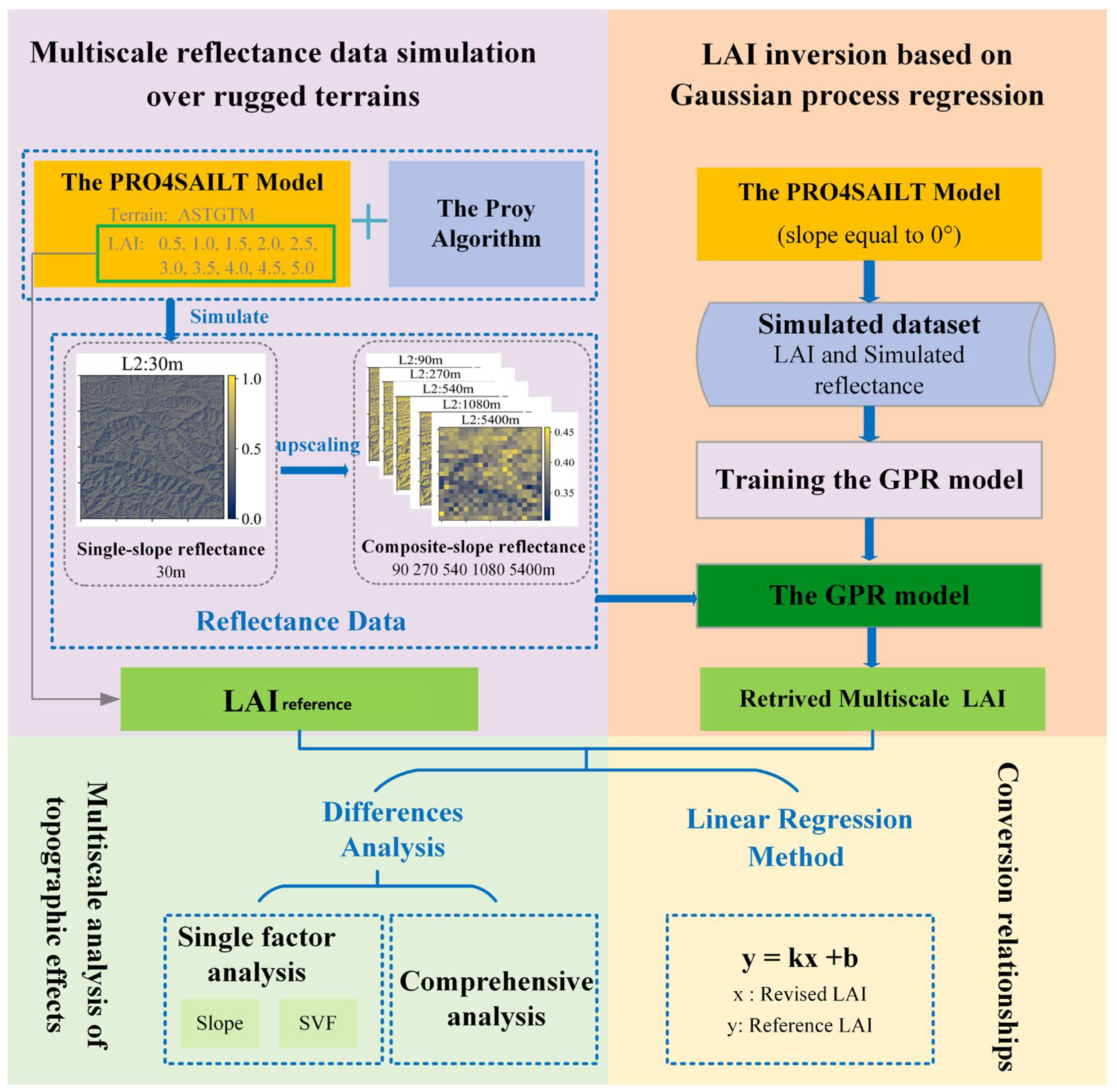
2.1. Multiscale Reflectance Data Simulation over Rugged Terrains
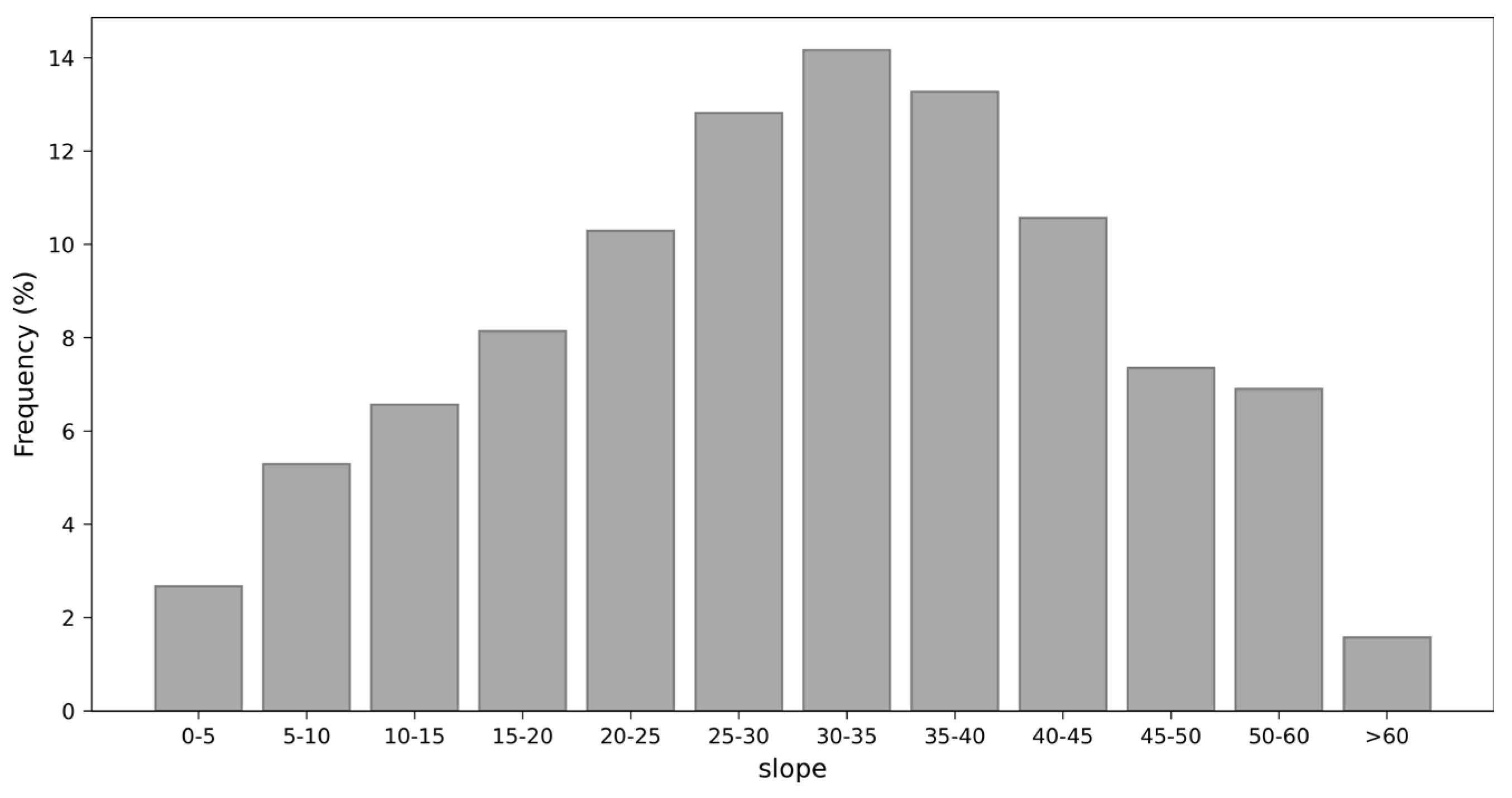
2.1.1. Study Area and Data
2.1.2. Reflectance Data Simulation Based on Topography Models
2.2. LAI Inversion Based on Gaussian Process Regression
2.2.1. Gaussian Process Regression
2.2.2. GPR Training and LAI Inversion
2.2.3. Multiscale Analysis of Topographic Effects
2.2.4. Conversion Relationships between the Flat LAI and Slope LAI Values
3. Results
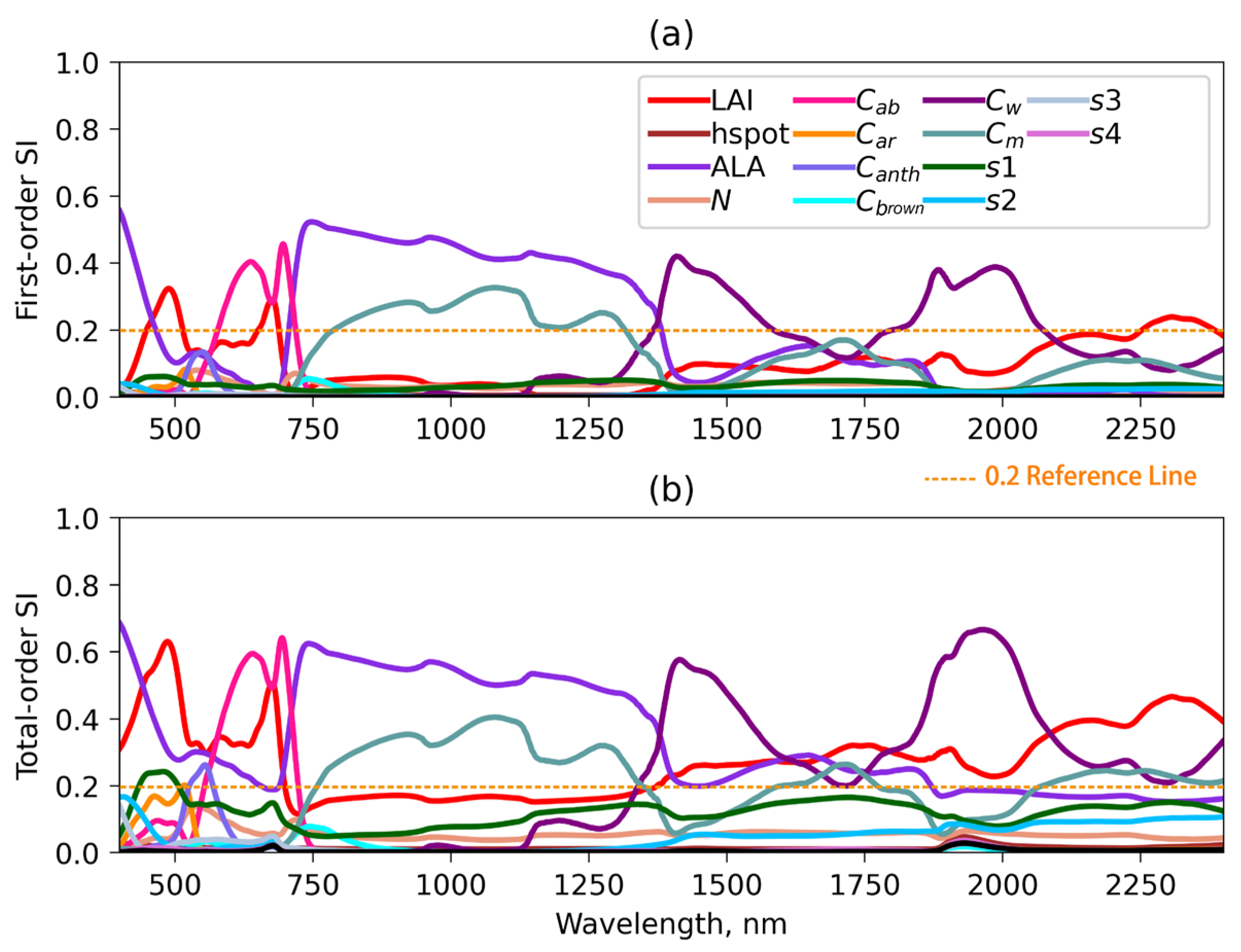
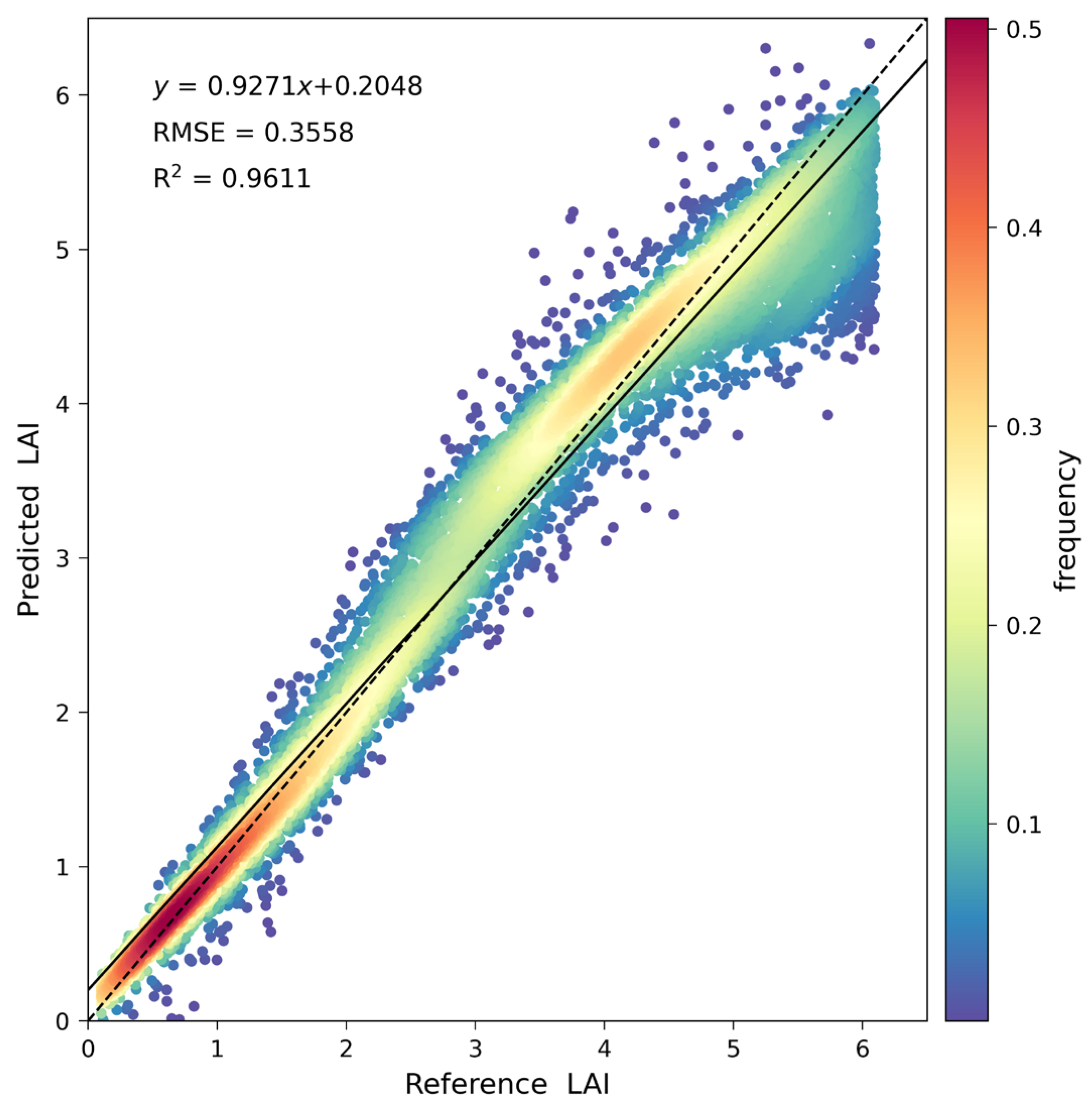
3.1. Analysis of the Simulation Data
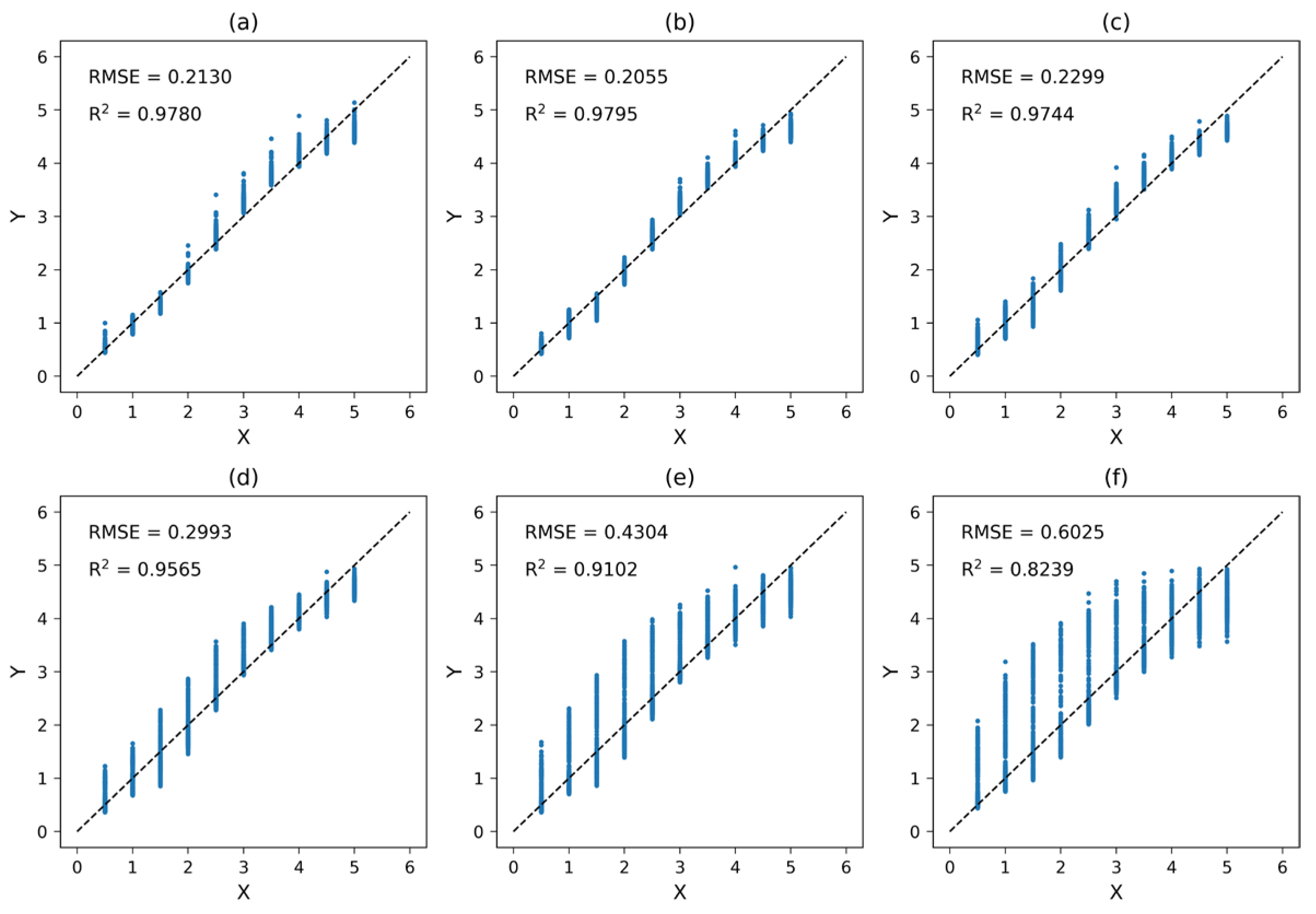
3.2. LAI Values Retrieved Using the Algorithm Ignoring Terrain Effects
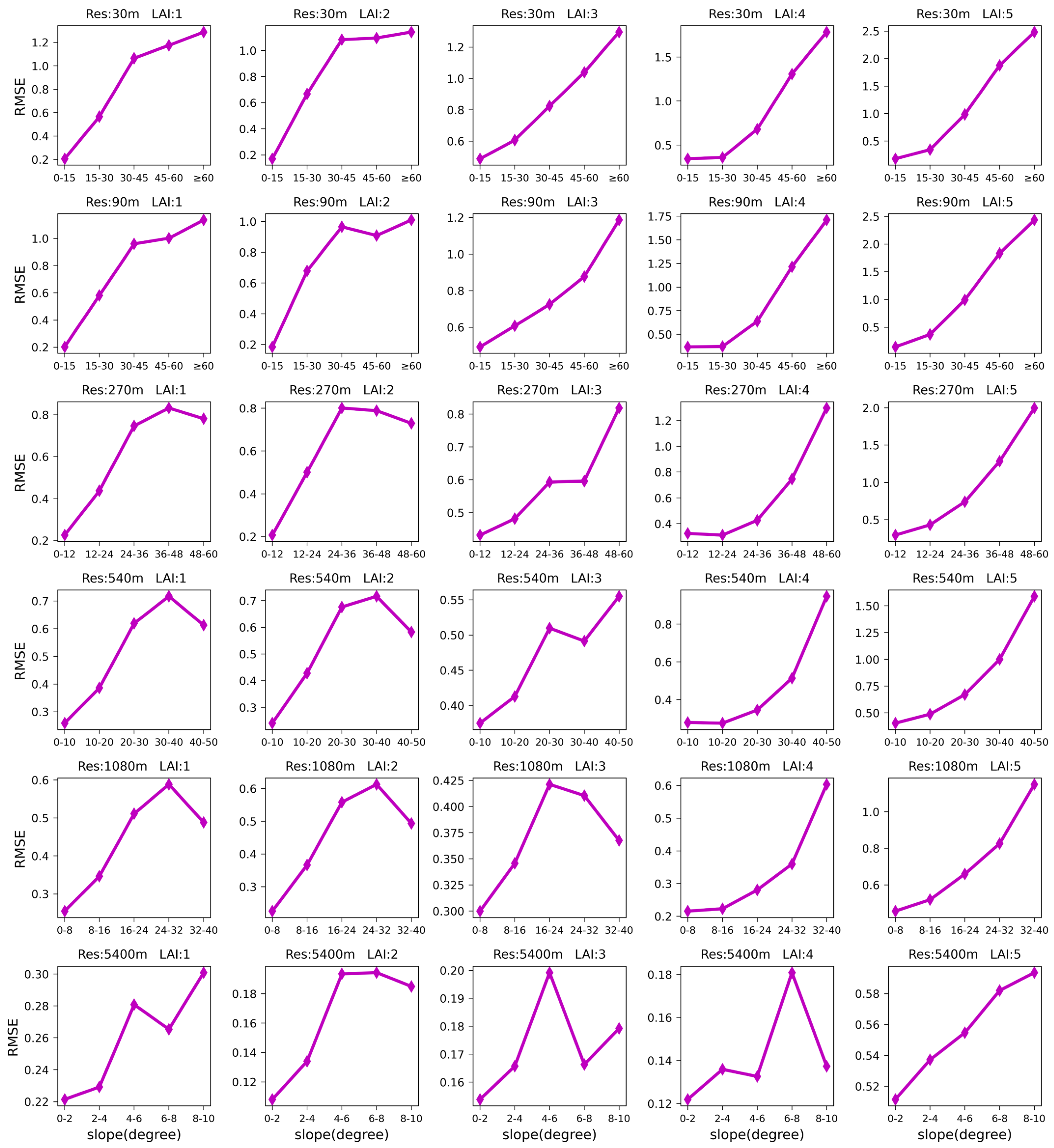
3.3. Multiscale Analysis of Topographic Effects on the Retrieved LAI Values
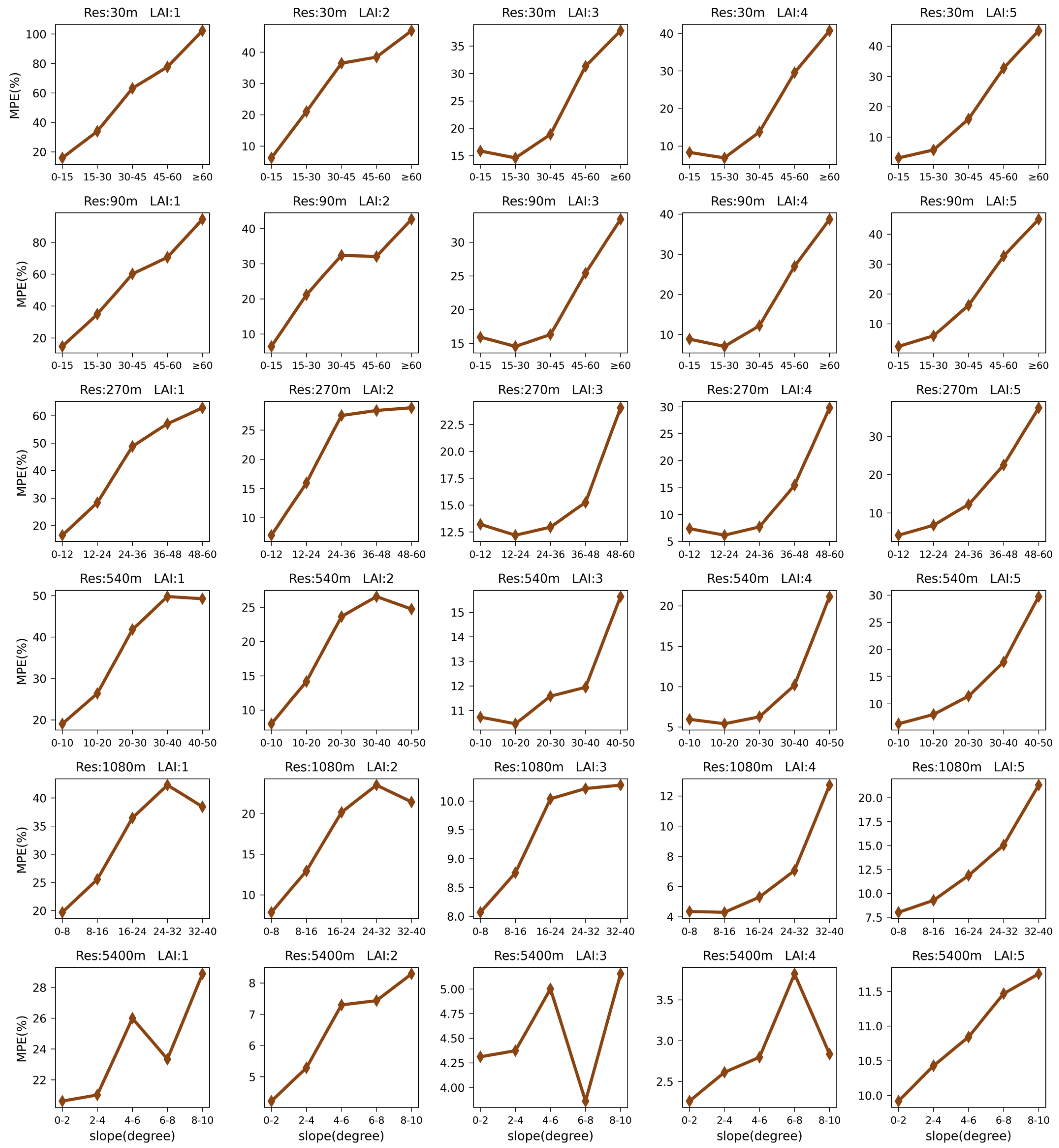
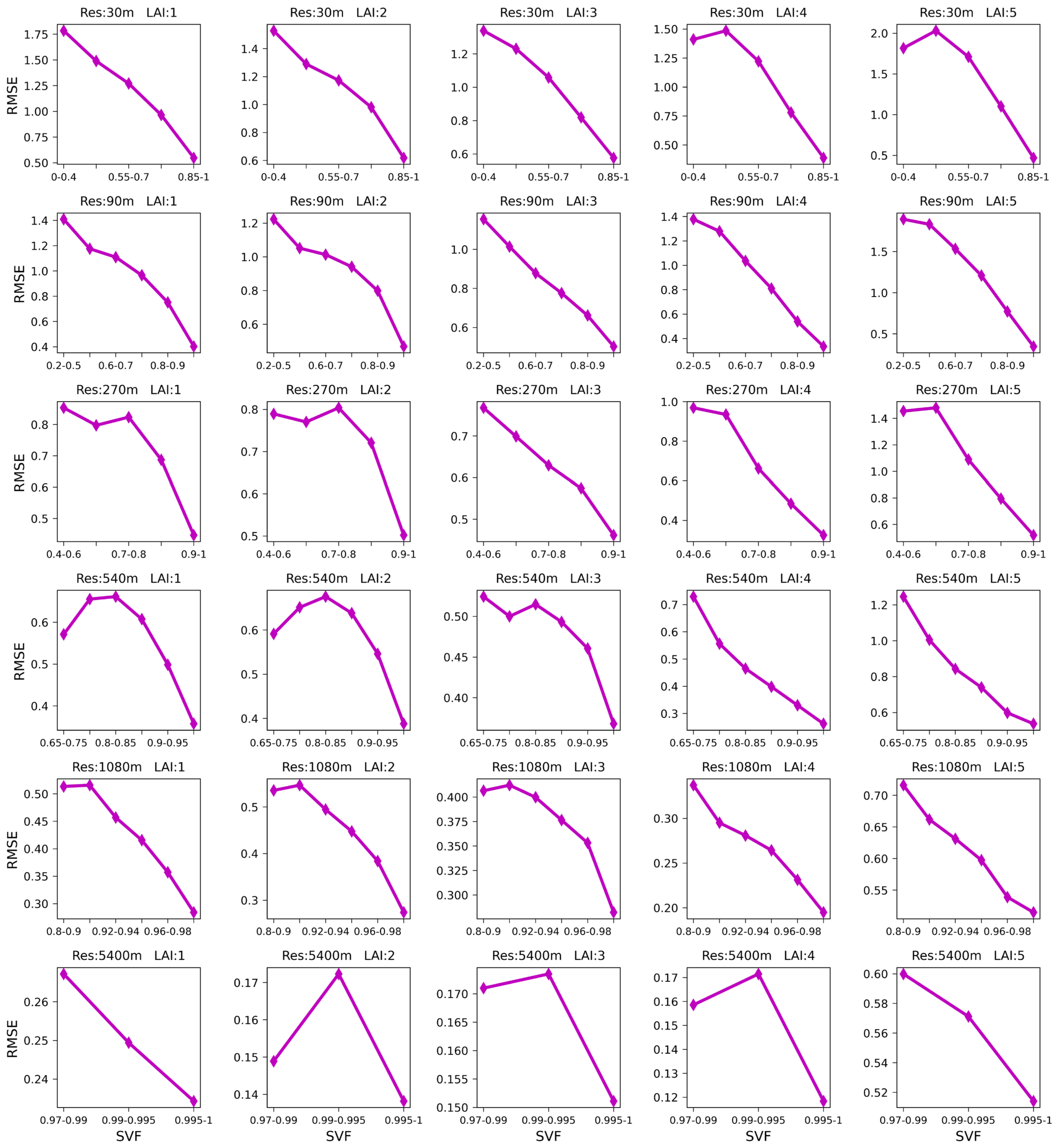
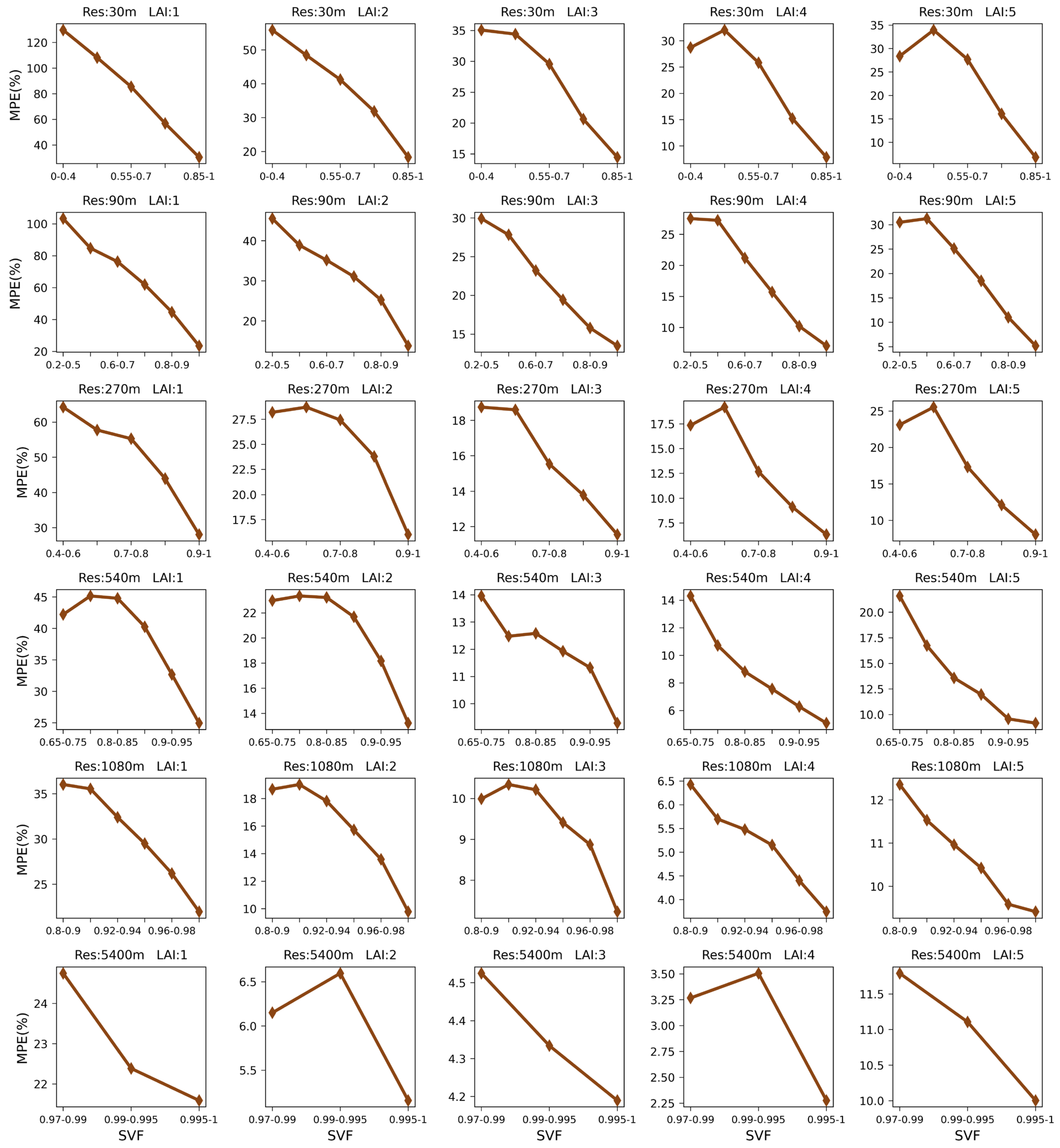
3.3.1. Single Factor Analysis
- (1)
- Impact analysis of the slope
- (2)
- Impact analysis of the SVF
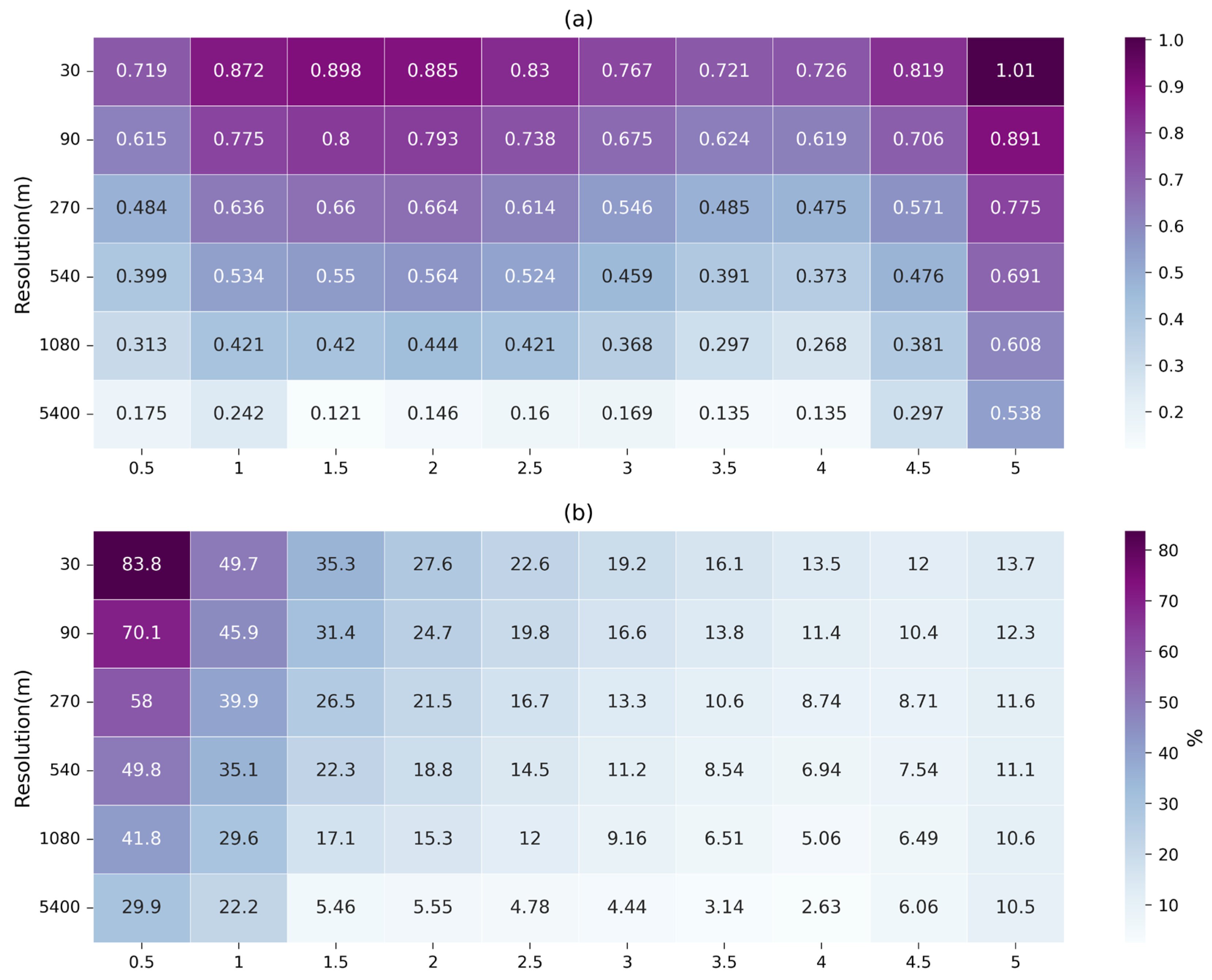
3.3.2. Comprehensive Analysis of Topographic Effects
3.4. Conversion Relationships between the LAI Values Retrieved Using the Algorithm Ignoring Terrain Effects and the Reference LAI Values
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jin, H.; Li, A.; Wang, J.; Bo, Y. Improvement of Spatially and Temporally Continuous Crop Leaf Area Index by Integration of CERES-Maize Model and MODIS Data. Eur. J. Agron. 2016, 78, 1–12. [Google Scholar] [CrossRef]
- Martin, C.; Jessica, M.; Eric, V.; Christopher, J. A 30+ Year AVHRR LAI and FAPAR Climate Data Record: Algorithm Description and Validation. Remote Sens. 2016, 8, 263. [Google Scholar] [CrossRef]
- Chen, J.M.; Black, T.A. Defining Leaf Area Index for Non-flat Leaves. Agric. For. Meteorol. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Niño, F.; Weiss, M.; Samain, O.; et al. LAI, fAPAR and fCover CYCLOPES Global Products Derived from VEGETATION Part 1: Principles of the Algorithm. Remote Sens. Environ. 2009, 110, 275–286. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Chen, P.; Yin, X.; Zhang, L.; Song, J. Use of General Regression Neural Networks for Generating the GLASS Leaf Area Index Product from Time-Series MODIS Surface Reflectance. IEEE Trans. Geosci. Remote Sens. 2014, 52, 209–223. [Google Scholar] [CrossRef]
- Baret, F.; Weiss, M.; Lacaze, R.; Camacho, F.; Makhmara, H.; Pacholcyzk, P.; Smets, B. GEOV1: LAI and FAPAR Essential Climate Variables and FCOVER Global Time Series Capitalizing over Existing Products. Part1: Principles of Development and Production. Remote Sens. Environ. 2013, 137, 299–309. [Google Scholar] [CrossRef]
- Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.; Nemani, R.R.; Myneni, R.B. Global Data Sets of Vegetation Leaf Area Index (LAI)3g and Fraction of Photosynthetically Active Radiation (FPAR)3g Derived from Global Inventory Modeling and Mapping Studies (GIMMS) Normalized Difference Vegetation Index (NDVI3g) for the Period 1981 to 2011. Remote Sens. 2013, 5, 927–948. [Google Scholar] [CrossRef]
- Atzberger, C. Object-Based Retrieval of Biophysical Canopy Variables Using Artificial Neural Nets and Radiative Transfer Models. Remote Sens. Environ. 2004, 93, 53–67. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Verrelst, J.; Munoz-Mari, J.; Laparra, V.; Mateo-Jimenez, F.; Gomez-Dans, J. A Survey on Gaussian Processes for Earth-Observation Data Analysis: A Comprehensive Investigation. IEEE Geosci. Remote Sens. Mag. 2016, 4, 58–78. [Google Scholar] [CrossRef]
- Gewali, U.B.; Monteiro, S.T.; Saber, E. Gaussian Processes for Vegetation Parameter Estimation from Hyperspectral Data with Limited Ground Truth. Remote Sens. 2019, 11, 1614. [Google Scholar] [CrossRef]
- Estévez, J.; Vicent, J.; Rivera-Caicedo, J.P.; Morcillo-Pallarés, P.; Vuolo, F.; Sabater, N.; Camps-Valls, G.; Moreno, J.; Verrelst, J. Gaussian Processes Retrieval of LAI from Sentinel-2 Top-of-Atmosphere Radiance Data. ISPRS J. Photogramm. Remote Sens. 2020, 167, 289–304. [Google Scholar] [CrossRef] [PubMed]
- Adeluyi, O.; Harris, A.; Verrelst, J.; Foster, T.; Clay, G.D. Estimating the Phenological Dynamics of Irrigated Rice Leaf Area Index Using the Combination of PROSAIL and Gaussian Process Regression. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102454. [Google Scholar] [CrossRef] [PubMed]
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.L.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.R.; et al. Global Products of Vegetation Leaf Area and Fraction Absorbed PAR from Year One of MODIS Data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar] [CrossRef]
- Allan, R.P.; Soden, B.J. Atmospheric Warming and the Amplification of Precipitation Extremes. Science 2008, 321, 1481–1484. [Google Scholar] [CrossRef] [PubMed]
- Jin, M.; Dickinson, R.E. New Observational Evidence for Global Warming from Satellite. Geophys. Res. Lett. 2002, 29, 39-1–39-4. [Google Scholar] [CrossRef]
- Vinnikov, K.Y.; Grody, N.C. Global Warming Trend of Mean Tropospheric Temperature Observed by Satellites. Science 2003, 302, 269–272. [Google Scholar] [CrossRef]
- Potter, C.S. Terrestrial Biomass and the Effects of Deforestation on the Global Carbon Cycle. BioScience 1999, 49, 769–778. [Google Scholar] [CrossRef]
- Jung, M. Global Patterns of Land-Atmosphere Fluxes of Carbon Dioxide, Latent Heat, and Sensible Heat Derived from Eddy Covariance, Satellite, and Meteorological Observations. J. Geophys. Res. Biogeosci. 2011, 116, G00J07. [Google Scholar] [CrossRef]
- Julien, Y.; Sobrino, J.A. Global Land Surface Phenology Trends from GIMMS Database. Int. J. Remote Sens. 2009, 30, 3495–3513. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.; Gao, F.; Reed, B.C.; Huete, A. Monitoring Vegetation Phenology Using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Townshend, J.; Justice, C.; Li, W.; Gurney, C.; Mcmanus, J. Global Land Cover Classification by Remote Sensing: Present Capabilities and Future Possibilities. Remote Sens. Environ. 1991, 35, 243–255. [Google Scholar] [CrossRef]
- Jin, H.; Li, A.; Bian, J.; Nan, X.; Zhao, W.; Zhang, Z.; Yin, G. Intercomparison and Validation of MODIS and GLASS Leaf Area Index (LAI) Products over Mountain Areas: A Case Study in Southwestern China. Int. J. Appl. Earth Obs. Geoinf. 2017, 55, 52–67. [Google Scholar] [CrossRef]
- Duveiller, G.; Defourny, P. A Conceptual Framework to Define the Spatial Resolution Requirements for Agricultural Monitoring Using Remote Sensing. Remote Sens. Environ. 2010, 114, 2637–2650. [Google Scholar] [CrossRef]
- Mulla, D.J. Twenty Five Years of Remote Sensing in Precision Agriculture: Key Advances and Remaining Knowledge Gaps. Biosyst. Eng. 2013, 114, 358–371. [Google Scholar] [CrossRef]
- Seelan, S.K.; Laguette, S.; Casady, G.M.; Seielstad, G.A. Remote Sensing Applications for Precision Agriculture: A Learning Community Approach. Remote Sens. Environ. 2003, 88, 157–169. [Google Scholar] [CrossRef]
- Asner, G.P.; Powell, G.V.N.; Mascaro, J.; Knapp, D.E.; Clark, J.K.; Jacobson, J.; Kennedy-Bowdoin, T.; Balaji, A.; Paez-Acosta, G.; Victoria, E.; et al. High-Resolution Forest Carbon Stocks and Emissions in the Amazon. Proc. Natl. Acad. Sci. USA 2010, 107, 16738–16742. [Google Scholar] [CrossRef] [PubMed]
- Sobrino, J.A.; Oltra-Carrió, R.; Sòria, G.; Bianchi, R.; Paganini, M. Impact of Spatial Resolution and Satellite Overpass Time on Evaluation of the Surface Urban Heat Island Effects. Remote Sens. Environ. 2012, 117, 50–56. [Google Scholar] [CrossRef]
- Welch, R. Spatial Resolution Requirements for Urban Studies. Int. J. Remote Sens. 1982, 3, 139–146. [Google Scholar] [CrossRef]
- Mousivand, A.; Verhoef, W.; Menenti, M.; Gorte, B. Modeling Top of Atmosphere Radiance over Heterogeneous Non-Lambertian Rugged Terrain. Remote Sens. 2015, 7, 8019–8044. [Google Scholar] [CrossRef]
- Yin, G.; Li, A.; Zhao, W.; Jin, H.; Bian, J.; Wu, S. Modeling Canopy Reflectance over Sloping Terrain Based on Path Length Correction. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4597–4609. [Google Scholar] [CrossRef]
- Gonsamo, A.; Chen, J.M. Improved LAI Algorithm Implementation to MODIS Data by Incorporating Background, Topography, and Foliage Clumping Information. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1076–1088. [Google Scholar] [CrossRef]
- Yu, W.; Li, J.; Liu, Q.; Yin, G.; Zeng, Y.; Lin, S.; Zhao, J. A Simulation-Based Analysis of Topographic Effects on LAI Inversion over Sloped Terrain. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 794–806. [Google Scholar] [CrossRef]
- Wen, J.; Liu, Q.; Xiao, Q.; Liu, Q.; You, D.; Hao, D.; Wu, S.; Lin, X. Characterizing Land Surface Anisotropic Reflectance over Rugged Terrain: A Review of Concepts and Recent Developments. Remote Sens. 2018, 10, 370. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, X.; Liu, J.; Sparrow, M. Estimating Surface Solar Radiation over Complex Terrain Using Moderate-resolution Satellite Sensor Data. Int. J. Remote Sens. 2005, 26, 47–58. [Google Scholar] [CrossRef]
- Wen, J.; Liu, Q.; Liu, Q.; Xiao, Q.; Li, X. Scale Effect and Scale Correction of Land-Surface Albedo in Rugged Terrain. Int. J. Remote Sens. 2009, 30, 5397–5420. [Google Scholar] [CrossRef]
- Burgess, D.W.; Lewis, P.; Muller, J.-P.A.L. Topographic Effects in AVHRR NDVI Data. Remote Sens. Environ. 1995, 54, 223–232. [Google Scholar] [CrossRef]
- Gonsamo, A.; Pellikka, P. The Computation of Foliage Clumping Index Using Hemispherical Photography. Agric. For. Meteorol. 2009, 149, 1781–1787. [Google Scholar] [CrossRef]
- María Luisa, E.; Frédéric, B.; Marie, W. Slope Correction for LAI Estimation from Gap Fraction Measurements. Agric. For. Meteorol. 2008, 148, 1553–1562. [Google Scholar] [CrossRef]
- Yan, G.; Hu, R.; Luo, J.; Weiss, M.; Jiang, H.; Mu, X.; Xie, D.; Zhang, W. Review of Indirect Optical Measurements of Leaf Area Index: Recent Advances, Challenges, and Perspectives. Agric. For. Meteorol. 2019, 265, 390–411. [Google Scholar] [CrossRef]
- Shi, H.; Xiao, Z. The 4SAILT Model: An Improved 4SAIL Canopy Radiative Transfer Model for Sloping Terrain. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5515–5525. [Google Scholar] [CrossRef]
- Proy, C.; Tanré, D.; Deschamps, P.Y. Evaluation of Topographic Effects in Remotely Sensed Data. Remote Sens. Environ. 1989, 30, 21–32. [Google Scholar] [CrossRef]
- Fujisada, H.; Urai, M.; Iwasaki, A. Technical Methodology for ASTER Global DEM. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3725–3736. [Google Scholar] [CrossRef]
- Feret, J.-B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the Leaf Optical Properties Model Separating Photosynthetic Pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Walthall, C.L.; Norman, J.M.; Welles, J.M.; Campbell, G.; Blad, B.L. Simple Equation to Approximate the Bidirectional Reflectance from Vegetative Canopies and Bare Soil Surfaces. Appl. Opt. 1985, 24, 383. [Google Scholar] [CrossRef] [PubMed]
- Verhoef, W.; Jia, L.; Xiao, Q.; Su, Z. Unified Optical-Thermal Four-Stream Radiative Transfer Theory for Homogeneous Vegetation Canopies. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1808–1822. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance Based Sensitivity Analysis of Model Output. Design and Estimator for the Total Sensitivity Index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Mousivand, A.; Menenti, M.; Gorte, B.; Verhoef, W. Global Sensitivity Analysis of the Spectral Radiance of a Soil–Vegetation System. Remote Sens. Environ. 2014, 145, 131–144. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; van der Tol, C.; Magnani, F.; Mohammed, G.; Moreno, J. Global Sensitivity Analysis of the SCOPE Model: What Drives Simulated Canopy-Leaving Sun-Induced Fluorescence? Remote Sens. Environ. 2015, 166, 8–21. [Google Scholar] [CrossRef]
- Prikaziuk, E.; van der Tol, C. Global Sensitivity Analysis of the SCOPE Model in Sentinel-3 Bands: Thermal Domain Focus. Remote Sens. 2019, 11, 2424. [Google Scholar] [CrossRef]
- Berger, K.; Atzberger, C.; Danner, M.; Wocher, M.; Mauser, W.; Hank, T. Model-Based Optimization of Spectral Sampling for the Retrieval of Crop Variables with the PROSAIL Model. Remote Sens. 2018, 10, 2063. [Google Scholar] [CrossRef]
- Yan, G.; Wang, T.; Jiao, Z.; Mu, X.; Zhao, J.; Chen, L. Topographic Radiation Modeling and Spatial Scaling of Clear-Sky Land Surface Longwave Radiation over Rugged Terrain. Remote Sens. Environ. 2016, 172, 15–27. [Google Scholar] [CrossRef]
- Yan, G.; Jiao, Z.-H.; Wang, T.; Mu, X. Modeling Surface Longwave Radiation over High-Relief Terrain. Remote Sens. Environ. 2020, 237, 111556. [Google Scholar] [CrossRef]
- Jiao, Z.-H.; Yan, G.; Wang, T.; Mu, X.; Zhao, J. Modeling of Land Surface Thermal Anisotropy Based on Directional and Equivalent Brightness Temperatures over Complex Terrain. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 410–423. [Google Scholar] [CrossRef]
- Shi, H.; Xiao, Z. Exploring Topographic Effects on Surface Parameters over Rugged Terrains at Various Spatial Scales. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4404616. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; Adaptive computation and machine learning; MIT Press: Cambridge, MA, USA, 2006; ISBN 978-0-262-18253-9. [Google Scholar]
- Riley, S.J.; DeGloria, S.D.; Elliot, R. Index That Quantifies Topographic Heterogeneity. Intermt. J. Sci. 1999, 5, 23–27. [Google Scholar]
- Liang, S.; Strahler, A.H. An Analytic Radiative Transfer Model for a Coupled Atmosphere and Leaf Canopy. J. Geophys. Res. Atmos. 1995, 100, 5085–5094. [Google Scholar] [CrossRef]
- Shi, H.; Xiao, Z.; Wen, J.; Wu, S. An Optical-Thermal Surface-Atmosphere Radiative Transfer Model Coupling Framework with Topographic Effects. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4400312. [Google Scholar] [CrossRef]
- Soenen, S.A.; Peddle, D.R.; Coburn, C.A. SCS+C: A Modified Sun-Canopy-Sensor Topographic Correction in Forested Terrain. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2148–2159. [Google Scholar] [CrossRef]

| Model | Parameter | Symbol | Model Parameter Range | Units | Parameter Setting for Reflectance Simulation over Rugged Terrains | Parameter Setting for Simulation of the Training Dataset | |
|---|---|---|---|---|---|---|---|
| Leaf Model PROSPECT-D | Leaf chlorophyll content | Cab | 0–100 | 50 | 5–75 | Uniform | |
| Carotenoids | Car | 0–30 | 10 | 10 | - | ||
| Anthocyanin | CAnth | 0–20 | 0 | 0 | - | ||
| Brown pigment content | Cbrown | 0–1 | 0 | 0 | - | ||
| Leaf water content | Cw | 0.0001–0.05 | 0.010 | 0.002–0.05 | Uniform | ||
| Leaf dry matter content | Cm | 0.0001–0.05 | 0.0080 | 0.001–0.03 | Uniform | ||
| Leaf structure index | N | 1–3.5 | None | 1.6 | 1.6 | - | |
| Canopy Model 4SAILT | Sun zenith angle | sza | 0–90 | ° | 30 | 30 | - |
| Sun azimuth angle | saa | 0–360 | ° | 130 | 130 | - | |
| View zenith angle | vza | 0–90 | ° | 10 | 10 | - | |
| View azimuth angle | vaa | 0–360 | ° | 40 | 40 | - | |
| Average leaf inclination angle | ALA | 0–90 | ° | 45 | 30–80 | Uniform | |
| Leaf area index | LAI | 0–8 | None | 0.5, 1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5 | 0.1–6 | Uniform | |
| Hot spot parameter | hspot | 0.001–0.1 | None | 0 | 0 | - | |
| Slope | slope | 0–90 | ° | From DEM | 0 | - | |
| Aspect | aspect | 0–360 | ° | From DEM | 0 | - | |
| Sky view factor | SVF | 0–1 | None | From DEM | 1 | - | |
| Soil Model Walthall | Soil parameter 1 | s1 | 0.05–0.4 | None | 0.4 | 0.05–0.4 | Uniform |
| Soil parameter 2 | s2 | −0.1–0.1 | None | 0 | 0 | - | |
| Soil parameter 3 | s3 | −0.05–0.05 | None | 0 | 0 | - | |
| Soil parameter 4 | s4 | −0.04–0.04 | None | 0 | 0 | - | |
| Slope Range | Conversion Relationships (x: Retrieved LAI; y: Reference LAI) |
|---|---|
| 0°–5° | y = 0.9712x − 0.1437 |
| 5°–10° | y = 0.9800x − 0.1604 |
| 10°–15° | y = 0.9898x − 0.1799 |
| 15°–20° | y = 0.9970x − 0.2134 |
| 20°–25° | y = 0.9786x − 0.1768 |
| 25°–30° | y = 0.9236x − 0.0455 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Xiao, Z.; Shi, H.; Song, J. Exploring the Effects of Topography on Leaf Area Index Retrieved from Remote Sensing Data at Various Spatial Scales over Rugged Terrains. Remote Sens. 2024, 16, 1404. https://doi.org/10.3390/rs16081404
Zheng Y, Xiao Z, Shi H, Song J. Exploring the Effects of Topography on Leaf Area Index Retrieved from Remote Sensing Data at Various Spatial Scales over Rugged Terrains. Remote Sensing. 2024; 16(8):1404. https://doi.org/10.3390/rs16081404
Chicago/Turabian StyleZheng, Yajie, Zhiqiang Xiao, Hanyu Shi, and Jinling Song. 2024. "Exploring the Effects of Topography on Leaf Area Index Retrieved from Remote Sensing Data at Various Spatial Scales over Rugged Terrains" Remote Sensing 16, no. 8: 1404. https://doi.org/10.3390/rs16081404
APA StyleZheng, Y., Xiao, Z., Shi, H., & Song, J. (2024). Exploring the Effects of Topography on Leaf Area Index Retrieved from Remote Sensing Data at Various Spatial Scales over Rugged Terrains. Remote Sensing, 16(8), 1404. https://doi.org/10.3390/rs16081404





