Coupling Downscaling and Calibrating Methods for Generating High-Quality Precipitation Data with Multisource Satellite Data in the Yellow River Basin
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.2.1. Remote Sensing Precipitation Data
2.2.2. Meteorological Station Precipitation Data
2.2.3. DEM and NDVI Data
2.3. Methodology
2.3.1. Downscaling Method
2.3.2. Data Calibration Method
- (1)
- Calculate the difference between downscaled data and meteorological station data.
- (2)
- Interpolate the point difference data into a 1 km resolution raster data using ordinary kriging.
- (3)
- The 1 km resolution precipitation predicted by the model is added to the 1 km resolution difference data in (2) to obtain the 1 km resolution precipitation data calibrated using meteorological station data.
2.3.3. Precision Evaluation
2.3.4. Analysis of Stages and Trends
3. Results
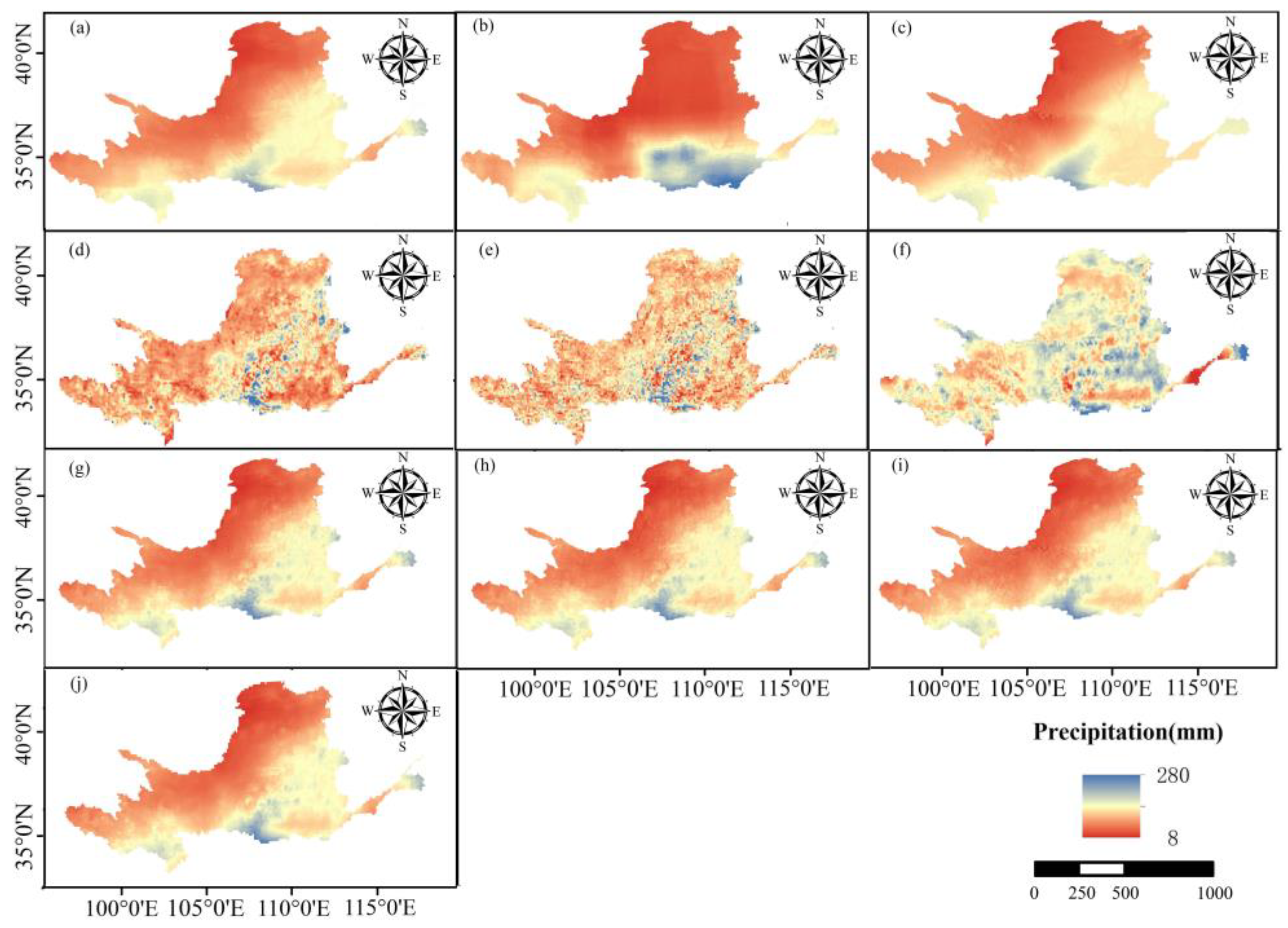
3.1. Optimal Combination of Remotely Sensed Precipitation Dataset
3.2. Downscaled Results
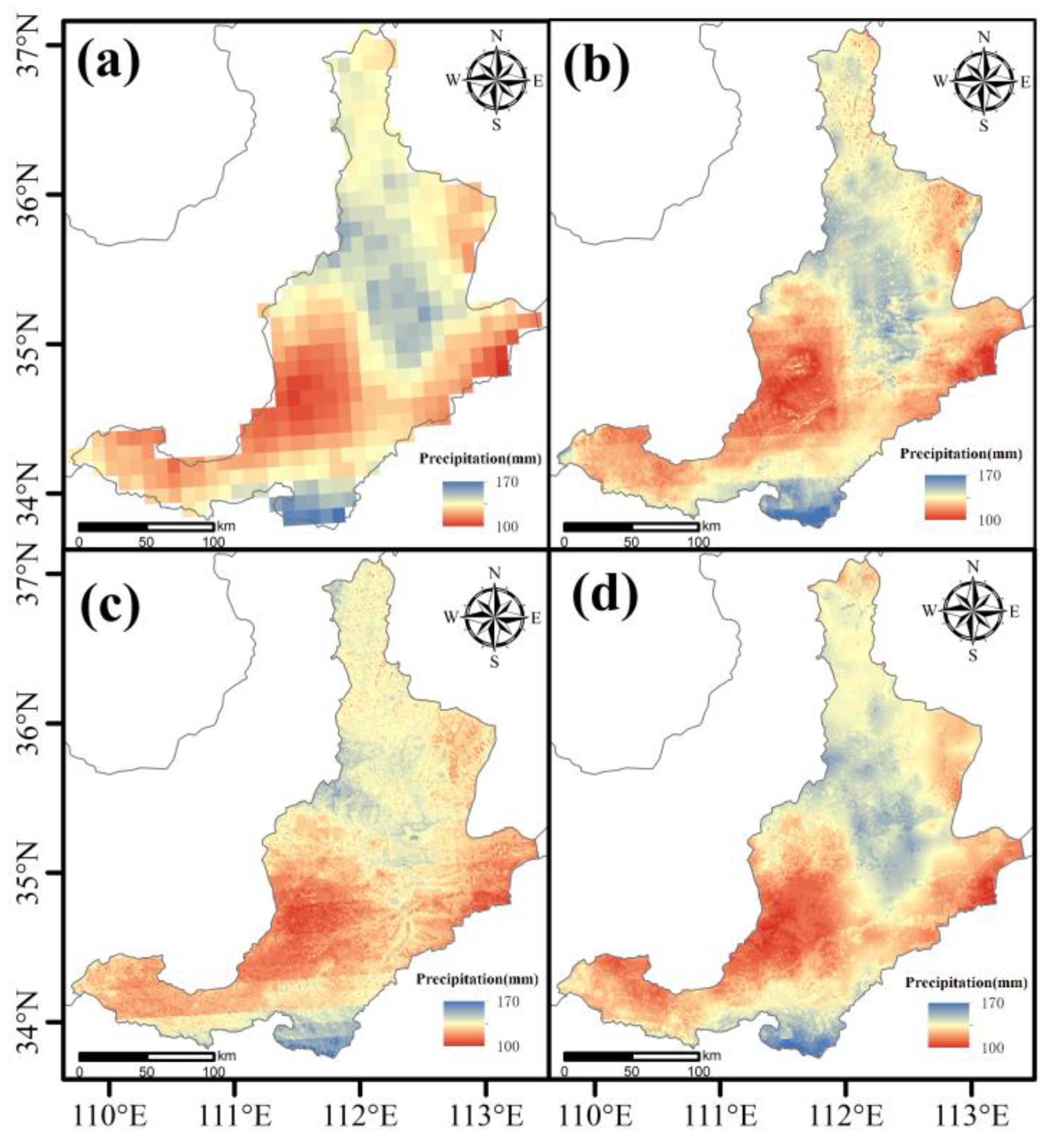
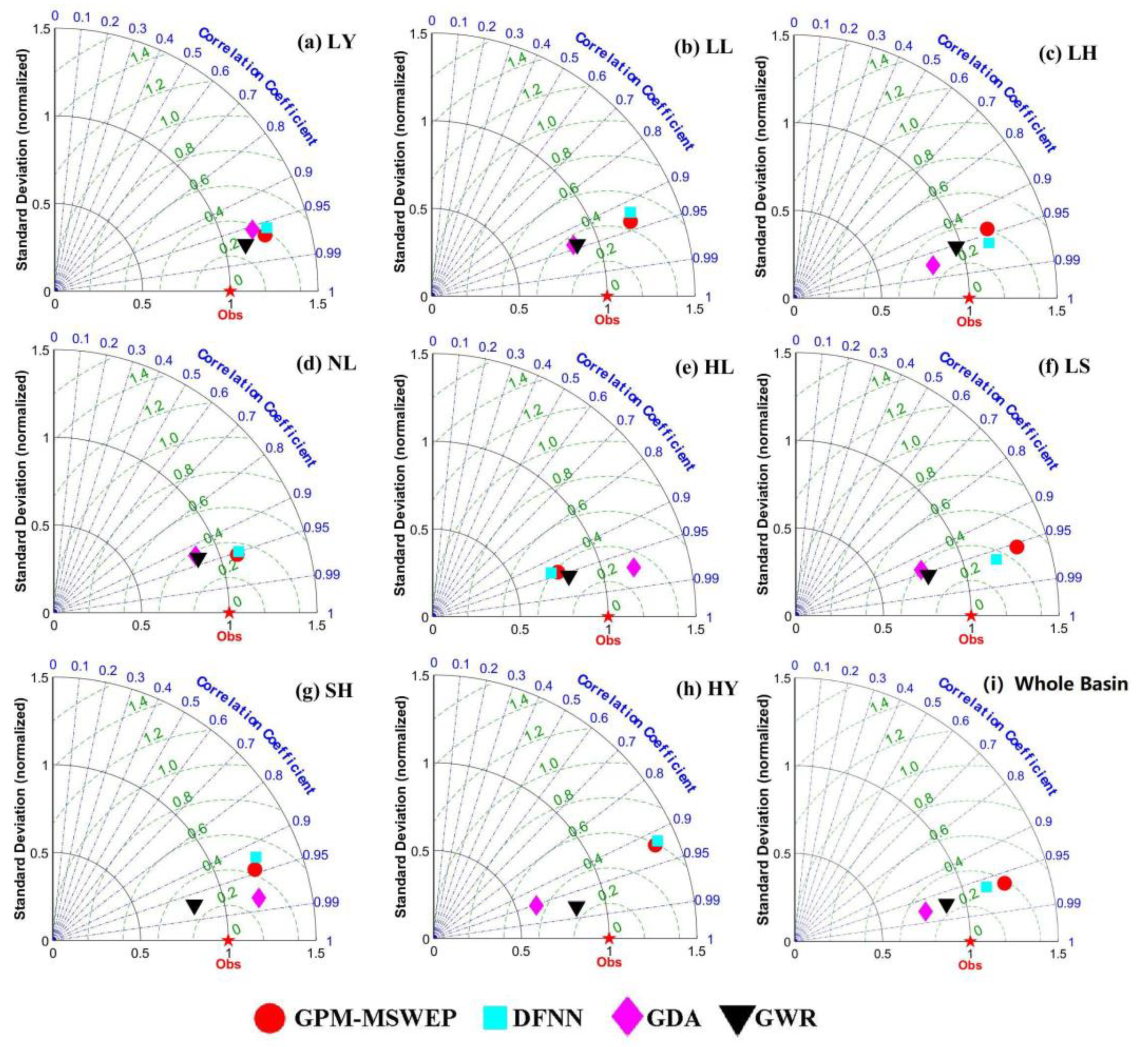
3.3. Calibration of Downscaled Results and Evaluation of Accuracy
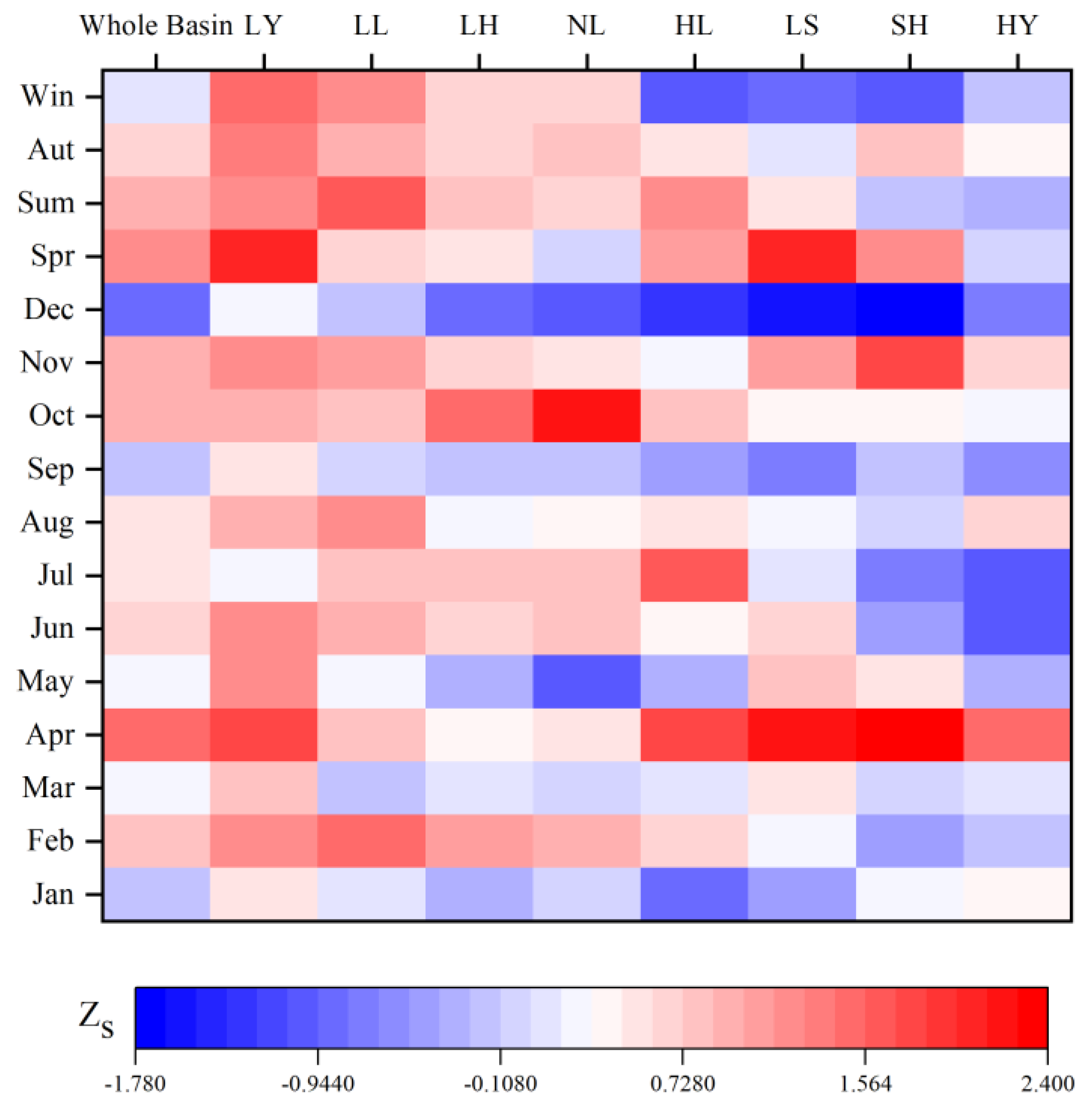
3.4. Stage Analysis and Spatial Trend Analysis
4. Discussion
5. Conclusions
- (1)
- On the temporal scale, GPM and MSWEP had the highest accuracy in the Yellow River basin, with R2 values of 0.92 and 0.90, respectively, and the smallest RMSE and FSE, with a BIAS close to 0. The TRMM and CHIRPS had the lowest accuracy. On the spatial scale, GPM had a better distribution of R2 and the smallest BIAS. The optimal combination of GPM and MSWEP was selected to construct a high-precision mixed dataset.
- (2)
- The DFNN downscaling results displayed better spatial details, more accurately reflecting the differences in regional localized precipitation. DFNN had a higher R2 and lower RMSE, FSE, and BIAS (R2 = 0.92, RMSE = 12.77, FSE = 1.92, BIAS = 1.4%), demonstrating better error control.
- (3)
- After calibration with GWR and GDA, the data accuracy was improved, and GWR’s calibration effect was superior to that of the GDA. After GWR calibration, the DFNN downscaling results saw an increase in R2 from 0.92 to 0.93, a decrease in RMSE from 12.77 to 12.00 mm, a decrease in FSE from 1.92 to 1.90, and a decrease in BIAS from 1.4% to 0.5%.
- (4)
- There were two abrupt changes in annual precipitation in the Yellow River basin in 2002 and 2016. On the monthly scale, the precipitation in January, September, and December showed a decreasing trend, and the precipitation in the remaining months showed an increasing trend. On the seasonal scale, the precipitation in spring, summer, fall, and winter showed an increasing trend.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Kubota, T.; Shige, S.; Hashizume, H.; Aonashi, K.; Takahashi, N.; Seto, S.; Hirose, M.; Takayabu, Y.N.; Ushio, T.; Nakagawa, K. Global precipitation map using satellite-borne microwave radiometers by the GSMaP project: Production and validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Funk, C.; Verdin, A.; Michaelsen, J.; Peterson, P.; Pedreros, D.; Husak, G. A global satellite-assisted precipitation climatology. Earth Syst. Sci. Data 2015, 7, 275–287. [Google Scholar]
- Li, Z.; Yang, D.; Gao, B.; Jiao, Y.; Hong, Y.; Xu, T. Multiscale hydrologic applications of the latest satellite precipitation products in the Yangtze River Basin using a distributed hydrologic model. J. Hydrometeorol. 2015, 16, 407–426. [Google Scholar] [CrossRef]
- Duan, Z.; Liu, J.; Tuo, Y.; Chiogna, G.; Disse, M. Evaluation of eight high spatial resolution gridded precipitation products in Adige Basin (Italy) at multiple temporal and spatial scales. Sci. Total Environ. 2016, 573, 1536–1553. [Google Scholar] [CrossRef]
- Lu, D.; Yong, B. A preliminary assessment of the gauge-adjusted near-real-time GSMaP precipitation estimate over Mainland China. Remote Sens. 2020, 12, 141. [Google Scholar] [CrossRef]
- Islam, M.A.; Yu, B.; Cartwright, N. Assessment and comparison of five satellite precipitation products in Australia. J. Hydrol. 2020, 590, 125474. [Google Scholar] [CrossRef]
- Aslami, F.; Ghorbani, A.; Sobhani, B.; Esmali, A. Comprehensive comparison of daily IMERG and GSMaP satellite precipitation products in Ardabil Province, Iran. Int. J. Remote Sens. 2019, 40, 3139–3153. [Google Scholar] [CrossRef]
- Yu, C.; Hu, D.; Liu, M.; Wang, S.; Di, Y. Spatio-temporal accuracy evaluation of three high-resolution satellite precipitation products in China area. Atmos. Res. 2020, 241, 104952. [Google Scholar] [CrossRef]
- McCollum, J.R.; Krajewski, W.F.; Ferraro, R.R.; Ba, M.B. Evaluation of BIASes of satellite rainfall estimation algorithms over the continental United States. J. Appl. Meteorol. Climatol. 2002, 41, 1065–1080. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhong, L.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA Version-7 legacy products over Mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Sa’adi, Z.; Shahid, S.; Chung, E.-S.; bin Ismail, T. Projection of spatial and temporal changes of rainfall in Sarawak of Borneo Island using statistical downscaling of CMIP5 models. Atmos. Res. 2017, 197, 446–460. [Google Scholar] [CrossRef]
- Wu, X.; Zhao, N. Evaluation and Comparison of Six High-Resolution Daily Precipitation Products in Mainland China. Remote Sens. 2022, 15, 223. [Google Scholar] [CrossRef]
- Atkinson, P.M. Downscaling in remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2013, 22, 106–114. [Google Scholar] [CrossRef]
- Legasa, M.; Manzanas, R.; Calviño, A.; Gutiérrez, J.M. A posteriori random forests for stochastic downscaling of precipitation by predicting probability distributions. Water Resour. Res. 2022, 58, e2021WR030272. [Google Scholar] [CrossRef]
- Wilby, R.L.; Wigley, T. Precipitation predictors for downscaling: Observed and general circulation model relationships. Int. J. Climatol. A J. R. Meteorol. Soc. 2000, 20, 641–661. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Chen, W.; Fu, K.; Zuo, J.; Zheng, X.; Huang, T.; Ren, W. Radar emitter classification for large data set based on weighted-xgboost. IET Radar Sonar Navig. 2017, 11, 1203–1207. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, W.; Nie, N. Spatial downscaling of TRMM precipitation data using an optimal subset regression model with NDVI and terrain factors in the Yarlung Zangbo River Basin, China. Adv. Meteorol. 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Mao, K.; Tang, H.; Wang, X.; Zhou, Q.; Wang, D. Near-surface air temperature estimation from ASTER data based on neural network algorithm. Int. J. Remote Sens. 2008, 29, 6021–6028. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, Z.; Crabbe, M.J.C.; Chandra Das, L. Statistical learning-based spatial downscaling models for precipitation distribution. Adv. Meteorol. 2022, 2022, 3140872. [Google Scholar] [CrossRef]
- Xu, R.; Chen, N.; Chen, Y.; Chen, Z. Downscaling and projection of multi-cmip5 precipitation using machine learning methods in the upper han river Basin. Adv. Meteorol. 2020, 2020, 8680436. [Google Scholar] [CrossRef]
- Ridgeway, G. Additive logistic regression: A statistical view of boosting: Discussion. Ann. Stat. 2000, 28, 393–400. [Google Scholar]
- Wager, S. Asymptotic theory for random forests. arXiv 2014, arXiv:1405.0352. [Google Scholar]
- Maji, D.; Santara, A.; Ghosh, S.; Sheet, D.; Mitra, P. Deep neural network and random forest hybrid architecture for learning to detect retinal vessels in fundus images. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Ha, V.K.; Ren, J.; Xu, X.; Zhao, S.; Xie, G.; Vargas, V.M. Deep learning based single image super-resolution: A survey. In Proceedings of the Advances in Brain Inspired Cognitive Systems: 9th International Conference, BICS 2018, Xi’an, China, 7–8 July 2018; Springer: Berlin, Germany, 2018. [Google Scholar]
- Baez-Villanueva, O.M.; Zambrano-Bigiarini, M.; Beck, H.E.; McNamara, I.; Ribbe, L.; Nauditt, A.; Birkel, C.; Verbist, K.; Giraldo-Osorio, J.D.; Thinh, N.X. RF-MEP: A novel Random Forest method for merging gridded precipitation products and ground-based measurements. Remote Sens. Environ. 2020, 239, 111606. [Google Scholar] [CrossRef]
- Cheema, M.J.M.; Bastiaanssen, W.G. Local calibration of remotely sensed rainfall from the TRMM satellite for different periods and spatial scales in the Indus Basin. Int. J. Remote Sens. 2012, 33, 2603–2627. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W. First results from Version 7 TRMM 3B43 precipitation product in combination with a new downscaling–calibration procedure. Remote Sens. Environ. 2013, 131, 1–13. [Google Scholar] [CrossRef]
- Yu, H.; Wang, L.; Yang, R.; Yang, M.; Gao, R. Temporal and spatial variation of precipitation in the Hengduan Mountains region in China and its relationship with elevation and latitude. Atmos. Res. 2018, 213, 1–16. [Google Scholar] [CrossRef]
- Khan, M.; Munoz-Arriola, F.; Rehana, S.; Greer, P. Spatial heterogeneity of temporal shifts in extreme precipitation across India. J. Clim. Chang. 2019, 5, 19–31. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Breiman, L. Classification and Regression Trees; Routledge: London, UK, 2017. [Google Scholar]
- Carlisle, D.M.; Falcone, J.; Wolock, D.M.; Meador, M.R.; Norris, R.H. Predicting the natural flow regime: Models for assessing hydrological alteration in streams. River Res. Appl. 2010, 26, 118–136. [Google Scholar] [CrossRef]
- Chaney, N.W.; Wood, E.F.; McBratney, A.B.; Hempel, J.W.; Nauman, T.W.; Brungard, C.W.; Odgers, N.P. POLARIS: A 30-meter probabilistic soil series map of the contiguous United States. Geoderma 2016, 274, 54–67. [Google Scholar] [CrossRef]
- Catani, F.; Lagomarsino, D.; Segoni, S.; Tofani, V. Landslide susceptibility estimation by random forests technique: Sensitivity and scaling issues. Nat. Hazards Earth Syst. Sci. 2013, 13, 2815–2831. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting (with discussion and a rejoinder by the authors). Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, W.; Huang, W.; Hong, Z.; Meng, L. Upscaling of surface soil moisture using a deep learning model with VIIRS RDR. ISPRS Int. J. Geo-Inf. 2017, 6, 130. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M. Spatial nonstationarity and autoregressive models. Environ. Plan. A 1998, 30, 957–973. [Google Scholar] [CrossRef]
- Bernaola-Galván, P.; Ivanov, P.C.; Amaral, L.A.N.; Stanley, H.E. Scale invariance in the nonstationarity of human heart rate. Phys. Rev. Lett. 2001, 87, 168105. [Google Scholar] [CrossRef] [PubMed]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Hamza, A.; Anjum, M.N.; Masud Cheema, M.J.; Chen, X.; Afzal, A.; Azam, M.; Kamran Shafi, M.; Gulakhmadov, A. Assessment of IMERG-V06, TRMM-3B42V7, SM2RAIN-ASCAT, and PERSIANN-CDR precipitation products over the Hindu Kush Mountains of Pakistan, South Asia. Remote Sens. 2020, 12, 3871. [Google Scholar] [CrossRef]
- Sharifi, E.; Saghafian, B.; Steinacker, R. Downscaling satellite precipitation estimates with multiple linear regression, artificial neural networks, and spline interpolation techniques. J. Geophys. Res. Atmos. 2019, 124, 789–805. [Google Scholar] [CrossRef]
- Beck, H.E.; Van Dijk, A.I.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; De Roo, A. MSWEP: 3-hourly 0.25 global gridded precipitation (1979–2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef]
- Zhao, C.; Ren, L.; Yuan, F.; Zhang, L.; Jiang, S.; Shi, J.; Chen, T.; Liu, S.; Yang, X.; Liu, Y. Statistical and hydrological evaluations of multiple satellite precipitation products in the yellow river source region of china. Water 2020, 12, 3082. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, L.; She, D.; Chen, J. Spatial downscaling of tropical rainfall measuring mission (TRMM) annual and monthly precipitation data over the middle and lower reaches of the Yangtze River Basin, China. Water 2019, 11, 568. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin, Germany, 2009; Volume 2. [Google Scholar]
- Tao, Y.; Gao, X.; Hsu, K.; Sorooshian, S.; Ihler, A. A deep neural network modeling framework to reduce BIAS in satellite precipitation products. J. Hydrometeorol. 2016, 17, 931–945. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, J.; Sheng, S.; Mansaray, L.R.; Liu, Z.; Wu, H.; Wang, X. A new downscaling-integration framework for high-resolution monthly precipitation estimates: Combining rain gauge observations, satellite-derived precipitation data and geographical ancillary data. Remote Sens. Environ. 2018, 214, 154–172. [Google Scholar] [CrossRef]






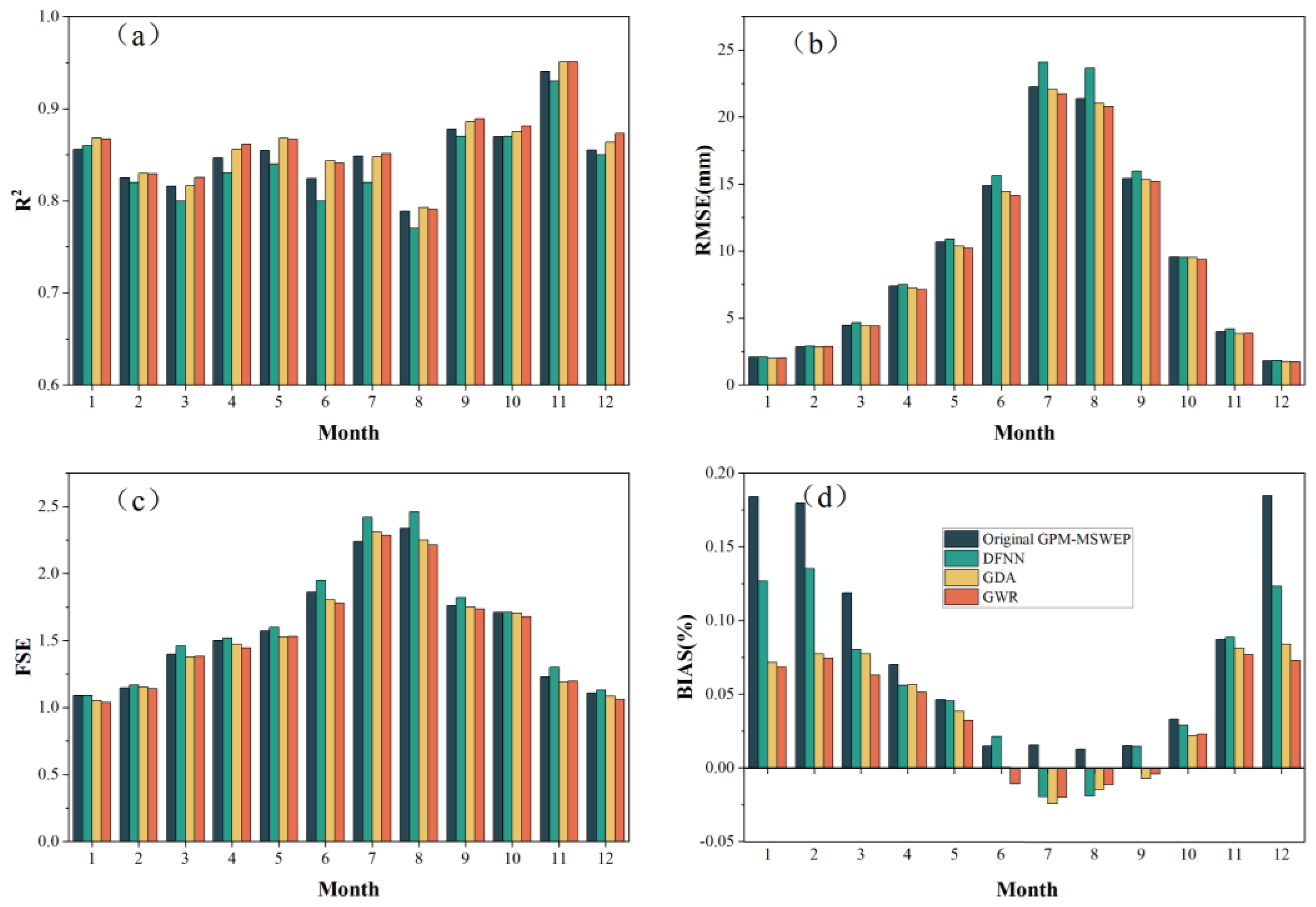




| R2 | RMSE (mm) | FSE | BIAS (%) | |
|---|---|---|---|---|
| Original GPM-MSWEP | 0.92 | 12.54 | 1.98 | 2.4 |
| DFNN | 0.92 | 12.77 | 1.92 | 1.4 |
| GDA | 0.93 | 12.03 | 1.93 | 1.0 |
| GWR | 0.93 | 12.00 | 1.90 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Cui, X.; Cai, Y.; Wu, Z.; Gao, S.; Yu, B.; Wang, Y.; Li, K.; Duan, Z.; Liang, Q. Coupling Downscaling and Calibrating Methods for Generating High-Quality Precipitation Data with Multisource Satellite Data in the Yellow River Basin. Remote Sens. 2024, 16, 1318. https://doi.org/10.3390/rs16081318
Yang H, Cui X, Cai Y, Wu Z, Gao S, Yu B, Wang Y, Li K, Duan Z, Liang Q. Coupling Downscaling and Calibrating Methods for Generating High-Quality Precipitation Data with Multisource Satellite Data in the Yellow River Basin. Remote Sensing. 2024; 16(8):1318. https://doi.org/10.3390/rs16081318
Chicago/Turabian StyleYang, Haibo, Xiang Cui, Yingchun Cai, Zhengrong Wu, Shiqi Gao, Bo Yu, Yanling Wang, Ke Li, Zheng Duan, and Qiuhua Liang. 2024. "Coupling Downscaling and Calibrating Methods for Generating High-Quality Precipitation Data with Multisource Satellite Data in the Yellow River Basin" Remote Sensing 16, no. 8: 1318. https://doi.org/10.3390/rs16081318
APA StyleYang, H., Cui, X., Cai, Y., Wu, Z., Gao, S., Yu, B., Wang, Y., Li, K., Duan, Z., & Liang, Q. (2024). Coupling Downscaling and Calibrating Methods for Generating High-Quality Precipitation Data with Multisource Satellite Data in the Yellow River Basin. Remote Sensing, 16(8), 1318. https://doi.org/10.3390/rs16081318








