Abstract
A regional aerosol model can complement globally averaged models and improve the accuracy of atmospheric numerical models in local applications. This study established a seasonal aerosol model based on data from the Aerosol Robotic Network (AERONET) of the sea area around eastern China, and its performance in calculating the aerosol optical depth (AOD) was evaluated. The seasonal columnar volume particle size distributions (VPSDs) illustrated a bimodal structure consisting of fine and coarse modes. The VPSDs of spring, autumn, and winter roughly agreed with each other, with their amplitudes of fine and coarse modes being almost equal; however, the fine mode of the summer VPSD was approximately twice as high as that of the coarse mode. Lognormal mode decomposition analysis revealed that fine and coarse modes comprised two sub-modes. Fitting the seasonal VPSDs to the four-mode lognormal distribution yielded a parameterized aerosol size distribution model. Furthermore, seasonal variations in complex refractive indices (CRIs) indicated unignorable changes in aerosol compositions. Overall, error analysis validated that the proposed model could meet accuracy requirements for optical engineering applications, with median AOD calculation errors of less than 0.01.
1. Introduction
Aerosols consist of particles suspended in the atmosphere, including dust, inorganic salts, and organic particulate matter, and they play significant roles in multiple research domains, such as climate change, optical engineering, and human health. Aerosols can act as cloud condensation nuclei in cloud formation, expediting the process and subsequently influencing weather [1]. The scatter and absorption effects of aerosols can reduce the signal-to-noise ratio of electro-optical signals, impacting the performance of optoelectronic devices in optical remote-sensing operations [2]. Moreover, environmental aerosols can also significantly influence human health, and prolonged exposure to a high concentration of PM2.5 substantially increases the risk of respiratory diseases [3]. Therefore, developing an accurate aerosol model has long been an atmospheric research hotspot.
Aerosol models in atmospheric numerical simulation tools usually focus on describing the microphysical characteristics of aerosol particle ensembles by distinguishing particle types based on the sources of air masses or their chemical compositions, and providing particle size distribution and refractive indices for various particles. A commonly used aerosol numerical forecast tool, Weather Research and Forecasting with Chemistry (WRF-Chem), includes several aerosol schemes, such as Modal Aerosol Module (MAM) [4]. The main differences among these models lie in the number of aerosol classification types and whether bin-based or modal-based methods describe the aerosol particle size distribution. There are also some standalone aerosol models used for optical engineering applications, such as Optical Properties of Aerosols and Cloud (OPAC), the Navy Aerosol Model (NAM), and the Mediterranean extinction code (MEDEX). OPAC is a software package used to calculate cloud and aerosol optical parameters released by M. Hess, categorizing aerosol particles into 10 types based on sources, size distribution, hygroscopicity, and refractive indices, which allows users to blend different types of aerosol components in proportions, then compute the optical parameters; the latest version of this software is 4.0 [5]. The NAM models aerosol particle size distributions using multiple lognormal distribution modes to describe different aerosol sources, with three basic modes: newly generated marine aerosols, aged sea salt aerosols, and background dust aerosols [6]. Its improved model, MEDEX, depicts aerosol characteristics in coastal areas based on the distance of air masses passing over the sea surface and the wind speed by parameterizing lognormal modes of particle size distribution [7]. In optical-remote-sensing-related research, some aerosol model datasets are commonly used. For example, Xie et al. [8] employed aerosol classification, size distribution, and refractive index data from others’ works in their composition inversion studies.
Although the abovementioned models are usually used to describe globally averaged aerosol conditions, their databases were mainly obtained from near-surface observation experiments in North America and Europe [9], which leads to a problem in that regional aerosol characteristics often deviate from global counterparts [10]. A zonal aerosol model might provide higher accuracy when dealing with local research. Cattrall et al. pointed out that considering vicinal-sourced black carbon aerosols can enhance the aerosol inversion accuracy of spaceborne lidar [11]. Shi et al. [12] improved the precision of MODIS aerosol inversion products in eastern China by establishing an area-specific aerosol model based on AERONET observations. Even for marine aerosols, a relatively stable type of aerosol, characteristics varied significantly among different oceans; for example, the cloud condensation nuclei concentration in the Pacific Ocean was much greater than that in the Arctic Ocean [13].
However, there are few aerosol models specifically tailored to the area around China, and most researchers have paid attention to inland regions [14]. For the surrounding sea areas, the majority of scholars have focused more on the analysis of variations in aerosol properties [15] by analyzing aerosol components, size distribution, sources, or the evolution of other microphysical parameters [16], with only a few summarizations from the perspective of optical utilizations in the South China Sea [17]. Therefore, this paper aims to establish a regional model suitable for describing the basic characteristics of aerosols in the eastern waters around China for optical engineering applications. The data products and the processing methods used in the study are introduced in Section 2. Section 3 delineates the characteristics of local aerosols and the aerosol model based on them, while a performance assessment of the proposed model is presented in Section 4.
2. Data and Method
2.1. AERONET Data
AERONET is a global confederation network of ground-based aerosol monitoring led by the National Aeronautics and Space Administration (NASA) and equipped with CE-318 sun photometers, manufactured by a French company in Paris, CIMEL Electronique. AERONET conducts observations from the ultraviolet to the near-infrared band, and performs multi-angle sky radiance measurements to retrieve columnar aerosol parameters based on the scatter effect of aerosols. The critical parameters of the inversion product are the VPSD and CRI [18]. AERONET provides three levels of data products—Level 1.0, Level 1.5, and Level 2.0—as unfiltered data, cloud-screened and quality-controlled data, and quality-assured products, respectively [19]. The presented work used Level 2.0 data produced by the version 3 retrieval algorithm [20], comprising the AOD, VPSD, and CRI. AOD at the wavelength of 550 nm was interpolated by the nearest available spectral AOD and Ångström Exponent [21] for the convenience of utilization and evaluation, since 550 nm AOD is a commonly used indicator in optical engineering [5]. There are two types of operation modes in AERONET: direct sun measurement and sky measurement [22]. Direct sun measurements are performed at standard 15 min intervals, and almucantar sky measurements are performed about eight times a day, from which the AOD and inversion product were obtained, respectively.
The sea area around eastern China includes various large cities in China, Korea, and Japan. The local aerosol is inevitably influenced by anthropogenic emissions, resulting in a spatial distribution pattern wherein aerosol concentrations over the sea are related to the offshore distance from the coast [23]. Five island sites of AERONET in the region were selected, listed in Table 1 and Figure 1, because of the lower impact of terrestrial aerosols compared to the coastal sites, which can better characterize the marine background aerosol. As shown in Figure 1, the five selected sites are scattered from north to south in the area, marked by red five-pointed stars labeled with names. The selected dataset contains over one hundred thousand AOD spectra and more than three thousand VPSDs, as detailed in Table 1. CRIs were provided with VPSDs in the inversion product of AERONET. The observations from these sites span a long period. Baengnyeong Station, for instance, has provided measurements for over 10 years, and is still being updated. In general, the selected dataset is adequate to describe regional aerosol features.

Table 1.
AERONET site information.
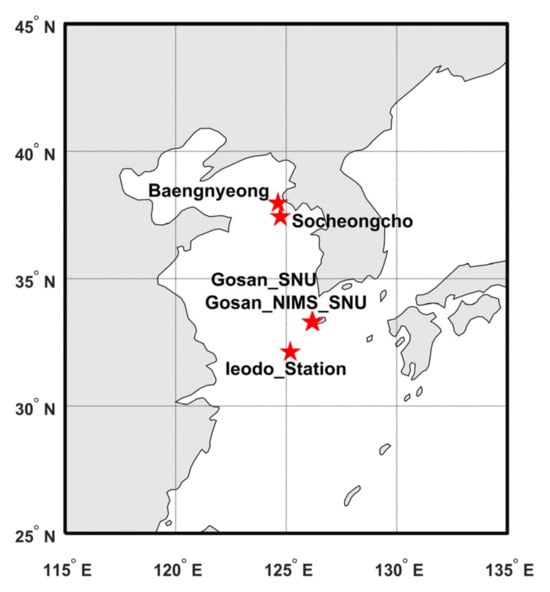
Figure 1.
Location of selected AERONET sites. Each red star represents one station and is labeled with the site name, except Gosan_SNU Station and Gosan_NIMS_SNU Station. These two stations are located on the same island, Gosan Island.
Because of the monsoonal characteristics of the local climate, VPSDs from selected AERONET sites were averaged to seasonal mean values that can represent the basic status of regional aerosols. To overcome the influence caused by the uneven temporal distribution of VPSD data, averaging was performed by calculating daily mean VPSDs and then obtaining monthly and seasonal mean results step-by-step. Although the counts of VPSDs among different seasons varied seriously, the results of the analysis mentioned after might still be valuable for AERONET’s relatively extended temporal coverage in the study area. CRIs followed the same process procedure as for VPSDs. AOD data served as the validation bases in this paper. The regional mean aerosol model obtained in Section 3 was used to calculate the AOD spectra, and comparisons were made between the calculated AOD and the measured counterparts.
2.2. Aerosol Model
The practical aerosol model in atmosphere-related optical applications consists of two key parameters: size distribution and complex refractive indices. Based on these two parameters, the optical properties can be estimated using Mie code calculations. In the aerosol model in OPAC, for instance [5], the size distribution was described by lognormal functions, and the complex refractive indices were obtained from the existing dataset based on aerosol components. This research followed the same method to establish a local aerosol model for optical applications.
The lognormal distribution function is often employed to describe the number concentration size distribution of aerosols [6], such as in Equation (1), where is the amount of modes, is the amplitude of the th mode, denotes the width, and signifies the mode radius. Different types of aerosols possess distinct modal parameters in OPAC [5]. As an example, the VPSD of black carbon aerosols has a single mode with a mode radius of 0.05 µm, while that of sea salt aerosols consists of two modes with mode radii of 0.94 µm and 7.9 µm. Marine aerosols were treated the same way in NAM, representing VPSDs using three or more modes assigned to different generation mechanisms [6]. The presented work adopted a modal decomposition method suggested by Cuesta et al. [24] to analyze the number of modes in VPSDs, which utilized the features of the second derivative of Gaussian functions.
The aerosol extinction coefficient can be computed from Mie theory, shown as Equation (2), where represents the extinction coefficient at the wavelength of , is the extinction efficiency factor obtained by means of Mie theory, and stands for the CRI at . The spectral CRIs were also retrieved in the inversion product of AERONET. The refractivity of local aerosol can reveal the composition variations, which are essential in evaluating optical characteristics.
The size distribution provided by AERONET is the volume size distribution, and the conversion to number concentration size distribution follows Equation (3). Observations from selected sites were averaged to obtain the seasonal VPSDs and CRIs for the area, and a model suitable for atmospheric optical engineering applications was established and evaluated based on AOD spectra acquired at the same sites.
2.3. Size Distribution Mode Decomposition
As mentioned above, the aerosol size distribution can be described using multiple lognormal modes. The mode parameters may be related to ambient meteorological conditions, like that in MEDEX [7]. It would be useful to separate VPSDs into appropriate modes because this might be the starting point for further analysis.
However, no widely accepted criterion for determining the required number of modes is currently available. The commonly used approach is to evaluate the goodness of fit for size distributions by statistical indicators obtained with different numbers of modes [25]. The selection of the value range of mode parameters is often based on empirical considerations, like the fitting scheme proposed by Hussein et al. [26]. To reconcile this arbitrariness, Cuesta et al. [24] proposed a method based on the characteristics of the second derivative of Gaussian curves to determine the number of modes and initial values of every mode parameter; the basic logic is illustrated in Figure 2.
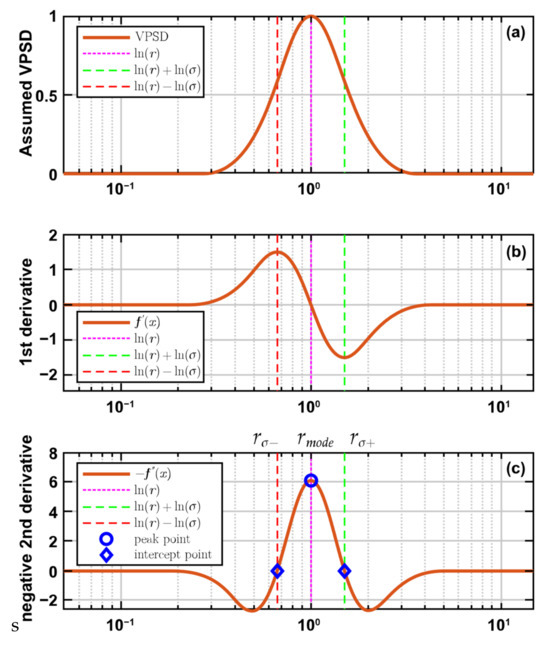
Figure 2.
Lognormal mode decomposition method. (a) Simulated single peak Gauss curve; (b) First derivative of simulated curve in (a); (c) Negative second derivative of simulated curve in (a).
Figure 2a shows the simulated aerosol size distribution curve, a single-peak Gauss curve. Figure 2b,c shows the first and negative second derivatives of the simulated curve in Figure 2a. The solid purple vertical line marks the mode radius of the lognormal mode peak, and the dashed lines on both sides mark the width of the simulated mode peak. The key idea of this method is that the number of modes can be estimated by the number of peaks of negative second derivatives. As for mode parameters, the mode radius can be guessed by the corresponding location of peaks, and the mode width can be obtained by the distance between the position of peaks and the zero points of the negative second derivative curve. Using the estimations of mode parameters as initial values, least square fitting can easily be performed to obtain fitted VPSDs.
3. Regional Aerosol Model
The climate of eastern Asia is a typical monsoonal climate; the Asian continent is under the control of the Siberian cold high-pressure systems during winter, while warm low-pressure systems control the mainland in summer, causing the north and northwest winds to prevail in the oceanic regions of eastern Asia in winter and the opposite wind directions to predominate in summer. Combined with the transition periods between them, the local climate exhibits a complete annual cycle [27]. Marine aerosols are significantly influenced by meteorological parameters such as wind speed [28], sea surface temperature [29], and humidity [30]. These influencing factors show distinct seasonal variations in the monsoonal zone, consequently driving the seasonal tendencies of aerosol parameters [31]. The season definition in this paper follows the meteorological convention, as the spring includes March, April, and May.
3.1. Seasonal Aerosol Model
Normalizing the aerosol size distribution before analysis is common in engineering applications [5]. A comparison among the seasonal averaged normalized VPSD of each station is shown in Figure 3, while subfigures a–d show the four seasons, respectively. The standard deviations of VPSDs are not shown in Figure 3 for conciseness, and the mean VPSD curves are situated well within the range marked by standard deviations.
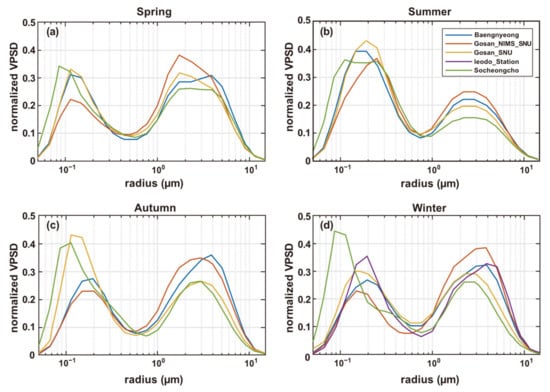
Figure 3.
Seasonal average VPSDs for each site. (a–d) were mean VPSDs for spring, summer, autumn, and winter, respectively.
Although the chosen sites were scattered at some distance in the Yellow Sea, their seasonal mean VPSDs showed many consistencies. The typical bimodal patterns can be observed in all seasonal mean VPSDs. Using the comparison between sites’ mean VPSDs of the same season, the categorization of aerosols into seasonal ones can be justified. The differences in mean VPSDs among stations were minor in spring and summer, as the positions and amplitudes of VPSD peaks did not vary severely. Though a slight shift of fine mode peak positions can be observed among sites’ VPSDs in autumn and winter, shown in Figure 3c,d, the deviations of the radius location of fine mode peaks were small. The shifted fine modes suggest the appearance of smaller particles, such as black carbon from North China [8,32], which is an indicator of pollution [33]. The amplitudes of both fine and coarse mode peaks of VPSDs in these two seasons were similar to those in spring and summer. Based on these comparisons, there were fewer differences among sites’ mean VPSDs in the same season, which indicates the feasibility of modeling the regional aerosol VPSD as a whole.
The CRI spectra of every season are illustrated in Figure 4 (the real part) and Figure 5 (the imaginary part); the error bars indicate standard deviations, and slight offsets in the wavelength of spectral CRI are added for distinctness. The real part of CRI (RCRI) can be used to describe the scattering effect of aerosols, and the imaginary part depicts the absorption ability. As shown in Figure 4, the spectral tendencies of RCRI from different stations are close in the same season. Considering the accuracy of RCRI inversion—about 0.04 [8]—and the standard deviations together, the aerosols in the study region can be modeled as a whole if we only focus on its macroscopical effects in optical engineering. This is because the gaps between spectral seasonal mean RCRI are slightly lower than 0.04, and the mean values are situated well inside the range of each other site’s standard deviations. Using such a preliminary quantitative baseline for establishing a general model is a good starting point, and the performance evaluation of the proposed model in Section 4 verifies the practicability of this criterion. Although the imaginary part of CRI (ICRI) illustrated greater variations and deviations, as shown in Figure 5, it can roughly be treated as having similar optical effects in the same season under this criterion.
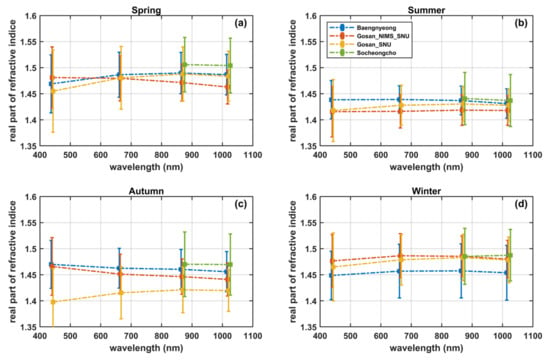
Figure 4.
Seasonal average of the real part of refractive indices for each site. (a–d) were mean RCRIs for spring, summer, autumn, and winter, respectively.
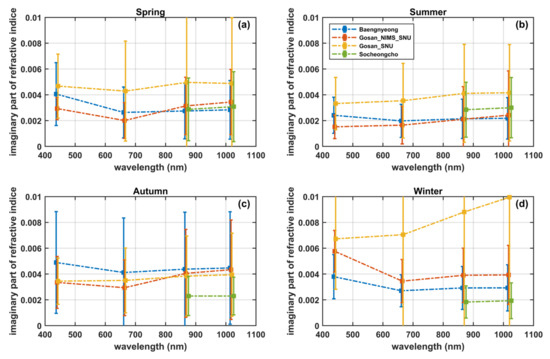
Figure 5.
Seasonal average of the imaginary part of refractive indices for each site. (a–d) were mean ICRIs for spring, summer, autumn, and winter, respectively.
The regional average seasonal VPSDs are illustrated in Figure 6a, and a reasonably stable mean status of local aerosol can be observed. The VPSDs of spring, autumn, and winter are close to each other, with only a tiny shift of both fine and coarse mode peaks in the VPSD of spring toward the direction of a smaller radius; the amplitudes of both peaks in VPSDs of these three seasons were roughly equal. The fine mode peaks of the VPSD in summer were almost twice as high as that of the corresponding coarse mode, though their radius locations were still close to that of VPSDs in other seasons.
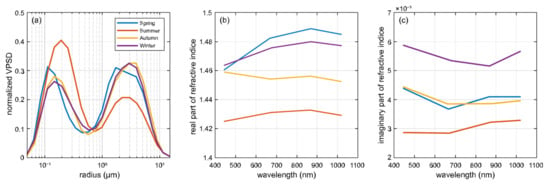
Figure 6.
Variation in local aerosol VPSDs and refractive indices across seasons. (a–c) were the comparison of seasonal VPSDs, RCRIs, and ICRIs in the whole area among different seasons, respectively.
The seasonally averaged CRI spectra are shown in Figure 6b,c, with Figure 6b indicating RCRI and Figure 6c indicating ICRI. The spectral dependencies of RCRI are similar in spring, summer, and winter, and the aerosol can refract light a little more efficiently in the visible band than in the ultraviolet (UV) band or near-infrared (NIR) band. In autumn, the spectral trend became monotonic, decreasing toward the infrared band. The differences in RCRI spectral trends, while the values of RCRI do not vary significantly, might suggest that the ratio of compositions changed while the species number remained more or less stable. The RCRI in summer was lowest, which may be due to the much cleaner ambient aerosol environment when this region received more precipitation in rainy periods of the monsoonal climate, and the relatively high atmospheric water vapor content and its uniformly distributed spectral RCRI with low values could cause the overall downward movement of the spectral RCRI curve [31]. The monotonic decreasing trend of the autumn RCRI spectrum suggests an increased ratio of highly refractive substances in the UV band, like sea salt and dust [8].
The spectra of seasonal ICRI illustrated in Figure 6c are concave, as the absorptions in the visible band were weaker than those in the UV and NIR bands for all seasons except for winter. The lowest absorption in winter occurred in the NIR band. The spectral ICRI of the summer was the lowest, and that of winter was the highest, while those of spring and autumn were medium and had roughly the same values. The high value of the imaginary part indicated pollution conditions in winter for the highly absorbing aerosols, which might be related to localized pollution sources such as North China [32,34,35]. The spectral curve of ICRI moved upwards synchronously, although there were slight discrepancies in spectral distributions as the time passed from summer to winter, implying changes in pollution compositions [36]. In spring, the absorption weakened, but the refraction did not decrease together, which could probably result from the intrusion of dust, one of the most highly refractive aerosols, taking the characteristics of regional climate into account [37]. Furthermore, it is worth noting that optical remote sensing could only provide rough estimations on composition variations; the detail analysis should include chemical measurements.
Generally, the comparisons of the seasonally averaged VPSD and CRI from selected sites in the same season demonstrated the reasonability of treating the aerosols in the study region as a whole in optical applications. The differences between the seasonal VPSD and CRI showed different characteristics of local aerosols, which can easily be utilized in optical applications.
3.2. Size Distribution Mode Decomposition
The aerosol model for optical usage consists of two key parameters: size distribution and complex refractive indices. The size distribution can be simplified by using modal representations such as Equation (1). AERONET divides VPSDs into coarse and fine modes [18], but studies have shown that some sub-modes exist, and using a multi-mode modal could benefit the analysis [38]. The modal decomposition method suggested by Cuesta et al. [24] was used to analyze the seasonal VPSDs obtained in Section 3.1; the least square fitting results are illustrated in Table 2 and Figure 7, where Figure 7 demonstrates the curve of each mode of the lognormal distribution, and Table 2 exhibits the values of modal parameters.

Table 2.
Mode parameters of fitted normalized VPSDs. The variables are defined as Equation (1), subscripts refer to corresponding mode, is the amplitude of the th mode, denotes the mode width, and signifies the mode radius. Units of and are μm. All modes are sequentially illustrated in Figure 7 as dashed lines with different colors.
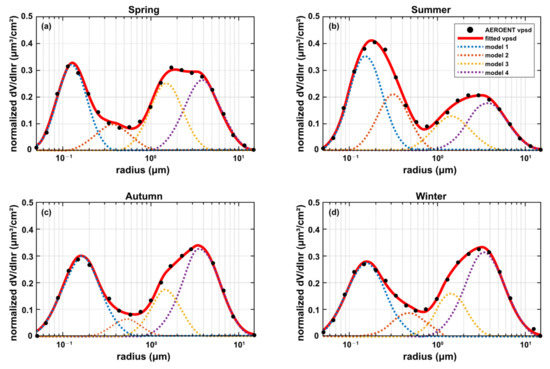
Figure 7.
Fitting result of seasonal VPSDs. (a–d) represents VPSD in spring, summer, autumn, and winter, respectively.
All seasonal VPSDs comprise four modes, and fine and coarse modes comprise two sub-modes. The inter-seasonal fluctuations of modal parameters are different; the first, third, and fourth modes were more stable than the second mode. The modal radius of the second mode could change from 0.31 μm to 0.53 μm, in contrast to the somewhat uniform range of variations for the first, third, and fourth modes, varying about 0.01 μm—around 0.15 μm, 1.45 μm, and 3.7 μm, respectively. The modal width of all modes shifted less compared to the modal radii, staying within 0.1 μm. The modal amplitudes showed the most obvious fluctuation among all modal parameters. The height of the first mode deviated the least from its mean value (about 0.35), and the third and fourth modes were more variable, with the third mode being nearly 50% higher in spring than that of other seasons. The fourth mode showed a similar tendency, but for autumn and winter. The second mode’s amplitude peaked in summer and was almost twice as high as autumn’s.
The number of lognormal modes did not necessarily have a strict physical meaning, but it could still reveal some physical realities of local aerosols. For example, the most stable mode, the first mode, may characterize mixing compositions of fine dust-like particles at higher altitudes with longer residence times and aged marine background aerosols no longer governed by current meteorological factors [6]. The AERONET observations were columnar measurements, which undoubtedly included information on such background aerosol particles. The mode radii of the first mode resolved from VPSD here were about 0.15 μm, which could be converted to about 0.08 μm for the corresponding mode of the number size distribution according to the method in Section 2.1.4.2 of [39]. This mode’s radius differed from that of the background dust-like component in NAM [6], the value of which was 0.03 μm. This might be because of the lower accuracy in inverting VPSDs in such a fine particle radius [18,40]. Still, AERONET can provide valuable long-term aerosol monitoring, especially for aerosol climatology. The mode parameters here could be an entry point for further analysis of meteorological controlling factors concerning aerosol types.
4. Evaluation
The aerosol extinction coefficient can be obtained using Mie code calculation based on the size distributions and CRI, as shown in Equation (2). If the VPSD is normalized, the calculation results can only represent the relative spectral tendency. In that case, the extinction coefficient at an arbitrary wavelength, , is usually normalized to that at 550 nm [5], i.e., , and . This kind of relative extinction coefficient spectrum is traditionally stored in atmospheric optical software as the intermediate result of the aerosol model to reduce computation. In applications, the measured extinction coefficient at 550 nm, , is required as a scale factor, and modal results of the extinction coefficient at any wavelength can be calculated as .
AOD is the integral of the extinction coefficient along the altitude. The AERONET inversion algorithm assumed a vertical homogeneous atmosphere, and the retrieved VPSD was a columnar parameter. The extinction coefficients obtained by the retrieved VPSD represent the columnar attenuation ability, which conforms to the definition of AOD. The evaluation of the proposed model was carried out by comparing the AOD spectrum calculation results, and the spectral residuals were analyzed to illustrate the capability of this model. The spectral AOD was computed using the corresponding seasonal VPSD and CRI according to the time that the measured AOD spectrum was acquired.
The aerosol model obtained in Section 3 was processed similarly, and its performance was evaluated based on AOD spectra measured from the same sites listed in Table 1. To depict the error of the proposed model when calculating AOD, the median and the quartile of residuals were adopted, and its probability density curves at specific wavelengths were also analyzed. All measured AOD spectra were retained to keep the test dataset as large as possible. The CRI in the AERONET inversions covered only four wavelengths within the range of 440–1020 nm; therefore, the real part and imaginary part of the refractive indices were linearly interpolated or extrapolated to the wavelengths at which AOD was measured. The median of AOD residuals and the 25% and 75% quartiles are shown in Figure 8a; probability density curves at six specific wavelengths are illustrated in Figure 8b. Generally, the wavelength combination of 440/675/870/1020 nm was used in sky radiance measurements, but 443/667/870/1020 nm were used in Ieodo Station and Socheongcho Station, so all six wavelengths’ probability densities were examined.
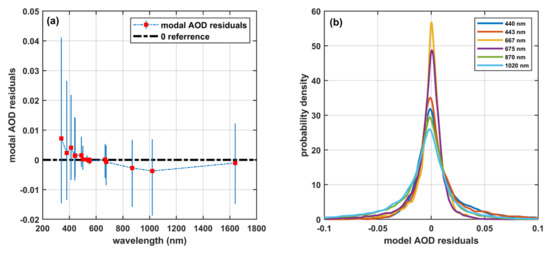
Figure 8.
Performance evaluation of the proposed model. (a) The median of residuals of AOD calculated by the proposed regional aerosol model; (b) The probability density of AOD error at several wavelengths.
As shown in Figure 8a, the median of the spectral AOD residuals (red dots) lay within ±0.01, which was similar to the AOD measurement accuracy of the CE-318 sun photometer [18]. In the UV band shorter than 400 nm, the upper quartile exceeded 0.04 (at 340 nm), while the lower quartile was greater than −0.02, which indicated the tendency of this model to overestimate AOD at the UV band. In the visible and NIR band, the medians of residuals were close to the zero reference line, and both upper and lower quartiles were near ±0.01, suggesting that the presented model could calculate AOD with accuracy similar to the sun photometer. All probability density curves in Figure 8b appeared Gaussian-like, showing only a single peak near zero and apparent symmetry. The similarity of probability density curves to Gaussian curves indicated that the errors of the proposed model in AOD calculations followed normal-like distributions, which implied that the model errors were close to naturally random errors. The statistics from probability density curves showed that, in most cases, the deviations of modeled AOD from actual values were close to zero. In about 70% of cases, the AOD errors were located within ±0.02. Combining the median and probability density of AOD errors, the proposed model can represent the mean status of regional aerosols.
5. Conclusions
This paper established a regional aerosol model for optical applications of the sea area around eastern China based on long-term observations from AERONET, by analyzing the characteristics of seasonal changes of aerosol microphysical parameters. The performance of the proposed model was evaluated, and the results illustrated the model’s good ability in AOD calculation.
The sea area around eastern China is a monsoonal climate zone; the meteorological parameters have periodic changes, which force the regional aerosol parameters to vary seasonally. The VPSDs of spring, autumn, and winter were close, with roughly equal high peaks in fine and coarse modes; but in summer, the amplitude of the fine mode was significantly higher, almost twice as high as that of the coarse mode. The real and imaginary parts of the CRI were both low in summer and gradually increased in autumn and winter with spectral synchronies. However, the imaginary part fell back in spring, while the real part climbed higher. These seasonal variations indicated significant changes in local aerosol compositions.
The VPSDs of all four seasons showed bimodal patterns, and each peak consisted of two sub-modes in the analysis of modal decomposition. Fitting the seasonal VPSDs to four modes of a lognormal function resulted in a simplified model that is easy to store. The modal parameters of the first mode were stable, and those of the third and fourth modes showed seasonal fluctuations. In contrast, more significant variations in the modal parameters of the second mode could be observed. Combined with the seasonal VPSDs and CRI, the AOD spectrum could be computed using the presented model. Evaluations validated that the accuracy of this model was adequate for use in optical applications, with comparable accuracy to sun photometers.
The regional aerosol model can be treated as a supplement to global models to improve the reliability of the numerical atmospheric model when applied locally. This research demonstrated a relatively simple way to establish a regional aerosol model, whereby the local climate pattern can be a clue for aerosol categorization, like the seasonal separation of aerosol for monsoonal climate areas in this paper. Moreover, gaining insight into the physical processes involved in aerosol changes is necessary to accurately characterize regional aerosols. The model presented here could be an entry point for relevant research, such as finding why the modal parameters of the second mode of seasonal VPSDs varied much more significantly than other modes, which might facilitate an understanding of local aerosol evolutions.
Author Contributions
S.C. (Shunping Chen) processed all data and organized the manuscript; C.D. provided original suggestions and funding support; N.L. provided the basic idea and part of the data analysis; W.L. and Y.Z. assisted in data processing; F.W. and C.Z. contributed to creating data visualizations; S.C. (Shengcheng Cui) and H.W. reviewed and edited the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
The National Key Research and Development Program of China (2019YFA0706004); the HFIPS Director’s Foundation (YZJJ2022QN06); the Independent Scientific Research Project of Nanhu Laser Laboratory (Grant No. 22-NHLL-ZZKY-005).
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request. The data are not publicly available due to privacy.
Acknowledgments
The authors would like to thank the (PI(s) and Co-I(s)) and their staff for establishing and maintaining the sites of AERONET used in this investigation, as well as Christian Mätzler for the MATLAB functions of Mie calculations. The authors acknowledge the editor’s and referees’ efforts in improving this manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, J.; Shilling, J.E.; Liu, J.; Zelenyuk, A.; Bell, D.M.; Petters, M.D.; Thalman, R.; Mei, F.; Zaveri, R.A.; Zheng, G. Cloud droplet activation of secondary organic aerosol is mainly controlled by molecular weight, not water solubility. Atmos. Chem. Phys. 2019, 19, 941–954. [Google Scholar] [CrossRef]
- Tan, W.; He, H.; Chen, X.; Qi, W.; Liu, J.; Wang, Y.; Ling, Z.; Sun, Y.; Jin, D. Analyzing the influence of atmosphere on optical remote sensing in 400 to 2500 nm wavelength spectrum. In AOPC 2020: Optical Spectroscopy and Imaging; and Biomedical Optics; SPIE: New York, NY, USA, 2020; Volume 11566, pp. 103–108. [Google Scholar]
- Contini, D.; Lin, Y.-H.; Hänninen, O.; Viana, M. Contribution of Aerosol Sources to Health Impacts. Atmosphere 2021, 12, 730. [Google Scholar] [CrossRef]
- Liu, X.; Easter, R.C.; Ghan, S.J. Toward a minimal representation of aerosol direct and indirect effects: Model description and evaluation. Geosci. Model Dev. 2012, 5, 709–735. [Google Scholar] [CrossRef]
- Hess, M.; Koepke, P.; Schult, I. Optical Properties of Aerosols and cloud: The Software Package OPAC. Bull. Am. Meteorol. Soc. 1998, 79, 831–844. [Google Scholar] [CrossRef]
- Van Eijk, A.M.J.; Kusmierczyk-Michulec, J.T.; Piazzola, J.J. The Advanced Navy Aerosol Model (ANAM): Validation of small-particle modes. In Proceedings of the SPIE Optical Engineering + Applications, San Diego, CA, USA, 21–25 August 2011; pp. 816108–816109. [Google Scholar]
- Piazzola, J.; Bouchara, F.; de Leeuw, G.; Van Eijk, A.M.J. Development of the Mediterranean extinction code (MEDEX). Opt. Eng. 2003, 42, 912–924. [Google Scholar] [CrossRef]
- Xie, Y.S.; Li, Z.Q.; Zhang, Y.X.; Zhang, Y.; Li, D.H.; Li, K.T.; Xu, H.; Zhang, Y.; Wang, Y.Q.; Chen, X.F.; et al. Estimation of atmospheric aerosol composition from ground-based remote sensing measurements of Sun-sky radiometer. J. Geophys. Res.-Atmos. 2017, 122, 498–518. [Google Scholar] [CrossRef]
- Tombette, M.; Sportisse, B. Aerosol modeling at a regional scale: Model-to-data comparison and sensitivity analysis over Greater Paris. Atmos. Environ. 2007, 41, 6941–6950. [Google Scholar] [CrossRef]
- Zhou, P.; Wang, Y.; Liu, J.; Xu, L.; Chen, X.; Zhang, L. Difference between global and regional aerosol model classifications and associated implications for spaceborne aerosol optical depth retrieval. Atmos. Environ. 2023, 300, 119674. [Google Scholar] [CrossRef]
- Cattrall, C.; Reagan, J.; Thome, K.; Dubovik, O. Variability of aerosol and spectral lidar and backscatter and extinction ratios of key aerosol types derived from selected Aerosol Robotic Network locations. J. Geophys. Res.-Atmos. 2005, 110, 15. [Google Scholar] [CrossRef]
- Shi, Y.R.; Levy, R.C.; Yang, L.; Remer, L.A.; Mattoo, S.; Dubovik, O. A Dark Target research aerosol algorithm for MODIS observations over eastern China: Increasing coverage while maintaining accuracy at high aerosol loading. Atmos. Meas. Tech. 2021, 14, 3449–3468. [Google Scholar] [CrossRef]
- Park, J.; Dall’Osto, M.; Park, K.; Gim, Y.; Kang, H.J.; Jang, E.; Park, K.-T.; Park, M.; Yum, S.S.; Jung, J.; et al. Shipborne observations reveal contrasting Arctic marine, Arctic terrestrial and Pacific marine aerosol properties. Atmos. Chem. Phys. 2020, 20, 5573–5590. [Google Scholar] [CrossRef]
- Fan, Y.; Sun, X.; Huang, H.; Ti, R.; Liu, X. The primary aerosol models and distribution characteristics over China based on the AERONET data. J. Quant. Spectrosc. Radiat. Transf. 2021, 275, 107888. [Google Scholar] [CrossRef]
- Pani, S.K.; Huang, H.-Y.; Wang, S.-H.; Holben, B.N.; Lin, N.-H. Long-term observation of columnar aerosol optical properties over the remote South China Sea. Sci. Total Environ. 2023, 905, 167113. [Google Scholar] [CrossRef]
- Lim, Y.-K.; Kim, J.; Lee, H.C.; Lee, S.-S.; Cha, J.-W.; Ryoo, S.B. Aerosol Physical Characteristics over the Yellow Sea During the KORUS-AQ Field Campaign: Observations and Air Quality Model Simulations. Asia-Pac. J. Atmos. Sci. 2019, 55, 629–640. [Google Scholar] [CrossRef]
- Pan, Y.; Cui, S.; Rao, R. A Model for Predicting Coastal Aerosol Size Distributions in Chinese Seas. Earth Space Sci. 2020, 7, 11. [Google Scholar] [CrossRef]
- Dubovik, O.; King, M.D. A flexible inversion algorithm for retrieval of aerosol optical properties from Sun and sky radiance measurements. J. Geophys. Res.-Atmos. 2000, 105, 20673–20696. [Google Scholar] [CrossRef]
- Che, Y.; Yu, B.; Parsons, K.; Desha, C.; Ramezani, M. Evaluation and comparison of MERRA-2 AOD and DAOD with MODIS DeepBlue and AERONET data in Australia. Atmos. Environ. 2022, 277, 119054. [Google Scholar] [CrossRef]
- Sinyuk, A.; Holben, B.N.; Eck, T.F.; Giles, D.M.; Slutsker, I.; Korkin, S.; Schafer, J.S.; Smirnov, A.; Sorokin, M.; Lyapustin, A. The AERONET Version 3 aerosol retrieval algorithm, associated uncertainties and comparisons to Version 2. Atmos. Meas. Tech. 2020, 13, 3375–3411. [Google Scholar] [CrossRef]
- Sayer, A.M.; Smirnov, A.; Hsu, N.C.; Holben, B.N. A pure marine aerosol model, for use in remote sensing applications. J. Geophys. Res.-Atmos. 2012, 117, 25. [Google Scholar] [CrossRef]
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanré, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A Federated Instrument Network and Data Archive for Aerosol Characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Kim, J.H.; Yum, S.S.; Lee, Y.G.; Choi, B.C. Ship measurements of submicron aerosol size distributions over the Yellow Sea and the East China Sea. Atmos. Res. 2009, 93, 700–714. [Google Scholar] [CrossRef]
- Cuesta, J.; Flamant, P.H.; Flamant, C. Synergetic technique combining elastic backscatter lidar data and sunphotometer AERONET inversion for retrieval by layer of aerosol optical and microphysical properties. Appl. Opt. 2008, 47, 4598–4611. [Google Scholar] [CrossRef] [PubMed]
- Taylor, M.; Kazadzis, S.; Gerasopoulos, E. Multi-modal analysis of aerosol robotic network size distributions for remote sensing applications: Dominant aerosol type cases. Atmos. Meas. Tech. 2014, 7, 839–858. [Google Scholar] [CrossRef]
- Hussein, T.; Dal Maso, M.; Petäjä, T.; Koponen, I.K.; Paatero, P.; Aalto, P.P.; Hämeri, K.; Kulmala, M. Evaluation of an automatic algorithm for fitting the particle number size distributions. Boreal Environ. Res. 2005, 10, 337. [Google Scholar]
- He, H.L.; Song, J.B.; Bai, Y.F.; Xu, Y.; Wang, J.J.; Bi, F. Climate and extrema of ocean waves in the East China Sea. Sci. China-Earth Sci. 2018, 61, 980–994. [Google Scholar] [CrossRef]
- Ganguly, D.; Raman, M. Estimating the Wind Dependency of Aerosol Optical Depth at Remote Oceanic Regions. Mar. Geod. 2023, 46, 359–375. [Google Scholar] [CrossRef]
- Liu, S.; Liu, C.-C.; Froyd, K.D.; Schill, G.P.; Murphy, D.M.; Bui, T.P.; Dean-Day, J.M.; Weinzierl, B.; Dollner, M.; Diskin, G.S.; et al. Sea spray aerosol concentration modulated by sea surface temperature. Proc. Natl. Acad. Sci. USA 2021, 118, 6. [Google Scholar] [CrossRef]
- Liu, N.; Luo, T.; Han, Y.; Yang, K.; Zhang, K.; Wu, Y.; Weng, N.; Li, X. Analysis of the atmospheric visibility influencing factors under sea–land breeze circulation. Opt. Express 2022, 30, 7356. [Google Scholar] [CrossRef]
- Shen, X.; Bilal, M.; Qiu, Z.; Sun, D.; Wang, S.; Zhu, W. Long-term spatiotemporal variations of aerosol optical depth over Yellow and Bohai Sea. Environ. Sci. Pollut. Res. 2019, 26, 7969–7979. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Yu, G.-H. Absorption properties and size distribution of aerosol particles during the fall season at an urban site of Gwangju, Korea. Environ. Eng. Res. 2019, 24, 159–172. [Google Scholar] [CrossRef]
- Wang, F.; Feng, T.; Guo, Z.; Li, Y.; Lin, T.; Rose, N.L. Sources and dry deposition of carbonaceous aerosols over the coastal East China Sea: Implications for anthropogenic pollutant pathways and deposition. Environ. Pollut. 2019, 245, 771–779. [Google Scholar] [CrossRef] [PubMed]
- Guan, X.; Wang, M.; Du, T.; Tian, P.; Zhang, N.; Shi, J.; Chang, Y.; Zhang, L.; Zhang, M.; Song, X.; et al. Wintertime aerosol optical properties in Lanzhou, Northwest China: Emphasis on the rapid increase of aerosol absorption under high particulate pollution. Atmos. Environ. 2021, 246, 118081. [Google Scholar] [CrossRef]
- Park, S.; Kim, S.-W.; Lin, N.-H.; Pani, S.K.; Sheridan, P.J.; Andrews, E. Variability of Aerosol Optical Properties Observed at a Polluted Marine (Gosan, Korea) and a High-altitude Mountain (Lulin, Taiwan) Site in the Asian Continental Outflow. Aerosol Air Qual. Res. 2019, 19, 1272–1283. [Google Scholar] [CrossRef]
- Schuster, G.L.; Dubovik, O.; Arola, A. Remote sensing of soot carbon—Part 1: Distinguishing different absorbing aerosol species. Atmos. Chem. Phys. 2016, 16, 1565–1585. [Google Scholar] [CrossRef]
- Kai, Z.; Huiwang, G. The characteristics of Asian-dust storms during 2000-2002: From the source to the sea. Atmos. Environ. 2007, 41, 9136–9145. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.; Xu, H.; Li, K.; Dubovik, O.; Goloub, P. The Fundamental Aerosol Models Over China Region: A Cluster Analysis of the Ground-Based Remote Sensing Measurements of Total Columnar Atmosphere. Geophys. Res. Lett. 2019, 46, 4924–4932. [Google Scholar] [CrossRef]
- Lewis, E.R.; Schwartz, S.E. Sea Salt Aerosol Production: Mechanisms, Methods, Measurements, and Models; American Geophysical Union: Washington, DC, USA, 2004; Volume 152. [Google Scholar]
- Dubovik, O.; Smirnov, A.; Holben, B.N.; King, M.D.; Kaufman, Y.J.; Eck, T.F.; Slutsker, I. Accuracy assessments of aerosol optical properties retrieved from Aerosol Robotic Network (AERONET) Sun and sky radiance measurements. J. Geophys. Res. Atmos. 2000, 105, 9791–9806. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).