LEO Satellite Downlink Distributed Jamming Optimization Method Using a Non-Dominated Sorting Genetic Algorithm

Abstract

Due to their low orbit, low-Earth-orbit (LEO) satellites possess advantages such as minimal transmission delay, low link loss, flexible deployment, diverse application scenarios, and low manufacturing costs. Moreover, by increasing the number of satellites, the system capacity can be enhanced, making them the core of future communication systems. However, there have been instances where malicious actors used LEO satellite communication equipment to illegally broadcast events in large sports stadiums or engage in unauthorized leakage of military secrets in sensitive military areas. This has become an urgent issue in the field of communication security. To combat and prevent abnormal and illegal communication activities using LEO satellites, this study proposes a LEO satellite downlink distributed jamming optimization method using a non-dominated sorting genetic algorithm. Firstly, a distributed jamming system model for the LEO satellite downlink is established. Then, using a non-dominated sorting genetic algorithm, the jamming parameters are optimized in the power, time, and frequency domains. Field jamming experiments were conducted in the southwest outskirts of Xi’an, China, targeting the LEO constellation of the China Satellite Network. The results indicate that under the condition that the jamming coverage rate is no less than 90%, the proposed method maximizes jamming power, minimizes time delay, and minimizes frequency compensation compared to existing jamming optimization methods, effectively improving the real-time jamming performance and success rate.

1. Introduction

As promising candidates for Beyond 5G (B5G) and 6G communication systems [1], LEO satellites, which can be applied in communications, remote sensing, navigation, and other fields [2,3], have attracted extensive attention in military and civilian fields due to their wide communication coverage and long transmission distances. With the explosive growth of wireless services, future wireless communication systems are expected to provide higher capacity and transmission rates. LEO satellite systems have been proposed to provide broadband access in unserved areas, especially in scenarios where ground network deployment is economically impractical [4,5,6]. However, some criminals have exploited the excellent characteristics of LEO satellites to engage in illegal activities, such as unauthorized broadcasting of events in large stadiums or illegal disclosure of information in military restricted areas. Unauthorized ships often generate extensive jamming to overwhelm satellite signals. These actions result in significant economic losses and pose serious security threats [7]. Therefore, preventing unauthorized actions and the illegal use of LEO satellites has become a crucial issue in the field of communication security.

In terms of electronic countermeasures, existing jamming techniques mainly consist of blanket jamming and deception jamming [8,9]. Blanket jamming is relatively easy to implement but may affect the communication ability of one’s own equipment, which is not an issue with deception jamming [10,11]. Deception jamming is mainly divided into repeater deception jamming and generative deception jamming [12,13,14]. Generative deception jamming primarily targets signals with known formats [15], the operational environment needed for which is lacking in LEO satellite communication. Repeater deception jamming involves adding time delays to various satellite signals before forwarding them. However, achieving precise synchronization is challenging in LEO satellite communication due to the fast movement of satellites [16]. Therefore, optimizing communication jamming for LEO satellites has become an important research direction. Existing jamming optimization methods mainly focus on a single domain. However, due to the frequent network switching in LEO satellite networks, single-domain jamming optimization methods cannot meet the needs of LEO satellite communication jamming. Therefore, finding a real-time multi-domain communication jamming optimization method with a high success rate is urgently needed in the field of LEO satellite countermeasures.

To address these issues, this study extensively studies the composition of LEO satellite communication systems and the time–frequency characteristics of communication signals. Combining the channel model of a LEO satellite and the spatial parameters of jammers, a LEO satellite downlink distributed jamming optimization method using a non-dominated sorting genetic algorithm is proposed. The main innovations of this study are as follows:

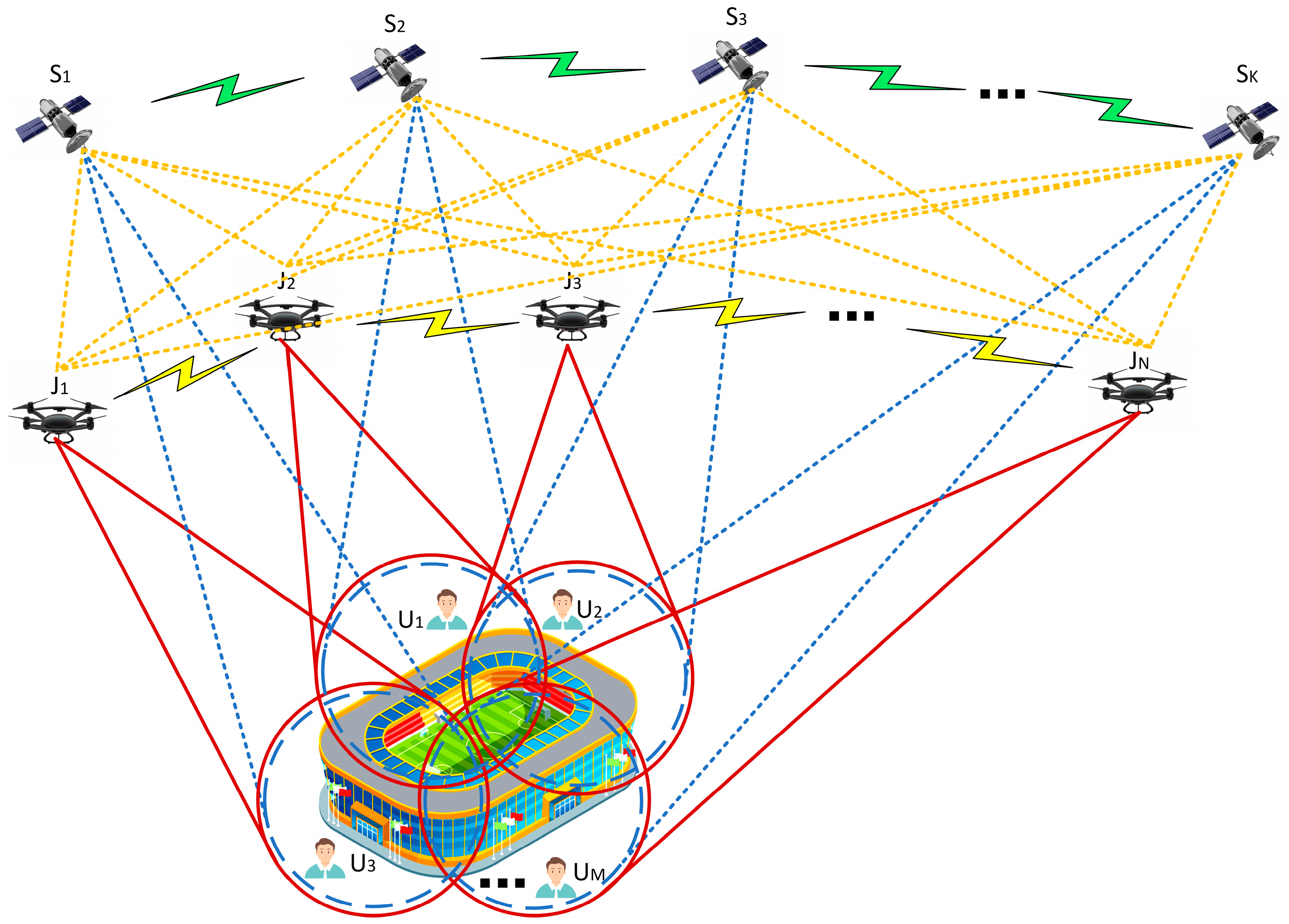
• This study proposes a distributed jamming cooperative control model. Distributed jammers determine the specific orientation of visible satellites through intercepting LEO satellite signals, exchange information with surrounding distributed jammers, continuously update and adjust their positions in real time, and achieve continuous switching for different LEO satellites with high speeds.
• This study utilizes the third-generation non-dominated sorting genetic algorithm for multi-objective optimization, optimizing jamming signals in the power, time, and frequency domains to maintain solution set diversity; improve optimization efficiency; avoid the algorithm falling into local optima; and jam the downlink of LEO satellites.
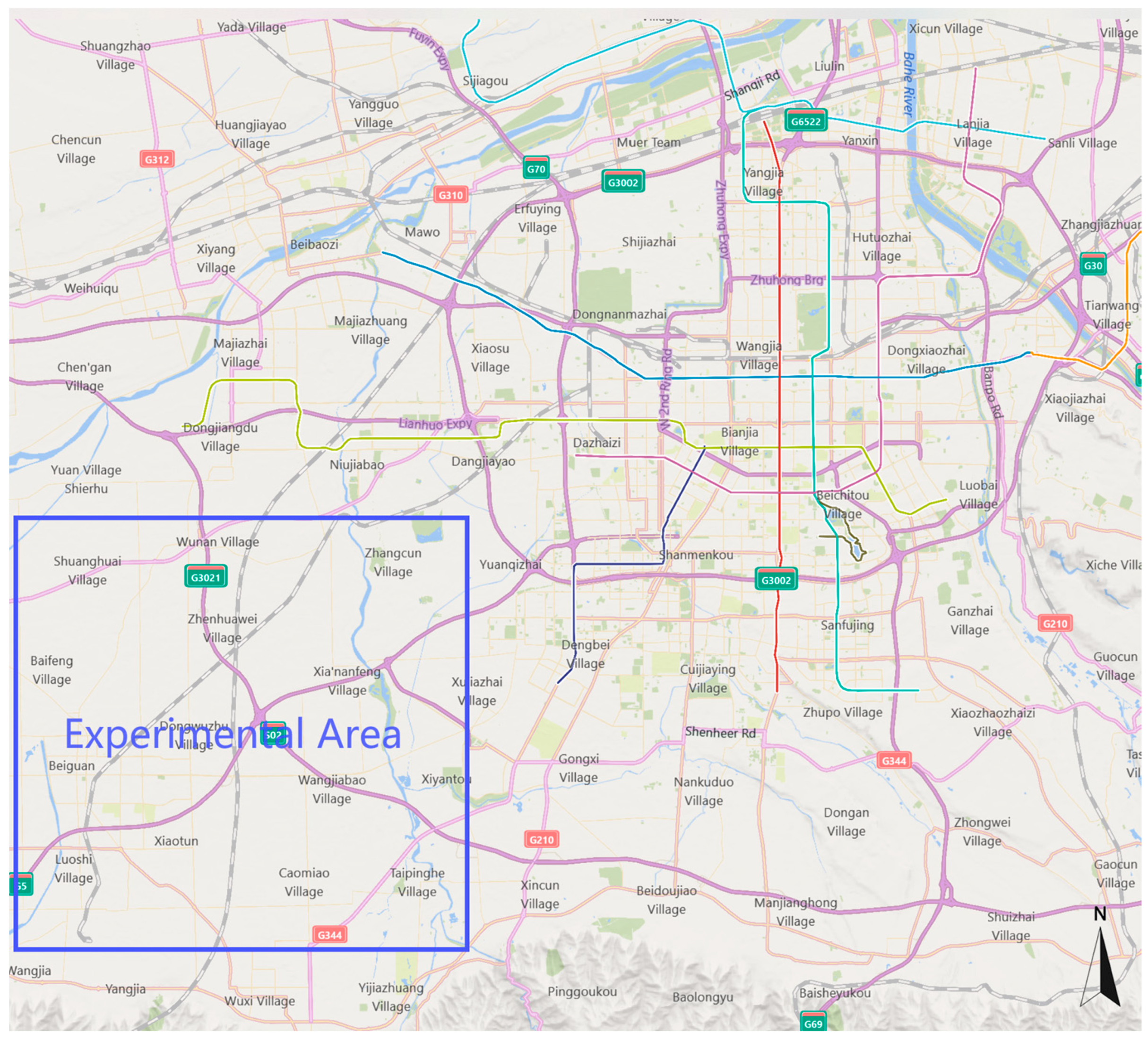
• This study constructs a jamming experimental comparison platform and implements it as hardware. Jamming optimization tests are conducted, targeting the LEO constellation of the China Satellite Network in the southwest outskirts of Xi’an, China, in order to verify the effectiveness of the proposed method for jamming the downlink of LEO satellites compared to existing methods.

The rest of the article is organized as follows: Section 2 introduces related works in the field of satellite countermeasures. Section 3 describes the distributed jamming system model for LEO satellite downlinks. Section 4 introduces the distributed jamming method for LEO satellites using the third-generation non-dominated sorting genetic algorithm. Section 5 details the experimental verification and analysis. Finally, Section 6 presents the conclusions.

2. Related Work

Early satellite communication had low coverage, and research into satellite signal jamming techniques primarily targeted the navigation field [17], which can be divided into three categories: jamming methods, jammer deployment, and jamming efficiency optimization.

Jamming methods mainly include blanket jamming and deception jamming. Blanket jamming involves emitting signals with certain bandwidths and higher power on the frequency band where the satellite operates, causing receivers to lose their lock [18,19]. Studies in the literature [20,21,22,23,24] have investigated various blanket jamming methods, such as wideband noise jamming, partial-band noise jamming, single-tone jamming, multi-tone jamming, and pulse jamming. Their results demonstrated that blanket jamming has a wide coverage area and can effectively jam target receivers within a certain range. However, blanket jamming also affects communication of other devices and is not suitable for jamming when considering LEO satellite communication. Deception jamming includes repeater deception jamming and generative deception jamming and involves generating deceptive signals that are highly similar to genuine satellite signals or re-transmitting genuine signals, causing receivers to lock onto deceptive signals as genuine ones, resulting in erroneous output. Studies in the literature [25] have carried out jamming with terminals through simulating satellite signals. However, generative deception jamming requires specific knowledge of the genuine signal’s format in advance and lacks practical use in LEO satellite communication jamming. Ref. [26] achieved the jamming of an unmanned aerial vehicle (UAV) integrated navigation system through controlling delays and subsequently re-transmitting of satellite signals. Repeater deception jamming does not require extensive prior information but is susceptible to being identified as multi-path jamming by receivers, limiting its effectiveness in LEO satellite communication jamming.

The deployment of jammers is an effective means to combat anti-jamming techniques, such as anti-adaptive nulling and beamforming [27]. In [28], a multi-station repeater deception jamming deployment method was proposed based on delay control, which protects fixed targets by analyzing the impact of delays of different magnitudes on the effective jamming region. In [29], a multi-station repeater deception jamming deployment method based on equivalent mapping was presented, which can realize area mapping and trajectory mapping while improving the jamming success rate. In [30], principles for the coordinated deployment of multiple jammers were formulated, and a deployment structure for the coordinated deployment of three jammers was obtained, thereby achieving full-domain coordinated deployment of multiple jammers. However, traditional jammer deployment methods lack flexibility and struggle to adapt to the high-speed movement of LEO satellites.

Jamming efficiency optimization can achieve better jamming effects under the same resource configuration conditions [31]. In [32], a particle swarm optimization-based jammer optimization algorithm was proposed, in which the packet delivery ratio was used as the objective function to select the optimal jamming position. However, such single-objective jamming optimization methods cannot counteract the anti-jamming measures of LEO satellites. The study [33] introduced a distributed communication jamming resource allocation method based on improved particle swarm optimization, optimizing the objectives of regional coverage rate and average danger coefficient to address issues such as low efficiency in resource allocation and uncertain jamming benefits in distributed communication jamming. However, such methods only consider two optimization objectives, making it difficult to directly obtain the optimal solution when there are more objective functions. In [34], a satellite navigation distributed blanket jamming resource scheduling method based on particle swarm optimization and a genetic algorithm was proposed, in which the objectives of bit error rate, pseudorange measurement error, and jamming cost were optimized. This method effectively scheduled limited resources. Such methods simplify multi-objective optimization into single-objective optimization using linear weighting, but the selection of weighting coefficients directly affects the bias of the final solution. In [35], a taboo search-artificial bee colony algorithm for cognitive cooperative jamming decision-making, which considers multiple objective functions for optimization, was proposed, making it less likely to fall into local optimal solutions. However, such methods have a slow convergence speed during optimization, making it difficult to ensure real-time jamming. Ref. [36] introduced an improved discrete particle swarm optimization algorithm, which can provide the most suitable allocation scheme according to the requirements of different tasks, effectively addressing the static allocation problem of jamming resources. However, the search space of the populations used in such methods is not broad enough, making it easy to fall into using local optimal solutions and difficult to guarantee a certain jamming success rate.

The limitations of existing jamming methods, poor flexibility in the deployment of jammers, and subpar decision-making performance in jamming efficiency optimization highlight the shortcomings of the current methods. In response to these deficiencies, this study proposes a LEO satellite downlink distributed jamming optimization method with a non-dominated sorting genetic algorithm, which offers strong flexibility and effectively enhances the real-time jamming performance and success rates.

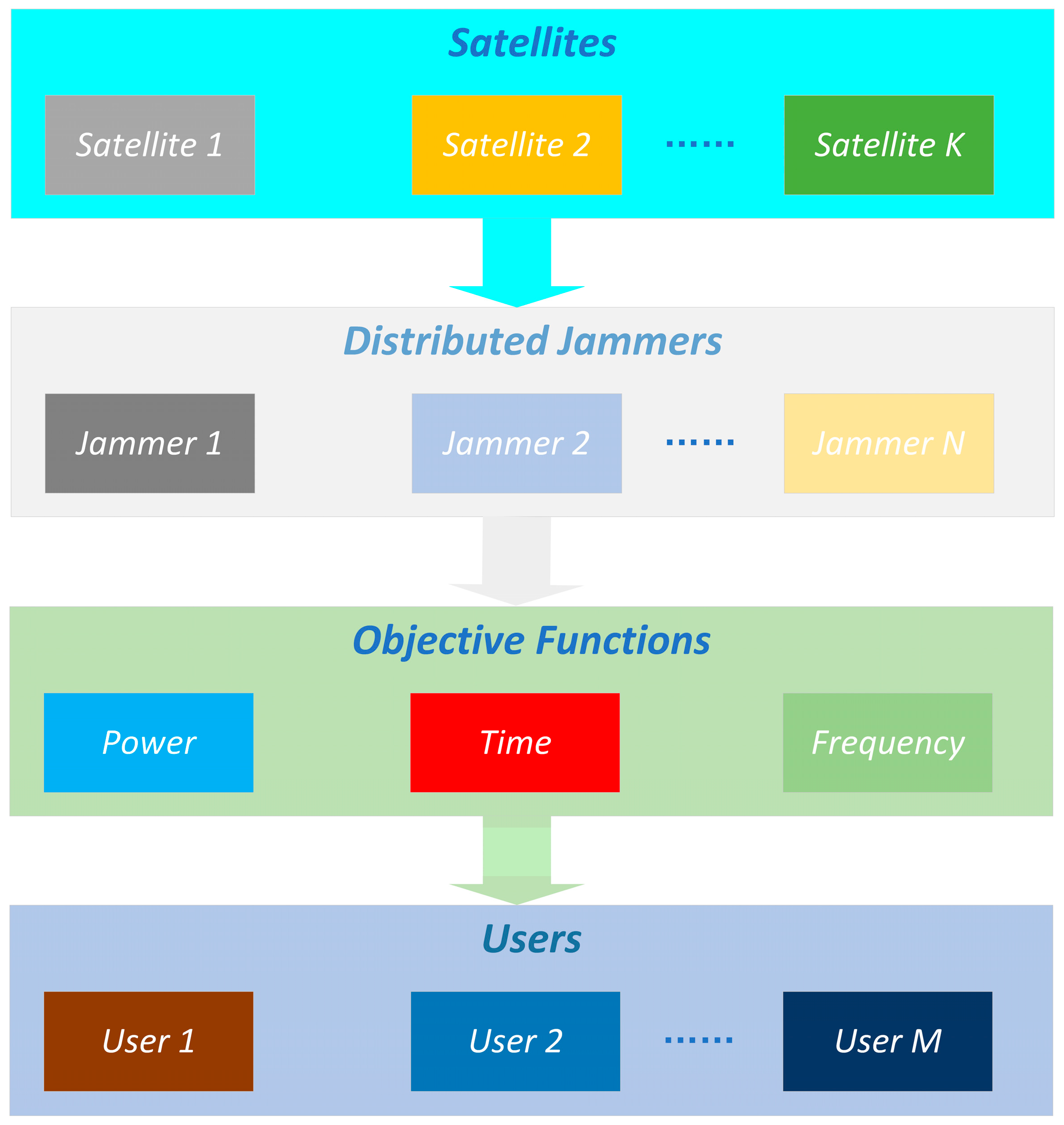
3. Distributed Jamming System Model for LEO Constellation Downlink

By identifying and separating the signals of LEO satellites and incorporating the positional information of distributed jammers and the satellite constellation, a LEO satellite downlink distributed jamming system model was constructed. The system consists of the LEO satellites, jammers, and ground jamming targets, as shown in Figure 1, where $J_N$ represents the $N$th distributed jammer, $S_k$ represents the $K$th LEO satellite, and $U_M$ represents the $M$th ground jamming target. The green lightning-like lines represent communication links between LEO satellites, yellow lightning-like lines represent communication links between onboard distributed jammers, orange dashed lines represent the interception links of onboard distributed jammers to signals from LEO satellites, blue dashed lines represent the beam coverage of LEO satellites to ground targets, and red solid lines represent the beam coverage of onboard distributed jammers to ground targets. The Maseng–Bakken model (MBM) [37,38], which assumes that the rate of change in rain attenuation is proportional to its instantaneous value, was adopted as the downlink channel model.

All distributed jammers were equipped with satellite navigation and communication receivers, providing the possibility for these jammers to collaboratively network with each other.

Based on the identification and localization of each satellite within the region, and utilizing the positional information of jammers in the satellite-to-ground link domain, a multi-objective jamming resource scheduling model was constructed, as illustrated in Figure 2. Considering the different deception strategies of distributed jammers in the power, time, and frequency domains, the optimization and coordinated control of distributed deceptive jammers are implemented. This allows for coordinated jamming in the satellite-to-ground links of multiple LEO satellites within the region, disrupting the downlink communication network of the LEO satellite constellation.

3.1. Jamming Evaluation Metrics

3.1.1. Total Jamming Power

In the downlink, satellite beams and ground user terminals often adopt a staring mode. Ground user terminals typically have multiple antenna transceiver capabilities. The main lobe and side lobes of the receiving antenna at the user terminal are susceptible to jamming signals from other systems and can encompass or accommodate the main characteristics of all potential jamming scenarios.

In practical scenarios, due to the large number of low-Earth-orbit satellite constellations, most jamming manifests as overlapping jamming from multiple jammers affecting the same ground user terminal, known as aggregate jamming. Therefore, the aggregate jamming power received at the ground user terminal is the sum of the jamming power caused by distributed jammers within the communication elevation angle range. This can be expressed as follows:

$$\left\{\begin{array}{c}{P}_{total}={\displaystyle \sum _i}{P}_{ri}\\ P_{ri}=P_t+G_t-L+G_r\\ G_{t/r}=10lg\left[4.5\times {\left(\frac{D}{\lambda }\right)}^2\right]\\ L=92.4+20lg\left(f\right)+20lg\left(d_i\right)\end{array}\right.$$

(1)

where $P_t$ represents the transmit power of the jamming signal, $G_t$ represents the gain of the jamming signal transmit antenna, $L$ represents the free-space loss, and $G_r$ represents the gain of the receiving antenna in the jammed system. Additionally, $D$ is the size of the antenna, $\lambda$ is the wavelength at the center frequency, $f$ is the signal frequency, and $d_i$ is the distance between the ground user and the $i$th jammer.

3.1.2. Time Delay

Distributed jamming systems operate on the principle of time delay deception. The system deceives the jamming device by receiving all currently available satellite signals, thus determining whether they are all visible to the ground receiver. After spatial separation, a time delay is applied to each visible satellite signal individually. The amalgamated deceptive signals are then broadcast to the target receiving device on the ground. By ensuring that the peaks of the deceptive signals surpass those of the genuine signals, the tracking loop of the target-receiving device can lock onto the deceptive signals and generate incorrect position solutions.

When the target receiving device tracks the deceptive signals, the pseudorange from the $j$th jamming device forwarding the signal from the $i$th satellite to the kth target point is given by

$$\rho =\left|{\mathit{r}}_{\mathit{i}}^{\mathit{L}}-{\mathit{r}}_{\mathit{j}}^{\mathit{Z}}\right|+\left|{\mathit{r}}_{\mathit{j}}^{\mathit{Z}}-{\mathit{r}}_{\mathit{k}}^{\mathit{T}}\right|+c·∆{\tau }_{ijk}+c·\delta ,$$

(2)

where ${\mathit{r}}_{\mathit{i}}^{\mathit{L}}$ represents the position of the $i$th satellite, ${\mathit{r}}_{\mathit{j}}^{\mathit{Z}}$ represents the position of the $j$th jammer, ${\mathit{r}}_{\mathit{k}}^{\mathit{T}}$ represents the position of the $k$th target receiver, $\delta$ represents the receiver clock bias, and $∆{\tau }_{ijk}$ represents the delay added when the $j$th jammer forwards the signal from the $i$th satellite to the $k$th user.

Assuming that the desired location is represented by the vector ${\mathit{r}}_{\mathit{k}}^{\mathit{C}}$, the pseudorange from the $i$th satellite to the $k$th fictitious target point is given by

$${\rho }^{\prime }=\left|{\mathit{r}}_{\mathit{i}}^{\mathit{L}}-{\mathit{r}}_{\mathit{k}}^{\mathit{C}}\right|+c·\delta .$$

(3)

By letting

$$\rho ={\rho }^{\prime },$$

(4)

the delay added when the $j$th jammer forwards the signal from the $i$th satellite to the $k$th user can be determined as follows:

$$∆{\tau }_{ijk}=\frac{\left|{\mathit{r}}_{\mathit{i}}^{\mathit{L}}-{\mathit{r}}_{\mathit{k}}^{\mathit{C}}\right|-\left|{\mathit{r}}_{\mathit{i}}^{\mathit{L}}-{\mathit{r}}_{\mathit{j}}^{\mathit{Z}}\right|-\left|{\mathit{r}}_{\mathit{j}}^{\mathit{Z}}{-\mathit{r}}_{\mathit{k}}^{\mathit{T}}\right|}{c}.$$

(5)

3.1.3. Frequency Compensation

Due to the high operational speeds of low-Earth-orbit satellites, the Doppler effect introduced by the relayed deceptive signals and genuine satellite signals reaching the receiver can result in deviations. Therefore, during the forwarding process, frequency compensation is necessary for the deceptive signals to ensure that the velocity measurements at the target-receiving device align with the actual values.

Assuming that the velocities of the $i$th satellite and the $j$th jammer are represented by the vectors ${\mathit{V}}_{\mathit{i}}^{\mathit{L}}$ and ${\mathit{V}}_{\mathit{j}}^{\mathit{Z}}$, respectively, and that the satellite’s emission frequency is $f_0$, then the Doppler frequency shift of the $i$th satellite and the $j$th jammer can be expressed as follows:

$$f_{ij}^Z=f_0\frac{V_{ij}^Z}{c}=\frac{f_0}{c}·\frac{\left({\mathit{r}}_{\mathit{i}}^{\mathit{L}}-{\mathit{r}}_{\mathit{j}}^{\mathit{Z}}\right)·\left({\mathit{V}}_{\mathit{i}}^{\mathit{L}}-{\mathit{V}}_{\mathit{j}}^{\mathit{Z}}\right)}{\left|{\mathit{r}}_{\mathit{i}}^{\mathit{L}}-{\mathit{r}}_{\mathit{j}}^{\mathit{Z}}\right|}.$$

(6)

Similarly, for the relative velocity and Doppler frequency shift between the $i$th satellite and the $k$th target receiver, we have

$$f_{ik}^T=f_0\frac{V_{ik}^T}{c}=\frac{f_0}{c}·\frac{\left({\mathit{r}}_{\mathit{i}}^{\mathit{L}}-{\mathit{r}}_{\mathit{k}}^{\mathit{T}}\right)·\left({\mathit{V}}_{\mathit{i}}^{\mathit{L}}-{\mathit{V}}_{\mathit{k}}^{\mathit{T}}\right)}{\left|{\mathit{r}}_{\mathit{i}}^{\mathit{L}}-{\mathit{r}}_{\mathit{k}}^{\mathit{T}}\right|}.$$

(7)

Therefore, the compensatory Doppler frequency shift is

$$∆f_{ijk}=f_{ik}^T-f_{ij}^Z.$$

(8)

3.1.4. Jamming Coverage Rate

In practical distributed jamming optimization, the jamming coverage rate is typically measured using the ratio or multiplicity of coverage from the beams formed by jammers after collaborative networking, targeting specific users in a given area. Therefore, in a specific jamming task, the jamming coverage rate can be expressed as follows:

$$\eta =\frac{num\left({Users}_{cover}\right)}{num\left(Users\right)}$$

(9)

where $num\left({Users}_{cover}\right)$ is the total number of targets covered by all the jammers, and $num\left(Users\right)$ is the total number of targets.

3.2. Multi-Objective Optimization Objective Functions and Constraints

In the distributed jamming system of LEO constellations, considering a given jamming success rate, the multi-objective optimization problem involves maximizing the total jamming power, minimizing relay delay, and minimizing frequency compensation. This can be formulated as follows:

$$\left\{\begin{array}{c}max\left(P_{total}\right)\\ min\left(∆{\tau }_{ijk}\right)\\ min\left(∆f_{ijk}\right)\\ s.t.:\eta \ge {\eta }_0\end{array}\right.$$

(10)

where ${\eta }_0$ is the minimum required jamming coverage rate.

4. Third-Generation Non-Dominated Sorting Genetic Algorithm

The third-generation non-dominated sorting genetic algorithm (NSGA-III) is an advanced multi-objective evolutionary algorithm designed to address optimization problems with multiple conflicting objectives. It primarily focuses on improving the diversity of solutions and enhancing efficiency to prevent the algorithm from becoming trapped in local optima. The algorithm’s specific process can be summarized as follows: population division into non-dominated levels, the determination of reference points on hyperplanes, adaptive normalization of population individuals, correlation operations, and genetic operations to generate offspring populations. The basic flow is illustrated in Figure 3.

This study proposes a distributed collaborative jamming optimization method based on NSGA-III. Leveraging the characteristics of distributed jammers collaborating and cross-validating each other through communication, the method involves real-time adjustments of individual positions within a small range. While ensuring a given jamming success rate, optimization is conducted in the power, time, and frequency domains. This results in a spatially distributed deceptive system within the region, contributing to system-level counteraction against LEO constellations.

4.1. Algorithm Flow

4.1.1. Population Division Based on Non-Dominated Layers

We let $P_t$ be the parent generation of the $t$th iteration, with a size of $N$. The offspring generated from this parent generation is denoted as $Q_t$, also with a size of $N$. Combining the offspring and parent populations, we obtain $R_t=P_t\cup Q_t$, with a size of $2N$. From this combined population, $N$ individuals are selected through the following steps:

• Perform non-dominated sorting on $R_t$, resulting in multiple non-dominated layers $\left(F_1,F_2,\cdots F_l\right)$.
• Starting from $F_1$, construct a new population $S_t$ by sequentially adding members from non-dominated layers ranked 1 to $l$. If $\left|S_t\right|=N$, set $P_{t+1}=S_t$ directly. If $\left|S_t\right|>N$, eliminate solutions from layers beyond $l$. The remaining part for the next generation ($K=N-\left|P_{t+1}\right|$) is selected from $F_l$, and these solutions constitute $P_{t+1}={\cup }_{i=1}^{l-1}{F}_i$.

4.1.2. Determination of Reference Points on the Hyperplane

NSGA-III uses a pre-defined set of reference points to ensure the diversity of the obtained solutions. In the context of a LEO distributed jamming system, the reference points lie on a two-dimensional hyperplane. Each objective is divided into 10 parts, resulting in 55 reference points. The algorithm used to select jamming reference points is as follows:

• Let $X$ be a two-dimensional variable, taking values from the set $\left\{0,\frac{1}{10},\cdots ,\frac{11}{10}\right\}$.
• For each $x_{ij}\in X$ (the $j$th element of the $i$th combination in $X$), $x_{ij}=x_{ij}-\frac{j - 1}{10}$.
• Use $S$ as the set of jamming reference points and obtain coordinates for each objective function:

  $$\left\{\begin{array}{ll}{s}_{ij}=x_{ij}-0,& j=1\\ s_{ij}=x_{ij}-x_{i\left(j-1\right)},& j=2\\ s_{ij}=1-x_{i\left(j-1\right)},& j=3\end{array}\right..$$

  (11)

4.1.3. Adaptive Normalization of Population Individuals

Adaptive normalization is applied in the NSGA-III algorithm to normalize the objective function values of each individual. This helps to maintain a uniform distribution of solutions on the Pareto front. The basic steps for adaptive normalization are as follows:

• Find the ideal point.

For each dimension of the objectives for individuals in the population $S_t$, find the minimum values $min\left(f_i\left(x\right)\right)\left(i=1,2,3\right)$ to construct the jamming ideal point $\overline{z}=\left(min\left(P_{total}\right),min\left(∆{\tau }_{ijk}\right),min\left(∆f_{ijk}\right)\right)$. Shift the population $S_t$ by $f_i^{\prime }\left(x\right)=f_i\left(x\right)-z_i^{min}\left(i=1,2,3\right)$ to bring the ideal point to the origin.

2.

Calculate extreme points and construct hyperplanes.

The jamming extreme points refer to points where one objective value is large while the others are small. The formula for generating jamming extreme points is as follows:

$$\left\{\begin{array}{c}ASF\left(x,\mathsf{\omega }\right)=max\frac{f_i^{\prime }\left(x\right)}{{\omega }_i},x\in S_t\\ {\omega }_i=\left(\tau ,\cdots {\omega }_j^i\cdots \tau \right),\tau ={10}^{-6},{\omega }_j^i=1\\ z^{i,max}=s:{argmin}_{s\in S_t}ASF\left(x,\mathsf{\omega }\right)\end{array}\right.$$

(12)

The lines connecting extreme points and ideal points form three extreme objective vectors $z^{i,max}\left(i=1,2,3\right)$, constituting a 3D jamming hyperplane.

3.

Objective Adaptive Normalization.

The intersection points of the 3D jamming hyperplane and the axes of the power, time, and frequency domains are intercepts $a_i\left(i=1,2,3\right)$. Normalization is carried out according to the following equation using these intercepts:

$$f_i^n\left(x\right)=\frac{f_i^{\prime }\left(x\right)}{a_i-z_i^{min}}=\frac{f_i\left(x\right)-z_i^{min}}{a_i-z_i^{min}}, for i=1,2,3.$$

(13)

4.1.4. Association Operation

The association operation involves associating individuals in the population with corresponding jamming reference points. The lines between the origin and reference points serve as reference lines. We calculate the distance from each individual in $S_t$ to each reference line and associate each individual with the reference line for which it has the shortest distance.

4.1.5. Individual Retention

During the process of individual selection, individuals with fewer associations with jamming reference points should be preserved to maintain diversity. The specific steps are as follows:

• Select the jamming reference point $J_{min}$ with the least number of associations. If there are multiple such jamming reference points, randomly choose one $\overline{J}$. $I_{\overline{J}}$ represents the individuals associated with jamming reference point $\overline{J}$ in the $F_l$ layer.
• If $I_{\overline{J}}$ is empty, re-select the jamming reference point. If $I_{\overline{J}}$ is not empty, check whether the number of associations ${\rho }_{\overline{J}}$ in all non-dominated layers before $F_l$ with jamming reference point $j$ is 0. If ${\rho }_{\overline{J}}=0$, select the individual with the minimum distance to $\overline{J}$ from $I_{\overline{J}}$ for the next generation. If ${\rho }_{\overline{J}}\ne 0$, randomly choose an individual from $I_{\overline{J}}$ for the next generation.
• Repeat the operation until the size of the next generation equals $N$.

5. Experimental Analysis

Field tests were conducted in the southwest outskirts of Xi’an, China, using the LEO satellite downlink distributed jamming optimization method with non-dominated sorting genetic algorithm proposed in this article, targeting the LEO constellation of the China Satellite Network. The experimental area is illustrated in Figure 4.

The jamming equipment carrier and the onboard jamming equipment used in the experiments are illustrated in Figure 5.

The specific jamming parameters for the experiments are outlined in

Table 1. Jamming scene parameter settings.

Parameter	Value
LEO Satellite Frequency Bands	37.5–42.5 GHz
Altitude of LEO Satellites	900 km
Number of Visible LEO Satellites	11
Number of Jammers	20
Altitude of Jammers	10–20 km
Jamming Radius	20 km
Area Size	$20 \mathrm{k}\mathrm{m}\times 20 \mathrm{k}\mathrm{m}$
Number of Target Central Points	25
Population Size	1000
Maximum Iteration Count	100

.

Three jamming scenarios were created:

• The first scenario compares the target function with the optimal solution set;
• The second scenario compares coverage optimization over time;
• The third scenario compares the success rate of jamming within a certain region.

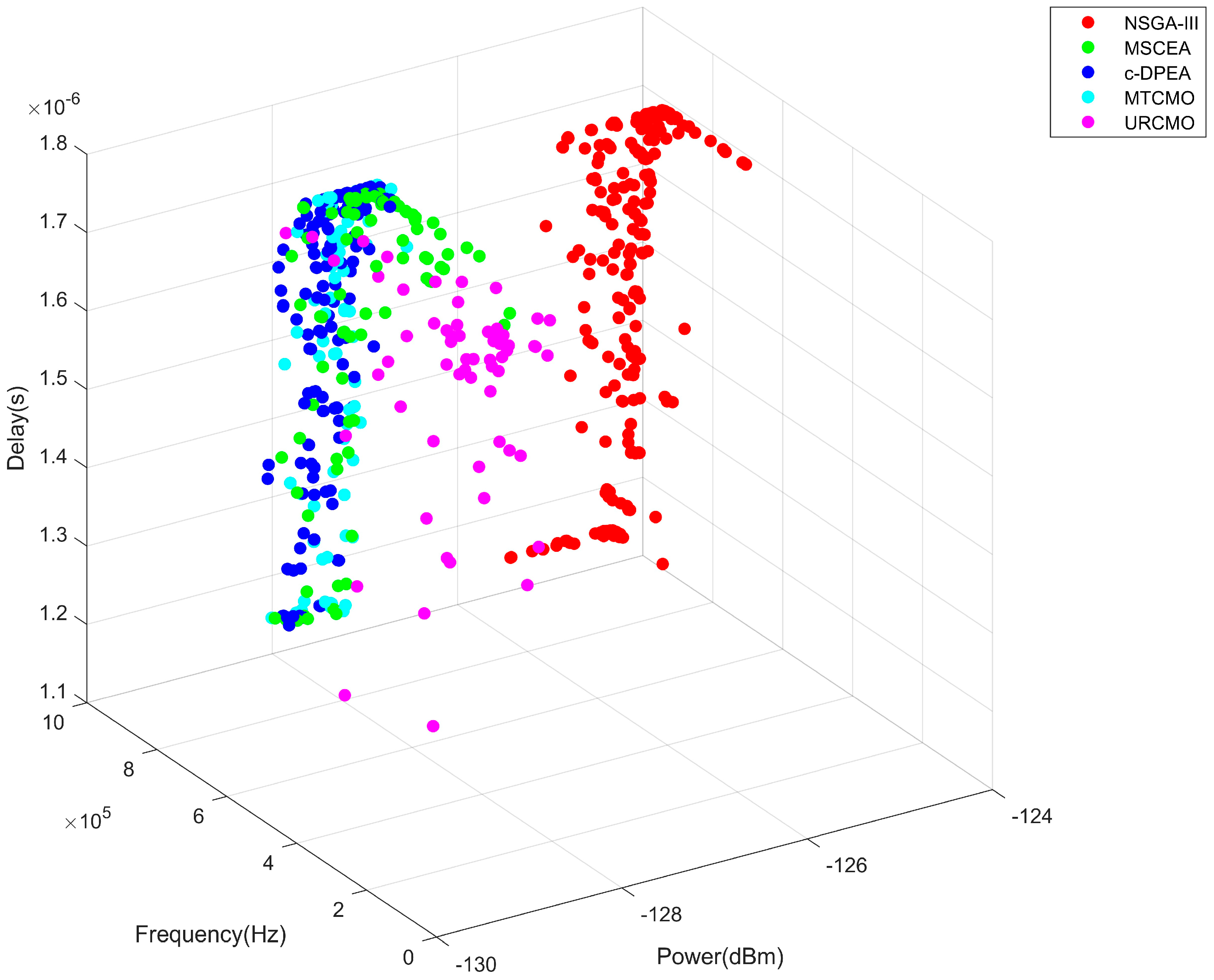
5.1. Objective Function and Optimal Solution Set Optimization

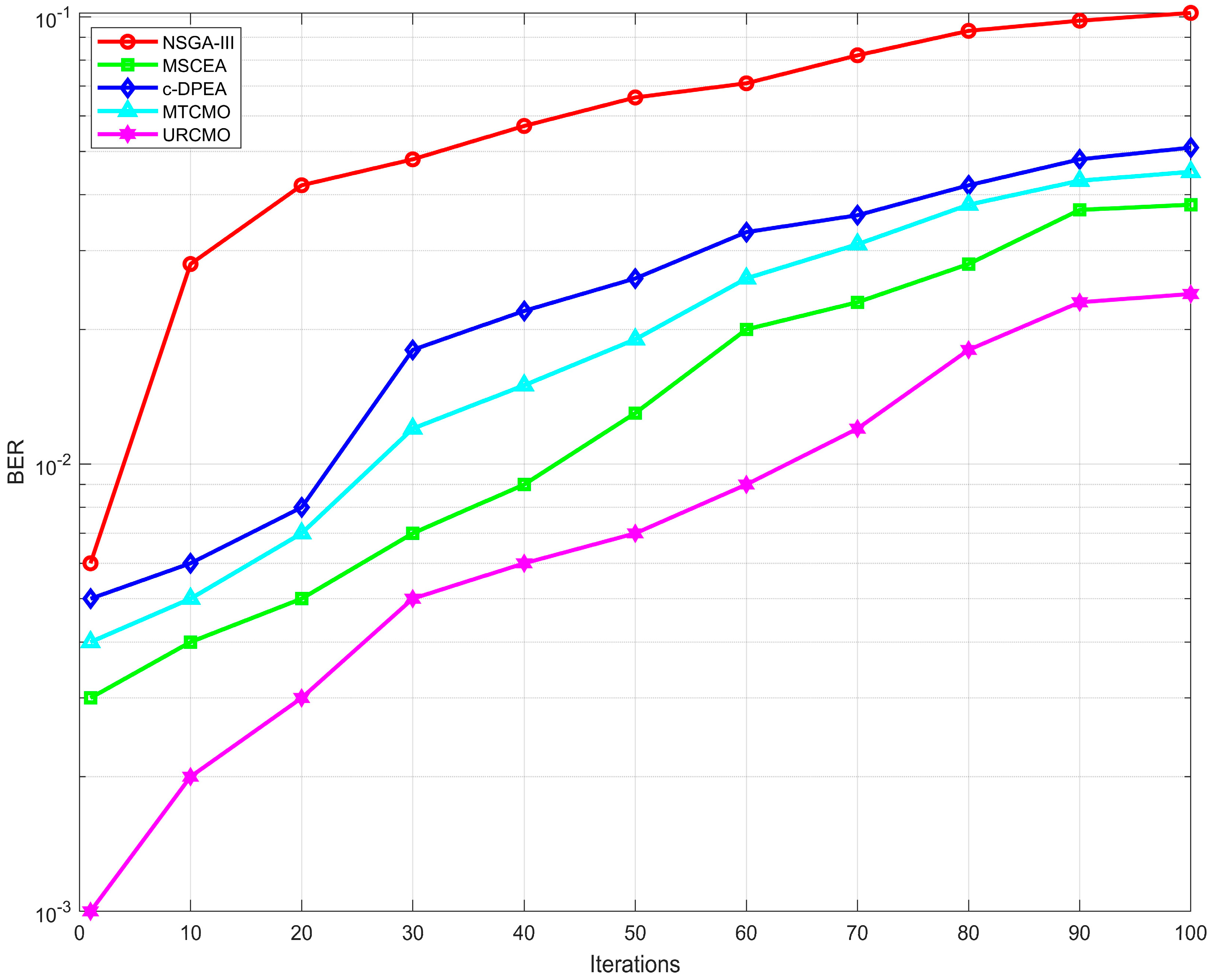
5.1.1. Objective Function Comparison

In the experimental testing of objective function optimization, the proposed third-generation non-dominated sorting genetic algorithm (NSGA-III) based on reference points for LEO satellite jamming was tested under the constraint of at least 90% jamming coverage. Subsequently, it was compared with the constraint-based dual-population evolutionary algorithm (c-DPEA), multi-task constraint multi-objective optimization algorithm (MTCMO), multi-strategy improved continuous explosive algorithm (MSCEA), and constraint-based multi-objective optimization algorithm utilizing unconstrained and constrained Pareto front relationships (URCMO). After 100 iterations, the multi-objective Pareto frontier sets for power, delay, and frequency compensation were obtained, as shown in Figure 6.

From Figure 6, it can be observed that the objective function values generated with the URCMO algorithm were scattered and did not converge to a stable Pareto frontier, while the other four algorithms all converged to a stable Pareto frontier, with the Pareto frontier generated with the MSCEA algorithm being relatively divergent. In terms of total jamming power, the NSGA-III algorithm optimization produced a jamming power of −125 dBm, while the jamming powers optimized with the MSCEA, c-DPEA, and MTCMO algorithms were all around −128 dBm, thus proving that the NSGA-III algorithm maximized the jamming power. Under similar total frequency compensation, the NSGA-III algorithm produced a smaller total delay compared to the other three algorithms, for instance, at a total relay delay of 1.2 μs with a total frequency compensation of 724 KHz for low-Earth-orbit constellations, while those of the other algorithms were all around 1.76 μs. Similarly, under a similar total delay, the NSGA-III algorithm produced smaller total frequency compensation compared to the other three algorithms; for example, at a total delay of 1.4 μs, a total frequency compensation of 695 KHz was obtained for low-Earth-orbit constellations, while those of the other algorithms were around 800 KHz, thereby demonstrating the effectiveness of the NSGA-III algorithm in optimizing in the power, time, and frequency domains for distributed jamming of the LEO satellites’ downlink.

5.1.2. Dominant Solution Set Comparison

The Feasible-Rate and Spread metrics were used to measure the feasibility and spread of the dominant solution set, respectively. Feasible-Rate assesses the proportion of solutions that satisfy all constraints and have variables within the upper and lower bounds among all generated solutions, where a higher Feasible-Rate indicates the better feasibility of the generated optimal solution set. Spread calculates the standard deviation of the distances between individuals that are farthest apart on each objective, where a larger Spread indicates a wider distribution of the algorithm’s generated solution set, making it less prone to local optima.

In the performance experiment regarding the solution set, under the same conditions as the objective function optimization test, the NSGA-III algorithm was tested first, followed by comparison with the c-DPEA, MTCMO, MSCEA, and URCMO algorithms. The Feasible-Rate and Spread values for the optimized dominant solution sets were obtained after testing, and they are shown in Figure 7 and Figure 8.

From Figure 7, it can be seen that the NSGA-III, MSCEA, c-DPEA, MTCMO, and URCMO algorithms converged to a Feasible-Rate of 1 at the 27th, 42nd, 55th, 49th, and 72nd iterations, respectively. This indicates that the dominant solution sets generated with all five algorithms satisfied the constraints and had extremely high feasibility. Additionally, the NSGA-III algorithm converged faster than the other four algorithms.

Taking the example of the last 20 iterations when the dominant solution sets generated with all five algorithms satisfied the constraints (Feasible-Rate = 1), Figure 8 shows that the Spread values obtained with the NSGA-III, MSCEA, c-DPEA, MTCMO, and URCMO algorithms were 1.157, 1.018, 1.036, 1.013, and 1.033, respectively. The NSGA-III algorithm produced the largest Spread, demonstrating the excellent spread of the dominant solution set generated with the NSGA-III algorithm when optimizing LEO satellite distributed jamming.

In summary, the feasibility, convergence, and spread of the dominant solution set generated with the NSGA-III algorithm were far superior to those of the other four algorithms. This confirms the strong overall performance of the NSGA-III algorithm in optimizing distributed jamming for LEO satellite constellations.

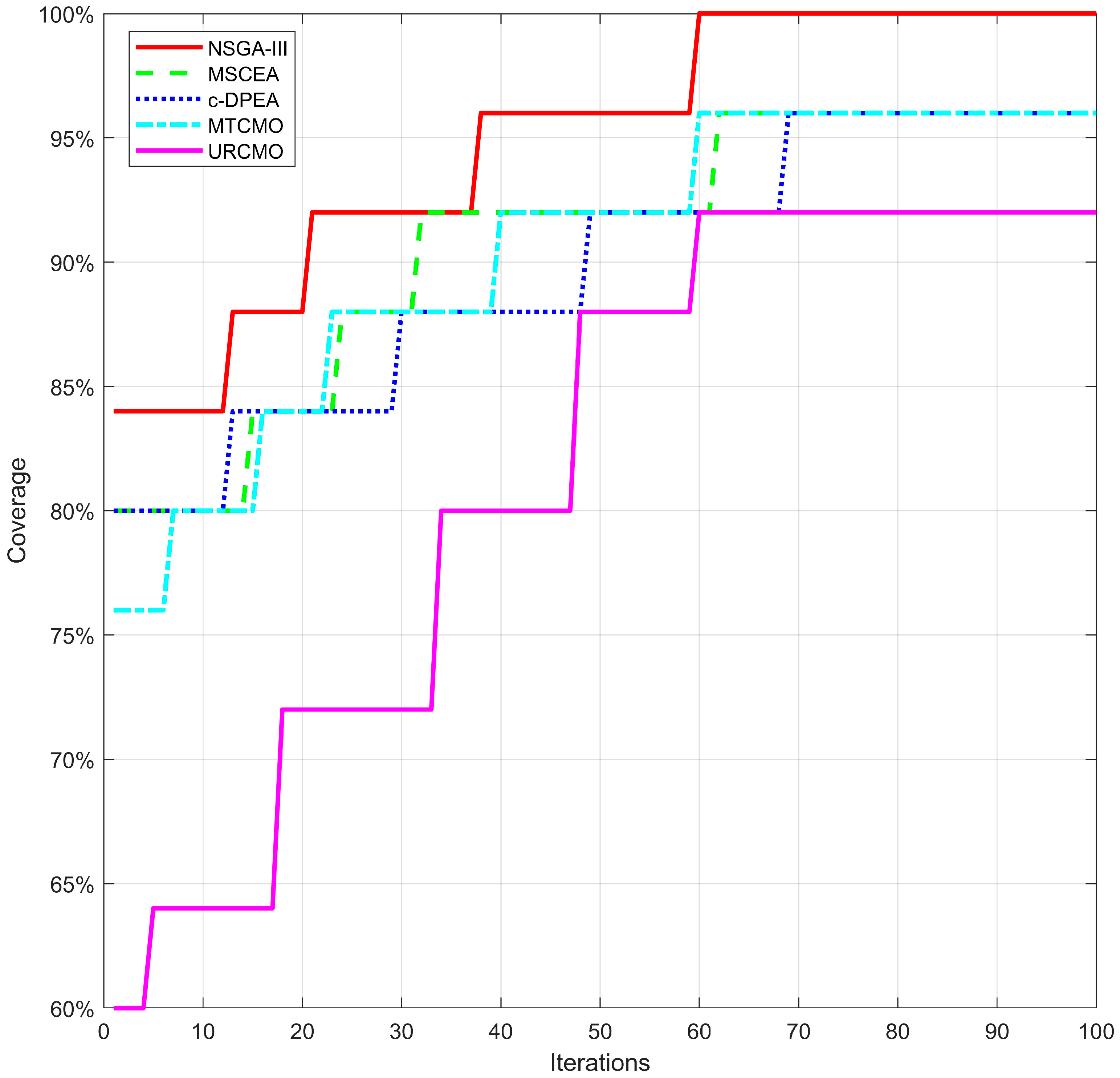
5.2. Coverage Optimization

Jamming coverage measures the degree to which key areas are covered by jamming beams. The proportion of ground users covered by jamming beams in a certain area was used as an indicator of jamming coverage. In the experiment testing jamming coverage optimization, the NSGA-III algorithm was tested first, followed by comparison with the c-DPEA, MTCMO, MSCEA, and URCMO algorithms. The changes in jamming coverage rates for the different optimization algorithms are plotted in Figure 9.

In Figure 9, it can be observed that the initial coverage rate of the NSGA-III algorithm was the highest (at 84%), while the URCMO algorithm had the lowest initial coverage rate (at 60%). With an increase in the number of iterations, the NSGA-III, MSCEA, c-DPEA, MTCMO, and URCMO algorithms reached jamming coverage rates of over 90% at the 21st, 32nd, 49th, 40th, and 60th iterations, respectively, satisfying the set jamming coverage rate constraint. At the end of the iterations, the coverage rate of the NSGA-III algorithm reached 100%; the coverage rates under the MSCEA, c-DPEA, and MTCMO algorithms were 96%; and the coverage rate of the URCMO algorithm was 92%. This demonstrates the efficiency of the NSGA-III algorithm in optimizing the jamming coverage rate in the context of LEO satellite downlink distributed jamming.

5.3. Jamming Success Rate Optimization

The jamming success rate is the core indicator of jamming optimization. The total receiver bit error rate in a certain area measured according to actual satellite signals was used to reflect the jamming success rate, where a higher bit error rate indicates a higher jamming success rate. In the experiment testing jamming success rate optimization, assuming that LEO satellites send a 1000-bit stream to ground users and under the constraint of at least 90% jamming coverage, the NSGA-III algorithm was tested first, followed by comparison with the c-DPEA, MTCMO, MSCEA, and URCMO algorithms. The changes in the bit error rates corresponding to different optimization algorithms are plotted in Figure 10.

From Figure 10, it can be observed that during the initial iterations, the NSGA-III algorithm produced the highest bit error rate, while the URCMO algorithm produced the lowest bit error rate. With an increase in the number of iterations, the bit error rate of the NSGA-III algorithm grew the most, surpassing the other four algorithms, while the bit error rate growth of the URCMO algorithm was the smallest. At the end of the iterations, the NSGA-III algorithm generated 102 bit errors; the c-DPEA and MTCMO algorithms produce 51 and 45 bit errors, respectively; the MSCEA algorithm produced 38 bit errors; and the URCMO algorithm produced only 24 bit errors. These results demonstrate the efficiency of the NSGA-III algorithm for optimizing the jamming success rate in distributed jamming of the LEO satellites’ downlinks.

6. Conclusions

This study aimed to prevent attacks on satellites by unauthorized ships in maritime scenarios, as well as activities such as illegal broadcasting in large sports stadiums or illegal leakage of military secrets in critical areas by taking advantage of the high transmission rate and low latency of LEO satellite communication systems, which pose serious threats to the national economy and security. In particular, a LEO satellite downlink distributed jamming optimization method using a non-dominated sorting genetic algorithm was proposed. Field jamming tests were conducted on the LEO constellation of the China Satellite Network in the southwest outskirts of Xi’an, China, and comparative experiments were performed against traditional jamming optimization methods, considering the objective functions, optimal solution sets, jamming coverage, and jamming success rates. The results indicated that under the condition of jamming coverage being no less than 90%, the proposed method outperformed the considered existing jamming optimization methods in terms of optimization in the power, time, and frequency domains, yielding a more extensive, scalable, and convergent solution set, thus effectively improving the real-time jamming performance and success rate. The method proposed in this article holds significant application value in both military and civilian security fields. In the future, we plan to conduct further research in order to explore its application in different communication jamming scenarios.