Selecting and Interpreting Multiclass Loss and Accuracy Assessment Metrics for Classifications with Class Imbalance: Guidance and Best Practices
Abstract
1. Introduction
2. Background
2.1. Accuracy Assessment Metrics
2.2. Averaged Multiclass Accuracy Measures
2.3. Loss Metrics
3. Methods
3.1. Data
3.2. Classification Experiments
3.2.1. CNN Scene Classification
3.2.2. Experiments Exploring the Effect of Changing Class Prevalences
4. Results, Discussion, and Recommendations
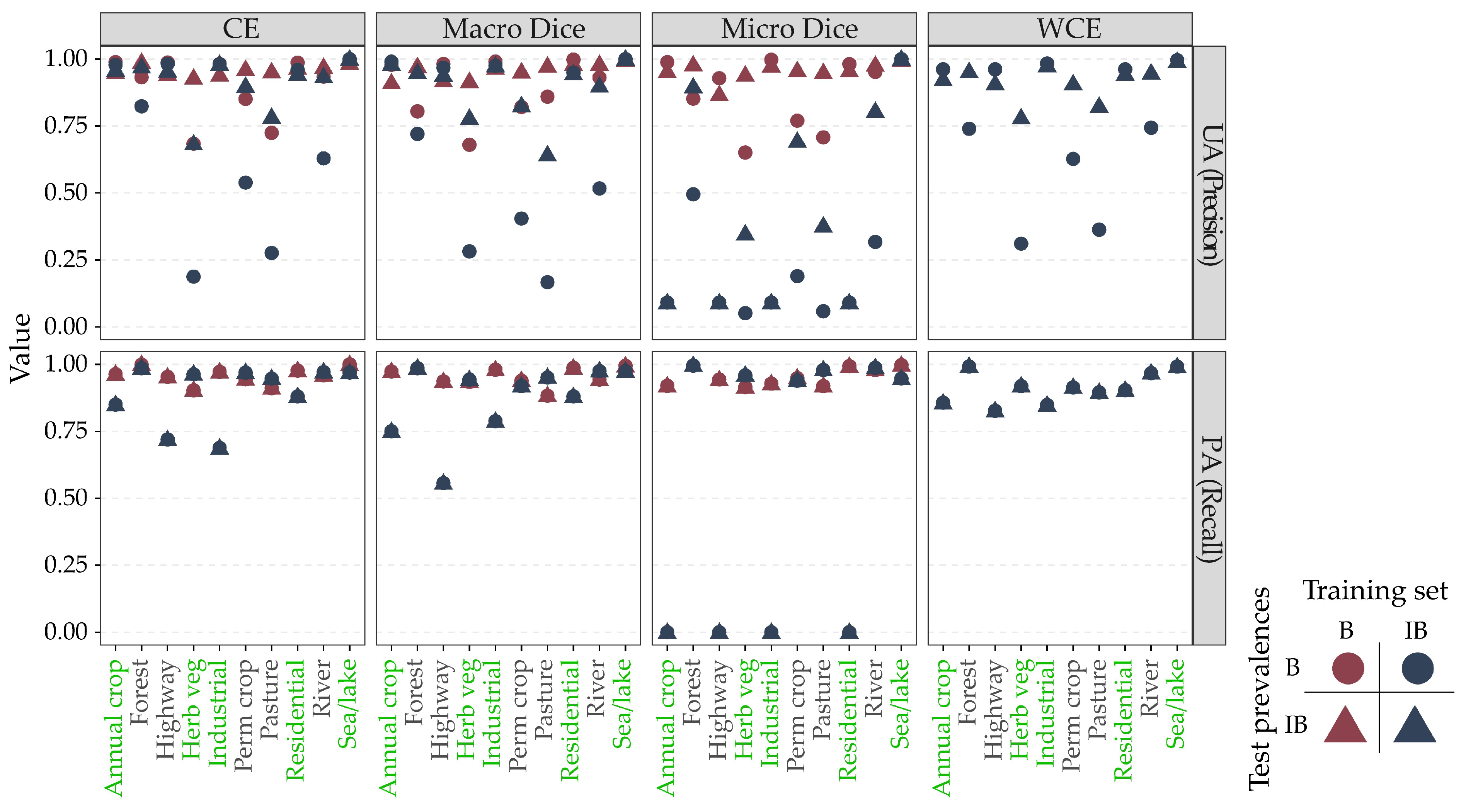
4.1. Micro- and Macro-Averaged Accuracy Assessment Metrics
4.2. Accuracy Assessment Metrics and Class Imbalance
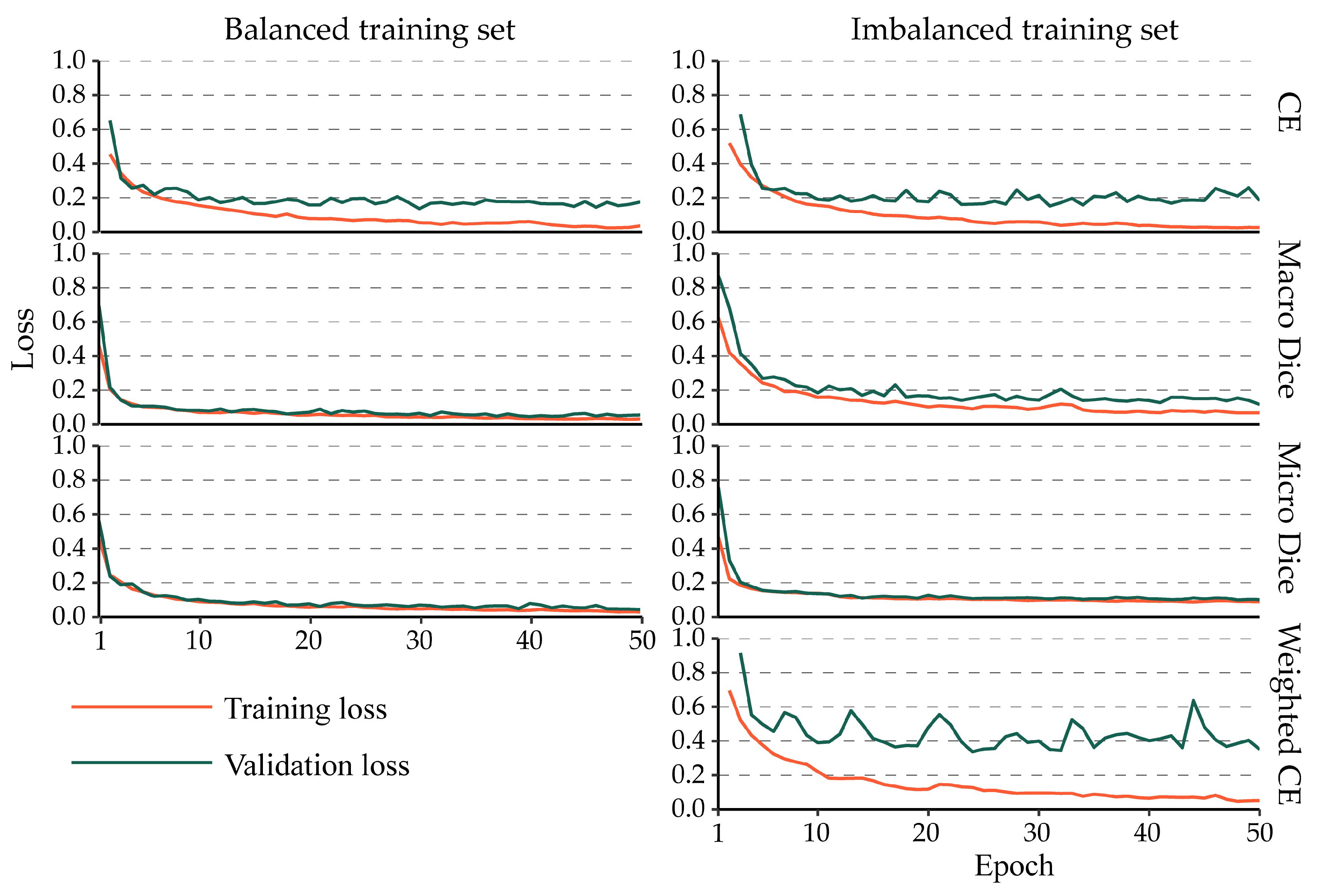
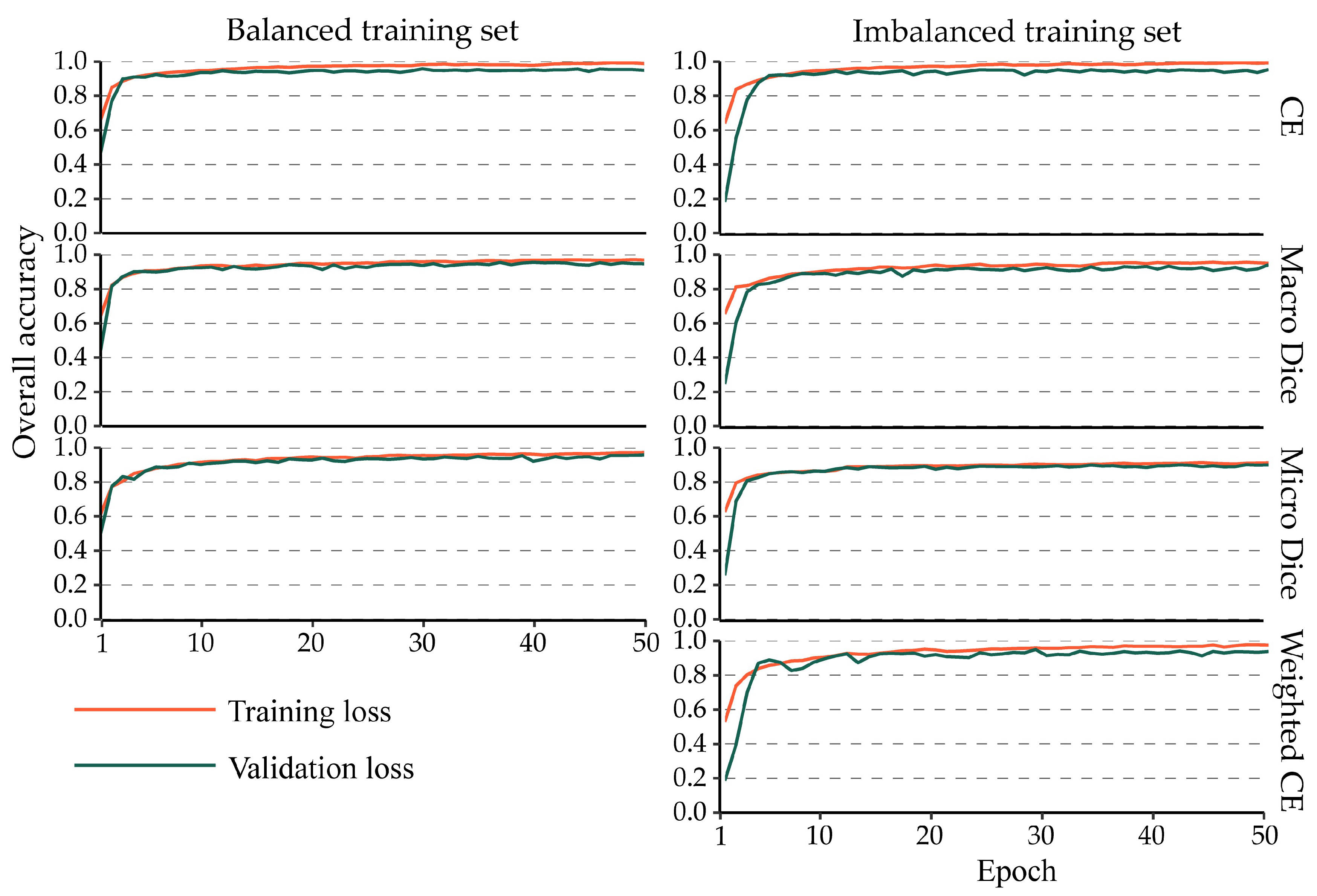
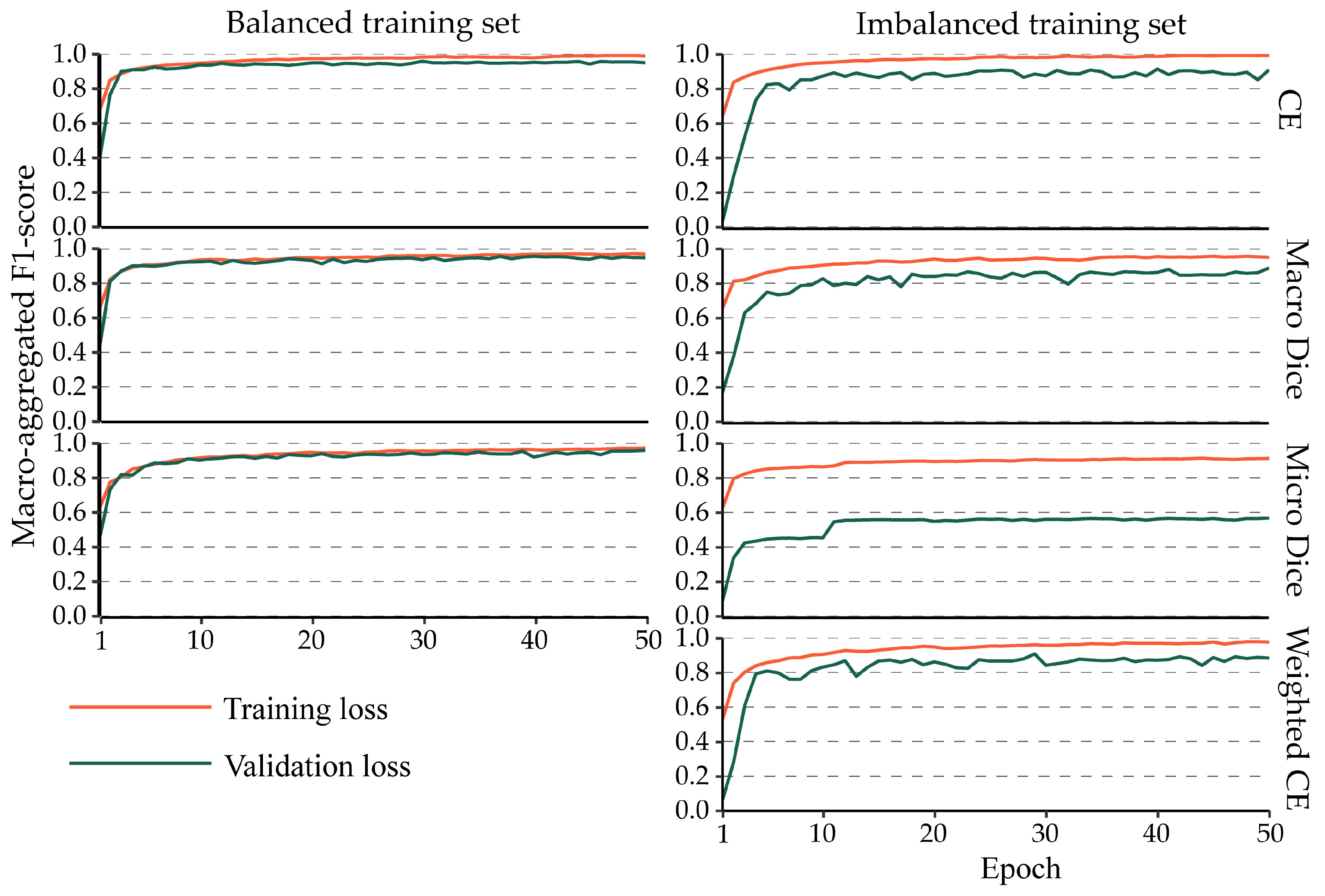
4.3. Impact of Class Imbalance on the Training Process
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Congalton, R.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Warner, T.A.; Nellis, M.D.; Foody, G.M. The SAGE Handbook of Remote Sensing; SAGE Publications, Inc.: Thousand Oaks, CA, USA, 2009. [Google Scholar] [CrossRef]
- Ma, J.; Chen, J.; Ng, M.; Huang, R.; Li, Y.; Li, C.; Yang, X.; Martel, A.L. Loss odyssey in medical image segmentation. Med. Image Anal. 2021, 71, 102035. [Google Scholar] [CrossRef]
- Yeung, M.; Sala, E.; Schönlieb, C.-B.; Rundo, L. Unified Focal loss: Generalising Dice and cross entropy-based losses to handle class imbalanced medical image segmentation. Comput. Med. Imaging Graph. 2022, 95, 102026. [Google Scholar] [CrossRef]
- Stehman, S.V.; Foody, G.M. Key issues in rigorous accuracy assessment of land cover products. Remote Sens. Environ. 2019, 231, 111199. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Guillén, L.A. Accuracy Assessment in Convolutional Neural Network-Based Deep Learning Remote Sensing Studies—Part 1: Literature Review. Remote Sens. 2021, 13, 2450. [Google Scholar] [CrossRef]
- Gowda, T.; You, W.; Lignos, C.; May, J. Macro-Average: Rare Types Are Important Too. In Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Online, 12 June 2021; pp. 1138–1157. [Google Scholar]
- Grandini, M.; Bagli, E.; Visani, G. Metrics for Multi-Class Classification: An Overview. arXiv 2020, arXiv:2008.05756. [Google Scholar]
- Stehman, S.V.; Czaplewski, R.L. Design and Analysis for Thematic Map Accuracy Assessment: Fundamental Principles. Remote Sens. Environ. 1998, 64, 331–344. [Google Scholar] [CrossRef]
- Stehman, S. Statistical Rigor and Practical Utility in Thematic Map Accuracy Assessment. Photogramm. Eng. Remote Sens. 2001, 67, 727–734. [Google Scholar]
- Stehman, S.V. Impact of sample size allocation when using stratified random sampling to estimate accuracy and area of land-cover change. Remote Sens. Lett. 2012, 3, 111–120. [Google Scholar] [CrossRef]
- Tharwat, A. Classification assessment methods. Appl. Comput. Inform. 2021, 17, 168–192. [Google Scholar] [CrossRef]
- Congalton, R.G.; Oderwald, R.G.; Mead, R.A. Assessing Landsat classification accuracy using discrete multivariate analysis statistical techniques. Photogramm. Eng. Remote Sens. 1983, 49, 1671–1678. [Google Scholar]
- Foody, G.M. Explaining the unsuitability of the kappa coefficient in the assessment and comparison of the accuracy of thematic maps obtained by image classification. Remote Sens. Environ. 2020, 239, 111630. [Google Scholar] [CrossRef]
- Pontius, R.G.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Xiao, R.; Zhong, C.; Zeng, W.; Cheng, M.; Wang, C. Novel Convolutions for Semantic Segmentation of Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5907313. [Google Scholar] [CrossRef]
- Singh, A.; Kalke, H.; Loewen, M.; Ray, N. River Ice Segmentation with Deep Learning. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7570–7579. [Google Scholar] [CrossRef]
- Zeng, Q.; Zhou, J.; Niu, X. Cross-Scale Feature Propagation Network for Semantic Segmentation of High-Resolution Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2023, 20, 6008305. [Google Scholar] [CrossRef]
- Subramanian, V. Deep Learning with PyTorch: A Practical Approach to Building Neural Network Models Using PyTorch; Packt Publishing: Birmingham, UK, 2018. [Google Scholar]
- Antiga, L.P.G.; Stevens, E.; Viehmann, T. Deep Learning with PyTorch; Manning: Shelter Island, NY, USA, 2020. [Google Scholar]
- Zhao, R.; Qian, B.; Zhang, X.; Li, Y.; Wei, R.; Liu, Y.; Pan, Y. Rethinking Dice Loss for Medical Image Segmentation. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM), Sorrento, Italy, 17–20 November 2020; pp. 851–860. [Google Scholar]
- Sudre, C.H.; Li, W.; Vercauteren, T.; Ourselin, S.; Jorge Cardoso, M. Generalised Dice Overlap as a Deep Learning Loss Function for Highly Unbalanced Segmentations. In Proceedings of the Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support, Québec City, QC, Canada, 14 September 2017; pp. 240–248. [Google Scholar]
- Li, X.; Sun, X.; Meng, Y.; Liang, J.; Wu, F.; Li, J. Dice Loss for Data-imbalanced NLP Tasks. arXiv 2020, arXiv:1911.02855. [Google Scholar]
- Bertels, J.; Eelbode, T.; Berman, M.; Vandermeulen, D.; Maes, F.; Bisschops, R.; Blaschko, M. Optimizing the Dice Score and Jaccard Index for Medical Image Segmentation: Theory & Practice. arXiv 2019, arXiv:1911.01685. [Google Scholar] [CrossRef]
- Wang, P.; Chung, A.C.S. Focal Dice Loss and Image Dilation for Brain Tumor Segmentation. In Proceedings of the Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support, Granada, Spain, 20 September 2018; pp. 119–127. [Google Scholar]
- Salehi, S.S.; Erdogmus, D.; Gholipour, A. Tversky Loss Function for Image Segmentation Using 3D Fully Convolutional Deep Networks. In Proceedings of the 8th International Workshop, MLMI 2017, Quebec City, QC, Canada, 10 September 2017. [Google Scholar]
- Abraham, N.; Khan, N.M. A Novel Focal Tversky Loss Function with Improved Attention U-Net for Lesion Segmentation. In Proceedings of the 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), Venice, Italy, 8–11 April 2019; pp. 683–687. [Google Scholar]
- Helber, P.; Bischke, B.; Dengel, A.; Borth, D. EuroSAT: A Novel Dataset and Deep Learning Benchmark for Land Use and Land Cover Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2217–2226. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- PyTorch [WWW Document], n.d. Available online: https://www.pytorch.org (accessed on 31 December 2020).
- Welcome to Python.org [WWW Document], n.d. Python.org. Available online: https://www.python.org/ (accessed on 5 January 2021).
- Bjorck, J.; Gomes, C.; Selman, B.; Weinberger, K.Q. Understanding Batch Normalization. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Buslaev, A.; Iglovikov, V.I.; Khvedchenya, E.; Parinov, A.; Druzhinin, M.; Kalinin, A.A. Albumentations: Fast and Flexible Image Augmentations. Information 2020, 11, 125. [Google Scholar] [CrossRef]
- Kuhn, M.; Vaughan, D.; Hvitfeldt, E. Yardstick: Tidy Characterizations of Model Performance. R Package Version 0.0. 2021; R Core Team: Vienna, Austria, 2021; Volume 8. [Google Scholar]
- Kuhn, M. Building Predictive Models in R Using the caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Evans, J.S.; Murphy, M.A. rfUtilities; R Core Team: Vienna, Austria, 2018. [Google Scholar]
- Pontius, R.G.; Santacruz, A. diffeR: Metrics of Difference for Comparing Pairs of Maps or Pairs of Variables; R Core Team: Vienna, Austria, 2023. [Google Scholar]
- Stehman, S.V. Estimating area and map accuracy for stratified random sampling when the strata are different from the map classes. Int. J. Remote Sens. 2014, 35, 4923–4939. [Google Scholar] [CrossRef]
- Stehman, S.V. Sampling designs for accuracy assessment of land cover. Int. J. Remote Sens. 2009, 30, 5243–5272. [Google Scholar] [CrossRef]
- Stehman, S. A Critical Evaluation of the Normalized Error Matrix in Map Accuracy Assessment. Photogramm. Eng. Remote Sens. 2004, 70, 743–751. [Google Scholar] [CrossRef]
- Stehman, S.V. Basic probability sampling designs for thematic map accuracy assessment. Int. J. Remote Sens. 1999, 20, 2423–2441. [Google Scholar] [CrossRef]
- Stehman, S.V. Comparison of systematic and random sampling for estimating the accuracy of maps generated from remotely sensed data. Photogramm. Eng. Remote Sens. 1992, 58, 1343–1350. [Google Scholar]
- Stehman, S.V.; Wagner, J.E. Choosing a sample size allocation to strata based on trade-offs in precision when estimating accuracy and area of a rare class from a stratified sample. Remote Sens. Environ. 2024, 300, 113881. [Google Scholar] [CrossRef]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Ghosh, K.; Bellinger, C.; Corizzo, R.; Branco, P.; Krawczyk, B.; Japkowicz, N. The class imbalance problem in deep learning. Mach. Learn. 2022. [Google Scholar] [CrossRef]
- Johnson, J.M.; Khoshgoftaar, T.M. Survey on deep learning with class imbalance. J. Big Data 2019, 6, 27. [Google Scholar] [CrossRef]
- Ding, W.; Huang, D.Y.; Chen, Z.; Yu, X.; Lin, W. Facial action recognition using very deep networks for highly imbalanced class distribution. In Proceedings of the 2017 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Kuala Lumpur, Malaysia, 12–15 December 2017; pp. 1368–1372. [Google Scholar]


| Reference | ||||||
|---|---|---|---|---|---|---|
| A | B | C | Row Total | UA | ||
| Classification | A | PAA | PAB | PAC | PA+ | PAA/PA+ |
| B | PBA | PBB | PBC | PB+ | PBB/PB+ | |
| C | PCA | PCB | PCC | PC+ | PCC/PC+ | |
| Column total | P+A | P+B | P+C | |||
| PA | PAA/P+A | PBB/P+B | PCC/P+C | |||
| Reference Data | |||||
|---|---|---|---|---|---|
| Positive | Negative | 1 – Commission Error | |||
| Classification Result | Positive | TP | FP | Precision | |
| Negative | FN | TN | NPV | ||
| 1 – omission error | Recall | Specificity | |||
| Type of Classification | Metric | Equation | Comments |
|---|---|---|---|
| Binary and multiclass | Overall accuracy (OA) | or | |
| Multiclass | User’s accuracy (UA) | 1 – commission error | |
| Producer’s accuracy (PA) | 1 – omission error | ||
| Binary | Recall | PA for positives (1 – positive case omission error) | |
| Precision | UA for positives (1 – positive case commission error) | ||
| Specificity | PA for negatives (1 – negative case omission error) | ||
| Negative predictive value (NPV) | UA for negatives (1 – negative case commission error) | ||
| F1-score (Dice score) | or |
| Loss | Equation |
|---|---|
| Binary cross-entropy (BCE) loss | |
| Cross-entropy (CE) loss | |
| Weighted CE loss |
| Band | B1 | B2 | B3 | B4 | B5 | B6 | B7 | B8 | B8a | B9 | B10 | B11 | B12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Central wavelength (nm) | 443 | 490 | 560 | 665 | 705 | 740 | 783 | 842 | 865 | 940 | 1375 | 1610 | 2190 |
| Description | Ultra blue | Blue | Green | Red | RE1 | RE2 | RE3 | NIR | NIR (narrow) | Water vapor | Cirrus cloud | SWIR 1 | SWIR 2 |
| Used in our experiment | Y | Y | Y | Y | Y | Y | Y | Y | Y | Y |
| Training | Validation | Testing | |||
|---|---|---|---|---|---|
| Balanced | Imbalanced | Balanced | Imbalanced | Both | |
| Annual crop | 1400 | 140 | 400 | 40 | 300 |
| Forest | 1400 | 1400 | 400 | 400 | 300 |
| Herb veg | 1400 | 140 | 400 | 40 | 300 |
| Highway | 1400 | 1400 | 400 | 400 | 250 |
| Industrial | 1400 | 140 | 400 | 40 | 250 |
| Pasture | 1400 | 1400 | 400 | 400 | 200 |
| Perm crop | 1400 | 1400 | 400 | 400 | 250 |
| Residential | 1400 | 140 | 400 | 40 | 300 |
| River | 1400 | 1400 | 400 | 400 | 250 |
| Sea/Lake | 1400 | 140 | 400 | 40 | 359 |
| Total | 14,000 | 7700 | 4000 | 2200 | 2509 |
| Reference | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Annual Crop | Forest | Herb Veg | Highway | Industrial | Pasture | Perm Crop | Residential | River | Sea/ Lake | Row Total | UA | ||
| Classification | Annual crop | 15.45 | 0.00 | 0.30 | 0.00 | 0.00 | 0.00 | 0.04 | 0.00 | 0.00 | 0.00 | 15.79 | 0.979 |
| Forest | 0.24 | 1.79 | 0.12 | 0.00 | 0.00 | 0.02 | 0.00 | 0.00 | 0.00 | 0.00 | 2.18 | 0.825 | |
| Herb veg | 0.06 | 0.00 | 13.09 | 0.01 | 0.07 | 0.03 | 0.01 | 0.06 | 0.00 | 0.00 | 13.33 | 0.982 | |
| Highway | 0.30 | 0.00 | 0.91 | 1.75 | 4.73 | 0.01 | 0.01 | 1.58 | 0.04 | 0.00 | 9.33 | 0.188 | |
| Industrial | 0.00 | 0.00 | 0.00 | 0.00 | 12.51 | 0.00 | 0.00 | 0.24 | 0.00 | 0.00 | 12.75 | 0.981 | |
| Pasture | 0.61 | 0.02 | 0.85 | 0.00 | 0.00 | 1.76 | 0.01 | 0.00 | 0.01 | 0.00 | 3.27 | 0.539 | |
| Perm crop | 1.52 | 0.00 | 2.67 | 0.03 | 0.00 | 0.00 | 1.72 | 0.30 | 0.00 | 0.00 | 6.24 | 0.276 | |
| Residential | 0.00 | 0.00 | 0.00 | 0.01 | 0.65 | 0.00 | 0.01 | 16.00 | 0.00 | 0.00 | 16.68 | 0.959 | |
| River | 0.00 | 0.00 | 0.24 | 0.01 | 0.22 | 0.00 | 0.01 | 0.00 | 1.77 | 0.56 | 2.81 | 0.630 | |
| Sea/lake | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 17.62 | 17.62 | 1.000 | |
| Column total | 18.18 | 1.82 | 18.18 | 1.82 | 18.18 | 1.82 | 1.82 | 18.18 | 1.82 | 18.18 | |||
| PA | 0.850 | 0.987 | 0.720 | 0.964 | 0.688 | 0.970 | 0.948 | 0.880 | 0.972 | 0.969 | |||
| Micro | Macro | |||||
|---|---|---|---|---|---|---|
| OA | UA (Precision) | PA (Recall) | F1-Score | UA (Precision) | PA (Recall) | F1-Score |
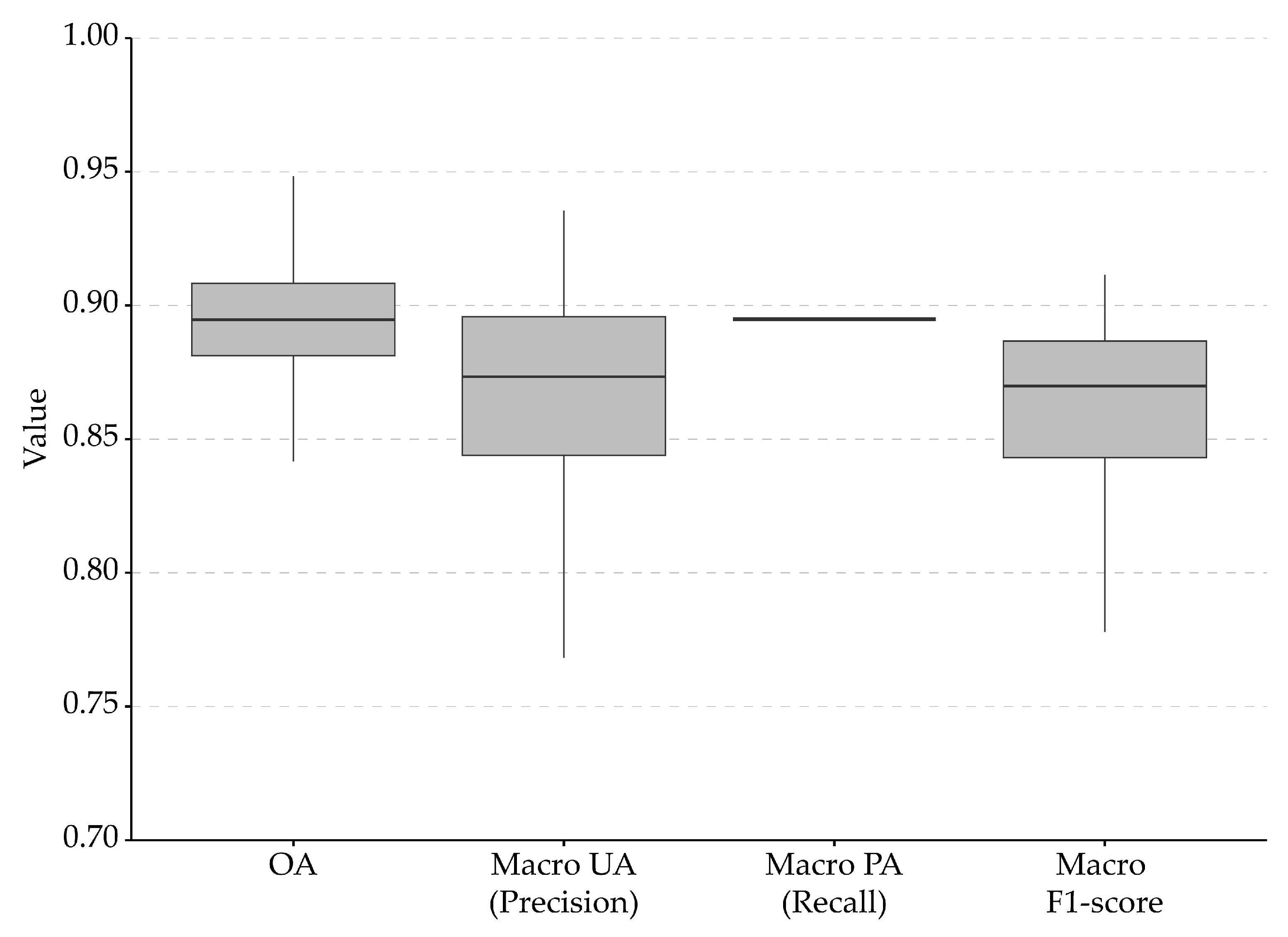
| 0.835 | 0.835 | 0.835 | 0.835 | 0.736 | 0.895 | 0.755 |
| Loss Metric | Training Set | Test Prevalences | OA | Macro-F1 | Macro-UA (Precision) | Macro-PA (Recall) |
|---|---|---|---|---|---|---|
| CE | Balanced | Balanced | 0.959 | 0.958 | 0.959 | 0.959 |
| Balanced | Imbalanced | 0.970 | 0.929 | 0.907 | 0.958 | |
| Imbalanced | Balanced | 0.895 | 0.895 | 0.911 | 0.895 | |
| Imbalanced | Imbalanced | 0.835 | 0.755 | 0.736 | 0.894 | |
| Weighted CE | Imbalanced | Balanced | 0.912 | 0.912 | 0.916 | 0.912 |
| Imbalanced | Imbalanced | 0.890 | 0.804 | 0.765 | 0.911 | |
| Micro-Dice (OA) | Balanced | Balanced | 0.954 | 0.954 | 0.955 | 0.954 |
| Balanced | Imbalanced | 0.956 | 0.913 | 0.883 | 0.954 | |
| Imbalanced | Balanced | 0.581 | 0.466 | 0.452 | 0.581 | |
| Imbalanced | Imbalanced | 0.261 | 0.264 | 0.251 | 0.581 | |
| Macro-Dice | Balanced | Balanced | 0.956 | 0.956 | 0.957 | 0.956 |
| Balanced | Imbalanced | 0.971 | 0.927 | 0.904 | 0.956 | |
| Imbalanced | Balanced | 0.873 | 0.872 | 0.894 | 0.873 | |
| Imbalanced | Imbalanced | 0.805 | 0.712 | 0.697 | 0.872 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farhadpour, S.; Warner, T.A.; Maxwell, A.E. Selecting and Interpreting Multiclass Loss and Accuracy Assessment Metrics for Classifications with Class Imbalance: Guidance and Best Practices. Remote Sens. 2024, 16, 533. https://doi.org/10.3390/rs16030533
Farhadpour S, Warner TA, Maxwell AE. Selecting and Interpreting Multiclass Loss and Accuracy Assessment Metrics for Classifications with Class Imbalance: Guidance and Best Practices. Remote Sensing. 2024; 16(3):533. https://doi.org/10.3390/rs16030533
Chicago/Turabian StyleFarhadpour, Sarah, Timothy A. Warner, and Aaron E. Maxwell. 2024. "Selecting and Interpreting Multiclass Loss and Accuracy Assessment Metrics for Classifications with Class Imbalance: Guidance and Best Practices" Remote Sensing 16, no. 3: 533. https://doi.org/10.3390/rs16030533
APA StyleFarhadpour, S., Warner, T. A., & Maxwell, A. E. (2024). Selecting and Interpreting Multiclass Loss and Accuracy Assessment Metrics for Classifications with Class Imbalance: Guidance and Best Practices. Remote Sensing, 16(3), 533. https://doi.org/10.3390/rs16030533







