Abstract
Accurate quantitative precipitation estimation (QPE) is fundamental for a large number of hydrometeorological applications, especially when addressing extreme rainfall phenomena. This paper presents a comprehensive comparison of various rainfall estimation methods, specifically those relying on weather radar data, rain gauge data, and their fusion. The study evaluates the accuracy and reliability of each method in estimating rainfall for a severe event that occurred in Tuscany, Italy. The results obtained confirm that merging radar and rain gauge data outperforms both individual approaches by reducing errors and improving the overall reliability of precipitation estimates. This study highlights the importance of data fusion in enhancing the accuracy of QPE and also supports its application in operational contexts, providing further evidence for the greater reliability of merging methods.
1. Introduction
Quantitative precipitation estimation (QPE) is a critical element in meteorology and hydrology, making accurate QPE methods essential for numerous applications, including flood forecasting. QPE methods typically employ data from two types of instrument: rain gauges and weather radars. Given the specific advantages and limitations of each instrument, the information about rainfall provided by these instruments are somehow complementary. Therefore, their combination represents a solid ground for achieving accurate precipitation estimation.
Rain gauges measure precipitation directly, providing highly accurate data on the amount of rainfall at specific locations. Given their precision, these instruments are used for calibrating and validating other precipitation estimation methods. However, rain gauge measurements may be affected by errors, both systematic and random, depending on the atmospheric conditions and the type of rain gauge [1,2]. Taking into account the point-wise nature of rain gauges, the rainfall measurements need to be spatially interpolated in order to generate a 2D rainfall map; for this purpose, deterministic (e.g., inverse distance weighting [3]) or geostatistical (e.g., kriging [4]) techniques are typically used (see [5,6] for a comparison). The nature of these instruments also represents their main limitation: in fact, a dense gauge network is required to capture the spatial variability of the rainfall patterns, especially in case of severe small-scale phenomena.
Weather radars, on the contrary, can monitor precipitation over large areas with high temporal and spatial resolution. Radars emit microwave pulses and measure the power backscattered from an ensemble of hydrometeors, providing a practically continuous monitoring of the spatial distribution of rainfall and of its intensity [7]. Despite their broad coverage and excellent resolution, both in time and space, radar-based QPE is subject to several sources of error, including signal attenuation due to rainfall itself, ground clutter and beam blockage [8]. Moreover, radars do not provide direct rainfall measures; thus, a conversion is required to obtain the QPE. This conversion is typically made by resorting to the so-called Z–R relationship [9]:
which relates the reflectivity factor Z (expressed in mm6·m−3), a parameter derived from the backscattered power measured by the radar, and the rainfall rate R (expressed in mm·h−1). Unfortunately, the choice of the coefficients a and b is critical. In fact, both Z and R depend on the drop size distribution (DSD), which is influenced by the type of event, the geographical area and the climatic conditions [8,10,11]. As a result, a and b are highly variable [12], and using the Z–R relation with a priori fixed coefficients can lead to significant rainfall estimation errors [13].
Since the advent of polarimetric (dual-polarized) radars, their use in meteorology has significantly increased. The additional variables they provide, such as differential reflectivity, differential phase, and specific attenuation, are instrumental in enhancing rainfall estimation [14,15]. In fact, using polarimetric variables—either alone or in combination—instead of only Z has been shown to improve the accuracy of rainfall rate estimates [16,17]. Furthermore, rainfall estimation through Z benefits from supplementary information on DSD and the hydrometeor type provided by the polarimetric parameters, allowing for the selection of an appropriate Z–R relationship that can be dynamically adjusted. Polarimetric data also help to reduce several sources of error previously mentioned, such as signal attenuation in rain [14,18], which is particularly important for C-band and X-band weather radars. However, as highlighted in [19], polarimetry cannot overcome the inherent limitations of radar in measuring rainfall, namely that it is measured indirectly and often at considerable heights and distances.
Due to the complementary features and issues of rain gauges and weather radars, the merging of their data can be usefully exploited to mitigate their limitations and to enhance the QPE accuracy. The advantages of combining these two instruments are well documented in the literature. In fact, numerous studies comparing QPE methods have shown that fusion strategies lead to superior estimation performance compared to using either radar or rain gauges alone (except when very dense rain gauge networks are available [19]). How to merge rain gauge and radar data has been investigated over several years, and various methods with different approaches have been developed. One criterion with which the different approaches can be categorized is based on how the two data types are employed during the fusion procedure [19].
Methods belonging to the geostatistical interpolation category use the rainfall point measurements provided by rain gauges as a primary quantitative information source and the radar rainfall field as auxiliary spatial information to improve the accuracy of the estimation. These methods derive mostly from the kriging technique and the most popular is that of kriging with external drift (KED), in which the external auxiliary variable (i.e., the radar-based QPE) is incorporated into the interpolation process of the primary variable (i.e., rainfall data provided by rain gauges) [4]. This category also includes the conditional merging (CM), in which the kriging-based QPE is corrected by adding an error obtained from radar rainfall observations [20]. According to multiple studies [19], KED generally outperforms other geostatistical interpolation methods and is considered the most reliable and preferred technique for merging rain gauge and radar data.
Different merging approaches consist of adjusting the radar-based QPE by exploiting the rain gauge measurements. In these kinds of methods—typically called radar bias adjustment methods because they address the issue of systematic bias in radar data—a multiplicative or additive correction factor obtained by comparing radar estimates with rain gauge measures is applied to the radar rainfall field. The simplest and most widely used method in this category is the mean field bias (MFB) adjustment, in which a spatially constant multiplicative correction factor is used [9]. Thanks to its simplicity, the mean field bias (MFB) adjustment is one of the most commonly adopted merging methods by national meteorological services for operational applications [19]. Other adjustment methods, such as that proposed by Brandes (Brandes spatial adjustment, BSA) [21], consider a correction factor that varies in space, so as to take into account the nonuniform bias across the radar coverage area. Also, the method presented in [22], which employs a space–time-varying Z–R relationship to account for the variable nature of the DSD, can be classified as a local bias adjustment method. Unlike MFB and BSA, which use radar-based QPE as the background field, this fusion approach, named the space-time adaptive coefficient conversion (STACC), utilizes the space–time average of the radar reflectivity factor. Rain gauge data are still used as true rainfall values to minimize the local bias between radar observations and rain gauge measurements; however, in STACC, they are exploited to dynamically calibrate the Z–R relationship. While radar bias adjustment methods are typically outperformed by geostatistical interpolation techniques [19], the STACC method has demonstrated superior robustness compared to the KED and CM in regions with a sparse rain gauge network and during intense rainfall events [23].
A third category of merging methods is radar–rain gauge integration, in which neither radar nor rain gauges serve as the primary source of rainfall data. In these methods, the rainfall at a specific location is estimated as a weighted average of both radar and rain gauge data, aiming to minimize overall estimation uncertainties [19]. The two principal methods within this category are co-kriging (CoK) [24], in which radar and rain gauge data are integrated in a single kriging system, and Bayesian data merging (BAY) [25], which minimizes overall estimation uncertainties by combining each individual data source after defining and quantifying the uncertainty associated with each. Due to the complexity involved in both formulation and implementation, as well as the computational cost, the use of these methods in operational contexts is particularly challenging. Consequently, only a limited number of studies have evaluated their performance and compared them to other QPE merging methods [19]. Based on these studies, CoK has demonstrated poorer performance compared to KED and BAY, while BAY have outperformed MFB, BSA, and KRE, exhibiting similar results to those of KED [19].
In this study, we aim to evaluate various QPE methods in the context of convective rainfall events, which pose significant challenges for accurate flood forecasting. Indeed, convective storms are characterized by intense, localized precipitation that are difficult to predict and can lead to flash flooding, resulting in extensive damage. Consequently, assessing the performance of QPE techniques under these severe conditions is critical for improving the accuracy and reliability of flood prediction models. Based on data collected during a severe convective rainfall event that occurred in Tuscany, Italy, we present a comparison of different QPE methods that rely solely on rain gauge data, solely on radar data, and on their fusion. Specifically, we consider merging methods belonging to the categories of geostatistical interpolation and radar bias adjustment. The paper is structured as follows: in Section 2, we first describe the rainfall event examined and the employed radar and rain gauge datasets; then, we introduce the different QPE methods considered, as well as the procedure adopted to evaluate and compare them. The experimental results are shown in Section 3 and discussed in Section 3. Finally, in Section 5, we draw some concluding remarks.
2. Materials and Methods
2.1. Meteorological Event Description
The information that follows, concerning the meteorological phenomenon considered in this study, comes from the meteorological report provided by the LaMMA (Environmental Modeling and Monitoring Laboratory for Sustainable Development) Consortium [26], to which the reader is referred for further details.
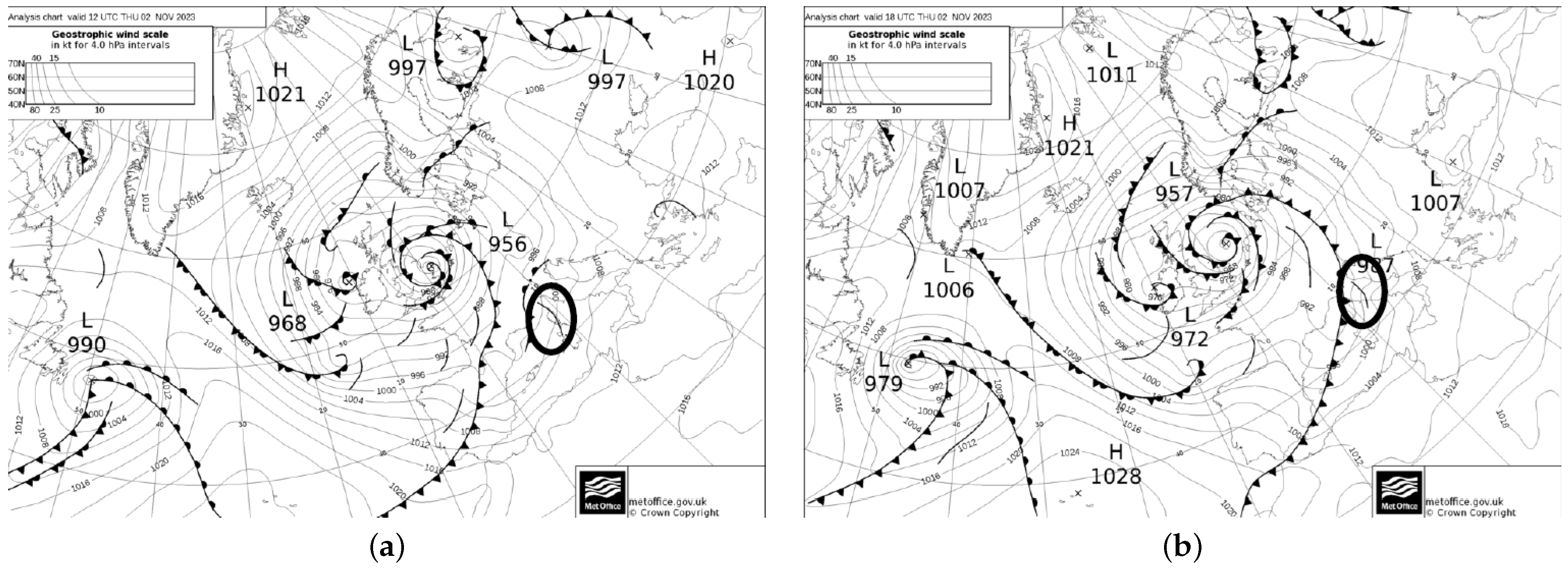
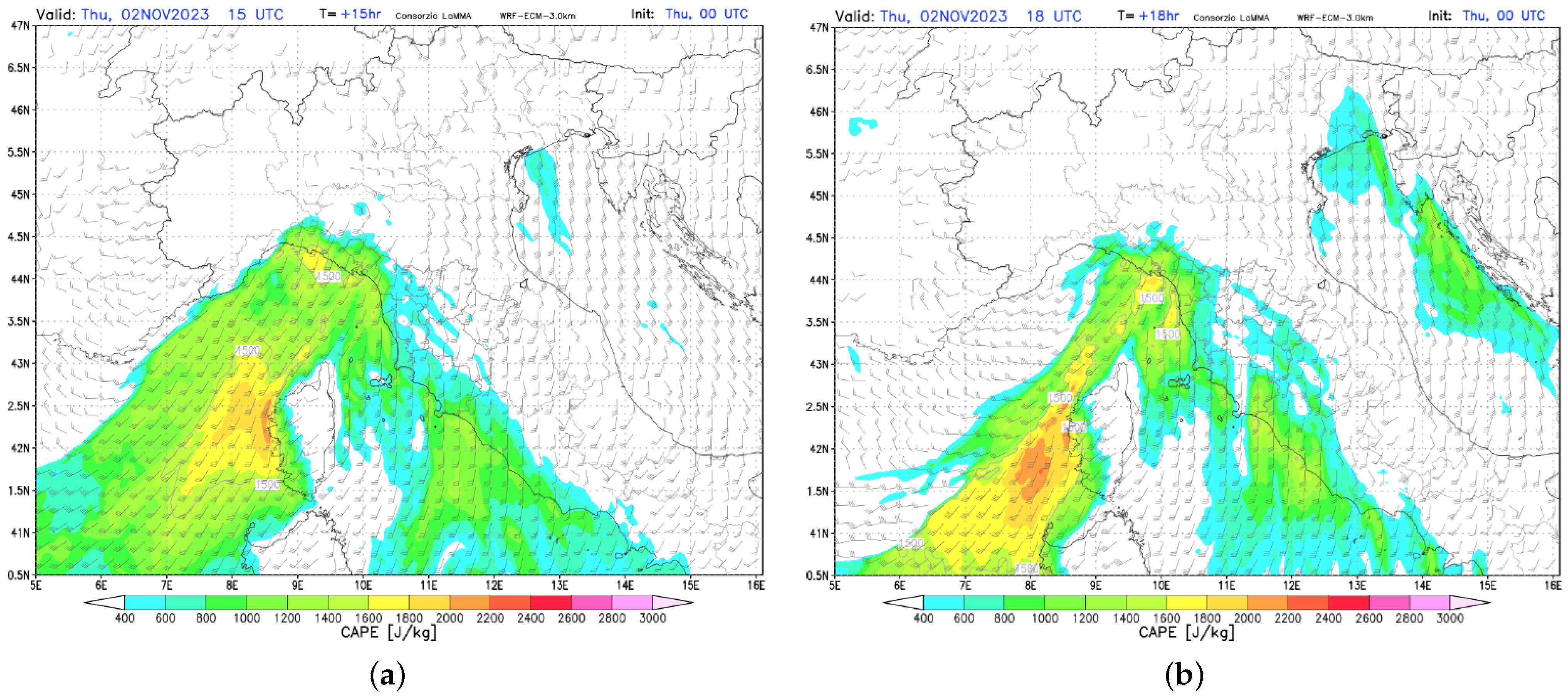
In the afternoon of 2 November 2023, in Tuscany, the movement of a relatively stationary instability line (Figure 1) ahead of a cold front facilitated the development of several thunderstorms. These storms were intensified by an energetically favorable atmosphere—meaning a major ability of supporting strong and sustained upward air movements that can trigger cloud formation and storms (see the high potential energy level in Figure 2)—along with highly humid low-level conditions, leading to an intense localized precipitation. Specifically, starting at 15:30 UTC, the convergence of strong winds in the southern parts of the region with the gradual influx of winds affecting the northern parts (see wind barbs in Figure 2), combined with the advance of cooler air aloft and favorable conditions in the lower levels, led to the formation of a thunderstorm line. This system remained nearly stationary until 20:30 UTC, extending from the provinces of Livorno and Pisa to the provinces of Pistoia, Prato, and Florence (see Figure 4, Section 2.2.1). The location, intensity, and stationary nature of this thunderstorm system exhibited nonlinear characteristics and presented significant forecasting challenges. As a result of the heavy precipitation (see Figure 6, Section 3.1), some rivers and creeks flooded, causing extensive damages to the environment and affecting local communities.
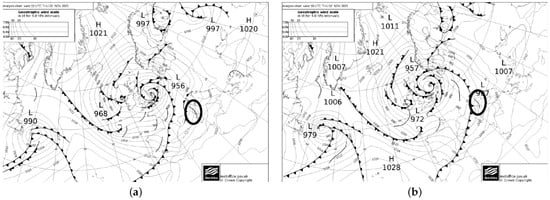
Figure 1.
Instability fronts and lines, 2 November 2023: (a) 12:00 UTC; (b) 18:00 UTC (source: MetOffice, U.K.). The instability line affecting Tuscany is circled in black. The figures are taken from [26].
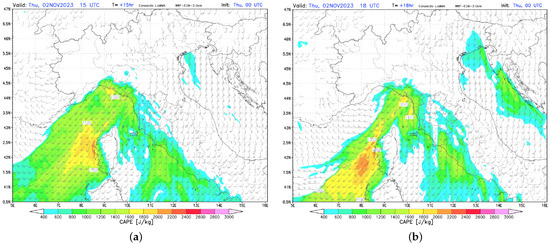
Figure 2.
Convective available potential energy (CAPE) and wind barbs, 2 November 2023: (a) 15:00 UTC; (b) 18:00 UTC. The figures are taken from [26].
2.2. Datasets
2.2.1. Radar Dataset
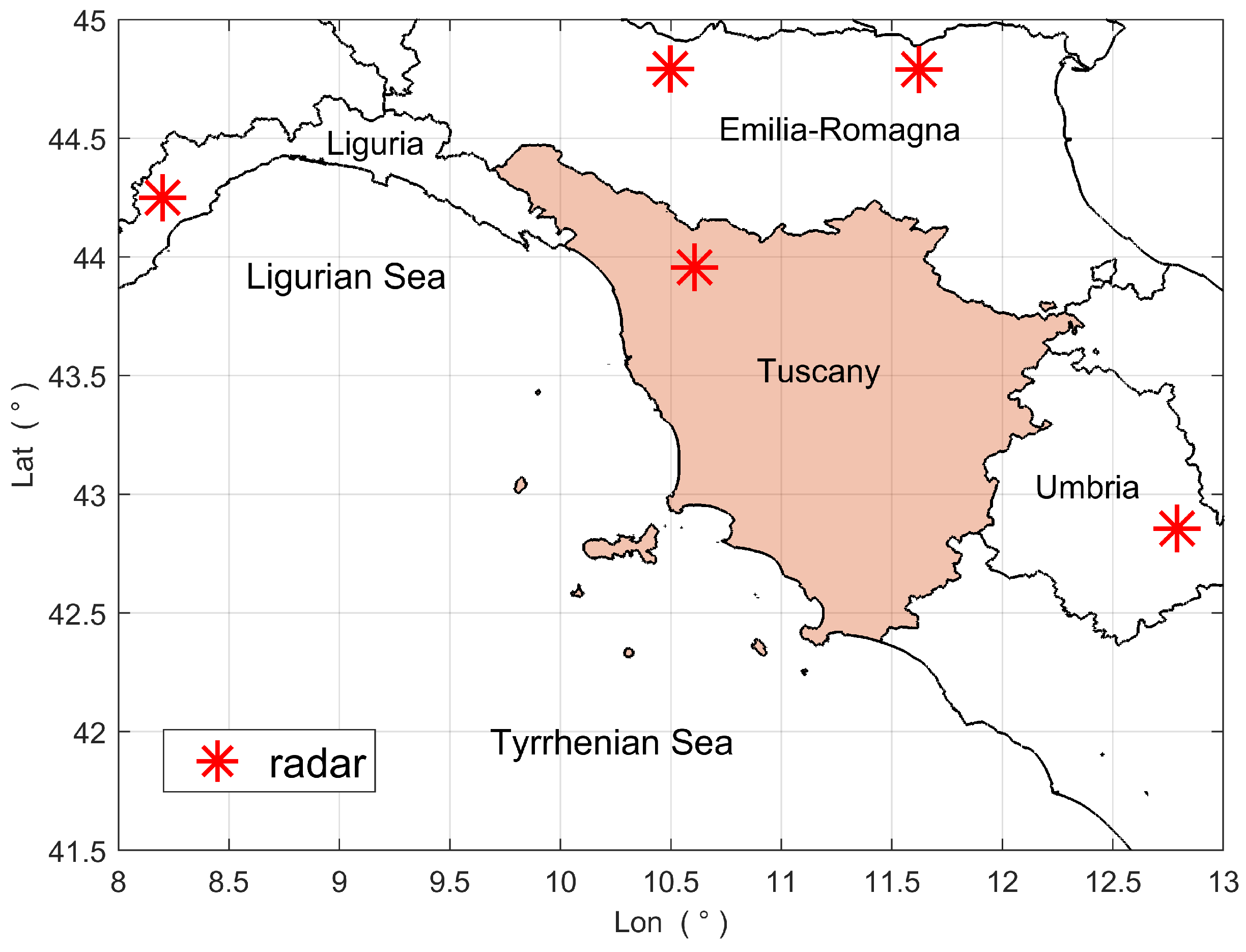
The weather radar data used in this study were collected by the Italian national weather radar network. Managed by the Italian National Civil Protection Department (DPCN), the network consists of 26 radar systems (22 C-band radars and 4 X-band radars, most of them dual-polarized) distributed to cover the entire national territory. Figure 3 shows the radar systems of the network that cover Tuscany. Specifically, these systems are C-band dual-polarized radars located in Monte Crocione (Tuscany, lat: 43.96°, lon: 10.61°, height: 1017 m a.s.l.), Monte Settepani (Liguria, lat: 44.25°, lon: 8.20°, height: 1390 m a.s.l.), Gattatico (Emilia Romagna, lat: 44.79°, lon: 10.50°, height: 34 m a.s.l.), San Pietro Capofiume (Emilia Romagna, lat: 44.66°, lon: 11.62°, height: 10 m a.s.l.), and Monte Serano (Umbria, lat: 42.86°, lon: 12.79°, height: 1428 m a.s.l.).
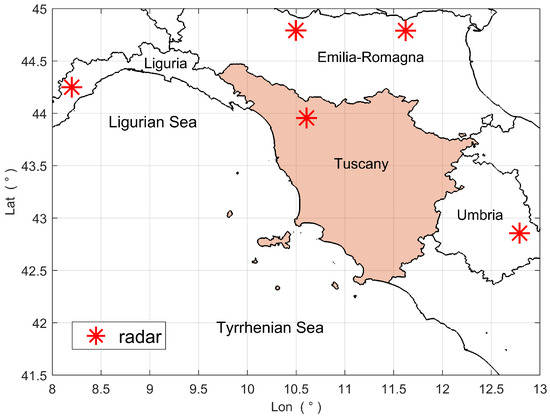
Figure 3.
Radar systems of the Italian national weather radar network that cover Tuscany. The red asterisks mark the radar sites, while the black lines indicate the Italian regional boundaries (Tuscany is highlighted in orange).
The radars of the network perform synchronous scans every 5 min. The raw data from all systems are processed by the DPCN, which performs several corrections (including ground clutter, partial beam blockage, and attenuation [17]), and afterward provides national-scale composite products derived from mosaicking. The radar reflectivity composite products include Constant Altitude Plan Position Indicator (CAPPI)—namely, the reflectivity at a specific altitude (from 1000 m up to 7000 m) obtained by interpolating data from scans made at multiple elevation angles—and Vertical Maximum Intensity (VMI), that is the maximum reflectivity value detected vertically above each ground pixel.
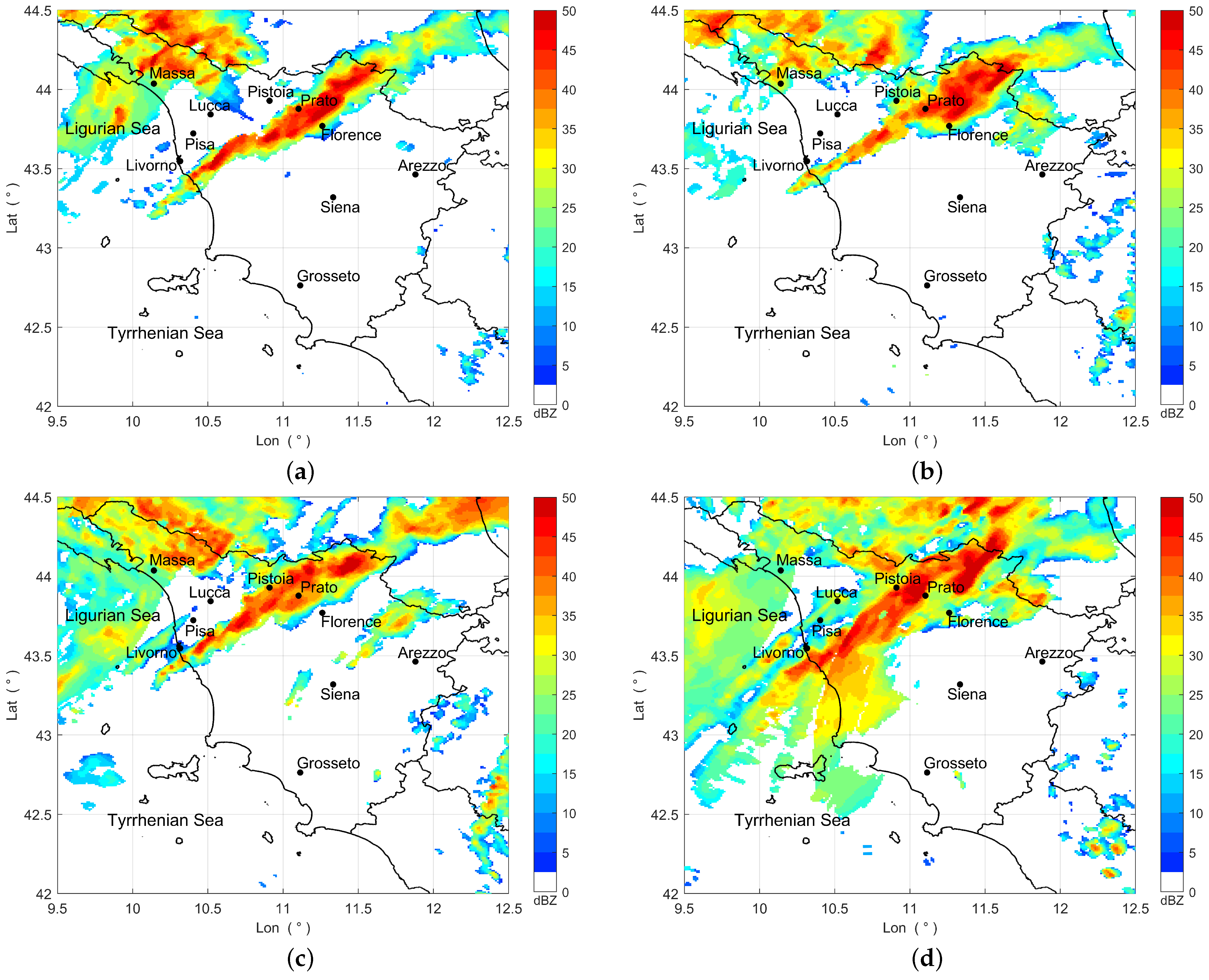
When facing the problem of merging radar and rain gauge data for QPE, the height of radar observations must be carefully considered, as it has an impact on estimation accuracy. In fact, several factors are involved in the choice of the most appropriate height for the reflectivity product, including local orography and topography, which may cause beam blockage and ground clutter, as well as vertical variations in precipitation resulting from evaporation, wind shear, and changes in hydrometeor type [8]. Considering the specific orography of Tuscany—particularly the presence of the Apennine mountain chain in the northern, eastern, and central areas of the region, with several peaks exceeding 1500 m—we chose to use the CAPPI radar reflectivity at an altitude of 2000 m. In this way, it is possible to balance the previously mentioned issues and achieve a reasonable compromise. The chosen reflectivity product, available with a time step of 10 min and a spatial resolution of 1 × 1 km2 (when mapped onto the x–y Cartesian coordinate system), is illustrated in Figure 4, which shows samples at different times on 2 November 2023. As can be seen, the stationary high-reflectivity stripe extending from the provinces of Livorno and Pisa to the provinces of Pistoia, Prato, and Florence represents the thunderstorm line that affected Tuscany beginning in the afternoon. Unfortunately, several uncorrected radar artifacts are evident, particularly in panel d. A comparison between Figure 3 and Figure 4d reveals beam blockage effects associated with the Monte Crocione (Tuscany) radar and highlights the extreme edge of the coverage provided by the Monte Serano (Umbria) and Monte Settepani (Liguria) radars. These artifacts are probably caused by an imperfect correction of the raw radar data, as well as an imperfect mosaicking of data from each individual radar. Certainly, this can be a factor that affects radar QPE and merging performance; in particular, it can be considered an operational (infrastructural) factor [19], since the reflectivity data are an elaborated product distributed by the DPCN.
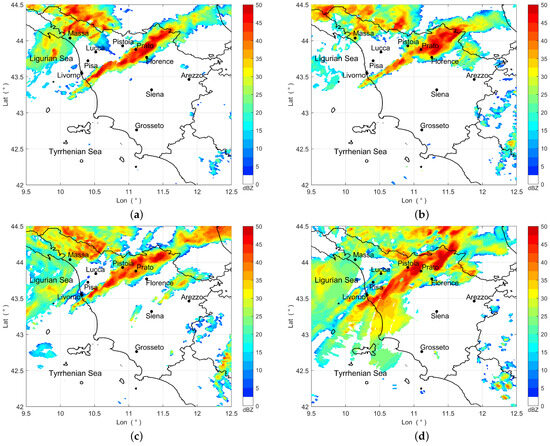
Figure 4.
CAPPI product at a height of 2000 m on 2 November 2023: (a) 16:00 UTC; (b) 17:00 UTC; (c) 18:00 UTC; (d) 19:00 UTC. The black lines indicate regional boundaries.
2.2.2. Rain Gauge Dataset
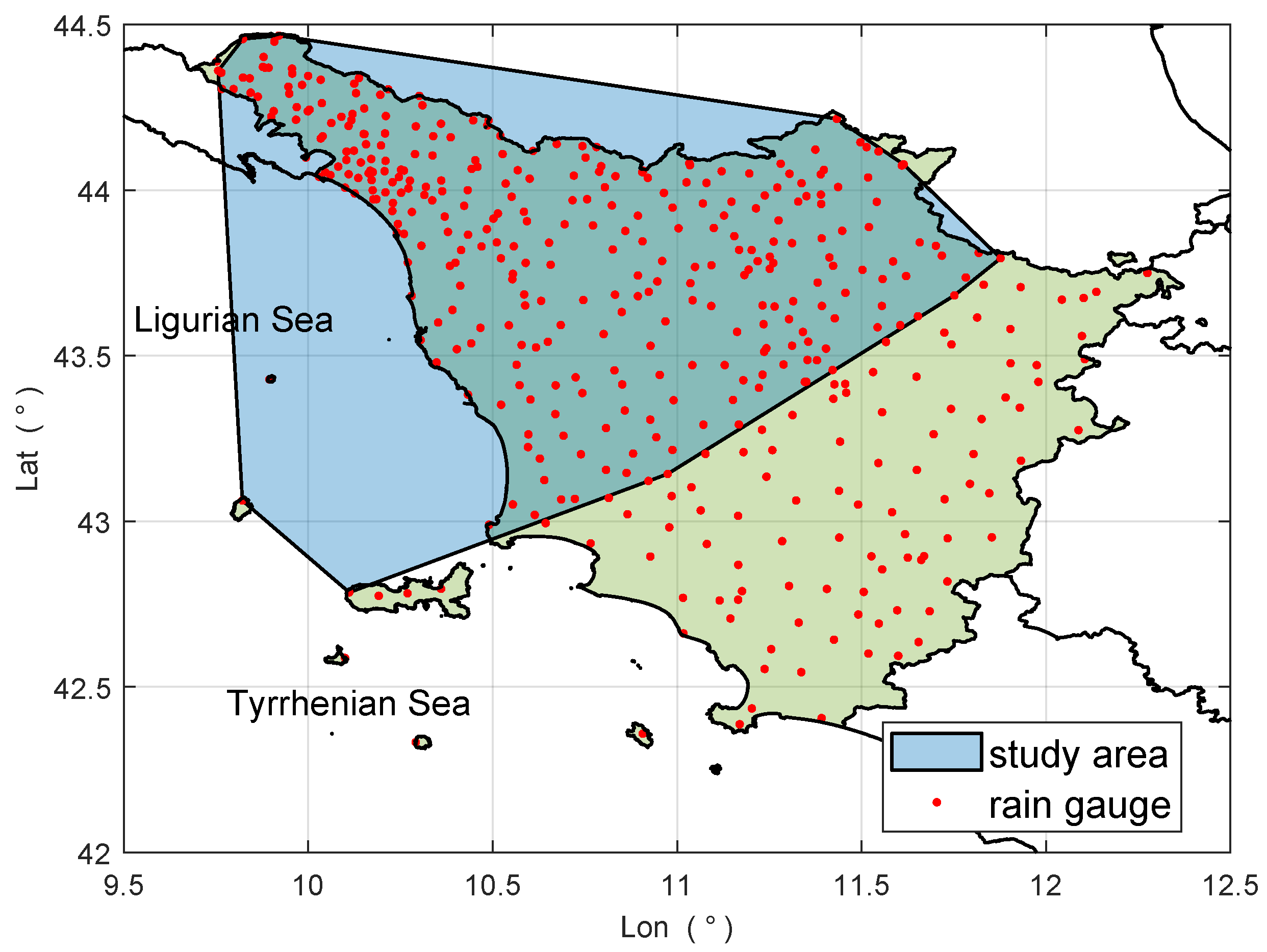
In this study, we used rainfall data from the rain gauge network of Tuscany, which is illustrated in Figure 5. The network is composed of 425 tipping-bucket rain gauges located across the entire 22,987 km2 area of Tuscany, which means approximately one gauge every 54 km2. Near real-time measurements of accumulated rainfall at 15-min intervals, recorded by all available stations, are made accessible online through a dedicated platform [27].
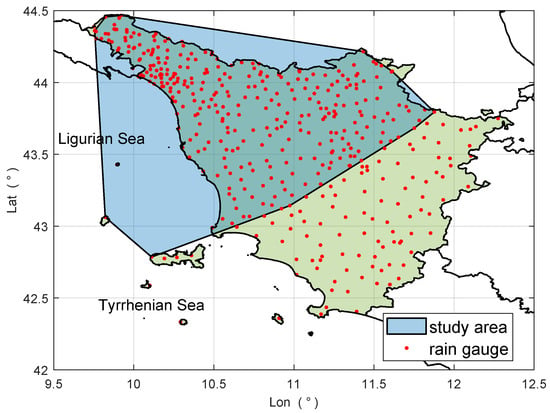
Figure 5.
Rain gauge network of Tuscany (total number of gauges: 425). Each rain gauge location is marked by a red dot, while the black lines indicate the Italian regional boundaries (Tuscany is highlighted in green). The study area is represented by the cyan polygon and contains 323 rain gauges.
By means of the rain gauge data, we defined the “study area” through the following procedure. First, we selected the time interval from 15:30 UTC to 20:30 UTC (i.e., when the considered rainfall event was most intense). Next, we calculated the convex hull encompassing all rain gauges that recorded an average rainfall rate of at least 1 mm·h−1 during that interval. The study area was then defined as the region enclosed by the convex hull also shown in Figure 5.
2.3. QPE Methods
2.3.1. Radar-Based Method
Estimating rainfall by using solely weather radar data is typically performed through the empirical relationship expressed in (1). In this work, we computed the rainfall field (in mm) as follows: first, the available 2D Z maps were averaged in space over a 3 × 3 window; then, they were converted into R maps with a fixed relationship; finally, the R maps were accumulated in time.
Different Z–R relationships were tested to evaluate which could be the most suitable for this case study. The following relationships were analyzed:
- , Marshall–Palmer [28].
- , Joss–Waldvogel [29].
- , utilized in the QPE algorithms of the Multi-Radar Multi-Sensor (MRMS) system for convective precipitation [30].
- , computed specifically for C-band radars, relying on experimental DSD measurements provided by disdrometers and collected in Rome (Italy) during convective events [31].
Based on the mean absolute error derived from the difference between the accumulated rainfall measured by the rain gauges from 15:30 UTC to 20:30 UTC (i.e., the highest intensity interval of the investigated event) and that estimated by the radar, the relationship proved to be the best. Consequently, it was the one used for comparisons with the other QPE methods. We refer to this radar-based method as ZR in the following.
2.3.2. Rain Gauge-Based Method
Creating a 2D rainfall map from rain gauge data involves using spatial interpolation techniques to estimate rainfall values at locations which are not directly covered by the rain gauge network. In this regard, we employed the ordinary kriging (OK) technique, which aims to produce an estimate at a given location by considering the values of nearby observations and their spatial distribution. The estimate is a weighted average of the known values, with weights derived from the spatial correlation pattern to minimize the variance of the estimation error (see [4] for a detailed description of OK).
A key component in kriging is the semivariogram, which quantifies the spatial autocorrelation of the data. Thus, it is necessary to calculate the empirical semivariogram from the observed rainfall values and then fit a theoretical model (e.g., spherical, exponential, Gaussian). In this study, we assumed a spherical model and used the open-source library GSTools [32] for semivariogram computation and kriging implementation.
2.3.3. Kriging with External Drift (KED)
KED is a fusion method for estimating rainfall that enhances traditional kriging by integrating external information (drift) provided by radar into the spatial interpolation process of rain gauge data (see [4] for an exhaustive explanation about how KED works). As to the implementation of KED, in this study, we used the GSTools library to set a spherical semivariogram model. As an external drift variable, we considered the radar-based QPE obtained by means of the procedure in Section 2.3.1.
2.3.4. Conditional Merging (CM)
Kriging with radar-based error correction, also known as conditional merging (CM), is a technique that refines the kriging-based rainfall field by exploiting the superior spatial information provided by radars [20]. In CM, the rainfall field obtained by using the kriging interpolation of rain gauge measures is corrected by adding an error field derived from radar data. The error field is calculated as follows: first, the radar-based rainfall field is estimated; next, the radar rainfall estimates at each rain gauge location are interpolated through kriging; finally, the resulting interpolated rainfall field is subtracted from the original radar-based rainfall field to derive the error field. In this work, we utilized OK (Section 2.3.2) and the rainfall map derived from ZR (Section 2.3.1) as the kriging technique and the radar-based rainfall field, respectively.
2.3.5. Mean Field Bias Adjustment (MFB)
MFB is a radar bias adjustment method that consists of applying a space-constant multiplicative adjustment factor to the radar-based QPE. The adjustment factor (AF) is derived from the rainfall estimated by the radar at rain gauge locations and the rainfall measured by the gauges [9], and is given by
where N is the number of available rain gauges, is the rainfall measured by the ith rain gauge, and is the rainfall estimated by radar at the ith rain gauge location.
For the implementation of MFB, we included in (2) only those rain gauges for which both the measured rainfall and the corresponding radar estimate exceeded 1 mm. The resulting adjustment factor was then applied to the rainfall map estimated through ZR (Section 2.3.1).
2.3.6. Brandes Spatial Adjustment (BSA)
BSA is an alternative radar bias adjustment method that, rather than applying a constant adjustment factor across space, uses a spatially varying correction. In the BSA method, a local adjustment factor is first computed at each rain gauge location by comparing the rainfall estimated by the radar with the rainfall measured by the gauge. These local adjustment factors are then spatially interpolated throughout the area of interest [21]. Specifically, to calculate the adjustment factor, we followed the procedure detailed in [33], excluding rain gauges for which either the measured rainfall or the corresponding radar estimate was less than 1 mm.
2.3.7. Space-Time Adaptive Coefficient Conversion (STACC)
STACC is a rain gauge and radar data fusion method designed to employ a Z–R relationship that varies both in time and space. This approach dynamically adapts the coefficients in (1) according to the spatial and temporal evolution of the observed phenomenon, ensuring a more accurate QPE compared to using a constant a priori selected relation. In the STACC method, the relationship used to convert the space–time average of Z into the time average of R is obtained through a two-step procedure consisting of local calibration and spatial interpolation. During the local calibration step, the optimal relationship coefficients are determined at each rain gauge location by applying a linear regression technique to the averaged values of rain gauge and radar data. In the successive step, these optimal coefficients are spatially interpolated across the study area. A more in-depth description of the STACC method can be found in [22].
Concerning the implementation of the STACC, we utilized a weighted least square regression method that accounts for the uncertainties of the two variables [34]. In particular, we set the temporal variability (i.e., the temporal standard deviation) of rain gauge and radar data as the uncertainties. The local coefficients obtained were assumed to be acceptable and employed in the subsequent spatial interpolation step if their values fell within an established range (typically found in the literature [35], and ). During the spatial interpolation step, the inverse distance weighting technique [36] was used.
2.4. Performance Analysis
Verifying the accuracy of QPE methods is challenging due to the unknown nature of the true rainfall field. Typically, this challenge is addressed by exploiting the high accuracy of rain gauge measurements, comparing the estimated rainfall values to those observed. Due to unavailability of an independent gauge network for the verification (i.e., a network different from that employed for the estimation), a leave-one-out cross-validation (LOOCV) was carried out to analyze the performance of the various QPE methods. The LOOCV procedure consists of the following steps:
- Remove one rain gauge from the dataset.
- Use a QPE method to estimate the rainfall at the location of the removed rain gauge.
- Compare the estimated rainfall y to the actual value x measured by the gauge.
- Repeat the above steps for all the available rain gauges.
To ensure a comprehensive analysis, this procedure is repeated throughout a designated observation period. Let T be the total observation time, during which the analysis is performed; assume that T is divided into several time slots of duration , where is a submultiple of T, yielding a total of time slots. For each time slot, the previously described LOOCV is applied to the available rain gauges. Therefore, for each ith rain gauge, , and for each jth time slot, , we denote the actual rainfall amount measured by the ith rain gauge during the jth time slot with , and its estimate obtained with a QPE method by excluding the ith rain gauge from the dataset with .
Finally, the accuracy of each QPE method is assessed by calculating the mean absolute error (MAE), the root-mean-squared error (RMSE), the coefficient of determination (), and the bias, defined as
where in (5) is the arithmetic mean of (, ). MAE and RMSE are the most common metrics employed in validation studies, with RMSE being more sensitive to large errors. The value helps to understand the correlation between predictions and observations; it normally ranges from 0 to 1 (the higher the index, the better the rainfall estimates fit the actual values). Finally, the bias provides insights about the trend of a method to overestimate (bias > 0) or underestimate (bias < 0) the actual rainfall values.
Another important aspect we would like to emphasize in this study is evaluating the different QPE methods in critical scenarios, such as when the rain gauge network fails to detect areas of very intense rainfall [23]. This critical situation may arise when a highly intense and localized precipitation event occurs, and the gauge network is not adequately dense to capture it effectively. Certainly, in such cases, meteorological radars are crucial for identifying high-risk areas. However, from a quantitative perspective, the lack of rain gauge data significantly impacts the accuracy of rainfall estimates. In this study, the robustness of the various QPE methods in critical scenarios is assessed by applying the LOOCV approach to selected rain gauges in specific areas where precipitation is intense.
3. Experimental Results
3.1. Leave-One-Out Cross-Validation (LOOCV)
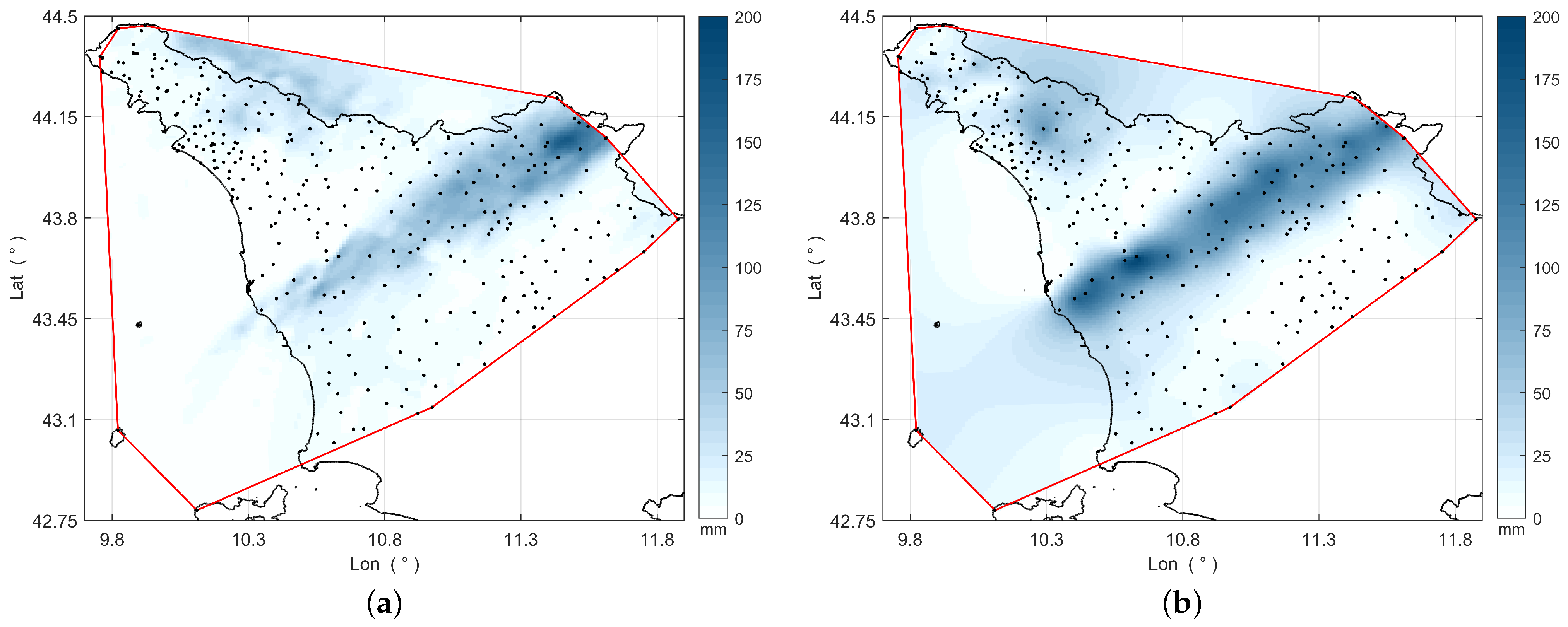
The LOOCV procedure detailed in Section 2.4 was applied to data collected between 15:30 UTC and 20:30 UTC, spanning a total duration of h. This period was chosen as it corresponds to the highest intensity interval of the investigated event. Figure 6 shows the rainfall accumulation over this period estimated through ZR and OK, which, among all methods, were chosen to contrast information coming from either radar or rain gauge data. The accumulated rainfall along the stationary thunderstorm line (see Section 2.1) is well highlighted in both maps. However, assuming the rain gauge measurements as the point-wise ground truth, the quantitative inaccuracy of radar-based estimates is apparent.
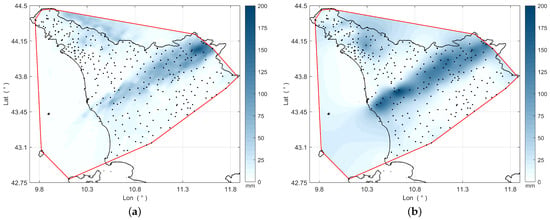
Figure 6.
Rainfall accumulation from 15:30 UTC to 20:30 UTC, 2 November 2023, estimated through (a) ZR and (b) OK. The dots mark the rain gauge locations, while the black line represents the Tuscany boundaries.
Rain gauges placed on the vertices of the convex hull that defines the study area (see Section 2.2.2) and those which recorded an average rainfall rate smaller than 1 mm·h−1 were excluded in the LOOCV procedure. In the case of kriging-based methods (i.e., OK, KED, and CM), data from only the 50 nearest gauges were used to estimate rainfall at the removed rain gauge location to reduce computational cost. In the following, we differentiate the QPE methods according to the these categories: methods that rely on a single data source, either radar and rain gauges (i.e., ZR and OK); geostatistical fusion methods (i.e., KED and CM); and radar bias adjustment methods (i.e., MFB, BSA, and STACC). For the sake of simplicity, the latter two categories are sometimes jointly referred to as fusion-based methods.
The results obtained for min are presented in Table 1. Among the methods that rely on a single data source, OK outperforms ZR according to all the considered metrics. Regarding fusion-based methods, the geostatistical ones perform better, with KED achieving the best overall performance. Among radar bias adjustment methods, MFB demonstrates the worst performance (providing just slightly better metrics than ZR), whereas the STACC produces the best results. In terms of bias, ZR, MFB, and STACC tend to underestimate the actual rainfall on average, while OK, KED, CM, and BSA tend to overestimate it. When comparing fusion-based and single-source methods, the fusion approaches outperform ZR; in contrast, only KED, CM, and STACC outperform OK, while MFB and BSA yield worse and similar results, respectively.

Table 1.
Leave-one-out cross-validation results: h (from 15:30 UTC to 20:30 UTC), min.
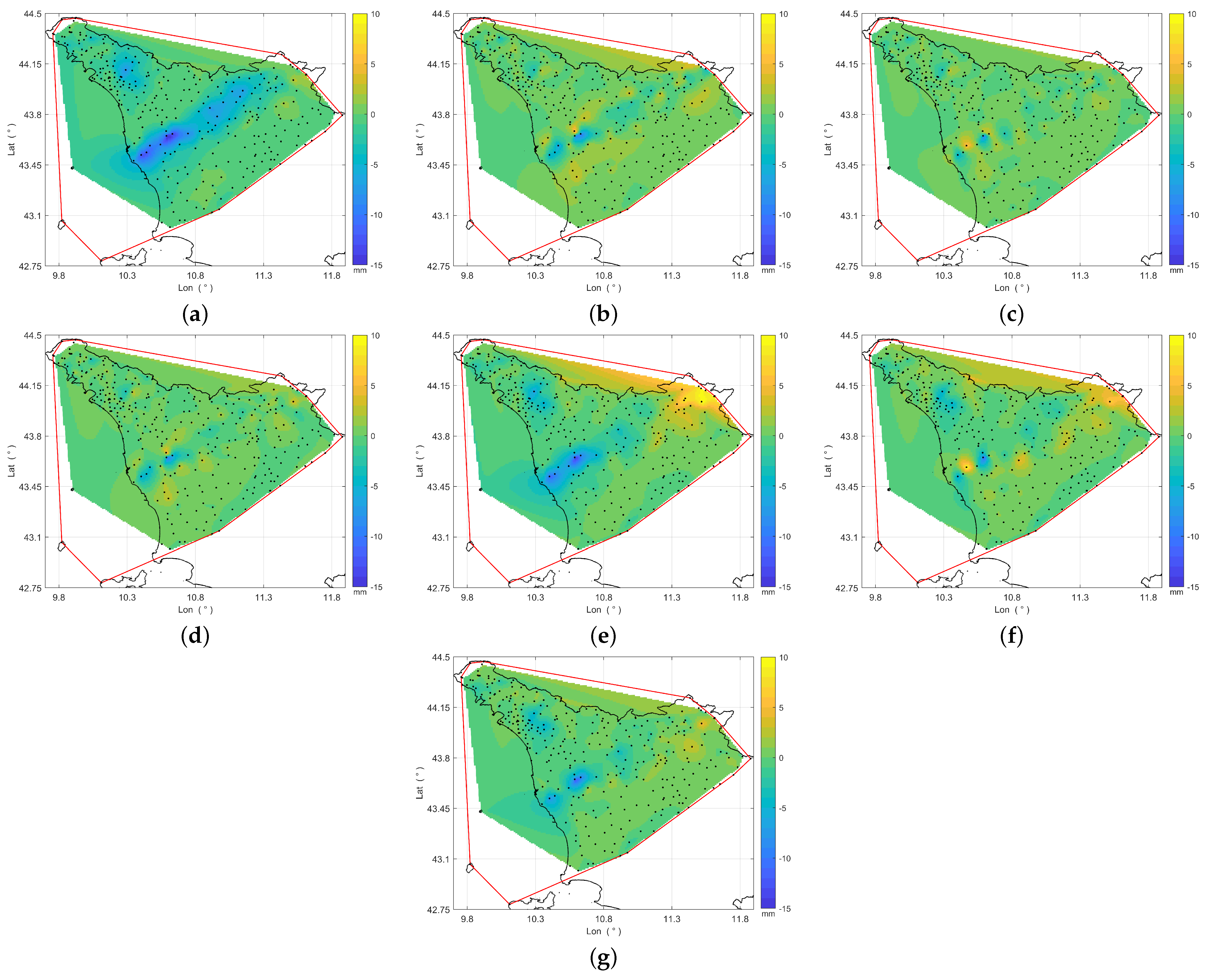
To identify the rain gauges where the evaluated methods tend to either overestimate or underestimate, the mean bias over time was calculated for each rain gauge. The results obtained were spatially interpolated to improve visualization, and the bias maps are shown in Figure 7. By comparing Figure 6 and Figure 7a, it is clear that ZR tends to underestimate the rainfall in areas with higher intensities. Similarly, the OK method (Figure 7b) also underestimates rainfall in these areas, even though less than ZR. Moreover, OK tends to overestimate rainfall in those areas where there is a transition from high to low rainfall intensity. Regarding geostatistical fusion methods, KED (Figure 7c) improves the bias level in both the underestimation and overestimation areas of OK, whereas CM (Figure 7d) yields results that are similar to those of OK. Among the radar bias adjustment methods, STACC (Figure 7g) significantly reduces the underestimation regions with respect to ZR, while introducing only slight overestimation. Conversely, MFB (Figure 7e) partly reduces underestimation and, like BSA (Figure 7f), introduces areas of strong overestimation.
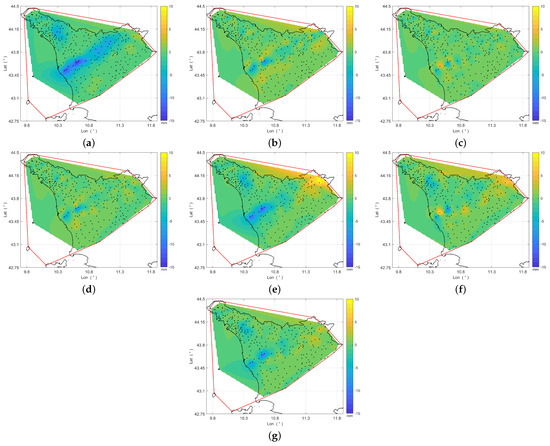
Figure 7.
Bias maps from 15:30 UTC to 20:30 UTC, 2 November 2023: (a) ZR, (b) OK, (c) KED, (d) CM, (e) MFB, (f) BSA, (g) STACC.
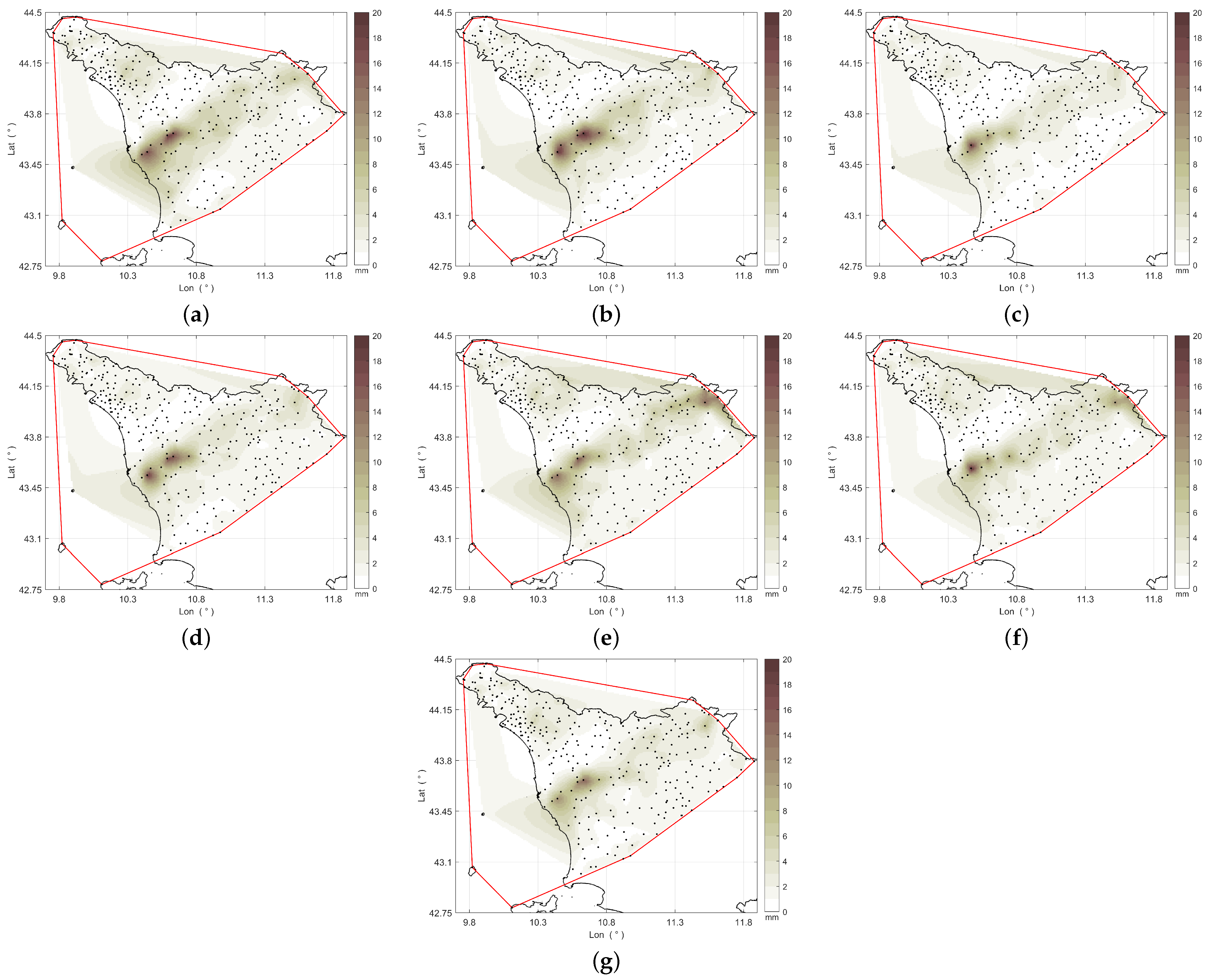
For a comprehensive analysis, we also calculated the temporal standard deviation () of the error associated with each rain gauge. For the jth rain gauge, is given by
where , and is the arithmetic mean of , . As for the bias, values were spatially interpolated for the sake of a better visualization. Figure 8 shows the results for each considered method. As can be noted, for all the methods, the highest values are observed for rain gauges located in areas with the highest rainfall intensity (see Figure 6). Additionally, when compared to Figure 7, these rain gauges are associated with significant underestimation or overestimation. Overall, the STACC map exhibits the lowest error variability (Figure 8g).
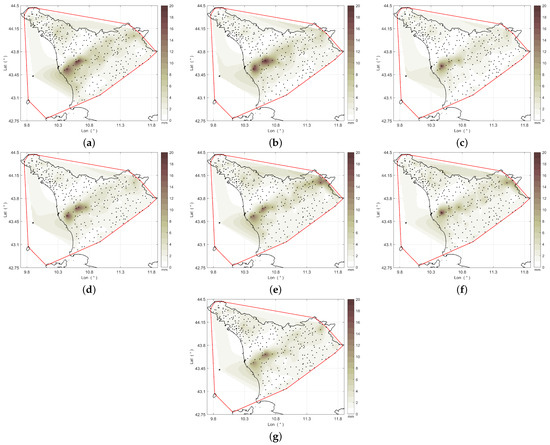
Figure 8.
Temporal standard deviation of the error from 15:30 UTC to 20:30 UTC, 2 November 2023: (a) ZR, (b) OK, (c) KED, (d) CM, (e) MFB, (f) BSA, and (g) STACC.
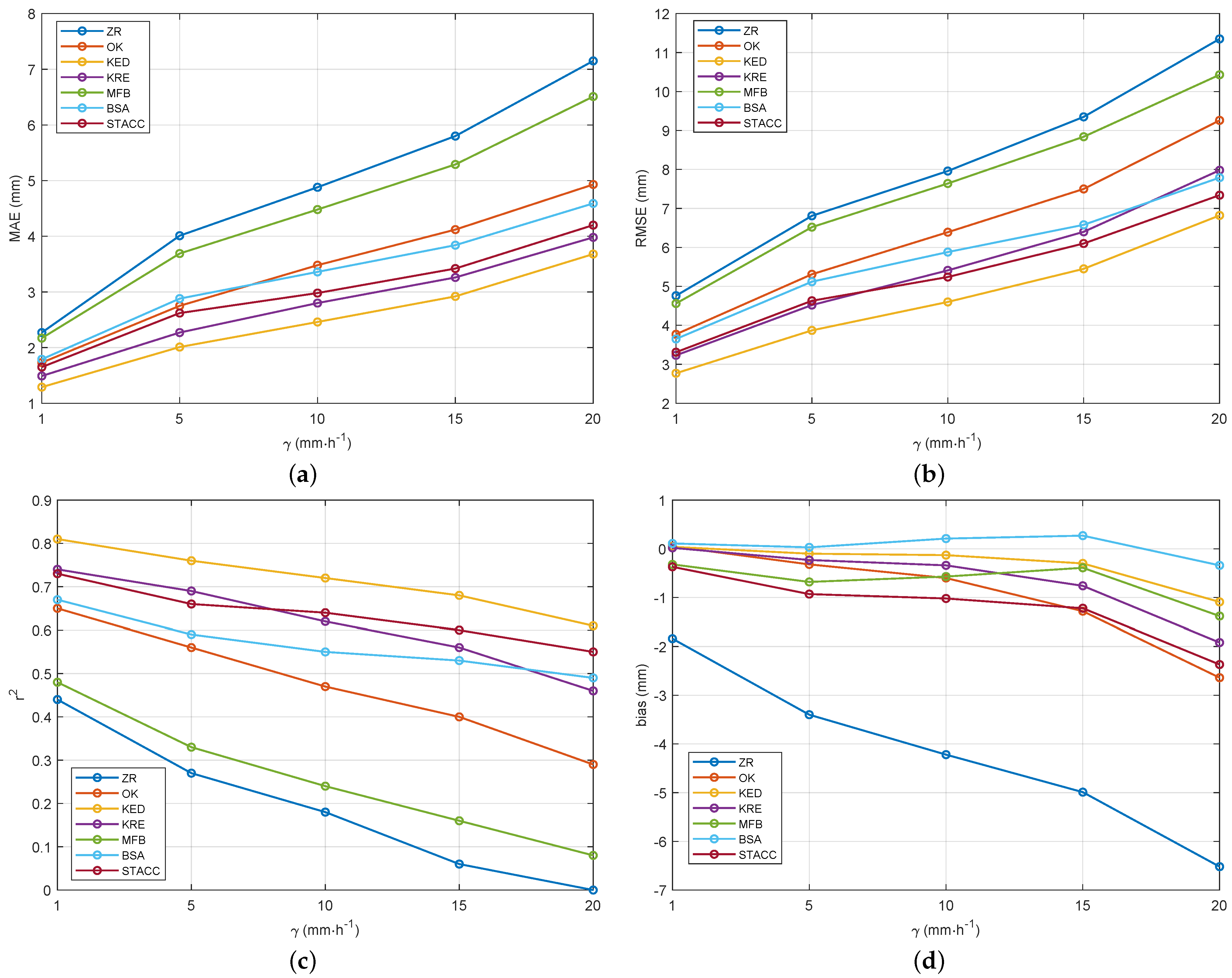
Since we are mostly interested in the areas with significant levels of rainfall, the LOOCV procedure was repeated by choosing exclusively those rain gauges that recorded an average rainfall rate greater than or equal to a specified threshold over the interval T. Four different thresholds were selected: , , , and ; set to 5, 10, 15, and 20 mm·h−1, respectively. Figure 9 shows, for each method, the trends of the chosen metrics vs. . From these results, it is noticeable that ZR remains the least effective among all QPE methods, especially at the highest values of , where the value drops to zero. Among fusion-based methods, MFB exhibits the worst performance (with approaching zero), while KED demonstrates the best results. As increases, the improvement of the fusion-based methods over single-source ones becomes more pronounced. Note also that all QPE methods show negative bias values, meaning an overall underestimation of the actual rainfall level.
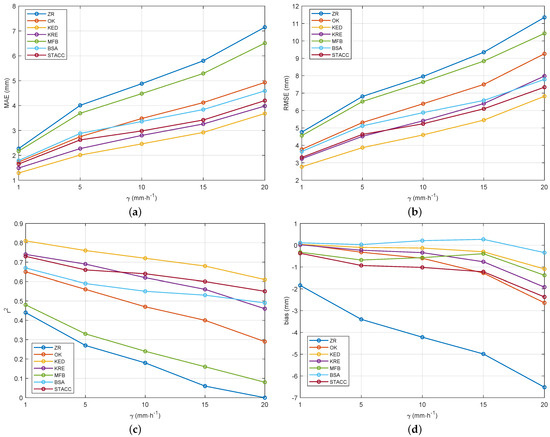
Figure 9.
Trend of (a) MAE, (b) RMSE, (c) , and (d) bias as a function of the threshold .
3.2. Critical Scenarios: Simulation and Analysis
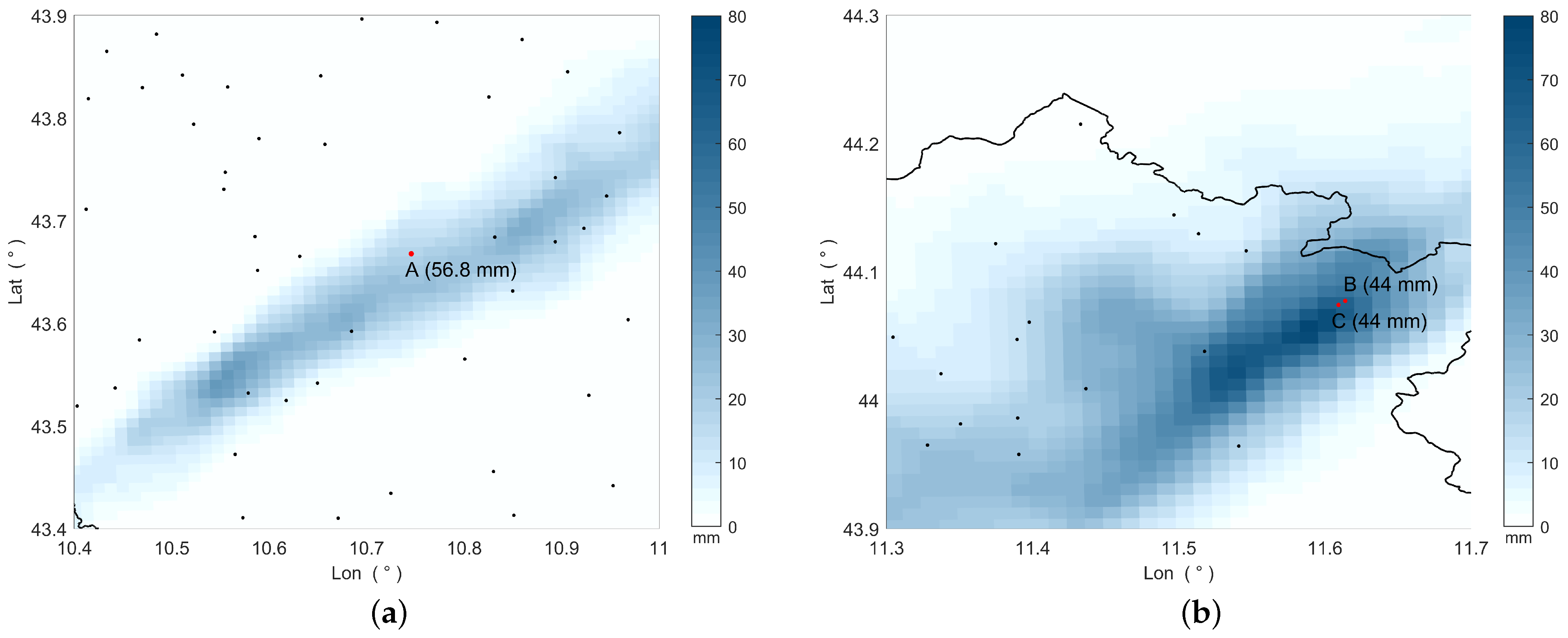
To assess the various QPE methods in critical situations (Section 2.4), we simulated and analyzed two scenarios by removing specific rain gauges from the dataset. Figure 10 shows the rainfall accumulation obtained by using the ZR method for two different time intervals. In both maps, the rain gauges that measured the highest rainfall amount (reported in brackets) are highlighted and labeled with a letter. These rain gauges are referred to as RGA, RGB, and RGC in the following.
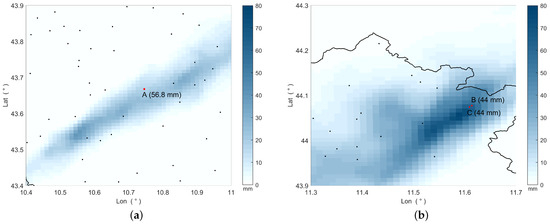
Figure 10.
Rainfall accumulation from (a) 15:30 UTC to 16:30 UTC and (b) 16:30 UTC to 17:30 UTC, 2 November 2023, estimated through ZR. The dots mark the rain gauge locations, while the black line represents the Tuscany boundaries. Rain gauges that measured the highest rainfall amount (indicated in brackets) are highlighted in red and labeled with a letter.
Starting from the scenario depicted in Figure 10a, we removed RGA from the rain gauge dataset and estimated the rainfall (y) at its location using the various QPE methods. These estimates were then compared to the actual measured value (x), and both the absolute estimation error () and the relative one expressed in percentage () were calculated to evaluate the accuracy of each method. The results are summarized in Table 2. As shown, all the QPE methods underestimate the actual rainfall, with the single-source ones yielding the largest errors. Among the fusion-based methods, CM and KED exhibit the poorest performance, while MFB and BSA show only minor improvements. The smallest error is achieved by the STACC method.

Table 2.
Estimation errors at the RGA location after its removal from the dataset (values without brackets) and after the additional removal of nearby rain gauges with high rainfall measures (values in brackets).
We also carried out an analogous simulation with the additional step of removing the nearby rain gauges that recorded high rainfall levels, further amplifying the impact of missing data in the analyzed area. As can be noted from observing the values in brackets in Table 2, only the STACC estimates improve (even if slightly), while the performance of all the other methods—in particular, OK, KED, and CM—are degraded.
With reference to Figure 10b, another critical sampling condition of the rain gauge network was simulated by removing RGB and RGC from the dataset. The rainfall estimate errors were then calculated at the RGB and RGC positions. Table 3 summarizes the estimation errors obtained. Also, in this case, OK underestimates the actual level of rainfall at both rain gauge sites. However, in contrast to the previous simulation, the ZR method results in an overestimation. Regarding fusion-based methods, MFB and BSA lead to significant overestimation, with much higher percentage errors than those of single-source methods (over 100% for MFB). CM results are similar to those obtained by ZR, while KED and STACC yield quite small errors (slight overestimation for RGC and underestimation for RGB). As in the previous simulation, the STACC method exhibits the best performance.

Table 3.
Estimation errors at RGB and RGC locations after their removal from the dataset.
4. Discussion
The results of the LOOCV analysis (Section 3.1) conducted in this study align with findings reported in the existing literature (see the review in [19]). All the fusion methods considered outperform the radar-based method (ZR). For what concerns the rain gauge-based method (OK), the situation is different. On average, OK performs better than MFB and also BSA. The good overall performance of OK can be attributed to the high density of the rain gauge network (see Section 2.2.2). This also positively impacts geostatistical fusion methods (i.e., KED and CM) [33], as these methods primarily rely on the spatial interpolation of rain gauge data. Typically, this category of methods tends to perform better than the radar bias adjustment one, with KED providing the best results [19]. This trend is confirmed by our results. However, the STACC method deserves a separate discussion, as it performs only slightly worse than KED and comparably to CM, outperforming the latter in some cases. Based on the results obtained, it proves to be the best method in the radar bias adjustment category, confirming the findings in [23]. As pointed out in [19], the quality of radar data, and thus radar QPE, plays an important role in the final results of the merging process. This is particularly true for the radar bias adjustment methods, which give greater weight to radar information than the geostatistical ones. Uncorrected errors in radar reflectivity maps (Figure 4) could have affected the performance of ZR and of the radar bias adjustment methods (MFB in particular, as it shows only slight improvements compared to radar-only estimation).
With regard to the analysis of critical rain gauge sampling scenarios, in both simulations (Section 3.2), OK yields the most significant underestimates at the locations of the rain gauges that measured the highest rainfall levels (i.e., RGA, RGB, and RGC), as expected. The main difference between the two critical cases simulated lies in the radar-based QPE as estimated through ZR. In the first case, RGA is not located where the radar estimates are the highest (Figure 10a), resulting in a high error when compared to the actual rainfall value provided by RGA. This remarkable underestimation, jointly with that caused by missing rain gauge, leads to an overall underestimation across all the considered fusion methods. In geostatistical fusion methods, additional spatial information from radar-based QPE is insufficient to compensate for the inaccuracy deriving from rain gauge data interpolation. In the case of MFB and BSA, the adjustment factor computed after the exclusion of RGA does not adequately correct the ZR underestimation. Conversely, in the second simulation, RGB and RGC are located in an area where the rainfall estimated by ZR is very high, leading to radar estimates that are higher than the rainfall measured by these gauges. In this situation, the radar-based QPE helps to correct kriging underestimation in geostatistical methods, with KED providing quite good results. Instead, in the case of MFB and BSA, the adjustment factor amplifies the radar overestimation, resulting in significant errors. In both simulations, the STACC method achieves the smallest errors among all QPE methods, confirming its superior robustness in these circumstances [23]. This robustness lies in the STACC’s fusion approach, which demonstrates low sensitivity to the absence of rain gauges in areas of high precipitation. When rain gauges recording the highest rainfall are removed, the Z–R relation coefficients at their locations are determined by spatial interpolation of the coefficients calibrated with the surrounding rain gauges. Since the calibration is performed using linear regression, the resulting relationship, although based on lower values of Z and R, can still be effectively applied to higher values of these quantities.
The findings of this study, in conjunction with those of [23], offer valuable insights into the most suitable QPE methods in case of severe convective rainfall systems. The key recommendations that emerge from these studies suggest the complementary use of KED and STACC, depending on the density of the available rain gauge network. Specifically, KED proves to be more effective when a dense network of rain gauges is available, ensuring higher accuracy in rainfall estimates. On the other hand, STACC demonstrates superior performance in cases of sparse rain gauge distribution, offering greater robustness and reliability under these conditions. The combination of these methods can significantly improve rainfall estimation accuracy for convective systems in various rain gauge sampling situations.
5. Conclusions
In this paper, a comprehensive comparison of different QPE methods based on rain gauge and weather radar data has been presented. To this end, data collected during a severe rainfall event that occurred in Tuscany, Italy, were employed.
We performed an LOOCV to assess the accuracy and the reliability of each considered method. The results have shown that relying exclusively on radar data leads to quantitatively inaccurate predictions, as expected. Additionally, merging radar and rain gauge data through the MFB approach does not significantly enhance estimation accuracy. The results have also demonstrated that a sufficiently dense rain gauge network, such as the one in Tuscany, can produce good results even when utilized alone, as in the OK method. In general, however, fusion methods like KED, CM, BSA, and STACC have achieved better results than OK. Regarding fusion methods, STACC has shown the best performance among radar bias adjustment methods, while KED has been the best overall among geostatistical interpolation methods.
A second type of analysis was also carried out in an attempt to highlight the robustness of the QPE methods on the lack of rain gauge data in high rainfall areas. This analysis was performed by removing specific rain gauges from the dataset available and by assessing the estimation obtained by the various methods. This analysis has disclosed, as expected, the main drawback of the methods relying solely on rain gauge data and has pointed out the essential role of spatial information provided by radar. Among fusion methods, the STACC has demonstrated the highest robustness under these challenging conditions, yielding the smallest estimation errors.
In general, this study has confirmed the advantages of merging rain gauge data with weather radar observations to improve QPE. In fact, by combining these two data sources, we have achieved more accurate rainfall estimates than by using either data source independently. The findings have offered further evidence of the validity of fusion techniques, particularly KED and STACC, for operational meteorology and hydrological applications such as flood forecasting, where precise precipitation measurements are essential.
Author Contributions
Conceptualization, A.B., L.F., F.A. and F.C.; methodology, A.B., L.F., F.A. and F.C.; software, A.B. and F.C.; validation, A.B.; formal analysis, A.B., L.F. and F.A.; investigation, A.B.; resources, L.F. and F.C.; data curation, A.B.; writing—original draft preparation, A.B.; writing—review and editing, A.B., L.F. and F.A.; visualization, A.B., L.F. and F.A.; supervision, L.F. and F.A.; project administration, L.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article; further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to thank the Italian National Civil Protection Department (DPCN) for providing the weather radar data and the LaMMA Consortium for providing rain gauge data.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lanza, L.G.; Vuerich, E. The WMO Field Intercomparison of Rain Intensity Gauges. Atmos. Res. 2009, 94, 534–543. [Google Scholar] [CrossRef]
- Michaelides, S.; Levizzani, V.; Anagnostou, E.; Bauer, P.; Kasparis, T.; Lane, J. Precipitation: Measurement, Remote Sensing, Climatology and Modeling. Atmos. Res. 2009, 94, 512–533. [Google Scholar] [CrossRef]
- Ahrens, B. Distance in spatial interpolation of daily rain gauge data. Hydrol. Earth Syst. Sci. 2006, 10, 197–208. [Google Scholar] [CrossRef]
- Wackernagel, H. Multivariate Geostatistics: An Introduction with Applications, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Piazza, A.D.; Conti, F.L.; Noto, L.V.; Viola, F.; Loggia, G.L. Comparative analysis of different techniques for spatial interpolation of rainfall data to create a serially complete monthly time series of precipitation for Sicily, Italy. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 396–408. [Google Scholar] [CrossRef]
- Mair, A.; Fares, A. Comparison of Rainfall Interpolation Methods in a Mountainous Region of a Tropical Island. J. Hydrol. Eng. 2011, 16, 371–383. [Google Scholar] [CrossRef]
- Doviak, R.J.; Zrnić, D.S. Doppler Radar and Weather Observations, 2nd ed.; Academic Press: San Diego, CA, USA, 1993. [Google Scholar]
- Villarini, G.; Krajewsky, W.F. Review of the Different Sources of Uncertainty in Single Polarization Radar-Based Estimates of Rainfall. Surv. Geophys. 2010, 31, 107–129. [Google Scholar] [CrossRef]
- Wilson, J.W.; Brandes, E.A. Radar Measurement of Rainfall—A Summary. Bull. Am. Meteorol. Soc. 1979, 60, 1048–1060. [Google Scholar] [CrossRef]
- Chapon, B.; Delrieu, G.; Gosset, M.; Boudevillain, B. Variability of rain drop size distribution and its effect on the Z–R relationship: A case study for intense Mediterranean rainfall. Atmos. Res. 2008, 87, 52–65. [Google Scholar] [CrossRef]
- Smith, J.A.; Hui, E.; Steiner, M.; Baeck, M.L.; Krajewski, W.F.; Ntelekos, A.A. Variability of rainfall rate and raindrop size distributions in heavy rain. Water Resour. Res. 2009, 45, W04430. [Google Scholar] [CrossRef]
- Atlas, D.; Ulbrich, C.W.; Meneghini, R. The multiparameter remote measurement of rainfall. Radio Sci. 1984, 19, 3–22. [Google Scholar] [CrossRef]
- Lee, G.W.; Zawadzki, I. Variability of Drop Size Distributions: Time-Scale Dependence of the Variability and Its Effects on Rain Estimation. J. Appl. Meteorol. 2005, 44, 241–255. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V. Polarimetric Doppler Weather Radar: Principles and Applications; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar] [CrossRef]
- Zrnic, D.S.; Ryzhkov, A.V. Polarimetry for Weather Surveillance Radars. Bull. Am. Meteorol. Soc. 1999, 80, 389–406. [Google Scholar] [CrossRef]
- Ryzhkov, A.; Zhang, P.; Bukovčić, P.; Zhang, J.; Cocks, S. Polarimetric Radar Quantitative Precipitation Estimation. Remote Sens. 2022, 14, 1695. [Google Scholar] [CrossRef]
- Vulpiani, G.; Montopoli, M.; Passeri, L.D.; Gioia, A.G.; Giordano, P.; Marzano, F.S. On the Use of Dual-Polarized C-Band Radar for Operational Rainfall Retrieval in Mountainous Areas. J. Appl. Meteorol. Climatol. 2012, 51, 405–425. [Google Scholar] [CrossRef]
- Gu, J.Y.; Ryzhkov, A.; Zhang, P.; Neilley, P.; Knight, M.; Wolf, B.; Lee, D.I. Polarimetric Attenuation Correction in Heavy Rain at C Band. J. Appl. Meteorol. Climatol. 2011, 50, 39–58. [Google Scholar] [CrossRef]
- Ochoa-Rodriguez, S.; Wang, L.P.; Willems, P.; Onof, C. A Review of Radar-Rain Gauge Data Merging Methods and Their Potential for Urban Hydrological Applications. Water Resour. Res. 2019, 55, 6356–6391. [Google Scholar] [CrossRef]
- Sinclair, S.; Pegram, G. Combining radar and rain gauge rainfall estimates using conditional merging. Atmos. Sci. Lett. 2005, 6, 19–22. [Google Scholar] [CrossRef]
- Brandes, E.A. Optimizing Rainfall Estimates with the Aid of Radar. J. Appl. Meteorol. Climatol. 1975, 14, 1339–1345. [Google Scholar] [CrossRef]
- Cuccoli, F.; Facheris, L.; Antonini, A.; Melani, S.; Baldini, L. Weather Radar and Rain-Gauge Data Fusion for Quantitative Precipitation Estimation: Two Case Studies. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6639–6649. [Google Scholar] [CrossRef]
- Biondi, A.; Facheris, L.; Argenti, F.; Cuccoli, F.; Antonini, A.; Melani, S. Assessing quantitative precipitation estimation methods based on the fusion of weather radar and rain-gauge data. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Krajewski, W.F. Cokriging radar-rainfall and rain gage data. J. Geophys. Res. 1987, 92, 9571–9580. [Google Scholar] [CrossRef]
- Todini, E. A Bayesian technique for conditioning radar precipitation estimates to rain-gauge measurements. Hydrol. Earth Syst. Sci. 2001, 5, 187–199. [Google Scholar] [CrossRef]
- Report Meteorologico: Evento 2 novembre 2023 (Consorzio LaMMA). Available online: https://www.lamma.toscana.it/clima/report/eventi/evento_02112023.pdf (accessed on 2 August 2024). (In Italian).
- Meteo-Hub Mistral (Meteo Italian Supercomputing Portal). Available online: https://www.mistralportal.it/opendata/ (accessed on 26 July 2024).
- Marshall, J.; Hitschfeld, W.; Gunn, K. Advances in Radar Weather. Adv. Geophys. 1955, 2, 1–56. [Google Scholar] [CrossRef]
- Joss, J.; Waldvogel, A. A method to improve the accuracy of radar measured amounts of precipitation. In Proceedings of the 14th Radar Meteorology Conference, Tucson, AZ, USA, 17–20 November 1970; pp. 237–238. [Google Scholar]
- Zhang, J.; Howard, K.; Langston, C.; Kaney, B.; Qi, Y.; Tang, L.; Grams, H.; Wang, Y.; Cocks, S.; Martinaitis, S.; et al. Multi-Radar Multi-Sensor (MRMS) Quantitative Precipitation Estimation: Initial Operating Capabilities. Bull. Am. Meteorol. Soc. 2016, 97, 621–638. [Google Scholar] [CrossRef]
- Adirosi, E.; Roberto, N.; Montopoli, M.; Gorgucci, E.; Baldini, L. Influence of Disdrometer Type on Weather Radar Algorithms from Measured DSD: Application to Italian Climatology. Atmosphere 2018, 9, 360. [Google Scholar] [CrossRef]
- Müller, S.; Schüler, L.; Zech, A.; Heße, F. GSTools v1.3: A toolbox for geostatistical modelling in Python. Geosci. Model Dev. 2022, 15, 3161–3182. [Google Scholar] [CrossRef]
- Goudenhoofdt, E.; Delobbe, L. Evaluation of radar-gauge merging methods for quantitative precipitation estimates. Hydrol. Earth Syst. Sci. 2009, 13, 195–203. [Google Scholar] [CrossRef]
- Orear, J. Least squares when both variables have uncertainties. Am. J. Phys. 1982, 50, 912–916. [Google Scholar] [CrossRef]
- Battan, L.J. Radar observation of the atmosphere. Q. J. R. Meteorol. Soc. 1973, 99, 793. [Google Scholar] [CrossRef]
- Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 23rd ACM National Conference, San Francisco, CA, USA, 27–29 August 1968; pp. 517–524. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).