Assessing Data Preparation and Machine Learning for Tree Species Classification Using Hyperspectral Imagery

Abstract

Tree species classification using hyperspectral imagery shows incredible promise in developing a large-scale, high-resolution model for identifying tree species, providing unprecedented details on global tree species distribution. Many questions remain unanswered about the best practices for creating a global, general hyperspectral tree species classification model. This study aims to address three key issues in creating a hyperspectral species classification model. We assessed the effectiveness of three data-labeling methods to create training data, three data-splitting methods for training/validation/testing, and machine-learning and deep-learning (including semi-supervised deep-learning) models for tree species classification using hyperspectral imagery at National Ecological Observatory Network (NEON) Sites. Our analysis revealed that the existing data-labeling method using the field vegetation structure survey performed reasonably well. The random tree data-splitting technique was the most efficient method for both intra-site and inter-site classifications to overcome the impact of spatial autocorrelation to avoid the potential to create a locally overfit model. Deep learning consistently outperformed random forest classification; both semi-supervised and supervised deep-learning models displayed the most promising results in creating a general taxa-classification model. This work has demonstrated the possibility of developing tree-classification models that can identify tree species from outside their training area and that semi-supervised deep learning may potentially utilize the untapped terabytes of unlabeled forest imagery.

1. Introduction

Timely and accurate mapping of tree species composition is crucial for many ecological applications and forest management. Tree species information is required for biodiversity assessment and monitoring. It facilitates the estimation of wildlife habitat [1]. Forest ecosystem conservation and restoration require detailed knowledge of the native plant compositions [2]. Accurate tree species classification enables better forest management decisions and contributes to overall forest conservation efforts [3]. Tree species information is recorded for forest inventory and input for species-specific allometric models for carbon-stock estimation [4,5].

Various remote-sensing data have been used for tree species classification, including passive optical multispectral, hyperspectral remote sensing, active light detection and ranging (lidar), synthetic aperture radar (SAR) data, and auxiliary data [1]. Passive optical remote-sensing data offer a valuable means for distinguishing between tree species by measuring the spectral response of directional electromagnetic radiation emitted by the sun and reflected by the canopy (and other surfaces) in sensor-specific wavelength regions. In particular, the hyperspectral imagery captures more than 400 bands, ranging from the ultraviolet to the infrared spectrum, with bands spaced approximately every 5 nm. It has been demonstrated repeatedly that this is enough to differentiate many species of vegetation [6,7,8,9,10]. Active remote-sensing sensors emit energy pulses and record the return time and amplitude to derive information about the tree species’ structure. Auxiliary data encompass a range of variables, including elevation, slope, slope direction, temperature, and precipitation. Combining spectral and structural remote-sensing data has been shown to improve tree species detection abilities compared to using any of them alone [8].

Various machine-learning and deep-learning algorithms have been developed to detect tree species using remote-sensing data. Currently, two primary types are widely employed with varying degrees of success, namely traditional machine-learning methods and deep-learning techniques. For the former, the most popular techniques since the dawn of the millennium have included using random forest and support vector machines to classify pixels, objects, or entire areas [1,3,8,11,12,13,14]. Both techniques involve a model iteratively learning a set of weights that informs a set of functions used to separate classes. In many cases, random forest or support vector machine classification remains the state of the art for remote-sensing applications. The latter mainly focuses on classic deep learning (convolutional neural network, CNN) applied to tree species classification [15]. However, most of the studies mentioned above focus on site-specific applications and rarely on the classification of individual trees [3,8,16]. Little is known about how well these approaches perform across broader geographic areas.

Creating forest species classification models includes multiple complex steps, ranging from creating accurately labeled tree data to accounting for spatial and environmental effects in the data. Fortunately, many remote-sensing data have become widely available in recent years to advance tree species classification efforts. In the continental US, large amounts of open ecological and remote-sensing data have been collected through the National Ecological Observatory Network (NEON). A concurrent field survey of individual trees, including stem locations, species, and crown diameter, along with the NEON Airborne Observation Platform (AOP) airborne remote-sensing imagery, including hyperspectral, multispectral, and lidar data products at high spatial resolutions, ranging from 0.1 to 1 m, have been collected at all of the NEON terrestrial sites [17,18].

With the widely available remote-sensing data, studies are emerging to develop automated and generalized species classification models. For example, Scholl et al. [8] developed an automated training-set preparation and a data-preprocessing workflow to classify the four dominant subalpine coniferous tree species at the Niwot Ridge Mountain Research Station forested NEON site in Colorado, USA, using in situ and NEON’s airborne hyperspectral and lidar data. Their method of creating the training dataset using the field survey of half of the maximum crown diameter per tree achieved the best accuracy for tree species classification [8]. Marconi et al. (2022) [16] developed a continental model for tree species classification for the continental US using field surveys and hyperspectral remote-sensing data from NEON. However, both models heavily use NEON field survey data to annotate the training data. Using other available lidar data might improve the annotation processes. In addition, those studies have not addressed the impact of spatial autocorrelation on model performance, nor have they tested the impact of deep learning on model performance.

Our study will address three fundamental questions that lead to developing a general model for tree species classification. First, a central problem when developing any classification model is creating accurate classification labels. Without accurate labels, the model will have no means of learning how to classify future inputs. For a classification model that works at a high resolution, such as the 1 m model developed in this study, all measurements must be precise, as being off by even a meter can lead to mislabeled pixels. Even if highly accurate coordinate measurements were taken at the base of a tree, depending on tree allometry and environmental conditions, the observed position of a tree crown in the remotely sensed imagery could be off by multiple meters. Additionally, from the ground, it can be impossible to know how visible [19] a tree crown will be when imaged from above, especially if the canopy is dense or multi-tiered. Accurately labeling tree pixels requires accounting for the possibility that any field-measured tree could be off by multiple meters or not visible. For this study, we intended to use the available concurrent lidar data collected at NEON sites to develop two annotation methods for training and testing and compare their performance with the previous annotation method, relying heavily on field surveys [8]. Once trained, hyperspectral imagery and lidar data are all the inputs a model would need to classify any tree species.

Second, many tree species classification models have not addressed the issues of spatial autocorrelation on model performance. Spatial autocorrelation is an essential concept to understand when creating any geographic model. In brief, it means that physically closer objects are more similar than objects further away from each other, and this similarity drops in a quantifiable fashion as the distance increases. In our case, two immediately adjacent pixels likely have much more similar values than pixels two kilometers apart. Unaccounted for spatial autocorrelation can lead to models that perform poorly outside their initial study area and are essentially overfitting a specific geographic space, even with a well-validated model [3]. This is a common issue when applying machine learning (ML)/deep learning (DL) to earth data, where the well-trained model reveals an apparent high predictive power, even when predictors have poor relationships with the variables of interest. Thus, ignoring spatial autocorrelation (SAC) in data can result in the over-optimistic assessment of model predictive power [19,20]. Using techniques without taking spatial relationships into account for tree species classification will lead to overconfident or otherwise ineffective models [3]. Karasiak et al. [19] suggested using a data-splitting design to ensure spatial independence between the training and test sets. For this study, we attempted to account for spatial autocorrelation by testing spatially aware methods of splitting training and evaluation data.

Lastly, previous studies [8,16] used classic machine-learning models and have not tested the improvement of deep-learning models compared to classical machine-learning models. While deep learning likely meets or surpasses existing machine-learning techniques for remote-sensing classification, the flexibility of deep learning to learn multiple functions and train for multiple objectives is most intriguing [15]. In addition, acquiring accurately labeled data for tree species classification is difficult and expensive. There are many orders of magnitude more unlabeled data than labeled data. Successful deep-learning models from other domains have demonstrated the capacity for deep learning to pre-train patterns in unlabeled data without any human instruction and then apply those patterns to a small corpus of labeled data [21,22]. This is referred to in the literature as semi-supervised or lightly supervised training; it has been shown to work with hyperspectral classification problems [10]. While multiple machine-learning models can be combined, with an initial model like K-nearest neighbors handling unlabeled data before feeding into a subsequent model like a random forest for labeled data, a single deep-learning model can train on multiple objectives simultaneously. It can first undergo unsupervised training and then transition to supervised training on a different task. To create a general species classification model, we will need to use a model that can take advantage of the enormous volume of unlabeled data available and learn the general patterns that allow for the separation of tree species. Due to the difficulty and expense of acquiring species labels for trees in the field, we attempted to design models that can be trained with as little labeled data as possible through the semi-supervised deep-learning method.

This study leverages the hyperspectral imagery data acquired through NEON to address the three fundamental questions toward developing a generalized machine-learning model for tree species classification. Many remote-sensing sources, including hyperspectral, lidar, and unmanned multispectral data, have been used for tree species classification [3,6,11,12,13,14,15,16,17,18]. Due to the computation limitation of running a deep-learning model on our system, we used hyperspectral data only to train the models in this study.

Tree species classification is typically performed in one of three manners, namely plot level, tree level, and pixel level [3]. The plot-level classification does not attempt to classify any single tree but instead attempts to quantify the proportion of a given species in a given area. Tree-level classification requires first segmenting observed tree crowns into individual trees and then, once trees have been segmented, classifying those trees as whole objects. Pixel-level classification attempts to classify each pixel in a remotely sensed image as belonging to a particular taxon. This requires first separating canopy pixels from other pixels, but no prior tree segmentation is needed. Pixel-level classification potentially allows for the classification of mixed pixels, where two or more tree crowns may overlap in a single pixel. This study focuses on pixel-level classification.

The goal of this study is to answer three research questions.

• Can we develop alternative annotation methods by using lidar to aid in the annotation of tree locations instead of using ground surveys, as presented in [8,16]?
• How can we account for spatial autocorrelation in training data using different data-splitting techniques to create a more capable general model for classifying taxa?
• Does deep learning, including self-supervised deep learning, offer an improvement over random forest classification for tree taxa classification?

2. Materials and Methods

2.1. Study Sites

Three NEON sites in the USA were utilized in this study (Figure 1). The primary subjects of experimentation were the Niwot Ridge (NIWO) and Rocky Mountain National Park (RMNP) sites. The other site, Steigerwaldt–Chequamegon (STEI), is the source of unlabeled data for a semi-supervised model.

The NIWO site was chosen as it is the same site used in [8], and testing the efficacy of the label selection method from that study was a primary goal of this work. The NIWO site is a mountainous, coniferous forest in Eastern Colorado, populated with Subalpine Fir, Lodgepole Pine, Englemann Spruce, and Limber Pine. The RMNP site was selected because of its geographic proximity to the NIWO site and the shared tree species in both locations. It is 11 km from the NIWO site and is a similar mountainous coniferous forest containing all the taxa sampled at the NIWO site. The taxa recorded at the RMNP site are Lodgepole Pine, Douglas Fir, Subalpine Fir, Quaking Aspen, Ponderosa Pine, Engelmann Spruce, and Limber Pine. The STEI was chosen because it offers a distinct mix of taxa from the other two sites. It is a mixed coniferous and deciduous forest in Northern Wisconsin, containing Sugar Maple, Red Maple, Balsam Fir, Black Spruce, Tamarack, and Eastern Hemlock.

2.2. Datasets

All data utilized in this study came from the National Ecological Observatory Network (NEON). NEON sites provide abundant, freely available data spanning all the major ecological domains in the United States. This includes 182 data products from 81 study sites, with airborne surveys run annually or semi-annually at all sites. These surveys collect hyperspectral imagery, lidar point clouds, and true-color imagery. Annual surveys of woody vegetation taxa, including geographic coordinates and allometric measurements for individual trees, are also conducted. The physical extent of the airborne observations is far greater than the areas in which tree surveys are conducted, leading to terabytes of unclassified data, representing hundreds of square kilometers of land over multiple years of collection [23]. Additionally, NEON provides software tools for accessing and managing NEON data. The NEON-OS, geoNEON, and NEON-utilities packages, version 3 (https://github.com/NEONScience, accessed on 5 January 2023) were utilized in this project.

2.2.1. Woody Vegetation Field Surveys

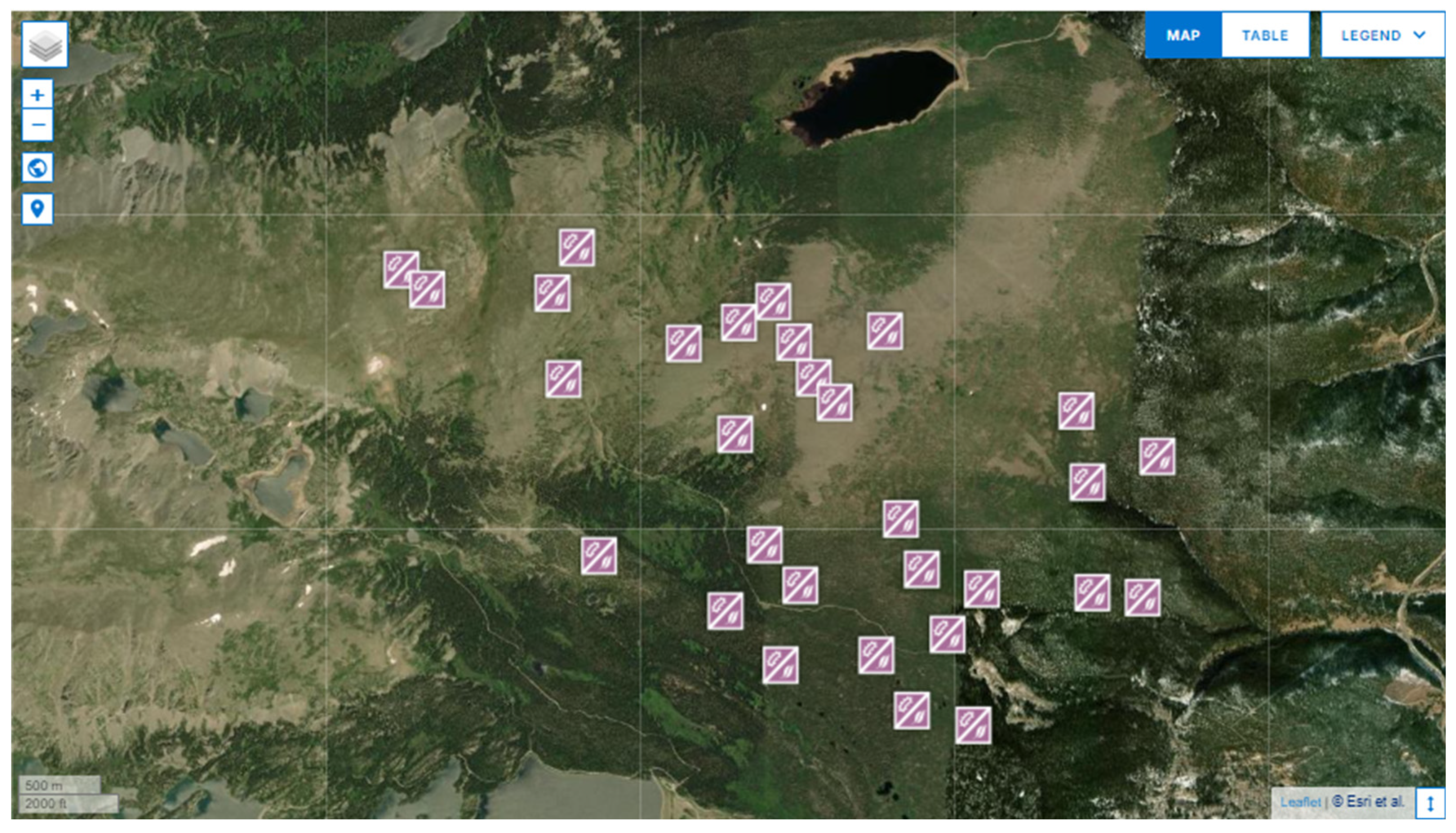
All NEON study sites contain a set of sampling plots in which regular vegetation and other ecological surveys are conducted. Any labeled vegetation data used in this study come from one of these sampling plots. The sampling plots are distributed throughout a site, as demonstrated in Figure 2, and are designed to capture the full gamut of ecological diversity present within a site [24]. They are not, however, designed to capture that diversity evenly, and specific taxa are much more highly sampled than others. Sample plots are either 40 m by 40 m or 20 m by 20 m, and different sites contain different plot numbers, generally around 50. Any reference to a ‘plot’ refers to one of these sample plots. The plots are identified using the 4-character site code and a 3-digit plot number, i.e., in Figure 3. All data used come from NIWO_057. That is, sampling plot 57 from the NIWO site.

Woody vegetation surveys are conducted annually at NEON sites. Data from these surveys include UTM coordinates for the stem location of woody vegetation and taxon label, crown diameter, and height measurements [25]. Locations are derived in the field by measuring distance and angle from a control point with known coordinates. This project’s precise stem location coordinates were calculated using the geoNEON R package, version 3. For the woody vegetation survey data, the most recent data from 2023 were downloaded for the RMNP and NIWO sites. Survey data were then filtered to utilize only the data collected before imagery acquisition at each site. After acquiring the woody vegetation data, duplicate trees were removed, trees measured after the remote-sensing acquisition date were removed, and any tree missing a height, taxon, coordinates, acquisition date, or was shorter than two meters was excluded from further analysis.

2.2.2. Airborne Remote-Sensing Data

NEON’s Airborne Observation Platform (AOP) consists of three remote-sensing instruments mounted into a DeHavilland DHC-6 Twin Otter aircraft to collect hyperspectral, multispectral, and lidar imagery [17]. During its annual flight campaign, the AOP surveys 75% of the core NEON sites on a rotating basis throughout the country. The AOP flight season runs from March to October. NEON terrestrial sites are scheduled to be flown during periods of at least 90% peak vegetation greenness for phenological consistency. The aircraft is flown at an altitude of 1000 m above ground level and a speed of 100 knots to achieve meter-scale hyperspectral and lidar raster data products and sub-meter multispectral imagery. The data products are publicly available on NEON’s data portal as flight lines and 1 km by 1 km mosaic tiles. When multiple flight lines cover a given tile, the most-nadir pixels are selected for the final mosaic. We utilized the mosaic data products in this study.

Hyperspectral Imagery

Hyperspectral scenes from the Spectrometer Orthorectified Surface Directional Reflectance–Mosaic data product [26] were utilized as the basis of the study. Each scene consists of a 1 km × 1 km tile at 1 m resolution, with 426 spectral bands ranging from 383 nm to 2512 nm and a spectral resolution of 5 nm. The scenes are orthorectified and projected to the appropriate UTM zone for each NEON site. The scenes are calibrated and atmospherically corrected so that all reflectance values fall between 0 and 1. The mosaics are created by using the most-nadir pixels from the most cloud-free flight lines from flights that are performed during 90% of maximum greenness or greater [27].

Canopy-Height Models

Discrete and waveform lidar were collected using the Optech ALTM Gemini system at a spatial resolution of approximately 1–4 points/waveforms per square meter, at 1064 nm spectrum. Using the discrete return point cloud data, NEON creates digital terrain model (DTM) and digital surface model (DSM) raster data products at 1 m spatial resolution to match the NIS imagery. Using the DTM and DSM, NEON also generates the ecosystem structure data product, a canopy-height model (CHM) raster where each pixel value quantifies the height of the top of the canopy above the ground [28]. This dataset consists of 1 km × 1 km canopy-height model (CHM) tiles at a 1 m resolution. The canopy heights under 2 m are set to 0 [29]. NEON’s CHM data were used to derive treetop locations using the lidR package version 3.1.0 and the “locate_trees” function, which utilizes a simple local maxima filter with a 3 m search radius. Treetop location was used during the data annotation process.

True-Color Images

True-color images, acquired concurrently with hyperspectral and lidar data at a 10 cm resolution, were used extensively in the development of this project but were not used as model inputs [30]. The AOP payload also includes an Optech D8900 commercial off-the-shelf digital camera that measures 8-bit light intensity reflected in the red, green, and blue (RGB) visible wavelengths. With a 70 mm focal length lens, the digital camera has a 42.1 deg cross-track field of view (FOV) and achieves a GSD of 0.086 m at a flight altitude of 1000 m. The raw RGB images are corrected for color balance and exposure, orthorectified to reduce geometric and topographic distortions and map the RGB imagery to the same geographic projection as the hyperspectral and lidar imagery, and ultimately resampled to a spatial resolution of 0.1 m (NEON data product ID: DP3.30010.001). The digital camera imagery can aid in identifying fine features such as boundaries of individual tree crowns in a dense canopy that are not as visible in the other airborne data products. Instead, these high-resolution true-color images were used to validate processes occurring with hyperspectral and other data visually.

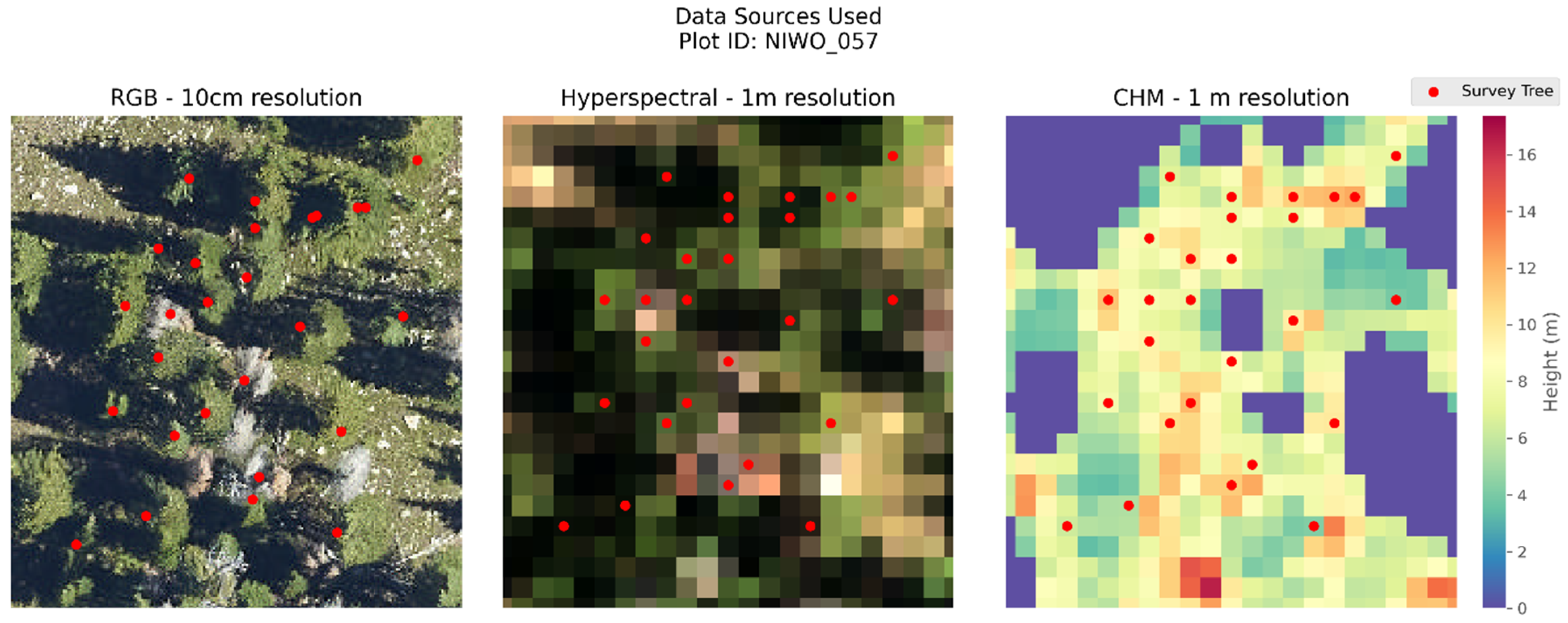
All scenes utilized for the NIWO, RMNP, and STEI sites were collected in August 2020. Figure 3 provides a visualization of all the data sources used in this study from a single plot at the NIWO site.

2.3. Workflow

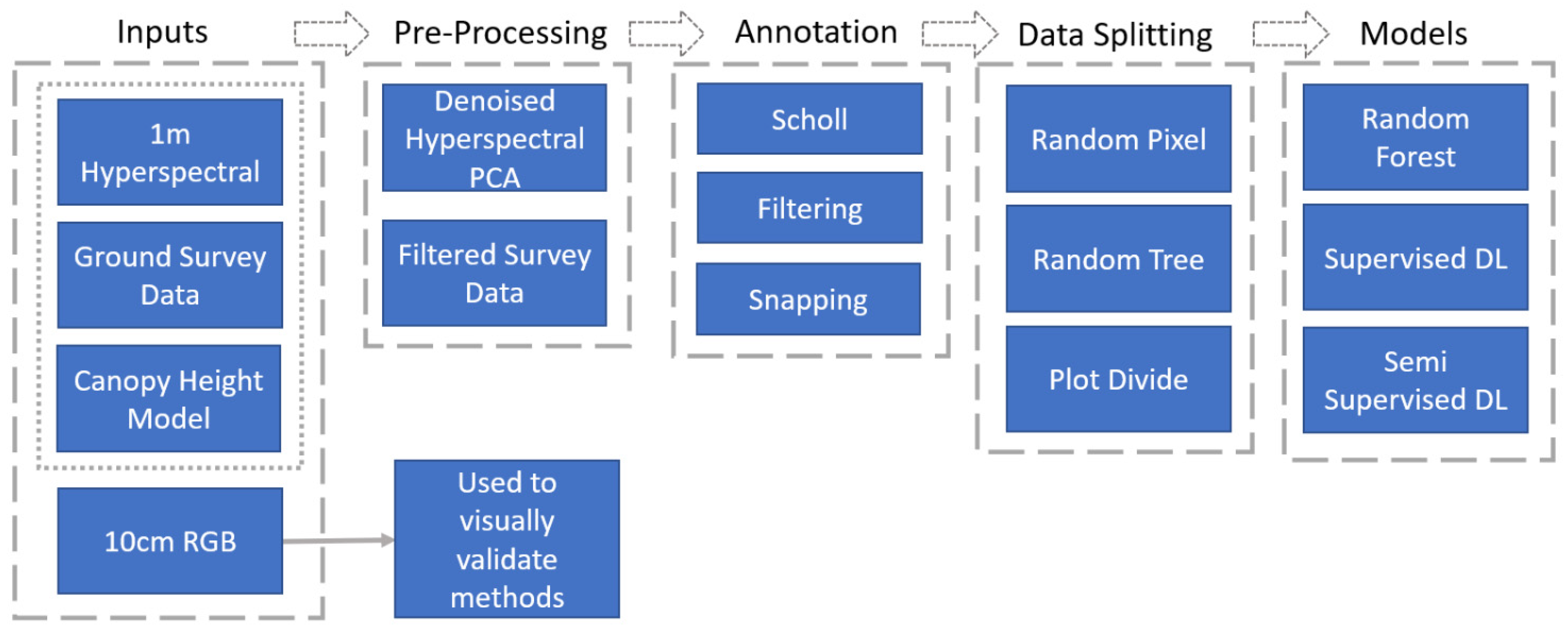
While there are many specifics to the experimental methods used in this study, and described in detail in the proceeding section, all the experiments followed the same flow (Figure 4). Those data were preprocessed and combined to create pixels labeled with a tree taxon. Those labels were then split into testing, training, and validation sets and used to train and evaluate a machine- or deep-learning model using different experimental parameters.

2.4. Pre-Processing

2.4.1. Hyperspectral Noise Reduction

Consistent with previous studies on the applications of hyperspectral imagery [7,9], it became evident during this research that certain hyperspectral bands exhibited higher levels of noise compared to others. Notably, bands that are highly absorbed by water molecules, as well as those situated at the extremes of the wavelength spectrum, tended to display noticeable noise or contained significantly lower values relative to the remaining bands. To account for this, we examined spectrographs from pixels throughout the NIWO study site and determined a range of bands to be included. The bands included fell between 410 and 1320 nm, 1450 and 1800 nm, and 2050 to 2475 nm.

Figure 5 illustrates the bands removed from the hyperspectral dataset, highlighting their influence on the resulting mean reflectance curve. This de-noising (mainly sensor noise) process dropped the total number of bands utilized in this study from 426 to 332. In some instances, isolated pixels exhibited reflectance values exceeding unity. To address this issue, any pixel with a reflectance value greater than 1 in any spectral band was masked out and subsequently disregarded from all subsequent processing and analyses.

2.4.2. Principal Component Analysis

Following de-noising, we decomposed all hyperspectral scenes using a principal component analysis (PCA). Prior studies working with hyperspectral imagery have shown promising results using either PCA [6,8,31] or other decomposition methods [11,13]. Since PCA is a well-established technique for dimensionality reduction and feature extraction, this study adopted the principal component analysis (PCA) to reduce the data dimension. The implementation of PCA is straightforward, computationally efficient, and consistently converges on a stable solution, making it an attractive choice for data decomposition. All PCA decomposition was conducted using the scikit-learn IncrementalPCA module, which was fitted to all scenes used from the NIWO site and then used to decompose scenes from other sites. We took the first 16 principal components for all scenes, as these accounted for 99.9% of the total variation found.

2.5. Tree Annotation

We tested three methods for labeling the NEON site data: Scholl, filtering, and snapping. All three methods remove some labeled trees from the NEON woody vegetation survey, illustrated in Figure 6. All three annotation methods attempt to ensure that only trees at the top of the canopy and visible in remotely sensed scenes are used to create tree labels. A tree recorded from the field survey but not visible from an aerial perspective could potentially result in inaccurately labeled pixels when used to generate a label for classification. The other two methods also attempt to address potential mismatches between field surveys and hyperspectral data due to geolocation errors in the field data.

2.5.1. Scholl Algorithm

The Scholl algorithm [8] compares each tree to the trees around it to determine which tree crown is most likely to be visible in a remote-sensing image. The algorithm performs this operation using standard GIS operations. It was initially implemented in QGIS but was re-implemented in Python for this study. The first step is to create a circular buffer around each identified tree from the NEON woody vegetation survey. The buffer size is determined using circular tree-crown polygons created with half the maximum crown diameter per tree. Once buffers are developed, the algorithm tests each tree to see if a neighboring tree may fully or partially occlude it. This comparison is performed by finding overlapping tree crowns and comparing the tree heights, as measured in the NEON woody vegetation survey. Any neighboring tree occluded from that tree is removed. Following filtering the NEON woody vegetation data by the Scholl algorithm, all remaining trees are selected for further use and labeled using their taxon label from the NEON survey.

2.5.2. Snapping Algorithm

This algorithm attempts to use a framework of mutual agreement to match the trees identified through the NEON woody vegetation survey with the treetops identified through the analysis of a local canopy-height model. The algorithm first searches through every survey-derived tree location in a given study plot. It finds the closest CHM-derived treetop location at each tree location within a user-supplied distance. Then, the algorithm searches through all CHM-derived tree locations and finds the closest survey-derived tree location within a user-supplied distance—3 m in our case. The algorithm tests each pair to find if the survey/CHM pair matches the CHM/survey pair. If that is the case, the survey location is ‘snapped’ to the CHM location as the actual location of the tree, and both the survey location and the CHM location are removed from further search iterations. The algorithm cycles through the survey- and CHM-derived tree locations until it reaches a maximum number of iterations, runs out of locations, or ceases to find new pairs. Once as many pairs as possible are found and snapped in a study plot, these are given a taxon label using the NEON woody vegetation survey and saved for further use.

2.5.3. Filtering Algorithm

The filtering algorithm selects trees from the NEON woody vegetation survey by first testing field-measured tree height against CHM-derived tree heights. For all trees in a given study site, the mean and standard deviation of height difference between measured tree height and height in the CHM at the exact coordinates were calculated. Any trees with absolute height differences between the survey and the CHM that were greater than the standard deviation of the height differences were removed from further analysis. Then, to handle potential overlapping or occluded tree crowns, a distance filtering procedure is applied. For each study plot in a study site, we select a minimum distance threshold of x − (1.5)σ, where x is the median distance between trees and σ is the standard deviation of the distance between trees. If any two trees are positioned closer together than the specified threshold, the tree within that pair that exhibits a shorter field-measured height is eliminated from consideration. The optimal outcome is a collection of distinct trees closely aligned with the canopy-height model (CHM). Once all trees have been filtered for height and lateral distance, labels are selected, as in the preceding methods.

2.5.4. Annotation Post-Processing

For all annotation methods, once a tree location had been identified, a 4 m × 4 m box centered around the identified tree was clipped from all input data sets and saved for model training and evaluation. A 4 m × 4 m box was chosen as it is a commonly used method for selecting a tree crown from a scene [9]. While the main model inputs used for experimentation were clips from PCA scenes, hyperspectral, canopy-height model, and RGB data were also clipped and saved for experimentation and visual validation. As all three algorithms select and filter trees differently, the total count of trees selected at a study site differs between algorithms.

Following annotation, non-canopy pixels are filtered out. If it is determined that a labeled tree contains no canopy pixels according to the CHM, as can occur with the Scholl annotation method, that tree is removed from the site. Each algorithm selected a different number of trees at the study sites, which is illustrated in

Table 1. Counts of trees labeled by each label selection algorithm at the NIWO and RMNP study sites.

Algorithm	Trees Labelled @ NIWO	Trees Labelled @ RMNP
Scholl	268	358
Snapping	317	487
Filtering	347	544

.

2.6. Data Splitting

We tested three techniques for splitting data into training, validation, and testing sets. This terminology is inconsistent between the computer science/deep-learning literature and the remote-sensing classification literature. For this paper, the training set refers to all data on which a given model is trained. The validation set is reserved for deep-learning models and is used to test if the deep-learning model overfits the training set. The random forest model utilized in these experiments self-validates using the supplied training data. So for the random forest experiments, training and validation sets were re-combined after being split. The testing set, comprising data reserved exclusively for evaluating the model’s performance, was not used until the completion of model training and the finalization of all parameter configurations. For all experiments on intra-site classification (testing on the same study site where a model was trained), we utilized a 60% training/20% validation/20% testing split. When performing inter-site classification (testing on a study site distinct from the one used for training), we maintained the same split for the original training site. Still, the testing data were completely from the testing site. Testing data from the original site were discarded; this was completed for consistency with intra-site classification methods.

We used three splitting methods, namely random pixel splitting, random tree splitting, and plot-divide splitting. To clarify, all classification tests are pixel level, and ‘random-tree splitting’ and ‘plot-divide splitting’ do not indicate that we are attempting to classify at the tree or plot level. In the case of these methods, the ‘tree’ and ‘plot’ are used to indicate the scale at which training/validation/testing pixels are divided.

2.6.1. Random Pixel Splitting

Despite findings that indicate the negative impact spatial autocorrelation can have on using this method [3], it is still used in remote-sensing studies when attempting pixel-level classification [8,32]. To perform the random pixel split, all labeled pixels are combined into a single array. These pixels are then randomly sampled without replacement to form the training, validation, and testing sets. A single tree can end up in all three sets.

2.6.2. Random Tree Splitting

This method divides pixels so that all pixels from a labeled tree remain together and distributions of tree taxa remain roughly equivalent across the testing, training, and validation sets. All labeled trees from a study site are grouped to perform this. These trees are then split into training, testing, and validation sets using a weighted random sampler, ensuring that all sets’ proportional taxa distributions are equivalent.

2.6.3. Plot-Divide Splitting

The plot-divide splitting method uses NEON sampling plots as a unit to divide labeled pixels. The goal is to split pixels into training, testing, and validation sets so that all pixels from the same sampling plot are contained within the same set while maintaining equivalent species distributions between all three sets. This approach makes sure that the pixels from the same plot can only be used for training or testing and validation. This is similar to the method used [16]. To perform this method, tree taxa count totals within all study plots at a study site are calculated. Then, the algorithm sets up and attempts to solve a non-linear optimization problem using the Google OR-Tools v9.6 package. In the case of a 60/20/20 split, this problem is framed as “60% of all sample plots from a given taxa should be in the training set, 20% should be in the validation set, and 20% should be in the testing set, while all trees from the same sample plot must be in the same set”. As tree taxa are not evenly distributed between sample plots, with some plots containing exclusively a single taxon, it is almost impossible to solve this problem perfectly. Therefore, instead of attempting to find a split that puts exactly 60% of the samples from a taxon into the training set, the solver tries to find a bounded optimal solution within a range of ±5 trees from any taxa. Once a solution has been found, the tree pixels are split into training, testing, and validation sets based on which plot they are found in. For example, the solution to the plot-divide problem could be:

• Training set: Plot NIWO_05, NIWO_07, NIWO_09, NIWO_30, NIWO_01, NIWO_0;
• Validation set: Plot NIWO_02, NIWO_16;
• Testing set: Plot NIWO_08, NIWO_11, NIWO_42.

The plot-divide splitting method is the most complicated and unwieldy. It does not always calculate a solution depending on the distribution of taxa across study plots. In that event, the solver’s tolerance can be adjusted.

2.7. Classification Models

We tested three model types, namely supervised deep learning, semi-supervised deep learning, and random forest. Both deep-learning models were implemented using PyTorch 1.13 and PyTorch Lightning 1.9. The random forest model used is from Scikit-Learn 1.1.3.

2.7.1. Deep Learning

For this project, we tested two different styles of deep learning, namely supervised and semi-supervised. Supervised deep learning (Figure 7) describes a model training procedure where a model is trained only on labeled pixels. Semi-supervised deep learning utilizes a pre-training procedure, where a model is first trained to perform a clustering task on unlabeled data and then re-trained to perform a classification task on labeled data. This is also called ‘lightly supervised’ training in the literature [22].

Based on the work of [10], we used a transformer architecture as the basis of all deep-learning models used in this work. The transformer architecture was initially developed for language translation models [33] but has shown excellent results in visual classification problems [34]. A typical transformer uses a transformer encoder–transformer decoder architecture. For this work, we used only the transformer encoder portion of the architecture, as the transformer decoder output is designed for decoding sequences in language and time-series modeling tasks. Instead, the transformer decoder is replaced with a simple, 2-layer multi-layer perception (MLP).

We used the same architectural parameters across both styles of deep-learning models. This allowed us to easily swap a pre-trained encoder into the supervised architecture, creating the semi-supervised architecture. For all deep-learning models testing PCA inputs, we used an embedding size of 128; a sequence length of 16, meaning that the model can address 16 pixels at a time, a feature length of 16; 12 encoding layers; a dropout rate of 0.2; and 4 attention heads. When performing supervised learning, the learning rate for all models was 5 × 10⁻⁴. When performing pre-training, the learning rate used was 5 × 10⁻⁵, as we found that a higher learning rate did not lead to stable results. The classification decoder is a 2-layer multilayer perception, with the number of parameters depending on the output classes. Loss, used to update model weights, was calculated using the binary cross-entropy loss function. No fine-tuning of model hyperparameters was performed. All deep-learning models were trained using a 60% training/20% validation/20% testing data split, with the validation data reserved to ensure our models had not overfit. All data were normalized to have unit mean and standard deviation before being fed to our deep-learning models.

Supervised Deep-Learning Model

The supervised deep-learning model, a transformer encoder, and an MLP decoder, with all model weights initialized with randomized values from the normal distribution, were trained for all experimental parameters for 200 epochs using a batch size of 128. A training epoch consisted of running a batch through the model, updating the model parameters, and running another batch until all training data had been consumed. Validation was performed after each epoch to test the model’s efficacy on the data it had not been exposed to. The loss on the validation set was used as a proxy for finding a model’s ‘best’ version. When testing a model, we utilized the model checkpoint, demonstrating the lowest loss on the validation set. This was often not the model from the 200th epoch, as the models had generally overfitted at that point.

Semi-Supervised Model

The semi-supervised model is significantly more complicated than the supervised model, as it requires creating and training a pre-training model on unlabeled data. While the pre-training model shares the same transformer encoder backbone as the supervised model, other components of the model and objective are different. For this work, we implemented the swapping assignments between views (SwAV) model for pre-training [22]. The SwAV model is an unsupervised clustering model with a similar output to other, more commonly used clustering methods like K-means. We chose to use the SwAV model specifically for deep-learning clustering as a technique in general because standard machine-learning clustering techniques, like the K-means above, did not provide coherent results in preliminary work when dealing with NEON hyperspectral scenes. The model was provided with two versions of the same unlabeled input. One of those versions is the original, and the other had pixel values randomly deleted. It is deemed a successful outcome if the model correctly assigns both input versions to the same class. Otherwise, it is considered a failure.

Pre-training using the SwAV model was tested on NIWO and STEI. For both sites, tests were run for 15 epochs. Each epoch consisted of running through all 4 × 4 contiguous canopy pixel patches from that site, using a batch size of 1024 patches.

After successfully training a pre-training model, we conducted semi-supervised training similar to supervised training. Model weights for the semi-supervised model encoder are not initialized randomly but instead copied from a pre-trained model. This gives us a model trained on a clustering objective, whose weights are then re-trained on a classification objective. Otherwise, all training proceeds in the same fashion as supervised model training.

2.7.2. Random Forest Model

We utilized the random forest classifier from the Scikit-Learn Python 1.2.1 package [35] for the random forest model. All model parameters were left as default values, using 100 estimators with no maximum depth. A random forest classification model is an ensemble model consisting of a set of decision trees trained on subsets of the provided training data. The probabilistic outputs from individual decision trees are combined to create a class prediction for a pixel. The model, as implemented, is self-validating, using a one-out-of-bag technique when building decision trees. This allows the model to control overfitting. As a result of this validation technique, different from the separate, per-epoch validation used in our deep-learning model, when training random forest models, all training and validation datasets are combined prior to being fed into the model.

2.8. Testing

Experimental parameters were chosen to test our three main variables, including the label-selection method, data-splitting method, and model type. We tested the three label-selection methods and three data-splitting methods using random forest and supervised deep-learning models for intra-site classification at the NIWO site. We also tested the label-selection and data-splitting methods for inter-site classification, with models trained on the NIWO site and tested on the RMNP site, using random forest and supervised deep-learning models. Finally, we tested semi-supervised deep learning on both intra-site and inter-site classification problems, using all label-selection methods but only the random tree and plot-divide data-splitting methods. We used semi-supervised models that were pre-trained on either the NIWO site or the STEI site for the semi-supervised tests.

3. Results

3.1. Intre-Species Spectrum Difference

The mean AOP hyperspectral reflectance curves appear very similar across all four tree species, including the peak reflectance at the green spectrum in the visible wavelength region and the steep slope at the edge between the red and near-infrared regions, the higher reflectance and three peak returns in the near-infrared region (NIR), and lowered reflectance in the mid-infrared spectrum (Figure 8). Inter-species comparison suggests that Limber Pine has the highest reflectance in the NIR and the mid-infrared spectrum, then followed by Englemann Spruce, Subalpine Fir, and Lodgepole Pine, the lowest. The spectral differences can be caused by leaf structure and leaf pigment, water content, leaf surface characteristics, and canopy structure.

3.2. Annotation Methods—Intra-Site Comparison

We tested our label-selection methods at the NIWO site, controlling for both data-splitting techniques and model type (Figure 9). The results show the following features in terms of accuracy. (1) The random forest model had no substantial disparities in performance across the three labeling methods and all three data-splitting methods employed. This result might suggest that the random forest model was able to best fit the data. (2) However, using the random forest model, the random pixel-splitting method resulted in higher accuracies (~0.7) than the other two splitting methods (random tree and plot-divide splitting methods) (~0.6–0.65). These higher accuracies using the random pixel-splitting method likely overstate the model’s actual performance due to the apparent spatial autocorrelation issue with this method discussed previously. (3) When employing the random pixel-splitting method, deep learning performed similarly to the random forest model among the various labeling methods. This result suggests that the random pixel-splitting method is not sensitive to different learning models and data-splitting methods. (4) However, with the plot-divide or random tree splitting methods, deep learning outperformed the random forest model using the filtering and Scholl labeling methods but performed similarly to the snapping labeling method. The highest accuracy can reach almost 0.8. Using the deep-learning model, the filtering method yielded the most optimal results. In contrast, the snapping method demonstrated the poorest performance, while the Scholl method exhibited intermediate effectiveness.

Table 2. Confusion matrix from experiment #42: a supervised deep-learning model trained on PCA scenes at the NIWO site using the Scholl algorithm and the plot-divide method, resulting in an overall accuracy of 0.721.

	Expected
Predicted	Subalpine Fir	Lodgepole Pine	Engelmann Spruce	Limber Pine	User’s Accuracy
Subalpine Fir	152	0	68	0	0.69
Lodgepole Pine	12	174	28	0	0.81
Engelmann Spruce	41	15	224	0	0.80
Limber Pine	47	0	6	10	0.16
Producer’s Accuracy	0.60	0.92	0.68	1.00	Overall: 0.72
F1 Score	0.64	0.86	0.74	0.27

illustrates the confusion matrix for an experiment using a supervised deep-learning model trained on PCA scenes at the NIWO site using the Scholl algorithm and the plot-divide method. The producer’s accuracies (PA) from highest to lowest are 1.0 (Limber Pine), 0.92 (Lodgepole Pine), 0.68 (Englemann Spruce), and 0.60 (Subalpine Fir). The user’s accuracies (UA) are 0.81(Lodgepole Pine), 0.8 (Englemann Spruce), 0.69 (Subalpine Fir), and 0.16 (Limber Pine). Limber Pine has the highest PA but the lowest UA. The F1 scores (combination of PA and UA) are 0.86 (Lodgepole Pine), 0.74 (Englemann Spruce), 0.64 (Subalpine Fir), and 0.27 (Limber Pine). The low accuracy for Limber Pine is likely due to its low sample size. Previous studies show that the model performance for each class depends on the training data size used [36]. Lower training size can result in lower accuracies. The Limber Pine class has the lowest samples compared to other species.

3.3. Splitting Methods for Training, Validation, and Testing

For intra-site classification, the random tree data-splitting method outperformed the plot-divide and random pixel-splitting methods when using the filtering annotation method and the deep-learning model (Figure 9). However, the differences between all three data-splitting methods were relatively small for the random forest model.

For inter-site classification, the random tree splitting method also demonstrated its superiority compared to the random pixel and the plot-divide splitting methods (Figure 10). For deep-learning models, the random pixel method, in which there is the greatest chance for a training pixel to be spatially proximate to a validation pixel, led to models with the least capacity for classifying taxa from outside their training site. The accuracies ranged from 0.32 to 0.45. The plot-divide method showed performance between the random pixel and random tree methods; their accuracies were from 0.4–0.6. The random tree data-splitting method ensures that no pixels from any individual tree are mixed between training, testing, and validation sets. It is the most successful method for both intra-site and inter-site classifications, with the highest accuracy of ~0.7. The random tree data-splitting method appears to be sufficient to partially overcome spatial autocorrelation’s impact and the potential to create a locally overfit model.

3.4. Random Forest vs. Deep Learning

For intra-site classification, the deep-learning models consistently outperformed random forest models when using the filtering and Scholl annotation methods and in conjunction with the plot-divide and random tree data-splitting methods (Figure 9). Conversely, DL showed no advantages compared to our random forest approach when using the snapping labeling and random pixel-splitting methods. The accuracies using the snapping labeling method and the random pixel-splitting method did not reflect the actual performance of the DL/ML methods. The higher accuracy of using the random pixel-splitting method is associated with the spatial autocorrelation feature of the dataset, as the models may be learning to recognize immediately adjacent pixels [19].

Deep-learning models consistently outperformed random forest models for inter-site classification when using all data-labeling and data-splitting methods (Figure 10). The random forest models appeared utterly incapable of inter-site classification, even between the relatively proximate NIWO and RMNP sites (11 km apart). Their accuracies went from 0.1 to 0.22. The snapping annotation method demonstrated the best results for deep-learning inter-site classification when using the random tree-splitting method, with the accuracy reaching 0.67. In contrast, the Scholl method showed the best results for the random tree data-splitting method, with the accuracy reaching ~0.69.

These results demonstrate that a deep-learning transformer model can consistently match or outperform standard random forest classification for intra-site classification tasks and that deep-learning transformer models are suitable for creating an inter-site hyperspectral species classification model with the data and parameters as configured, while random forest models are not.

3.5. Supervised and Semi-Supervised Deep Learning

Pre-training did not improve the model accuracies for intra-site classification (Figure 11; top row), while pre-training improved the results for inter-site classification only when pre-training on the STEI site (Figure 11; bottom row). Pre-training on the NIWO site, training on the NIWO site, and testing on either the NIWO or RMNP sites have led to worse results than not pre-training. These results indicate that, while semi-supervised training may hold promise for creating a general classification model, significant investigation must be conducted to fully understand the impact of unsupervised pre-training as a model-training component and if it can be utilized to create a more capable general classification model. Meanwhile, we caution readers about over-complicated models that might perform worse than parsimonious ones.

4. Discussion

4.1. Pros and Cons of Different Labeling Methods

While different label selections worked better under different circumstances, there are distinctions between all three methods, in addition to their potential impact on classification accuracy. Most immediately, the Scholl method requires more information from the NEON woody vegetation survey than the other two methods, which require access to a canopy-height model to work. The Scholl method needs the maximum crown diameter and tree height parameters to assess whether an individual tree might have its crown obscured by another crown. These parameters, measured in the field, are unavailable for all trees in the NEON woody vegetation survey. Therefore, the Scholl method works with a more limited data set than the other two. This is most apparent regarding the number of individuals selected to make up the data set for a study site (Table 1).

As a general rule for training models, more data are better. However, the quality of that data is essential, and the maximum crown diameter parameter could indicate data quality. We performed preliminary tests to see if requiring the maximum crown diameter significantly affected the classification results when using the snapping and filtering methods. While our tests were not exhaustive, we did not find that requiring the maximum crown diameter offered improved the results when using the snapping and filtering methods.

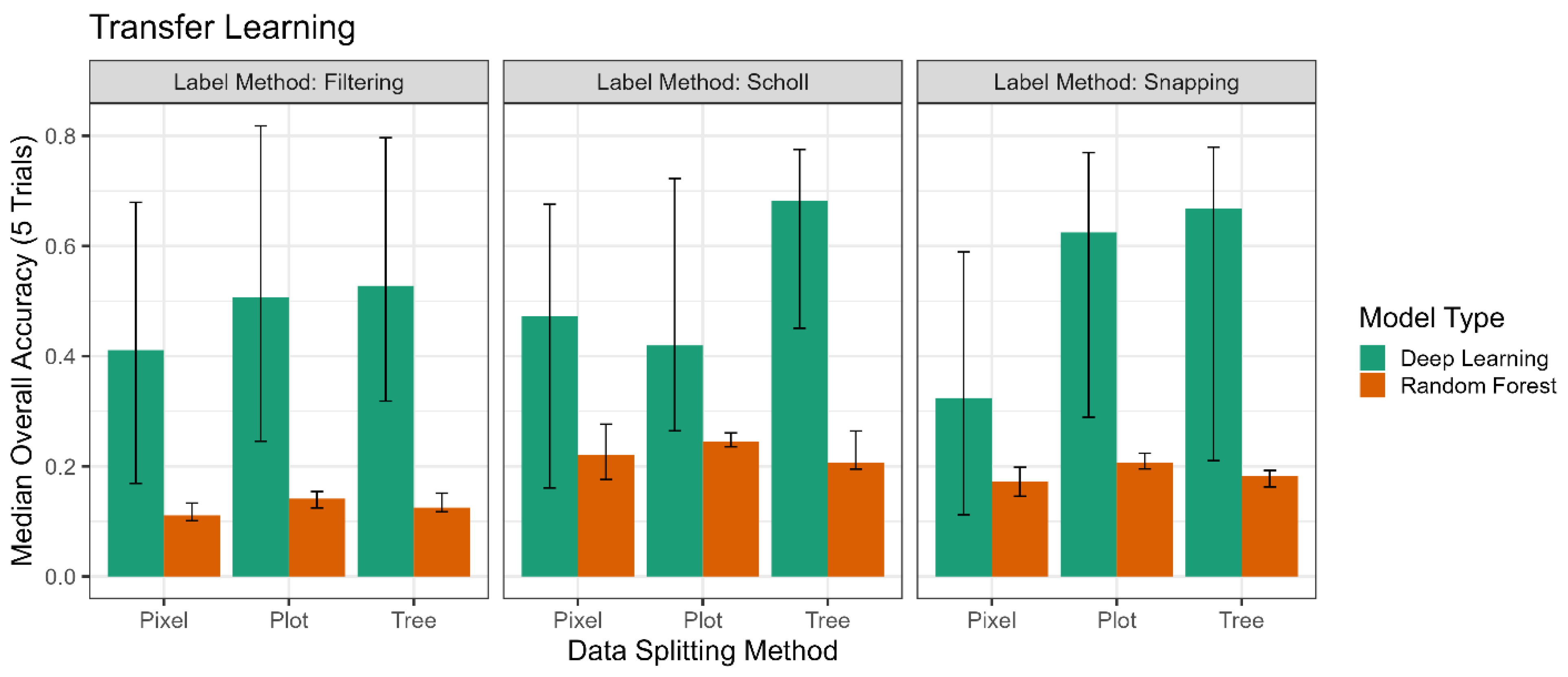
While the Scholl method performed generally well, there were certain circumstances in which it was outperformed by our two proposed methods, particularly the filtering method. The filtering method produced the best overall results of all the experiments (Figure 11) and generally performed well at intra-site classification at NIWO (Figure 9). In the tests of inter-site classification with no pre-training (Figure 10), the filtering method underperformed. The filtering method requires two parameters, namely the acceptable range of standard deviations from the mean height difference between ground observations and the canopy-height model and the acceptable minimum standard deviation from the mean regarding the lateral distance between trees. For these experiments, we found these parameters (±1.5 standard deviations for height difference, ≥1.5 standard deviation for lateral distance) based on visual observations of the data from the NIWO site. We may get better results by tuning these parameters per site by using the filtering method. It should also be noted that the filtering method performed best at the pre-training inter-site classification task, indicating, again, that the data-labeling selection method is not the controlling factor in model accuracy.

One drawback that both the filtering and snapping methods share is that they depend on the canopy-height model for work. Using the canopy-height model increases the number of model parameters. The performance of these two labeling methods might be affected by the accuracy of the rasterized canopy-height model process derived from lidar point clouds.

For the test cases utilized in this work, the snapping algorithm performed the worst overall, and we would not recommend it for building a tree species identification model from NEON data. However, it still may offer good results for building classification models using noisier data where there are potential registration issues between tree locations and remotely sensed imagery. This could appear, for example, if users did not have access to survey-grade GPS equipment when developing their tree locations. Another possible use would be if remote-sensing data were gathered on a particularly windy day, where the wind could bend treetops to be meters from their trunk base. In essence, we recommend using the Scholl method when extensive crown diameter measurements are available or the filtering method when only a canopy-height model is available. In the future, it may best work towards a tree labeling method that does not depend on a measured crown diameter or a canopy-height model.

4.2. Spatially Aware Data Splitting of Evaluation Data

One of the most significant findings of this work, and one that is occasionally ignored or uninterrogated in the literature, is that potential spatial autocorrelation must be considered when developing any remote-sensing classification model, particularly a fine-scale hyperspectral-based model where local lighting and environmental conditions will have an outsized impact on observed reflectance. We have successfully demonstrated that combining all labeled pixels and then randomly splitting those into training, testing, and validation sets without consideration for the spatial and object relationships between pixels leads to a less successful general model and may lead to overconfidence in model performance. With these results, we argue that any spatially based classification model validated by comparing immediately adjacent pixels, particularly those that may belong to an object also present in the training set, requires re-evaluation using a spatially aware data-splitting technique.

When creating remote-sensing classification models, the same fundamental principle of variety in exposure to data applies. To create a well-performing model, the model must be exposed to various inputs in training and testing, which account for the spatial autocorrelation that is essentially guaranteed to be present in the data. Two trees near each other are more likely to have experienced similar environmental conditions and life history than two trees far apart, and the proximate trees are, therefore, more likely to resemble each other. This is merely an application of Tobler’s first law [37] and is a fundamental feature of geographic problems.

Digging into our other two data-splitting methods, we demonstrated what, at first, appeared to be counterintuitive results. The random tree data-splitting method largely outperformed the plot-divide data-splitting method, even though the plot-divide method ensures a greater physical gap between the training, testing, and validation sets.

To see why the plot-divide method consistently underperforms relative to the random tree method, even though the plot-divide method would seem to give the most spatially disparate training and validation sets, we must consider the principle of providing model access to the greatest variety of data possible to ensure more general training. Fundamentally, we can see that the random tree method is superior in variety, as it provides tree samples from across as large a swath as possible from the study site. In contrast, because of how trees are distributed at NEON sampling plots, the plot-divide method may provide a minimal range of training and validation data. NEON sampling plots are not evenly spaced, and each plot does not contain a proportional number of taxa relative to the distribution of taxa throughout the site.

4.3. Random Forest vs. Deep Learning

Deep learning outperformed random forest classification across almost all combinations of experimental parameters outside of using the random pixel data-splitting method. However, we also notice the large error bars in the deep-learning results. While we do not believe these significantly impact our conclusions thus far, they provide valuable insight for future model development and training techniques.

The error bars for intra-site classification (Figure 8) are relatively similar between the deep-learning and random forest models; the subsequent increase in range as we progress through the inter-site classification results (Figure 9 and Figure 10) demonstrates the stochasticity in training deep-learning models. The minimum and maximum values of the error bars in Figure 9 follow the trend of the median values. However, they become noisier when looking at Figure 9. Part of this is due to the stochastic nature of deep-learning model training, where weights are populated and updated in a non-deterministic fashion. This issue can likely be addressed through model initialization and training techniques.

The range in the deep-learning model results for inter-site classification may also be due to how validation was performed to select the ‘best’ model for testing. This is best demonstrated by the differences in error range in the two rows of Figure 10. In the top row, for intra-site classification, the validation set used to determine the ‘best’ model comes from the same site as the testing set, so there is some consistency between what will work well between both sets. For inter-site classification, the ‘best’ model is determined by using a validation set from the original training site. Perhaps in the future, using a validation set from the testing site would give less noisy results. Even better, since this work aims toward developing a general model, developing a general validation set would allow for testing and training throughout our entire potential classification area.

4.4. Uncertainties of the Models

Many tree species classification studies use multi-source data, including hyperspectral, lidar, and unmanned multispectral data [9,14,38,39,40,41,42,43,44,45]. This study trains the models using hyperspectral data only. Adding other data sources, such as lidar and environmental, will improve the model’s accuracy. Even though this study used lidar data for data splitting for training and testing, it was not used for training the model. Including other data sources, such as lidar data and environment and topography data, will potentially improve the model’s performance.

5. Conclusions

While our two proposed methods (filtering and snapping) occasionally outperformed the Scholl method for annotating woody vegetation from NEON science sites, the Scholl method was the most consistently superior method across all experimental parameters. Two proposed methods in this study depend on additional data in the canopy-height model, and both require user-supplied parameters that the Scholl method does not. Meanwhile, the filtering method produced the best overall accuracy of all the experiments when using pre-training and performing an inter-site classification task. Though the Scholl method requires a measurement of crown diameter to operate, it can still be used with crown diameters estimated from observation or known allometry. The Scholl method can be easily implemented in GIS software, such as ArcPro, or code utilizing GIS libraries. The consistency of results across the different NEON sites suggests that the Scholl method works well and would be a good starting point for any classification model where ground survey points have to be registered with remote-sensing data.

Of the three data-splitting techniques tested, namely random pixel, random tree, and plot divide, the random tree method performed best when testing inter-site classification. We used inter-site classification capabilities as a proxy for overcoming spatial autocorrelation. At least partially, the random tree method can account for spatial autocorrelation by ensuring pixels from the same object are not spread across our training, testing, and validation sets. Having pixels from the same object spread in training, testing, and validation sets, such as the random pixel method, leads to overconfident validation results and, therefore, to a lower capacity for use as a general, inter-site classification model.

In testing the two methods that attempted to account for the impact of spatial autocorrelation, we found that the random tree method was both easy to implement and provided strong results. The plot-divide method required solving a non-linear optimization problem and was clumsy to implement and execute. We propose that the random tree data-splitting method is sufficient to overcome the impact of spatial autocorrelation for creating a general, inter-site classification model. The study by [3] suggested that a minimum distance between classification objects be maintained to account for spatial autocorrelation. Our analysis suggests that enforcing a minimum distance to prevent individual tree crowns from overlapping may be sufficient for accurate tree taxa classification. Additionally, we dismiss the random pixel-splitting method as a valid approach for creating training, testing, and validation sets when dealing with geographic data exhibiting spatial autocorrelation.

We demonstrated that deep learning provides consistently better classification results than random forest classification. While deep learning performed moderately better than random forest at intra-site classification when using the random tree and plot-divide splitting methods, it significantly outperformed random forest when tested on inter-site classification. Using a self-supervised model of deep learning, wherein the model was pre-trained on unlabeled data before being exposed to labeled training data, showed the best results for inter-site classification. As part of this, we demonstrate that the lightweight SwAV architecture is suitable for the unsupervised clustering of high-dimensional remote-sensing pixels. This type of semi-supervised model training shows great promise for creating future general taxa-classification models. Although our findings with this semi-supervised model were preliminary, gaining deeper insights into how the pre-training stage operates to classify data could contribute to an improved theoretical understanding of classification models.

Building a general tree-classification model that can operate globally and identify thousands of taxa will be an enormous undertaking. By testing methods of data annotation, data splitting, and classification of tree species outside of the study area, we have taken a few small steps toward constructing a large general model. We have shown that the existing Scholl data-annotation method works well but that our proposed filtering method also works well, with lower field data gathering required. We conclude that the random pixel data-splitting method proves inadequate and invalid for training and classifying individual trees. We found that ensuring trees remain treated as whole objects when splitting training and testing data is enough to account for local overfitting. Finally, our analysis also demonstrates that taking advantage of the terabytes of unlabeled tree imagery possibly improves our model’s capacity for classification outside of the boundaries of its original training set. Our findings from the study provide valuable insights that will help to develop the next generation of tree species classification models. Future work will train the models using multi-data sources for better accuracies.