Research on SAR Active Anti-Jamming Imaging Based on Joint Random Agility of Inter-Pulse Multi-Parameters in the Presence of Active Deception

Abstract

Synthetic aperture radar (SAR) inter-pulse parameter agility technology involves dynamically adjusting parameters such as the pulse width, chirp rate, carrier frequency, and pulse repetition interval within a certain range; this effectively increases the complexity and uncertainty of radar waveforms, thereby countering active deceptive interference signals from multiple dimensions. With the development of active deceptive interference technology, single-parameter agility can no longer meet the requirements, making multi-parameter joint agility one of the main research directions. However, inter-pulse carrier frequency agility can cause azimuth Doppler chirp rate variation, making azimuth compression difficult and compensation computationally intensive, thus hindering imaging. Additionally, pulse repetition interval (PRI) agility leads to non-uniform azimuth sampling, severely deteriorating image quality. To address these issues, this paper proposes a multi-parameter agile SAR imaging scheme based on traditional frequency domain imaging algorithms. This scheme can handle joint agility of pulse width, chirp rate polarity, carrier frequency, and PRI, with relatively low computational complexity, making it feasible for engineering implementation. By inverting SAR images, the echoes with multi-parameter joint agility are obtained, and active deceptive interference signals are added for processing. The interference-suppressed imaging results verify the effectiveness of the proposed method. Furthermore, simulation results of point targets with multiple parameters under the proposed processing algorithm show that the peak sidelobe ratio (PSLR) and integrated sidelobe ratio (ISLR) are improved by 12 dB and 10 dB, respectively, compared to the traditional fixed waveform scheme.

1. Introduction

Synthetic aperture radar (SAR), as a crucial tool for modern reconnaissance, is widely used in electronic countermeasures [1]. How to effectively acquire target information while reducing the probability of being intercepted and identified and minimizing the impact of active deceptive interference has become one of the research hotspots in the SAR field [2,3,4]. To address these challenges, two approaches are commonly employed: (1) transmitting low-power signals or noise-like signals to reduce the likelihood of interception [5,6]; (2) using methods based on characteristic parameters and time–frequency analysis to identify and eliminate false target information [7,8]; however, with the advancement of jamming technology, these methods may not provide sufficient protection in certain scenarios [9,10]. Therefore, researching new anti-jamming techniques has become increasingly important.

Reducing transmission power often leads to a decline in radar performance, while eliminating interference signals through back-end signal processing can easily cause echo signal distortion and incomplete interference suppression [11,12]. With the maturity of waveform generation technology and advancements in hardware equipment, active anti-jamming methods based on waveform design have gradually become a research hotspot [13,14]. Among these methods, using complex waveforms generated by random agility of inter-pulse parameters can effectively reduce the probability of interception and actively suppress active deceptive signals [15,16,17]. Traditional LFM signals primarily include parameters such as pulse width, bandwidth, chirp rate, carrier frequency, and PRI. To ensure consistent range resolution, the bandwidth is typically not altered. Therefore, on the basis of fixed parameters, random agility is applied within a certain range to the pulse width, chirp rate, carrier frequency, and PRI. This randomness disrupts the timing of the jamming receiver, increasing the difficulty of analysis. As a result, the retransmitted jamming signals cannot match the time sequence of the original pulses during processing, thereby actively suppressing the imaging of deceptive targets [18].

Different agile parameters have varying impacts on imaging, requiring distinct processing methods. In terms of suppressing active jamming signals, pulse width and chirp rate primarily suppress jamming signal energy in the range dimension, while carrier frequency and PRI mainly function in the azimuth dimension. By applying random agility to these parameters, active jamming signals can be effectively suppressed from different dimensions, thereby enhancing the anti-jamming capability of radar imaging. Pulse width agility disrupts the energy distribution of the jamming signal by altering the time-domain characteristics of the echo signal [19]. Chirp rate agility changes the frequency-domain characteristics of the signal, preventing the jamming signal from maintaining consistency in the range dimension [20].

Carrier frequency agility suppresses azimuthal jamming signals by altering the signal’s center frequency [21,22]; for example, B. Yang significantly improved radar’s anti-jamming performance under electronic interference by alternating the use of pulse repetition frequency agile radar and traditional fixed pulse repetition frequency pulse Doppler radar in different scenarios [23]. Mobley S. G. and Maier M. W. addressed the issue of high Doppler sidelobes in radar echoes with non-uniform pulse repetition intervals by proposing a method to process radar echoes using an interpolation filter; this method achieved synthetic aperture radar signal processing with non-uniform pulse repetition intervals, enhancing radar sensitivity and anti-jamming capability [24,25].

Additionally, some studies have pointed out that joint agility of different parameters can achieve effects that single-parameter agility cannot accomplish. For example, the joint agility of phase and frequency-coded waveforms can effectively suppress repeater jamming; intra-pulse carrier frequency combined with inter-pulse chirp rate polarity agility can effectively suppress intermittent sampling repeater jamming; the combination of frequency and PRI random agility can reduce the probability of interception and effectively enhance anti-jamming capability [26].

However, agility in pulse width and PRI can result in uneven target energy distribution. Carrier frequency agility can cause variations in the azimuth Doppler chirp rate, leading to signal confusion in the range-Doppler domain. Additionally, agility in PRI can generate non-uniform azimuth signals. Some studies have discussed the impact of inter-pulse carrier frequency agility on SAR imaging under the spotlight SAR polar format algorithm and derived theoretical compensation models. These studies indicate that the instantaneous slant range is closely related to the position of each scatterer target in the imaging scene, leading to substantial computational demands for phase compensation [17]. Therefore, to optimize the reconstruction process of inter-pulse frequency agile signals, it is necessary to seek a processing scheme that is computationally efficient and provides excellent imaging performance. Additionally, there is a lack of systematic analysis of the anti-active deceptive performance of joint agility of multiple parameters, which requires further research.

Based on existing methods, a consensus has been reached on the processing of traditional phase, frequency modulation polarity, and pulse width agility. This can be accurately corrected by constructing multiple corresponding range–direction matched filters. However, there is still considerable controversy regarding the processing of carrier frequency and PRF, especially since carrier frequency agility significantly affects azimuth focusing. Traditional classical frequency-domain imaging algorithms (such as RD and ω-k) theoretically struggle to achieve accurate correction, requiring complex decoupling formula derivation and difficult-to-estimate computational effort [27]. Although classical time-domain imaging algorithms (such as BP) can adapt to a certain extent by changing wavelength parameters to accommodate agile carrier frequencies, their adaptation range is limited, and the computational burden is high, rendering them ineffective against active deceptive interference. Furthermore, while new imaging algorithms based on compressed sensing have emerged in recent years, their application in the domain of carrier frequency agility is limited due to uncertainties in resolution and the requirement for target sparsity. Research on PRF agility is relatively advanced, primarily applied in the field of high-resolution wide-swath SAR imaging, which emphasizes the gradual accumulation of PRF intervals. The use of non-uniform Fourier transform in this context leads to the disadvantage of high sidelobes [28,29]. This paper, however, focuses on PRF agility in the context of countering active interference, where PRF intervals do not accumulate gradually and are instead modeled using a Gaussian random distribution.

To address the above issues, the structure of this paper is as follows: Section 2 analyzes the impact of different parameter agility on SAR imaging in detail; Section 3 proposes the imaging algorithm and processing flow for joint multi-parameter agility, along with corresponding solutions; Section 4 establishes an SAR model with multi-parameter agility, introduces active deceptive interference, and conducts step-by-step validation of the proposed algorithm; Section 5 provides discussion and conclusions.

The main innovations and research content of this paper are as follows:

(1)

To address the issues of large computational demands and difficult compensation brought by inter-pulse carrier frequency agility, this paper proposes a non-search fast time domain compensation algorithm based on range axis matrix. This algorithm achieves azimuthal signal reconstruction, enhancing target imaging performance while suppressing active deceptive interference. The computational complexity is comparable to that of fixed waveform processing, providing a feasible solution for engineering implementation.

(2)

Previous studies on random agility waveforms have mostly been limited to the agility of one or two parameters. This paper, however, presents a systematic design of joint agility based on the four most fundamental parameters in LFM signals. Under the same conditions, the anti-active deceptive interference performance of each parameter was further analyzed, providing a foundation for waveform processing and experimental conditions for future intelligent agile waveform countermeasure technologies.

2. Analysis of the Impact of Different Agile Parameters on SAR Imaging and the Interference Signal Model

2.1. Radar Transmitted Signal

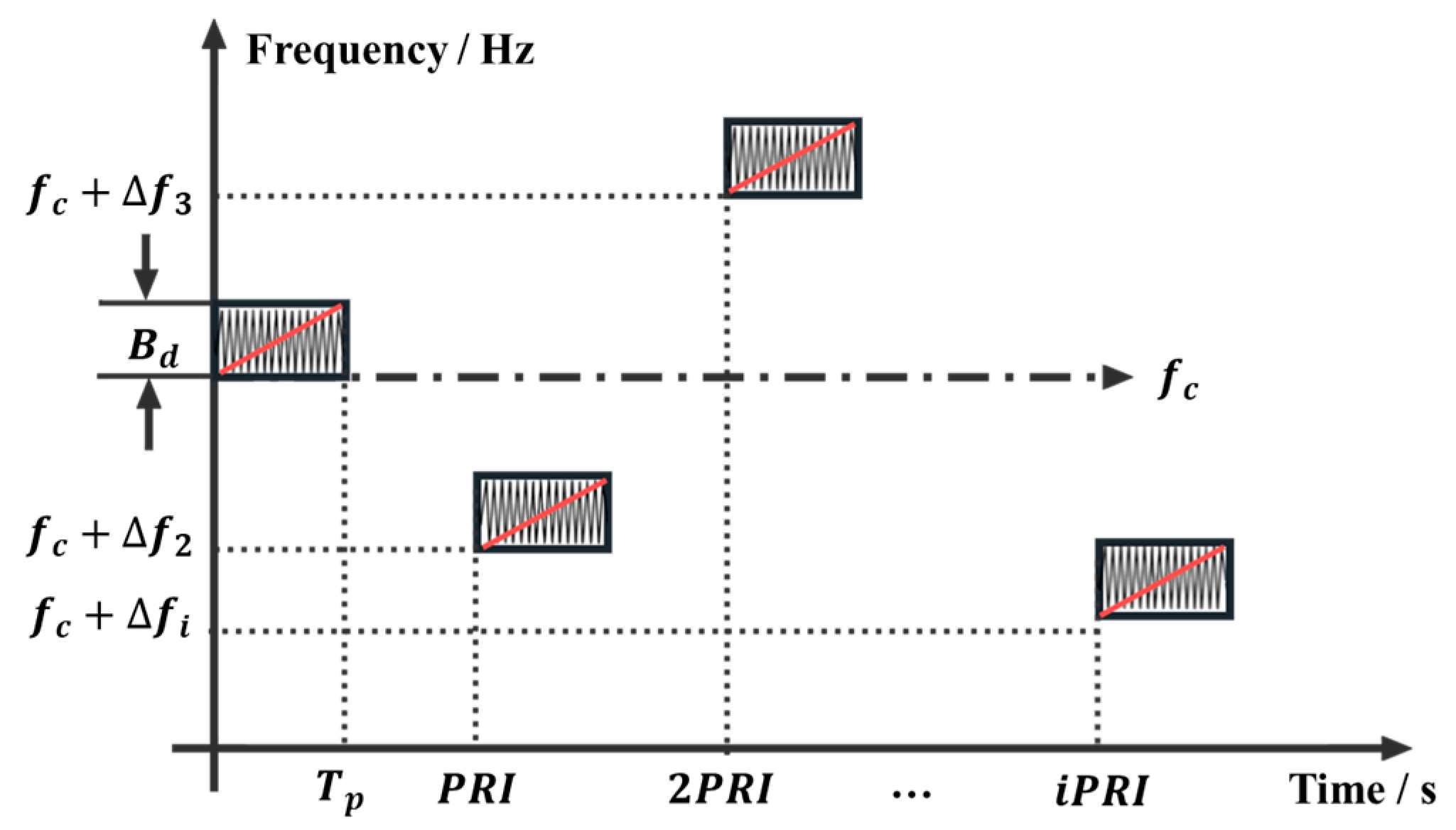
By ensuring a constant bandwidth, agility is achieved during each pulse transmission by randomly generating a set of values for pulse width, chirp rate, and carrier frequency parameters. The agility of the PRI is realized by varying the pulse transmission times; a multi-parameter joint agile waveform schematic diagram is shown in Figure 1. Each pulse signal is spaced at a fixed interval with an additional random jitter of σ, resulting in different PRF for each pulse. The signal polarity is represented using different colors.

The baseband signal of a single pulse echo can be represented as Equation (1). In this context, $\tau$represents the fast time in the range direction and$\eta$represents the slow time in the azimuth direction. Assuming that the carrier frequency, frequency modulation polarity, pulse width, and pulse repetition period vary with the continuous pulse interval$n$. On the right side of the equation, $A_0$ is an arbitrary constant, ${\omega }_r\left(\tau \right)$is the range envelope, $T_p$ represents the time width of a single pulse, ${\omega }_a\left({\eta }_n\right)$ is the azimuth envelope, and $f_c$is the standard carrier frequency. The carrier frequency is randomly shifted between pulses through ${∆f}_n$; $a_n$ is the randomly assigned frequency modulation polarity, taking values of 1 and −1. $K_r^n$is the corresponding frequency modulation polarity, which also varies with the pulses.

$$s_0\left(\tau ,{\eta }_n\right)=A_0·{\omega }_r\left[{\displaystyle \frac{\tau -2\frac{R_{\left({\eta }_n\right)}}{c}}{T_p}}\right]·{\omega }_a\left[\eta -{\eta }_c\right]·exp[-j4\pi {(f}_c+{∆f}_n){\displaystyle \frac{R_{\left({\eta }_n\right)}}{c}}+j\pi a_n{K}_r^n{\left(t-{\displaystyle \frac{R_{\left({\eta }_n\right)}}{c}}\right)}^2]$$

(1)

The effect of each parameter on SAR imaging is analyzed as follows.

2.2. Agility of Carrier Frequency

Frequency Agile Linear Frequency Modulation Signal (FA-LFM) is achieved by randomly increasing or decreasing the carrier frequency of each pulse within the hardware’s allowable range, while maintaining a fixed bandwidth. In principle, this can enhance the radar’s anti-jamming capability. A schematic diagram of the transmitted signal waveform is shown in Figure 2.

Assuming the baseband echo of the pulse interval carrier frequency agile signal is represented as Equation (2), in this context, $t$ is the pulse transmission time, $n$ is the continuous pulse sequence, and $\tau$represents the echo delay.

$$S_0\left(t,n\right)=rect\left({\displaystyle \frac{t-\tau }{T_p}}\right)·exp\left[-j2\pi \left(f_c+∆f_n\right)\tau +j\pi K{\left(t-\tau \right)}^2\right]$$

(2)

The inter-pulse carrier frequency agility does not affect range direction pulse compression. By applying the principle of stationary phase to the baseband signal, the range direction matched filtering yields the following equation:

$$S_0\left(t,n\right)=T_p·sinc\left[K_r{T}_p\left(t-\tau \right)\right]·exp\left(-j2\pi (f_c+∆f_{n)}\tau \right)$$

(3)

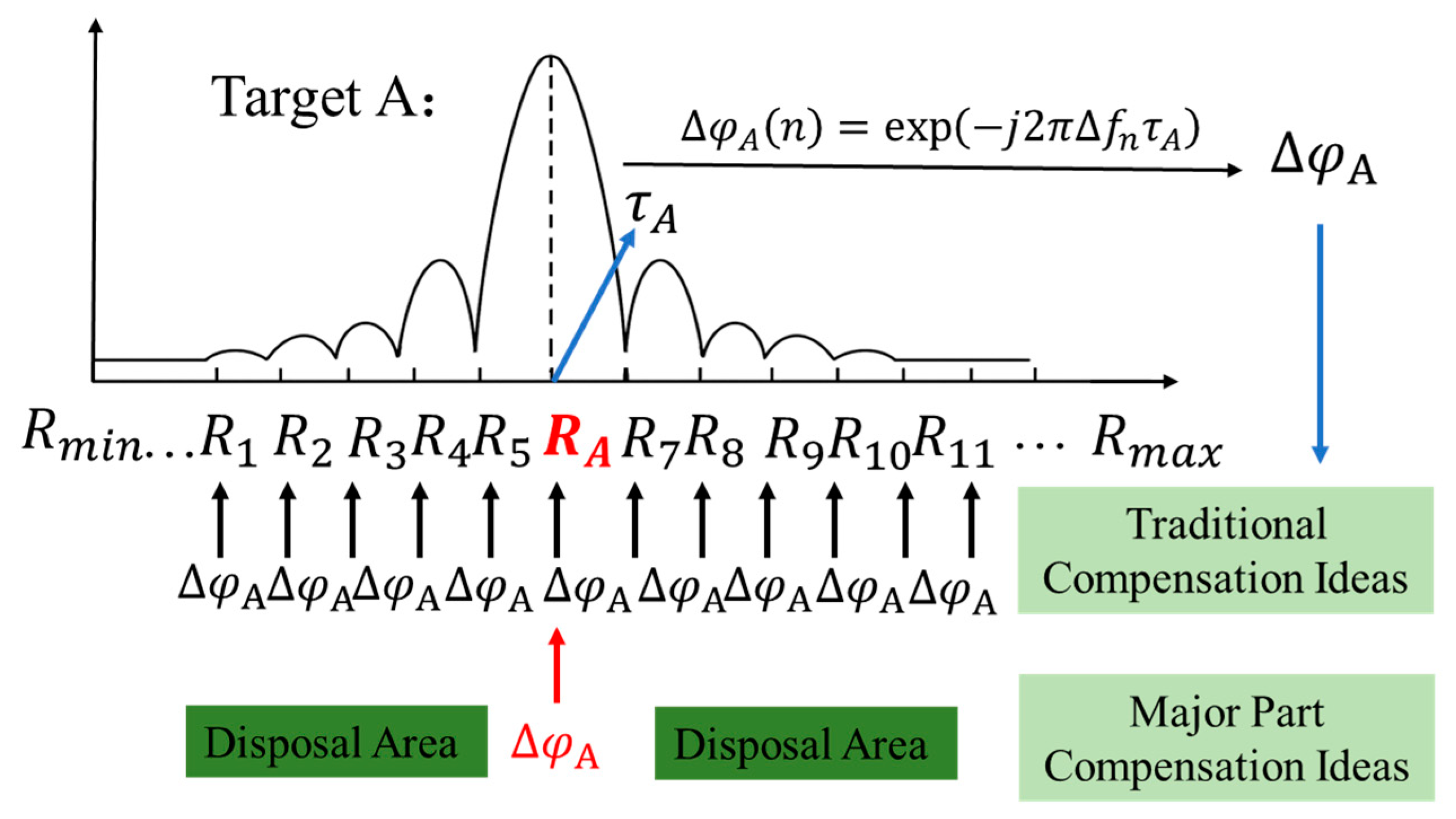
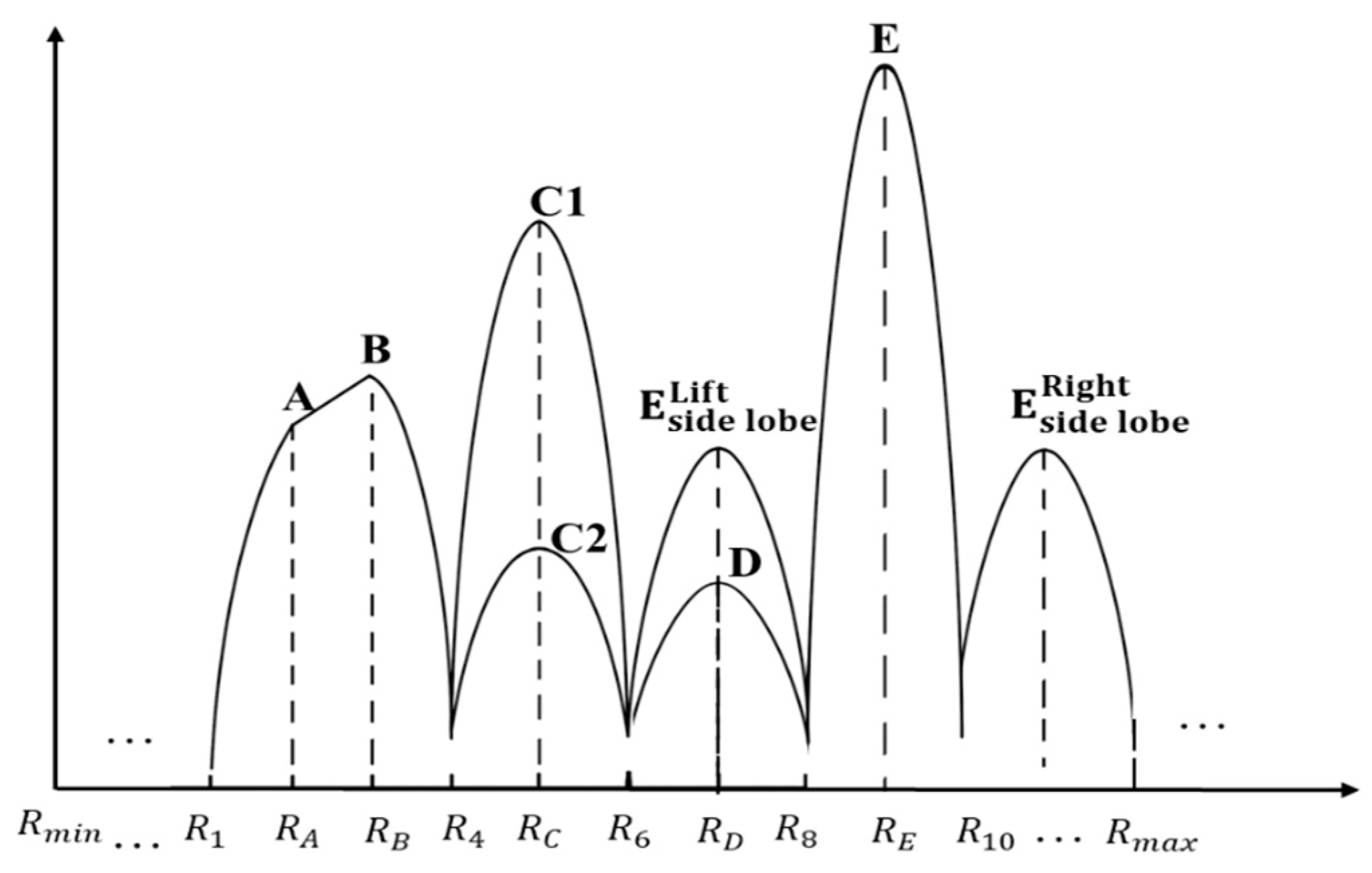
From Equation (3), it is understood that the second phase term contains the basic imaging information necessary for locating and focusing on scene targets. However, the third phase term resulting from random frequency offset is undesirable and must be compensated for to restore the correct phase. Mathematically, compensating each target to the standard carrier frequency phase is extremely difficult and computationally intensive due to varying delays for different targets. Additionally, echoes from adjacent targets overlap on the same range axis but require different compensation values, as illustrated in Figure 3. The functions $\mathrm{g}\left(x\right)$ and $\mathrm{f}\left(x\right)$ represent the signal expressions of targets A and B, respectively, within the same slow-time echo. The phase compensation amounts required for each are $\mathsf{\phi }\left(A\right)$and$\mathsf{\phi }\left(B\right)$, with a portion of the signals overlapping.

Therefore, the compensation methods used in the existing literature are challenging, and it is difficult to effectively complete signal reconstruction within a reasonable time frame.

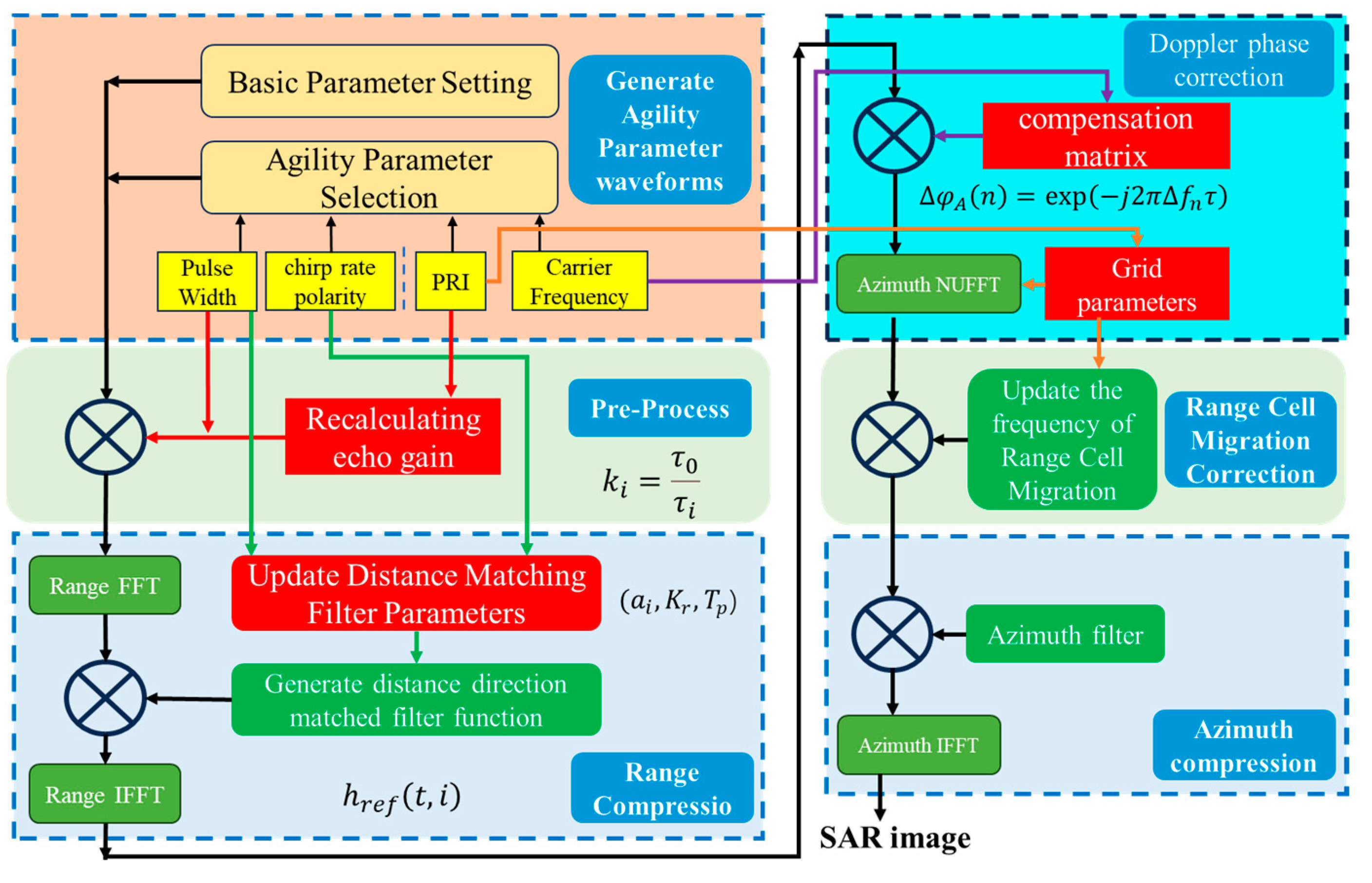
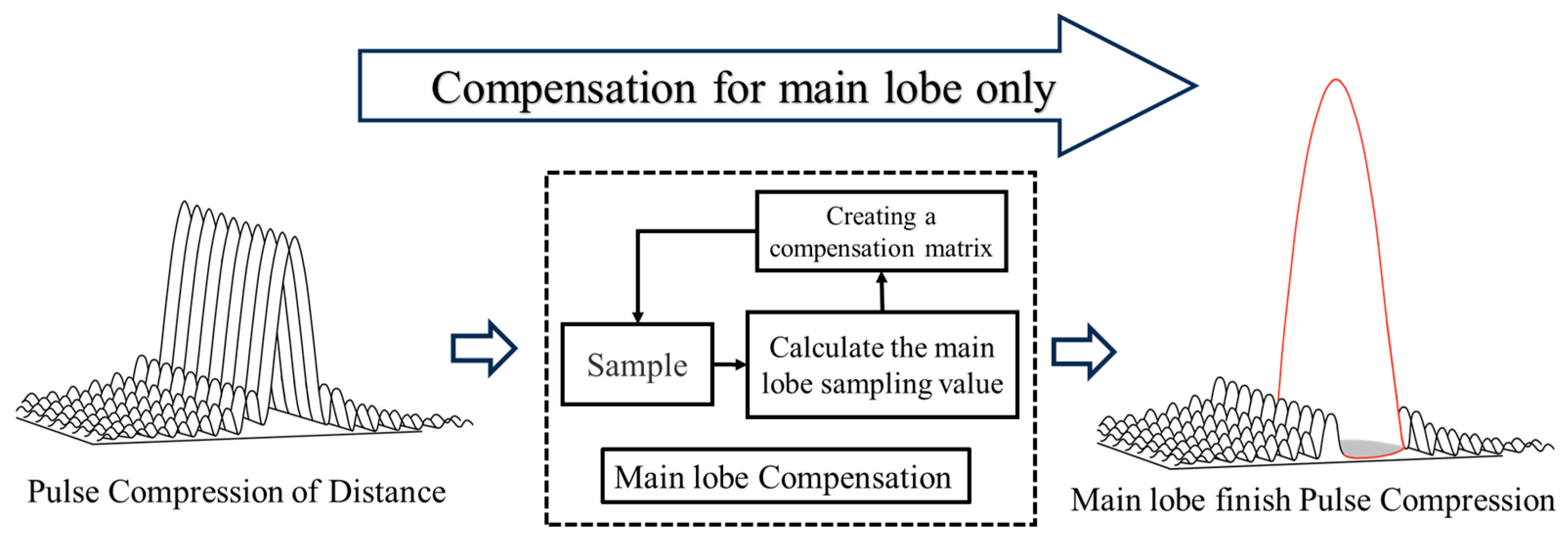
Traditional compensation methods face two key issues: first, they require backcalculating the compensation amount based on the target, and second, they need to disentangle the interactions between targets to apply corresponding compensations. This paper proposes a novel compensation approach to circumvent these issues. Firstly, instead of searching for targets, it considers that each sampling point may contain echoes from multiple point targets. Therefore, it assumes that each sampling point on every range axis carries point target information. Secondly, instead of compensating the entire echo segment, it only compensates the main lobe region of the target after range compression. This approach significantly avoids the mutual influence of target compensation values.

2.3. Agility of PRI

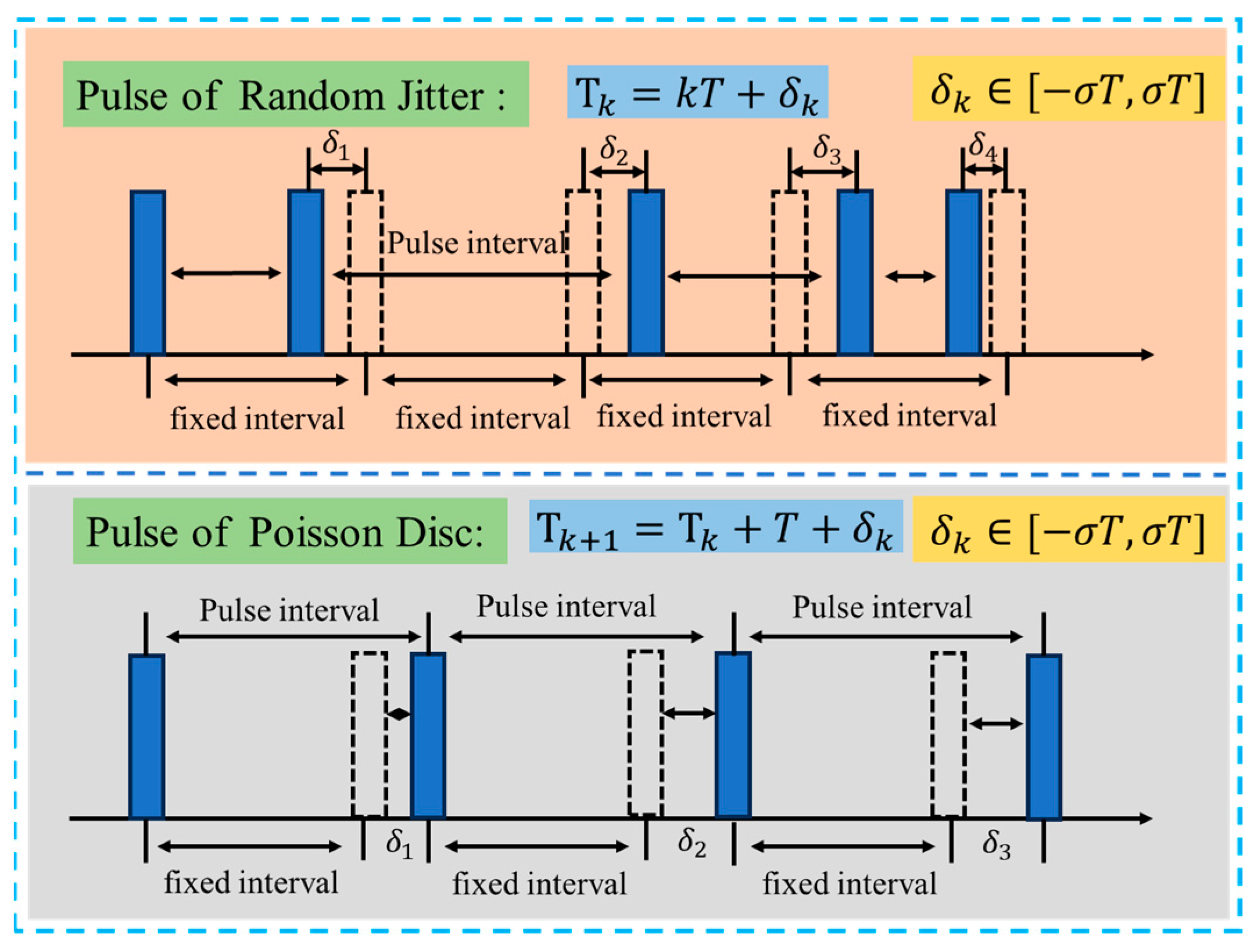
The random agility of the pulse repetition frequency (PRF) makes it difficult for jammers to generate fully coherent jamming signals, leading to misalignment in the azimuth direction and resulting in the failure of two-dimensional focusing to some extent. There are two main methods of PRF agility: random pulse jitter and Poisson disk pulse, with their interval patterns shown in Figure 4.

The random variation in the PRF results in non-uniform azimuth sampling further deteriorate SAR image quality. In this context, the error from random pulse jitter does not accumulate, and the number of transmitted pulses remains constant over a given period, similar to fixed-interval pulses. In contrast, Poisson disk pulses gradually accumulate non-uniform intervals, leading to larger errors, but they can significantly enhance the system’s anti-jamming performance.

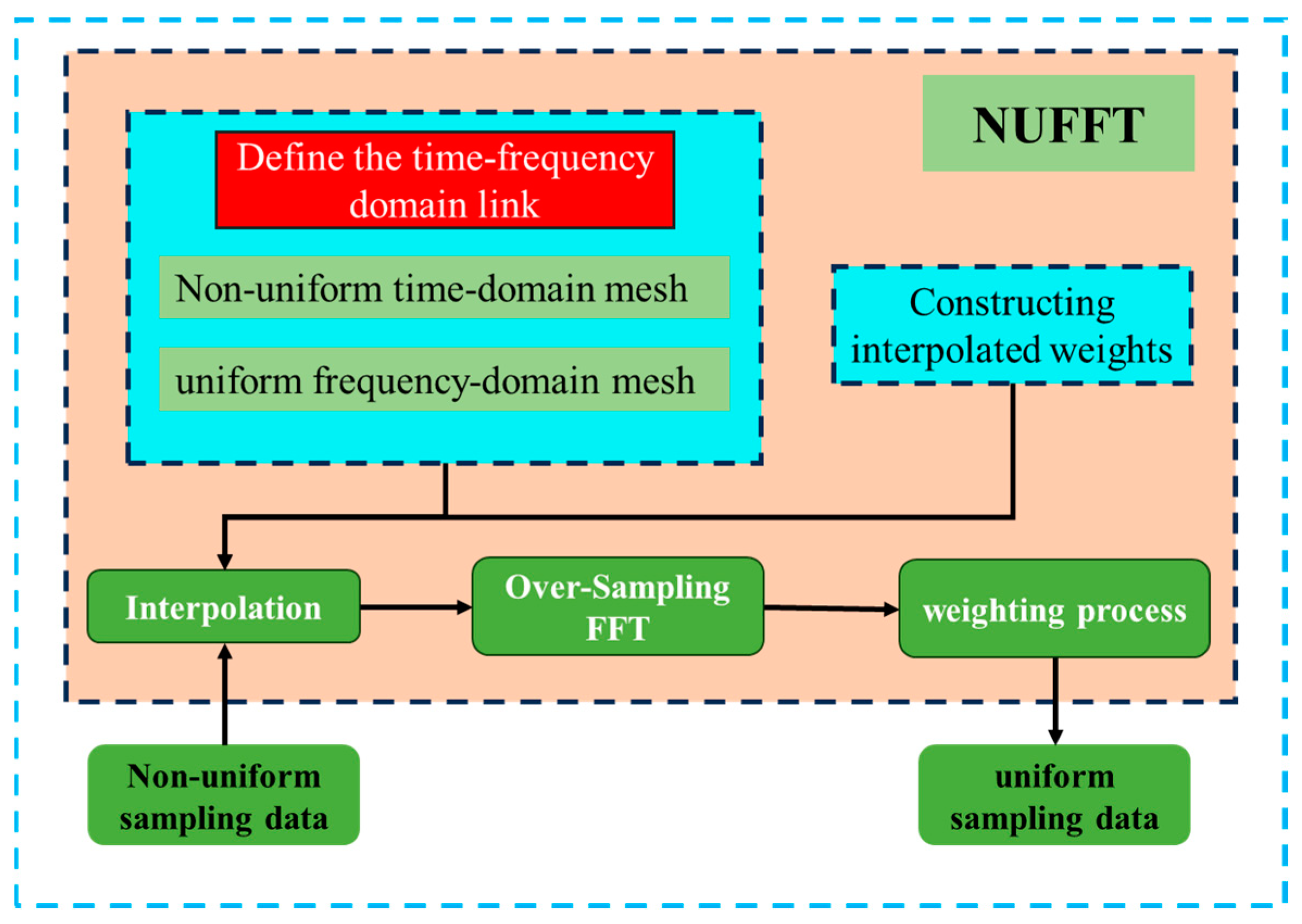
This paper addresses the issue of non-uniform azimuth sampling in echo signals using Non-Uniform Fast Fourier Transform (NUFFT). In essence, various NUFFT algorithms are implemented based on conventional FFT, and the processing flow is illustrated in Figure 5. For PRF agile signals, the non-uniform time-domain sampled signals are known. Based on this known information, a non-uniform time-domain grid and the target uniform frequency-domain grid are defined. Then, interpolation is performed to reconstruct the signal, which is subsequently transformed to the frequency domain using FFT, ultimately yielding a uniformly sampled frequency-domain signal [30].

The sampling values obtained from the non-uniform grid points $x_l\in (-N/2,N/2)$are transformed using the Fourier transform to obtain the sampling values at uniform grid points. The expression for this transformation is given in Equation (4) as follows:

$$z\left(x_k\right)=\sum _{l=1}^M{e}^{-2\pi i{x}_{l}k/N}{z}_l,k=-N/2,\cdots N/2$$

(4)

The ingenuity of NUFFT lies in the fact that it does not interpolate the data directly, as this would increase the complexity with each read, interpolation, and calculation. Instead, it interpolates $e^{-ix\xi }$ to make it uniform. For a band-limited signal $f\left(x\right)$with a bandwidth less than $\mathsf{\pi }$, it can be reconstructed from its sampled signal $f\left(m\right)$ using the Shannon sampling theorem, as expressed in Equation (5).

$$f\left(x\right)=\sum _{m\in Z}\varnothing \left(\pi \left(x-m\right)\right)f\left(m\right)$$

(5)

Here, $\mathrm{\varnothing }\in C_0^{\infty }$ is the interpolation function. Substituting $e^{-ix\xi }$ into the above equation yields Equation (6).

$$e^{-ix\xi }={\displaystyle \frac{(2\pi {)}^{-1/2}}{\varnothing \left(\xi \right)}}\sum _{m\in Z}\varnothing \left(\pi \left(x-m\right)\right)e^{-im\xi },\left|\xi \right|<\pi$$

(6)

The choice of interpolation function directly impacts the efficiency of the final result, and typically, an approximate solution is considered sufficient. Let $\xi =2\pi k/cN,x=c{x}_l$. By substituting the interpolated signal into the first equation, we obtain Equation (7), which completes the time–frequency transformation from non-uniformly sampled signals to uniformly sampled signals:

$$\widehat{z}\left(x_l\right)={\displaystyle \frac{(2\pi {)}^{-1/2}}{\varnothing \left(2\pi k/cN\right)}}\sum _{l=1}^M\sum _{m\in Z}\widehat{z_l\varnothing }\left(c{x}_l-m\right)e^{-2\pi imk/cN},K=-N/2,\cdots N/2-1$$

(7)

2.4. Agility of Chirp Rate Polarity

The inter-pulse chirp rate polarity agile signal is achieved by keeping other parameters constant while randomly selecting the chirp rate polarity from either 1 or -1, following a binomial random distribution. A schematic diagram of the transmitted signal waveform is shown in Figure 6.

Assuming the baseband echo signal obtained from the agile signal is represented as Equation (8):

$$s_0\left(t,n\right)=\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}\left({\displaystyle \frac{t-\tau }{T_p}}\right)·exp\left[-j2\pi f_c\tau +j\pi a_{n}K{\left(t-\tau \right)}^2\right]$$

(8)

based on the recorded variation sequence, a new range direction matched filter function can be regenerated in each synthetic aperture echo segment, as shown in Equation (9). $R_0$represents the reference center slant range.

$$h_{ref}\left(t,n\right)=\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}\left({\displaystyle \frac{t-\frac{2R_0}{c}}{T_p}}\right)\mathrm{e}\mathrm{x}\mathrm{p}\left[-j\pi a_{n}K{\left(t-{\displaystyle \frac{2R_0}{c}}\right)}^2\right]$$

(9)

Each chirp pulse with frequency agility emitted by the SAR corresponds to a pre-determined matched filter function sequence, enabling complete range direction gain. In contrast, the jamming signal cannot match the randomly generated polarities, and probabilistically, it can only achieve general range direction compression gain.

2.5. Agility of Pulse Width

For LFM signals, when the bandwidth remains constant, the pulse width is inversely proportional to the chirp rate, as shown in Equation (10). Therefore, inter-pulse pulse width agility requires simultaneous adjustment of the chirp rate to ensure the signal bandwidth remains constant; $B_d$ represents the pulse bandwidth.

$$B_d=K_r·T_p$$

(10)

A schematic diagram of the transmitted signal waveform is shown in Figure 7:

Assuming the baseband signal of the echo for this agile pulse width signal is represented as Equation (11), to ensure that the signal bandwidth remains constant, both the signal time width and the chirp rate must be adjusted simultaneously.

$$S_0\left(t,n\right)=rect\left({\displaystyle \frac{t-\tau }{T_p^n}}\right)·exp\left[-j2\pi f_c\tau +j\pi K_r^n{\left(t-\tau \right)}^2\right]$$

(11)

In this case, $T_p$and$K_r$vary synchronously. Based on the recorded sequences of pulse width and chirp rate changes, a new range direction matched filter function can be regenerated in each synthetic aperture echo segment, as shown in Equation (12):

$$h_{ref}\left(t\right)=rect\left({\displaystyle \frac{t-\frac{2R_0}{c}}{T_p^n}}\right)exp\left[-j\pi K_r^n{\left(t-{\displaystyle \frac{2R_0}{c}}\right)}^2\right]$$

(12)

Due to the fact that the energy gain after range compression is approximately equal to the time–bandwidth product, inter-pulse variable pulse width signals can cause energy non-uniformity in the azimuth direction. Each echo needs to be multiplied by the corresponding energy gain factor to return to the standard value, as shown in Equation (13).

$$B_d{\tau }_0={{\displaystyle \frac{A_0}{A_n}}·B}_d{\tau }_n$$

(13)

Based on Equation (13), the gain factor $k_n$ required for compensating each echo can be derived as shown in Equation (14).

$$k_n={\displaystyle \frac{{\tau }_0}{{\tau }_n}}$$

(14)

Therefore, by multiplying each echo segment by an energy gain factor and updating the range match filter, the azimuth energy fluctuations and imaging issues caused by inter-pulse variable pulse width signals can be resolved.

2.6. Principle of SAR Deception Jamming

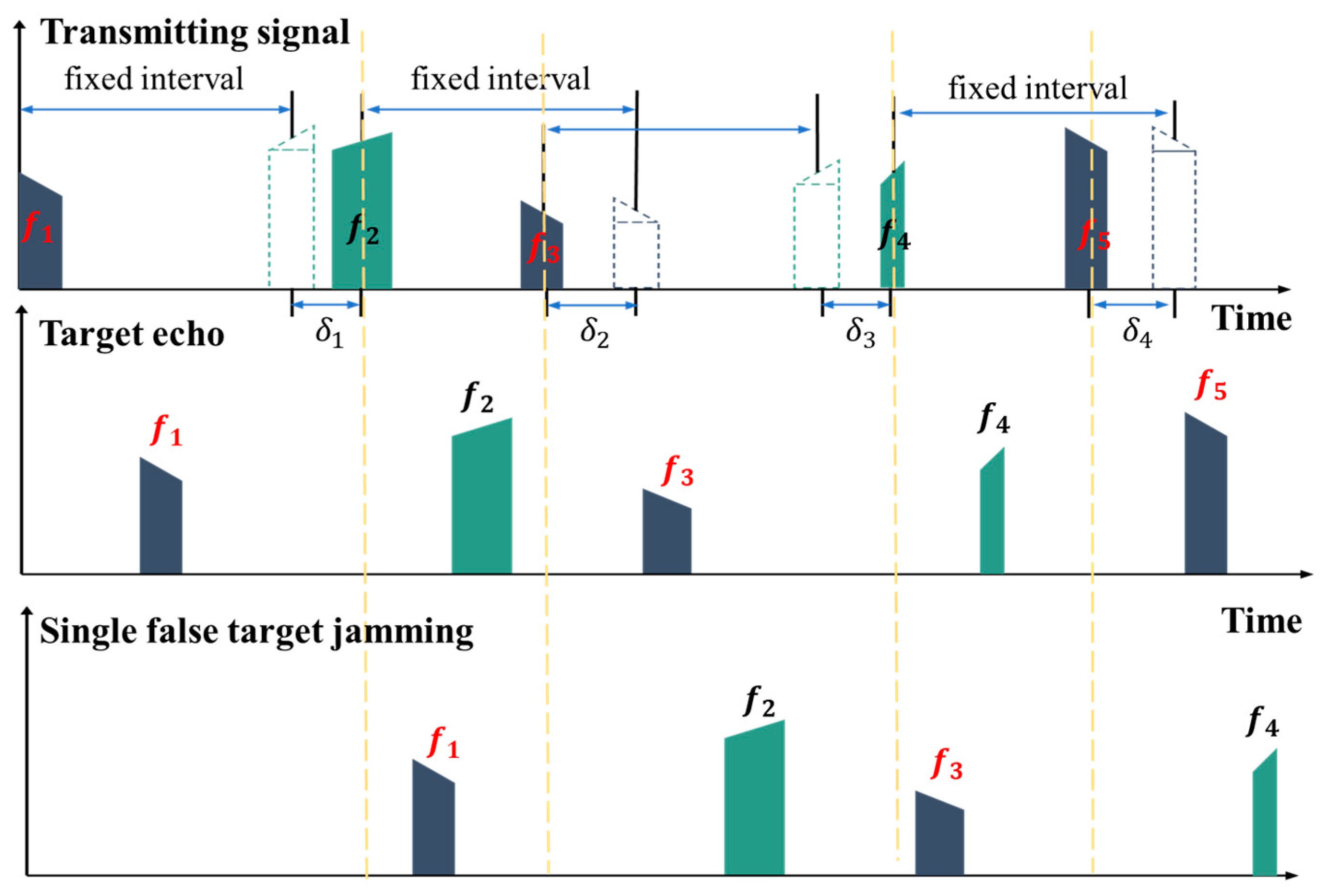
Inter-pulse carrier frequency agile signals are frequency diversity signals. When a jammer replicates and retransmits full-pulse deception jamming, there is a significant delay, causing a mismatch between the reference signal and the jamming signal during azimuth compression. This prevents the jamming signal from accumulating sufficient gain during coherent integration. Additionally, inter-pulse chirp rate polarity and pulse width agility can further cause mismatches during range compression, thereby suppressing active coherent jamming signals in multiple dimensions. Traditional fixed signals have a certain regularity and are easily accurately replicated by jammers. However, the random agility of the pulse repetition interval further increases the difficulty for jammers to accurately recognize the signal. Therefore, multi-parameter joint agility SAR theoretically has better electronic counter-counter measure (ECCM) performance [31].

As shown in Figure 8, due to the longer sampling time of a single false target jamming and the increased difficulty for the jammer to analyze the multi-parameter agile waveform and frequency diversity, the jammer’s transmitted signal has a time delay. Therefore, the retransmitted jamming generally lags by one pulse. By utilizing this jamming delay, it is possible to distinguish between real targets and false targets during the phase compensation process of parameter agility.

Assuming that the jammer can successfully intercept and accurately replicate the radar’s transmitted signal, with the retransmission delay being at least one pulse duration behind the transmitted signal, the sequence of jamming signals intercepted by the jammer is given by Equation (15).

$${\mathrm{f}}_{\mathrm{J}}=[{\mathrm{f}}_{\mathrm{J}1},{\mathrm{f}}_{\mathrm{J}1},\dots ,{\mathrm{f}}_{\mathrm{J}\mathrm{N}}{]}^T$$

(15)

Thus, for a false target at a jamming distance $R_J$ generated by the jammer, with a jamming delay of $\tau =2R_J/c$, the jamming echo received by the n pulse is given by Equation (16).

$$y_{JN}\left(\mathrm{t}\right)=Y_J·rect\left({\displaystyle \frac{t-\tau }{T_p}}\right)·exp-j2\pi f_{N-1}\tau +j\pi K_{N-1}{\left(t-\tau \right)}^2$$

(16)

where $Y_J$ is the amplitude of the false target echo; according to Gaussian probability law, the jamming signal has only a 50% chance of matching the chirp rate polarity.

3. Inter-Pulse Multi-Parameter Joint Random Agile SAR Imaging Algorithm

The purpose of SAR echo imaging processing is to obtain the two-dimensional distribution of the scattering coefficient of the target area. This two-dimensional correlation processing is typically divided into range processing and azimuth processing. In the second section of this paper, it is derived that the pulse width and chirp rate polarity primarily affect the range processing part, while the carrier frequency and pulse repetition interval mainly affect the azimuth processing part. The main differences among various existing algorithms lie in how they define the distance model between the radar and the target and how they address the range-azimuth coupling issue. These differences result in variations in imaging quality and computational complexity among the algorithms.

This paper focuses on exploring the impact of parameter agility on SAR imaging models and systematically addressing the effects brought by each parameter to establish a comprehensive multi-parameter agile SAR imaging and processing model. For this purpose, the classical range-Doppler algorithm (RDA) is selected as the basis for imaging processing, and improvements are made to adapt it to the multi-parameter agile SAR model. The specific imaging advantages of various algorithms are not within the scope of this discussion. In fact, the compensation modules proposed for agile parameters in this paper can still be applied to other algorithms (such as the Wavenumber algorithm (ω-k) and Back Projection (BP) algorithm), which will be demonstrated later.

3.1. Imaging Algorithm Processing Flow

Unlike traditional constant-parameter waveform imaging, as shown in Figure 9, the effects of various parameters need to be addressed. These effects are also crucial for suppressing the imaging of false targets. The impacts of pulse width and chirp rate polarity in the one-dimensional range direction can be directly handled by updating the matched filter parameters, making the engineering implementation relatively simple. The image quality non-uniformity caused by pulse width and PRI agility can be resolved by multiplying the echo with an energy gain factor. Azimuth frequency domain disorder caused by carrier frequency agility has been approximately solved by the rapid phase compensation method proposed in this paper. Meanwhile, the azimuth non-uniform sampling issue caused by PRI agility is addressed using the NUFFT.

The imaging process proposed in this paper is shown in Figure 10. In the preprocessing part, the energy fluctuations between pulses caused by pulse width and PRI agility are compensated for, as shown in the green block diagram. The light blue block diagram section represents the range compression and azimuth compression processing of the traditional RD imaging algorithm. Using the known information, the range matched filter parameters are successively updated between each pulse to complete the range matched filtering. Next, as shown in the blue block diagram, carrier frequency compensation is achieved through a phase compensation matrix, enabling the reconstruction of Doppler frequency aliased signals. Then, a non-uniform to uniform time–frequency grid is constructed, and the NUFFT is performed to convert the signals to the range-Doppler domain, where range cell migration correction is applied. The range cell migration correction values need to be updated based on the newly generated frequency domain grid. Finally, azimuth matched filtering is performed, and the image is output.

3.2. Carrier Frequency Agility Compensation Algorithm

3.2.1. Introduction to the Range Axis Compensation Algorithm

Since the inter-pulse frequency agile signal does not affect the range compression of the two-dimensional signal, for point target A, the compressed signal is shown in Figure 11.

According to the analysis in Section 2.1, the compensation value required for target A is given by Equation (17); $∆{\phi }_A$ represents the phase compensation required for each pulse, $∆f_n$ represents the carrier frequency agility across different pulses, and ${\tau }_A$ is the echo delay corresponding to the target.

$$∆{\phi }_A\left(n\right)=\mathit{exp}\left(j2\pi ∆f_n{\tau }_A\right)$$

(17)

The carrier frequency variable is known, and the delay can be determined from the sampling points within the main lobe where target A is located. As shown in Figure 12, for target A after range pulse compression, compensating for all sampling points within the entire signal duration would not only increase computational load but could also potentially interfere with other targets. The core of the algorithm proposed in this paper is to achieve signal reconstruction by compensating only the main lobe units, thereby effectively reducing computational load and minimizing interference between target signals.

According to Equation (17), since the target delay $\tau$ is only coupled with the sampling point position on the range axis where its main lobe unit is located, this provides a foundation for main lobe and side lobe filtering. That is, a linear compensation matrix is constructed using the range axis and carrier frequency variation, as shown in Equations (18) and (19). Due to the strict coupling of the compensation values with the range axis, the unique compensation mechanism of the range axis compensation matrix enables accurate compensation of the main lobe and natural suppression of the side lobes.

In Formula (19), $\tau \left(x\right)$ represents the delay of the target reflected to the imaging distance axis.

$$\begin{gathered} A_0{p}_r{w}_r.exp\left(-j{\displaystyle \frac{4\pi f\left(\eta \right)R_0}{c}}\right)exp\left(-j{\displaystyle \frac{2\pi f\left(\eta \right)V_r^2}{c{R}_0}}{\eta }^2\right).{\left[\begin{array}{ccc}\exp \left(j2\pi ∆f_1{\tau }_1\right)& \cdots & \exp \left(j2\pi ∆f_1{\tau }_m\right)\\ ⋮& \ddots & ⋮\\ \exp \left(j2\pi ∆f_n{\tau }_1\right)& \cdots & \exp \left(j2\pi ∆f_n{\tau }_m\right)\end{array}\right]}_{n\times m} \\ =S\left(\tau ,\eta \right)\exp \left(j2\pi \right).\left[\begin{array}{c}∆f_1\\ ⋮\\ ∆f_n\end{array}\right].\left[\begin{array}{ccc}{\tau }_1& \cdots & {\tau }_m\end{array}\right] \end{gathered}$$

(18)

$$\tau \left(x\right)={\displaystyle \frac{2·\left(R_{max}-R_{min}\right)}{c·\left(f_s-1\right)}}·\left(x-1\right)+{\displaystyle \frac{2R_{min}}{c}}$$

(19)

The compensation matrix constructed using the range axis is also applicable to multi-target situations. In real SAR imaging scenarios, multiple strong and weak target echoes are often present in the same echo segment, as shown in Figure 13. The main lobes of targets A and B are separated by adjacent sampling points; targets C1 and C2 are overlapped at one sampling point; targets D and E are separated by different sampling points, with E’ being the first side lobe of target E and D being a weak target adjacent to E. In such cases, the range axis compensation matrix can achieve accurate compensation for the main lobes of each target and naturally suppress the side lobe effects, ensuring imaging quality in multi-target scenarios.

For targets A and B, decomposing their overlapping parts increases computational load. Using the range axis compensation matrix may cause some energy loss and generate background noise, but it ensures peak reconstruction of targets A and B, achieving an effective balance between computational efficiency and imaging quality. If C1 and C2 are two targets located at different positions but overlapping within one synthetic aperture time, according to the compensation principle, the compensation value is only related to the target’s delay. Therefore, for two targets with the same delay, their main lobes can be effectively reconstructed simultaneously. In the case of adjacent strong and weak targets, such as D and E, since the side lobe of E shifts further from the main lobe, the compensation accuracy decreases, leading to poorer reconstruction. However, compared to traditional methods, the compensation scheme proposed in this paper can effectively reconstruct target D under the same sampling point. This means that weak targets are less likely to be obscured by the side lobes of adjacent strong targets during processing, resulting in clearer details in two-dimensional imaging.

3.2.2. Compensation Processing Flow

The core of the rapid compensation frequency domain imaging algorithm proposed in this paper is to reduce the computational load when searching for targets by abandoning the compensation for side lobes of the targets after range compression. This method provides a novel and efficient solution for the engineering challenge of inter-pulse frequency agile imaging. The reconstructed signal can continue to be processed using existing frequency domain algorithms for imaging, enabling rapid application.

Figure 14 shows the comparison of point target focusing in the azimuth direction before and after compensation. The left side is a schematic diagram of the point target after range pulse compression, and the right side is the azimuth focusing result after compensating only the main lobe units of the target in the range direction. For traditional LFM signals, when azimuth compression is performed on the main and side lobes after range pulse compression, the gain enhancement is consistent, so it does not affect the range compression. This paper improves the range imaging metrics by selectively and accurately compensating the main lobe of the target in the range direction. The side lobes of the target, due to the sampling point offset, have significant compensation errors. As a result, the main lobe energy is fully focused in the azimuth direction, while the side lobe energy remains defocused in the azimuth direction.

4. Imaging Validation

To validate the inter-pulse multi-parameter agile processing algorithm proposed in this paper, the following validation steps were conducted based on a simulation platform and real data from a frequency-hopping airborne SAR: first, point targets were simulated to evaluate imaging performance metrics; then, the image quality was assessed using simulated data for extended targets.

4.1. Simulation Parameter Platform

With the maturity of digital waveform generation technology, radar can easily perform random agility on inter-pulse waveform parameters such as pulse width, chirp rate polarity, carrier frequency, and PRI at each PRF moment. Based on an airborne SAR simulation platform, this paper upgrades the traditional fixed-parameter LFM signal to achieve multi-parameter joint agility between pulses.

The basic parameter information of the radar simulation platform is shown in

Table 1. Multi-Parameter Joint Agile SAR Simulation Platform Parameter Table.

Parameter	Value	Parameter	Value
Carrier Frequency	$5.4 \mathrm{G}\mathrm{H}\mathrm{z}$	Platform Height	$2000 \mathrm{m}$
PRF	1000 Hz	Platform Velocity	$100 \mathrm{m}/\mathrm{s}$
Pulse Width	$4 \mathsf{\mu }\mathrm{s}$	Antenna Length	$1.2 \mathrm{m}$
Band Width	$200 \mathrm{M}\mathrm{H}\mathrm{z}$	Sampling Rate	400 MHz
Incidence Angle	45°	Squint Angle	0°
Azimuth Sampling Points	1024	Range Sampling Points	2048

:

The information of agile parameters is shown in

Table 2. Agile Parameter Variation Range Table.

Parameter	Default Value	Variation Range	Step Frequency
Pulse Width	4 μs	2–4 μs	1/10
Chirp Rate Polarity	1	−1 or 1	1/2
Carrier Frequency	$5.4 \mathrm{G}\mathrm{H}\mathrm{z}$	$200 \mathrm{M}\mathrm{H}\mathrm{z}$	1/100
PRF	1000 Hz	600–1400 Hz	1/9

:

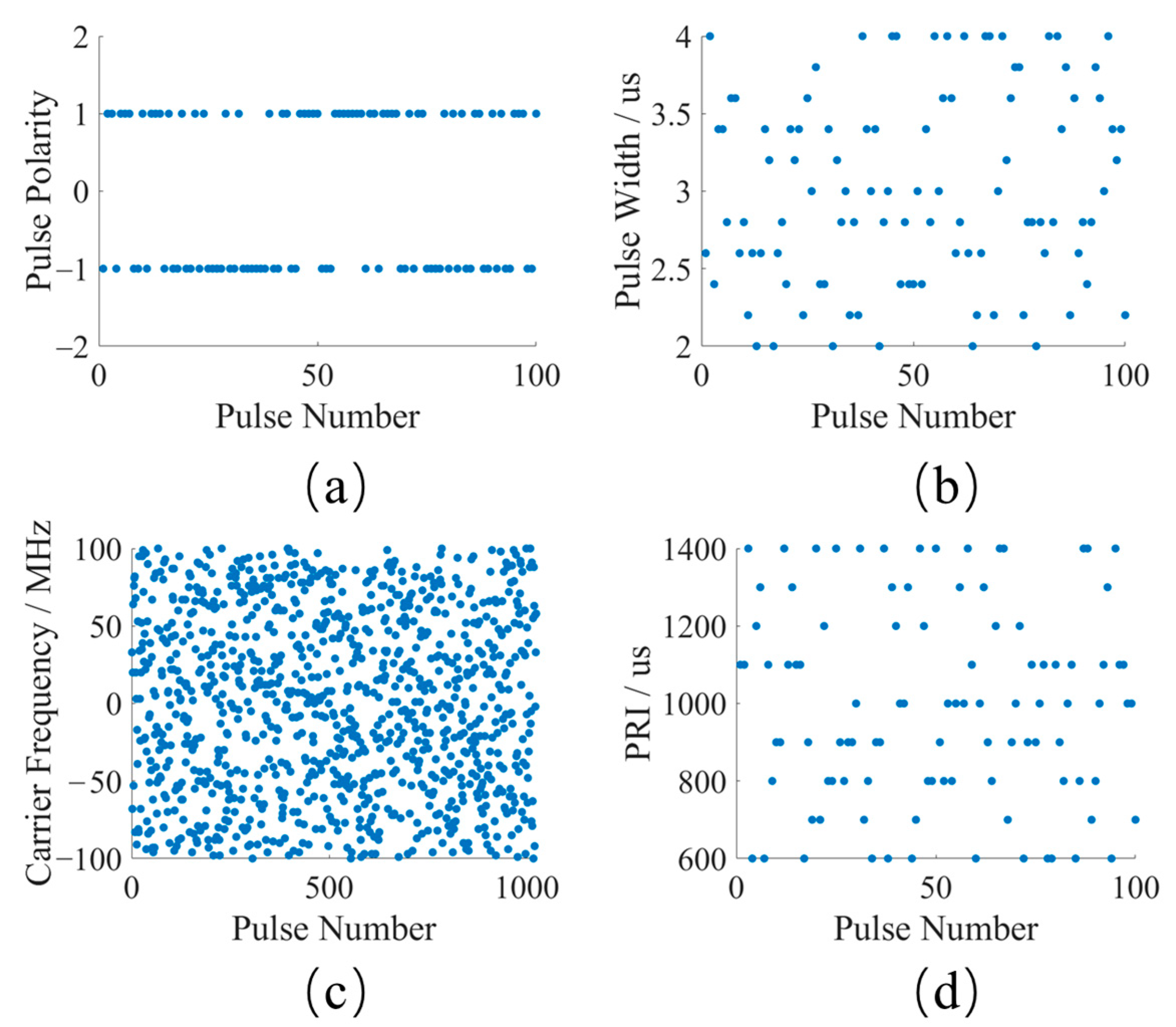
In the simulation platform, 1024 pulses were transmitted, with the width, chirp rate polarity, carrier frequency, and PRI of each pulse varying as shown in Figure 15. It can be seen that at each PRF moment, these four parameters vary flexibly and simultaneously, greatly increasing the complexity and uncertainty of the radar waveform. In the following sections, the ability to resist active coherent interference will be verified by applying interference.

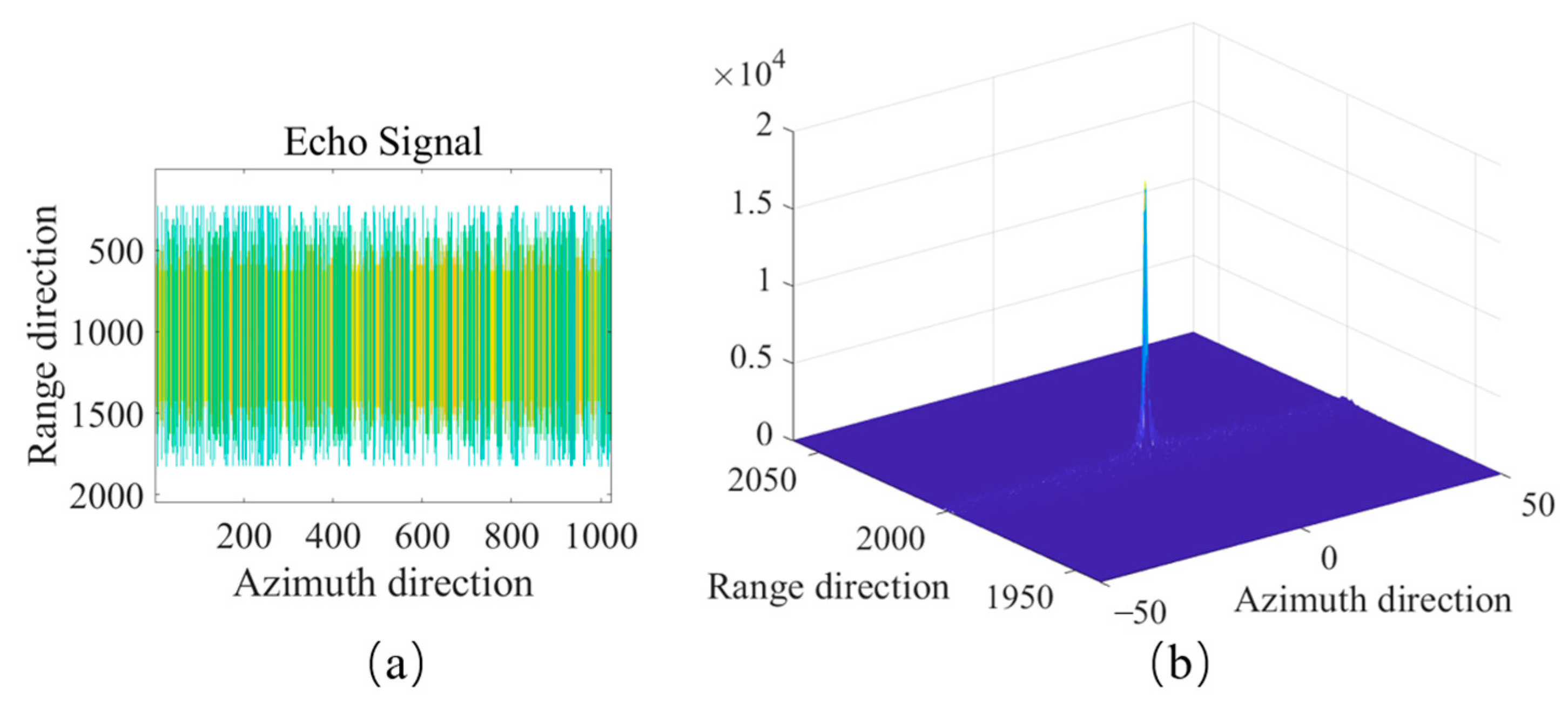
The simulation scenarios include imaging for point targets and scenario targets: point target location: 2000 m, 0 m; simulation scenario target data source: real remote sensing images from the Aerospace Information Research Institute, Chinese Academy of Sciences.

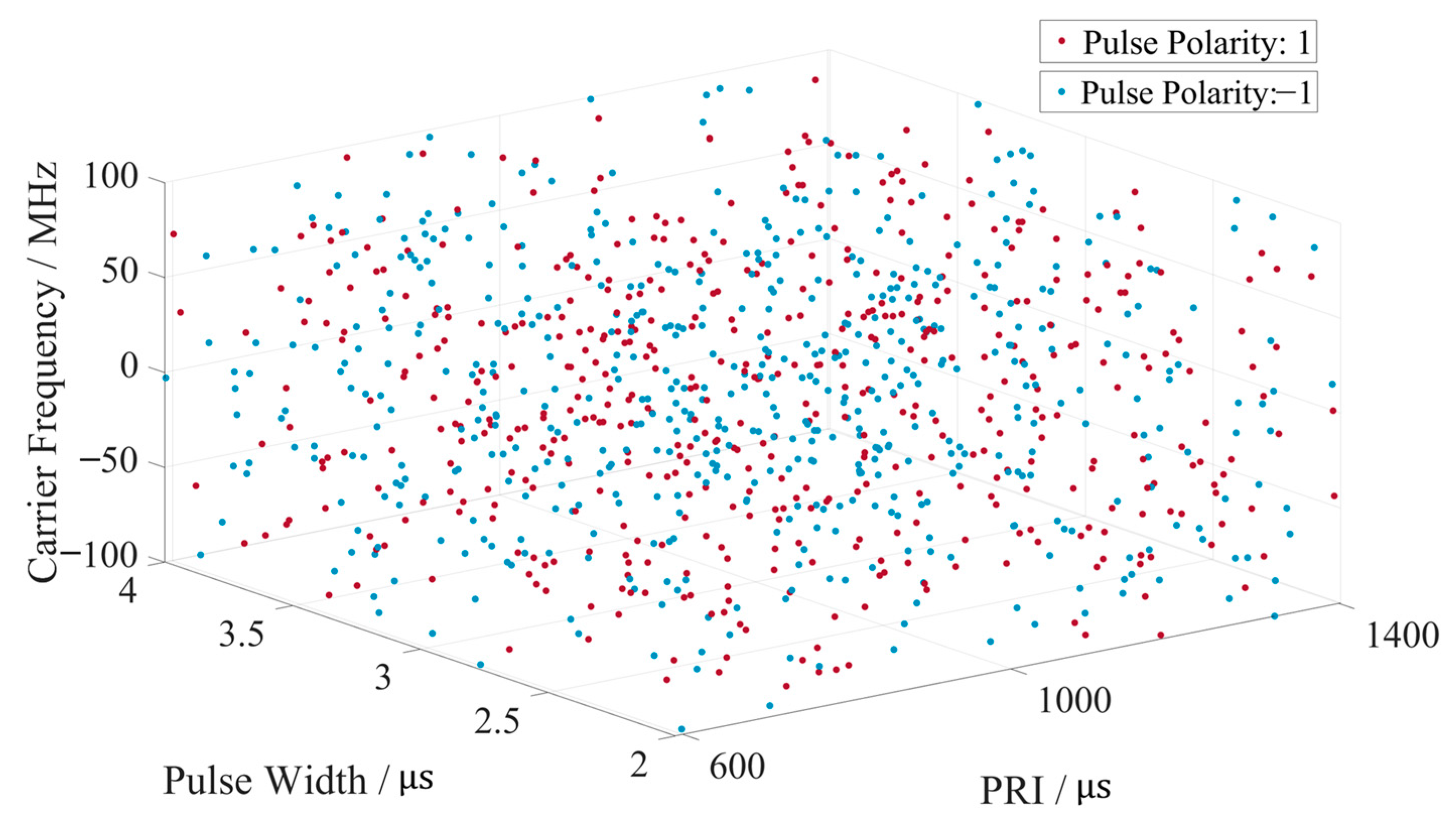
The multi-parameter joint agile waveform characteristics proposed in this paper are shown in Figure 16. The chirp rate polarity, pulse width, and carrier frequency of the signal vary with the pulse transmission time. This multi-parameter joint agile waveform greatly exceeds single-parameter agility in four-dimensional complexity, significantly enhancing the system’s ability to resist active coherent interference.

4.2. Point Target Simulation—Evaluation of Imaging Metrics

This section first verifies the feasibility of the compensation algorithm based on point targets and then presents the results of experiments conducted to evaluate the performance metrics after simulation compensation under different agile parameter ranges.

As shown in Figure 17, the compensation algorithm proposed in this paper can reconstruct the signal under the condition of four-parameter joint agility without causing high side lobes and other impacts. Next, an analysis of the point target imaging metrics was conducted.

As shown in Figure 18, the compression results in both the range and azimuth directions under single- or multi-parameter joint agility were compared with those of fixed linear frequency modulation signals. It can be observed that, under the processing of the proposed algorithm, the carrier frequency agility caused by azimuth compression has the greatest impact on the range imaging metrics, verifying the theoretical effects of the algorithm proposed in Section 2. Since the compensation for parameters such as pulse width and chirp rate polarity is relatively simple and has minimal impact on imaging, this subsection will not discuss their effects on imaging metrics.

4.2.1. The Impact of Multi-Parameter Joint Agility on Range Imaging

Under the current radar platform and waveform signal agile parameters, even within the same agile range, the imaging metrics will fluctuate within a certain range due to different agile values generated randomly each time. Therefore, the average of five measurements is taken to replace a single measurement for all fluctuating metrics. This section focuses on analyzing the impact of carrier frequency agility: as shown in

Table 3. Different Algorithms for Processing LFM and Multi-Parameter Agile Signals: Range Imaging Results.

Algorithm and Signal Type	PSLR	ISLR
RD, LFM	−12.64 dB	−9.77dB
BP, LFM	−13.94 dB	−10.77 dB
ω-k, LFM	−13.26 dB	−9.67 dB
RD+ proposed method, Agile Signals	−25.86 dB	−21.90dB
BP, Agile Signals	−15.36 dB	−16.28 dB
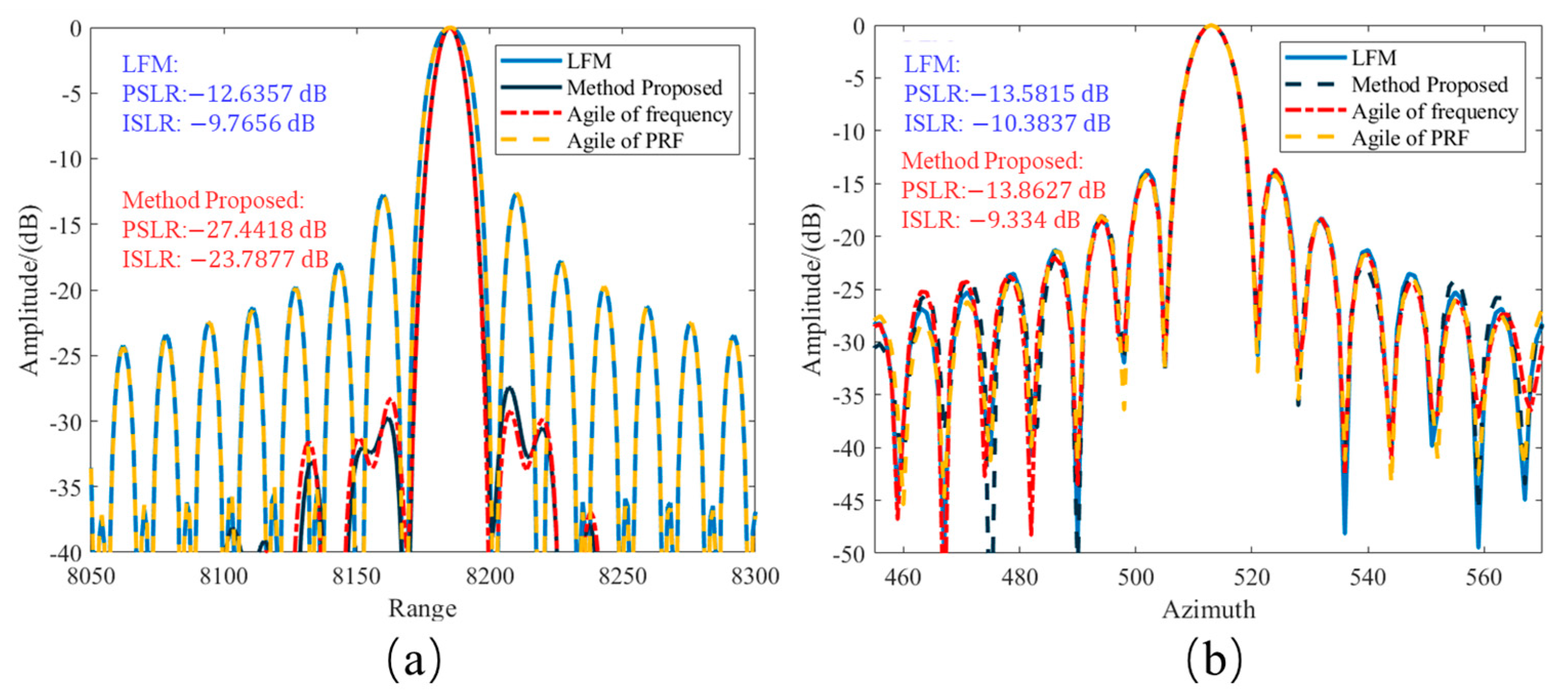
ω-k+ proposed method, Agile Signals	−26.86 dB	−24.57 dB

, for point targets sampled at twice the bandwidth and evaluated with 16x fine interpolation, under a 200 MHz agility range and without windowing, the carrier frequency processing algorithm proposed in this paper can effectively improve the peak side lobe ratio by 12 dB and the integrated side lobe ratio by 10 dB in the range direction compared to linear frequency modulation signals, without causing main lobe broadening.

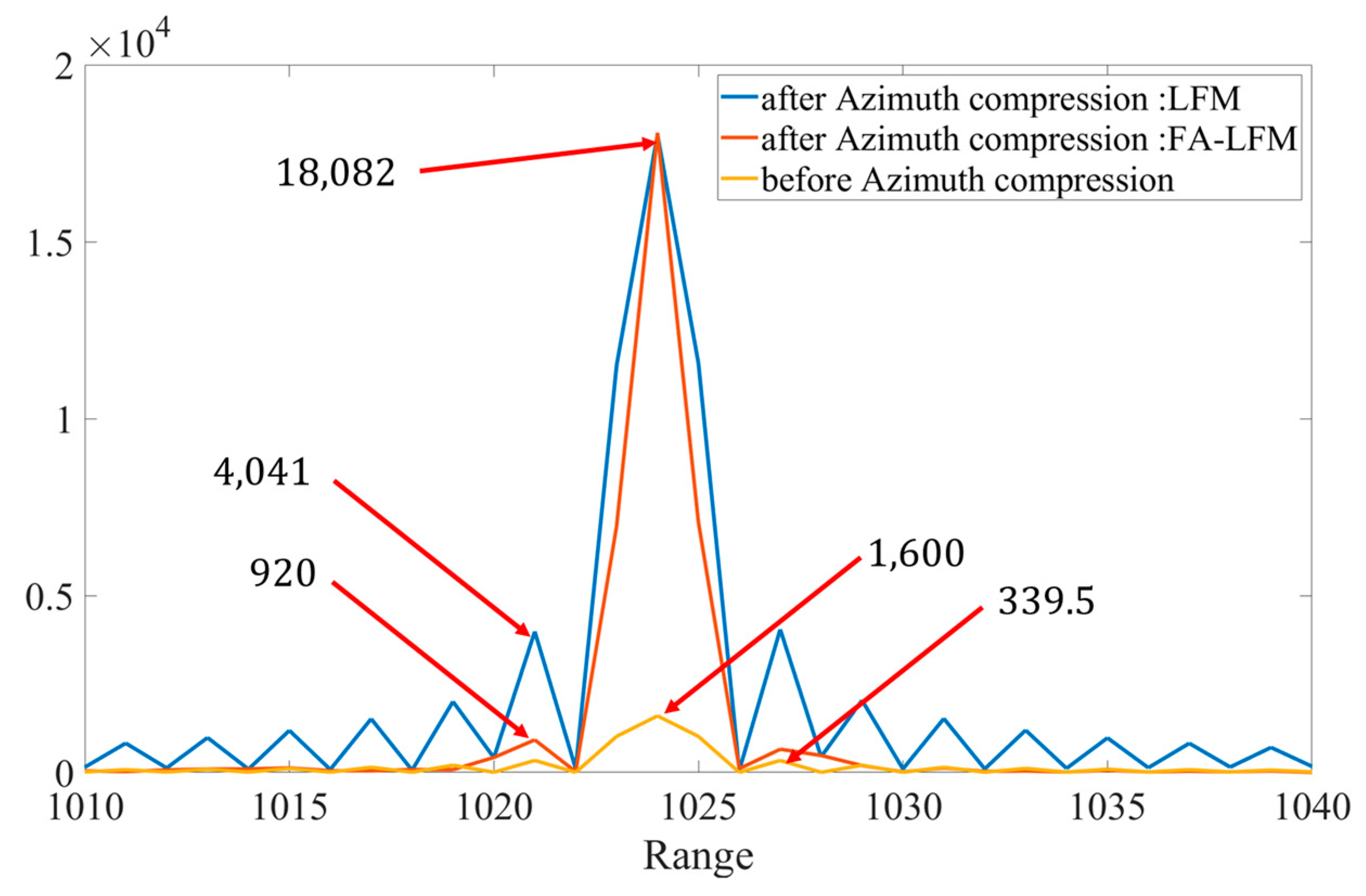
Based on the data in the imaging stages, the range gain brought by this carrier frequency agile processing algorithm is explained: as shown in Figure 19, the range profiles of the two signals before and after azimuth compression are quite clear. According to the peak values of the main and side lobes in the range direction, the processing gain of the inter-pulse frequency agile signal under the proposed algorithm can be directly calculated. The yellow line in the figure shows the range slices after pulse compression of the linear frequency modulation signal and the inter-pulse frequency agile signal with only the main lobe compensated. At this point, the range compression effect is basically consistent. The peak values of the main and side lobes are 1600 and 339.5, respectively. At this time, the range peak side lobe ratio of the two signals after range pulse compression is 13.46 dB.

After azimuth focusing, as shown by the blue and orange lines in the figure, the range profiles of the target after 2D imaging for LFM and FA-LFM are illustrated. The peak values of their main lobes are both approximately 18,082. However, the maximum side lobe peak value of the linear frequency modulation signal is 4041, and after azimuth compression, the main and side lobes are increased by 11.30 and 11.90 times, respectively. On the other hand, the maximum side lobe peak value of the inter-pulse frequency agile signal is only 920, and after azimuth compression, it is increased by 2.71 times. It can be observed that the main and side lobes of the linear frequency modulation signal are nearly equally amplified in the range direction, resulting in minimal impact on the target’s range metrics after azimuth focusing. However, the inter-pulse frequency agile signal shows a significant difference in the amplification of the main and side lobes in the range direction. As shown in Equation (20), the processed peak side lobe ratio integration is 25.86 dB.

$${PSLR}_{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}}=13.46+20·\mathit{log}\left({\displaystyle \frac{{11.30}_{\mathrm{m}\mathrm{i}\mathrm{a}\mathrm{n}}}{{2.71}_{\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{e}}}}\right)=25.86 \mathrm{d}\mathrm{B}$$

(20)

The effective improvement in range metrics can greatly prevent strong targets from obscuring adjacent weak targets. Two targets with different strengths are set at one resolution unit apart in the range direction, located at (2000 m, 0 m) and (2002 m, 0 m) respectively, with an energy difference of four times, or −12.04 dB. The point target imaging results produced by LFM signal and inter-pulse agile signal are shown in Figure 20.

As shown in Figure 21, compared to the imaging effect of linear frequency modulation (LFM) signals, the algorithm proposed in this paper allows weak targets, originally obscured by the side lobes of strong targets, to remain clearly visible when processing inter-pulse FA-LFM signals. After normalization, the energy of the weak target is consistent with the original amplitude ratio, validating the effectiveness of the proposed algorithm in highlighting weak targets.

4.2.2. Impact of Multi-Parameter Joint Agility on Azimuth Imaging

As shown in

Table 4. Different Algorithms for Processing LFM and Multi-Parameter Agile Signals: Azimuth Imaging Results.

Algorithm and Signal Type	PSLR	ISLR
RD, LFM	−13.58 dB	−10.38 dB
BP, LFM	−15.08 dB	−11.40 dB
ω-k, LFM	−13.22 dB	−9.94 dB
RD+ proposed method, Agile Signals	−13.57 dB	−9.52 dB
BP, Agile Signals	−14.88 dB	−5.22 dB
ω-k+ proposed method, Agile Signals	−13.30 dB	−9.43 dB

, the effect of azimuth compression processing is similar to that of LFM signals. However, the improved BP algorithm, when handling 200 MHz agility, results in an excessively high integrated side lobe ratio, making it unsuitable for agile frequency imaging.

4.2.3. Impact of Parameter Variation Range on Imaging

The carrier frequency agility range has a direct impact on the final imaging metrics of inter-pulse frequency agile SAR. A smaller agility range may not effectively achieve the purposes of anti-interference and side lobe suppression, thus limiting the improvement of imaging quality. However, an excessively large carrier frequency agility range may increase compensation errors, leading to a decline in imaging performance. As shown in

Table 5. Range and Azimuth Imaging Metrics Based on RD Algorithm under Different Carrier Frequency Variation Ranges.

Carrier Frequency Variation Ranges	PSLR		ISLR
	Range	Azimuth	Range	Azimuth
20 MHz	−13.04 dB	−13.61 dB	−11.19 dB	−10.35 dB
300 MHz	−20.54 dB	−14.50 dB	−15.38 dB	−9.32 dB
400 MHz	−15.21 dB	−16.07 dB	−10.29 dB	−8.59 dB
600 MHz	−15.21 dB	−15.60 dB	−10.40 dB	−8.36 dB
800 MHz	−16.61 dB	−13.95 dB	−10.88 dB	−7.50 dB

, since the target delay, which constitutes the compensation value, is derived from the range axis, its accuracy is affected by the number of range axis sampling points. When the agility range increases, the system errors caused by sampling accuracy are amplified, resulting in a continuous decrease in the integrated side lobe ratio in the azimuth direction.

4.3. Extended Target Simulation—Evaluation of Image Quality

Based on existing real remote sensing images, this paper uses the pixel grayscale values of the images as reference values for the backscattering coefficient of the extended targets. The target positions are divided according to the theoretical resolutions of 0.6 m in the azimuth direction and 1.1 m in the range direction to obtain the imaging results processed by each parameter, as shown in Figure 22.

This paper also simulates the echoes of multi-parameter joint agile waveforms in various dense extended target scenarios and compares the imaging results with traditional LFM signals and different processing algorithms, as shown in Figure 23.

As shown in

Table 6. The image quality of the proposed algorithm and the BP algorithm in handling LFM signals for different targets: second-order entropy and speed comparison.

Scenario/Algorithm	LFM Signal Using RD Algorithm	Agile Signal with RD Algorithm+ Proposed Method	Agile Signal Using BP Algorithm
Ships	6.0421 dB	5.9435 dB	5.3362 dB
Planes	6.3238 dB	6.0376 dB	5.7275 dB
Docks	9.5404 dB	9.5092 dB	9.2142 dB
Average Time	2.35 s	2.59 s	51.91 s

,

Table 7. The image quality of the proposed algorithm and the BP algorithm in handling LFM signals for different targets: average gradient.

Scenario/Algorithm	LFM Signal Using RD Algorithm	Agile Signal with RD Algorithm+ Proposed Method	Agile Signal with ω-k Algorithm+ Proposed Method	Agile Signal Using BP Algorithm
Ships	2.59 dB	3.59 dB	3.60 dB	2.68 dB
Planes	1.54 dB	2.79 dB	2.44 dB	1.59 dB
Docks	6.59 dB	7.03 dB	7.7 dB	6.62 dB
Figure 21	8.66 dB	9.30 dB	9.95 dB	8.67 dB

and

Table 8. The image quality of the proposed algorithm and the BP algorithm in handling LFM signals for different targets: contrast.

Scenario/Algorithm	LFM Signal Using RD Algorithm	Agile Signal with RD Algorithm+ Proposed Method	Agile Signal with ω-k Algorithm+ Proposed Method	Agile Signal Using BP Algorithm
Ships	37.11 dB	73.44 dB	64.76 dB	68.85 dB
Planes	47.22 dB	59.23 dB	59.21 dB	54.83 dB
Docks	1.76 dB	2.87 dB	2.66 dB	2.13 dB
Figure 21	331.84 dB	387.51 dB	389.49 dB	362.38 dB

, the algorithm proposed in this paper can be directly applied to RD, ω-k, and other frequency domain algorithms. It is evaluated based on imaging quality metrics: second-order entropy, average gradient, and contrast, as well as computational speed. The proposed algorithm achieves results closer to the theoretical values attainable by LFM signals compared to the BP algorithm, indicating better performance [32,33,34]. Additionally, in terms of processing time on a Windows platform, with echo data of 2048 × 1024 sampling points, the proposed algorithm takes significantly less time on average than the BP algorithm, demonstrating higher efficiency.

5. Evaluation of Effectiveness against Active Deception Jamming

The complexity and uncertainty of inter-pulse parameter agile waveforms greatly enhance the SAR system’s ability to resist active coherent interference. However, existing studies mostly focus on single-parameter agility and lack systematic research on multi-parameter joint agility. This section systematically introduces active coherent interference and analyzes the anti-jamming performance of single and combined agility of pulse width, chirp rate polarity, carrier frequency, and pulse repetition interval.

5.1. Dense Point Target Jamming

To simulate the suppression of deception jamming, a real target is placed at the center of the scene (2000 m, 0 m), and eight false target points are generated around the real target every 10 m to simulate dense false targets. It is also assumed that the jamming echo has at least one pulse delay.

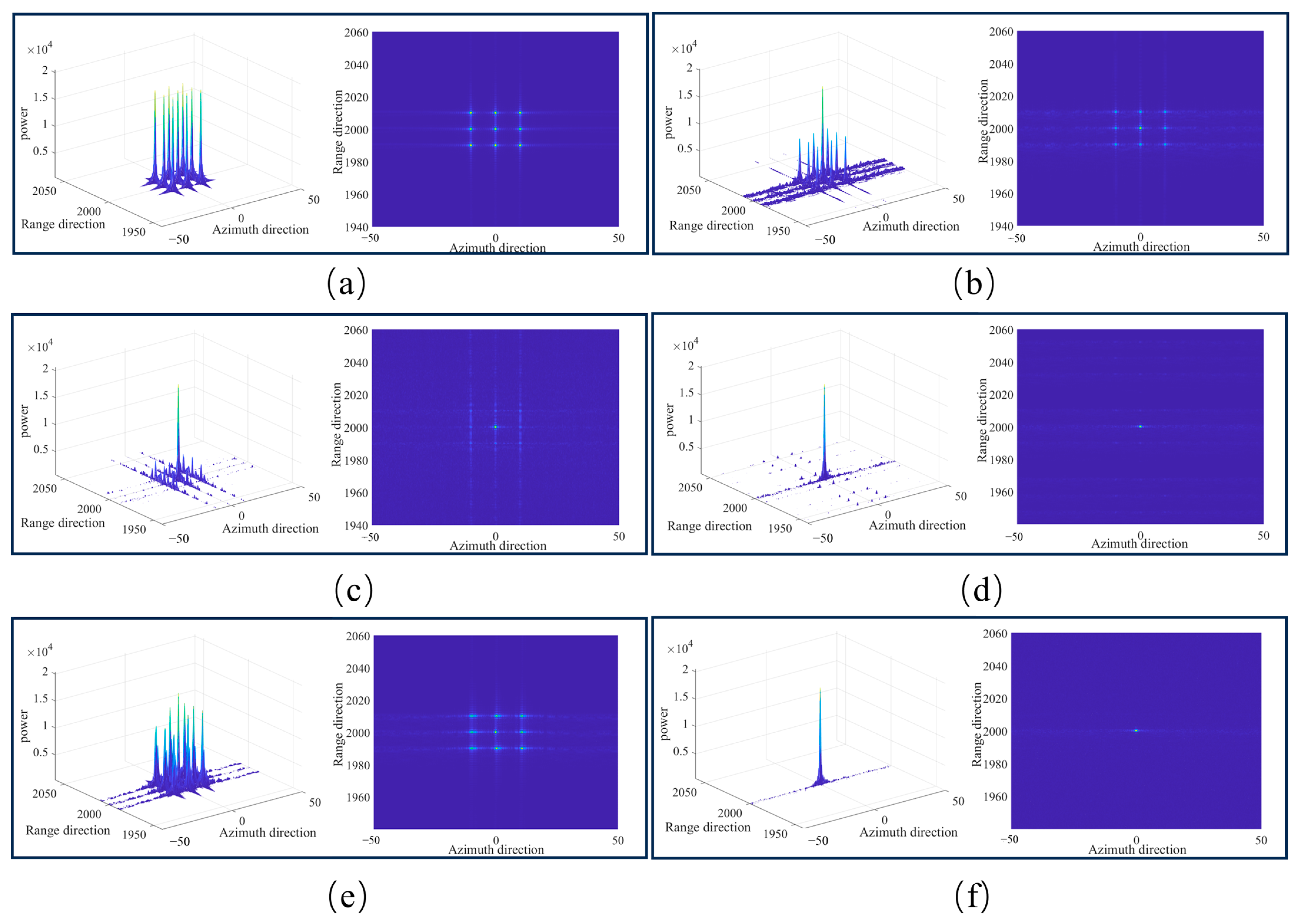
As shown in Figure 24, part (a) demonstrates that the impulse response of false target points almost matches that of the central real target when facing deception jamming from a jammer. Since this model does not yet consider the direct impact of PRF variation on the jammer, under the conditions of this paper, PRF variation exhibits the weakest suppression effect on false targets, only attenuating false target energy to a certain extent. Chirp rate polarity agility effectively reduces the range gain of the jamming signal by half but still generates interference targets. Pulse width agility better suppresses the compression of jamming signals in the range direction. However, compared to the carrier frequency parameter, carrier frequency agility under the proposed algorithm clearly shows that false targets are directly suppressed, only exhibiting periodic minimal points that cannot compare in amplitude to the real target. The multi-parameter joint agility combines the suppression advantages of each agile parameter, suppressing false target jamming signals across multiple stages and dimensions, thereby significantly enhancing the radar system’s resistance to active interference.

5.2. Evaluation of Large-Scale Deception Jamming Suppression Effectiveness

There are two main types of scene deception: first, using jamming templates to conceal real targets, such as airports and bases; second, using jamming templates to generate deceptive targets to confuse the enemy’s judgment, such as airplanes and ships.

First, using methods proposed in the related literature, scene deception jamming is applied to a concealed airport in mountainous terrain. The scene and jamming templates are shown in Figure 25a,b. Deception jamming is applied using the simulation platform, and the processing results of LFM signals and multi-parameter agile signals are observed, as shown in Figure 25c,d.

Secondly, deception jamming with false targets is applied to a coastal dock area. The scene and jamming templates are shown in Figure 26a,b. Deception jamming is applied using the simulation platform, and the processing results of LFM signals and multi-parameter agile signals are observed, as shown in Figure 26c,d.

Simulation results show that the LFM signal is deceived by the jamming signal, causing the real scene in Scenario 1 to be obscured, and false targets, such as ships, to appear in Scenario 2. In contrast, the multi-parameter agile signal processed by the proposed algorithm successfully suppresses the jamming signal and achieves effective imaging. This comparison demonstrates the algorithm’s ability to directly suppress deception signals in large-scale scenes, providing strong support for the improvement of radar system anti-jamming performance using multi-parameter agile signals.

6. Discussion

Currently, parameter agile signals, as an emerging active method to counter active coherent jamming based on waveform design, are gradually becoming a research hotspot. In previous studies, SAR active waveform countermeasure methods tended to focus on single agile parameters or mainly considered relatively simple and easy-to-handle joint agility of parameters such as pulse width, chirp rate polarity, or initial phase. Agile PRF has also been primarily applied in high-resolution wide-swath fields, but the anti-active coherent jamming capability of these parameters is limited. Experimental results demonstrate that carrier frequency agility has better anti-active jamming capabilities, but compensating for carrier frequency entails significant computational load, a problem mentioned in many studies. Therefore, it is necessary to reconsider the mode of carrier frequency compensation. According to the theoretical model, this paper proposes a principal component approximate reconstruction method based on the range axis to address the underdetermined estimation problem of the echo matrix, reducing the computational load to the $O\left(n\right)$ level while retaining the maximum amount of signal information.

As seen in the experiments explored in Section 4, the proposed algorithm not only reconstructs carrier frequency agile echo signals but also improves range imaging metrics. Moreover, in the case of full parameter agility, it achieves imaging results close to linear frequency modulation signals. In Section 5, an active coherent jamming model was established to systematically test the anti-jamming performance of different parameters and multi-parameter joint agility from the aspects of dense point targets and large-scale jamming, which is relatively rare in previous studies. It should be noted that, although this paper has achieved multi-parameter joint agile imaging to some extent and has retained anti-jamming capabilities, there are still several limitations. For example, when the frequency agility range is too large, the errors introduced by digital sampling are amplified, leading to a decline in imaging metrics and a deterioration in image quality. Additionally, as active jamming techniques evolve, the traditional assumption based on jamming signal delays may no longer hold, necessitating further upgrades to radar systems. Furthermore, the impact of errors in actual systems has not yet been considered, and further validation and implementation are required [35].

In the future, we will attempt to establish an active coherent system for practical countermeasures and, based on the random agility model presented in this paper, further consider intelligent waveform countermeasures to fully exploit the flexibility of parameter agile SAR; the next steps will include improving the algorithm to increase the range of signal parameter agility, thereby enhancing the unpredictability and anti-jamming capabilities of the agile signal. These improvements will also focus on enhancing imaging quality and achieving additional effects such as high-resolution and wide-swath imaging [36].

7. Conclusions

Inter-pulse parameter agility technology can effectively enhance the anti-active coherent jamming capability of airborne SAR. However, different parameters have varying impacts on the imaging model and differing jamming suppression effects, posing challenges for achieving high-resolution imaging with SAR. The main research work of this paper systematically analyzed the primary parameters in traditional linear frequency modulation signals that can be made agile, investigated their effects on imaging, and addressed the difficulties in carrier frequency compensation. Experiments verified the imaging effects of single and joint inter-pulse parameter agility compared to traditional fixed parameter signals. The study also analyzed the suppression effects of four parameters on active coherent jamming signals at the imaging results level. The main research conclusions of this paper are as follows:

• Multi-Parameter Analysis and Carrier Frequency Processing Method: The impact of four agile parameters on the SAR imaging model was analyzed. Pulse width and chirp rate polarity are parameters that are simple to compensate for and have minimal impact on imaging results after processing. The use of NUFFT for PRI can result in fluctuating side lobes to some extent, and there are existing methods in the literature to address this. Due to the significant impact of carrier frequency agility on the model and the large computational load for compensation, which is unfavorable for engineering implementation, an approximate compensation method was proposed. This method reduces the computational load to an acceptable level while preserving the principal component information and can be applied to various frequency domain imaging algorithms;
• Multi-Parameter Joint Agile Signal Imaging System: A full-parameter agile signal imaging system was established, and a compensation + non-uniform reconstruction method was proposed. This method is suitable for SAR image processing of inter-pulse parameter agile waveforms and yielded results similar to those of traditional fixed LFM signal images;
• Anti-Jamming Effect Analysis: Assuming the jammer can accurately replicate the signal, without considering the impact of parameter agility on the jammer itself, the suppression effects of the four agile parameters on active jamming signals are as follows: carrier frequency > pulse width > chirp rate polarity > PRI. Joint parameter agility can further combine the suppression advantages of individual parameters to achieve the best suppression effect.

In summary, the proposed processing flow for multi-parameter joint agile signals is simple and efficient, with significant suppression effects on active coherent jamming. This work is expected to be applied in the field of SAR to counter active deception jamming, addressing the issue of traditional LFM signals being jammed. This has certain reference significance and practical value in engineering applications.