Rapid Prediction of the Lithium Content in Plants by Combining Fractional-Order Derivative Spectroscopy and Wavelet Transform Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Sampling
2.2. Spectral Measurements and Preprocessing
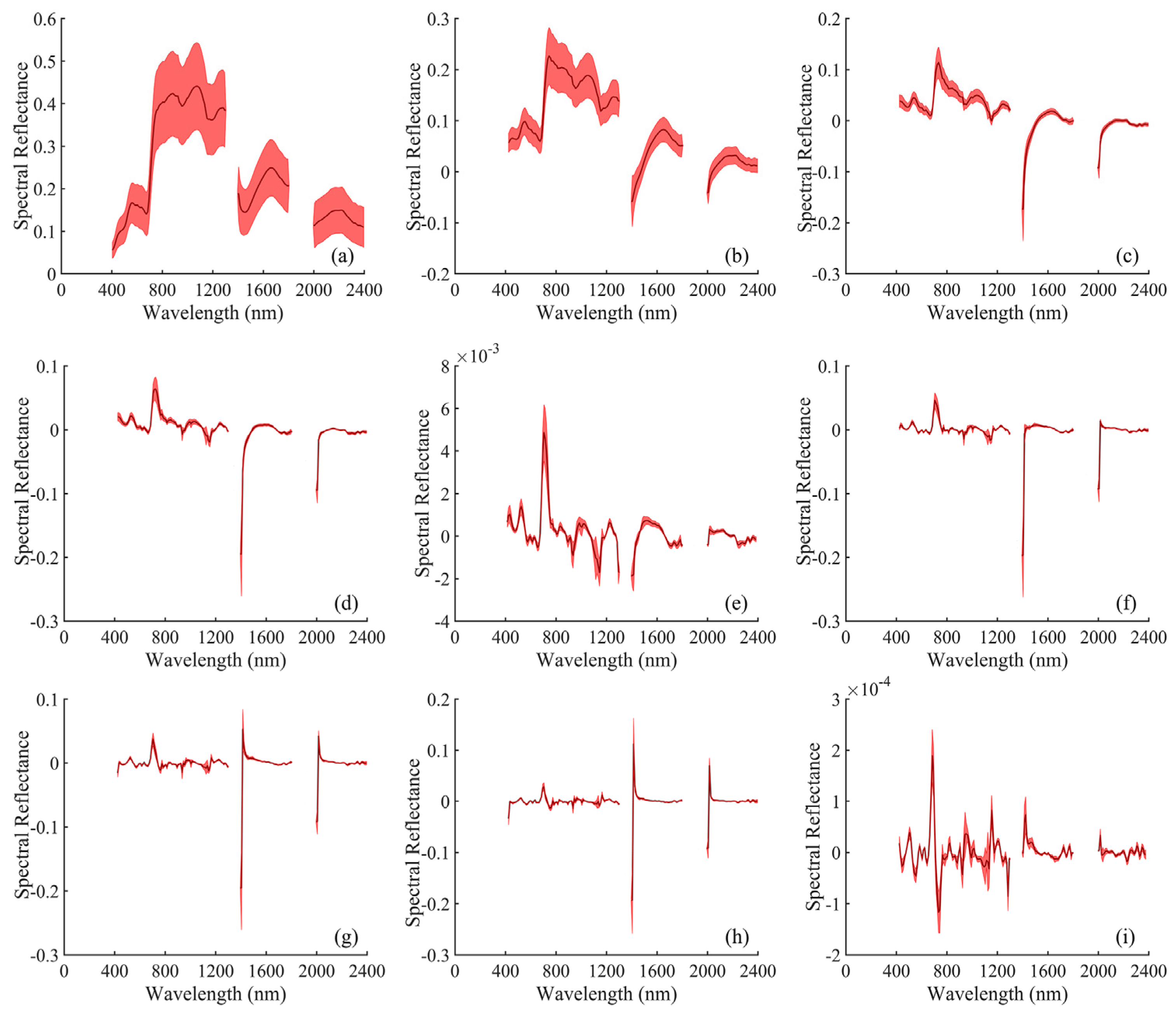
2.3. Spectral Transformation
2.4. Partial Least Squares Regression
2.5. Wavelet Transform Method
2.6. Model Establishment and Accuracy Evaluation
2.7. Kruskal–Wallis Test
3. Results
3.1. Statistical Analysis of the Li Content in Plants
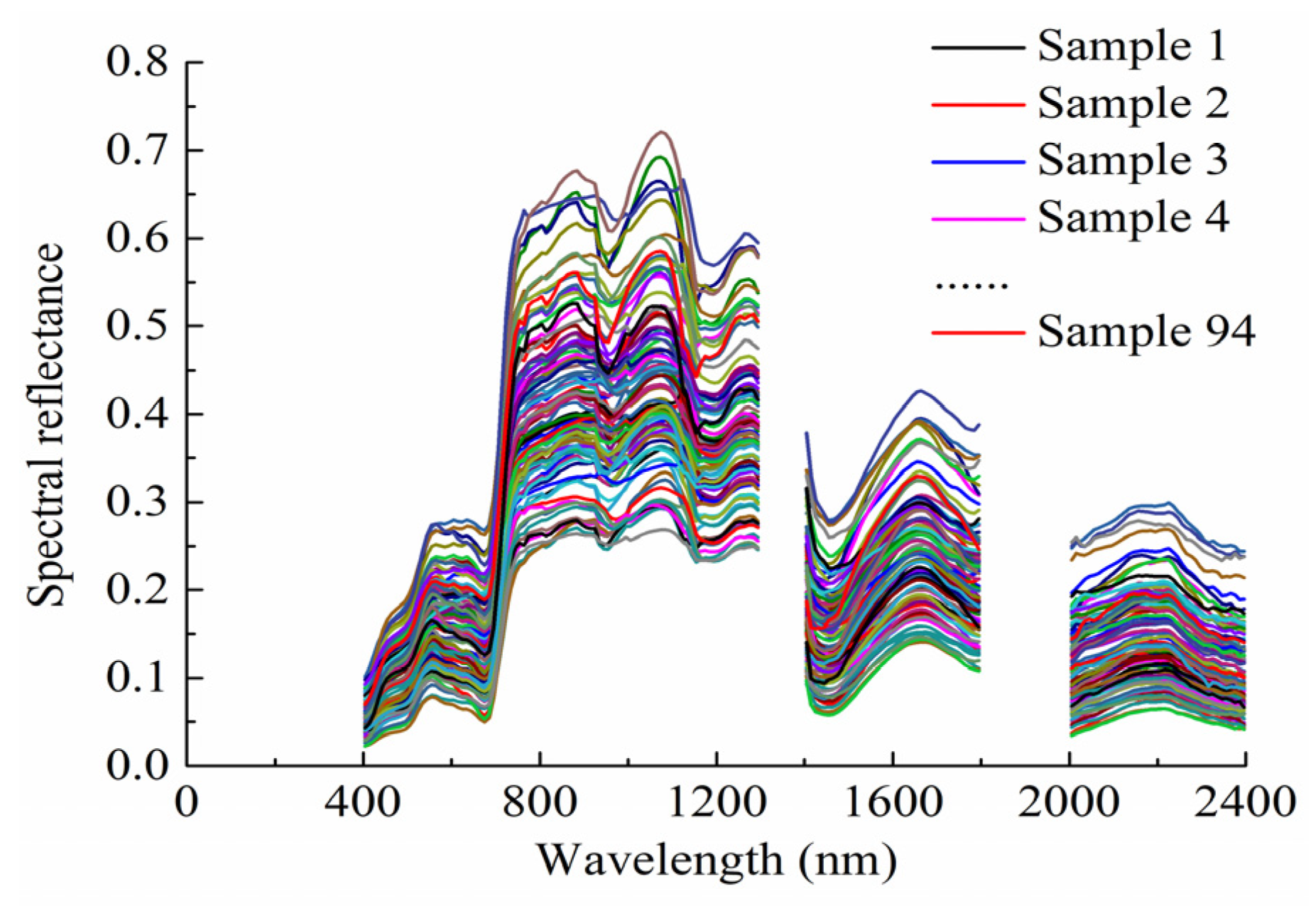
3.2. Spectral Characteristics
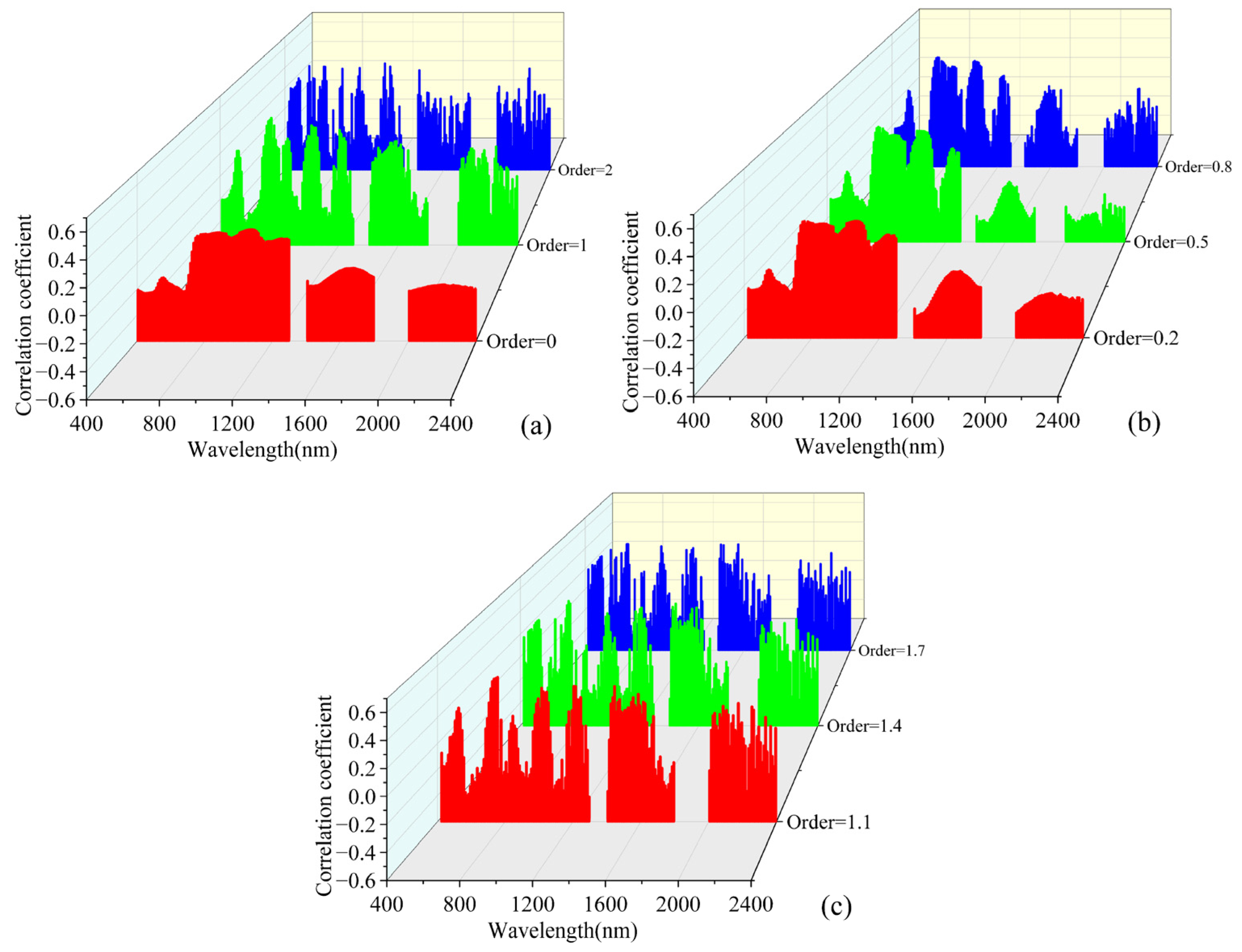
3.3. Correlation Analysis between the Transformed Spectra and the Li Content
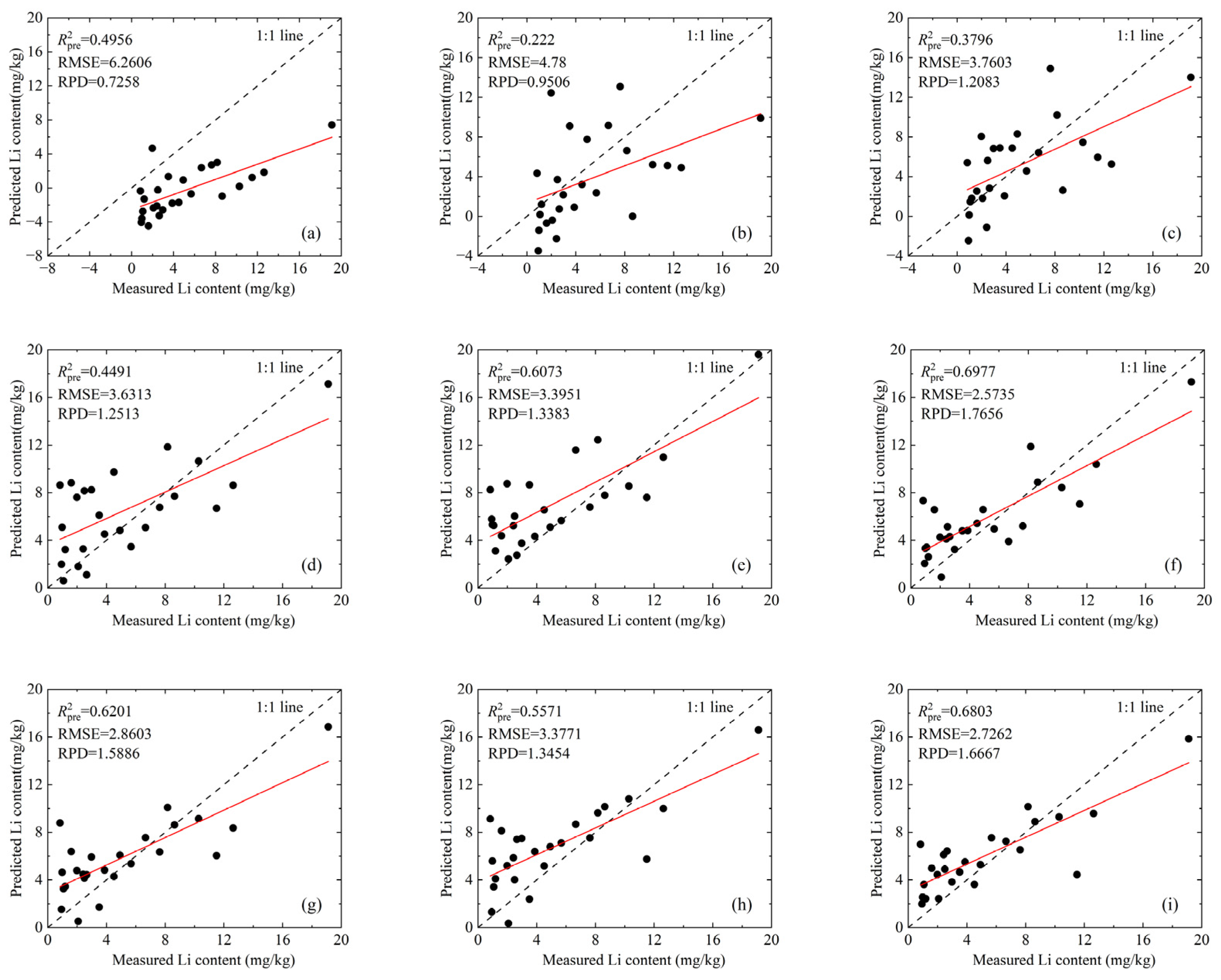
3.4. Establishment of the Estimation Model
3.5. Construction of an Estimation Model Based on the Wavelet Coefficient
4. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Naranjo, M.A.; Romero, C.; Belles, J.M.; Montesinos, C.; Vicente, O.; Serrano, R. Lithium treatment induces a hypersensitive-like response in tobacco. Planta 2003, 217, 417–424. [Google Scholar] [CrossRef] [PubMed]
- Hawrylak-Nowak, B.; Kalinowska, M.; Szymanska, M. A Study on Selected Physiological Parameters of Plants Grown Under Lithium Supplementation. Biol. Trace Elem. Res. 2012, 149, 425–430. [Google Scholar] [CrossRef] [PubMed]
- Martinez, N.E.; Sharp, J.L.; Johnson, T.E.; Kuhne, W.W.; Stafford, C.T.; Duff, M.C. Reflectance-Based Vegetation Index Assessment of Four Plant Species Exposed to Lithium Chloride. Sensors 2018, 18, 2750. [Google Scholar] [CrossRef]
- Hayyat, M.U.; Nawaz, R.; Siddiq, Z.; Shakoor, M.B.; Mushtaq, M.; Ahmad, S.R.; Ali, S.; Hussain, A.; Irshad, M.A.; Alsahli, A.A.; et al. Investigation of Lithium Application and Effect of Organic Matter on Soil Health. Sustainability 2021, 13, 1705. [Google Scholar] [CrossRef]
- Zhai, M.; Wu, F.; Hu, R.; Jiang, S.; Li, W.; Wang, R.; Wang, D.; Qi, T.; Qin, K.; Wen, H. Crtical metal mineral resources: Current research status and scientific issues. Bull. Natl. Nat. Sci. Found. China 2019, 33, 106–111. (In Chinese) [Google Scholar]
- Wang, D.H. Study on critical mineral resources: Significance of research, determination of types, attributes of resources, progress of prospecting, problem of utilization and direction of exploitation. Acta Geol. Sin. 2019, 93, 1189–1209. (In Chinese) [Google Scholar]
- Köhler, M.; Hanelli, D.; Schaefer, S.; Barth, A.; Knobloch, A.; Hielscher, P.; Cardoso-Fernandes, J.; Lima, A.; Teodoro, A.C. Lithium Potential Mapping Using Artificial Neural Networks: A Case Study from Central Portugal. Minerals 2021, 11, 1046. [Google Scholar] [CrossRef]
- Cardoso-Fernandes, J.; Lima, A.; Roda-Robles, E.; Teodoro, A.C. Constraints and potentials of remote sensing data/techniques applied to lithium (Li)-pegmatites. Can. Miner. 2019, 57, 723–725. [Google Scholar] [CrossRef]
- Cardoso-Fernandes, J.; Teodoro, A.C.; Lima, A. Remote sensing data in lithium (Li) exploration: A new approach for the detection of Li-bearing pegmatites. Int. J. Appl. Earth Obs. Geoinf. 2019, 76, 10–25. [Google Scholar] [CrossRef]
- Cardoso-Fernandes, J.; Silva, J.; Dias, F.; Lima, A.; Teodoro, A.C.; Barrès, O.; Cauzid, J.; Perrotta, M.; Roda-Robles, E.; Ribeiro, M.A. Tools for Remote Exploration: A Lithium (Li) Dedicated Spectral Library of the Fregeneda-Almendra Aplite-Pegmatite Field. Data 2021, 6, 33. [Google Scholar] [CrossRef]
- Gao, Y.B.; Bagas, L.; Li, K.; Jin, M.S.; Liu, Y.G.; Teng, J.X. Newly Discovered Triassic Lithium Deposits in the Dahongliutan Area, North West China: A Case Study for the Detection of Lithium-Bearing Pegmatite Deposits in Rugged Terrains Using Remote-Sensing Data and Images. Front. Earth Sci. 2020, 8, 591966. [Google Scholar] [CrossRef]
- Chen, Y.J.; Xue, L.Z.; Wang, X.L.; Zhao, Z.B.; Han, J.S.; Zhou, K.F. Progress in geological study of pegmatite-type lithium deposits in the world. Acta Geol. Sin. 2021, 95, 2971–2995. (In Chinese) [Google Scholar]
- Cardoso-Fernandes, J.; Teodoro, A.C.; Lima, A.; Roda-Robles, E. Semi-Automatization of Support Vector Machines to Map Lithium (Li) Bearing Pegmatites. Remote Sens. 2020, 12, 2319. [Google Scholar] [CrossRef]
- Cardoso-Fernandes, J.; Teodoro, A.C.; Lima, A.; Perrotta, M.; Roda-Robles, E. Detecting Lithium (Li) Mineralizations from Space: Current Research and Future Perspectives. Appl. Sci. 2020, 10, 1785. [Google Scholar] [CrossRef]
- Perrotta, M.M.; Souza Filho, C.R.; Leite, C.A.S. Mapeamento espectral de intrusões pegmatíticas relacionadas a mineralizações de lítio, gemas e minerais industriais na região do vale do Jequitinhonha (MG) a partir de imagens ASTER. In Proceedings of the Anais do XII Simpósio Brasileiro de Sensoriamento Remoto, Goiânia, Brazil, 16–21 April 2005; pp. 1855–1862. [Google Scholar]
- Mendes, D.; Perrotta, M.M.; Costa, M.A.C.; Paes, V.J.C. Mapeamento espectral para identificação de assinaturas espectrais de minerais de lítio em imagens ASTER (NE/MG). In Proceedings of the Anais do XVIII Simpósio Brasileiro de Sensoriamento Remoto, Santos-SP, Brazil, 28–29 May 2017; pp. 5273–5280. [Google Scholar]
- Cardoso-Fernandes, J.; Teodoro, A.C.; Lima, A. Potential of Sentinel-2 data in the detection of lithium (Li)-bearing pegmatites: A study case. In Proceedings of the SPIE, SPIE Remote Sensing, Berlin, Germany, 10–13 September 2018; Michel, U., Schulz, K., Eds.; SPIE: Bellingham, WA, USA, 2018; p. 15. [Google Scholar]
- Cardoso-Fernandes, J.; Silva, J.; Perrotta, M.M.; Lima, A.; Teodoro, A.C.; Ribeiro, M.A.; Dias, F.; Barrès, O.; Cauzid, J.; Roda-Robles, E. Interpretation of the Reflectance Spectra of Lithium (Li) Minerals and Pegmatites: A Case Study for Mineralogical and Lithological Identification in the Fregeneda-Almendra Area. Remote Sens. 2021, 13, 3688. [Google Scholar] [CrossRef]
- Santos, D.; Teodoro, A.; Lima, A.; Cardoso-Fernandes, J. Remote sensing techniques to detect areas with potential for lithium exploration in Minas Gerais, Brazil. In Proceedings of the SPIE, SPIE Remote Sensing, Strasbourg, France, 9–12 September 2019; Schulz, K., Michel, U., Nikolakopoulos, K.G., Eds.; SPIE: Bellingham, WA, USA, 2019. [Google Scholar]
- Dai, J.J.; Wang, D.H.; Dai, H.Z.; Liu, L.J.; Ling, D.Y. Reflectance spectral characteristics of rocks and mineral in Jiajika lithium deposits in west Sichuan. Rock Miner. Anal. 2019, 37, 507–517. (In Chinese) [Google Scholar]
- Dai, J.J.; Wang, D.H.; Dai, H.Z.; Liu, L.J.; Wu, Y.N. Geological mapping and ore-prospecting study using remote sensing technology in Jiajika area of Western Sichuan Province. Geol. China 2017, 44, 389–398. (In Chinese) [Google Scholar]
- Dai, J.J.; Wang, D.H.; Ling, T.Y. Quantitative estimation of content of lithium using reflectance spectroscopy. Remote Sens. Technol. Appl. 2019, 34, 992–997. (In Chinese) [Google Scholar]
- Gemusse, U.; Lima, A.; Teodoro, A. Pegmatite spectral behavior considering ASTER and Landsat 8 OLI data in Naipa and Muiane mines (Alto Ligonha, Mozambique). In Proceedings of the SPIE, SPIE Remote Sensing, Berlin, Germany, 10–13 September 2018; Michel, U., Schulz, K., Eds.; SPIE: Bellingham, WA, USA, 2018. [Google Scholar]
- Gemusse, U.; Lima, A.; Teodoro, A.C.M.; Schulz, K.; Nikolakopoulos, K.G.; Michel, U. Comparing different techniques of satellite imagery classification to mineral mapping pegmatite of Muiane and Naipa: Mozambique). In Proceedings of the Earth Resources and Environmental Remote Sensing/GIS Applications X, Strasbourg, France, 10–12 September 2019. [Google Scholar]
- Chakraborty, R.; Kereszturi, G.; Pullanagari, R.; Durance, P.; Ashraf, S.; Anderson, C. Mineral prospecting from biogeochemical and geological information using hyperspectral remote sensing-Feasibility and challenges. J. Geochem. Explor. 2022, 232, 106900. [Google Scholar] [CrossRef]
- Hu, X.S.; Meng, G.L. Method of plant geochemical measurement and its prospecting result. Miner. Resour. Geol. 2005, 19, 610–616. (In Chinese) [Google Scholar]
- McInnes, B.I.A.; Dunn, C.E.; Cameron, E.M.; Kameko, L. Biogeochemical exploration for gold in tropical rain forest regions of Papua New Guinea. J. Geochem. Explor. 1996, 57, 227–243. [Google Scholar] [CrossRef]
- Özdemir, Z.; Saǧıroǧlu, A. Salix acmophylla, Tamarix smyrnensis and Phragmites australis as biogeochemical indicators for copper deposits in Elazıǧ, Turkey. J. Asian Earth Sci. 2000, 18, 595–601. [Google Scholar] [CrossRef]
- Özdemir, Z. Pinus brutia as a biogeochemical medium to detect iron and zinc in soil analysis, chromite deposits of the area mersin, Turkey. Geochemistry 2005, 65, 79–88. [Google Scholar] [CrossRef]
- Pratas, J.; Prasad, M.N.V.; Freitas, H.; Conde, L. Plants growing in abandoned mines of portugal are useful for biogeochemical exploration of arsenic, antimony, tungsten and mine reclamation. J. Geochem. Explor. 2005, 85, 99–107. [Google Scholar] [CrossRef]
- Lottermoser, B.G.; Ashley, P.M.; Munksgaard, N.C. Biogeochemistry of Pb–Zn gossans, northwest Queensland, Australia: Implications for mineral exploration and mine site rehabilitation. Appl. Geochem. 2008, 23, 723–742. [Google Scholar] [CrossRef]
- Miao, L.; Xu, R.; Ma, Y.; Xu, J.; Wang, J.; Cai, R.; Chen, Y. Biogeochemical characteristics of the Hetai goldfield, Guangdong Province. China. J. Geochem. Explor. 2008, 96, 43–52. [Google Scholar] [CrossRef]
- Reid, N.; Hill, S.M. Biogeochemical sampling for mineral exploration in arid terrains: Tanami Gold Province. Australia. J. Geochem. Explor. 2010, 104, 105–117. [Google Scholar] [CrossRef]
- Reid, N.; Hill, S.M. Spinifex biogeochemistry across Arid Australia: Mineral exploration potential and chromium accumulation. Appl. Geochem. 2013, 29, 92–101. [Google Scholar] [CrossRef]
- Filippidis, A.; Papastergios, G.; Kantiranis, N.; Michailidis, K.; Chatzikirkou, A.; Katirtzoglou, K. The species of Silene compacta Fischer as indicator of zinc. iron and copper mineralization. Geochemistry 2012, 72, 71–76. [Google Scholar] [CrossRef]
- Noble, R.R.P.; Anand, R.R.; Gray, D.J.; Cleverley, J.S. Metal migration at the DeGrussa Cu-Au sulphide deposit, Western Australia: Soil, vegetation and groundwater studies. Geochem. Explor. Environ. Anal. 2017, 17, 124–142. [Google Scholar] [CrossRef]
- Song, C.A.; Song, W.; Ding, R.F.; Lei, L.Q. Phytogeochemical Characteristics of Seriphidium terrae-albae (Krasch) Poljak in the Metallic Ore Deposits in North Part of East Junggar Desert Area, Xinjiang and their Prospecting Significance. Geotecton. Metallog. 2017, 41, 122–132. (In Chinese) [Google Scholar]
- Johnsen, A.R.; Thomsen, T.B.; Thaarup, S.M. Test of vegetation-based surface exploration for detection of Arctic mineralizations: The deep buried Kangerluarsuk Zn-Pb-Ag anomaly. J. Geochem. Explor. 2021, 220, 106665. [Google Scholar] [CrossRef]
- Sun, J.; Zhou, X.; Wu, X.H.; Lu, B.; Dai, C.X.; Shen, J.F. Research and analysis of cadmium residue in tomato leaves based on WT-LSSVR and Vis-NIR hyperspectral imaging. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2019, 212, 215–221. [Google Scholar]
- He, L.; Li, A.N.; Nan, X. Study of vegetation spectral anomaly behaviour in a porphyry copper mine area based on hyperspectral indices. Int. J. Remote Sens. 2020, 41, 911–928. [Google Scholar] [CrossRef]
- Lin, D.; Li, G.; Zhu, Y.; Liu, H.; Li, L.; Fahad, S.; Zhang, X.; Wei, C.; Jiao, Q. Predicting copper content in chicory leaves using hyperspectral data with continuous wavelet transforms and partial least squares. Comput. Electron. Agric. 2021, 187, 106293. [Google Scholar] [CrossRef]
- Feng, X.; Chen, H.; Chen, Y.; Zhang, C.; Liu, X.; Weng, H.; Xiao, S.; Nie, P.; He, Y. Rapid detection of cadmium and its distribution in Miscanthus sacchariflorus based on visible and near-infrared hyperspectral imaging. Sci. Total Environ. 2019, 659, 1021–1031. [Google Scholar] [CrossRef]
- Mirzaei, M.; Verrelst, J.; Marofi, S.; Abbasi, M.; Azadi, H. Eco-Friendly Estimation of Heavy Metal Contents in Grapevine Foliage Using In-Field Hyperspectral Data and Multivariate Analysis. Remote Sens. 2019, 11, 2731. [Google Scholar] [CrossRef]
- Cao, Y.; Sun, J.; Yao, K.S.; Xu, M.; Tang, N.Q.; Zhou, X. Non-destructive detection of lead content in oilseed rape leaves based on MRF-HHO-SVR and hyperspectral technology. J. Food Process Eng. 2021, 44, e13793. [Google Scholar] [CrossRef]
- Hede, A.; Kashiwaya, K.; Koike, K.; Sakurai, S. A new vegetation index for detecting vegetation anomalies due to mineral deposits with application to a tropical forest area. Remote Sens. Environ. 2015, 171, 83–97. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Ren, H.Z.; Ersoy, O.K. A new narrow band vegetation index for characterizing the degree of vegetation stress due to copper: The copper stress vegetation index (CSVI). Remote Sens. Lett. 2017, 8, 576–585. [Google Scholar] [CrossRef]
- Zhang, C.; Ren, H.; Huang, Z.; Li, J.; Qin, Q.; Zhang, T.; Sun, Y. Assessment of the application of copper stress vegetation index on Hyperion image in Dexing Copper Mine, China. J. Appl. Remote Sens. 2019, 13, 014511. [Google Scholar] [CrossRef]
- Zhang, C.; Ren, H.; Dai, X.; Qin, Q.; Li, J.; Zhang, T.; Sun, Y. Spectral characteristics of copper-stressed vegetation leaves and further understanding of the copper stress vegetation index. Int. J. Remote Sens. 2019, 40, 4473–4488. [Google Scholar] [CrossRef]
- Wang, G.D.; Wang, Q.X.; Su, Z.L.; Zhang, J.H. Predicting copper contamination in wheat canopy during the full growth period using hyperspectral data. Environ. Sci. Pollut. Res. Int. 2021, 27, 39029–39040. [Google Scholar] [CrossRef]
- Lassalle, G.; Fabre, S.; Credoz, A.; Hédacq, R.; Dubucq, D.; Elger, A. Mapping leaf metal content over industrial brownfields using airborne hyperspectral imaging and optimized vegetation indices. Sci. Rep. 2021, 11, 2. [Google Scholar] [CrossRef]
- Shi, G.Q.; Yang, K.M.; Sun, Y.Y.; Liu, F.; Wei, H.F. Spectral red edge position responding and pollution moitoring of core leaves stressed by heavy metal copper. Hubei Agric. Sci. 2015, 54, 3234–3239. (In Chinese) [Google Scholar]
- Chen, S.M.; Tu, Y.; Zhao, Y.L.; Liu, Z.Y.; Xu, J.S.; Wei, L.; Shao, R. Relational model between the hyperspectral variability of Celosia argentea L. growing in manganese stress environment and the content of metal element in the canopy. J. Guilin Univ. Technol. 2018, 38, 744–751. (In Chinese) [Google Scholar]
- Li, Y.X.; Chen, X.Y.; Luo, D.; Li, B.Y.; Wang, S.R.; Zhang, L.W. Effects of Cuprum Stress on Position of Red Edge of Maize Leaf Reflection Hyperspectra and Relations to Chlorophyll Content. Spectrosc. Spect. Anal. 2018, 38, 546–551. [Google Scholar]
- Liu, M.L.; Wang, T.J.; Skidmore, A.K.; Liu, X.N. Heavy metal-induced stress in rice crops detected using multi-temporal Sentinel-2 satellite images. Sci. Total Environ. 2018, 637, 18–29. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, K.M.; Wang, M.; Gao, P.; Cheng, F.; Liu, Y. LD-CR-SIDSCA(tan) Detection Model for the Weak Spectral Information of Maize Leaves under Copper and Lead Stresses. Spectrosc. Spect. Anal. 2019, 39, 2091–2099. [Google Scholar]
- Li, X.; Gao, P.; Gjetvaj, B.; Westcott, N.; Gruber, M.Y. Analysis of the metabolome and transcriptome of Brassica carinata seedlings after lithium chloride exposure. Plant. Sci. 2009, 177, 68–80. [Google Scholar] [CrossRef]
- Kalinowska, M.; Hawrylak-Nowak, B.; Szymanska, M. The influence of two lithium forms on the growth, L-ascorbic acid content and lithium accumulation in lettuce plants. Biol. Trace Elem. Res. 2013, 152, 251–257. [Google Scholar] [CrossRef]
- Shahzad, B.; Tanveer, M.; Hassan, W.; Shah, A.N.; Anjum, S.A.; Cheema, S.A.; Ali, I. Lithium toxicity in plants: Reasons, mechanisms and remediation possibilities-A review. Plant Physiol. Biochem. 2016, 107, 104–115. [Google Scholar] [CrossRef]
- Hayyat, M.U.; Khan, A.U.; Ali, S.; Siddiq, Z.; Sharif, F. Alleviation of lithium toxicity in sorghum (Sorghum vulgare pers.) by inoculation with lithium resistant bacteria. Appl. Ecol. Environ. Res. 2020, 18, 7989–8008. [Google Scholar] [CrossRef]
- Li, J.B.; Zhang, H.; Lv, Z.H. Genetic linkage between pegmatites and granites from Jingerquan, East Tianshan Mountains: Evidence from zircon U-Pb geochronological and Hf isotopic data. Geochinica 2020, 49, 385–403. (In Chinese) [Google Scholar]
- Yao, F.J.; Xu, X.W.; Yang, J.M.; Wu, L.N.; Geng, X.X. A technology for identifying Li-Be pegmatite using ASTER remote sensing data in granite of Gobi shallow-covered area: A case study of recognition and prediction of Li-Be pegmatite in Jingerquan, Xinjiang. Miner. Deposit. 2020, 39, 686–696. (In Chinese) [Google Scholar]
- Wang, J.J.; Cui, L.J.; Gao, W.X.; Shi, T.Z.; Chen, Y.Y.; Gao, Y. Prediction of low heavy metal concentrations in agricultural soils using visible and near-infrared reflectance spectroscopy. Geoderma 2014, 216, 1–9. [Google Scholar] [CrossRef]
- Hong, Y.; Liu, Y.; Chen, Y.; Liu, Y.; Yu, L.; Liu, Y.; Cheng, H. Application of fractional-order derivative in the quantitative estimation of soil organic matter content through visible and near-infrared spectroscopy. Geoderma 2019, 337, 758–769. [Google Scholar] [CrossRef]
- Jia, X.Y.; O’Connor, D.; Shi, Z.; Hou, D.Y. VIRS based detection in combination with machine learning for mapping soil pollution. Environ. Pollut. 2021, 268, 115845. [Google Scholar] [CrossRef]
- Wang, J.; Tiyip, T.; Ding, J.; Zhang, D.; Liu, W.; Wang, F.; Tashpolat, N. Desert soil clay content estimation using reflectance spectroscopy preprocessed by fractional derivative. PLoS ONE 2017, 12, e0184836. [Google Scholar] [CrossRef]
- Zhao, L.; Hu, Y.-M.; Zhou, W.; Liu, Z.-H.; Pan, Y.-C.; Shi, Z.; Wang, L.; Wang, G.-X. Estimation Methods for Soil Mercury Content Using Hyperspectral Remote Sensing. Sustainability. 2018, 10, 2474. [Google Scholar] [CrossRef]
- Zhou, W.; Yang, H.; Xie, L.; Li, H.; Huang, L.; Zhao, Y.; Yue, T. Hyperspectral inversion of soil heavy metals in Three-River Source Region based on random forest model. Catena 2021, 202, 105222. [Google Scholar] [CrossRef]
- Schmitt, J.M. Fractional derivative analysis of diffuse reflectance spectra. Appl. Spectrosc. 1998, 52, 840–846. [Google Scholar] [CrossRef]
- Li, C.C.; Shi, J.J.; Ma, C.Y.; Cui, Y.Q.; Wang, Y.L.; Li, Y.C. Estimation of Chlorophyll Content in Winter Wheat Based on Wavelet Transform and Fractional Differential. Trans. Chin. Soc. Agric. Mach. 2019, 52, 172–182. (In Chinese) [Google Scholar]
- Xiao, Y.; Xin, H.B.; Wang, B.; Cui, L.; Jiang, Q.G. Hyperspectral estimation of black soil organic matter content based on wavelet transform and successive projections algorithm. Remote Sens. Land Resour. 2021, 33, 33–39. (In Chinese) [Google Scholar]
- Wold, S.; Sjostrom, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemometr. Intell. Lab. 2021, 58, 109–130. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Walvoort, D.J.J.; Mcbratney, A.B.; Janik, L.J.; Skjemstad, J.O. Visible, near infrared, mid infrared or combined diffuse reflectance spectroscopy for simultaneous assessment of various soil properties. Geoderma 2006, 131, 59–75. [Google Scholar] [CrossRef]
- Vasques, G.M.; Grunwald, S.; Sickman, J.O. Comparison of multivariate methods for inferential modeling of soil carbon using visible/near-infrared spectra. Geoderma 2008, 146, 14–25. [Google Scholar] [CrossRef]
- Shi, T.Z.; Chen, Y.Y.; Liu, Y.L.; Wu, G.F. Visible and near-infrared reflectance spectroscopy—An alternative for monitoring soil contamination by heavy metals. J. Hazard. Mater. 2014, 265, 166–176. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Ding, J.; Yu, D.; Ma, X.; Zhang, Z.; Ge, X.; Teng, D.; Li, X.; Liang, J.; Lizaga, I.; et al. Capability of Sentinel-2 MSI data for monitoring and mapping of soil salinity in dry and wet seasons in the Ebinur Lake region, Xinjiang, China. Geoderma. 2019, 353, 172–187. [Google Scholar] [CrossRef]
- Yin, F.; Wu, M.M.; Liu, L.; Zhu, Y.Q.; Feng, J.L.; Yin, D.W. Predicting the abundance of copper in soil using reflectance spectroscopy and GF5 hyperspectral imagery. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102420. [Google Scholar] [CrossRef]
- Zhang, S.; Shen, Q.; Nie, C.; Huang, Y.; Wang, J.; Hu, Q.; Ding, X.; Zhou, Y.; Chen, Y. Hyperspectral inversion of heavy metal content in reclaimed soil from a mining wasteland based on different spectral transformation and modeling method. Spectrochim. Acta Part A 2019, 211, 393–400. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.H.; Gao, J.; Zha, Y. Hyperspectral sensing of heavy metals in soil and vegetation: Feasibility and challenges. ISPRS J. Photogramm. Remote Sens. 2018, 136, 73–84. [Google Scholar]
- Lao, C.; Chen, J.; Zhang, Z.; Chen, Y.; Ma, Y.; Chen, H.; Gu, X.; Ning, J.; Jin, J.; Li, X. Predicting the contents of soil salt and major water-soluble ions with fractional-order derivative spectral indices and variable selection. Comput. Electron. Agric. 2021, 182, 106031. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, Y.; Yu, L.; Liu, Y.; Liu, Y.; Zhang, Y.; Liu, Y.; Cheng, H. Combining Fractional Order Derivative and Spectral Variable Selection for Organic Matter Estimation of Homogeneous Soil Samples by VIS–NIR Spectroscopy. Remote Sens. 2018, 10, 479. [Google Scholar] [CrossRef]
- Kharintsev, S.; Salakhov, M.K. A simple method to extract spectral parameters using fractional derivative spectrometry. Spectrochim. Acta Part A 2004, 60, 2125–2133. [Google Scholar] [CrossRef] [PubMed]
- Tong, P.J.; Du, Y.P.; Zheng, K.Y.; Wu, T.; Wang, J.J. Improvement of NIR model by fractional order Savitzky–Golay derivation (FOSGD) coupled with wavelength selection. Chemometr. Intell. Lab. 2015, 143, 40–48. [Google Scholar] [CrossRef]
- Wang, T.; Wei, H.; Zhou, C.; Gu, Y.; Li, R.; Chen, H.; Ma, W. Estimating cadmium concentration in the edible part of Capsicum annuum using hyperspectral models. Environ. Monit. Assess. 2017, 189, 548. [Google Scholar] [CrossRef] [PubMed]
- Nawar, S.; Buddenbaum, H.; Hill, J.; Kozak, J.; Mouazen, A.M. Estimating the soil clay content and organic matter by means of different calibration methods of vis-NIR diffuse reflectance spectroscopy. Soil Tillage Res. 2016, 155, 510–552. [Google Scholar] [CrossRef]
- Hong, Y.S.; Chen, S.T.; Liu, Y.L.; Zhang, Y.; Yu, L.; Chen, Y.Y. Combination of fractional order derivative and memory-based learning algorithm to improve the estimation accuracy of soil organic matter by visible and near-infrared spectroscopy. Catena 2019, 174, 104–116. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, J.; Zou, M.; Liu, X.; Du, X.; Wang, Q.; Liu, Y.; Liu, Y.; Li, J. Feasibility of Using Rice Leaves Hyperspectral Data to estimate CaCl2-extractable concentrations of Heavy Metals in Agricultural Soil. Sci. Rep. 2019, 9, 16084. [Google Scholar] [CrossRef]
- Tan, K.; Ma, W.B.; Chen, L.H.; Wang, H.M.; Du, Q.; Du, P.J. Estimating the distribution trend of soil heavy metals in mining area from HyMap airborne hyperspectral imagery based on ensemble learning. J. Hazard. Mater. 2021, 401, 123288. [Google Scholar] [CrossRef]
- Cui, S.C.; Zhou, K.F.; Ding, R.F.; Zhao, J.; Du, X.S.H. Comparing the effects of different spectral transformations on the estimation of the copper content of Seriphidium terrae-albae. J. Appl. Remote Sens. 2018, 12, 036003. [Google Scholar] [CrossRef]
- Abdugheni, A.; Nija, K.; Shi, O.D.; Rukeya, S.; Bilal, I. Estimating Heavy Metal Contents in Anabasis L. Using Hyperspectral Data. J. Xinjiang Univ. 2020, 37, 309–320. (In Chinese) [Google Scholar]
- Zhang, Z.P.; Ding, J.L.; Wang, J.Z.; Ge, X.Y. Prediction of soil organic matter in northwestern China using fractional order derivative spectroscopy and modified normalized difference indices. Catena 2020, 185, 104257. [Google Scholar] [CrossRef]
- Ge, X.Y.; Ding, J.L.; Jin, X.L.; Wang, J.Z.; Chen, X.Y.; Li, X.H. Estimating Agricultural Soil Moisture Content through UAV-Based Hyperspectral Images in the Arid Region. Remote Sens. 2021, 13, 1562. [Google Scholar] [CrossRef]
- Hong, Y.; Guo, L.; Chen, S.; Linderman, M.; Mouazen, A.M.; Yu, L.; Chen, Y.; Liu, Y.; Liu, Y.; Cheng, H.; et al. Exploring the potential of airborne hyperspectral image for estimating topsoil organic carbon: Effects of fractional-order derivative and optimal band combination algorithm. Geoderma 2020, 365, 114228. [Google Scholar] [CrossRef]
- Hong, Y.; Shen, R.; Cheng, H.; Chen, Y.; Zhang, Y.; Liu, Y.; Zhou, M.; Yu, L.; Liu, Y.; Liu, Y. Estimating lead and zinc concentrations in peri-urban agricultural soils through reflectance spectroscopy: Effects of fractional-order derivative and random forest. Sci. Total Environ. 2019, 651, 1969–1982. [Google Scholar] [CrossRef]
- Shi, T.Z.; Liu, H.Z.; Chen, Y.Y.; Fei, T.; Wang, J.J.; Wu, G.F. Spectroscopic Diagnosis of Arsenic Contamination in Agricultural Soils. Sensors 2017, 17, 1036. [Google Scholar] [CrossRef] [PubMed]
- Kemper, T.; Sommer, S. Estimate of heavy metal contamination in soils after a mining accident using reflectance spectroscopy. Environ. Sci. Technol. 2002, 36, 2742–2747. [Google Scholar] [CrossRef]
- Shi, T.Z.; Liu, H.Z.; Wang, J.J.; Chen, Y.Y.; Fei, T.; Wu, G.F. Monitoring Arsenic Contamination in Agricultural Soils with Reflectance Spectroscopy of Rice Plants. Environ. Sci. Technol. 2014, 48, 6264–6272. [Google Scholar] [CrossRef]
- Shi, T.Z.; Wang, J.J.; Chen, Y.Y.; Wu, G.F. Improving the prediction of arsenic contents in agricultural soils by combining the reflectance spectroscopy of soils and rice plants. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 95–103. [Google Scholar] [CrossRef]
- Cheng, H.; Shen, R.; Chen, Y.; Wan, Q.; Shi, T.; Wang, J.; Wan, Y.; Hong, Y.; Li, X. Estimating heavy metal concentrations in suburban soils with reflectance spectroscopy. Geoderma 2019, 336, 59–67. [Google Scholar] [CrossRef]
- Wang, J.Z.; Shi, T.Z.; Yu, D.L.; Teng, D.X.; Ge, X.Y.; Zhang, Z.P. Ensemble machine-learning-based framework for estimating total nitrogen concentration in water using drone-borne hyperspectral imagery of emergent plants: A case study in an arid oasis, NW China. Environ. Pollut. 2020, 266, 115422. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.L.; Liu, X.N.; Ding, W.C.; Wu, L. Monitoring stress levels on rice with heavy metal pollution from hyperspectral reflectance data using wavelet-fractal analysis. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 246–255. [Google Scholar] [CrossRef]


| Dataset | Number | Min (mg/kg) | Max (mg/kg) | Mean (mg/kg) | SD (mg/kg) | CV (%) |
|---|---|---|---|---|---|---|
| Whole dataset | 94 | 0.84 | 22.60 | 4.94 | 4.06 | 82.19 |
| Calibration dataset | 69 | 0.86 | 22.60 | 4.86 | 3.90 | 80.25 |
| Validation dataset | 25 | 0.84 | 19.11 | 5.14 | 4.54 | 88.32 |
| Spectral Transformation Form | Number of Principal Components | Calibration Set | Validation Set | |||
|---|---|---|---|---|---|---|
| RMSEc (mg/kg) | RMSEpre (mg/kg) | RPD | ||||
| Order = 0 | 9 | 0.5897 | 2.4784 | 0.4956 | 6.2606 | 0.7258 |
| Order = 0.2 | 9 | 0.6939 | 2.1407 | 0.222 | 4.78 | 0.9506 |
| Order = 0.5 | 8 | 0.678 | 2.1955 | 0.3796 | 3.7603 | 1.2083 |
| Order = 0.8 | 8 | 0.7639 | 1.8798 | 0.4491 | 3.6313 | 1.2513 |
| Order = 1 | 6 | 0.6903 | 2.1531 | 0.6073 | 3.3951 | 1.3383 |
| Order = 1.1 | 5 | 0.6583 | 2.2616 | 0.6977 | 2.5735 | 1.7656 |
| Order = 1.4 | 5 | 0.6944 | 2.1387 | 0.6201 | 2.8603 | 1.5886 |
| Order = 1.7 | 5 | 0.7033 | 2.1073 | 0.5571 | 3.3771 | 1.3454 |
| Order = 2 | 5 | 0.6748 | 2.2064 | 0.6803 | 2.7262 | 1.6667 |
| Layers of Wavelet Transform | Number of Principal Components | Validation Set | |||
|---|---|---|---|---|---|
| RMSEpre (mg/kg) | RPD | Number of Variables | |||
| 1 | 3 | 0.38 | 3.5488 | 1.2804 | 90 |
| 2 | 9 | 0.7044 | 2.4633 | 1.8446 | 51 |
| 3 | 3 | 0.6388 | 2.8778 | 1.5789 | 32 |
| 4 | 4 | 0.556 | 3.4974 | 1.2992 | 22 |
| 5 | 8 | 0.34 | 5.5283 | 0.8219 | 17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, S.; Jiang, G.; Bai, Y. Rapid Prediction of the Lithium Content in Plants by Combining Fractional-Order Derivative Spectroscopy and Wavelet Transform Analysis. Remote Sens. 2024, 16, 3071. https://doi.org/10.3390/rs16163071
Cui S, Jiang G, Bai Y. Rapid Prediction of the Lithium Content in Plants by Combining Fractional-Order Derivative Spectroscopy and Wavelet Transform Analysis. Remote Sensing. 2024; 16(16):3071. https://doi.org/10.3390/rs16163071
Chicago/Turabian StyleCui, Shichao, Guo Jiang, and Yong Bai. 2024. "Rapid Prediction of the Lithium Content in Plants by Combining Fractional-Order Derivative Spectroscopy and Wavelet Transform Analysis" Remote Sensing 16, no. 16: 3071. https://doi.org/10.3390/rs16163071
APA StyleCui, S., Jiang, G., & Bai, Y. (2024). Rapid Prediction of the Lithium Content in Plants by Combining Fractional-Order Derivative Spectroscopy and Wavelet Transform Analysis. Remote Sensing, 16(16), 3071. https://doi.org/10.3390/rs16163071






