Optimization on the Polarization and Waveform of Radar for Better Target Detection Performance under Rainy Condition
Abstract
1. Introduction
- Assume that the TIRM is perfectly known;
- Only energy constraints are considered in the optimization process;
- Clutter is modeled as polarization-dependent but independent of the range bin.
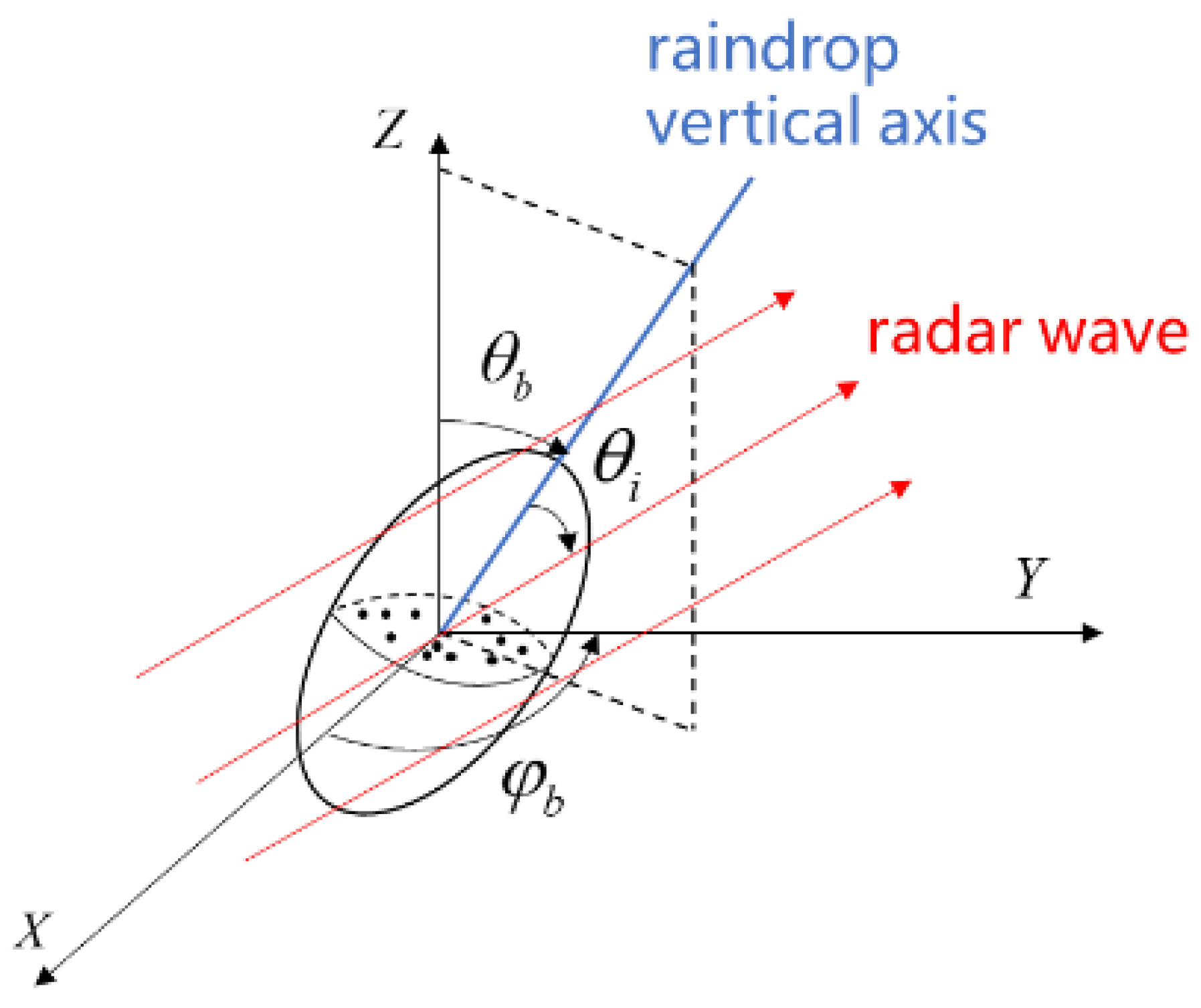
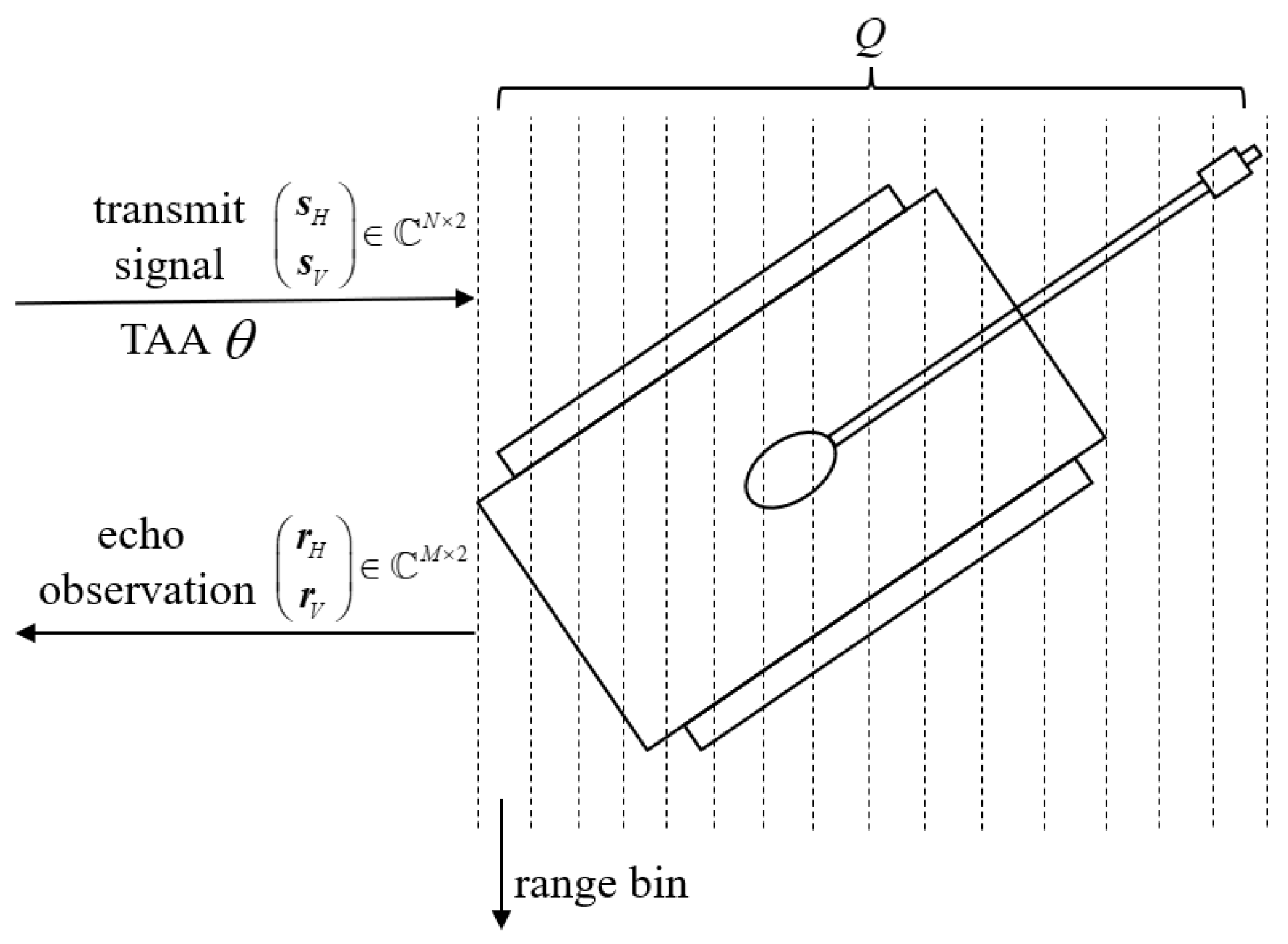
2. System Model
3. Materials and Methods
3.1. Joint Optimization of Transmit Signals and Receive Filters
- The transmit signal power constraint, which requires in general.
- the similarity constraint, which requires in order to control the correlation characteristics of the signals not to be too cluttered. Where the parameter restricts the feasible domain of similarity and is a preset waveform [32].
| Algorithm 1 Joint Transmitter/Receiver Design Under Rainy Condition. |
| Input: , , , , Output: The solution to and
|
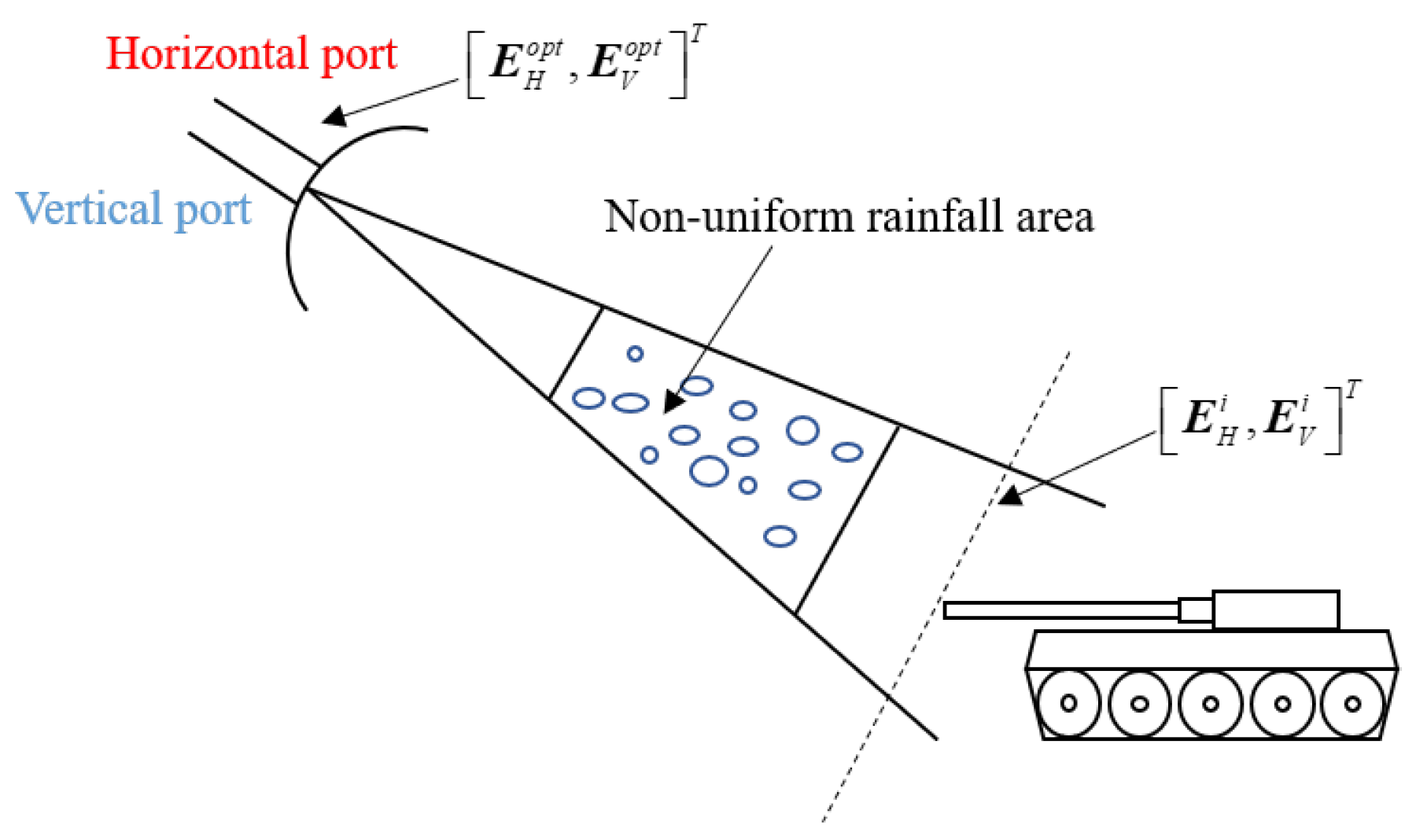
3.2. Polarization and Waveform Optimization Design Based on Fully Polarized Radar Observation Parameters
- (i)
- Finding the radar signal that optimally extracts the target information at the target.
- (ii)
- Designing the optimal radar transmit signal and receive filter based on the transmission effect to reduce the influence of the rain medium.
- (iii)
- Designing the optimal transmit signal without the information of rainfall.
4. Results
4.1. Experimental Setup Considered
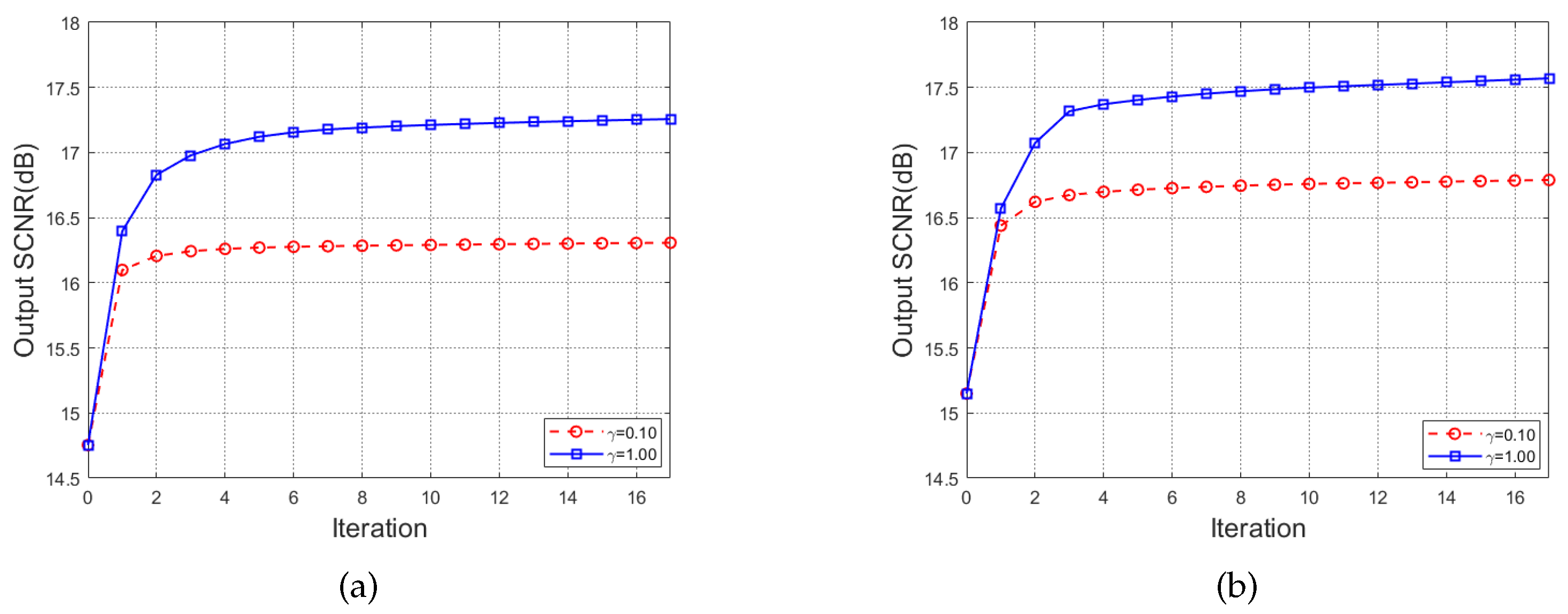
4.2. Effectiveness of the Proposed Method in Section 3.1
4.3. Effects of the Filter Bank Size in Method of Section 3.1
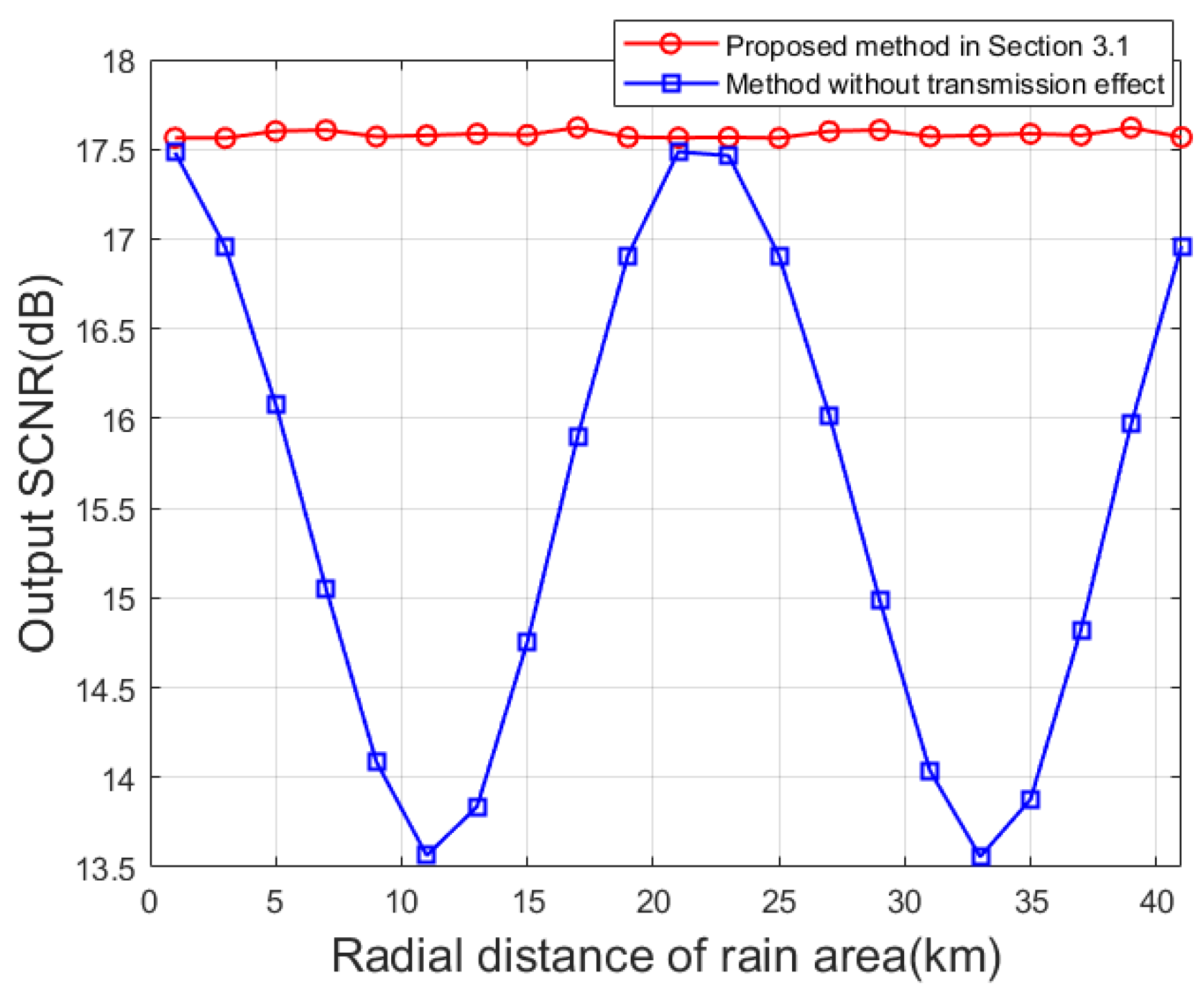
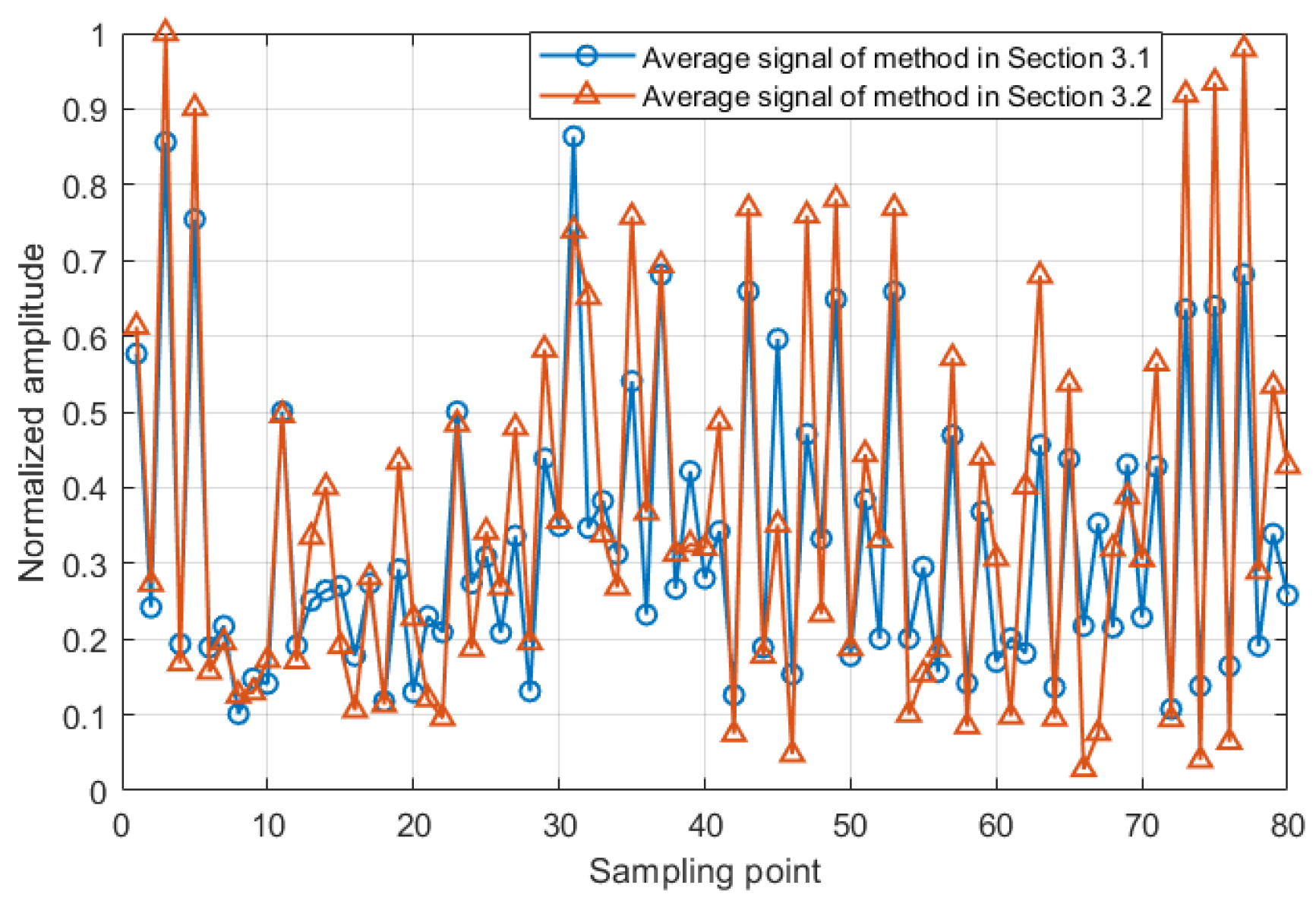
4.4. Effectiveness of the Proposed Method in Section 3.2
4.5. Detection Probability Analysis
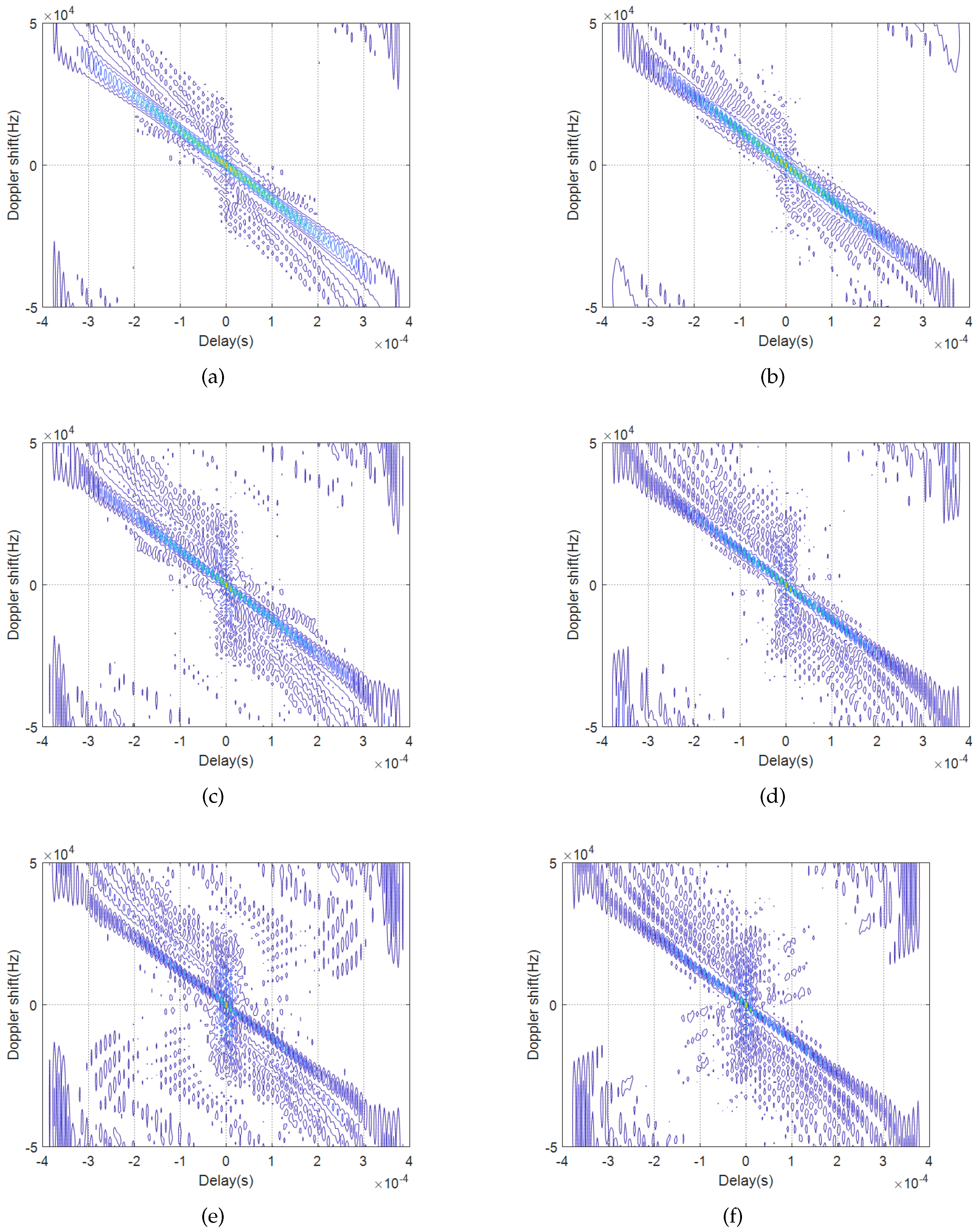
4.6. Signal Ambiguity Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Calculation of the Rain Media Transmission Matrix
References
- Lu, C.S.; Zhao, Z.W.; Wu, Z.S.; Lin, L.K.; Thiennviboon, P.; Zhang, X.; Lv, Z.F. A new rain attenuation prediction model for the earth-space links. IEEE Trans. Antennas Propag. 2018, 66, 5432–5442. [Google Scholar] [CrossRef]
- Han, C.; Bi, Y.; Duan, S.; Lu, G. Rain rate retrieval test from 25-GHz, 28-GHz, and 38-GHz millimeter-wave link measurement in Beijing. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2019, 12, 2835–2847. [Google Scholar] [CrossRef]
- Lin, D.P.; Chen, H.Y. Volume integral equation solution of extinction cross section by raindrops in the range 0.6–100 GHz. IEEE Trans. Antennas Propag. 2001, 49, 494–499. [Google Scholar]
- AIasseur, C.; Husson, L.; Pérez-Fontán, F. Simulation of rain events time series with Markov model. In Proceedings of the 2004 IEEE 15th International Symposium on Personal, Indoor and Mobile Radio Communications (IEEE Cat. No. 04TH8754), Barcelona, Spain, 5–8 September 2004; Volume 4, pp. 2801–2805. [Google Scholar]
- Zhang, W.; Tervonen, J.K.; Salonen, E.T. Backward and forward scattering by the melting layer composed of spheroidal hydrometeors at 5–100 GHz. IEEE Trans. Antennas Propag. 1996, 44, 1208–1219. [Google Scholar] [CrossRef]
- Ajewole, M.O.; Kolawole, L.B.; Ajayi, G.O. Theoretical study of the effect of different types of tropical rainfall on microwave and millimeter-wave propagation. Radio Sci. 1999, 34, 1103–1124. [Google Scholar] [CrossRef]
- Oguchi, T. Scattering from hydrometeors: A survey. Radio Sci. 1981, 16, 691–730. [Google Scholar] [CrossRef]
- Alhujaili, K.; Yu, X.; Cui, G.; Monga, V. Spectrally compatible MIMO radar beampattern design under constant modulus constraints. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4749–4766. [Google Scholar] [CrossRef]
- Alhujaili, K.; Monga, V.; Rangaswamy, M. Transmit MIMO radar beampattern design via optimization on the complex circle manifold. IEEE Trans. Signal Process. 2019, 67, 3561–3575. [Google Scholar] [CrossRef]
- Aubry, A.; De Maio, A.; Govoni, M.A.; Martino, L. On the design of multi-spectrally constrained constant modulus radar signals. IEEE Trans. Signal Process. 2020, 68, 2231–2243. [Google Scholar] [CrossRef]
- Tang, B.; Li, J. Spectrally constrained MIMO radar waveform design based on mutual information. IEEE Trans. Signal Process. 2018, 67, 821–834. [Google Scholar] [CrossRef]
- Stoica, P.; He, H.; Li, J. New algorithms for designing unimodular sequences with good correlation properties. IEEE Trans. Signal Process. 2009, 57, 1415–1425. [Google Scholar] [CrossRef]
- Wang, F.; Pang, C.; Li, Y.; Wang, X. Orthogonal Polyphase Coded Waveform Design Method for Simultaneous Fully Polarimetric Radar. J. Radars. 2017, 6, 340–348. [Google Scholar]
- Fan, W.; Liang, J.; Lu, G.; Fan, X.; So, H.C. Spectrally-agile waveform design for wideband MIMO radar transmit beampattern synthesis via majorization-ADMM. IEEE Trans. Signal Process. 2021, 69, 1563–1578. [Google Scholar] [CrossRef]
- Li, H.; Chen, S. Electromagnetic scattering characteristics and radar identification of sea corner reflectors: Advances and prospects. J. Radars. 2023, 12, 738–761. [Google Scholar]
- Chen, C.Y.; Vaidyanathan, P. MIMO radar waveform optimization with prior information of the extended target and clutter. IEEE Trans. Signal Process. 2009, 57, 3533–3544. [Google Scholar] [CrossRef]
- Garren, D.A.; Odom, A.C.; Osborn, M.K.; Goldstein, J.S.; Pillai, S.U.; Guerci, J.R. Full-polarization matched-illumination for target detection and identification. IEEE Trans. Aerosp. Electron. Syst 2002, 38, 824–837. [Google Scholar] [CrossRef]
- Goodman, N.A.; Venkata, P.R.; Neifeld, M.A. Adaptive waveform design and sequential hypothesis testing for target recognition with active sensors. IEEE J. Sel. Top. Signal Process. 2007, 1, 105–113. [Google Scholar] [CrossRef]
- Bell, M.R. Information theory and radar waveform design. IEEE Trans. Inf. Theory 1993, 39, 1578–1597. [Google Scholar] [CrossRef]
- Yang, J.; Cui, G.; Yu, X.; Kong, L. Dual-use signal design for radar and communication via ambiguity function sidelobe control. IEEE Trans. Veh. Technol. 2020, 69, 9781–9794. [Google Scholar] [CrossRef]
- Tsinos, C.G.; Arora, A.; Chatzinotas, S.; Ottersten, B. Joint transmit waveform and receive filter design for dual-function radar-communication systems. IEEE J. Sel. Top. Signal Process. 2021, 15, 1378–1392. [Google Scholar] [CrossRef]
- Beauchamp, R.M.; Tanelli, S.; Peral, E.; Chandrasekar, V. Pulse compression waveform and filter optimization for spaceborne cloud and precipitation radar. IEEE Trans. Geosci. Remote Sens. 2016, 55, 915–931. [Google Scholar] [CrossRef]
- Li, Q.; Rothwell, E.J.; Chen, K.M.; Nyquist, D.P. Scattering center analysis of radar targets using fitting scheme and genetic algorithm. IEEE Trans. Antennas Propag. 1996, 44, 198–207. [Google Scholar]
- Liu, W.; Liu, J.; Liu, T.; Chen, H.; Wang, Y. Detector Design and Performance Analysis for Target Detection in Subspace Interference. IEEE Signal Process. Lett. 2023, 30, 618–622. [Google Scholar] [CrossRef]
- Liu, W.; Liu, J.; Gao, Y.; Wang, G.; Wang, Y. Multichannel signal detection in interference and noise when signal mismatch happens. Signal Process. 2020, 166, 107268. [Google Scholar] [CrossRef]
- Liu, W.; Liu, J.; Hao, C.; Gao, Y.; Wang, Y. Multichannel adaptive signal detection: Basic theory and literature review. Sci. China Inf. Sci. 2022, 65, 121301. [Google Scholar] [CrossRef]
- Romero, R.; Goodman, N. Waveform design in signal-dependent interference and application to target recognition with multiple transmissions. IET Radar Sonar Navig. 2009, 3, 328–340. [Google Scholar] [CrossRef]
- Karbasi, S.M.; Aubry, A.; De Maio, A.; Bastani, M.H. Robust transmit code and receive filter design for extended targets in clutter. IEEE Trans. Signal Process. 2015, 63, 1965–1976. [Google Scholar] [CrossRef]
- Wang, F.; Xia, X.G.; Pang, C.; Cheng, X.; Li, Y.; Wang, X. Joint design methods of unimodular sequences and receiving filters with good correlation properties and Doppler tolerance. IEEE Trans. Geosci. Remote Sens. 2022, 61, 1–14. [Google Scholar] [CrossRef]
- Rabaste, O.; Savy, L. Mismatched filter optimization for radar applications using quadratically constrained quadratic programs. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 3107–3122. [Google Scholar] [CrossRef]
- Qian, J.; Venturino, L.; Lops, M.; Wang, X. Radar and communication spectral coexistence in range-dependent interference. IEEE Trans. Signal Process. 2021, 69, 5891–5906. [Google Scholar] [CrossRef]
- Cheng, X.; Aubry, A.; Ciuonzo, D.; De Maio, A.; Wang, X. Robust waveform and filter bank design of polarimetric radar. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 370–384. [Google Scholar] [CrossRef]
- Baden, J.M.; O’Donnell, B.; Schmieder, L. Multiobjective sequence design via gradient descent methods. IEEE Trans. Aerosp. Electron. Syst. 2017, 54, 1237–1252. [Google Scholar] [CrossRef]
- Wu, L.; Alaee-Kerahroodi, M.; Shankar, B.M. Improving pulse-compression weather radar via the joint design of subpulses and extended mismatch filter. In Proceedings of the IGARSS 2022–2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 469–472. [Google Scholar]
- Kumar, M.; Chandrasekar, V. Intrapulse polyphase coding system for second trip suppression in a weather radar. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3841–3853. [Google Scholar] [CrossRef]
- Aubry, A.; De Maio, A.; Jiang, B.; Zhang, S. Ambiguity function shaping for cognitive radar via complex quartic optimization. IEEE Trans. Signal Process. 2013, 61, 5603–5619. [Google Scholar] [CrossRef]
- Novak, L.M.; Sechtin, M.B.; Cardullo, M.J. Studies of target detection algorithms that use polarimetric radar data. IEEE Trans. Aerosp. Electron. Syst. 1989, 25, 150–165. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P.; Wang, Z. On robust Capon beamforming and diagonal loading. IEEE Trans. Signal Process. 2003, 51, 1702–1715. [Google Scholar] [CrossRef]
- Barros, A.I.; Frenk, J.; Schaible, S.; Zhang, S. A new algorithm for generalized fractional programs. Math. Program. 1996, 72, 147–175. [Google Scholar] [CrossRef][Green Version]
- GTRI Public Dataset. Sensor Data Management System. 2014. Available online: https://www.sdms.afrl.af.mil/index.php?collection=gtri (accessed on 6 April 2024).
- Ben-Tal, A.; Nemirovski, A. Lectures on Modern Convex Optimization; Spring Semester; 2012 ed.; Department ISYE, Georgia Institute of Technology: Atlanta, GA, USA, 2012; pp. 335–375. [Google Scholar]
- Peng, Y.; Li, J.; Yin, J.; Chan, P.W.; Kong, W.; Wang, X. Retrieval of the Characteristic Size of Raindrops for Wind Sensing Based on Dual-Polarization Radar. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9974–9986. [Google Scholar] [CrossRef]
- Tao, M.; Zhou, F.; Liu, Y.; Zhang, Z. Tensorial Independent Component Analysis-Based Feature Extraction for Polarimetric SAR Data Classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2481–2495. [Google Scholar] [CrossRef]
- Oguchi, T. Electromagnetic wave propagation and scattering in rain and other hydrometeors. Proc. IEEE Proc. 1983, 71, 1029–1078. [Google Scholar] [CrossRef]
- De Wolf, D.; Russchenberg, H.; Ligthart, L. Modelling of particle distribution in the melting layer. In Proceedings of the IEE Proceedings H-Microwaves, Antennas and Propagation; IET: London, UK, 1990; Volume 137, pp. 389–395. [Google Scholar]
- Liebe, H.J.; Hufford, G.A.; Manabe, T. A model for the complex permittivity of water at frequencies below 1 THz. Int. J. Infrared Milli Waves. 1991, 12, 659–675. [Google Scholar] [CrossRef]
- Willis, P.T. Functional fits to some observed drop size distributions and parameterization of rain. J. Atmos. Sci. 1984, 41, 1648–1661. [Google Scholar] [CrossRef]






| Parameter | Content |
|---|---|
| Operating system | Windows10 |
| CPU type | i7-12700 H |
| GPU type | RTX 3060 |
| RAM | 16 GB |
| MATLAB | 2021b |
| Parameter | Value |
|---|---|
| Temperature | |
| Longitudinal distance of rainy area | 1 km |
| Radar operating frequency | 10 GHz |
| Radar wave incidence angle | |
| Raindrop axial inclination and | , |
| Normalized intercept parameter | 3000 |
| Raindrop shape parameter | 11.5 |
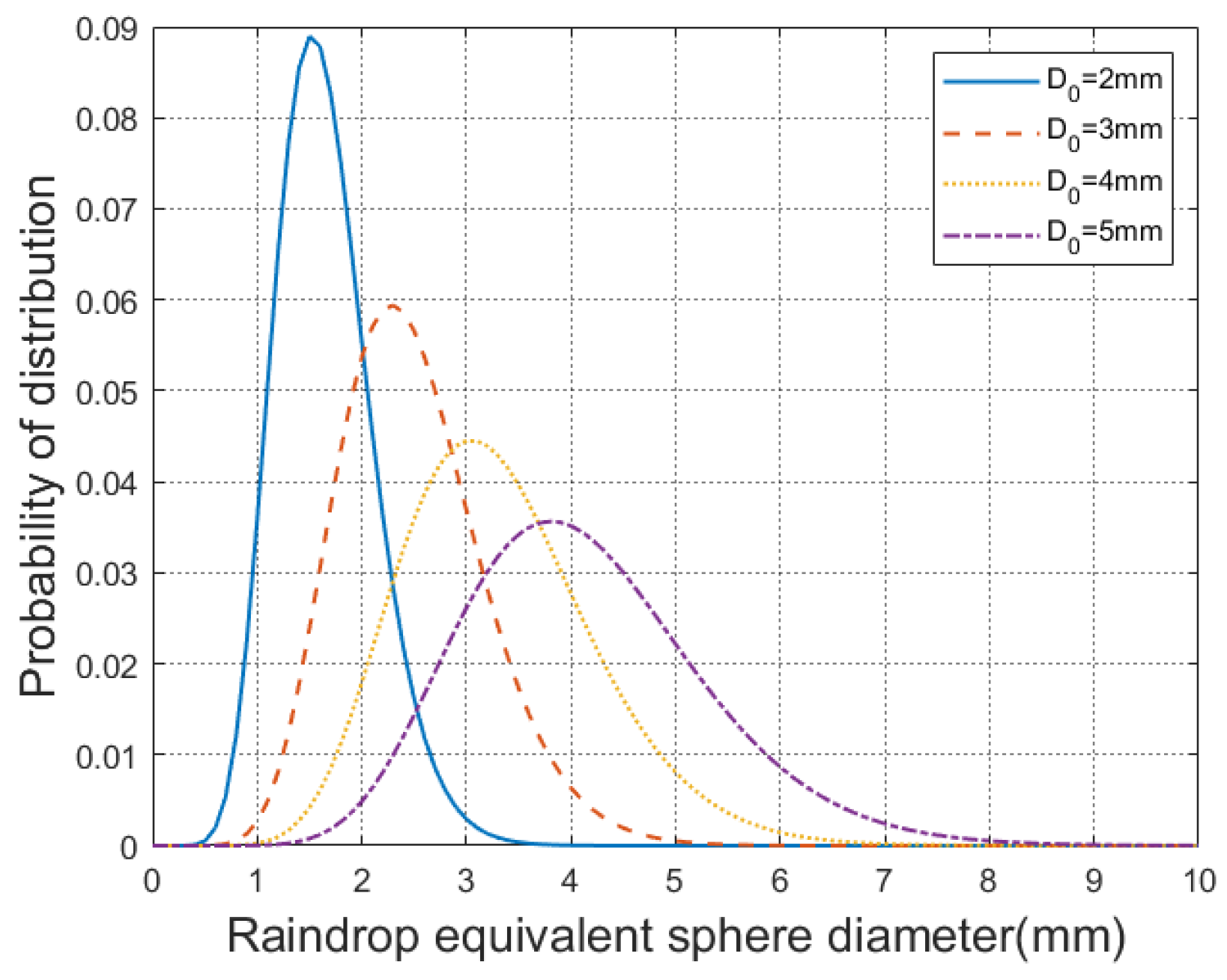
| Median diameter | (2, 3, 4, 5) mm |
| Axial ratio of raindrop particles | 1.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Cheng, X.; Ju, X.; Peng, Y.; Hu, J.; Li, J. Optimization on the Polarization and Waveform of Radar for Better Target Detection Performance under Rainy Condition. Remote Sens. 2024, 16, 2557. https://doi.org/10.3390/rs16142557
Li X, Cheng X, Ju X, Peng Y, Hu J, Li J. Optimization on the Polarization and Waveform of Radar for Better Target Detection Performance under Rainy Condition. Remote Sensing. 2024; 16(14):2557. https://doi.org/10.3390/rs16142557
Chicago/Turabian StyleLi, Xinda, Xu Cheng, Xinjie Ju, Yunli Peng, Jinzhu Hu, and Jianbing Li. 2024. "Optimization on the Polarization and Waveform of Radar for Better Target Detection Performance under Rainy Condition" Remote Sensing 16, no. 14: 2557. https://doi.org/10.3390/rs16142557
APA StyleLi, X., Cheng, X., Ju, X., Peng, Y., Hu, J., & Li, J. (2024). Optimization on the Polarization and Waveform of Radar for Better Target Detection Performance under Rainy Condition. Remote Sensing, 16(14), 2557. https://doi.org/10.3390/rs16142557








