Enhancement of Comparative Assessment Approaches for Synthetic Aperture Radar (SAR) Vegetation Indices for Crop Monitoring and Identification—Khabarovsk Territory (Russia) Case Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
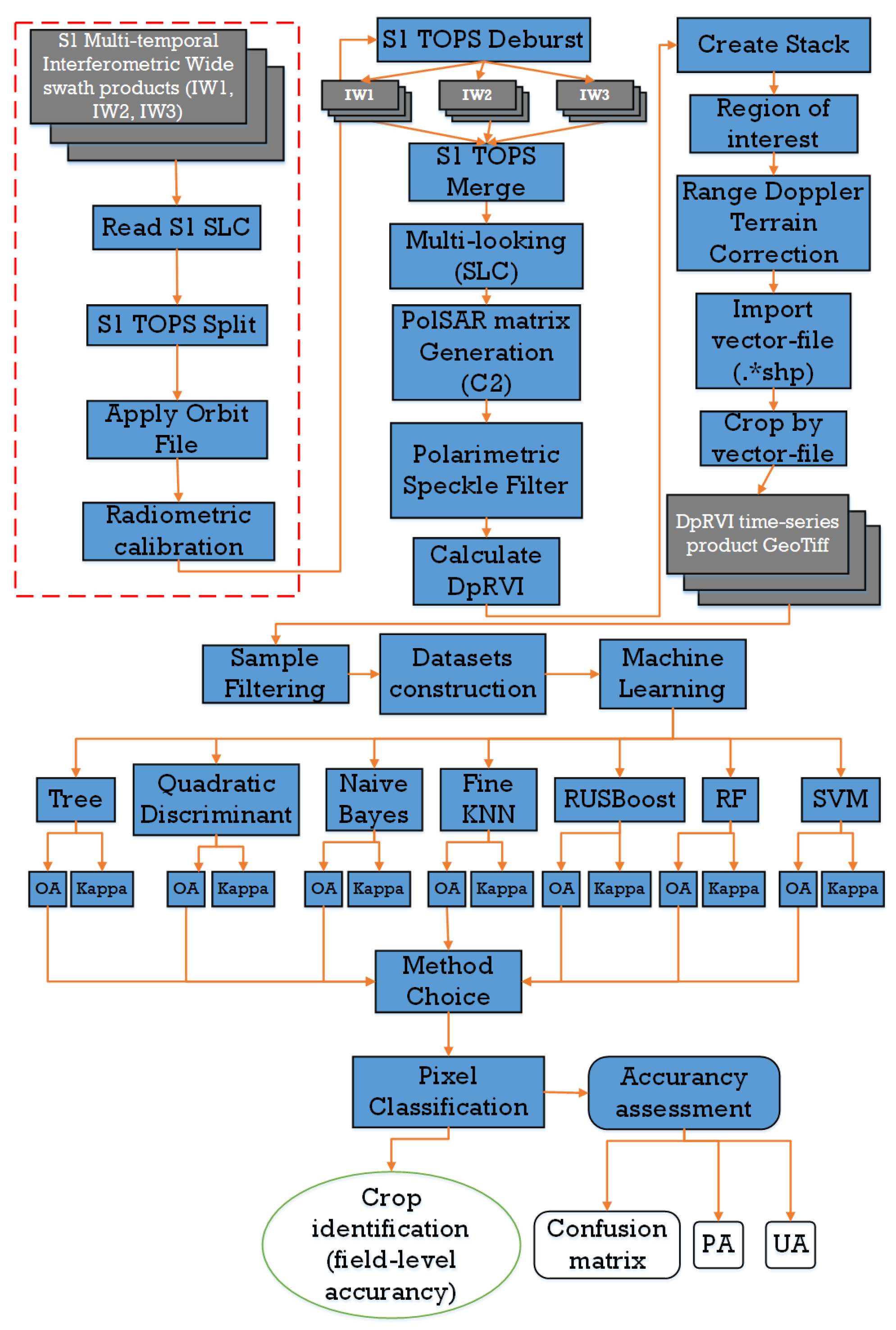
2.2. Data Acquisition and Processing
2.3. Generation of the DpRVI Time-Series Product
2.4. NDVI Time-Series
2.5. Estimation of SAR Time Series
2.6. Sample Filtering
2.7. Construction of the Training and Test Datasets
2.8. Crop Classification Methods
2.9. Accuracy Assessment of the Classification Results
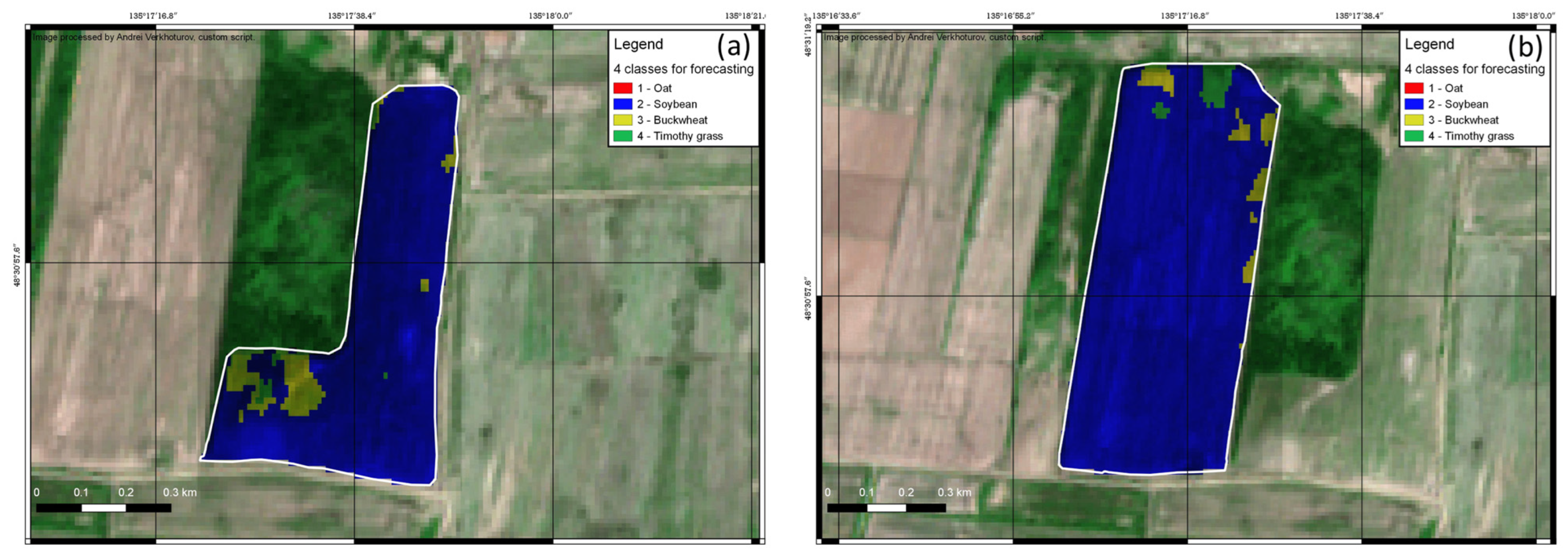
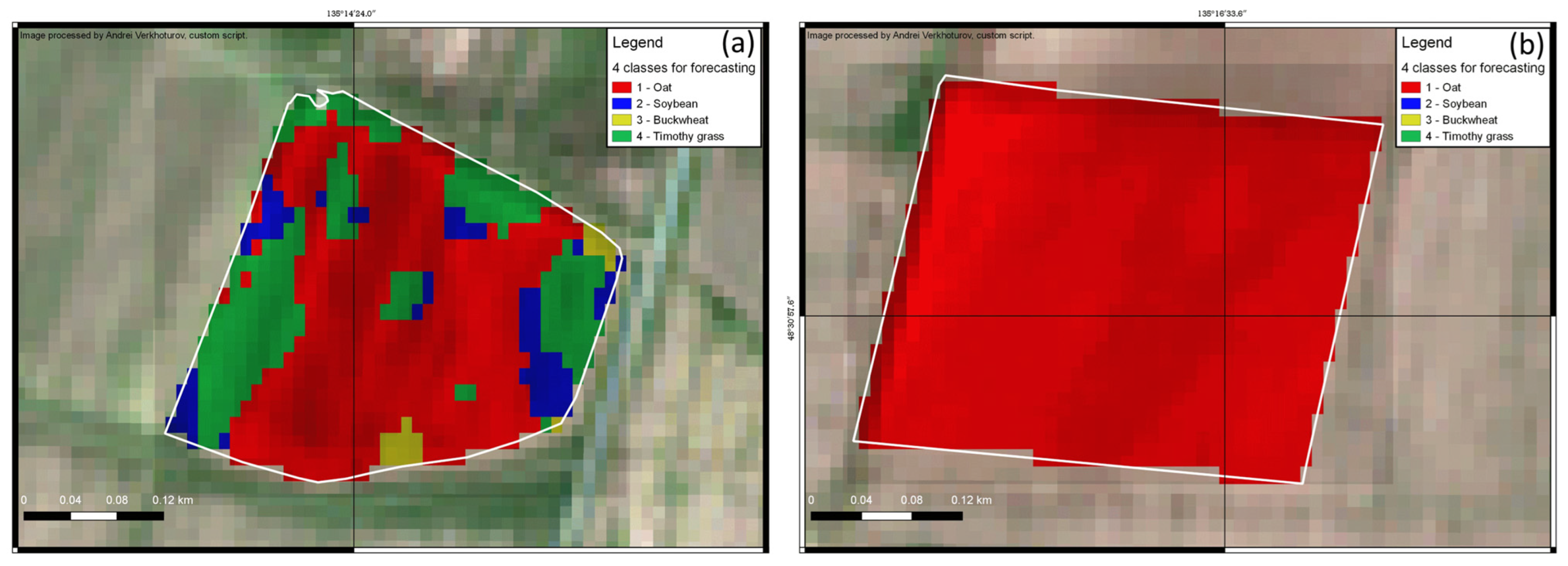
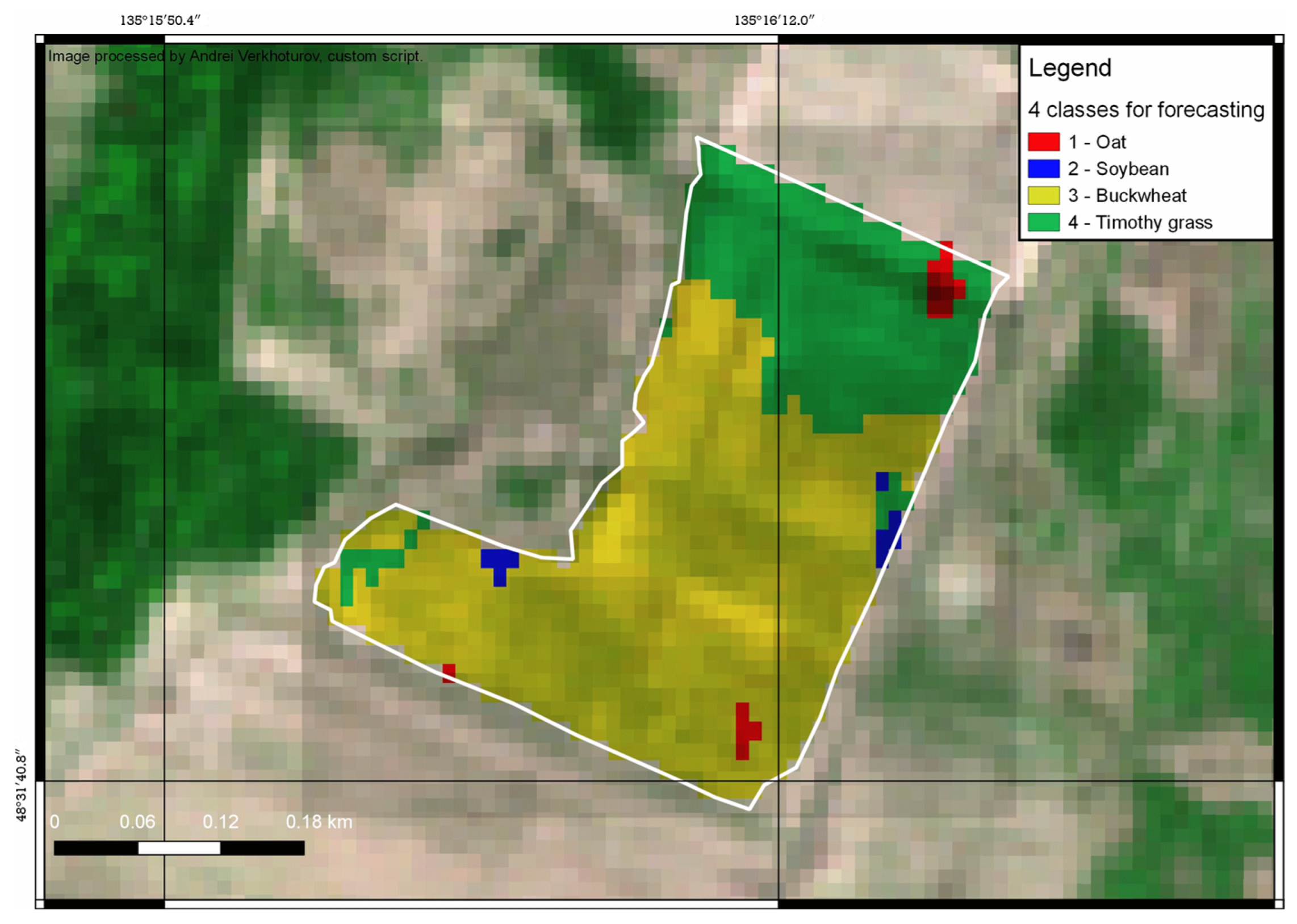
2.10. Crop Identification at the Field Level
3. Results
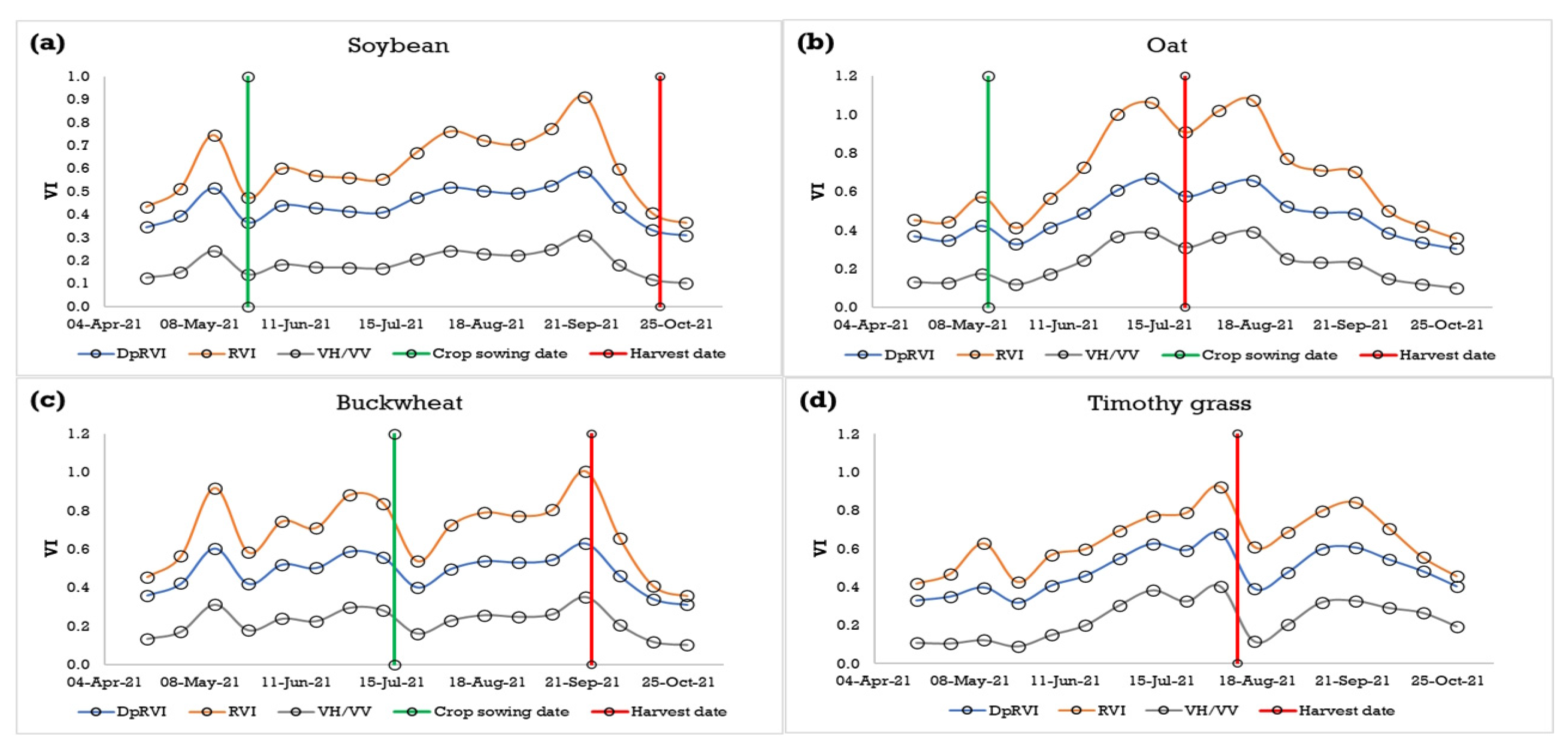
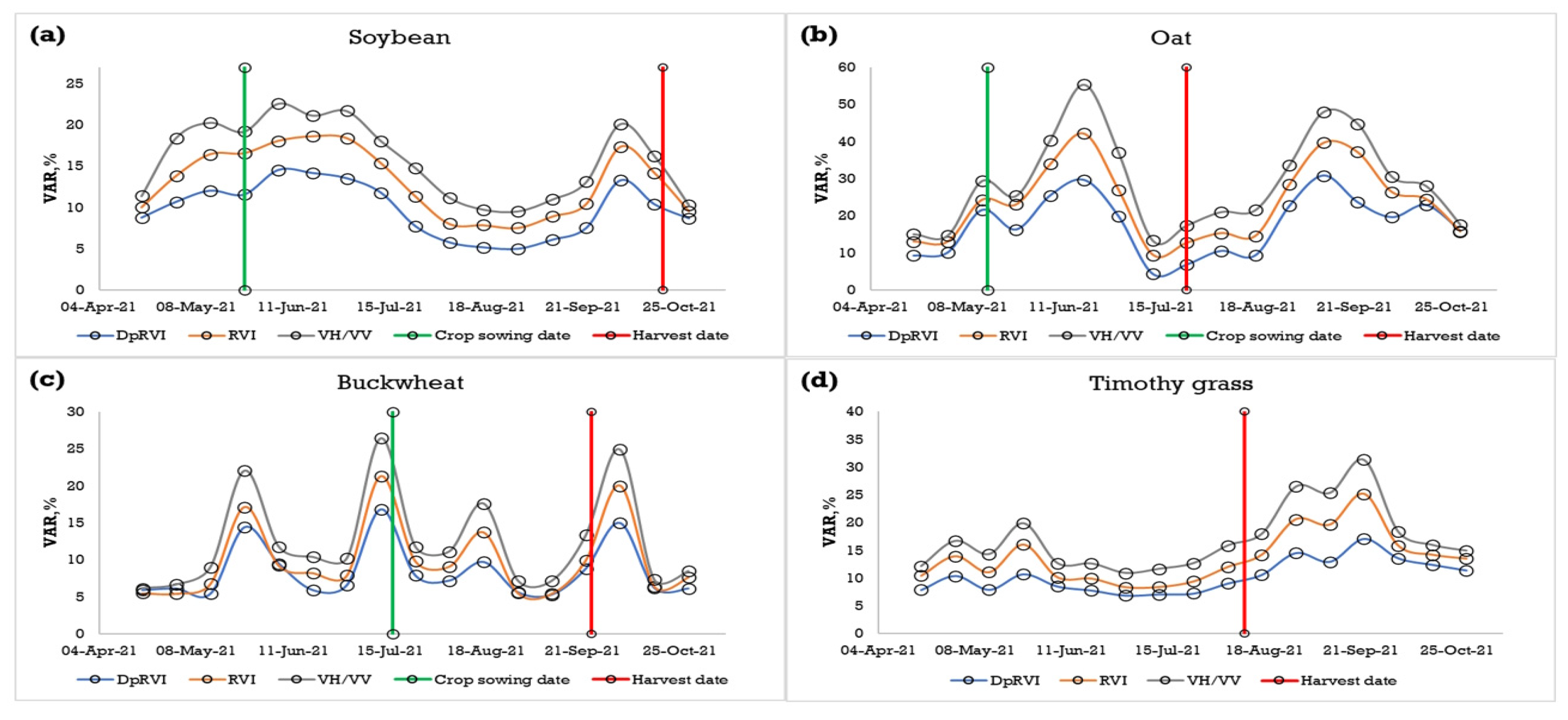
3.1. Comparative Analysis of SAR Indices
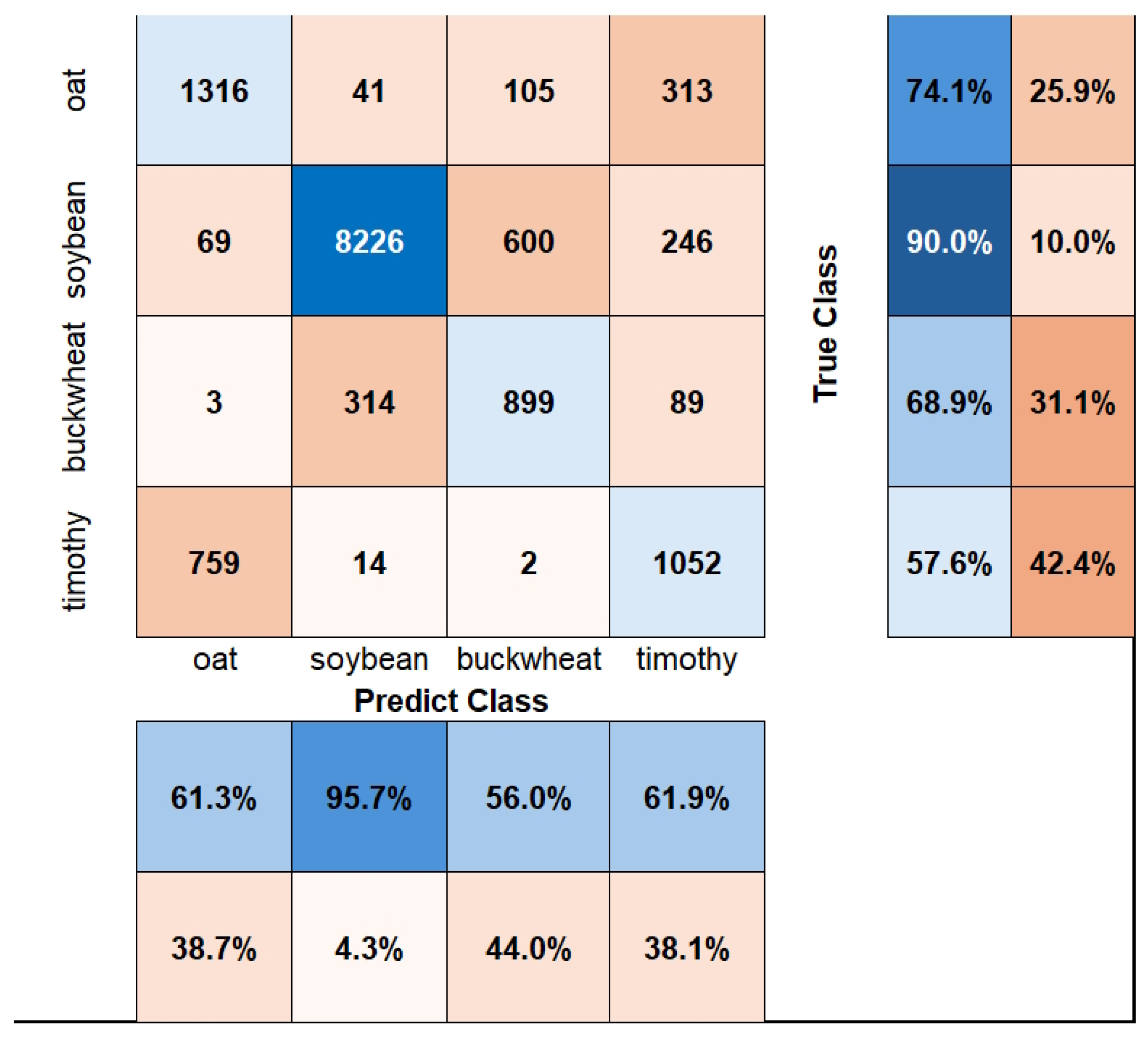
3.2. Accuracy Estimation for ML Methods
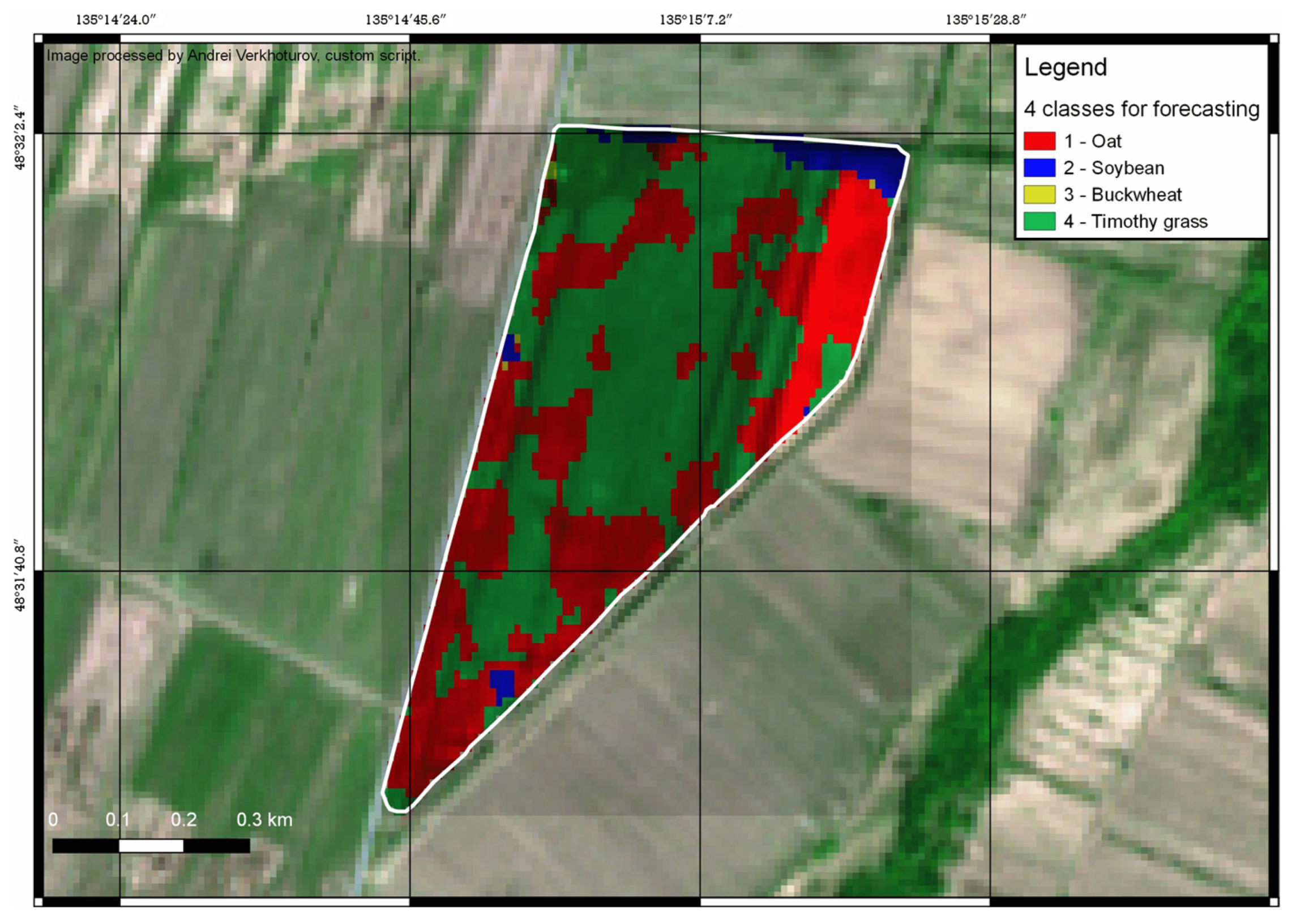
3.3. Crop Identification
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gumma, M.K.; Kadiyala, M.D.M.; Panjala, P.; Ray, S.S.; Radha, A.V.; Dubey, S.K.; Smith, A.P.; Das, R.; Whitbread, A.M. Assimilation of Remote Sensing Data into Crop Growth Model for Yield Estimation: A Case Study from India. J. Indian Soc. Remote Sens. 2021, 50, 257–270. [Google Scholar] [CrossRef]
- Pasha, S.V.; Behera, M.D.; Mahawar, S.K.; Barik, S.K.; Joshi, S.R. Assessment of shifting cultivation fallows in Northeastern India using Landsat imageries. Trop. Ecol. 2020, 61, 65–75. [Google Scholar] [CrossRef]
- Zhang, H.; Kang, J.; Xu, X.; Zhang, L. Accessing the temporal and spectral features in crop type mapping using multi-temporal Sentinel-2 imagery: A case study of Yi’an County, Heilongjiang province, China. Comput. Electron. Agric. 2020, 176, 105618. [Google Scholar] [CrossRef]
- Hao, P.; Tang, H.; Chen, Z.; Meng, Q.; Kang, Y. Early-season crop type mapping using 30-m reference time series. J. Integr. Agric. 2020, 19, 1897–1911. [Google Scholar]
- Chen, Y.; Lu, D.; Moran, E.; Batistella, M.; Dutra, L.V.; Sanches, I.D.; da Silva, R.F.B.; Huang, J.; Luiz, A.J.B. Mapping croplands, cropping patterns, and crop types using MODIS time-series data. Int. J. Appl. Earth Obs. Geoinf. 2018, 69, 133–147. [Google Scholar] [CrossRef]
- Bellón, B.; Bégué, A.; Lo Seen, D.; Lebourgeois, V.; Evangelista, B.A.; Simões, M.; Ferraz, R.P.D. Improved regional-scale Brazilian cropping systems’ mapping based on a semi-automatic object-based clustering approach. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 127–138. [Google Scholar] [CrossRef]
- Griffiths, P.; Nendel, C.; Hostert, P. Intra-annual reflectance composites from Sentinel-2 and Landsat for national-scale crop and land cover mapping. Remote Sens. Environ. 2019, 220, 135–151. [Google Scholar] [CrossRef]
- Boiarskii, B.; Hasegawa, H.; Muratov, A.; Sudeykin, V. Application of UAV-Derived Digital Elevation Model in Agricultural Field to Determine Waterlogged Soil Areas in Amur Region, Russia. Int. J. Eng. Adv. Technol. 2019, 8, 520–523. [Google Scholar]
- Su, Z.; Wang, Y.; Xu, Q.; Gao, R.; Kong, Q. LodgeNet: Improved rice lodging recognition using semantic segmentation of UAV high-resolution remote sensing images. Comput. Electron. Agric. 2022, 196, e106873. [Google Scholar] [CrossRef]
- Wang, F.; Yi, Q.; Hu, J.; Xie, L.; Yao, X.; Xu, T.; Zheng, J. Combining spectral and textural information in UAV hyperspectral images to estimate rice grain yield. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102397. [Google Scholar] [CrossRef]
- Pandey, A.; Jain, K. An intelligent system for crop identification and classification from UAV images using conjugated dense convolutional neural network. Comput. Electron. Agric. 2022, 192, e106543. [Google Scholar] [CrossRef]
- Blaes, X.; Defourny, P.; Wegmuller, U.; Della Vecchia, A.; Guerriero, L.; Ferrazzoli, P. C-band polarimetric indexes for maize monitoring based on a validated radiative transfer model. IEEE Trans. Geosci. Remote Sens. 2006, 44, 791–800. [Google Scholar] [CrossRef]
- McNairn, H.; Champagne, C.; Shang, J.; Holmstrom, D.; Reichert, G. Integration of Optical and Synthetic Aperture Radar (SAR) Imagery for Delivering Operational Annual Crop Inventories. ISPRS J. Photogramm. Remote Sens. 2009, 64, 434–449. [Google Scholar] [CrossRef]
- Inglada, J.; Vincent, A.; Arias, M.; Marais-Sicre, C. Improved Early Crop Type Identification by Joint Use of High Temporal Resolution SAR And Optical Image Time Series. Remote Sens. 2016, 8, 362. [Google Scholar] [CrossRef]
- Larranaga, A.; Alvarez-Mozos, J.; Albizua, L. Crop Classification in Rain-fed and Irrigated Agricultural Areas Using Landsat TM and ALOS/PALSAR Data. Can. J. Remote Sens. 2011, 37, 157–170. [Google Scholar] [CrossRef]
- Robertson, L.D.; Davidson, A.M.; McNairn, H.; Hosseini, M.; Mitchell, S.; de Abelleyra, D.; Verón, S.; le Maire, G.; Plannells, M.; Valero, S.; et al. C-band synthetic aperture radar (SAR) imagery for the classification of diverse cropping systems. Int. J. Remote Sens. 2020, 41, 9628–9649. [Google Scholar] [CrossRef]
- Skakun, S.; Kussul, N.; Shelestov, A.Y.; Lavreniuk, M.; Kussul, O. Efficiency Assessment of Multitemporal C-Band Radarsat-2 Intensity and Landsat-8 Surface Reflectance Satellite Imagery for Crop Classification in Ukraine. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3712–3719. [Google Scholar] [CrossRef]
- van Tricht, K.; Gobin, A.; Gilliams, S.; Piccrad, I. Synergistic Use of Radar Sentinel-1 and Optical Sentinel-2 Imagery for Crop Mapping: A Case Study for Belgium. Remote Sens. 2018, 10, 1642. [Google Scholar] [CrossRef]
- Wozniak, E.; Rybicki, M.; Kofman, W.; Aleksandrowicz, S.; Wojtkowski, C.; Lewiński, S.; Bojanowski, J.; Musiał, J.; Milewski, T.; Slesiński, P.; et al. Multi-temporal phenological indices derived from time series Sentinel-1 images to country-wide crop classification. Int. J. Appl. Earth Obs. Geoinf. 2022, 107, 102683. [Google Scholar] [CrossRef]
- Mercier, A.; Betbeder, J.; Baudry, V.; Le Roux, V.; Spicher, F.; Lacoux, J.; Roger, D.; Hubert-Moy, L. Evaluation of Sentinel-1 & 2 time series for predicting wheat and rapeseed phenological stages. ISPRS J. Photogramm. Remote Sens. 2020, 163, 231–256. [Google Scholar]
- Mengmeng, L.; Bijker, W. Potential of Multi-Temporal Sentinel-1A Dual Polarization SAR Images for Vegetable Classification in Indonesia. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 3820–3823. [Google Scholar]
- Harfenmeister, K.; Itzerott, S.; Weltzien, C.; Spengler, D. Detecting Phenological Development of Winter Wheat and Winter Barley Using Time Series of Sentinel-1 and Sentinel-2. Remote Sens. 2021, 13, 5036. [Google Scholar] [CrossRef]
- Löw, J.; Ullmann, T.; Conrad, C. The Impact of Phenological Developments on Interferometric and Polarimetric Crop Signatures Derived from Sentinel-1: Examples from the DEMMIN Study Site (Germany). Remote Sens. 2021, 13, 2951. [Google Scholar] [CrossRef]
- Gururaj, P.; Umesh, P.; Shetty, A. Assessment of spatial variation of soil moisture during maize growth cycle using SAR observations. In Remote Sensing for Agriculture, Ecosystems, and Hydrology XXI; SPIE: Strasbourg, France, 2019; Volume 11149, p. 8. [Google Scholar]
- Nasirzadehdizaji, R.; Balik Sanli, F.; Abdikan, S.; Cakir, Z.; Sekertekin, A.; Ustuner, M. Sensitivity analysis of multi-temporal Sentinel-1 SAR parameters to crop height and canopy coverage. Appl. Sci. 2019, 9, 655. [Google Scholar] [CrossRef]
- Periasamy, S. Significance of dual polarimetric synthetic aperture radar in biomass retrieval: An attempt on Sentinel-1. Remote Sens. Environ. 2018, 217, 537–549. [Google Scholar] [CrossRef]
- Mandal, D.; Ratha, D.; Bhattacharya, A.; Kumar, V.; McNairn, H.; Rao, Y.S.; Flery, A.C. A Radar Vegetation Index for Crop Monitoring Using Compact Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6321–6335. [Google Scholar] [CrossRef]
- Ratha, D.; Mandal, D.; Kumar, V.; Mcnairn, H.; Bhattacharya, A.; Frery, A.C. A Generalized Volume Scattering Model-Based Vegetation Index from Polarimetric SAR Data. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1791–1795. [Google Scholar] [CrossRef]
- Jiao, X.; McNairn, H.; Yekkehkhany, B.; Robertson, L.D.; Ihuoma, S. Integrating Sentinel-1 SAR and Sentinel-2 optical imagery with a crop structure dynamics model to track crop condition. Int. J. Remote Sens. 2022, 43, 6509–6537. [Google Scholar] [CrossRef]
- Mandal, D.; Kumar, V.; Ratha, D.; Dey, S.; Bhattacharya, A.; Lopez-Sanchez, J.M.; McNairn, H.; Rao, Y.S. Dual polarimetric radar vegetation index for crop growth monitoring using Sentinel-1 SAR data. Remote Sens. Environ. 2020, 247, e111954. [Google Scholar] [CrossRef]
- Stepanov, A.; Dubrovin, K.; Sorokin, A.; Aseeva, T. Predicting Soybean Yield at the Regional Scale Using Remote Sensing and Climatic Data. Remote Sens. 2020, 12, 1936. [Google Scholar] [CrossRef]
- Lee, J.S.; Pottier, E. Polarimetric SAR Radar Imaging: From Basic to Applications; CRC Press: Boca Raton, FL, USA, 2009; p. 438. [Google Scholar]
- Barakat, R. Degree of polarization and the principal idempotents of the coherency matrix. Opt. Commun. 1977, 23, 147–150. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Prudente, V.H.R.; Skakun, S.; Oldoni, L.V.; Xaud, H.A.M.; Xaud, M.R.; Adami, M.; Sanches, I.D. Multisensor approach to land use and land cover mapping in Brazilian Amazon. ISPRS J. Photogramm. Remote Sens. 2022, 189, 95–109. [Google Scholar] [CrossRef]
- Tufail, R.; Ahmad, A.; Javed, M.A.; Ahmad, S.R. A machine learning approach for accurate crop type mapping using combined SAR and optical time series data. Adv. Space Res. 2022, 69, 331–346. [Google Scholar] [CrossRef]
- Ghojogh, B.; Crowley, M. Linear and Quadratic Discriminant Analysis: Tutorial. arXiv 2019, arXiv:1906.02590. [Google Scholar]
- Choubin, B.; Moradi, E.; Golshan, M.; Adamowski, J.; Sajedi-Hosseini, F.; Mosavi, A. An ensemble prediction of flood susceptibility using multivariate discriminant analysis, classification and regression trees, and support vector machines. Sci. Total Environ. 2019, 651, 2087–2096. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H. The Optimality of Naive Bayes. In Proceedings of the Seventeenth International Florida Artificial Intelligence Research Society Conference; FLAIRS: Miami Beach, FL, USA, 2004. [Google Scholar]
- Castro, W.; De-la-Torre, M.; Avila-George, H.; Torres-Jimenez, J.; Guivin, A.; Acevedo-Juárez, B. Amazonian cacao-clone nibs discrimination using NIR spectroscopy coupled to naïve Bayes classifier and a new waveband selection approach. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2022, 270, 120815. [Google Scholar] [CrossRef] [PubMed]
- Hechenbichler, K.; Schliep, K. Weighted k-Nearest-Neighbor Techniques and Ordinal Classification. Master’s Thesis, Massey University, Palmerston North, New Zealand, 2004. [Google Scholar] [CrossRef]
- Ohmann, J.L.; Gregory, M.J.; Roberts, H.M.; Cohen, W.B.; Kennedy, R.E.; Yang, Z. Mapping change of older forest with nearest-neighbor imputation and Landsat time-series. For. Ecol. Manag. 2012, 272, 13–25. [Google Scholar] [CrossRef]
- Wilson, B.T.; Lister, A.J.; Riemann, R.I. A nearest-neighbor imputation approach to mapping tree species over large areas using forest inventory plots and moderate resolution raster data. For. Ecol. Manag. 2012, 271, 182–198. [Google Scholar] [CrossRef]
- Seiffert, C.; Khoshgoftaar, T.; Van Hulse, J.; Napolitano, A. RUSBoost: Improving Classification Performance when Training Data is Skewed. In Proceedings of the 19th IEEE International Conference on Pattern Recognition, Tampa, FL, USA, 8–11 December 2008. [Google Scholar]
- Piiroinen, R.; Heiskanen, J.; Mottus, M.; Pellikka, P. Classification of crops across heterogeneous agricultural landscape in Kenya using AisaEAGLE imaging spectroscopy data. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 1–8. [Google Scholar] [CrossRef]
- Ben-Hur, A.; Weston, J. A User’s Guide to Support Vector Machines; Data Mining Techniques for the Life Sciences; Springer: Berlin/Heidelberg, Germany, 2010; pp. 223–239. [Google Scholar]
- Asgarian, A.; Soffianian, A.; Pourmanafi, S. Crop type mapping in a highly fragmented and heterogeneous agricultural landscape: A case of central Iran using multi-temporal Landsat 8 imagery. Comput. Electron. Agric. 2016, 127, 531–540. [Google Scholar] [CrossRef]
- Ouzemou, J.-E.; El Harti, A.; Lhissou, R.; El Moujahid, A.; Bouch, N.; El Ouazzani, R.; Bachaoui, E.M.; El Ghmari, A. Crop type mapping from pansharpened Landsat 8 NDVI data: A case of a highly fragmented and intensive agricultural system. Remote Sens. Appl. Soc. Environ. 2018, 11, 94–103. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Blickensdörfer, L.; Schwieder, M.; Pflugmacher, D.; Nendel, C.; Erasmi, S.; Hostert, P. Mapping of crop types and crop sequences with combined time series of Sentinel-1, Sentinel-2 and Landsat 8 data for Germany. Remote Sens. Environ. 2022, 269, e112831. [Google Scholar] [CrossRef]
- Tran, K.H.; Zhang, H.K.; McMaine, J.T.; Zhang, X.; Luo, D. 10 m crop type mapping using Sentinel-2 reflectance and 30 m cropland data layer product. Int. J. Appl. Earth Obs. Geoinf. 2022, 107, 102692. [Google Scholar] [CrossRef]
- Bishop, Y.M.; Fienberg, S.E.; Holland, P.W. Discrete Multivariate Analysis: Theory and Practice; Springer: New York, NY, USA, 1975; p. 568. [Google Scholar]
- Konduri, V.S.; Kumar, J.; Hargrove, W.W.; Hoffman, F.M.; Ganguly, A.R. Mapping crops within the growing season across the United States. Remote Sens. Environ. 2020, 251, e112048. [Google Scholar] [CrossRef]
- Dietterich, T.G. Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithms. Neural. Comput. 1998, 10, 1895–1923. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Patel, N.R.; Danodia, A. Deriving Phenological Metrics from Landsat-OLI for Sugarcane Crop Type Mapping: A Case Study in North India. J. Indian Soc. Remote Sens. 2022, 50, 1021–1030. [Google Scholar] [CrossRef]
- Arias, M.; Campo-Bescós, M.Á.; Álvarez-Mozos, J. Crop Classification Based on Temporal Signatures of Sentinel-1 Observations over Navarre Province, Spain. Remote Sens. 2020, 12, 278. [Google Scholar] [CrossRef]

| Oat | Soybean | Buckwheat | Timothy Grass | Total | |
|---|---|---|---|---|---|
| Fields | 9 | 18 | 12 | 4 | 43 |
| Area, ha | 181.4 | 460.8 | 243.1 | 124.5 | 1009.8 |
| Crop | W | p-Value |
|---|---|---|
| Oat | 0.91885 | 0.24 * |
| Soybean | 0.93707 | 0.42 * |
| Buckwheat | 0.88407 | 0.08 * |
| Timothy grass | 0.90323 | 0.15 * |
| Dataset | Metric | Oat | Soybean | Buckwheat | Timothy Grass | Total |
|---|---|---|---|---|---|---|
| Training | Number | 9380 | 16,459 | 8783 | 4906 | 39,528 |
| Share, % | 24 | 42 | 22 | 12 | 100 | |
| Test | Number | 1775 | 9141 | 1305 | 1827 | 14,048 |
| Share, % | 13 | 65 | 9 | 13 | 100 |
| Method | Parameters |
|---|---|
| Fine Tree | Maximum Number of splits: 3321 Split criterion: Maximum Deviance Reduction Optimizer: Bayesian optimization |
| Quadratic Discriminant Analysis | Covariance Structure: Full |
| Gaussian Naïve Bayes | Distribution names: Kernel Kernel type: Triangle Support: Unbounded |
| K Nearest Neighbors | Number of neighbors: 30 Distance metric: Euclidean Distance weight: Squared inverse |
| RUSBoost | Maximum number of splits: 5455 Number of learners: 72 Learning rate: 0.1 |
| Support Vector Machine | Kernel: Radial Basis Function C (regularization): 1 Gamma (kernel coefficient): 0.07 |
| Random Forest | Estimators: 100 Criterion: Gini Min_samples_split: 2 |
| Crop | Indicator | VI | |||
|---|---|---|---|---|---|
| DpRVI | RVI | VH/VV | NDVI | ||
| Soybean | 0.59 ± 0.08 | 0.92 ± 0.16 | 0.31 ± 0.07 | 0.80 ± 0.11 | |
| 6.7 | 9.1 | 11.7 | 6.8 | ||
| 263.4 ± 8.2 | 261.0 ± 21.3 | 260.7 ± 21.4 | 238.2 ± 15.0 | ||
| 1.5 | 3.8 | 4.4 | 3.4 | ||
| Oat | 0.69 ± 0.11 | 0.96 ± 0.34 | 0.44 ± 0.20 | 0.69 ± 0.24 | |
| 6.2 | 11.3 | 17.8 | 8.1 | ||
| 193.3 ± 33.8 | 203.0 ± 35.4 | 200.7 ± 42.4 | 200.3 ± 34.8 | ||
| 6.8 | 7.8 | 8.7 | 5.9 | ||
| Buckwheat | 0.63 ± 0.08 | 0.94 ± 0.15 | 0.40 ± 0.09 | 0.71 ± 0.11 | |
| 5.9 | 8.7 | 9.9 | 6.9 | ||
| 262.4 ± 15.0 | 257.1 ± 16.6 | 259.7 ± 18.5 | 254.0 ± 23.7 | ||
| 2.6 | 3.7 | 4.5 | 4.3 | ||
| Timothy | 0.68 ± 0.08 | 0.94 ± 0.13 | 0.42 ± 0.08 | 0.83 ± 0.09 | |
| 4.9 | 6.7 | 8.0 | 5.4 | ||
| 214.2 ± 16.4 | 212.7 ± 17.9 | 216.7 ± 19.3 | 180.1 ± 24.3 | ||
| 3.6 | 4.4 | 5.5 | 5.2 | ||
| Method | FT | QD | Gaussian NB | Fine KNN | RUSBoost | RF | SVM |
|---|---|---|---|---|---|---|---|
| Time, seconds | 61.8 | 30.3 | 3612.5 | 526.4 | 95.9 | 422.1 | 1325.6 |
| Test accuracy, % | 71.1 | 81.9 | 73.4 | 72.4 | 74.4 | 76.7 | 79.1 |
| κ | 0.49 | 0.67 | 0.52 | 0.50 | 0.54 | 0.58 | 0.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sorokin, A.; Stepanov, A.; Dubrovin, K.; Verkhoturov, A. Enhancement of Comparative Assessment Approaches for Synthetic Aperture Radar (SAR) Vegetation Indices for Crop Monitoring and Identification—Khabarovsk Territory (Russia) Case Study. Remote Sens. 2024, 16, 2532. https://doi.org/10.3390/rs16142532
Sorokin A, Stepanov A, Dubrovin K, Verkhoturov A. Enhancement of Comparative Assessment Approaches for Synthetic Aperture Radar (SAR) Vegetation Indices for Crop Monitoring and Identification—Khabarovsk Territory (Russia) Case Study. Remote Sensing. 2024; 16(14):2532. https://doi.org/10.3390/rs16142532
Chicago/Turabian StyleSorokin, Aleksei, Alexey Stepanov, Konstantin Dubrovin, and Andrey Verkhoturov. 2024. "Enhancement of Comparative Assessment Approaches for Synthetic Aperture Radar (SAR) Vegetation Indices for Crop Monitoring and Identification—Khabarovsk Territory (Russia) Case Study" Remote Sensing 16, no. 14: 2532. https://doi.org/10.3390/rs16142532
APA StyleSorokin, A., Stepanov, A., Dubrovin, K., & Verkhoturov, A. (2024). Enhancement of Comparative Assessment Approaches for Synthetic Aperture Radar (SAR) Vegetation Indices for Crop Monitoring and Identification—Khabarovsk Territory (Russia) Case Study. Remote Sensing, 16(14), 2532. https://doi.org/10.3390/rs16142532









