Abstract
Surface longwave radiation (SLR) plays a pivotal role in the Earth’s energy balance, influencing a range of environmental processes and climate dynamics. As the demand for high spatial resolution remote sensing products grows, there is an increasing need for accurate SLR retrieval with enhanced spatial detail. This study focuses on the development and validation of models to estimate SLR using measurements from the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) sensor. Given the limitations posed by fewer spectral bands and data products in ASTER compared to moderate-resolution sensors, the proposed approach combines an atmospheric radiative transfer model MODerate resolution atmospheric TRANsmission (MODTRAN) with the Light Gradient Boosting Machine algorithm to estimate SLR. The MODTRAN simulations were performed to construct a representative training dataset based on comprehensive global atmospheric profiles and surface emissivity spectra data. Global sensitivity analyses reveal that key inputs influencing the accuracy of SLR retrievals should reflect surface thermal radiative signals and near-surface atmospheric conditions. Validated against ground-based measurements, surface upward longwave radiation (SULR) and surface downward longwave radiation (SDLR) using ASTER thermal infrared bands and surface elevation estimations resulted in root mean square errors of 17.76 W/m2 and 25.36 W/m2, with biases of 3.42 W/m2 and 3.92 W/m2, respectively. Retrievals show systematic biases related to extreme temperature and moisture conditions, e.g., causing overestimation of SULR in hot humid conditions and underestimation of SDLR in arid conditions. While challenges persist, particularly in addressing atmospheric variables and cloud masking, this work lays a foundation for accurate SLR retrieval from high spatial resolution sensors like ASTER. The potential applications extend to upcoming satellite missions, such as the Landsat Next, and contribute to advancing high-resolution remote sensing capabilities for an improved understanding of Earth’s energy dynamics.
1. Introduction
Surface longwave radiation (SLR) stands as a foundational factor governing the energy equilibrium of the Earth’s surface. As the surface warms, it triggers fluctuations in surface downward longwave radiation (SDLR) at a pace of 7 Wm−2K−1, representing one of the most responsive fluxes within the Earth’s climatic system [1]. The role of SLR extends to affecting the interchange of energy and substances within the land–atmosphere structure, with consequential effects on attributes of vegetation, soil climate, hydrology, and zoology [2,3,4]. In this context, the comprehensive monitoring of SLR on a global scale emerges as indispensable for comprehending the dynamism of our evolving planet.
As applied research progresses, investigations such as those focusing on small-scale regions or watersheds, including studies related to understanding snow processes in glacier melting, regional ecology, and precision agriculture involving phenomena like evapotranspiration, necessitate remote sensing products of SLR with higher spatial resolutions (such as less than 100 m) to serve as input parameters for modeling efforts [5,6]. Furthermore, high spatial resolution remote sensing data of SLR prove invaluable in constraining the evolving resolution of global climate models, thereby reducing the uncertainties of cloud and radiation processes simulations [7]. Major earthquakes tend to occur near active fault zones within mountainous regions due to strong tectonic activities. Previous studies suggest that variations in surface temperature and water vapor prior to seismic events may be associated with the seismogenic process [8,9]. SLR serves as an integrated geophysical parameter reflecting changes in surface and atmospheric thermal radiation. High spatial resolution SLR data can contribute to the study of spatiotemporal evolution characteristics of pre-seismic thermal anomalies within fault zones in a detailed pattern. Moreover, coarse-resolution products fall short in meeting the demands of applications including urban, extreme environmental, and agricultural domains, and the current availability of medium- to high-resolution remote sensing thematic data products remains inadequate. Hence, it is important to explore remote sensing retrieval methods for SLR, facilitating the acquisition of reliable surface thermal radiation product at high spatial resolutions.
After many years of development, SLR estimations based on satellite observations have evolved into three major types of retrieval methods: parameterization, physically based, and hybrid methods. Parameterization methods establish linear or non-linear statistical relationships between SLR and readily available surface or atmospheric variables, such as surface temperature, humidity, and cloud cover. For instance, the study [10] used Moderate Resolution Imaging Spectroradiometer (MODIS) land surface temperature/emissivity products to estimate SLR. A widely used parameterization is the formula from the study [11], which relates SDLR to screen-level air temperature and water vapor pressure. While parameterization methods are simple and computationally efficient, they may lack accuracy, particularly for diverse landscapes. Physically based methods directly employ radiative transfer calculations to simulate the atmospheric emission and absorption of longwave radiation based on atmospheric profiles of temperature, water vapor, and other relevant parameters. The Moderate Resolution Atmospheric Radiance and Transmittance Model (MODTRAN) [12] is commonly used for this purpose and is employed in this study. This approach can be coupled with atmospheric profiles derived from satellite observations or reanalysis data. Although this approach offers a physically interpretable basics, it requires accurate atmospheric data and complex model calculations, resulting in a deep dependence on input data and significant computational costs. Hybrid methods combine parameterization and physically based models to leverage the strengths of both, resulting in more robust and accurate SLR estimates. In these methods, radiative transfer models generate training datasets, and parameterization methods build the statistical relationships. Beyond using linear models, machine learning approaches, particularly neural networks, are increasingly employed for SLR estimation due to their ability to handle large datasets and complex relationships. For example, SLR under cloudy sky conditions was estimated by combining parameterization and artificial neural networks from remotely sensed data [13], highlighting the effectiveness of machine learning in capturing non-linear relationships. Such approach holds promise for improved accuracy but requires careful construction of training data and thorough model validation, and remains an active area of research. Note that each retrieval method has its respective strengths and limitations, and the choice of method often depends on factors such as the availability of input data, computational resources, and the desired accuracy and resolution of the SLR estimates.
Ongoing studies aim to further improve the accuracy and spatiotemporal resolution of SLR estimates from remote sensing data, as well as to account for complex atmospheric conditions and surface properties. However, in contrast to the algorithms for retrieving SLR at medium to low resolutions [14,15,16,17], only a few studies have been dedicated to SLR retrieval from high-resolution remote sensing data. Such studies necessitate the integration of satellite imagery, typically Landsat and Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) data, with meteorological observations including air temperature, humidity, atmospheric pressure, and atmospheric sounding data. Employing parameterization approaches, these investigations achieve remote sensing estimations of SLR [18,19,20]. An early method for SLR estimation was introduced by the study [21], using Landsat imagery and ground-based meteorological observations to estimate surface radiation balance. Relative to results from airborne observations, satellite-derived net radiation exhibited discrepancies of less than 12%. SDLR is estimated from air temperature and humidity, while surface upward longwave radiation (SULR) is computed via Landsat-derived surface temperature. Subsequent investigations predominantly followed analogous retrieval strategies. Application of this approach to radiation balance studies in wetland areas has demonstrated its efficacy, though universality remains an area for enhancement [22].
Influenced by local circulation patterns, the retrieval of SLR using Landsat data necessitates the integration of land cover types and ground-based observational data [23]. Sparse ground-based parameters, such as air temperature and humidity, require spatial interpolation to extend over larger regions, unavoidably incurring significant errors. Consequently, the study [24] incorporated the MODIS atmospheric water vapor products into their inversion model. Reference [25], on the other hand, employed the atmospheric radiative transfer model MODTRAN, inputting ASTER and site-based observational data for direct simulation and computation of SDLR [26]. This approach leads to a substantial increase in computational burden and requires plenty of atmospheric and surface parameters from various field observations, thereby challenging its scalability to broader regions. Reference [27] directly utilized atmospheric sounding data of field measurements and a spatial interpolation method to retrieve SDLR. Landsat and meteorological data have also been used for estimating instantaneous, daily, and daytime surface net radiation under clear-sky conditions [28].
Meanwhile, when comparing data products with moderate spatial resolution (e.g., MODIS) to high spatial resolution multispectral satellite data from instruments such as ASTER or Landsat, the latter often reveals limitations. ASTER possesses five thermal infrared (TIR) bands, a 16-day revisit interval, a higher spatial resolution of 90 m, and a restricted array of data products (e.g., land surface temperature (LST) and band emissivity) pertinent to the estimation of SLR. In contrast, MODIS features 16 TIR bands and a more comprehensive suite of data products (including LST, emissivity, column water vapor, air temperature and humidity profiles, and cloud parameters) available at least four times per day. These limitations in the ASTER data products complicate the direct application of common SLR retrieval models developed for sensors with more comprehensive atmospheric and surface information. For instance, parameterization methods necessitate additional atmospheric or ground-based data, somewhat constraining the global applicability of this approach. Reanalysis data are frequently employed as model input. However, they consistently exhibit a coarse spatial resolution (e.g., 0.25 degrees), and the process of downscaling the data to 90 m introduces significant uncertainties. Therefore, developing an SLR retrieval model specifically tailored for high spatial resolution satellite remote sensing data is crucial to ensure its relevance and effectiveness in scientific research.
Notably, advancements in high-resolution remote sensing and machine learning algorithms hold the potential for further refinement of SLR estimations. The Light Gradient Boosting Machine (LightGBM) machine learning model has been widely explored in remote sensing parameter retrievals and object recognition. It stands out as a prominent open-source gradient boosting framework, developed by Microsoft, that enjoys widespread employment in machine learning tasks. An exceptional attribute of LightGBM is its application of the “Gradient-based One-Side Sampling” technique during training. This method prioritizes and selects the most informative data instances, contributing to reduced memory consumption and accelerated training. While conventional gradient boosting frameworks opt for depth-wise tree growth, LightGBM innovatively adopts leaf-wise tree growth. This approach expands the tree’s leaves based on the maximum loss reduction, leading to a more precise and efficacious model. LightGBM has been employed in various applications, such as estimating water depth, salinity and lithium concentration from Landsat data [29], wind power forecasting [30], forest canopy height retrieval based on ICESat-2, Landsat-8 and Sentinel-2 data [31], and dynamic water extent mapping in high spatiotemporal resolution using Sentinel-2 data [32], and ground-level PM2.5 estimation from Himawari-8 and auxiliary environmental variables data [33]. As a result, the LightGBM model often outperforms other machine learning frameworks like XGBoost and CatBoost in terms of both speed and accuracy in certain cases [30,34]. Its fast performance and ability to handle large-scale tasks make it a top choice for both academic research and practical industrial applications. Notably, limited input features were utilized in constructing the retrieval models in this study. Unlike the LightGBM model, which excels with simpler features, deep learning models typically require more complex features and are trained on larger datasets [35]. This distinction underscores the different needs and considerations when applying various machine learning techniques in different contexts.
ASTER remote sensing data possess five thermal infrared bands (8–12 μm), higher spatial resolution (90 m), and an extended time series observation (from 2000 to present), rendering them conducive for validation and analysis after SLR retrievals compared with Landsat data. These attributes establish ASTER observations as a better dataset for constructing high spatial resolution SLR retrieval models. A summary of common surface longwave radiation products is shown in Table 1. While the temporal resolution of the MDSLF (MSG Downward Surface Longwave Flux) product can be as fine as 30 min, the highest spatial resolution is 1 km as provided by the GLASS (Global Land Surface Satellite) product. In comparison, ASTER can generate SLR data with a much higher spatial resolution of 90 m, albeit with a limited revisit interval, highlighting the necessity of developing high spatial resolution SLR products.

Table 1.
A summary of common surface longwave radiation products.
In this study, we showcase the utilization of ASTER remote sensing data to develop clear-sky SLR models. This is achieved through a combination of atmospheric radiative transfer model and a machine learning technique, specifically the LightGBM algorithm. The upcoming Landsat Next satellite, projected for launch around 2030, is anticipated to feature a thermal infrared band configuration similar to the ASTER sensor [43]. As such, this study provides a methodological precursor and a foundational reserve of shared technologies for the prospective retrieval of SLR and product generation, utilizing Landsat Next data. Moreover, leveraging the SLR dataset derived from ASTER retrieval serves as a cornerstone for validating medium to low-resolution products, facilitating judicious selection of spatial scales for validation, informing future observational site placements, and furnishing scientific reference for enhancing authenticity assessment methodologies.
2. Data
2.1. ASTER Product
The ASTER sensor operates aboard the polar orbit satellite Terra and has been operational since 8 March 2000. It is equipped to capture Earth-atmosphere radiance data, with its viewing zenith angles maintained within a range of ±8.55°. It can capture high-resolution images of the Earth across 14 distinct wavelengths (0.52–11.65 μm) at a spatial resolution of 90 m for the TIR bands and a swath width of ~60 km. The radiometric precision of ASTER TIR bands (10–14) is at a value of ≤0.3 K in terms of the noise equivalent temperature difference (NE∆T) [44]. Importantly, the ASTER instrument can acquire data synchronously with Terra/MODIS and delivers intricate details regarding geophysical parameters, including land surface temperature, emissivity, reflectance, and altitude. This capability enables comprehensive insights into Earth’s surface characteristics.
For this study, the ASTER Level 1T (L1T) Version 3.1 product (AST_L1T) was used as the foundational dataset. It offers calibrated and terrain-corrected at-sensor radiance information at Level 1. The integration of this dataset into the research framework enables the exploration and development of the SLR retrieval models with expected better accuracy.
2.2. MODIS Cloud Product
Cloud contamination poses a significant challenge in satellite remote sensing, as clouds can obscure underlying land surface features and degrade the accuracy of retrieved geophysical parameters. However, the release of an office version of the ASTER cloud mask product remains absent. An ASTER cloud mask database (http://tonolab.cis.ibaraki.ac.jp/ASTER/cloud, accessed on 24 June 2024) is to use MODIS cloud product MOD35 Collection 6. In this study, MOD35 Collection 6.1 was used to identify the clear-sky pixels in ASTER granules as advised by the study [45]. The MOD35 cloud mask product is designed to identify and categorize clouds in the satellite imagery captured by MODIS. It uses a series of visible and infrared threshold and consistency tests to specify confidence that an unobstructed view of the Earth’s surface is observed [46]. The spatial resolution of MOD35 is 1 km, which covers pixels of ASTER thermal infrared bands. Only ASTER pixels with a confident clear sky flag in the MOD35 data that they are collocated with were used in subsequent ground validation.
2.3. Atmospheric Profile Data
The development of SLR retrieval algorithms requires representative databases of atmospheric profiles and surface conditions. A new Fifth Generation of European ReAnalysis (ERA5)-based profile dataset derived by the study [47] was utilized. This dataset includes 82,828 atmospheric profiles and surface conditions derived from ERA5 reanalysis data and multiple satellite products, which is aimed at developing and testing LST retrieval algorithms from satellite thermal infrared observations. This database provides global coverage of clear and cloudy conditions, incorporating realistic variability of surface temperature and emissivity from different satellite sensors and landcover types. Compared to existing databases like SeeBor [48], the new compilation encompasses a broader range of atmospheric profiles and associated brightness temperatures. Specifically, the database contains temperature, specific humidity, and ozone at 137 pressure levels as well as 2 m air temperature, skin temperature, total column water vapor, and total cloud cover.
To focus on clear-sky conditions, only profiles with a cloud fraction below 0.1 were retained. The adoption of a 0.1 threshold represents a more stringent criterion compared to the value of 0.3 employed by a previous study [30]. Given the spatial resolution of this dataset at 1° × 1°, acquiring entirely clear-sky atmospheric profiles poses a significant challenge. As a consequence of employing this threshold, approximately 47% of profiles were removed from the original dataset. This selection criterion serves as a compromise, maintaining a substantial amount of data for constructing the simulation dataset.
2.4. Spectral Emissivity Dataset
The Combined ASTER MODIS Emissivity over Land (CAMEL) V2 product [49] was employed to represent real surface spectral emissivity at the pixel level. The CAMEL database harmonizes infrared emissivity measurements by amalgamating two existing emissivity products: the University of Wisconsin-Madison MODIS Baseline Fit (UWBF) and ASTER Global Emissivity Dataset (GED) v4. The database uses a high spectral resolution algorithm designed to generate monthly mean emissivity spectra within the range of 3.6–14.3 µm, across 417 distinct hinge points. Operating at a spatial resolution of 5 km at a global scale, this dataset spans the period from April 2000 to December 2016. The utilization of the CAMEL dataset is anticipated to mitigate errors in LST estimation stemming from satellites with moderate spatial resolutions. It is achieved by providing more representative surface emissivity estimates offering comprehensive global coverage with a monthly temporal sampling frequency.
The CAMEL emissivity product was compared using lab measurements, a long-term spectral emissivity dataset derived from remote sensing observation, and simulated brightness temperatures [50]. This evaluation revealed enhanced accuracy in identifying features of snow, quartz, and carbonate in the Earth’s surface. By tracking monthly changes in emissivity, the CAMEL product effectively captures dynamic changes in land surfaces. Differences at 8.6 µm were mostly below 0.1, and for wavelengths of 10.8 µm or more, differences were mainly under 0.02. Notably, statistical analysis of simulated brightness temperature in the 3.6–5 and 8–9 µm regions indicated that CAMEL provides a more accurate emissivity estimate than a fixed value. The CAMEL dataset therefore offers effective representation of surface spectral emissivity at the pixel scale. When compared to lab-measured spectral emissivity libraries, CAMEL could be a preferable option, and its uncertainties do not significantly impact the retrieval model, as was observed when relying solely on lab spectra [51,52].
2.5. Ground Measurements
The Surface Radiation Budget Network (SURFRAD) measurements were used to verify the proposed SLR retrieval models. This network, active since 1993, comprises a collection of stations scattered across the United States. These stations routinely monitor the fluxes of surface radiation and meteorological conditions, ensuring the acquisition of high-quality and long-term data [53]. To ensure precision, measurements are conducted using specialized instruments called pyranometers and pyrgeometers, which are regularly calibrated to maintain data accuracy. This network plays a pivotal role in climate research within the United States, providing ground-truth measurements against which satellite observations and retrieval models can be compared. It also serves to validate the performance of land surface models.
The collected data include SDLR, SULR, air temperature, and relative humidity. These measurements were taken at 3 min intervals before 2009 and at 1 min intervals after 2009. The network consists of seven stations, strategically situated in climatically diverse regions, as detailed in Table 2. The land cover type of each site is obtained from the official website (https://gml.noaa.gov/grad/surfrad/index.html, accessed on 24 June 2024) and Google Earth (https://earth.google.com, accessed on 24 June 2024). Upon reviewing Google Earth, we noticed a slight deviation in the coordinates of the GWN site and have corrected it.

Table 2.
Description of SURFRAD sites used in ground validations.
3. Methods
The SLR estimations from ASTER TIR measurements involve several steps, as illustrated in Figure 1. Initially, a spatial-temporal match was performed based on an ERA5-based atmospheric profile dataset and a spectral emissivity dataset known as CAMEL. An SDLR-based screening method was proposed in above dataset to achieve a relatively even distribution of SDLR, representing the hydrothermal condition of the near-surface atmosphere. Subsequently, a representative atmospheric profile and corresponding spectral emissivity dataset were constructed. Thirdly, the simulation dataset, including ASTER TIR band radiances and SLR components, was generated using MODTRAN v5.2 from this dataset. To emulate real ASTER observations, random white noise was added to the simulated TIR bands based on ASTER band NE∆T. Fourthly, an initial full band model was created using LightGBM v4.2.0, which was employed in global sensitivity analysis to identify optimal bands for both SDLR and SULR retrievals. The hyperparameters of the LightGBM model were determined using the Optuna v 3.5.0 framework based on the optimal bands from the representative dataset. The final SLR models were then constructed based on the optimal bands and hyperparameters and were validated using ground measurements from SURFRAD.
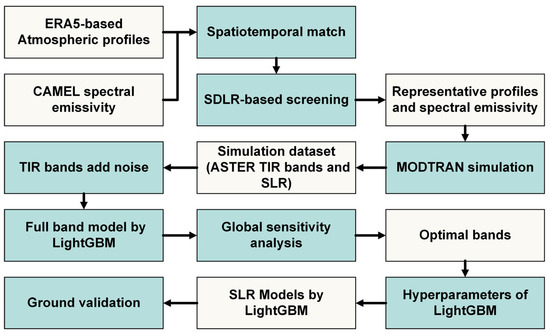
Figure 1.
Workflow of constructing a retrieval model for surface longwave radiation from the ASTER data. The blue-green blocks represent the data processing steps, while the white blocks represent the data.
3.1. Rationale of SLR Retrieval Method
The physical basis for this hybrid method in SLR retrieval is introduced in the work [52]. Based on the radiative transfer theory, the spectral radiance received at the top of the atmosphere (TOA) in cloud-free conditions can be approximated as the sum of the radiance contributions from the Earth’s surface and all atmospheric levels, as expressed in (1). This formula underpins the retrieval algorithms that derive SLR from measured TOA radiances in the TIR region.
where is the surface emissivity at wavenumber v; B indicates the Planck function; is the surface temperature; is the total atmospheric transmittance from the surface at pressure to the TOA at v; is the air temperature at pressure P; and denote the zenith angle and azimuth angle, respectively. The first term on the right-hand side of (1) is the spectral radiance emitted directly from the surface and transmitted to the TOA. The second term denotes the hemispheric atmospheric downwelling longwave radiation at reflected by the surface and subsequently attenuated by the atmosphere along the path from the surface to the TOA. Lastly, the third term represents the atmospheric upwelling path radiation at . The terms account for the radiative contributions from the surface, atmospheric reflection and emission, respectively, enabling the retrieval of information related to the surface and atmospheric state.
As shown in (1), the coupling of upwelling and downwelling radiative components in the atmospheric radiative transfer equation poses a challenge for the direct estimation of SDLR from TOA measurements. While the connection between SDLR and TOA radiances is inherently non-linear and complex, statistical methods have been proposed to approximate this relationship through linear or non-linear models [52,54,55]. These approaches aim to establish mathematical functions that relate the measured TOA radiances to the desired SDLR quantity, enabling its direct retrieval from satellite observations.
The TOA radiances in TIR bands are strongly dependent on band weighting functions [52]. Therefore, different bands of the ASTER sensor exhibit specific sensitivities to atmospheric and surface information. The band correlation between ASTER and MODIS is presented in Figure 2, demonstrating their spectral interrelated characteristics in this critical range. ASTER bands 10 and 11 partly overlap with MODIS band 29, and ASTER bands 13 and 14 partly overlap with MODIS band 31. The MODIS window bands 31 and 32 have been utilized in LST retrieval [56], and LST has a strong correlation with near-surface air temperature and SULR. Radiance measurements obtained from MODIS bands 29, 31, and 32 are known to provide valuable insights into atmospheric moisture content owing to the weak water vapor absorption observed within these spectral regions [57], and affirmed by the study [52]. Therefore, the spectral characteristics of the TIR bands play a crucial role in determining the information content of the measured radiances. By exploiting the spectral overlap and correlations between ASTER and MODIS bands, it is possible to leverage the well-established retrieval techniques for LST and SULR from MODIS to extract relevant information from ASTER observations. Despite the relatively weak signals related to near-surface air temperature and water vapor in the ASTER bands, their presence suggests the feasibility of retrieving SDLR, analogous to the approach using MODIS data [52,58].
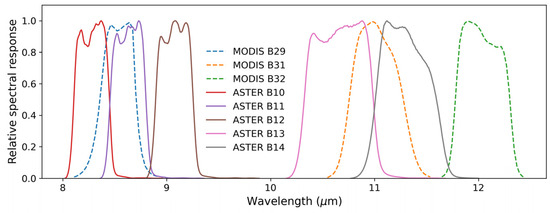
Figure 2.
Spectral response functions of thermal infrared bands of ASTER (bands 10–14) and MODIS (bands 29, 31, and 32) within the spectrum range of 8–13 .
3.2. Generation of Atmosphere Profiles and Emissivity Spectra Matchups
Atmospheric radiative transfer simulations by the MODTRAN model necessitate specific inputs: atmospheric profiles containing temperature and moisture data, as well as surface emissivity spectra. For every atmospheric profile, surface elevation information based on ERA5 land orography data was added, matched to its latitude and longitude coordinates. Initially, the dataset provided 25 potential emissivity pairs at around 11 and 12 µm [47]. However, this proved insufficient for MODTRAN simulations. Consequently, the CAMEL database was utilized, offering high spectral resolution within the 3.6–14.3 µm range, to complement each atmospheric profile.
For each profile, emissivity spectra were extracted from a window around it monthly, forming an initial dataset from April 2000 to December 2016. These emissivity spectra exhibit relative uniformity attributable to analogous land cover characteristics, with their fluctuations primarily attributed to phenomena associated with vegetation, snow, or alterations in land cover, all of which are responsive to atmospheric profiles.
Through an iterative process, this dataset was refined using a method based on maximum covariance, see (2). The covariance was calculated between emissivity spectra in the subset and a potential candidate. If the covariance exceeded a predetermined threshold , the candidate spectrum was added to the subset. When the spectra count within the subset surpassed 20, the threshold increased by 20%, and the process was repeated.
where m is the number of emissivity spectra in the subset; n is the number of points in the emissivity spectra; is the i-th emissivity value of a spectra in the subset, and is its average emissivity value; is the i-th emissivity value of a potential candidate, and is its average emissivity value.
Ultimately, a new emissivity spectra dataset for each atmospheric profile was generated. In Figure 3, it becomes evident that out of 1746 emissivity spectra, only 7 spectra were selected to stand as representatives. These chosen spectra were deemed to sufficiently capture the diverse variations seen in the MODTRAN simulation, meanwhile significantly reducing the computational resources required for this analysis.
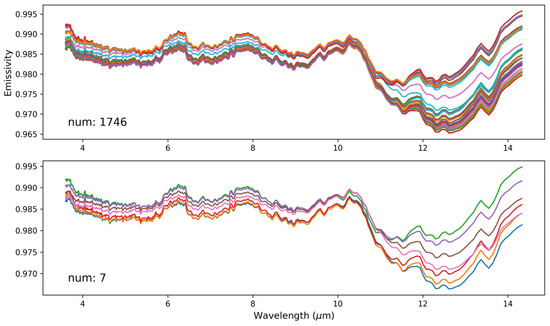
Figure 3.
An illustration of emissivity spectra dataset for an atmospheric profile before (upper) and after (lower) dissimilarity calculation. From an initial pool of 1746 emissivity spectra, just 7 were retained. Different colors distinguish the various spectra.
It is evident that an increased number of atmospheric profiles can lead to a more accurate representation of atmospheric conditions. However, this expansion may potentially impede radiative transfer simulations, which are computationally intensive. Additionally, unbalanced samples can distort the fitness of machine learning models. To tackle this challenge and optimize computational efficiency, two approaches were applied.
First, a constraint by considering the SDLR values associated with each profile was introduced. Given that temperature and humidity profiles significantly influence SDLR, this metric serves as a valuable indicator of the collective hydrothermal state of the atmosphere. To calculate the SDLR value, MODTRAN simulations were employed that utilized the temperature and humidity profiles from the newly generated dataset. The SDLR range, spanning from 50 to 500 W/m2, was systematically divided into 50 bins with intervals of 10 W/m2. Subsequently, all atmospheric profiles were categorized based on their respective SDLR bins.
Then, in order to ensure that each bin contained no more than 400 profiles—an empirical value established through iterative experimentations—a screening procedure was carried out. Initially, one atmospheric profile was randomly selected to form the initial dataset. This dataset was then updated iteratively by evaluating the similarity between newly extracted atmospheric profiles and those already present in the dataset. A similarity indicator (Λ) was employed to ascertain that each newly selected profile sufficiently differed from the existing ones. The value of Λ for each new atmospheric profile was determined according to the following formula:
where and represent either the air temperature or specific humidity of a new atmospheric profile at the i-th layer in the initial dataset and as the candidate profile, respectively; n denotes the total number of effective layers in an atmospheric profile; m is the number of atmospheric profiles in the new dataset; and denotes the geopotential height at the i-th layer. The initial threshold values for air temperature and specific humidity are set at 0.5 K and 0.05 g/kg, respectively. If Λ exceeded 0.5 K for air temperature or 0.05 g/kg for specific humidity, the new atmospheric profile was incorporated into the dataset. Following each epoch, if the new dataset exceeded 400 profiles in a bin, this procedure was reiterated, gradually increasing the air temperature and specific humidity thresholds by 20%.
A uniform sample distribution in terms of SDLR was achieved, aiming to enhance the performance of regression models and mitigate the likelihood of both overestimation and underestimation at extreme SDLR values [58]. Figure 4a illustrates the distribution of sample numbers in each bin, highlighting a satisfactory overall evenness. However, it is worth noting that the count is relatively lower for SDLR values <180 W/m2 or >460 W/m2. Finally, a comprehensive and representative atmospheric profile dataset was generated spanning global land areas. The spatial and statistical attributes of this dataset are showcased in Figure 4b–e. While these profiles cover a substantial portion of land, their representation in tropical zones is relatively sparse. This could be attributed to the comparable extremely hot and humid conditions prevalent in these regions, and limited samples is sufficient to effectively capture such variations. The air temperature typically ranges from 200–350 K, with a notable peak around 300 K. Total Column Water Vapor (TCWV) observations cluster around values close to 0, while the second peak appears around 5.0 cm, with a maximum of 8.0 cm. In summary, this database signifies a refined subset of atmospheric profiles across different regions worldwide.
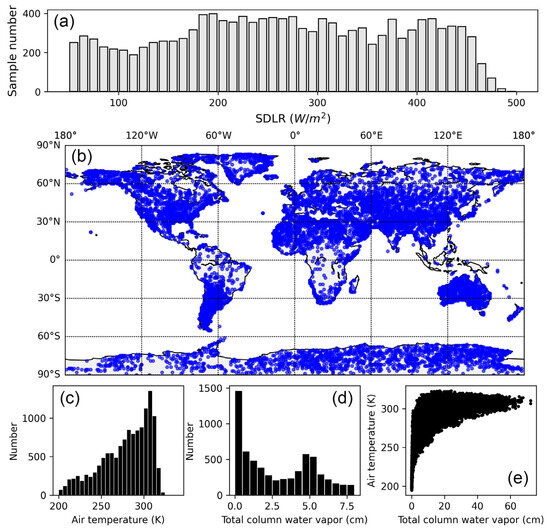
Figure 4.
Characteristics of refined atmospheric profile database. (a) The histogram of atmospheric profiles in terms of SDLR bins; (b) spatial distribution of atmospheric profiles represented by blue circles, providing insights into their global coverage and distribution; (c) the histogram of air temperature, depicting the number distribution of air temperatures; (d) the histogram of total column water vapor (TCWV); (e) the scatter plot between air temperature and TCWV across atmospheric profiles.
3.3. MODTRAN Simulations
Both SDLR and SULR, as well as TOA band radiances from the ASTER sensor, were simulated using MODTRAN version 5 [59]. The ASTER sensor’s viewing zenith angle falls within a range of ±8.55°, making the nadir viewing angle the suitable choice for the MODTRAN simulation. To emulate SDLR, essential input data included the profiles of air temperature, humidity, ozone, and surface elevation. The atmosphere model for additional gases, such as CH4, N2O, and CO, was adjusted based on the specific time and latitude of the given atmospheric profile. All other settings were kept at their default values. Following this, the calculation of TOA spectral radiance () is performed according to the following formula:
where is the wavenumber; is the LST, derived from the ERA5-based atmospheric profile dataset, containing six distinct values; is the emissivity spectrum extracted from CAMEL database at ; is the upwelling atmospheric transmittance at ; is the surface downward spectral radiances simulated by MODTRAN at ; is the spectrum of path radiance towards the TOA and is also simulated by MODTRAN at .
The ASTER band radiances () are calculated as:
where and are the lower and upper boundaries of the spectral response function (SRF) of the ASTER TIR band; is the SRF, which can be obtained from https://asterweb.jpl.nasa.gov/characteristics.asp, accessed on 24 June 2024.
The SULR (, W/m2) can be calculated as:
where is the broadband emissivity that is integrated from emissivity spectrum of CAMEL data and corresponds to each atmospheric profile as illustrated in Figure 3; is the Stefan–Boltzmann constant (); is SDLR (W/m2) simulated by MODTRAN. Subsequently, a comprehensive dataset was assembled. This dataset incorporates the inputs of band radiance values () across five ASTER TIR bands, as well as surface elevation. On the output side, it consists of the SULR and SDLR, both simulated by MODTRAN. This dataset was then employed to effectively train the machine learning model.
3.4. The LightGBM Model and Determination of Its Hyperparameters
The LightGBM model was used for establishing the statistical linkage between SLR and the band radiances of ASTER TIR bands. Nevertheless, such a model has a range of hyperparameters that require careful tuning to achieve optimal peak model performance. Hyperparameters are parameters that govern the learning process of the algorithm, influencing the way the model learns from the training data and makes predictions on unseen data. However, they cannot be trained and must be predetermined before model training commences. Consequently, techniques for hyperparameter tuning emerge as a critical endeavor. By tuning hyperparameters, we essentially undertake a search for the optimal combination of settings that enable the model to generalize effectively to new, unseen data. This process entails exploring various values for hyperparameters and evaluating the model’s performance using methodologies such as cross-validation.
To facilitate this essential process, we employed Optuna, an open-source hyperparameter optimization framework designed to automate the search for optimal hyperparameter configurations [60]. Utilizing a 10-fold cross-validation approach, Optuna navigated through the hyperparameter space to identify the optimal parameter combination, guided by the Root Mean Square Error (RMSE) metric as criterion. The resultant parameter settings, along with their corresponding optimal values for both the SULR and SDLR retrieval models, have been compiled in Table 3. Notably, the optimal configuration for the SDLR retrieval model exhibits a greater degree of complexity when compared to the configuration for the SULR model.

Table 3.
Hyperparameters and optimal values of the constructed LightGBM model for SULR and SDLR estimations.
3.5. Global Sensitivity Analysis
The optional inputs for the SLR retrieval models include ASTER’s bands 10–14 and the surface elevation from the AW3D30 (ALOS World 3D—30 m) DEM product [61]. To identify the optimal inputs for the SULR and SDLR models, a comprehensive global sensitivity analysis was conducted, drawing from methodologies outlined in the studies [62,63]. Sensitivity analysis refers to the study of uncertainty in the output of a model or system and further determining the sources of that uncertainty, specifically investigating the extent to which changes in input parameters result in variations in the output. Therefore, sensitivity analysis is an essential and routine step in the process of system modeling. The Sobol method is a variance-based global sensitivity analysis approach that can handle non-linear responses and measure the effects of interactions in non-additive systems [64]. While the global approach captures interactions among inputs, particularly in non-linear and non-additive models, it often necessitates probabilistic data and thus incurs computational demands. It falls within the realm of probability theory, characterizing uncertainties in both input and output as probability distributions, dissecting output variance into segments assignable to individual input variables and their interplays. Consequently, this method facilitates quantification of the effects of model inputs or external factors on desired outputs. By conducting a global sensitivity analysis, the most influential input parameters can be pinpointed, thus enhancing the overall model’s reliability and effectiveness.
3.6. Training of SLR Models
The TIR bands of the ASTER sensor exhibit a NE∆T of ≤0.3 K [44]. Therefore, instrument noise was introduced to the calculated spectral band radiance. Employing a lookup table (LUT) methodology, the transformation of ASTER band radiance from the MODTRAN simulated dataset to band brightness temperature (BT) was executed. Subsequently, random additive white noise, with an average of 0 K and a standard deviation of 0.3 K, is superimposed onto this BT dataset to emulate ASTER observations. This process culminates in the calculation of five band radiances from the noise-affected band BTs through the same LUT.
The inputs undergo normalization using the min-max approach as expressed in (7), which linearly transforms the raw input features to a common range, typically spanning from 0 to 1.
where is the value of an input feature; and are the minimum and maximum values of that feature, respectively. Normalization can accelerate the training convergence for identifying optimal solutions and potentially elevate the model’s predictive accuracy.
The MODTRAN simulated dataset is then randomly partitioned into three distinct segments: training (60%), validation (20%), and test (20%) datasets. The validation dataset assumes a pivotal role in the model training phase, while the test dataset serves to assess the model’s performance as a separate dataset. Employing an early stopping strategy, measures are taken to forestall model overfitting. This strategy ensures continued training until the validation score ceases to improve by a user-defined minimum threshold.
3.7. Validation
The ASTER data collocated with SURFRAD sites spanning the period from 2000 to 2021 were acquired for validation and analysis. The derived ASTER SLR data underwent validation against in situ measurements within a neighboring window (i.e., a radius of 135 m), along with a temporal window of 12 min. Notably, all pixels within the window needed to exhibit clear sky conditions [5], and subsequently, their average value was considered when their standard deviation was less than 10 W/m2 to ensure a relatively homogeneous scene. Temporally, all ground measurements (comprising 4 samples prior to 2009 and 12 samples post-2009) had to be valid, with their standard deviation being less than 5 W/m2. This consideration is rooted in the relatively stable nature of SDLR variations under clear sky conditions over a short timeframe. To assess accuracy, commonly utilized evaluation metrics including the bias, RMSE, and the Coefficient of Determination (R2) were employed. Their definitions are defined as follows:
where N is the total count of validation samples; is the retrieved SULR/SDLR value for the i-th sample; is the true SULR/SDLR value for the i-th sample, which is the ground measurement; is the average of all ; and is the average of all .
4. Results
4.1. Global Sensitivity Analysis and Feature Selection
The outcomes of the global sensitivity analysis for ASTER SLR models are depicted in Figure 5, where larger values correspond to heightened sensitivity or significance of input parameters in influencing the model output. The sensitivity indices are presented in terms of S1, the first-order sensitivity index, representing the proportion of total variance attributed solely to a given parameter (e.g., surface altitude). Additionally, ST, the total sensitivity index, showcases the proportion of total variance that a parameter influences, accounting for interactions with other parameters (e.g., surface altitude vs. radiance of Band 11). The sensitivity indices, both ST and S1, exhibit consistent trends for each input parameter. Notably, as ST consistently surpasses S1 due to its comprehensive nature. It is worth mentioning that radiances from Bands 13 and 14 predominantly encapsulate surface thermal radiative signals, while those from Bands 10 to 12 are more responsive to atmospheric water vapor content. In the case of the SULR model, the most critical inputs are Bands 13 and 14, which demonstrate sensitivity to ground surface conditions. For the SDLR model, the significance shifts towards Bands 10 to 12. This is attributed to the fact that in clear sky conditions, the near-surface atmospheric temperature and moisture play important roles in influencing SDLR. Moreover, surface altitude emerges as the second most influential parameter (Figure 5b), capable of reflecting variations in air temperature along the altitudinal axis. Based on these insights, the first four sensitive parameters were chosen as model inputs for further analysis. Specifically, the SULR model was built using Bands 13, 14, 12, and 11, while the SDLR model employed Band 10, surface altitude, Band 11, and Band 12 as its primary input parameters.
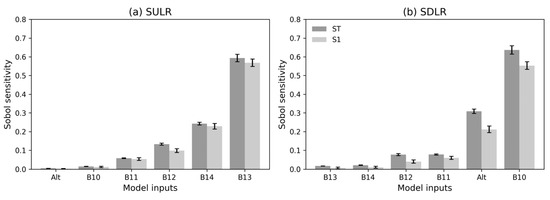
Figure 5.
Sensitivity analysis of model inputs using the global sensitivity analysis approach. Error bars are indicative of the confidence intervals associated with ST (dark grey) or S1 (light grey) values. B10–B14 are ASTER thermal infrared band radiances from 10–14. Alt denotes surface altitude.
4.2. Fitting Performance Based on MODTRAN-Simulated Dataset
The theoretical performance of the ASTER SLR retrieval models, based on MODTRAN simulations is shown in Figure 6. Both models exhibit similar performance levels across the training and test datasets. The biases for all cases are found to be closely approximating zero. During the training phase, the RMSEs for SULR and SDLR estimations amount to 5.45 W/m2 and 13.13 W/m2, respectively. In the subsequent testing phase, these figures slightly increase to 5.52 W/m2 for SULR and 15.00 W/m2 for SDLR. Comparably, the performance of the SULR model aligns with the findings of the study [52], with a RMSE around 12.4 W/m2, and Wang and Liang [54], who reported approximately 14 W/m2. Moreover, the SULR models’ RMSE range in the training phase, spanning 1.75–7.37 W/m2 [51], is in line with our results. The fitting of SULR values below ~500 W/m2 signifies a notable consistency, whereas for higher SULR values, some dispersions are observed (Figure 6a,b). With our refined atmospheric profile dataset, the distribution of SDLR aligns more evenly along the 1:1 line, indicating the potential for a more stable retrieval model.
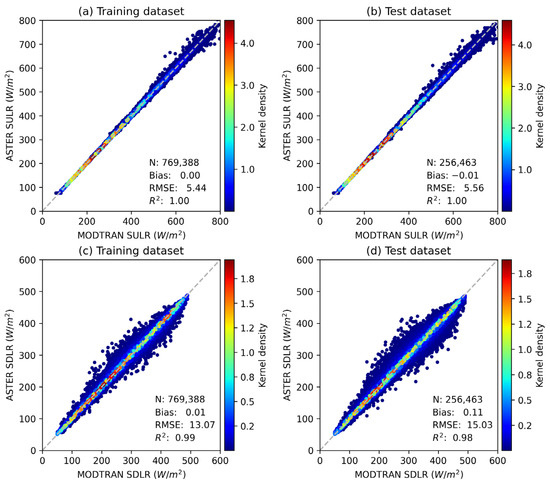
Figure 6.
Comparison of proposed ASTER retrieval models and MODTRAN simulations for (a,b) SULR and (c,d) SDLR estimations in training and test stages, respectively. The light grey dashed line represents the 1:1 line.
SDLR values exhibit a greater degree of dispersion compared to MODTRAN simulations than SULR values do (Figure 6). From the perspective of the retrieval algorithm, SULR values are easier to estimate from ASTER thermal bands than SDLR values. This is because ASTER can directly measure the upwelling thermal flux, and the algorithm performs atmospheric correction to remove its effect and obtain the surface outgoing flux. Although this correction is not exactly identical to the target, it explains most of the SULR estimation model. In contrast, estimating SDLR involves using indirect signals from ASTER bands, which are influenced by radiance differences due to water vapor and air temperature. Therefore, the accuracy and precision of SDLR are expected to be lower than those of SULR. Incorporating bands that are more sensitive to water vapor and air temperature into the retrieval model can improve SDLR performance, as observed when using MODIS data [58].
4.3. Validation Using In Situ Measurements
The validation results based on ground measurements are depicted in Figure 7, indicating favorable performance for both SULR and SDLR models. The SULR model exhibits a bias of 3.42 W/m2, RMSE of 17.76 W/m2, and R2 of 0.98. Meanwhile, the SDLR model showcases evaluation metrics of a bias of 3.92 W/m2, RMSE of 25.36 W/m2, and R2 of 0.80. Retrieving SDLR from ASTER band radiances can pose challenges due to the indirect nature of the process [52], but these results are acceptable given that the retrieval accuracy aligns with outcomes achieved through a broader validation using MODIS data [58]. Similar accuracy has been obtained for SLR estimations on Mt. Qomolangma over the Tibetan Plateau using Landsat data and parameterization methods, with an RMSE of 27.2 W/m2 for SDLR and 16.4 W/m2 for SULR [27].
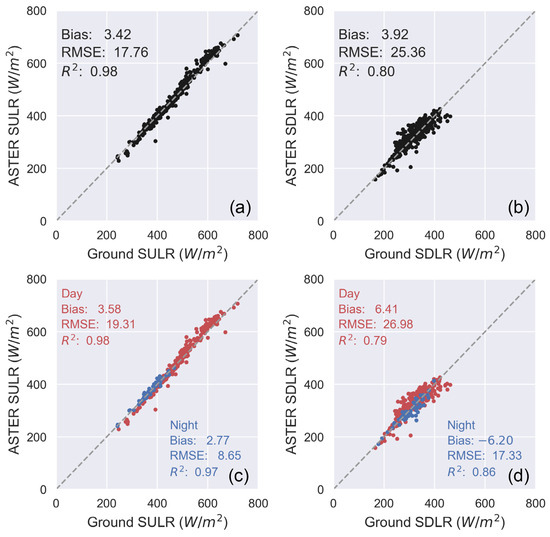
Figure 7.
Ground validation of ASTER-derived (a) SULR and (b) SDLR data, and (c,d) their daytime and nighttime performances. The grey dashed line represents the 1:1 line.
The diurnal variation in SLR retrieval is presented in Figure 7c,d. Overestimations of SULR are evident during both daytime and nighttime periods. Notably, the daytime retrievals exhibit poorer agreement with ground measurements, characterized by a higher RMSE of 19.31 W/m2. The biases of SDLR are 6.41 W/m2 and −6.20 W/m2 for the daytime and nighttime, respectively. It is noticeable that the SDLR model tends to overestimate during daytime and underestimate during nighttime [58]. The model’s performance during daytime consistently lags behind its nighttime counterpart. The spatial representativeness of ground measurements could be a contributing factor, as daytime conditions are more susceptible to surface thermal heterogeneity due to solar radiation and land cover variations or even topographic effects [65,66,67].
5. Discussion
5.1. Impacts of Threshold Number of Surface Emissivity Spectra
We established different threshold numbers for surface emissivity spectra for each atmospheric profile and tested their influence on model fitting. The thresholds for spectral emissivity were set to 20, 40, 60, 80, and 100. The generated datasets, which included matched atmospheric profiles and surface emissivity spectra, were input into the ASTER SDLR and SULR models to evaluate fitting performance for both training and test data. The results are presented in Table 4. As the threshold increases, the bias values of SDLR for the training data gradually decrease from 0.11 W/m2 to 0.04 W/m2. A similar trend is observed in RMSE values, which decreases from 15.03 W/m2 to 13.71 W/m2. However, the model performance during the training stage shows minimal variation with increased threshold numbers. For the SULR model, only the RMSE values show a slight decrease from 5.56 to 5.24 W/m2. These results indicate that more diversified surface emissivity spectra can reduce fitting errors during the test stage. However, these benefits are limited, and the simulation cost significantly increases with the increment of surface emissivity spectra. Consequently, we chose a threshold number of 20 for this study.

Table 4.
Model performances for ASTER SDLR and SULR estimations with varying threshold numbers (No.) of surface emissivity spectra for each atmospheric profile. The values in the brackets are for test data, and others are for training data.
5.2. Impacts of Atmospheric Temperature and Moisture
This section analyzes the impact of air temperature and relative humidity, as measured at ground stations, on the precision of satellite-derived SLR estimations (Figure 8). In the case of SULR, there is a noticeable negative bias within the air temperature range of 240–283 K. However, this bias progressively turns positive as the air temperature surpasses 297 K. Turning to SDLR, the average bias demonstrates relative stability when air temperature remains below 280 K, except for instances above 302 K where a negative bias emerges (Figure 8b). In a broader perspective, as the air temperature climbs, the discrepancy between satellite-derived SLR and ground measurements widens, holding true for both SULR and SDLR models. This divergence is more pronounced for SDLR as compared to SULR, particularly at higher air temperatures. While biases for SULR largely hover around zero across most relative humidity ranges, SDLR presents a distinct pattern. Here, lower humidity levels result in substantial negative biases, which then transition to positive biases at higher humidity levels, with the shift occurring around the 20% level of relative humidity.
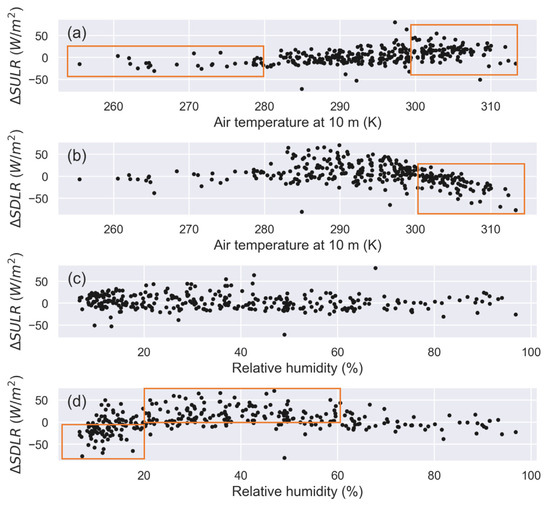
Figure 8.
Biases between retrieved and ground measured SLR. Retrieval error variance for (a) SULR and (c) SDLR as functions of air temperature; retrieval error variance for (b) SULR and (d) SDLR as functions of relative humidity. The orange boxes highlight the areas emphasized in the text.
The outcomes highlight the impact of air temperature and humidity on the inherent biases within existing satellite-driven SLR models [39,58]. Notably, these biases are more pronounced in arid climates when contrasted with more humid conditions. The study proves that uncertainties within input data, such as water vapor scale height and temperature lapse rate, can introduce systematic biases particularly in dry and hot environments [39]. The convergence of low humidity and high temperature conditions, often characteristic of desert or barren landscapes, exacerbates the margin of retrieval errors, with a more pronounced effect on SDLR. This phenomenon can be attributed to the intricate interaction between such conditions and the atmospheric radiative transfer modeling integral to satellite algorithms.
In regions characterized by low humidity, the reduction in downwelling thermal radiation from the atmosphere to the surface leads to pronounced discrepancies. Under extremely dry circumstances, current radiative transfer models may tend to overestimate the atmospheric contribution. The impact of elevated temperatures is noteworthy, as it accentuates the role of atmospheric dust and aerosols in attenuating downwelling thermal radiation. However, prevailing satellite algorithms inadequately account for this phenomenon [68]. The observed diminished accuracy in SLR retrieval, particularly within arid zones, appears to stem from the suboptimal representation of radiative transfer dynamics and limitations in input data, especially under exceedingly hot and dry conditions. Addressing these inherent limitations presents an opportunity to enhance satellite-driven SLR estimates for applications in climate studies across desert landscapes and water-constrained areas.
5.3. Benefits and Limitations
The presented approach leverages ASTER band radiance data in conjunction with surface elevation information to estimate SLR. This hybrid method offers a distinct advantage by obviating the necessity for meteorological data input and powerful non-linear fitting capabilities. It can expedite the retrieval process when dealing with vast volumes of remote sensing data. Moreover, there is promise in integrating multiple satellite datasets to mitigate the input limitations of ASTER data products and improve the resilience of the SLR retrieval algorithm. Synchronous MODIS observations furnish a spectrum of geophysical parameters, including water vapor content, air temperature profile, and vegetation parameters, which can be aptly utilized as inputs for the SLR model provided reasonable downscaling methods are available. Lastly, to ensure the wider applicability and global relevance of the developed model, radiative transfer simulations can be adopted as an alternative to relying solely on localized ground measurements [69].
It is imperative to emphasize the need for validation across a broader spectrum of geographical locations, transcending the confines of the United States and grounded in high-quality ground measurements. This requisite step will further promote the robustness and reliability of the proposed model, validating its efficacy across diverse environments.
The uncertainties associated with the MODIS cloud mask product are of significant importance in this study. To simplify, the cloud mask, operating at a 1 km resolution, faces limitations when trying to spot clouds that are as small as 90 m, like those observed by the ASTER pixel scale. This limitation becomes evident when examining specific data samples in Figure 7, where their values are noticeably underestimated. One plausible explanation for these discrepancies lies in the possibility of not detecting cloud covers, which can have a substantial impact. This is because clouds emit less radiation due to their lower temperatures compared to the warmer land surface, resulting in unexpectedly low values for SLR retrieval. The influence of clouds on the SLR estimates is demonstrated in Figure 9. The MODIS cloud mask excels at identifying clear sky conditions, as seen in Figure 9f. However, upon closer examination of Figure 9e, we can identify instances where clouds, along with their accompanying shadows, persist within the ASTER false-color composite map. Meanwhile, the MODIS cloud mask product detect a broader range of cloud-covered areas. For instance, Figure 9h exhibits complete cloud coverage according to the 1 km cloud mask, while ASTER’s false-color composite map reveals clear-sky regions.

Figure 9.
The cloud effect on SLR data derived from ASTER observations in the vicinity of the BON site within SURFRAD. (a) The ASTER SULR data, where white areas indicate the data that is unreliable due to the presence of clouds or due to the granule margins; (b) the ASTER SDLR data; (c) the false-color composite map from an ASTER granule where dark red areas correspond to vegetated regions, and the white areas represent cloud cover; (d) MODIS cloud mask data depicted in light gray for cloudy regions and in blue for clear sky condition; (e) a subgraph of (c) depicting area A; (f) a subgraph of (d) in area A where the blue denotes clear sky conditions; (g) a subgraph of (c) focusing on area B; (h) a subgraph of (d) in area B where the light gray indicates clouds.
Despite the good performance of the MODIS cloud mask product under most conditions [70], it is crucial to recognize that there are greater uncertainties associated with remote sensing data when working at finer spatial resolutions. On one hand, the presence of unidentified clouds in the MODIS cloud mask product leads to an underestimation of SLR, thereby potentially misleading assessments regarding the performance of retrieval algorithms. On the other hand, misclassification of clouds notably diminishes the number of valid ASTER pixels, consequently compromising the adequacy of validation samples and the validity of assessment outcomes. This conclusion is reinforced by the findings from the research conducted by the study [45]. Furthermore, it is worth noting that accurately detecting clouds in snow-covered or nighttime images using the ASTER instrument presents a formidable challenge due to the instrument’s lack of specific spectral bands [45]. Nevertheless, the need to develop a cloud mask at the same fine resolution remains an essential work, with the potential to significantly enhance the precision and reliability of proposed remote sensing retrieval methodologies.
The performance of the SLR model is better during nighttime, as clearly depicted in Figure 7c,d. However, we should consider the spatial characteristics of the SURFRAD sites during the validation phase. It is worth noting that surface thermal uniformity is notably better during the night compared to daytime conditions [71], even at the fine-grained 90 m resolution. Furthermore, the degree of surface spatial heterogeneity plays a pivotal role in assessing the accuracy of satellite-derived SLR data [17]. Thus, evaluating the spatial representativeness of ground measurements emerges as a crucial factor in validating retrieval models and remote sensing data products. To improve the dependability of validation for medium- to low-resolution products, we envision the creation of a repository of prior knowledge on spatial representativeness for SLR at observational sites. This repository has the potential to enhance the credibility of validation efforts and pave the way for more reliable assessments in the realm of SLR modeling and remote sensing.
A single machine learning model, LightGBM, has been utilized to create the primary retrieval model. To broaden our insights, it would be beneficial to explore other advanced gradient boosting methods in future research, such as gradient boosting decision tree (GBDT), XGBoost, and CatBoost. This investigation can facilitate a comparison of their performances, potentially improving the accuracy and efficiency of SLR retrieval models. Furthermore, applying deep learning approaches presents an exciting opportunity. Exploring different architectures for statistical models could leverage the potential of deep learning models in the parameter inversion of Earth science. This pathway holds significant promise for advancing our capabilities in comprehending and interpreting intricate Earth science data.
6. Conclusions
SLR is a fundamental climate variable that governs the radiation budget and energy balance at the Earth’s surface. As an integrated parameter reflecting land surface emission and atmospheric thermal radiation, the estimation of high spatial resolution SLR is essential for climate studies and environmental modeling from local to global scales. This investigation constructed and validated a hybrid statistical-physical approach to retrieve SLR from ASTER TIR satellite data at 90 m resolution. A global database of land surface emissivity spectra and reanalysis-based atmospheric profiles was generated. The MODTRAN was used with these datasets to simulate TOA radiances and SLR components under a range of surface and atmospheric conditions. A LightGBM machine learning algorithm was trained on the simulation results to establish quantitative relationships between ASTER band radiances, surface elevation, and SLR fluxes. Global sensitivity analysis determined the optimal input variables to be ASTER bands 13, 14, 12, and 11 for SULR, and bands 10, 11, 12 and surface elevation for SDLR.
Validated against ground-based measurements from the SURFRAD network, the SULR model achieved a bias of 3.42 W/m2 and a RMSE of 17.76 W/m2, while the SDLR model had a bias of 3.92 W/m2, and a RMSE of 25.36 W/m2. Retrievals exhibited systematic biases related to extreme temperature and moisture conditions, with SULR overestimating in hot humid atmospheres while underestimating in cold dry conditions. SDLR showed large negative biases in very arid atmospheric conditions. These errors likely stem from deficiencies in current radiative transfer models under such non-standard temperature and humidity regimes.
Overall, this study demonstrates the potential for a hybrid statistical-physical modeling approach to generate global, long-term SLR datasets at 90 m resolution from ASTER and comparable TIR sensors. The method established provides a pathfinder for SLR retrieval from future missions like Landsat Next. With further refinements to the radiative transfer modeling for extreme atmospheric conditions, this approach could produce valuable high-resolution SLR data for studies of urban climate, ecosystems, evapotranspiration, and land–atmosphere interactions from local to global scales.
Author Contributions
Conceptualization, Z.J.; Formal analysis, Z.J.; Funding acquisition, Z.J. and X.F.; Methodology, Z.J.; Writing—original draft, Z.J.; Writing—review and editing, Z.J. and X.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Key Research and Development Program of China, grant number 2020YFA0608702; Independent Research Project of State Key Laboratory of Earthquake Dynamics, grant number LED2023A07; National Natural Science Foundation of China, grant numbers 42071337; and Basic Science Research Plan of the Institute of Geology, China Earthquake Administration, grant numbers IGCEA2002.
Data Availability Statement
The ASTER data are available from NASA Earthdata Search at https://search.earthdata.nasa.gov/search (accessed on 20 May 2024). The MODIS cloud mask product is available from the Level-1 and Atmosphere Archive & Distribution System Distributed Active Archive Center (LAADS DAAC) at https://ladsweb.modaps.eosdis.nasa.gov (accessed on 20 May 2024).
Acknowledgments
The authors wish to extend their gratitude to the reviewers and editors for their invaluable comments and suggestions, which have significantly contributed to enhancing the quality of this work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Stephens, G.L.; Li, J.; Wild, M.; Clayson, C.A.; Loeb, N.; Kato, S.; L’Ecuyer, T.; Stackhouse, P.W.; Lebsock, M.; Andrews, T. An update on Earth’s energy balance in light of the latest global observations. Nat. Geosci. 2012, 5, 691–696. [Google Scholar] [CrossRef]
- Liang, S.; Wang, D.; He, T.; Yu, Y. Remote sensing of earth’s energy budget: Synthesis and review. Int. J. Digit. Earth 2019, 12, 737–780. [Google Scholar] [CrossRef]
- Wang, T.; Shi, J.; Yu, Y.; Husi, L.; Gao, B.; Zhou, W.; Ji, D.; Zhao, T.; Xiong, C.; Chen, L. Cloudy-sky land surface longwave downward radiation (LWDR) estimation by integrating MODIS and AIRS/AMSU measurements. Remote Sens. Environ. 2018, 205, 100–111. [Google Scholar] [CrossRef]
- Rogora, M.; Frate, L.; Carranza, M.L.; Freppaz, M.; Stanisci, A.; Bertani, I.; Bottarin, R.; Brambilla, A.; Canullo, R.; Carbognani, M.; et al. Assessment of climate change effects on mountain ecosystems through a cross-site analysis in the Alps and Apennines. Sci. Total Environ. 2018, 624, 1429–1442. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Q.; Cheng, J.; Dong, L. Assessment of the Long-Term High-Spatial-Resolution Global Land Surface Satellite (GLASS) Surface Longwave Radiation Product Using Ground Measurements. IEEE J.-STARS 2020, 13, 2032–2055. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Marshall, S.J. Parameterization of incoming longwave radiation at glacier sites in the Canadian Rocky Mountains. J. Geophys. Res. Atmos. 2015, 120, 12536–12556. [Google Scholar] [CrossRef]
- Wild, M. The global energy balance as represented in CMIP6 climate models. Clim. Dyn. 2020, 55, 553–577. [Google Scholar] [CrossRef] [PubMed]
- Picozza, P.; Conti, L.; Sotgiu, A. Looking for Earthquake Precursors from Space: A Critical Review. Front. Earth Sci. 2021, 9, 676775. [Google Scholar] [CrossRef]
- Jiao, Z.-H.; Zhao, J.; Shan, X. Pre-seismic anomalies from optical satellite observations: A review. Nat. Hazards Earth Syst. Sci. 2018, 18, 1013–1036. [Google Scholar] [CrossRef]
- Wang, K.; Wan, Z.; Wang, P.; Sparrow, M.; Liu, J.; Zhou, X.; Haginoya, S. Estimation of surface long wave radiation and broadband emissivity using Moderate Resolution Imaging Spectroradiometer (MODIS) land surface temperature/emissivity products. J. Geophys. Res. Atmos. 2005, 110, D11109. [Google Scholar] [CrossRef]
- Prata, A.J. A new long-wave formula for estimating downward clear-sky radiation at the surface. Q. J. R. Meteorol. Soc. 1996, 122, 1127–1151. [Google Scholar]
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Bernstein, L.S.; Muratov, L.; Lee, J.; Fox, M.; Adler-Golden, S.M.; Chetwynd, J.H.; Hoke, M.L.; et al. MODTRAN 5: A reformulated atmospheric band model with auxiliary species and practical multiple scattering options: Update. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XI; Shen, S.S., Lewis, P.E., Eds.; International Society for Optics and Photonics: San Diego, CA, USA, 2005; Volume 5806, pp. 662–667. [Google Scholar]
- Jiang, Y.; Tang, B.-H.; Zhao, Y. Estimation of Downwelling Surface Longwave Radiation with the Combination of Parameterization and Artificial Neural Network from Remotely Sensed Data for Cloudy Sky Conditions. Remote Sens. 2022, 14, 2716. [Google Scholar] [CrossRef]
- Yu, S.; Xin, X.; Liu, Q.; Zhang, H.; Li, L. An Improved Parameterization for Retrieving Clear-Sky Downward Longwave Radiation from Satellite Thermal Infrared Data. Remote Sens. 2019, 11, 425. [Google Scholar] [CrossRef]
- Yang, F.; Cheng, J. A framework for estimating cloudy sky surface downward longwave radiation from the derived active and passive cloud property parameters. Remote Sens. Environ. 2020, 248, 111972. [Google Scholar] [CrossRef]
- Wang, T.; Shi, J.; Ma, Y.; Letu, H.; Li, X. All-sky longwave downward radiation from satellite measurements: General parameterizations based on LST, column water vapor and cloud top temperature. ISPRS J. Photogramm. Remote Sens. 2020, 161, 52–60. [Google Scholar] [CrossRef]
- Jiao, Z.-H.; Mu, X. Single-footprint retrieval of clear-sky surface longwave radiation from hyperspectral AIRS data. Int. J. Appl. Earth Obs. Geoinf. 2022, 110, 102802. [Google Scholar] [CrossRef]
- da Silva, B.B.; Montenegro, S.M.G.L.; da Silva, V.d.P.R.; da Rocha, H.R.; Galvíncio, J.D.; de Oliveira, L.M.M. Determination of instantaneous and daily net radiation from TM—Landsat 5 data in a subtropical watershed. J. Atmos. Sol. Terr. Phys. 2015, 135, 42–49. [Google Scholar] [CrossRef]
- Mira, M.; Olioso, A.; Gallego-Elvira, B.; Courault, D.; Garrigues, S.; Marloie, O.; Hagolle, O.; Guillevic, P.; Boulet, G. Uncertainty assessment of surface net radiation derived from Landsat images. Remote Sens. Environ. 2016, 175, 251–270. [Google Scholar] [CrossRef]
- Nedbal, V.; Láska, K.; Brom, J. Mitigation of Arctic Tundra Surface Warming by Plant Evapotranspiration: Complete Energy Balance Component Estimation Using LANDSAT Satellite Data. Remote Sens. 2020, 12, 3395. [Google Scholar] [CrossRef]
- Moran, M.S.; Jackson, R.D.; Raymond, L.H.; Gay, L.W.; Slater, P.N. Mapping surface energy balance components by combining landsat thematic mapper and ground-based meteorological data. Remote Sens. Environ. 1989, 30, 77–87. [Google Scholar] [CrossRef]
- Goodin, D.G. Mapping the surface radiation budget and net radiation in a sand hills wetland using a combined modeling/remote sensing method and Landsat thematic Mapper Imagery. Geocarto Int. 1995, 10, 19–29. [Google Scholar] [CrossRef]
- Kuang, W.; Liu, A.; Dou, Y.; Li, G.; Lu, D. Examining the impacts of urbanization on surface radiation using Landsat imagery. GIScience Remote Sens. 2018, 56, 462–484. [Google Scholar] [CrossRef]
- Hu, D.; Cao, S.; Chen, S.; Deng, L.; Feng, N. Monitoring spatial patterns and changes of surface net radiation in urban and suburban areas using satellite remote-sensing data. Int. J. Remote Sens. 2017, 38, 1043–1061. [Google Scholar] [CrossRef]
- Ma, W.; Ma, Y.; Li, M.; Hu, Z.; Zhong, L.; Su, Z.; Ishikawa, H.; Wang, J. Estimating surface fluxes over the north Tibetan Plateau area with ASTER imagery. Hydrol. Earth Syst. Sci. 2009, 13, 57–67. [Google Scholar] [CrossRef]
- Frey, C.M.; Parlow, E. Flux Measurements in Cairo. Part 2: On the Determination of the Spatial Radiation and Energy Balance Using ASTER Satellite Data. Remote Sens. 2012, 4, 2635–2660. [Google Scholar] [CrossRef]
- Chen, X.; Su, Z.; Ma, Y.; Yang, K.; Wang, B. Estimation of surface energy fluxes under complex terrain of Mt. Qomolangma over the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2013, 17, 1607–1618. [Google Scholar] [CrossRef]
- Carmona, F.; Rivas, R.; Caselles, V. Development of a general model to estimate the instantaneous, daily, and daytime net radiation with satellite data on clear-sky days. Remote Sens. Environ. 2015, 171, 1–13. [Google Scholar] [CrossRef]
- Dai, J.; Liu, T.; Zhao, Y.; Tian, S.; Ye, C.; Nie, Z. Remote sensing inversion of the Zabuye Salt Lake in Tibet, China using LightGBM algorithm. Front. Earth Sci. 2023, 10, 1022280. [Google Scholar] [CrossRef]
- Ju, Y.; Sun, G.; Chen, Q.; Zhang, M.; Zhu, H.; Rehman, M.U. A Model Combining Convolutional Neural Network and LightGBM Algorithm for Ultra-Short-Term Wind Power Forecasting. IEEE Access 2019, 7, 28309–28318. [Google Scholar] [CrossRef]
- Sang, M.; Xiao, H.; Jin, Z.; He, J.; Wang, N.; Wang, W. Improved Mapping of Regional Forest Heights by Combining Denoise and LightGBM Method. Remote Sens. 2023, 15, 5436. [Google Scholar] [CrossRef]
- Li, B.; Liu, K.; Wang, M.; Wang, Y.; He, Q.; Zhuang, L.; Zhu, W. High-spatiotemporal-resolution dynamic water monitoring using LightGBM model and Sentinel-2 MSI data. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103278. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Pinker, R.T.; Wang, J.; Sun, L.; Xue, W.; Li, R.; Cribb, M. Himawari-8-derived diurnal variations in ground-level PM2.5 pollution across China using the fast space-time Light Gradient Boosting Machine (LightGBM). Atmos. Chem. Phys. 2021, 21, 7863–7880. [Google Scholar] [CrossRef]
- Daoud, E.A. Comparison between XGBoost, LightGBM and CatBoost Using a Home Credit Dataset. Int. J. Comput. Inf. Eng. 2019, 145, 6–10. [Google Scholar]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, F. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Rossow, W.B. Global Radiative Flux Profile Data Set: Revised and Extended. J. Geophys. Res. Atmos. 2023, 128, e2022JD037340. [Google Scholar] [CrossRef]
- Zhang, T.; Stackhouse, P.W.; Gupta, S.K.; Cox, S.J.; Mikovitz, J.C. The validation of the GEWEX SRB surface longwave flux data products using BSRN measurements. J. Quant. Spectrosc. Radiat. Transf. 2015, 150, 134–147. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Kratz, D.P.; Gupta, S.K.; Wilber, A.C.; Sothcott, V.E. Validation of the CERES Edition-4A Surface-Only Flux Algorithms. J. Appl. Meteorol. Climatol. 2020, 59, 281–295. [Google Scholar] [CrossRef]
- Stengel, M.; Stapelberg, S.; Sus, O.; Finkensieper, S.; Würzler, B.; Philipp, D.; Hollmann, R.; Poulsen, C.; Christensen, M.; McGarragh, G. Cloud_cci Advanced Very High Resolution Radiometer post meridiem (AVHRR-PM) dataset version 3: 35-year climatology of global cloud and radiation properties. Earth Syst. Sci. Data 2020, 12, 41–60. [Google Scholar] [CrossRef]
- Trigo, I.F.; Barroso, C.; Viterbo, P.; Freitas, S.C.; Monteiro, I.T. Estimation of downward long-wave radiation at the surface combining remotely sensed data and NWP data. J. Geophys. Res. Atmos. 2010, 115, D24118. [Google Scholar] [CrossRef]
- Liang, S.; Cheng, J.; Jia, K.; Jiang, B.; Liu, Q.; Xiao, Z.; Yao, Y.; Yuan, W.; Zhang, X.; Zhao, X.; et al. The Global Land Surface Satellite (GLASS) Product Suite. Bull. Am. Meteorol. Soc. 2021, 102, E323–E337. [Google Scholar] [CrossRef]
- Wulder, M.A.; Roy, D.P.; Radeloff, V.C.; Loveland, T.R.; Anderson, M.C.; Johnson, D.M.; Healey, S.; Zhu, Z.; Scambos, T.A.; Pahlevan, N.; et al. Fifty years of Landsat science and impacts. Remote Sens. Environ. 2022, 280, 113195. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Kahle, A.B.; Tsu, H.; Kawakami, T.; Pniel, M. Overview of Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER). IEEE Trans. Geosci. Remote Sens. 1998, 36, 1062–1071. [Google Scholar] [CrossRef]
- Tonooka, H.; Tachikawa, T. ASTER Cloud Coverage Assessment and Mission Operations Analysis Using Terra/MODIS Cloud Mask Products. Remote Sens. 2019, 11, 2798. [Google Scholar] [CrossRef]
- King, M.D.; Menzel, W.P.; Kaufman, Y.J.; Tanre, D.; Gao, B.-C.; Platnick, S.; Ackerman, S.A.; Remer, L.A.; Pincus, R.; Hubanks, P.A. Cloud and aerosol properties, precipitable water, and profiles of temperature and water vapor from MODIS. IEEE Trans. Geosci. Remote Sens. 2003, 41, 442–458. [Google Scholar] [CrossRef]
- Ermida, S.L.; Trigo, I.F. A Comprehensive Clear-Sky Database for the Development of Land Surface Temperature Algorithms. Remote Sens. 2022, 14, 2329. [Google Scholar] [CrossRef]
- Borbas, E.; Seemann, S.W.; Huang, H.-L.; Li, J.; Menzel, W.P. Global profile training database for satellite regression retrievals with estimates of skin temperature and emissivity. In Proceedings of the XIV International ATOVS Study Conference, Beijing, China, 25–31 May 2005. [Google Scholar]
- Borbas, E.; Hulley, G.; Feltz, M.; Knuteson, R.; Hook, S. The Combined ASTER MODIS Emissivity over Land (CAMEL) Part 1: Methodology and High Spectral Resolution Application. Remote Sens. 2018, 10, 643. [Google Scholar] [CrossRef]
- Feltz, M.; Borbas, E.; Knuteson, R.; Hulley, G.; Hook, S. The Combined ASTER MODIS Emissivity over Land (CAMEL) Part 2: Uncertainty and Validation. Remote Sens. 2018, 10, 664. [Google Scholar] [CrossRef]
- Qin, B.; Cao, B.; Li, H.; Bian, Z.; Hu, T.; Du, Y.; Yang, Y.; Xiao, Q.; Liu, Q. Evaluation of Six High-Spatial Resolution Clear-Sky Surface Upward Longwave Radiation Estimation Methods with MODIS. Remote Sens. 2020, 12, 1834. [Google Scholar] [CrossRef]
- Tang, B.; Li, Z.-L. Estimation of instantaneous net surface longwave radiation from MODIS cloud-free data. Remote Sens. Environ. 2008, 112, 3482–3492. [Google Scholar] [CrossRef]
- Driemel, A.; Augustine, J.; Behrens, K.; Colle, S.; Cox, C.; Cuevas-Agulló, E.; Denn, F.M.; Duprat, T.; Fukuda, M.; Grobe, H.; et al. Baseline Surface Radiation Network (BSRN): Structure and data description (1992–2017). Earth Syst. Sci. Data 2018, 10, 1491–1501. [Google Scholar] [CrossRef]
- Wang, W.; Liang, S. Estimation of high-spatial resolution clear-sky longwave downward and net radiation over land surfaces from MODIS data. Remote Sens. Environ. 2009, 113, 745–754. [Google Scholar] [CrossRef]
- Wang, T.; Yan, G.; Chen, L. Consistent retrieval methods to estimate land surface shortwave and longwave radiative flux components under clear-sky conditions. Remote Sens. Environ. 2012, 124, 61–71. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the collection-6 MODIS land-surface temperature/emissivity product. Remote Sens. Environ. 2014, 140, 36–45. [Google Scholar] [CrossRef]
- Seemann, S.W.; Li, J.; Menzel, W.P.; Gumley, L.E. Operational retrieval of atmospheric temperature, moisture, and ozone from MODIS infrared radiances. J. Appl. Meteorol. 2003, 42, 1072–1091. [Google Scholar] [CrossRef]
- Jiao, Z.-H.; Mu, X. Global validation of clear-sky models for retrieving land-surface downward longwave radiation from MODIS data. Remote Sens. Environ. 2022, 271, 112903. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Bernstein, L.S.; Muratov, L.; Lee, J.; Fox, M.; Adler-Golden, S.M.; Chetwynd, J.J.H.; Hoke, M.L.; et al. MODTRAN5: 2006 update. In Proceedings of the SPIE 6233, Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XII, Kissimmee, FL, USA, 8 May 2006; p. 62331F. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; Association for Computing Machinery: Anchorage, AK, USA, 2019; pp. 2623–2631. [Google Scholar]
- Takaku, J.; Tadono, T.; Doutsu, M.; Ohgushi, F.; Kai, H. Updates of ‘AW3D30’ ALOS global digital surface model in Antarctica with other open access datasets. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, XLIII-B4-2021, 401–408. [Google Scholar]
- Herman, J.; Usher, W. SALib: An open-source Python library for Sensitivity Analysis. J. Open Source Softw. 2017, 2, 97. [Google Scholar] [CrossRef]
- Pianosi, F.; Beven, K.; Freer, J.; Hall, J.W.; Rougier, J.; Stephenson, D.B.; Wagener, T. Sensitivity analysis of environmental models: A systematic review with practical workflow. Environ. Model. Softw. 2016, 79, 214–232. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Corbari, C.; Sobrino, J.A.; Mancini, M.; Hidalgo, V. Land surface temperature representativeness in a heterogeneous area through a distributed energy-water balance model and remote sensing data. Hydrol. Earth Syst. Sci. 2010, 14, 2141–2151. [Google Scholar] [CrossRef]
- García-Santos, V.; Cuxart, J.; Jiménez, M.A.; Martínez-Villagrasa, D.; Simó, G.; Picos, R.; Caselles, V. Study of temperature heterogeneities at sub-kilometric scales and influence on surface–atmosphere energy interactions. IEEE Trans. Geosci. Remote Sens. 2019, 57, 640–654. [Google Scholar] [CrossRef]
- Yan, G.; Jiao, Z.-H.; Wang, T.; Mu, X. Modeling surface longwave radiation over high-relief terrain. Remote Sens. Environ. 2020, 237, 111556. [Google Scholar] [CrossRef]
- Maghrabi, A.H.; Almutayri, M.M.; Aldosary, A.F.; Allehyani, B.I.; Aldakhil, A.A.; Aljarba, G.A.; Altilasi, M.I. The influence of atmospheric water content, temperature, and aerosol optical depth on downward longwave radiation in arid conditions. Theor. Appl. Climatol. 2019, 138, 1375–1394. [Google Scholar] [CrossRef]
- Liu, M.; Zheng, X.; Zhang, J.; Xia, X. A revisiting of the parametrization of downward longwave radiation in summer over the Tibetan Plateau based on high-temporal-resolution measurements. Atmos. Chem. Phys. 2020, 20, 4415–4426. [Google Scholar] [CrossRef]
- Frey, R.A.; Ackerman, S.A.; Holz, R.E.; Dutcher, S.; Griffith, Z. The Continuity MODIS-VIIRS Cloud Mask. Remote Sens. 2020, 12, 3334. [Google Scholar] [CrossRef]
- Duan, S.-B.; Li, Z.-L.; Li, H.; Göttsche, F.-M.; Wu, H.; Zhao, W.; Leng, P.; Zhang, X.; Coll, C. Validation of Collection 6 MODIS land surface temperature product using in situ measurements. Remote Sens. Environ. 2019, 225, 16–29. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).