Exterior Orientation Parameter Refinement of the First Chinese Airborne Three-Line Scanner Mapping System AMS-3000
Abstract
1. Introduction
- We developed an EOP refinement method that integrates cubic spline interpolation with a first-order Gaussian Markov process, reducing reliance on reference data.
- We conducted comparative experiments with the LIM and PPM, demonstrating superior flexibility in the EOP refinement of airborne three-line scanners, resulting in improved visual outcomes and higher geometric processing accuracy.
- The proposed method was applied to the AMS-3000 data processing system, addressing the challenges faced by the AMS-3000 camera due to the low sampling rate and accuracy of its POS system, providing significant support for its product application.
- The remainder of this paper is organized as follows. Section 2 reviews related work on EOP refinement. Section 3 describes the characteristics of the AMS-3000 camera and the experimental data. Section 4 details the proposed method. Section 5 presents and discusses the experimental results. Section 6 concludes the study.
2. Related Work
3. Materials
3.1. AMS-300 Mapping System
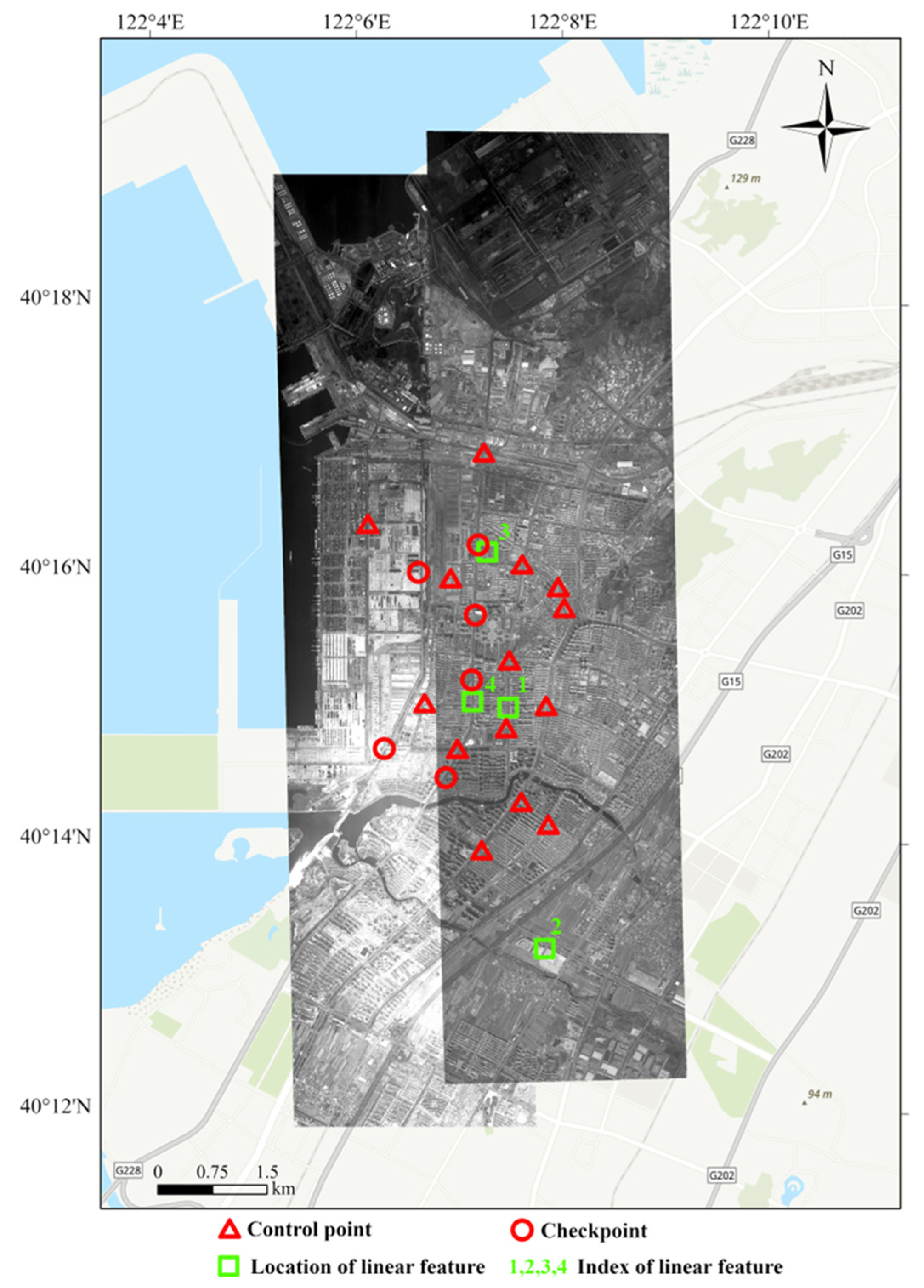
3.2. Experimental Data
3.3. EOP Problem Caused by the Self-Developed POS
4. Method
- Level 1 image generation: This step addresses severe distortions in the original images, setting the stage for further processing.
- Tie point matching: This involves obtaining tie points across images from different views to collect extensive observations critical for the bundle adjustment.
- Bundle adjustment: Utilizing the Gaussian Markov model, this stage accurately models the motion of the sensor and is incorporated into the bundle adjustment process.
- Cubic spline interpolation: Applying cubic spline interpolation, EOPs of lines without observations are obtained.
4.1. Modeling the Sensor Motion with the First-Order Gauss-Markov Model
4.2. EOP Refinement Workflow
4.2.1. Level 1 Image Generation
4.2.2. Tie Point Matching
4.2.3. Bundle Adjustment
4.2.4. Cubic Spline Interpolation
5. Results and Discussion
5.1. Experimental Settings
5.2. Overall Comparison
5.2.1. Quantitative Evaluation
5.2.2. Comparison of Residual Distributions at Tie Points
5.2.3. Visual Performance of EOP Refinement
5.3. Effectiveness of Cubic Spline Interpolation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gruen, A.; Zhang, L.; Wang, X. 3D City Modeling with TLS (Three Line Scanner) Data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2003, 34, 24–27. [Google Scholar]
- Müller, J.; Gärtner-Roer, I.; Thee, P.; Ginzler, C. Accuracy Assessment of Airborne Photogrammetrically Derived High-Resolution Digital Elevation Models in a High Mountain Environment. ISPRS J. Photogramm. Remote Sens. 2014, 98, 58–69. [Google Scholar] [CrossRef]
- Zhu, X.; Pang, G.; Chen, P.; Tao, Y.; Zhang, Y.; Zuo, X. Research on Urban Construction Land Change Detection Method Based on Dense DSM and TDOM of Aerial Images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 42, 205–210. [Google Scholar] [CrossRef]
- Xi, K.; Duan, Y. AMS-3000 Large Field View Aerial Mapping System: Basic Principles and the Workflow. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 79–84. [Google Scholar] [CrossRef]
- Gruen, A.; Zhang, L. Sensor Modeling for Aerial Mobile Mapping with Three-Line-Scanner (TLS) Imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2002, 34, 139–146. [Google Scholar]
- Zhai, F.; Li, J.; Ye, W.; Gu, B.; Lu, Z.; Qiu, H.; Li, J. An Airborne Position and Orientation System (POS) for Remote Sensing and Its Current State. In Proceedings of the 2017 IEEE International Conference on Imaging Systems and Techniques (IST), Beijing, China, 18–20 October 2017; IEEE: New York, NY, USA; pp. 1–6. [Google Scholar]
- Li, J.; Ma, L.; Fan, Y.; Wang, N.; Duan, K.; Han, Q.; Zhang, X.; Su, G.; Li, C.; Tang, L. An Image Stitching Method for Airborne Wide-Swath Hyperspectral Imaging System Equipped with Multiple Imagers. Remote Sens. 2021, 13, 1001. [Google Scholar] [CrossRef]
- Pivnicka, F.; Kemper, G.; Geissler, S. Calibration Procedures in Mid Format Camera Setups. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 149–152. [Google Scholar] [CrossRef]
- Yotumata, T.; Okagawa, M.; Fukuzawa, Y.; Tachibana, K.; Sasagawa, T. Investigation for Mapping Accuracy of the Airborne Digital Sensor-ADS40. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2002, 34, 304–315. [Google Scholar]
- Hinsken, L.; Miller, S.; Tempelmann, U.; Uebbing, R.; Walker, A.S. Triangulation of LH Systems ADS40 Imagery Using Orima GPS/IMU. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2002, 34, 156–162. [Google Scholar]
- Marks, R.J.I. Introduction to Shannon Sampling and Interpolation Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; ISBN 1-4613-9708-1. [Google Scholar]
- Zhu, Y.; Yang, T.; Wang, M.; Hong, H.; Zhang, Y.; Wang, L.; Rao, Q. Jitter Detection Method Based on Sequence CMOS Images Captured by Rolling Shutter Mode for High-Resolution Remote Sensing Satellite. Remote Sens. 2022, 14, 342. [Google Scholar] [CrossRef]
- Amberg, V.; Dechoz, C.; Bernard, L.; Greslou, D.; De Lussy, F.; Lebegue, L. In-Flight Attitude Perturbances Estimation: Application to PLEIADES-HR Satellites; SPIE: San Diego, CA, USA, 2013; p. 886612. [Google Scholar]
- Kirk, R.L.; Howington-Kraus, E.; Redding, B.; Galuszka, D.; Hare, T.M.; Archinal, B.A.; Soderblom, L.A.; Barrett, J.M. High-resolution Topomapping of Candidate MER Landing Sites with Mars Orbiter Camera Narrow-angle Images. J.Geophys.Res. 2003, 108, JE002131. [Google Scholar] [CrossRef]
- Girod, L.; Nuth, C.; Kääb, A.; McNabb, R.; Galland, O. MMASTER: Improved ASTER DEMs for Elevation Change Monitoring. Remote Sens. 2017, 9, 704. [Google Scholar] [CrossRef]
- Schwind, P.; Schneider, M.; Palubinskas, G.; Storch, T.; Muller, R.; Richter, R. Processors for ALOS Optical Data: Deconvolution, DEM Generation, Orthorectification, and Atmospheric Correction. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4074–4082. [Google Scholar] [CrossRef]
- Ayoub, F.; Leprince, S.; Binet, R.; Lewis, K.W.; Aharonson, O.; Avouac, J.-P. Influence of Camera Distortions on Satellite Image Registration and Change Detection Applications. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 6–11 July 2008; IEEE: New York, NY, USA; pp. II-1072–II-1075. [Google Scholar]
- Zhang, Z.; Iwasaki, A.; Xu, G. Attitude Jitter Compensation for Remote Sensing Images Using Convolutional Neural Network. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1358–1362. [Google Scholar] [CrossRef]
- Weser, T.; Rottensteiner, F.; Willneff, J.; Poon, J.; Fraser, C.S. Development and Testing of a Generic Sensor Model for Pushbroom Satellite Imagery. Photogramm. Rec. 2008, 23, 255–274. [Google Scholar] [CrossRef]
- Breit, H.; Fritz, T.; Balss, U.; Lachaise, M.; Niedermeier, A.; Vonavka, M. TerraSAR-X SAR Processing and Products. IEEE Trans. Geosci. Remote Sens. 2010, 48, 727–740. [Google Scholar] [CrossRef]
- Pan, H.; Zou, Z. Penalized Spline: A General Robust Trajectory Model for Ziyuan-3 Satellite. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B1, 365–372. [Google Scholar] [CrossRef]
- Bostelmann, J.; Heipke, C. Modeling Spacecraft Oscillations in HRSC Images of Mars Express. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 38, 51–56. [Google Scholar] [CrossRef]
- Geng, X.; Xu, Q.; Wang, J.; Lan, C.; Qin, F.; Xing, S. Generation of Large-Scale Orthophoto Mosaics Using MEX HRSC Images for the Candidate Landing Regions of China’s First Mars Mission. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–20. [Google Scholar] [CrossRef]
- Zhang, X.; Pan, H.; Zhou, S.; Zhu, X. Self-Calibration Strip Bundle Adjustment of High-Resolution Satellite Imagery. Remote Sens. 2024, 16, 2196. [Google Scholar] [CrossRef]
- Li, R.; Hwangbo, J.; Chen, Y.; Di, K. Rigorous Photogrammetric Processing of HiRISE Stereo Imagery for Mars Topographic Mapping. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2558–2572. [Google Scholar]
- McGlone, J.C. Photogrammetric Analysis of Aircraft Multispectral Scanner Data; School of Civil Engineering, Purdue University: West Lafayette, Indiana, 1982; p. 178. [Google Scholar]
- Lee, C.; Theiss, H.J.; Bethel, J.S.; Mikhail, E.M. Rigorous Mathematical Modeling of Airborne Pushbroom Imaging Systems. Photogramm. Eng. Remote Sens. 2000, 66, 385–392. [Google Scholar]
- Jonsson, E.; Riso, C.; Lupp, C.A.; Cesnik, C.E.S.; Martins, J.R.R.A.; Epureanu, B.I. Flutter and Post-Flutter Constraints in Aircraft Design Optimization. Prog. Aerosp. Sci. 2019, 109, 100537. [Google Scholar] [CrossRef]
- Zhang, H.; Duan, Y.; Zhou, Q.; Chen, Q.; Cai, B.; Tao, P.; Zhang, Z. Calibrating an Airborne Linear-Array Multi-Camera System on the Master Focal Plane with Existing Bundled Images. Geo-Spat. Inf. Sci. 2024, 1–19. [Google Scholar] [CrossRef]
- Tong, X.; Ye, Z.; Xu, Y.; Tang, X.; Liu, S.; Li, L.; Xie, H.; Wang, F.; Li, T.; Hong, Z. Framework of Jitter Detection and Compensation for High Resolution Satellites. Remote Sens. 2014, 6, 3944–3964. [Google Scholar] [CrossRef]
- Barker, J.L.; Seiferth, J.C. Landsat Thematic Mapper Band-to-Band Registration. In Proceedings of the IGARSS ’96. 1996 International Geoscience and Remote Sensing Symposium, Lincoln, NE, USA, 31 May 1996; IEEE: New York, NY, USA; Volume 3, pp. 1600–1602. [Google Scholar]
- Delevit, J.M.; Greslou, D.; Amberg, V.; Dechoz, C.; De Lussy, F.; Lebegue, L.; Latry, C.; Artigues, S.; Bernard, L. Attitude Assessment Using Pleiades-HR Capabilities. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 525–530. [Google Scholar] [CrossRef]
- Iwata, T.; Kawahara, T.; Muranaka, N.; Laughlin, D. High-Bandwidth Attitude Determination Using Jitter Measurements and Optimal Filtering. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 August 2009; American Institute of Aeronautics and Astronautics: Chicago, IL, USA, 2009. [Google Scholar]
- Pan, H.; Huang, T.; Zhou, P.; Cui, Z. Self-Calibration Dense Bundle Adjustment of Multi-View Worldview-3 Basic Images. ISPRS J. Photogramm. Remote Sens. 2021, 176, 127–138. [Google Scholar] [CrossRef]
- Pan, H.; Zou, Z.; Zhang, G.; Zhu, X.; Tang, X. A Penalized Spline-Based Attitude Model for High-Resolution Satellite Imagery. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1849–1859. [Google Scholar] [CrossRef]
- Teshima, Y.; Iwasaki, A. Correction of Attitude Fluctuation of Terra Spacecraft Using ASTER/SWIR Imagery with Parallax Observation. IEEE Trans. Geosci. Remote Sens. 2007, 46, 222–227. [Google Scholar] [CrossRef]
- Mattson, S.; Boyd, A.; Kirk, R.; Cook, D.; Howington-Kraus, E. HiJACK: Correcting Spacecraft Jitter in HiRISE Images of Mars. Health Manag. Technol 2009, 33, A162. [Google Scholar]
- Tong, X.; Xu, Y.; Ye, Z.; Liu, S.; Tang, X.; Li, L.; Xie, H.; Xie, J. Attitude Oscillation Detection of the ZY-3 Satellite by Using Multispectral Parallax Images. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3522–3534. [Google Scholar] [CrossRef]
- Liu, S.; Tong, X.; Wang, F.; Sun, W.; Guo, C.; Ye, Z.; Jin, Y.; Xie, H.; Chen, P. Attitude Jitter Detection Based on Remotely Sensed Images and Dense Ground Controls: A Case Study for Chinese ZY-3 Satellite. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5760–5766. [Google Scholar] [CrossRef]
- Jung, W.; Bethel, J. Stochastic Modeling and Triangulation for an Airborne Three-Line Scanner. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 653–656. [Google Scholar]
- Kocaman, S.; Zhang, L. Investigations on the Triangulation Accuracy of Starimager Imagery. In Proceedings of the ASPRS Annual Convention, Baltimore, MD, USA, 7–11 March 2005. [Google Scholar]
- Wang, T.; Zhang, Y.; Zhang, Y.; Jiang, G.; Zhang, Z.; Yu, Y.; Dou, L. Geometric Calibration for the Aerial Line Scanning Camera GFXJ. Photogramm. Eng. Remote Sens. 2019, 85, 643–658. [Google Scholar] [CrossRef]
- Jia, G.; Wang, X.; Wei, H.; Zhang, Z. Modeling Image Motion in Airborne Three-Line-Array (TLA) Push-Broom Cameras. Photogramm. Eng. Remote Sens. 2013, 79, 67–78. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Wang, M.; Hu, F.; Li, J.; Pan, J. A Fast Approach to Best Scanline Search of Airborne Linear Pushbroom Images. Photogramm. Eng. Remote Sens. 2009, 75, 1059–1067. [Google Scholar] [CrossRef]
- Zhang, Z.; He, J.; Huang, S.; Duan, Y. Dense Image Matching with Two Steps of Expansion. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 143–149. [Google Scholar] [CrossRef]
- Cao, J.; Fu, J.; Yuan, X.; Gong, J. Nonlinear Bias Compensation of ZiYuan-3 Satellite Imagery with Cubic Splines. ISPRS J. Photogramm. Remote Sens. 2017, 133, 174–185. [Google Scholar] [CrossRef]
- Toutin, T. Review Article: Geometric Processing of Remote Sensing Images: Models, Algorithms and Methods. Int. J. Remote Sens. 2004, 25, 1893–1924. [Google Scholar] [CrossRef]
- Liu, S.; Tong, X.; Li, L.; Ye, Z.; Lin, F.; Zhang, H.; Jin, Y.; Xie, H. Geometric Modeling of Attitude Jitter for Three-Line-Array Imaging Satellites. Opt. Express 2021, 29, 20952–20969. [Google Scholar] [CrossRef]
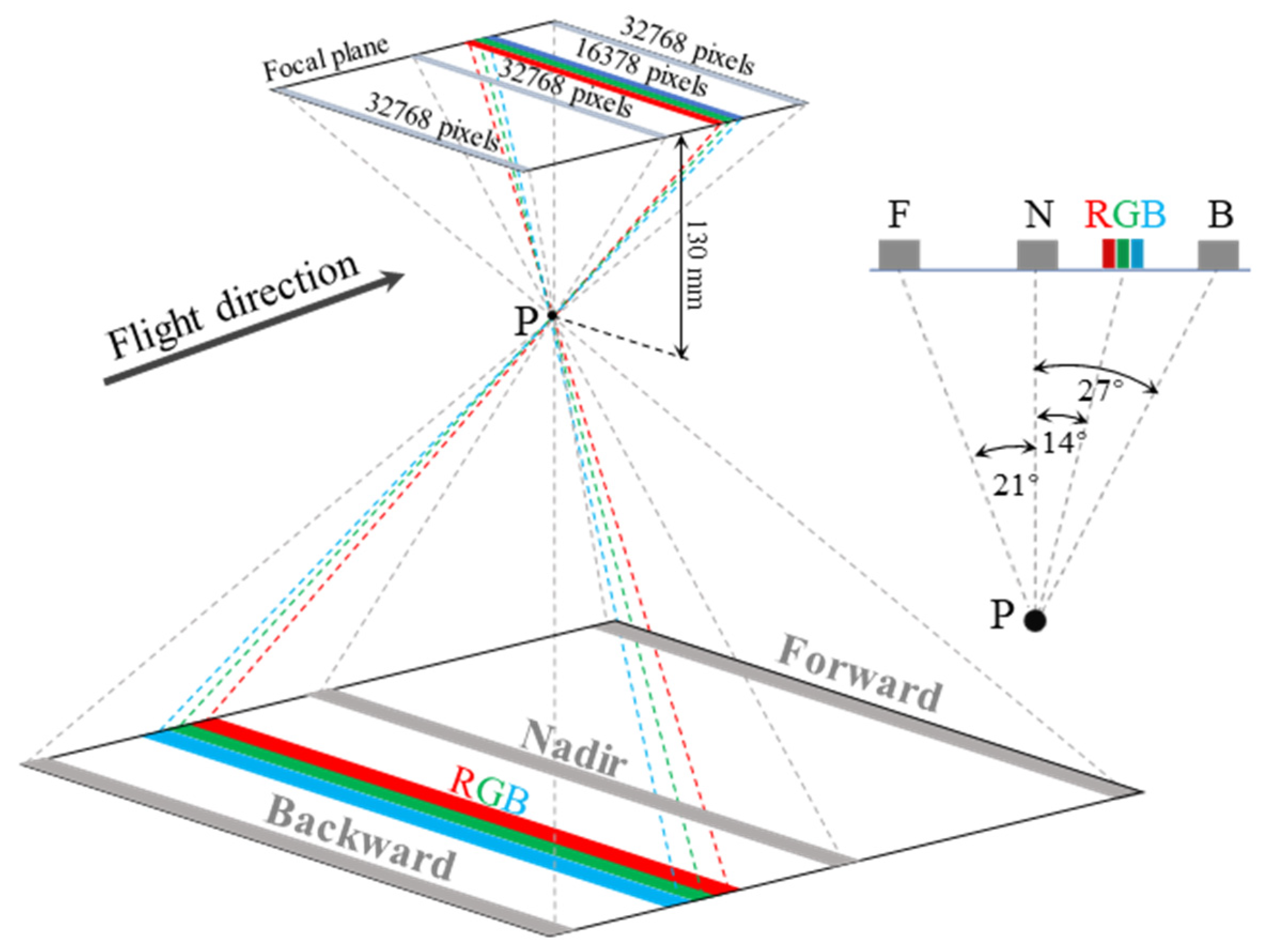






| Item | Designed Parameter |
|---|---|
| Focal length (mm) | 130 |
| Radiometric resolution (bit) | 16 |
| Pixel size (μm) | Panchromatic: 5, RGB: 10 |
| Spectrum (nm) | Panchromatic: 465–680, R: 608–662, G: 428–492, B: 428–492 |
| Field of view (degree) | 64 |
| Weight (kg) | 72.5 |
| Topographic Mapping Scale | Planar RMSE | Height RMSE | ||||
|---|---|---|---|---|---|---|
| Flat | Hills | Mountains | Flat | Hills | Mountains | |
| 1:1000 | 0.5 | 0.5 | 0.7 | 0.28 | 0.4 | 0.6 |
| 1:2000 | 1.0 | 1.0 | 1.4 | 0.28 | 0.4 | 1.0 |
| Performance | POS AV610 | Self-Developed POS Product |
|---|---|---|
| Position (m) | Horizontal: 0.05, vertical: 0.1 | Horizontal: 0.05, vertical: 0.1 |
| Velocity (m/s) | 0.005 | 0.02 |
| Roll and pitch (degree) | 0.0025 | 0.015 |
| True heading (degree) | 0.005 | 0.030 |
| GNSS frequency (Hz) | 200 | 2 |
| IMU frequency (Hz) | 1000 | 200 |
| Post-processing software | POS Pac 8 | self-developed software |
| Method | X | Y | Z | |||
|---|---|---|---|---|---|---|
| Std | RMSE | Std | RMSE | Std | RMSE | |
| DR | 3.943 | 4.040 | 3.835 | 3.947 | 0.587 | 6.007 |
| PPM | 0.102 | 0.115 | 0.079 | 0.089 | 0.200 | 0.208 |
| LIM | 0.097 | 0.112 | 0.074 | 0.083 | 0.198 | 0.205 |
| Ours | 0.076 | 0.088 | 0.069 | 0.078 | 0.145 | 0.150 |
| Method | Line 1 | Line 2 | Line 3 | Line 4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Max | Min | RMSE | Max | Min | RMSE | Max | Min | RMSE | Max | Min | RMSE | |
| DR | 1.55 | 0.01 | 0.85 | 2.36 | 0.00 | 1.01 | 2.68 | 0.03 | 1.24 | 2.87 | 0.02 | 1.50 |
| PPM | 0.7 | 0.01 | 0.31 | 2.00 | 0.02 | 0.91 | 3.86 | 0.07 | 1.55 | 1.7 | 0.01 | 0.71 |
| LIM | 1.23 | 0.01 | 0.54 | 1.18 | 0.01 | 0.51 | 1.59 | 0.02 | 0.67 | 1.78 | 0.01 | 0.65 |
| Ours | 0.65 | 0.01 | 0.27 | 0.71 | 0.00 | 0.28 | 1.02 | 0.00 | 0.47 | 0.93 | 0.01 | 0.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Duan, Y.; Qin, W.; Zhou, Q.; Zhang, Z. Exterior Orientation Parameter Refinement of the First Chinese Airborne Three-Line Scanner Mapping System AMS-3000. Remote Sens. 2024, 16, 2362. https://doi.org/10.3390/rs16132362
Zhang H, Duan Y, Qin W, Zhou Q, Zhang Z. Exterior Orientation Parameter Refinement of the First Chinese Airborne Three-Line Scanner Mapping System AMS-3000. Remote Sensing. 2024; 16(13):2362. https://doi.org/10.3390/rs16132362
Chicago/Turabian StyleZhang, Hao, Yansong Duan, Wei Qin, Qi Zhou, and Zuxun Zhang. 2024. "Exterior Orientation Parameter Refinement of the First Chinese Airborne Three-Line Scanner Mapping System AMS-3000" Remote Sensing 16, no. 13: 2362. https://doi.org/10.3390/rs16132362
APA StyleZhang, H., Duan, Y., Qin, W., Zhou, Q., & Zhang, Z. (2024). Exterior Orientation Parameter Refinement of the First Chinese Airborne Three-Line Scanner Mapping System AMS-3000. Remote Sensing, 16(13), 2362. https://doi.org/10.3390/rs16132362







