Fast and Reliable Network RTK Positioning Based on Multi-Frequency Sequential Ambiguity Resolution under Significant Atmospheric Biases

Abstract

The positioning performance of the Global Navigation Satellite System (GNSS) network real-time kinematic (NRTK) depends on regional atmospheric error modeling. Under normal atmospheric conditions, NRTK positioning provides high accuracy and rapid initialization. However, fluctuations in atmospheric conditions can lead to poor atmospheric error modeling, resulting in significant atmospheric biases that affect the positioning accuracy, initialization speed, and reliability of NRTK positioning. Consequently, this decreases the efficiency of NRTK operations. In response to these challenges, this paper proposes a fast and reliable NRTK positioning method based on sequential ambiguity resolution (SAR) of multi-frequency combined observations. This method processes observations from extra-wide-lane (EWL), wide-lane (WL), and narrow-lane (NL) measurements; performs sequential AR using the LAMBDA algorithm; and subsequently constrains other parameters using fixed ambiguities. Ultimately, this method achieves high precision, rapid initialization, and reliable positioning. Experimental analysis was conducted using Continuous Operating Reference Station (CORS) data, with baseline lengths ranging from 88 km to 110 km. The results showed that the proposed algorithm offers positioning accuracy comparable to conventional algorithms in conventional NRTK positioning and has higher fixed rate and positioning accuracy in single-epoch positioning. On two datasets, the proposed algorithm demonstrated over 30% improvement in time to first fix (TTFF) compared to conventional algorithms. It provides higher precision in suboptimal positioning solutions when conventional NRTK algorithms fail to achieve fixed solutions during the initialization phase. These experiments highlight the advantages of the proposed algorithm in terms of initialization speed and positioning reliability.

1. Introduction

Network real-time kinematic (NRTK) positioning, as a comprehensive high-precision positioning technology, has been extensively utilized in geodetic surveys, engineering measurements, and industries related to location information. However, achieving high precision in NRTK positioning relies on precise modeling of spatially correlated errors. Among these spatially correlated errors, ionospheric delay and tropospheric delay are predominant. Due to its strong spatial correlation, tropospheric delay can be effectively mitigated through well-established modeling, with tropospheric delay modeling residual typically measuring only a few centimeters, exerting minimal impact on ambiguity resolution (AR). Corresponding to it, ionospheric delay presents significant uncertainty, especially during periods of ionospheric activity, resulting in suboptimal modeling outcomes. Ionospheric delay modeling residual can adversely affect the initialization speed, positioning accuracy, and reliability of real-time kinematic (RTK) positioning [1,2,3]. With the modernization of global navigation systems [4,5], BDS-3 and Galileo satellite systems support the broadcast of five-frequency signals. In the modernization process of GPS, new satellites are also beginning to support the broadcast of third-frequency signals. GLONASS satellite systems employ dual-frequency signals based on Frequency Division Multiple Access (FDMA). In their modernization process, GLONASS satellites are also introducing third-frequency Code Division Multiple Access (CDMA) signals. Currently, all satellite systems support the broadcast of triple-frequency or five-frequency signals. Multi-frequency observations offer numerous solutions for solving problems such as long baseline AR, AR between NRTK reference stations, and fast and reliable positioning affected by atmospheric biases [6,7,8].

In the realm of single-epoch positioning research, Forssell et al. [9] and Vollath et al. [10] first put forward a fast ambiguity fixing method using triple-frequency observations, known as TCAR. The traditional TCAR method resolves the integer ambiguity of the selected linear combination by rounding, starting from the longest wavelength to the shortest, thus achieving rapid resolution of the combination ambiguity. Geng and Guo [11] achieved precise point positioning (PPP) at the decimeter level in a single epoch using Galileo satellites with observations from three or more frequencies, and they subsequently enhanced positioning accuracy through filtering. Ji et al. [12] studied the performance of single-epoch AR using cascading ambiguity resolution (CAR) and LAMBDA methods using Galileo quad-frequency data. The results indicate that overall, the LAMBDA method outperforms the CAR method. The speed of AR is closely related to the accuracy of carrier phase measurement. Gao et al. [13] investigated the quad-frequency observations from BDS and Galileo. They initially fixed two ambiguities for EWL observations based on the geometric-free (GF) and IF models and then jointly fixed the EWL ambiguities using the geometric-base (GB) model. This approach achieves decimeter-level positioning for medium to long baselines. Zhang et al. [14] studied the AR method for multi-frequency carrier observations based on three-frequency, quad-frequency, and five-frequency observations, and they discussed high-quality signals and optimal linear combinations under different baseline lengths. Finally, the experiments indicated that MCAR can effectively resolve single-epoch ambiguities, and increasing the number of frequencies can significantly improve the success rate of AR. Liu et al. [15] proposed a long baseline RTK positioning method based on BDS-3 five-frequency ionosphere–reduce (IR) combination. The measured data results show that the step-by-step fixed model of the IR EWL/WL combination can achieve long baseline instantaneous decimeter level positioning. Wang et al. [16] used BDS-3 multi-frequency observations to initially resolve an EWL and WL ambiguities, obtaining high-precision WL ambiguity through linear combination. Subsequently, they constrained the IR combination NL ambiguity This method effectively improves the success rate and positioning accuracy of NL ambiguity fixation.

In the research focused on fast and reliable positioning or rapid AR, Li et al. [17] proposed the use of the triple-frequency observations of BDS to fix two EWL ambiguities first, then use the ionosphere-fixed model or ionosphere-float model to achieve decimeter-level fast positioning, as well as using Kalman filter to calculate NL ambiguity, altogether to achieve a NL ambiguity fixing rate as high as 84% in five epochs. Xie et al. [18] proposed a method that first rapidly fixed two EWL ambiguities of BDS using a high success rate and then derived WL ambiguities through transformation. They further used BDS WL to aid in fixing GPS WL ambiguities and parameterized ionospheric and tropospheric delay to expedite the convergence of NL ambiguity floating solutions. This approach shortened the time for the first fix of ambiguities. Tian et al. [19] improved the conventional TCAR method by utilizing the observations of the BDS triple-frequency, smoothing the ionospheric delay derived from the EWL using the ionospheric delay containing ambiguity information derived from the original observations. Subsequently, they mitigated the ionospheric effects in single-epoch positioning using the ionospheric delay derived from EWL. This method achieved rapid AR for medium to long baselines. Pu et al. [20] used GPS/Galileo/BDS triple-frequency observations and the C-TCAR method to initially fix two EWL ambiguities. By subsequently transforming the WL ambiguities, they employed the IW-TCAR model to resolve narrow-lane (NL) ambiguities based on the ambiguities fixed in EWL, WL, and NL observations. Their experiments demonstrated that the IW-TCAR algorithm significantly improved the time to first fix (TTFF) compared to the C-TCAR algorithm. Henkel and Günther [21] studied the Galileo triple-frequency combination observation and achieved a fixing success rate of over 90% within two seconds. The proposed method can achieve reliable AR in a short period of time.

Regarding long baseline positioning or positioning reliability, Zhao et al. [22] explored the limitations of the classical TCAR method and modified it by eliminating ionospheric delay and geometric terms using ambiguities fixed in EWL, WL, and three pseudo-range observations. The data results indicate that the improved TCAR method outperformed the classical TCAR method. Wang et al. [23] proposed a single-epoch rapid resolution model. They first resolved ambiguities of triple-frequency carrier phase observations and then resolved ambiguities of dual-frequency carrier phase observations. This process led to rapid AR in a single epoch. Gong et al. [24] proposed a fast AR method based on GPS/BDS multi-frequency observation measurements. This method first uses double-difference non-combined observations to obtain a float solution for ambiguities, and atmospheric biases are estimated as random walk parameters through a Kalman filter. The EWL, WL, and NL ambiguity are sequentially fixed using the LAMBDA algorithm. Subsequently, experiments indicate that only approximately one, two, and six epochs (30 s intervals) are needed to fix the ambiguities of EWL, WL, and NL, respectively. Regarding reconvergence time during ionospheric activity periods, 90% of the epochs can be fixed within two epochs by using atmospheric bias information obtained from the previous 5 min. Finally, the positioning accuracy of EWL, WL, and NL fixed solutions reached the meter level, decimeter level, and centimeter level, respectively. Tang et al. [25] introduced the IF-TCAR method to address AR between reference stations in long baseline positioning. Based on known reference station positions, easy to fix EWL ambiguities, and ionosphere-free combinations, they reliably fixed WL ambiguities. Finally, they restored the original ambiguities using the fixed WL ambiguities and ionosphere-free combinations, achieving a 100% correct AR rate. Li et al. [26] analyzed the advantages of BDS-3 B1C/B1I/B2a triple-frequency observations in long baseline positioning. They proposed optimal ionosphere-free and IR combinations, resulting in a 20% improvement in positioning accuracy compared to BDS-3 B1C/B2a or GPS L1/L5 dual-frequency combinations. Experiments indicate that the triple-frequency ionosphere-free combination improved RTK positioning accuracy by 7–9%, while the IR combination achieved an 88.4% fix rate for 1600 km baselines. Ji et al. [27] used full-frequency data to progressively resolve EWL, WL, system-wide WL, NL subsets, and NL ambiguities between reference stations. This method achieved long baseline NRTK single-epoch AR, with fixed rates exceeding 90%.

Based on the preceding research, in order to solve the issues of slow initialization of NRTK positioning caused by atmospheric biases, low positioning accuracy during the initialization phase, and reduced positioning reliability, this paper proposes a solution based on multi-frequency combined observations. The structure of this paper is as follows. In the first section, the combination methods of multi-frequency combined observations are introduced, followed by a description of the combination observations and algorithm used in this paper in the second section. Finally, this paper demonstrates the advantages of the proposed NRTK fast and reliable positioning algorithm from multiple perspectives using Continuous Operating Reference Station (CORS) data.

2. Fundamental Mathematical Model

With the original single-frequency double-differenced (DD) pseudo-range and carrier phase measurements, the combined multi-frequency DD observations can be expressed as

$$\Delta \nabla P_{\left(i,j,k,t\right)}=\frac{i\cdot f_1\cdot \Delta \nabla P_1+j\cdot f_2\cdot \Delta \nabla P_2+k\cdot f_3\cdot \Delta \nabla P_3+t\cdot f_4\cdot \Delta \nabla P_4}{i\cdot f_1+j\cdot f_2+k\cdot f_3+t\cdot f_4}$$

(1)

$$\Delta \nabla {\varphi }_{\left(i,j,k,t\right)}=\frac{i\cdot f_1\cdot \Delta \nabla {\varphi }_1+j\cdot f_2\cdot \Delta \nabla {\varphi }_2+k\cdot f_3\cdot \Delta \nabla {\varphi }_3+t\cdot f_4\cdot \Delta \nabla {\varphi }_4}{i\cdot f_1+j\cdot f_2+k\cdot f_3+t\cdot f_4}$$

(2)

$$\Delta \nabla {\phi }_{\left(i,j,k,t\right)}=i\cdot \Delta \nabla {\phi }_1+j\cdot \Delta \nabla {\phi }_2+k\cdot \Delta \nabla {\phi }_3+t\cdot \Delta \nabla {\phi }_4$$

(3)

where $\Delta \nabla$ is the DD operation to the term immediately to the right; the combination coefficients $i,j,k,t$ are integers; for the i-th frequency $f_i$, $\Delta \nabla P_i$ and $\Delta \nabla {\varphi }_i$ are the DD code and DD phase measurements in meters, respectively; and $\Delta \nabla {\phi }_i$ is the DD phase measurement in cycles. The combined frequency $f_{\left(i,j,k,t\right)}$, the corresponding wavelength ${\lambda }_{\left(i,j,k,t\right)}$, the combined integer ambiguity $\Delta \nabla N_{\left(i,j,k,t\right)}$, the combined first-order ionospheric scale factor ${\beta }_{\left(i,j,k,t\right)}$, and the phase noise factor ${\mu }_{\left(i,j,k,t\right)}^2$ are defined, respectively, as

$$f_{\left(i,j,k,t\right)}=i\cdot f_1+j\cdot f_2+k\cdot f_3+t\cdot f_4$$

(4)

$${\lambda }_{\left(i,j,k,t\right)}=\frac{c}{i\cdot f_1+j\cdot f_2+k\cdot f_3+t\cdot f_4}$$

(5)

$$\Delta \nabla N_{\left(i,j,k,t\right)}=i\cdot \Delta \nabla N_1+j\cdot \Delta \nabla N_2+k\cdot \Delta \nabla N_3+t\cdot \Delta \nabla N_4$$

(6)

$${\beta }_{\left(i,j,k,t\right)}=\frac{f_1^2\left(\raisebox{1ex}{$i$}\!\left/ \!\raisebox{-1ex}{$f_1$}\right.+\raisebox{1ex}{$j$}\!\left/ \!\raisebox{-1ex}{$f_2$}\right.+\raisebox{1ex}{$k$}\!\left/ \!\raisebox{-1ex}{$f_3$}\right.+\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$f_4$}\right.\right)}{i\cdot f_1+j\cdot f_2+k\cdot f_3+t\cdot f_4}$$

(7)

$${\mu }_{\left(i,j,k,t\right)}^2=\frac{{\left(i\cdot f_1\right)}^2+{\left(j\cdot f_2\right)}^2+{\left(k\cdot f_3\right)}^2+{\left(t\cdot f_4\right)}^2}{i\cdot f_1+j\cdot f_2+k\cdot f_3+t\cdot f_4}$$

(8)

From the single-frequency DD observation Equations (1) and (2), the $\Delta \nabla P_{\left(i,j,k,t\right)}$ and $\Delta \nabla {\varphi }_{\left(i,j,k,t\right)}$ observation of the selected combination can be derived, respectively, as

$$\Delta \nabla {\varphi }_{\left(i,j,k,t\right)}=\Delta \nabla \rho +\Delta \nabla {\delta }_{orb}+\Delta \nabla {\delta }_{trop}-{\beta }_{\left(i,j,k,t\right)}\frac{\Delta \nabla I}{f_1^2}-{\lambda }_{\left(i,j,k,t\right)}\Delta \nabla N_{\left(i,j,k,t\right)}+{\epsilon }_{\Delta \nabla \varphi \left(i,j,k,t\right)}$$

(9)

$$\Delta \nabla P_{\left(i,j,k,t\right)}=\Delta \nabla \rho +\Delta \nabla {\delta }_{orb}+\Delta \nabla {\delta }_{trop}+{\beta }_{\left(i,j,k,t\right)}\frac{\Delta \nabla I}{f_1^2}+{\epsilon }_{\Delta \nabla P\left(i,j,k,t\right)}$$

(10)

where $\Delta \nabla \rho$ represents the DD geometric distance between satellite and receiver, $\Delta \nabla {\delta }_{orb}$ is the DD satellite orbital error, $\Delta \nabla {\delta }_{trop}$ is the DD tropospheric delay, and $\Delta \nabla I$ is the DD first-order ionospheric delay. The integer ambiguity of the phase measurement in cycles is $N_i$, and ${\epsilon }_{\Delta \nabla P}$ and ${\epsilon }_{\Delta \nabla \varphi }$ are the observation noise for the code and phase observation, respectively.

In RTK, ionospheric delay and tropospheric delay are corrected through prior models or estimated as parameters. Different from this, in NRTK, ionospheric delay and tropospheric delay are modeled and corrected between reference stations. In conventional NRTK positioning, it is assumed that these delays have been fully corrected and have not been further adjusted [28]. Therefore, the positioning performance of NRTK is affected by the effectiveness of ionospheric delay modeling and tropospheric delay modeling.

3. Multi-Frequency Sequential Ambiguity Resolution (SAR)

In this section, we listed the public signals used in the proposed algorithm as shown in

Table 1. NL observations used in experiments.

Satellite Systems	Frequency	Signals	Wavelength/m
GPS	$f_1$	L1	0.19
	$f_2$	L2	0.24
	$f_3$	L5	0.25
BDS-2	$f_1$	B1I	0.19
	$f_2$	B2I	0.24
	$f_3$	B3I	0.23
BDS-3	$f_1$	B1I	0.19
	$f_2$	B3I	0.23
	$f_3$	B1C	0.19
	$f_4$	B2a	0.25

, and the types of combined observations used are shown in

Table 2. Combined observations used in the sequential solution NRTK algorithm.

Satellite Systems	$\mathit{i}$	$\mathit{j}$	$\mathit{k}$	$\mathit{t}$	Combined Observations	Wavelength/m	$\mathit{\beta }$	$\mathit{\mu }$
GPS	0	1	−1	/	L2-L5 (EWL)	4.98	−1.7186	33.2415
	1	−1	0	/	L1-L2 (WL)	0.86	−1.2833	5.7422
	1	0	0	/	L1 (NL)	0.19	1	1
BDS-2	0	−1	1	/	B3I-B2I (EWL)	4.88	−1.5915	28.5287
	1	−1	0	/	B1I-B2I (WL)	0.84	−1.2932	5.5752
	1	0	0	/	B1I (NL)	0.19	1	1
BDS-3	−1	0	1	0	B1C-B1I (EWL)	20.93	−0.9909	154.8580
	0	1	0	−1	B3I-B2a (EWL)	3.26	−1.6330	18.7909
	0	0	1	−1	B1C-B2a (WL)	0.75	−1.3148	4.9282
	1	0	0	0	B1I (NL)	0.19	1	1

. We also analyzed the impact of atmospheric error modeling residuals on various types of ambiguity. Subsequently, we introduce the solution model and the processing workflow of the algorithm proposed in this paper.

In NRTK positioning, the accuracy of atmospheric error modeling is the primary influence factor on positioning precision. Under typical atmospheric conditions, both ionospheric delay and tropospheric delay can be effectively modeled. However, during periods of ionospheric activity, the accuracy of ionospheric delay modeling decreases and often results in significant modeling residuals. When the ionospheric delay modeling residual reaches one NL wavelength or more, it poses challenges to the resolution of NL ambiguity. Nevertheless, due to the longer wavelengths of EWL and WL, even when the ionospheric delay modeling residual modeling reaches an NL wavelength, the impact on the WL combination remains within one quarter-wavelength. For the EWL combination, the impact is even smaller. This indicates that the EWL and WL combinations are better able to withstand the influence of atmospheric biases.

Therefore, this paper presents a method for sequentially resolves ambiguities using EWL, WL, and NL combinations to achieve fast and reliable NRTK positioning.

The single-system model for this method (using four frequencies as an example) is as follows:

$$\left[\begin{array}{c}\Delta \nabla {\phi }_{EWL1}\\ \Delta \nabla {\phi }_{EWL2}\\ \Delta \nabla {\phi }_{WL}\\ \Delta \nabla {\phi }_1\\ \Delta \nabla P_1\\ \Delta \nabla P_2\\ \Delta \nabla P_3\\ \Delta \nabla P_4\end{array}\right]=\left[\begin{array}{ccccc}A& {\lambda }_{EWL1}& 0& 0& 0\\ A& 0& {\lambda }_{EWL2}& 0& 0\\ A& 0& 0& {\lambda }_{WL}& 0\\ A& 0& 0& 0& {\lambda }_1\\ A& 0& 0& 0& 0\\ A& 0& 0& 0& 0\\ A& 0& 0& 0& 0\\ A& 0& 0& 0& 0\end{array}\right]\cdot \left[\begin{array}{c}\delta X\\ \Delta \nabla N_{EWL1}\\ \Delta \nabla N_{EWL2}\\ \Delta \nabla N_{WL}\\ \Delta \nabla N_1\end{array}\right]$$

(11)

where $\Delta \nabla$ represents the double-difference operator; ${\phi }_1$ denotes the L1 carrier phase observation, where ${\phi }_{EW{L}_j}$ represents the carrier phase observation of the $j$ EWL combination, and ${\phi }_{WL}$ represents the carrier phase observation of the WL combination; $P_i$ is the pseudo-range observation for the $i$ frequency; $\lambda$ represents the wavelength corresponding to the carrier phase observation; $N$ represents the ambiguity corresponding to the carrier phase observation; $A$ stands for the direction cosine coefficient matrix; and $\delta X$ represents the parameters to be estimated in the geometric position.

This method uses Kalman filtering for AR and employs the LAMBDA algorithm for ambiguity search.

Table 3. Details of the Kalman filter.

Items	Setting
Cutoff elevation	10°
Sampling rate	30 s
Observation weighting	Elevation-dependent weighting
A priori STD of observation	0.3 m and 0.003 m undifferenced code and phase signals, respectively
Ionospheric delay	Modeling by NRTK
Tropospheric delay	Modeling by NRTK
AR	Partial ambiguity resolution (PAR) by elevation (from 10 to 40, step-10)
Position	Estimated in an epoch-wise manner with a priori value obtained from code-based positioning and a priori sigma = 302 (m2)

presents the details of the Kalman filter.

The sequential AR process proceeds as follows:

Initially, a selection matrix is used to filter out the ambiguities of EWL combinations. Subsequently, the LAMBDA algorithm is employed to search for these ambiguities. A PAR strategy is applied to select and resolve the ambiguities of EWL combinations. Satellites for which EWL combinations cannot be resolved are removed from further processing. Following this, the subsequent steps do not address fixing WL ambiguities or NL ambiguities. If it is not possible to resolve any of the EWL ambiguities, a EWL float solution is output.

Following the resolution of EWL ambiguities, the state transition matrix is utilized to update the ambiguities of WL combinations, NL combinations, and geometric position parameters [29].

$${\tilde{X}}_b=X_b-Q_{ab}\cdot Q_{aa}^{-1}\cdot \left(X_a^{float}-X_a^{fix}\right)$$

(12)

$${\tilde{Q}}_{bb}=Q_{bb}-Q_{ab}\cdot Q_{aa}^{-1}\cdot Q_{aa}^T$$

(13)

In the above equations, ${\tilde{X}}_b$ represents the updated matrix for WL ambiguities, NL ambiguities, and geometric position parameters; $X_b$ stands for the pre-update matrix for WL ambiguities, NL ambiguities, and geometric position parameters; $Q_{ab}$ represents the covariance matrix for EWL ambiguities, WL ambiguities, NL ambiguities, and geometric position parameters before the update; ${\tilde{Q}}_{bb}$ stands for the covariance matrix for updated WL ambiguities, NL ambiguities, and geometric position parameters; $Q_{bb}$ represents the covariance matrix for WL ambiguities, NL ambiguities, and geometric position parameters before the update; $X_a^{float}$ represents the float solution for EWL ambiguities; and $X_a^{fix}$ stands for the fixed solution for EWL ambiguities.

Following a strategy similar to that for fixing EWL ambiguities, after resolving the WL ambiguities, a selection matrix is used again to update the NL ambiguities and geometric position parameters. If WL ambiguities cannot be resolved, a EWL fixed solution is output.

Employing a PAR strategy, NL ambiguities are addressed after constraints from both EWL and WL ambiguities. Following the resolution of NL ambiguities, the geometric position parameters are updated using the state transition matrix to achieve a fixed solution for NL ambiguities. If NL ambiguities cannot be resolved, a WL fixed solution is output.

The flowchart of the multi-frequency SAR algorithm is shown in Figure 1.

The method proposed in this paper achieves sequential constraint by utilizing EWL, WL, and NL ambiguities, thus reducing the impact of atmospheric errors on WL and NL ambiguities to some extent. Particularly in single-epoch positioning scenarios, conventional NRTK algorithms are susceptible to significant atmospheric error effects on NL ambiguities. However, the NL ambiguities in the SAR algorithm are constrained through the fixed solutions of EWL and WL ambiguities, leading to reduced susceptibility to atmospheric error influences and faster convergence. In the case of continuous multi-epoch filtering, the Kalman filter has already mitigated the impact of atmospheric errors on ambiguities. Consequently, the constraint effect of the method proposed in this paper on NL ambiguities is somewhat diminished compared to single-epoch positioning.

4. Experiments and Analysis

The experimental data utilized in this study consisted of two sets of CORS reference station data. The experiments were conducted using data from two different time periods: the CORS station data from western China on DOY 148, 2020 (Dataset 1), and the AUSCORS reference station data from DOY 249, 2023, to DOY 254, 2023 (Dataset 2), were collected with a data sampling interval of 30 s. For the western China CORS data, the primary reference station was STA1, and the network employed Virtual Reference Station (VRS) technology to generate a virtual reference station at STA4. STA4 was used as the simulated rover station for zero-baseline NRTK positioning. In the case of the AUSCORS data, the main reference station was MSWL, and the network performed zero-baseline NRTK positioning using MTHR station as the simulated rover station. The geographical distribution of reference stations for the two sets of CORS reference stations used in this paper are depicted in Figure 2.

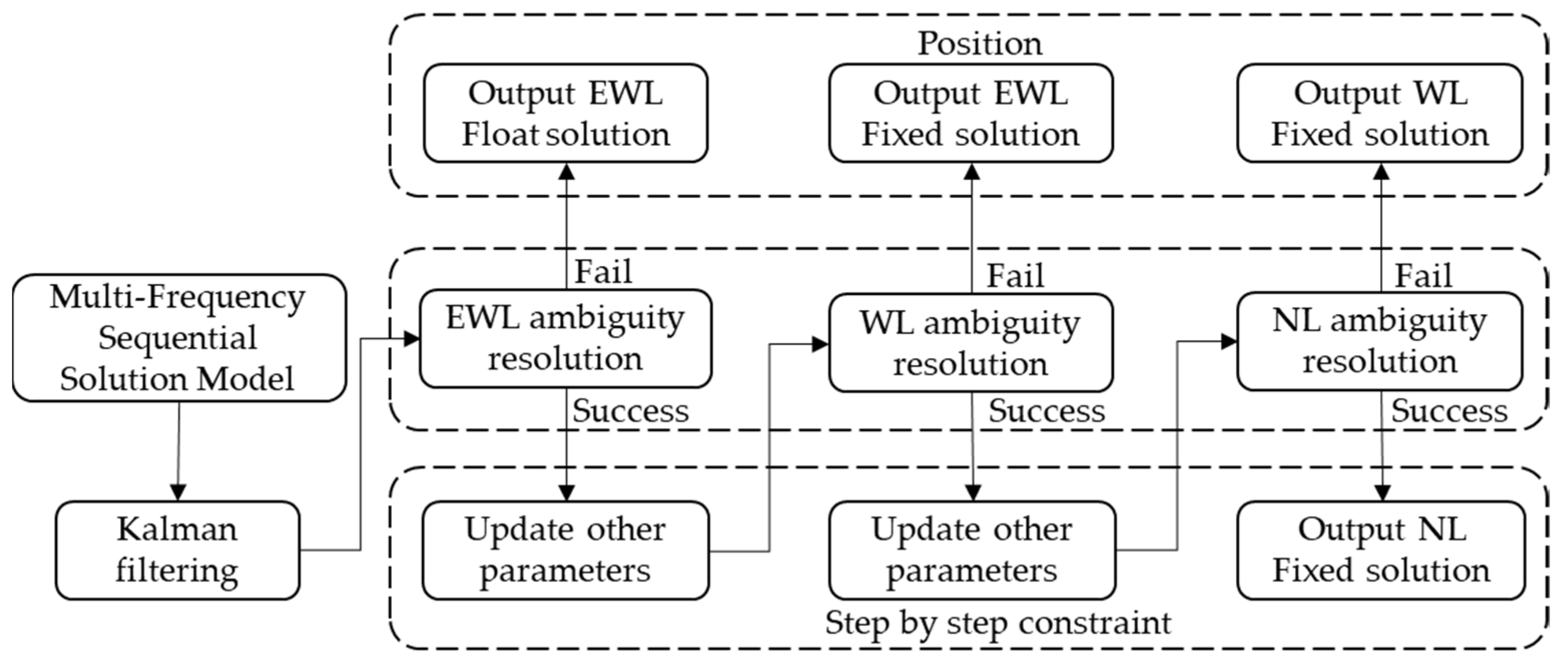
In the NRTK positioning experiments, the SAR algorithm proposed in this paper was compared to the conventional NRTK algorithm. The conventional NRTK algorithm refers to the direct involvement of carrier and pseudo-range observations from various base frequencies in the Kalman filter, with the unknown parameters being geometric parameters and NL ambiguities, and the algorithm proposed in this paper incorporates EWL, WL, and L1 carrier observations, as well as pseudo-range observations, into the filtering process. The unknown parameters include geometric parameters, as well as EWL, WL, and NL ambiguities. Both algorithms employ the Kalman filter algorithm and the LAMBDA algorithm for AR and ambiguity fixing. Additionally, a partial ambiguity fixing strategy is used to enhance the AR success rate. A chi-squared test [5] is also applied to validate the reliability of AR.

4.1. Atmospheric Biases Analysis

In the two sets of static experiments, we obtained the atmospheric biases at the rover station location through atmospheric error modeling. Subsequently, we used the simulated rover station as a reference station to perform baseline solutions, obtaining the actual atmospheric biases on that baseline (as a reference true value). By subtracting the atmospheric errors modeling value from the actual atmospheric biases obtained through baseline solutions, we obtained the atmospheric biases (consisting of ionospheric delay modeling residuals and tropospheric delay modeling residuals) on that baseline. When these atmospheric biases are sufficiently large, they can affect AR. Figure 3a illustrates the tropospheric delay modeling residuals and ionospheric delay modeling residuals at station STA4 in dataset 1. Figure 3b shows the tropospheric delay modeling residuals and ionospheric delay modeling residuals at station MTHR in dataset 2. Different colors in both figures are used to distinguish different satellite pairs. From the tropospheric delay modeling residuals in both datasets, it can be observed that the tropospheric modeling method used in this paper can effectively capture the tropospheric variations. Most of the tropospheric delay modeling residuals are less than 8 cm, and nearly all satellite tropospheric delay modeling residuals are less than half a wavelength. Figure 3a shows fluctuations in ionospheric delay modeling residuals from 12:00 to 18:00, with residuals exceeding one wavelength. Figure 3b indicates that although the ionospheric delay modeling residuals in dataset 2 are relatively stable, there are still fluctuations in the overall trend (e.g., from 22:00 to 4:00 every day). From Figure 3, it can be observed that the main factor causing atmospheric bias disturbance is the disturbance of ionospheric delay, which is also the main factor affecting the reliability of NRTK positioning.

4.2. Positioning Analysis

In order to illustrate the performance of the SAR algorithm, we first conducted single-epoch positioning experiments. The ratio threshold was set to 2.5.

Table 4. Single-epoch positioning experiment results.

Dataset	Conventional Algorithm				SAR Algorithm
	North/m	East/m	Up/m	NL Fixed Rate	North/m	East/m	Up/m	NL Fixed Rate
Set 1	0.061	0.066	0.169	48.9%	0.024	0.020	0.061	64.6%
Set 2	0.072	0.071	0.256	71.8%	0.022	0.031	0.083	77.9%

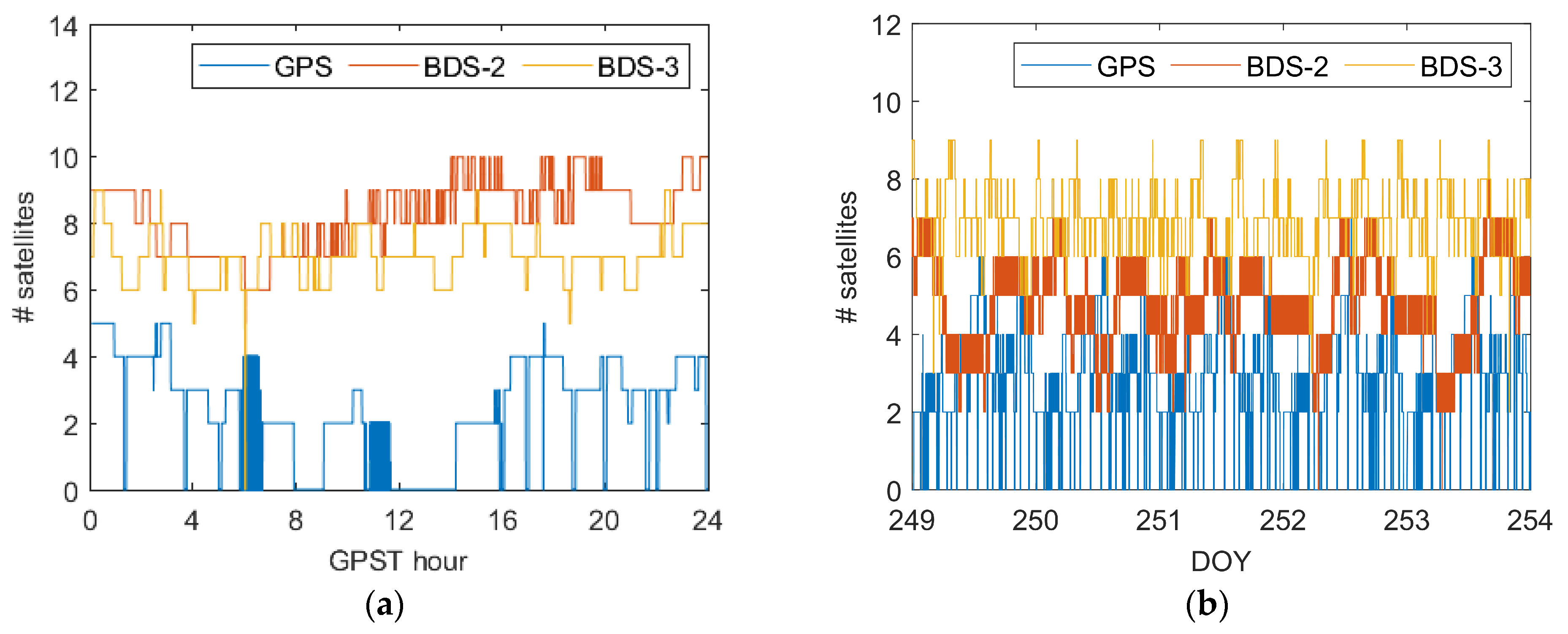
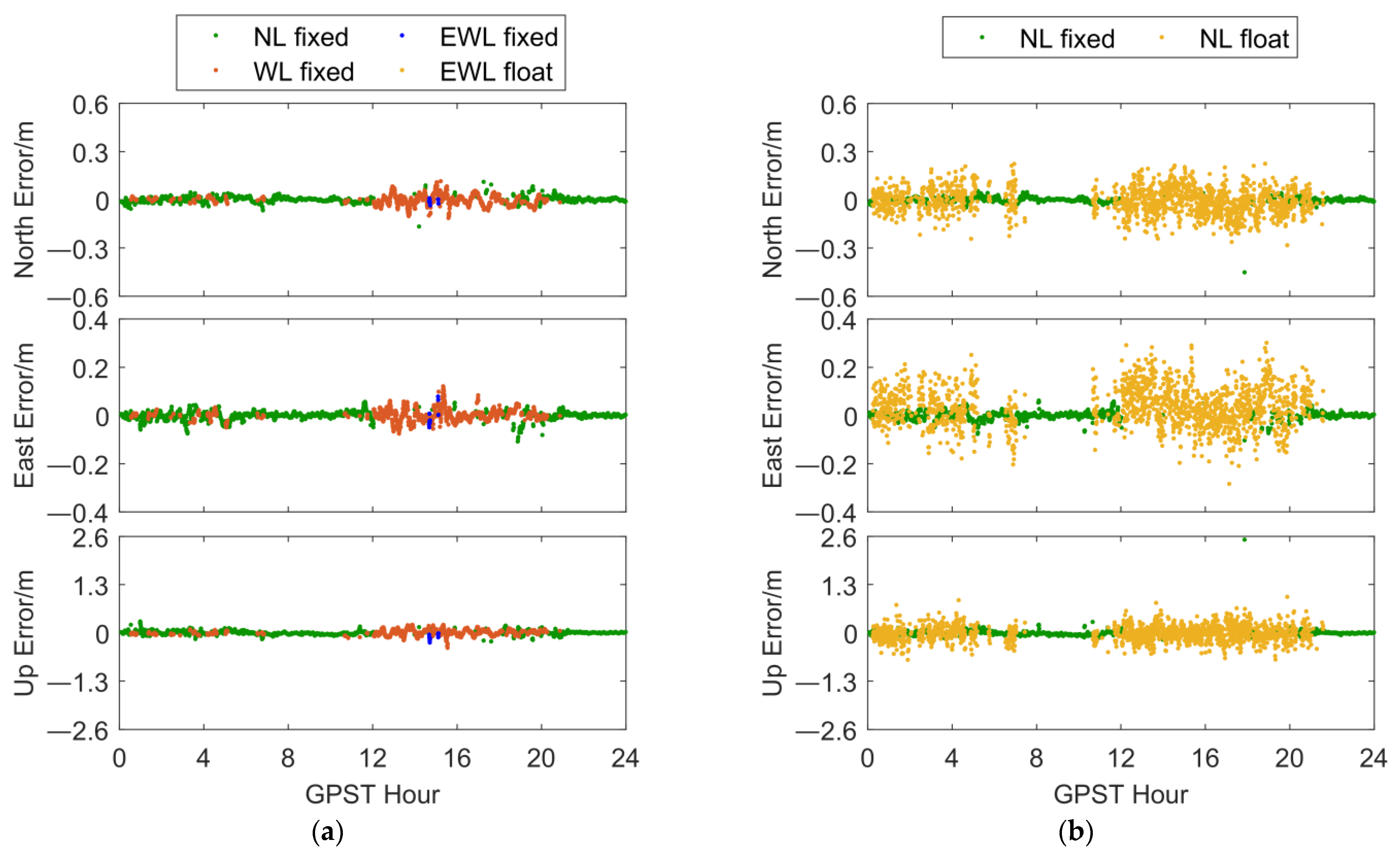
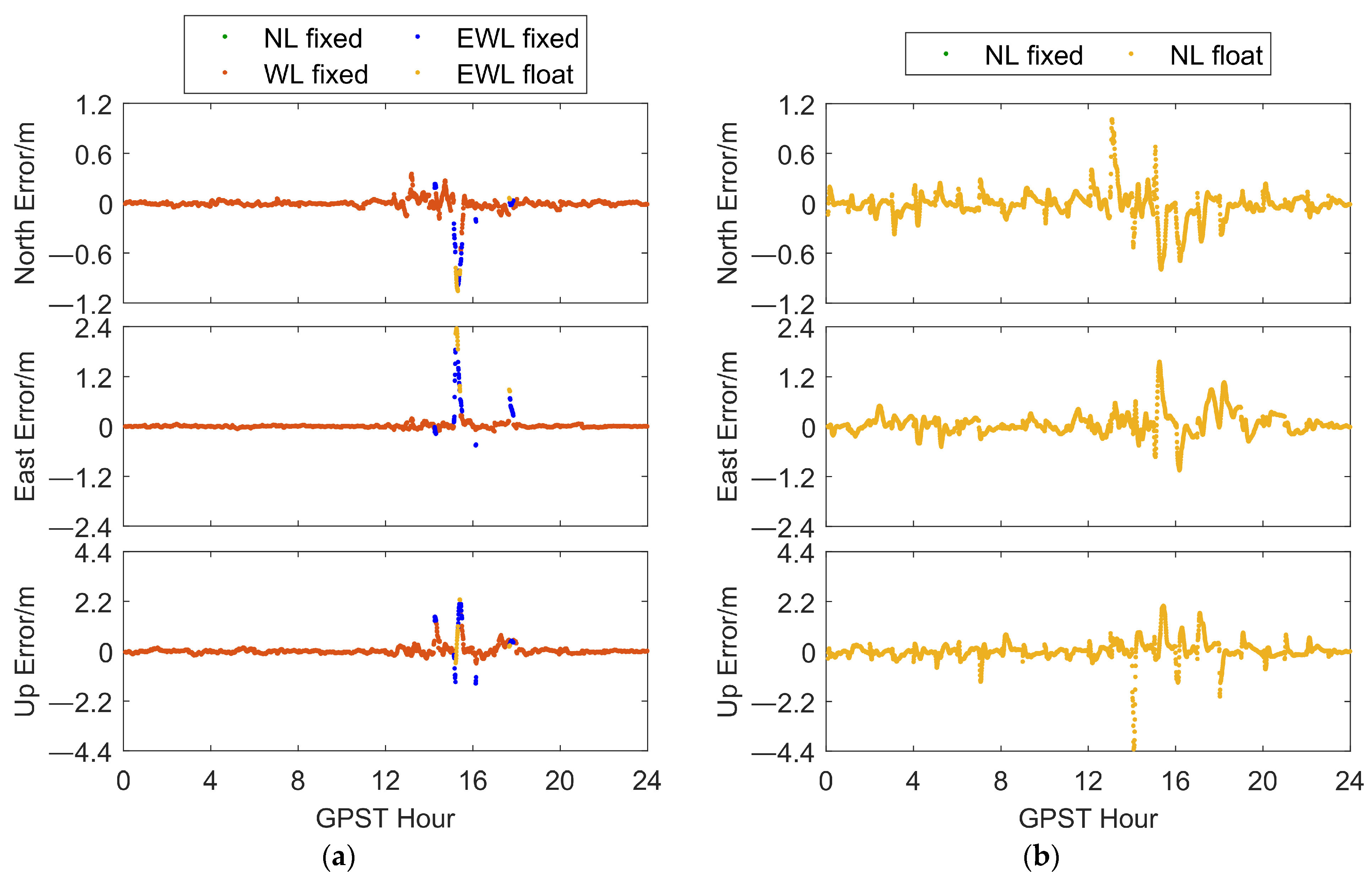
presents the positioning results of the two positioning algorithms in the two datasets for the conventional positioning experiments. Figure 4 shows the number of satellites in two datasets, and Figure 5a,b shows the positioning results of the SAR algorithm and the conventional NRTK positioning algorithm in dataset 1. The NL fixed solution accuracies in three directions (North, East, Up) for the conventional NRTK algorithm were as follows: 0.018 m, 0.016 m, and 0.091 m, respectively. On the other hand, the SAR algorithm achieved NL fixed solution accuracies of 0.016 m, 0.016 m, and 0.050 m in the same three directions. 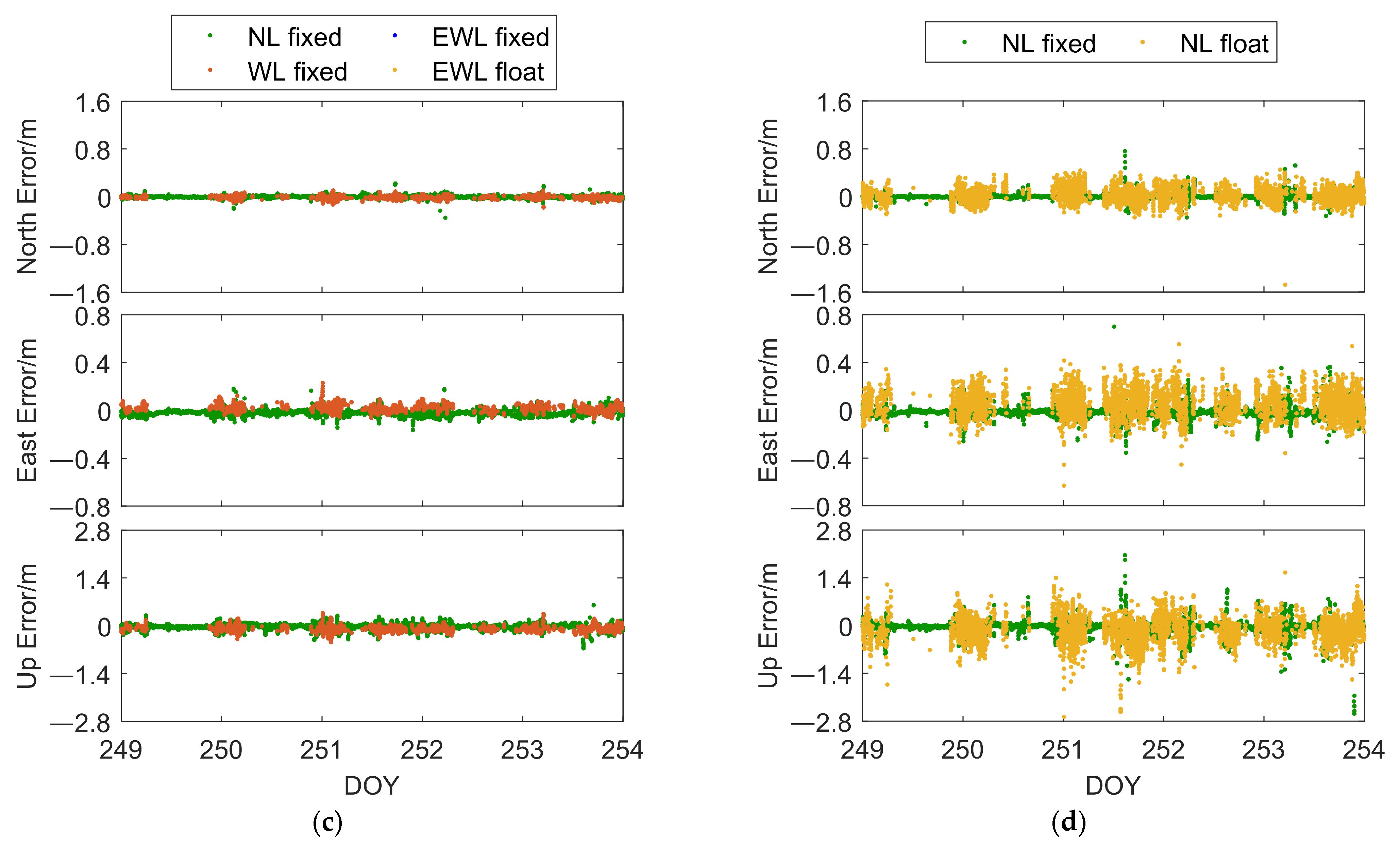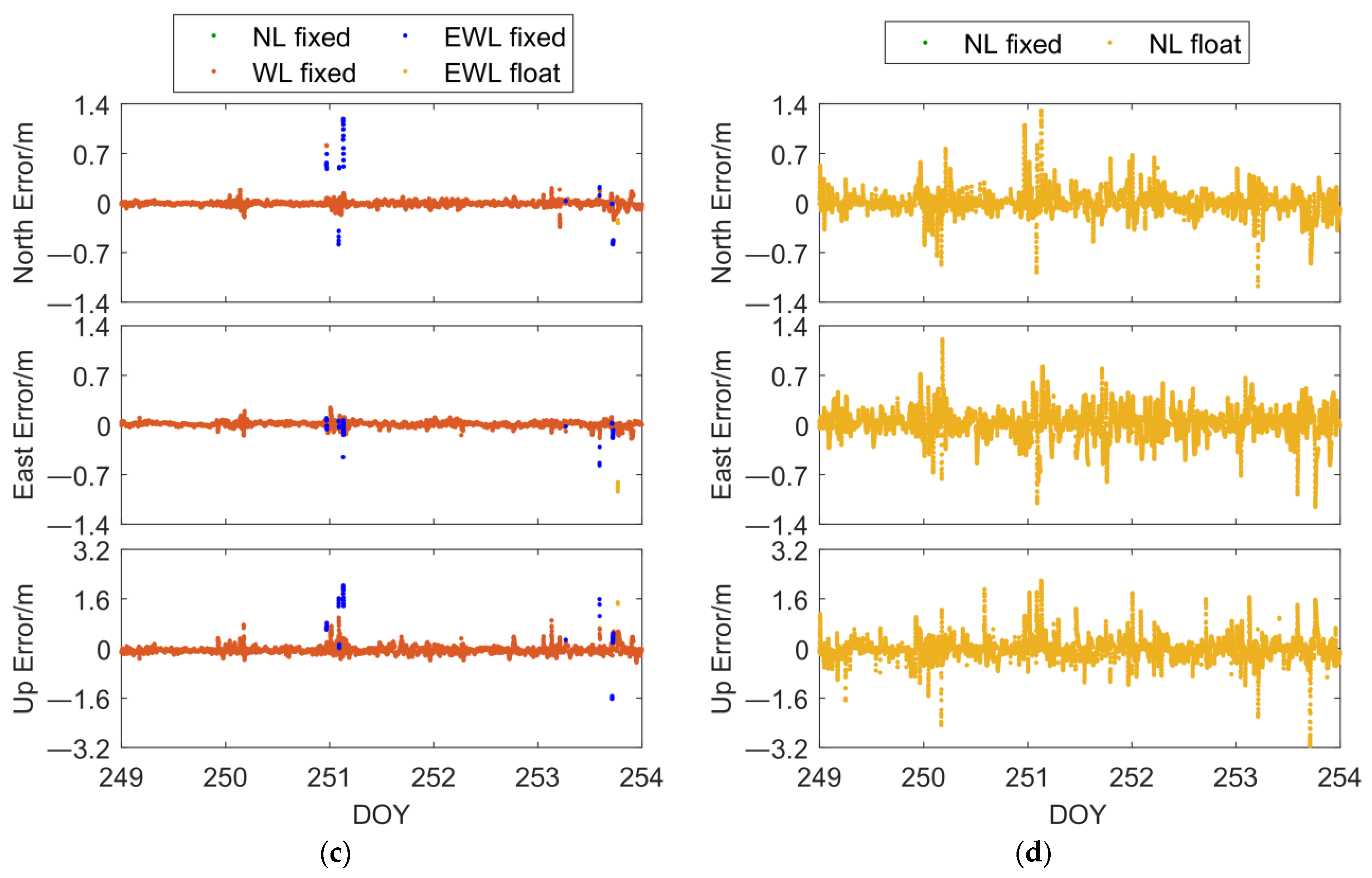Meanwhile, Figure 5c,d depicts the results of both algorithms in dataset 2. In this case, the conventional NRTK algorithm yielded NL fixed solution accuracies of 0.034 m, 0.039 m, and 0.149 m in the three directions, while the SAR algorithm achieved NL fixed solution accuracies of 0.018 m, 0.029 m, and 0.069 m in the same three directions. In both datasets, the SAR algorithm exhibited improvements in positioning accuracy and fixed rate. Regarding fixed solution positioning accuracy, the proposed algorithm showed slight improvements, highlighting its advantages in positioning reliability. It is worth noting that in the positioning results for dataset 1, the conventional NRTK algorithm exhibited significant biased pseudo-fixed solutions around 18:00, due to increased ionospheric activity during that period, which resulted in ionospheric delay modeling residuals reaching one wavelength. Ionospheric errors directly affect NL ambiguities, affecting AR. In the positioning results for dataset 2, the conventional NRTK algorithm exhibited pseudo-fixed solutions ranging from a few centimeters to several tens of centimeters in several periods (e.g., around 14:40 on DOY 251), which impacts the reliability of positioning. In both datasets, the SAR algorithm did not produce significantly erroneous NL fixed solutions, further demonstrating its superiority in positioning reliability.

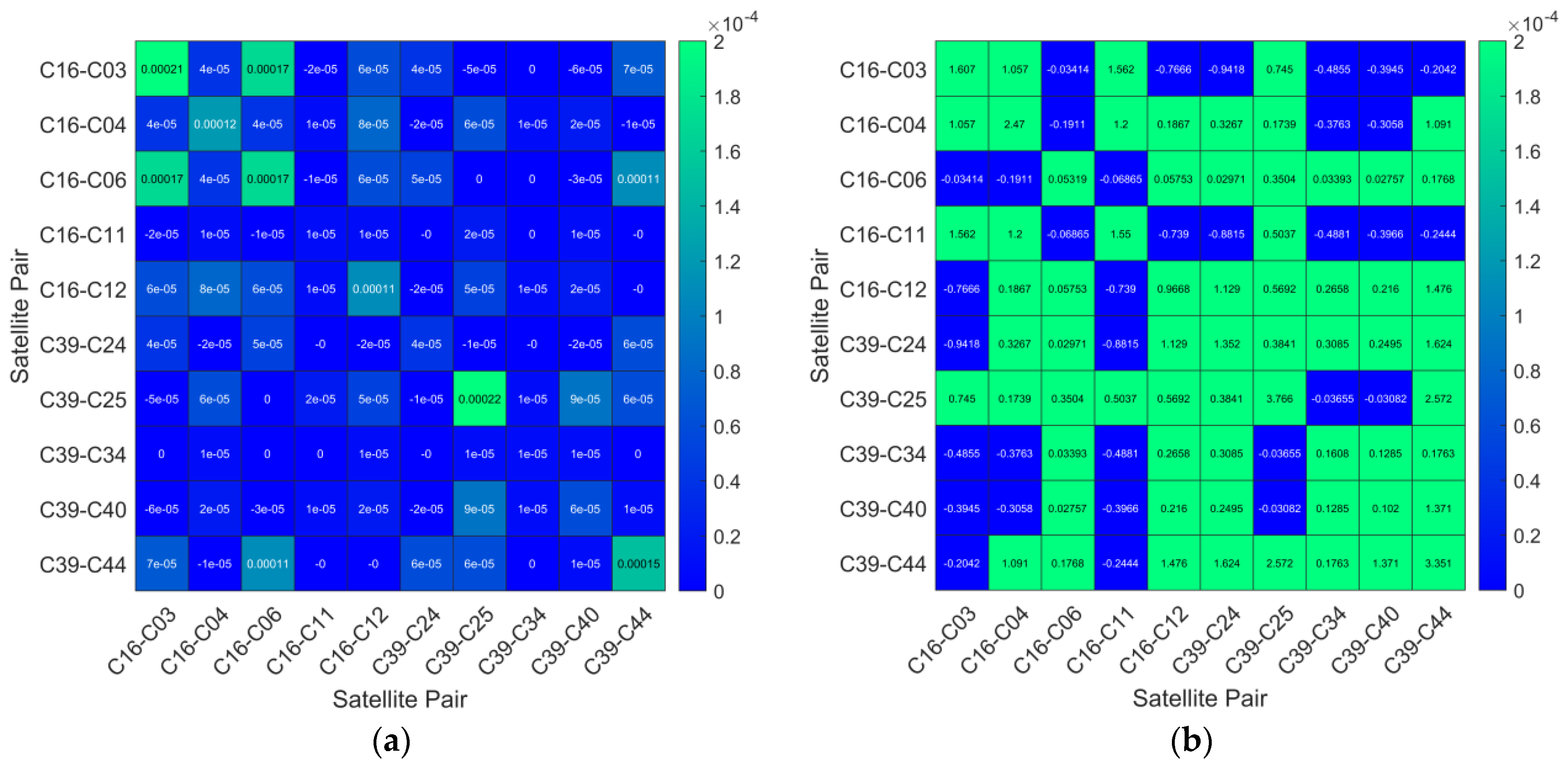
To investigate the impact of the EWL and WL ambiguity fixed solutions in the proposed algorithm on NL ambiguities, we analyzed the fraction of NL ambiguity of the conventional NRTK positioning algorithm in dataset 2 and compared it with the fraction of NL ambiguity constrained by the EWL ambiguity fixed solution and the WL ambiguity fixed solution in the SAR algorithm. Figure 6 provides the fraction of NL ambiguity for 10 satellite pairs at epoch 358530 (GPST-3:35:30 on DOY 250) in dataset 2. It is important to note that there were a total of 11 satellite pairs in this epoch, with only one pair from the GPS satellite system. Due to the MTHR-MSWL baseline failing to resolve the ambiguity true value for this satellite pair, this resulted in the inability to calculate the fraction of this satellite pair. Therefore, this satellite pair is not included in Figure 6.

Figure 7 shows the covariance matrix for NL ambiguities of two algorithms at epoch 358530 (GPST-3:35:30 on DOY 250) in the SAR algorithm. Due to the constraints applied by the EWL ambiguity fixed solution and WL ambiguity fixed solution on the NL ambiguities, the covariance matrix for NL ambiguities approached convergence, resulting in higher ambiguity precision. By comparing the float solution fraction of NL ambiguities constrained by the EWL and WL ambiguity fixed solutions with the float solution fraction of NL ambiguities in the conventional NRTK algorithm, it can be seen that for some satellites, the fraction of NL ambiguities constrained by the EWL ambiguity fixed solutions were reduced. After being further constrained by the WL ambiguity fixed solution, the fraction of NL ambiguities for half of the satellites was less than 0.3 cycles, and all fractions of NL ambiguities were less than 0.5 cycles. This demonstrates the effective constraint of NL ambiguities by the proposed algorithm, and NL ambiguity was shown to exhibit better integer characteristics.

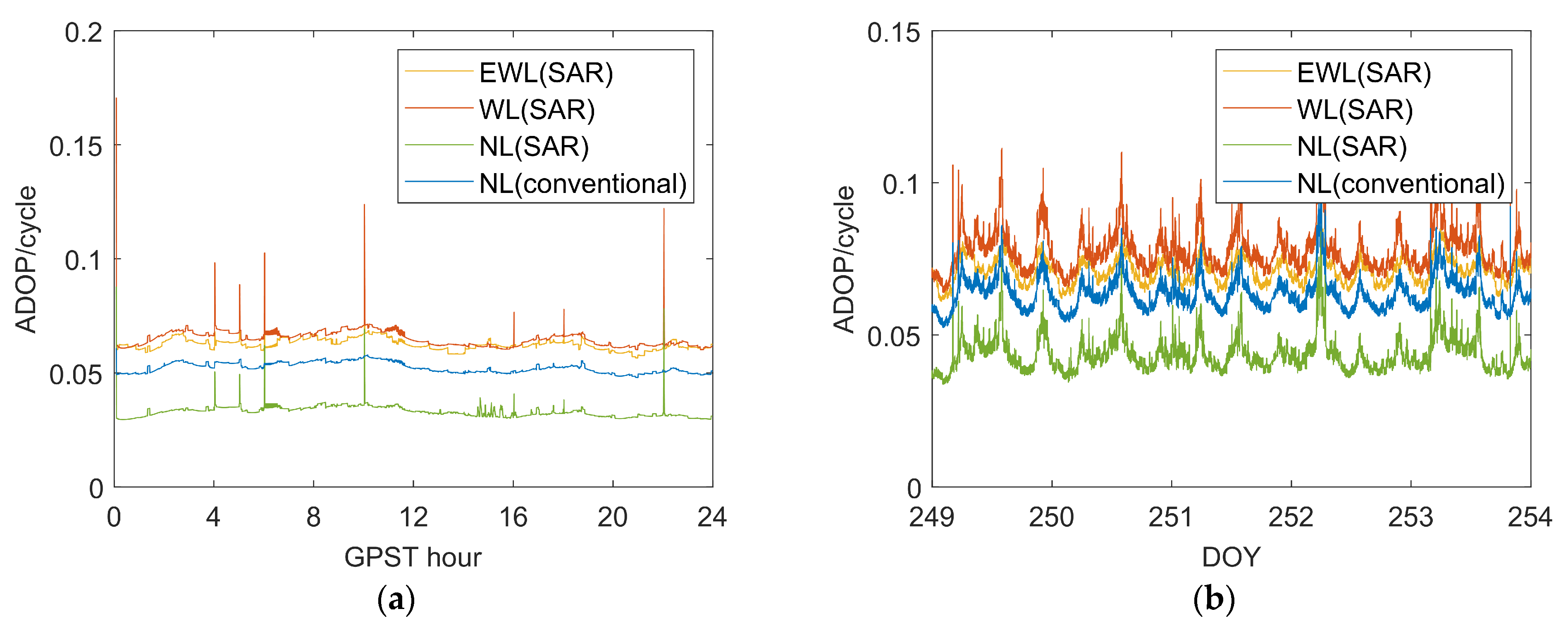
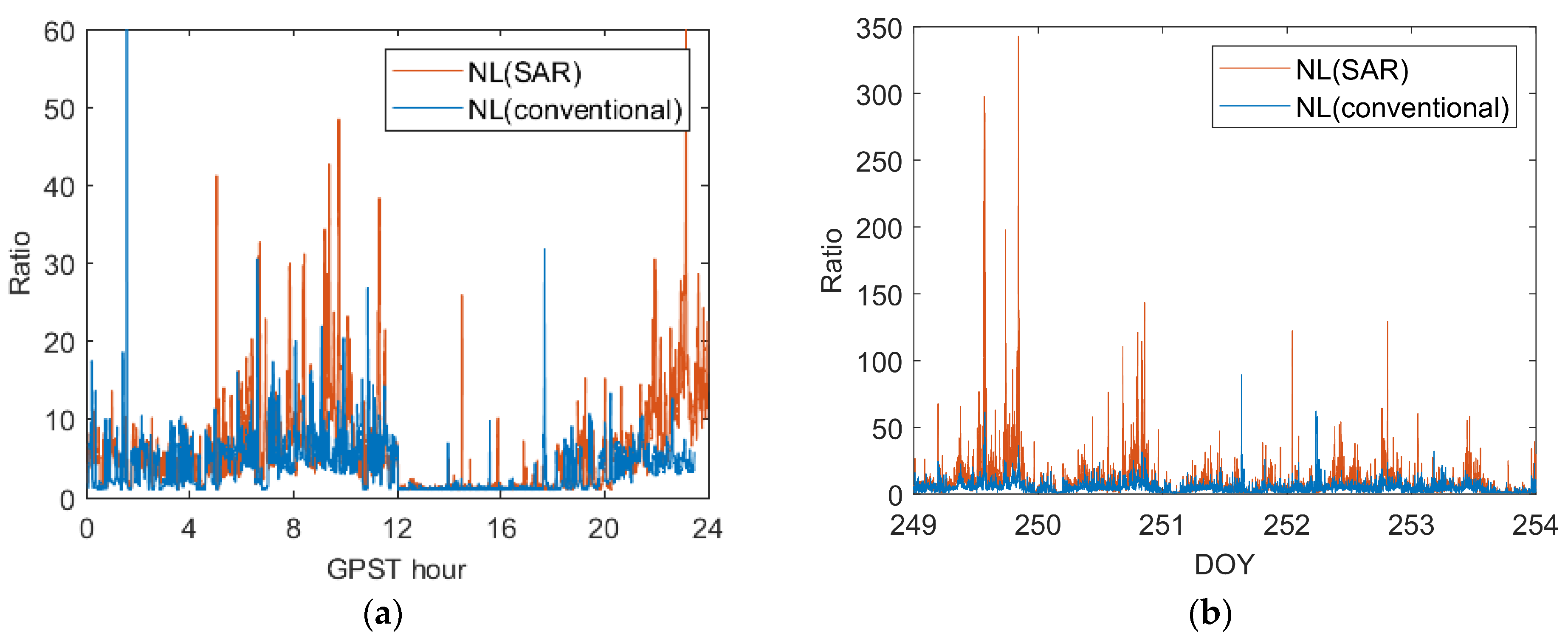
To further illustrate the effect of EWL and WL on the speed and success rate of NL AR, Figure 8 shows the ADOP values of various ambiguities in two sets of experiments, and Figure 9 shows the ratio values of NL ambiguity in both sets of experiments. From Figure 8, it is evident that the NL ambiguity ADOP value in the SAR algorithm was generally lower than that in the conventional algorithm, indicating that NL ambiguity constrained by EWL and WL contributes to a higher AR success rate [30,31]. Figure 9 illustrates that the ratio value of the SAR algorithm was relatively higher during periods with smaller atmospheric biases. However, during periods with larger atmospheric biases, the ratio value of the SAR algorithm aligned closely with that of conventional algorithms. This further supports the conclusion that the NL ambiguity handled by the SAR algorithm leads to a higher success rate in AR.

To quantitatively illustrate the advantages of the SAR algorithm in terms of convergence speed, we conducted an initialization positioning experiment. The experiment involved initializing every 5 min (10 epochs) and calculating the time it took for the first fix within the current time window where all subsequent epochs remained fixed. The ambiguity test ratio threshold was set to 2.5.

Table 5. Initialization (5 min) positioning experiment results.

Dataset	Conventional Algorithm				SAR Algorithm
	North/m	East/m	Up/m	NL Fixed Rate	North/m	East/m	Up/m	NL Fixed Rate
Set 1	0.191	0.142	0.478	49.7%	0.110	0.029	0.110	66.1%
Set 2	0.132	0.089	0.386	72.0%	0.033	0.032	0.097	79.2%

provides the positioning results for the two datasets with both NRTK positioning algorithms used in the initialization experiments.

Table 6. Average TTFF for two algorithms.

Dataset	Conventional Algorithm/Epoch	SAR Algorithm/Epoch	Improvement
Set 1	5.36	3.66	31.7%
Set 2	2.19	1.65	24.6%

presents the TTFF for both algorithms in the two datasets, and it clearly indicates that the SAR algorithm outperformed the conventional NRTK algorithm in terms of convergence speed. Figure 10 shows the hourly average TTFF for two algorithms. It can be clearly seen that although the SAR algorithm also requires a large number of epochs for initialization or cannot be initialized as a fixed solution during periods with large atmospheric biases, the initialization time of the SAR algorithm is better than that of conventional algorithms when conventional algorithms require more epochs for initialization during periods with slightly smaller atmospheric biases. 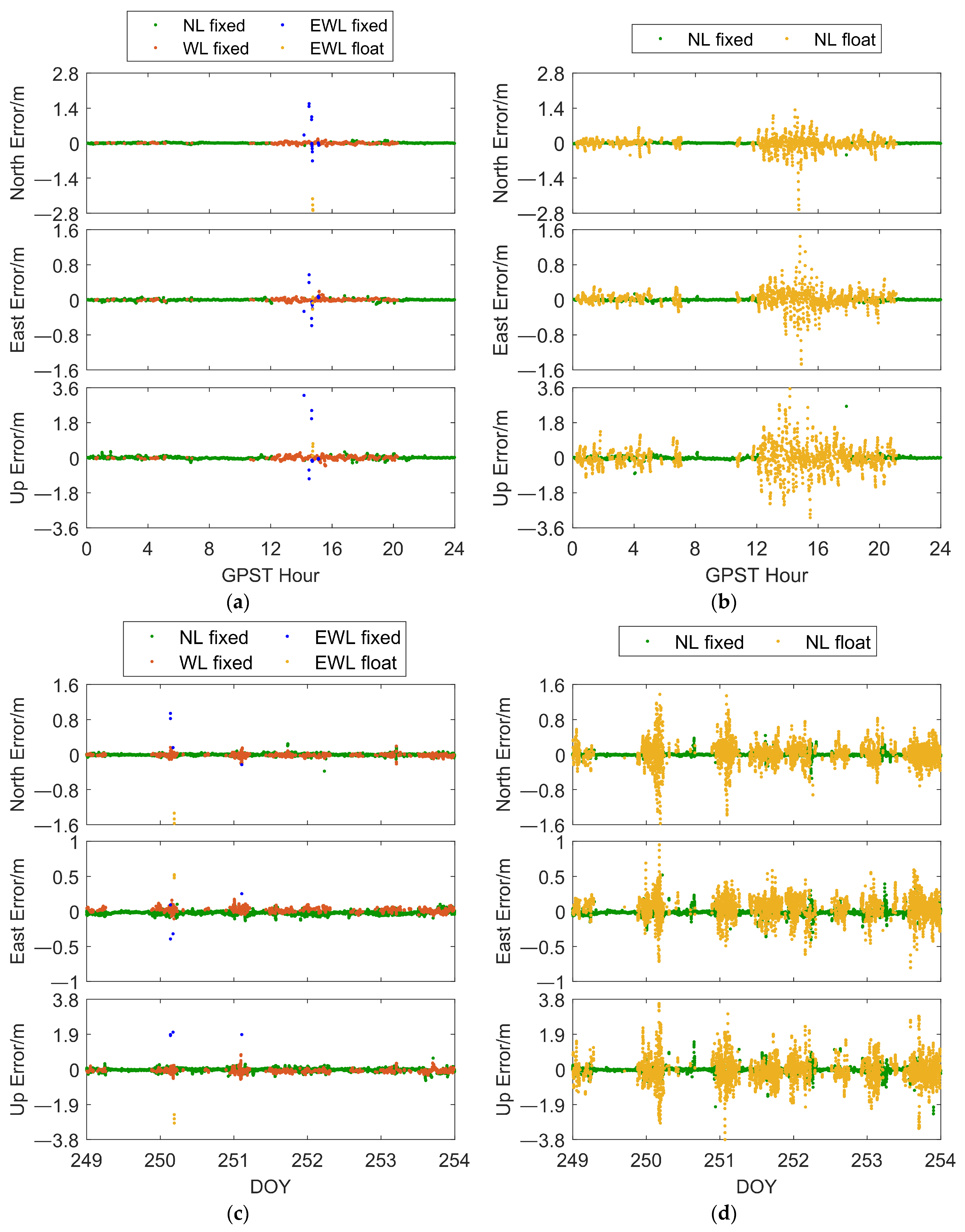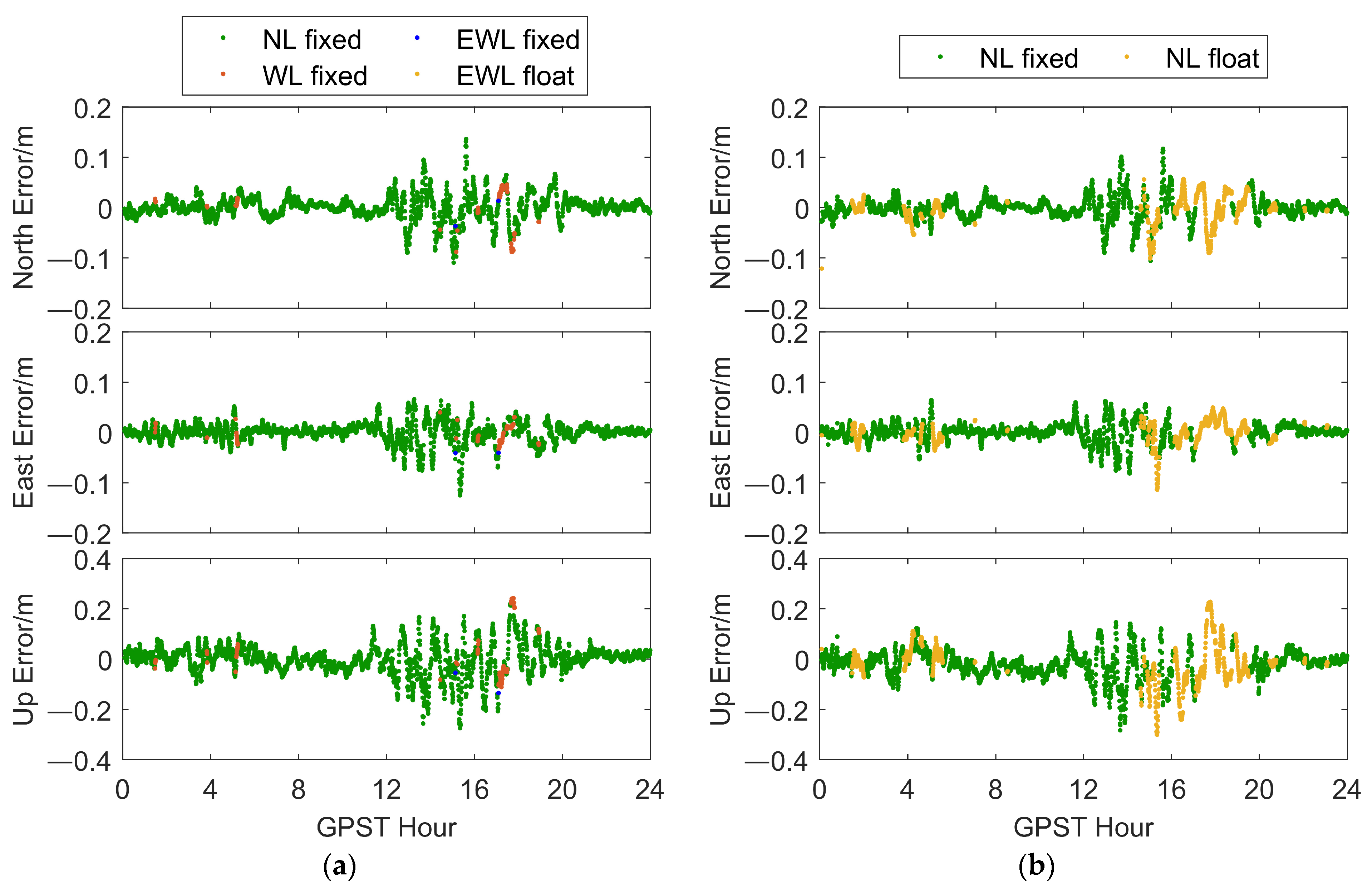Figure 11a,b illustrates the positioning results for the SAR algorithm and the conventional NRTK positioning algorithm in dataset 1, while Figure 11c,d shows the positioning results for both algorithms in dataset 2. Through these two sets of experiments, we observed that the SAR algorithm consistently achieved a higher NL fixed rate compared to the conventional NRTK algorithm. In particular, during 0:00 to 6:00 in dataset 1 and 22:00 to 24:00 in dataset 2, the conventional NRTK algorithm failed to initialize as a NL fixed solution. In contrast, the SAR algorithm was able to initialize as a NL fixed solution, demonstrating its superiority in terms of convergence speed. During 12:00 to 20:00 in dataset 1 and 0:00 to 6:00 in dataset 2, the conventional NRTK algorithm only provided low-accuracy NL float solutions. In these scenarios, the SAR algorithm achieved high-accuracy WL fixed solutions. Comparing Figure 11a,b, as well as Figure 11c,d, it is evident that the accuracy of the WL fixed solutions in the SAR algorithm was significantly higher than the accuracy of the NL float solutions obtained by the conventional NRTK algorithm. Although the accuracy of the EWL fixed solutions was relatively lower, it still matched the accuracy level of the NL float solutions in the conventional NRTK algorithm.

In the above experiment, it can be found that both the SAR algorithm and the conventional algorithm cannot be NL fixed during periods of significant atmospheric biases. During this period, the positioning accuracy provided by the conventional algorithm was poor. To demonstrate that the SAR algorithm can provide more reliable positioning when it cannot provide a NL fixed solution, we conducted another initialization experiment. In this experiment, the NL ambiguity test ratio value was set to maximum, with this resulting in both algorithms being unable to obtain NL fixed solutions. Due to the slow convergence speed of NL float solutions in conventional algorithms, we initialized the algorithms once every hour to compare their positioning accuracy and reliability during initialization. Table 6 displays the positioning accuracy of both algorithms in two datasets, demonstrating that the SAR algorithm had significantly improved positioning accuracy in both cases. Figure 12 illustrates the positioning results of both algorithms in two datasets, while Figure 13 presents the ADOP values of NL ambiguities in the experiments. Combining

Table 7. Initialization (1 h) positioning experiment results.

Dataset	Conventional Algorithm			SAR Algorithm
	North/m	East/m	Up/m	North/m	East/m	Up/m
Set 1	0.166	0.270	0.429	0.108	0.191	0.238
Set 2	0.146	0.200	0.324	0.053	0.039	0.141

and Figure 12 and Figure 13, we conclude that the SAR algorithm exhibited higher initialization speed and can deliver higher accuracy and more reliable positioning during the initialization phase.

Due to the fact that atmospheric biases are not always significant, atmospheric biases were relatively small in most scenarios. In order to illustrate the general positioning performance of the SAR algorithm proposed in this paper in most scenarios, we conducted conventional positioning experiments (i.e., continuous filtering using regular NRTK). The ratio threshold was set to 2.5.

Table 8. Conventional positioning experimental results.

Dataset	Conventional Algorithm				SAR Algorithm
	North/m	East/m	Up/m	NL Fixed Rate	North/m	East/m	Up/m	NL Fixed Rate
Set 1	0.025	0.020	0.068	77.5%	0.025	0.020	0.065	97.3%
Set 2	0.042	0.042	0.089	97.7%	0.034	0.031	0.078	99.2%

presents the positioning results of the two positioning algorithms in the two datasets for the conventional positioning experiments.

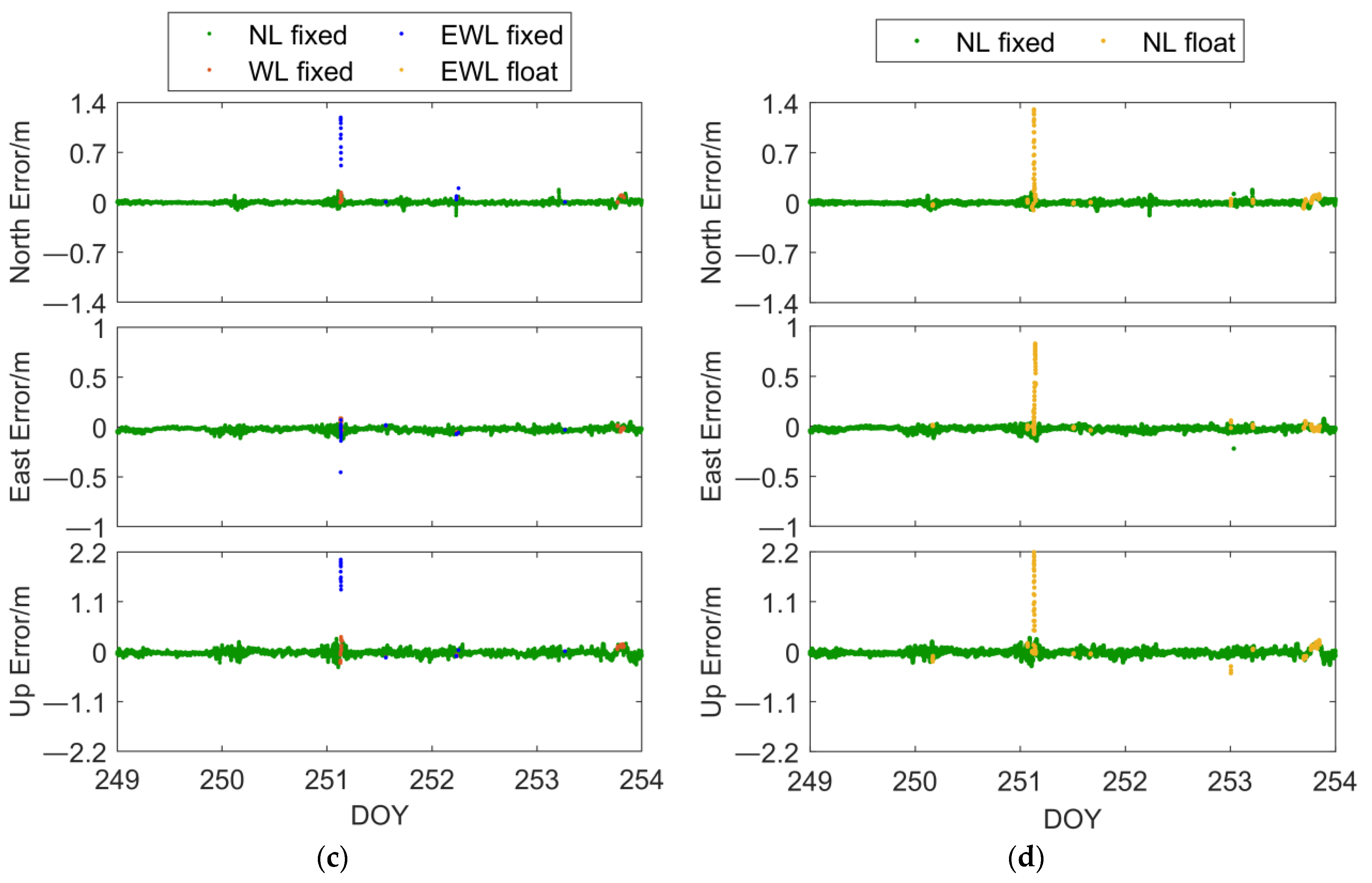
Figure 14a,b shows the positioning results of the SAR algorithm and the conventional NRTK positioning algorithm in dataset 1. The positioning accuracy of the two algorithms was generally comparable. In terms of NL fixed rate, the SAR algorithm showed an improvement of approximately 20%. This improvement was mainly observed from 12:00 to 18:00. However, the increased fixed solutions did not exhibit a significant improvement in positioning accuracy. Figure 3 indicates an increase in ionospheric delay modeling residuals during this time period, leading to a decrease in positioning accuracy. This suggests that the algorithm proposed in this paper is also affected by significant atmospheric error modeling residuals, and its positioning accuracy is comparable to conventional NRTK positioning.

Figure 14c,d depicts the results of both algorithms in dataset 2. The SAR algorithm showed a significant improvement in positioning accuracy compared to the conventional NRTK positioning algorithm. The positioning accuracy improvements in the North, East, and Up directions were 19%, 26%, and 12%, respectively. The lower positioning accuracy of conventional NRTK positioning was mainly due to the initialization phase not converging, resulting in many large NL float solutions biases. However, the SAR algorithm quickly converged to NL fixed solutions in the initialization phase, demonstrating its advantage. In terms of NL fixed solution positioning accuracy, both algorithms were generally consistent. Both sets of datasets demonstrated that the SAR algorithm can achieve positioning accuracy at a similar level to conventional NRTK positioning algorithms under general positioning conditions and exhibited an advantage in the initialization phase.

5. Discussion

In single-epoch positioning experiments, we compared the fraction of NL ambiguities constrained by the WL ambiguity fixed solution with atmospheric biases. In Figure 15, it was observed that the fraction of NL ambiguities was consistent with atmospheric biases, indicating that atmospheric error modeling residuals are the primary factors affecting the integer properties of NL ambiguities. To further investigate the impact on the integer properties of NL ambiguities, we examined ionospheric delay modeling residuals and tropospheric delay modeling residuals. It was found that the tropospheric delay modeling residuals for the listed satellites in this epoch were all less than 1.4 cm, with an impact on NL ambiguities of less than 0.073 cycles. However, eight of the listed satellites had ionospheric delay modeling residuals exceeding 2 cm, with four of them exceeding 5 cm, which resulted in an impact on NL ambiguities of over 0.26 cycles.

In NRTK positioning, typically utilized for short baseline solutions algorithms, ignoring the impact of atmospheric errors on AR can lead to suboptimal positioning performance during periods of atmospheric activity. In studying the impact of atmospheric errors on ambiguity resolution, some researchers have addressed the influence of atmospheric errors on ambiguity resolution in long baseline scenarios by utilizing multi-frequency observations or parameterizing atmospheric errors. In such scenarios, where atmospheric errors continuously affect ambiguity resolution, these algorithms have shown favorable results for long baseline solutions. From Figure 3, it is evident that in NRTK positioning, atmospheric errors do not continuously affect AR; they only impact it during periods of atmospheric activity. Therefore, employing long baseline positioning algorithms in NRTK positioning would degrade performance during calm atmospheric conditions. The SAR algorithm is based on ionosphere-fixed modeling, which maintains performance comparable to conventional NRTK positioning algorithms during calm atmospheric conditions while providing more reliable positioning during active atmospheric periods. This achieves a good balance between model robustness and positioning performance.

6. Conclusions

We studied the modeling of atmospheric biases in medium to long baselines and found that tropospheric delay modeling is effective. Ionospheric delay modeling performs well during quiet ionospheric conditions but poorly during ionospheric activity, with modeling residuals reaching one wavelength. Under typical atmospheric conditions, when the combined impact of ionospheric and tropospheric delay modeling residuals is significant, NRTK faces significant challenges. Conventional NRTK algorithms directly estimate NL ambiguities for each basic frequency. Due to the shorter wavelength of NL observations, ambiguities are strongly influenced by atmospheric biases. This can lead to AR mistakes or even an inability to NL fixed ambiguities, resulting in poor quality pseudo-fixed or float solutions. If NRTK initialization occurs during periods of poor atmospheric error modeling, conventional NRTK algorithms struggle to converge to NL fixed solutions or require extended filtering times. Additionally, the accuracy of float solutions during the initialization phase is inadequate to meet NRTK positioning accuracy and reliability requirements, severely impacting NRTK operational efficiency.

To address these issues, we propose a multi-frequency sequential solution NRTK fast and reliable positioning method. This method combines the observation of EWL, WL, and NL with Kalman filtering. Taking advantage of the ease of fixing EWL ambiguity, the LAMBDA algorithm is first used to resolve the EWL ambiguity, and then the already fixed ambiguity is used to constrain other parameters. Then, the same method was used to gradually resolve the ambiguity of WL and NL, achieving high-precision, fast, and reliable positioning. Subsequently, this paper conducted NRTK positioning experiments with CORS data from two medium to long baselines, illustrating that the proposed algorithm maintains comparable positioning accuracy to conventional NRTK algorithms under typical scenarios. Furthermore, the proposed algorithm provides higher-precision suboptimal positioning solutions when conventional NRTK algorithms cannot provide NL fixed solutions positioning during the initialization phase. It also offers faster convergence and more reliable fixed solutions compared to conventional NRTK algorithms, highlighting the advantages of the proposed algorithm.

In conclusion, this paper presents a high-precision, fast, and reliable NRTK positioning method that uses multi-frequency combined observations and sequential AR. This method achieves faster convergence, higher positioning accuracy, and greater positioning reliability compared to conventional NRTK algorithms when atmospheric biases significantly impact positioning quality or result in an inability to fix ambiguities during initialization.