Abstract
Plant traits are often measured in the field or laboratory to characterize stress responses. However, direct measurements are not always cost effective for broader sampling efforts, whereas indirect approaches such as reflectance spectroscopy could offer efficient and scalable alternatives. Here, we used field spectroscopy to assess whether (1) existing vegetation indices could predict leaf trait responses to heat stress, or if (2) partial least squares regression (PLSR) spectral models could quantify these trait responses. On several warm, sunny days, we measured leaf trait responses indicative of photosynthetic mechanisms, plant water status, and morphology, including electron transport rate (ETR), photochemical quenching (qP), leaf water potential (Ψleaf), and specific leaf area (SLA) in 51 urban trees from nine species. Concurrent measures of hyperspectral leaf reflectance from the same individuals were used to calculate vegetation indices for correlation with trait responses. We found that vegetation indices predicted only SLA robustly (R2 = 0.55), while PLSR predicted all leaf trait responses of interest with modest success (R2 = 0.36 to 0.58). Using spectral band subsets corresponding to commercially available drone-mounted hyperspectral cameras, as well as those selected for use in common multispectral satellite missions, we were able to estimate ETR, qP, and SLA with reasonable accuracy, highlighting the potential for large-scale prediction of these parameters. Overall, reflectance spectroscopy and PLSR can identify wavelengths and wavelength ranges that are important for remote sensing-based modeling of important functional trait responses of trees to heat stress over broad ranges.
1. Introduction
Trees in many regions are likely to experience more frequent and intense heat and water-stress events as the climate warms [1,2,3,4]. Many urban trees are at the leading edge of this shift given the urban heat island effect [5], thus providing examples of what other trees are likely to exhibit in the coming decades and making urban trees a management and research priority [6]. Temperature and drought-induced impairments could decrease photosynthetic rates and lead to increased mortality in extreme cases [7]. Plant functional traits associated with chlorophyll fluorescence [8,9,10] and leaf water potential (Ψleaf) [11,12] can serve as indicators of photosynthetic rates and plant water status, making them valuable metrics of heat and water-stress responses in trees. However, it is challenging to monitor these physiological responses at different scales because they are dynamic, influenced by fluctuating environmental conditions, and require sophisticated measurement techniques.
Recent technological developments in remote sensing show the potential to monitor forest ecophysiological responses to climate warming. Specifically, satellite [13,14,15,16] and airborne imaging spectrometers [17,18,19,20] may enable remote detection of stress levels and physiological responses over broad spatial ranges. To support remote sensing, empirical relationships between selected traits and spectral signatures at the leaf level must be established. Therefore, field-based studies that integrate leaf-level physiological measurements and proximal sensing spectroscopy are essential for developing a basis for comparison with remote sensing imagery, ultimately improving the extensive quantification of plant traits [21,22,23,24].
Plant physiological responses to heat and water stress are well documented. For instance, chlorophyll fluorescence parameters like electron transport rate (ETR) and photochemical quenching (qP) are known to respond to physiological stress under drought and high-temperature conditions [25,26,27,28]. ETR is an indicator of photosynthetic potential that is highly sensitive to light and temperature [8,9,10]. As long as light is not limiting, ETR is tightly correlated with carbon assimilation via photosynthesis. However, excessive light and temperature can damage photosynthetic apparatuses. As a response, plants perform non-stomatal regulation by qP and non-photochemical quenching (NPQ) to protect themselves from photodamage and heat-induced impairment [29]. Under fluctuating light conditions, qP is a more critical limiting factor than NPQ for photosynthesis, and qP tends to be more responsive to temperature [30]. Therefore, the field-measured ETR and qP values can be used as input parameters for modeling spatiotemporal variability in plant photosynthetic activity and biome-specific gross primary productivity [16,31].
Leaf water potential (Ψleaf) is a responsive and useful measure of heat and water stress as it declines (becomes more negative) when the tension on water flowing through the xylem increases [11,12,32]. Diurnal variation in Ψleaf can help to identify plants as being more isohydric or anisohydric [33], or more risk-averse versus risk-taking in their management of water use. Isohydric species maintain a relatively steady daytime Ψleaf to prevent xylem embolism, whereas anisohydric species exhibit a greater variation in daytime Ψleaf under water stress [34].
Specific leaf area (SLA) is the ratio of a leaf’s area to its dry mass, and it therefore varies as a function of tissue density and leaf thickness [35,36]. Variation in SLA or leaf mass per area (LMA; the inverse of SLA) is known to describe strategies that plants use when constructing leaf tissue, i.e., whether they prioritize longevity or rapid return on their energetic investment [37,38]. Investing in short-lived, lower LMA leaves may be advantageous when environmental conditions are more stressful [39,40]. Therefore, differences in SLA across individual trees and species capture variability in structural attributes as well as light interception, light absorption, leaf chlorophyll content, nutrient concentrations, and gas exchange rates.
Hyperspectral leaf reflectance can provide an efficient means of estimating leaf functional trait responses. A hyperspectral sensor can detect high-resolution spectral reflectance across hundreds of narrow bands. This is helpful in identifying the specific bands or spectral regions that correspond to each functional trait. For example, the chlorophyll fluorescence emission from photosystem I and II has a peak reflectance in the red region at 640–750 nm [41] and therefore has the potential to spectrally predict ETR and qP. Likewise, there could be a relationship between leaf reflectance and Ψleaf for some tree species, but the wavelength range associated with Ψleaf is not consistent across studies. One study found visible, near-infrared, and shortwave infrared regions (VNIR–SWIR; 350–2500 nm) to be predictive of Ψleaf [42], whereas others found that only the SWIR region (1100 to 2000 nm [43] or 1300 to 2500 nm [44]) was needed to predict Ψleaf. In addition to Ψleaf, SWIR can detect leaf structural properties, including cellulose and lignin content; thus, SWIR [45,46] or SWIR integrated with VNIR [47] may estimate SLA better than VNIR alone can. Regardless, uncertainty remains with respect to which spectral regions are most useful for estimating these trait responses and how much information will be retrieved using solely VNIR.
Leaf traits have been estimated from vegetation indices composed of either narrowband or broadband spectral reflectance. For example, the double-peak optical index was developed with wavelengths in the red-edge region (688, 697, and 710 nm) for predicting steady-state chlorophyll a fluorescence [48], the photochemical reflectance index was developed with green-yellow wavelengths (531 and 570 nm) for photosynthetic radiation use efficiency [49], and the water index was developed with near-infrared wavelengths (900 and 970 nm) for plant water status [50]. Many vegetation indices were developed for estimating selected traits of vegetation in general, whereas others were developed for one or a few tree species. Consequently, the applicability of vegetation indices needs to be evaluated for common urban tree species, especially when they are measured under stressful environmental conditions.
Although vegetation indices benefit from simplicity, they include limited spectral information. As an alternative, partial least squares regression (PLSR) leverages machine learning to develop robust statistical models from wide portions of hyperspectral reflectance datasets. In particular, PLSR shows promise in analyzing high-dimensional hyperspectral data containing multiple correlated and noisy predictor variables [51,52]. The PLSR models developed with hyperspectral leaf and canopy reflectance have proven useful for high-throughput phenotyping in the field and are increasingly being used for predicting key physicochemical and structural parameters, including but not limited to chlorophyll fluorescence, Ψleaf, photosynthetic capacity, leaf nitrogen concentration, and cellulose and lignin content [51,53,54,55,56]. Therefore, PLSR modeling with reflectance spectroscopy may be able to predict the trait responses selected in our study as well.
The combination of air temperature (Ta) with leaf reflectance data may improve model prediction due to its capacity to capture physiological responses to diurnal and seasonal shifts in heat loading. Trees in cites can be physiologically more stressed than those in outlying rural areas and forested landscapes because they experience elevated urban temperatures and limited space for root growth [57]. In addition, factors such as photosynthetic phenology and the timing and length of the growing season can vary across heterogeneous urban landscapes due largely to their temperature gradients [58,59,60]. These findings suggest that Ta may serve as a useful complementary predictor of physiological responses in urban trees.
When upscaling leaf-specific measures to broader remote sensing applications, it is important to understand whether leaf-level spectral models can be applied to airborne and satellite data. This translation requires empirical results from leaf-level research that suggests the spectral resolution, individual wavelengths, and wavelength ranges needed to detect each trait response. Hyperspectral sensors mounted on drones can collect high spatial resolution imagery, thus enabling digitization of individual tree crowns and extraction of canopy reflectance spectra. However, commercially available hyperspectral cameras (e.g., Cubert Firefleye S185 and Ultris X20 Plus; Cubert GmbH, Ulm, Baden-Württemberg, Germany) that are capable of being deployed on drones can detect only the VNIR region [61,62,63]. Therefore, the extent to which drone-mounted hyperspectral VNIR systems can monitor key plant trait responses remains unclear. Alternatively, satellite remote sensing remains a reliable approach to broad-scale monitoring. Among readily accessible and high temporal resolution multispectral satellite data, the Copernicus Sentinel-2 delivers relatively high spatial resolution (10 m), with 13 multispectral bands encompassing the VNIR–SWIR region, that is comparable with the wavelength range (400–2500 nm) of hyperspectral data collected in this study. However, it is not clear if the limited number of bands available in the multispectral data will be useful for broad-scale monitoring of plant trait responses.
In this study, we sought to determine the accuracy with which functional trait responses to heat and moisture stress could be estimated using reflectance spectroscopy. Our objectives were to (1) assess the capacity of existing vegetation indices to predict selected trait responses, and to (2) predict selected trait responses using PLSR on all available bands and band subsets corresponding to realistic remote sensing scenarios. To address these questions, we conducted a field-based, proximal sensing study using trees that were growing on a university campus outside Baltimore, Maryland, USA. We measured trait responses using conventional methods (e.g., leaf fluorometry) and concurrently recorded hyperspectral reflectance. We then used statistical modeling to determine the extent to which vegetation indices, the full spectral range, and portions of the range corresponding to drone- and satellite-borne sensors could predict stress-related physiological and morphological trait responses.
2. Materials and Methods
2.1. Study Area
This study took place on the campus of the University of Maryland, Baltimore County (UMBC; 39°15′20.37″N, 76°42′39.59″W). The campus has a heterogeneous mix of land cover features that are commonly observed in cities, such as medium-rise buildings, parking lots, sidewalks, grass, and other impervious surfaces. In addition, the campus has a diverse tree community that includes many common species in eastern North American cities. We focused on a set of 51 mature trees representing nine species and six genera (Table 1) that were distributed across the UMBC campus. Mature, medium-stature trees were selected such that each species spanned a gradient of surrounding impervious cover up to 15 m. This was done so the broad range of growing conditions experienced in urbanized landscapes would be included in our data.

Table 1.
Tree species included in this study. Sample size (n) indicates the number of samples collected from all trees in the species at multiple times spanning July–October in 2022; total number of trees = 51. ETR—electron transport rate, qP—photochemical quenching, Ψleaf—leaf water potential, SLA—specific leaf area, and ρ—fresh leaf reflectance.
2.2. Air Temperature
Ambient Ta can indicate heat loading as well as seasonality that can impact the physiological mechanisms and spectral response patterns of tree species. In this study, we used Ta as an ancillary environmental parameter in developing models to predict trees’ morphological and physiological responses. We measured Ta every minute using a Type-T thermocouple shaded by a RAD06 METSPEC 6-plate solar radiation shield (Campbell Scientific Inc., Logan, UT, USA). During all field visits, the sensor was placed in a shaded, centralized location on the UMBC campus so that it could provide continuous, site-level data concurrent with leaf-level physiological and hyperspectral measurements.
2.3. Physiological and Morphological Measurements
2.3.1. Leaf Sampling
We conducted field campaigns on sunny days during each month from July to October 2022. This allowed us to capture high heat conditions and evaluate the implications of summer stress on end-of-season functionality (i.e., photosynthetic phenology). Each campaign spanned 2–3 days per month (20–22 July, 24–25 August, 26–27 September, and 20–21 October). Measurements were made between 11:00 AM and 4:00 PM Eastern Daylight Time when heat loading and water limitation were near their daily peaks.
During each field visit, we collected fresh leaf samples from 51 trees located along a gradient of urban-like site conditions on the UMBC campus. We repeatedly sampled the same trees each month from July to October, making about 200 measurements of each trait by the time the field campaigns ended (Table 1). During sample collection, we used a long pole pruner to cut a shoot (30–50 cm long) from the sunlit portion of each tree’s middle or upper canopy. The cut end of the shoot was recut underwater, and measurements were taken immediately.
2.3.2. Chlorophyll Fluorescence
We measured chlorophyll fluorescence parameters from a representative leaf while it was still attached to the cut shoot. We clamped the leaf into a Portable Photosynthesis System equipped with a pulse amplitude-modulated fluorometer (LI-6800F, LI-COR Biosciences Inc., Lincoln, NE, USA). Leaves were allowed to equilibrate to chamber conditions (typically 2–3 min), which included irradiance equivalent to full sun (2000 µmol m−2 s−1) and ambient CO2 (400 ppm). Target leaf temperatures were set to mimic afternoon temperatures each month (35 °C in July and August, 25 °C in September, and 20 °C in October) and the chamber’s vapor-pressure deficit was set to 1.5 kPa.
Once equilibrated, leaves were subjected to a multi-phase flash to determine light-adapted maximum fluorescence (F′m). Steady-state fluorescence (Fs) was measured once the leaf returned to actinic light conditions. Light-adapted minimum fluorescence (F′o) was measured after the removal of actinic light and a brief exposure to far-red light [64]. From these values, we derived (a) qP, which is related to the maximum efficiency of photosystem II (PSII) or, equivalently, the proportion of PSII centers that are open, qP = (F′m − Fs)/(F′m − F′o) [65] and (b) the quantum yield of PSII (ΦPSII; (F′m − Fs)/F′m). ETR was then calculated as follows: ETR—PFDa × ΦPSII × 0.5, where PFDa is the photon flux density of absorbed light and 0.5 is a correction factor for the partitioning of energy [65].
2.3.3. Leaf Water Potential
We measured leaf water potential (Ψleaf) on one fully developed leaf from each tree. Leaves were typically taken from the same shoots as those selected for chlorophyll fluorescence, with measurements made 2–3 min apart. A sample leaf was excised with a razor blade and immediately sealed in a pressure chamber (Model 615, PMS Instrument Company, Albany, OR, USA). Nitrogen gas was slowly added until sap first emerged from the xylem visible in the petiole’s cut surface; the valve was closed at this moment and the pressure was recorded. Because an overabundance of foam precluded measurements from Acer spp. [66,67], the Ψleaf dataset was smaller than the others (Table 1).
2.3.4. Specific Leaf Area
We measured the SLAs of sample leaves taken from the same shoots as those used in physiological measurements. After petioles had been removed, leaves were sealed in plastic bags and kept cool until their areas could be measured in the laboratory with a LI-3100C Area Meter (LI-COR Biosciences Inc., Lincoln, NE, USA). Leaves were then transferred to paper bags and oven-dried at 60 °C for at least 48 h, allowed to cool in a desiccation chamber, and weighed. SLA was calculated as the ratio of fresh leaf area to dry leaf mass.
2.4. Leaf-Level Spectroscopy: Hyperspectral Leaf Reflectance
Hyperspectral measurements were made concurrently with physiological and morphological measurements, with leaves excised from the same shoot. We used a handheld spectroradiometer (SVC HR-1024i, Spectra Vista Corporation, Poughkeepsie, NY, USA) equipped with a leaf clip and a Spectralon white reference panel (99% reflectance). This device samples the spectral range of 350–2500 nm with nominal bandwidths of ≤1.5 nm for the range of 350–1000 nm, ≤3.8 nm for 1000–1890 nm, and ≤2.5 nm for 1890–2500 nm. For each measurement, we collected spectral data by first scanning the white reference plate and then the target sample leaf that was placed in the SVC leaf clip (which was connected to a calibrated light source). For large leaves, we measured three leaves per shoot separately. For small or narrow leaves, we arranged a leaf mat comprised of 2–3 leaves arranged side by side to fill the field of view (FOV) and minimize the gaps and overlaps between leaves during measurement [68], and we separately measured this for 2–3 leaf mats per tree. In rare cases where leaves could not be arranged to fill the FOV (e.g., 90% FOV coverage), leaf reflectance values were normalized to 100% FOV.
After the field measurements were completed, hyperspectral leaf reflectance data were post-processed. Overlapping portions of spectra were joined by setting the detector overlap controls within the wavelength range of 990 to 1900 nm and applying the NIR-SWIR overlap algorithm within the matching region; this was available in the SVC HR-1024i PC Data Acquisition Software version 1.22 and yielded a single set of values. Next, samples that showed atypical green leaf spectra in the VNIR region were discarded (n = 7); these were mainly found in senescing leaves collected in October. Finally, the spectra measured from replicate leaves or leaf mats were averaged to yield one spectrum per tree. The resultant curve of hyperspectral reflectance followed a characteristic pattern across the VNIR–SWIR wavelength range (400 to 2500 nm), though it varied strongly by species (Figure 1).
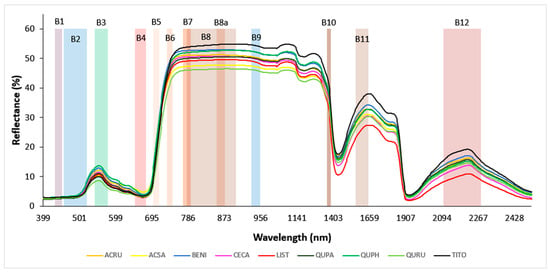
Figure 1.
Hyperspectral leaf reflectance curves of nine tree species. The reflectance values of all trees within each species were averaged to give mean spectra for each species. The species code abbreviations are explained in Table 1. The twelve color-shaded rectangles represent full spectral widths of Sentinel-2 bands; B1—Aerosol (433–453 nm), B2—Blue (457.5–522.5 nm), B3—Green (542.5–577.5 nm), B4—Red (650–680 nm), B5—Red Edge 1 (697.5–712.5 nm), B6—Red Edge 2 (732.5–747.5 nm), B7—Red Edge 3 (773–793 nm), B8—NIRwide (784.5–899.5 nm), B8a—NIRnarrow (855–875 nm), B9—Water Vapor (935–955 nm), B10—Cirrus (1360–1390 nm), B11—SWIR 1 (1565–1655 nm), and B12—SWIR 2 (2100–2280 nm).
2.5. Data Analysis
2.5.1. Vegetation Indices
One of our study objectives was to gain insight into whether, and the extent to which, each leaf trait response could be modeled with existing vegetation indices. Accordingly, we tested a total of 58 published vegetation indices selected for their potential biochemical or biophysical relevance to our leaf trait responses of interest (e.g., [46,48,49,50,69,70,71,72,73]) (Table S1). We calculated these vegetation indices from our hyperspectral leaf reflectance data and fitted them to our measured data of leaf trait responses using linear models. To evaluate their prediction capacity, we calculated their model-fit indicators (R2 and root mean square error (RMSE)) and then identified the top three vegetation indices that were the most linearly associated with each of the trait responses measured in this study.
2.5.2. Correlation Analysis
Using R version 4.2.3 [74], we calculated a Pearson correlation matrix to evaluate relationships among measure leaf trait responses (ETR, qP, Ψleaf, and SLA) and to assess which of the responses were affected by Ta. Those that were significantly correlated with Ta were likely to be better predicted by models in which Ta was included with hyperspectral bands.
2.5.3. Model Development: Partial Least Squares Regression
To predict trait responses of urban tree species under heat and moisture stress, we developed partial least squares regression (PLSR) models by using the ‘pls’ package version 2.8-1 [75]. Initial models used reflectance over the full range of VNIR–SWIR hyperspectral wavelengths (400 to 2500 nm) that were detected with our spectroradiometer (hereafter referred to as “full spectral scenario”). We built two PLSR models for each trait response—one with hyperspectral leaf reflectance and Ta, and the other with hyperspectral leaf reflectance only. Comparing these two models could provide insight into whether Ta captured variation in trait responses that were associated with weekly changes in temperature or diurnal temperature fluxes.
We also evaluated model performance using subsets of the full spectral dataset limited to the VNIR range, which was typical of data from drone-mounted hyperspectral cameras (hereafter referred to as “drone scenario”) or selected bands within the VNIR–SWIR range matching those available in Sentinel-2 data (as a stand-in for any common multispectral satellite; hereafter referred to as “multispectral scenario”). As before, we developed separate PLSR models for each trait response but with restrictions on band inclusion corresponding to the scenario in question. To establish independent training and testing datasets, we randomly divided observations into training (80% of samples) and validation (20%) subsets using the ‘caret’ package version 6.0-94 [76]. During model development, we assigned the initial input number of PLS components to 30 [77,78,79]. We selected the best-fit PLSR model with the number of components having the smallest RMSE based on the results of a 10-fold cross-validation with ten repetitions [80]. For the “full spectral scenario” and “drone scenario”, we identified the 20 most important raw spectral bands involved in model fits using the ‘varImp’ function available in the ‘caret’ package [76]. For model validation, fitted models were used to predict the validation response and were evaluated by calculating model-fit indicators, such as R2, RMSE, and root mean square error percentage (RMSE%; calculated as (RMSE/ × 100%). As RMSE% was reported as a percentage, its results were more interpretable, especially when comparing model performance across leaf trait responses with different value ranges.
The entire model-fitting process was repeated 500 times with different randomizations of training and validation sets to assess the sensitivity of model outputs to sampling variation. From these 500 iterations, we calculated the mean and standard error (SE) of model-fit indicators in each model-fit scenario. To visualize the observed-vs.-modeled leaf trait responses, we created scatterplots for each tested scenario using our measured data as observed values and the average of predicted values resulted from 500 iterated runs as modeled values. Only for the most likely best-fit scenario, viz., the “full spectral scenario” with hyperspectral leaf reflectance and Ta, did we report the total number of times that the most important 20 wavelengths were selected for predicting each leaf trait response.
For the “full spectral scenario”, we first counted the frequencies of the 20 most important wavelengths selected from the 500 model runs within the full spectral width of each Sentinel-2 band, which were illustrated as shaded areas in Figure 1 [81]. Then, we calculated the normalized selection frequency of Sentinel-2 bands by dividing the sum of the counts of the 20 most important wavelengths within each band and then scaling the resultant values between 0 and 1.
3. Results
3.1. Vegetation Indices
We reported the three vegetation indices that best predicted each leaf trait response via linear relationships (Table 2). Results for remaining vegetation indices are in the supplement (Table S1). The top three vegetation indices had R2 values of 0.23–0.28 for ETR, 0.13–0.17 for qP, 0.11–0.13 for Ψleaf, and 0.48–0.55 for SLA. The double-peak optical index (DPi) was able to account for variation in chlorophyll fluorescence (ETR and qP) as well as Ψleaf probably because DPi was made up of red-edge wavelengths only (Table 2). Overall, the tested vegetation indices had relatively low predictive capacity for trait responses; however, they were more successful at predicting SLA (especially mNDLMA [46]; R2 = 0.55).

Table 2.
The best vegetation indices for predicting ETR, qP, Ψleaf, and SLA. The top three vegetation indices for predicting their respective leaf trait responses are bolded in green. Asterisk indicates the significance level of linear relationship between vegetation index and leaf trait response (***—p < 0.001, **—p < 0.01, *—p < 0.05, and ns—p > 0.05). ρ represents fresh leaf reflectance of corresponding wavelengths (expressed as percentage).
3.2. Leaf Trait Responses and Air Temperature
Initial analysis revealed that physiological trait values (ETR, qP, and Ψleaf) were significantly correlated with Ta (Table 3), suggesting that their stress responses could be influenced by changes in Ta and that spectral models may benefit from the inclusion of this widely available parameter. In contrast, the morphological trait, SLA, was not correlated with Ta. Summary statistics for ETR, qP, Ψleaf, SLA, and Ta are presented in the supplement (Table S2).

Table 3.
Pearson correlation coefficient (r) matrix for electron transport rate (ETR), photochemical quenching (qP), leaf water potential (Ψleaf), specific leaf area (SLA), and air temperature (Ta). Correlations are bolded if statistically significant (p < 0.05). Asterisks indicate the significance level of each pairwise correlation (***—p < 0.001, **—p < 0.01, and *—p < 0.05).
3.3. Model Performance
All PLSR model outputs were stable, as evidenced by the size of the standard errors (SE) relative to corresponding means (calculated from 500 iterations; Table 4). Predictions based on the “full spectral scenario” accounted for substantial yet available portions of variation in each functional trait response. Inclusion of Ta in the “full spectral scenario” improved the prediction of ETR (R2 = 0.56 vs. 0.51) and qP (R2 = 0.33 vs. 0.28), but not Ψleaf or SLA. In Figure 2, we showed scatterplots of models with Ta only because the ability of a model to predict Ψleaf and SLA was not generally decreased by the inclusion of Ta. Among the tested scenarios, the “full spectral scenario” best predicted Ψleaf (R2 = 0.36) and SLA (R2 = 0.56). However, chlorophyll fluorescence predictions were somewhat improved in the “drone scenario” vs. the “full spectral scenario”, but not the “multispectral scenario”.

Table 4.
Performance of partial least squares regression models using leaf reflectance (ρ) & air temperature (Ta) vs. only ρ as predictors. Model fit indicators of test data (R2 and RMSE%) are averaged over 500 model runs, with SEs indicated in parentheses. Bold indicates the best model for predicting a leaf trait across the three scenarios evaluated.
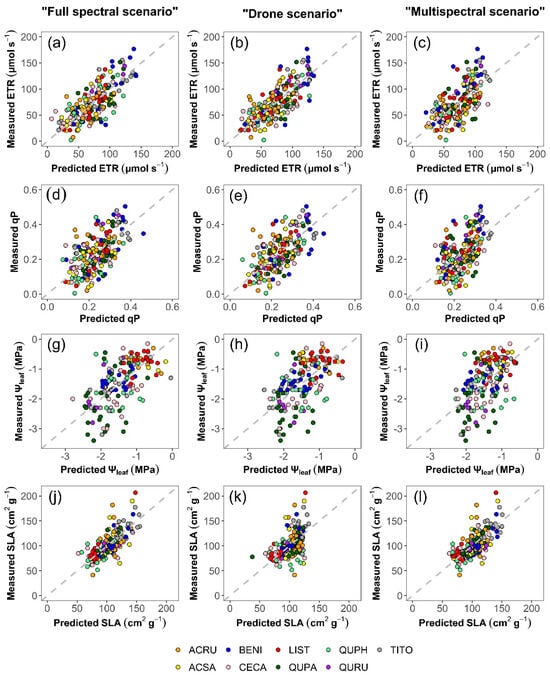
Figure 2.
Scatterplots comparing measured and modeled values of ETR (a–c), qP (d–f), Ψleaf (g–i), and SLA (j–l) among the “full spectral”, “drone”, and “multispectral” scenarios. Modeled values represent the final, modeled results, calculated from the average of predicted values obtained from 500 iterations, with Ta included as a predictor in all models. Table 1 explains the species abbreviations. Dashed grey lines depict 1:1 relationships.
Models based on the “drone scenario” somewhat improved predictions of ETR (R2 = 0.58 vs. 0.56) and qP (R2 = 0.42 vs. 0.33) over the “full spectral scenario”, even though only the VNIR spectral region was used. Once again, Ta offered some predictive benefit when included in ETR and qP predictions, as well as in estimates of Ψleaf (ETR, R2 = 0.58 vs. 0.55; qP, R2 = 0.42 vs. 0.40; and Ψleaf, R2 = 0.28 vs. 0.21).
The “multispectral scenario” also benefited modestly from the inclusion of Ta in the spectral models predicting trait responses. Under the “multispectral scenario”, the inclusion of Ta improved the prediction of trait responses—ETR (R2 = 0.43 vs. 0.36), qP (R2 = 0.31 vs. 0.26), and Ψleaf (R2 = 0.27 vs. 0.20) but, as anticipated, did not improve SLA prediction. The “multispectral scenario” had a comparable capacity to the “full spectral scenario” in predicting SLA (R2 = 0.56 vs. 0.53). Across all models under the “multispectral scenario”, prediction of SLA was most accurate, followed by the prediction of ETR, qP, and Ψleaf. Figure 2 compares observed and modeled values for each leaf trait response under tested scenarios.
3.4. Important Wavelengths
In the spectral models that included Ta developed under “full spectral scenario”, the VNIR wavelength range was a significant predictor of ETR and qP (Figure 3). For ETR, the most selected wavelength ranges were mainly within the visible light region (including 696–699 nm, i.e., the red edge 1 band in Sentinel-2), followed by SWIR and NIR. This was the same for qP in the order of importance; however, spectral widths of both red edge 1 (695–707 nm) and blue (521–533 nm) bands in Sentinel-2 were important for qP prediction. Overall, many of the chosen wavelengths did not overlap with Sentinel-2 bands, indicating the importance of blue–green (only for qP), green–red, and SWIR 1–SWIR 2 wavelengths for predicting chlorophyll fluorescence.
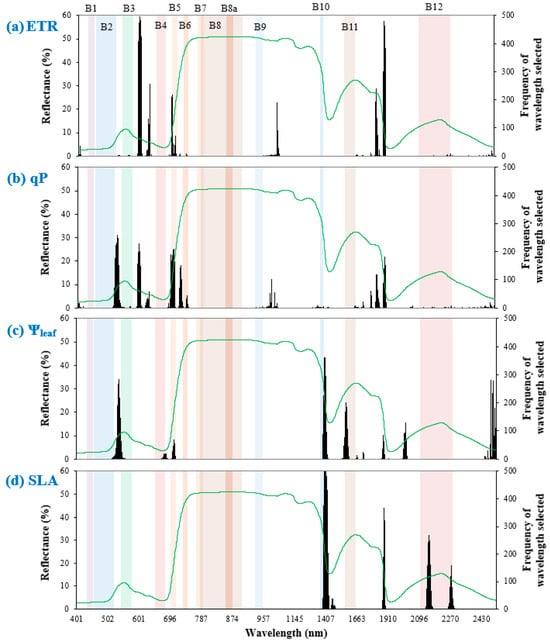
Figure 3.
Frequency of important wavelengths selected out of 500 model runs in predicting leaf trait responses (a) ETR, (b) qP, (c) Ψleaf, and (d) SLA, shown by black bars. Colored rectangles represent full spectral widths of Sentinel-2 bands. The green line depicts the grand mean spectrum across all leaf samples.
The Ψleaf models required visible light and SWIR regions. Between the two regions, PLSR mostly selected SWIR wavelengths, including portions of cirrus (1385–1422 nm) and SWIR 1 (1561–1580 nm) bands in Sentinel-2. The importance of SWIR and visible light regions concurred with Table 4, which recommended the “full spectral scenario” to best predict Ψleaf.
Models of SLA required only the SWIR region. These models also selected portions of Sentinel-2 bands such as cirrus (1385–1422 nm) and SWIR 2 (2139–2160 nm and 2265–2275 nm). This indicates that SLA prediction mainly requires SWIR bands under the “multispectral scenario”.
3.5. Important Sentinel-2 Bands
We assessed the potential of satellite-based sensors to predict functional trait responses by identifying the Sentinel-2 spectral bands with greatest importance in prediction. In correspondence with Table 4 and as shown in Figure 4 that highlighted the most selected, important Sentinel-2 bands for predicting each trait response, the visible light region, specifically red edge 1 (697.5–712.5 nm) was useful for the prediction of ETR and qP. In addition to red edge 1, Figure 3 and Figure 4 generally indicated the importance of having wavelengths among the Sentinel-2 bands in predicting ETR and qP, particularly in the visible light region, such as blue–green, green–red, and red edge 1–red edge 2 bands.
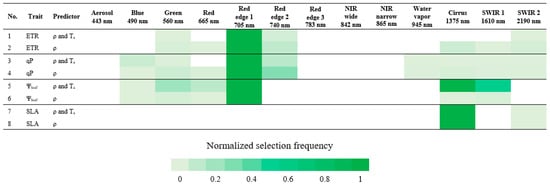
Figure 4.
Normalized selection frequency of Sentinel-2 bands. Normalized selection frequency is scaled between 0 and 1, in which 1 is the score most selected. Band center wavelength (nm) is described beneath its corresponding band.
For Ψleaf prediction, red edge 1, cirrus (1360–1390 nm), SWIR 1 (1565–1655 nm), and green (542.5–577.5 nm) bands were the most important, in this order, in the model that included Ta, whereas only red edge 1 was selected as important in the model without Ta. Even though important wavelength selections aligned with Sentinel-2 bands, intervals in the blue–green and SWIR 1–SWIR 2 spectral ranges (Figure 3 and Figure 4) could also be important for Ψleaf prediction, as was the case for ETR and qP.
Only cirrus and SWIR 2 (2100–2280 nm) bands were important for SLA prediction, whereas Figure 3 also highlighted the possible contribution of wavelengths between SWIR 1 and SWIR 2. There was no contribution of VNIR bands in predicting SLA (Figure 3 and Figure 4). Inclusion or exclusion of Ta in the SLA models did not affect the determination of important Sentinel-2 bands.
4. Discussion
4.1. Vegetation Indices
Vegetation indices were nearly as effective as PLSR for predicting the leaf structural trait, SLA (R2 = 0.48–0.55; Table 2). In particular, mNDLMA, a vegetation index formerly developed for the estimation of leaf-level LMA in broad-leaved forest [46], was as able to predict the SLA of urban trees as the predictive models developed with PLSR (R2 = 0.55–0.56; Table 2 and Table 4). There was also considerable agreement between the top vegetation indices and PLSR models in terms of input wavelength and wavelength range of importance. For instance, both mSRLMA and the PLSR models required the contribution of 2265 nm for SLA estimation (Table 2 and Figure 3). In terms of wavelength range, both PLSR models and top vegetation indices required SWIR for SLA prediction, i.e., the wavelength region spectrally responsive to changes in biochemical and structural traits (including cellulose, lignin, carbon, nutrients, and proteins), as well as water absorption [85,86,87].
Although SLA, a leaf structural trait, was well-modeled using vegetation indices, the more ephemeral or transient physiological parameters were not. Although the predictive power of the vegetation indices was low, we did see wavelength-range agreement between the top vegetation indices and the PLSR models selected to model ETR and qP. This makes sense because chlorophyll fluorescence emission mainly takes place in the VNIR region [88,89]. In contrast, vegetation indices and PLSR band selection did not perfectly align for Ψleaf prediction (Figure 3 and Table 4). The top vegetation indices for Ψleaf estimation included only VNIR wavelengths (Table 2); however, PLSR models indicated use of the full VNIR–SWIR spectral range (preferably the SWIR wavelengths as shown in Figure 3) to better model Ψleaf (Table 4), potentially explaining why these indices had significantly lower predictive capacity than the PLSR model. Overall, our results suggested that the vegetation indices severely reduced the available spectral information, and that retaining the original bands for use in PLSR (or perhaps some other machine-learning-based methods) was required to spectroscopically quantify these dynamic physiological trait responses.
4.2. Predicting Trait Responses with PLSR
Field spectroscopy method allowed us to estimate leaf functional trait expression with modest success in this study (e.g., R2 = 0.36–0.56). Spectral models were particularly successful at predicting chlorophyll fluorescence and SLA, though they were less successful for Ψleaf. Here, we focus on the potential to quantify variation in these trait responses over large areas using narrowband drone data or broadband satellite remote sensing data.
Under the “full spectral scenario”, PLSR models mainly selected VNIR wavelengths, as well as a few bands in the SWIR region such as 1817–1832 nm and 1881–1899 nm for ETR and 1881–1892 nm for qP. Prior studies used strong water absorption bands in the SWIR region together with VNIR wavelengths to estimate leaf chlorophyll fluorescence in spring wheat cultivars [53], mango (Mangifera indica) [90], and the salt marsh plant (Suaeda salsa). This combination is possible when photons emitted during chlorophyll fluorescence are reabsorbed by chlorophyll pigments; thus, longer wavelengths (beyond the chlorophyll and carotenoid absorption range) might also be useful for detecting chlorophyll fluorescence [73]. Nonetheless, inclusion of the SWIR region as in the “full spectral scenario” did not outperform predictions derived solely from VNIR, suggesting that comparable predictive capacity could be achieved with the use of drone-borne hyperspectral data.
With slightly better predictive capacity than the “full spectral scenario”, our “drone scenario” indicated that chlorophyll fluorescence monitoring from a VNIR hyperspectral remote sensing system was feasible. Like other studies [91,92,93], we confirmed that VNIR (without SWIR) was the best predictor of ETR and qP across the three tested scenarios. From a physiological standpoint, the chlorophyll fluorescence emission from photosystem I and II has a peak or a shoulder near the red and far-red spectral regions (680–695 nm and 720–740 nm) [88,89,91,92,94]. Correspondingly, PLSR models for predicting chlorophyll fluorescence dynamics (particularly qP) selected wavelength ranges at or near these regions. Moreover, the most frequent selections for predicting ETR and qP included the O2-B band range (682–698 nm), which represents the sun-induced chlorophyll fluorescence band widely recommended as a proxy for photosynthetic efficiency of vegetation from space [19,95,96]. Not surprisingly, the “multispectral scenario” also showed potential for the remote detection of ETR and qP. Among the Sentinel-2 bands, red edge 1 was the one most selected for predicting fluorescence in our study. This finding was relevant to satellite remote sensing because the European Space Agency specifically designed the red edge 1 band of Sentinel-2 as the baseline for fluorescence studies [81].
The “drone scenario” and “multispectral scenario” showed comparable performance in predicting Ψleaf. However, both were weaker predictors than the “full spectral scenario”, indicating an even more limited capacity to quantify Ψleaf over extensive areas with remote sensing. On the other hand, our findings correspond with previous work in highlighting red edge 1 and SWIR 1 as important bands for broad-scale monitoring with Sentinel-2 data [97]. Based on our results, the best scenario for predicting Ψleaf required hyperspectral wavelengths across the full spectrum of VNIR–SWIR, yet these models were only able to explain just over one third of the observed variation. However, previous modeling efforts using hyperspectral wavelengths within or near red-edge and cirrus regions had twice the explained variation of Ψleaf as in our study [42], where Ψleaf models showed notably weaker predictive performance than other trait responses. One plausible explanation may stem from the lack of observations from Acer species during model development (n = 169 for Ψleaf vs. n = 194 to 199 for other leaf trait responses). We were not able to measure Ψleaf from 30 samples of Acer rubrum and Acer saccharum due to foam formation in the cut petiole (as noted by Bahari et al. [66] and Hauer et al. [67]), especially during the warmer months. Eitel et al. [44] noted a similar pattern when limited data was available for their predictions of Populus species (R2 = 0.34 for entire dataset vs. 0.08 for data without highly stressed samples). The exclusion of highly water-stressed samples certainly lowered our sample size and might have affected the capacity for Ψleaf prediction.
Our results demonstrated the potential of satellite-based SLA prediction with Sentinel-2 data. The models based on the “multispectral scenario” outperformed the “drone scenario” and were also comparable to the best-case “full spectral scenario” (R2 = 0.53 vs. 0.56), reaffirming the observation that the inclusion of SWIR wavelengths, even at multispectral resolution, could significantly improve SLA prediction. Our study also found that SWIR, particularly the cirrus and SWIR 2 bands of Sentinel-2, was a key predictor of SLA. This was consistent with previous reports that the wavelength range of 1300–1800 nm was predictive of SLA in broadleaf, conifer, and mixed forest stands [45]. This range overlapped with the most-selected wavelengths in the urban tree types investigated here (Figure 3). Even though the “multispectral scenario” showed great potential, possibly due to the inclusion of the SWIR region, modeling SLA under the “drone scenario” lost a significant amount of predictive power compared to the best-case “full spectral scenario” (R2 = 0.56 vs. 0.30), indicating the potential limitation of a drone-mounted hyperspectral VNIR system to remotely sense SLA.
Spectral models developed with PLSR had modest success in predicting key leaf functional trait responses (R2 = 0.36 to 0.58). To potentially improve the predictive capacity, or as an alternative, using the machine learning methods that have non-linear fitting capacities (e.g., random forest [98] or support vector machine [99]) might capture more variability in the data of one or more trait responses. Although not conducted in this study, calculating radiance from reflectance data may offer an additional opportunity to evaluate correlations between spectral features and chlorophyll fluorescence. This would present radiance–trait relationships, providing insight into the mechanistic link with, and validation of, upcoming satellite remote sensing products such as Fluorescence Explorer (FLEX). This mission will carry a high-resolution Fluorescence Imaging Spectrometer (FLORIS), which will measure radiance between 500 and 780 nm and provide fluorescence estimates to map photosynthesis and monitor vegetation health [100,101,102].
Across functional traits and predictive scenarios, we found that inclusion of Ta in spectral models better predicted tree physiological responses to heat and moisture stress at our urbanized site. Like other studies [103,104,105,106], our tree physiological trait responses were associated with temperature changes. This suggested that large-scale and global studies of plant ecophysiology, tree cooling in urban cities, and their responses to heat could benefit from the integration of satellite-based reflective and thermal (e.g., land surface temperature) remote sensing data [107,108,109]. In our study, Ta was able to improve the estimation of physiological traits more effectively than the morphological trait SLA since, as expected, SLA was less sensitive to temperature variation. In particular, including Ta improved predictions of trait responses related to chlorophyll fluorescence, but its effect on Ψleaf estimation was equivocal. Even though there was no improvement in the “full spectral scenario”, inclusion of Ta did increase the R2 of Ψleaf models by 7% in both the “drone scenario” and “multispectral scenario”, suggesting its potential value in remote sensing models. Overall, physiological trait responses appear to be sensitive to, and dependent upon, ambient Ta as a covariate; therefore, we recommend including it in remote sensing-based predictions of tree responses to heat and moisture stress.
5. Conclusions
This study used proximal spectral sensing to assess (1) whether existing published vegetation indices could predict trees’ functional trait responses to heat in an urbanized setting and (2) if predictive models developed with PLSR could quantify these trait responses. Success would indicate that these trait responses may be predictable remotely, and thus over broad scales. We found that SLA was well predicted with some vegetation indices, which were comparably as effective as PLSR models. However, physiological trait responses (ETR, qP, and Ψleaf) were not well predicted by vegetation indices; thus, the more robust PLSR models were needed to predict these dynamic parameters with reasonable accuracy. Across the evaluated scenarios, traits associated with chlorophyll fluorescence (ETR and qP) showed great potential to be remotely sensed with drone-mounted sensors due to their important wavelengths being confined to the VNIR region, whereas SLA could potentially be sensed with the satellite-borne multispectral sensors due to the Sentinel-2 bands extending to the SWIR region. Remote sensing-based scenarios had a limited capacity to predict Ψleaf. This limitation may have come from our inability to measure a wide range of Ψleaf in Acer species when they were highly heat-stressed during warmer months (n = 30 measurements). For satellite-based monitoring, red edge 1 band of Sentinel-2 may be useful for ETR and qP prediction; green, red edge 1, cirrus, and SWIR 1 may be useful for Ψleaf prediction; and cirrus and SWIR 2 may be useful for SLA prediction. We recommend including both Ta and spectral remote sensing data to predict physiological responses to heat due to these traits’ sensitivity to Ta. We conclude that field-based reflectance spectroscopy and PLSR can identify wavelengths and wavelength ranges that have the potential to be leveraged when developing remote sensing-based monitoring tools for broad-scale predictions of trees’ heat stress responses.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs16132291/s1. Table S1. List of tested vegetation indices: The top three vegetation indices for predicting their corresponding leaf trait responses are bolded in green. ρ represents fresh leaf reflectance of corresponding wavelengths (expressed as percentage). The “ns” superscript on R2 indicates no significant relationship between vegetation index and its corresponding trait response. Table S2: The mean, standard error (SE), median, minimum, maximum, and sample size (n) of electron transport rate (ETR), photochemical quenching (qP), leaf water potential (Ψleaf), specific leaf area (SLA), and air temperature (Ta). References [110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133] are cited in the Supplementary Materials.
Author Contributions
Conceptualization, T.Y.K., M.A., M.E.B. and J.S.C.; methodology, T.Y.K., M.A. and J.S.C.; software, T.Y.K., M.A. and J.S.C.; validation, T.Y.K., M.A. and J.S.C.; formal analysis, T.Y.K.; investigation, T.Y.K. and M.A.; resources, M.A., M.E.B. and S.W.E.; data curation, T.Y.K., M.A., M.E.B., S.W.E. and J.S.C.; writing—original draft preparation, T.Y.K.; writing—review and editing, T.Y.K., M.A., M.E.B., S.W.E. and J.S.C.; visualization, T.Y.K.; supervision, M.A.; project administration, M.A., M.E.B., S.W.E. and J.S.C.; funding acquisition, M.A., M.E.B., S.W.E. and J.S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the U.S. National Science Foundation (award number 1951647) to. The Article Processing Charge (APC) was funded by American University.
Data Availability Statement
Data available in a publicly accessible repository. Here is the DOI link to access the data at FigShare repository: https://doi.org/10.6084/m9.figshare.26384242.v1.
Acknowledgments
We thank student volunteers from the American University and the University of Maryland, Baltimore County for assistance with field data collection.
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to Data Availability Statement. This change does not affect the scientific content of the article.
References
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Kitzberger, T.; Rigling, A.; Breshears, D.D.; Hogg, E.T. A Global Overview of Drought and Heat-Induced Tree Mortality Reveals Emerging Climate Change Risks for Forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef]
- Anderegg, W.R.; Kane, J.M.; Anderegg, L.D. Consequences of Widespread Tree Mortality Triggered by Drought and Temperature Stress. Nat. Clim. Change 2013, 3, 30–36. [Google Scholar] [CrossRef]
- Park Williams, A.; Allen, C.D.; Macalady, A.K.; Griffin, D.; Woodhouse, C.A.; Meko, D.M.; Swetnam, T.W.; Rauscher, S.A.; Seager, R.; Grissino-Mayer, H.D. Temperature as a Potent Driver of Regional Forest Drought Stress and Tree Mortality. Nat. Clim. Change 2013, 3, 292–297. [Google Scholar] [CrossRef]
- Teskey, R.; Wertin, T.; Bauweraerts, I.; Ameye, M.; McGuire, M.A.; Steppe, K. Responses of Tree Species to Heat Waves and Extreme Heat Events. Plant Cell Environ. 2015, 38, 1699–1712. [Google Scholar] [CrossRef] [PubMed]
- Oke, T.R. The Energetic Basis of the Urban Heat Island. Q. J. R. Meteorol. Soc. 1982, 108, 1–24. [Google Scholar] [CrossRef]
- Barona, C.O.; Trammell, T.L. Urban Trees in a Changing Climate: Science and Practice to Enhance Resilience. Front. Ecol. Evol. 2022, 10, 882510. [Google Scholar]
- Choat, B.; Brodribb, T.J.; Brodersen, C.R.; Duursma, R.A.; López, R.; Medlyn, B.E. Triggers of Tree Mortality under Drought. Nature 2018, 558, 531–539. [Google Scholar] [CrossRef]
- Gupta, R.; Sharma, R.D.; Rao, Y.R.; Siddiqui, Z.H.; Verma, A.; Ansari, M.W.; Rakwal, R.; Tuteja, N. Acclimation Potential of Noni (Morinda citrifolia L.) Plant to Temperature Stress Is Mediated through Photosynthetic Electron Transport Rate. Plant Signal. Behav. 2021, 16, 1865687. [Google Scholar] [CrossRef]
- Zhang, R.; Sharkey, T.D. Photosynthetic Electron Transport and Proton Flux under Moderate Heat Stress. Photosynth. Res. 2009, 100, 29–43. [Google Scholar] [CrossRef]
- Zivcak, M.; Brestic, M.; Balatova, Z.; Drevenakova, P.; Olsovska, K.; Kalaji, H.M.; Yang, X.; Allakhverdiev, S.I. Photosynthetic Electron Transport and Specific Photoprotective Responses in Wheat Leaves under Drought Stress. Photosynth. Res. 2013, 117, 529–546. [Google Scholar] [CrossRef]
- Mrema, A.; Granhall, U.; Sennerby-Forsse, L. Plant Growth, Leaf Water Potential, Nitrogenase Activity and Nodule Anatomy in Leucaena leucocephala as Affected by Water Stress and Nitrogen Availability. Trees 1997, 12, 42–48. [Google Scholar] [CrossRef]
- Patakas, A.; Nikolaou, N.; Zioziou, E.; Radoglou, K.; Noitsakis, B. The Role of Organic Solute and Ion Accumulation in Osmotic Adjustment in Drought-Stressed Grapevines. Plant Sci. 2002, 163, 361–367. [Google Scholar] [CrossRef]
- Buman, B.; Hueni, A.; Colombo, R.; Cogliati, S.; Celesti, M.; Julitta, T.; Burkart, A.; Siegmann, B.; Rascher, U.; Drusch, M. Towards Consistent Assessments of In Situ Radiometric Measurements for the Validation of Fluorescence Satellite Missions. Remote Sens. Environ. 2022, 274, 112984. [Google Scholar] [CrossRef]
- Jänicke, L.K.; Preusker, R.; Celesti, M.; Tudoroiu, M.; Fischer, J.; Schüttemeyer, D.; Drusch, M. OLCI-A/B Tandem Phase: Evaluation of FLuorescence EXplorer (FLEX)-like Radiances and Estimation of Systematic Differences between OLCI-A and OLCI-FLEX. Atmos. Meas. Tech. 2023, 16, 3101–3121. [Google Scholar] [CrossRef]
- Julitta, T.; Corp, L.A.; Rossini, M.; Burkart, A.; Cogliati, S.; Davies, N.; Hom, M.; Mac Arthur, A.; Middleton, E.M.; Rascher, U. Comparison of Sun-Induced Chlorophyll Fluorescence Estimates Obtained from Four Portable Field Spectroradiometers. Remote Sens. 2016, 8, 122. [Google Scholar] [CrossRef]
- Li, X.; Xiao, J.; He, B. Chlorophyll Fluorescence Observed by OCO-2 Is Strongly Related to Gross Primary Productivity Estimated from Flux Towers in Temperate Forests. Remote Sens. Environ. 2018, 204, 659–671. [Google Scholar] [CrossRef]
- Bandopadhyay, S.; Rastogi, A.; Rascher, U.; Rademske, P.; Schickling, A.; Cogliati, S.; Julitta, T.; Mac Arthur, A.; Hueni, A.; Tomelleri, E. Hyplant-Derived Sun-Induced Fluorescence—A New Opportunity to Disentangle Complex Vegetation Signals from Diverse Vegetation Types. Remote Sens. 2019, 11, 1691. [Google Scholar] [CrossRef]
- Rascher, U.; Alonso, L.; Burkart, A.; Cilia, C.; Cogliati, S.; Colombo, R.; Damm, A.; Drusch, M.; Guanter, L.; Hanus, J. Sun-induced Fluorescence–a New Probe of Photosynthesis: First Maps from the Imaging Spectrometer HyPlant. Glob. Change Biol. 2015, 21, 4673–4684. [Google Scholar] [CrossRef]
- Rossini, M.; Nedbal, L.; Guanter, L.; Ač, A.; Alonso, L.; Burkart, A.; Cogliati, S.; Colombo, R.; Damm, A.; Drusch, M. Red and Far Red Sun-induced Chlorophyll Fluorescence as a Measure of Plant Photosynthesis. Geophys. Res. Lett. 2015, 42, 1632–1639. [Google Scholar] [CrossRef]
- Siegmann, B.; Alonso, L.; Celesti, M.; Cogliati, S.; Colombo, R.; Damm, A.; Douglas, S.; Guanter, L.; Hanuš, J.; Kataja, K. The High-Performance Airborne Imaging Spectrometer HyPlant—From Raw Images to Top-of-Canopy Reflectance and Fluorescence Products: Introduction of an Automatized Processing Chain. Remote Sens. 2019, 11, 2760. [Google Scholar] [CrossRef]
- Habyarimana, E.; Baloch, F.S. Machine Learning Models Based on Remote and Proximal Sensing as Potential Methods for In-Season Biomass Yields Prediction in Commercial Sorghum Fields. PLoS ONE 2021, 16, e0249136. [Google Scholar] [CrossRef] [PubMed]
- Schuster, J.; Hagn, L.; Mittermayer, M.; Maidl, F.-X.; Hülsbergen, K.-J. Using Remote and Proximal Sensing in Organic Agriculture to Assess Yield and Environmental Performance. Agronomy 2023, 13, 1868. [Google Scholar] [CrossRef]
- Tao, H.; Xu, S.; Tian, Y.; Li, Z.; Ge, Y.; Zhang, J.; Wang, Y.; Zhou, G.; Deng, X.; Zhang, Z. Proximal and Remote Sensing in Plant Phenomics: Twenty Years of Progress, Challenges and Perspectives. Plant Commun. 2022, 3, 100344. [Google Scholar] [CrossRef] [PubMed]
- Tattaris, M.; Reynolds, M.P.; Chapman, S.C. A Direct Comparison of Remote Sensing Approaches for High-Throughput Phenotyping in Plant Breeding. Front. Plant Sci. 2016, 7, 1131. [Google Scholar] [CrossRef] [PubMed]
- Kitao, M.; Lei, T.T.; Koike, T.; Tobita, H.; Maruyama, Y. Higher Electron Transport Rate Observed at Low Intercellular CO2 Concentration in Long-term Drought-acclimated Leaves of Japanese Mountain Birch (Betula ermanii). Physiol. Plant. 2003, 118, 406–413. [Google Scholar] [CrossRef]
- Peguero-Pina, J.J.; Sancho-Knapik, D.; Morales, F.; Flexas, J.; Gil-Pelegrín, E. Differential Photosynthetic Performance and Photoprotection Mechanisms of Three Mediterranean Evergreen Oaks under Severe Drought Stress. Funct. Plant Biol. 2009, 36, 453–462. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Liu, X.; Zhai, H.; Gao, H.; Yao, Y.; Du, Y. Responses of Photosystem II Photochemistry and the Alternative Oxidase Pathway to Heat Stress in Grape Leaves. Acta Physiol. Plant. 2016, 38, 232. [Google Scholar] [CrossRef]
- Yu, Z.-C.; Zheng, X.-T.; Lin, W.; Cai, M.-L.; Zhang, Q.-L.; Peng, C.-L. Different Photoprotection Strategies for Mid-and Late-Successional Dominant Tree Species in a High-Light Environment in Summer. Environ. Exp. Bot. 2020, 171, 103927. [Google Scholar] [CrossRef]
- Foyer, C.; Furbank, R.; Harbinson, J.; Horton, P. The Mechanisms Contributing to Photosynthetic Control of Electron Transport by Carbon Assimilation in Leaves. Photosynth. Res. 1990, 25, 83–100. [Google Scholar] [CrossRef]
- Han, J.; Gu, L.; Warren, J.M.; Guha, A.; Mclennan, D.A.; Zhang, W.; Zhang, Y. The Roles of Photochemical and Non-Photochemical Quenching in Regulating Photosynthesis Depend on the Phases of Fluctuating Light Conditions. Tree Physiol. 2022, 42, 848–861. [Google Scholar] [CrossRef]
- Norton, A.J.; Rayner, P.J.; Koffi, E.N.; Scholze, M.; Silver, J.D.; Wang, Y.-P. Estimating Global Gross Primary Productivity Using Chlorophyll Fluorescence and a Data Assimilation System with the BETHY-SCOPE Model. Biogeosciences 2019, 16, 3069–3093. [Google Scholar] [CrossRef]
- Caplan, J.S.; Galanti, R.C.; Olshevski, S.; Eisenman, S.W. Water Relations of Street Trees in Green Infrastructure Tree Trench Systems. Urban For. Urban Green. 2019, 41, 170–178. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, S.; Gentine, P.; Xiao, X. Can Vegetation Optical Depth Reflect Changes in Leaf Water Potential during Soil Moisture Dry-down Events? Remote Sens. Environ. 2019, 234, 111451. [Google Scholar] [CrossRef]
- Martínez-Vilalta, J.; Poyatos, R.; Aguadé, D.; Retana, J.; Mencuccini, M. A New Look at Water Transport Regulation in Plants. New Phytol. 2014, 204, 105–115. [Google Scholar] [CrossRef] [PubMed]
- Witkowski, E.; Lamont, B.B. Leaf Specific Mass Confounds Leaf Density and Thickness. Oecologia 1991, 88, 486–493. [Google Scholar] [CrossRef] [PubMed]
- Xiong, D.; Wang, D.; Liu, X.; Peng, S.; Huang, J.; Li, Y. Leaf Density Explains Variation in Leaf Mass per Area in Rice between Cultivars and Nitrogen Treatments. Ann. Bot. 2016, 117, 963–971. [Google Scholar] [CrossRef]
- Reich, P.B. The World-wide ‘Fast–Slow’ Plant Economics Spectrum: A Traits Manifesto. J. Ecol. 2014, 102, 275–301. [Google Scholar] [CrossRef]
- Wright, I.J.; Reich, P.B.; Westoby, M.; Ackerly, D.D.; Baruch, Z.; Bongers, F.; Cavender-Bares, J.; Chapin, T.; Cornelissen, J.H.; Diemer, M. The Worldwide Leaf Economics Spectrum. Nature 2004, 428, 821–827. [Google Scholar] [CrossRef]
- Caplan, J.S.; Yeakley, J.A. Functional Morphology Underlies Performance Differences among Invasive and Non-Invasive Ruderal Rubus Species. Oecologia 2013, 173, 363–374. [Google Scholar] [CrossRef]
- Salisbury, A.B.; Gallagher, F.J.; Caplan, J.S.; Grabosky, J.C. Maintenance of Photosynthesis by Betula populifolia in Metal Contaminated Soils. Sci. Total Environ. 2018, 625, 1615–1627. [Google Scholar] [CrossRef]
- Croce, R.; Zucchelli, G.; Garlaschi, F.M.; Bassi, R.; Jennings, R.C. Excited State Equilibration in the Photosystem I—Light-Harvesting I Complex: P700 Is Almost Isoenergetic with Its Antenna. Biochemistry 1996, 35, 8572–8579. [Google Scholar] [CrossRef] [PubMed]
- El-Hendawy, S.E.; Al-Suhaibani, N.A.; Elsayed, S.; Hassan, W.M.; Dewir, Y.H.; Refay, Y.; Abdella, K.A. Potential of the Existing and Novel Spectral Reflectance Indices for Estimating the Leaf Water Status and Grain Yield of Spring Wheat Exposed to Different Irrigation Rates. Agric. Water Manag. 2019, 217, 356–373. [Google Scholar] [CrossRef]
- Giovenzana, V.; Beghi, R.; Parisi, S.; Brancadoro, L.; Guidetti, R. Potential Effectiveness of Visible and near Infrared Spectroscopy Coupled with Wavelength Selection for Real Time Grapevine Leaf Water Status Measurement. J. Sci. Food Agric. 2018, 98, 1935–1943. [Google Scholar] [CrossRef] [PubMed]
- Eitel, J.U.; Gessler, P.E.; Smith, A.M.; Robberecht, R. Suitability of Existing and Novel Spectral Indices to Remotely Detect Water Stress in Populus Spp. For. Ecol. Manag. 2006, 229, 170–182. [Google Scholar] [CrossRef]
- Ali, A.M.; Darvishzadeh, R.; Skidmore, A.K.; van Duren, I. Specific Leaf Area Estimation from Leaf and Canopy Reflectance through Optimization and Validation of Vegetation Indices. Agric. For. Meteorol. 2017, 236, 162–174. [Google Scholar] [CrossRef]
- Le Maire, G.; François, C.; Soudani, K.; Berveiller, D.; Pontailler, J.-Y.; Bréda, N.; Genet, H.; Davi, H.; Dufrêne, E. Calibration and Validation of Hyperspectral Indices for the Estimation of Broadleaved Forest Leaf Chlorophyll Content, Leaf Mass per Area, Leaf Area Index and Leaf Canopy Biomass. Remote Sens. Environ. 2008, 112, 3846–3864. [Google Scholar] [CrossRef]
- Asner, G.P.; Martin, R.E.; Knapp, D.E.; Tupayachi, R.; Anderson, C.; Carranza, L.; Martinez, P.; Houcheime, M.; Sinca, F.; Weiss, P. Spectroscopy of Canopy Chemicals in Humid Tropical Forests. Remote Sens. Environ. 2011, 115, 3587–3598. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Pushnik, J.; Dobrowski, S.; Ustin, S. Steady-State Chlorophyll a Fluorescence Detection from Canopy Derivative Reflectance and Double-Peak Red-Edge Effects. Remote Sens. Environ. 2003, 84, 283–294. [Google Scholar] [CrossRef]
- Gamon, J.A.; Serrano, L.; Surfus, J.S. The Photochemical Reflectance Index: An Optical Indicator of Photosynthetic Radiation Use Efficiency across Species, Functional Types, and Nutrient Levels. Oecologia 1997, 112, 492–501. [Google Scholar] [CrossRef]
- Penuelas, J.; Filella, I.; Biel, C.; Serrano, L.; Save, R. The Reflectance at the 950–970 nm Region as an Indicator of Plant Water Status. Int. J. Remote Sens. 1993, 14, 1887–1905. [Google Scholar] [CrossRef]
- Barnes, M.L.; Breshears, D.D.; Law, D.J.; Van Leeuwen, W.J.; Monson, R.K.; Fojtik, A.C.; Barron-Gafford, G.A.; Moore, D.J. Beyond Greenness: Detecting Temporal Changes in Photosynthetic Capacity with Hyperspectral Reflectance Data. PLoS ONE 2017, 12, e0189539. [Google Scholar] [CrossRef]
- Nigon, T.J.; Yang, C.; Dias Paiao, G.; Mulla, D.J.; Knight, J.F.; Fernández, F.G. Prediction of Early Season Nitrogen Uptake in Maize Using High-Resolution Aerial Hyperspectral Imagery. Remote Sens. 2020, 12, 1234. [Google Scholar] [CrossRef]
- El-Hendawy, S.; Al-Suhaibani, N.; Elsayed, S.; Alotaibi, M.; Hassan, W.; Schmidhalter, U. Performance of Optimized Hyperspectral Reflectance Indices and Partial Least Squares Regression for Estimating the Chlorophyll Fluorescence and Grain Yield of Wheat Grown in Simulated Saline Field Conditions. Plant Physiol. Biochem. 2019, 144, 300–311. [Google Scholar] [CrossRef]
- Fu, P.; Meacham-Hensold, K.; Guan, K.; Bernacchi, C.J. Hyperspectral Leaf Reflectance as Proxy for Photosynthetic Capacities: An Ensemble Approach Based on Multiple Machine Learning Algorithms. Front. Plant Sci. 2019, 10, 730. [Google Scholar] [CrossRef]
- Meacham-Hensold, K.; Montes, C.M.; Wu, J.; Guan, K.; Fu, P.; Ainsworth, E.A.; Pederson, T.; Moore, C.E.; Brown, K.L.; Raines, C. High-Throughput Field Phenotyping Using Hyperspectral Reflectance and Partial Least Squares Regression (PLSR) Reveals Genetic Modifications to Photosynthetic Capacity. Remote Sens. Environ. 2019, 231, 111176. [Google Scholar] [CrossRef]
- Nakaji, T.; Oguma, H.; Nakamura, M.; Kachina, P.; Asanok, L.; Marod, D.; Aiba, M.; Kurokawa, H.; Kosugi, Y.; Kassim, A.R. Estimation of Six Leaf Traits of East Asian Forest Tree Species by Leaf Spectroscopy and Partial Least Square Regression. Remote Sens. Environ. 2019, 233, 111381. [Google Scholar] [CrossRef]
- Percival, G.C. Heat Tolerance of Urban Tree Species-A Review. Urban For. Urban Green. 2023, 86, 128021. [Google Scholar] [CrossRef]
- Alonzo, M.; Baker, M.E.; Caplan, J.S.; Williams, A.; Elmore, A.J. Canopy Composition Drives Variability in Urban Growing Season Length More than the Heat Island Effect. Sci. Total Environ. 2023, 884, 163818. [Google Scholar] [CrossRef]
- Hara, C.; Inoue, S.; Ishii, H.R.; Okabe, M.; Nakagaki, M.; Kobayashi, H. Tolerance and Acclimation of Photosynthesis of Nine Urban Tree Species to Warmer Growing Conditions. Trees 2021, 35, 1793–1806. [Google Scholar] [CrossRef]
- Wang, S.; Ju, W.; Peñuelas, J.; Cescatti, A.; Zhou, Y.; Fu, Y.; Huete, A.; Liu, M.; Zhang, Y. Urban−rural Gradients Reveal Joint Control of Elevated CO2 and Temperature on Extended Photosynthetic Seasons. Nat. Ecol. Evol. 2019, 3, 1076–1085. [Google Scholar] [CrossRef]
- Guo, A.; Ye, H.; Huang, W.; Qian, B.; Wang, J.; Lan, Y.; Wang, S. Inversion of Maize Leaf Area Index from UAV Hyperspectral and Multispectral Imagery. Comput. Electron. Agric. 2023, 212, 108020. [Google Scholar] [CrossRef]
- Liu, S.; Yan, Z.; Wang, Z.; Serbin, S.; Visser, M.; Zeng, Y.; Ryu, Y.; Su, Y.; Guo, Z.; Song, G. Mapping Foliar Photosynthetic Capacity in Sub-Tropical and Tropical Forests with UAS-Based Imaging Spectroscopy: Scaling from Leaf to Canopy. Remote Sens. Environ. 2023, 293, 113612. [Google Scholar] [CrossRef]
- Wijesingha, J.; Astor, T.; Schulze-Brüninghoff, D.; Wengert, M.; Wachendorf, M. Predicting Forage Quality of Grasslands Using UAV-Borne Imaging Spectroscopy. Remote Sens. 2020, 12, 126. [Google Scholar] [CrossRef]
- Kramer, D.M.; Johnson, G.; Kiirats, O.; Edwards, G.E. New Fluorescence Parameters for the Determination of QA Redox State and Excitation Energy Fluxes. Photosynth. Res. 2004, 79, 209–218. [Google Scholar] [CrossRef]
- Maxwell, K.; Johnson, G.N. Chlorophyll Fluorescence—A Practical Guide. J. Exp. Bot. 2000, 51, 659–668. [Google Scholar] [CrossRef]
- Bahari, Z.; Pallardy, S.; Parker, W. Photosynthesis, Water Relations, and Drought Adaptation in Six Woody Species of Oak-Hickory Forests in Central Missouri. For. Sci. 1985, 31, 557–569. [Google Scholar]
- Hauer, R.J.; Wei, H.; Koeser, A.K.; Dawson, J.O. Gas Exchange, Water Use Efficiency, and Biomass Partitioning among Geographic Sources of Acer saccharum Subsp. saccharum and Subsp. nigrum Seedlings in Response to Water Stress. Plants 2021, 10, 742. [Google Scholar]
- Huemmrich, K.; Campbell, P. Tundra Plant Leaf-Level Spectral Reflectance and Chlorophyll Fluorescence, 2019–2021; ORNL DAAC: Oak Ridge, TN, USA, 2022. [Google Scholar] [CrossRef]
- Barnes, E.; Clarke, T.; Richards, S.; Colaizzi, P.; Haberland, J.; Kostrzewski, M.; Waller, P.; Choi, C.; Riley, E.; Thompson, T. Coincident Detection of Crop Water Stress, Nitrogen Status and Canopy Density Using Ground Based Multispectral Data. In Proceedings of the Fifth International Conference on Precision Agriculture, Bloomington, MN, USA, 16–19 July 2000; Volume 1619. [Google Scholar]
- Gao, B.-C. NDWI—A Normalized Difference Water Index for Remote Sensing of Vegetation Liquid Water from Space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Rouse, J.W. Monitoring the Vernal Advancement and Retrogradation of Natural Vegetation; National Aeronautics and Space Administration, Goddard Space Flight Center: Greenbelt, MD, USA, 1973. [Google Scholar]
- Zarco-Tejada, P.J.; González-Dugo, V.; Williams, L.E.; Suarez, L.; Berni, J.A.J.; Goldhamer, D.; Fereres, E. A PRI-Based Water Stress Index Combining Structural and Chlorophyll Effects: Assessment Using Diurnal Narrow-Band Airborne Imagery and the CWSI Thermal Index. Remote Sens. Environ. 2013, 138, 38–50. [Google Scholar] [CrossRef]
- Dobrowski, S.; Pushnik, J.; Zarco-Tejada, P.J.; Ustin, S.L. Simple Reflectance Indices Track Heat and Water Stress-Induced Changes in Steady-State Chlorophyll Fluorescence at the Canopy Scale. Remote Sens. Environ. 2005, 97, 403–414. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Liland, K.H.; Mevik, B.-H.; Wehrens, R.; Hiemstra, P. Pls: Partial Least Squares and Principal Component Regression. In R Package Version 2.8-1; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Kuhn, M. Building Predictive Models in R Using the Caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Baek, J.; Kim, M. Face Recognition Using Partial Least Squares Components. Pattern Recognit. 2004, 37, 1303–1306. [Google Scholar] [CrossRef]
- Reiss, P.T.; Ogden, R.T. Functional Principal Component Regression and Functional Partial Least Squares. J. Am. Stat. Assoc. 2007, 102, 984–996. [Google Scholar] [CrossRef]
- Wentzell, P.D.; Montoto, L.V. Comparison of Principal Components Regression and Partial Least Squares Regression through Generic Simulations of Complex Mixtures. Chemom. Intell. Lab. Syst. 2003, 65, 257–279. [Google Scholar] [CrossRef]
- Moreno-Torres, J.G.; Sáez, J.A.; Herrera, F. Study on the Impact of Partition-Induced Dataset Shift on k-Fold Cross-Validation. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1304–1312. [Google Scholar] [CrossRef] [PubMed]
- European Space Agency Sentinel-2 User Handbook. 2015. Available online: https://sentinels.copernicus.eu/Documents/247904/685211/Sentinel-2_User_Handbook.Pdf/8869acdf-Fd84-43ec-Ae8c-3e80a436a16c?T=1438278087000 (accessed on 16 June 2024).
- Gitelson, A.A.; Buschmann, C.; Lichtenthaler, H.K. The Chlorophyll Fluorescence Ratio F735/F700 as an Accurate Measure of the Chlorophyll Content in Plants. Remote Sens. Environ. 1999, 69, 296–302. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between Leaf Pigment Content and Spectral Reflectance across a Wide Range of Species, Leaf Structures and Developmental Stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Datt, B. Remote Sensing of Water Content in Eucalyptus Leaves. Aust. J. Bot. 1999, 47, 909–923. [Google Scholar] [CrossRef]
- Ely, K.S.; Burnett, A.C.; Lieberman-Cribbin, W.; Serbin, S.P.; Rogers, A. Spectroscopy Can Predict Key Leaf Traits Associated with Source–Sink Balance and Carbon–Nitrogen Status. J. Exp. Bot. 2019, 70, 1789–1799. [Google Scholar] [CrossRef]
- Kokaly, R.F.; Asner, G.P.; Ollinger, S.V.; Martin, M.E.; Wessman, C.A. Characterizing Canopy Biochemistry from Imaging Spectroscopy and its Application to Ecosystem Studies. Remote Sens. Environ. 2009, 113, S78–S91. [Google Scholar] [CrossRef]
- Serbin, S.P.; Townsend, P.A. Scaling Functional Traits from Leaves to Canopies. In Remote Sensing of Plant Biodiversity; Springer International Publishing: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Kalaji, H.M.; Schansker, G.; Brestic, M.; Bussotti, F.; Calatayud, A.; Ferroni, L.; Goltsev, V.; Guidi, L.; Jajoo, A.; Li, P. Frequently Asked Questions about Chlorophyll Fluorescence, the Sequel. Photosynth. Res. 2017, 132, 13–66. [Google Scholar] [CrossRef] [PubMed]
- Pedrós, R.; Moya, I.; Goulas, Y.; Jacquemoud, S. Chlorophyll Fluorescence Emission Spectrum inside a Leaf. Photochem. Photobiol. Sci. 2008, 7, 498–502. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, J.; Wang, Q.; Song, G.; Jin, J. Validating and Developing Hyperspectral Indices for Tracing Leaf Chlorophyll Fluorescence Parameters under Varying Light Conditions. Remote Sens. 2023, 15, 4890. [Google Scholar] [CrossRef]
- Buschmann, C. Variability and Application of the Chlorophyll Fluorescence Emission Ratio Red/Far-Red of Leaves. Photosynth. Res. 2007, 92, 261–271. [Google Scholar] [CrossRef] [PubMed]
- Porcar-Castell, A.; Tyystjärvi, E.; Atherton, J.; Van der Tol, C.; Flexas, J.; Pfündel, E.E.; Moreno, J.; Frankenberg, C.; Berry, J.A. Linking Chlorophyll a Fluorescence to Photosynthesis for Remote Sensing Applications: Mechanisms and Challenges. J. Exp. Bot. 2014, 65, 4065–4095. [Google Scholar] [CrossRef] [PubMed]
- van der Tol, C.; Rossini, M.; Cogliati, S.; Verhoef, W.; Colombo, R.; Rascher, U.; Mohammed, G. A Model and Measurement Comparison of Diurnal Cycles of Sun-Induced Chlorophyll Fluorescence of Crops. Remote Sens. Environ. 2016, 186, 663–677. [Google Scholar] [CrossRef]
- Franck, F.; Juneau, P.; Popovic, R. Resolution of the Photosystem I and Photosystem II Contributions to Chlorophyll Fluorescence of Intact Leaves at Room Temperature. Biochim. Biophys. Acta (BBA)-Bioenerg. 2002, 1556, 239–246. [Google Scholar] [CrossRef]
- Amir, M.; Chen, J.; Chen, B.; Wang, S.; Zhu, K.; Li, Y.; Meng, Z.; Ma, L.; Wang, X.; Liu, Y. Reflectance and Chlorophyll Fluorescence-Based Retrieval of Photosynthetic Parameters Improves the Estimation of Subtropical Forest Productivity. Ecol. Indic. 2021, 131, 108133. [Google Scholar] [CrossRef]
- Chen, J.; Wang, S.; Chen, B.; Li, Y.; Amir, M.; Ma, L.; Zhu, K.; Yang, F.; Wang, X.; Liu, Y. Comparative Analysis on the Estimation of Diurnal Solar-Induced Chlorophyll Fluorescence Dynamics for a Subtropical Evergreen Coniferous Forest. Remote Sens. 2021, 13, 3143. [Google Scholar] [CrossRef]
- Lin, Y.; Zhu, Z.; Guo, W.; Sun, Y.; Yang, X.; Kovalskyy, V. Continuous Monitoring of Cotton Stem Water Potential Using Sentinel-2 Imagery. Remote Sens. 2020, 12, 1176. [Google Scholar] [CrossRef]
- Richter, R.; Reu, B.; Wirth, C.; Doktor, D.; Vohland, M. The Use of Airborne Hyperspectral Data for Tree Species Classification in a Species-Rich Central European Forest Area. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 464–474. [Google Scholar] [CrossRef]
- Karimi, Y.; Prasher, S.; Madani, A.; Kim, S. Application of Support Vector Machine Technology for the Estimation of Crop Biophysical Parameters Using Aerial Hyperspectral Observations. Can. Biosyst. Eng. 2008, 50, 13–20. [Google Scholar]
- Drusch, M.; Moreno, J.; Del Bello, U.; Franco, R.; Goulas, Y.; Huth, A.; Kraft, S.; Middleton, E.M.; Miglietta, F.; Mohammed, G. The Fluorescence Explorer Mission Concept—ESA’s Earth Explorer 8. IEEE Trans. Geosci. Remote Sens. 2016, 55, 1273–1284. [Google Scholar] [CrossRef]
- Coppo, P.; Taiti, A.; Pettinato, L.; Francois, M.; Taccola, M.; Drusch, M. Fluorescence Imaging Spectrometer (FLORIS) for ESA FLEX Mission. Remote Sens. 2017, 9, 649. [Google Scholar] [CrossRef]
- Van Wittenberghe, S.; Sabater, N.; Cendrero-Mateo, M.P.; Tenjo, C.; Moncholi, A.; Alonso, L.; Moreno, J. Towards the Quantitative and Physically-Based Interpretation of Solar-Induced Vegetation Fluorescence Retrieved from Global Imaging. Photosynthetica 2021, 59, 438–457. [Google Scholar] [CrossRef]
- He, M.; Lian, X.; Cui, J.; Xu, H.; Piao, S. Vegetation Physiological Response to Increasing Atmospheric CO2 Slows the Decreases in the Seasonal Amplitude of Temperature. Geophys. Res. Lett. 2022, 49, e2022GL097829. [Google Scholar] [CrossRef]
- Rennenberg, H.; Loreto, F.; Polle, A.; Brilli, F.; Fares, S.; Beniwal, R.; Gessler, A. Physiological Responses of Forest Trees to Heat and Drought. Plant Biol. 2006, 556–571. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Baldocchi, D.D. Seasonal Trends in Photosynthetic Parameters and Stomatal Conductance of Blue Oak (Quercus Douglasii) under Prolonged Summer Drought and High Temperature. Tree Physiol. 2003, 23, 865–877. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.-Q.; Zhao, F.; Fan, Z.-X.; Panthi, S.; Fu, P.-L.; Braeuning, A.; Griessinger, J.; Li, Z.-S. Long-Term Growth Trends of Abies Delavayi and Its Physiological Responses to a Warming Climate in the Cangshan Mountains, Southwestern China. For. Ecol. Manag. 2022, 505, 119943. [Google Scholar] [CrossRef]
- Xu, X.; Zhou, G.; Du, H.; Mao, F.; Xu, L.; Li, X.; Liu, L. Combined MODIS Land Surface Temperature and Greenness Data for Modeling Vegetation Phenology, Physiology, and Gross Primary Production in Terrestrial Ecosystems. Sci. Total Environ. 2020, 726, 137948. [Google Scholar] [CrossRef]
- Zhang, P.; Liu, H.; Li, H.; Yao, J.; Chen, X.; Feng, J. Using Enhanced Vegetation Index and Land Surface Temperature to Reconstruct the Solar-Induced Chlorophyll Fluorescence of Forests and Grasslands across Latitude and Phenology. Front. For. Glob. Change 2023, 6, 1257287. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, X.; Wu, D.; Meili, N.; Fatichi, S. Satellite-based Evidence Highlights a Considerable Increase of Urban Tree Cooling Benefits from 2000 to 2015. Glob. Change Biol. 2023, 29, 3085–3097. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.; Merzlyak, M.N. Quantitative Estimation of Chlorophyll-a Using Reflectance Spectra: Experiments with Autumn Chestnut and Maple Leaves. J. Photochem. Photobiol. B Biol. 1994, 22, 247–252. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Remote Estimation of Chlorophyll Content in Higher Plant Leaves. Int. J. Remote Sens. 1997, 18, 2691–2697. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Miller, J.R.; Mohammed, G.H.; Noland, T.L. Chlorophyll Fluorescence Effects on Vegetation Apparent Reflectance: I. Leaf-Level Measurements and Model Simulation. Remote Sens. Environ. 2000, 74, 582–595. [Google Scholar] [CrossRef]
- Clevers, J.G.; Gitelson, A.A. Remote Estimation of Crop and Grass Chlorophyll and Nitrogen Content Using Red-Edge Bands on Sentinel-2 and-3. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 344–351. [Google Scholar] [CrossRef]
- Gupta, R.K.; Vijayan, D.; Prasad, T.S. Comparative Analysis of Red-Edge Hyperspectral Indices. Adv. Space Res. 2003, 32, 2217–2222. [Google Scholar] [CrossRef]
- Le Maire, G.; François, C.; Dufrene, E. Towards Universal Broad Leaf Chlorophyll Indices Using PROSPECT Simulated Database and Hyperspectral Reflectance Measurements. Remote Sens. Environ. 2004, 89, 1–28. [Google Scholar] [CrossRef]
- Maccioni, A.; Agati, G.; Mazzinghi, P. New Vegetation Indices for Remote Measurement of Chlorophylls Based on Leaf Directional Reflectance Spectra. J. Photochem. Photobiol. B Biol. 2001, 61, 52–61. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P. The MERIS Terrestrial Chlorophyll Index. Int. J. Remote Sens. 2004, 25, 5403–5413. [Google Scholar] [CrossRef]
- Datt, B. A New Reflectance Index for Remote Sensing of Chlorophyll Content in Higher Plants: Tests Using Eucalyptus Leaves. J. Plant Physiol. 1999, 154, 30–36. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Miller, J.R.; Noland, T.L.; Mohammed, G.H.; Sampson, P.H. Scaling-up and Model Inversion Methods with Narrowband Optical Indices for Chlorophyll Content Estimation in Closed Forest Canopies with Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1491–1507. [Google Scholar] [CrossRef]
- Guyot, G.; Baret, F.; Major, D. High Spectral Resolution: Determination of Spectral Shifts between the Red and near Infrared. In The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; FAO: Rome, Italy, 1988. [Google Scholar]
- Carter, G.A. Ratios of Leaf Reflectances in Narrow Wavebands as Indicators of Plant Stress. Remote Sens. 1994, 15, 697–703. [Google Scholar] [CrossRef]
- McMurtrey Iii, J.E.; Chappelle, E.W.; Kim, M.S.; Meisinger, J.J.; Corp, L.A. Distinguishing Nitrogen Fertilization Levels in Field Corn (Zea mays L.) with Actively Induced Fluorescence and Passive Reflectance Measurements. Remote Sens. Environ. 1994, 47, 36–44. [Google Scholar] [CrossRef]
- Wen, P.-F.; Wang, R.; Shi, Z.-J.; Ning, F.; Wang, S.-L.; Zhang, Y.-J.; Zhang, Y.-H.; Wang, Q.; Li, J. Effects of N Application Rate on N Remobilization and Accumulation in Maize (Zea mays L.) and Estimating of Vegetative N Remobilization Using Hyperspectral Measurements. Comput. Electron. Agric. 2018, 152, 166–181. [Google Scholar] [CrossRef]
- Vogelmann, J.E.; Rock, B.N.; Moss, D.M. Red Edge Spectral Measurements from Sugar Maple Leaves. Int. J. Remote Sens. 1993, 14, 1563–1575. [Google Scholar] [CrossRef]
- Daughtry, C.S.; Walthall, C.; Kim, M.; De Colstoun, E.B.; McMurtrey Iii, J. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Stimson, H.C.; Breshears, D.D.; Ustin, S.L.; Kefauver, S.C. Spectral Sensing of Foliar Water Conditions in Two Co-Occurring Conifer Species: Pinus edulis and Juniperus monosperma. Remote Sens. Environ. 2005, 96, 108–118. [Google Scholar] [CrossRef]
- Datt, B. Remote Sensing of Chlorophyll a, Chlorophyll b, Chlorophyll a+b, and Total Carotenoid Content in Eucalyptus Leaves. Remote Sens. Environ. 1998, 66, 111–121. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a Green Channel in Remote Sensing of Global Vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated Narrow-Band Vegetation Indices for Prediction of Crop Chlorophyll Content for Application to Precision Agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Elsayed, S.; Mistele, B.; Schmidhalter, U. Can Changes in Leaf Water Potential Be Assessed Spectrally? Funct. Plant Biol. 2011, 38, 523–533. [Google Scholar] [CrossRef] [PubMed]
- Penuelas, J.; Baret, F.; Filella, I. Semi-Empirical Indices to Assess Carotenoids/Chlorophyll a Ratio from Leaf Spectral Reflectance. Photosynthetica 1995, 31, 221–230. [Google Scholar]
- Feret, J.-B.; François, C.; Gitelson, A.; Asner, G.P.; Barry, K.M.; Panigada, C.; Richardson, A.D.; Jacquemoud, S. Optimizing Spectral Indices and Chemometric Analysis of Leaf Chemical Properties Using Radiative Transfer Modeling. Remote Sens. Environ. 2011, 115, 2742–2750. [Google Scholar] [CrossRef]
- Apan, A.; Held, A.; Phinn, S.; Markley, J. Detecting Sugarcane ‘Orange Rust’ Disease Using EO-1 Hyperion Hyperspectral Imagery. Int. J. Remote Sens. 2004, 25, 489–498. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).