Voids Filling of DEM with Multiattention Generative Adversarial Network Model
Abstract
:1. Introduction
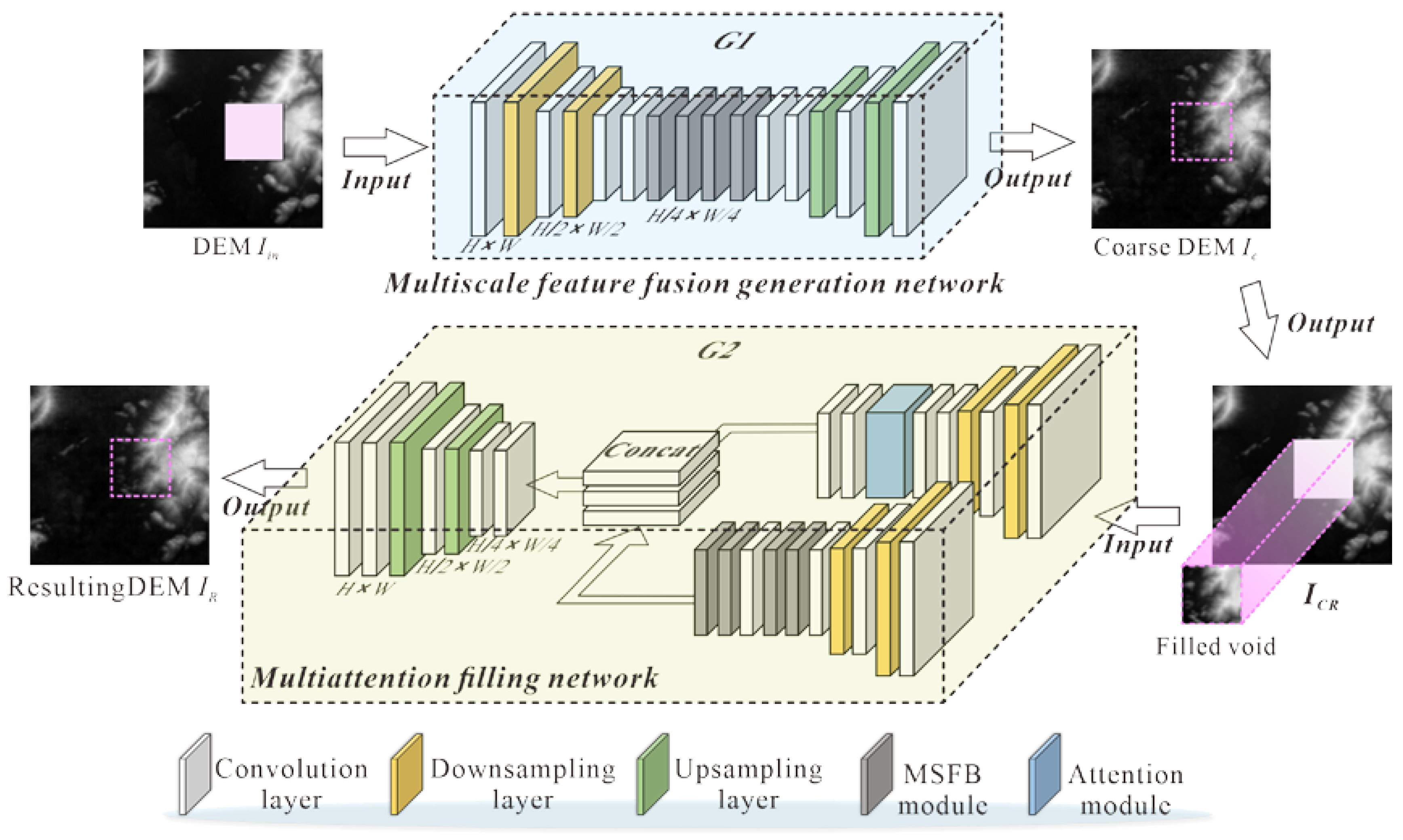
2. A Multiattention Generative Adversarial Network Filling Model
2.1. Multiscale Feature Fusion Generation Network
2.1.1. Network Structure Design
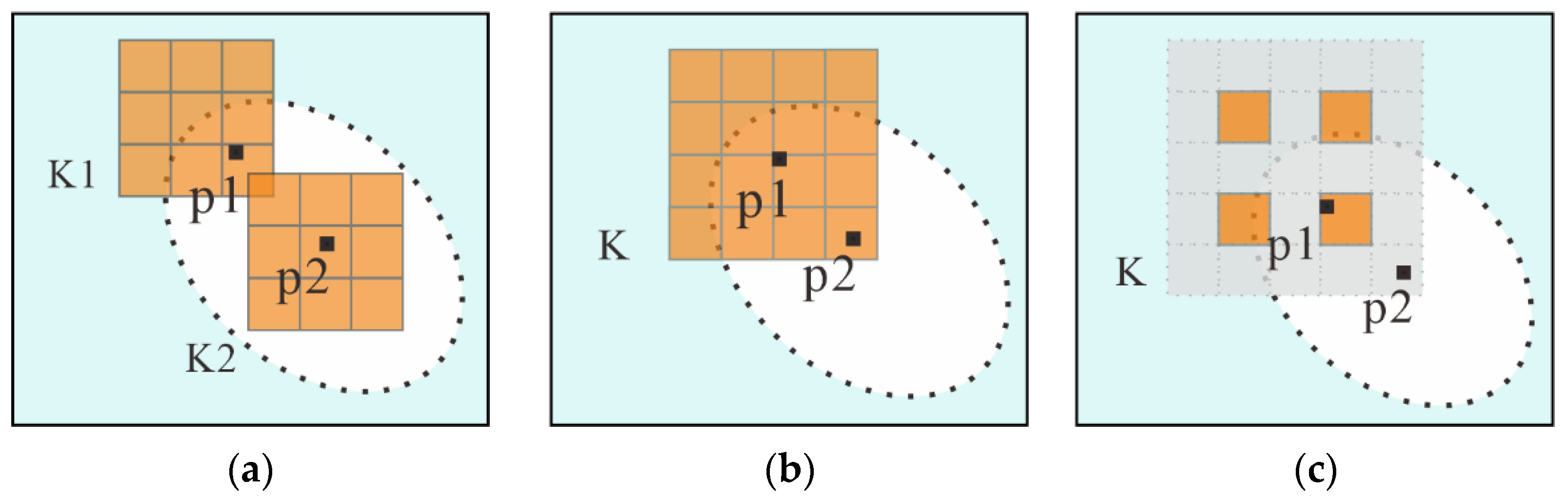
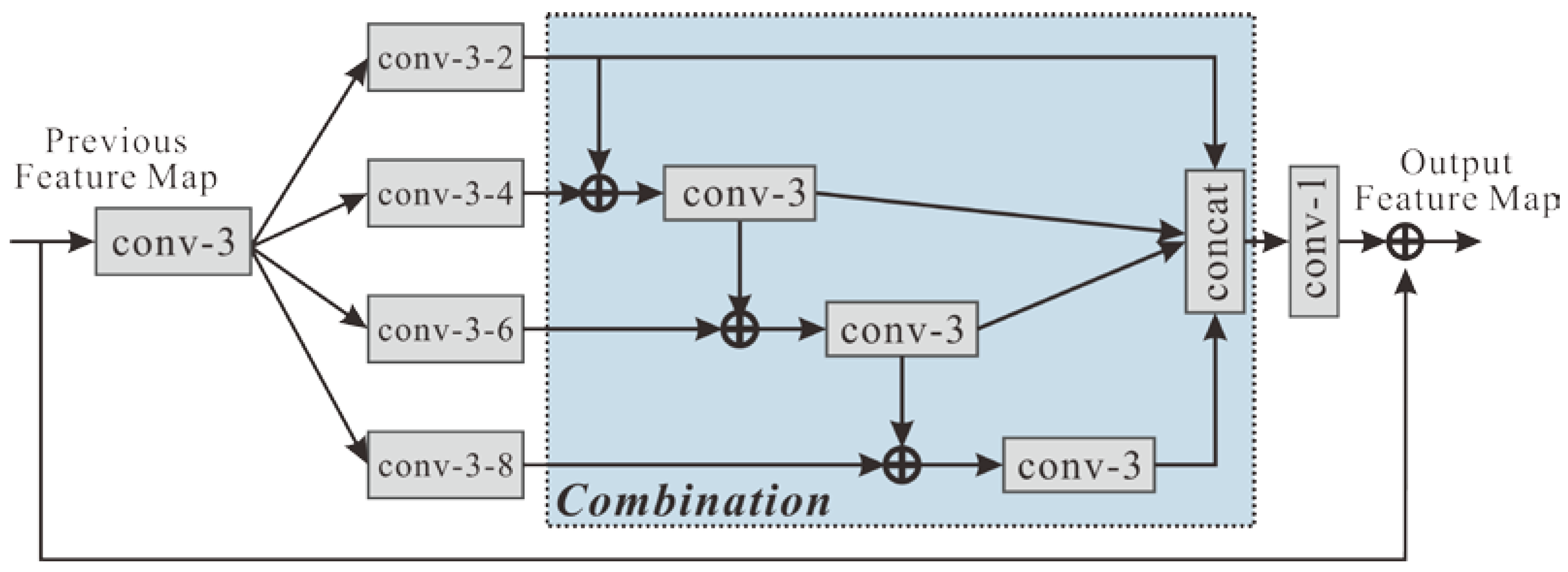
2.1.2. Multiscale Feature Fusion Module
2.2. Multiattention Filling Network
2.2.1. Network Structure Designs
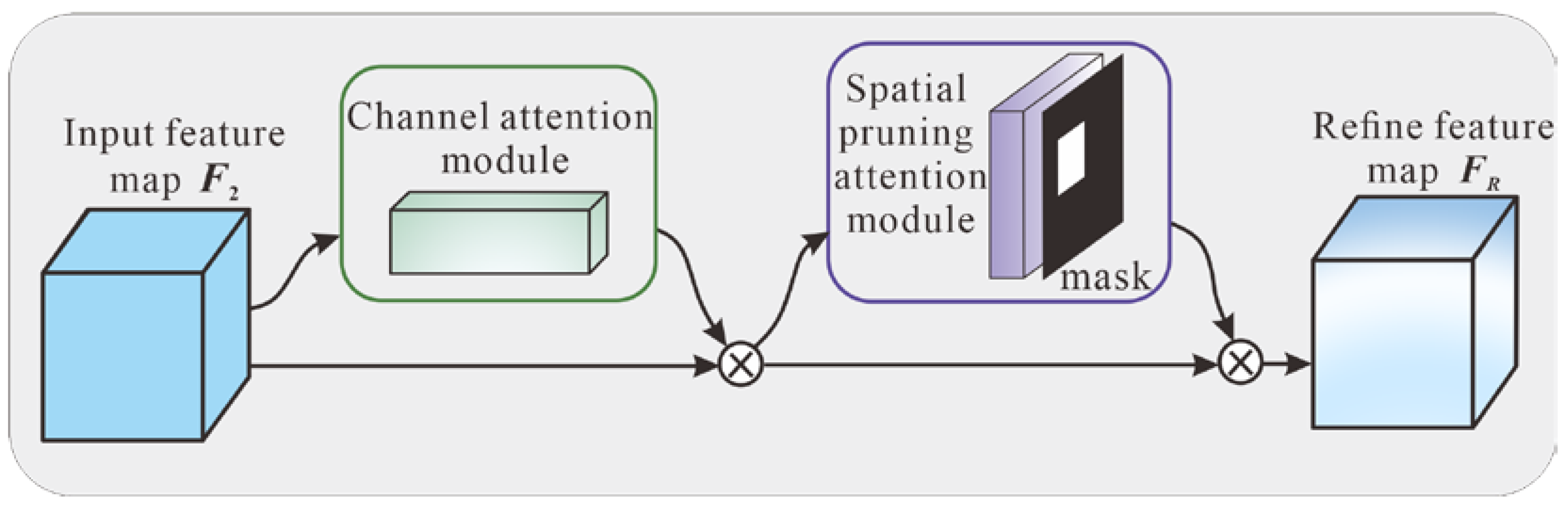
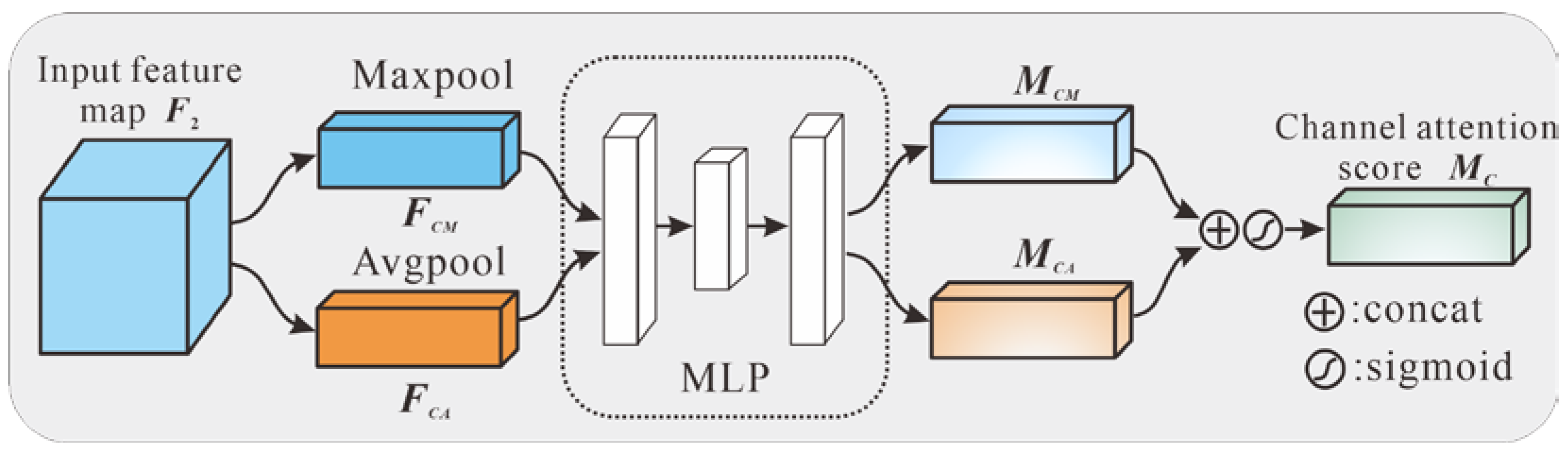
2.2.2. Multiattention Mechanism Module
2.3. Global-Local Adversarial Network
2.4. Combined Loss Function
3. Experiment and Analysis
3.1. Experimental Data and Preprocessing
3.1.1. Datasets
3.1.2. Data Preprocessing
3.1.3. Evaluation Metrics
3.2. The Filled Results in Four Test Areas
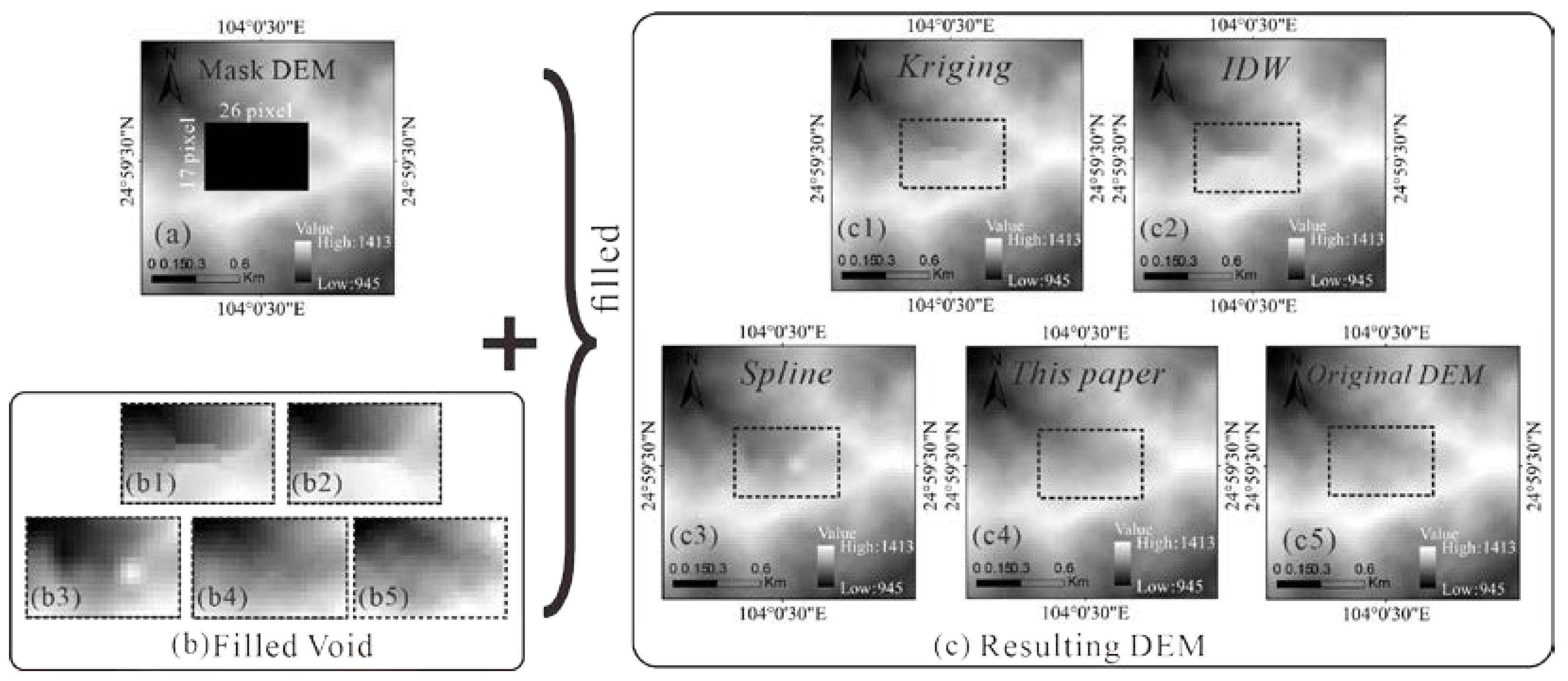
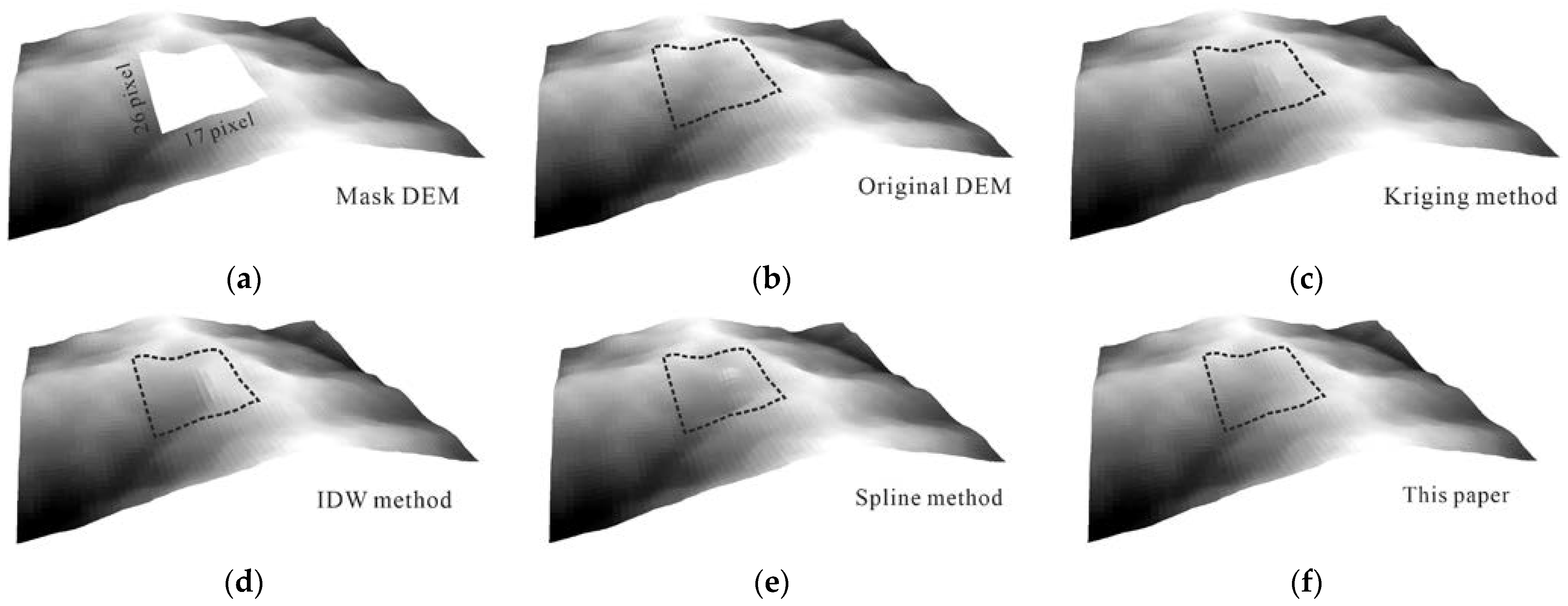
3.3. Comparison Analysis with Traditional Methods
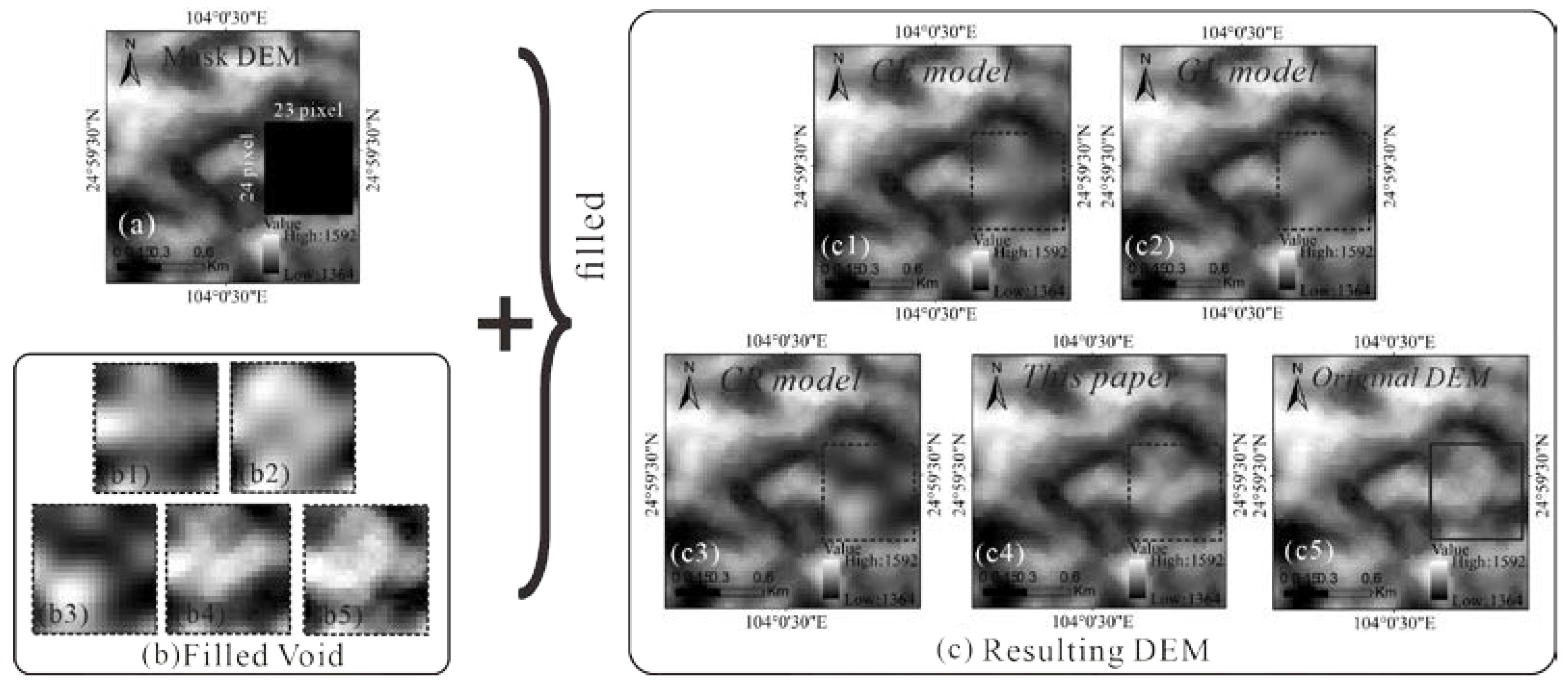
3.4. Comparison Analysis with Other Deep Learning Models
3.5. Discussion
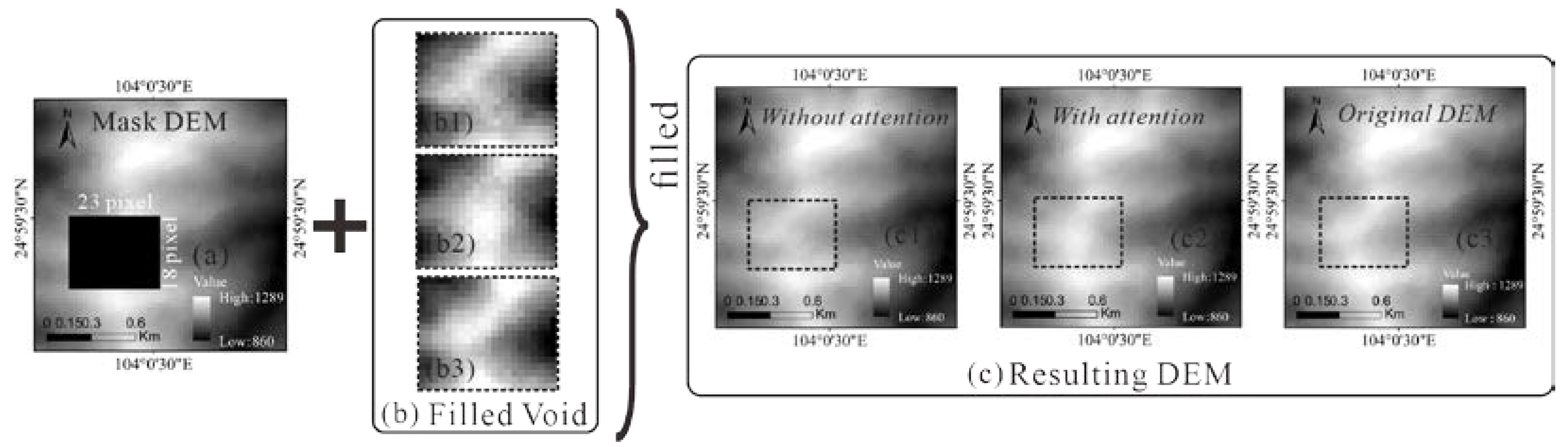
3.5.1. Impact Analysis of the Attention Mechanism vs. Filling Accuracy
3.5.2. Impact Analysis of the Loss Function Type vs. Filling Accuracy
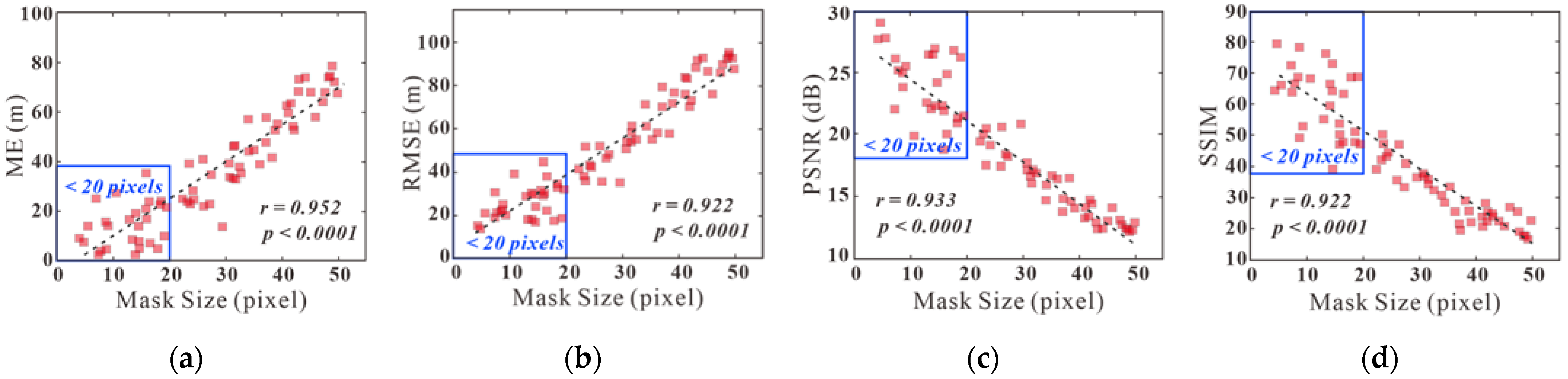
3.5.3. Impact Analysis of the Size of DEM Void vs. Filling Accuracy
4. Conclusions
- (1)
- A multiscale feature fusion generation network in the model is proposed, with which the receptive field is enlarged while maintaining the density of the dilated convolution.
- (2)
- A channel-spatial cropping attention mechanism module is proposed for the multiattention filling network, with which the correlation between the front and back feature maps is enhanced and the global-local dependence of the feature maps is improved.
- (3)
- To overcome the difficulty of balancing generator and discriminator adversarial training in generative adversarial networks, this paper proposes a global-local adversarial network and uses the spectral normalization on the output of the network layer, enhancing the stability of network training as a result.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Han, H.; Zeng, Q.; Jiao, J. Quality Assessment of TanDEM-X DEMs, SRTM and ASTER GDEM on Selected Chinese Sites. Remote Sens. 2021, 13, 1304. [Google Scholar] [CrossRef]
- Zhou, G. Urban High-Resolution Remote Sensing Algorithms and Modeling; CRC Press, Tylor& Francis Group: Boca Raton, FL, USA, 2021; pp. 135–136. [Google Scholar]
- Div, A.; Aas, B. TanDEM-X DEM: Comparative performance review employing LIDAR data and DSMs. ISPRS J. Photogramm. 2020, 160, 33–50. [Google Scholar]
- Liu, Z.; Han, L.; Yang, Z.; Cao, H.; Guo, F.; Guo, J.; Ji, Y. Evaluating the Vertical Accuracy of DEM Generated from ZiYuan-3 Stereo Images in Understanding the Tectonic Morphology of the Qianhe Basin, China. Remote Sens. 2021, 13, 1203. [Google Scholar] [CrossRef]
- Sukcharoenpong, A.; Yilmaz, A.; Li, R. An Integrated Active Contour Approach to Shoreline Mapping Using HSI and DEM. IEEE T. Geosci. Remote. 2016, 54, 1586–1597. [Google Scholar] [CrossRef]
- Zhou, G.; Huang, J.; Zhang, G. Evaluation of the wave energy conditions along the coastal waters of Beibu Gulf, China. Energy 2015, 85, 449–457. [Google Scholar] [CrossRef]
- Yue, L.; Shen, H.; Yu, W.; Zhang, L. Monitoring of Historical Glacier Recession in Yulong Mountain by the Integration of Multisource Remote Sensing Data. IEEE J.-Stars 2018, 11, 1–13. [Google Scholar] [CrossRef]
- Zhou, G.; Bao, X.; Ye, S.; Wang, H.; Yan, H. Selection of Optimal Building Facade Texture Images From UAV-Based Multiple Oblique Image Flows. IEEE T. Geosci. Remote. 2021, 59, 1534–1552. [Google Scholar] [CrossRef]
- Zhou, G.; Wang, H.; Chen, W.; Zhang, G.; Luo, Q.; Jia, B. Impacts of Urban land surface temperature on tract landscape pattern, physical and social variables. Int. J. Remote Sens. 2020, 41, 683–703. [Google Scholar] [CrossRef]
- Maune, D.F.; Nayegandhi, A. Digital Elevation Model Technologies and Applications: The DEM Users Manual; ASPRS: Baton Rouge, LA, USA, 2019; pp. 38–39. [Google Scholar]
- Zhou, Q.; Liu, X. Analysis of errors of derived slope and aspect related to DEM data properties. Comput. Geosci. UK 2004, 30, 369–378. [Google Scholar] [CrossRef]
- Zhou, G.; Xie, M. Coastal 3-D Morphological Change Analysis Using LiDAR Series Data: A Case Study of Assateague Island National Seashore. J. Coastal Res. 2009, 25, 400–435. [Google Scholar] [CrossRef]
- Hirt, C. Artefact detection in global digital elevation models (DEMs): The Maximum Slope Approach and its application for complete screening of the SRTM v4. 1 and MERIT DEMs. Remote Sens. Environ. 2018, 207, 27–41. [Google Scholar] [CrossRef] [Green Version]
- Ma, H.; Zhou, W.; Zhang, L. DEM refinement by low vegetation removal based on the combination of full waveform data and progressive TIN densification. ISPRS J. Photogramm. 2018, 146, 260–271. [Google Scholar] [CrossRef]
- Uss, M.L.; Vozel, B.; Lukin, V.V.; Chehdi, K. Estimation of Variance and Spatial Correlation Width for Fine-Scale Measurement Error in Digital Elevation Model. IEEE T. Geosci. Remote 2020, 58, 1941–1956. [Google Scholar] [CrossRef]
- Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 1968 23rd ACM National Conference, New York, NY, USA, 27–29 August 1968; pp. 517–524. [Google Scholar]
- Reuter, H.I.; Nelson, A.; Jarvis, A. An evaluation of void-filling interpolation methods for SRTM data. Int. J. Geogr. Inf. Sci. 2007, 21, 983–1008. [Google Scholar] [CrossRef]
- Grohman, G.; Kroenung, G.; Strebeck, J. Filling SRTM voids: The delta surface fill method. Photogramm. Eng. Remote Sens. 2006, 72, 213–216. [Google Scholar]
- Luedeling, E.; Siebert, S.; Buerkert, A. Filling the voids in the SRTM elevation model—A TIN-based delta surface approach. ISPRS J. Photogramm. 2007, 62, 283–294. [Google Scholar] [CrossRef]
- Vallé, B.L.; Pasternack, G.B. Field mapping and digital elevation modelling of submerged and unsubmerged hydraulic jump regions in a bedrock step–pool channel. Earth Surf. Proc. Land. 2006, 31, 646–664. [Google Scholar] [CrossRef]
- Dokken, T.; Lyche, T.; Pettersen, K.F. Polynomial splines over locally refined box-partitions. Comput. Aided Geom. Des. 2013, 30, 331–356. [Google Scholar] [CrossRef]
- Skytt, V.; Barrowclough, O.; Dokken, T. Locally refined spline surfaces for representation of terrain data. Comput. Graph. 2015, 49, 58–68. [Google Scholar]
- Heritage, G.L.; Milan, D.J.; Large, A.R.; Fuller, I.C. Influence of survey strategy and interpolation model on DEM quality. Geomorphology 2009, 112, 334–344. [Google Scholar] [CrossRef]
- Arun, P.V. A comparative analysis of different DEM interpolation methods. Egypt. J. Remote Sens. Space Sci. 2013, 16, 133–139. [Google Scholar]
- Ling, F.; Zhang, Q.W.; Wang, C. Filling voids of SRTM with Landsat sensor imagery in rugged terrain. Int. J. Remote Sens. 2007, 28, 465–471. [Google Scholar] [CrossRef]
- Hogan, J.; Smith, W.A. Refinement of digital elevation models from shadowing cues. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Francisco, CA, USA, 13–18 June 2010; pp. 1181–1188. [Google Scholar]
- Yue, T.; Chen, C.; Li, B. A high-accuracy method for filling voids and its verification. Int. J. Remote Sens. 2012, 33, 2815–2830. [Google Scholar] [CrossRef]
- Yue, T.; Zhao, M.; Zhang, X. A high-accuracy method for filling voids on remotely sensed XCO2 surfaces and its verification. J. Clean. Prod. 2015, 103, 819–827. [Google Scholar] [CrossRef]
- Yue, L.; Shen, H.; Zhang, L.; Zheng, X.; Zhang, F.; Yuan, Q. High-quality seamless DEM generation blending SRTM-1, ASTER GDEM v2 and ICESat/GLAS observations. ISPRS J. Photogramm. 2017, 123, 20–34. [Google Scholar] [CrossRef] [Green Version]
- Dong, G.; Chen, F.; Ren, P. Filling SRTM void data via conditional adversarial networks. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 7441–7443. [Google Scholar]
- Liu, J.; Liu, D.; Alsdorf, D. Extracting Ground-Level DEM From SRTM DEM in Forest Environments Based on Mathematical Morphology. IEEE T. Geosci. Remote 2014, 52, 6333–6340. [Google Scholar] [CrossRef]
- Pathak, D.; Krahenbuhl, P.; Donahue, J.; Darrell, T.; Efros, A.A. Context Encoders: Feature Learning by Inpainting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2536–2544. [Google Scholar]
- Guangyun, Z.; Rongting, Z.; Guoqing, Z.; Xiuping, J. Hierarchical spatial features learning with deep CNNs for very high-resolution remote sensing image classification. Int. J. Remote Sens. 2018, 39, 1–19. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. arXiv 2014, arXiv:1406.266. Available online: https://arxiv.org/abs/1406.2661 (accessed on 10 June 2014). [CrossRef]
- Iizuka, S.; Simo-Serra, E.; Ishikawa, H. Globally and locally consistent image completion. ACM Trans. Graph. 2017, 36, 107. [Google Scholar] [CrossRef]
- Liu, G.; Reda, F.A.; Shih, K.J.; Wang, T.C.; Tao, A.; Catanzaro, B. Image Inpainting for Irregular Holes Using Partial Convolutions. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 85–100. [Google Scholar]
- Qiu, Z.; Yue, L.; Liu, X. Void Filling of Digital Elevation Models with a Terrain Texture Learning Model Based on Generative Adversarial Networks. Remote Sens. 2019, 11, 2829. [Google Scholar] [CrossRef] [Green Version]
- Dong, G.; Huang, W.; Smith, W.A.P.; Ren, P. A shadow constrained conditional generative adversarial net for SRTM data restoration. Remote Sens. Environ. 2020, 237, 111602. [Google Scholar] [CrossRef]
- Hui, Z.; Li, J.; Wang, X.; Gao, X. Image fine-grained inpainting. arXiv 2020, arXiv:2002.02609. Available online: https://arxiv.org/abs/2002.02609 (accessed on 4 October 2020).
- Jaderberg, M.; Simonyan, K.; Zisserman, A.; Kavukcuoglu, K. Spatial Transformer Networks. arXiv 2015, arXiv:1506.02025. Available online: https://arxiv.org/abs/1506.02025 (accessed on 4 February 2016).
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 1181–1188. [Google Scholar]
- Yu, J.; Lin, Z.; Yang, J.; Shen, X.; Lu, X.; Huang, T.S. Generative image inpainting with contextual attention. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 5505–5514. [Google Scholar]
- Wang, N.; Li, J.; Zhang, L.; Du, B. MUSICAL: Multi-Scale Image Contextual Attention Learning for Inpainting. In Proceedings of the 28th International Joint Conference on Artificial Intelligence (IJCAI), Macao, China, 10–16 August 2019; pp. 3748–3754. [Google Scholar]
- Gavriil, K.; Muntingh, G.; Barrowclough, O.J. Void filling of digital elevation models with deep generative models. IEEE Geosci. Remote Sens. 2019, 16, 1645–1649. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Shi, S.; Ge, Y.; Liu, H.; Cui, W. DEM Void Filling Based on Context Attention Generation Model. ISPRS Int. J. Geo-Inf. 2020, 9, 734. [Google Scholar] [CrossRef]
- Zhu, D.; Cheng, X.; Zhang, F.; Yao, X.; Gao, Y.; Liu, Y. Spatial interpolation using conditional generative adversarial neural networks. Int. J. Geogr. Inf. Sci. 2020, 34, 735–758. [Google Scholar] [CrossRef]
- Li, S.; Hu, G.; Cheng, X.; Xiong, L.; Tang, G.; Strobl, J. Integrating topographic knowledge into deep learning for the void-filling of digital elevation models. Remote Sens. Environ. 2022, 269, 112818. [Google Scholar] [CrossRef]
- Yu, J.; Lin, Z.; Yang, J.; Shen, X.; Lu, X.; Huang, T.S. Free-form image inpainting with gated convolution. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 4471–4480. [Google Scholar]
- Mehta, S.; Rastegari, M.; Caspi, A.; Shapiro, L.; Hajishirzi, H. Espnet: Efficient spatial pyramid of dilated convolutions for semantic segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 552–568. [Google Scholar]
- Miyato, T.; Kataoka, T.; Koyama, M.; Yoshida, Y. Spectral normalization for generative adversarial networks. arXiv 2018, arXiv:1802.05957. Available online: https://arxiv.org/abs/1802.05957 (accessed on 16 February 2018).
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein GAN. arXiv 2017, arXiv:1701.07875. Available online: https://arxiv.org/abs/1701.07875 (accessed on 26 January 2017).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2017, arXiv:1412.6980. Available online: https://arxiv.org/abs/1412.6980 (accessed on 30 January 2017).
- Jiang, B.; Chen, G.; Wang, J.; Ma, H.; Wang, L.; Wang, Y.; Chen, X. Deep Dehazing Network for Remote Sensing Image with Non-Uniform Haze. Remote Sens. 2021, 13, 4443. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]







| Input: Original DEM, Mask matrix |
| Output: Initial generation of the data for G1, Refined filling data of G2, Discriminator loss value |
| Step 1: Dividing the original DEM into a training set, test set and setting the network training hyperparameters. |
| Step 2: Generating random mask masks for each DEM image to obtain simulated hole DEM images. |
| Step 3: When i < T do |
| Sampling m samples from the training set as mini_batchsize and entering the corresponding mask matrix. |
| for i < TC |
| Calculating the reconstruction loss values and updating the G1 network using the Adam optimization algorithm. |
| else: |
| Inputting the generated image and the original image into the discriminator, calculating the adversarial loss and L2 loss values of the discriminator D, and updating the discriminator parameters. |
| Finishing TC pretraining, calculating L2 reconstruction loss, adversarial loss, and updating G1, G2 and D networks using Adam optimization until training is completed and saving the model. |
| end |
| Step 4: Sampling m sample data from the test set as mini_batchsize, randomly generating mask, inputting to the trained filling model, putting the test data through G1 and G2 networks, respectively, getting the repaired DEM images, and calculating the repair accuracy. |
| ME (m) | MAE (m) | RMSE (m) | PSNR (dB) | SSIM | |
|---|---|---|---|---|---|
| Area 1 | 1.37 | 4.69 | 5.77 | 29.33 | 83.74% |
| Area 2 | 4.22 | 10.13 | 12.80 | 33.52 | 92.93% |
| Area 3 | 8.61 | 12.23 | 15.79 | 28.27 | 82.94% |
| Area 4 | 6.06 | 11.88 | 15.85 | 21.71 | 59.84% |
| ME (m) | MAE (m) | RMSE (m) | PSNR (dB) | SSIM | |
|---|---|---|---|---|---|
| Kriging | 14.54 | 20.14 | 27.01 | 24.76 | 74.10% |
| IDW | 19.82 | 30.21 | 38.04 | 21.80 | 61.90% |
| Spline | 0.27 | 14.82 | 21.48 | 26.77 | 66.18% |
| This paper | 2.99 | 9.74 | 11.90 | 31.90 | 84.42% |
| ME (m) | MAE (m) | RMSE (m) | PSNR (dB) | SSIM | |
|---|---|---|---|---|---|
| CE | 3.94 | 9.64 | 17.02 | 20.18 | 43.05% |
| GL | 10.80 | 25.97 | 34.66 | 16.36 | 17.07% |
| CR | 7.13 | 17.19 | 22.19 | 20.23 | 11.42% |
| This paper | 4.20 | 13.13 | 16.72 | 22.69 | 57.40% |
| ME (m) | MAE (m) | RMSE (m) | PSNR (dB) | SSIM | |
|---|---|---|---|---|---|
| Without attention | 9.76 | 13.51 | 19.90 | 26.67 | 59.25% |
| With attention | 2.56 | 12.50 | 15.73 | 28.72 | 75.57% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, G.; Song, B.; Liang, P.; Xu, J.; Yue, T. Voids Filling of DEM with Multiattention Generative Adversarial Network Model. Remote Sens. 2022, 14, 1206. https://doi.org/10.3390/rs14051206
Zhou G, Song B, Liang P, Xu J, Yue T. Voids Filling of DEM with Multiattention Generative Adversarial Network Model. Remote Sensing. 2022; 14(5):1206. https://doi.org/10.3390/rs14051206
Chicago/Turabian StyleZhou, Guoqing, Bo Song, Peng Liang, Jiasheng Xu, and Tao Yue. 2022. "Voids Filling of DEM with Multiattention Generative Adversarial Network Model" Remote Sensing 14, no. 5: 1206. https://doi.org/10.3390/rs14051206
APA StyleZhou, G., Song, B., Liang, P., Xu, J., & Yue, T. (2022). Voids Filling of DEM with Multiattention Generative Adversarial Network Model. Remote Sensing, 14(5), 1206. https://doi.org/10.3390/rs14051206







