Assessment and Prediction of Sea Level Trend in the South Pacific Region
Abstract
1. Introduction
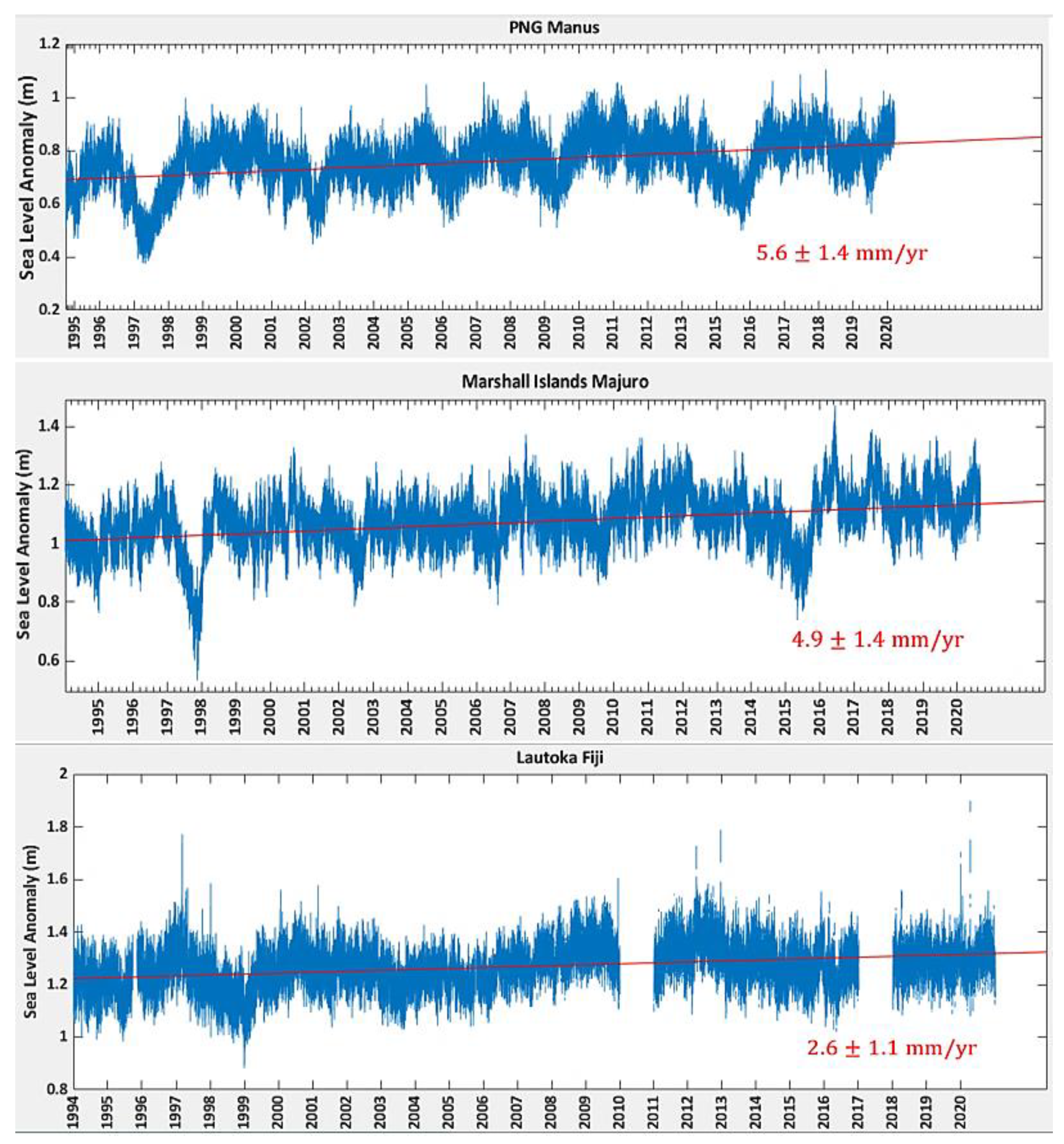
2. Study Area and Data
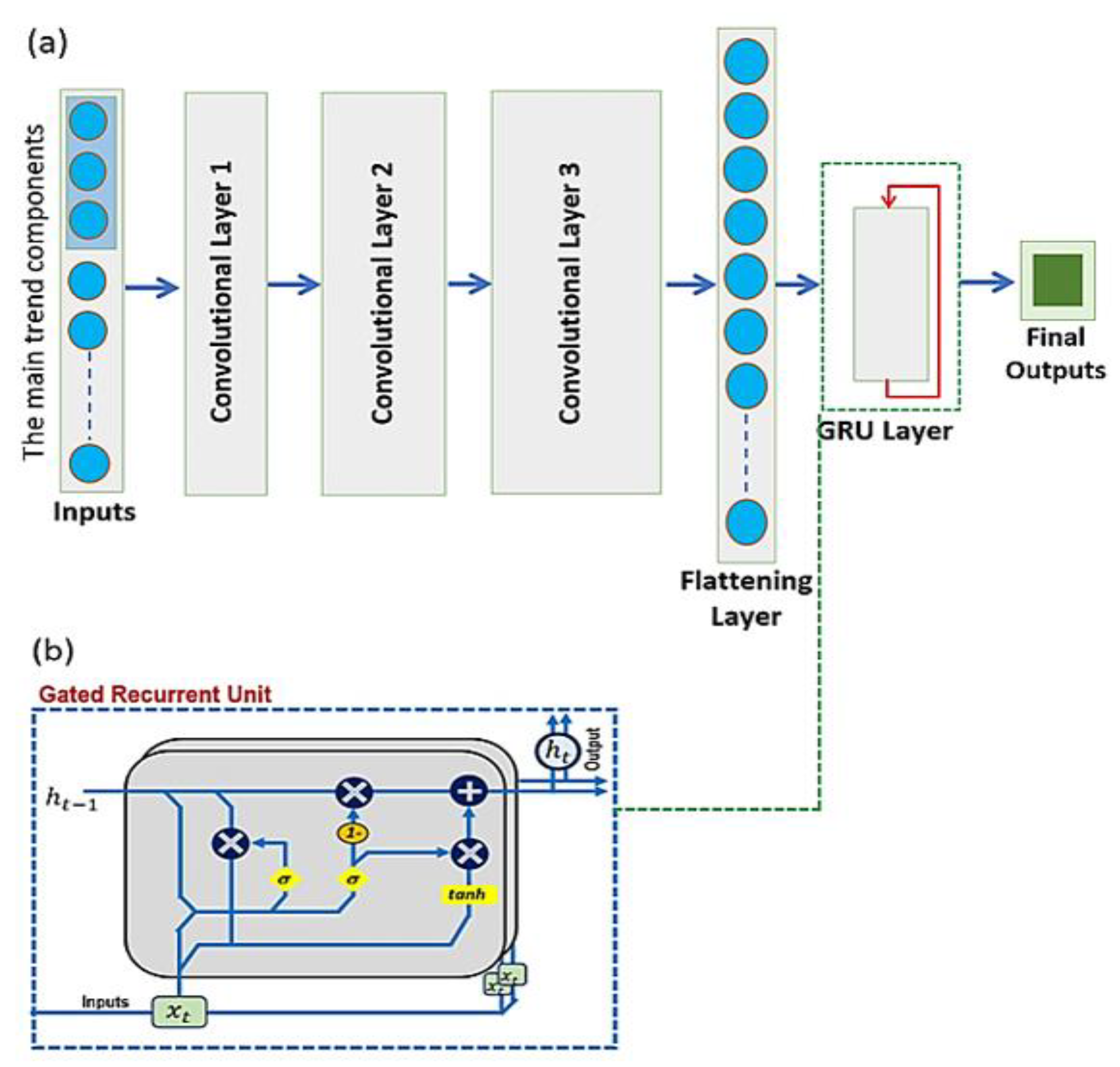
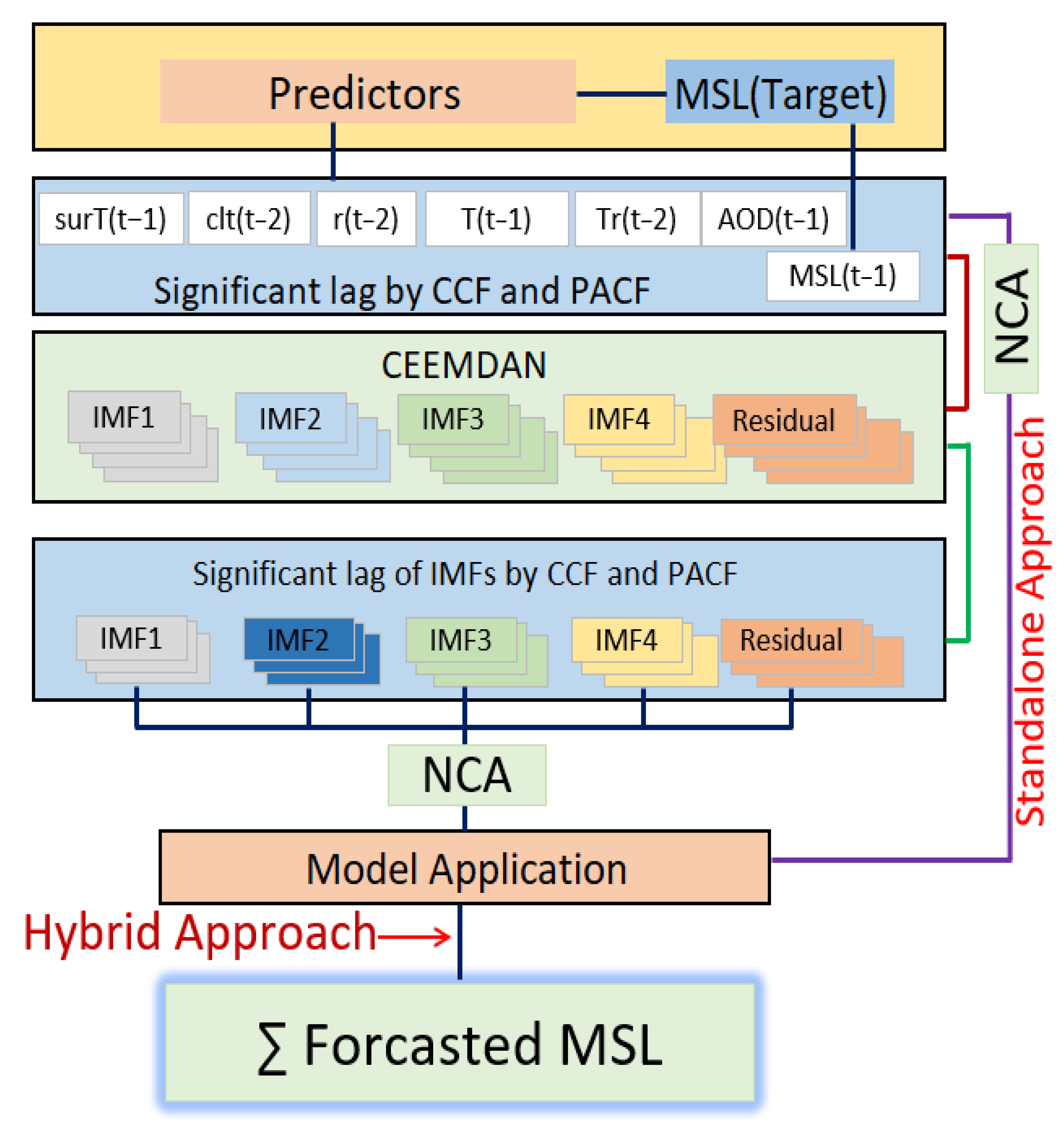
3. Materials and Methods
4. Results
- Correlation Coefficient (r)
- Nash–Sutcliffe Coefficient (NS)
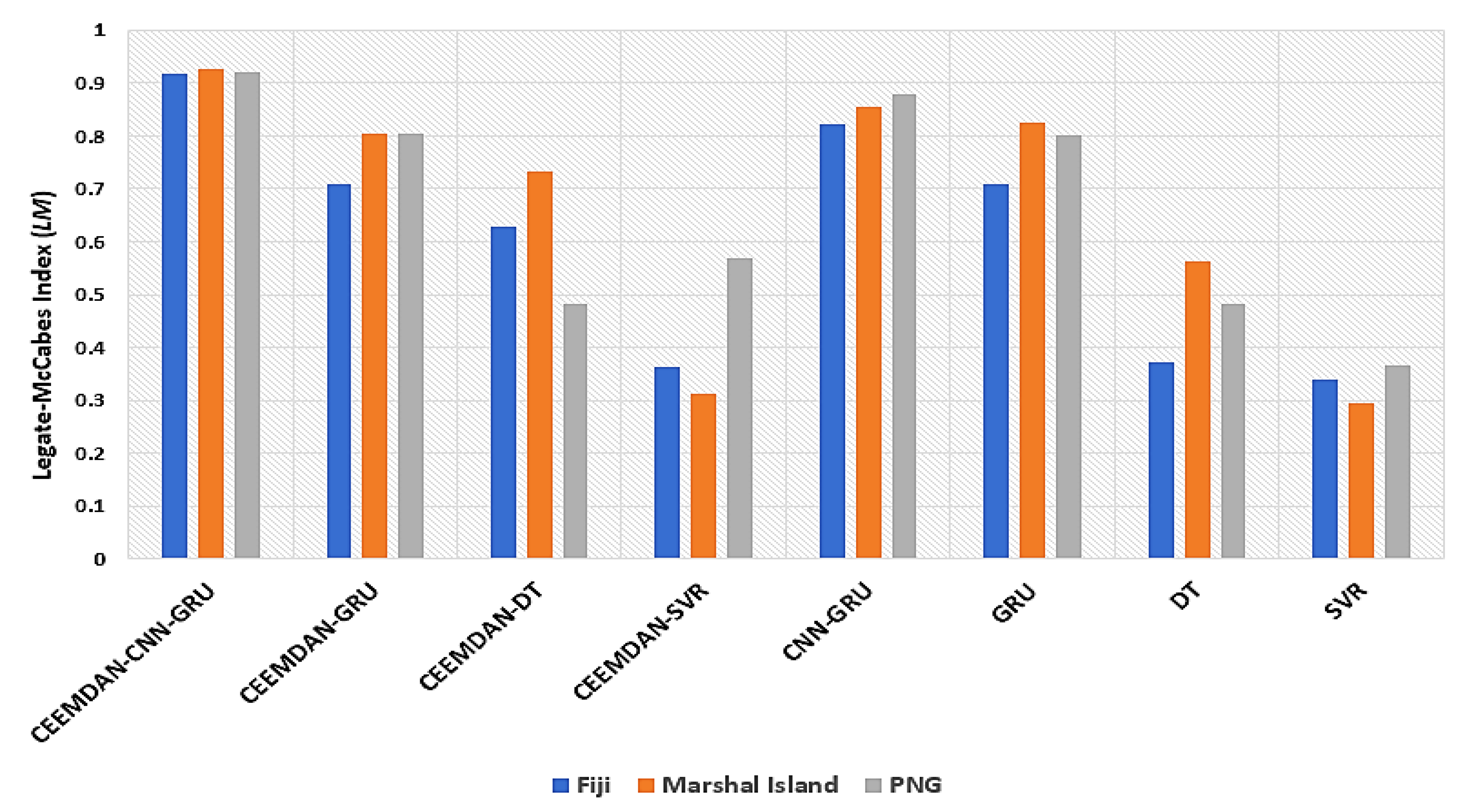
- Legates and McCabe index (LM)
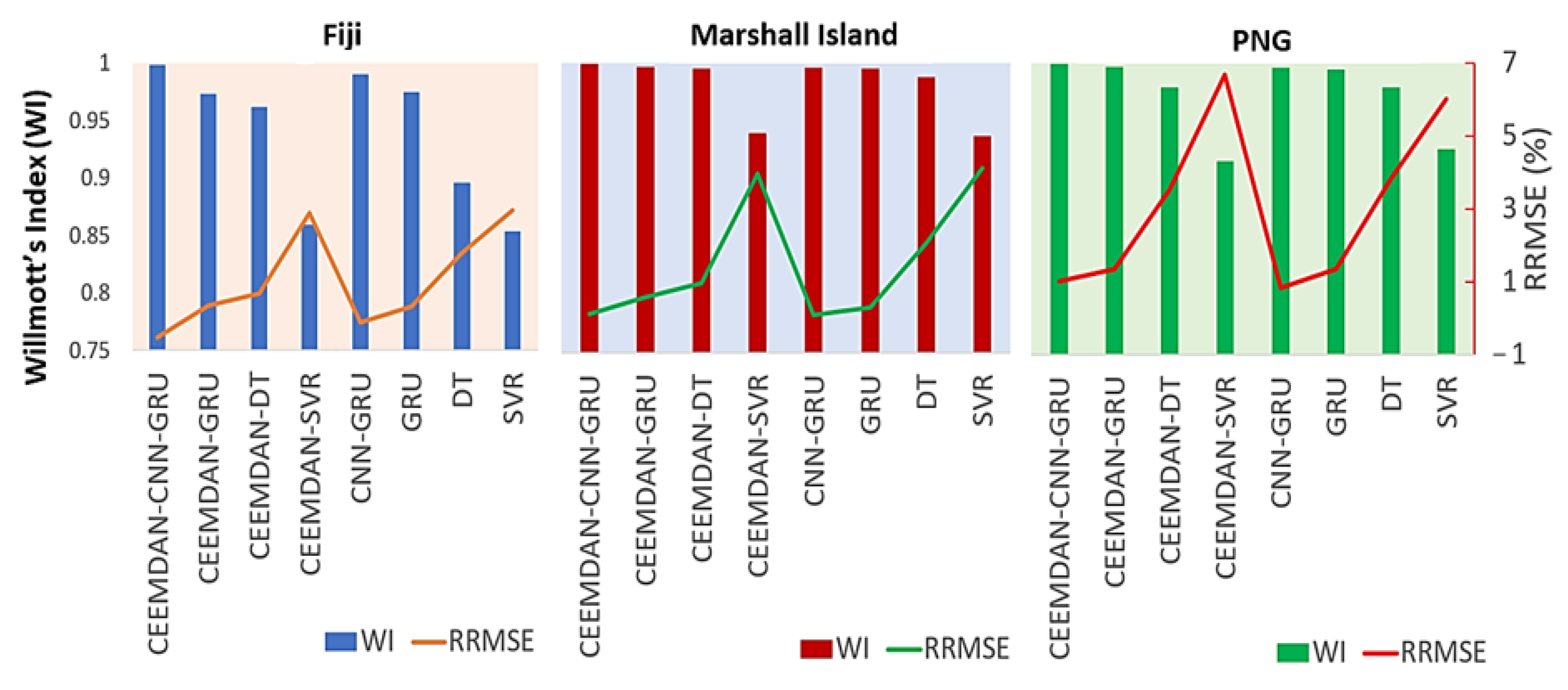
- Willmott’s Index of agreement (d)
- Root Mean Square Error (RMSE)
- Mean Absolute Error (MAE)
- Root Mean Absolute Error (RMAE)
- Relative Root Mean Square Error (RRMSE)
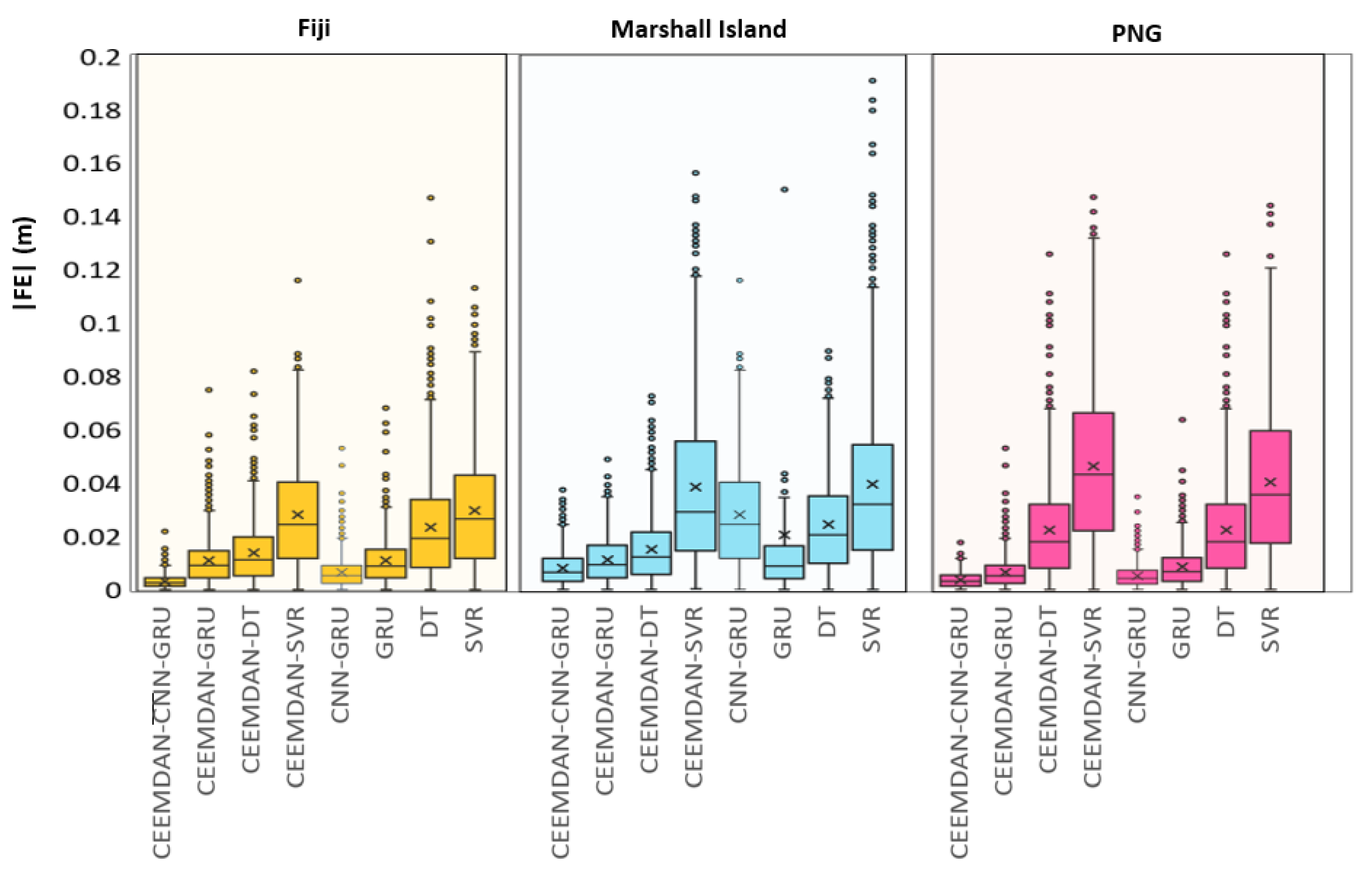
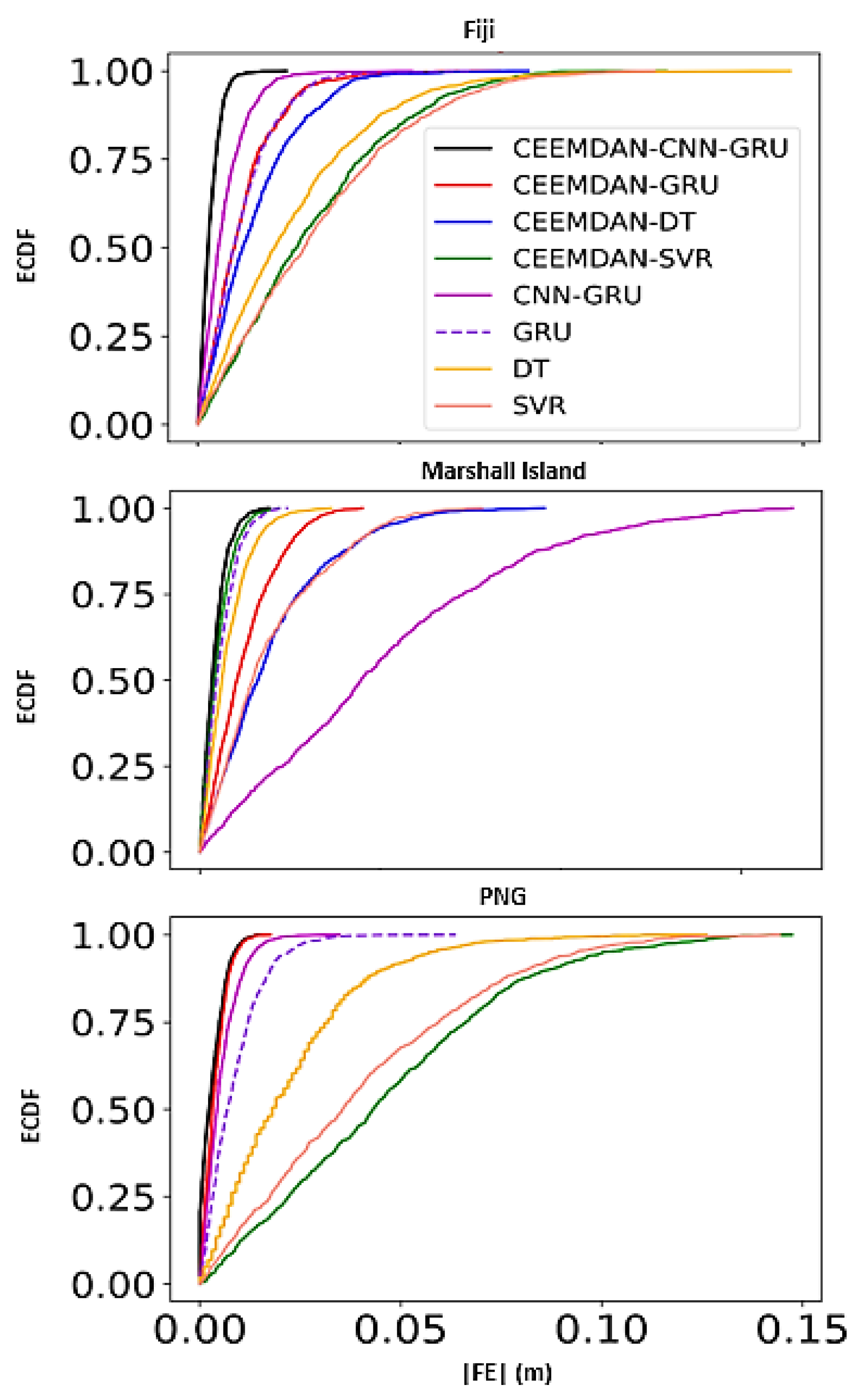
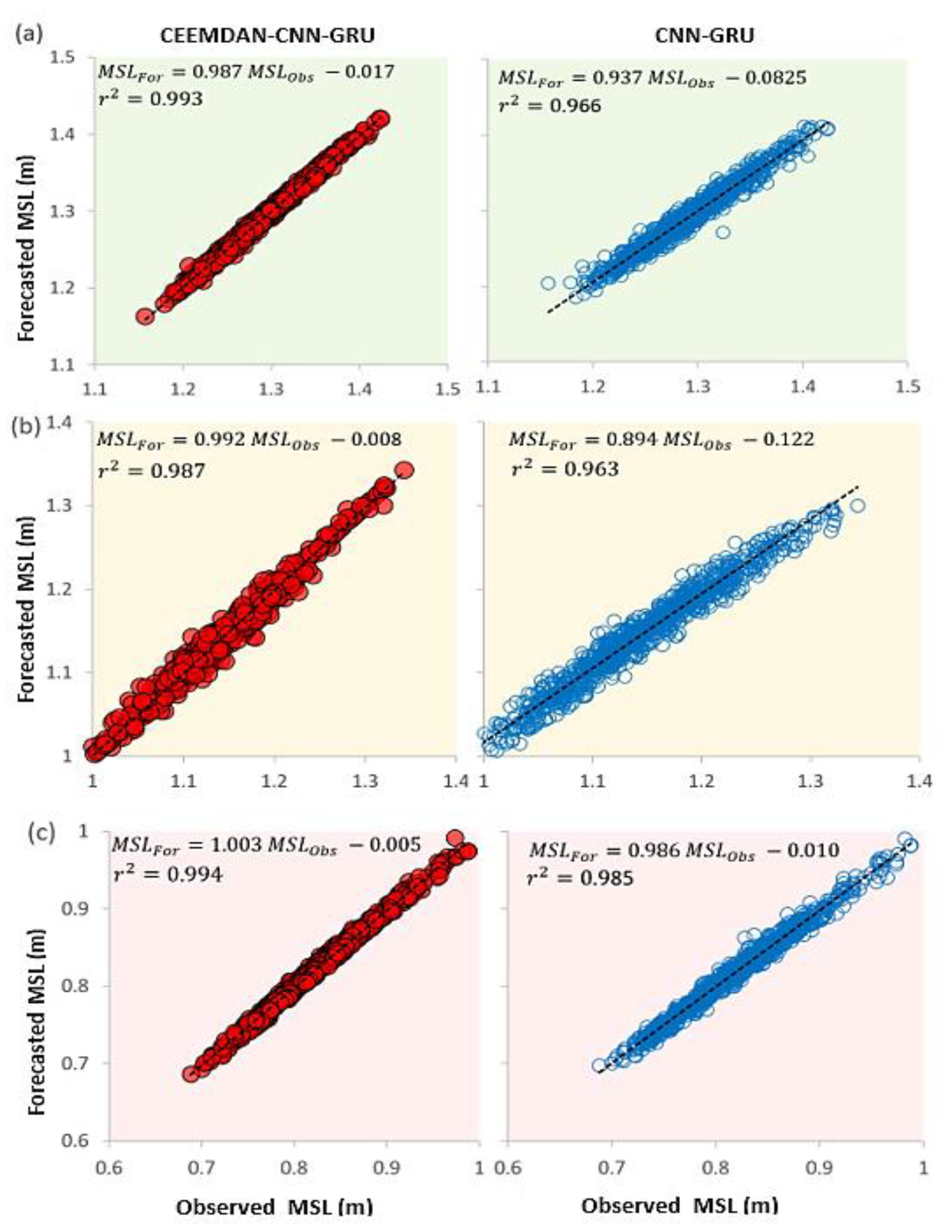
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MSL | Mean Sea Level |
| CEEMDAN | Complete Ensemble Empirical Mode Decomposition with Adaptive Noise |
| GRU | Gated Recurrent Unit |
| CNN | Convolutional Neural Network |
| DL | Deep Learning (DL) |
| NCA | Neighbourhood Component Analysis |
| BOM | Bureau of Mereology |
| ACF | Auto Correlation Function |
| PACF | Partial Auto Correlation Function |
| CCF | Cross-Correlation Function |
| r | Correlation Coefficient |
| NS | Nash–Sutcliffe Coefficient |
| L | Legates and McCabe Index |
Appendix A
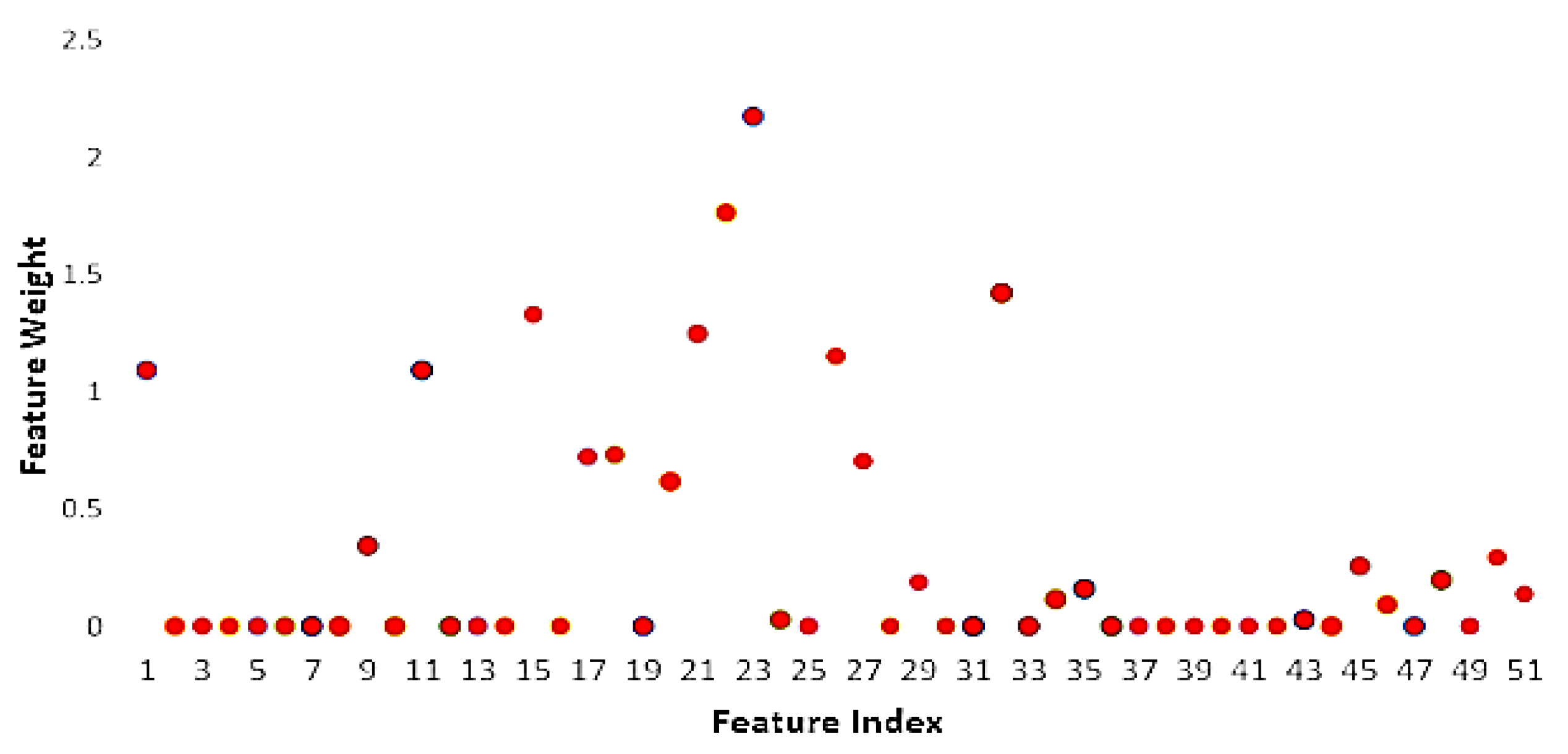
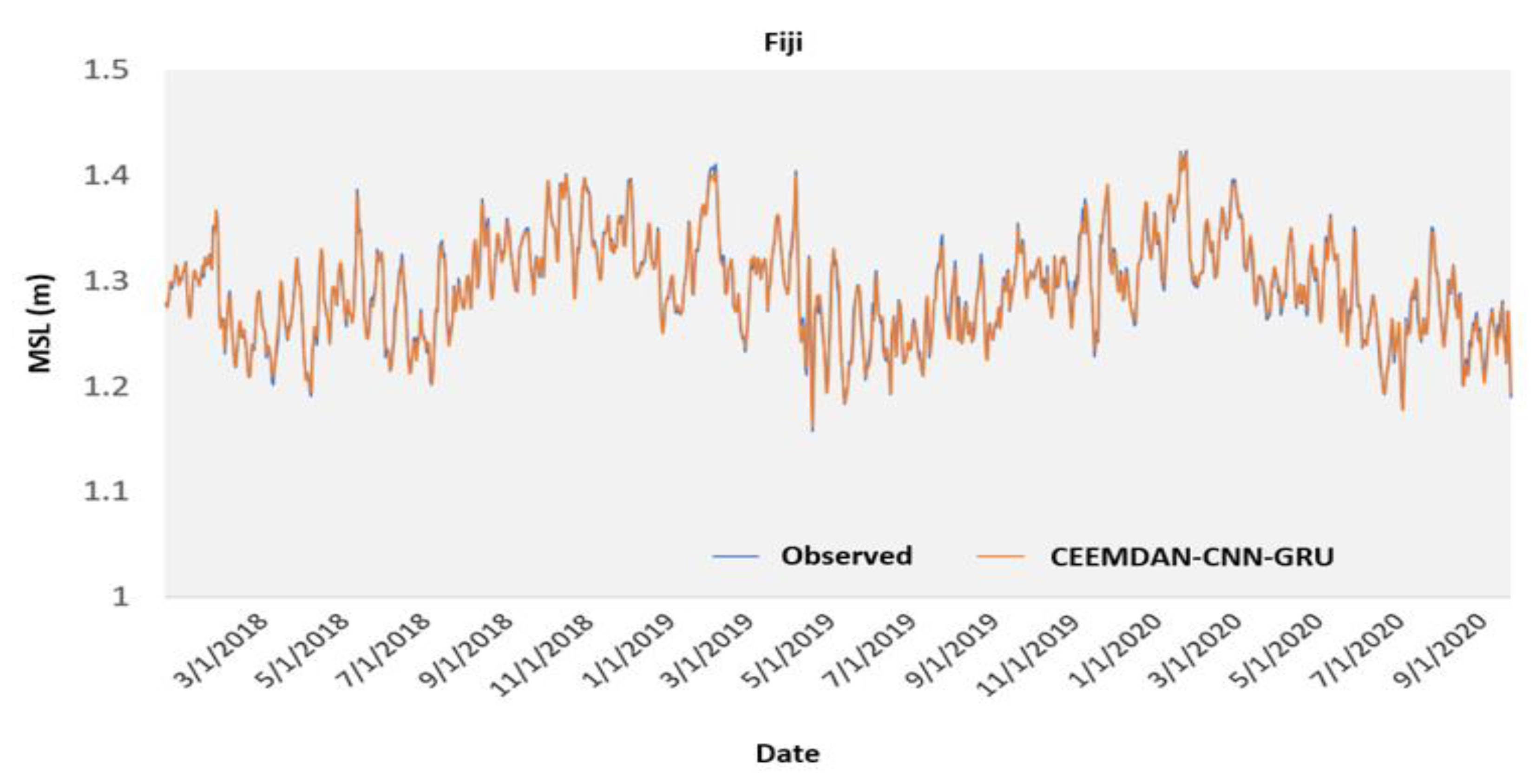
Appendix A.1. Figures
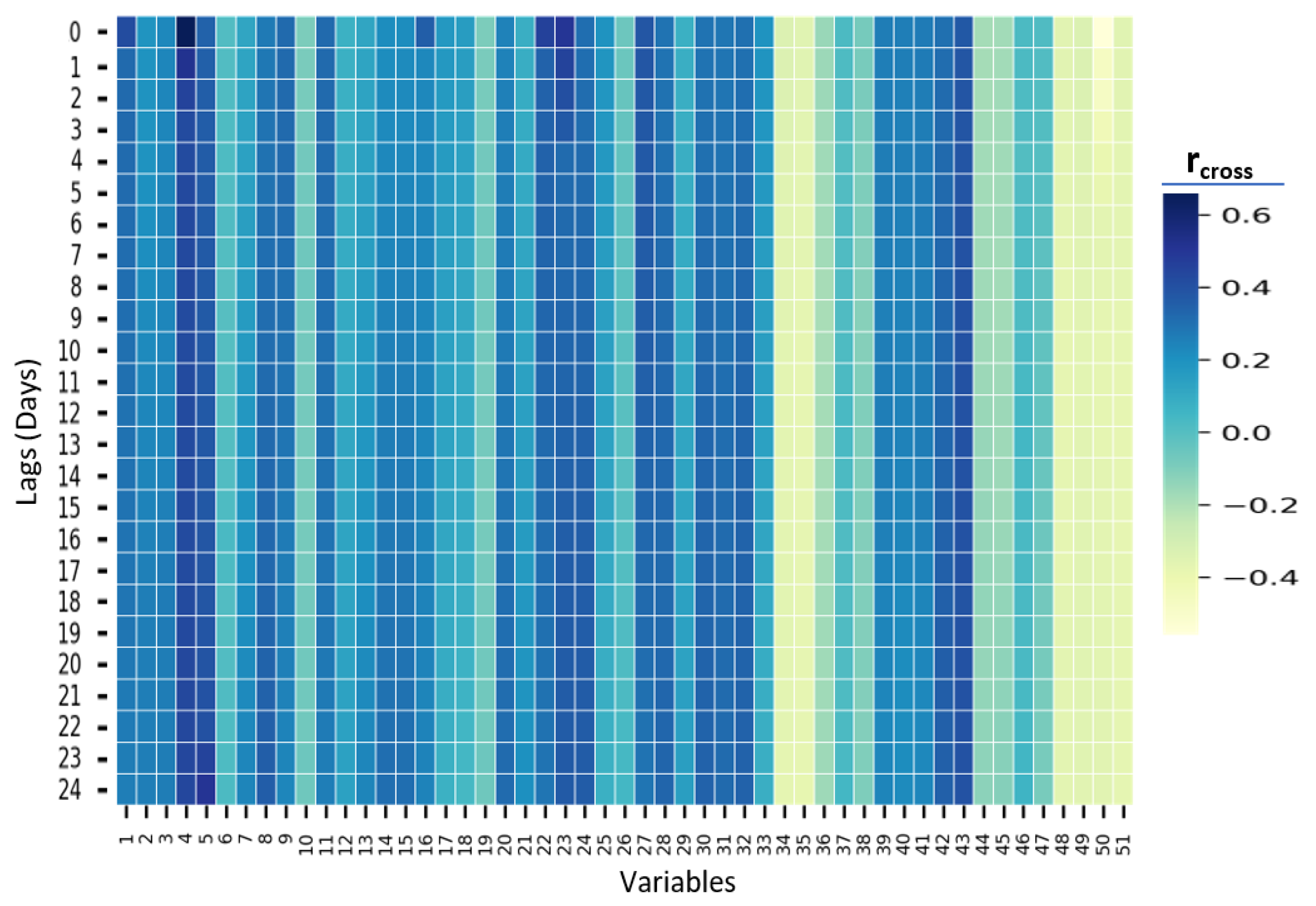
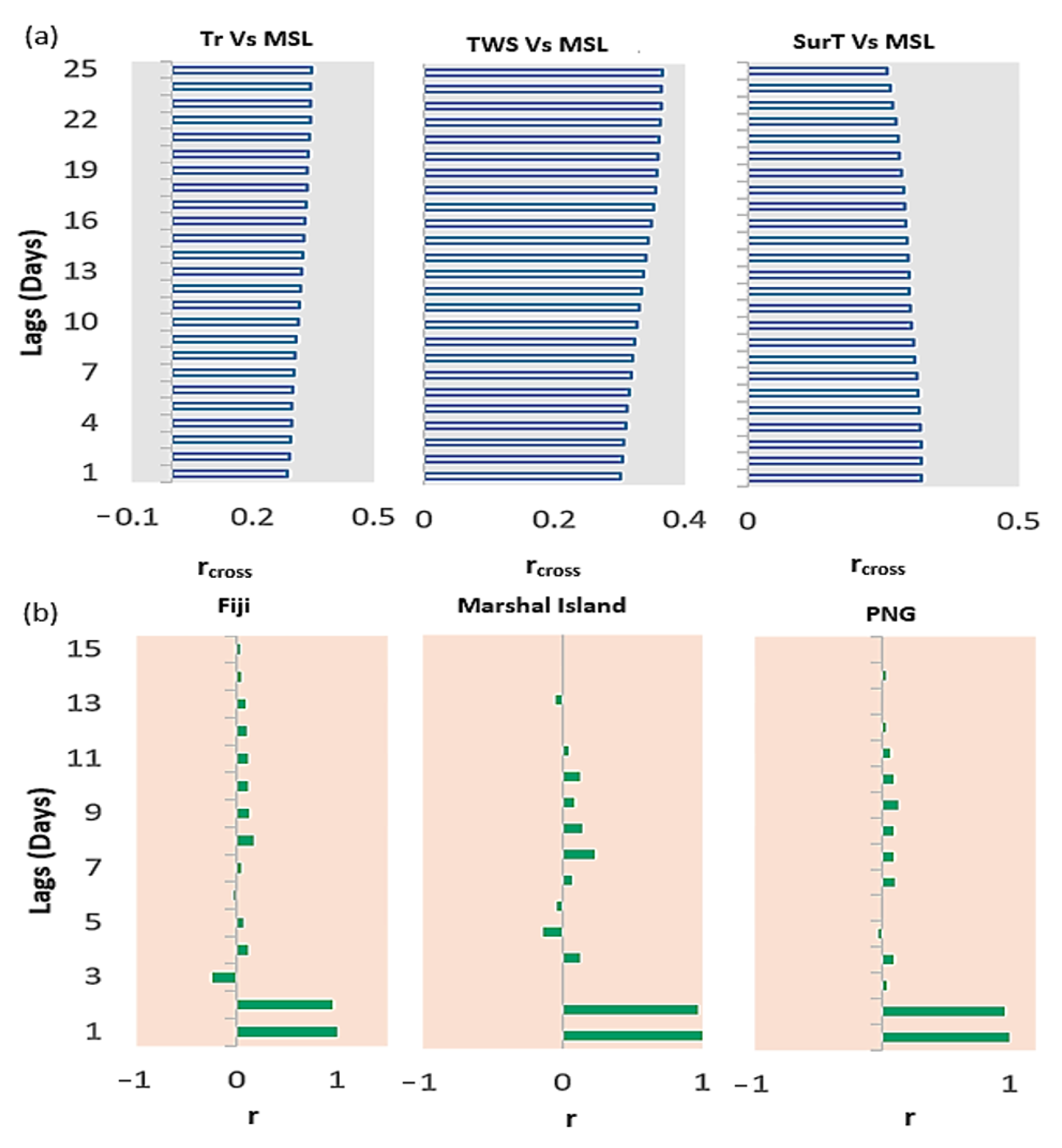
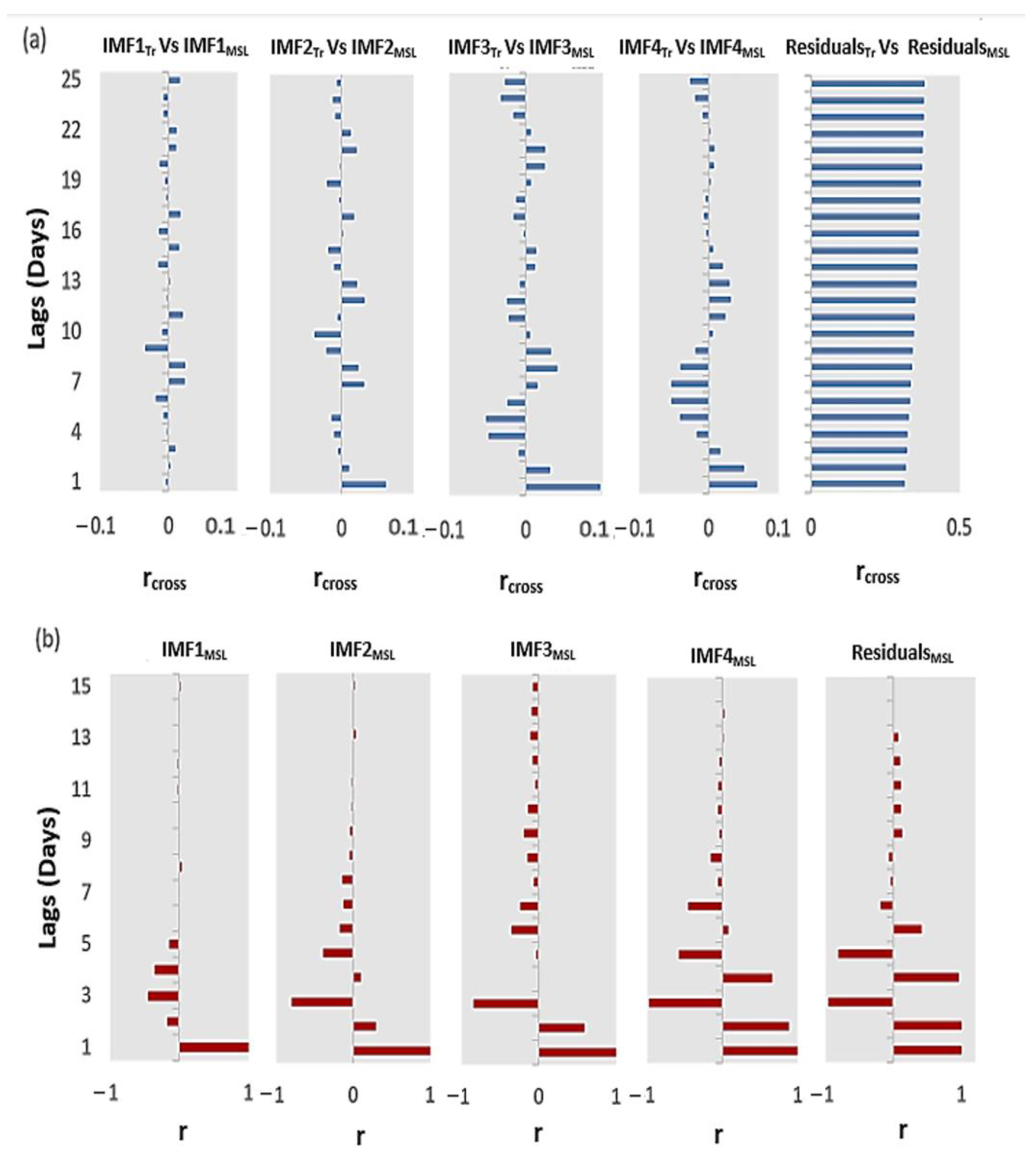
Appendix A.2. Tables
| Variable ID | Description of Variables | Acronyms | Units |
|---|---|---|---|
| Model: GLDAS 2.0 | |||
| 1 | Average Surface Skin temperature | SurT | K |
| 2 | Plant canopy surface water | P | kg m−2 s−1 |
| 3 | Canopy water evaporation | Cw | kg m−2 s−1 |
| 4 | Direct evaporation from bare soil | Ev | W m−2 |
| 5 | Snow evaporation | Sn | W m−2 |
| 6 | Evapotranspiration | Evp | W m−2 |
| 7 | Ground water storage | GWS | W m−2 |
| 8 | Net long-wave radiation flux | Lw | kg m−2 s−1 |
| 9 | Ground heat flux | Gh | m |
| 10 | Sensible heat net flux | Sh | K |
| 11 | Latent heat net flux | Lat | kg m−2 |
| 12 | Baseflow-groundwater runoff | Bg | W m−2 |
| 13 | Snow melt daily 0.25 | Snm | kg m−2 s−1 |
| 14 | Storm surface runoff | SSR | kg m−2 s−1 |
| 15 | Snow depth daily | S | kg m−2 |
| 16 | Snow surface temperature | St | kg m−2 s−1 |
| 17 | Profile soil moisture | PSM | kg m−2 |
| 18 | Root zone soil moisture | Szn | kg m−2 |
| 19 | Surface soil moisture | Ssm | kg m−2 |
| 20 | Snow depth water equivalent | Sdw | kg m−2 s−1 |
| 21 | Net short-wave radiation flux | Swr | kg m−2 s−1 |
| 22 | Transpiration | Tr | mm |
| 23 | Terrestrial water storage | TWS | mm |
| Model: MODIS-Terra | |||
| 24 | Aerosol optical depth 550 nm (Dark Target) | AOD | - |
| 25 | Scattering angle: mean of daily mean | S | degrees |
| 26 | Combined dark target and deep blue AOD at 0.55 µ for land | C | - |
| 27 | Precipitable water vapor 440 to 10 mb: Mean | r | cm |
| 28 | Precipitable water vapor surface to 680 mb | rw | cm |
| 29 | Precipitable water vapor total col: Mean of level-3 QA weighted | rvp | cm |
| 30 | Cirrus reflectance: Daily mean | Cr | - |
| 31 | Ice Cloud Effective Particle Radius: Daily mean | Ice | - |
| 32 | Liquid Water Cloud Effective Particle Radius: Daily mean | LW | - |
| 33 | Cloud Fraction from Cloud Mask: Day Mean | CF | - |
| 34 | Cloud Fraction from Cloud Mask: Mean | CFm | - |
| 35 | Cloud Fraction from Cloud Mask: Night Mean | Cnm | - |
| 36 | Combined Cloud Optical Thickness: Mean | CC | - |
| 37 | Ice Cloud Optical Thickness: Mean | IC | microns |
| 38 | Liquid Water Cloud Optical Thickness: Mean | Lm | microns |
| 39 | Cloud Top Pressure (Day): Mean | CP | hPa |
| 40 | Cloud Top Pressure: Mean | CPm | hPa |
| 41 | Cloud Top Pressure (Night): Mean | CPnm | hPa |
| 42 | Cloud Top Temperature: Mean | CTm | K |
| 43 | Cloud Top Temperature (Day): Mean | CTdm | K |
| 44 | Cloud Top Temperature (Night): Mean | CTnm | K |
| 45 | Ice Cloud Water Path: Mean | IC | g/m2 |
| 46 | Liquid Water Cloud Water Path: Mean | LQ | g/m2 |
| 47 | Aerosol Optical Depth 550 nm (Deep Blue, Land-only) | A550 | - |
| 48 | Deep Blue Angstrom Exponent for land (0.412–0.47µ): Mean | D | - |
| 49 | Water vapor near-infrared—clear column (bright land and ocean sunlight only) | Wvi | cm |
| 50 | Water vapor near infrared—cloudy column: Mean | Wvm | cm |
| Model: MERRA-2 | |||
| 51 | 2 m air temperature—daily max | Tmax | K |
| 52 | 2 m air temperature—daily mean | Tr | K |
| 53 | 2 m air temperature—daily min | Tmin | K |
| Objective Variable | |||
| 54 | Mean sea level | MSL | m |
| Model | Model Hyper-Parameter Names | Search Space for Optimal Hyper-Parameters |
|---|---|---|
| (a) Tested Range of Model Hyper-Parameters | ||
| CNN-GRU | Filter 1 | [70, 80, 100, 150] |
| Filter 2 | [70, 80, 100, 150] | |
| Filter 3 | [70, 80, 100, 150] | |
| GRU Cell Units | [40, 50, 70, 80, 100, 150] | |
| Epochs | [500, 800, 1000] | |
| Activation function | [ReLU] | |
| Optimiser | [Adam], [SGD] | |
| Batch Size | [5, 10, 20, 50, 100] | |
| GRU | GRU Cell1 | [70, 80, 100, 110] |
| GRU Cell 2 | [70, 80, 100,150, 200, 210] | |
| Epochs | [500, 800, 1000] | |
| Activation function | [ReLU] | |
| Optimiser | [Adam], [SGD] | |
| Batch Size | [5, 10, 20, 50, 100] | |
| (b) Optimally Selected Hyper-parameters | ||
| CNN-GRU | Convolution Layer 1 (C1) | 80 |
| C1- Activation function | ReLU | |
| C1-Pooling Size | 1 | |
| Convolution Layer 2 (C2) | 70 | |
| C2- Activation function | ReLU | |
| C2-Pooling Size | 1 | |
| Convolution Layer 3 (C3) | 80 | |
| C3- Activation function | ReLU | |
| C3-Pooling Size | 1 | |
| GRU Layer 1 (L1) | 200 | |
| L1- Activation function | ReLU | |
| GRU Layer 2 (L2) | 60 | |
| L2- Activation function | ReLU | |
| Dropout rate | 0.2 | |
| Optimiser | Adam | |
| Padding | Same | |
| Batch Size | 5 | |
| Epochs | 1000 | |
| GRU | GRU Cell 1 (G1) | 110 |
| G1- Activation function | ReLU | |
| GRU Cell 2 (G2) | 250 | |
| G2- Activation function | ReLU | |
| Epochs | ||
| Optimiser | SGD | |
| Dropout rate | 0.2 | |
| Batch Size | 15 | |
| Epochs | 1000 | |
References
- Walsh, K.J.; McInnes, K.L.; McBride, J.L. Climate change impacts on tropical cyclones and extreme sea levels in the South Pacific—A regional assessment. Glob. Planet. Chang. 2012, 80, 149–164. [Google Scholar] [CrossRef]
- Barnett, J.; Campbell, J. Climate Change and Small Island States: Power, Knowledge and the South Pacific; Earthscan: London, UK, 2010. [Google Scholar]
- Tadesse, M.; Wahl, T.; Cid, A. Data-driven modeling of global storm surges. Front. Mar. Sci. 2020, 7, 260. [Google Scholar] [CrossRef]
- Scicchitano, G.; Scardino, G.; Monaco, C.; Piscitelli, A.; Milella, M.; De Giosa, F.; Mastronuzzi, G. Comparing impact effects of common storms and Medicanes along the coast of south-eastern Sicily. Mar. Geol. 2021, 439, 106556. [Google Scholar] [CrossRef]
- Crain, C.M.; Halpern, B.S.; Beck, M.W.; Kappel, C.V. Understanding and managing human threats to the coastal marine environment. Ann. N. Y. Acad. Sci. 2009, 1162, 39–62. [Google Scholar] [CrossRef] [PubMed]
- Nunn, P.D.; Mimura, N. Vulnerability of South Pacific island nations to sea-level rise. J. Coast. Res. 1997, 12, 133–151. [Google Scholar]
- Vacchi, M.; Marriner, N.; Morhange, C.; Spada, G.; Fontana, A.; Rovere, A. Multiproxy assessment of Holocene relative sea-level changes in the western Mediterranean: Sea-level variability and improvements in the definition of the isostatic signal. Earth-Sci. Rev. 2016, 155, 172–197. [Google Scholar] [CrossRef]
- Lambeck, K.; Antonioli, F.; Purcell, A.; Silenzi, S. Sea-level change along the Italian coast for the past 10,000 yr. Quat. Sci. Rev. 2004, 23, 1567–1598. [Google Scholar] [CrossRef]
- Cazenave, A.; Nerem, R.S. Present-day sea level change: Observations and causes. Rev. Geophys. 2004, 42. [Google Scholar] [CrossRef]
- Raj, N.; Brown, J. An EEMD-BiLSTM Algorithm Integrated with Boruta Random Forest Optimiser for Significant Wave Height Forecasting along Coastal Areas of Queensland, Australia. Remote Sens. 2021, 13, 1456. [Google Scholar] [CrossRef]
- Gharineiat, Z.; Deng, X. Application of the multi-adaptive regression splines to integrate sea level data from altimetry and tide gauges for monitoring extreme sea level events. Mar. Geod. 2015, 38, 261–276. [Google Scholar] [CrossRef]
- Imani, M.; Kao, H.-C.; Lan, W.-H.; Kuo, C.-Y. Daily sea level prediction at Chiayi coast, Taiwan using extreme learning machine and relevance vector machine. Glob. Planet. Chang. 2018, 161, 211–221. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Deo, R.C.; Ghahramani, A.; Raj, N.; Feng, Q.; Yin, Z.; Yang, L. LSTM integrated with Boruta-random forest optimiser for soil moisture estimation under RCP4. 5 and RCP8. 5 global warming scenarios. Stoch. Environ. Res. Risk Assess. 2021, 35, 1851–1881. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Deo, R.C.; Feng, Q.; Ghahramani, A.; Raj, N.; Yin, Z.; Yang, L. Deep learning hybrid model with Boruta-Random forest optimiser algorithm for streamflow forecasting with climate mode indices, rainfall, and periodicity. J. Hydrol. 2021, 599, 126350. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Deo, R.C.; Feng, Q.; Ghahramani, A.; Raj, N.; Yin, Z.; Yang, L. Hybrid Deep Learning for Week-Ahead Evapotranspiration Forecasting. Research Square. Available online: https://assets.researchsquare.com/files/rs-424493/v1_covered.pdf?c=1631863211 (accessed on 10 November 2021).
- Ghimire, S.; Deo, R.C.; Downs, N.J.; Raj, N. Global solar radiation prediction by ANN integrated with European Centre for medium range weather forecast fields in solar rich cities of Queensland Australia. J. Clean. Prod. 2019, 216, 288–310. [Google Scholar] [CrossRef]
- Sharma, E.; Deo, R.C.; Prasad, R.; Parisi, A.V.; Raj, N. Deep Air Quality Forecasts: Suspended Particulate Matter Modeling With Convolutional Neural and Long Short-Term Memory Networks. IEEE Access 2020, 8, 209503–209516. [Google Scholar] [CrossRef]
- Moishin, M.; Deo, R.C.; Prasad, R.; Raj, N.; Abdulla, S. Designing deep-based learning flood forecast model with ConvLSTM hybrid algorithm. IEEE Access 2021, 9, 50982–50993. [Google Scholar] [CrossRef]
- Thomson, S.W. The tide gauge, tidal harmonic analyser, and tide predicter. In Minutes of the Proceedings of the Institution of Civil Engineers; Thomas Telford-ICE Virtual Library: London, UK, 1881; Volume 65, pp. 2–25. [Google Scholar]
- Emery, K. Relative sea levels from tide-gauge records. Proc. Natl. Acad. Sci. USA 1980, 77, 6968–6972. [Google Scholar] [CrossRef]
- Zubier, K.M.; Eyouni, L.S. Investigating the role of atmospheric variables on sea level variations in the Eastern Central Red Sea using an artificial neural network approach. Oceanologia 2020, 62, 267–290. [Google Scholar] [CrossRef]
- Watson, C.S.; White, N.J.; Church, J.A.; King, M.A.; Burgette, R.J.; Legresy, B. Unabated global mean sea-level rise over the satellite altimeter era. Nat. Clim. Chang. 2015, 5, 565–568. [Google Scholar] [CrossRef]
- Ablain, M.; Meyssignac, B.; Zawadzki, L.; Jugier, R.; Ribes, A.; Spada, G.; Benveniste, J.; Cazenave, A.; Picot, N. Uncertainty in satellite estimates of global mean sea-level changes, trend and acceleration. Earth Syst. Sci. Data 2019, 11, 1189–1202. [Google Scholar] [CrossRef]
- Bindoff, N.L.; Willebrand, J.; Artale, V.; Cazenave, A.; Gregory, J.M.; Gulev, S.; Hanawa, K.; Le Quere, C.; Levitus, S.; Nojiri, Y. Observations: Oceanic Climate Change and Sea Level. Available online: http://nora.nerc.ac.uk/id/eprint/15400/1/ar4-wg1-chapter5.pdf (accessed on 15 April 2007).
- Shukla, J.; Verma, M.; Misra, A. Effect of global warming on sea level rise: A modeling study. Ecol. Complex. 2017, 32, 99–110. [Google Scholar] [CrossRef]
- Levermann, A.; Clark, P.U.; Marzeion, B.; Milne, G.A.; Pollard, D.; Radic, V.; Robinson, A. The multimillennial sea-level commitment of global warming. Proc. Natl. Acad. Sci. USA 2013, 110, 13745–13750. [Google Scholar] [CrossRef] [PubMed]
- Rahmstorf, S. A semi-empirical approach to projecting future sea-level rise. Science 2007, 315, 368–370. [Google Scholar] [CrossRef] [PubMed]
- Douglas, B.C.; Kearney, M.S.; Leatherman, S.P. Sea level rise: History and consequences. In International Geophysics Series; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Houston, J.R.; Dean, R.G. Sea-level acceleration based on US tide gauges and extensions of previous global-gauge analyses. J. Coast. Res. 2011, 27, 409–417. [Google Scholar]
- Houston, J. Reply to: Donoghue, J.F. and Parkinson, R.W. 2011. Discussion of: Houston, J.R.; Dean, R.G. Sea-Level Acceleration Based on US Tide Gauges and Extensions of Previous Global-Gauge Analyses. J. Coast. Res. 2011, 27, 409–417. J. Coast. Res. 2011, 27, 997. [Google Scholar]
- Tomasicchio, G.R.; Lusito, L.; D’Alessandro, F.; Frega, F.; Francone, A.; De Bartolo, S. A direct scaling analysis for the sea level rise. Stoch. Environ. Res. Risk Assess. 2018, 32, 3397–3408. [Google Scholar] [CrossRef]
- Hünicke, B.; Zorita, E. Influence of temperature and precipitation on decadal Baltic Sea level variations in the 20th century. Tellus A Dyn. Meteorol. Oceanogr. 2006, 58, 141–153. [Google Scholar] [CrossRef]
- Vadrevu, K.P.; Lasko, K.; Giglio, L.; Justice, C. Analysis of Southeast Asian pollution episode during June 2013 using satellite remote sensing datasets. Environ. Pollut. 2014, 195, 245–256. [Google Scholar] [CrossRef]
- Xu, Y.; Ho, H.C.; Wong, M.S.; Deng, C.; Shi, Y.; Chan, T.-C.; Knudby, A. Evaluation of machine learning techniques with multiple remote sensing datasets in estimating monthly concentrations of ground-level PM2.5. Environ. Pollut. 2018, 242, 1417–1426. [Google Scholar] [CrossRef]
- Dardel, C.; Kergoat, L.; Hiernaux, P.; Mougin, E.; Grippa, M.; Tucker, C. Re-greening Sahel: 30 years of remote sensing data and field observations (Mali, Niger). Remote Sens. Environ. 2014, 140, 350–364. [Google Scholar] [CrossRef]
- Maul, G.A.; Martin, D.M. Sea level rise at Key West, Florida, 1846-1992: America’s longest instrument record? Geophys. Res. Lett. 1993, 20, 1955–1958. [Google Scholar] [CrossRef]
- Gharineiat, Z.; Deng, X. Spectral analysis of satellite altimeter and tide gauge data around the Northern Australian Coast. Remote Sens. 2020, 12, 161. [Google Scholar] [CrossRef]
- Gharineiat, Z.; Deng, X. Description and assessment of regional sea-level trends and variability from altimetry and tide gauges at the northern Australian coast. Adv. Space Res. 2018, 61, 2540–2554. [Google Scholar] [CrossRef]
- Parker, R.L.; Parker, R.L. Geophysical Inverse Theory; Princeton University Press: Princeton, NJ, USA, 1994; Volume 1. [Google Scholar]
- Pope, A.J. The Statistics of Residuals and the Detection of Outliers; US Department of Commerce, National Oceanic and Atmospheric Administration: Silver Spring, MD, USA, 1976. [Google Scholar]
- Ketkar, N. Introduction to keras. In Deep Learning with Python; Springer: Berlin/Heidelberg, Germany, 2017; pp. 97–111. [Google Scholar]
- Brownlee, J. Deep Learning with Python: Develop Deep Learning Models on Theano and TensorFlow Using Keras; Machine Learning Mastery: San Juan, PR, USA, 2016. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th Symposium on Operating Systems Design and Implementation ({OSDI} 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Barrett, P.; Hunter, J.; Miller, J.T.; Hsu, J.-C.; Greenfield, P. Matplotlib—A Portable Python Plotting Package. In Proceedings of the Astronomical Data Analysis Software And Systems XIV, Pasadena, CA, USA, 24–27 October 2004; p. 91. [Google Scholar]
- Waskom, M.; Botvinnik, O.; Gelbart, M.; Ostblom, J.; Hobson, P.; Lukauskas, S.; Gemperline, D.C.; Augspurger, T.; Halchenko, Y.; Warmenhoven, J. Seaborn: Statistical Data Visualization; Astrophysics Source Code Library: College Park, MD, USA, 2020. [Google Scholar]
- Tiwari, M.K.; Adamowski, J. Urban water demand forecasting and uncertainty assessment using ensemble wavelet-bootstrap-neural network models. Water Resour. Res. 2013, 49, 6486–6507. [Google Scholar] [CrossRef]
- Tiwari, M.K.; Chatterjee, C. A new wavelet–bootstrap–ANN hybrid model for daily discharge forecasting. J. Hydroinformatics 2011, 13, 500–519. [Google Scholar] [CrossRef]
- Wang, J.; Cao, J.; Yuan, S.; Cheng, M. Short-term forecasting of natural gas prices by using a novel hybrid method based on a combination of the CEEMDAN-SE-and the PSO-ALS-optimized GRU network. Energy 2021, 233, 121082. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L. Drought Prediction Method Based on an Improved CEEMDAN-QR-BL Model. IEEE Access 2021, 9, 6050–6062. [Google Scholar] [CrossRef]
- Adamowski, J.; Fung Chan, H.; Prasher, S.O.; Ozga-Zielinski, B.; Sliusarieva, A. Comparison of multiple linear and nonlinear regression, autoregressive integrated moving average, artificial neural network, and wavelet artificial neural network methods for urban water demand forecasting in Montreal, Canada. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Yang, W.; Wang, K.; Zuo, W. Neighborhood component feature selection for high-dimensional data. J. Comput. 2012, 7, 161–168. [Google Scholar] [CrossRef]
- Goldberger, J.; Hinton, G.E.; Roweis, S.; Salakhutdinov, R.R. Neighbourhood components analysis. Adv. Neural Inf. Processing Syst. 2004, 17. Available online: https://proceedings.neurips.cc/paper/2004/file/42fe880812925e520249e808937738d2-Paper.pdf (accessed on 10 November 2021).
- Goryachkin, Y.I.; Ivanov, V.; Stepanyants, Y.A. Oscillations of the Black Sea sea level in the north part of the coast. Phys. Oceanogr. 1999, 10, 123–130. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Hanson, S.E.; Lowe, J.A.; Warrick, R.A.; Lu, X.; Long, A.J. Sea-level scenarios for evaluating coastal impacts. Wiley Interdiscip. Rev. Clim. Chang. 2014, 5, 129–150. [Google Scholar] [CrossRef]
- Hunter, J. Estimating sea-level extremes under conditions of uncertain sea-level rise. Clim. Chang. 2010, 99, 331–350. [Google Scholar] [CrossRef]
- Willis, J.K.; Chambers, D.P.; Kuo, C.-Y.; Shum, C. Global sea level rise: Recent progress and challenges for the decade to come. Oceanography 2010, 23, 26–35. [Google Scholar] [CrossRef]
- Sweet, W.V.; Kopp, R.E.; Weaver, C.P.; Obeysekera, J.; Horton, R.M.; Thieler, E.R.; Zervas, C. Global and Regional Sea Level Rise Scenarios for the United States (No. CO-OPS 083); National Oceanic and Atmospheric Administration: Washington, DC, USA, 2017. [Google Scholar]
- Taylor, R. Interpretation of the correlation coefficient: A basic review. J. Diagn. Med. Sonogr. 1990, 6, 35–39. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- McCuen, R.H.; Knight, Z.; Cutter, A.G. Evaluation of the Nash–Sutcliffe efficiency index. J. Hydrol. Eng. 2006, 11, 597–602. [Google Scholar] [CrossRef]
- Knoben, W.J.; Freer, J.E.; Woods, R.A. Inherent benchmark or not? Comparing Nash–Sutcliffe and Kling–Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robeson, S.M.; Matsuura, K. A refined index of model performance. Int. J. Climatol. 2012, 32, 2088–2094. [Google Scholar] [CrossRef]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; Legates, D.R.; O’donnell, J.; Rowe, C.M. Statistics for the evaluation and comparison of models. J. Geophys. Res. Ocean. 1985, 90, 8995–9005. [Google Scholar] [CrossRef]
- Pachauri, R.K.; Reisinger, A. IPCC Fourth Assessment Report; IPCC: Geneva, Switzerland, 2007; Volume 2007. [Google Scholar]
- Nicholls, R.J.; Mimura, N. Regional issues raised by sea-level rise and their policy implications. Clim. Res. 1998, 11, 5–18. [Google Scholar] [CrossRef][Green Version]
- Anzidei, M.; Scicchitano, G.; Scardino, G.; Bignami, C.; Tolomei, C.; Vecchio, A.; Serpelloni, E.; De Santis, V.; Monaco, C.; Milella, M. Relative Sea-Level Rise Scenario for 2100 along the Coast of South Eastern Sicily (Italy) by InSAR Data, Satellite Images and High-Resolution Topography. Remote Sens. 2021, 13, 1108. [Google Scholar] [CrossRef]
- Scardino, G.; Sabatier, F.; Scicchitano, G.; Piscitelli, A.; Milella, M.; Vecchio, A.; Anzidei, M.; Mastronuzzi, G. Sea-level rise and shoreline changes along an open sandy coast: Case study of gulf of taranto, Italy. Water 2020, 12, 1414. [Google Scholar] [CrossRef]
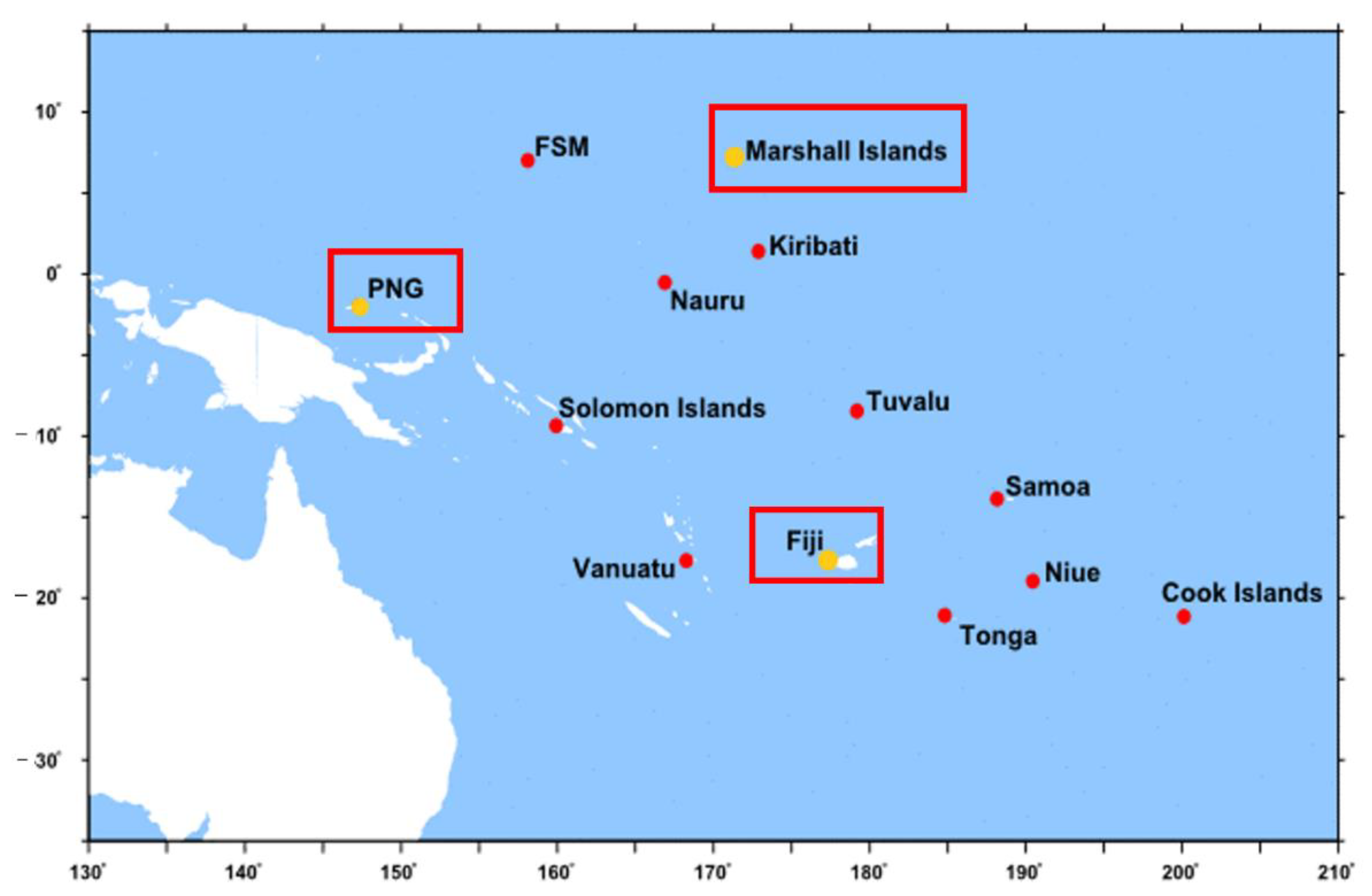

| Country | Place | Latitude | Longitude |
|---|---|---|---|
| Fiji | Lautoka | −2.0420 | 147.3737 |
| Marshall Islands | Majuro | 7.1060 | 171.3725 |
| PNG | Manus | −17.6053 | 177.4381 |
| Partition | Training (70%) | Validation (15%) | Testing (15%) |
|---|---|---|---|
| Dataset | January 1994–December 2012 | January 2013–December 2016 | January 2017–December 2020 |
| Model | r | NS | RMSE | MAE | RMAE |
|---|---|---|---|---|---|
| Station: Fiji | |||||
| CEEMDAN-CNN-GRU | 0.996 | 0.993 | 0.004 | 0.003 | 0.239 |
| CEEMDAN-GRU | 0.959 | 0.907 | 0.014 | 0.011 | 0.844 |
| CEEMDAN-DT | 0.927 | 0.850 | 0.018 | 0.014 | 1.075 |
| CEEMDAN-SVR | 0.806 | 0.605 | 0.043 | 0.035 | 2.767 |
| CNN-GRU | 0.982 | 0.964 | 0.009 | 0.007 | 0.513 |
| GRU | 0.955 | 0.909 | 0.014 | 0.011 | 0.841 |
| DT | 0.812 | 0.564 | 0.031 | 0.024 | 1.819 |
| SVR | 0.793 | 0.586 | 0.044 | 0.036 | 2.871 |
| Station: Marshall Island | |||||
| CEEMDAN-CNN-GRU | 0.996 | 0.991 | 0.010 | 0.006 | 0.628 |
| CEEMDAN-GRU | 0.979 | 0.957 | 0.011 | 0.009 | 1.022 |
| CEEMDAN-DT | 0.962 | 0.924 | 0.019 | 0.015 | 1.301 |
| CEEMDAN-SVR | 0.829 | 0.492 | 0.049 | 0.038 | 3.289 |
| CNN-GRU | 0.989 | 0.977 | 0.011 | 0.008 | 0.711 |
| GRU | 0.984 | 0.967 | 0.013 | 0.010 | 0.851 |
| DT | 0.909 | 0.810 | 0.030 | 0.024 | 2.133 |
| SVR | 0.766 | 0.459 | 0.051 | 0.039 | 3.385 |
| Station: PNG | |||||
| CEEMDAN-CNN-GRU | 0.995 | 0.989 | 0.007 | 0.005 | 0.650 |
| CEEMDAN-GRU | 0.979 | 0.957 | 0.011 | 0.009 | 1.022 |
| CEEMDAN-DT | 0.846 | 0.708 | 0.029 | 0.022 | 2.705 |
| CEEMDAN-SVR | 0.721 | 0.459 | 0.055 | 0.046 | 5.463 |
| CNN-GRU | 0.992 | 0.984 | 0.007 | 0.005 | 0.637 |
| GRU | 0.979 | 0.958 | 0.011 | 0.009 | 1.032 |
| DT | 0.846 | 0.708 | 0.029 | 0.022 | 2.705 |
| SVR | 0.735 | 0.451 | 0.049 | 0.040 | 4.759 |
| Models | Fiji | Marshal Island | PNG |
|---|---|---|---|
| CEEMDAN-CNN-GRU | 0.9168 | 0.9271 | 0.9207 |
| CEEMDAN-GRU | 0.7087 | 0.8034 | 0.8034 |
| CEEMDAN-DT | 0.6289 | 0.7321 | 0.4824 |
| CEEMDAN-SVR | 0.3626 | 0.3139 | 0.5702 |
| CNN-GRU | 0.8213 | 0.8545 | 0.8778 |
| GRU | 0.7085 | 0.8254 | 0.8026 |
| DT | 0.372 | 0.5631 | 0.4824 |
| SVR | 0.3392 | 0.2943 | 0.3672 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raj, N.; Gharineiat, Z.; Ahmed, A.A.M.; Stepanyants, Y. Assessment and Prediction of Sea Level Trend in the South Pacific Region. Remote Sens. 2022, 14, 986. https://doi.org/10.3390/rs14040986
Raj N, Gharineiat Z, Ahmed AAM, Stepanyants Y. Assessment and Prediction of Sea Level Trend in the South Pacific Region. Remote Sensing. 2022; 14(4):986. https://doi.org/10.3390/rs14040986
Chicago/Turabian StyleRaj, Nawin, Zahra Gharineiat, Abul Abrar Masrur Ahmed, and Yury Stepanyants. 2022. "Assessment and Prediction of Sea Level Trend in the South Pacific Region" Remote Sensing 14, no. 4: 986. https://doi.org/10.3390/rs14040986
APA StyleRaj, N., Gharineiat, Z., Ahmed, A. A. M., & Stepanyants, Y. (2022). Assessment and Prediction of Sea Level Trend in the South Pacific Region. Remote Sensing, 14(4), 986. https://doi.org/10.3390/rs14040986










