An Analysis of Arctic Sea Ice Leads Retrieved from AMSR-E/AMSR2
Abstract
:1. Introduction
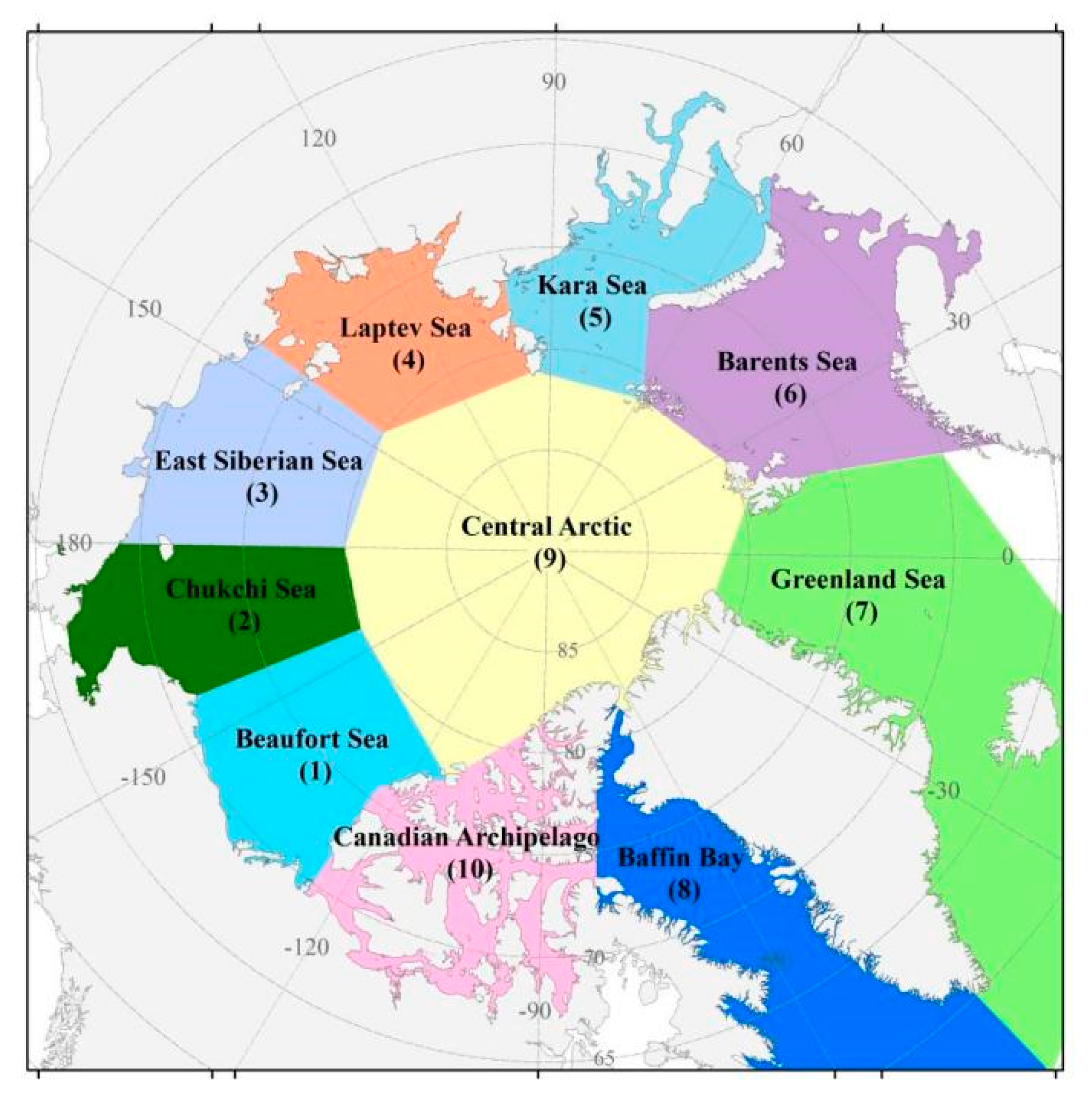
2. Data
2.1. AMSR2 Data
2.2. MODIS Datasets
3. Method
3.1. Retrieve Sea Ice Leads from the AMSR2 Brightness Temperature
- (1)
- Interpolate the AMSR2 L1B brightness temperatures at frequencies of 18.7 GHz (TB,18.7V) and 89.0 GHz (TB,89V) onto the National Snow and Ice Data Center (NSIDC) EASE grid with a spatial resolution of 6.25 km. For 89.0 GHz data, a bilinear interpolation scheme is used. For 18.7 GHz data, a nearest-neighbor interpolation scheme is used;
- (2)
- Calculate the brightness temperature ratio (r) following Equation (1):
- (3)
- Calculate the brightness temperature ratio anomalies () according to Equation (2):where Medianw(r) represents the utilization of a median filter to r in all grid points surrounding the target grid point with a w × w search window. The large AMSR2 sensor’s footprint means that a potential lead signal might be a mixture of narrow lead and thick ice; thus, sea ice leads in the pack ice zone are more representative by than by r;
- (4)
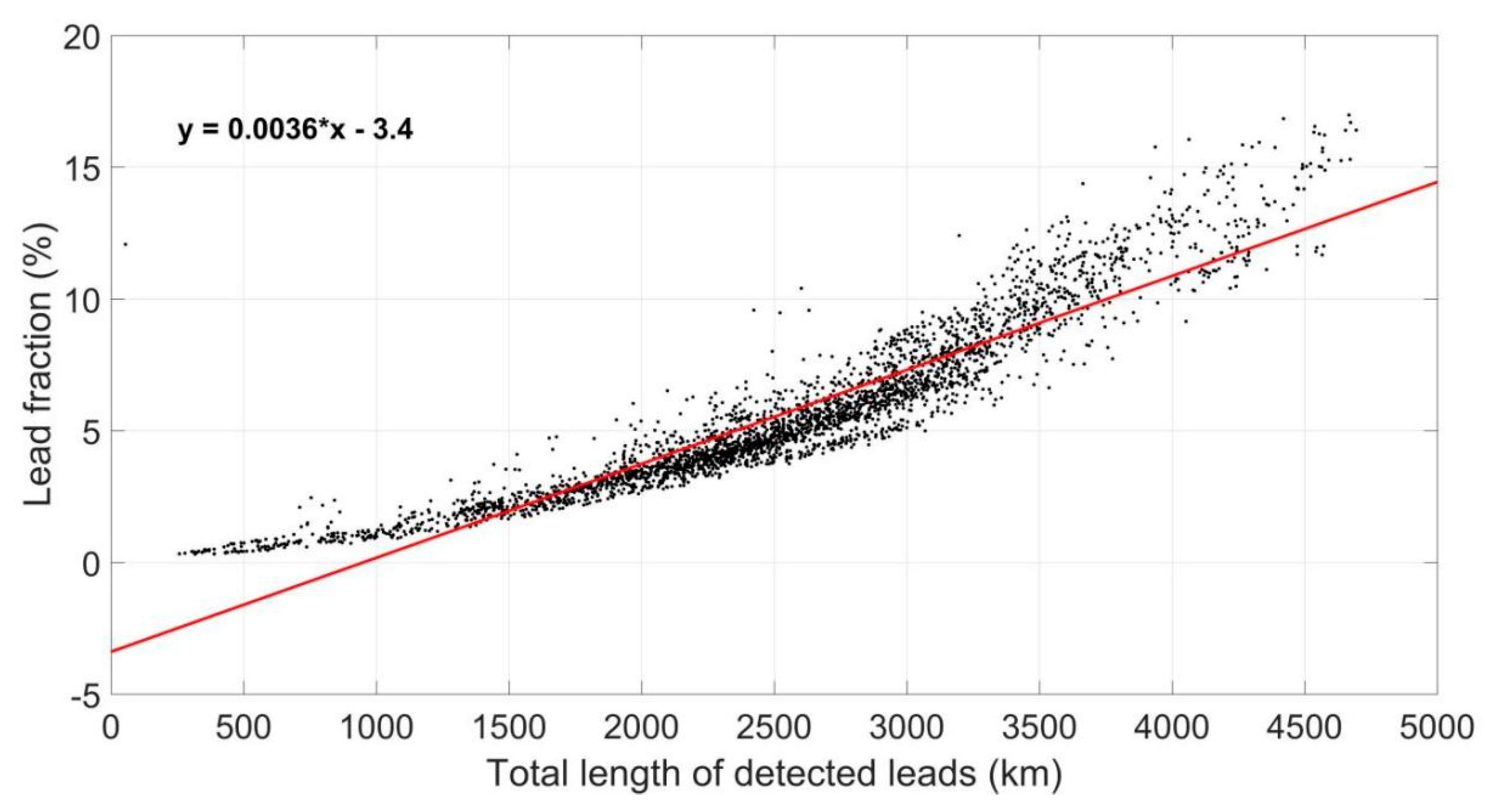
- Calculate the lead fraction (LF) following Equation (3). The lead fraction is defined as the area fraction of thin ice compared to the area fraction of other ice classes.
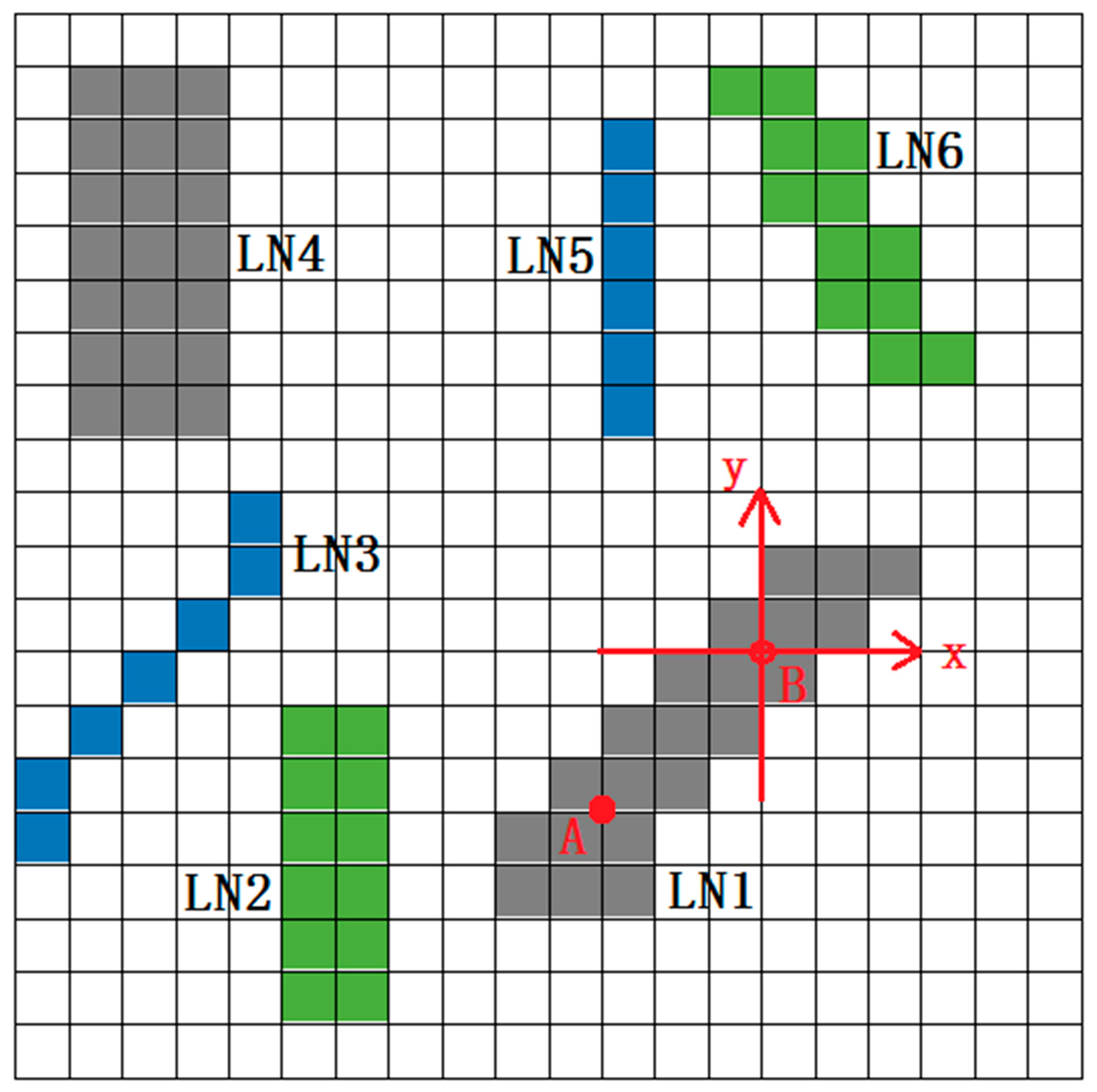
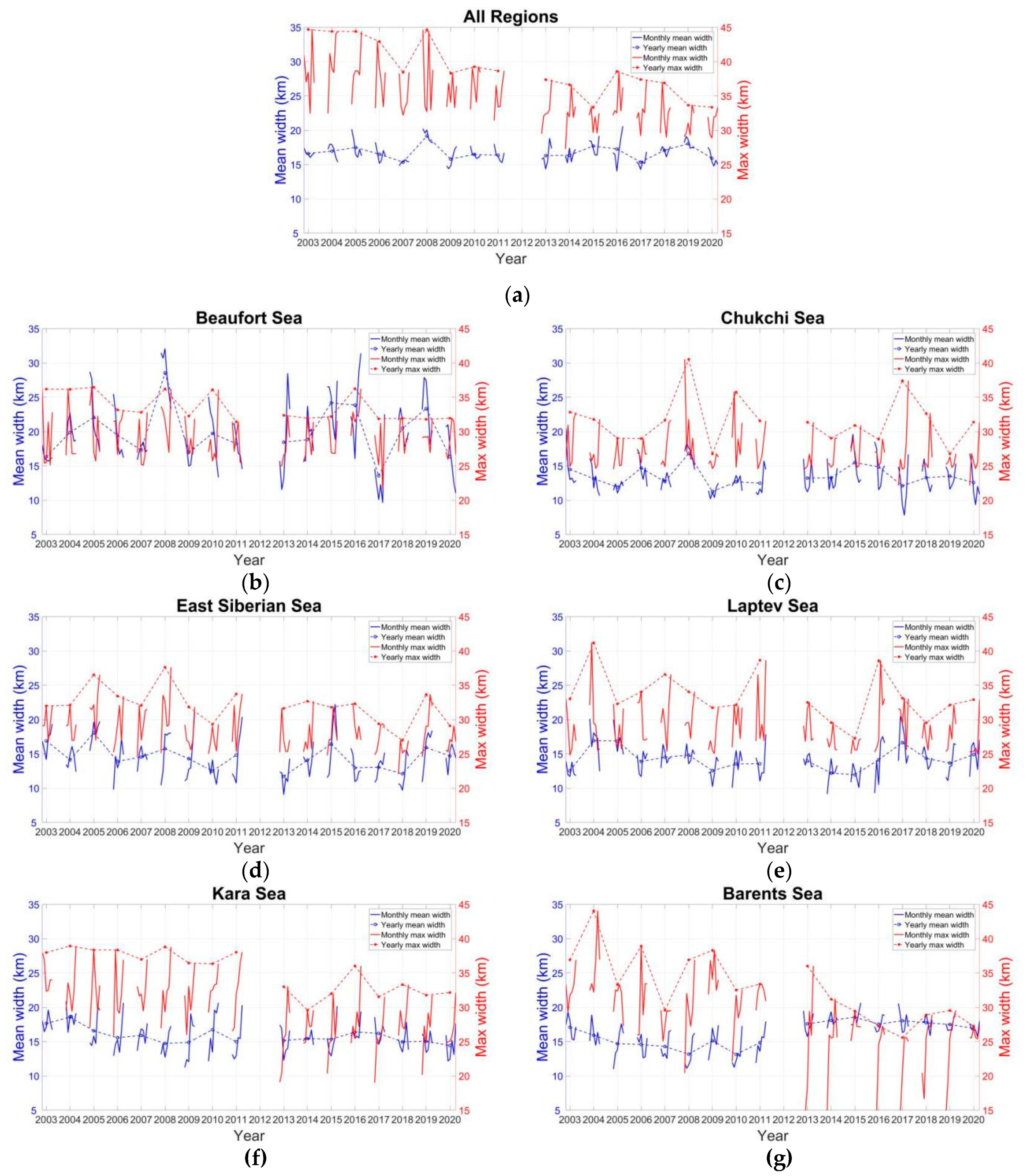
3.2. Statistics of Lead Geometry
4. Results
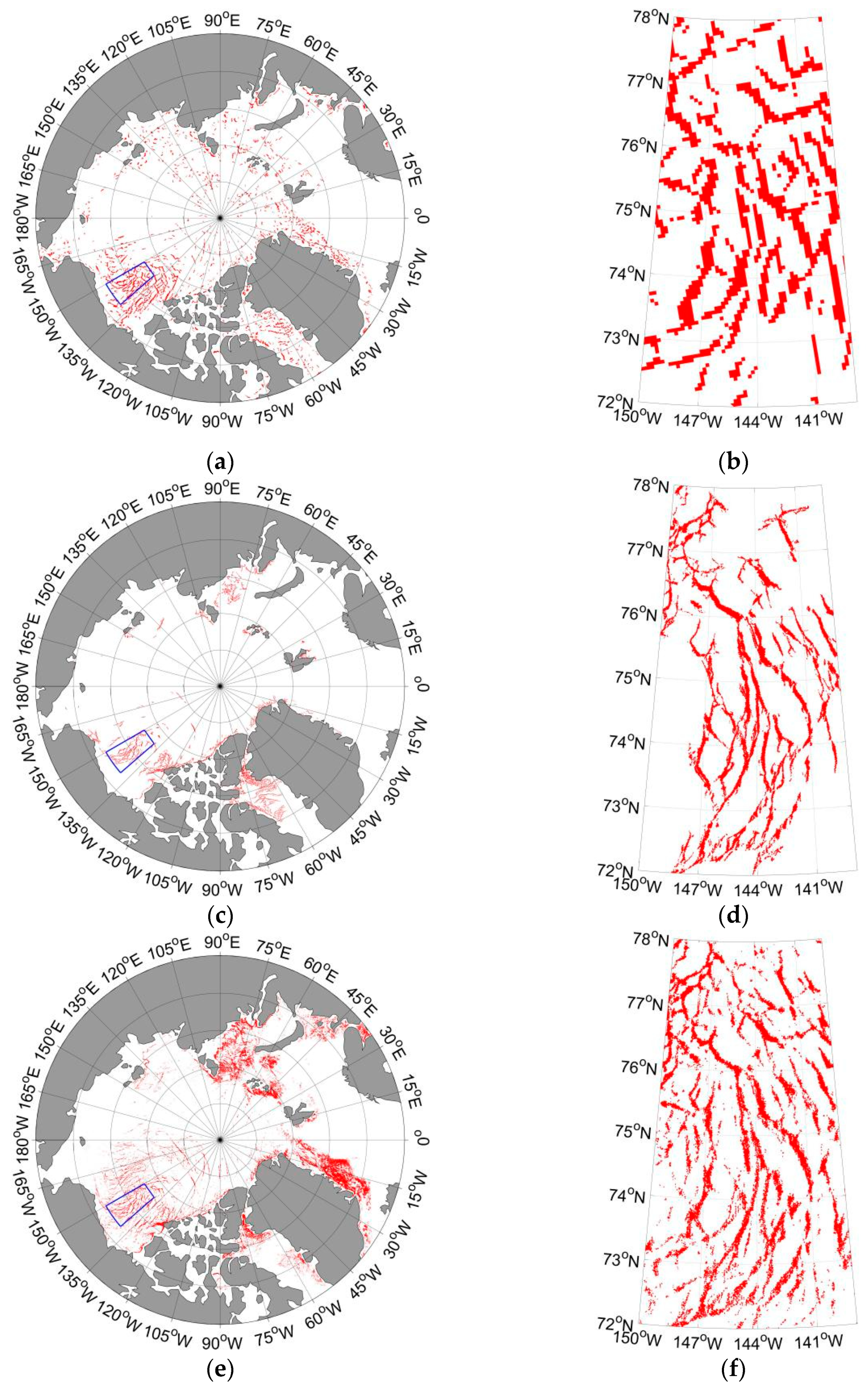
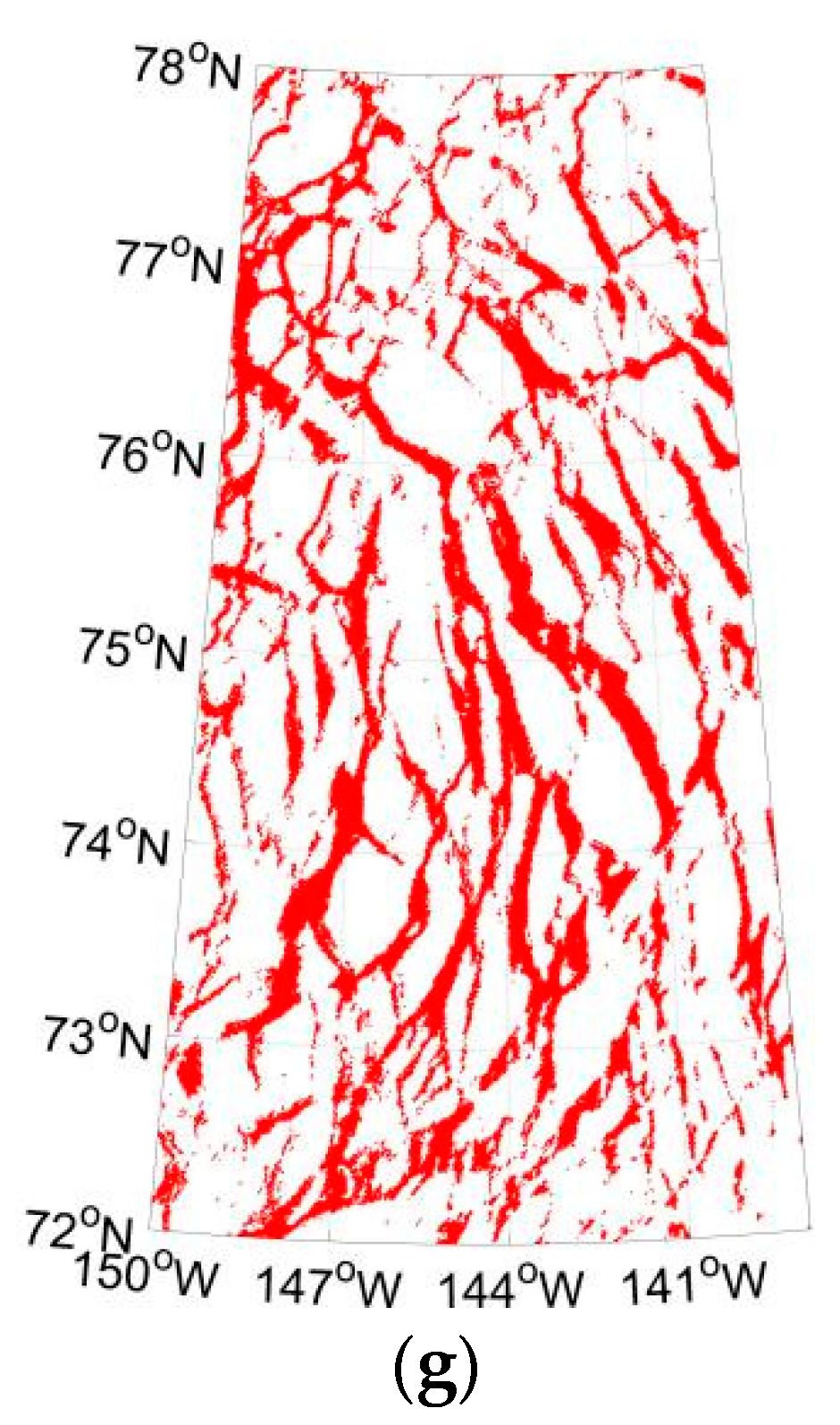
4.1. Validation of the Derived Sea Ice Leads on 3 April 2013
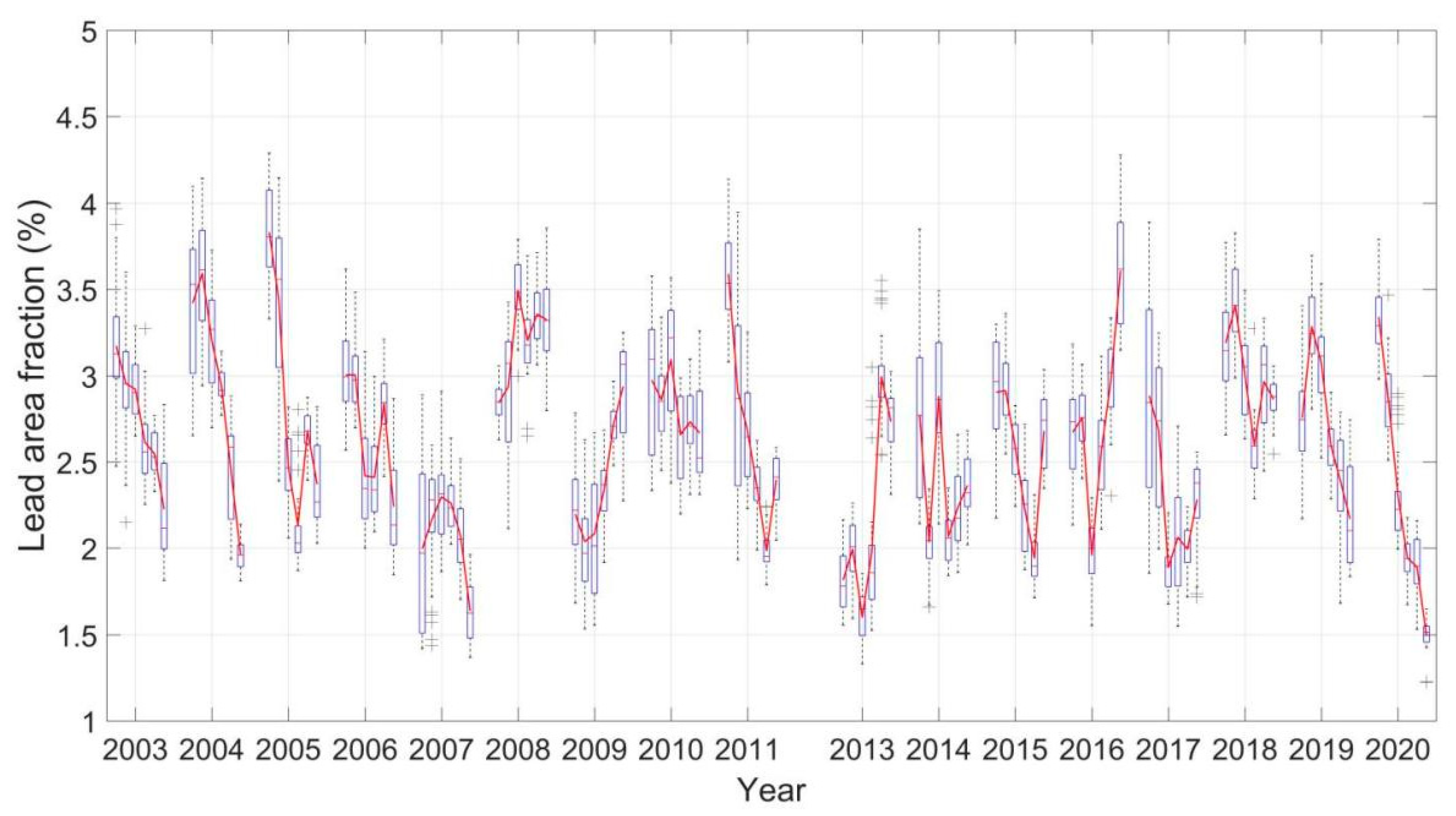
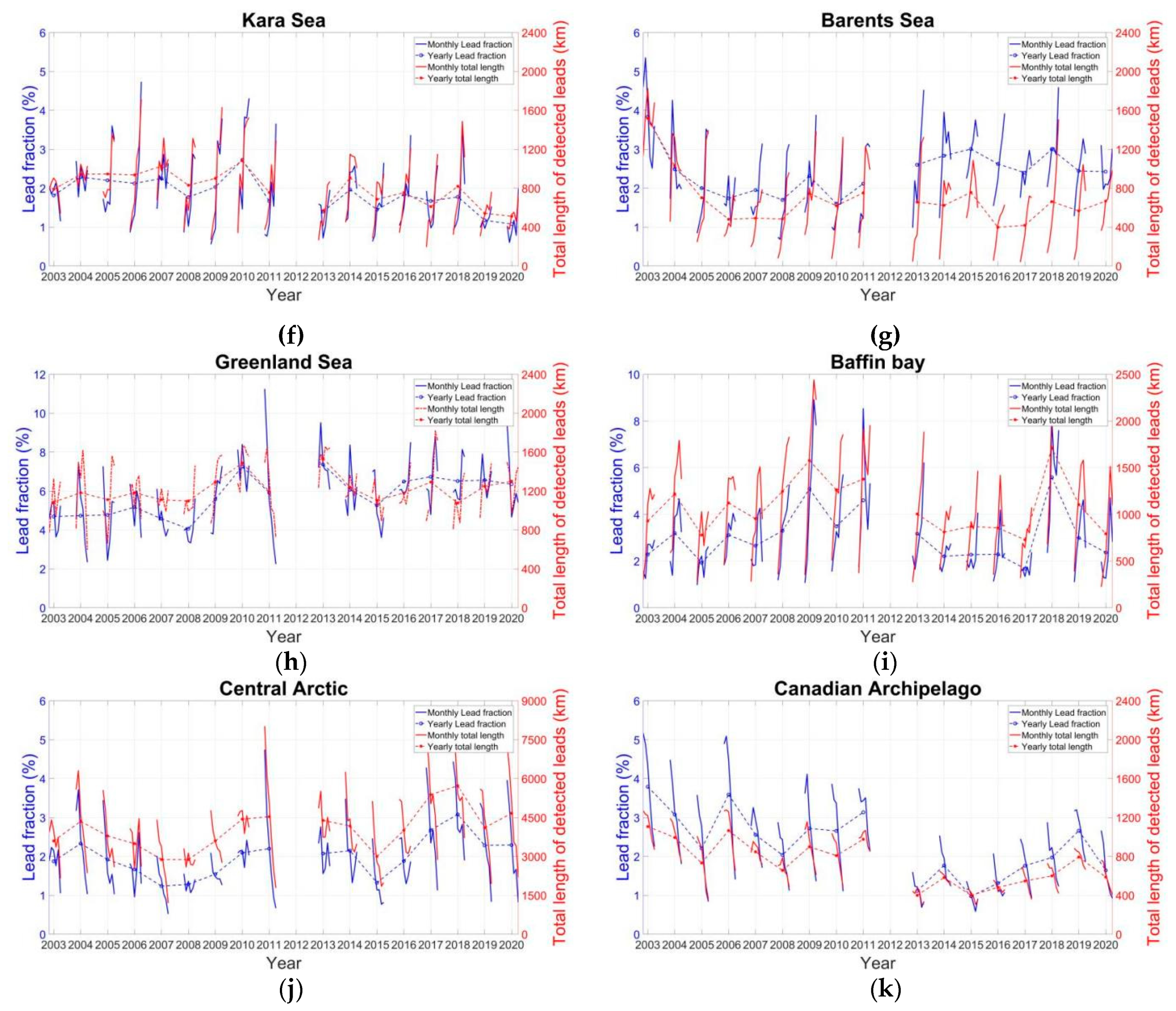
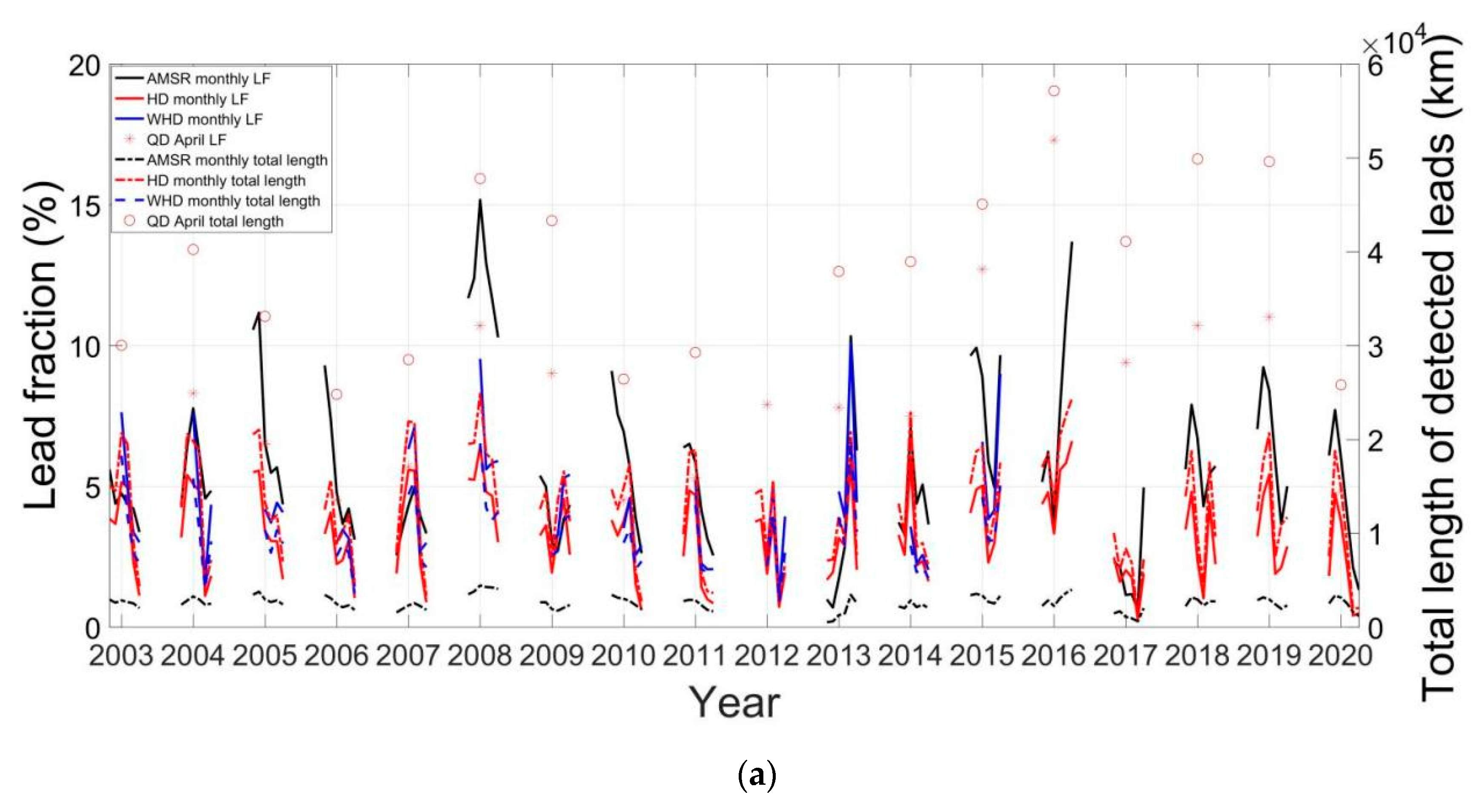
4.2. Long-Term Evolution of Lead Fraction and Geometry in the AMSR Family Data
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Parkinson, C.L.; Cavalieri, D.J.; Gloersen, P.; Zwally, H.J.; Comiso, J.C. Arctic Sea ice extents, areas, and trends, 1978–1996. J. Geophys. Res. Earth Surf. 1999, 104, 20837–20856. [Google Scholar] [CrossRef]
- Comiso, J.C.; Parkinson, C.L.; Gersten, R.; Stock, L. Accelerated decline in the Arctic Sea ice cover. Geophys. Res. Lett. 2008, 35, L01703. [Google Scholar] [CrossRef] [Green Version]
- Kwok, R.; Sulsky, D. Arctic Ocean Sea ice thickness and kinematics: Satellite retrievals and modeling. Oceanography 2010, 23, 134–143. [Google Scholar] [CrossRef]
- Lindsay, R.; Schweiger, A. Arctic Sea ice thickness loss determined using subsurface, aircraft, and satellite observations. Cryosphere 2015, 9, 269–283. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Song, M.; Horton, R.M.; Hu, Y. Reducing spread in climate model projections of a September ice-free Arctic. Proc. Natl. Acad. Sci. USA 2013, 110, 12571–12576. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lindsay, R.W.; Rothrock, D.A. Arctic Sea ice leads from advanced very high resolution radiometer images. J. Geophys. Res. Earth Surf. 1995, 100, 4533–4544. [Google Scholar] [CrossRef]
- Inoue, J.; Kawashima, M.; Fujiyoshi, Y.; Wakatsuchi, M. Aircraft observations of air-mass modification over the sea of Okhotsk during seaice growth. Bound. Layer Meteorol. 2005, 117, 111–129. [Google Scholar] [CrossRef]
- Barry, R.G.; Serreze, M.C.; Maslanik, J.A.; Preller, R.H. The Arctic Sea ice climate system: Observations and modeling. Rev. Geophys. 1993, 31, 397–422. [Google Scholar]
- Miles, M.W.; Barry, R.G. A 5-year satellite climatology of winter sea ice leads in the western Arctic. J. Geophys. Res. Earth Surf. 1998, 103, 21723–21734. [Google Scholar] [CrossRef]
- Makshtas, A.P. The Heat Budget of Arctic Ice in the Winter; International Glaciological Society: Cambridge, UK, 1991; p. 77. [Google Scholar]
- Eisen, O.; Kottmeier, C. On the importance of leads in sea ice to the energy balance and ice formation in the Weddell Sea. J. Geophys. Res. Earth Surf. 2000, 105, 14045–14060. [Google Scholar] [CrossRef]
- Lüpkes, C.; Vihma, T.; Birnbaum, G.; Wacker, U. Influence of leads in sea ice on the temperature of the atmospheric boundary layer during polar night. Geophys. Res. Lett. 2008, 35, 03805. [Google Scholar] [CrossRef] [Green Version]
- Marcq, S.; Weiss, J. Influence of sea ice lead-width distribution on turbulent heat transfer between the ocean and the atmosphere. Cryosphere 2012, 6, 143–156. [Google Scholar] [CrossRef] [Green Version]
- Tetzlaff, A.; Lüpkes, C.; Hartmann, J. Aircraft-based observations of atmospheric boundary-layer modification over Arctic leads. Q. J. R. Meteorol. Soc. 2015, 141, 2839–2856. [Google Scholar] [CrossRef]
- Chechin, D.G.; Makhotina, I.A.; Lüpkes, C.; Makshtas, A.P. Effect of wind speed and leads on clear-sky cooling over Arctic sea ice during polar night. J. Atmos. Sci. 2019, 76, 2481–2503. [Google Scholar] [CrossRef]
- Li, X.; Krueger, S.K.; Strong, C.; Mace, G.G.; Benson, S. Midwinter Arctic leads form and dissipate low clouds. Nat. Commun. 2020, 11, 1–8. [Google Scholar]
- Michaelis, J.; Lüpkes, C.; Schmitt, A.U.; Hartmann, J. Modelling and parametrization of the convective flow over leads in sea ice and comparison with airborne observations. Q. J. R. Meteorol. Soc. 2021, 147, 914–943. [Google Scholar] [CrossRef]
- Hartmann, J.; Kottmeier, C.; Wamser, C.; Augstein, E. The Polar Oceans and Their Role in Shaping the Global Environment. In Aircraft Measured Atmospheric Momentum, Heat and Radiation Fluxes over Arctic Sea Ice; Johannessen, O.M., Muench, R.D., Overland, J.E., Eds.; American Geophysical Union Geophysical Monograph Series; American Geophysical Union: Washington, DC, USA, 1994; Volume 85, pp. 443–454. [Google Scholar]
- Ruffieux, D.; Persson, P.O.G.; Fairall, C.W.; Wolfe, D.E. Ice pack and lead surface energy budgets during LEADEX. J. Geophys. Res. 1995, 100, 4593–4612. [Google Scholar] [CrossRef]
- Paluch, I.R.; Lenschow, D.H.; Wang, Q. The Arctic boundary layer in the fall season over open and frozen sea. J. Geophys. Res. 1997, 102, 25955–25971. [Google Scholar] [CrossRef] [Green Version]
- Wensnahan, M.; Maykut, G.; Grenfell, T.; Winebrenner, D. Passive microwave remote sensing of thin sea ice using principal component analysis. J. Geophys. Res. 1993, 98, 12453–12468. [Google Scholar] [CrossRef]
- Cavalieri, D. A microwave technique for mapping thin sea ice. J. Geophys. Res. Ocean. 1994, 99, 12561–12572. [Google Scholar] [CrossRef]
- Jacobi, H.; Kaleschke, L.; Richter, A.; Rozanov, A.; Burrows, J.P. Observation of a fast ozone loss in the marginal ice zone of the Arctic Ocean. J. Geophys. Res. Atmos. 2006, 111, D15309. [Google Scholar] [CrossRef] [Green Version]
- Röhrs, J.; Kaleschke, L. An algorithm to detect sea ice leads using AMSR-E passive microwave imagery. Cryosphere 2012, 6, 343–352. [Google Scholar] [CrossRef] [Green Version]
- Bröhan, D.; Kaleschke, L. A Nine-Year Climatology of Arctic Sea Ice Lead Orientation and Frequency from AMSR-E. Remote Sens. 2014, 6, 1451–1475. [Google Scholar] [CrossRef] [Green Version]
- Willmes, S.; Heinemann, G. Daily Pan-Arctic Sea-Ice Lead Maps for 2003–2015, with Links to Maps in NetCDF Format. PANGAEA, 2015. Available online: https://doi.pangaea.de/10.1594/PANGAEA.854411 (accessed on 15 August 2020).
- Willmes, S.; Heinemann, G. Pan-Arctic lead detection from MODIS thermal infrared imagery. Ann. Glaciol. 2015, 56, 29–37. [Google Scholar] [CrossRef] [Green Version]
- Willmes, S.; Heinemann, G. Sea-ice wintertime lead frequencies and regional characteristics in the Arctic, 2003–2015. Remote Sens. 2016, 8, 4. [Google Scholar] [CrossRef] [Green Version]
- Reiser, F.; Willmes, S.; Heinemann, G. A new algorithm for daily sea ice lead identification in the arctic and antarctic winter from thermal-infrared satellite imagery. Remote Sens. 2020, 12, 1957. [Google Scholar] [CrossRef]
- Hoffman, J.; Ackerman, S.; Liu, Y.; Key, J. Sea-Ice Leads in the Arctic Algorithm Theoretical Basis Document; Cooperative Institute for Meteorological Satellite Studies, University of Wisconsin-Madison NOAA/NESDIS: Madison, WI, USA, 2018; pp. 4–22. [Google Scholar]
- Hoffman, J.; Ackerman, S.; Liu, Y.; Key, J. The detection and characterization of Arctic Sea ice leads with satellite imagers. Remote Sens. 2019, 11, 521. [Google Scholar] [CrossRef] [Green Version]
- Qu, M.; Pang, X.; Zhao, X.; Zhang, J.; Ji, Q.; Fan, P. Estimation of turbulent heat flux over leads using satellite thermal images. Cryosphere 2019, 13, 1565–1582. [Google Scholar] [CrossRef] [Green Version]
- Qu, M.; Pang, X.; Zhao, X.; Lei, R.; Ji, Q.; Liu, Y.; Chen, Y. Spring leads in the Beaufort Sea and its interannual trend using Terra/MODIS thermal imagery. Remote Sens. Environ. 2021, 256, 112342. [Google Scholar] [CrossRef]
- Hoffman, J.; Ackerman, S.; Liu, Y.; Key, J.; McConnell, I. Application of a convolutional neural network for the detection of sea ice leads. Remote Sens. 2021, 13, 4571. [Google Scholar] [CrossRef]
- Kern, S.; Kaleschke, L.; Clausi, D.A. A comparison of two 85-GHz SSM/I ice concentration algorithms with AVHRR and ERS-2 SAR imagery. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2294–2306. [Google Scholar] [CrossRef]
- Zakharova, E.A.; Fleury, S.; Guerreiro, K.; Willmes, S.; Rémy, F.; Kouraev, A.V.; Heinemann, G. Sea ice leads detection using Saral/Altika altimeter. Mar. Geod. 2015, 38, 522–533. [Google Scholar] [CrossRef]
- Wernecke, A.; Kaleschke, L. Lead detection in arctic sea ice from Cryosat-2: Quality assessment, lead area fraction and width distribution. Cryosphere 2015, 9, 1955–1968. [Google Scholar] [CrossRef] [Green Version]
- Ivanova, N.; Rampal, P.; Bouillon, S. Error assessment of satellite-derived lead fraction in the arctic. Cryosphere 2016, 10, 585–595. [Google Scholar] [CrossRef] [Green Version]
- Murashkin, D.; Spreen, G.; Huntemann, M.; Dierking, W. Method for detection of leads from Sentinel-1 SAR images. Ann. Glaciol. 2018, 59, 124–136. [Google Scholar] [CrossRef] [Green Version]
- Fetterer, F.; Holyer, R. A Hough Transform Technique for Extracting Lead Features from Sea Ice Imagery; Naval Ocean R&D Activity: Stennis Space Center, MS, USA, 1989; pp. 1125–1128. [Google Scholar]
- Wang, Q.; Danilov, S.; Jung, T.; Kaleschke, L.; Wernecke, A. Sea ice leads in the Arctic Ocean: Model assessment, interannual variability and trends. Geophys. Res. Lett. 2016, 43, 7019–7027. [Google Scholar] [CrossRef] [Green Version]
- Fetterer, F.; Savoie, M.; Helfrich, S.; Clemente-Colón, P. Multisensor Analyzed Sea Ice Extent—Northern Hemisphere (MASIE-NH); Version 1; National Snow and Ice Data Center: Boulder, CO, USA, 2010. [Google Scholar] [CrossRef]




| Period. | All Regions | Beaufort Sea | Chukchi Sea | East Siberian Sea | Laptev Sea | Kara Sea | Barents Sea | Greenland Sea | Baffin Bay | Central Arctic | Canadian Archipelago |
|---|---|---|---|---|---|---|---|---|---|---|---|
| MW1 (km) | MW1 (km) | MW1 (km) | MW1 (km) | MW1 (km) | MW1 (km) | MW1 (km) | MW1 (km) | MW1 (km) | MW1 (km) | MW1 (km) | |
| MW2 (km) | MW2 (km) | MW2 (km) | MW2 (km) | MW2 (km) | MW2 (km) | MW2 (km) | MW2 (km) | MW2 (km) | MW2 (km) | MW2 (km) | |
| TL (103 km) | TL (103 km) | TL (103 km) | TL (103 km) | TL (103 km) | TL (103 km) | TL (103 km) | TL (103 km) | TL (103 km) | TL (103 km) | TL (103 km) | |
| LF (%) | LF (%) | LF (%) | LF (%) | LF (%) | LF (%) | LF (%) | LF (%) | LF (%) | LF (%) | LF (%) | |
| 2002/ 2003 | 44.7 | 36.2 | 32.8 | 32.0 | 33.0 | 38.0 | 36.9 | 44.7 | 36.2 | 40.9 | 31.8 |
| 16.6 | 16.3 | 14.5 | 16.9 | 12.6 | 17.6 | 17.1 | 19.1 | 14.4 | 15.6 | 20.4 | |
| 16.2 | 2.60 | 1.67 | 1.91 | 0.68 | 0.79 | 1.52 | 1.09 | 0.93 | 3.60 | 1.11 | |
| 2.73 | 4.45 | 3.01 | 3.35 | 1.12 | 1.81 | 3.84 | 4.69 | 2.28 | 1.87 | 3.79 | |
| 2003/ 2004 | 44.4 | 36.2 | 31.8 | 32.1 | 41.2 | 38.9 | 44.1 | 44.4 | 32.3 | 33.4 | 31.6 |
| 17.0 | 19.9 | 13.1 | 14.1 | 16.9 | 18.6 | 15.9 | 18.9 | 15.5 | 15.5 | 18.3 | |
| 16.7 | 2.72 | 1.24 | 1.36 | 1.49 | 0.94 | 1.03 | 1.18 | 1.22 | 4.35 | 0.99 | |
| 2.91 | 5.69 | 2.08 | 2.01 | 3.36 | 2.28 | 2.49 | 4.73 | 3.20 | 2.33 | 3.07 | |
| 2004/ 2005 | 44.4 | 36.5 | 29.0 | 36.5 | 32.3 | 38.4 | 33.3 | 44.4 | 33.2 | 37.0 | 33.8 |
| 17.5 | 22.1 | 11.9 | 18.1 | 16.9 | 16.6 | 14.7 | 18.3 | 14.7 | 14.5 | 18.0 | |
| 15.1 | 3.02 | 0.87 | 1.71 | 1.28 | 0.95 | 0.70 | 1.11 | 0.78 | 3.79 | 0.73 | |
| 2.81 | 7.30 | 1.28 | 3.20 | 2.86 | 2.20 | 2.00 | 4.77 | 1.92 | 1.92 | 2.20 | |
| 2005/ 2006 | 42.9 | 33.1 | 29.0 | 33.4 | 34.0 | 38.4 | 38.9 | 42.9 | 32.1 | 39.0 | 33.2 |
| 16.5 | 19.5 | 14.7 | 13.0 | 13.9 | 15.6 | 14.6 | 18.8 | 15.9 | 13.9 | 19.2 | |
| 15.0 | 2.54 | 1.63 | 1.27 | 0.94 | 0.94 | 0.48 | 1.18 | 1.12 | 3.49 | 1.07 | |
| 2.64 | 5.41 | 3.07 | 1.91 | 1.67 | 2.12 | 1.74 | 5.17 | 3.11 | 1.67 | 3.59 | |
| 2006/ 2007 | 38.4 | 32.8 | 31.7 | 32.1 | 36.6 | 37.0 | 29.6 | 38.3 | 33.4 | 38.4 | 31.6 |
| 15.4 | 17.3 | 12.7 | 14.5 | 14.5 | 15.9 | 14.3 | 17.8 | 15.2 | 12.8 | 17.8 | |
| 12.5 | 2.07 | 0.92 | 1.21 | 0.82 | 1.03 | 0.49 | 1.11 | 0.95 | 2.88 | 0.85 | |
| 2.06 | 3.76 | 1.46 | 1.86 | 1.51 | 2.25 | 1.95 | 4.57 | 2.65 | 1.24 | 2.55 | |
| 2007/ 2008 | 44.6 | 36.2 | 40.5 | 37.6 | 34.1 | 38.8 | 36.9 | 44.6 | 32.7 | 33.5 | 31.8 |
| 19.2 | 28.6 | 16.8 | 15.8 | 14.8 | 14.7 | 13.2 | 17.0 | 15.7 | 13.4 | 19.0 | |
| 15.6 | 4.05 | 1.48 | 1.61 | 1.10 | 0.83 | 0.48 | 1.10 | 1.25 | 2.88 | 0.66 | |
| 3.18 | 12.35 | 3.20 | 2.91 | 2.10 | 1.77 | 1.70 | 4.06 | 3.29 | 1.28 | 2.03 | |
| 2008/ 2009 | 38.3 | 32.3 | 26.8 | 31.8 | 31.7 | 36.5 | 38.3 | 33.4 | 33.4 | 33.4 | 33.4 |
| 15.8 | 17.0 | 11.3 | 14.3 | 12.6 | 14.9 | 15.1 | 19.4 | 18.2 | 12.9 | 17.1 | |
| 14.3 | 2.23 | 0.62 | 0.96 | 1.13 | 0.90 | 0.75 | 1.29 | 1.58 | 3.60 | 0.90 | |
| 2.37 | 4.05 | 0.85 | 1.49 | 1.89 | 2.03 | 2.31 | 5.58 | 5.09 | 1.54 | 2.72 | |
| 2009/ 2010 | 39.3 | 36.1 | 35.8 | 29.3 | 32.1 | 36.3 | 32.5 | 33.3 | 36.5 | 39.0 | 31.9 |
| 16.5 | 19.7 | 12.7 | 12.5 | 13.5 | 16.7 | 13.1 | 21.2 | 15.3 | 13.9 | 18.8 | |
| 16.1 | 2.77 | 1.46 | 1.27 | 0.61 | 1.08 | 0.62 | 1.49 | 1.26 | 4.43 | 0.81 | |
| 2.82 | 5.97 | 2.31 | 1.68 | 1.08 | 2.73 | 1.60 | 7.25 | 3.48 | 2.09 | 2.65 | |
| 2010/ 2011 | 38.6 | 31.4 | 31.6 | 33.7 | 38.6 | 38.0 | 33.4 | 32.4 | 32.7 | 34.1 | 29.6 |
| 16.4 | 18.2 | 12.5 | 14.8 | 13.6 | 15.0 | 14.9 | 19.4 | 16.2 | 13.3 | 19.0 | |
| 15.0 | 2.40 | 0.96 | 1.08 | 0.68 | 0.76 | 0.75 | 1.20 | 1.38 | 4.53 | 0.98 | |
| 2.64 | 4.76 | 1.51 | 1.79 | 1.21 | 1.67 | 2.11 | 5.91 | 4.60 | 2.20 | 3.13 | |
| 2012/ 2013 | 37.4 | 32.4 | 31.4 | 31.6 | 32.5 | 33.0 | 36.0 | 32.4 | 37.4 | 29.6 | 29.3 |
| 16.3 | 18.4 | 13.2 | 11.7 | 14.0 | 15.2 | 17.6 | 21.3 | 18.5 | 13.6 | 15.6 | |
| 12.2 | 1.64 | 0.57 | 0.57 | 0.71 | 0.57 | 0.66 | 1.54 | 1.00 | 4.39 | 0.40 | |
| 2.15 | 3.81 | 0.86 | 0.70 | 1.28 | 1.40 | 2.60 | 7.37 | 3.17 | 2.07 | 1.11 | |
| 2013/ 2014 | 36.6 | 32.0 | 29.0 | 32.7 | 29.6 | 29.6 | 31.2 | 36.6 | 32.5 | 33.4 | 29.2 |
| 16.4 | 18.8 | 13.3 | 14.1 | 12.2 | 15.4 | 18.1 | 20.5 | 16.3 | 14.9 | 16.7 | |
| 13.4 | 2.27 | 1.13 | 1.04 | 0.47 | 0.91 | 0.62 | 1.24 | 0.81 | 4.17 | 0.58 | |
| 2.35 | 4.53 | 1.87 | 1.50 | 0.79 | 1.96 | 2.83 | 6.07 | 2.20 | 2.15 | 1.77 | |
| 2014/ 2015 | 33.3 | 32.2 | 30.9 | 31.8 | 27.2 | 32.0 | 29.5 | 33.3 | 30.9 | 32.0 | 26.9 |
| 17.7 | 24.2 | 15.5 | 16.4 | 12.0 | 15.3 | 18.6 | 19.7 | 15.4 | 13.0 | 14.0 | |
| 13.4 | 3.14 | 1.53 | 1.23 | 0.54 | 0.68 | 0.76 | 1.10 | 0.87 | 2.99 | 0.40 | |
| 2.51 | 8.16 | 3.10 | 2.15 | 0.86 | 1.45 | 3.00 | 5.26 | 2.27 | 1.32 | 0.97 | |
| 2015/ 2016 | 38.6 | 36.3 | 28.9 | 32.3 | 38.6 | 36.0 | 27.2 | 32.4 | 33.3 | 32.5 | 25.4 |
| 17.3 | 23.9 | 14.8 | 13.0 | 14.1 | 16.4 | 17.5 | 20.7 | 16.1 | 13.7 | 15.3 | |
| 14.3 | 3.01 | 1.42 | 1.24 | 0.80 | 0.75 | 0.40 | 1.18 | 0.85 | 4.00 | 0.48 | |
| 2.72 | 7.94 | 2.76 | 1.70 | 1.59 | 1.83 | 2.62 | 6.49 | 2.29 | 1.88 | 1.31 | |
| 2016/ 2017 | 37.4 | 31.9 | 37.4 | 29.4 | 33.1 | 31.5 | 25.6 | 32.5 | 28.5 | 32.6 | 26.9 |
| 15.4 | 13.6 | 12.1 | 13.1 | 16.6 | 16.2 | 18.0 | 20.9 | 13.8 | 13.7 | 17.1 | |
| 13.0 | 1.30 | 0.60 | 0.98 | 1.01 | 0.61 | 0.42 | 1.29 | 0.73 | 5.38 | 0.55 | |
| 2.26 | 2.06 | 0.99 | 1.33 | 2.20 | 1.67 | 2.39 | 6.73 | 1.67 | 2.68 | 1.76 | |
| 2017/ 2018 | 36.9 | 31.9 | 32.6 | 27.0 | 29.5 | 33.3 | 28.9 | 36.9 | 31.9 | 29.6 | 25.5 |
| 17.1 | 20.5 | 13.3 | 12.1 | 14.4 | 15.0 | 17.8 | 20.9 | 18.9 | 15.2 | 18.1 | |
| 15.7 | 2.69 | 0.99 | 0.70 | 0.56 | 0.82 | 0.66 | 1.08 | 1.71 | 5.72 | 0.60 | |
| 2.96 | 5.94 | 1.68 | 0.85 | 1.03 | 1.77 | 3.00 | 6.51 | 5.58 | 3.08 | 1.97 | |
| 2018/ 2019 | 33.7 | 31.8 | 26.8 | 33.7 | 32.1 | 31.8 | 29.5 | 32.5 | 31.8 | 29.6 | 27.2 |
| 18.0 | 23.3 | 13.5 | 15.9 | 13.7 | 15.0 | 17.5 | 20.3 | 16.7 | 15.8 | 18.3 | |
| 13.7 | 2.61 | 0.81 | 1.25 | 0.53 | 0.54 | 0.57 | 1.25 | 1.10 | 4.10 | 0.79 | |
| 2.70 | 6.54 | 1.33 | 2.11 | 0.99 | 1.17 | 2.44 | 6.56 | 2.99 | 2.28 | 2.66 | |
| 2019/ 2020 | 33.3 | 31.9 | 31.4 | 29.1 | 32.9 | 32.2 | 27.3 | 31.9 | 26.8 | 33.3 | 29.5 |
| 15.9 | 16.3 | 12.6 | 14.7 | 14.9 | 14.4 | 16.9 | 20.5 | 16.4 | 13.9 | 15.2 | |
| 13.0 | 2.39 | 0.58 | 0.91 | 0.52 | 0.51 | 0.67 | 1.30 | 0.79 | 4.66 | 0.59 | |
| 2.27 | 4.55 | 1.20 | 1.39 | 0.99 | 1.08 | 2.42 | 6.35 | 2.36 | 2.29 | 1.64 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Liu, J.; Qu, M.; Zhang, Z.; Liang, X. An Analysis of Arctic Sea Ice Leads Retrieved from AMSR-E/AMSR2. Remote Sens. 2022, 14, 969. https://doi.org/10.3390/rs14040969
Li M, Liu J, Qu M, Zhang Z, Liang X. An Analysis of Arctic Sea Ice Leads Retrieved from AMSR-E/AMSR2. Remote Sensing. 2022; 14(4):969. https://doi.org/10.3390/rs14040969
Chicago/Turabian StyleLi, Ming, Jiping Liu, Meng Qu, Zhanhai Zhang, and Xi Liang. 2022. "An Analysis of Arctic Sea Ice Leads Retrieved from AMSR-E/AMSR2" Remote Sensing 14, no. 4: 969. https://doi.org/10.3390/rs14040969
APA StyleLi, M., Liu, J., Qu, M., Zhang, Z., & Liang, X. (2022). An Analysis of Arctic Sea Ice Leads Retrieved from AMSR-E/AMSR2. Remote Sensing, 14(4), 969. https://doi.org/10.3390/rs14040969







