Cascaded U-Net with Training Wheel Attention Module for Change Detection in Satellite Images
Abstract
1. Introduction
- (1)
- A cascaded U-Net change detection model was proposed with ConvNeXT blocks, and with the help of a patch embedding layer more U-Nets can be cascaded.
- (2)
- A novel attention module was proposed to facilitate the training process of cascaded U-Nets which increases accuracy of the model without extra cost at inference time.
- (3)
- Extensive experiments on two change detection datasets validated the effectiveness and efficiency of the proposed method.
2. Materials and Methods
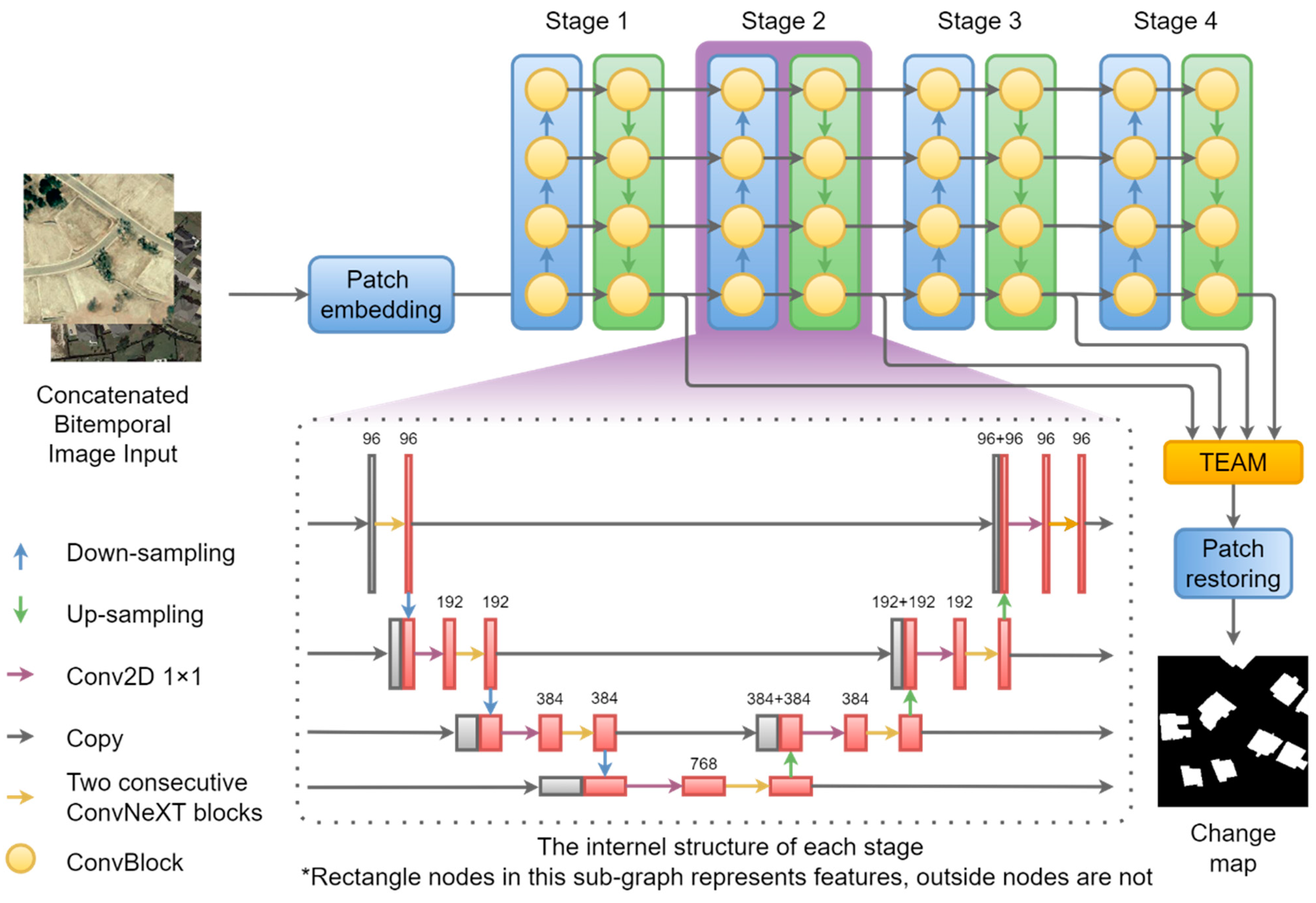
2.1. Overall Structure of Proposed Neural Network
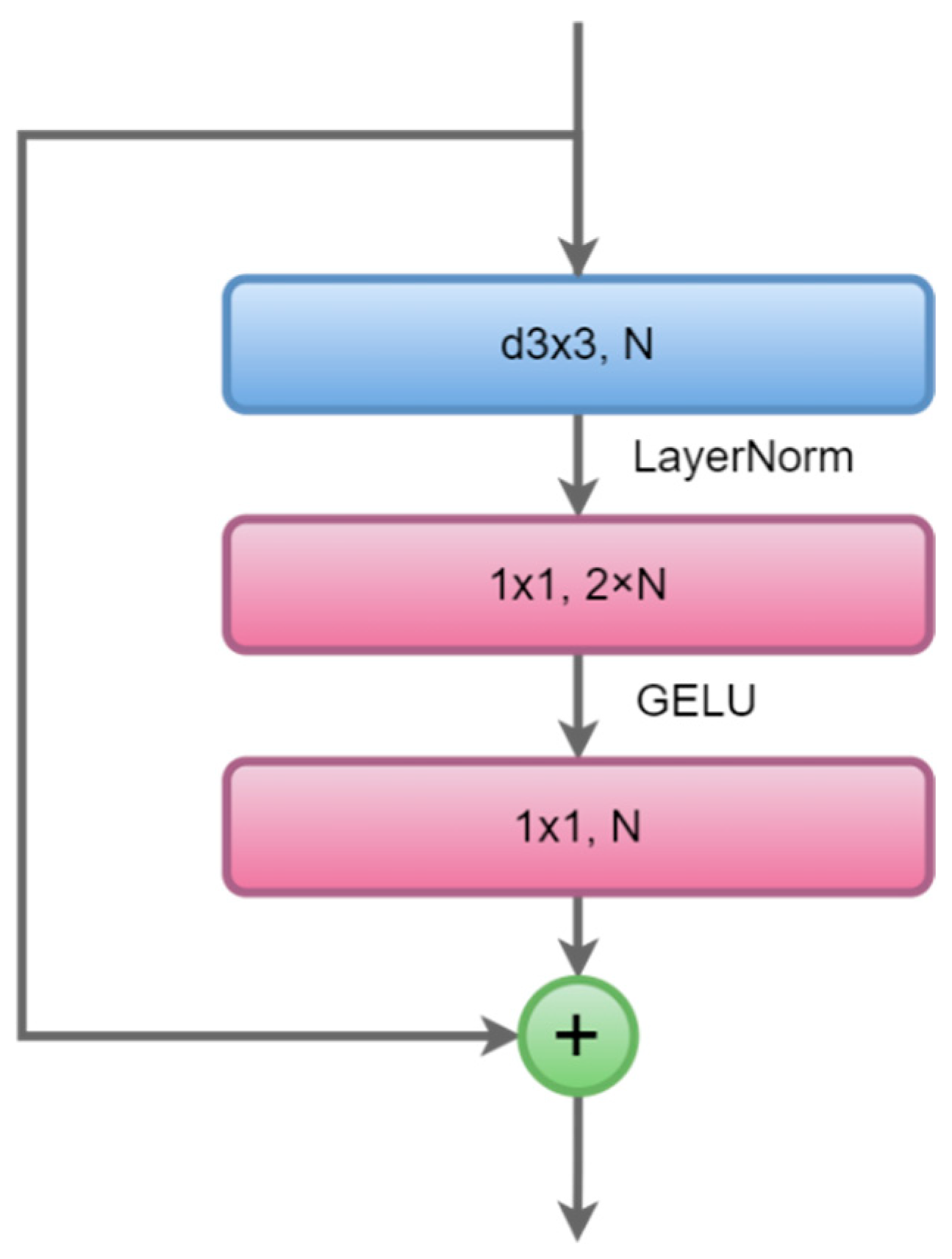
2.2. Details of Proposed Neural Network
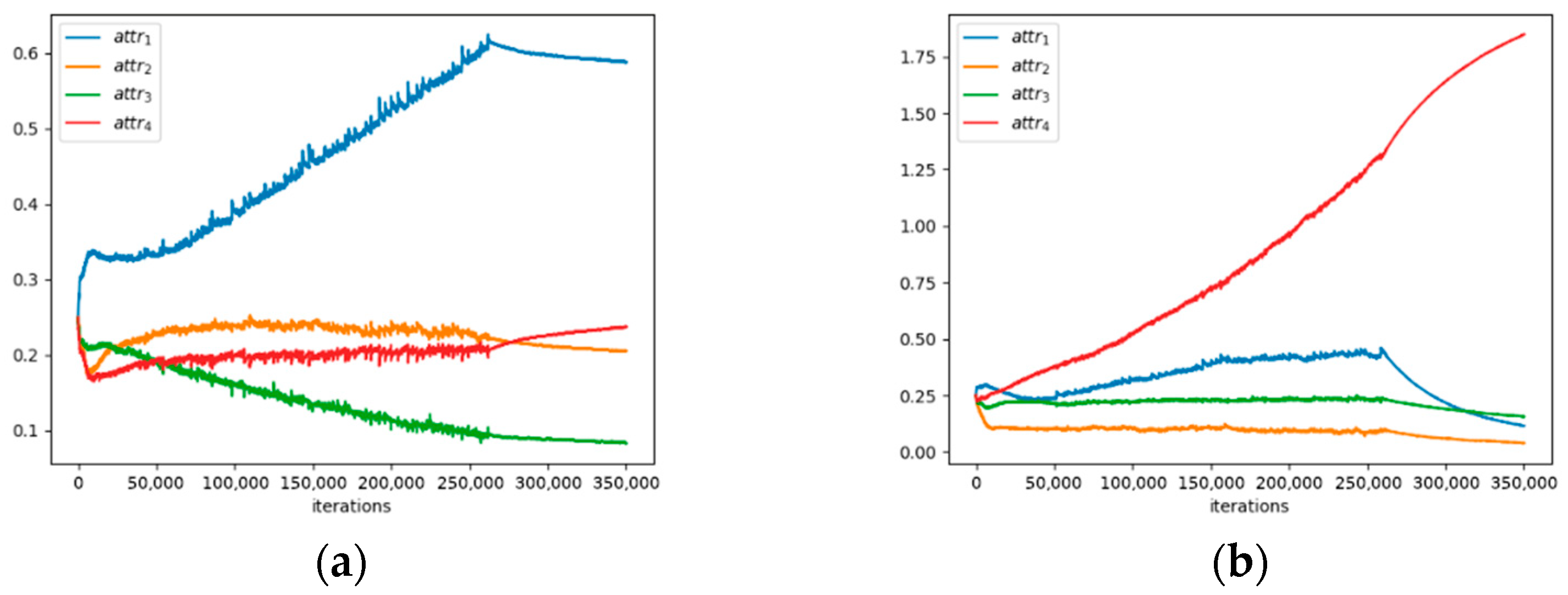
2.3. Training whEels Attention Module (TEAM)
| Algorithm 1: Weight shifting strategy of TEAM | |
| 1. | Input: = weights of different stages, = initial learning rate, = impact of shifting strategy |
| Output: = shifted weights | |
| 2. | begin |
| 3. | |
| 4. | for |
| 5. | |
| 6. | |
| 7. | end |
2.4. Loss Function
3. Experiments
3.1. Datasets and Evaluation Metrics
3.1.1. Datasets
3.1.2. Evaluation Metrics
3.2. Comparison Methods
3.3. Experimental Details
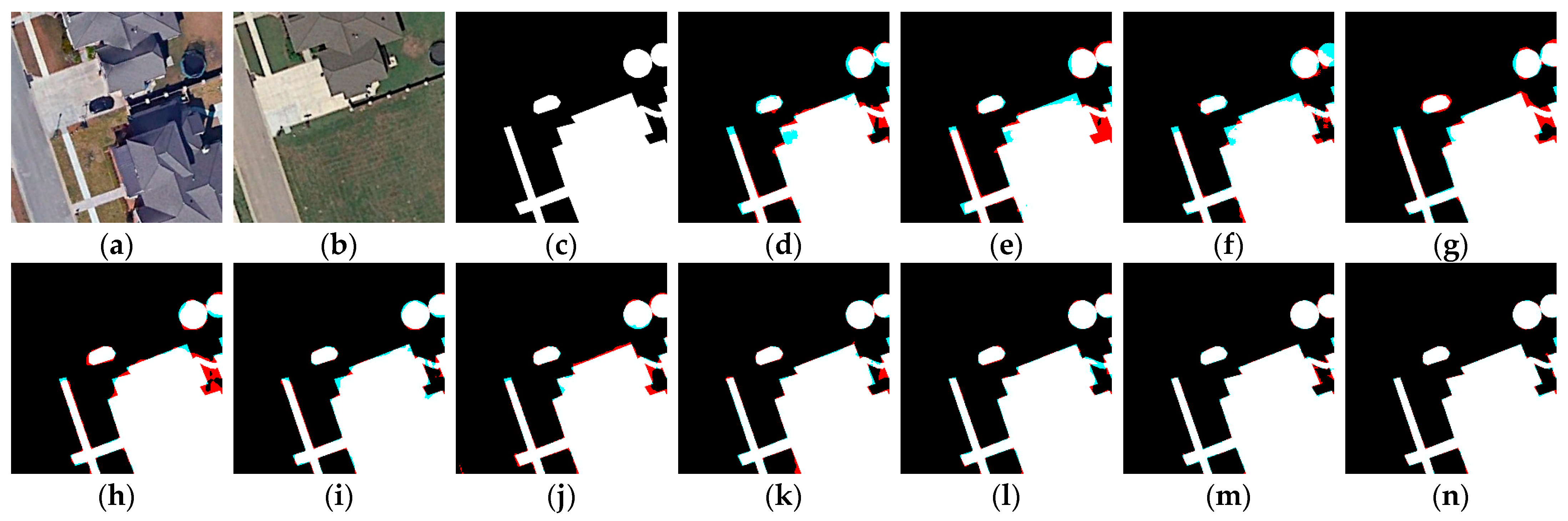
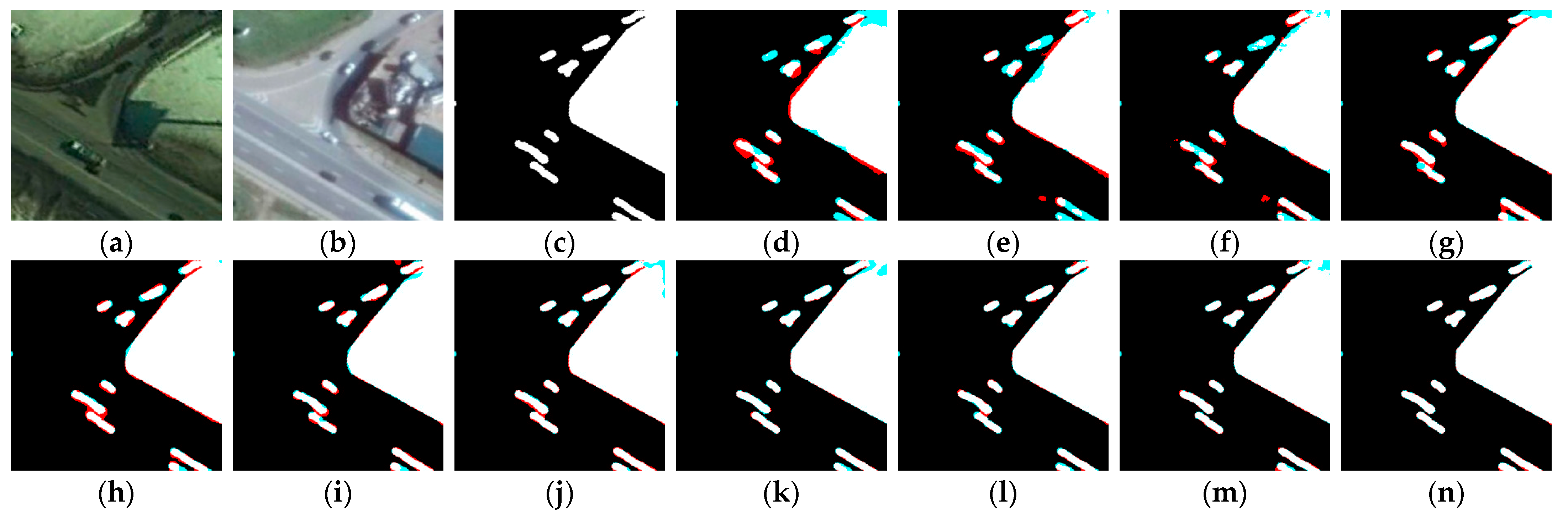
4. Experimental Results
4.1. Experimental Results on LEVIR-CD
4.2. Experimental Results on CCD
5. Discussion
5.1. Effectiveness of Cascaded Stages
5.2. Ablation Study
5.3. More Efficient Cascaded Stages
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mehrotra, A.; Singh, K.K.; Nigam, M.J.; Pal, K. Detection of tsunami-induced changes using generalized improved fuzzy radial basis function neural network. Nat. Hazards 2015, 77, 367–381. [Google Scholar] [CrossRef]
- Sublime, J.; Kalinicheva, E. Automatic post-disaster damage mapping using deep-learning techniques for change detection: Case study of the Tohoku tsunami. Remote Sens. 2019, 11, 1123. [Google Scholar] [CrossRef]
- Bennie, J.; Duffy, J.P.; Davies, T.W.; Correa-Cano, M.E.; Gaston, K.J. Global Trends in Exposure to Light Pollution in Natural Terrestrial Ecosystems. Remote Sens. 2015, 7, 2715–2730. [Google Scholar] [CrossRef]
- Chen, H.; Hua, Y.; Ren, Q.; Zhang, Y. Comprehensive analysis of regional human-driven environmental change with multitemporal remote sensing images using observed object-specified dynamic Bayesian network. J. Appl. Remote Sens. 2016, 10, 016021. [Google Scholar] [CrossRef]
- Khan, S.H.; He, X.; Porikli, F.; Bennamoun, M. Forest Change Detection in Incomplete Satellite Images with Deep Neural Networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5407–5423. [Google Scholar] [CrossRef]
- Solé Gómez, À.; Scandolo, L.; Eisemann, E. A learning approach for river debris detection. Int. J. Appl. Earth Obs. Geoinf. 2022, 107, 102682. [Google Scholar] [CrossRef]
- Chen, X.L.; Zhao, H.M.; Li, P.X.; Yin, Z.Y. Remote sensing image-based analysis of the relationship between urban heat island and land use/cover changes. Remote Sens. Environ. 2006, 104, 133–146. [Google Scholar] [CrossRef]
- Georg, I.; Blaschke, T.; Taubenböck, H. A Global Inventory of Urban Corridors Based on Perceptions and Night-Time Light Imagery. ISPRS Int. J. Geo-Information 2016, 5, 233. [Google Scholar] [CrossRef]
- Lyu, H.; Lu, H.; Mou, L.; Li, W.; Wright, J.; Li, X.; Li, X.; Zhu, X.X.; Wang, J.; Yu, L.; et al. Long-term annual mapping of four cities on different continents by applying a deep information learning method to Landsat data. Remote Sens. 2018, 10, 471. [Google Scholar] [CrossRef]
- Liu, S.; Marinelli, D.; Bruzzone, L.; Bovolo, F. A Review of Change Detection in Multitemporal Hyperspectral Images: Current Techniques, Applications, and Challenges. IEEE Geosci. Remote Sens. Mag. 2019, 7, 140–158. [Google Scholar] [CrossRef]
- Bruzzone, L.; Prieto, D.F. Automatic analysis of the difference image for unsupervised change detection. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1171–1182. [Google Scholar] [CrossRef]
- Deng, J.S.; Wang, K.; Deng, Y.H.; Qi, G.J. PCA-based land-use change detection and analysis using multitemporal and multisensor satellite data. Int. J. Remote Sens. 2008, 29, 4823–4838. [Google Scholar] [CrossRef]
- Benedek, C.; Sziranyi, T. Change Detection in Optical Aerial Images by a Multilayer Conditional Mixed Markov Model. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3416–3430. [Google Scholar] [CrossRef]
- Cao, G.; Zhou, L.; Li, Y. A new change-detection method in high-resolution remote sensing images based on a conditional random field model. Int. J. Remote Sens. 2016, 37, 1173–1189. [Google Scholar] [CrossRef]
- Lv, P.; Zhong, Y.; Zhao, J.; Zhang, L. Unsupervised Change Detection Based on Hybrid Conditional Random Field Model for High Spatial Resolution Remote Sensing Imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4002–4015. [Google Scholar] [CrossRef]
- Celik, T. Unsupervised Change Detection in Satellite Images Using Principal Component Analysis and $k$-Means Clustering. IEEE Geosci. Remote Sens. Lett. 2009, 6, 772–776. [Google Scholar] [CrossRef]
- Jian, P.; Chen, K.; Zhang, C. A hypergraph-based context-sensitive representation technique for VHR remote-sensing image change detection. Int. J. Remote Sens. 2016, 37, 1814–1825. [Google Scholar] [CrossRef]
- Zhu, X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Review. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Shi, W.; Zhang, M.; Zhang, R.; Chen, S.; Zhan, Z. Change Detection Based on Artificial Intelligence: State-of-the-Art and Challenges. Remote Sens. 2020, 12, 1688. [Google Scholar] [CrossRef]
- Alcantarilla, P.F.; Stent, S.; Ros, G.; Arroyo, R.; Gherardi, R. Street-view change detection with deconvolutional networks. Auton. Robots 2018, 42, 1301–1322. [Google Scholar] [CrossRef]
- Chen, H.; Pu, F.; Yang, R.; Tang, R.; Xu, X. RDP-Net: Region Detail Preserving Network for Change Detection. arXiv 2022, arXiv:2202.09745. [Google Scholar] [CrossRef]
- Peng, D.; Zhang, Y.; Guan, H. End-to-End Change Detection for High Resolution Satellite Images Using Improved UNet++. Remote Sens. 2019, 11, 1382. [Google Scholar] [CrossRef]
- Caye Daudt, R.; Le Saux, B.; Boulch, A. Fully convolutional siamese networks for change detection. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 4063–4067. [Google Scholar] [CrossRef]
- Zhang, C.; Yue, P.; Tapete, D.; Jiang, L.; Shangguan, B.; Huang, L.; Liu, G. A deeply supervised image fusion network for change detection in high resolution bi-temporal remote sensing images. ISPRS J. Photogramm. Remote Sens. 2020, 166, 183–200. [Google Scholar] [CrossRef]
- Bandara, W.G.C.; Patel, V.M. A Transformer-Based Siamese Network for Change Detection. arXiv 2022, arXiv:2201.01293. [Google Scholar]
- Chen, H.; Qi, Z.; Shi, Z. Remote Sensing Image Change Detection with Transformers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5607514. [Google Scholar] [CrossRef]
- Zhan, Y.; Fu, K.; Yan, M.; Sun, X.; Wang, H.; Qiu, X. Change Detection Based on Deep Siamese Convolutional Network for Optical Aerial Images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1845–1849. [Google Scholar] [CrossRef]
- Chen, H.; Shi, Z. A spatial-temporal attention-based method and a new dataset for remote sensing image change detection. Remote Sens. 2020, 12, 1662. [Google Scholar] [CrossRef]
- Liu, J.; Gong, M.; Qin, A.K.; Tan, K.C. Bipartite Differential Neural Network for Unsupervised Image Change Detection. IEEE Trans. Neural Networks Learn. Syst. 2020, 31, 876–890. [Google Scholar] [CrossRef]
- Yang, K.; Xia, G.-S.; Liu, Z.; Du, B.; Yang, W.; Pelillo, M.; Zhang, L. Asymmetric Siamese Networks for Semantic Change Detection in Aerial images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–18. [Google Scholar] [CrossRef]
- Liu, J.; Chen, K.; Xu, G.; Sun, X.; Yan, M.; Diao, W.; Han, H. Convolutional Neural Network-Based Transfer Learning for Optical Aerial Images Change Detection. IEEE Geosci. Remote Sens. Lett. 2020, 17, 127–131. [Google Scholar] [CrossRef]
- Pan, J.; Li, X.; Cai, Z.; Sun, B.; Cui, W. A Self-Attentive Hybrid Coding Network for 3D Change Detection in High-Resolution Optical Stereo Images. Remote Sens. 2022, 14, 2046. [Google Scholar] [CrossRef]
- Liu, M.; Shi, Q. Dsamnet: A Deeply Supervised Attention Metric Based Network for Change Detection of High-Resolution Images. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 6159–6162. [Google Scholar] [CrossRef]
- Song, F.; Zhang, S.; Lei, T.; Song, Y.; Peng, Z. MSTDSNet-CD: Multiscale Swin Transformer and Deeply Supervised Network for Change Detection of the Fast-Growing Urban Regions. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, L.; Cheng, S.; Li, Y. SwinSUNet: Pure Transformer Network for Remote Sensing Image Change Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-CNN. arXiv 2017, arXiv:1703.06870. [Google Scholar]
- Quispe, D.A.J.; Sulla-Torres, J. Automatic Building Change Detection on Aerial Images using Convolutional Neural Networks and Handcrafted Features. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 679–684. [Google Scholar] [CrossRef]
- Maiya, S.R.; Babu, S.C. Slum Segmentation and Change Detection: A Deep Learning Approach. arXiv 2018, arXiv:1811.07896. [Google Scholar]
- Adam, A.; Sattler, T.; Karantzalos, K.; Pajdla, T. Objects Can Move: 3D Change Detection by Geometric Transformation Consistency. In Computer Vision—ECCV 2022, Proceedings of the 17th European Conference; Tel Aviv, Israel, 23–27 October 2022, Avidan, S., Brostow, G., Cissé, M., Farinella, G.M., Hassner, T., Eds.; Springer Nature: Cham, Switzerland, 2022; pp. 108–124. [Google Scholar]
- Tan, M.; Pang, R.; Le, Q.V. EfficientDet: Scalable and Efficient Object Detection. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; IEEE Computer Society: Los Alamitos, CA, USA, 2020; pp. 10778–10787. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Liu, H.; Shen, X.; Shang, F.; Ge, F.; Wang, F. CU-Net: Cascaded U-Net with Loss Weighted Sampling for Brain Tumor Segmentation. arXiv 2019, arXiv:1907.07677. [Google Scholar]
- Bao, L.; Yang, Z.; Wang, S.; Bai, D.; Lee, J. Real Image Denoising Based on Multi-Scale Residual Dense Block and Cascaded U-Net with Block-Connection. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Los Alamitos, CA, USA, 14–19 June 2020; pp. 1823–1831. [Google Scholar]
- Ma, K.; Shu, Z.; Bai, X.; Wang, J.; Samaras, D. DocUNet: Document Image Unwarping via a Stacked U-Net. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 4700–4709. [Google Scholar]
- Ghosh, A.; Ehrlich, M.; Shah, S.; Davis, L.S.; Chellappa, R. Stacked U-Nets for Ground Material Segmentation in Remote Sensing Imagery. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 252–2524. [Google Scholar]
- Liu, G.; Li, L.; Jiao, L.; Dong, Y.; Li, X. Stacked Fisher autoencoder for SAR change detection. Pattern Recognit. 2019, 96, 106971. [Google Scholar] [CrossRef]
- López-Fandiño, J.; Garea, A.S.; Heras, D.B.; Argüello, F. Stacked autoencoders for multiclass change detection in hyperspectral images. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1906–1909. [Google Scholar]
- Liu, Z.; Mao, H.; Wu, C.-Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A ConvNet for the 2020s. arXiv 2022, arXiv:2201.03545. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Gaussian Error Linear Units (GELUs). arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer Normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Guo, M.H.; Xu, T.X.; Liu, J.J.; Liu, Z.N.; Jiang, P.T.; Mu, T.J.; Zhang, S.H.; Martin, R.R.; Cheng, M.M.; Hu, S.M. Attention mechanisms in computer vision: A survey. Comput. Vis. Media 2022, 8, 331–368. [Google Scholar] [CrossRef]
- Lebedev, M.A.; Vizilter, Y.V.; Vygolov, O.; Knyaz, V.A.; Rubis, A.Y. Change detection in remote sensing images using conditional adversarial networks. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-2, 565–571. [Google Scholar] [CrossRef]
- Chen, L.-C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]







| Methods | Precision (%) | Recall (%) | F1-Score (%) | IoU (%) | GMACs (%) | Inference Time (s) |
|---|---|---|---|---|---|---|
| FC-Siam-Diff | 95.34 | 72.88 | 82.61 | 70.37 | 4.72 | 0.01680 |
| FC-Siam-Conc | 91.26 | 81.83 | 86.29 | 75.88 | 5.32 | 0.01713 |
| CDNet | 91.34 | 87.66 | 89.46 | 80.93 | 23.46 | 0.01662 |
| DSAMNet | 70.61 | 96.41 | 81.52 | 68.80 | 65.64 | 0.03378 |
| IFNet | 92.84 | 86.81 | 89.72 | 81.36 | 82.35 | 0.03298 |
| DeepLab V3 | 88.77 | 86.03 | 87.38 | 77.59 | 41.15 | 0.02783 |
| DeepLab V3+ | 90.30 | 86.79 | 88.51 | 79.39 | 43.47 | 0.02868 |
| UNet++ MSOF | 93.80 | 85.89 | 89.67 | 81.27 | 18.25 | 0.02262 |
| BIT | 92.66 | 88.02 | 90.28 | 82.28 | 8.47 | 0.01381 |
| RDPNet | 90.77 | 87.54 | 89.13 | 80.39 | 27.15 | 0.03388 |
| DUNE-CD | 92.27 | 88.83 | 90.52 | 82.68 | 25.86 | 0.02451 |
| Methods | Precision (%) | Recall (%) | F1-Score (%) | IoU (%) | GMACs (%) | Inference Time (s) |
|---|---|---|---|---|---|---|
| FC-Siam-Diff | 94.56 | 86.43 | 90.31 | 82.34 | 4.72 | 0.01452 |
| FC-Siam-Conc | 93.63 | 86.69 | 90.03 | 81.86 | 5.32 | 0.01442 |
| CDNet | 95.29 | 88.19 | 91.60 | 84.51 | 23.46 | 0.01576 |
| DSAMNet | 97.22 | 95.35 | 96.28 | 92.83 | 65.64 | 0.03238 |
| IFNet | 98.71 | 93.25 | 95.90 | 92.13 | 82.35 | 0.03165 |
| DeepLab V3 | 94.74 | 93.87 | 94.30 | 89.22 | 41.15 | 0.02545 |
| DeepLab V3+ | 95.00 | 94.24 | 94.62 | 89.79 | 43.47 | 0.02640 |
| UNet++ MSOF | 96.63 | 94.89 | 95.75 | 91.85 | 18.25 | 0.02044 |
| BIT | 98.85 | 94.15 | 96.44 | 93.13 | 8.47 | 0.01285 |
| RDPNet | 99.25 | 94.26 | 96.69 | 93.59 | 27.15 | 0.03281 |
| DUNE-CD | 98.10 | 96.90 | 97.50 | 95.12 | 25.86 | 0.02451 |
| Methods | Precision (%) | Recall (%) | F1-Score (%) | IoU (%) | GMACs | Inference Time (s) |
|---|---|---|---|---|---|---|
| DUNE-1 | 99.02 | 94.19 | 96.55 | 93.32 | 6.47 | 0.01447 |
| DUNE-2 | 99.49 | 94.75 | 97.06 | 94.29 | 12.93 | 0.01781 |
| DUNE-3 | 99.47 | 94.81 | 97.08 | 94.33 | 19.39 | 0.02122 |
| DUNE-CD | 98.10 | 96.90 | 97.50 | 95.12 | 25.86 | 0.02451 |
| Methods | Precision (%) | Recall (%) | F1-Score (%) | IoU (%) | GMACs | Inference Time (s) |
|---|---|---|---|---|---|---|
| DUNE-CD w/o TEAM | 99.47 | 94.71 | 97.03 | 94.24 | 25.86 | 0.02441 |
| DUNE-CD w/o weighted sum | 99.22 | 94.41 | 96.75 | 93.71 | 25.86 | 0.02437 |
| DUNE-CD | 98.10 | 96.90 | 97.50 | 95.12 | 25.86 | 0.02451 |
| Method | Modules | Metrics | GMACs | Inference Time (s) | |||||
|---|---|---|---|---|---|---|---|---|---|
| 2C | PE | CX | Precision (%) | Recall (%) | F1-Score (%) | IoU (%) | |||
| Baseline | - | - | - | 84.91 | 65.85 | 74.18 | 58.95 | 65.74 | 0.029 |
| Proposed 1 | - | - | ✓ | 97.37 | 96.08 | 96.72 | 93.65 | 61.22 | 0.043 |
| Proposed 2 | - | ✓ | ✓ | 97.33 | 95.42 | 96.37 | 92.99 | 4.04 | 0.012 |
| DUNE-1 | ✓ | ✓ | ✓ | 99.02 | 94.19 | 96.55 | 93.32 | 6.47 | 0.013 |
| Methods | Precision (%) | Recall (%) | F1-Score (%) | IoU (%) | GMACs | Inference Time (s) |
|---|---|---|---|---|---|---|
| DUNE-CD | 92.27 | 88.83 | 90.52 | 82.68 | 25.86 | 0.02451 |
| DUNE-CD (Reduced) | 91.74 | 88.74 | 90.22 | 82.18 | 15.40 | 0.01950 |
| Methods | Precision (%) | Recall (%) | F1-Score (%) | IoU (%) | GMACs | Inference Time (s) |
|---|---|---|---|---|---|---|
| DUNE-CD | 98.10 | 96.90 | 97.50 | 95.12 | 25.86 | 0.02451 |
| DUNE-CD (Reduced) | 99.61 | 94.89 | 97.19 | 94.54 | 15.40 | 0.02196 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adil, E.; Yang, X.; Huang, P.; Liu, X.; Tan, W.; Yang, J. Cascaded U-Net with Training Wheel Attention Module for Change Detection in Satellite Images. Remote Sens. 2022, 14, 6361. https://doi.org/10.3390/rs14246361
Adil E, Yang X, Huang P, Liu X, Tan W, Yang J. Cascaded U-Net with Training Wheel Attention Module for Change Detection in Satellite Images. Remote Sensing. 2022; 14(24):6361. https://doi.org/10.3390/rs14246361
Chicago/Turabian StyleAdil, Elyar, Xiangli Yang, Pingping Huang, Xiaolong Liu, Weixian Tan, and Jianxi Yang. 2022. "Cascaded U-Net with Training Wheel Attention Module for Change Detection in Satellite Images" Remote Sensing 14, no. 24: 6361. https://doi.org/10.3390/rs14246361
APA StyleAdil, E., Yang, X., Huang, P., Liu, X., Tan, W., & Yang, J. (2022). Cascaded U-Net with Training Wheel Attention Module for Change Detection in Satellite Images. Remote Sensing, 14(24), 6361. https://doi.org/10.3390/rs14246361






