Abstract
The concept of the phase space plays a key role in the analysis of oscillating signals. For a 1-D signal, the coordinates of the 2-D phase space are the observation time and the instant frequency. For measurements of propagating wave fields, the time and instant frequency are linked to the spatial location and wave normal, defining a ray. In this case, the phase space is also termed the ray space. Distributions in the ray space find important applications in the analysis of radio occultation (RO) data because they allow the separation of interfering rays in multipath zones. Examples of such distributions are the spectrogram, Wigner distribution function (WDF), and Kirkwood distribution function (KDF). In this study, we analyze the application of the fractional Fourier transform (FrFT) to the construction of distributions in the ray space. The FrFT implements the phase space rotation. We consider the KDF averaged over the rotation group and demonstrate that it equals the WDF convolved with a smoothing kernel. We give examples of processing simple test signals, for which we evaluate the FrFT, KDF, WDF, and smoothed WDF (SWDF). We analyze the advantages of the SWDF and show examples of its application to the analysis of real RO observations.
1. Introduction
The power of radio occultation (RO) sounding of the Earth’s atmosphere [1] by the signals of global navigation satellite systems (GNSS) is based on the fact that it is possible to measure both their amplitude and phase. This enables the application of radio holographic (RH) methods, allowing a high resolution in the inversion, not limited by the Fresnel zone size [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36].
The central idea of RH methods is the identification of rays in radio holograms, i.e., cross-sections of the wave field recorded by a moving space-borne receiver, , where is the amplitude and is the phase of the signal, which in RO processing is represented as the optical path, eikonal multiplied by wavenumber , and is the wavelength. Rays are understood as normals to wavefronts and, therefore, each ray has a specific Doppler frequency, which depends on the ray direction and the orbit data of the receiver.
The simplest approach to separating rays that are observed simultaneously is Fourier analysis in the sliding apertures [2,17]. It uses the reference signal defined for a climatological model of the atmosphere and the actual observation geometry. The reference signal describes most of the regular variations due to the satellite movement, atmospheric decay with altitude, etc. The normalized signal is defined as follows:
The maximums of its spectra in sliding apertures identify the interfering rays, provided that the sliding aperture size is chosen in the optimal way [6].
If each spectrum indicates a single maximum, the single-ray propagation is inferred. In this case, it is possible to apply the simplest geometric-optical (GO) retrieval scheme, where the bending angle is evaluated from the optical path derivative [37]. Such signals can be termed quasi-monochromatic because their amplitudes and instantaneous frequencies are smooth functions of time.
In the general case, the observed signal is represented as a superposition of quasi-monochromatic signals. It is convenient to define the normalized frequency, or momentum , which is, generally speaking, a multi-valued function. Its graph represents a curve in the 2-D space . From the physical viewpoint, the elements of this space are rays. Accordingly, the curve is referred to as the ray manifold, and the space is termed the phase or ray space. The concept of the phase space provides the link between the wave optical (WO) and GO descriptions, or quantum and classical mechanics.
For RO processing, it is important that can be transformed into , where p is the ray impact height and is the bending angle [21,22]. This transform conserves the volume of the phase space, and, therefore, it is canonical and can be associated with a Fourier integral operator (FIO) [21]. FIOs are linear operators mapping the original wave field to a function of impact parameter , which can be represented as , in terms of the amplitude and eikonal in the transformed space. The bending angle is evaluated from the derivative of . In other words, these operators change the type of the ray manifold projection in such a way that it should be single-valued. This idea is the basis of different methods of processing RO data, including back propagation [4,38], full spectrum inversion [12,18,27], canonical transform [14,21,36], and phase matching [20].
Despite their power, these methods have limitations: their applicability condition may be broken in the presence of horizontal gradients, which result in the variations of ray impact parameter [19,39,40,41]. This explains the need for data analysis methods that provide an access to the whole phase space rather than to specific projections of the ray manifold. This is achieved by applying time-frequency analysis [42].
The simplest variant of the time-frequency analysis is the aforementioned Fourier analysis in sliding apertures, also referred to as the spectrogram [2,17]. The more advanced technique uses the Wigner distribution function (WDF) [28,29].
The WDF was first introduced in theoretical physics [43,44,45], where it played the role of the symbol of the quantum-mechanical density operator. The symbol is a function of the classical coordinates and momenta, which after their substitution as quantum-mechanical operators turns into the density operator. Because the coordinate and momenta operators do not commute with each other, the substitution must follow specific rules of their ordering. In particular, the symmetric ordering results in the WDF. The WDF has found important applications in signal processing [42,46], including RO signals [28,29].
The WDF achieves a better resolution in the phase space, as compared to the spectrogram. Its drawback is that it is computationally expensive: for each sample of the signal, it requires one long-term Fourier transform, whereas the spectrogram only requires one short-term Fourier transform. Less known is the Kirkwood distribution function (KDF) [47]. The KDF has a strong computational advantage: it only requires one long-term Fourier transform for the whole record. Its drawback is that it does not achieve the same quality of visualization of the ray space as the WDF. The application of the KDF to the analysis of RO observations was first introduced by Gorbunov et al. [48], Gorbunov and Koval [49].
The idea of this work consists in utilizing the link between the WDF and KDF in order to develop an algorithm for the evaluation of the smoothed WDF (SWDF), using the rotations of the ray space and averaging KDFs for different rotation angles. The operator of the ray space rotation is the FIO describing the dynamics of the quantum harmonic oscillator. This approach is similar to the phase space tomography [28], and the choice of a reasonable number of projections allows the optimization of computational expenses.
The paper is organized as follows. In Section 2, we present the mathematical basis of the algorithm. In Section 3, we describe its numerical implementation. In Section 4, we present the results for simple test signals. In Section 5, we apply the developed algorithm to the analysis of real RO observations. In Section 6, we present the discussion of the results. In Section 7, we offer our conclusions.
2. Algorithm Description
2.1. Quasiprobability Distribution Functions
Consider a generic signal as a function of coordinate x. This signal can be both or . If the signal is quasi-monochromatic, it can be written as follows:
where is the momentum conjugated to the coordinate x, and k is the wavenumber in wave propagation problems, or the inverse Planck constant in quantum mechanics. More generally, k is a problem-specific scaling factor. In the general case, the signal is a superposition of quasi-monochromatic signals (2). The dependence in the simplest case, or the set of dependencies for multiple quasi-monochromatic components of the signal, specify the structure of the ray manifold.
Momentum plays a double role. On the one hand, it is the derivative of the eikonal or the normalized frequency. On the other hand, it is associated with a differential operator:
where the second equation is understood as a short-wave asymptotic. Coordinate x can also be thought of as operator of the multiplication by x.
In the interpretation of RO data, we have observations of and we need to recover the complicated structure of ray manifold [22,28]. There are different approaches to this problem. One of them uses the linear representations of wave fields implemented by FIOs [22]: the wave field is transformed into the representation of the impact parameter, which in most cases ensures the single-valued projection of the ray manifold. The other approach uses the non-linear representations of wave fields and operates with the pseudo-density in the whole phase space. The maximums of the pseudo-density follow the ray manifold, regardless of the type of its projection to any specific coordinate axis. In this study, we follow the latter approach.
The distribution function in the ray space is the symbol of the quantum density operator. Because operators and do not commute, the symbol depends on the chosen ordering of these operators. If we choose the symmetric, or Weyl ordering, we arrive at the WDF [28,43,44,45,50]:
where is the complex conjugate of . If, however, we choose the ordering, we arrive at the KDF [47,48,49]:
where is the Fourier transform of .
There is a relationship between these two distributions [48]:
where the asterisk denotes convolution, and vice versa:
2.2. Phase Space Scaling
The further idea is to study the transformation laws of and with respect to rotations of the phase space. However, a rotation mixes x and , which, generally speaking, have different units and characteristic scales. Therefore, the first step should be to scale the coordinate and momentum to make them unitless. The wavenumber k will also be scaled. Because the basic waveform is , the scaling transform must keep the unitless product , and the most general form of a group of such transforms is as follows:
where a and b are the group parameters. In our case, has the dimension of inverse length, x has the dimension of length, and is unitless. Unitless and can only be obtained for unitless . Therefore, it is convenient to choose to get rid of k. Then we arrive at the following transform:
where just one unitless scaling parameter b remains. Given the characteristic variations X and of x and along the ray manifold or its piece under analysis, we require:
and infer:
Finally, we can write the scaling as follows:
This transform, too, has just one scaling parameter, .
In our further discourse, we will keep the notation for the scaled coordinates, because, generally, the choice of measurement units is arbitrary. The reader must just bear in mind that all the considerations where x and play symmetric roles operate with unitless coordinates.
2.3. Phase Space Rotation
Consider the rotation of the phase space :
and, accordingly:
This is a canonical transform, whose generating function is defined by the differential equation [22,28]:
which results in the following expression:
The corresponding FIO has the following form [22,28]:
This transform is termed the fractional Fourier transform (FrFT) [51]. For it turns into the Fourier transform, and it possesses the group property:
If , the kernel of this operator aims at -function, which makes it possible to define as the unity operator. Therefore, these operators form a group. Because , this is a representation of the rotation group.
Deep links between the FrFT and quasiprobability distribution functions were discussed in [52]. We will follow this approach and study the transformation properties of the WDF and KDF with respect to phase space rotations. Denote and as the WDF and KDF for the transformed function .
From the tomographic definition of the WDF [28] it follows that it is invariant with respect to phase space rotations:
Unlike the WDF, the KDF does not possess such a nice property. However, we can consider its averaging over phase space rotations. Then, using (9) along with the fact that convolution commutes with rotations, we can infer:
The integral in the right-hand part evaluates analytically:
where it the Bessel function. Therefore, the averaging of the KDF evaluated for the FrFTs of the signal, with different rotation angles, results in the WDF convolved with the smoothing kernel (26), and (25) is close to the Fresnel transform of the WDF [52]. We will denote the smoothed WDF (SWDF) .
3. Numerical Implementation
3.1. Discretization
Because the coordinate x and momentum in the phase space play fully symmetric roles, their discretization must use identical grids. Given the total number of points N, the duality relations can be written:
where and are the discretization steps. Because , we infer the relation between N and :
3.2. Fractional Fourier Transform
Our numerical implementation of the FrFT is close to that described in [53]. First, we notice that the numerical evaluation of transform (22) for small angles may represent difficulties. Using the group property (23), we represent the FrFT as follows:
where is the usual Fourier transform, , and K is chosen in such a way that . K may take the four values representing the four basic directions , each one serving in two octants: and . The values of K and the corresponding are summarized in Table 1:

Table 1.
Basic directions and transforms .
We represent as follows:
The overall numerical algorithm consists of the following steps:
- Determination of K and evaluation of . For , the standard fast Fourier transform (FFT) is employed;
- Evaluation of ;
- Evaluation of , where . The standard FFT is employed. This function is obtained for the standard grid , where the corresponding grid of y is ;
- Interpolation of from the grid to the standard grid , producing ;
- Final evaluation of .
3.3. Kirkwood Distribution Function and Its Averaging over Rotations
The numerical evaluation of the KDF for function is straightforward and follows (6). For the KDF interpolated to the original non-rotated coordinates, we can write:
In the last expression, the first term is evaluated analytically, and the other two require 1-D interpolation.
In (25), the integration is spread over the full circle . However, as follows from Table 1, rotations by correspond to coordinate inversions and, therefore, they leave the KDF transformed to unrotated coordinates, unchanged:
This allows limiting the averaging to the interval of . In fact, it is possible to make one more step to reduce the averaging interval. First, we can write:
Because rotations by correspond to the Fourier transform, this KDF equals:
From this, we can infer:
Therefore, rotations by correspond to the complex conjugation of the KDF. Because the WDF is real, the imaginary part of the KDF becomes zero when averaging over rotations. Finally, we conclude that it is enough to average the real part of the KDF over the interval of .
Averaging over rotation angles is discretized. Given the number of projections , the step of equals , and the projections are evaluated for angles , .
3.4. Wigner Distribution Function
In our numerical tests, we will evaluate the WDF for a comparison with the other distributions. For each , is evaluated as the inverse FFT over j from the function . In order to evaluate the function values for the half-integer indexes, we up-sample the signal using the Fourier interpolation. To this end, we evaluate the FFT of the signal, enlarge the frequency grid twice, pad the missing spectrum values for high frequencies with zero, and evaluate the inverse FFT. This produces the signal up-sampled to the twice denser grid.
4. Tests with Simple Signals
We will illustrate the previous considerations with the distributions in the phase space for simple test signals, where we can easily anticipate the intuitive results. We employ the following model of the signal:
where are the model parameters, and amplitude is shown in Figure 1. This form of amplitude smoothly decreasing to zero at the borders is used to prevent the boundary effects in FFT, resulting in the propagation of energy from one grid border to the other. Function describes the form of the ray manifold in the phase space. The distributions are expected to have maximums in their vicinity. In the test examples, the number of samples is , and, in compliance with (27), .

Figure 1.
Signal amplitude.
The simplest model is the pure linear trend of the frequency: (“button”). The results for this model are presented in Figure 2, Figure 3, Figure 4 and Figure 5. Figure 2 shows the evolution of the KDF for for different rotation angles. The FrFT transforms a linear frequency trend into another linear frequency trend or a -function, which can be understood as a “vertical” trend. The latter situation is realized for = 120°. This figure is a good illustration of the fact that the KDF has a different resolution for different orientations of the ray manifold in the phase space. The best resolution is achieved for the vertical orientation of the ray manifold. The “maximum” of the KDF must be understood in the generalized sense. In fact, it has an oscillating structure all over the phase space, and it is the ray manifold, where it has a stationary phase point. Therefore, when integrating the KDF multiplied by a smooth probe function, the maximum contribution comes from the vicinity of the ray manifold. Figure 3 shows the same KDF interpolated to the original coordinates. Here, the KDF traces the original unrotated ray manifold with different resolutions.
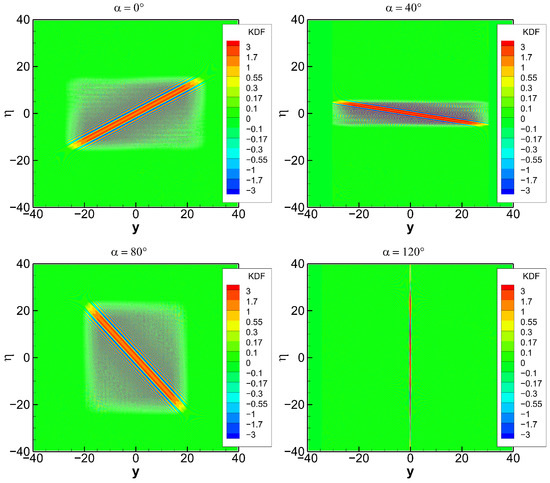
Figure 2.
KDF of function in rotated coordinates . The rotation angle takes the values of 0°, 40°, 80°, and 120°.
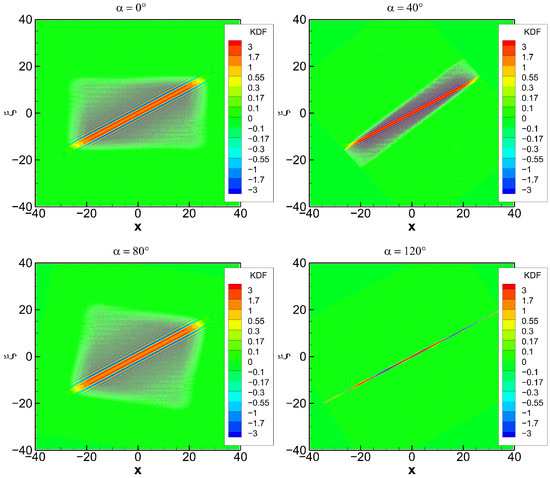
Figure 3.
KDF of function interpolated to the unrotated coordinates . The rotation angle takes the values of 0°, 40°, 80°, and 120°.
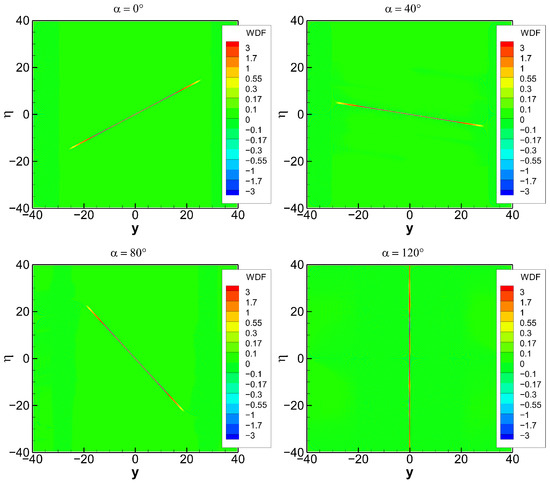
Figure 4.
WDF of function in rotated coordinates . The rotation angle takes the values of 0°, 40°, 80°, and 120°.
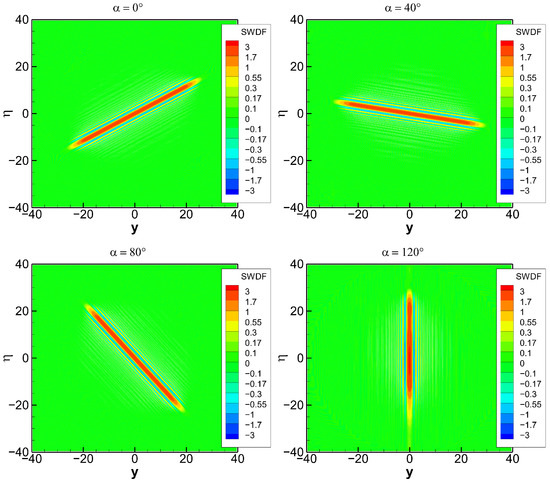
Figure 5.
SWDF of function in rotated coordinates . The rotation angle takes the values of 0°, 40°, 80°, and 120°.
Figure 4 illustrates the fact that the WDF has an ideal performance for any linear frequency trend [28]. This fact is linked to the invariance of the WDF with respect to the rotations of the phase space. Figure 5 shows the SWDF evaluated for the number of projections . has an intermediate resolution independent from the orientation of the ray manifold. It indicates a clear maximum at the ray manifold and decaying oscillations elsewhere.
The parameter set produces another, more interesting model (“snake”). The results for this model are presented in Figure 6, Figure 7, Figure 8 and Figure 9. Figure 6 shows the evolution of the KDF. In the original orientation , the energy, which is concentrated on the ray manifold, is evenly distributed over y coordinate, but in the Fourier space, it is very inhomogeneous due to the ray manifold geometry and its projection to the axis. The rotations result in the re-distribution of energy over both y and coordinates. Although the original situation indicates a single-valued projection of the ray manifold to the y axis, for the other chosen rotations it is not the case. For = 40°, there are narrow regions, where the original wave-like structure starts crashing. These regions become wider for = 80°. For = 120°, the original structure acquires a vertical orientation, and the whole projection becomes multi-valued. Figure 7 shows the same KDF interpolated to the original coordinates, revealing the same original structure surrounded by different oscillating patterns.
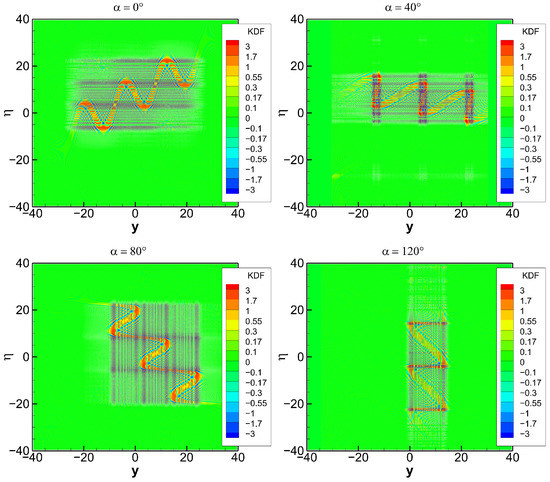
Figure 6.
KDF of function in rotated coordinates . The rotation angle takes the values of 0°, 40°, 80°, and 120°.
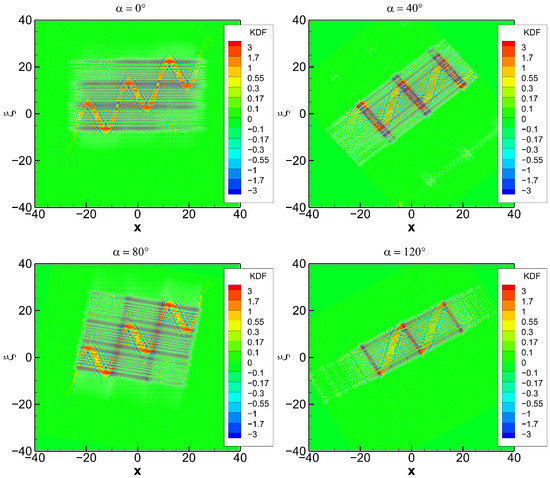
Figure 7.
KDF of function interpolated to the unrotated coordinates . The rotation angle takes the values of 0°, 40°, 80°, and 120°.
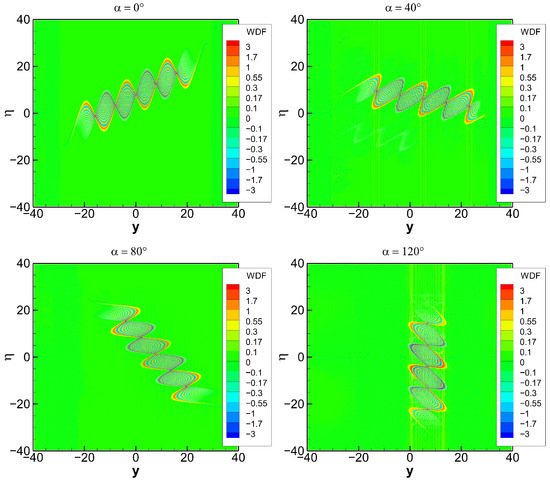
Figure 8.
WDF of function in rotated coordinates . The rotation angle takes the values of 0°, 40°, 80°, and 120°.
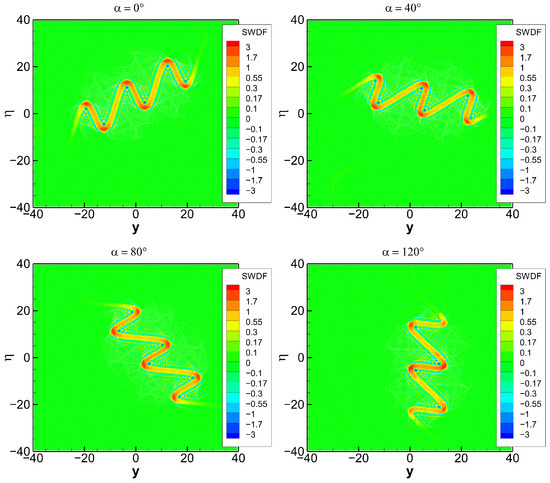
Figure 9.
SWDF of function in rotated coordinates . The rotation angle takes the values of 0°, 40°, 80°, and 120°.
The performance of the WDF, as shown in Figure 8, is far from ideal. Although the original snake-like structure is traced very well, it is duplicated in an antisymmetric way, with oscillating patterns between these two structures. Finally, the SWDF shown in Figure 9 indicates the same resolution as in the previous case.
5. Results of Processing RO Data
Figure 10, Figure 11, Figure 12 and Figure 13 show four examples of processing COSMIC-2 data. We chose RO events with deep penetration, indicating a complicated multipath propagation structure. The analysis was performed in the time domain, and its starting point was the original complex signal normalized to the reference signal (1). For the analysis, we chose the tropospheric part of the signal. COSMIC-2 observations have a sampling rate of 100 Hz. We down-sampled the signals to 50 Hz because in most cases the signal spectrum lies within a 50 Hz band [54,55,56]. Examples of spectrograms of deep COSMIC-2 events with a sampling rate of 100 Hz can be found in [57]. We plotted the WDF and SWDF in the time–frequency coordinates, where the frequency is understood as the difference between the Doppler frequencies of the measured signal and the reference one. According to the sampling rate, the frequency lies between and 25 Hz. In all the cases, the WDF indicates a complicated structure, where the ray manifold is traced at a high resolution, but it is mixed with a lot of additional oscillating structures. The SWDF allows a significantly clearer visualization of the ray manifold and suppresses most of the additional oscillating structures. This is achieved at a price of a lower resolution.
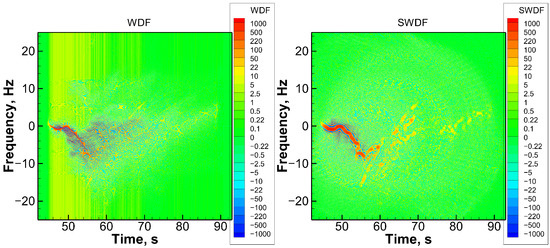
Figure 10.
COSMIC-2 setting RO event observed on 15 May 2020 UTC 20:05, 16.69°N 163.45°W. Left: WDF, right: SWDF.
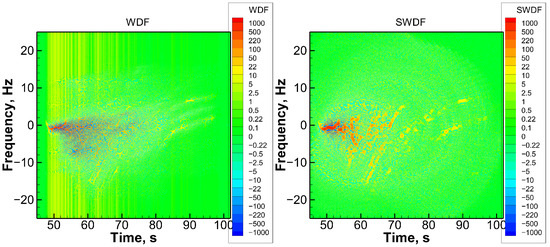
Figure 11.
COSMIC-2 setting RO event observed on 15 May 2020 UTC 20:31, 13.07°N 70.83°W. Left: WDF, right: SWDF.
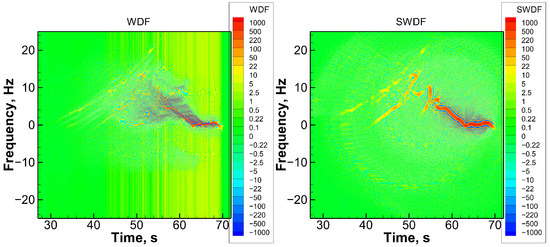
Figure 12.
COSMIC-2 rising RO event observed on 15 May 2020 UTC 20:42, 24.36°S 14.18°E. Left: WDF, right: SWDF.
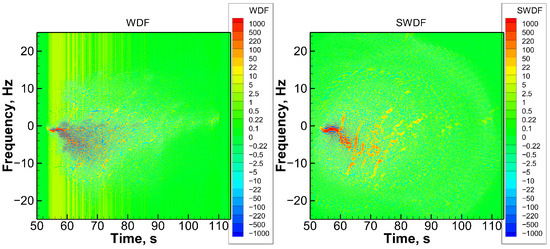
Figure 13.
COSMIC-2 setting RO event observed on 15 May 2020 UTC 12:29, 0.65°N 167.78°E. Left: WDF, right: SWDF.
6. Discussion
The uncertainty relation is a fundamental limitation of the time–frequency analysis, defining the size of the cell in the phase space, which limits the resolution of the determination of the ray manifold structure. For time and frequency, it dictates that , which indicates that the phase space cell volume is 1. However, the manifestations of this principle are different for different quasiprobability distributions in the phase space. For the WDF, it defines the characteristic scale of “quantum oscillations” [28]. For the SWDF, it defines the characteristic width of its maximum.
The uncertainty relation is written without any assumption about the signal, which can have a wide spectrum. Given some a priori information about the signal structure, the uncertainty relation can be overridden. An example of this is the use of the canonical transform method [22]. The observed wave field is transformed into the representation of the impact parameter , where, in most cases, the ray manifold projection becomes single-valued, and the signal becomes quasi-monochromatic. This information allows the determination of the instant frequency of the signal even if , i.e., from one oscillation period, although the uncertainty relation tells us that in this case, , and, therefore, the frequency cannot be determined. This property of the ray manifold projection in the impact parameter representation allows achieving a high resolution in the retrieval of the bending angle profiles (see the numerical simulation in [22]).
The time–frequency analysis is most useful in situations where such a single-valued projection of the ray manifold is not known a priori. This happens in the presence of strong horizontal gradients, which perturb the ray impact parameter [10], resulting in the multipath in the impact parameter space [41]. In such cases, a spectrogram of the signal can tell us much more about the structure of the signal than the bending angle profile retrieved by using the FIO approach. While FIOs implement linear representations of the wave field, different types of quasiprobability distributions in the phase space implement non-linear (quadratic) representations.
The SWDF possesses properties that make it a prospective candidate for the time–frequency analysis of RO observations:
- It effectively suppresses the “quantum oscillations”, which are imminent to the WDF.
- Its resolution is good enough for practical purposes.
- It has no preferred direction in the phase space because it is invariant with respect to the phase space rotation.
7. Conclusions
This study is a continuation of the work on the application of the technique of quantum distributions for the analysis of RO observations. Previously, the WDF and KDF were introduced in this context [28,48,49]. The advantage of the KDF is the simplicity of its evaluation. However, it cannot provide such a good quality of ray manifold detection as the WDF. On the other hand, the WDF produces a lot of “quantum oscillations” in the phase space, which are manifestations of the wave nature of the signal.
We follow the idea of using the FrFT, which implements rotations in the phase space [28,52,53]. Averaging the KDF over the rotation group results in the WDF convolved with a smoothing kernel, which is close to the Fresnel transform of the WDF. We introduce this type of quasiprobability density in the phase space for the analysis of RO observations. We describe the numerical algorithm of the evaluation of the SWDF. We analyze two simple test signals, which demonstrate its advantages. Finally, we apply the SWDF for the analysis of real RO observations. We demonstrate that it allows a clearer visualization of the ray manifold compared to the WDF due to the suppression of the oscillating structures. The SWDF is invariant with respect to the phase space rotation. It achieves an optimal resolution without any externally defined parameter, such as the sliding aperture size [6]. This makes the SWDF a prospective technique of time–frequency analysis of RO observations.
Author Contributions
Conceptualization and methodology, M.G.; software, O.D. and M.G.; validation, M.G. and O.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Russian Foundation for Basic Research, grant number 20-05-00189 A.
Data Availability Statement
The COSMIC2 data used in this study are freely available on the CDAAC website.
Acknowledgments
The authors acknowledge Taiwan’s National Space Organization (NSPO) and the University Corporation for Atmospheric Research (UCAR) for providing the COSMIC-2 data. The authors are grateful to Kent B. Lauritsen (Danish Meteorological Institute) and to Christian Marquardt (EUMETSAT) for the discussions of time–frequency analysis.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FIO | Fourier Integral Operators |
| FFT | Fast Fourier Transform |
| FrFT | Fractional Fourier Transform |
| GNSS | Global Navigation Satellite Systems |
| GO | Geometrical Optics |
| KDF | Kirkwood Distribution Function |
| RH | Radio Holography |
| RO | Radio Occultation |
| SWDF | Smoothed Wigner Distribution Function |
| WDF | Wigner Distribution Function |
| WO | Wave Optics |
References
- Anthes, R.A. Exploring Earth’s atmosphere with radio occultation: Contributions to weather, climate and space weather. Atmos. Meas. Tech. 2011, 4, 1077–1103. [Google Scholar] [CrossRef]
- Pavelyev, A.G. On the Feasibility of Radioholographic Investigations of Wave Fields Near the Earth’s Radio-Shadow Zone on the Satellite-to-Satellite Path. J. Commun. Technol. Electron. 1998, 43, 875–879. [Google Scholar]
- Mortensen, M.D.; Høeg, P. Inversion of GPS occultation measurements using Fresnel diffraction theory. Geophys. Res. Lett. 1998, 25, 2441–2444. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Gurvich, A.S. Algorithms of inversion of Microlab-1 satellite data including effects of multipath propagation. Int. J. Remote Sens. 1998, 19, 2283–2300. [Google Scholar] [CrossRef]
- Mortensen, M.D.; Linfield, R.P.; Kursinski, E.R. Vertical resolution approaching 100 m for GPS occultations of the Earth’s atmosphere. Radio Sci. 1999, 36, 1475–1484. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Gurvich, A.S.; Kornblueh, L. Comparative analysis of radioholographic methods of processing radio occultation data. Radio Sci. 2000, 35, 1025–1034. [Google Scholar] [CrossRef]
- Høeg, P.; Jensen, A.S.; Nielsen, A.S.; Lohmann, M.; Schroder, T.M.; Grove-Rasmussen, J.; Larsen, G.B. Radio Occultation Signal Analysis; ACE-Scientific Support Study WP6300(1); Atmosphere Ionosphere Research Division, Danish Meteorological Institute: Copenhagen, Denmark, 2001.
- Beyerle, G.; Hocke, K. Observation and simulation of direct and reflected GPS signals in radio occultation experiments. Geophys. Res. Lett. 2001, 28, 1895–1898. [Google Scholar] [CrossRef]
- Gorbunov, M.E. Radioholographic Methods for Processing Radio Occultation Data in Multipath Regions; Scientific Report 01-02; Danish Meteorological Institute: Copenhagen, Denmark, 2001.
- Gorbunov, M.E.; Kornblueh, L. Analysis and validation of GPS/MET radio occultation data. J. Geophys. Res. 2001, 106, 17161–17169. [Google Scholar] [CrossRef]
- Beyerle, G.; Hocke, K.; Wickert, J.; Schmidt, T.; Marquardt, C.; Reigber, C. GPS radio occultations with CHAMP: A radio holographic analysis of GPS signal propagation in the troposphere and surface reflections. J. Geophys. Res. 2002, 107, 4802. [Google Scholar] [CrossRef]
- Jensen, A.S.; Benzon, H.H.; Lohmann, M.S. A New High Resolution Method for Processing Radio Occultation Data; Scientific Report 02-06; Danish Meteorological Institute: Copenhagen, Denmark, 2002.
- Gorbunov, M.E.; Gurvich, A.S.; Shmakov, A.V. Back-propagation and radio-holographic methods for investigation of sporadic ionospheric E-layers from Microlab-1 data. Int. J. Remote Sens. 2002, 23, 675–685. [Google Scholar] [CrossRef]
- Gorbunov, M.E. Canonical transform method for processing radio occultation data in the lower troposphere. Radio Sci. 2002, 37, 9-1–9-10. [Google Scholar] [CrossRef]
- Gorbunov, M.E. Radio-holographic analysis of Microlab-1 radio occultation data in the lower troposphere. J. Geophys. Res. 2002, 107, 7-1–7-10. [Google Scholar] [CrossRef]
- Gorbunov, M.E. Radioholographic analysis of radio occultation data in multipath zones. Radio Sci. 2002, 37, 14-1–14-9. [Google Scholar] [CrossRef]
- Pavelyev, A.; Igarashi, K.; Reigber, C.; Hocke, K.; Wickert, J.; Beyerle, G.; Matyugov, S.; Kucherjavenkov, A.; Pavelyev, D.; Yakovlev, O. First application of the radioholographic method to wave observations in the upper atmosphere. Radio Sci. 2002, 37, 1043. [Google Scholar] [CrossRef]
- Jensen, A.S.; Lohmann, M.S.; Benzon, H.H.; Nielsen, A.S. Full spectrum inversion of radio occultation signals. Radio Sci. 2003, 38, 1040. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Kornblueh, L. Analysis and validation of Challenging Minisatellite Payload (CHAMP) radio occultation data. J. Geophys. Res. 2003, 108, 4584. [Google Scholar] [CrossRef]
- Jensen, A.S.; Lohmann, M.S.; Nielsen, A.S.; Benzon, H.H. Geometrical optics phase matching of radio occultation signals. Radio Sci. 2004, 39, RS3009. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Benzon, H.H.; Jensen, A.S.; Lohmann, M.S.; Nielsen, A.S. Comparative analysis of radio occultation processing approaches based on Fourier integral operators. Radio Sci. 2004, 39, RS6004. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Lauritsen, K.B. Analysis of wave fields by Fourier integral operators and its application for radio occultations. Radio Sci. 2004, 39, RS4010. [Google Scholar] [CrossRef]
- Gorbunov, M.E. Wave Optics Algorithms for Processing Radio Occultation Data in the Lower Troposphere: A Review and Synthesis. In Occultations for Probing Atmosphere and Climate; Kirchengast, G., Foelsche, U., Steiner, A.K., Eds.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2004; pp. 11–24. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Lauritsen, K.B. Canonical Transform Methods for Radio Occultation Data. In Occultations for Probing Atmosphere and Climate; Kirchengast, G., Foelsche, U., Steiner, A.K., Eds.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2004; pp. 61–68. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Lauritsen, K.B. Radio Holographic Filtering of Noisy Radio Occultations; Scientific Report 05-06; Danish Meteorological Institute: Copenhagen, Denmark, 2005. Available online: https://www.dmi.dk/fileadmin/Rapporter/SR/sr05-06.pdf (accessed on 29 September 2022).
- Gorbunov, M.E.; Lauritsen, K.B.; Rodin, A.; Tomassini, M.; Kornblueh, L. Analysis of the CHAMP experimental data on radio-occultation sounding of the Earth’s atmosphere. Izv. Atm. Ocean. Phys. 2005, 41, 726–740. [Google Scholar]
- Jensen, A.S.; Benzon, H.H.; Lohmann, M.S.; Nielsen, A.S. Processing radio occultation data by full spectrum inversion techniques: An overview and recent developments. In Atmosphere and Climate, Studies by Radio Occultation Methods; Foelsche, U., Kirchengast, G., Steiner, A., Eds.; Springer: New York, NY, USA, 2006; pp. 96–112. [Google Scholar]
- Gorbunov, M.E.; Lauritsen, K.B.; Leroy, S.S. Application of Wigner distribution function for analysis of radio occultations. Radio Sci. 2010, 45, RS6011. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Lauritsen, K.B.; Leroy, S.S. Analysis of RO data retrieved from the Wigner distribution function. In Proceedings of the International Radio Occultation Working Group, 2nd Workshop, Estes Park, CO, USA, 28 March–3 April 2012. [Google Scholar]
- Pavelyev, A.G.; Liou, Y.A.; Matyugov, S.S.; Pavelyev, A.A.; Gubenko, V.N.; Zhang, K.; Kuleshov, Y. Application of the locality principle to radio occultation studies of the Earth’s atmosphere and ionosphere. Atmos. Meas. Tech. 2015, 8, 2885–2899. [Google Scholar] [CrossRef]
- Sievert, T.; Rasch, J.; Carlström, A.; Pettersson, M.I. Analysis of reflections in GNSS radio occultation measurements using the phase matching amplitude. Atmos. Meas. Tech. 2018, 11, 569–580. [Google Scholar] [CrossRef]
- Koval, O.A.; Gorbunov, M.E. The theory of fluctuations of radio occultation signals: Geometric optical approximation of the Canonical Transform Method. In Proceedings of the IGL-1 2018: First International Workshop on Innovating GNSS and LEO Occultations & Reflections for Weather, Climate and Space Weather, Beijing, China, 6–11 September 2018; p. 87. [Google Scholar]
- Gorbunov, M.E.; Cardellach, E.; Lauritsen, K.B. Reflected ray retrieval from radio occultation data using radio holographic filtering of wave fields in ray space. Atmos. Meas. Tech. 2018, 11, 1181–1191. [Google Scholar] [CrossRef]
- Koval, O.A.; Gorbunov, M.E.; Kan, V. The fluctuation theory of radio occultation signals: Geometric optical approximation of the Canonical Transform method. IOP Conf. Ser. Earth Environ. Sci. 2019, 231, 012029. [Google Scholar] [CrossRef]
- Sievert, T.; Rasch, J.; Carlström, A.; Barbosa, V.L.; Pettersson, M.I.; Vu, V. Using A Sliding Window Phase Matching Method for Imaging of GNSS Radio Occultation Signals. Remote Sens. 2021, 13, 970. [Google Scholar] [CrossRef]
- Gorbunov, M.; Kirchengast, G.; Lauritsen, K.B. Generalized canonical transform method for radio occultation sounding with improved retrieval in the presence of horizontal gradients. Atmos. Meas. Tech. 2021, 14, 853–867. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Sokolovskiy, S.V. Remote Sensing of Refractivity from Space for Global Observations of Atmospheric Parameters; Report 119; Max-Planck Institute for Meteorology: Hamburg, Germany, 1993; 58p. [Google Scholar]
- Gorbunov, M.E.; Gurvich, A.S. Microlab-1 experiment: Multipath effects in the lower troposphere. J. Geophys. Res. 1998, 103, 13819–13826. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Lauritsen, K.B. Error Estimate of Bending Angles in the Presence of Strong Horizontal Gradients. In New Horizons in Occultation Research; Steiner, A., Pirscher, B., Foelsche, U., Kirchengast, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 17–26. [Google Scholar] [CrossRef]
- Healy, S.B. Radio occultation bending angle and impact parameter errors caused by horizontal refractive index gradients in the troposphere: A simulation study. J. Geophys. Res. 2001, 106, 11875–11890. [Google Scholar] [CrossRef]
- Zou, X.; Liu, H.; Kuo, Y.H. Occurrence and detection of impact multipath simulations of bending angle. Quart. J. R. Meteor. Soc. 2019, 145, 1690–1704. [Google Scholar] [CrossRef]
- Cohen, L. Time-frequency distributions—A review. Proc. IEEE 1989, 77, 941–981. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Note on Exchange Phenomena in the Thomas Atom. Proc. Camb. Philos. Soc. 1930, 26, 376–395. [Google Scholar] [CrossRef]
- Heisenberg, W. Über Die Inkohärente Streuung Von Röntgenstrahlen. Physik. Zeitschr. 1931, 32, 737–740. [Google Scholar]
- Wigner, E.P. On the Quantum Correction for Thermodynamic Equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
- Ville, J. Théorie et Applications de la Notion de Signal Analytique. Cables Transm. 1948, 2, 61–74. [Google Scholar]
- Kirkwood, J.G. Quantum statistics of almost classical assemblies. Phys. Rev. 1933, 44, 31–37. [Google Scholar] [CrossRef]
- Gorbunov, M.; Koval, O.; Kirchengast, G. Kirkwood Distribution Function and its Application for the Analysis of Radio Occultation Observations. In Proceedings of the Joint 6th ROM SAF User Workshop and 7th IROWG Workshop, EUMETSAT ROM SAF, Elsinore, Denmark, 19–25 September 2019. [Google Scholar]
- Gorbunov, M.E.; Koval, O.A. Kirkwood and Wigner Quantum Densities, Their Properties, and Applications in Radiophysics. Radiophys. Quantum Electron. 2021, 64, 140–148. [Google Scholar] [CrossRef]
- Mello, P.A.; Revzen, M. Wigner function and the successive measurement of position and momentum. Phys. Rev. A 2014, 89, 012106. [Google Scholar] [CrossRef]
- Condon, E.U. Immersion of the Fourier Transform in a Continuous Group of Functional Transformations. Proc. Natl. Acad. Sci. USA 1937, 23, 158–164. [Google Scholar] [CrossRef]
- Anaya-Contreras, J.; Zúñiga-Segundo, A.; Moya-Cessa, H. Quasiprobability Distribution Functions from Fractional Fourier Transforms. Symmetry 2019, 11, 344. [Google Scholar] [CrossRef]
- Marinho, F.J.; Bernardo, L.M. Numerical calculation of fractional Fourier transforms with a single fast-Fourier-transform algorithm. J. Opt. Soc. Am. A 1998, 15, 2111. [Google Scholar] [CrossRef]
- Sokolovskiy, S.V. Modeling and inverting radio occultation signals in the moist troposphere. Radio Sci. 2001, 36, 441–458. [Google Scholar] [CrossRef]
- Sokolovskiy, S.V. Tracking tropospheric radio occultation signals from low Earth orbit. Radio Sci. 2001, 36, 483–498. [Google Scholar] [CrossRef]
- Sokolovskiy, S.; Schreiner, W.; Zeng, Z.; Hunt, D.; Lin, Y.C.; Kuo, Y.H. Observation, analysis, and modeling of deep radio occultation signals: Effects of tropospheric ducts and interfering signals. Radio Sci. 2014, 49, 954–970. [Google Scholar] [CrossRef]
- Hordyniec, P.; Kuleshov, Y.; Choy, S.; Norman, R. Observation of Deep Occultation Signals in Tropical Cyclones With COSMIC-2 Measurements. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).