VLF/LF Lightning Location Based on LWPC and IRI Models: A Quantitative Study

Abstract

The group velocity of lightning electromagnetic signals plays an important role in lightning location systems using the time difference of arrival (TDOA) method. Accurate estimation of group velocity is difficult due to the space- and time-varying properties of the Earth-ionosphere waveguide. Besides, the analytical solution of the group velocity is difficult to obtain from the classic mode theory, especially when higher-order modes, anisotropic geomagnetic background, diffuse ionosphere profile, and propagation path segmentation are all taken into consideration. To overcome these challenges, a novel numerical method is proposed in this paper to estimate the group velocity of the lightning signal during ionospheric quiet periods. The well-known Long Wavelength Propagation Capability (LWPC) code is used to model the propagation of VLF/LF radio waves. Since LWPC uses a simplified ionospheric model which is unable to describe the subtle variations of ionospheric parameters over time and space, the IRI-2016 model is incorporated into the numerical modeling process to provide more accurate ionosphere parameters. Experimental results of a VLF/LF lightning location network are demonstrated and analyzed to show the effectiveness of our method. The proposed method is also applicable when there is a sudden ionospheric disturbance as long as the parameters of the ionosphere are obtained in real time by remote sensing methods.

1. Introduction

Electromagnetic waves in the VLF/LF frequency band can travel long distances in the so-called earth-ionosphere waveguide and are widely used in communication, navigation, nuclear electromagnetic pulse detection, lightning detection, etc. [1,2,3,4]. Among these, lightning detection systems find the locations of sferics by measuring the arrival times of electromagnetic signals and solving the inverse problem with the estimated or empirical propagation velocity of lightning signals. This propagation velocity is the average velocity of the propagated lightning energy for each frequency component and is also known as the group velocity [5]. The group velocity, which can be further interpreted as time or distance, is one of the most important parameters to be estimated for lightning detection systems.

Although a complete theory of VLF/LF radio wave propagation was established in the 1960s [6], there is no analytical solution for the group velocity of lightning electromagnetic pulses, especially when considering multiple modes, anisotropic geomagnetic background, a diffuse ionosphere profile, and segmentation propagation path. Wait [6] derived the phase velocity of the nth-order mode of radio waves passing through the Earth-ionosphere waveguide (EIWG), assuming the Earth and the ionosphere possess infinite conductivity. Later, a non-sharp or diffuse ionosphere with exponentially varying conductivity was considered by Wait to obtain a more accurate analytical solution of the phase velocity. While these simplified versions of phase velocity reveal the underlying physical nature and are convenient for fast computation, they are not sufficiently accurate due to various approximations. A general theory of radio propagation by wave-guide modes is given by Budden [7] which simultaneously makes allowance for the gradualness of the lowest part of the ionosphere, the Earth’s curvature, and the Earth’s magnetic field. However, this method requires solving partial differential equations and, therefore, also does not yield an analytical solution for the phase or group velocity.

After the development of the detection of lightning discharges in the 1990s, various methods for estimating the group velocity of the lightning waveform were proposed. The World Wide Lightning Location Network (WWLLN) [8] uses an approximate group velocity of about 0.9922c (0.9922 times the speed of light in vacuum), corresponding to a representative group velocity in the middle of the detection frequency range, for all paths at all times and frequencies, as recommended by Watt [9]. This fixed group velocity, although partially eliminating the effects of wave propagation on the path, still does not fully reflect the time- and space-dependent properties of the EIWG.

Said et al. [10] proposed a semi-empirical method for long-range lightning geolocation which avoids explicit estimation of group velocity. This technique catalogs the dominant variation in expected received waveforms in a set of waveform banks, which are then used to estimate the propagation distance and accurately determine the arrival time. Using only three sensors in a trial network, this technique demonstrated a median accuracy of 1–4 km, depending on the time of day. This ingenious method considers the effect of Earth-ionosphere waveguides while avoiding the need to estimate the group velocity. However, this method requires the creation of a filter bank containing a large number of typical lightning waveforms, which is difficult to implement in most scientific and engineering applications.

Liu et al. [11] proposed a technique with a variable propagation velocity which is implemented in the time of arrival (TOA) method. The lightning locations obtained by this method improve the accuracy of locations by 0.89–1.06 km compared with the lightning locations reported by the UK Met Office. Li et al. [12] establish a long-range lightning location network to verify the feasibility of the variable propagation velocity proposed by Liu. It is found that the average location error of the equivalent propagation method is 9.17 km, which improves the average location accuracy by about 1.16 km, compared with the assumed light speed of lightning-radiated sferic from the lightning stroke point to the observation station. However, this conceptually novel method makes an implicit assumption that the lightning wave traveling over different paths shares the same propagation velocity, which is not true. It is also not feasible to use different velocities for each path because this would make the number of unknowns in the equations of the TOA method larger than that of observations.

Accurately estimating the group velocity requires high-precision modeling of the propagation of VLF/LF waves. With long wave propagation modeling tools such as LWPC [13] and appropriate ionospheric models [14], the phase characteristics of electromagnetic waves can be accurately calculated numerically. For low-power VLF propagation, the ionosphere can be fully characterized by its electron density profile, the corresponding collision frequency profile, and the direction and intensity of the ambient magnetic field. The former two parameters, i.e., the electron density profile and the collision frequency profile, are two of the most important and unstable parameters of the ionosphere D region. Wait and Spies [15] used laboratory measurements, ionospheric sounding rocket measurements, and VLF propagation measurements to empirically derive a parameterized model with an exponential profile for them. This two-parameter model, which is parameterized by the reference height (h’) and the slope of the logarithm of the electron density profile (β), has been widely used and verified in various scenarios since then. Based on previous works, the CCIR recommended typical values for h’ and β during the daytime and nighttime. According to this recommendation, the ionospheric parameters are relatively stable during the day and are only affected by the season and latitude. The changes in the ionosphere at night are more complicated. In addition to the seasonal and latitude factors, they are also affected by the working frequency and the geomagnetic field of the location. LWPC also uses Wait’s two-parameter model for the ionosphere, and the values for h′ and β are determined by the solar zenith angle, which in turn, is determined by parameters such as time and location [13]. In the LWPC model, when the solar zenith angle meets the conditions of daytime or nighttime, the corresponding β and h′ are both fixed values. Therefore, for such regions, the electron density and collision frequency do not change with the geographical location but are only related to the height from the ground. This is different from the distribution of actual electron density and collision frequency. A more sophisticated model of the ionosphere is needed to facilitate precise modeling of VLF/LF propagation.

The International Reference Ionosphere (IRI) is an empirical standard model of the ionosphere produced by a working group based on all available data sources [14]. Since the first version of the model was released in the 1960s, it has been widely used in various fields [16,17,18,19,20]. Pal [16] coupled the Fortran code of the IRI model with the LWPC code for propagation simulation of the VLF signal of the Indian Navy’s transmitter (VTX) at 18.2 kHz. The electron-ion density profiles along the propagation path, which are computed from the IRI-2007 model, are used as the inputs in the LWPC code. Chowdhury [17] uses the electron density profile from the IRI model to fit Wait’s two-parameter exponential model to obtain the values of h’ and β, and then uses LWPC to simulate the amplitude variations of the VTX 18.2 kHz signal for comparison with the observations from available VLF/LF sites. Yi [18] updated both the electron density and collision frequency modules originally embedded in LWPC by the IRI model for improved simulation performance compared with the observed amplitude variations of VLF signals of the Australian Navy’s transmitter (NWC) by the Wuhan University VLF receiver. In addition to the narrowband VLF modeling described above, the IRI model is also used for wideband VLF propagation simulation. Hu [19] developed a full-wave two-dimensional finite-difference time-domain (FDTD) model to simulate lightning-generated electromagnetic wave propagation in the ionosphere with high altitude and long-distance capabilities. The density and collision frequency profiles of electrons and ions are calculated using the IRI model. Results of this FDTD model agree with the mode theory very well, with the agreement between the models better than 5% over the frequency range from 0 to 30 kHz for typical nighttime ionosphere profiles. Marshall [20] incorporated the IRI model into a time-domain model of the lightning electromagnetic pulse (EMP) interaction with the lower ionosphere. In addition to modeling lightning, this model can be used for long-distance VLF wave propagation in the Earth-ionosphere waveguide, heating of the lower ionosphere by VLF transmitters, etc. The IRI model is generally considered to be a description of the average and quiet state of the ionosphere. When the ionosphere is disturbed by sudden events such as solar flares, earthquakes, and volcanoes, the ionospheric parameters obtained by the IRI model have great deviations from the real situation. In this case, the real-time ionospheric state parameters can be retrieved by the VLF ionospheric remote sensing method [21], which is not described here in detail.

Inspired by the previous research results mentioned earlier, this paper develops a lightning positioning scheme with a novel numerical method to estimate the group velocity of the lightning signal during ionospheric quiet periods. The well-known LWPC program is used to model the propagation of the electromagnetic wave at the frequency band of interest, and the IRI-2016 model is incorporated into the numerical modeling process to provide more accurate ionosphere parameters such as the electron density profile. Experimental results of a VLF/LF lightning location network are demonstrated and analyzed to show the effectiveness of our method. Extensive comparisons of lightning location accuracy between our proposed method and others are also made. The results show that when the average ionospheric reflection height on the path is accurately obtained (based on the IRI model), the first-order mode group velocity analytic solution yields a very good localization accuracy. The default LWPC model yields a similar localization accuracy, and the combined use of the LWPC and IRI models allows for further improvement in localization accuracy.

This article is organized as follows. In Section 2, the background of the lightning location principle, i.e., the TDOA and the arrival time estimation method, is briefly introduced, and the proposed group velocity estimation method applicable to broadband lightning signals is described in detail with an emphasis on the VLF/LF electromagnetic wave propagation modeling scheme based on the LWPC and IRI models. In Section 3, the performance of our proposed group velocity estimation method is analyzed based on the experimental results of the VLF/LF lightning detection network and compared with other group velocity estimation methods. The results of the analysis are discussed in Section 4. Finally, conclusions are drawn in Section 5.

2. Materials and Methods

2.1. Lightning Location via the TDOA Method

Suppose the position of lightning occurrence is (φ, λ) where φ and λ are latitude and longitude, respectively, and the time of occurrence of the lightning sferic is T₀. The positions of the N lightning detection stations are (φ_n, λ_n), and the arrival times of the received lightning are T_n, n = 1, 2,…, N, respectively. The TDOA method estimates the lightning position and time of occurrence by minimizing the following cost function:

$$\left(\widehat{\phi },\widehat{\lambda },{\widehat{T}}_0\right)\triangleq \underset{\left(\phi ,\lambda ,T_0\right)}{\min }{\displaystyle \sum _{n=2}^N\frac{1}{{\sigma }_{t,n}^2}{\left[T_n-T_1-\frac{D\left(\phi ,\lambda ,{\phi }_n,{\lambda }_n\right)}{v_n}+\frac{D\left(\phi ,\lambda ,{\phi }_1,{\lambda }_1\right)}{v_1}\right]}^2}$$

(1)

where σ_t,n is the standard deviation of the synchronization time error of the nth receiver, and D(φ, λ, φ_n, λ_n) and v_n are the distance and the propagation velocity from the lightning location to the nth receiver, respectively. The optimization problem in Equation (1) can be solved by well-established optimization tools such as the Levenberg–Marquardt algorithm [22].

It can be found from Equation (1) that in addition to the receiver synchronization error σ_t,n, the arrival time T_n and the group velocity v_n are two of the most important factors that affect the lightning location accuracy. Accurate estimation of arrival time can be achieved using the time of group arrival (TOGA) method or cross-correlation described in Section 2.2. To reduce the location error caused by the inaccuracy of the group velocity, a relocation scheme is adopted. First, the approximate location of the lightning is estimated via Equation (1) using the speed of light in the air, and then the group velocity is estimated using methods described in Section 2.3 with the approximate location of the lightning event. Finally, a more accurate location of the lightning event is obtained by minimizing Equation (1) again using the estimated group velocity.

2.2. Arrival Time Estimation of Lightning Signals

According to the classic theory of VLF/LF electromagnetic propagation, when the lightning occurs at a short distance to the receiver, the ground wave dominates, and there is a sharp peak in the received time-domain waveform of the lightning electric field. In this case, the time stamp of the electric field waveform peak is commonly used as the arrival time of the lightning, and the location error caused by the inaccuracy of the arrival time is very small. In contrast, when the lightning source is far away from the receiver, due to the filtering effect of the EIWG, the high-frequency components of the lightning electric field are filtered out and the sharp peak is broadened. The time stamp corresponding to the electric field waveform peak should no longer be used as the arrival time of the lightning; otherwise, it causes large arrival time errors, which lead to large location errors.

Two well-known methods can be used to accurately determine the time (difference) of the arrival of long-range lightning fields. One is the cross-correlation method [23], which calculates the time difference between the arrival of lightning at the two stations by cross-correlating their electric field waveforms. The other is the TOGA method proposed by Dowden et al. [5], which calculates the group arrival time of the lightning electric field by performing least-squares linear fitting on the phase spectrum and is successfully applied to the WWLLN lightning detection network. The latter method is described in detail since it is very closely related to the group velocity estimation method described in Section 2.3. The TOGA method is briefly summarized as follows.

The phase of the lightning signal at time t and distance r is:

$$\varphi \left(\omega ;t,r\right)=\omega \left(t-T_0\right)-k\left(\omega \right)r+{\varphi }_0$$

(2)

where ω is the angular frequency, T₀ is the time of lightning occurrence, k(ω) is the wave number of the electromagnetic wave, and ϕ₀ is the initial phase of the lightning signal. Note that the above formula assumes that the initial phase of each frequency component of lightning is constant at the time T₀, which is generally true for fast-rising lightning signals. Taking the derivative of the phase to the angular frequency ω yields the slope of the phase spectrum as:

$$t_{slope}\left(\omega \right)=\frac{\partial \varphi \left(\omega ;t,r\right)}{\partial \omega }=\left(t-T_0\right)-r\frac{\partial k\left(\omega \right)}{\partial \omega }=\left(t-T_0\right)-\frac{r}{v_g\left(\omega \right)}$$

(3)

The last step in Equation (3) uses the definition of group velocity. Group travel time is defined as the time it takes for the lightning signal to travel distance r at group velocity v_g, i.e., t_g(ω) = r/v_g(ω). Correspondingly, the group arrival time is defined as t_TOGA(ω) = T₀ + t_g(ω). Together with Equation (3) we can immediately obtain:

$$t_{slope}\left(\omega \right)=t-\left(T_0+t_g\left(\omega \right)\right)=t-t_{TOGA}\left(\omega \right)$$

(4)

Therefore, the group arrival time t_TOGA(ω) can be obtained from the above formula:

$$t_{TOGA}\left(\omega \right)=t-t_{slope}\left(\omega \right)$$

(5)

The arrival time of the main energy of the broadband lightning electromagnetic pulse, i.e., TOGA, is defined as the average of the group arrival time t_TOGA(ω):

$$TOGA=\overline{t_{TOGA}}\left(\omega \right)=t-\overline{t_{slope}}\left(\omega \right)$$

(6)

where the bar in Equation (6) implies an average. In practice, a robust estimate of the mean of t_slope(ω) is replaced by the slope of the regression line of the phase spectrum ϕ(ω) in the frequency band of interest. Recall that t represents the sampling time which can be defined arbitrarily as long as the lightning waveform is completely recorded. Dowden [5] suggests using the trigger time as the sampling time t in Equation (6). Since the trigger time is earlier than the TOGA, the phase spectrum always shows a negative slope for the measured lighting electric waveform.

2.3. Group Velocity Estimation Methods

The group velocity is the velocity with which the envelope of a signal propagates in a medium and it is well-defined for narrowband applications. The spectrum of lightning signals occupies a very wide bandwidth, and the traditional definition of group velocity is no longer applicable. Meanwhile, researchers in the VLF/LF community have found that most of the lightning energy is concentrated in a certain frequency range, and there is a peak point in the spectrum. Therefore, the group velocity at the spectral peak frequency can be used to approximate the group velocity of lightning signals. The phase velocity v_p(ω) and the group velocity v_g(ω) for a narrow band of energy centered about frequency ω are defined as:

$$v_p\left(\omega \right)=\frac{\omega }{k\left(\omega \right)}$$

(7)

$$v_g\left(\omega \right)=\frac{\partial \omega }{\partial k\left(\omega \right)}$$

(8)

Combining Equations (7) and (8) and eliminating k(ω), we can obtain the relationship between v_p(ω) and v_g(ω) as follows:

$$v_g\left(\omega \right)=\frac{v_p^2}{\left[v_p-\omega \left(d{v}_p/d\omega \right)\right]}$$

(9)

By assuming the Earth and the ionosphere to possess infinite conductivity, Wait [15] has shown that the phase velocity of the nth-order mode of radio waves passing through the Earth and a sharply bounded ionosphere is approximately given by:

$$v_p=c{\left(1-C_n^2\right)}^{-\frac{1}{2}}\left(1-\frac{h}{2a}\right)$$

(10)

where c is the velocity of light in free space, $C_n=\left(n-1/2\right)\lambda /2h$, h is the height of reflection of the VLF wave from the ionosphere, and a and λ are the Earth’s radius and wavelength of the wave, respectively. Therefore, given the frequency ω, waveguide mode order n, and ionospheric reflection height h, the phase velocity along the path can be calculated from Equation (10), and then the corresponding group velocity can be obtained from Equation (9).

Generally, Equations (9) and (10) are used to estimate the group velocity and phase velocity of the first-order mode for large distances where higher-order modes vanish. For short or medium distances, analytical calculation of the group velocity of lightning sferics by the above method is not feasible due to the superposition of multiple modes. In addition, when the propagation path is long enough that the ionospheric day–night transition occurs, the average reflection height h in Equation (10) is difficult to determine accurately, despite the presence of only the first-order mode.

Since the analytical group velocity of the first-order mode based on the mode theory has the above-mentioned limitations, we propose a novel and more accurate group velocity estimation method applicable to wideband lightning signals. Our proposed method is inspired by the TOGA method mentioned in Section 2.2 and transforms the problem of solving the group velocity into the problem of solving the group delay time as described below.

First, we rewrite the relation between the group velocity v_g(ω) and the group travel time t_g(ω) as follows:

$$v_g\left(\omega \right)=\frac{r}{t_g\left(\omega \right)}$$

(11)

According to the definition of the group velocity, by combining Equations (8) and (11) the group travel time can be reformulated as:

$$t_g\left(\omega \right)=\frac{r}{v_g\left(\omega \right)}=\frac{\partial \left[k\left(\omega \right)r\right]}{\partial \omega }$$

(12)

The $k\left(\omega \right)r$ term in Equation (12) is the phase change resulting from radio propagation. This phase term cannot be extracted from the experimental data but can be easily obtained by numerical simulations such as those performed using the LWPC program. In particular, the phase spectrum of any frequency calculated by LWPC is the phase relative to the propagation of electromagnetic waves in free space, namely:

$$\varphi \left(\omega \right)=\omega T_r-k\left(\omega \right)r$$

(13)

where T_r = r/c. Note that the expression of Equation (13) is a special case of Equation (2) where the initial phase ϕ₀ is set to 0 and the time t is set to be the instant after the electromagnetic wave travels the distance r at the speed of light in the vacuum from time T₀. Taking the derivation of (13) about ω, we obtain:

$$\frac{\partial \varphi \left(\omega \right)}{\partial \omega }=t_{slope}\left(\omega \right)=T_r-\frac{\partial \left[k\left(\omega \right)r\right]}{\partial \omega }$$

(14)

Combining Equations (12) and (14) we obtain:

$$t_g\left(\omega \right)=T_r-t_{slope}\left(\omega \right)$$

(15)

The group velocity can be obtained by Equations (11), (14) and (15). To obtain the group velocity of wideband lightning signals, the same measure can be taken as in Equation (6), i.e., either by taking the mean of t_slope(ω) or by the least square fitting of the regression line slope of the phase spectrum ϕ(ω) in the frequency band of interest.

The computational procedure of our proposed group velocity estimation method is shown in

Table 1. The computational procedure of the proposed group velocity estimation method.

Input: latitude and longitude of the source position (φsource, λsource),    latitude and longitude of the receiver position (φreceiver, λreceiver),    the frequency band of interest [ωmin, ωmax],    time of occurrence t. Output: group velocity vg.

Steps: For ω = ωmin:∆ω:ωmax, compute the phase spectrum ϕ(ω) by the LWPC and IRI models (see Section 2.4 for details). $$\varphi \left(\omega \right)=LWPC\left({\phi }_{source},{\lambda }_{source},{\phi }_{receiver},{\lambda }_{receiver},\omega ,t\right)$$ Compute the slope of the phase spectrum by Equation (14) or by the least square fitting of the regression line of the phase spectrum ϕ(ω); Compute the group velocity vg by Equations (11) and (15).

.

2.4. Long Wave Propagation Modeling Based on LWPC and IRI Models

From the previous subsection, it can be seen that the modeling of VLF/LF wave propagation is one of the most important steps in group velocity estimation. The propagation of VLF electromagnetic waves in the Earth-ionospheric waveguide is affected by many factors such as ionospheric parameters, ground parameters, and geomagnetic parameters. Among these space-varying parameters, ground conductivity, permittivity, and geomagnetic field are almost invariant with time, so existing measured or empirical models for them can be used. In contrast, ionospheric parameters vary dramatically not only within a day but also with seasons and years. Meanwhile, ionospheric parameters are also affected by sudden disturbances such as solar flares, volcanic eruptions, earthquakes, etc.

We use the well-known LWPC program for VLF/LF propagation modeling and simulation. LWPC is a very powerful software based on the mode theory [13]. After the user inputs the location, frequency, time of the source, and the location of the receiving point, the software can automatically determine the ionosphere, ground conductivity, and the Earth’s magnetic field parameters distribution along the path and calculate the field strength and phase at the receiving point.

For the most important ionospheric parameters, i.e., electron density N_e(h) and electron-neutral collision frequency V(h), LWPC uses the classical Wait two-parameter model exponential model to calculate them:

$$N_e\left(h\right)=1.43\times {10}^7\times \exp \left(-0.15h^{\prime }\right)\times \exp \left[\left(\beta -0.15\right)\left(h-h^{\prime }\right)\right]$$

(16)

$$V\left(h\right)=1.82\times {10}^{11}\times \exp \left(-0.15h\right)$$

(17)

where β and h’ are the electron density slope (km⁻¹) and reference height (km), respectively. The built-in model of LWPC sets the value of β and h’ for the daytime and nighttime ionosphere separately. The daytime ionosphere has a constant value of β equal to 0.3 km^–1 and a constant value of h’ equal to 74 km. The nighttime ionosphere is more complicated in that β varies with frequency while h’ is constant at 87 km.

Despite the great success of LWPC, the ionosphere model it uses is far from perfect because the electron density does not vary with geographic location when the solar zenith angle meets daytime or nighttime conditions. Following previous works, we combine the IRI-2016 ionospheric model with the LWPC model to obtain better modeling results of VLF electromagnetic wave propagation. Specifically, the electron density profile in Equation (16) is substituted by IRI-2016’s output, and the models of collision frequency, conductivity, permittivity, and geomagnetic field remain unchanged as the built-in models of LWPC. For any given transmitter and receiver pair, the great circle path is divided into no more than 100 equal segments due to the limitations of LWPC. The length of each segment is set to be no less than 50 km, which is a compromise between accuracy and efficiency. The electron density output from the IRI-2016 model is extrapolated down to a height of 65 km employing linear logarithmic interpolation, which is also generally considered to be the lowest height of the ionosphere during the daytime.

2.5. A Detailed Example for Group Velocity Estimation

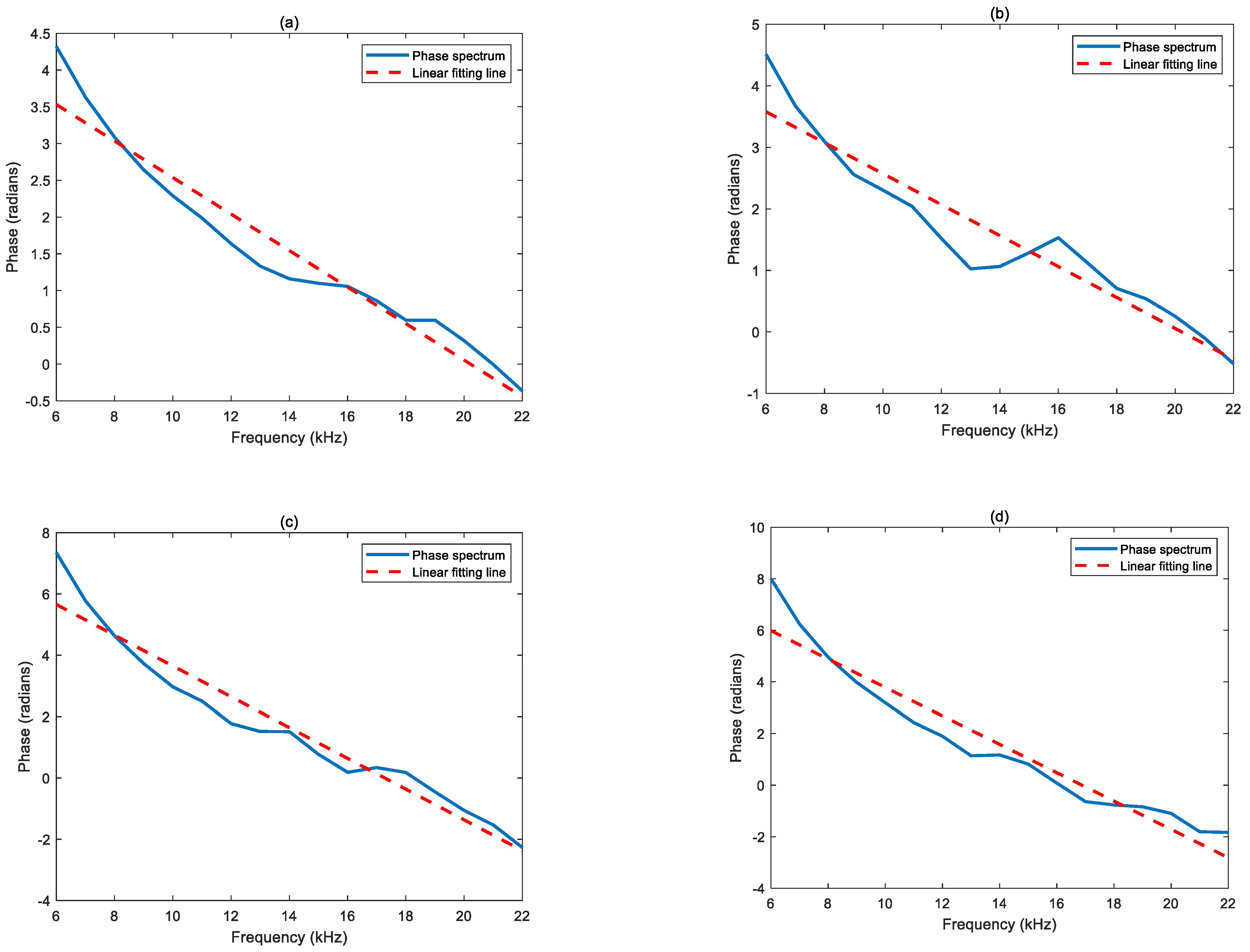
In this section, we give an example to illustrate how to estimate the group velocity of a lightning signal using our proposed method. A set of data from the lightning detection experiment introduced in Section 3.1 is used for the following calculations. By TDOA localization with the speed of light in the air, the initial solution of the location (31°3′N, 91°35′E) and the occurrence time (UTC 2021/09/20 08:25:59) of the lightning source are obtained, so that the path from the source to each station can be determined, and the corresponding distances are 1286 km, 1310 km, 2770 km, and 3126 km. The phase spectrums of Equation (13) are calculated using the VLF/LF propagation model introduced in Section 2.4, as shown by the blue curves in Figure 1. The frequency range of the phase spectrum is from 6 kHz to 22 kHz, covering most of the energy of the lightning signal. The red dotted lines in Figure 1 are the linear fitting lines of the spectrum curves based on the least square criterion. The linear fitting line with a negative slope indicates that the lightning propagation time along the path is longer than the time required for the electromagnetic wave to travel the same distance in the air, and the time difference equals the slope of the linear fitting line. From Figure 1 and Equation (2), it can be calculated that the time differences (t_slope) are $-40 \mathsf{\mu }\mathrm{s}$, $-40 \mathsf{\mu }\mathrm{s}$, $-80 \mathsf{\mu }\mathrm{s}$, and $-88 \mathsf{\mu }\mathrm{s}$. Accordingly, the group travel times t_g and the group velocities v_g can be calculated via Equations (11) and (15), respectively. The results are summarized in column v₄ of

Table 2. Intermediate and final calculation results of different methods of group velocity estimation.

Station	Distance (km)	v21			v3			v4
		h’2	vp/c	vg/c	tslope	tg	vg/c	tslope	tg	vg/c
Urumqi	1286	72	0.9976	0.9911	−36	4326	0.9918	−40	4330	0.9909
Yuxi	1310	72	0.9975	0.9911	−37	4405	0.9916	−40	4408	0.9909
Taizhou	2770	73	0.9974	0.9911	−75	9313	0.9920	−80	9318	0.9914
Baishan	3126	73	0.9973	0.9911	−86	10,514	0.9918	−88	10,516	0.9917

¹ v₂, v₃, and v₄ represent the three group velocity estimation methods defined in Section 3.1. ² h’ is in kilometers. v_p/c and v_g/c are unitless where c is the speed of light in the air. t_slope and t_g are in microseconds.

.

Table 2 also presents the intermediate and final results of the calculation of the group velocity of the first-order mode and the group velocity estimated by LWPC only, which are defined as v₂ and v₃ and are described in detail in Section 3.1. The calculation process of v₃ is similar to that of v₄, and will not be repeated here. For v₂, the calculation results include the average ionospheric reflection height h’, the phase velocity v_p, and the group velocity v_g, as shown in column v₂ of Table 2.

3. Results

3.1. Experiment Description

A quantitative analysis of location accuracy is performed based on the data of an experimental long-baseline lightning network (ELLN) built in the summer of 2021. ELLN consists of four lightning stations distributed over China. These stations are located in Urumqi (43°49′N, 87°38′E), Yuxi (24°20′N, 102°33′E), Taizhou (28°40′N, 121°24′E), and Baishan (41°57′N, 126°25′E), as illustrated in Figure 2. Each station continuously collects the vertical electric field between 3 kHz and 400 kHz with a sampling frequency of 1 MHz. The recorded length of the waveform is 1000 μs with the trigger time at 250 μs. The timing accuracy of the Beidou clock used in each receiver is 18 ns which enables the network to record lightning signals with high temporal resolution.

The lightning location results of ELLN are compared with those of the Global Lightning Dataset (GLD360) operated by Vaisala [24]. GLD360 is the first ground-based lightning detection network capable of providing both worldwide coverage and uniform, high performance without significant detection differences between daytime and nighttime conditions. After the 2020 upgrade to version 4.0, the GLD360 lightning location network announced a one-kilometer location accuracy for lightning strikes globally [25]. A GLD360 event is defined to be matched with an event of ELLN if the time difference is within 1 millisecond and the distance difference is within 50 km.

The lightning location data collected from ELLN are processed with different group velocity estimation methods, including our proposed method and other methods to be compared. The localization results obtained from different data processing methods are matched with those of GLD360 to count the localization errors. In particular, we define, analyze and compare the following four kinds of group velocity estimation methods:

• v₁, the speed of light in the air

The speed of light in the air is used as a benchmark for others. According to the theory of electromagnetic waves, the speed of light in the air is:

$$v_1=\frac{c}{\sqrt{{\epsilon }_r{\mu }_r}}$$

(18)

where ε_r and μ_r are the relative permittivity and the relative permeability of air, respectively. Note that in this case, the optimization problem of lightning location in Section 2.1 only needs to be solved once, and the resulting location errors should be the largest among all cases.

• v₂, the group velocity of the first-order mode

The group velocity of the first-order mode, v₂, is calculated via Equations (9) and (10). Instead of using the daytime and nighttime ionospheric reflection heights recommended by the CCIR, the average reflection height along any given path is estimated via the IRI model. Specifically, first, the IRI model is used to obtain the electron density profile of each position along the path, and then the electron density is fitted with Wait’s two-parameter model to obtain the reflection height. Finally, the average reflection height is obtained by arithmetically averaging the reflection heights at each position along the propagation path. For short paths, the reflection height at the middle point of the path is used.

• v₃, the group velocity estimated by LWPC

The group velocity v₃ is based on the LWPC program calculation of the phase spectrum over a given frequency range on the propagation path, and the estimation of the group velocity is achieved by Equations (11), (14) and (15). LWPC is a classical and widely used model for VLF/LF propagation calculations, and the localization performance based on group velocity v₃ is improved relative to the speed of light v₁. However, due to the simplicity of the built-in ionospheric model of LWPC, this method does not achieve optimal localization performance.

• v₄, the group velocity estimated by LWPC and IRI

The group velocity v₄ is also calculated from Equations (11), (14) and (15) as v₃ does. The only difference between them is the use of the ionosphere model. While v₃ uses a simple ionosphere model, v₄ uses the IRI model in the hope of obtaining a more accurate group velocity. The electron density profiles of each position along the path are integrated into a path-segmented ionospheric model. For short paths without path segmentation, the electron density profile of the middle point along the path is used. The complete computational procedure for group velocity v₄ is summarized in Table 1.

3.2. Analysis of Lightning Location Results

One month of lightning location data of ELLN are used to complete the analysis in this section. After matching the location results with those of GLD360, a total of 11,126 matched events are obtained. They are plotted on the map according to their latitudes and longitudes, as shown in Figure 3. In this figure, the cyan triangles are the locations of stations, the blue asterisks are the positions of lightning events of ELLN, and the red circles are the corresponding positions of lightning events matched with GLD360. As seen from Figure 3, most of the lightning events are located in mainland China, and there are also many lightning events outside of ELLN, located in southeast Asia and the South China Sea.

The lightning localization results of ELLN in Figure 3 are calculated using v₁, the speed of light in the air. In order to compare the localization accuracies of different group velocity estimation methods, for each lightning event in Figure 3, we also calculated the lightning location of occurrence using the other three group velocities introduced in Section 3.1. Figure 4 plots the statistical results of the localization errors obtained using the four different group velocity estimation methods: the speed of light in the air (v₁), the group velocity of the first-order mode (v₂), the group velocity estimated by LWPC (v₃), and the group velocity estimated by LWPC and IRI (v₄). From the corresponding location error statistics of the four methods in Figure 4, it can be seen that v₁ has the largest positioning error, with different counts of lightning events distributed in all intervals within 50 km. The location errors corresponding to the other three group velocities are mainly distributed in the 0–20 km interval, and the group velocity based on LWPC and IRI, i.e., v₄, corresponds to the smallest positioning error. In summary, the four group velocity estimation methods are ranked in descending order of localization errors as follows: v₁, v₂, v₃, and v₄.

The distances between the four stations of ELLN vary from 2000 to 4000 km, and the histogram distributions of the minimum, mean and maximum distances from the lightning events to the stations are shown in Figure 5. Among them, the minimum distances range from 0–1700 km, the mean distances range from 1300–2800 km, and the maximum distances range from 1500–4500 km. The statistics in Figure 5 show that the distance of lightning events varies considerably under different definitions. To better and quantitatively reveal how the positioning errors vary with distance, we define the maximum distance from a lightning event to the ELLN stations as the distance from the event to the ELLN network in all subsequent analyses. According to this definition, the vast majority of distances corresponding to all lightning localization events in Figure 3 are distributed in the range of 1500 to 4000 km.

For all the lightning localization events in Figure 3, we sorted the localization errors obtained from each group velocity estimation method by distance from near to far and counted the mean and the standard deviation of localization errors per 200 km interval within 1500 to 4000 km, and the results are shown in Figure 6. Note that in Figure 6, the mean and standard deviation of the localization error correspond to the left and right y-axes respectively. From the figure, it can be seen more clearly that the four group velocity estimation methods, in descending order of localization error, are arranged as follows: the speed of light in the air (v₁), the group velocity of the first-order mode (v₂), the group velocity estimated by LWPC (v₃), and the group velocity estimated by LWPC and IRI (v₄). This is the same as the conclusion obtained in Figure 4. Among them, v₁ has the largest localization error due to the use of the speed of light in air, with an error range of 13–30 km; v₂ has the second largest localization error, with an error range of 4–17 km; v₃ has the third largest localization error, with an error range of 3–14 km; and v₄ has the smallest localization error, with an error range of 2–10 km.

Although there is a large improvement in the localization error for our proposed group velocity estimation method, v₄, relative to v₁, we also find the following interesting points: (1) the group velocity of the first-order mode, v₂, and the group velocity estimated by LWPC, v₃, also have large improvements in the localization error relative to v₁, and the localization errors of v₂ and v₃ are comparable. This indicates that both the analytical solution of the first-order mode group velocity and the LWPC model are very close to the real situation of VLF/LF wave propagation; (2) v₄, shows limited improvement in localization error relative to v₂ and v₃, and the improvement in localization error increases with distance. This may be due to the greater influence of the ionosphere on VLF/LF wave propagation as the distance becomes greater, and the effect of the combined use of the LWPC and IRI models is subsequently more pronounced; and (3) the standard deviation of v₁’s localization error is relatively large but it changes little with distance. The standard deviation of v₃’s localization error varies greatly with distance, exceeding all other methods at 4000 km. This could be due to the simplified ionospheric model used by LWPC.

It is well known that the ionospheric state varies greatly throughout the day. To analyze the localization performance of the four group velocity estimation methods at different moments of the day, we further divided the lightning events into three groups according to the time of occurrence: daytime, nighttime, and day–night transition. As can be seen in Figure 3, the lightning event is located in an area approximately centered near Xi’an, which corresponds to the actual time zone of East 7. We define the local time in Xi’an from 8:00 a.m. to 6:00 p.m. as daytime (corresponding to UTC from 0100 to 1100), from 8:00 p.m. to 6:00 a.m. as nighttime (corresponding to UTC from 1300 to 2300), and the other periods as day-night transitions (corresponding to UTC from 1100 to 1300 and 2300 to 0100). According to the above definitions, for each group of lightning events and each group velocity estimation method, we sorted the localization errors obtained by distance from near to far and counted the mean and the standard deviation of localization errors per 200 km interval within 1500 to 4000 km, and the results are shown in Figure 7, Figure 8 and Figure 9.

The general trend of localization errors with distance in Figure 7, Figure 8 and Figure 9 is similar to that in Figure 6. We summarized all the localization error curves in Figure 6, Figure 7, Figure 8 and Figure 9, and the results are shown in

Table 3. The statistics of location errors (km) for different group velocity estimation methods.

	v1	v2	v3	v4
All data	13 to 30	4 to 17	3 to 14	2 to 10
Daytime	10 to 34	4 to 17	4 to 13	3 to 12
Nighttime	11 to 28	3 to 17	3 to 14	2 to 8
Day-night transition	14 to 29	4 to 17	4 to 21	3 to 7

. From the figures and the table, we can see several new interesting points: (1) During the night or day-night transition period, the localization error curves of v₂ and v₃ fluctuate more drastically with distance than those of daytime, whereas those of v₄ fluctuate less with distance. This indicates that the ionospheric variation is more complicated at night or during the daytime transition; on the other hand, it also illustrates the effectiveness of our proposed group velocity estimation method based on the LWPC and IRI models. (2) Most of the time, the localization error of v₂ is larger than that of v₃, but in a few cases at longer distances, the localization error of v₂ is smaller than that of v₃. This may be due to the fact that the ionospheric reflection height in v₂ is calculated based on the IRI model, which is better than the simple ionospheric model in LWPC. (3) The improvement of the localization error of v₄ relative to v₂ and v₃ is more obvious as the distance increases. This shows the superiority of using the group velocity estimation method proposed in this paper when the propagation distance becomes longer and the path is more complex.

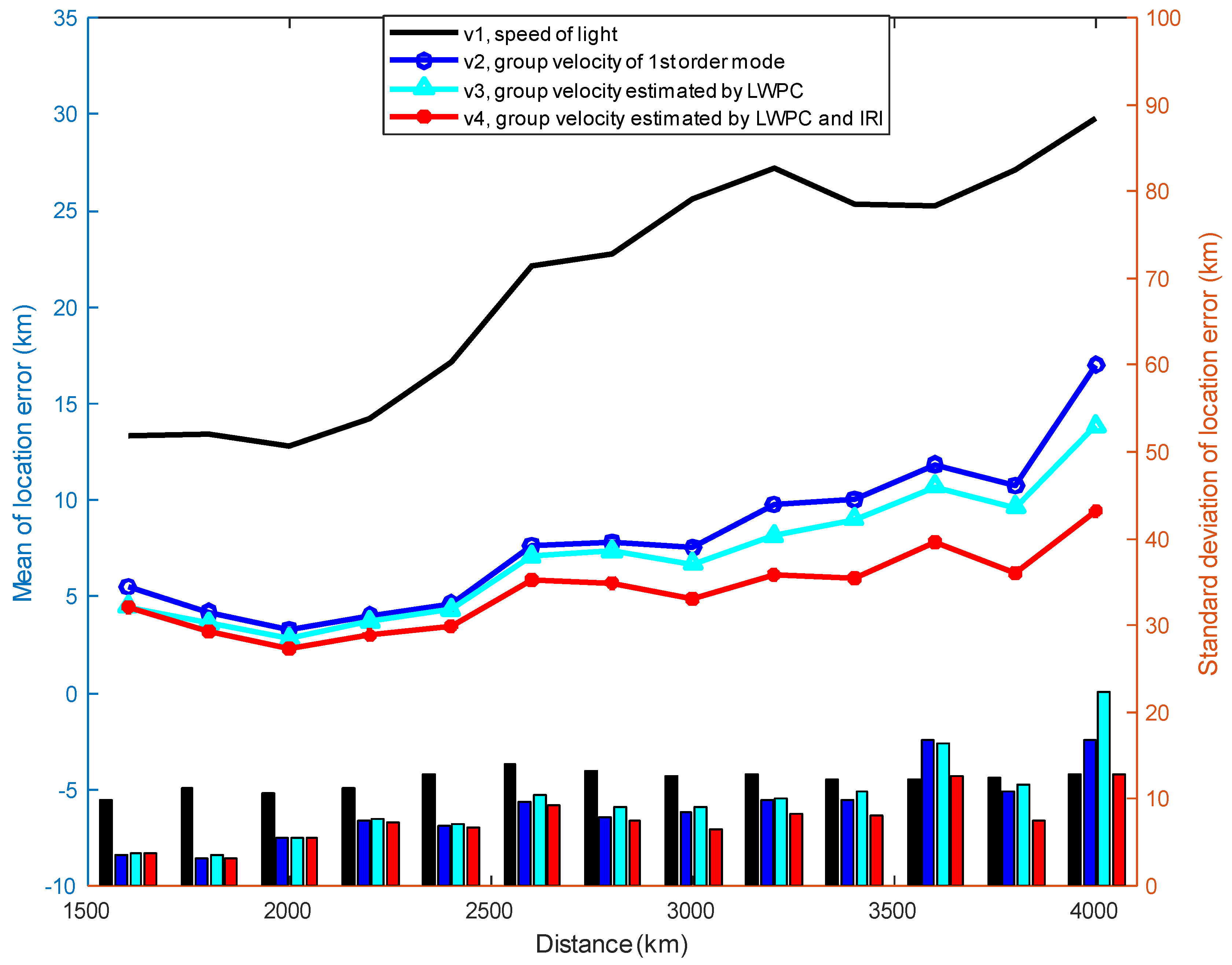
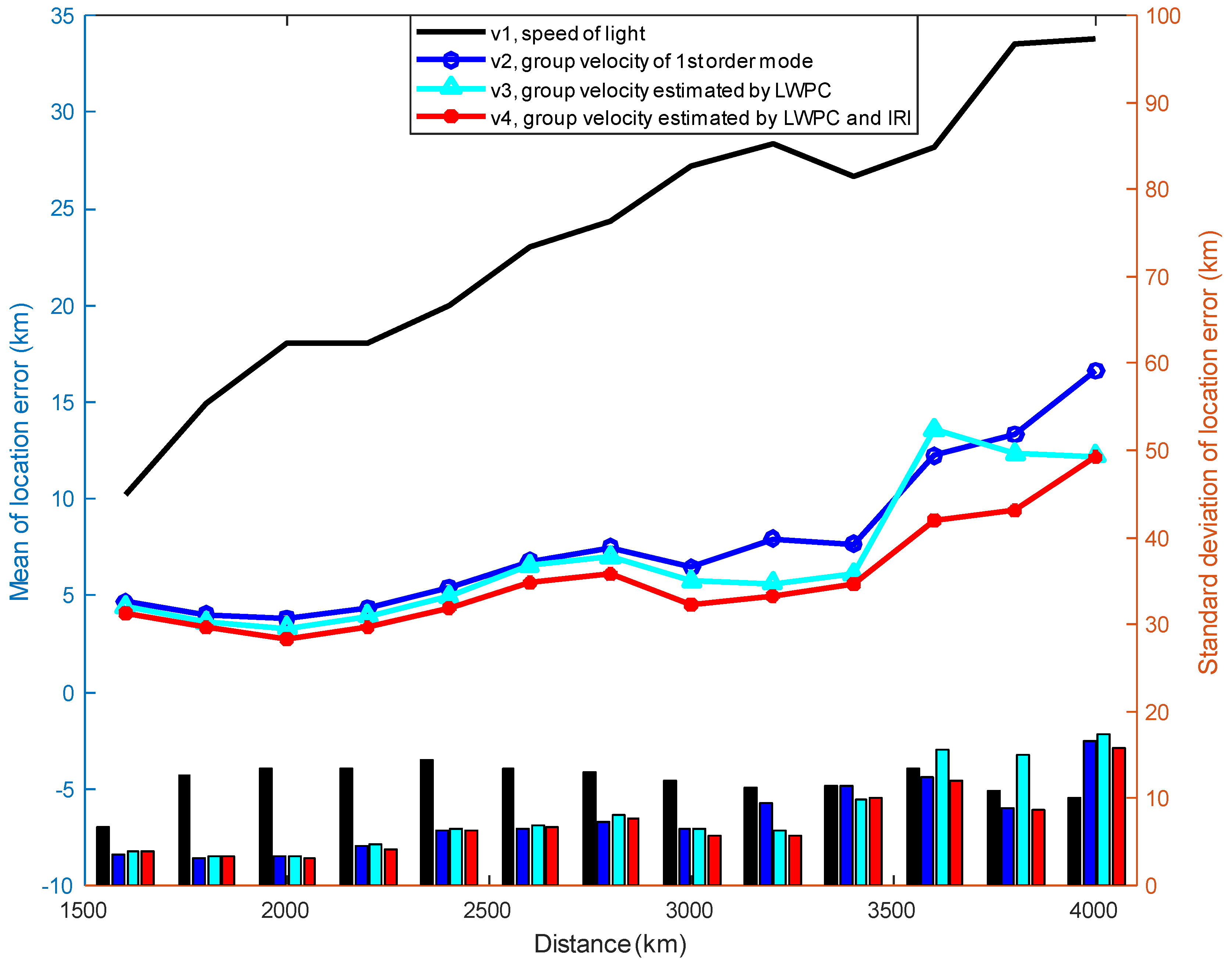
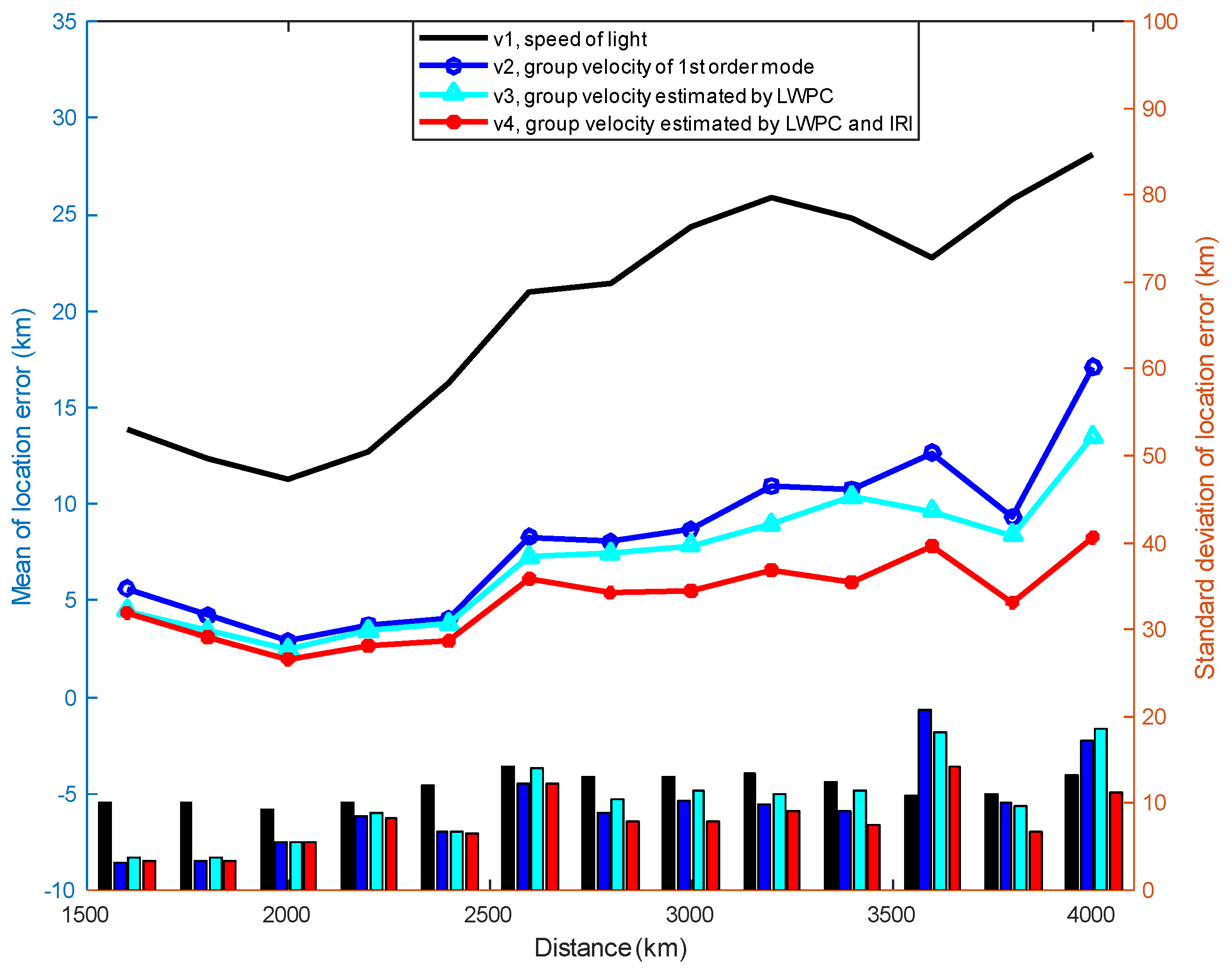
4. Discussion

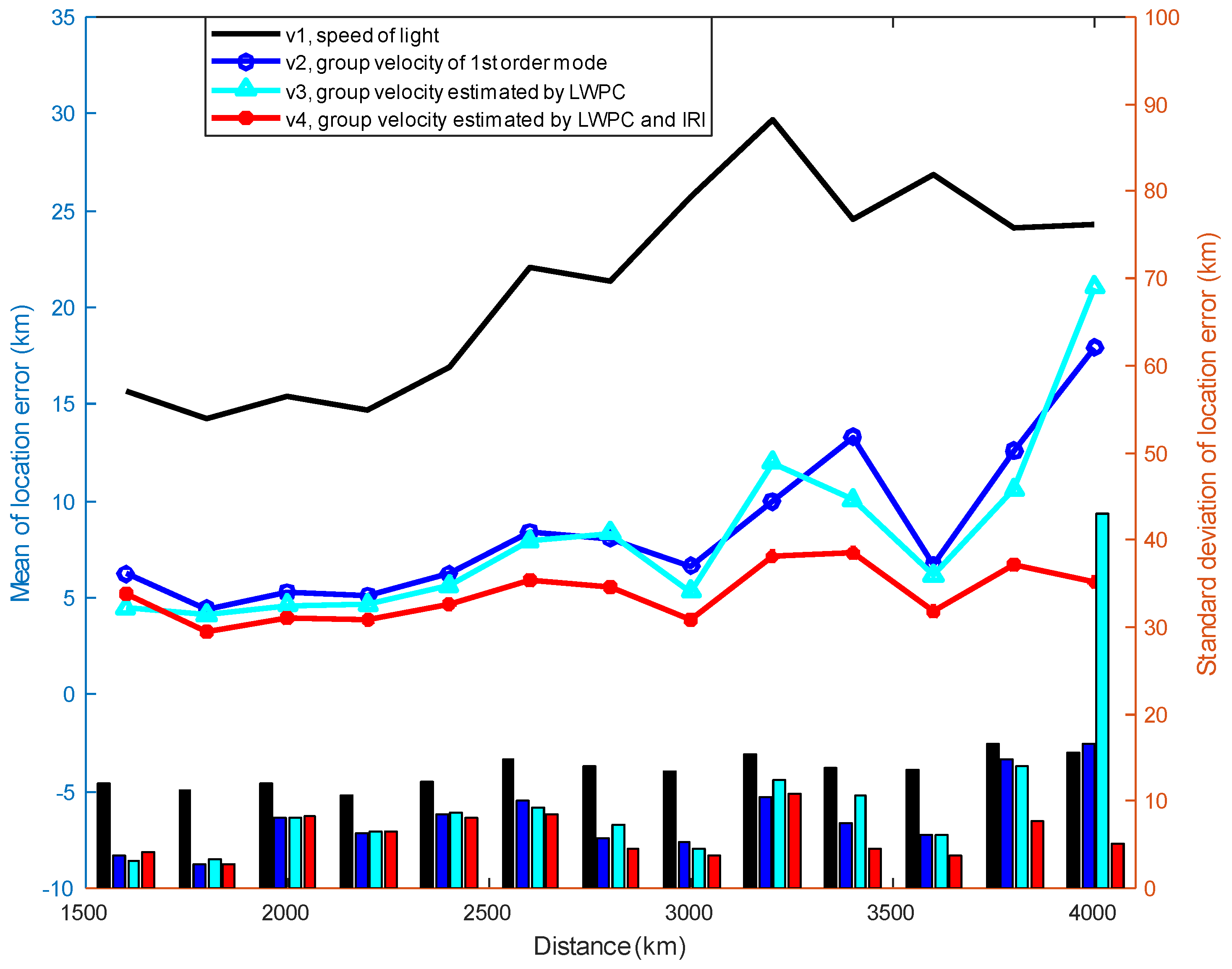
From the results in Section 3.2, it can be seen that, on the one hand, due to the joint use of LWPC and IRI models, group velocity v₄ has the best localization accuracy relative to other group velocity estimation methods; on the other hand, the first-order mode group velocity, v₂, also achieves very high localization accuracy by calculating the equivalent reflection height of the ionosphere on the path using the IRI model, and therefore, it is necessary to analyze the group velocities calculated by different methods of group velocity estimation. 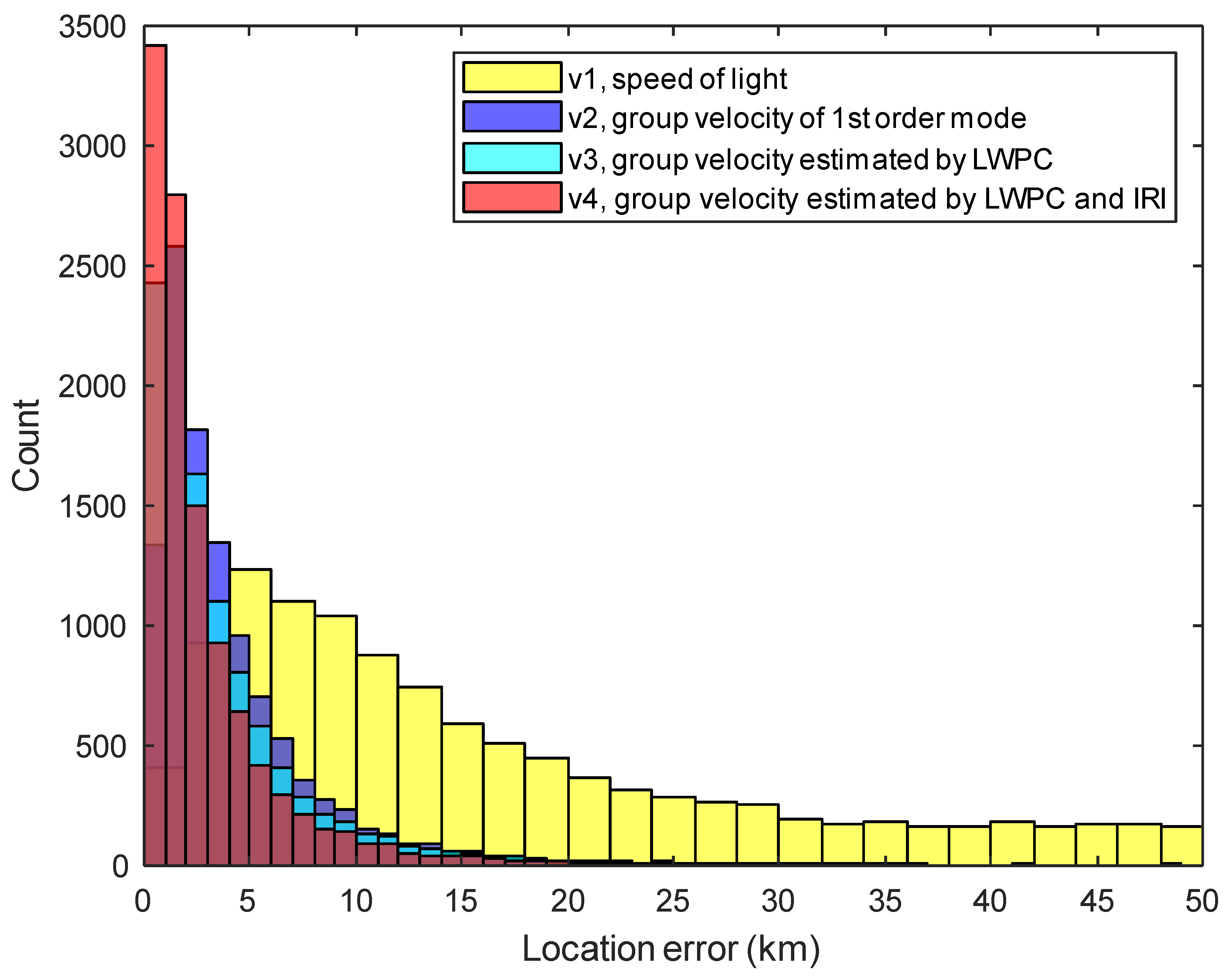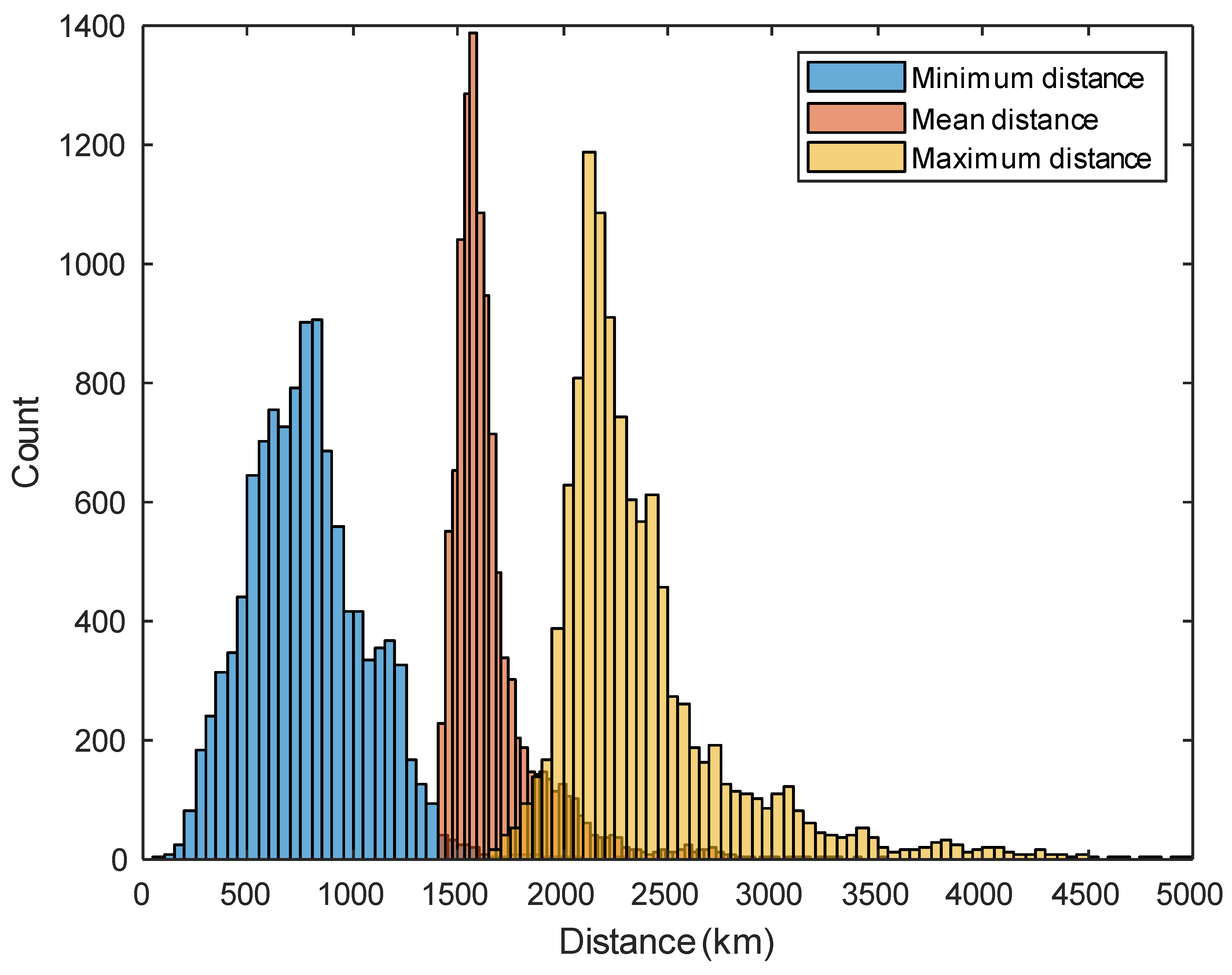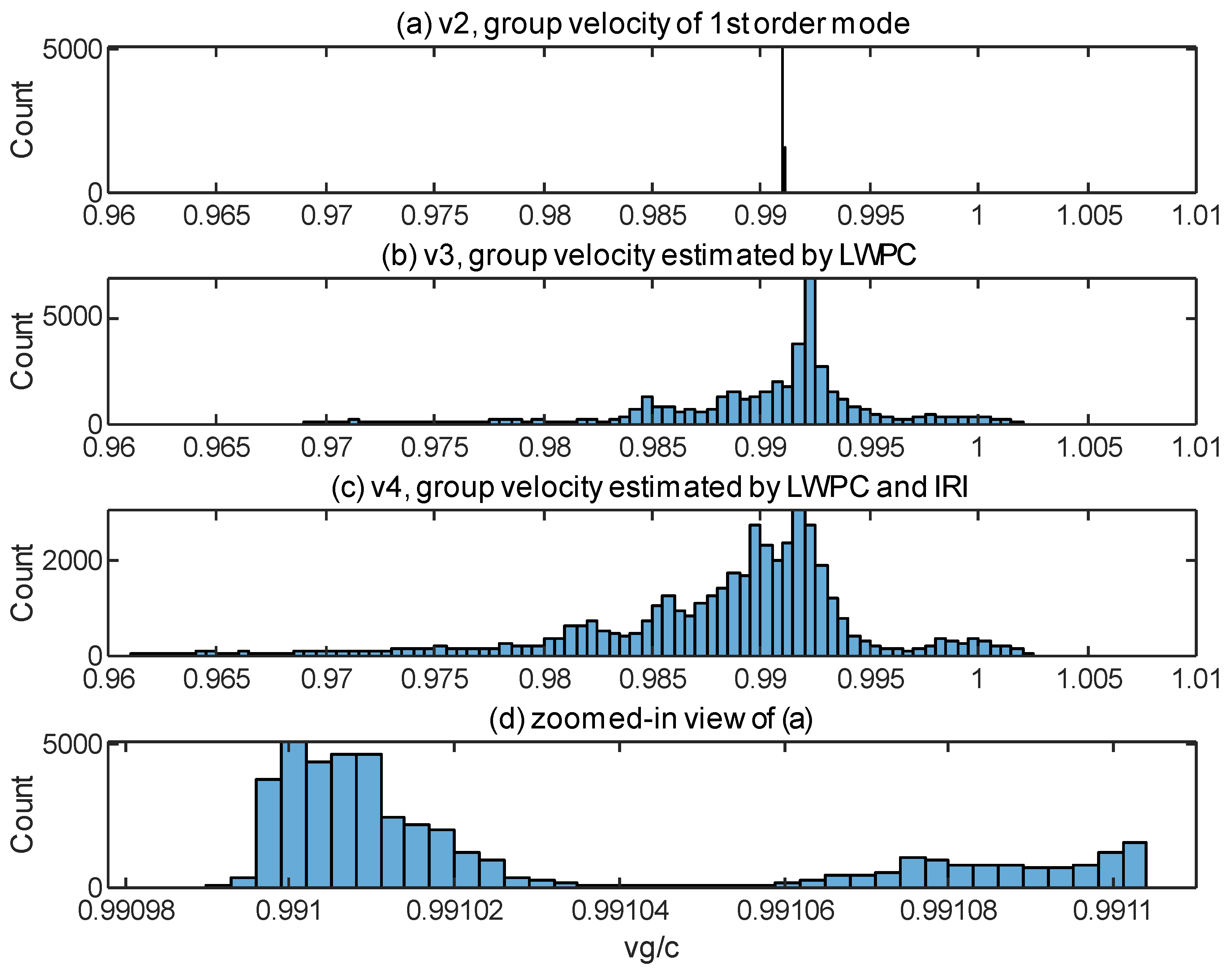We perform a statistical analysis of the group velocities of all lightning events in Figure 3, and the histograms of the group velocity distributions are plotted as shown in Figure 10. Figure 10a–c show the propagation velocity distribution of v₂, v₃, and v₄, respectively. Figure 10d is a zoomed-in view of the group velocity distribution in Figure 10a, and it can be seen that almost all of the group velocity values are concentrated in a very narrow interval around 0.991c.

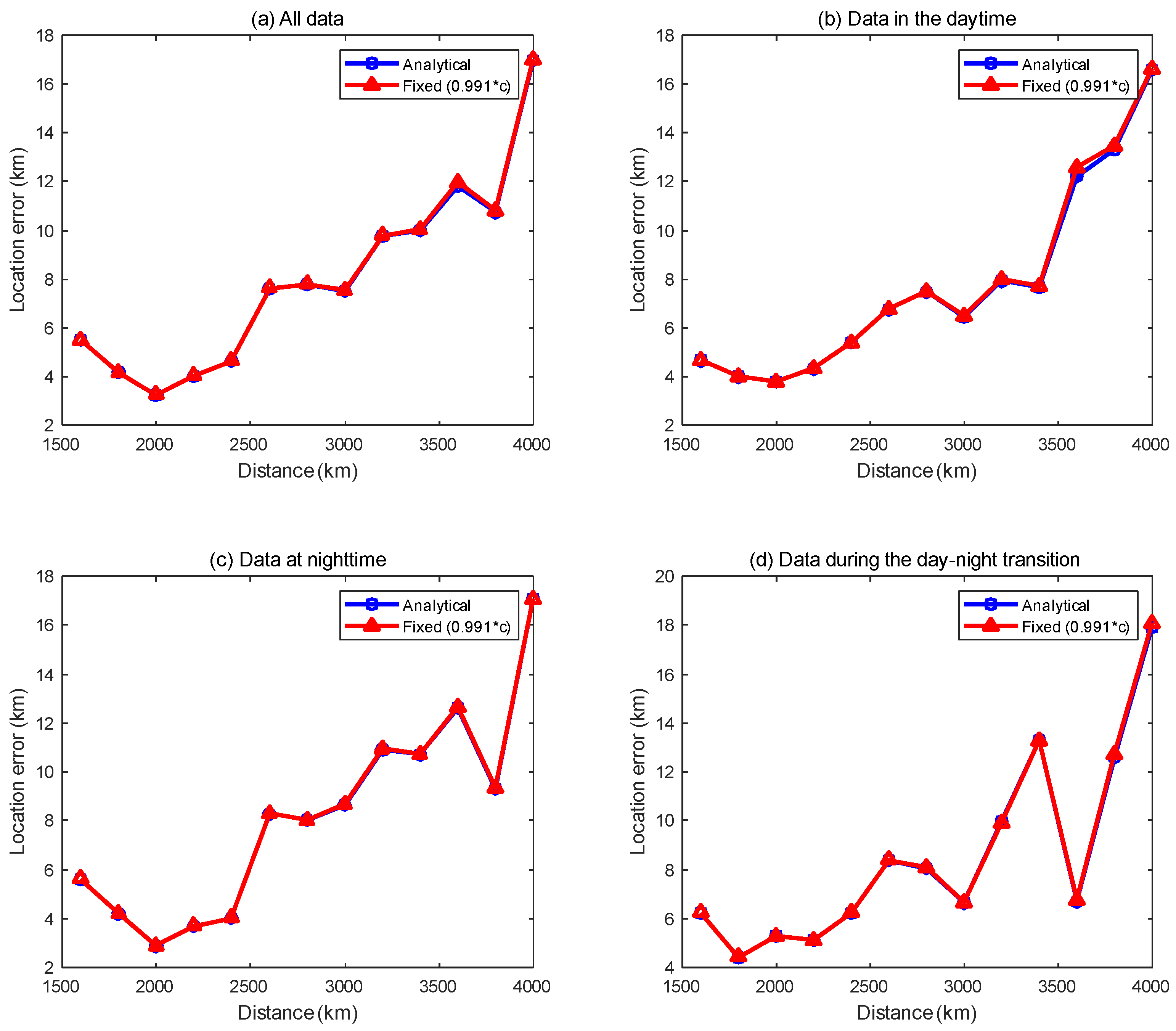
After the analysis of group velocity distribution in Figure 10 and the localization error in the previous section, a natural question arises: Since the group velocities of the first-order waveguide mode are mostly concentrated around 0.991c and have high localization accuracy, can similar localization accuracy be obtained by directly applying a fixed group velocity of 0.991c to all lightning detection data? Figure 11 shows the comparison of the localization error curves between the fixed group velocity (0.991c) and the group velocity of the first-order mode. Figure 11a–d show the comparison of the localization error curves using all data, daytime data, nighttime data and day–night transition data, respectively. As seen in the figure, the fixed group velocity achieves almost the same localization performance as the first-order mode group velocity, while the former does not need to use either the IRI model to calculate the equivalent reflection height of the ionosphere on the path or the LWPC model to calculate the phase of multiple frequency points. In other words, for our experimental detection network and a limited surrounding area, a fixed group velocity can be used to localize the lightning event and obtain a good localization accuracy similar to the first-order mode group velocity.

Nevertheless, we should note that the experimental data used in this paper are located in a very restricted area. When the lightning signal propagates farther and the propagation path is more complex, it is generally difficult to use a certain fixed group velocity to meet the diverse scenarios, and then the group velocity estimation method proposed in this paper can be used to improve the localization accuracy.

5. Conclusions

In this paper, we propose a group velocity estimation method based on the LWPC and IRI models for VLF/LF lightning localization. The performance of the method is quantitatively analyzed by a large amount of measured lightning location data and is fully compared with the speed of light in the air, the group velocity of the first-order waveguide mode, and the LWPC-based group velocity. The results show that the localization accuracy of both the group velocity of the first-order mode and the LWPC-based group velocity improve substantially with respect to the speed of light in the air, and our proposed method in this paper has the smallest localization error due to the joint use of the LWPC and IRI models. Although our proposed method is designed for the quiet state of the ionosphere, it can also be combined with the real-time remote sensing technique of the ionospheric D-layer to improve the lightning location accuracy when there are sudden ionospheric disturbances.