A Robust Track Error Estimation Method for Airborne SAR Based on Accuracy Analysis Model
Abstract
1. Introduction
- From the above literature, quite a lot of methods use the phase errors obtained by autofocus algorithms to estimate motion errors. However, they lack the theoretical analysis of the motion error estimation model. Therefore, this paper derives the accuracy limits, the CRLB, of this model for the first time. The CRLB specifies the factors affecting the estimation accuracy.
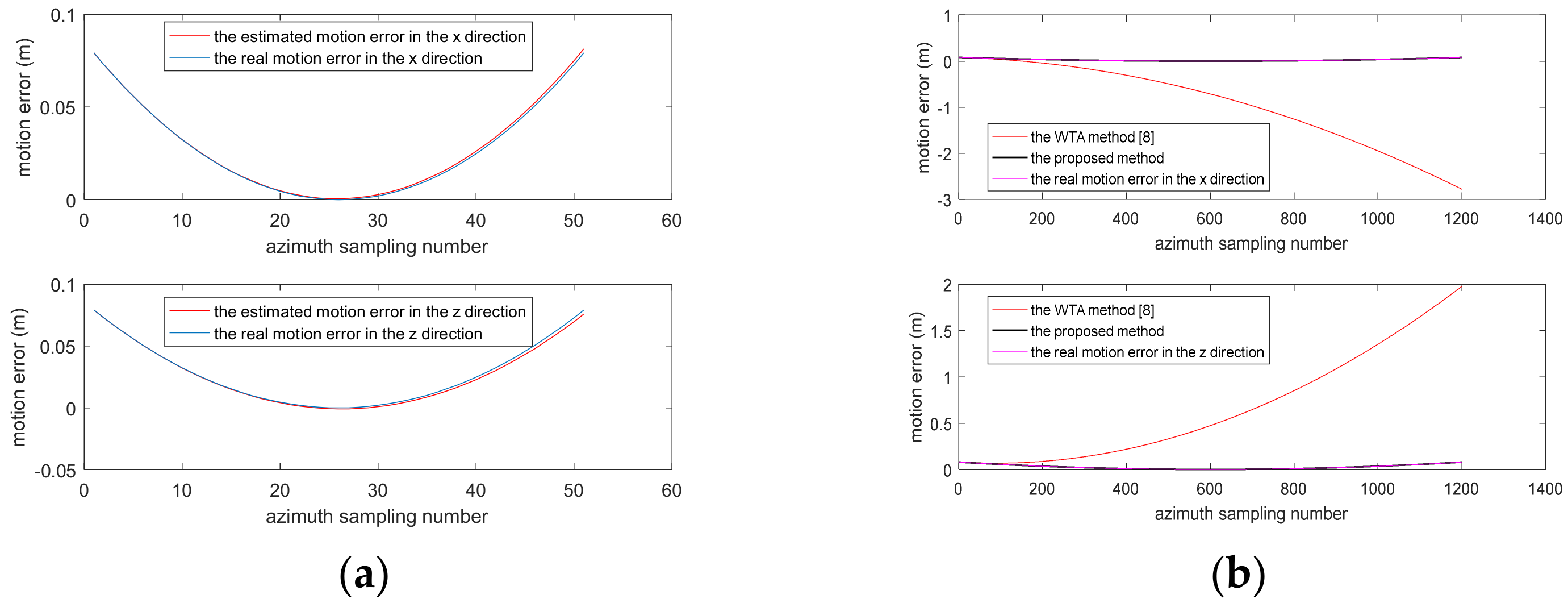
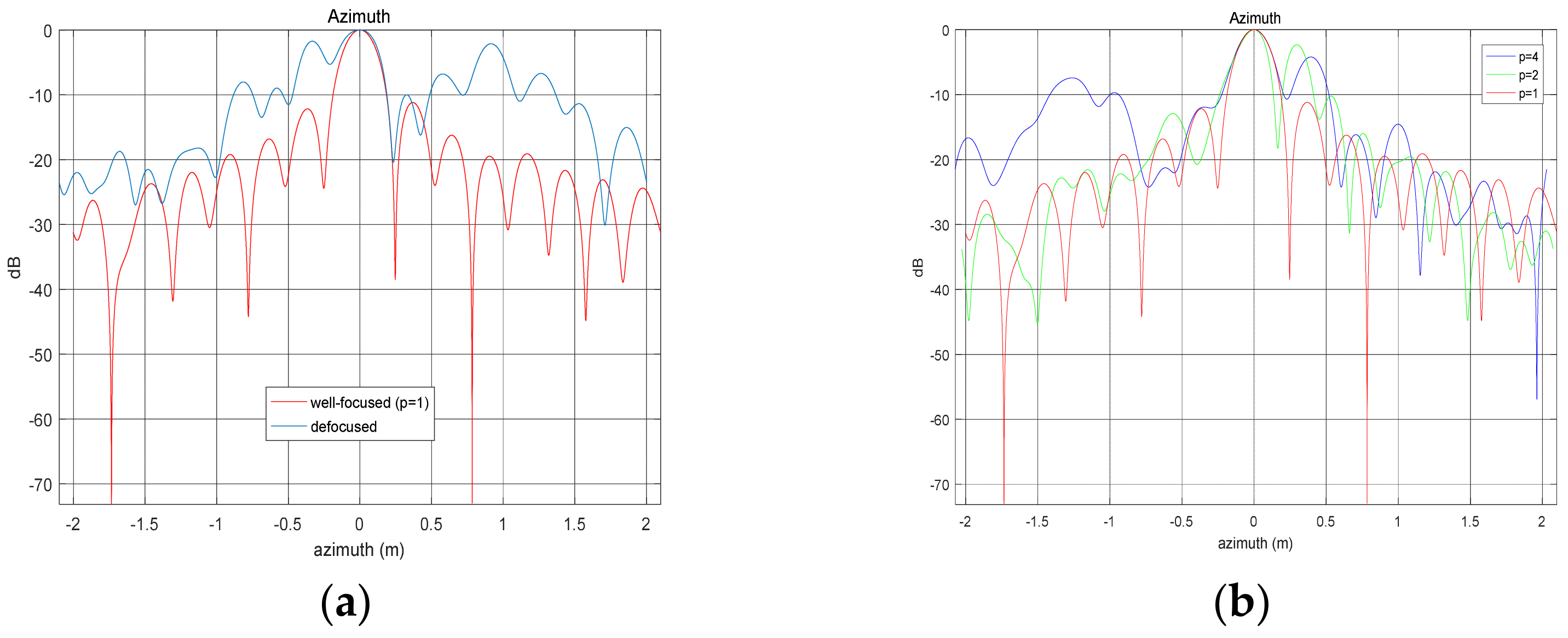
- The step length of the estimation kernel in WTA [6] is not considered, but is directly set to one. However, when the pulse repetition frequency (PRF) is relatively high because of the high azimuth resolution or velocity, this unconsidered way of setting is not reasonable. It will cause the estimated phase error gradients to be drowned in the noise. The noise accumulation of the double integration of these gradients has a very poor effect on the final track estimation results. So, based on the accuracy analysis model, we propose a more robust improvement of the WTA algorithm by selecting the appropriate step length. The proposed method can better resist the effects of noise and further ensure estimation accuracy compared to WTA.
2. Fundamentals
2.1. Signal Model of Phase Error Estimation
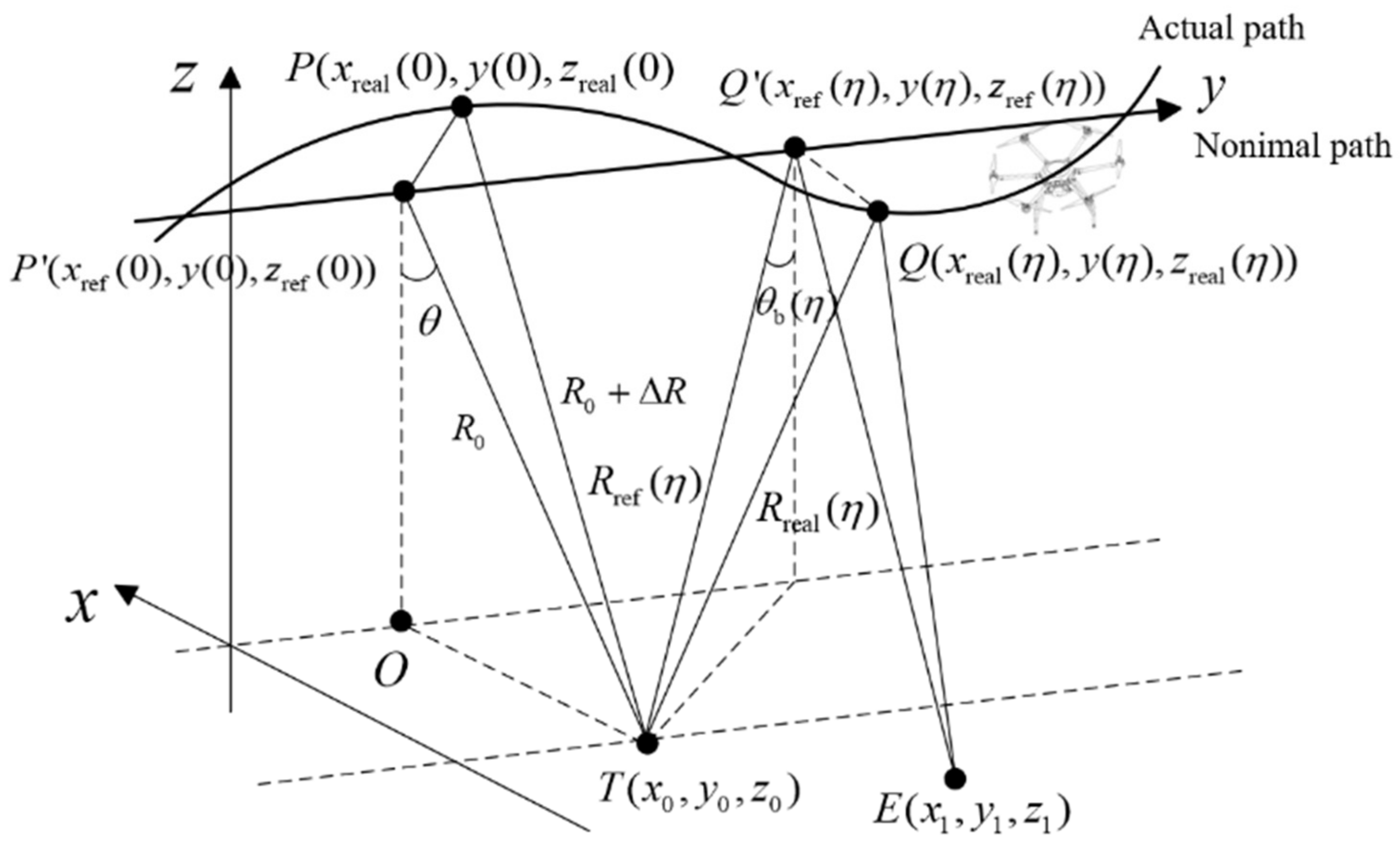
2.2. Motion Error Estimation Model
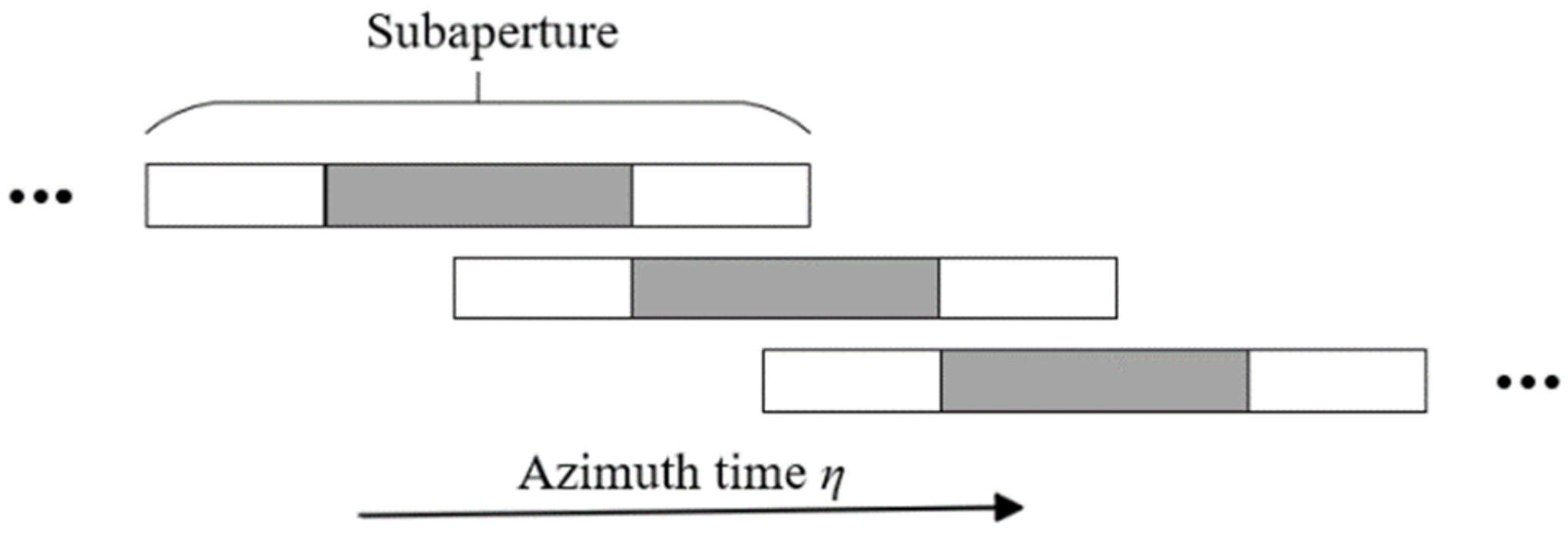
2.3. The Main Steps of WTA
- Estimating the double phase error gradients by PGA-based autofocus method: In the azimuth subapertures, dozens of strong targets are chosen to calculate the double phase error gradients based on the signals after the azimuth dechirp. The target-selection criteria [17] are used, which consider both the Doppler flatness and the energy.
- Filtering the double phase error gradients by polynomial fitting: By double integrating the estimated double phase error gradients and performing the polynomial fitting, the filtered phases are obtained. Then, the filtered double-phase gradients can be obtained by taking the second derivative of the above-fitted phases.
3. Accuracy Limits Analysis of Motion Error Estimation
3.1. Derivation of the CRLB
3.2. Correctness Verification of the Derived CRLB
3.3. Analysis of Influencing Factors of CRLB
- The shorter the wavelength, the smaller the CRLB.
- The smaller the variance , the smaller the CRLB.
- The more targets, the smaller the CRLB. When adding one target, the numerator of the formula increases by one term, while the denominator increases by terms. Because the denominator increases more than the numerator, the CRLB becomes smaller.
- The more extensive the incident angle range, the smaller the CRLB. When the range of incident angles increases, the difference between the incident angles increases. So, in the denominator increases and CRLB becomes smaller.
- When the incident angles increase, the CRLB in the x direction decreases and increases in the z direction. When the angles become larger, the numerator in the x direction is , which becomes smaller. The numerator in the z direction is , which becomes larger.
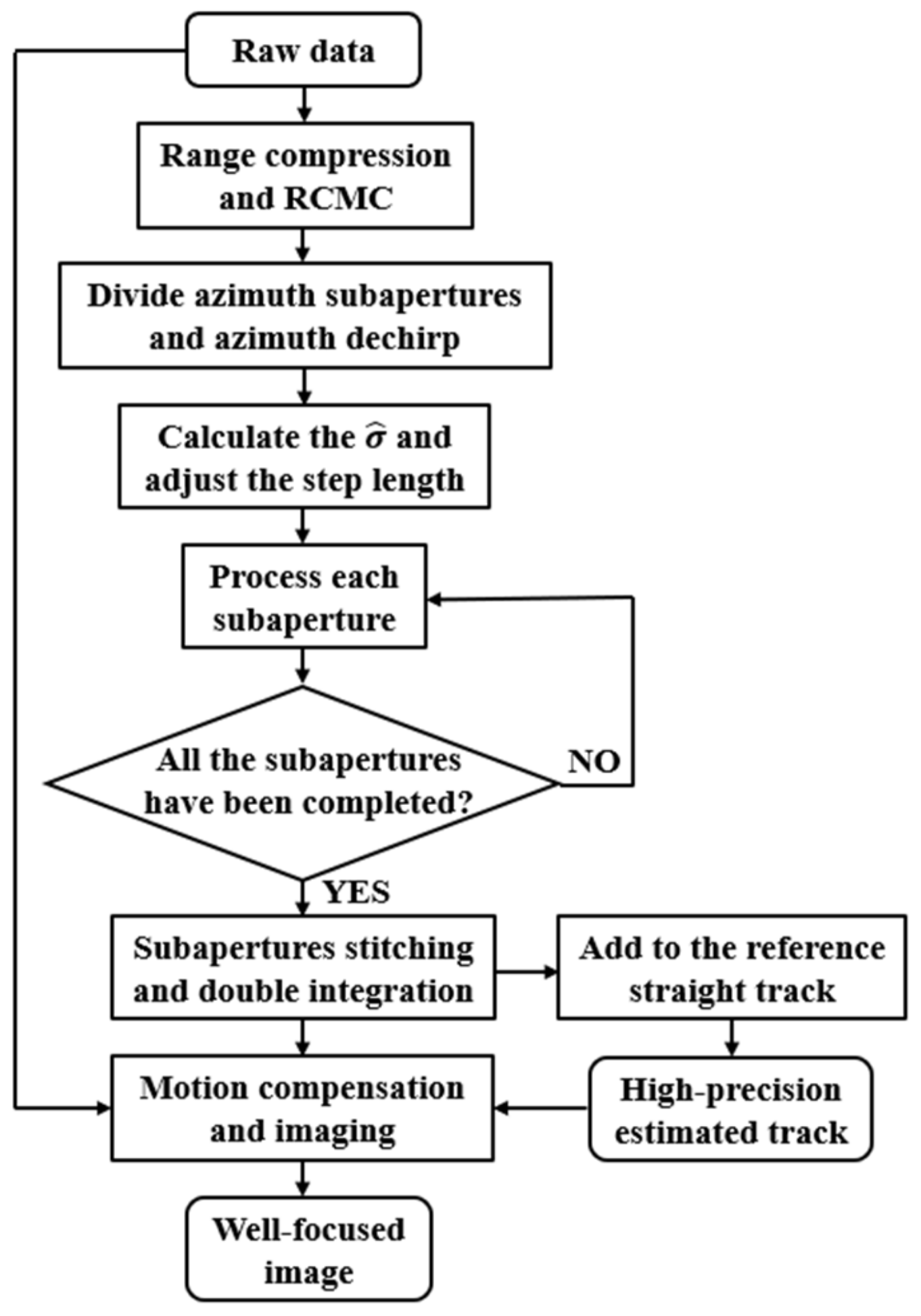
4. An Improved Track Error Estimation Method
4.1. Criteria of Step Length Selection
- The estimated double phase gradients should not be so large that Equation (36) exceeds the principal value interval. Otherwise, it will lead to phase wrapping [23].
- Track variation information cannot be lost. Increasing the step length is equivalent to down-sampling the track. We can use the a priori upper limit frequency information of the actual track to ensure that the track loss is within an acceptable range.
4.2. Method of Selecting Step Length
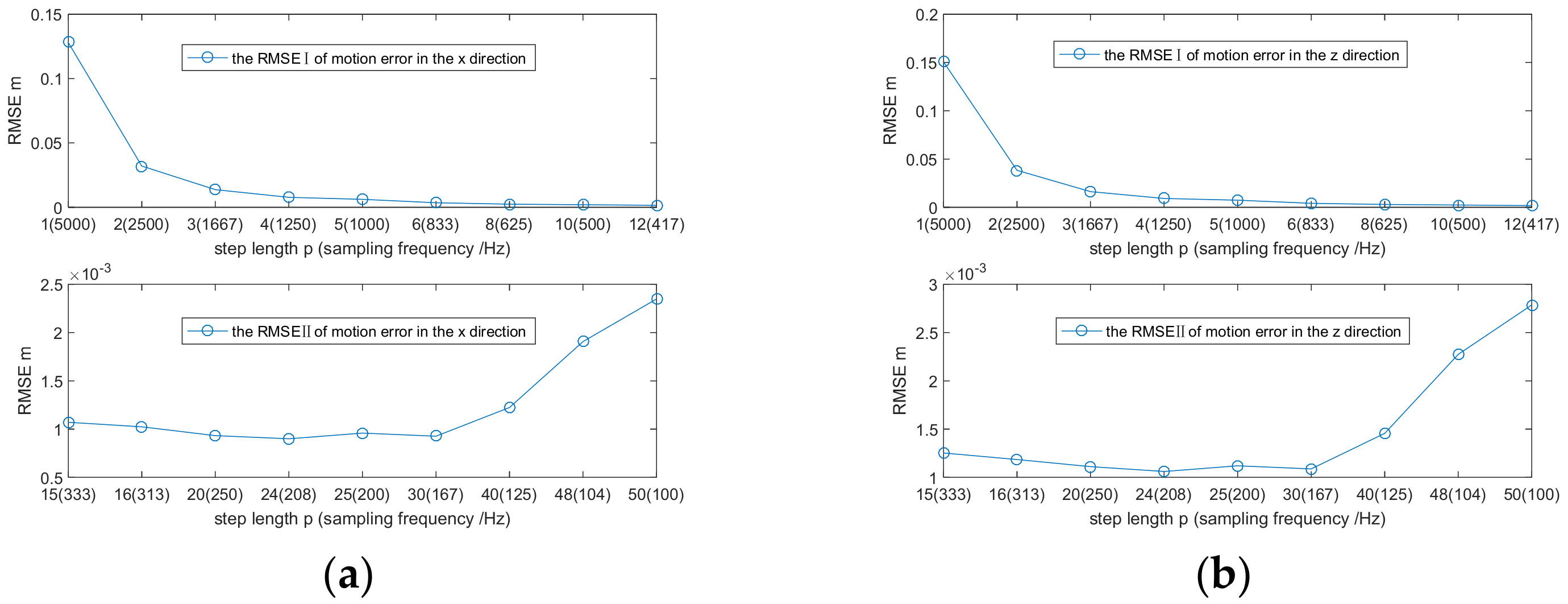
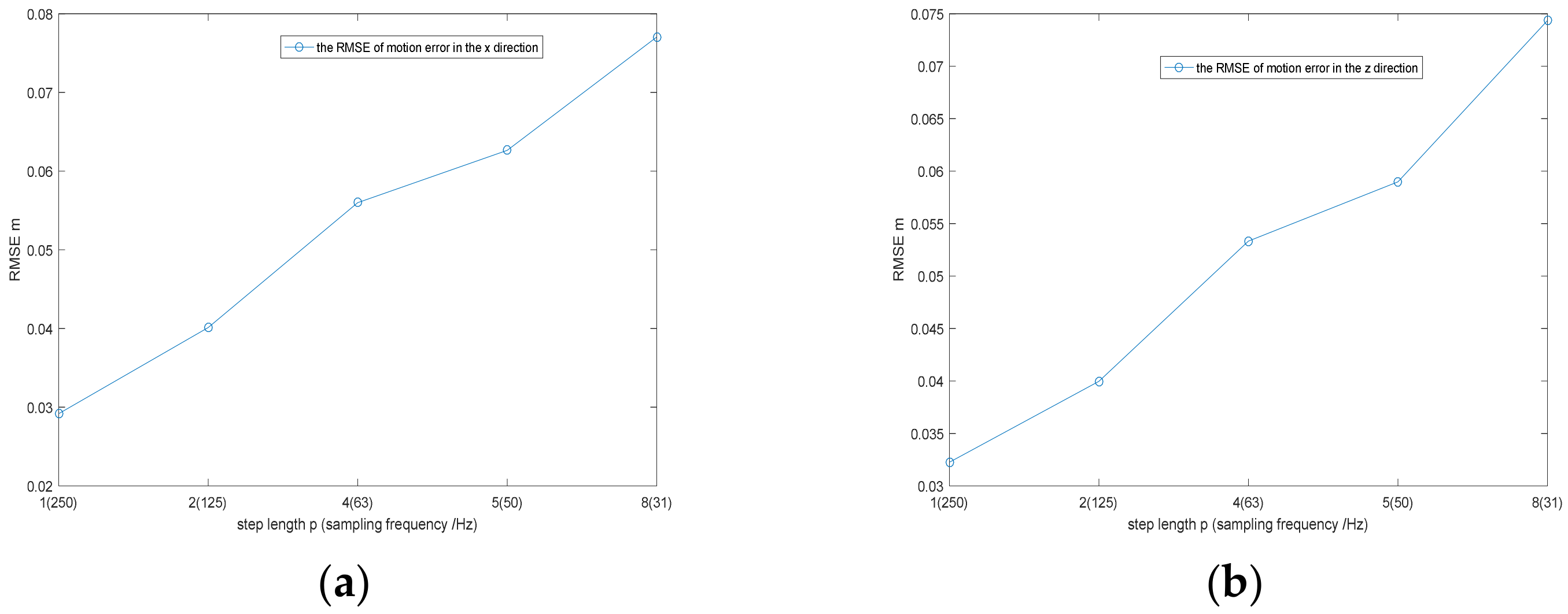
- When the step length defaults to one, like the WTA, we can obtain the estimated double-phase gradients. We use them to approximately calculate the standard deviation of phase estimation errors [6]. Then, we use the standard deviation and the other known parameters to calculate the CRLB. We can take the square root of CRLB to obtain . measures the estimation errors of the double-motion gradients. When is larger than the ground truth of the double motion gradients, the estimation errors lead to a pretty negative impact, which means we must select the appropriate step.
- To select the suitable step, we use the a priori weak navigation information and the basic parameters of scenes to conduct random experiments to estimate motion errors. From the experiments, we can obtain the root mean square error (RMSE) curve of estimation errors. The step length that minimizes the RMSE should be chosen as the appropriate one.
4.3. Overall Process of the Improved Method
5. Experiments and Results
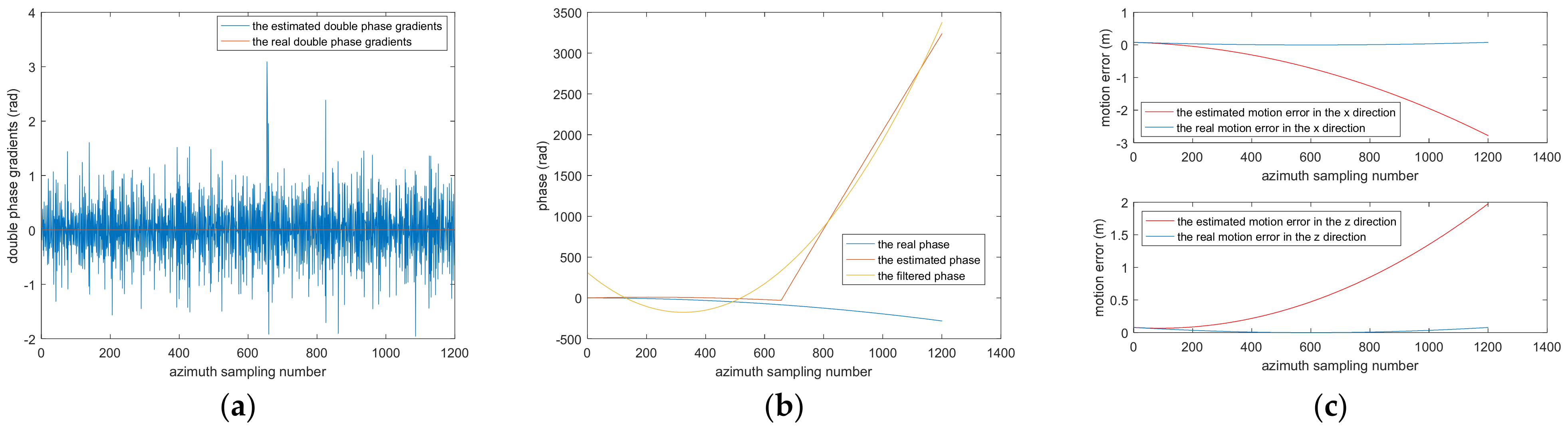
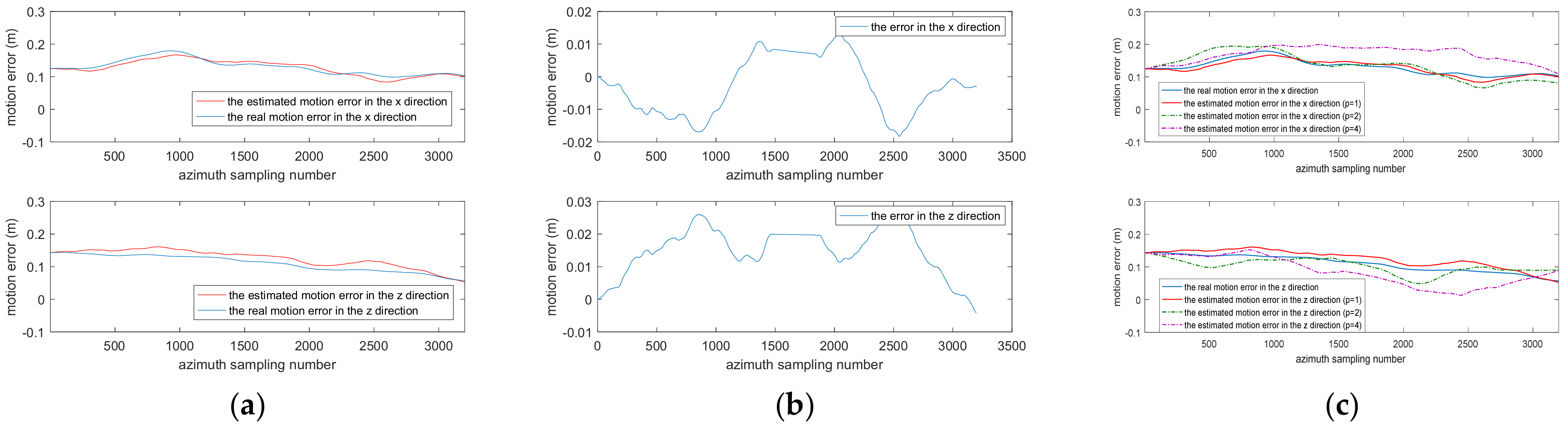
5.1. Simulation Experiment Where PRF Is High
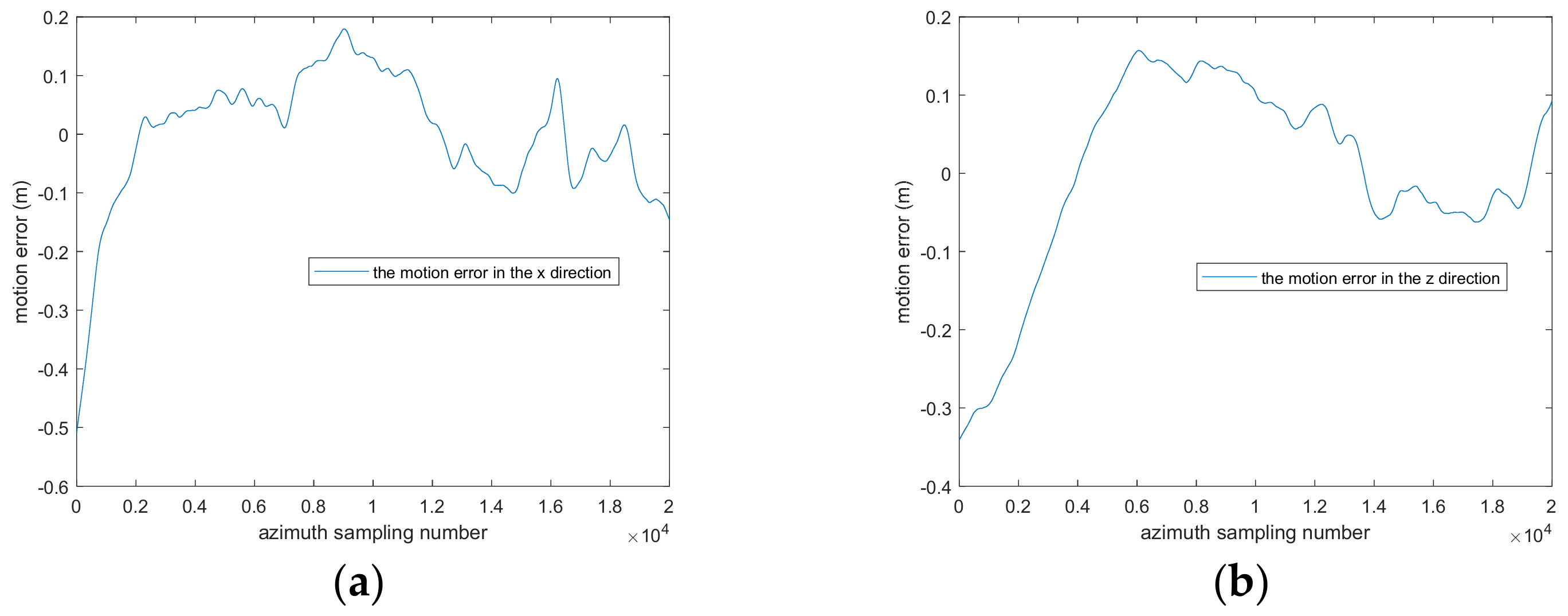
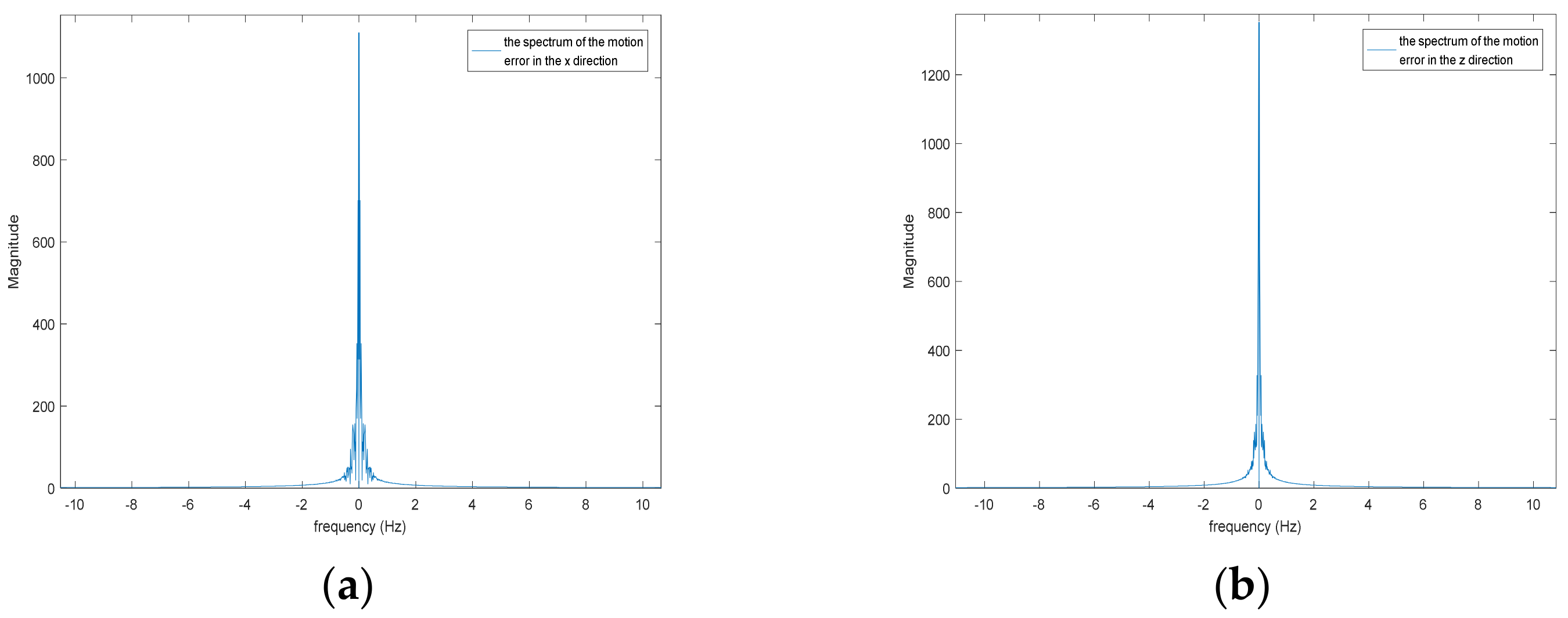
5.2. Airborne SAR Data Experiment Where PRF Is Low
6. Discussions
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wiley, C.A. Synthetic Aperture Radars. IEEE Trans. Aerosp. Electron. Syst. 1985, AES-21, 440–443. [Google Scholar] [CrossRef]
- Xing, M.; Jiang, X.; Wu, R.; Zhou, F.; Bao, Z. Motion compensation for UAV SAR based on raw radar data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2870–2883. [Google Scholar] [CrossRef]
- Bejiga, M.B.; Zeggada, A.; Nouffidj, A.; Melgani, F. A convolutional neural network approach for assisting avalanche search and rescue operations with UAV imagery. Remote Sens. 2017, 9, 100. [Google Scholar] [CrossRef]
- Liang, Y.; Li, G.; Wen, J.; Zhang, G.; Dang, Y.; Xing, M. A fast time-domain SAR imaging and corresponding autofocus method based on hybrid coordinate system. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8627–8640. [Google Scholar] [CrossRef]
- Bezvesilniy, O.O.; Gorovyi, I.M.; Vavriv, D.M. Autofocusing SAR images via local estimates of flight trajectory. Int. J. Microw. Wirel. Technol. 2016, 8, 881–889. [Google Scholar] [CrossRef]
- Li, Y.; Liu, C.; Wang, Y.; Wang, Q. A robust motion error estimation method based on raw data. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2780–2790. [Google Scholar] [CrossRef]
- Li, J.; Chen, J.; Wang, P.; Loffeld, O. A Coarse-to-Fine Autofocus Approach for Very High-Resolution Airborne Stripmap SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3814–3829. [Google Scholar] [CrossRef]
- Ran, L.; Liu, Z.; Zhang, L.; Li, T.; Xie, R. An autofocus algorithm for estimating residual trajectory deviations in synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3408–3425. [Google Scholar] [CrossRef]
- Sjanic, Z.; Gustafsson, F. Simultaneous navigation and SAR auto-focusing. In Proceedings of the 2010 13th International Conference on Information Fusion, Edinburgh, UK, 26–29 July 2010; pp. 1–7. [Google Scholar]
- Pu, W.; Wu, J.; Huang, Y.; Yang, J.; Yang, H. Fast factorized backprojection imaging algorithm integrated with motion trajectory estimation for bistatic forward-looking SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3949–3965. [Google Scholar] [CrossRef]
- Hu, K.; Zhang, X.; He, S.; Zhao, H.; Shi, J. A less-memory and high-efficiency autofocus back projection algorithm for SAR imaging. IEEE Geosci. Remote Sens. Lett. 2014, 12, 890–894. [Google Scholar]
- Torgrimsson, J.; Dammert, P.; Hellsten, H.; Ulander, L.M.H. An efficient solution to the factorized geometrical autofocus problem. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4732–4748. [Google Scholar] [CrossRef]
- Chen, J.; Xing, M.; Yu, H.; Liang, B.; Peng, J.; Sun, G.C. Motion Compensation/Autofocus in Airborne Synthetic Aperture Radar: A Review. IEEE Geosci. Remote Sens. Mag. 2022, 10, 185–206. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Z.; Zhou, Y.; Wang, P.; Qiu, J. A novel motion compensation scheme for airborne very high resolution SAR. Remote Sens. 2021, 13, 2729. [Google Scholar] [CrossRef]
- Wahl, D.E.; Eichel, P.H.; Ghiglia, D.C.; Jakowatz, C.V. Phase gradient autofocus-a robust tool for high resolution SAR phase correction. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 827–835. [Google Scholar] [CrossRef]
- Prats, P.; Camara, D.; Reigber, A.; Scheiber, R.; Mallorqui, J.J. Comparison of Topography- and Aperture-Dependent Motion Compensation Algorithms for Airborne SAR. IEEE Geosci. Remote Sens. Lett. 2007, 4, 349–353. [Google Scholar] [CrossRef]
- Chan, H.L.; Yeo, T.S. Noniterative quality phase-gradient autofocus (QPGA) algorithm for spotlight SAR imagery. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1531–1539. [Google Scholar] [CrossRef]
- Chen, J.; Liang, B.; Zhang, J.; Yang, D.G.; Deng, Y.; Xing, M. Efficiency and Robustness Improvement of Airborne SAR Motion Compensation With High Resolution and Wide Swath. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Zhang, L.; Qiao, Z.; Xing, M.; Yang, L.; Bao, Z. A Robust Motion Compensation Approach for UAV SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3202–3218. [Google Scholar] [CrossRef]
- Scharf, L.L. Statistical Signal Processing: Detection, Estimation, and Time Series Analysis; Addison-Wesley Publishing Company: Boston, MA, USA, 1991. [Google Scholar]
- Stoica, P.; Moses, R.L. Spectral Analysis of Signals; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2005; Volume 452. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1993. [Google Scholar]
- Pu, L.; Zhang, X.; Zhou, Z.; Li, L.; Zhou, L.; Shi, J.; Wei, S. A Robust InSAR Phase Unwrapping Method via Phase Gradient Estimation Network. Remote Sens. 2021, 13, 4564. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, J.; Yu, H.; Xu, G.; Liang, B.; Yang, D.G.; Wang, H. Blind NCS-Based Autofocus for Airborne Wide-Beam SAR Imaging. IEEE Trans. Comput. Imaging 2022, 8, 626–638. [Google Scholar] [CrossRef]
- Macedo, K.A.C.d.; Scheiber, R. Precise topography- and aperture-dependent motion compensation for airborne SAR. IEEE Geosci. Remote Sens. Lett. 2005, 2, 172–176. [Google Scholar] [CrossRef]





| Target | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Incident angle (°) | 19.19 | 27.57 | 34.84 | 41.03 | 46.24 | 50.62 | 54.31 | 57.44 | 60.12 |
| Real Phase error (rad) | −112.15 | −117.53 | −120.16 | −120.88 | −120.40 | −119.22 | −117.69 | −116.00 | −114.29 |
| Target | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Group 1 (°) | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 | 6.5 | 7 |
| Group 2 (°) | 8 | 8.5 | 9 | 9.5 | 10 | 10.5 | 11 | 11.5 | 12 |
| Group 3 (°) | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 | 16 | 16.5 | 17 |
| Group 4 (°) | 18 | 18.5 | 19 | 19.5 | 20 | 20.5 | 21 | 21.5 | 22 |
| Group 5 (°) | 23 | 23.5 | 24 | 24.5 | 25 | 25.5 | 26 | 26.5 | 27 |
| Group 6 (°) | 28 | 28.5 | 29 | 29.5 | 30 | 30.5 | 31 | 31.5 | 32 |
| Parameter | Value |
|---|---|
| Carrier frequency | 15.14 GHz |
| PRF | 5000 Hz |
| Velocity | 66.56 m/s |
| Target | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Incident angle (°) | 42.58 | 44.43 | 46.16 | 47.80 | 49.33 | 50.78 | 52.14 | 53.42 | 54.64 | 55.78 |
| Parameter | Value |
|---|---|
| Carrier frequency | 15.2 GHz |
| Bandwidth | 1.2 GHz |
| PRF | 249.99 Hz |
| Velocity | 8.01 m/s |
| Flight altitude | 402.2585 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, M.; Qiu, X.; Cheng, Y.; Lv, J.; Ding, C. A Robust Track Error Estimation Method for Airborne SAR Based on Accuracy Analysis Model. Remote Sens. 2022, 14, 5769. https://doi.org/10.3390/rs14225769
Gao M, Qiu X, Cheng Y, Lv J, Ding C. A Robust Track Error Estimation Method for Airborne SAR Based on Accuracy Analysis Model. Remote Sensing. 2022; 14(22):5769. https://doi.org/10.3390/rs14225769
Chicago/Turabian StyleGao, Ming, Xiaolan Qiu, Yao Cheng, Junwei Lv, and Chibiao Ding. 2022. "A Robust Track Error Estimation Method for Airborne SAR Based on Accuracy Analysis Model" Remote Sensing 14, no. 22: 5769. https://doi.org/10.3390/rs14225769
APA StyleGao, M., Qiu, X., Cheng, Y., Lv, J., & Ding, C. (2022). A Robust Track Error Estimation Method for Airborne SAR Based on Accuracy Analysis Model. Remote Sensing, 14(22), 5769. https://doi.org/10.3390/rs14225769







