Development of a New Vertical Water Vapor Model for GNSS Water Vapor Tomography
Abstract
1. Introduction
2. Voxel-Based GNSS Tropospheric WV Tomography
3. GNSS Tomographic Experiment
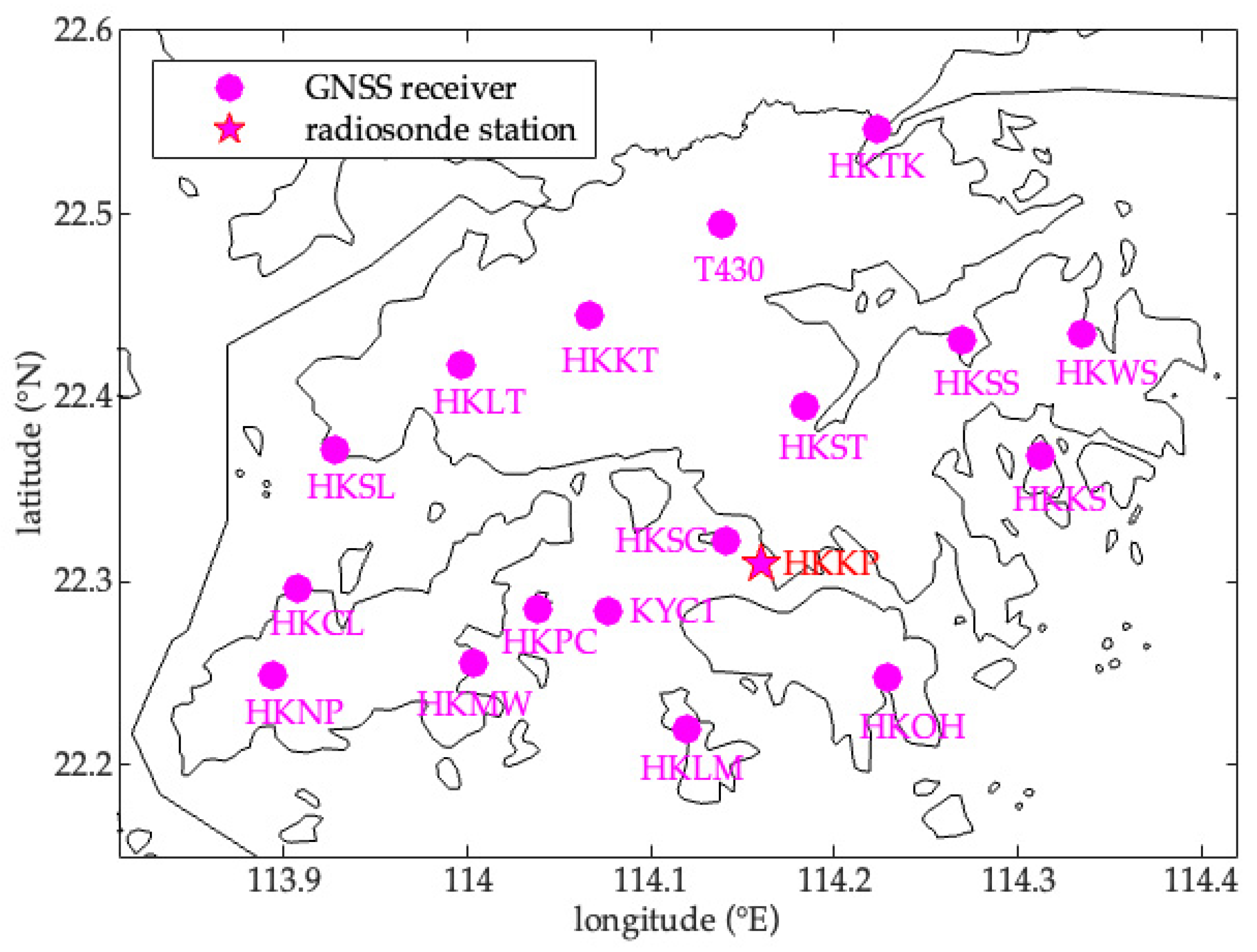
3.1. Data Description and Data Processing
3.1.1. GNSS Data
3.1.2. Radiosonde Data
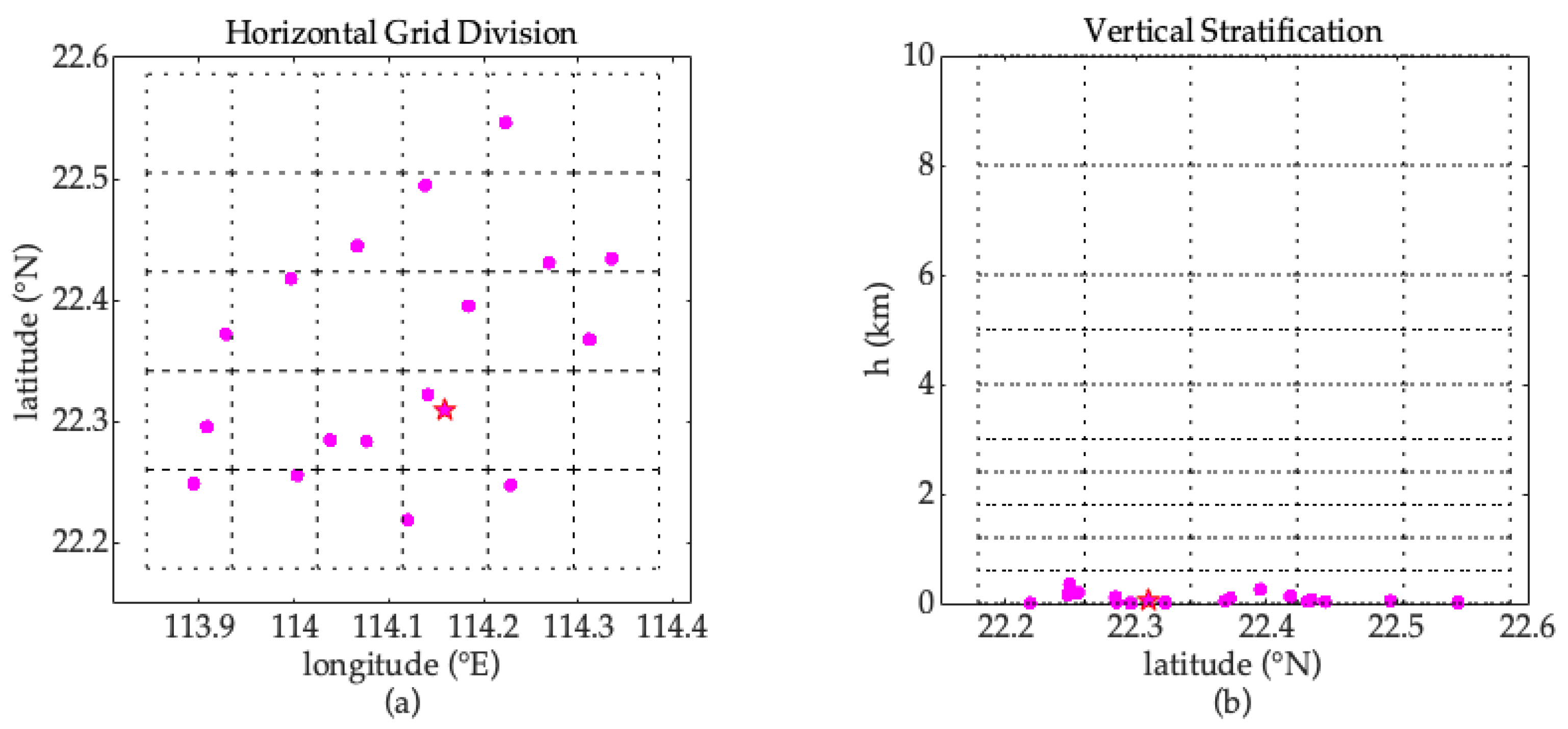
3.2. Division Strategy for Tomographic Voxel
3.3. Vertical Constraint Conditions
3.3.1. Traditional Vertical Constraint Condition
3.3.2. Newly Proposed Vertical Constraint Model
4. Test Results of Using Different Vertical Constraints
4.1. RE of Layered WVD
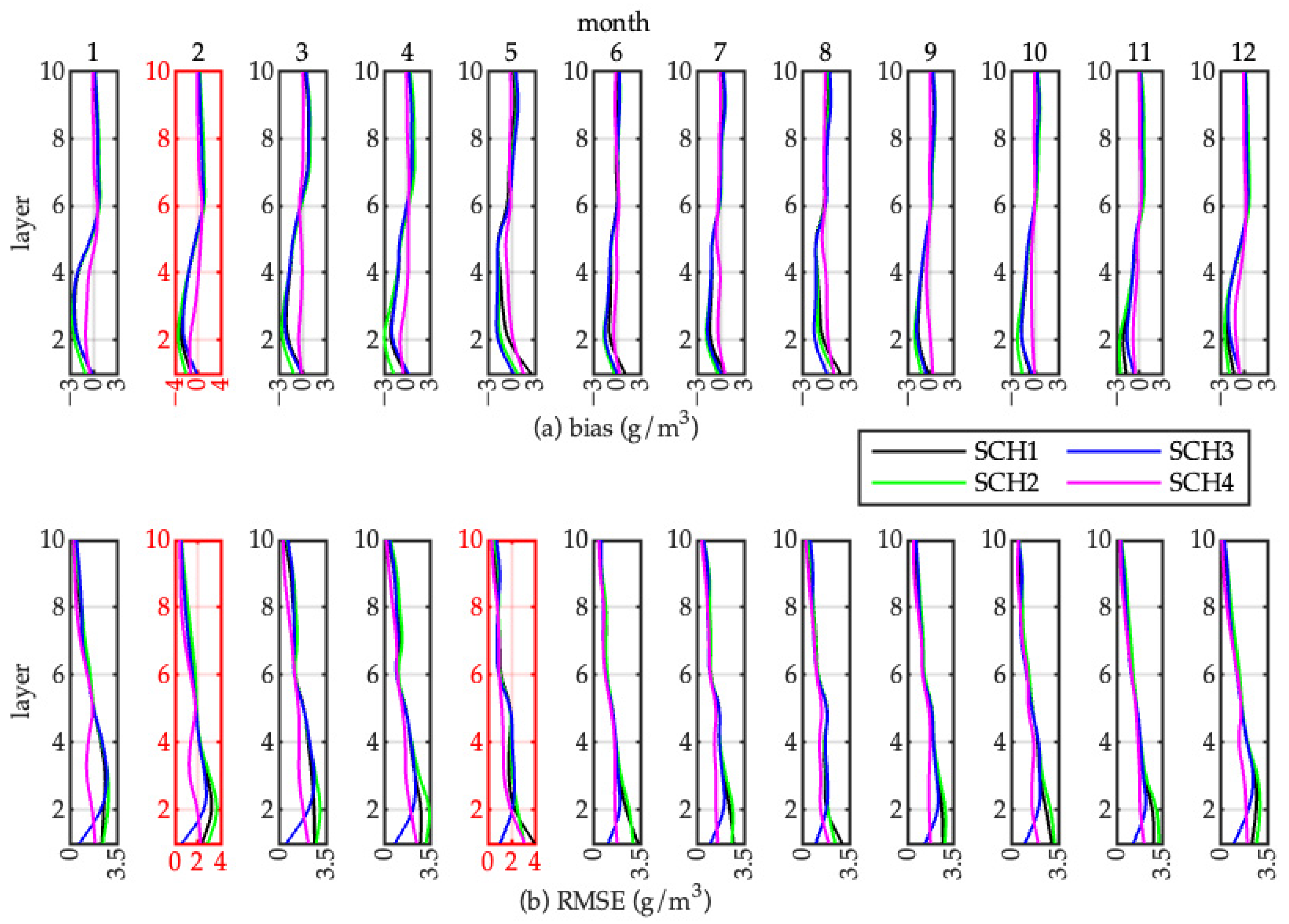
4.2. Bias and RMSE of Layered WVD
4.2.1. Monthly Bias and RMSE
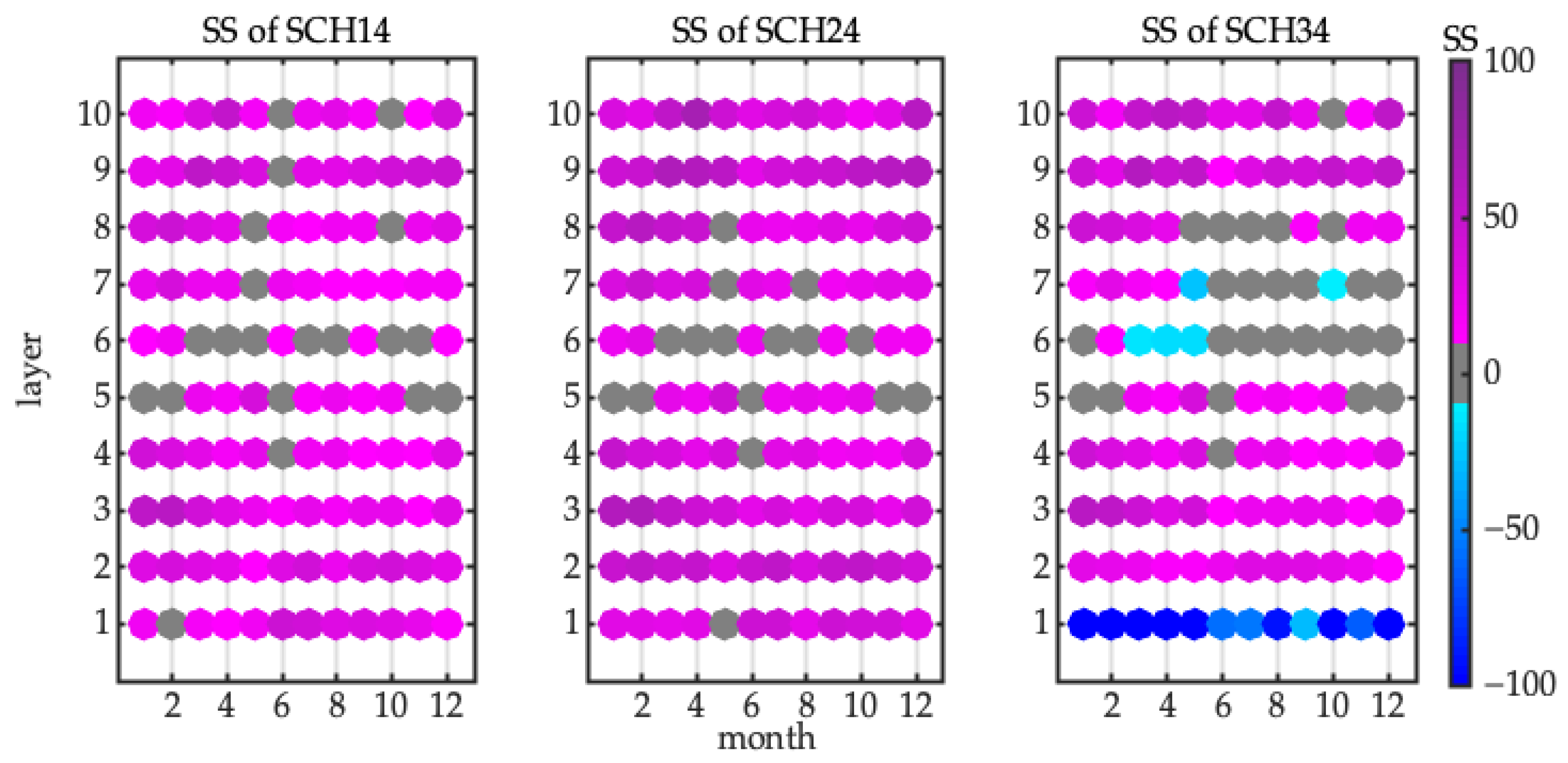
4.2.2. Skill Score of Monthly RMSE
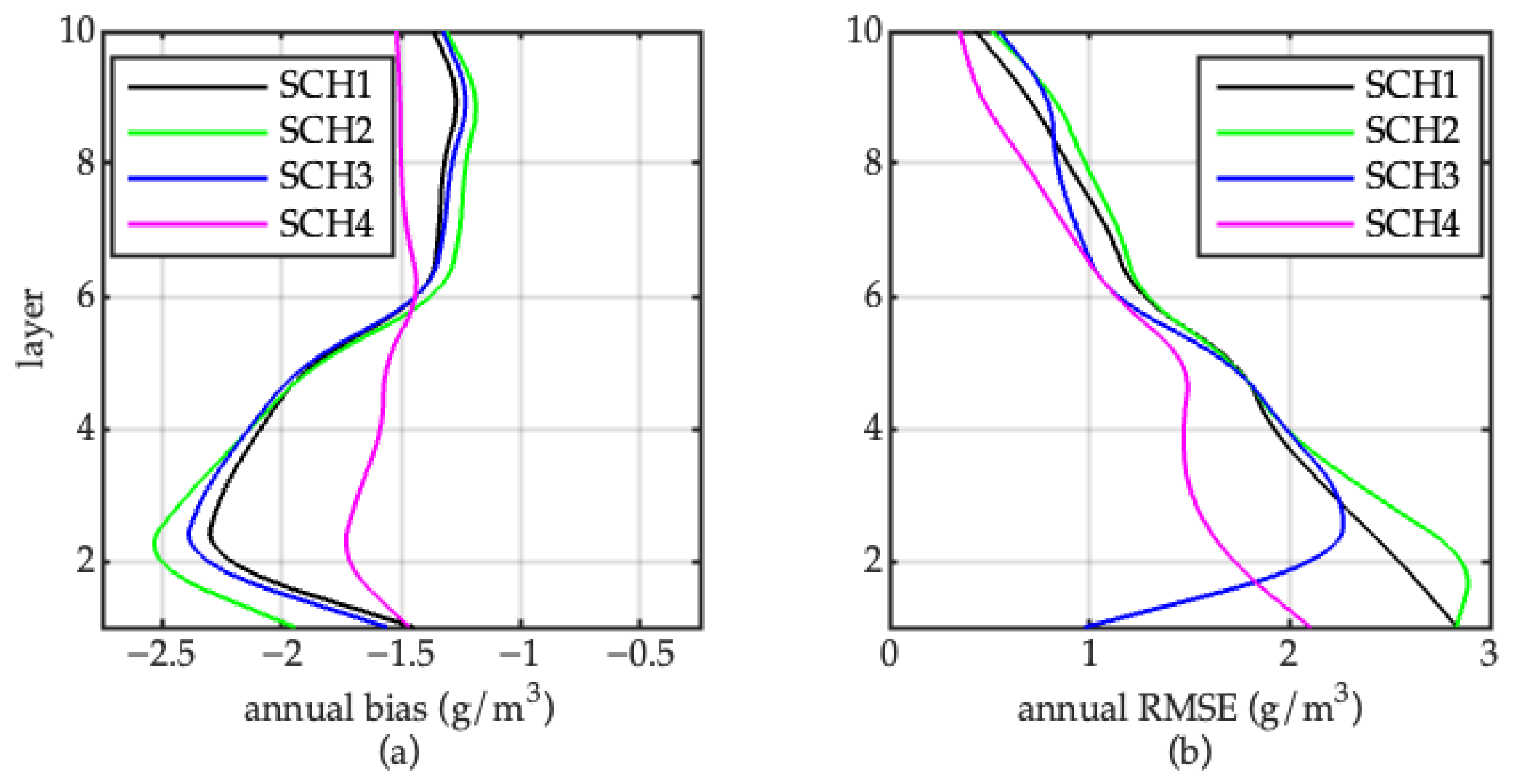
4.2.3. Annual Bias and RMSE
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| 42.90 | −16.97 | −4.18 | −1.50 | −0.92 | |
| 8.67 | 0.68 | −0.75 | 0.01 | −1.02 |
| Coefficient of PWV Range | Tomographic Layer | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 1 | 0.478 | 0.363 | 0.249 | 0.183 | 0.130 | 0.088 | 0.047 | 0.026 | 0.013 | 0.005 | |
| 0.030 | 0.011 | −0.018 | 0.000 | 0.007 | −0.005 | −0.011 | −0.005 | 0.000 | 0.000 | ||
| −0.002 | −0.017 | −0.006 | 0.001 | 0.012 | 0.002 | 0.000 | 0.001 | 0.002 | 0.001 | ||
| 0.020 | 0.003 | −0.016 | 0.020 | 0.003 | −0.012 | −0.007 | −0.002 | 0.000 | 0.000 | ||
| 0.008 | 0.001 | 0.011 | 0.005 | −0.001 | −0.004 | −0.005 | 0.000 | −0.001 | 0.000 | ||
| −0.014 | −0.017 | −0.005 | 0.016 | 0.008 | −0.002 | −0.002 | 0.003 | 0.002 | 0.000 | ||
| 0.012 | 0.012 | 0.013 | −0.006 | −0.010 | −0.011 | −0.003 | −0.001 | −0.001 | 0.000 | ||
| 2 | 0.409 | 0.343 | 0.274 | 0.215 | 0.147 | 0.094 | 0.049 | 0.027 | 0.011 | 0.003 | |
| 0.012 | 0.019 | 0.030 | 0.016 | 0.009 | −0.019 | −0.021 | −0.010 | −0.003 | −0.001 | ||
| −0.012 | −0.006 | 0.010 | 0.011 | 0.010 | 0.002 | −0.007 | −0.003 | −0.001 | 0.000 | ||
| 0.016 | 0.008 | 0.007 | 0.009 | −0.005 | −0.014 | −0.008 | 0.001 | 0.001 | 0.000 | ||
| 0.006 | 0.007 | 0.010 | 0.011 | 0.003 | −0.006 | −0.008 | −0.003 | −0.002 | 0.000 | ||
| −0.003 | −0.005 | −0.001 | 0.005 | 0.000 | −0.004 | 0.002 | 0.001 | 0.001 | 0.000 | ||
| 0.001 | 0.003 | 0.005 | −0.001 | −0.004 | −0.003 | 0.001 | 0.000 | −0.001 | 0.000 | ||
| 3 | 0.387 | 0.338 | 0.270 | 0.216 | 0.153 | 0.099 | 0.052 | 0.028 | 0.012 | 0.004 | |
| 0.008 | 0.027 | 0.032 | 0.021 | 0.011 | −0.018 | −0.020 | −0.014 | −0.005 | −0.001 | ||
| −0.013 | 0.002 | 0.012 | 0.011 | 0.008 | −0.001 | −0.007 | −0.004 | −0.001 | 0.000 | ||
| 0.011 | 0.006 | 0.007 | 0.007 | −0.001 | −0.011 | −0.005 | −0.001 | 0.001 | 0.000 | ||
| −0.002 | 0.002 | 0.012 | 0.015 | 0.000 | −0.007 | −0.007 | −0.002 | −0.001 | 0.000 | ||
| 0.003 | 0.001 | 0.002 | 0.004 | 0.000 | −0.005 | −0.001 | 0.000 | 0.000 | 0.000 | ||
| −0.001 | −0.001 | 0.004 | 0.001 | −0.003 | −0.004 | 0.002 | 0.002 | 0.000 | 0.000 | ||
| 4 | 0.365 | 0.325 | 0.265 | 0.218 | 0.157 | 0.105 | 0.056 | 0.031 | 0.014 | 0.004 | |
| 0.003 | 0.025 | 0.037 | 0.025 | 0.017 | −0.014 | −0.022 | −0.016 | −0.007 | −0.002 | ||
| −0.001 | 0.012 | 0.012 | 0.007 | 0.004 | −0.005 | −0.010 | −0.005 | −0.002 | 0.000 | ||
| 0.006 | 0.003 | 0.006 | 0.005 | −0.001 | −0.009 | −0.006 | 0.000 | 0.001 | 0.001 | ||
| 0.007 | 0.013 | 0.010 | 0.007 | 0.000 | −0.008 | −0.007 | −0.003 | −0.001 | 0.000 | ||
| −0.001 | −0.002 | 0.000 | 0.003 | −0.002 | −0.002 | 0.001 | 0.001 | 0.000 | 0.000 | ||
| 0.000 | 0.003 | 0.002 | −0.001 | 0.000 | −0.007 | 0.000 | 0.002 | 0.001 | 0.000 | ||
| 5 | 0.347 | 0.310 | 0.257 | 0.215 | 0.157 | 0.112 | 0.064 | 0.037 | 0.016 | 0.005 | |
| 0.000 | 0.020 | 0.031 | 0.024 | 0.017 | −0.006 | −0.016 | −0.015 | −0.009 | −0.003 | ||
| 0.001 | 0.016 | 0.015 | 0.010 | 0.006 | −0.004 | −0.010 | −0.006 | −0.003 | −0.001 | ||
| −0.002 | −0.004 | 0.003 | 0.002 | 0.000 | −0.003 | −0.003 | 0.000 | 0.000 | 0.000 | ||
| 0.006 | 0.010 | 0.009 | 0.006 | 0.004 | −0.007 | −0.008 | −0.004 | −0.001 | 0.000 | ||
| −0.003 | −0.005 | −0.002 | 0.000 | −0.001 | 0.003 | 0.001 | 0.002 | 0.000 | 0.000 | ||
| −0.001 | −0.001 | 0.001 | 0.002 | −0.001 | −0.003 | 0.001 | 0.001 | 0.001 | 0.000 | ||
| 6 | 0.321 | 0.293 | 0.244 | 0.209 | 0.155 | 0.121 | 0.074 | 0.044 | 0.020 | 0.006 | |
| −0.010 | 0.013 | 0.022 | 0.018 | 0.013 | 0.004 | −0.007 | −0.012 | −0.009 | −0.004 | ||
| 0.005 | 0.017 | 0.013 | 0.010 | 0.005 | −0.004 | −0.008 | −0.008 | −0.004 | −0.001 | ||
| −0.007 | −0.004 | 0.001 | 0.002 | 0.000 | 0.004 | −0.002 | 0.000 | 0.000 | 0.000 | ||
| 0.005 | 0.009 | 0.006 | 0.004 | 0.002 | −0.003 | −0.006 | −0.004 | −0.001 | 0.000 | ||
| −0.006 | −0.009 | −0.005 | −0.001 | −0.002 | 0.003 | 0.004 | 0.003 | 0.001 | 0.000 | ||
| 0.000 | −0.001 | −0.002 | −0.002 | −0.002 | −0.002 | −0.001 | 0.002 | 0.001 | 0.000 | ||
References
- Chahine, M.T. The Hydrological Cycle and Its Influence on Climate. Nature 1992, 359, 373–380. [Google Scholar] [CrossRef]
- Held, I.M.; Soden, B.J. Robust Responses of the Hydrological Cycle to Global Warming. J. Clim. 2006, 19, 5686–5699. [Google Scholar] [CrossRef]
- Niell, A.E.; Coster, A.J.; Solheim, F.S.; Mendes, V.B.; Toor, P.C.; Langley, R.B.; Upham, C.A. Comparison of Measurements of Atmospheric Wet Delay by Radiosonde, Water Vapor Radiometer, GPS, and VLBI. J. Atmos. Ocean. Technol. 2001, 18, 830–850. [Google Scholar] [CrossRef]
- Champollion, C.; Masson, F.; Bouin, M.N.; Walpersdorf, A.; Doerflinger, E.; Bock, O.; Van Baelen, J. GPS Water Vapour Tomography: Preliminary Results from the ESCOMPTE Field Experiment. Atmos. Res. 2005, 74, 253–274. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System. J. Geophys. Res. 1992, 97, 15787. [Google Scholar] [CrossRef]
- Flores, A.; Ruffini, G.; Rius, A. 4D Tropospheric Tomography Using GPS Slant Wet Delays. Ann. Geophys. 2000, 18, 223–234. [Google Scholar] [CrossRef]
- Seko, H.; Shimada, S.; Nakamura, H.; Kato, T. Three-Dimensional Distribution of Water Vapor Estimated from Tropospheric Delay of GPS Data in a Mesoscale Precipitation System of the Baiu Front. Earth Planets Space 2000, 52, 927–933. [Google Scholar] [CrossRef]
- Flores, A.; De Arellano, J.V.G.; Gradinarsky, L.P.; Rius, A. Tomography of the Lower Troposphere Using a Small Dense Network of GPS Receivers. IEEE Trans. Geosci. Remote Sens. 2001, 39, 439–447. [Google Scholar] [CrossRef]
- Gradinarsky, L.; Jarlemark, P. GPS Tomography Using the Permanent Network in Göteborg: Simulations. In Proceedings of the Record—IEEE PLANS, Position Location and Navigation Symposium, Palm Springs, CA, USA, 15–18 April 2002; pp. 128–133. [Google Scholar]
- Troller, M.; Bürki, B.; Cocard, M.; Geiger, A.; Kahle, H.-G. 3-D Refractivity Field from GPS Double Difference Tomography. Geophys. Res. Lett. 2002, 29, 2-1–2-4. [Google Scholar] [CrossRef]
- Nilsson, T.; Gradinarsky, L. Water Vapor Tomography Using GPS Phase Observations: Simulation Results. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2927–2941. [Google Scholar] [CrossRef]
- Song, S.; Zhu, W.; Ding, J.; Peng, J. 3D Water-Vapor Tomography with Shanghai GPS Network to Improve Forecasted Moisture Field. Chin. Sci. Bull. 2006, 51, 607–614. [Google Scholar] [CrossRef]
- Perler, D.; Geiger, A.; Hurter, F. 4D GPS Water Vapor Tomography: New Parameterized Approaches. J. Geod. 2011, 85, 539–550. [Google Scholar] [CrossRef]
- Manning, T.; Zhang, K.; Rohm, W.; Choy, S.; Hurter, F. Detecting Severe Weather Using GPS Tomography: An Australian Case Study. J. Glob. Position. Syst. 2012, 11, 59–70. [Google Scholar] [CrossRef]
- Rohm, W.; Zhang, K.; Bosy, J. Unconstrained, Robust Kalman for GNSS Troposphere Tomography. Atmos. Meas. Tech. 2013, 6, 9133–9162. [Google Scholar] [CrossRef]
- Chen, B.; Liu, Z. Voxel-Optimized Regional Water Vapor Tomography and Comparison with Radiosonde and Numerical Weather Model. J. Geod. 2014, 88, 691–703. [Google Scholar] [CrossRef]
- Manning, T.; Rohm, W.; Zhang, K.; Hurter, F.; Wang, C. Determining the 4D Dynamics of Wet Refractivity Using GPS Tomography in the Australian Region; Springer: Berlin/Heidelberg, Germany, 2013; Volume 139, pp. 41–49. [Google Scholar]
- Chen, B.; Liu, Z. Assessing the Performance of Troposphere Tomographic Modeling Using Multi-Source Water Vapor Data during Hong Kong’s Rainy Season from May to October 2013. Atmos. Meas. Tech. 2016, 9, 5249–5263. [Google Scholar] [CrossRef]
- Ding, N.; Zhang, S.B.; Wu, S.Q.; Wang, X.M.; Zhang, K.F. Adaptive Node Parameterization for Dynamic Determination of Boundaries and Nodes of GNSS Tomographic Models. J. Geophys. Res. Atmos. 2018, 123, 1990–2003. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, W.; Yao, Y.; Li, X. An Improved GNSS Tropospheric Tomography Method with the GPT2w Model. GPS Solut. 2020, 24, 1–13. [Google Scholar] [CrossRef]
- Liu, C.; Yao, Y.; Xu, C. Conventional and Neural Network-Based Water Vapor Density Model for GNSS Troposphere Tomography. GPS Solut. 2022, 26, 4. [Google Scholar] [CrossRef]
- Mousavian, R.; Hossainali, M.; Lorenz, C.; Kunstmann, H. Copula, a New Approach for Optimum Design of Voxel-Based GNSS Tropospheric Tomography Based on the Atmospheric Dynamics. GPS Solut. 2022, 26, 149. [Google Scholar] [CrossRef]
- Sadeghi, E.; Hossainali, M.; Safari, A. Development of a Hybrid Tomography Model Based on Principal Component Analysis of the Atmospheric Dynamics and GPS Tracking Data. GPS Solut. 2022, 26, 77. [Google Scholar] [CrossRef]
- Adavi, Z.; Weber, R.; Glaner, M.F. Assessment of Regularization Techniques in GNSS Tropospheric Tomography Based on Single- and Dual-Frequency Observations. GPS Solut. 2022, 26, 21. [Google Scholar] [CrossRef]
- Wilgan, K.; Hurter, F.; Geiger, A.; Rohm, W.; Bosy, J. Tropospheric Refractivity and Zenith Path Delays from Least-Squares Collocation of Meteorological and GNSS Data. J. Geod. 2017, 91, 117–134. [Google Scholar] [CrossRef]
- Mishra, M.R.; Behera, R.K.; Jha, S.; Panda, A.K.; Mishra, A.; Pradhan, D.K.; Choudary, P.R. A Brief Review on Phytoconstituents and Ethnopharmacology of Scoparia Dulcis Linn. (Scrophulariaceae). Int. J. Phytomedicine 2011, 3, 422–438. [Google Scholar] [CrossRef]
- Bender, M.; Raabe, A. Preconditions to Ground Based GPS Water Vapour Tomography. Ann. Geophys. 2007, 25, 1727–1734. [Google Scholar] [CrossRef]
- Rohm, W. The Precision of Humidity in GNSS Tomography. Atmos. Res. 2012, 107, 69–75. [Google Scholar] [CrossRef]
- Haji-Aghajany, S.; Amerian, Y.; Verhagen, S. B-Spline Function-Based Approach for GPS Tropospheric Tomography. GPS Solut. 2020, 24, 88. [Google Scholar] [CrossRef]
- Haji-Aghajany, S.; Amerian, Y.; Verhagen, S.; Rohm, W.; Schuh, H. The Effect of Function-Based and Voxel-Based Tropospheric Tomography Techniques on the GNSS Positioning Accuracy. J. Geod. 2021, 95, 78. [Google Scholar] [CrossRef]
- Troller, M.; Geiger, A.; Brockmann, E.; Bettems, J.M.; Bürki, B.; Kahle, H.G. Tomographic Determination of the Spatial Distribution of Water Vapor Using GPS Observations. Adv. Space Res. 2006, 37, 2211–2217. [Google Scholar] [CrossRef]
- Zhang, K.; Manning, T.; Wu, S.; Rohm, W.; Silcock, D.; Choy, S. Capturing the Signature of Severe Weather Events in Australia Using GPS Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1839–1847. [Google Scholar] [CrossRef]
- Mateus, P.; Miranda, P.M.A.; Nico, G.; Catalão, J.; Pinto, P.; Tomé, R. Assimilating InSAR Maps of Water Vapor to Improve Heavy Rainfall Forecasts: A Case Study With Two Successive Storms. J. Geophys. Res. Atmos. 2018, 123, 3341–3355. [Google Scholar] [CrossRef]
- Yao, Y.; Xin, L.; Zhao, Q. An Improved Pixel-Based Water Vapor Tomography Model. Ann. Geophys. 2019, 37, 89–100. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, K.; Wu, S.; Shi, J.; Li, L.; Wu, H.; Liu, S. A New Method for Tropospheric Tomography Using GNSS and Fengyun-4A Data. Atmos Res 2022, 280, 106460. [Google Scholar] [CrossRef]
- Notarpietro, R.; Cucca, M.; Gabella, M.; Venuti, G.; Perona, G. Tomographic Reconstruction of Wet and Total Refractivity Fields from GNSS Receiver Networks. Adv. Space Res. 2011, 47, 898–912. [Google Scholar] [CrossRef]
- Yao, Y.; Zhao, Q. Maximally Using GPS Observation for Water Vapor Tomography. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7185–7196. [Google Scholar] [CrossRef]
- Benevides, P.; Catalao, J.; Nico, G.; Miranda, P.M.A. 4D Wet Refractivity Estimation in the Atmosphere Using GNSS Tomography Initialized by Radiosonde and AIRS Measurements: Results from a 1-Week Intensive Campaign. GPS Solut. 2018, 22, 91. [Google Scholar] [CrossRef]
- Rohm, W. The Ground GNSS Tomography-Unconstrained Approach. Adv. Space Res. 2013, 51, 501–513. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y. An Improved Troposphere Tomographic Approach Considering the Signals Coming from the Side Face of the Tomographic Area. Ann. Geophys. 2017, 35, 87–95. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Yao, W.; Xia, P. An Optimal Tropospheric Tomography Approach with the Support of an Auxiliary Area. Ann. Geophys. 2018, 36, 1037–1046. [Google Scholar] [CrossRef]
- Yang, F.; Guo, J.; Shi, J.; Zhao, Y.; Zhou, L.; Song, S. A New Method of GPS Water Vapor Tomography for Maximizing the Use of Signal Rays. Appl. Sci. 2019, 9, 1446. [Google Scholar] [CrossRef]
- Benevides, P.; Nico, G.; Catalao, J.; Miranda, P.M.A. Analysis of Galileo and GPS Integration for GNSS Tomography. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1936–1943. [Google Scholar] [CrossRef]
- Dong, Z.; Jin, S. 3-D Water Vapor Tomography in Wuhan from GPS, BDS and GLONASS Observations. Remote Sens. 2018, 10, 62. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Cao, X.; Yao, W.Q. Accuracy and Reliability of Tropospheric Wet Refractivity Tomography with GPS, BDS, and GLONASS Observations. Adv. Space Res. 2019, 63, 2836–2847. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, S.; Ding, N.; Holden, L.; Wang, X.; Zheng, N. GNSS-RS Tomography: Retrieval of Tropospheric Water Vapor Fields Using GNSS and RS Observations. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Xiong, S.; Ma, F.; Ren, X.; Chen, J.; Zhang, X. LEO Constellation-Augmented Multi-GNSS for 3D Water Vapor Tomography. Remote Sens. 2021, 13, 3056. [Google Scholar] [CrossRef]
- Benevides, P.; Nico, G.; Catalão, J.; Miranda, P.M.A. Bridging InSAR and GPS Tomography: A New Differential Geometrical Constraint. IEEE Trans. Geosci. Remote Sens. 2016, 54, 697–702. [Google Scholar] [CrossRef]
- Jaberi Shafei, M.; Mashhadi-Hossainali, M. Application of the GNSS-R in Tomographic Sounding of the Earth Atmosphere. Adv. Space Res. 2018, 62, 71–83. [Google Scholar] [CrossRef]
- Miranda, P.M.A.; Mateus, P. A New Unconstrained Approach to GNSS Atmospheric Water Vapor Tomography. Geophys. Res. Lett. 2021, 48, e2021GL094852. [Google Scholar] [CrossRef]
- Elósegui, P.; Ruis, A.; Davis, J.L.; Ruffini, G.; Keihm, S.J.; Bürki, B.; Kruse, L.P. An Experiment for Estimation of the Spatial and Temporal Variations of Water Vapor Using GPS Data. Phys. Chem. Earth 1998, 23, 125–130. [Google Scholar] [CrossRef]
- Cao, Y. GPS Tomographying Three-Dimensional Atmospheric Water Vapor and Its Meteorological Applications. Ph.D. Thesis, The Chinese Academy of Sciences, Beijing, China, 2012. [Google Scholar]
- Xia, P.; Ye, S.; Jiang, P.; Pan, L.; Guo, M. Assessing Water Vapor Tomography in Hong Kong with Improved Vertical and Horizontal Constraints. Ann. Geophys. 2018, 36, 969–978. [Google Scholar] [CrossRef]
- Haji-Aghajany, S.; Amerian, Y.; Verhagen, S.; Rohm, W.; Ma, H. An Optimal Troposphere Tomography Technique Using the WRF Model Outputs and Topography of the Area. Remote Sens. 2020, 12, 1442. [Google Scholar] [CrossRef]
- Jacob, D. The Role of Water Vapour in the Atmosphere. A Short Overviewfrom a Climate Modeller’s Point of View. Phys. Chem. Earth Part A Solid Earth Geod. 2001, 26, 523–527. [Google Scholar] [CrossRef]
- Andritsch, F.; Dach, R.; Grahsl, A.; Schildknecht, T.; Jäggi, A. Bernese GNSS Software Version 5.2. User manual; Astronomical Institute, University of Bern, Bern Open Publishing: Bern, Switzerland, 2015. [Google Scholar]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A New Empirical Mapping Function Based on Numerical Weather Model Data. Geophys. Res. Lett. 2006, 33, 7. [Google Scholar] [CrossRef]
- Bar-Sever, Y.E.; Kroger, P.M.; Borjesson, J.A. Estimating Horizontal Gradients of Tropospheric Path Delay with a Single GPS Receiver. J. Geophys. Res. Solid Earth 1998, 103, 5019–5035. [Google Scholar] [CrossRef]
- Chen, G.; Herring, T.A. Effects of Atmospheric Azimuthal Asymmetry on the Analysis of Space Geodetic Data. J. Geophys. Res. Solid Earth 1997, 102, 20489–20502. [Google Scholar] [CrossRef]
- Shoji, Y.; Nakamura, H.; Iwabuchi, T.; Aonashi, K.; Seko, H.; Mishima, K.; Itagaki, A.; Ichikawa, R.; Ohtani, R. Tsukuba GPS Dense Net Campaign Observation: Improvement in GPS Analysis of Slant Path Delay by Stacking One-Way Postfit Phase Residuals. J. Meteorol. Soc. Jpn. 2004, 82, 301–314. [Google Scholar] [CrossRef]
- Tomasi, C. Determination of the Total Precipitable Water by Varying the Intercept in Reitan’s Relationship. J. Appl. Meteorol. 1981, 20, 1058–1069. [Google Scholar] [CrossRef]
- Ye, S.; Xia, P.; Cai, C. Optimization of GPS Water Vapor Tomography Technique with Radiosonde and COSMIC Historical Data. Ann. Geophys. 2016, 34, 789–799. [Google Scholar] [CrossRef]
- Kennett, E.J.; Toumi, R. Temperature Dependence of Atmospheric Moisture Lifetime. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Otarola, A.C.; Querel, R.; Kerber, F. Precipitable Water Vapor: Considerations on the Water Vapor Scale Height, Dry Bias of the Radiosonde Humidity Sensors, and Spatial and Temporal Variability of the Humidity Field. Available online: https://arxiv.org/abs/1103.3025 (accessed on 1 August 2022).
- Wan, M.; Zhang, K.; Wu, S.; Shen, Z.; Sun, P.; Li, L. New Model for Vertical Distribution and Variation of Tropospheric Water Vapor—A Case Study for China. Available online: https://www.researchsquare.com/article/rs-1497870/v1.pdf (accessed on 1 August 2022).

| Scheme | Vertical Constraint | Type of Parameter |
|---|---|---|
| SCH1 | ||
| SCH2 | 1 | |
| SCH3 | ||
| SCH4 |
| Tomographic Layer (km) | RE < 30% | RE > 50% | ||||||
|---|---|---|---|---|---|---|---|---|
| SCH1 | SCH2 | SCH3 | SCH4 | SCH1 | SCH2 | SCH3 | SCH4 | |
| 1 (0–0.6) | 86 | 85 | 99 | 94 | 2.3 | 1.9 | 0.0 | 1.6 |
| 2 (0.6–1.2) | 85 | 77 | 94 | 96 | 0.8 | 1.5 | 0.1 | 0.6 |
| 3 (1.2–1.8) | 75 | 75 | 78 | 92 | 2 | 2 | 2 | 2 |
| 4 (1.8–2.4) | 75 | 75 | 76 | 86 | 5 | 5 | 5 | 5 |
| 5 (2.4–3) | 70 | 71 | 70 | 74 | 12 | 12 | 11 | 14 |
| 6 (3–4) | 63 | 63 | 66 | 64 | 26 | 28 | 24 | 25 |
| 7 (4–5) | 52 | 51 | 56 | 55 | 38 | 41 | 36 | 33 |
| 8 (5–6) | 41 | 39 | 44 | 45 | 48 | 52 | 45 | 38 |
| 9 (6–8) | 23 | 19 | 21 | 32 | 68 | 73 | 69 | 47 |
| 10 (8–10) | 14 | 9 | 9 | 21 | 79 | 86 | 82 | 57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, M.; Zhang, K.; Wu, S.; Sun, P.; Li, L. Development of a New Vertical Water Vapor Model for GNSS Water Vapor Tomography. Remote Sens. 2022, 14, 5656. https://doi.org/10.3390/rs14225656
Wan M, Zhang K, Wu S, Sun P, Li L. Development of a New Vertical Water Vapor Model for GNSS Water Vapor Tomography. Remote Sensing. 2022; 14(22):5656. https://doi.org/10.3390/rs14225656
Chicago/Turabian StyleWan, Moufeng, Kefei Zhang, Suqin Wu, Peng Sun, and Longjiang Li. 2022. "Development of a New Vertical Water Vapor Model for GNSS Water Vapor Tomography" Remote Sensing 14, no. 22: 5656. https://doi.org/10.3390/rs14225656
APA StyleWan, M., Zhang, K., Wu, S., Sun, P., & Li, L. (2022). Development of a New Vertical Water Vapor Model for GNSS Water Vapor Tomography. Remote Sensing, 14(22), 5656. https://doi.org/10.3390/rs14225656






