Abstract
A Doppler lidar mounted on a rotary platform has been developed for measuring wind fields in the upper troposphere and stratosphere. The rotating platform was used to support a large system for the detection of wind velocities of sight (VOS) in four directions. The principle, structure, and parameters of the lidar system are introduced. The Fabry-Perot interferometer (FPI), the core component of the wind measurement system, was designed after comprehensively considering the measurement uncertainty and the influence of Mie scattering. Its dual-edge channel bandwidth is 1.05 GHz with 3.48 GHz spacing. In operation, the FPI channels are locked to the laser frequency with a stability of 14.8 MHz. Compared with the local radiosonde, it was found that the deviation in wind speed below 28 km was generally less than 10 m/s, and the deviation in wind direction below 19 km was less than 10 degrees. The 42-day profile comparison between lidar in Hefei and radiosondes in Anqing and Fuyang was analyzed. The statistical results show that the wind speed and wind direction deviations between lidar and radiosondes below 20 km were approximately 10 m/s and 20 degrees, respectively, which are comparable to the regional differences in the wind field. However, as altitudes exceed 20 km, the deviations increased rapidly with height. The experiments indicate that the Doppler lidar could measure wind fields from 7 km to 30 km, with better detection accuracy below 20 km.
1. Introduction
Wind field measurements are essential for exploring the middle and upper atmosphere, especially in studies of climate and atmospheric dynamics, and in meteorological models, where wind profiles with high accuracy and resolution are urgently needed [1,2,3]. As active, optical remote-sensing instruments with a high temporal-spatial resolution, Doppler lidars based on the coherent technique have been put into commercial use for measuring wind in the planetary boundary layer (PBL) [4,5,6]. However, in the middle atmosphere, only direct detection (incoherent) Doppler lidars with a powerful laser and large-aperture telescope are competent for continuous wind measurements, which are still rarely reported due to their high cost and complexity. Chanin et al. first implemented wind measurements between 25 and 50 km by using a Fabry-Perot interferometer (FPI) and three receiver telescopes of 445 mm diameter that were pointing in different directions [7]. Tepley et al. developed another lidar system at Arecibo for wind measurements up to 60 km by using a single etalon FPI [8]. The receiver was constructed with a 380-mm-diameter roof-mounted azimuth-elevation mirror and a telescope. Korb et al. proposed the theory of the double-edge technique for wind lidar measurements and developed the Goddard Lidar Observatory for Winds (GLOW) system [9,10]. A series of Doppler lidars based on FPI has been manufactured by the team at the University of Science and Technology of China, for measuring wind fields at different altitude ranges [11,12,13]. Aside from optical interferometers, iodine vapor filters, such as the mobile Doppler lidar of Ocean University of China [14,15], are also employed as Doppler frequency shift discriminators. The Doppler Rayleigh/Mie/Raman lidar system that deployed at the ALOMAR research station in Norway has been reformed to analyze the Doppler shift of Rayleigh echoes, by using iodine filters, and has detected wind and temperature simultaneously up to 80 km [16]. The Doppler lidars acquire wind fields using the vector synthesis method by combining the wind velocities of at least two radial directions. For wind lidars with middle-sized and small telescopes, scanning mirrors are usually equipped to change the radial directions [8,13,14]. However, for telescopes with an aperture greater than 0.5 m, the optical scanner is too heavy and expensive to adopt. Almost all of the large devices have needed at least two lidar subsystems to observe wind velocities of sight (VOS) at orthogonal directions [11,16,17]. Following this design, the mass, cost, and maintenance of the device are almost double that of the single lidar system.
In view of this, a large-aperture Doppler wind lidar mounted on a rotary platform has been developed by the Anhui Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, at Hefei, China (117.18°E, 31.91°N). The wind-measurement core-component FPI has obtained an excellent performance after design optimization of the response sensitivity and signal-to-noise ratio. The effective range of wind measurement is significantly expanded after the AD and PC signals are glued together by a fusion algorithm. A statistical-comparison experiment was carried out on the wind fields observed by the lidar and the sondes in Hefei, Fuyang, and Anqing, at the same time. The Doppler wind lidar can measure wind fields of between 7 and 30 km.
2. Detection Principle and Lidar System
2.1. The Principle of Doppler Lidar
For direct-detection wind lidars, the Doppler shifts of the lidar echoes can be derived from the intensity changes of signals that pass through the frequency discriminator. In this lidar, a Fabry-Perot interferometer was adopted as the frequency discriminator. As depicted in Figure 1, there are three optical channels on the FPI: two edge channels (blue and cyan lines) to filter the atmospheric backscattered echoes; one lock channel (black line) to maintain the center frequency of the FPI consistent with the laser frequency by adjusting the cavity length of the FPI. The signal intensities of the two edge channels were determined by the spectral convolutions between the atmospheric echoes and the edge channels. The Doppler shifts will change the relative position of the atmospheric backscattered spectrum, followed by the rise or fall of the two edge signals. The Doppler shifts can be achieved by applying the frequency discrimination curve:
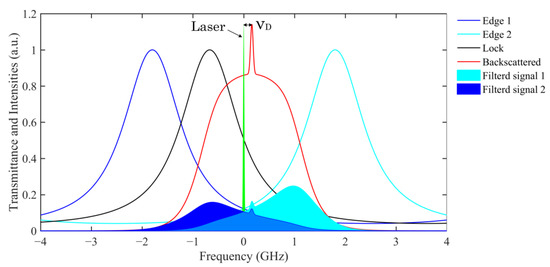
Figure 1.
Principle of frequency discrimination of FPI.
The subscripts 1, 2, or i indicate the edge channels, is the frequency, z is the height at which the echo was produced. T is calculated from the channel detection constant C and the convolution of the transmittance spectrum of edge channels, , and the atmospheric backscattering spectrum, . The channel transmittance curves, combined with their detection constants, can be calibrated by scanning the FPI. For stratospheric observation, the lidar echoes are mainly generated by Rayleigh–Brillouin scattering, which is described by the Tenti 6 model in the spectrum [18]. Significantly, the small amount of Mie scattering from aerosols that is depicted as a peak of the red line in Figure 1 should also be considered and will be discussed in Section 2.2.2 of this paper. The whole frequency shifts are obtained by interpolating the measured signal ratios into the calibrated frequency discrimination curve. Then the velocity of sight (VOS) can be derived:
where is the laser wavelength and is the Doppler shift, which is derived from the difference in the whole frequency shift and locking frequency .
The wind lidar measured VOSs in four directions, successively. By assuming the vertical wind velocity is zero, the horizontal wind field can be calculated by vector synthesis:
where and are the horizontal wind velocity and direction, respectively. and are, respectively, the X and Y vector components of horizontal wind velocity. , , , and are the VOSs of east, west, north, and south, respectively and is the zenith angle of the telescope pointing direction.
2.2. The Doppler Lidar System
2.2.1. Structure and Parameters
This Doppler Lidar system was designed for wind measurements from 7 km to 30 km, with height resolutions of 0.55 km (changeable). The whole system has been integrated into an equipment shelter with a size of 5 m × 2.7 m × 2.4 m, which is mounted on a rotary platform with a diameter of 6 m, as shown in Figure 2. In operation, the platform rotates with a speed of 2 degrees per second, and stays at 0, 90, 180, and 270 degrees, to measure the four VOSs. Considering the time for the rotary platform to return to zero, the rotation process takes about 4.5 min in a wind measurement period. For each VOS measurement, it takes 333 s for signal acquisition, in the case where 10,000 laser shots are accumulated, 15 s for laser warming, and 10 s for pre-measured frequency locking of the FPI. About 6 min are needed for each VOS measurement. So, the time consumption of the whole wind measurement period is 28.5 min.

Figure 2.
Structure diagram and photo of the rotary lidar system.
A Q-switched Nd:YAG laser (Powerlite 9030, Continuum Ltd., Winchester, UK) working at 532 nm is employed as the transmitter in the lidar system. In order to obtain a single longitudinal-mode laser output, the Nd:YAG laser is injection seeded by a 1064 nm-fiber laser (SI-2000, NP Photonics Ltd., Tucson, AZ, USA) with a bandwidth narrower than 5 kHz. Due to the fact that the laser frequency is sensitive to the ambient temperature, the seed laser and the Nd:YAG laser are installed in thermostatic boxes that are controlled within ±2 °C and ±0.3 °C, respectively, achieving a frequency shift of about 200 MHz per hour at 532 nm. The output laser energy is approximately 350 mJ per pulse with a repetition rate of 30 Hz. The laser pulse spectrum follows a Gaussian distribution with an FWHM of 70 MHz, much less than the spectral width of the atmospheric backscattering echoes and the FPI channels. The laser beam is expanded by 10 times to reduce the transmitted divergence angle to about 50 μrad, in order to decrease the field of view (FOV) of telescope. A very small fraction (less than 1%) of the transmitted laser is split into an integrating sphere (IS) and is then led into the receiver by an optical fiber and a collimator for frequency locking of the FPI in operation. The IS is used to homogenize the optical field that is coupled to the fiber.
A Cassegrain telescope with a diameter of 800 mm and focal length of 1961 mm is pointing to an atmosphere with a zenith angle of 24 degrees to gather the laser echoes. An optical fiber is used for light transmission from the telescope to the receiver. One end face of the fiber is fixed at the focal point of the telescope and acts as an aperture. The fiber core diameter of 200 μm leads to a receiving FOV of 100 μrad. The other end of the fiber is fixed to a collimator in the receiver, achieving a divergence angle of 2.5 mrad. Narrowband interference filters centered at 532.1 nm, with a bandwidth (FWHM) of 0.3 nm, are mounted on the two collimators for background suppression. The receiver consists of five photomultiplier tubes (PMT) in the system. As shown in Figure 3, 10% of the received atmospheric echo is detected directly by PMT 1 as a reference signal for the alignment between the transmitter and the receiver. The remaining backscattered signal is equally divided into two edge channels of the FPI and measured by PMTs 2 and 3 for Doppler shift discrimination. PMTs 4 and 5 are used to measure the transmittance of the frequency-locking channel on the FPI. The PMTs of the two edge channels are gated by an electronic gating card to avoid signal saturation in lower altitudes. Normally the gate is triggered by the Q-switch with an 80 μs delay, corresponding to 12 km distance.
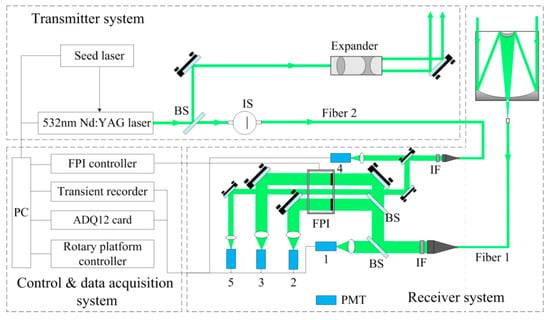
Figure 3.
Schematic view of the Doppler lidar. BS, beam splitter; IS, integrating sphere; IF, interference filter.
A computer is used to control the whole lidar system, including the laser, FPI, rotary platform, and data acquisition devices. A transient recorder (TR20-160, Licel GmbH, Berlin, Germany) with a 12-bit, 20 MHz AD (analog to digital) converter is employed to acquire the atmospheric backscattering signals of PMTs 1–3. This transient recorder can acquire AD and PC (photon counting) signals simultaneously. PMTs 4 and 5 measure signals from the transmitted laser pulses, which are ~10 ns width in the time domain. So, a high-speed acquisition card (ADQ12, Queentest Ltd., Hongkong, China) with a sampling rate of 1 GHz is used to acquire the pulse signals. The system parameters are summarized in Table 1.

Table 1.
Lidar system parameters.
2.2.2. Design of the Fabry-Perot Interferometer
An FPI designed for working at 532 nm is the critical device for Doppler shift discrimination. The whole optical aperture of the FPI is 80 mm. There are three coated channels of a circular shape on it: two edge channels with a diameter of 38 mm and a frequency- locking channel with a diameter of 19 mm. As observed in Figure 1, the spectra of FPI channels follow Lorentz curves. The spectral bandwidth and spacing between the two edge channels have a significant impact on the signal-to-noise ratio (SNR) of the two channels and the sensitivity of the frequency discrimination; they then affect the random errors in VOS measurement. Figure 4a shows the simulated random errors in VOS, with respect to different FPI bandwidths and the spacing between the two edge channels, by considering molecular backscattering only. The red dot marks the optimized bandwidth and spacing, with values of 1.05 GHz and 2.92 GHz, respectively. However, as mentioned in Section 2, there exists a Mie scattering component in the lidar echoes, which must be considered in the FPI design due to the fact that its spectrum is much narrower than that of Rayleigh-Brillouin scattering. Figure 4b shows the simulated VOS errors caused by Mie signals (with a backscattering ratio of 1.5) when pure molecular scattering is assumed in the calculation. The red dotted line indicates the optimized parameter pairs. Taking the two aspects into account, the designed value of the FPI bandwidth and the spacing between two edge channels were determined as 1.05 GHz and 3.48 GHz, respectively.
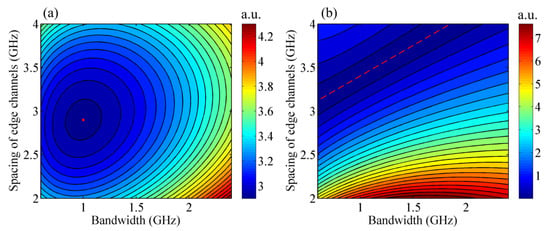
Figure 4.
Simulated (a) random errors of VOS and (b) VOS errors caused by Mie signals with respect to different bandwidths and spacing of edge channels. A red dot or dotted line marks the optimized parameters.
2.2.3. Frequency Locking of the FPI
Although equipped with thermostatic boxes, the output laser suffers a frequency drift of about 100 MHz per hour. In addition, the FPI spectrum drifts and vibrates with time due to temperature variation and mechanical vibration. In operation, a frequency-locking channel on the FPI (black line in Figure 1) is used to avoid the relative displacement of spectral lines between the FPI channels and the transmitted laser. The procedure of frequency locking is presented in Figure 5. Specifically, a small fraction of the transmitted laser pulses are introduced into the receiver and split in a ratio of 30:70. The 30% part of the laser energy is detected directly by PMT 4, and the other 70% passes through the frequency-locking channel on the FPI and is detected by PMT 5 (see Figure 3). Then, the relative transmittance of the frequency-locking channel is probed by the ratio of the two signals. In operation, the deviation values between the measured signal ratios and a reference ratio are obtained constantly with a 10-s interval. The reference ratio is set to the position where the spectrum curves of the two edge channels intersect with each other. By fitting the segment of the locking channel spectrum around the reference point linearly, the deviations in signal ratio could be converted to FPI steps. If the number of steps is greater than a threshold (here, that is 3), it is fed back to the FPI controller; then, the signal ratio returns to the reference value. Figure 6a shows the movement of FPI steps in a frequency-locking process of 140 min. Corresponding to the 150 steps, the equivalent frequency adjustment is about 0.56 GHz, which is larger than the linear response range of the Doppler frequency, as shown in Figure 6b. Figure 6c,d show the signal ratios and the related frequency variation, respectively. In this case, the signal ratios fluctuated around a reference value of 0.508, controlled in a range of ±0.024. This fluctuation of signal ratios can be converted to frequency dithers by interpolating the transmittance curve of the FPI lock channel, which is depicted in Figure 1 with the black line. Finally, a frequency stability of 14.8 MHz (standard deviation) is achieved, according to Equation (3), corresponding to an uncertainty of 3.94 m/s in VOS measurement.
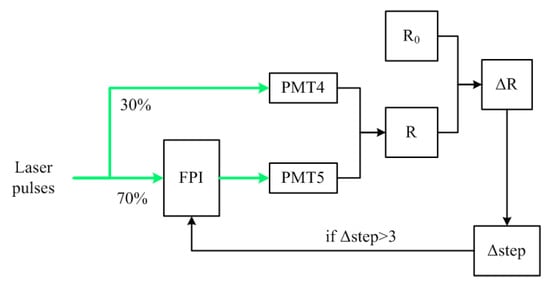
Figure 5.
The procedure of frequency locking. R is the ratio of the two signals; R0 is the reference ratio; ΔR is the deviation of the signal ratio; Δstep is the converted FPI step.
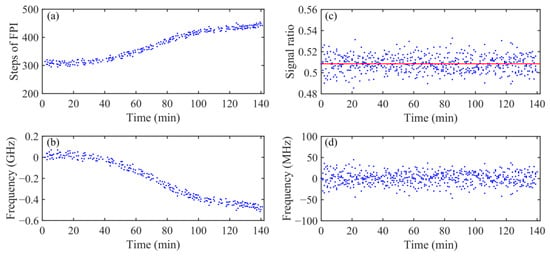
Figure 6.
(a) The movement of FPI steps in a frequency locking process; (b) the equivalent frequency adjustment of FPI; (c) the locked signal ratios, accompanied by the reference ratio of 0.508 (red line); (d) the final frequency variation.
2.3. Signals Gluing
The lidar signals are acquired by a licel transient recorder in AD and PC modes simultaneously. The AD signals are reliable at lower altitudes but have poor SNR at higher altitudes, while the PC signals could reach higher detection altitudes but suffer saturation distortion due to the pulse pileup effect at lower heights [19,20,21]. Thus, the AD and PC profiles have been glued together to improve the dynamic range of detection.
Firstly, the electronic delay of AD channels relative to PC channels is corrected by shifting the AD signal profiles forward by nine bins. Secondly, the pileup effect is corrected for PC signals before the implementation of the gluing process. Assuming the photon counter is a non-paralyzable system, the real photon counting rate can be calculated from the measured values [22]:
where is the real photon counting rate, P is the measured photon counting rate, and is the dead time, about 4 ns for the licel products. Finally, The AD and PC signal profiles are glued together with a merging method. The segments with a PC amplitude from 2 to 4 MHz were chosen for merging. The AD and PC signals were weighted for merging [23]:
where PAD is the converted AD signal that multiplied the original AD signal by the PC/AD ratio which was obtained from the merging signal segments. PPC and PGlue are the corrected PC signal and the glued signal, respectively. W and (1 − W) are the weight coefficients of the AD signals and PC signals. Cmin and Cmax are the minimum and maximum PC signals of the merging segment. For example, the signal gluing process of the edge 1 channel is illustrated in Figure 7. The raw PC signal (blue solid line) is obviously distorted when larger than 10 MHz. Despite having undergone dead-time correction, the PC signal (blue dashed line) diverged slightly from the converted AD signal (black solid line), which is regarded as the “actual PC signal”. By applying the merging method of Equations (9) and (10), the AD and PC signals were glued. The glued signal agreed well with the AD signal and is much better in terms of SNR, especially at higher altitude ranges.
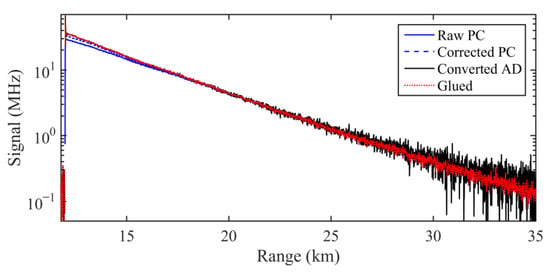
Figure 7.
The signal profiles of the edge 1 channel: the raw PC signal, the PC signal with dead-time correction, the converted AD signal that is regarded as the “actual PC signal” and the glued signal.
3. Results
A comparative observation of wind fields between Doppler lidar and radiosonde was carried out at about 23:00 on 29 December 2021 (LT). The Doppler lidar transmitted 8000 laser shots in each radial direction and took a total of 24 min for the four VOS measurements. In order to improve the SNR, the original data bins were spatially averaged to achieve a range resolution of 300 m. At a lidar-telescope with a zenith angle of 23.5 degrees, the height resolution was 275 m. Since the open time of signal gates was delayed by 80 μs after Q-switch, the lidar profiles were effective from 11 km. At the same location, a weather balloon lifted off. The balloon reached an altitude of 28.01 km in 69 min, covering the lidar working time. The GPS data show that the balloon drifted 165.6 km eastward during the lifting period. The profiles of horizontal wind speed (WS) as measured by Doppler lidar and radiosonde are presented in Figure 8a with a blue line and red dots, respectively. Figure 8b shows the absolute deviations and the relative deviations between the two devices. The absolute deviations were less than 10 m/s except for a thin layer at around 25 km. The relative deviations were less than 12% below 18.5 km but increased seriously above 19 km where the wind speed is low. The horizontal wind speed reached its maximum of 88.7 m/s at 11.77 km, near the tropopause, then decreased to several meters per second around an altitude of 21.5 km. A weak wind layer appeared from 21.5 to 26.5 km, with a peak speed of about 15 m/s. Figure 8c shows the wind direction (WD) profiles of the Doppler lidar and the radiosonde. The altitudes from 10 to 25 km were dominated by a west wind (227~292 degrees). A wind direction shear appeared at around 28 km and was captured by both the lidar and the radiosonde. The wind direction deviations of the two devices were less than 10 degrees below 19 km, but the profile measured by the lidar oscillated seriously above 20 km, as shown in Figure 8d.
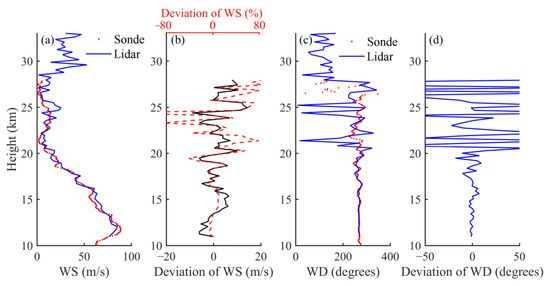
Figure 8.
(a,c) Profiles of horizontal wind speed and direction measured by lidar (blue line) and radiosonde (red line). (b,d) Deviation between the two devices.
Due to the lack of local radiosonde data in Hefei, we used radiosonde data from Anqing (117.11°E, 30.53°N) and Fuyang (115.81°E, 32.91°N), which are, respectively, 154 km and 170 km from the lidar location, for comparison and subsequent statistics and analysis. The radiosonde data were obtained from the China Meteorological Data Service Centre (http://data.cma.cn (accessed on 30 December 2021)). From 25 February to 5 April, there were 42 lidar profiles that were close to the weather balloons’ lifting time at night and were employed for comparison with the radiosonde profiles from Anqing and Fuyang. All the data were normalized at a height resolution of 550 m. Figure 9 illustrates six cases of wind speed and direction comparisons. The wind fields of the two places were similar to each other above 5 km and generally consistent with the wind profiles measured by lidar in Hefei. Figure 10a shows the root mean square deviations (RMSD) between wind speed profiles as measured by lidar in Hefei and radiosondes in Anqing and Fuyang, respectively. The two lidar-sonde-RMSD profiles followed the same trend. For comparison, the RMSDs between the radiosonde profiles from Fuyang and Anqing (290 km apart from each other) are also shown with a black dashed line and reflect the regional difference in horizontal wind speed. The three RMSD profiles were comparable with values around 10 m/s from 7 to 14 km, decreased up to 20 km, and then increased up to 30 km. Due to the decrease in lidar SNR, the divergences between the lidar-sondes-RMSD profiles and the Anqing-Fuyang-RMSD profile gradually expanded with height. Similarly, Figure 10b presents the RMSD profiles of the wind directions. The lidar-sonde RMSDs of the wind directions are less than 20 degrees under 15 km, which is comparable to the Anqing–Fuyang RMSDs, and increased to more than 50 degrees above 20 km. Figure 10c shows the data quantities involved in the statistics at different heights. Since the original data points of the radiosonde are sparse and distributed irregularly, the normalized radiosonde profiles are occasionally missing data in some height bins, especially above 28 km. The bins under 11 km lack data because most of the lidar profiles were gated from 11 km.
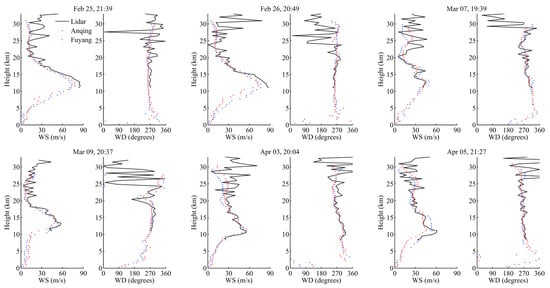
Figure 9.
Comparison cases of wind speed and direction measured by lidar in Hefei (black lines) and radiosondes in Anqing (blue dots) and Fuyang (red dots).
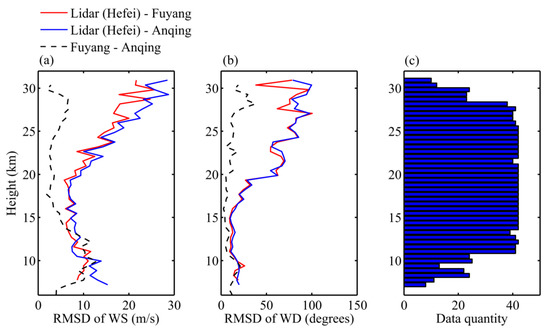
Figure 10.
RMSD profiles of (a) wind speeds and (b) wind directions between different locations: lidar—Fuyang (red lines), lidar—Anqing (blue lines), and Fuyang—Anqing (black dashed lines); (c) data quantities at different heights.
4. Conclusions
A Doppler lidar that is mounted on a rotary platform has been developed for measuring wind fields in the upper troposphere and stratosphere, from 7 km to 30 km height. The rotary platform was designed to enable the measurement of four VOSs using a single transmitter-receiver system. The system structures and parameters were described in Section 2.2.1 The FPI spectrum was designed and optimized, after comprehensively considering the influence of signal-to-noise ratio and Mie signal, forming two edge channels with a bandwidth of 1.05 GHz and a spacing of 3.48 GHz. The FPI channels were locked to the laser frequency with a stability of 14.8 MHz for several hours, corresponding to a VOS uncertainty of 3.94 m/s. After the AD and PC signals are combined and glued, the effective range of wind measurement is significantly improved.
As a comparison, the wind fields were observed by lidar and radiosonde at the same time, in Hefei. The results show that the deviation in horizontal wind speed was generally less than 10 m/s in the comparing heights; the deviation of wind directions was less than 20 degrees below 19 km, but oscillations became serious above 20 km. In order to overcome the lack of radiosonde data in Hefei, the radiosonde data of Anqing and Fuyang were used for statistical comparison with lidar. Overall, the wind fields of the three locations were relatively uniform between 15 and 25 km, with slight differences at higher altitudes and at the tropopause. The lidar–sonde RMSDs of the wind speeds and wind directions below 20 km were approximately in 10 m/s and 20 degrees, respectively. Above 20 km, the RMSDs increased rapidly with height. The above results verified that the Doppler lidar has detection capability for wind fields between 7 and 30 km, with better accuracy below 20 km. In the future, the Doppler lidar system could be used for wind field observations in different regions and seasons to provide more accurate information about wind fields in the upper troposphere and stratosphere.
Author Contributions
Conceptualization, C.X.; methodology, K.X.; software, B.W.; validation, L.C.; formal analysis, M.Z.; investigation, J.C. and Z.F.; resources, K.X.; data curation, B.W.; writing—original draft preparation, M.Z.; writing—review and editing, J.C.; visualization, M.Z.; supervision, C.X.; project administration, C.X.; funding acquisition, C.X. and L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Civil Aerospace Technology Pre-research Project (D040103) and the Key Project of Natural Science Research of Anhui Provincial Department of Education (KJ2021A0945).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, J.F.; Xiao, C.Y.; Hu, X.; Xu, Q. Responses of zonal wind at ~40°N to stratospheric sudden warming events in the stratosphere, mesosphere and lower thermosphere. Sci. China 2017, 60, 935–945. [Google Scholar] [CrossRef]
- Zhao, R.; Dou, X.; Xue, X.; Sun, D.; Han, Y.; Chen, C.; Zheng, J.; Li, Z.; Zhou, A.; Han, Y.; et al. Stratosphere and lower mesosphere wind observation and gravity wave activities of the wind field in China using a mobile Rayleigh Doppler lidar. J. Geophys. Res. Space Phys. 2017, 122, 8847–8857. [Google Scholar] [CrossRef]
- Hedin, A.E.; Fleming, E.L.; Manson, A.H.; Schmidlin, F.J.; Avery, S.K.; Clark, R.R.; Franke, S.J.; Fraser, G.J.; Tsuda, T.; Vial, F.; et al. Empirical wind model for the upper, middle and lower atmosphere. J. Atmos. Terr. Phys. 1996, 58, 1421–1447. [Google Scholar] [CrossRef]
- Prasad, N.S.; Sibell, R.; Vetorino, S.; Higgins, R.; Tracy, A. All-Fiber, Modular, Compact Wind Lidar for Wind Sensing and Wake Vortex Applications. Proc. SPIE 2015, 9465, 94650C. [Google Scholar]
- Lombard, L.; Valla, M.; Planchat, C.; Goular, D.; Augère, B.; Bourdon, P.; Canat, G. Eyesafe coherent detection wind lidar based on a beam-combined pulsed laser source. Opt. Lett. 2015, 40, 1030–1033. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, X.; Fan, C.; Bi, D.; Liu, J.; Zhang, X.; Zhu, X.; Chen, W. Field Performance of All-Fiber Pulsed Coherent Doppler Lidar. Eur. Phys. J. Conf. 2020, 237, 08009. [Google Scholar] [CrossRef]
- Chanin, M.L.; Garnier, A.; Hauchecorne, A.; Porteneuve, J. A doppler lidar for measuring winds in the middle atmosphere. Geophys. Res. Lett. 1989, 16, 1273–1276. [Google Scholar] [CrossRef]
- Tepley, C.A.; Sargoytchev, S.I.; Hines, C.O. Initial doppler rayleigh lidar results from arecibo. Geophys. Res. Lett. 1991, 18, 167–170. [Google Scholar] [CrossRef]
- Korb, C.L.; Gentry, B.M.; Li, X.; Flesia, C. Theory of the double-edge technique for Doppler lidar wind measurement. Appl. Opt. 1998, 37, 3097–3104. [Google Scholar] [CrossRef]
- Gentry, B.M.; Chen, H. Tropospheric wind measurements obtained with the Goddard Lidar Observatory for Winds (GLOW): Validation and performance. Proc. SPIE 2002, 4484, 74–81. [Google Scholar]
- Dou, X.; Han, Y.; Sun, D.; Xia, H.; Shu, Z.; Zhao, R.; Shangguan, M.; Guo, J. Mobile rayleigh Doppler lidar for wind and temperature measurements in the stratosphere and lower mesosphere. Opt. Express 2014, 22, A1203–A1221. [Google Scholar] [CrossRef] [PubMed]
- Shangguan, M.; Xia, H.; Wang, C.; Qiu, J.; Shentu, G.; Zhang, Q.; Dou, X.; Pan, J. All-fiber upconversion high spectral resolution wind lidar using a Fabry-Perot interferometer. Opt. Express 2016, 24, 19322. [Google Scholar] [CrossRef] [PubMed]
- Xia, H.; Shangguan, M.; Wang, C.; Shentu, G.; Qiu, J.; Zhang, Q.; Dou, X.; Pan, J. Micro-pulse upconversion Doppler lidar for wind and visibility detection in the atmospheric boundary layer. Opt. Lett. 2016, 41, 5218–5221. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, B.; Li, Z.; Yan, Z.; Wu, S.; Sun, Z. Wind measurements with incoherent Doppler lidar based on iodine filters at night and day. Appl. Phys. B 2007, 88, 327–335. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Z.; Liu, L.; Wu, S.; Liu, B.; Li, Z.; Chu, X. Iodine-filter-based mobile doppler lidar to make continuous and full-azimuth-scanned wind measurements: Data acquisition and analysis system, data retrieval methods, and error analysis. Appl. Opt. 2010, 49, 6960–6978. [Google Scholar] [CrossRef] [PubMed]
- Baumgarten, G. Doppler Rayleigh/Mie/Raman lidar for wind and temperature measurements in the middle atmosphere up to 80 km. Atmos. Meas. Tech. 2010, 3, 1509–1518. [Google Scholar] [CrossRef]
- Claude, S.; Anne, G.; Albert, H.; Hauchecorne, A.; Porteneuve, J. Rayleigh–mie doppler wind lidar for atmospheric measurements. 1. instrumental setup, validation, and first climatological results. Appl. Opt. 1999, 38, 2410–2421. [Google Scholar]
- Tenti, G.; Boley, C.D.; Desai, R.C. On the kinetic model description of rayleigh-brillouin scattering from molecular gases. Can. J. Phys. 1974, 52, 285–290. [Google Scholar] [CrossRef]
- Omote, K. Dead-time effects in photon counting distributions. Nucl. Instrum. Methods Phys. Res. 1990, A293, 582–588. [Google Scholar] [CrossRef]
- Donovan, D.P.; Whiteway, J.A.; Carswell, A.I. Correction for nonlinear photon counting effects in lidar systems. Appl. Opt. 1993, 32, 6742–6753. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Z.; Liu, B.; Li, R. Analysis of saturation signal correction of the troposphere lidar. Chin. Opt. Lett. 2009, 7, 1051–1054. [Google Scholar] [CrossRef]
- Whiteman, D.N.; Melfi, S.H.; Ferrare, R.A. Raman lidar system for the measurement of water vapor and aerosols in the Earth’s atmosphere. Appl. Opt. 1992, 31, 3068–3082. [Google Scholar] [CrossRef] [PubMed]
- Feng, C.; Wu, S.; Liu, B. Gluing Method of Detected Signal Based on Lidar. Acta Photonica Sin. 2018, 47, 0601101. (In Chinese) [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).