Abstract
The backscatter coefficients of Synthetic Aperture Radar (SAR) images that observe the Greenland Ice Sheet (GrIS) are incidence angle dependent, which impedes subsequent applications, such as monitoring its surface melting. Therefore, backscatter intensities with varying incidence angles should be normalized. This study proposes an incidence angle normalization method for dual-polarized Sentinel-1 images for GrIS. A multiple linear regression model is trained using the ratio between the backscatter coefficient differences and the incidence angle differences of quasi-simultaneously observed ascending and descending image pairs. Regression factors include the geographical position and elevation. The precision evaluation to the ascending and descending images suggests better normalization results than the widely used cosine-square correction method for horizontal transmit and horizontal receive (HH) images and a slight improvement for horizontal transmit and vertical receive (HV) images. Another dataset of GrIS Sentinel-1 mosaics in four 6-day repeating periods in 2020 is also tested to evaluate the proposed method and yields similar results. For HH images, the proposed method performs better than the cosine-square method, reducing 0.34 dB RMSE on average. The overall accuracy of our proposed method is 0.77 and 0.75 dB for HH and HV images, respectively. The proposed incidence angle normalization method can benefit the application of wide-swath SAR images to the study of large-scale and long-period observation on GrIS.
1. Introduction
Synthetic Aperture Radar (SAR), as an active microwave remote sensing technology, usually provides phase and intensity information of the ground surface observations. The former is applied by the interferometry technique to monitor ground surface deformation [1,2,3]. The latter is of great importance for monitoring dielectric features of the Earth’s surface, including snowmelt [4], soil moisture [5], oil spill detection [6], and building damage detection [7], etc. The dielectric features are affected by the dielectric coefficients, surface characteristics, incidence angle, etc. In polar regions, where optical images are limited due to polar night, SAR observations play a greater role. For homogeneous and stable surfaces, such as sea surface and/or ice sheets, the backscatter intensity generally decreases as the incidence angle increases from near range to far range [8]. For one specific ground object, even if other backscatter influencing factors remain unchanged, the backscatter coefficients vary with the incidence angles, which encumbers the direct intercomparison of data from different platforms that have different viewing geometries [9].
Various methods were proposed for incidence angle normalization of SAR images. A widely used one is the cosine-square correction method derived from Lambert’s law for optics. It assumes that the amount of power that is re-radiated in the upper hemisphere follows the cosine law, and because the radiation variability of the observed area also follows the cosine law, the measured backscatter coefficient is related to the cosine square of the incidence angle [10]. This method was applied to different types of land cover, including vegetation [11], ice sheets [12], ocean [13], etc. Other normalization methods for SAR images were based on statistical approaches. Mladenova et al. [9] and Menges et al. [14] eliminated the systematic differences in the mean value and variance between the model and independent datasets based on the frequency distribution or histogram matching. Ye et al. [15] proposed a normalization method based on the cumulative distribution function, which normalized the variable-angle observations for each incidence angle, using the information from multiple partially overlap swaths. The linear relationship between the incidence angle and the backscatter coefficient was investigated on different surfaces, including wet snow in mountains [16]. More investigations were conducted on sea ice. Some studies [17,18,19,20,21] utilized SAR data to perform linear regression between the incidence angle and backscatter coefficient on different types of sea ice. Others [22,23,24] focused on the empirical regression of backscatter differences and incidence angle differences on multiple observations in the same area.
To normalize the backscatter coefficient to a reference angle, this study develops a linear regression model of incidence angle compensation for the backscatter coefficient of Sentinel-1 EW images over the Greenland Ice Sheet (GrIS). This method helps isolate the contribution of incidence angle changes to the backscatter variability. The SAR mosaics of GrIS are therefore produced utilizing Sentinel-1 images, which is beneficial to the image interpretation of monitoring surface freezing/melting states of GrIS and the study of radar glacier zones.
2. Study Area and Data Sets
2.1. Greenland Ice Sheet
Greenland is the largest island in the world. As the second biggest ice sheet after the Antarctica Ice Sheet, GrIS, located in the northeastern of North America, extends 72–15°W and 60–83°N. Its elevation drops from above 3500 m at the center to the periphery. In recent decades, the increases in the glacier flow velocity and surface melting have made GrIS a major contributor to the rise in the global sea-level [25]. The typical melting period starts in June and ends in late August. Daily microwave radiometers and scatterometers have found that GrIS experiences strong melting in summer, and its surface melting duration increased at 4.5 days per decade, with the extension of the surface melting area increasing by 6.9% per decade during 1979–2019 [26,27]. In 2022, the melt duration of GrIS lasted until September, with an unusual late-season melt event [28].
Compared to passive microwave sensors, SAR offers a combination of a short revisit time and high spatial measurement of GrIS, enabling better monitoring of the surface melting. SAR mosaics derived from numerous images of different tracks, such as products provided by National Snow and Ice Data Center (NSIDC), NSIDC-0633, and NSIDC-0723 (discussed in Section 4.3), are not well-balanced without incidence angle normalization. The different backscatter coefficients in near-time acquisitions in the same area affect the snowmelt detection of GrIS.
2.2. Sentinel-1 EW SAR Imagery
Sentinel-1 Extra Wide (EW) mode provides horizontal transmit and receive (HH) and horizontal transmit and vertical receive (HV) images with an incidence angle range of 18.9–47.0° at GrIS. It contains 5 sub-swaths, covering a swath width of 400 km. This study adopts the EW ground range detected with medium-resolution (40 m × 40 m) products.
Sentinel-1 A/B SAR image pairs acquired from July 2019 to June 2021 at the five experimental areas (EA) were used in this study. Each quasi-simultaneously observed overlapping image pair comprises one image observed with an ascending orbit and another with a descending orbit. Since not enough quasi-simultaneous EW observations were found at the southern GrIS, it was not involved in the training process. Images acquired during July 2019 to June 2020 were employed for model training, and those during July 2020 to June 2021 were taken as a testing dataset. The image coverage is shown in Figure 1. T and F refer to the relative orbit number and frame number of the Sentinel-1 products.
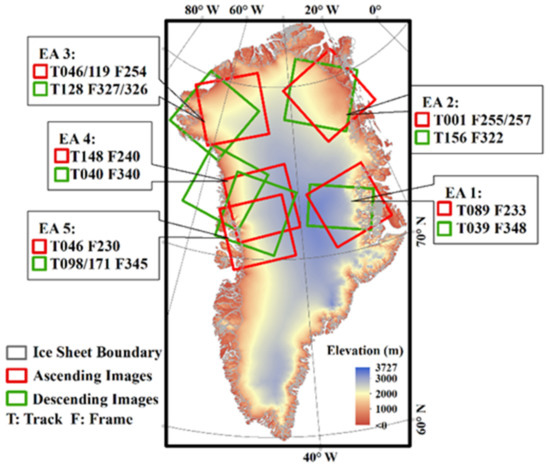
Figure 1.
Five experimental areas (EAs) and Sentinel-1 image pairs coverage on GrIS.
Another dataset applied for testing includes all ascending (more than descending acquisitions) Sentinel-1 A/B EW images covering the GrIS of four 6-day repeat cycles: 11 January 2020~16 January 2020, 16 April 2020~21 April 2020, 9 July 2020~14 July 2020, and 13 October 2020~18 October 2020, containing 52, 66, 59, and 63 frames, respectively.
All images were pre-processed with the Sentinel Application Platform (SNAP) using the following steps: precise orbit → thermal noise removal → calibration to σ0→ multilook (2∗2) → speckle filter (Refined Lee) → terrain correction → ice sheet mask. For HV polarized images, their EW1 sub-swaths were cut out because of irremovable thermal noise [29] despite the thermal noise removal step being performed in our processing steps.
2.3. Other Relevant Data
The elevation model applied in this study is the NSIDC-0715 dataset provided by National Snow and Ice Data Center (NSIDC) [30], with a resolution of 30 m. The GrIS mask is provided by the Ice sheet Mass Balance Inter-comparison Exercise [31]. The land freeze/thaw status images product is the NSIDC-0728 dataset [32], and the 2 m air temperature of the ERA5 model hourly data was downloaded from the Copernicus Climate Change Service (C3S) Climate Data Store [33].
3. Methodology
3.1. Linear Normalization Method
Different glacier facies for GrIS are identifiable by different radar characteristics on SAR images. The C-band microwave can easily penetrate the dry snow zone, where forward scattering dominates. The percolation zone, with large grain sizes and ice lens, is dominated by volume scattering and thus shows high backscattering coefficients. The wet snow zone with surface melting is dominated by surface scattering, showing low backscatter coefficients, and the scabrous bare ice zone along the shoreline shows stronger backscattering than the wet snow zone but still smaller than the percolation zone [34]. The microwave backscattering properties of GrIS are complex and show significant seasonal variations [27].
Assuming that the quasi-simultaneously obtained ascending and descending observation of one image pair share the same scattering characteristics on GrIS, their backscatter coefficients difference () in dB should only relate to the local incidence angles’ difference () in the same area. By presuming a linear model [22,23,24], the ratio () depends on the backscattering characteristics, which also relates to the freeze-thaw states of the ice surface.
Since the freeze-thaw state of GrIS is unknown before image interpretation and one aim of SAR observation is to detect such a state, this study takes other influence factors to represent such a ratio, including the elevation (H), latitude (Lat), longitude (Lon) of corresponding pixels, and a freeze/thaw-related factor (T). Three alternative factors for the freeze/thaw-related factor were tested. The first one is the absolute value of the image acquisition date’s distance from the summer solstice (), which is the estimation of the temporal distance to the most violent melting days of the year (DOY). The second is the historic average of the past decade of ERA5 2 m air temperature (K) calculated for each DOY () [33]. The last one utilizes land freeze/thaw status binary images from NSIDC-0728, regarding 0 as freezing and 1 as melting. The historic average of the past decade for each DOY is calculated.
The multiple linear regression model is expressed as Equations (1)–(3):
where are the regression coefficients of the four independent variables, and is the intercept of the regression result. The subscript a and d refer to the ascending and descending acquisition, and i refers to the pixel samples of each image pair. refers to three alternative variables: , and .
Pixel samples were extracted within image pairs during July 2019 to June 2020 upon the five EAs. An equal interval sampling with 1:1000 was conducted on all available samples. The samples were trained with (1) to obtain regression coefficients.
After the model was trained, the backscatter coefficients in dB were normalized to a fixed reference angle as Equation (4):
where is the normalized backscatter coefficients, and is a fixed reference angle, set as 30° in this study. and are the local incidence angles and measured backscatter coefficients in decibel of the original images. i refers to every image pixel.
3.2. Precision Evaluation
To evaluate the proposed normalization method, the widely used square-cosine correction was adopted as a reference method [10]. The backscatter coefficient is given by:
where the variables are the same as in Equation (4).
The mean value of multiple backscatter () for each pixel represents the average backscattering. Therefore, the root-mean-square error is calculated as (6):
where k = 1,2,3,…n represents the observation times in the same resolution cell and is the backscatter coefficient at the observation. The backscatter coefficients are measured in dB for Equation (6). For pixels in the overlap area, their mean RMSE was applied to evaluate the precision of different incidence angle normalization methods. The lower the value of RMSE, the better the performance. The precision evaluation was conducted on the two datasets in this study.
4. Results and Validation
4.1. Regression Coefficients Estimation
With the other variables remaining unchanged, , and were substituted into Equation (1), respectively, and three sets of regression coefficients were derived. The regression results of the HH images show that the coefficients of are almost equal (shown in Table 1), and those of are 2.82 × 10−5, −7.17 × 10−5, and −4.83 × 10−2, respectively. Regardless of which freeze/thaw-related factor was used, it had little effect on the backscatter correction, with no more than 0.1 dB. The introduction of such a parameter or into consideration does not alter the normalized results. Such a phenomenon is possibly caused by the limited melted samples, which could only be extracted from the very short melting period and the small melting area in the image pairs used in this study, compared to a large number of frozen samples.

Table 1.
Regression coefficient estimation.
Table 1 shows the regression coefficients estimation of variables except T, with all p < 0.01. The negative coefficients of H and Lat show that with higher elevation or latitude, the value of decreases. The coefficient of Lon is positive, indicating that as the longitude increase, also increases.
Without taking T into account, the ratio () variation of GrIS is shown in Figure 2 for both the HH and HV polarization channels. The absolute value of the ratio along the shoreline is generally smaller than those of the central ice sheet, suggesting that the backscatter coefficients of the central ice sheet are more sensitive to incidence angle variation than the coastal part. As for the different polarization mode, the overall absolute value of the ratio of HH polarization is bigger than that of HV polarization, which means that the HH backscatter coefficients are more sensitive to incidence angle variation than HV polarization. The ratio differs from −0.325 to −0.011 dB/°, with a mean value of −0.231 dB/° for the HH images. While for the HV images, the ratio ranges from −0.277 to 0.054 dB/° and is −0.166 dB/° on average. The incidence angle dependence of the backscatter coefficients for the HH images is stronger than for the HV images. Considering the incidence angle variation of Sentinel-1 EW mode is 18.9~47.0°, the incidence angle variation could lead to backscatter coefficient changes of 6.49 and 4.66 dB for the HH and HV images, respectively.
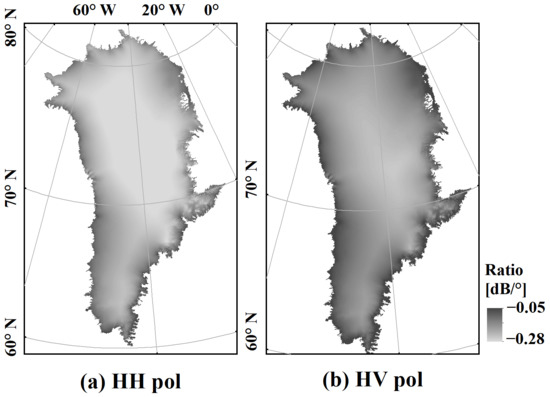
Figure 2.
The ratio of HH and HV polarization over the whole GrIS, calculated by Equation (1) with the regression coefficients shown in Table 1.
4.2. Evaluation Based on Ascending/Descending Image Pairs
To test whether the model fits images observed in other years, the image pairs observed during July 2020 to June 2021, the next year of the training data, were chosen to test the temporal independence of the proposed method (hereinafter referred to as the “incidence angle correction method”). The RMSEs of them, together with the training dataset, were calculated as in Equation (6), and the results are shown in Table 2.

Table 2.
RMSE results of the image pairs upon the five EAs (dB).
The incidence angle correction method reduces RMSE of the backscatter coefficient compared to the traditional cosine-square method. For HH images, the incidence angle correction method performs better for all EAs and seasons while for HV images, it shows a slight improvement. For the images observed during July 2019 to June 2020, the method performs well on EA1 and EA5 in the central GrIS, with a reduction of 0.86 and 0.70 dB RMSE for the HH images and 0.09 and 0.12 dB RMSE for the HV images, respectively. The results of the other 3 EAs also show a. 0.42 and 0.03 dB RMSE reduction on average for the HH and HV images.
The results of RMSE for the ascending and descending image pairs during July 2020 to June 2021 are similar to the training data during July 2019 to June 2020. For all 5 EAs, the incidence angle correction method achieves a 0.70 and 0.07 dB RMSE reduction for the HH and HV images, respectively, for the training dataset, and 0.74 and 0.08 dB for the validation dataset.
Figure 3 shows the mosaic images of one image pair acquired in EA1 in April 2021. The backscatter coefficient profiles along the red line in Figure 3a of the ascending image and descending image are shown in Figure 4. For the part of the incidence angle smaller than the reference incidence angle (30° in this study), the corresponding backscatter coefficients decrease after normalization by the incidence angle correction method. Conversely, for the other pixels whose incidence angle is larger than the reference angle, their normalized backscatter coefficients increase. The normalized backscatter coefficients of the ascending image and the descending image show less discrepancy than the unnormalized images and the normalized images with the cosine-square method, and the mosaics of their corrected images are well-balanced, and their edges are less obvious.
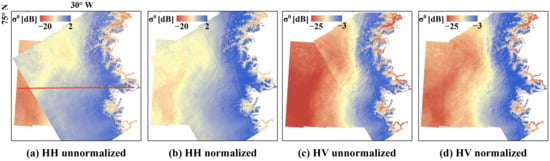
Figure 3.
Mosaics of the image pair in EA1 (Eastern Greenland, ascending image on top) before (a,c) and after (b,d) incidence angle normalization by the incidence angle correction method. EW1 of the HV images was removed. The ascending image was acquired on 19 April 2021 and the descending one was acquired on 16 April 2021.
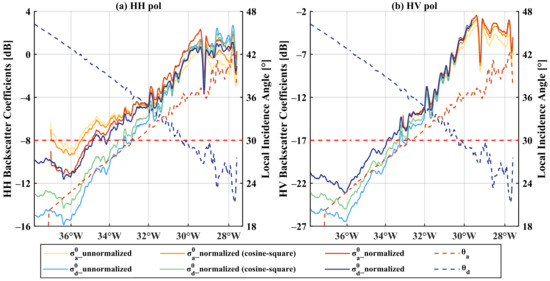
Figure 4.
The profile obtained along the red line in Figure 3a of the backscatter coefficient before and after incidence angle normalization by the cosine-square method and the incidence angle correction method. The left vertical axis shows the backscatter coefficient variation and the right one shows the corresponding incidence angle change. The subscripts a and d refer to the ascending and descending images. The horizontal red dashed line indicates the reference incidence angle of 30°.
Figure 5 and Figure 6 show the details of the mosaic images and profiles of another image pair acquired in EA3 on 3 February 2021. Similarly, the backscatter coefficients are compensated by the larger incidence angle than the reference angle while the part with a smaller incidence angle is weakened. Thus, the ascending image and the descending one are balanced. However, the discrepancy between the normalized ascending and descending images in Figure 6 is more obvious than in Figure 4. In northwest GrIS, the incidence angle correction method does not perform as well as in the central GrIS, which is in line with the RMSE improvement results shown in Table 2.
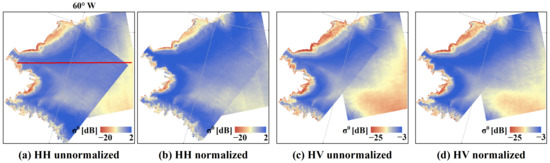
Figure 5.
Mosaics of the image pair in EA3 (northwest Greenland, descending image on top) before (a,c) and after (b,d) incidence angle normalization by the incidence angle correction method. EW1 of HV images was removed. Both the ascending image and descending image were acquired on 3 February 2021. The temporal interval of the two images is about 9 h.
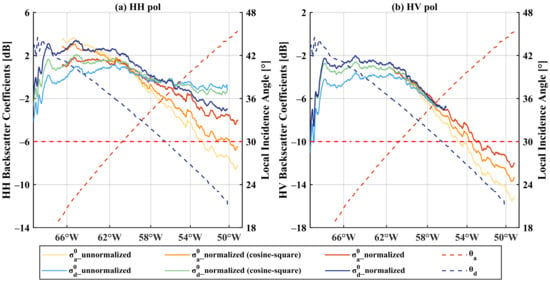
Figure 6.
The profile obtained along the red line in Figure 5a of the backscatter coefficient before and after incidence angle normalization by the cosine-square method and the incidence angle correction method. The left vertical axis shows the backscatter coefficient variation and the right one shows the corresponding incidence angle change. The subscripts a and d refer to the ascending and descending images. The red dashed line indicates the reference incidence angle of 30°.
Combining the two examples above, it can be seen that the backscatter coefficients of the SAR images on central GrIS are stable and display a better normalization effect while the part near the shoreline is more variable. In melting periods, the normalization effects of the melting ice sheet are limited, which is discussed in Section 5.2. In this study, the incidence angle correction method does not change the ice sheet characteristics as reflected by the backscatter intensity, but it removes the backscatter coefficient ramp induced by the large range of the incidence angle.
Compared to the cosine-square method, the improvement of the incidence angle correction method is more obvious for HH images than HV images. A possible reason is that the original backscatter difference between the HV ascending and descending images shown in Figure 4b and Figure 6b is much smaller than the HH images (Figure 4a and Figure 6a). The discrepancy between the HV ascending and descending images could be eliminated by both the cosine-square method and the incidence angle correction method, with similar improvements.
4.3. Evaluation of Greenland Ice Sheet Mosaic
The GrIS mosaics of Sentinel-1 with a temporal resolution of 6 or 12 days have been provided by NSIDC-0723 since 2015 [35]. The mosaics are produced by Sentinel-1 IW products of seven tracks, and the images have simply been overlaid without incidence angle normalization. Another GrIS SAR mosaicking dataset is NSIDC-0633, which provides annual winter mosaics produced by different SAR sensors, including RADARSAT-1 and ALOS PALSAR before 2013 [36].
In this study, incidence angle normalization was conducted for all ascending Sentinel-1 images observed in EW mode upon GrIS during four 6-day acquisition periods and then joined into mosaics. The mean backscatter coefficient was adopted for overlapped orbits. Figure 7 shows the mosaics before and after incidence angle normalization by the incidence angle correction method acquired in January 2020, April 2020, July 2020, and October 2020.
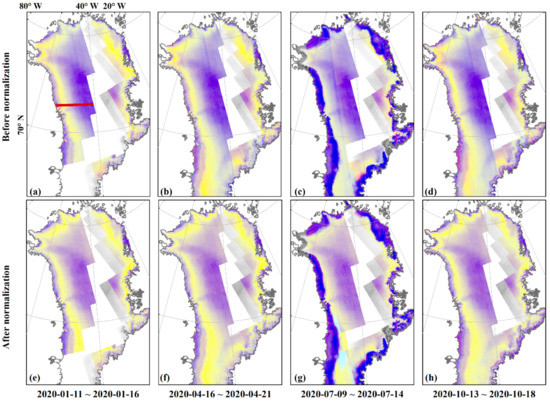
Figure 7.
Sentinel-1 mosaics of the GrIS images before (a–d) and after (e–h) incidence angle normalization by the incidence angle correction method. The mosaics are RGB pseudo-color composite images, R: HH, G: HV, B: HH/HV (all in dB values). EW1 of the HV images was removed.
The sharp edge of the backscatter coefficient on the four normalized Sentinel-1 mosaics (Figure 7e–h) is eliminated compared to the mosaics that were not normalized (Figure 7a–d). The mosaics in January 2020, April 2020, and October 2020 are well-balanced while the obvious superimposed traces of the different tracks or frames still exist in the southern GrIS in the mosaic of July 2020, possibly due to the quick surface freezing and thawing status changes in the melting seasons.
Any pixel of the GrIS SAR mosaic is produced by one or more overlap tracks. Figure 8 shows the backscatter variation before and after incidence angle normalization of the three tracks along the red line in Figure 7a, including the tracks T017, T046, and T148. Because the incidence angles of T017 are all above the reference angle, its normalized backscatter coefficients are compensated accordingly. This is similar for most of T046. The western part of T148 decreases and the rest increases for the backscatter coefficients, bounded by an incidence angle equal to the reference incidence angle setting at 30°. The values of the backscatter coefficients of the three tracks are closer after incidence angle normalization. The backscatter coefficient corrections for the other overlapping tracks show similar results, which are not shown in detail.
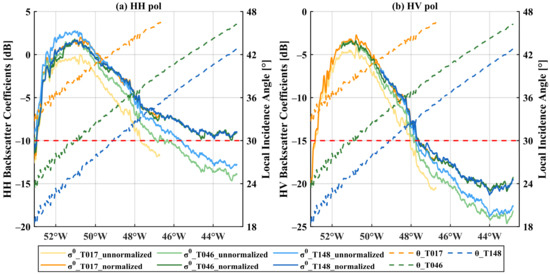
Figure 8.
The backscatter coefficients profile along the red line in Figure 7a, covering the tracks 017, 046, and 148. The left vertical axis shows the backscatter coefficients’ variation and the right one shows the corresponding incidence angle change. EW1 of the HV images was removed. The red dashed line indicates the reference incidence angle of 30°.
RMSEs of Sentinel-1 GrIS mosaics are shown in Table 3. For the HH images, RMSE of the image mosaics corrected by the incidence angle correction method was reduced by 0.34, 0.33, 0.32, and 0.37 dB in January 2020, April 2020, July 2020, and October 2020, respectively, relative to that corrected by the cosine-square method. For the HV images, the method performs slightly better, with a reduction of 0.04, 0.01, 0.05, and 0.04 dB RMSE, respectively, in the four periods.

Table 3.
RMSE of SAR images mosaics on Greenland ice sheet (dB).
5. Discussion
5.1. Comparison with the Cosine-Square Method
Due to its easy implementation, the cosine-square method based on a physical mechanism has been applied to SAR image correction of various land surfaces [11,12,13]. However, the backscattering characteristics vary considerably over the different surfaces of Earth, which could not simply be regarded as Lambertian. Recent studies updated the square power of Equation (5) over a particular type of observation surface, for which the power value is roughness-dependent, and the method can be improved by adjusting the power value [9,11,37]. However, this improvement has not been studied on the ice sheet.
According to Equation (5), the ratio of the change in the backscatter coefficients to the change in the incidence angle () can be calculated for the cosine-square correction method. Presuming a reference angle of 30°, the ratio changes with the change in the incidence angle, varying from −0.069 to -0.122 dB/° in the range of 18.9–47.0°. Such a value is much less negative than the ratio for the HH images (−0.231 dB/°) and relatively closer to that of the HV images (−0.166 dB/°). This may also explain why the incidence angle correction method achieves a 0.34 dB prevision improvement for the HH images but similar results for the HV images on the GrIS mosaics validation to the cosine-square method. The Lambertian assumption of the cosine-square method is not reasonable for GrIS because the scattering characteristics change between the different zones of glaciers and a state of isotropic reflection is not maintained [38]. Electromagnetic wave penetration dominates in the dry snow zone while the wet-snow zone is dominated by surface scattering [34]. The scattering characteristics of different glacial radar zones to different polarizations and carrier frequencies require further study. Therefore, it is inappropriate to apply the cosine-square method to normalize the SAR images of the ice sheet with varying incidence angles, although the results show some improvements.
5.2. Limitation of the Study
For the incidence angle correction method to achieve a better performance for SAR images, more image pairs and more thawing samples are needed for the training process. This method is based on the empirical model, which is expected to perform better if more ascending and descending image pairs on the entire GrIS are involved in the training process, especially at the southern part of GrIS. Due to the Sentinel-1 observation plan on GrIS, quasi-simultaneous ascending and descending observations in EW mode are constrained, particularly in the southern GrIS. This possibly explains why normalized mosaics (Figure 7) perform better in the northern and central GrIS than in the southern GrIS.
The ratio () in Equation (4) should be related to the freeze-thaw states of the ice surface. However, an inadequate number of thawing samples of GrIS were taken for the linear model training due to a small number of SAR images observed in EW mode by Sentinel-1 being found in the southern part and/or summer for Greenland. Although ascending acquisitions in EW mode are usually available for southern GrIS, Sentinel-1 usually works in IW mode in the descending track. This could explain why the three freeze/thaw-related factors were tested and found to be invalid.
As for the issue of thermal noise, although noise vectors are provided in the EW product to eliminate the thermal noise for HV-polarized images, under- or over-compensation and unbalancing can still be noticed between different sub-swaths, especially between EW1 and EW2 [29]. This study removed EW1 for all HV images instead of denoising them, resulting in a smaller incidence angle range than the HH images. Thus, the RMSE evaluation shows limited improvement because the incidence angle differences between the descending and ascending angles are less than expected due to the lack of the EW1 subswath, resulting in a smaller RMSE. The RMSE analysis (Table 2 and Table 3) of the HH images and HV images can only be compared within the same polarization channel but not compared between different polarization channels.
6. Conclusions
This study utilized Sentinel-1 dual-polarized images to observe GrIS and proposed an incidence angle normalization method for the backscatter coefficient. This incidence angle correction method normalizes the variability in the backscatter intensities caused by the large incidence angle variations of the Extra Wide (EW) mode of Sentinel-1 dual-polarized images, which were used to observe GrIS. Our method reduced RMSE of multiple observations in the overlapping area by an average of 0.72 dB for the 5 experiment areas and 0.34 dB for the GrIS mosaics compared with the widely used cosine-square method for the HH images. For the HV images, the results normalized by our method showed a slight improvement. It can reduce the uncertainty of the subsequent application of Sentinel-1 images to observe GrIS, such as large-scale and time-series studies to monitor its surface freeze-thaw status. Given the small improvement of our incidence angle correction method compared to the traditional cosine square method for normalizing HV images, more training data and/or more effective incidence angle normalization methods need to be explored. Our method can also be applied to the incidence angle normalization of other SAR sensors such as ENVISAT, RADARSAT, and ALOS, if they provide quasi-simultaneous ascending and descending observations with the same mode.
Author Contributions
Methodology, X.C. (Xiao Chen) and G.L.; software, X.C. (Xiao Chen); validation, X.C. (Xiao Chen) and G.L.; writing—original draft preparation, X.C. (Xiao Chen); writing—review and editing, G.L.; visualization, X.C. (Xiao Chen) and Q.J.; supervision, Z.C.; funding acquisition, Z.C. and X.C. (Xiao Cheng). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China (Grant No. 2019YFC1509104), the National Natural Science Foundation of China (Grant No. 41901384), Science and Technology Projects in Guangzhou (Grant No. 20210202033), and by the Innovation Group Project of Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai) (Grant No. 311021008).
Data Availability Statement
The NSIDC products analyzed in this study are freely available at https://nsidc.org/data (accessed on 21 September 2022), and the Sentinel-1 images utilized can be downloaded from https://search.asf.alaska.edu/ (accessed on 21 September 2022).
Acknowledgments
We thank the European Space Agency (ESA) for providing the easily accessible Sentinel-1 SAR imagery, NSIDC for the product 0715 and 0728, the IMBIE Team for the Greenland ice sheet mask vector, and the ERA5 model data from the Copernicus Climate Change Service (C3S) Climate Data Store.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hooper, A.; Segall, P.; Zebker, H. Persistent scatterer interferometric synthetic aperture radar for crustal deformation analysis, with application to Volcán Alcedo, Galápagos. J. Geophys. Res. 2007, 112, B07407. [Google Scholar] [CrossRef]
- Jiang, M.; Guarnieri, A.M. Distributed scatterer interferometry with the refinement of spatiotemporal coherence. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3977–3987. [Google Scholar] [CrossRef]
- Lanari, R.; Mora, O.; Manunta, M.; Mallorqui, J.J.; Berardino, P.; Sansosti, E. A small-baseline approach for investigating deformations on full-resolution differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1377–1386. [Google Scholar] [CrossRef]
- Scher, C.; Steiner, N.C.; McDonald, K.C. Mapping seasonal glacier melt across the Hindu Kush Himalaya with time series synthetic aperture radar (SAR). Cryosphere 2021, 15, 4465–4482. [Google Scholar] [CrossRef]
- Paloscia, S.; Pettinato, S.; Santi, E.; Notarnicola, C.; Pasolli, L.; Reppucci, A. Soil moisture mapping using Sentinel-1 images: Algorithm and preliminary validation. Remote Sens. Environ. 2013, 134, 234–248. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, H.; Luo, Q.; Li, Y.; Wei, J.; Li, J. Oil spill detection in quad-polarimetric SAR Images using an advanced convolutional neural network based on SuperPixel model. Remote Sens. 2020, 12, 944. [Google Scholar] [CrossRef]
- Dong, L.; Shan, J. A comprehensive review of earthquake-induced building damage detection with remote sensing techniques. ISPRS-J. Photogramm. Remote Sens. 2013, 84, 85–99. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Long, D.G. Microwave Radar and Radiometric Remote Sensing; Univ. of Michigan Press: Ann Arbor, MI, USA, 2014. [Google Scholar]
- Mladenova, I.E.; Jackson, T.J.; Bindlish, R.; Hensley, S. Incidence angle normalization of radar backscatter data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1791–1804. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Volume II—Radar Remote Sensing and Surface Scattering and Emission Theory. In Microwave Remote Sensing: Active and Passive; Artech House: Norwood, MA, USA, 1982. [Google Scholar]
- Ardila, J.P.; Tolpekin, V.; Bijker, W. Angular backscatter variation in L-Band ALOS ScanSAR images of tropical forest areas. IEEE Geosci. Remote Sens. Lett. 2010, 7, 821–825. [Google Scholar] [CrossRef]
- Zhou, C.; Zheng, L. Mapping radar glacier zones and dry snow line in the Antarctic Peninsula using Sentinel-1 images. Remote Sens. 2017, 9, 1171. [Google Scholar] [CrossRef]
- Topouzelis, K.; Singha, S. Incidence angle normalization of Wide Swath SAR data for oceanographic applications. Open Geosci. 2016, 8, 450–464. [Google Scholar] [CrossRef]
- Menges, C.H.; Zyl, J.J.V.; Hill, G.J.E.; Ahmad, W. A procedure for the correction of the effect of variation in incidence angle on AIRSAR data. Int. J. Remote Sens. 2010, 22, 829–841. [Google Scholar] [CrossRef]
- Ye, N.; Walker, J.P.; Rüdiger, C. A cumulative distribution function method for normalizing variable-angle microwave observations. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3906–3916. [Google Scholar] [CrossRef]
- Nagler, T.; Rott, H. Retrieval of wet snow by means of multitemporal SAR data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 754–765. [Google Scholar] [CrossRef]
- Brath, M.; Kern, S.; Stammer, D. Sea ice classification during freeze-up conditions with multifrequency scatterometer data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3336–3353. [Google Scholar] [CrossRef]
- Gill, J.P.S.; Yackel, J.J.; Geldsetzer, T.; Fuller, M.C. Sensitivity of C-band synthetic aperture radar polarimetric parameters to snow thickness over landfast smooth first-year sea ice. Remote Sens. Environ. 2015, 166, 34–49. [Google Scholar] [CrossRef]
- Komarov, A.S.; Buehner, M. Detection of first-year and multi-year sea ice from dual-polarization SAR images under cold conditions. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9109–9123. [Google Scholar] [CrossRef]
- Mahmud, M.S.; Geldsetzer, T.; Howell, S.E.L.; Yackel, J.J.; Nandan, V.; Scharien, R.K. Incidence angle dependence of HH-polarized C- and L-band wintertime backscatter over Arctic sea ice. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6686–6698. [Google Scholar] [CrossRef]
- Zakhvatkina, N.Y.; Alexandrov, V.Y.; Johannessen, O.M.; Sandven, S.; Frolov, I.Y. Classification of sea ice types in ENVISAT Synthetic Aperture Radar images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2587–2600. [Google Scholar] [CrossRef]
- Aldenhoff, W.; Eriksson, L.E.B.; Ye, Y.; Heuzé, C. First-year and multiyear sea ice incidence angle normalization of dual-polarized Sentinel-1 SAR images in the Beaufort Sea. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 1540–1550. [Google Scholar] [CrossRef]
- Mäkynen, M.P.; Manninen, A.T.; Simila, M.H.; Karvonen, J.A.; Hallikainen, M.T. Incidence angle dependence of the statistical properties of C-band HH-polarization backscattering signatures of the Baltic Sea ice. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2593–2605. [Google Scholar] [CrossRef]
- Mäkynen, M.; Karvonen, J. Incidence angle dependence of first-year sea ice backscattering coefficient in Sentinel-1 SAR imagery over the Kara Sea. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6170–6181. [Google Scholar] [CrossRef]
- The IMBIE Team. Mass balance of the Greenland Ice Sheet from 1992 to 2018. Nature 2020, 579, 233–239. [Google Scholar] [CrossRef]
- Bhattacharya, I.; Jezek, K.C.; Wang, L.; Liu, H. Surface melt area variability of the Greenland ice sheet: 1979-2008. Geophys. Res. Lett. 2009, 36, L20502. [Google Scholar] [CrossRef]
- Colosio, P.; Tedesco, M.; Ranzi, R.; Fettweis, X. Surface melting over the Greenland ice sheet derived from enhanced resolution passive microwave brightness temperatures (1979–2019). Cryosphere 2021, 15, 2623–2646. [Google Scholar] [CrossRef]
- National Snow & Ice Data Center. Available online: https://nsidc.org/greenland-today/ (accessed on 28 October 2022).
- Sun, Y.; Li, X.M. Denoising Sentinel-1 Extra-Wide mode cross-polarization images over sea ice. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2116–2131. [Google Scholar] [CrossRef]
- Howat, I.M.; Negrete, A.; Smith, B.E. MEaSUREs Greenland Ice Mapping Project (GIMP) Digital Elevation Model from GeoEye and WorldView Imagery, Version 1. NASA National Snow and Ice Data Center Distributed Active Archive Center; Boulder, Colorado USA, 2017. Available online: https://nsidc.org/data/NSIDC-0715/versions/1 (accessed on 21 September 2022).
- Zwally; Jay, H.; Giovinetto, M.B.; Beckley, M.A.; Saba, J.L. Antarctic and Greenland Drainage Systems. GSFC Cryospheric Sciences Laboratory. 2012. Available online: http://icesat4.gsfc.nasa.gov/cryo_data/ant_grn_drainage_systems.php (accessed on 21 September 2022).
- Kim, Y.; Kimball, J.S.; Du, J.; Glassy, J. MEaSUREs Polar EASE-Grid 2.0 Daily 6 km Land Freeze/Thaw Status from AMSR-E and AMSR2, Version 2; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2021. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Hourly Data on Single Levels from 1979 to Present; Copernicus Climate Change Service (C3S) Climate Data Store (CDS): Reading, UK, 2018. [Google Scholar] [CrossRef]
- Rees, W.G. Remote sensing of glacier, ice sheets and ice shelves. In Remote Sensing of Snow and Ice; CRC Press: Boca Raton, FL, USA, 2006; pp. 212–217. [Google Scholar]
- Joughin, I. MEaSUREs Greenland Image Mosaics from Sentinel-1A and 1B, Version 3; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2020. [Google Scholar] [CrossRef]
- Joughin, I. MEaSUREs Greenland Ice Sheet Mosaics from SAR Data, Version 1; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2015. [Google Scholar] [CrossRef]
- O’Grady, D.; Leblanc, M.; Gillieson, D. Relationship of local incidence angle with satellite radar backscatter for different surface conditions. Int. J. Appl. Earth Obs. Geoinf. 2013, 24, 42–53. [Google Scholar] [CrossRef]
- Liu, H.; Wang, L.; Jezek, K.C. Automated delineation of dry and melt snow zones in Antarctica using active and passive microwave observations from space. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2152–2163. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).