Globally Scalable Approach to Estimate Net Ecosystem Exchange Based on Remote Sensing, Meteorological Data, and Direct Measurements of Eddy Covariance Sites
Abstract
1. Introduction
2. Data and Methods
2.1. Data
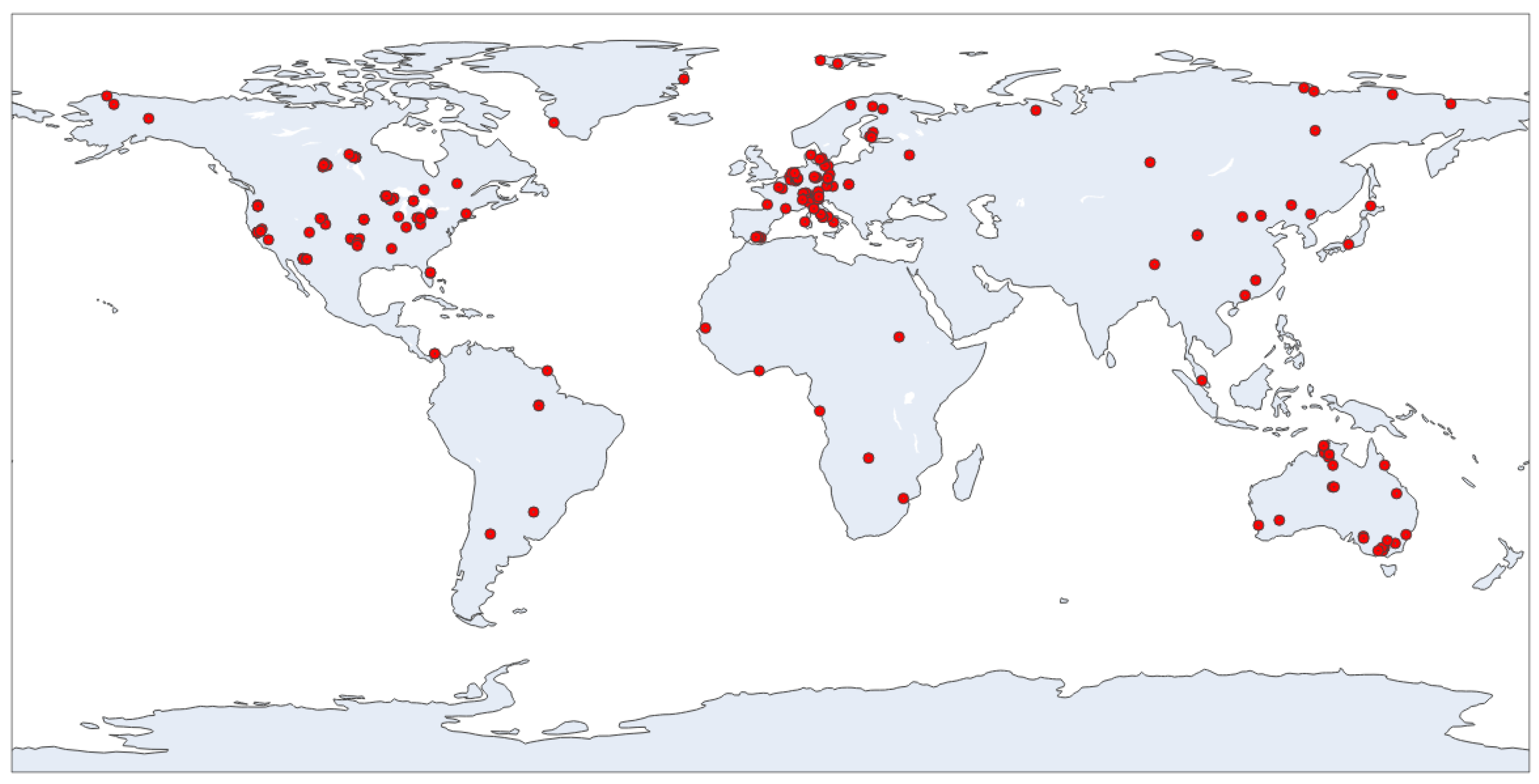
2.1.1. Eddy Covariance Data
2.1.2. Remote Sensing Data
2.1.3. Meteorological Data
2.2. Simulation Experiment
2.2.1. Footprint Calculation with LPDM
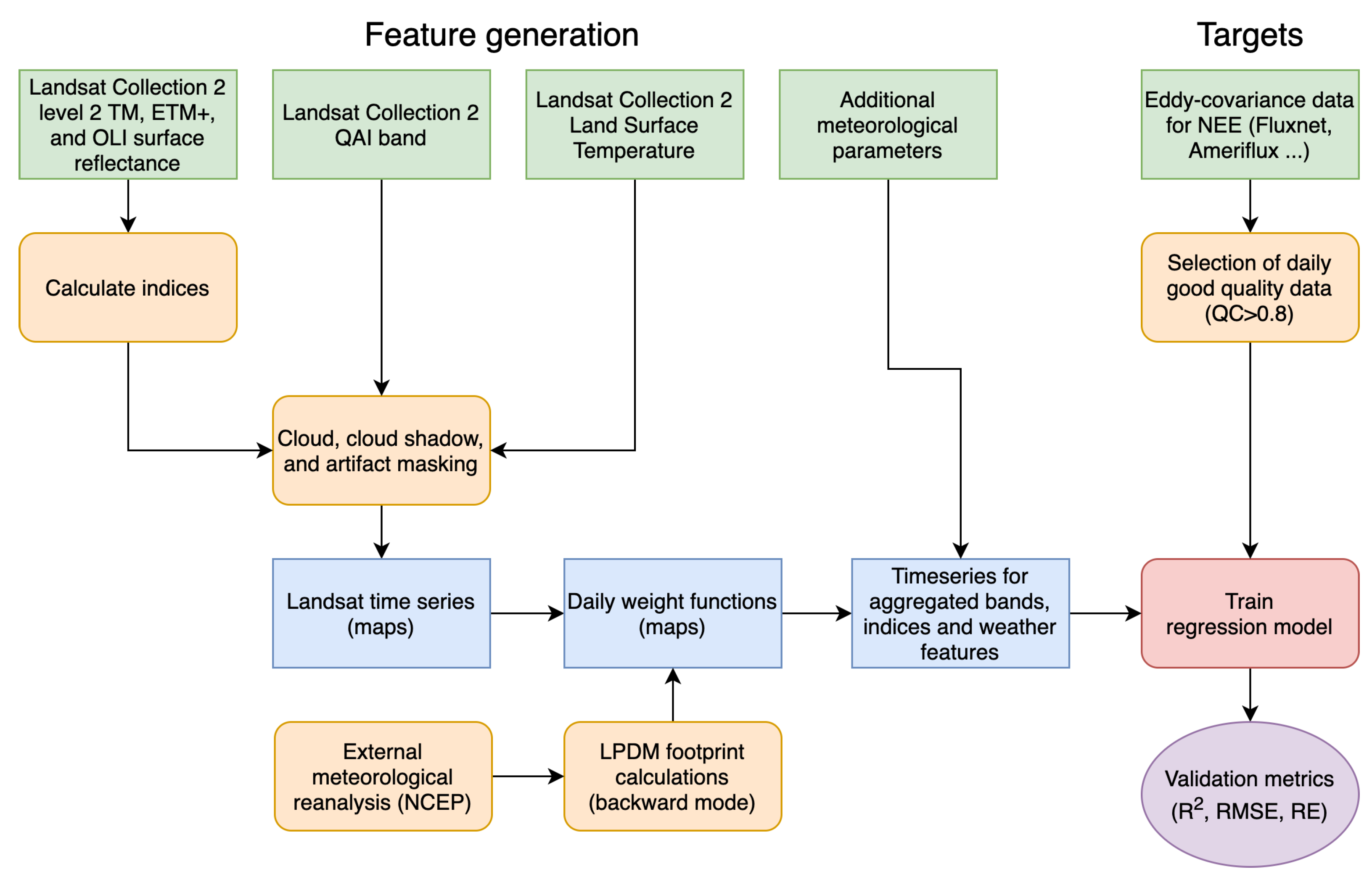
2.2.2. Feature Generation and Data Augmentation
2.2.3. Building Regression Model
2.2.4. Metrics for Accuracy Assessment
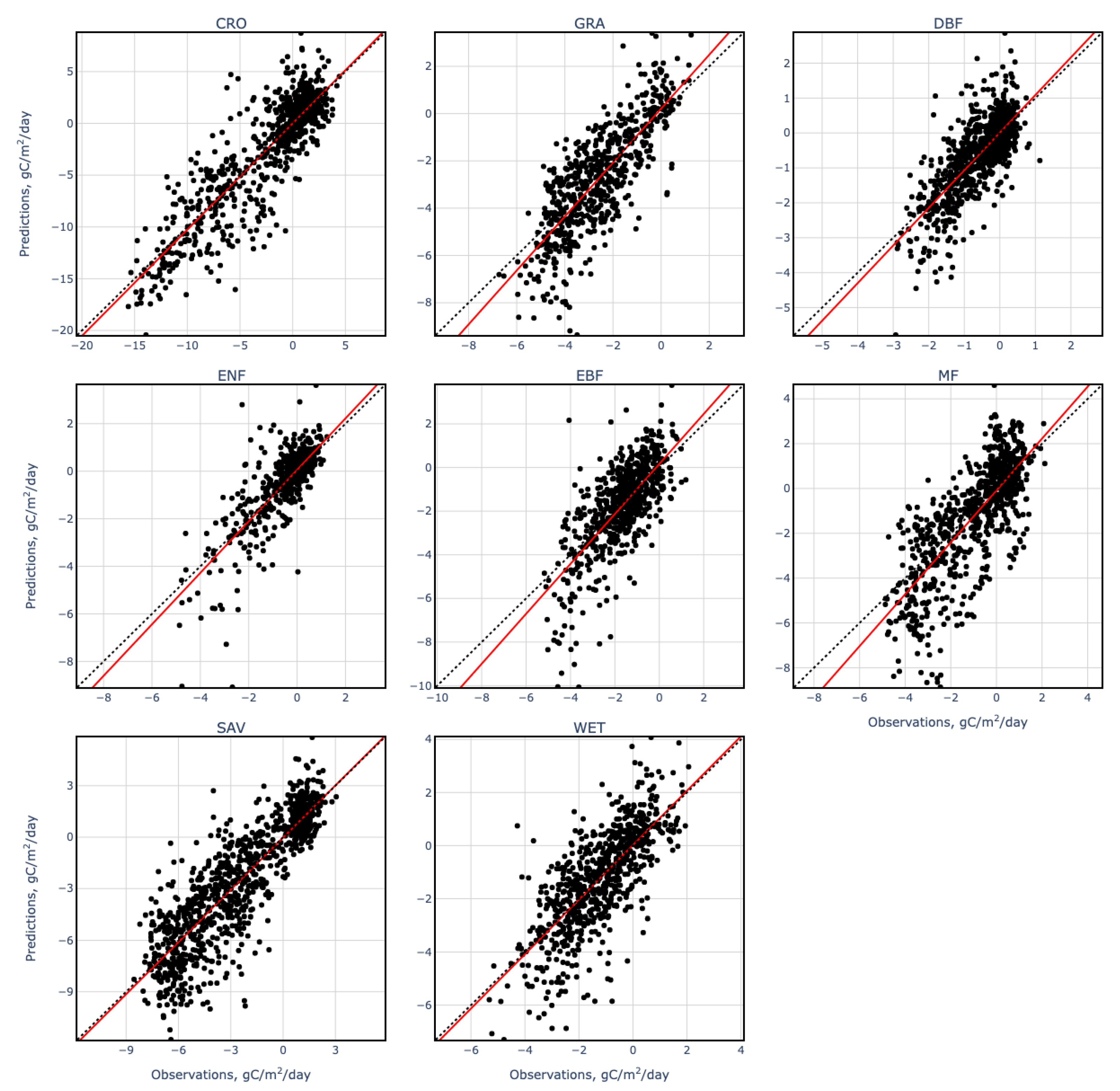
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Input Data Description
| Site Code | Lat | Lon | IGBP | Start Year | End Year |
|---|---|---|---|---|---|
| BE-Lon | 50.5516 | 4.7462 | CRO | 2004 | 2014 |
| CH-Oe2 | 47.2864 | 7.7337 | CRO | 2004 | 2014 |
| DE-Geb | 51.0997 | 10.9146 | CRO | 2001 | 2014 |
| DE-Kli | 50.8931 | 13.5224 | CRO | 2004 | 2014 |
| FR-Gri | 48.8442 | 1.9519 | CRO | 2004 | 2014 |
| IT-BCi | 40.5237 | 14.9574 | CRO | 2004 | 2014 |
| IT-CA2 | 42.3772 | 12.026 | CRO | 2011 | 2014 |
| US-ARM | 36.6058 | −97.4888 | CRO | 2003 | 2012 |
| US-CRT | 41.6285 | −83.3471 | CRO | 2011 | 2013 |
| US-Lin | 36.3566 | −119.0922 | CRO | 2009 | 2010 |
| US-Ne1 | 41.1651 | −96.4766 | CRO | 2001 | 2013 |
| US-Ne2 | 41.1649 | −96.4701 | CRO | 2001 | 2013 |
| US-Ne3 | 41.1797 | −96.4397 | CRO | 2001 | 2013 |
| US-Twt | 38.1087 | −121.6531 | CRO | 2009 | 2014 |
| DE-Hai | 51.0792 | 10.4522 | DBF | 2000 | 2012 |
| DE-Lnf | 51.3282 | 10.3678 | DBF | 2002 | 2012 |
| DK-Sor | 55.4859 | 11.6446 | DBF | 2000 | 2014 |
| FR-Fon | 48.4764 | 2.7801 | DBF | 2005 | 2014 |
| IT-CA1 | 42.3804 | 12.0266 | DBF | 2011 | 2014 |
| IT-CA3 | 42.38 | 12.0222 | DBF | 2011 | 2014 |
| IT-Col | 41.8494 | 13.5881 | DBF | 2000 | 2014 |
| IT-Isp | 45.8126 | 8.6336 | DBF | 2013 | 2014 |
| IT-PT1 | 45.2009 | 9.061 | DBF | 2002 | 2004 |
| IT-Ro1 | 42.4081 | 11.93 | DBF | 2000 | 2008 |
| IT-Ro2 | 42.3903 | 11.9209 | DBF | 2002 | 2012 |
| US-Ha1 | 42.5378 | −72.1715 | DBF | 2000 | 2012 |
| US-Oho | 41.5545 | −83.8438 | DBF | 2004 | 2013 |
| US-UMB | 45.5598 | −84.7138 | DBF | 2000 | 2014 |
| US-UMd | 45.5625 | −84.6975 | DBF | 2007 | 2014 |
| US-WCr | 45.8059 | −90.0799 | DBF | 2000 | 2014 |
| AU-Cum | −33.6152 | 150.7236 | EBF | 2012 | 2014 |
| AU-Wac | −37.4259 | 145.1878 | EBF | 2005 | 2008 |
| AU-Whr | −36.6732 | 145.0294 | EBF | 2011 | 2014 |
| AU-Wom | −37.4222 | 144.0944 | EBF | 2010 | 2014 |
| CN-Din | 23.1733 | 112.5361 | EBF | 2003 | 2005 |
| FR-Pue | 43.7413 | 3.5957 | EBF | 2000 | 2014 |
| IT-Cpz | 41.7052 | 12.3761 | EBF | 2000 | 2009 |
| CZ-BK1 | 49.5021 | 18.5369 | ENF | 2004 | 2014 |
| DE-Obe | 50.7867 | 13.7213 | ENF | 2008 | 2014 |
| DE-Tha | 50.9626 | 13.5651 | ENF | 2000 | 2014 |
| IT-Ren | 46.5869 | 11.4337 | ENF | 2000 | 2013 |
| IT-SRo | 43.7279 | 10.2844 | ENF | 2000 | 2012 |
| US-Blo | 38.8953 | −120.6328 | ENF | 2000 | 2007 |
| AU-DaP | −14.0633 | 131.3181 | GRA | 2007 | 2013 |
| AU-Stp | −17.1507 | 133.3502 | GRA | 2008 | 2014 |
| AU-TTE | −22.287 | 133.64 | GRA | 2012 | 2014 |
| CH-Cha | 47.2102 | 8.4104 | GRA | 2005 | 2014 |
| CH-Fru | 47.1158 | 8.5378 | GRA | 2005 | 2014 |
| CH-Oe1 | 47.2858 | 7.7319 | GRA | 2002 | 2008 |
| CN-Cng | 44.5934 | 123.5092 | GRA | 2007 | 2010 |
| ES-Amo | 36.8336 | −2.2523 | OSH | 2007 | 2012 |
| ES-LJu | 36.9266 | −2.7521 | OSH | 2004 | 2013 |
| US-AR1 | 36.4267 | −99.42 | GRA | 2009 | 2012 |
| US-AR2 | 36.6358 | −99.5975 | GRA | 2009 | 2012 |
| US-Goo | 34.2547 | −89.8735 | GRA | 2002 | 2006 |
| US-Igreen | 41.8406 | −88.241 | GRA | 2004 | 2011 |
| US-SRC | 31.9083 | −110.8395 | OSH | 2008 | 2014 |
| US-SRG | 31.7894 | −110.8277 | GRA | 2008 | 2014 |
| US-Var | 38.4133 | −120.9508 | GRA | 2000 | 2014 |
| US-Whs | 31.7438 | −110.0522 | OSH | 2007 | 2014 |
| US-Wkg | 31.7365 | −109.9419 | GRA | 2004 | 2014 |
| AR-SLu | −33.4648 | −66.4598 | MF | 2009 | 2011 |
| BE-Bra | 51.3076 | 4.5198 | MF | 2000 | 2014 |
| BE-Vie | 50.3049 | 5.9981 | MF | 2000 | 2014 |
| CA-Gro | 48.2167 | −82.1556 | MF | 2003 | 2014 |
| CH-Lae | 47.4783 | 8.3644 | MF | 2004 | 2014 |
| CN-Cha | 42.4025 | 128.0958 | MF | 2003 | 2005 |
| US-Syv | 46.242 | −89.3477 | MF | 2001 | 2014 |
| AU-ASM | −22.283 | 133.249 | SAV | 2010 | 2014 |
| AU-Ade | −13.0769 | 131.1178 | WSA | 2007 | 2009 |
| AU-Cpr | −34.0021 | 140.5891 | SAV | 2010 | 2014 |
| AU-Dry | −15.2588 | 132.3706 | SAV | 2008 | 2014 |
| AU-Gin | −31.3764 | 115.7138 | WSA | 2011 | 2014 |
| AU-How | −12.4943 | 131.1523 | WSA | 2001 | 2014 |
| US-SRM | 31.8214 | −110.8661 | WSA | 2004 | 2014 |
| US-Ton | 38.4309 | −120.966 | WSA | 2001 | 2014 |
| AU-Fog | −12.5452 | 131.3072 | WET | 2006 | 2008 |
| CN-Ha2 | 37.6086 | 101.3269 | WET | 2003 | 2005 |
| DE-Spw | 51.8922 | 14.0337 | WET | 2010 | 2014 |
| US-Los | 46.0827 | −89.9792 | WET | 2000 | 2014 |
| US-Myb | 38.0499 | −121.765 | WET | 2010 | 2014 |
| US-Tw1 | 38.1074 | −121.6469 | WET | 2012 | 2014 |
| US-Tw4 | 38.1027 | −121.6413 | WET | 2013 | 2014 |
Appendix B. Features Description
- LST/SWIR2·Mean_Solar_1week—LST divided by SWIR2 and multiplied by 1 week mean solar radiation
- LST/SWIR2·Solar—LST divided by SWIR2 and multiplied by current daily solar radiation
- Cum_Solar_2week—2 week cumulative solar radiation
- Cum_Solar_4days—4 days cumulative solar radiation
- Cum_Temperature_1week—1 week cumulative temperature
- Cum_Temperature_4days—4 days cumulative temperature
- Cum_Temperature_over_2_1week—1 week cumulative temperature over 2 Celsius degree
- Cum_Temperature_over_2_3week—3 week cumulative temperature over 2 Celsius degree
- Cum_Temperature_over_3_3week—3 week cumulative temperature over 3 Celsius degree
- Cum_Temperature_over_4_3week—week cumulative temperature over 4 Celsius degree
- Cum_Temperature_over_5_2week—2 week cumulative temperature over 5 Celsius degree
- Cum_Temperature_over_5_3week—3 week cumulative temperature over 5 Celsius degree
- Cum_precipitation_2days—2 days cumulative precipitation
- Cum_precipitation_3days—3 days cumulative precipitation
- Cum_precipitation_5days—5 days cumulative precipitation
- Delta_T—difference between current daily temperature and daily dew-point temperature
- EVI·DewPoint—EVI multiplied by dew-point temperature
- Mean_Solar_2week—2 week averaged solar radiation
- Mean_Solar_4days—4 days averaged solar radiation
- Mean_Solar_4week—4 week averaged solar radiation
- Mean_Temperature_1week—1 week averaged temperature
- NDVI · Cum_Solar_3week—NDVI multiplied by 3 week cumulative solar radiation
- NDVI·Mean_Solar_3week—NDVI multiplied by 3 week averaged solar radiation
- NDVI·Mean_Solar_4week—NDVI multiplied by 4 week averaged solar radiation
- NDVI·Solar—NDVI multiplied by current daily solar radiation
- TCG·Cum_Solar_3week—TCG multiplied by 3 week cumulative solar radiation
- TCG·Cum_Solar_4days—TCG multiplied by 4 days cumulative solar radiation
- TCG·DewPoint—TCG multiplied by dew-point temperature
- TCG·Mean_Temperature_2week—TCG multiplied by 2 week averaged temperature
- TCG·Solar—TCG multiplied by current daily solar radiation
- blue·SWIR—blue multiplied by SWIR
- blue/green—blue divided by green
- blue/red—blue divided by red
- blue/NIR—blue divided by NIR
- blue/SWIR2—blue divided by SWIR2
- green red—green multiplied by red
- green/red—green divided by red
- green/NIR—green divided by NIR
- red/blue—red divided by blue
- red/green—red divided by green
- red/NIR—red divided by NIR
- red/SWIR—red divided by SWIR
- red/SWIR2·Cum_Solar_2week—red divided by SWIR2 and multiplied by 2 week cumulative solar radiation
- NIR·SWIR—NIR multiplied by SWIR
- NIR/LST—NIR divided by LST
- NIR/LST·Solar—NIR divided by LST and multiplied by current daily solar radiation
- NIR/green—NIR divided by green
- NIR/SWIR—NIR divided by SWIR
- NIR/SWIR2—NIR divided by SWIR2
- NIR/SWIR2·Mean_Solar_2week—NIR divided by SWIR2 and multiplied by 2 week averaged solar radiation
- NIR/SWIR2·Solar—NIR divided by SWIR2 and multiplied by current daily solar radiation
- NIR·Cum_Solar_3week—NIR multiplied by 3 week cumulative solar radiation
- NIR·Solar—NIR multiplied by current daily solar radiation
- SWIR/green—SWIR divided by green
- SWIR/red—SWIR divided by red
- SWIR/NIR—SWIR divided by NIR
- SWIR/NIR·Cum_Temperature_over_5_4week—SWIR divided by NIR and multiplied by 4 week cumulative temperature over 5 Celsius degree
- SWIR2/blue—SWIR2 divided by blue
- SWIR2/green—SWIR2 divided by green
- SWIR2/NIR—SWIR2 divided by NIR
- SWIR2/SWIR—SWIR2 divided by SWIR
References
- Fargione, J.E.; Bassett, S.; Boucher, T.; Bridgham, S.D.; Conant, R.T.; Cook-Patton, S.C.; Ellis, P.W.; Falcucci, A.; Fourqurean, J.W.; Gopalakrishna, T.; et al. Natural climate solutions for the United States. Sci. Adv. 2018, 4, 1869. [Google Scholar] [CrossRef] [PubMed]
- Novick, K.A.; Metzger, S.; Anderegg, W.R.L.; Barnes, M.; Cala, D.S.; Guan, K.; Hemes, K.S.; Hollinger, D.Y.; Kumar, J.; Litvak, M.; et al. Informing Nature-based Climate Solutions for the United States with the best-available science. Glob. Chang. Biol. 2022, 28, 3778–3794. [Google Scholar] [CrossRef] [PubMed]
- Seddon, N.; Chausson, A.; Berry, P.; Girardin, C.A.; Smith, A.; Turner, B. Understanding the value and limits of nature-based solutions to climate change and other global challenges. Philos. Trans. R. Soc. B Biol. Sci. 2020, 375, 1794. [Google Scholar] [CrossRef] [PubMed]
- Cook-Patton, S.C.; Leavitt, S.M.; Gibbs, D.; Harris, N.L.; Lister, K.; Anderson-Teixeira, K.J.; Briggs, R.D.; Chazdon, R.L.; Crowther, T.W.; Ellis, P.W.; et al. Mapping carbon accumulation potential from global natural forest regrowth. Nature 2020, 585, 545–550. [Google Scholar] [CrossRef] [PubMed]
- Heavens, N.G.; Ward, D.S.; Natalie, M.M. Studying and Projecting Climate Change with Earth System Models. Nat. Educ. Knowl. 2013, 4, 4. [Google Scholar]
- Fisher, R.A.; Koven, C.D.; Anderegg, W.R.L.; Christoffersen, B.O.; Dietze, M.C.; Farrior, C.E.; Holm, J.A.; Hurtt, G.C.; Knox, R.G.; Lawrence, P.J.; et al. Vegetation demographics in Earth System Models: A review of progress and priorities. Glob. Chang. Biol. 2018, 24, 35–54. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, F.; Wang, J.; Ju, W.; Chen, J.M. Terrestrial ecosystem carbon flux estimated using GOSAT and OCO-2 XCO2 retrievals. Atmos. Chem. Phys. 2019, 19, 12067–12082. [Google Scholar] [CrossRef]
- Kondo, M.; Patra, P.K.; Sitch, S.; Friedlingstein, P.; Poulter, B.; Chevallier, F.; Ciais, P.; Canadell, J.G.; Bastos, A.; Lauerwald, R.; et al. State of the science in reconciling top-down and bottom-up approaches for terrestrial CO2 budget. Glob. Chang. Biol. 2020, 26, 1068–1084. [Google Scholar] [CrossRef]
- Dara, A.; Baumann, M.; Kuemmerle, T.; Pflugmacher, D.; Rabe, A.; Griffiths, P.; Hölzel, N.; Kamp, J.; Freitag, M.; Hostert, P. Mapping the timing of cropland abandonment and recultivation in northern Kazakhstan using annual Landsat time series. Remote. Sens. Environ. 2018, 213, 49–60. [Google Scholar] [CrossRef]
- Quegan, S.; Le Toan, T.; Chave, J.; Dall, J.; Exbrayat, J.-F.; Minh, D.H.T.; Lomas, M.; D’Alessandro, M.M.; Paillou, P.; Papathanassiou, K.; et al. The European Space Agency BIOMASS mission: Measuring forest above-ground biomass from space. Remote. Sens. Environ. 2019, 227, 44–60. [Google Scholar] [CrossRef]
- Rodríguez-Veiga, P.; Wheeler, J.; Louis, V.; Tansey, K.; Balzter, H. Quantifying forest biomass carbon stocks from space. Curr. For. Rep. 2017, 3, 1–18. [Google Scholar] [CrossRef]
- Yuan, W.; Cai, W.; Xia, J.; Chen, J.; Liu, S.; Dong, W.; Merbold, L.; Law, B.; Arain, A.; Beringer, J.; et al. Global comparison of light use efficiency models for simulating terrestrial vegetation gross primary production based on the LaThuile database. Agric. For. Meteorol. 2014, 192–193, 108–120. [Google Scholar] [CrossRef]
- Zhang, L.X.; Zhou, D.C.; Fan, J.W.; Hu, Z.M. Comparison of four light use efficiency models for estimating terrestrial gross primary production. Ecol. Model. 2015, 300, 30–39. [Google Scholar] [CrossRef]
- Wu, C.; Munger, J.W.; Niu, Z.; Kuang, D. Comparison of multiple models for estimating gross primary production using MODIS and eddy covariance data in Harvard Forest. Remote. Sens. Environ. 2010, 114, 2925–2939. [Google Scholar] [CrossRef]
- Wu, C.; Chen, J.M.; Huang, N. Predicting gross primary production from the enhanced vegetation index and photosynthetically active radiation: Evaluation and calibration. Remote. Sens. Environ. 2011, 115, 3424–3435. [Google Scholar] [CrossRef]
- Ueyama, M.; Ichii, K.; Iwata, H.; Euskirchen, E.S.; Zona, D.; Rocha, A.V.; Harazono, Y.; Iwama, C.; Nakai, T.; Oechel, W.C. Upscaling terrestrial carbon dioxide fluxes in Alaska with satellite remote sensing and support vector regression. J. Geophys. Res. Biogeosci. 2013, 118, 1266–1281. [Google Scholar] [CrossRef]
- Xie, X.; Li, A.; Tan, J.; Jin, H.; Nan, X.; Zhang, Z.; Bian, J.; Lei, G. Assessments of gross primary productivity estimations with satellite data-driven models using eddy covariance observation sites over the northern hemisphere. Agric. For. Meteorol. 2020, 280, 107771. [Google Scholar] [CrossRef]
- Gardin, L.; Chiesi, M.; Fibbi, L.; Maselli, F. Mapping soil organic carbon in Tuscany through the statistical combination of ground observations with ancillary and remote sensing data. Geoderma 2021, 404, 115386. [Google Scholar] [CrossRef]
- Tramontana, G.; Jung, M.; Schwalm, C.R.; Ichii, K.; Camps-Valls, G.; Ráduly, B.; Reichstein, M.; Arain, M.A.; Cescatti, A.; Kiely, G.; et al. Predicting carbon dioxide and energy fluxes across global FLUXNET sites with regression algorithms. Biogeosciences 2016, 13, 4291–4313. [Google Scholar] [CrossRef]
- Dubovik, O.; Schuster, G.L.; Xu, F.; Hu, Y.; Bösch, H.; Landgraf, J.; Li, Z. Grand Challenges in Satellite Remote Sensing. Front. Remote. Sens. 2021, 2, 9818. [Google Scholar] [CrossRef]
- Burba, G. Eddy Covariance Method for Scientific, Regulatory, and Commercial Applications; LI-COR Biosciences Publisher: Lincoln, NE, USA, 2022; p. 702. [Google Scholar]
- Campioli, M.; Malhi, Y.; Vicca, S.; Luyssaert, S.; Papale, D.; Penuelas, J.; Reichstein, M.; Migliavacca, M.; Arain, A.; Janssens, A. Evaluating the convergence between eddy-covariance and biometric methods for assessing carbon budgets of forests. Nat. Commun. 2016, 7, 13717. [Google Scholar] [CrossRef]
- Kirschbaum, M.U.F.; Eamus, D.; Gifford, R.M.; Roxburgh, S.H.; Sands, P.J. Definitions of some ecological terms commonly used in carbon accounting. In Proceedings of the Net Ecosystem Exchange CRC Workshop, Canberra, Australia, 18–20 April 2001; pp. 2–5. [Google Scholar]
- Luyssaert, S.; Reichstein, M.; Schulze, E.-D.; Janssens, I.A.; Law, B.E.; Papale, D.; Dragoni, D.; Goulden, M.L.; Granier, A.; Kutsch, W.L.; et al. Toward a consistency cross-check of eddy covariance flux-based and biometric estimates of ecosystem carbon balance. Glob. Biogeochem. Cycl. 2009, 23, 3377. [Google Scholar] [CrossRef]
- Aubinet, M.; Vesala, T.; Papale, D. Eddy Covariance: A Practical Guide to Measurement and Data Analysis, 1st ed.; Springer: Dordrecht, The Netherlands, 2012; p. 438. [Google Scholar]
- Foken, T. Micrometeorology, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2017; p. 362. [Google Scholar]
- Pastorello, G.Z.; Papale, D.; Chu, H.; Trotta, C.; Agarwal, D.A.; Canfora, E.; Baldocchi, D.D.; Torn, M.S. A new dataset to keep a sharper eye on land-air exchanges. Eos 2017, 98. [Google Scholar] [CrossRef]
- Burba, G. Illustrative Maps of Past and Present Eddy Covariance Measurement Locations: II. High-Resolution Images. 2019, 9. Available online: https://www.researchgate.net (accessed on 1 June 2022).
- Baldocchi, D. How eddy covariance flux measurements have contributed to our understanding of global change biology. Glob. Chang. Biol. 2020, 26, 242–260. [Google Scholar] [CrossRef] [PubMed]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A New Tool to Study the Temporal and Spatial Variability of Ecosystem-Scale Carbon Dioxide, Water Vapor, and Energy Flux Densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Friend, A.D.; Arneth, A.; Kiang, N.Y.; Lomas, M.; Ogée, J.; Rödenbeck, C.; Running, S.W.; Santaren, J.-D.; Sitch, S.; Viovy, N.; et al. FLUXNET and modelling the global carbon cycle. Glob. Chang. Biol. 2007, 13, 610–633. [Google Scholar] [CrossRef]
- Pastorello, G.; Trotta, C.; Canfora, E.; Chu, H.; Christianson, D.; Cheah, Y.-W.; Pointdexter, C.; Chen, J.; Elbashandy, A.; Humphrey, M.; et al. The FLUXNET2015 dataset and the ONEFlux processing pipeline for eddy covariance data. Sci. Data 2020, 7, 225. [Google Scholar] [CrossRef]
- Williams, M.; Richardson, A.D.; Reichstein, M.; Stoy, P.C.; Peylin, P.; Verbeeck, H.; Carvalhais, N.; Jung, M.; Hollinger, D.Y.; Kattge, J.; et al. Improving land surface models with FLUXNET data. Biogeosciences 2009, 6, 1341–1359. [Google Scholar] [CrossRef]
- Fu, D.; Chen, B.; Zhang, H.; Wang, J.; Black, T.A.; Amiro, B.D.; Bohrer, G.; Bolstad, P.; Coulter, R.; Rahman, A.F.; et al. Estimating Landscape Net Ecosystem Exchange At High Spatial–Temporal Resolution Based On Landsat Data, An Improved Upscaling Model Framework, And Eddy Covariance Flux Measurements. Remote. Sens. Environ. 2014, 141, 90–104. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2008; p. 200. [Google Scholar]
- Crist, E.P. A TM tasseled cap equivalent transformation for reflectance factor data. Remote Sens. Environ. 1985, 17, 301–306. [Google Scholar] [CrossRef]
- Ren, H.; Zhou, G.; Zhang, F. Using negative soil adjustment factor in soil-adjusted vegetation index (SAVI) for aboveground living biomass estimation in arid grasslands. Remote Sens. Environ. 2018, 209, 439–445. [Google Scholar] [CrossRef]
- Dara, A.; Baumann, M.; Freitag, M.; Hölzel, N.; Hostert, P.; Kamp, J.; Müller, D.; Prishchepov, A.V.; Kuemmerle, T. Annual Landsat time series reveal post-Soviet changes in grazing pressure. Remote Sens. Environ. 2020, 239, 111667. [Google Scholar] [CrossRef]
- Boogaard, H.; Schubert, J.; De Wit, A.; Lazebnik, J.; Hutjes, R.; Van der Grijn, G. Agrometeorological Indicators from 1979 to Present Derived from Reanalysis, Version 1.0. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2020. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/sis-agrometeorological-indicators?tab=overview (accessed on 30 June 2022).
- Leclerc, M.Y.; Foken, T. Footprints in Micrometeorology and Ecology, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2014; p. 239. [Google Scholar]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A simple two-dimensional parameterisation for flux footprint prediction (FFP). Geosci. Model Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef]
- Griebel, A.; Bennett, L.T.; Metzen, D.; Cleverly, J.; Burba, G.; Arndt, S.K. Effects of inhomogeneities within the flux footprint on the interpretation of seasonal, annual, and interannual ecosystem carbon exchange. Agric. For. Meteorol. 2016, 221, 50–60. [Google Scholar] [CrossRef]
- Griebel, A.; Metzen, D.; Pendall, E.; Burba, G.; Metzger, S. Generating spatially robust carbon budgets from flux tower observations. Geophys. Res. Lett. 2020, 47, 5942. [Google Scholar] [CrossRef]
- Stohl, A.; Forster, C.; Frank, A.; Seibert, P.; Wotawa, G. Technical note: The Lagrangian particle dispersion model FLEXPART version 6.2. Atmos. Chem. Phys. 2005, 5, 2461–2474. [Google Scholar] [CrossRef]
- Stohl, A.; Seibert, P.; Arduini, J.; Eckhardt, S.; Fraser, P.; Greally, B.R.; Lunder, C.; Maione, M.; Mhle, J.; O’Doherty, S.; et al. An analytical inversion method for determining regional and global emissions of greenhouse gases: Sensitivity studies and application to halocarbons. Atmos. Chem. Phys. 2009, 9, 1597–1620. [Google Scholar] [CrossRef]
- Murphy, K.P. 14.4.3. Kernelized ridge regression. In Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012; pp. 492–493. [Google Scholar]
- Shawe-Taylor, J.; Cristianini, N. Kernel Methods for Pattern Analysis; Cambridge University Press: Cambridge, MA, USA, 2004; p. 462. [Google Scholar]
- Vapnik, V.; Golowich, S.E.; Smola, A. Support Vector Method for Function Approximation, Regression Estimation, and Signal Processing. In Advances in Neural Information Processing Systems 9; MIT Press: Cambridge, MA, USA, 1996; pp. 281–287. [Google Scholar]
- Raschka, S. MLxtend: Providing machine learning and data science utilities and extensions to Python’s scientific computing stack. J. Open Source Softw. 2018, 3, 638. [Google Scholar] [CrossRef]
- Kozachenko, L.F.; Leonenko, N.N. Sample Estimate of the Entropy of a Random Vector. Probl. Inform. Transmiss. 1987, 95–101, 9–16. [Google Scholar]
- Jung, M.; Reichstein, M.; Margolis, H.A.; Cescatti, A.; Richardson, A.D.; Arain, M.A.; Arneth, A.; Bernhofer, C.; Bonal, D.; Chen, J.; et al. Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations. J. Geophys. Res.-Biogeol. 2011, 116, 1566. [Google Scholar] [CrossRef]
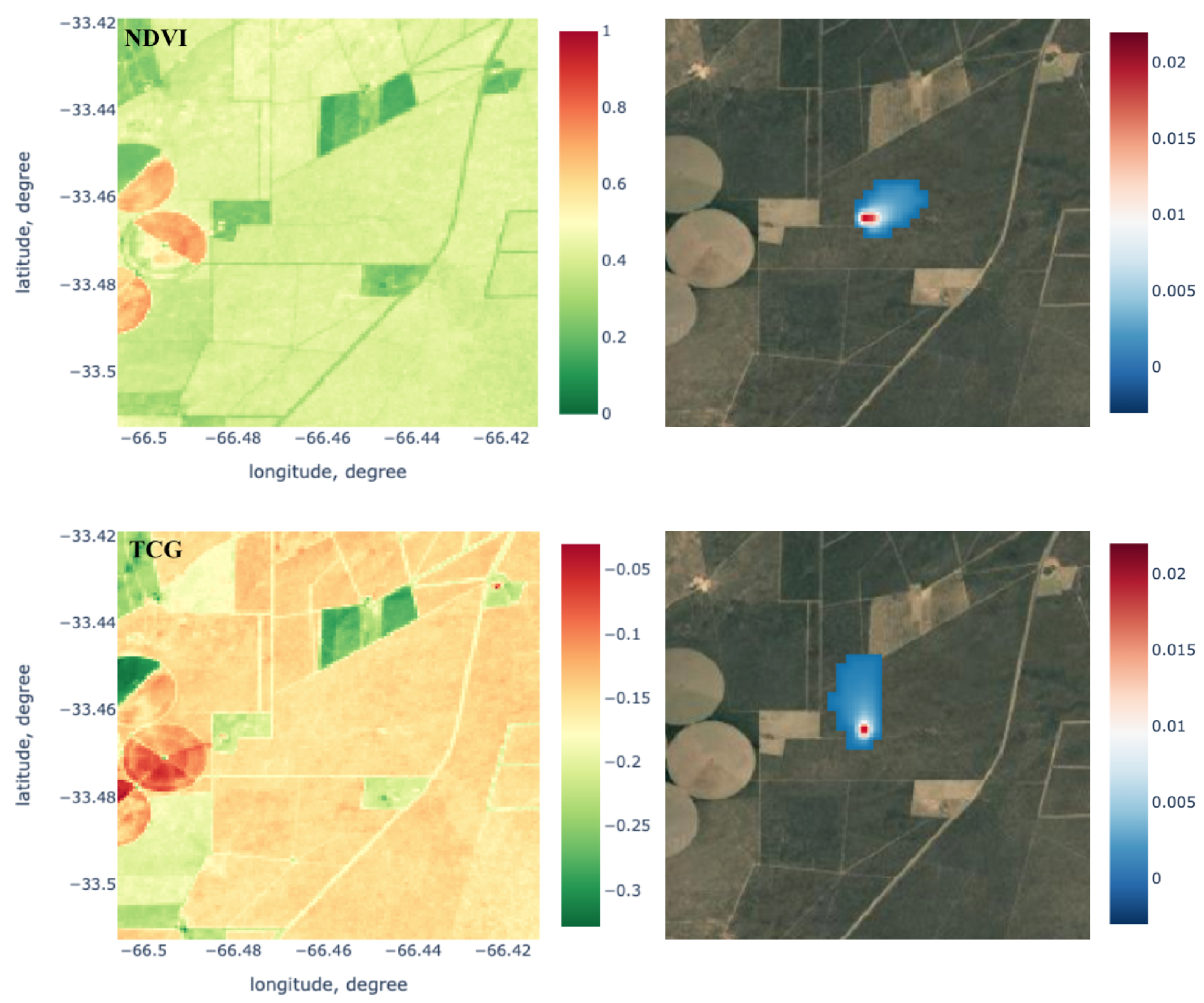
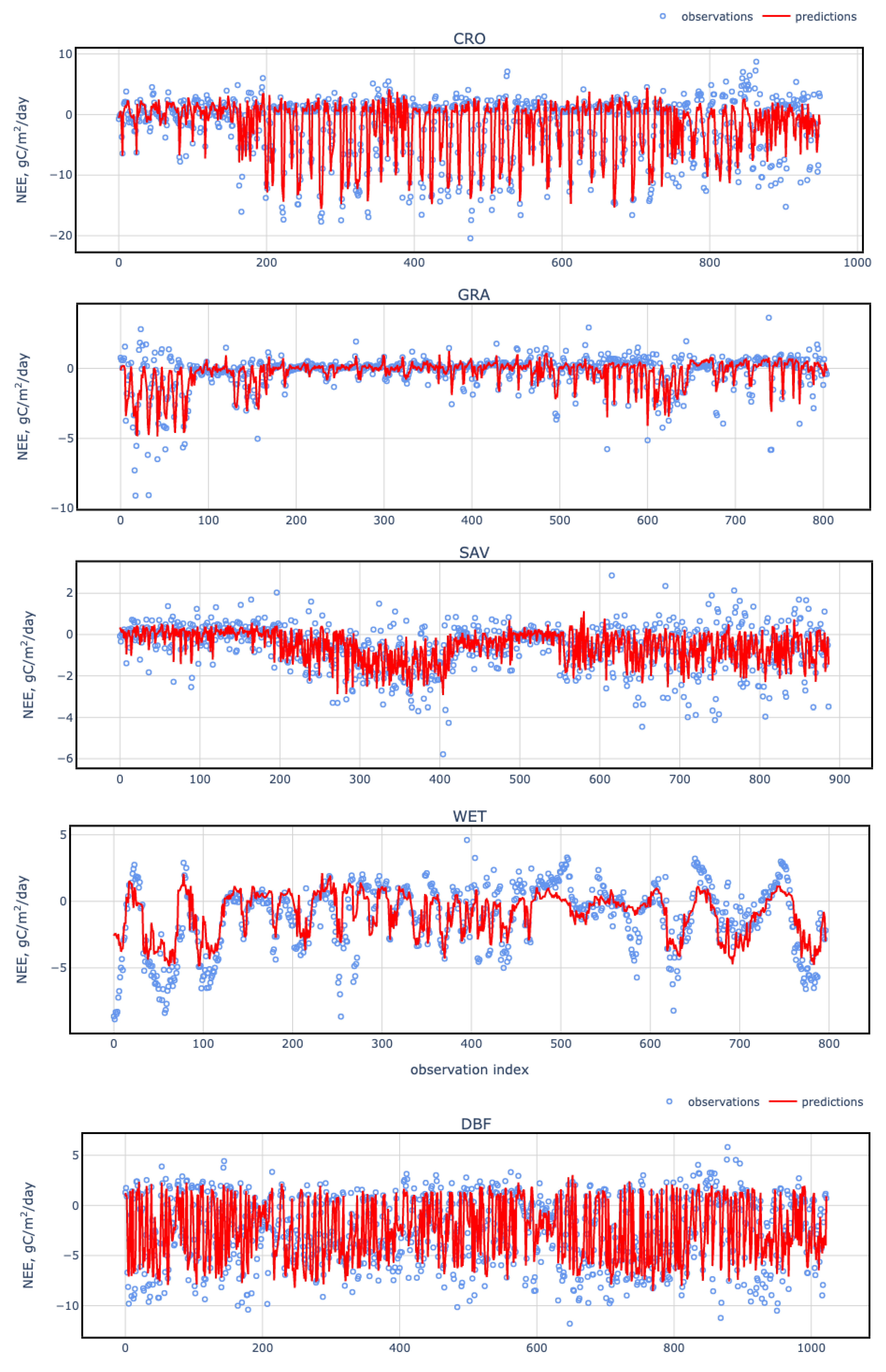
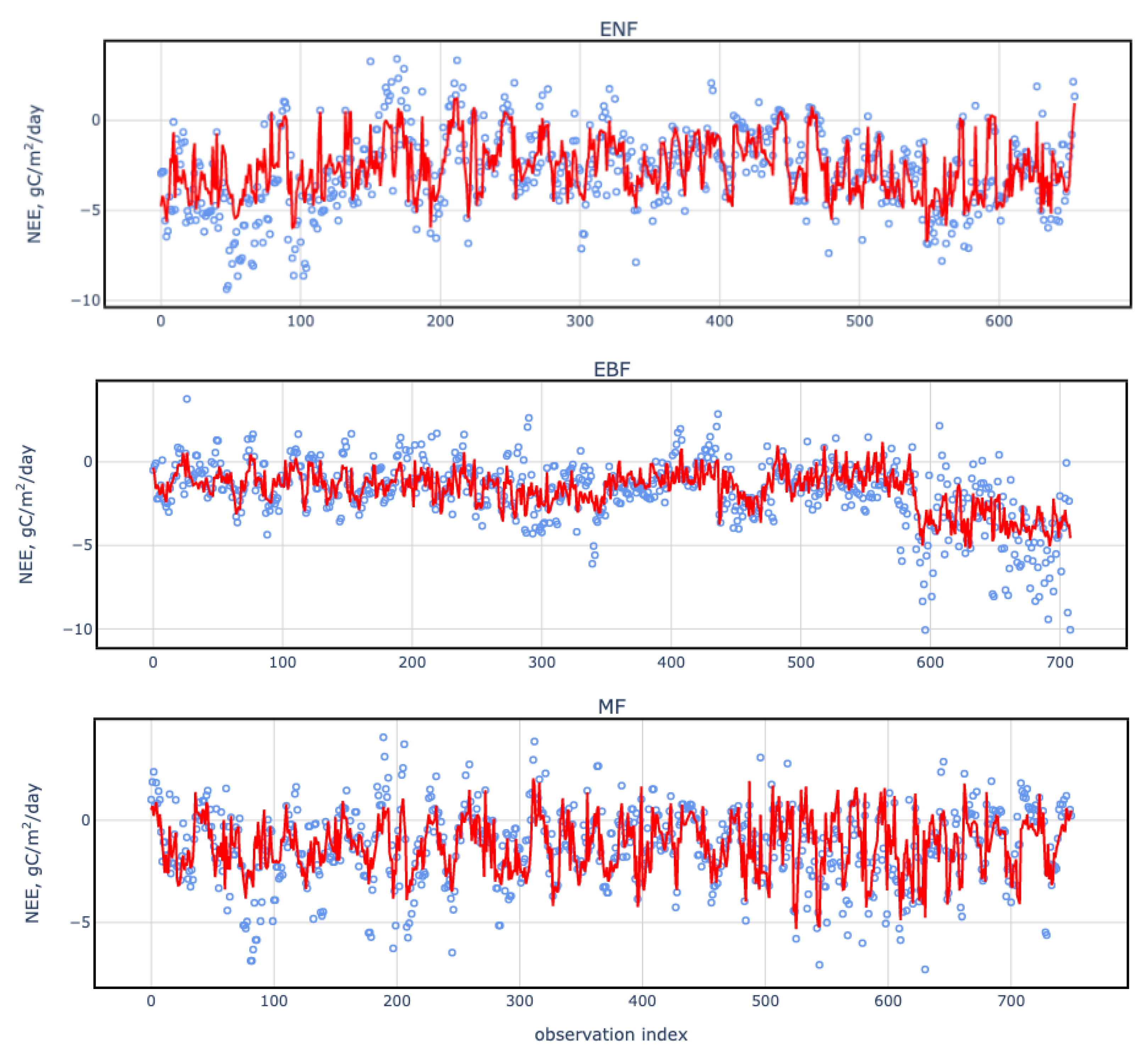
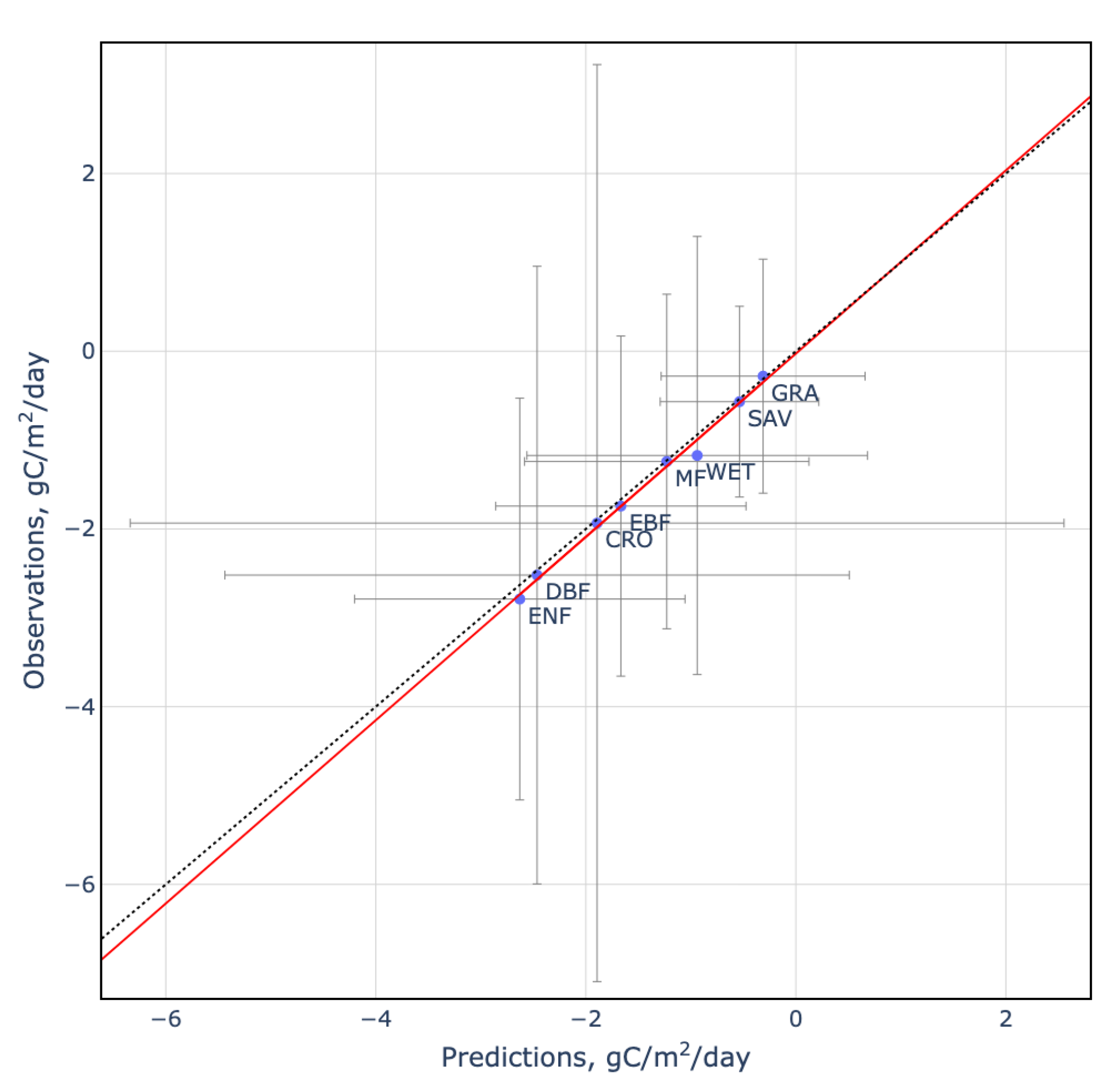
| Date | Blue | NDMI | SAVI |
|---|---|---|---|
| 27 December 2009 | 344.9 | 327.6 | 2314.2 |
| 28 December 2009 | 346.8 | 345.2 | 2335.3 |
| 29 December 2009 | 338.3 | 315.5 | 2276.5 |
| 30 December 2009 | 342.1 | 317.5 | 2289.9 |
| 31 December 2009 | 355.2 | 355.5 | 2392.7 |
| 1 January 2010 | 351.3 | 356.4 | 2354.5 |
| 2 January 2010 | 349.3 | 325.1 | 2346.3 |
| 3 January 2010 | 351.4 | 361.2 | 2373.4 |
| 4 January 2010 | 355.4 | 363.2 | 2382.4 |
| 5 January 2010 | 352.2 | 348.9 | 2367.3 |
| Date | |
|---|---|
| 27 December 2009 | −5.77 |
| 28 December 2009 | −7.43 |
| 29 December 2009 | −10.24 |
| 30 December 2009 | −5.49 |
| 31 December 2009 | −7.83 |
| 1 January 2010 | −5.47 |
| 2 January 2010 | −5.24 |
| 3 January 2010 | −3.87 |
| 4 January 2010 | −5.52 |
| 5 January 2010 | −3.45 |
| ⋯ | ⋯ |
| Land Cover | List of Features |
|---|---|
| DBF | , , , , , , , , , , |
| GRA | , , , , , , , , , , , , , , , |
| CRO | , , , , , , , , , |
| ENF | , , , , , , , , , , , |
| MF | , , , , , , , , |
| EBF | , , , , , , |
| WET | , , , , , , , , , , , , , , , , , , |
| SAV | , , , , , , , , , |
| IGBP | |||
|---|---|---|---|
| CRO | 0.73 (0.17) | 2.32 (0.67) | 0.44 (0.19) |
| GRA | 0.61 (0.04) | 0.70 (0.35) | 0.60 (0.05) |
| DBF | 0.76 (0.05) | 1.64 (0.16) | 0.42 (0.04) |
| ENF | 0.62 (0.05) | 1.30 (0.22) | 0.60 (0.06) |
| MF | 0.55 (0.02) | 1.25 (0.18) | 0.64 (0.01) |
| EBF | 0.42 (0.06) | 1.28 (0.32) | 0.73 (0.05) |
| WET | 0.53 (0.06) | 1.55 (0.19) | 0.64 (0.08) |
| SAV | 0.56 (0.03) | 0.68 (0.14) | 0.63 (0.02) |
| IGBP | ||
|---|---|---|
| CRO | 0.83 | 1.94 |
| GRA | 0.60 | 0.54 |
| DBF | 0.84 | 1.23 |
| ENF | 0.78 | 0.89 |
| MF | 0.70 | 0.75 |
| EBF | 0.70 | 0.80 |
| WET | 0.66 | 1.25 |
| SAV | 0.69 | 0.49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuravlev, R.; Dara, A.; Santos, A.L.D.d.; Demidov, O.; Burba, G. Globally Scalable Approach to Estimate Net Ecosystem Exchange Based on Remote Sensing, Meteorological Data, and Direct Measurements of Eddy Covariance Sites. Remote Sens. 2022, 14, 5529. https://doi.org/10.3390/rs14215529
Zhuravlev R, Dara A, Santos ALDd, Demidov O, Burba G. Globally Scalable Approach to Estimate Net Ecosystem Exchange Based on Remote Sensing, Meteorological Data, and Direct Measurements of Eddy Covariance Sites. Remote Sensing. 2022; 14(21):5529. https://doi.org/10.3390/rs14215529
Chicago/Turabian StyleZhuravlev, Ruslan, Andrey Dara, André Luís Diniz dos Santos, Oleg Demidov, and George Burba. 2022. "Globally Scalable Approach to Estimate Net Ecosystem Exchange Based on Remote Sensing, Meteorological Data, and Direct Measurements of Eddy Covariance Sites" Remote Sensing 14, no. 21: 5529. https://doi.org/10.3390/rs14215529
APA StyleZhuravlev, R., Dara, A., Santos, A. L. D. d., Demidov, O., & Burba, G. (2022). Globally Scalable Approach to Estimate Net Ecosystem Exchange Based on Remote Sensing, Meteorological Data, and Direct Measurements of Eddy Covariance Sites. Remote Sensing, 14(21), 5529. https://doi.org/10.3390/rs14215529






