A Novel Method to Derive Exospheric Temperatures from Swarm Thermospheric Densities during Quiet Times
Abstract
1. Introduction
2. Data and Methods
2.1. Data and Model
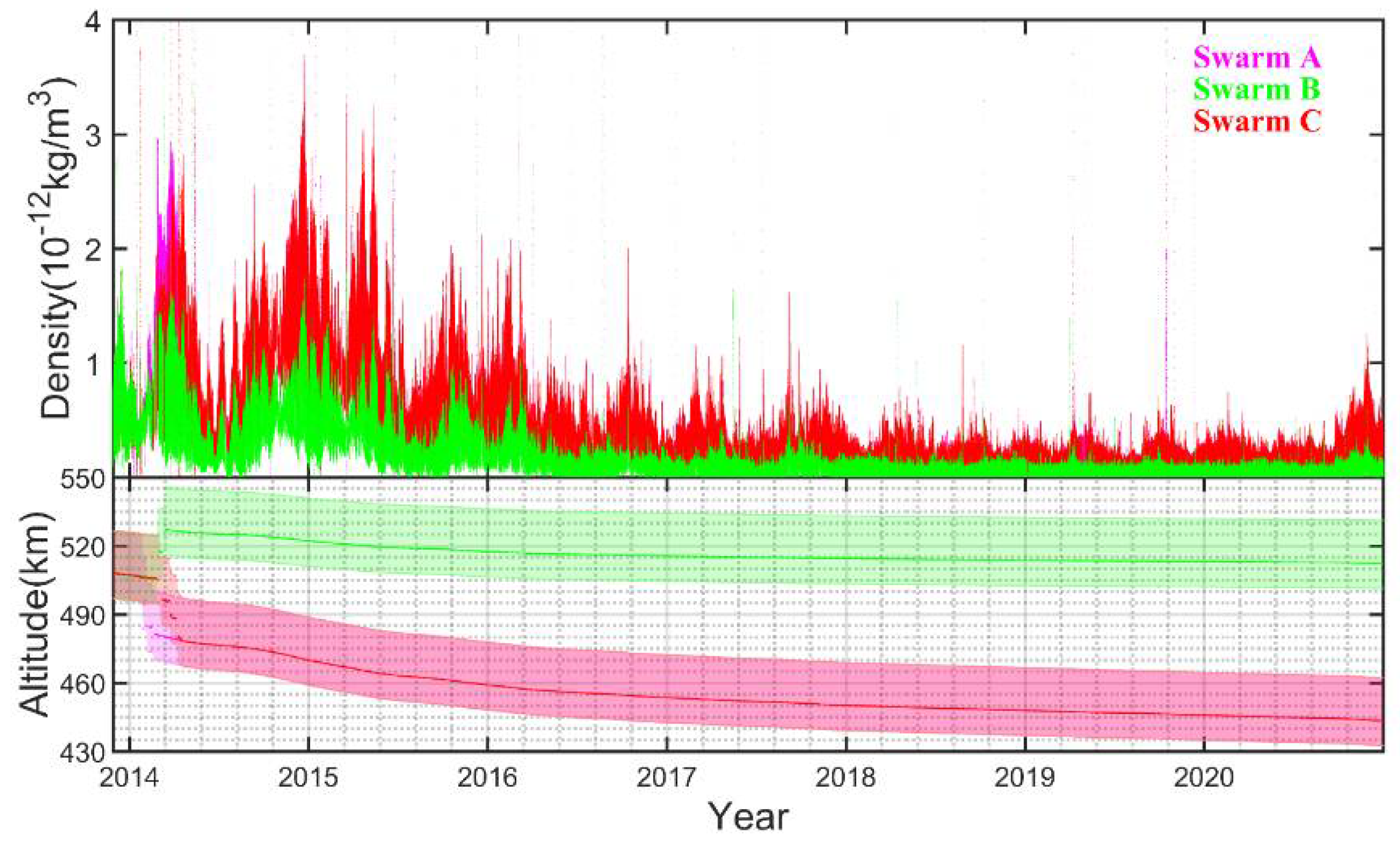
2.1.1. Swarm Satellites
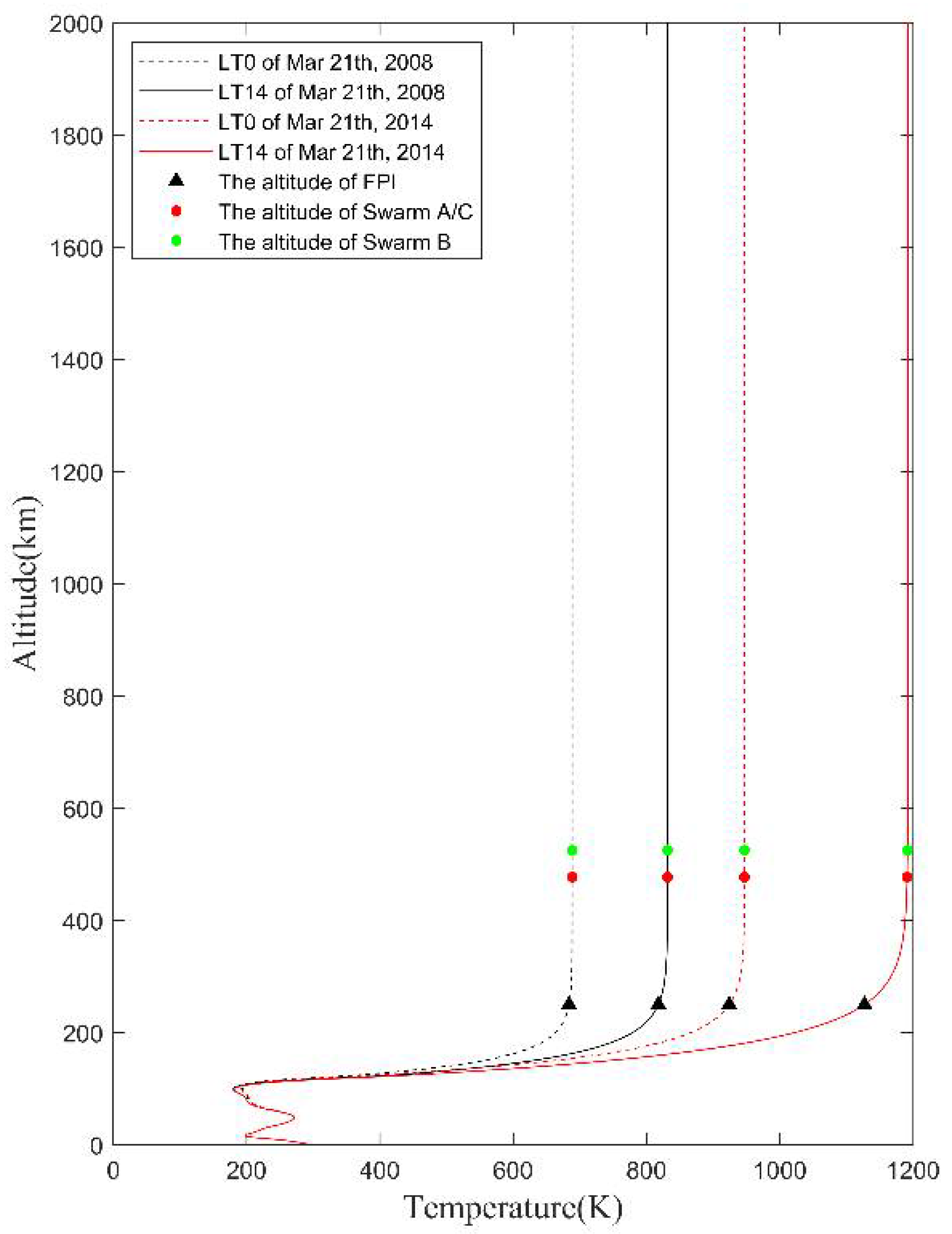
2.1.2. The Ground-Based Fabry-Perot Interferometer
2.1.3. NRL-MSISE00 Model
2.2. New Method for Temperature Calculation
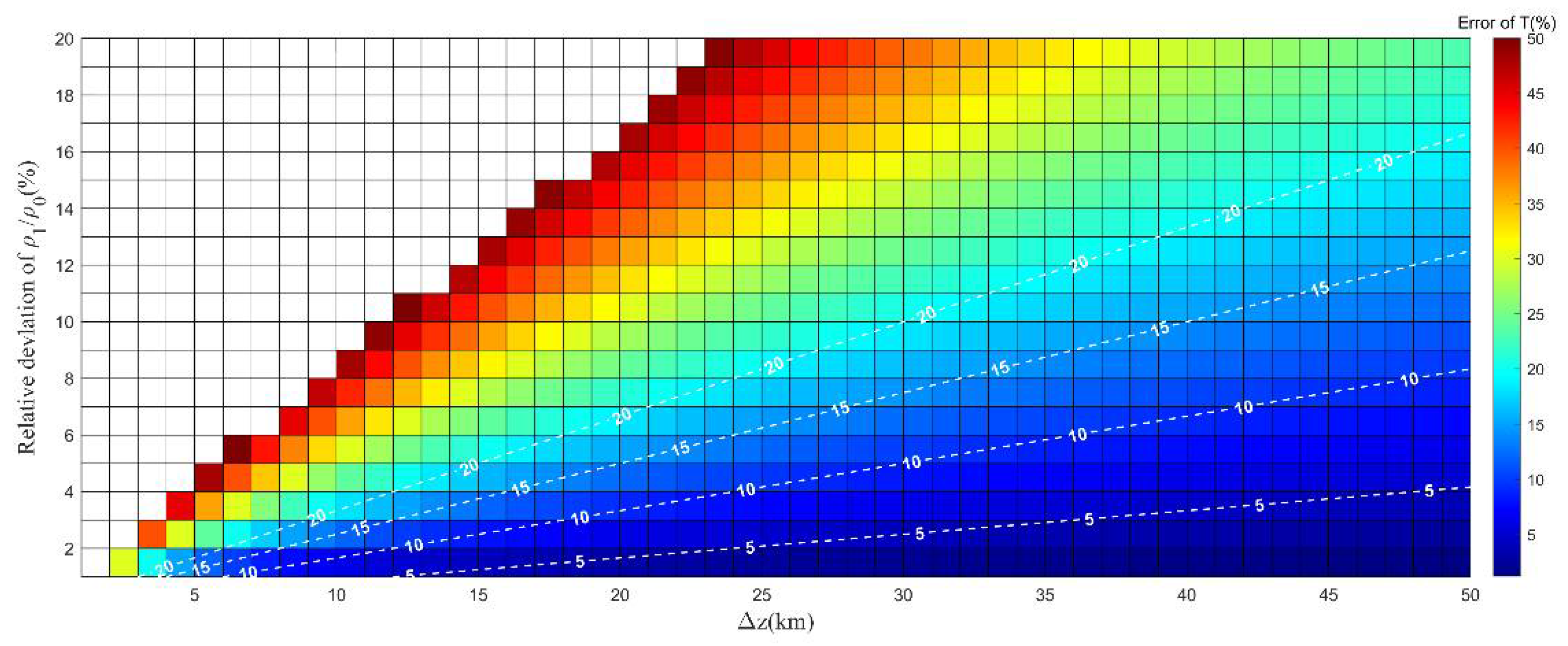
2.3. Sources of Uncertainty
3. Temperature Comparisons between Observations, Model Simulations, and Inversion Temperatures
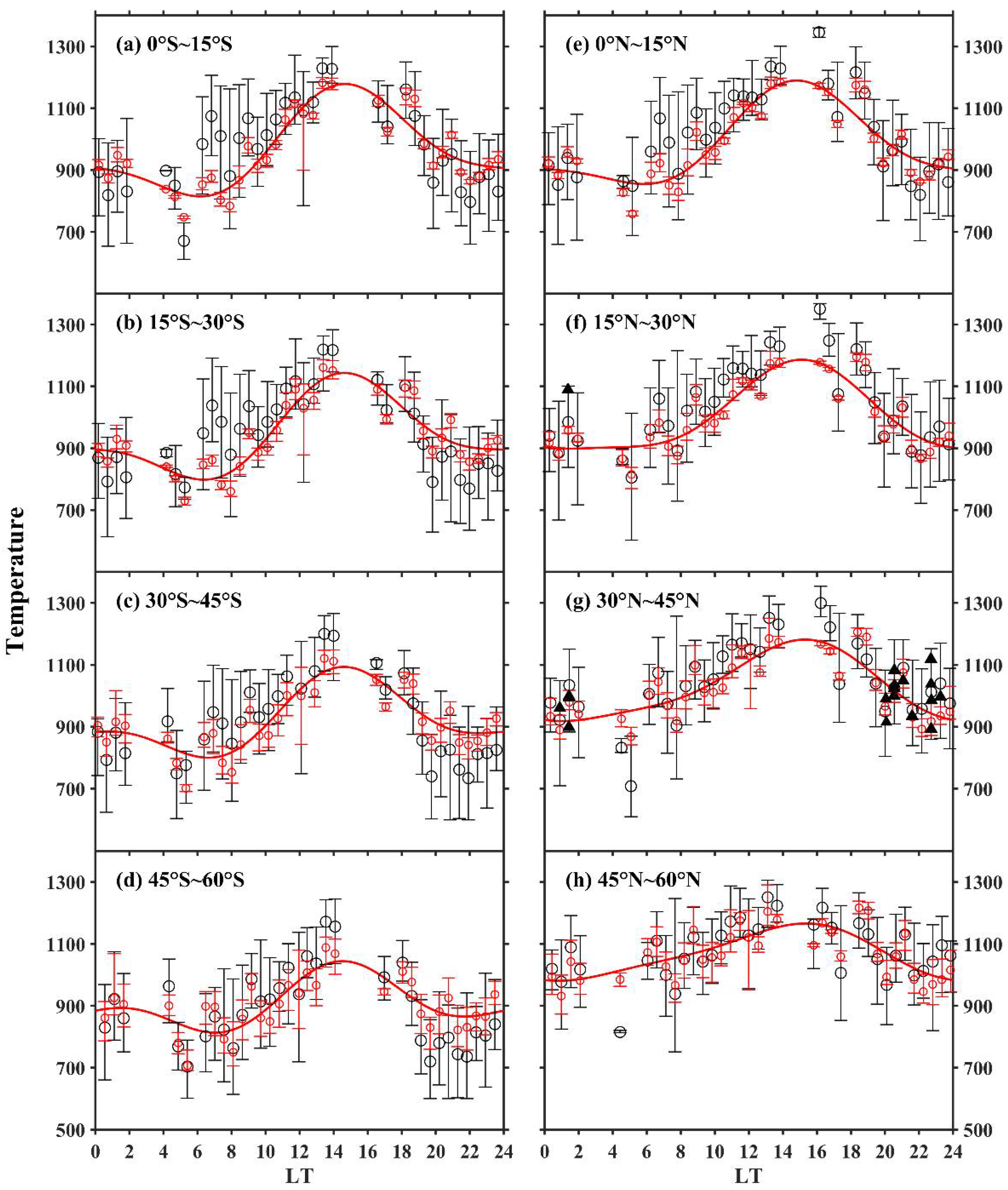
3.1. Quantitative Comparison between Derived Temperatures, Ground-Based FPI Measured Temperatures and MSIS Simulations
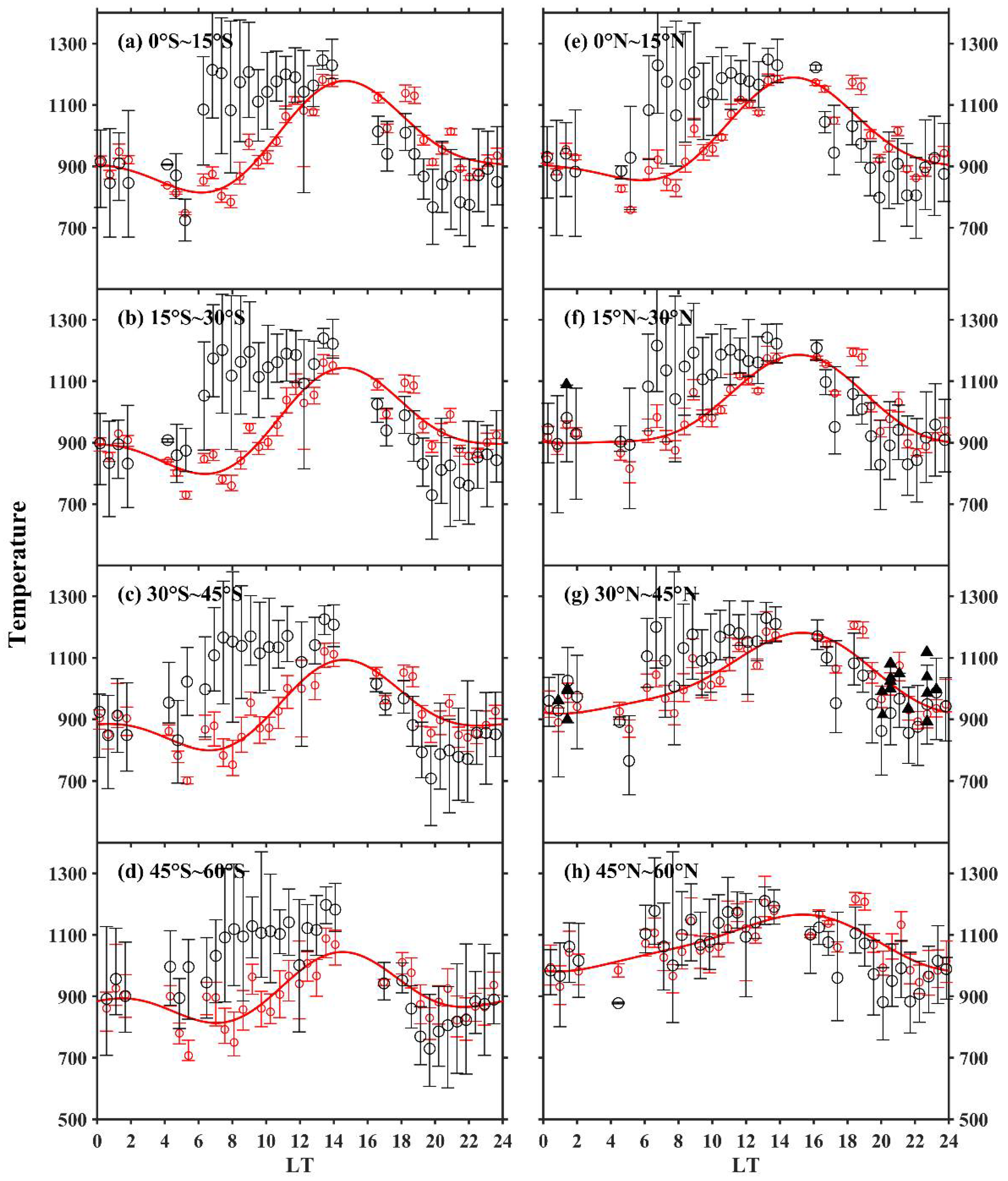
3.2. Comparison between Inversion Temperatures Calculated with , Ground-Based FPI Measured Temperatures and MSIS Simulations
4. A New Concept “Satellite-Tethered Mass Spectrometer Detection”
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Name and Location of FPI Stations | DOY | UT, h | LT, h | Location of Swarm B,° | Average Location, ° | ALT-B, km | AverageALT, km | Temperature of FPI, k | Temperature of Swarm, k |
| Location of Swarm A/C, ° | ALT-A/C, km | ||||||||
| Arecibo (18.34°, −66.75°) | 112 | 5.4500 | 1.3837 | 16.30, −62 | 15.85, −61 | 515.66 | 492 | 1088.68 | 887.57 |
| 15.39 −59.99 | 468.33 | ||||||||
| 112 | 5.4542 | 1.3392 | 17.66, −63.46 | 16.53, −61.73 | 515.66 | 492.01 | 1088.73 | 837.66 | |
| 15.39 −59.99 | 468.35 | ||||||||
| 112 | 5.4542 | 1.3385 | 15.73, −63.43 | 16.51, −61.74 | 515.67 | 492 | 1088.73 | 894.91 | |
| 17.29, −60.04 | 468.33 | ||||||||
| 112 | 5.4542 | 1.3862 | 16.3, −62 | 16.8, −61.02 | 515.67 | 492 | 1088.73 | 922.71 | |
| 17.29, −60.04 | 468.33 | ||||||||
| 112 | 5.4583 | 1.3417 | 17.66, −63.46 | 17.48, −61.75 | 515.67 | 492.01 | 1088.77 | 868.91 | |
| 17.29, −60.04 | 468.35 | ||||||||
| 112 | 5.4583 | 1.3893 | 18.22, −62.03 | 17.76, −61.04 | 515.67 | 492.02 | 1088.77 | 893.26 | |
| 17.29, −60.04 | 468.36 | ||||||||
| 112 | 5.4625 | 1.3448 | 19.58, −63.49 | 18.44, −61.77 | 515.67 | 492.04 | 1088.82 | 843.63 | |
| 17.29, −60.04 | 468.4 | ||||||||
| 112 | 5.4625 | 1.3445 | 17.66, −63.46 | 18.43, −61.77 | 515.71 | 492.03 | 1088.82 | 903.36 | |
| 19.2, −60.08 | 468.35 | ||||||||
| 112 | 5.4625 | 1.3922 | 18.22, −62.03 | 18.71, −61.06 | 515.71 | 492.04 | 1088.82 | 929.69 | |
| 19.2, −60.08 | 468.36 | ||||||||
| 112 | 5.4667 | 1.3477 | 19.58, −63.49 | 19.39, −61.79 | 515.71 | 492.06 | 1088.86 | 876.11 | |
| 19.2, −60.08 | 468.4 | ||||||||
| 112 | 5.4667 | 1.3953 | 20.15, −62.06 | 19.68, −61.07 | 515.71 | 492.07 | 1088.86 | 898.58 | |
| 19.2, −60.08 | 468.43 | ||||||||
| 112 | 5.4708 | 1.3512 | 21.51, −63.51 | 20.36, −61.8 | 515.71 | 492.1 | 1088.9 | 849.12 | |
| 19.2, −60.08 | 468.49 | ||||||||
| 112 | 5.4708 | 1.3505 | 19.58, −63.49 | 20.34 −61.81 | 515.79 | 492.1 | 1088.9 | 912.78 | |
| 21.1, −60.12 | 468.4 | ||||||||
| 112 | 5.4708 | 1.3982 | 20.15, −62.06 | 20.63, −61.09 | 515.71 | 492.11 | 1088.9 | 937.18 | |
| 21.1, −60.12 | 468.43 | ||||||||
| Easter Kentucky (37.75°, −84.29°) | 143 | 3.8583 | 22.6973 | 34.74, −80.55 | 35.34, −77.42 | 517.39 | 493.02 | 1038.31 | 1063.6 |
| 35.93, −74.28 | 468.65 | ||||||||
| 143 | 3.8625 | 22.7018 | 36.66, −80.54 | 36.3, −77.41 | 517.39 | 493.18 | 1038.62 | 1037.24 | |
| 35.93, −74.28 | 468.97 | ||||||||
| 143 | 3.8667 | 22.7057 | 36.66, −80.54 | 37.25, −77.42 | 517.73 | 493.35 | 1038.48 | 1062.43 | |
| 37.83, −74.29 | 468.97 | ||||||||
| 143 | 3.8708 | 22.7105 | 38.58, −80.52 | 38.21, −77.41 | 517.73 | 493.52 | 1038.34 | 1035.98 | |
| 37.83, −74.29 | 469.31 | ||||||||
| 143 | 3.875 | 22.7147 | 38.58, −80.52 | 39.16, −77.41 | 518.09 | 493.7 | 1038.2 | 1060.56 | |
| 39.73, −74.29 | 469.31 | ||||||||
| 143 | 3.8792 | 22.7195 | 40.5, −80.5 | 40.12, −77.4 | 518.09 | 493.88 | 1038.06 | 1034.47 | |
| 39.73, −74.29 | 469.66 | ||||||||
| 168 | 2.0542 | 20.5625 | 34.51, −85.29 | 35.43, −82.38 | 517.96 | 493.27 | 1081.03 | 944.58 | |
| 36.34, −79.46 | 468.57 | ||||||||
| 168 | 2.0542 | 20.5632 | 36.43, −85.28 | 35.44, −82.37 | 517.65 | 493.27 | 1081.03 | 903.84 | |
| 34.44, −79.45 | 468.89 | ||||||||
| 168 | 2.0583 | 20.5183 | 35.67, −86.74 | 36.01, −83.1 | 517.96 | 493.35 | 1081.15 | 910.72 | |
| 36.34, −79.46 | 468.74 | ||||||||
| 168 | 2.0583 | 20.567 | 36.43, −85.28 | 36.39, −82.37 | 517.96 | 493.43 | 1081.15 | 926.49 | |
| 36.34, −79.46 | 468.89 | ||||||||
| 168 | 2.0625 | 20.5232 | 37.59, −86.72 | 36.97, −83.09 | 517.96 | 493.52 | 1081.2 | 893.85 | |
| 36.34, −79.46 | 469.07 | ||||||||
| 168 | 2.0625 | 20.5708 | 36.43, −85.28 | 37.34, −82.38 | 518.28 | 493.59 | 1081.2 | 949.9 | |
| 38.24, −79.47 | 468.89 | ||||||||
| 168 | 2.0625 | 20.5715 | 38.35, −85.27 | 37.35, −82.37 | 517.96 | 493.59 | 1081.2 | 909.78 | |
| 36.34, −79.46 | 469.22 | ||||||||
| 168 | 2.0667 | 20.527 | 37.59, −86.72 | 37.92, −83.1 | 518.28 | 493.68 | 1081.25 | 915.91 | |
| 38.24, −79.47 | 469.07 | ||||||||
| 168 | 2.0667 | 20.5753 | 38.35, −85.27 | 38.3, −82.37 | 518.28 | 493.75 | 1081.25 | 932.6 | |
| 38.24, −79.47 | 469.22 | ||||||||
| 168 | 2.0708 | 20.5318 | 39.51, −86.7 | 38.88, −83.09 | 518.28 | 493.85 | 1081.3 | 898.69 | |
| 38.24, −79.47 | 469.41 | ||||||||
| 168 | 2.0708 | 20.5795 | 38.35, −85.27 | 39.25, −82.37 | 518.62 | 493.92 | 1081.3 | 955.56 | |
| 40.14, −79.47 | 469.22 | ||||||||
| 168 | 2.0708 | 20.5802 | 40.27, −85.25 | 39.26, −82.36 | 518.28 | 493.93 | 1081.3 | 915.65 | |
| 38.24, −79.47 | 469.57 | ||||||||
| 168 | 2.075 | 20.536 | 39.51, −86.7 | 39.83, −83.09 | 518.62 | 494.02 | 1081.34 | 920.31 | |
| 40.14, −79.47 | 469.41 | ||||||||
| 168 | 2.075 | 20.5844 | 40.27, −85.25 | 40.21, −82.36 | 518.62 | 494.1 | 1081.34 | 938.06 | |
| 40.14, −79.47 | 469.57 | ||||||||
| 174 | 2.0875 | 20.0379 | 35.28, −94.18 | 35.57, −90.75 | 517.65 | 493.16 | 990.56 | 920.98 | |
| 35.86, −87.31 | 468.67 | ||||||||
| 174 | 2.0917 | 20.0417 | 35.28, −94.18 | 36.52, −90.75 | 517.97 | 493.32 | 990.68 | 930.27 | |
| 37.76, −87.32 | 468.67 | ||||||||
| 174 | 2.0917 | 20.0424 | 37.2, −94.17 | 36.53, −90.74 | 517.65 | 493.32 | 990.68 | 910.9 | |
| 35.86, −87.31 | 468.99 | ||||||||
| 174 | 2.0958 | 20.0462 | 37.2, −94.17 | 37.48, −90.75 | 517.97 | 493.48 | 990.88 | 920.11 | |
| 37.76, −87.32 | 468.99 | ||||||||
| 174 | 2.1 | 20.05 | 37.2, −94.17 | 38.43, −90.75 | 518.3 | 493.65 | 991.08 | 928.83 | |
| 39.66, −87.33 | 468.99 | ||||||||
| 174 | 2.1 | 20.0507 | 39.12, −94.16 | 38.44, −90.74 | 517.97 | 493.65 | 991.08 | 910.08 | |
| 37.76, −87.32 | 469.33 | ||||||||
| 174 | 2.1042 | 20.0545 | 39.12, −94.16 | 39.39, −90.75 | 518.3 | 493.82 | 991.27 | 918.73 | |
| 39.66, −87.33 | 469.33 | ||||||||
| Peach mountain (42.27°, −83.75°) | 168 | 2.0958 | 20.5602 | 43.35, −86.64 | 44.59, −83.04 | 519.7 | 494.92 | 1036.22 | 949.87 |
| 45.83, −79.43 | 470.13 | ||||||||
| 168 | 2.0958 | 20.5609 | 45.26, −86.59 | 44.6, −83.03 | 519.33 | 494.92 | 1036.22 | 912.71 | |
| 43.93, −79.46 | 470.51 | ||||||||
| 174 | 2.125 | 20.0787 | 42.95, −94.1 | 44.15, −90.7 | 519.35 | 494.7 | 914.79 | 920.76 | |
| 45.35, −87.29 | 470.04 | ||||||||
| 174 | 2.125 | 20.0797 | 44.87, −94.05 | 44.16, −90.68 | 518.99 | 494.7 | 914.79 | 905.27 | |
| 43.45, −87.31 | 470.41 | ||||||||
| Pisgah (35.2°, −82.85°) | 112 | 7.1 | 1.3897 | 33.11, −87.17 | 32.88, −85.66 | 516.91 | 493.28 | 898.09 | 1001.83 |
| 32.64, −84.14 | 469.65 | ||||||||
| 112 | 7.1 | 1.4377 | 33.67, −85.73 | 33.16, −84.94 | 516.91 | 493.33 | 898.09 | 991.8 | |
| 32.64, −84.14 | 469.74 | ||||||||
| 112 | 7.1042 | 1.3938 | 35.03, −87.17 | 33.84, −85.66 | 516.91 | 493.43 | 898.36 | 965.39 | |
| 32.64, −84.14 | 469.94 | ||||||||
| 112 | 7.1042 | 1.3932 | 33.11, −87.17 | 33.83, −85.67 | 517.18 | 493.42 | 898.36 | 1044.64 | |
| 34.54, −84.16 | 469.65 | ||||||||
| 112 | 7.1042 | 1.4412 | 33.67, −85.73 | 34.11, −84.95 | 517.18 | 493.46 | 898.36 | 1033.88 | |
| 34.54, −84.16 | 469.74 | ||||||||
| 112 | 7.1083 | 1.3973 | 35.03, −87.17 | 34.79, −85.67 | 517.18 | 493.56 | 898.29 | 1005.55 | |
| 34.54, −84.16 | 469.94 | ||||||||
| 112 | 7.1083 | 1.4453 | 35.59, −85.73 | 35.07, −84.95 | 517.18 | 493.61 | 898.29 | 994.54 | |
| 34.54, −84.16 | 470.03 | ||||||||
| 112 | 7.1125 | 1.4018 | 36.95, −87.16 | 35.75, −85.66 | 517.18 | 493.71 | 898.22 | 968.96 | |
| 34.54, −84.16 | 470.24 | ||||||||
| 112 | 7.1125 | 1.4012 | 35.03, −87.17 | 35.74, −85.67 | 517.48 | 493.71 | 898.22 | 1048.81 | |
| 36.44, −84.17 | 469.94 | ||||||||
| 112 | 7.1125 | 1.4492 | 35.59, −85.73 | 36.02, −84.95 | 517.48 | 493.76 | 898.22 | 1037 | |
| 36.44, −84.17 | 470.03 | ||||||||
| 112 | 7.1167 | 1.4057 | 36.95, −87.16 | 36.7, −85.67 | 517.48 | 493.86 | 898.15 | 1009.58 | |
| 36.44, −84.17 | 470.24 | ||||||||
| 112 | 7.1167 | 1.4537 | 37.51, −85.72 | 36.98, −84.95 | 517.48 | 493.91 | 898.15 | 997.47 | |
| 36.44, −84.17 | 470.34 | ||||||||
| 112 | 7.1208 | 1.4105 | 38.87, −87.14 | 37.66, −85.66 | 517.48 | 494.03 | 898.08 | 972.57 | |
| 36.44, −84.17 | 470.57 | ||||||||
| 112 | 7.1208 | 1.4095 | 36.95, −87.16 | 37.65, −85.67 | 517.79 | 494.02 | 898.08 | 1053.3 | |
| 38.34, −84.18 | 470.24 | ||||||||
| 143 | 3.8458 | 22.7335 | 31.54, −79.11 | 32.79, −76.69 | 517.06 | 492.62 | 893.31 | 1076.3 | |
| 34.03, −74.26 | 468.17 | ||||||||
| 143 | 3.8458 | 22.7342 | 33.46, −79.11 | 32.8, −76.68 | 516.76 | 492.61 | 893.31 | 1025.52 | |
| 32.13, −74.24 | 468.45 | ||||||||
| 143 | 3.85 | 22.6897 | 32.82, −80.55 | 33.43, −77.41 | 517.06 | 492.71 | 893.05 | 1064.71 | |
| 34.03, −74.26 | 468.35 | ||||||||
| 143 | 3.85 | 22.7377 | 33.46, −79.11 | 33.75, −76.69 | 517.06 | 492.76 | 893.05 | 1049.78 | |
| 34.03, −74.26 | 468.45 | ||||||||
| 143 | 3.8542 | 22.6938 | 34.74, −80.55 | 34.39, −77.41 | 517.06 | 492.86 | 892.78 | 1038.25 | |
| 34.03, −74.26 | 468.65 | ||||||||
| 143 | 3.8542 | 22.7411 | 33.46, −79.11 | 34.7, −76.7 | 517.39 | 492.92 | 892.78 | 1075.51 | |
| 35.93, −74.28 | 468.45 | ||||||||
| 143 | 3.8542 | 22.7422 | 35.38, −79.1 | 34.71, −76.68 | 517.06 | 492.91 | 892.78 | 1023.8 | |
| 34.03, −74.26 | 468.76 | ||||||||
| 143 | 3.8583 | 22.6973 | 34.74, −80.55 | 35.34, −77.42 | 517.39 | 493.02 | 891.82 | 1063.6 | |
| 35.93, −74.28 | 468.65 | ||||||||
| 143 | 3.8583 | 22.7456 | 35.38, −79.1 | 35.66, −76.69 | 517.39 | 493.08 | 891.82 | 1048.6 | |
| 35.93, −74.28 | 468.76 | ||||||||
| 143 | 3.8625 | 22.7018 | 36.66, −80.54 | 36.3, −77.41 | 517.39 | 493.18 | 891.57 | 1037.24 | |
| 35.93, −74.28 | 468.97 | ||||||||
| 143 | 3.8625 | 22.7495 | 35.38, −79.1 | 36.61, −76.7 | 517.73 | 493.25 | 891.57 | 1074.14 | |
| 37.83, −74.29 | 468.76 | ||||||||
| 143 | 3.8625 | 22.7501 | 37.3, −79.09 | 36.62, −76.69 | 517.39 | 493.24 | 891.57 | 1022.68 | |
| 35.93, −74.28 | 469.08 | ||||||||
| 143 | 3.8667 | 22.7057 | 36.66, −80.54 | 37.25, −77.42 | 517.73 | 493.35 | 891.32 | 1062.43 | |
| 37.83, −74.29 | 468.97 | ||||||||
| 143 | 3.8667 | 22.754 | 37.3, −79.09 | 37.57, −76.69 | 517.73 | 493.41 | 891.32 | 1047.32 | |
| 37.83, −74.29 | 469.08 | ||||||||
| 168 | 2.0458 | 20.5069 | 33.75, −86.74 | 33.15, −83.09 | 517.36 | 492.9 | 1000.05 | 883.9 | |
| 32.54, −79.43 | 468.43 | ||||||||
| 168 | 2.0458 | 20.5545 | 32.59, −85.29 | 33.52, −82.37 | 517.65 | 492.97 | 1000.05 | 939.43 | |
| 34.44, −79.45 | 468.28 | ||||||||
| 168 | 2.0458 | 20.5551 | 34.51, −85.29 | 33.53, −82.36 | 517.36 | 492.97 | 1000.05 | 898.59 | |
| 32.54, −79.43 | 468.57 | ||||||||
| 168 | 2.05 | 20.5104 | 33.75, −86.74 | 34.1, −83.1 | 517.65 | 493.04 | 999.8 | 905.9 | |
| 34.44, −79.45 | 468.43 | ||||||||
| 168 | 2.05 | 20.5587 | 34.51, −85.29 | 34.48, −82.37 | 517.65 | 493.11 | 999.8 | 921.31 | |
| 34.44, −79.45 | 468.57 | ||||||||
| 168 | 2.0542 | 20.5145 | 35.67, −86.74 | 35.06, −83.1 | 517.65 | 493.2 | 999.22 | 888.8 | |
| 34.44, −79.45 | 468.74 | ||||||||
| 168 | 2.0542 | 20.5625 | 34.51, −85.29 | 35.43, −82.38 | 517.96 | 493.27 | 999.22 | 944.58 | |
| 36.34, −79.46 | 468.57 | ||||||||
| 168 | 2.0542 | 20.5632 | 36.43, −85.28 | 35.44, −82.37 | 517.65 | 493.27 | 999.22 | 903.84 | |
| 34.44, −79.45 | 468.89 | ||||||||
| 168 | 2.0583 | 20.5183 | 35.67, −86.74 | 36.01, −83.1 | 517.96 | 493.35 | 998.98 | 910.72 | |
| 36.34, −79.46 | 468.74 | ||||||||
| 168 | 2.0583 | 20.567 | 36.43, −85.28 | 36.39, −82.37 | 517.96 | 493.43 | 998.98 | 926.49 | |
| 36.34, −79.46 | 468.89 | ||||||||
| 168 | 2.0625 | 20.5232 | 37.59, −86.72 | 36.97, −83.09 | 517.96 | 493.52 | 998.73 | 893.85 | |
| 36.34, −79.46 | 469.07 | ||||||||
| 168 | 2.0625 | 20.5708 | 36.43, −85.28 | 37.34, −82.38 | 518.28 | 493.59 | 998.73 | 949.9 | |
| 38.24, −79.47 | 468.89 | ||||||||
| 168 | 2.0625 | 20.5715 | 38.35, −85.27 | 37.35, −82.37 | 517.96 | 493.59 | 998.73 | 909.78 | |
| 36.34, −79.46 | 469.22 | ||||||||
| Urbana (40.13°, −88.2°) | 112 | 7.1208 | 1.4105 | 38.87, −87.14 | 37.66, −85.66 | 517.48 | 494.03 | 994.39 | 972.57 |
| 36.44, −84.17 | 470.57 | ||||||||
| 112 | 7.1208 | 1.4095 | 36.95, −87.16 | 37.65, −85.67 | 517.79 | 494.02 | 994.39 | 1053.3 | |
| 38.34, −84.18 | 470.24 | ||||||||
| 112 | 7.1208 | 1.4575 | 37.51, −85.72 | 37.93, −84.95 | 517.79 | 494.07 | 994.39 | 1040.3 | |
| 38.34, −84.18 | 470.34 | ||||||||
| 112 | 7.125 | 1.4143 | 38.87, −87.14 | 38.61, −85.66 | 517.79 | 494.18 | 993.78 | 1013.64 | |
| 38.34, −84.18 | 470.57 | ||||||||
| 112 | 7.125 | 1.4623 | 39.43, −85.7 | 38.89, −84.94 | 517.79 | 494.23 | 993.78 | 1000.54 | |
| 38.34, −84.18 | 470.67 | ||||||||
| 112 | 7.1292 | 1.4192 | 40.78, −87.12 | 39.56, −85.65 | 517.79 | 494.35 | 993.74 | 977.73 | |
| 38.34, −84.18 | 470.9 | ||||||||
| 112 | 7.1292 | 1.4185 | 38.87, −87.14 | 39.56, −85.66 | 518.12 | 494.35 | 993.74 | 1056.14 | |
| 40.24, −84.18 | 470.57 | ||||||||
| 112 | 7.1292 | 1.4665 | 39.43, −85.7 | 39.84, −84.94 | 518.12 | 494.4 | 993.74 | 1042.11 | |
| 40.24, −84.18 | 470.67 | ||||||||
| 112 | 7.1333 | 1.4233 | 40.78, −87.12 | 40.51 −85.65 | 518.12 | 494.51 | 993.7 | 1017.76 | |
| 40.24, −84.18 | 470.9 | ||||||||
| 112 | 7.1333 | 1.4717 | 41.34, −85.67 | 40.79, −84.93 | 518.12 | 494.57 | 993.7 | 1002.4 | |
| 40.24, −84.18 | 471.01 | ||||||||
| 112 | 7.1375 | 1.4288 | 42.7, −87.08 | 41.47, −85.63 | 518.12 | 494.69 | 993.66 | 982.72 | |
| 40.24, −84.18 | 471.25 | ||||||||
| 112 | 7.1375 | 1.4278 | 40.78, −87.12 | 41.46, −85.65 | 518.47 | 494.69 | 993.66 | 1059.24 | |
| 42.14, −84.17 | 470.9 | ||||||||
| 112 | 7.1375 | 1.4762 | 41.34, −85.67 | 41.74, −84.92 | 518.47 | 494.74 | 993.66 | 1042.83 | |
| 42.14, −84.17 | 471.01 | ||||||||
| 112 | 7.1417 | 1.4333 | 42.7, −87.08 | 42.42 −85.63 | 518.47 | 494.86 | 993.46 | 1021.89 | |
| 42.14, −84.17 | 471.25 | ||||||||
| 137 | 5.3958 | 23.2755 | 38.97, −93.49 | 37.8, −91.81 | 517.17 | 493.29 | 996.4 | 1018.72 | |
| 36.63, −90.12 | 469.4 | ||||||||
| 137 | 5.3958 | 23.2749 | 37.05, −93.5 | 37.79, −91.82 | 517.52 | 493.29 | 996.4 | 1095.5 | |
| 38.53, −90.13 | 469.06 | ||||||||
| 137 | 5.4 | 23.2314 | 38.36, −94.93 | 38.45, −92.53 | 517.52 | 493.42 | 996.24 | 1055.53 | |
| 38.53, −90.13 | 469.31 | ||||||||
| 137 | 5.4 | 23.2794 | 38.97, −93.49 | 38.75, −91.81 | 517.52 | 493.46 | 996.24 | 1056.11 | |
| 38.53, −90.13 | 469.4 | ||||||||
| 137 | 5.4042 | 23.2362 | 40.28, −94.91 | 39.41, −92.52 | 517.52 | 493.59 | 996.01 | 1021.46 | |
| 38.53, −90.13 | 469.66 | ||||||||
| 137 | 5.4042 | 23.2355 | 38.36, −94.93 | 39.4, −92.53 | 517.89 | 493.6 | 996.01 | 1094.6 | |
| 40.43, −90.13 | 469.31 | ||||||||
| 137 | 5.4042 | 23.2845 | 40.88, −93.46 | 39.71, −91.8 | 517.52 | 493.64 | 996.01 | 1019.53 | |
| 38.53, −90.13 | 469.75 | ||||||||
| 137 | 5.4042 | 23.2835 | 38.97, −93.49 | 39.7, −91.81 | 517.89 | 493.65 | 996.01 | 1095.3 | |
| 40.43, −90.13 | 469.4 | ||||||||
| 137 | 5.4083 | 23.2404 | 40.28, −94.91 | 40.36, −92.52 | 517.89 | 493.78 | 995.85 | 1058.55 | |
| 40.43, −90.13 | 469.66 | ||||||||
| 137 | 5.4083 | 23.2887 | 40.88, −93.46 | 40.66, −91.8 | 517.89 | 493.82 | 995.85 | 1056.57 | |
| 40.43, −90.13 | 469.75 | ||||||||
| 137 | 5.4125 | 23.2455 | 42.2, −94.88 | 41.32, −92.51 | 517.89 | 493.96 | 995.7 | 1025.08 | |
| 40.43, −90.13 | 470.02 | ||||||||
| 137 | 5.4125 | 23.2445 | 40.28, −94.91 | 41.31, −92.52 | 518.26 | 493.96 | 995.7 | 1096.58 | |
| 42.33, −90.13 | 469.66 | ||||||||
| 137 | 5.4125 | 23.2939 | 42.8, −93.43 | 41.62, −91.78 | 517.89 | 494.01 | 995.7 | 1019.87 | |
| 40.43, −90.13 | 470.12 | ||||||||
| 137 | 5.4125 | 23.2928 | 40.88, −93.46 | 41.61, −91.8 | 518.26 | 494.01 | 995.7 | 1094.54 | |
| 42.33, −90.13 | 469.75 | ||||||||
| 137 | 5.4167 | 23.2497 | 42.2, −94.88 | 42.27, −92.51 | 518.26 | 494.14 | 995.54 | 1061.25 | |
| 42.33, −90.13 | 470.02 | ||||||||
| 137 | 5.4167 | 23.298 | 42.8, −93.43 | 42.57, −91.78 | 518.26 | 494.19 | 995.54 | 1055.78 | |
| 42.33, −90.13 | 470.12 | ||||||||
| 156 | 3.5667 | 21.5716 | 38.77, −92.34 | 37.78, −89.93 | 517.8 | 493.57 | 934.33 | 874.53 | |
| 36.78, −87.51 | 469.33 | ||||||||
| 156 | 3.5708 | 21.5759 | 38.77, −92.34 | 38.72, −89.93 | 518.15 | 493.74 | 933.98 | 894.65 | |
| 38.67, −87.51 | 469.33 | ||||||||
| 156 | 3.5708 | 21.6245 | 39.5, −90.88 | 39.09, −89.2 | 518.15 | 493.8 | 933.98 | 897.76 | |
| 38.67, −87.51 | 469.45 | ||||||||
| 156 | 3.575 | 21.581 | 40.69, −92.31 | 39.68, −89.91 | 518.15 | 493.92 | 933.57 | 877.68 | |
| 38.67, −87.51 | 469.69 | ||||||||
| 156 | 3.5792 | 21.5852 | 40.69, −92.31 | 40.63, −89.91 | 518.51 | 494.1 | 933.16 | 897.64 | |
| 40.57, −87.51 | 469.69 | ||||||||
| 156 | 3.5792 | 21.6339 | 41.42, −90.85 | 41, −89.18 | 518.51 | 494.17 | 933.16 | 900.69 | |
| 40.57, −87.51 | 469.82 | ||||||||
| 156 | 3.5833 | 21.5904 | 42.61, −92.28 | 41.59, −89.9 | 518.51 | 494.29 | 932.75 | 881.13 | |
| 40.57, −87.51 | 470.06 | ||||||||
| 156 | 3.5875 | 21.5945 | 42.61, −92.28 | 42.54, −89.9 | 518.88 | 494.47 | 932.34 | 900.72 | |
| 42.47, −87.51 | 470.06 | ||||||||
| Virginia (37.2°, −80.42°) | 112 | 7.1083 | 1.3973 | 35.03, −87.17 | 34.79, −85.67 | 469.94 | 493.56 | 997.97 | 1005.55 |
| 34.54, −84.16 | 493.56 | ||||||||
| 112 | 7.1083 | 1.4453 | 35.59, −85.73 | 35.07, −84.95 | 470.03 | 493.61 | 997.97 | 994.54 | |
| 34.54, −84.16 | 493.61 | ||||||||
| 112 | 7.1125 | 1.4018 | 36.95, −87.16 | 35.75, −85.66 | 470.24 | 493.71 | 997.55 | 968.96 | |
| 34.54, −84.16 | 493.71 | ||||||||
| 112 | 7.1125 | 1.4012 | 35.03, −87.17 | 35.74, −85.67 | 469.94 | 493.71 | 997.55 | 1048.81 | |
| 36.44, −84.17 | 493.71 | ||||||||
| 112 | 7.1125 | 1.4492 | 35.59, −85.73 | 36.02, −84.95 | 470.03 | 493.76 | 997.55 | 1037 | |
| 36.44, −84.17 | 493.76 | ||||||||
| 112 | 7.1167 | 1.4057 | 36.95, −87.16 | 36.7, −85.67 | 470.24 | 493.86 | 997.57 | 1009.58 | |
| 36.44, −84.17 | 493.86 | ||||||||
| 112 | 7.1167 | 1.4537 | 37.51, −85.72 | 36.98, −84.95 | 470.34 | 493.91 | 997.57 | 997.47 | |
| 36.44, −84.17 | 493.91 | ||||||||
| 112 | 7.1208 | 1.4105 | 38.87, −87.14 | 37.66, −85.66 | 470.57 | 494.03 | 997.59 | 972.57 | |
| 36.44, −84.17 | 494.03 | ||||||||
| 112 | 7.1208 | 1.4095 | 36.95, −87.16 | 37.65, −85.67 | 470.24 | 494.02 | 997.59 | 1053.3 | |
| 38.34, −84.18 | 494.02 | ||||||||
| 112 | 7.1208 | 1.4575 | 37.51, −85.72 | 37.93, −84.95 | 470.34 | 494.07 | 997.59 | 1040.3 | |
| 38.34, −84.18 | 494.07 | ||||||||
| 112 | 7.125 | 1.4143 | 38.87, −87.14 | 38.61, −85.66 | 470.57 | 494.18 | 998.09 | 1013.64 | |
| 38.34, −84.18 | 494.18 | ||||||||
| 112 | 7.125 | 1.4623 | 39.43, −85.7 | 38.89, −84.94 | 470.67 | 494.23 | 998.09 | 1000.54 | |
| 38.34, −84.18 | 494.23 | ||||||||
| 112 | 7.1292 | 1.4192 | 40.78, −87.12 | 39.56, −85.65 | 470.9 | 494.35 | 998.11 | 977.73 | |
| 38.34, −84.18 | 494.35 | ||||||||
| 112 | 7.1292 | 1.4185 | 38.87, −87.14 | 39.56, −85.66 | 470.57 | 494.35 | 998.11 | 1056.14 | |
| 40.24, −84.18 | 494.35 | ||||||||
| 143 | 3.8583 | 22.6973 | 34.74, −80.55 | 35.34, −77.42 | 468.65 | 493.02 | 984.75 | 1063.6 | |
| 35.93, −74.28 | 493.02 | ||||||||
| 143 | 3.8583 | 22.7456 | 35.38, −79.1 | 35.66, −76.69 | 468.76 | 493.08 | 984.75 | 1048.6 | |
| 35.93, −74.28 | 493.08 | ||||||||
| 143 | 3.8625 | 22.7018 | 36.66, −80.54 | 36.3, −77.41 | 468.97 | 493.18 | 984.66 | 1037.24 | |
| 35.93, −74.28 | 493.18 | ||||||||
| 143 | 3.8625 | 22.7495 | 35.38, −79.1 | 36.61, −76.7 | 468.76 | 493.25 | 984.66 | 1074.14 | |
| 37.83, −74.29 | 493.25 | ||||||||
| 143 | 3.8625 | 22.7501 | 37.3, −79.09 | 36.62, −76.69 | 469.08 | 493.24 | 984.66 | 1022.68 | |
| 35.93, −74.28 | 493.24 | ||||||||
| 143 | 3.8667 | 22.7057 | 36.66, −80.54 | 37.25, −77.42 | 468.97 | 493.35 | 984.57 | 1062.43 | |
| 37.83, −74.29 | 493.35 | ||||||||
| 143 | 3.8667 | 22.754 | 37.3, −79.09 | 37.57, −76.69 | 469.08 | 493.41 | 984.57 | 1047.32 | |
| 37.83, −74.29 | 493.41 | ||||||||
| 143 | 3.8708 | 22.7105 | 38.58, −80.52 | 38.21, −77.41 | 469.31 | 493.52 | 984.48 | 1035.98 | |
| 37.83, −74.29 | 493.52 | ||||||||
| 143 | 3.8708 | 22.7582 | 37.3, −79.09 | 38.52, −76.69 | 469.08 | 493.59 | 984.48 | 1072.23 | |
| 39.73, −74.29 | 493.59 | ||||||||
| 143 | 3.8708 | 22.7585 | 39.22, −79.08 | 38.53, −76.69 | 469.43 | 493.58 | 984.48 | 1021.35 | |
| 37.83, −74.29 | 493.58 | ||||||||
| 143 | 3.875 | 22.7147 | 38.58, −80.52 | 39.16, −77.41 | 469.31 | 493.7 | 984.39 | 1060.56 | |
| 39.73, −74.29 | 493.7 | ||||||||
| 143 | 3.875 | 22.7627 | 39.22, −79.08 | 39.48, −76.69 | 469.43 | 493.76 | 984.39 | 1045.4 | |
| 39.73, −74.29 | 493.76 | ||||||||
| 162 | 2.0167 | 21.0857 | 34.53, −76.35 | 34.92, −73.97 | 468.71 | 493.24 | 1048.98 | 980.04 | |
| 35.3, −71.58 | 493.24 | ||||||||
| 162 | 2.0208 | 21.0418 | 35.67, −77.79 | 35.49, −74.69 | 468.87 | 493.32 | 1048.52 | 957.52 | |
| 35.3, −71.58 | 493.32 | ||||||||
| 162 | 2.0208 | 21.0902 | 36.45, −76.34 | 35.88, −73.96 | 469.03 | 493.4 | 1048.52 | 958.83 | |
| 35.3, −71.58 | 493.4 | ||||||||
| 162 | 2.025 | 21.0463 | 37.58, −77.78 | 36.44, −74.68 | 469.2 | 493.48 | 1048.2 | 937.99 | |
| 35.3, −71.58 | 493.48 | ||||||||
| 162 | 2.025 | 21.0457 | 35.67, −77.79 | 36.44, −74.69 | 468.87 | 493.48 | 1048.2 | 982.09 | |
| 37.2, −71.59 | 493.48 | ||||||||
| 162 | 2.025 | 21.094 | 36.45, −76.34 | 36.83, −73.97 | 469.03 | 493.56 | 1048.2 | 983.54 | |
| 37.2, −71.59 | 493.56 | ||||||||
| 162 | 2.0292 | 21.0502 | 37.58, −77.78 | 37.39, −74.69 | 469.2 | 493.64 | 1047.88 | 961.85 | |
| 37.2, −71.59 | 493.64 | ||||||||
| 162 | 2.0292 | 21.0989 | 38.36, −76.32 | 37.78, −73.96 | 469.36 | 493.72 | 1047.88 | 962.74 | |
| 37.2, −71.59 | 493.72 | ||||||||
| 162 | 2.0333 | 21.055 | 39.5, −77.76 | 38.35, −74.68 | 469.55 | 493.82 | 1047.56 | 942.48 | |
| 37.2, −71.59 | 493.82 | ||||||||
| 162 | 2.0333 | 21.054 | 37.58, −77.78 | 38.34, −74.69 | 469.2 | 493.81 | 1047.56 | 986.25 | |
| 39.1, −71.6 | 493.81 | ||||||||
| 162 | 2.0333 | 21.1027 | 38.36, −76.32 | 38.73, −73.96 | 469.36 | 493.89 | 1047.56 | 987.27 | |
| 39.1, −71.6 | 493.89 | ||||||||
| 162 | 2.0375 | 21.0589 | 39.5, −77.76 | 39.3, −74.68 | 469.55 | 493.99 | 1047.25 | 966.22 | |
| 39.1, −71.6 | 493.99 | ||||||||
| 162 | 2.0375 | 21.1075 | 40.28, −76.3 | 39.69, −73.95 | 469.71 | 494.07 | 1047.25 | 966.66 | |
| 39.1, −71.6 | 494.07 | ||||||||
| 168 | 2.0542 | 20.5145 | 35.67, −86.74 | 35.06, −83.1 | 468.74 | 493.2 | 1023.73 | 888.8 | |
| 34.44, −79.45 | 493.2 | ||||||||
| 168 | 2.0542 | 20.5625 | 34.51, −85.29 | 35.43, −82.38 | 468.57 | 493.27 | 1023.73 | 944.58 | |
| 36.34, −79.46 | 493.27 | ||||||||
| 168 | 2.0542 | 20.5632 | 36.43, −85.28 | 35.44, −82.37 | 468.89 | 493.27 | 1023.73 | 903.84 | |
| 34.44, −79.45 | 493.27 | ||||||||
| 168 | 2.0583 | 20.5183 | 35.67, −86.74 | 36.01, −83.1 | 468.74 | 493.35 | 1023.57 | 910.72 | |
| 36.34, −79.46 | 493.35 | ||||||||
| 168 | 2.0583 | 20.567 | 36.43, −85.28 | 36.39, −82.37 | 468.89 | 493.43 | 1023.57 | 926.49 | |
| 36.34, −79.46 | 493.43 | ||||||||
| 168 | 2.0625 | 20.5232 | 37.59, −86.72 | 36.97, −83.09 | 469.07 | 493.52 | 1023.42 | 893.85 | |
| 36.34, −79.46 | 493.52 | ||||||||
| 168 | 2.0625 | 20.5708 | 36.43, −85.28 | 37.34, −82.38 | 468.89 | 493.59 | 1023.42 | 949.9 | |
| 38.24, −79.47 | 493.59 | ||||||||
| 168 | 2.0625 | 20.5715 | 38.35, −85.27 | 37.35, −82.37 | 469.22 | 493.59 | 1023.42 | 909.78 | |
| 36.34, −79.46 | 493.59 | ||||||||
| 168 | 2.0667 | 20.527 | 37.59, −86.72 | 37.92, −83.1 | 469.07 | 493.68 | 1023.26 | 915.91 | |
| 38.24, −79.47 | 493.68 | ||||||||
| 168 | 2.0667 | 20.5753 | 38.35, −85.27 | 38.3, −82.37 | 469.22 | 493.75 | 1023.26 | 932.6 | |
| 38.24, −79.47 | 493.75 | ||||||||
| 168 | 2.0708 | 20.5318 | 39.51, −86.7 | 38.88, −83.09 | 469.41 | 493.85 | 1022.9 | 898.69 | |
| 38.24, −79.47 | 493.85 | ||||||||
| 168 | 2.0708 | 20.5795 | 38.35, −85.27 | 39.25, −82.37 | 469.22 | 493.92 | 1022.9 | 955.56 | |
| 40.14, −79.47 | 493.92 | ||||||||
| 168 | 2.0708 | 20.5802 | 40.27, −85.25 | 39.26, −82.36 | 469.57 | 493.93 | 1022.9 | 915.65 | |
| 38.24, −79.47 | 493.93 | ||||||||
| Xing Long (40.2°, 117.4°) | 118 | 16.6333 | 0.8973 | 38.19, 123.23 | 37.88, 123.96 | 517.47 | 493.81 | 959.93 | 922.82 |
| 37.57, 124.69 | 470.15 | ||||||||
| 118 | 16.6375 | 0.8542 | 39.55, 121.81 | 38.56, 123.25 | 517.47 | 493.93 | 959.84 | 895.31 | |
| 37.57, 124.69 | 470.39 | ||||||||
| 118 | 16.6375 | 0.8535 | 37.63, 121.79 | 38.55, 123.24 | 517.8 | 493.93 | 959.84 | 959.91 | |
| 39.47, 124.69 | 470.06 | ||||||||
| 118 | 16.6375 | 0.9015 | 38.19, 123.23 | 38.83, 123.96 | 517.8 | 493.98 | 959.84 | 958.39 | |
| 39.47, 124.69 | 470.15 | ||||||||
| 118 | 16.6417 | 0.8583 | 39.55, 121.81 | 39.51, 123.25 | 517.8 | 494.1 | 959.74 | 929.13 | |
| 39.47, 124.69 | 470.39 | ||||||||
| 118 | 16.6417 | 0.9067 | 40.11, 123.26 | 39.79, 123.98 | 517.8 | 494.14 | 959.74 | 927.44 | |
| 39.47, 124.69 | 470.48 | ||||||||
| 118 | 16.6458 | 0.8635 | 41.47, 121.84 | 40.47, 123.27 | 517.8 | 494.27 | 959.65 | 900.2 | |
| 39.47, 124.69 | 470.73 | ||||||||
| 118 | 16.6458 | 0.8625 | 39.55, 121.81 | 40.46, 123.25 | 518.15 | 494.27 | 959.65 | 964.76 | |
| 41.37, 124.69 | 470.39 | ||||||||
| 118 | 16.6458 | 0.9108 | 40.11, 123.26 | 40.74, 123.98 | 518.15 | 494.32 | 959.65 | 963.02 | |
| 41.37, 124.69 | 470.48 | ||||||||
| 118 | 16.65 | 0.8677 | 41.47, 121.84 | 41.42, 123.27 | 518.15 | 494.44 | 959.56 | 934.08 | |
| 41.37, 124.69 | 470.73 | ||||||||
| 118 | 16.65 | 0.9157 | 42.03, 123.28 | 41.7, 123.99 | 518.15 | 494.49 | 959.56 | 932.15 | |
| 41.37, 124.69 | 470.82 | ||||||||
| 118 | 16.6542 | 0.8732 | 43.38, 121.88 | 42.38, 123.29 | 518.15 | 494.62 | 959.47 | 905.01 | |
| 41.37, 124.69 | 471.09 | ||||||||
| 118 | 16.6542 | 0.8722 | 41.47, 121.84 | 42.37, 123.27 | 518.51 | 494.62 | 959.47 | 969.58 | |
| 43.26, 124.7 | 470.73 | ||||||||
| 118 | 16.6542 | 0.9202 | 42.03, 123.28 | 42.65, 123.99 | 518.51 | 494.67 | 959.47 | 967.59 | |
| 43.26, 124.7 | 470.82 | ||||||||
| 143 | 14.8875 | 22.7149 | 38.39, 115.87 | 37.74, 117.41 | 517.61 | 493.47 | 1118.16 | 900.95 | |
| 37.08, 118.95 | 469.32 | ||||||||
| 143 | 14.8917 | 22.6707 | 37.76, 114.43 | 38.37, 116.69 | 517.96 | 493.59 | 1117.94 | 927.64 | |
| 38.98, 118.94 | 469.22 | ||||||||
| 143 | 14.8917 | 22.7186 | 38.39, 115.87 | 38.69, 117.41 | 517.96 | 493.64 | 1117.94 | 930.77 | |
| 38.98, 118.94 | 469.32 | ||||||||
| 143 | 14.8958 | 22.6752 | 39.68, 114.44 | 39.33, 116.69 | 517.96 | 493.77 | 1117.73 | 899.96 | |
| 38.98, 118.94 | 469.57 | ||||||||
| 143 | 14.8958 | 22.7235 | 40.31, 115.89 | 39.65, 117.42 | 517.96 | 493.82 | 1117.73 | 902.19 | |
| 38.98, 118.94 | 469.68 | ||||||||
| 143 | 14.8958 | 22.7229 | 38.39, 115.87 | 39.64, 117.41 | 518.33 | 493.83 | 1117.73 | 961.69 | |
| 40.88, 118.94 | 469.32 | ||||||||
| 143 | 14.9 | 22.6794 | 39.68, 114.44 | 40.28, 116.69 | 518.33 | 493.95 | 1117.51 | 929.23 | |
| 40.88, 118.94 | 469.57 | ||||||||
| 143 | 14.9 | 22.7277 | 40.31, 115.89 | 40.6, 117.42 | 518.33 | 494.01 | 1117.51 | 931.65 | |
| 40.88, 118.94 | 469.68 | ||||||||
| 143 | 14.9042 | 22.6845 | 41.59, 114.47 | 41.24, 116.71 | 518.33 | 494.13 | 1117.3 | 902.39 | |
| 40.88, 118.94 | 469.93 | ||||||||
| 143 | 14.9042 | 22.7329 | 42.23, 115.92 | 41.56, 117.43 | 518.33 | 494.19 | 1117.3 | 903.65 | |
| 40.88, 118.94 | 470.04 | ||||||||
| 143 | 14.9042 | 22.7322 | 40.31, 115.89 | 41.54, 117.42 | 518.71 | 494.2 | 1117.3 | 961.81 | |
| 42.77, 118.95 | 469.68 | ||||||||
| 143 | 14.9083 | 22.689 | 41.59, 114.47 | 42.18, 116.71 | 518.71 | 494.32 | 1117.09 | 931.03 | |
| 42.77, 118.95 | 469.93 | ||||||||
| 143 | 14.9083 | 22.7374 | 42.23, 115.92 | 42.5, 117.44 | 518.71 | 494.38 | 1117.09 | 932.43 | |
| 42.77, 118.95 | 470.04 |
References
- Burke, W.J.; Lin, C.S.; Hagan, M.P.; Huang, C.Y.; Weimer, D.R.; Wise, J.O.; Gentile, L.C.; Marcos, F.A. Storm time global thermosphere: A driven-dissipative thermodynamic system. J. Geophys. Res.-Space Phys. 2009, 114, A06306. [Google Scholar] [CrossRef]
- Wise, J.O.; Burke, W.J.; Sutton, E.K. Globally averaged exospheric temperatures derived from CHAMP and GRACE accelerometer measurements. J. Geophys. Res.-Space Phys. 2012, 117. [Google Scholar] [CrossRef]
- Picone, J.M.; Hedin, A.E.; Drob, D.P.; Aikin, A.C. Nrlmsise-00 Empirical Model of the Atmosphere: Statistical Comparisons and Scientific Issues. J. Geophys. Res.-Space Phys. 2002, 107, SIA 15-1–SIA 15-16. [Google Scholar] [CrossRef]
- Forbes, J.M.; Zhang, X.; Bruinsma, S.L. New perspectives on thermosphere tides: 2. Penetration to the upper thermosphere. Earth Planets Space 2014, 66, 1–11. [Google Scholar] [CrossRef]
- Weimer, D.R.; Sutton, E.K.; Mlynczak, M.G.; Hunt, L.A. Intercalibration of neutral density measurements for mapping the thermosphere. J. Geophys. Res. Space Phys. 2016, 121, 5975–5990. [Google Scholar] [CrossRef]
- Weng, L.; Lei, J.; Sutton, E.; Dou, X.; Fang, H. An exospheric temperature model from CHAMP thermospheric density. Space Weather 2017, 15, 343–351. [Google Scholar] [CrossRef]
- Evans, J.S.; Lumpe, J.D.; Correira, J.; Veibell, V.; Kyrwonos, A.; McClintock, W.E.; Solomon, S.C.; Eastes, R.W. Neutral Exospheric Temperatures From the GOLD Mission. J. Geophys. Res.-Space Phys. 2020, 125, e2020JA027814. [Google Scholar] [CrossRef]
- Friis-Christensen, E.; Luhr, H.; Knudsen, D.; Haagmans, R. Swarm—An Earth Observation Mission investigating Geospace. Adv. Space Res. 2008, 41, 210–216. [Google Scholar] [CrossRef]
- Doornbos, E.; van den Ijssel, J.; Luhr, H.; Forster, M.; Koppenwallner, G. Neutral Density and Crosswind Determination from Arbitrarily Oriented Multiaxis Accelerometers on Satellites. J. Spacecr. Rockets 2010, 47, 580–589. [Google Scholar] [CrossRef]
- Van den Ijssel, J.; Doornbos, E.; Iorfida, E.; March, G.; Siemes, C.; Montenbruck, O. Thermosphere densities derived from Swarm GPS observations. Adv. Space Res. 2020, 65, 1758–1771. [Google Scholar] [CrossRef]
- Yuan, W.; Xu, J.; Ma, R.; Wu, Q.; Jiang, G.; Gao, H.; Liu, X.; Chen, S. First observation of mesospheric and thermospheric winds by a Fabry-Perot interferometer in China. Chin. Sci. Bull. 2010, 55, 4046–4051. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, X.; Xu, J.; Zhou, Q.; Jiang, G.; Ma, R. FPI observations of nighttime mesospheric and thermospheric winds in China and their comparisons with HWM07. Ann. Geophys. 2013, 31, 1365–1378. [Google Scholar] [CrossRef]
- Chen, G.-m.; Xu, J.; Wang, W.; Burns, A.G. A comparison of the effects of CIR- and CME-induced geomagnetic activity on thermospheric densities and spacecraft orbits: Statistical studies. J. Geophys. Res. Space Phys. 2014, 119, 7928–7939. [Google Scholar] [CrossRef]
- Cai, X.; Burns, A.G.; Wang, W.; Qian, L.; Solomon, S.C.; Eastes, R.W.; Pedatella, N.; Daniell, R.E.; McClintock, W.E. The Two-Dimensional Evolution of Thermospheric ΣO/N2 Response to Weak Geomagnetic Activity During Solar-Minimum Observed by GOLD. Geophys. Res. Lett. 2020, 47, e2020GL088838. [Google Scholar] [CrossRef]
- Buonsanto, M.J.; Pohlman, L.M. Climatology of neutral exospheric temperature above Millstone Hill. J. Geophys. Res.-Space Phys. 1998, 103, 23381–23392. [Google Scholar] [CrossRef]


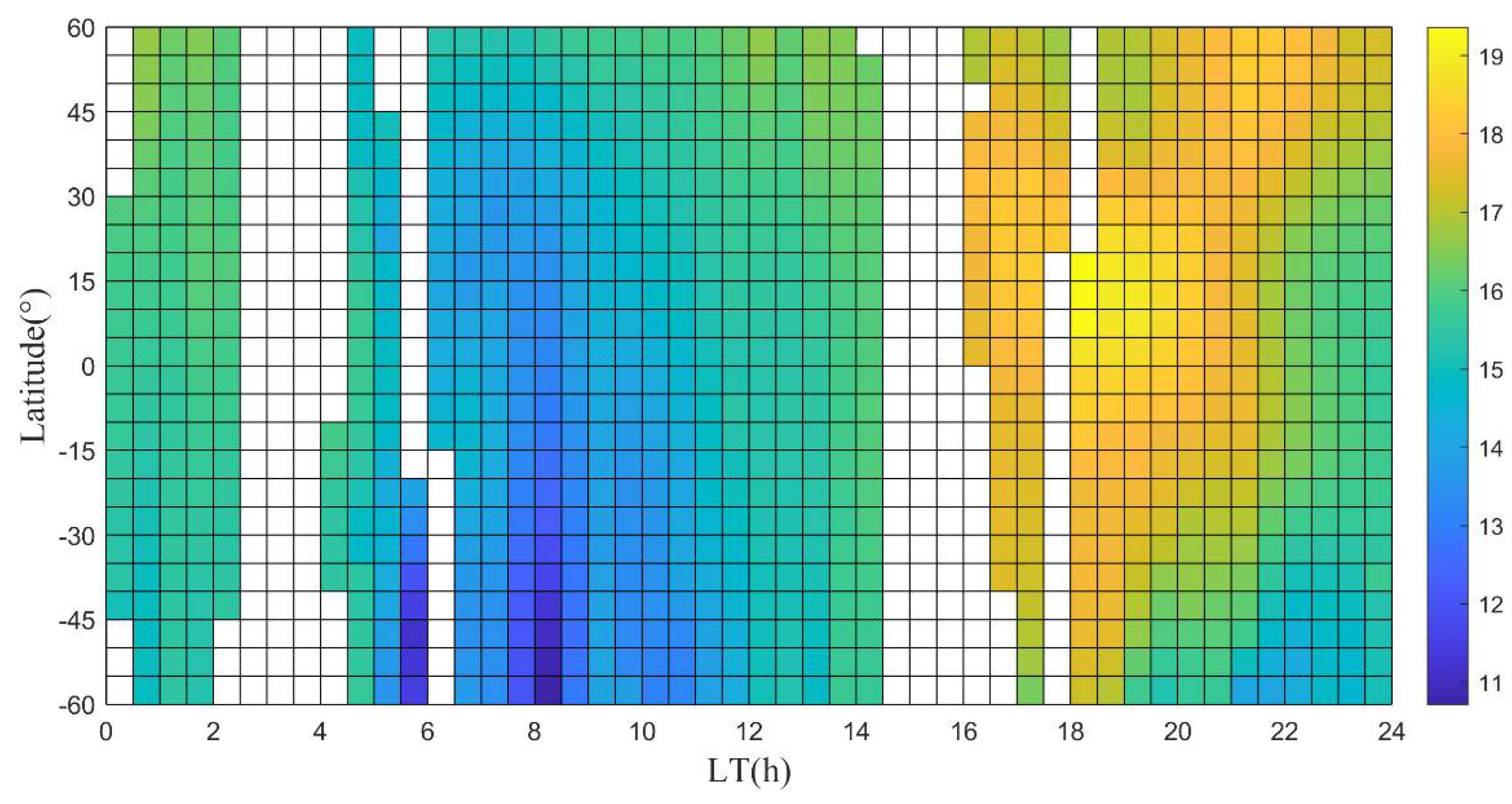

| FPI Station | Latitude | Longitude | Used Observations in the Comparison |
|---|---|---|---|
| Arecibo | 18.34° | −66.75° | 14 |
| Pisgah | 35.2° | −82.85° | 41 |
| Virginia | 37.2° | −80.42° | 52 |
| Eastern Kentucky | 37.75° | −84.29° | 27 |
| Urbana | 40.13° | −88.2° | 38 |
| Xinglong | 40.2° | 117.4° | 27 |
| Peach mountain | 42.27° | −83.75° | 4 |
| Temperatures for Comparison | Sample Points | Mean Deviation, K | Standard Deviation, K |
|---|---|---|---|
| T () & T(FPI) | 203 | 30.80 | 106.20 |
| T () & T(FPI) | 203 | −30.67 | 108.03 |
| T (MSIS at 500 km) & T (MSIS at 250 km) | 203 | 23.52 | 14.53 |
| T () & T(MSIS) | 81011 | 16.52 | 84.46 |
| T () & T(MSIS) | 81011 | 45.90 | 140.73 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Xu, J.; van den IJssel, J.; Yuan, W. A Novel Method to Derive Exospheric Temperatures from Swarm Thermospheric Densities during Quiet Times. Remote Sens. 2022, 14, 5382. https://doi.org/10.3390/rs14215382
Lin Y, Xu J, van den IJssel J, Yuan W. A Novel Method to Derive Exospheric Temperatures from Swarm Thermospheric Densities during Quiet Times. Remote Sensing. 2022; 14(21):5382. https://doi.org/10.3390/rs14215382
Chicago/Turabian StyleLin, Yingyun, Jiyao Xu, Jose van den IJssel, and Wei Yuan. 2022. "A Novel Method to Derive Exospheric Temperatures from Swarm Thermospheric Densities during Quiet Times" Remote Sensing 14, no. 21: 5382. https://doi.org/10.3390/rs14215382
APA StyleLin, Y., Xu, J., van den IJssel, J., & Yuan, W. (2022). A Novel Method to Derive Exospheric Temperatures from Swarm Thermospheric Densities during Quiet Times. Remote Sensing, 14(21), 5382. https://doi.org/10.3390/rs14215382







