Triangle Water Index (TWI): An Advanced Approach for More Accurate Detection and Delineation of Water Surfaces in Sentinel-2 Data
Abstract
1. Introduction
2. Study Areas
3. Materials and Methods
3.1. Sentinel-2 Data
3.2. MNDWI
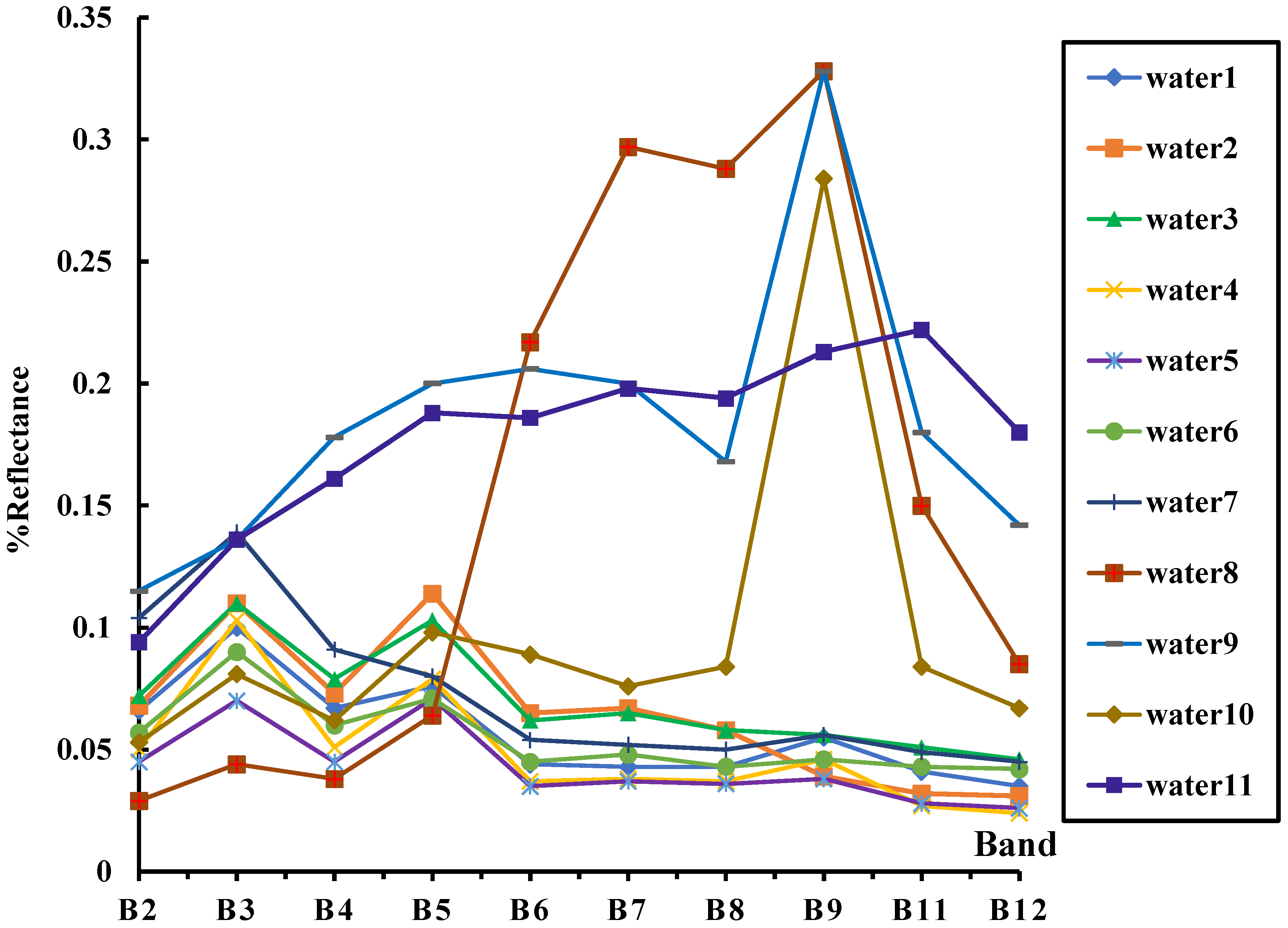
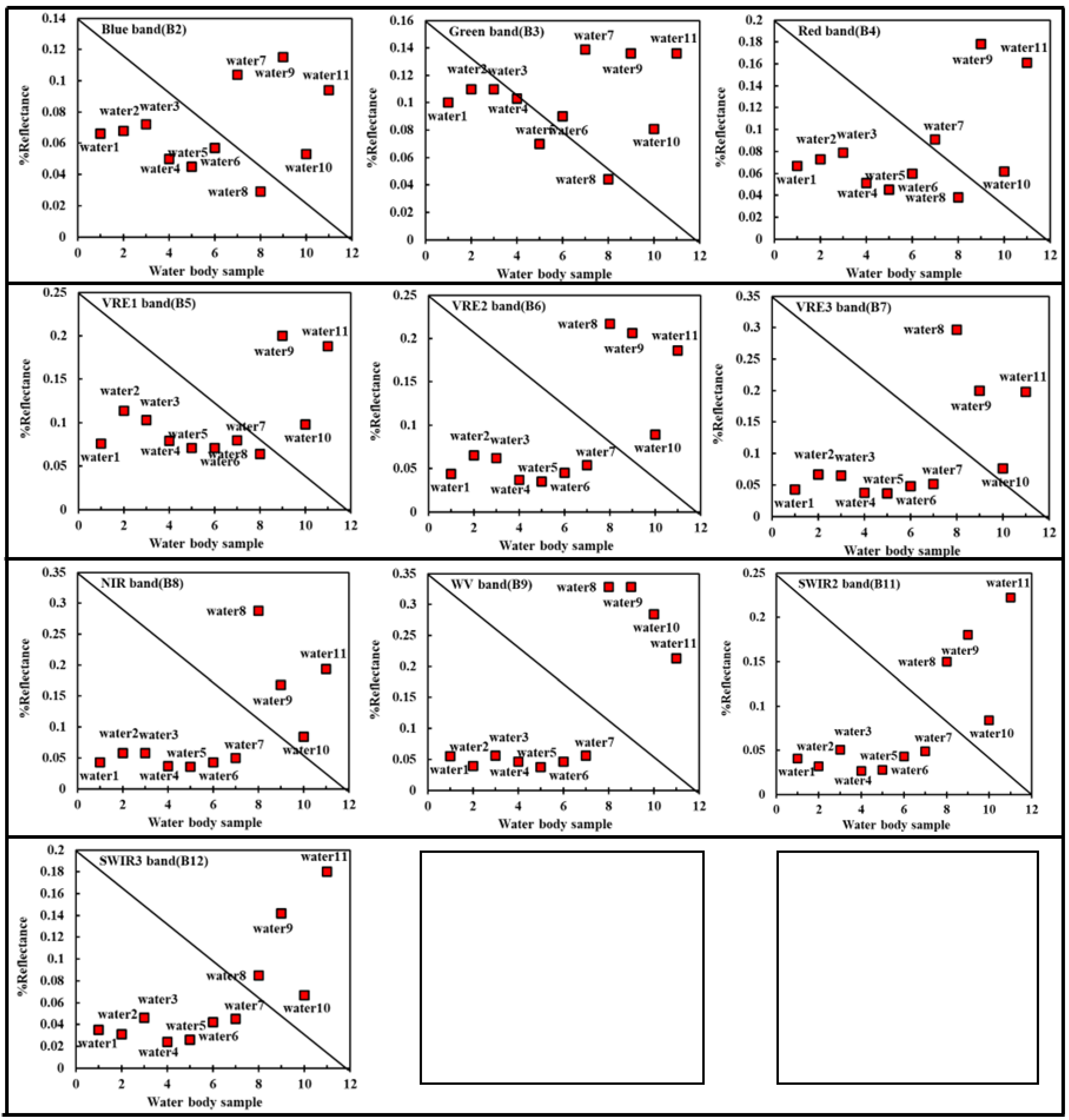
3.3. Analysis of the Spectral Response Characteristics of Water Bodies
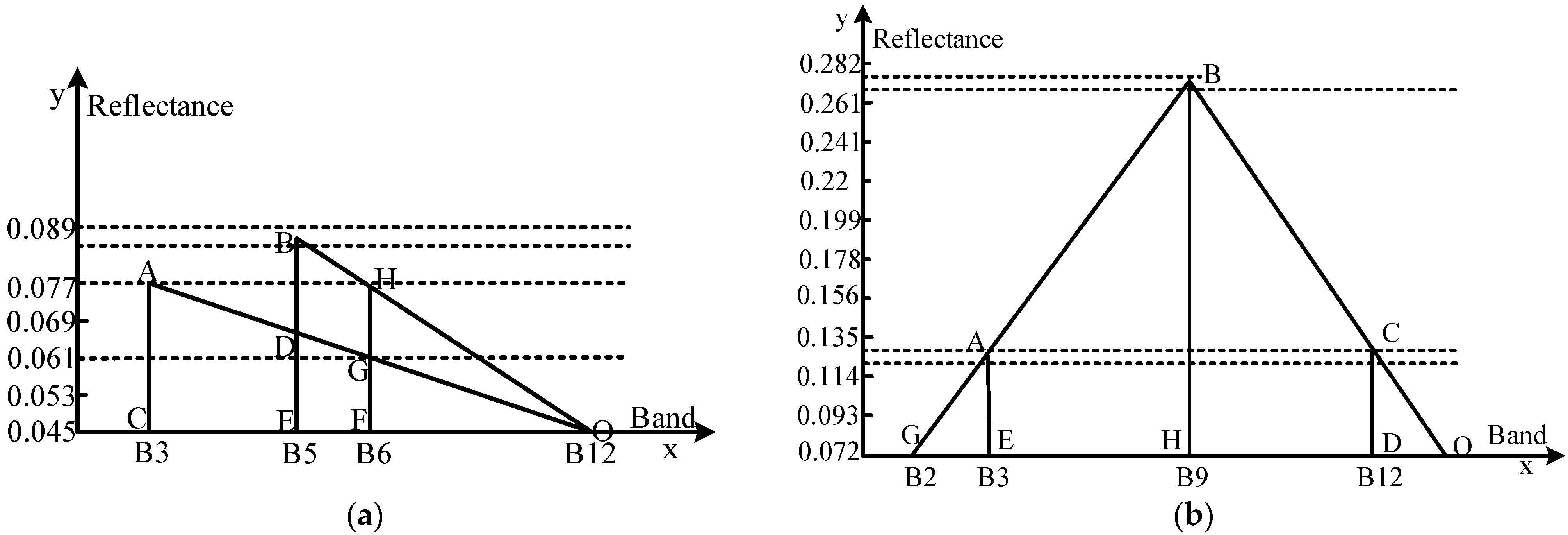
3.4. Formulation of the Triangle Water Index (TWI)
3.5. The Otsu Automatic Threshold
3.6. Accuracy Assessment
4. Results and Discussion
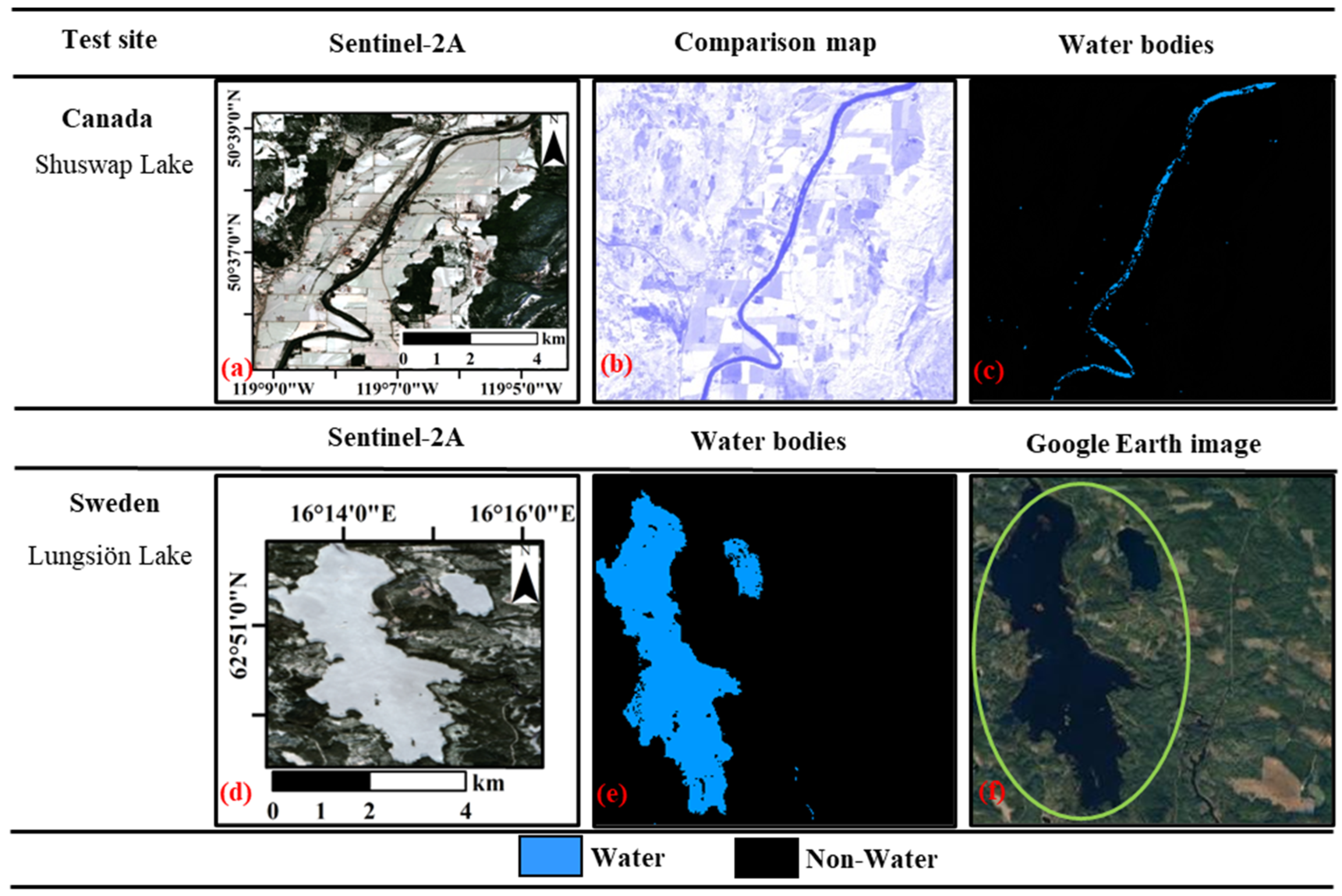
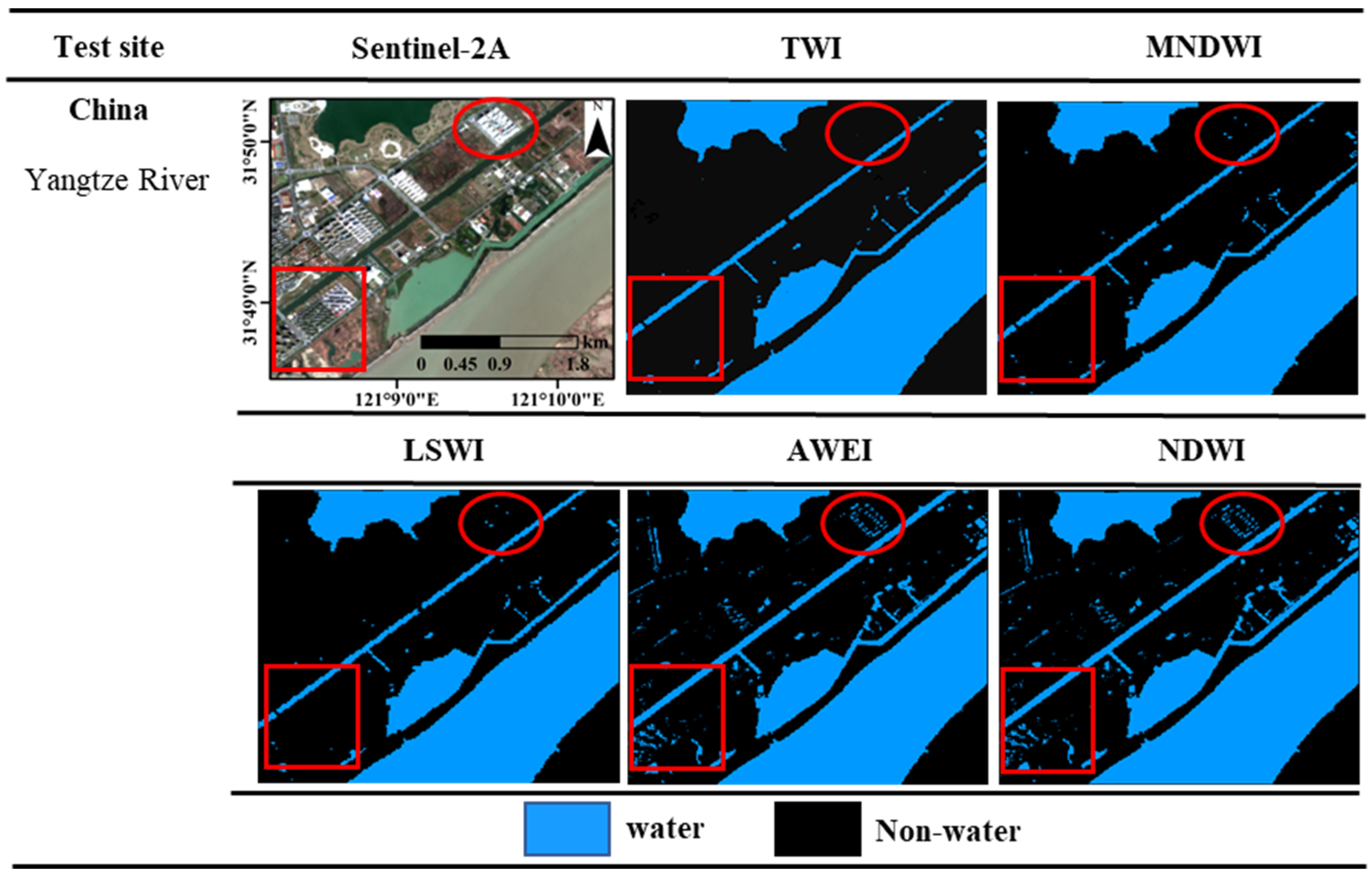
4.1. Water Extraction Maps
4.2. Classification Accuracy
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dang, T.D.; Cochrane, T.A.; Arias, M.E. Quantifying suspended sediment dynamics in mega deltas using remote sensing data: A case study of the Mekong floodplains. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 105–115. [Google Scholar] [CrossRef]
- Ji, L.; Zhang, L.; Wylie, B. Analysis of Dynamic Thresholds for the Normalized Difference Water Index. Photogramm. Eng. Remote Sens. 2009, 75, 1307–1317. [Google Scholar] [CrossRef]
- Chen, Y.; Fan, R.; Yang, X.; Wang, J.; Latif, A. Extraction of Urban Water Bodies from High-Resolution Remote-Sensing Imagery Using Deep Learning. Water 2018, 10, 585. [Google Scholar] [CrossRef]
- Rishikeshan, C.A.; Ramesh, H. An automated mathematical morphology driven algorithm for water body extraction from remotely sensed images. ISPRS J. Photogramm. Remote Sens. 2018, 146, 11–21. [Google Scholar] [CrossRef]
- Habeeb, R.; Gupta, Y.; Chinwan, H.; Barker, E. Assessing Demographic and Water Sensitivities Arising due to Urban Water Insecurity in Haldwani, Uttarakhand (India): A GIS-Based Spatial Analysis. J. Geovis. Spat. Anal. 2019, 3, 8. [Google Scholar] [CrossRef]
- Feng, W.; Sui, H.; Huang, W.; Xu, C.; An, K. Water Body Extraction From Very High-Resolution Remote Sensing Imagery Using Deep U-Net and a Superpixel-Based Conditional Random Field Model. IEEE Geosci. Remote Sens. Lett. 2019, 16, 618–622. [Google Scholar] [CrossRef]
- Moser, G.; Zerubia, J.; Serpico, S.B.; Benediktsson, J.A. Mathematical Models for Remote Sensing Image Processing. In Signals and Communication Technology; Moser, G., Zerubia, J., Eds.; Springer: Cham, Switzerland, 2018; pp. 1–36. [Google Scholar] [CrossRef]
- Matsushita, B.; Yang, W.; Chang, P.; Yang, F.; Fukushima, T. A simple method for distinguishing global Case-1 and Case-2 waters using SeaWiFS measurements. ISPRS J. Photogramm. Remote Sens. 2012, 69, 74–87. [Google Scholar] [CrossRef]
- Nguyen, U.N.T.; Pham, L.T.H.; Dang, T.D. An automatic water detection approach using Landsat 8 OLI and Google Earth Engine cloud computing to map lakes and reservoirs in New Zealand. Environ. Monit. Assess. 2019, 191, 235. [Google Scholar] [CrossRef]
- Sun, F.; Sun, W.; Chen, J.; Gong, P. Comparison and improvement of methods for identifying waterbodies in remotely sensed imagery. Int. J. Remote Sens. 2012, 33, 6854–6875. [Google Scholar] [CrossRef]
- Pham, L.T.H.; Brabyn, L. Monitoring mangrove biomass change in Vietnam using SPOT images and an object-based approach combined with machine learning algorithms. ISPRS J. Photogramm. Remote Sens. 2017, 128, 86–97. [Google Scholar] [CrossRef]
- Chawla, I.; Karthikeyan, L.; Mishra, A.K. A review of remote sensing applications for water security: Quantity, quality, and extremes. J. Hydrol. 2020, 585, 124826. [Google Scholar] [CrossRef]
- Nandi, D.; Chowdhury, R.; Mohapatra, J.; Mohanta, K.; Ray, D. Automatic delineation of water bodies using multiple spectral indices. Int. J. Sci. Res. Sci. Eng. Technol. IJSRSET 2018, 4, 14. [Google Scholar]
- Acharya, T.D.; Lee, D.H.; Yang, I.T.; Lee, J.K. Identification of Water Bodies in a Landsat 8 OLI Image Using a J48 Decision Tree. Sensors 2016, 16, 1075. [Google Scholar] [CrossRef] [PubMed]
- Mueller, N.; Lewis, A.; Roberts, D.; Ring, S.; Melrose, R.; Sixsmith, J.; Lymburner, L.; McIntyre, A.; Tan, P.; Curnow, S.; et al. Water observations from space: Mapping surface water from 25 years of Landsat imagery across Australia. Remote Sens. Environ. 2016, 174, 341–352. [Google Scholar] [CrossRef]
- Yang, J.; Du, X. An enhanced water index in extracting water bodies from Landsat TM imagery. Ann. GIS 2017, 23, 141–148. [Google Scholar] [CrossRef]
- Acharya, T.D.; Subedi, A.; Lee, D.H. Evaluation of Water Indices for Surface Water Extraction in a Landsat 8 Scene of Nepal. Sensors 2018, 18, 2580. [Google Scholar] [CrossRef]
- Rokni, K.; Ahmad, A.; Solaimani, K.; Hazini, S. A new approach for surface water change detection: Integration of pixel level image fusion and image classification techniques. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 226–234. [Google Scholar] [CrossRef]
- Liu, W.; Chen, X.; Ran, J.; Liu, L.; Wang, Q.; Xin, L.; Li, G. LaeNet: A Novel Lightweight Multitask CNN for Automatically Extracting Lake Area and Shoreline from Remote Sensing Images. Remote Sens. 2020, 13, 56. [Google Scholar] [CrossRef]
- Skakun, S. A neural network approach to flood mapping using satellite imagery. Comput. Inform. 2010, 29, 1013–1024. [Google Scholar]
- Weng, Q. Remote sensing of impervious surfaces in the urban areas: Requirements, methods, and trends. Remote Sens. Environ. 2012, 117, 34–49. [Google Scholar] [CrossRef]
- Bofana, J.; Zhang, M.; Nabil, M.; Wu, B.; Tian, F.; Liu, W.; Zeng, H.; Zhang, N. Comparison of Different Cropland Classification Methods under Diversified Agroecological Conditions in the Zambezi River Basin. Remote Sens. 2020, 12, 2096. [Google Scholar] [CrossRef]
- Sun, F.; Zhao, Y.; Gong, P.; Ma, R.; Dai, Y. Monitoring dynamic changes of global land cover types: Fluctuations of major lakes in China every 8 days during 2000–2010. Chin. Sci. Bull. 2013, 59, 171–189. [Google Scholar] [CrossRef]
- Mallet, C.; Bretar, F.; Roux, M.; Soergel, U.; Heipke, C. Relevance assessment of full-waveform lidar data for urban area classification. ISPRS J. Photogramm. Remote Sens. 2011, 66, S71–S84. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Acharya, T.D.; Subedi, A.; Lee, D.H. Evaluation of Machine Learning Algorithms for Surface Water Extraction in a Landsat 8 Scene of Nepal. Sensors 2019, 19, 2769. [Google Scholar] [CrossRef]
- Ji, L.; Geng, X.; Sun, K.; Zhao, Y.; Gong, P. Target Detection Method for Water Mapping Using Landsat 8 OLI/TIRS Imagery. Water 2015, 7, 794–817. [Google Scholar] [CrossRef]
- Wu, X.; Kumar, V.; Ross Quinlan, J.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Yu, P.S.; et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2007, 14, 1–37. [Google Scholar] [CrossRef]
- Kaplan, G.; Avdan, U. Object-based water body extraction model using Sentinel-2 satellite imagery. Remote Sens. 2017, 50, 137–143. [Google Scholar] [CrossRef]
- Khalid, H.W.; Khalil, R.M.Z.; Qureshi, M.A. Evaluating spectral indices for water bodies extraction in western Tibetan Plateau. Egypt. J. Remote Sens. Space Sci. 2021, 24, 619–634. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 2007, 17, 1425–1432. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2007, 27, 3025–3033. [Google Scholar] [CrossRef]
- Wang, S.; Baig, M.H.A.; Zhang, L.; Jiang, H.; Ji, Y.; Zhao, H.; Tian, J. A Simple Enhanced Water Index (EWI) for Percent Surface Water Estimation Using Landsat Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 90–97. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Engler, R.; Waser, L.T.; Zimmermann, N.E.; Schaub, M.; Berdos, S.; Ginzler, C.; Psomas, A. Combining ensemble modeling and remote sensing for mapping individual tree species at high spatial resolution. For. Ecol. Manag. 2013, 310, 64–73. [Google Scholar] [CrossRef]
- Jiang, W.; Ni, Y.; Pang, Z.; Li, X.; Ju, H.; He, G.; Lv, J.; Yang, K.; Fu, J.; Qin, X. An Effective Water Body Extraction Method with New Water Index for Sentinel-2 Imagery. Water 2021, 13, 1647. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Schalles, J.; Binding, C.; Cao, Z.; Ma, R.; Alikas, K.; Kangro, K.; Gurlin, D.; Hà, N.; et al. Seamless retrievals of chlorophyll-a from Sentinel-2 (MSI) and Sentinel-3 (OLCI) in inland and coastal waters: A machine-learning approach. Remote Sens. Environ. 2020, 240, 11604. [Google Scholar] [CrossRef]
- Wieland, M.; Martinis, S. Large-scale surface water change observed by Sentinel-2 during the 2018 drought in Germany. Int. J. Remote Sens. 2020, 41, 4742–4756. [Google Scholar] [CrossRef]
- Tamiminia, H.; Salehi, B.; Mahdianpari, M.; Quackenbush, L.; Adeli, S.; Brisco, B. Google Earth Engine for geo-big data applications: A meta-analysis and systematic review. ISPRS J. Photogramm. Remote Sens. 2020, 164, 152–170. [Google Scholar] [CrossRef]
- Huang, C.; Chen, Y.; Zhang, S.; Wu, J. Detecting, Extracting, and Monitoring Surface Water From Space Using Optical Sensors: A Review. Rev. Geophys. 2018, 56, 333–360. [Google Scholar] [CrossRef]
- Matsushita, B.; Yang, W.; Yu, G.; Oyama, Y.; Yoshimura, K.; Fukushima, T. A hybrid algorithm for estimating the chlorophyll-a concentration across different trophic states in Asian inland waters. ISPRS J. Photogramm. Remote Sens. 2015, 102, 28–37. [Google Scholar] [CrossRef]
- Gao, H.; Wang, L.; Jing, L.; Xu, J. An effective modified water extraction method for Landsat-8 OLI imagery of mountainous plateau regions. IOP Conf. Ser. Earth Environ. Sci. 2016, 34, 012010. [Google Scholar] [CrossRef]
- Waser, L.T.; Rüetschi, M.; Psomas, A.; Small, D.; Rehush, N. Mapping dominant leaf type based on combined Sentinel-1/-2 data—Challenges for mountainous countries. ISPRS J. Photogramm. Remote Sens. 2021, 180, 209–226. [Google Scholar] [CrossRef]
- Main-Knorn, M.; Pflug, B.; Louis, J.; Debaecker, V.; Müller-Wilm, U.; Gascon, F. Sen2Cor for Sentinel-2. Image Signal Process. Remote Sens. 2017, 10427, 37–48. [Google Scholar]
- Segl, K.; Richter, R.; Küster, T.; Kaufmann, H. End-to-end sensor simulation for spectral band selection and optimization with application to the Sentinel-2 mission. Appl. Opt. 2012, 51, 439–449. [Google Scholar] [CrossRef]
- Picciotto, H. Triangle Congruence and Similarity A Common-Core-Compatible Approach. Available online: https://www.mathed.page/transformations/triangle-congruence-similarity-v1.pdf (accessed on 3 May 2022).
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Xu, X.; Xu, S.; Jin, L.; Song, E. Characteristic analysis of Otsu threshold and its applications. Pattern Recognit. Lett. 2011, 32, 956–961. [Google Scholar] [CrossRef]
- Powers, D.M.W. Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation. J. Mach. Learn. Technol. 2011, 2, 29. [Google Scholar] [CrossRef]
- Foody, G.M. Classification accuracy comparison: Hypothesis tests and the use of confidence intervals in evaluations of difference, equivalence and non-inferiority. Remote Sens. Environ. 2009, 113, 1658–1663. [Google Scholar] [CrossRef]
- Foody, G.M. Explaining the unsuitability of the kappa coefficient in the assessment and comparison of the accuracy of thematic maps obtained by image classification. Remote Sens. Environ. 2020, 239, 111630. [Google Scholar] [CrossRef]
- Morales-Barquero, L.; Lyons, M.B.; Phinn, S.R.; Roelfsema, C.M. Trends in Remote Sensing Accuracy Assessment Approaches in the Context of Natural Resources. Remote Sens. 2019, 11, 2305. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, L.; Li, J.; Luo, L.; Yin, Y.; Liu, M.; Li, Y. Seasonal-spatial variation and remote sensing of phytoplankton absorption in Lake Taihu, a large eutrophic and shallow lake in China. J. Plankton Res. 2010, 32, 1023–1037. [Google Scholar] [CrossRef]



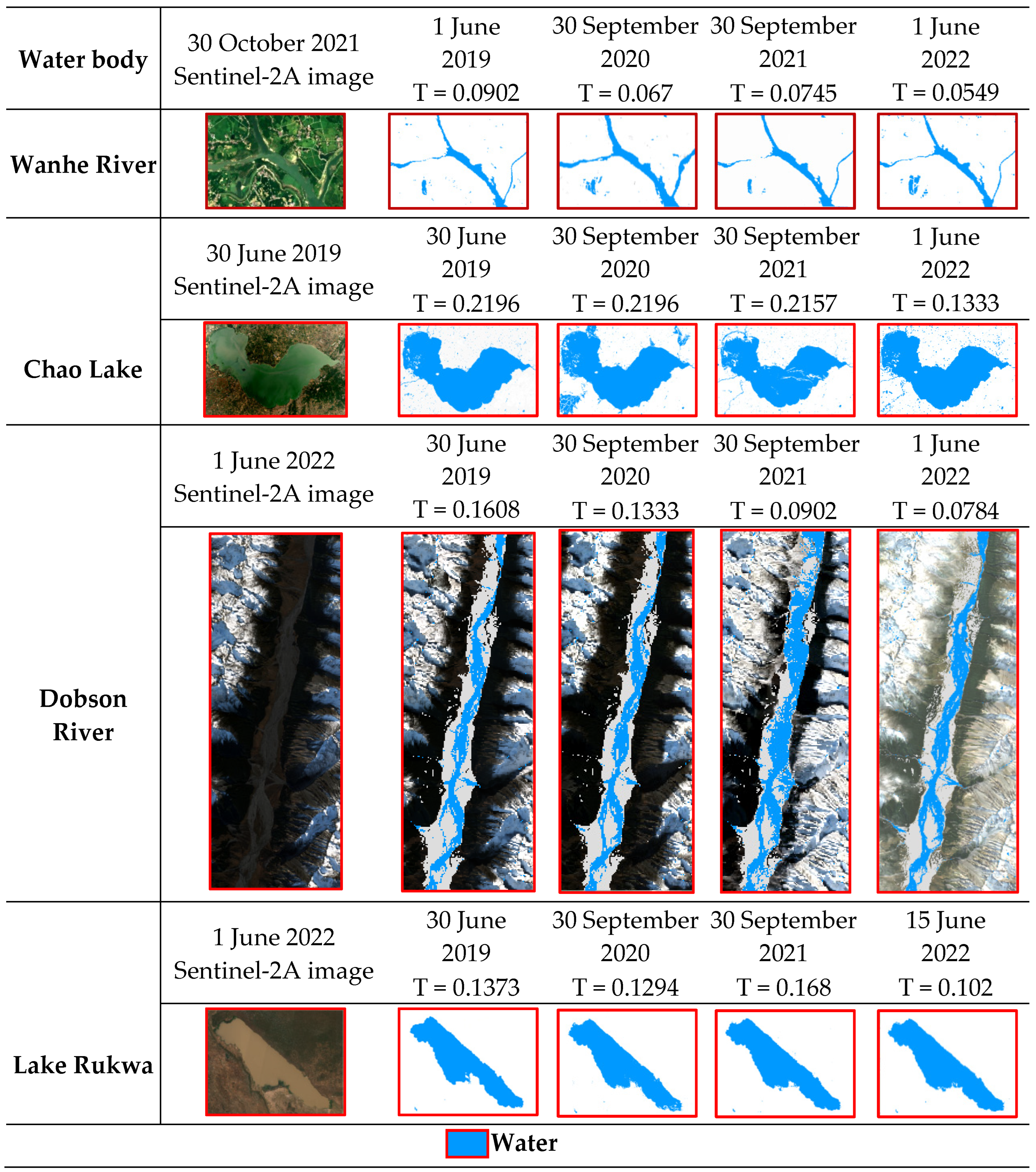
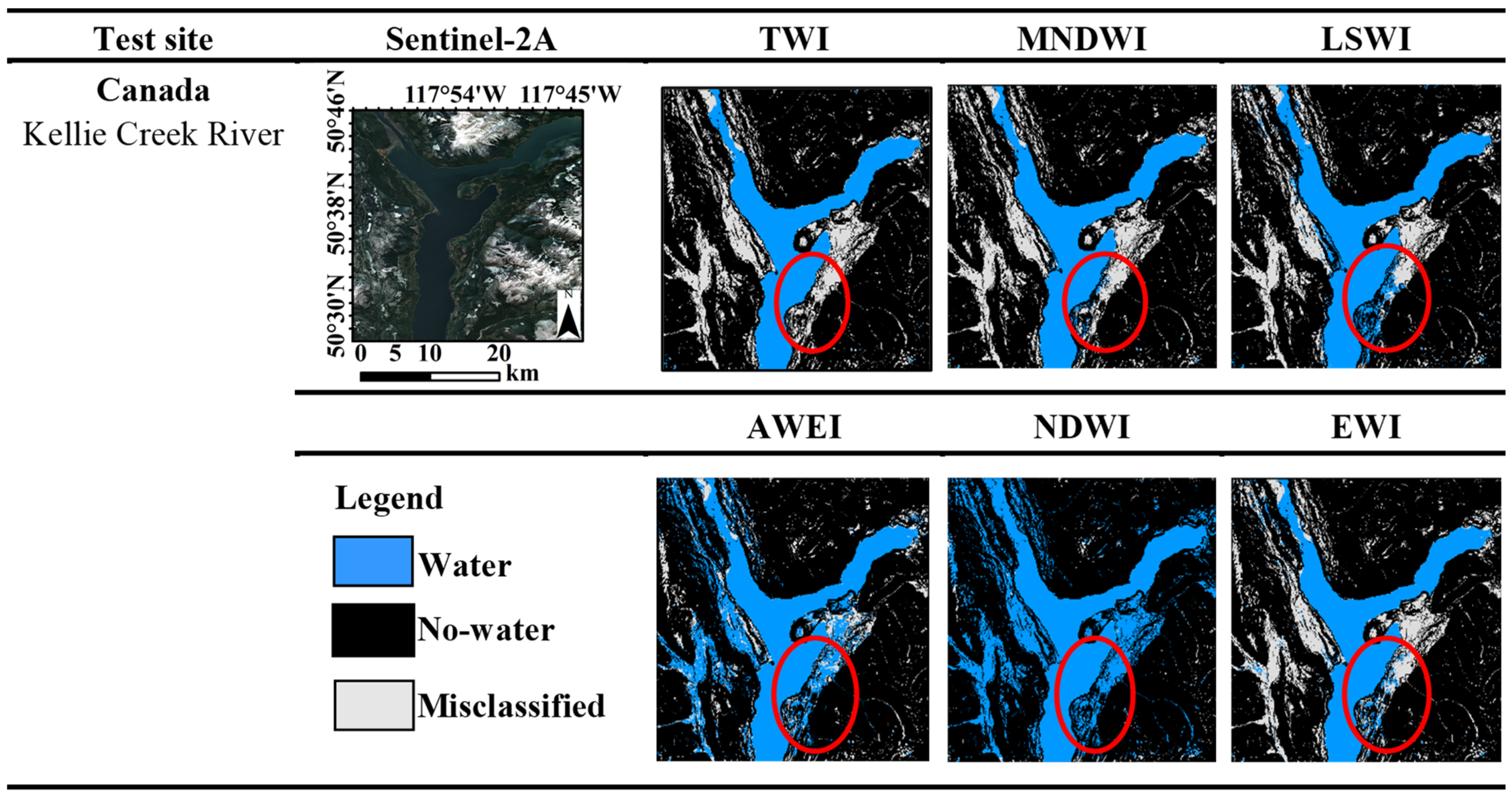
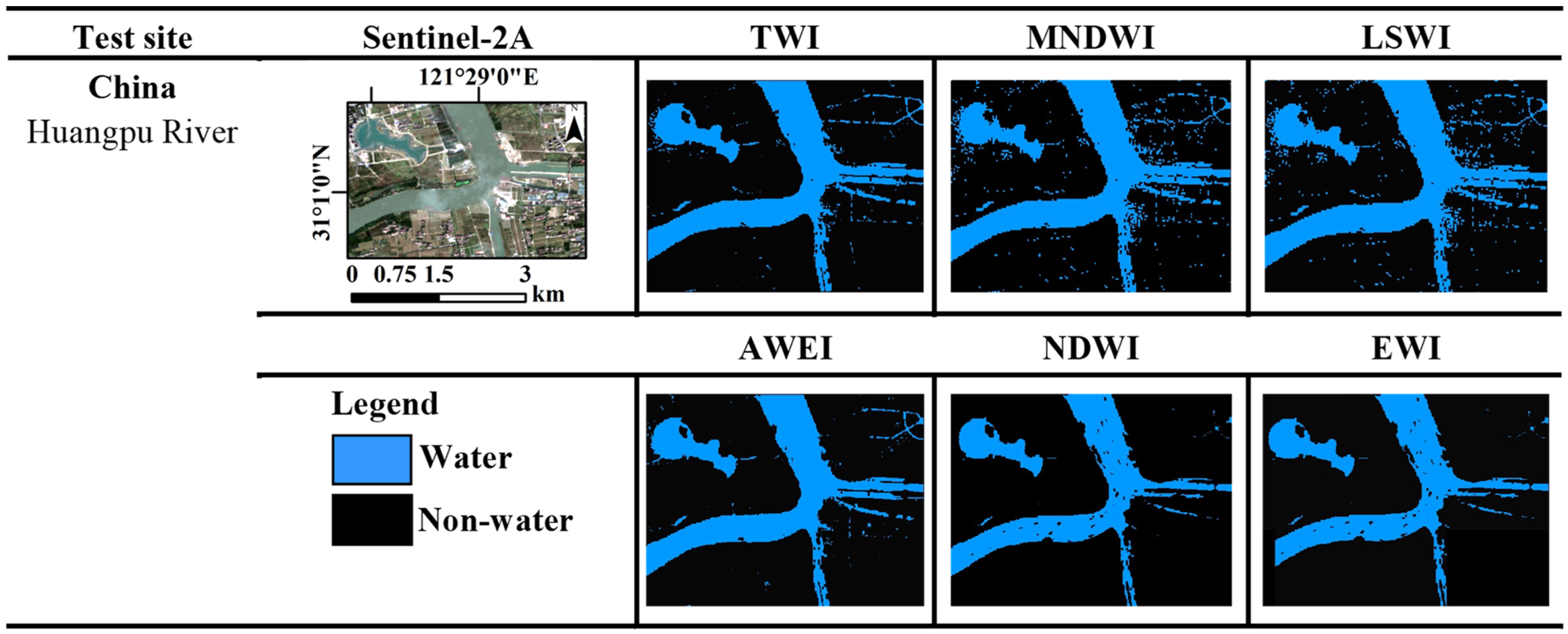
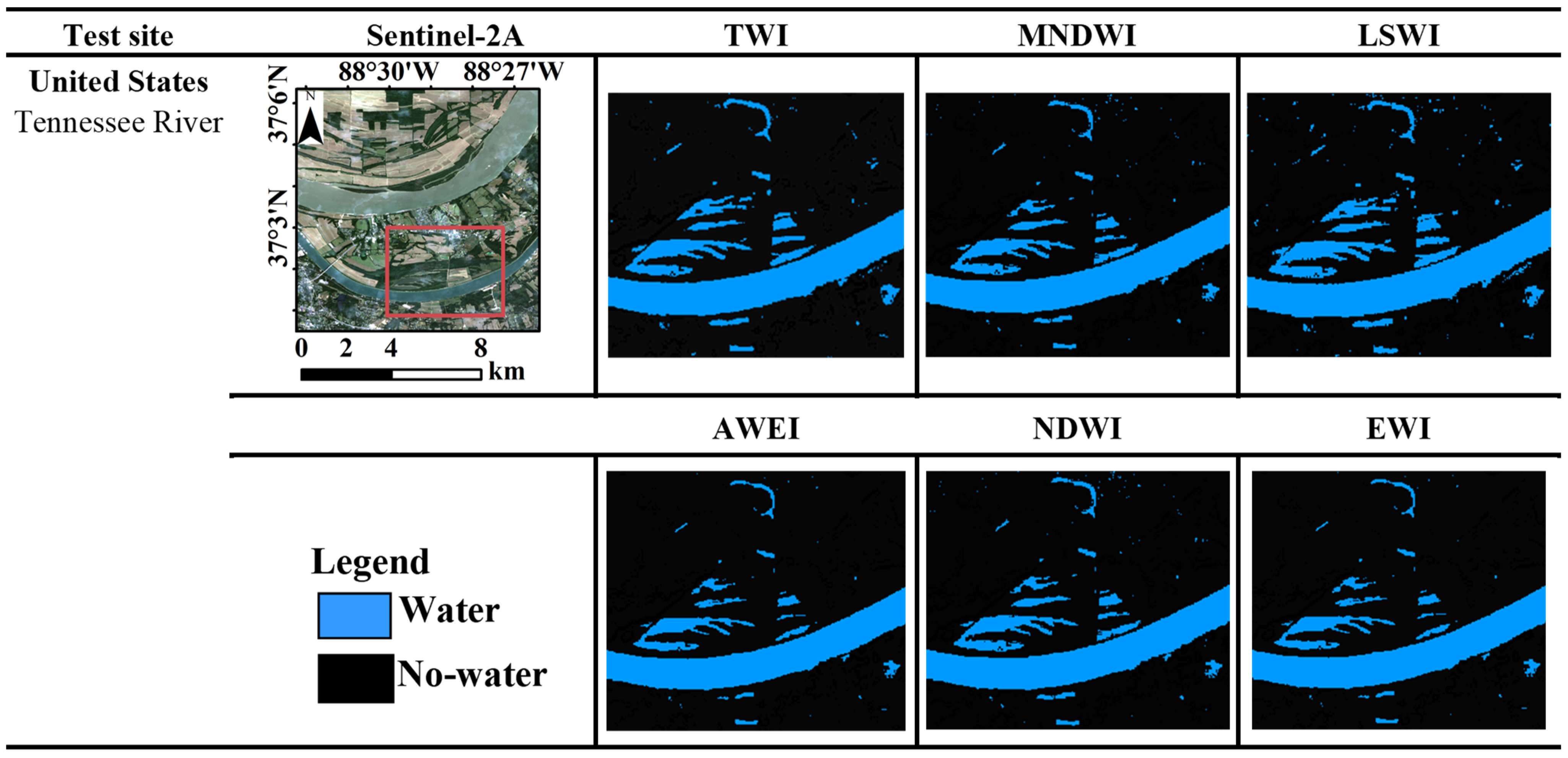


| Countries and Names of Water Bodies | Center Point Coordinates of Test Sites (WGS84) | Topography | Characteristics |
|---|---|---|---|
| Mongolia | |||
| Khar-Us Lake | 47.97°N, 92.22°E | Basin predominantly flat | Freshwater pollution |
| United States | |||
| Tennessee River | 37.06°N, 88.51°W | Predominantly flat | Normal water |
| Canada | |||
| Kellie Creek | 50.65°N,117.78°W | Hills, rugged terrain | Normal water |
| Shuswap Lake | 50.69°N, 119.05°W | Predominantly flat | River surrounded by snow and ice |
| China | |||
| Qinghai Lake | 36.90°N, 100.17°E | Predominantly flat | Inland saltwater |
| East China Sea | 31.27°N, 121.92°E | Flat | Muddy water |
| Huangpu River | 31.02°N, 121.49°E | Freshwater Clear water | |
| Yangtze River | 31.82°N, 121.15°E | Water body including suspended matter | |
| Sweden | |||
| Lungsiön Lake | 62.84°N, 16.24°E | Terrain slopes from northwest to southeast | Water covered by snow and ice. |
| Bands and Description | WR/μm | GSD/m | Main Utility Conc. Water |
|---|---|---|---|
| Band 1—Blue Coastal Aerosol | 0.433–0.453 | 60 | Aerosol monitoring |
| Band 2—Blue | 0.4575–0.5225 | 10 | Relative maximum for phytoplankton in band 3; strong chlorophyll absorptions in bands 2 and 4 |
| Band 3—Green | 0.5425–0.5775 | 10 | |
| Band—Red | 0.65–0.68 | 10 | |
| Band 5—Vegetation Red Edge 1 (VRE 1) | 0.6975–0.7125 | 20 | Blue and red shift phenomenon; iron rich sediments |
| Band 6—Vegetation Red Edge 2 (VRE2) | 0.7325–0.7475 | 20 | |
| Band 7—Vegetation Red Edge 3 (VRE 3) | 0.773-0.793 | 20 | |
| Band 8—Near-Infrared (NIR) | 0.7845–0.8995 | 10 | Reduced reflectance peak of phytopigments; biomass |
| Band 8A—Near-Infrared (VRE 4) | 0.855–0.875 | 20 | |
| Band 9—Water Vapor (WV) | 0.935–0.955 | 60 | Water vapor monitoring |
| Band 10—Shortwave Infrared 1 (SWIR 1) | 1.36–1.39 | 60 | Cirrus clouds detection |
| Band 11—Shortwave Infrared 2 (SWIR 2) | 1.565–1.655 | 20 | Floating sediments, soils |
| Band 12—Shortwave Infrared 3 (SWIR 3) | 2.10–2.28 | 20 |
| Test Site | Sentinel-2 Data | Reference Image on GEE | |
|---|---|---|---|
| Acquisition Data | Season | ||
| Mongolia | Autumn | Google Earth Map data @2021 imagery @2021CNES/Airbus. | |
| Khar-Us Lake | 30 October 2021 | ||
| Canada | Autumn | Google Earth Map data @2021imagery@2021, CNES/Airbus, Landsat/Copernicus | |
| Kellie Creek | 30 September 2021 | ||
| China | |||
| Qinghai Lake | 30 October 2019 | Autumn | Google Earth Map data @2021imagery @2021,CNES/Airbus, Landsat/Copernicus, Maxar Technologies |
| East China Sea | 30 December 2020 | Autumn | Google Earth Map data @2021imagery @2021CNES/Airbus, Maxar Technologies |
| Huangpu River | 30 June 2021 | Summer | Google Earth Map data @2021imagery, @2021CNES/Airbus, Maxar Technologies |
| Yangtze River | 09 June 2020 | Summer | Google Earth Map data @2021imagery@2021, Maxar Technologies, USDA/FPAC/GEO |
| United States | Winter | ||
| Tennessee River | 30 November 2019 | ||
| Sweden | 30 November 2021 | Winter | Google Earth Map data @2021 imagery @2021, Terra Metrics |
| Lungsiön Lake | 09 September 2020 | Autumn | |
| Water Body Index | Canada | United States | Sweden | Mongolia |
|---|---|---|---|---|
| Kappa Coeff. | Kappa Coeff. | Kappa Coeff. | Kappa Coeff. | |
| TWI | 0.940 | 0.929 | 0.926 | 0.897 |
| EWI | 0.923 | 0.873 | 0.913 | 0.847 |
| AWEI | 0.929 | 0.900 | 0.916 | 0.845 |
| LSWI | 0.936 | 0.895 | 0.913 | 0.884 |
| NDWI | 0.936 | 0.929 | 0.882 | 0.857 |
| MNDWI | 0.936 | 0.925 | 0.923 | 0.884 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, L.; Kaufmann, H.; Xu, G.; Zhang, G.; Ji, C.; He, Y.; Sun, M. Triangle Water Index (TWI): An Advanced Approach for More Accurate Detection and Delineation of Water Surfaces in Sentinel-2 Data. Remote Sens. 2022, 14, 5289. https://doi.org/10.3390/rs14215289
Niu L, Kaufmann H, Xu G, Zhang G, Ji C, He Y, Sun M. Triangle Water Index (TWI): An Advanced Approach for More Accurate Detection and Delineation of Water Surfaces in Sentinel-2 Data. Remote Sensing. 2022; 14(21):5289. https://doi.org/10.3390/rs14215289
Chicago/Turabian StyleNiu, Lifeng, Hermann Kaufmann, Guochang Xu, Guangzong Zhang, Chaonan Ji, Yufang He, and Mengfei Sun. 2022. "Triangle Water Index (TWI): An Advanced Approach for More Accurate Detection and Delineation of Water Surfaces in Sentinel-2 Data" Remote Sensing 14, no. 21: 5289. https://doi.org/10.3390/rs14215289
APA StyleNiu, L., Kaufmann, H., Xu, G., Zhang, G., Ji, C., He, Y., & Sun, M. (2022). Triangle Water Index (TWI): An Advanced Approach for More Accurate Detection and Delineation of Water Surfaces in Sentinel-2 Data. Remote Sensing, 14(21), 5289. https://doi.org/10.3390/rs14215289







