Next Article in Journal
Early Monitoring of Cotton Verticillium Wilt by Leaf Multiple “Symptom” Characteristics
Previous Article in Journal
Generative-Model-Based Data Labeling for Deep Network Regression: Application to Seed Maturity Estimation from UAV Multispectral Images
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 14
Issue 20
10.3390/rs14205239
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Estimating PM2.5 Concentrations Using the Machine Learning RF-XGBoost Model in Guanzhong Urban Agglomeration, China

by
Lujun Lin
1,2,†,
Yongchun Liang
1,
Lei Liu
1,2,*,
Yang Zhang
3,†,
Danni Xie
4,
Fang Yin
4 and
Tariq Ashraf
1
1
School of Earth Science and Resources, Chang’an University, Xi’an 710054, China
2
State Key Laboratory of Tibetan Plateau Earth System, Environment and Resources (TPESER), Institute of Tibetan Plateau Research, Chinese Academy of Sciences, Beijing 100101, China
3
School of Human Settlements and Civil Engineering, Xi’an Jiaotong University, Xi’an 710049, China
4
Shaanxi Key Laboratory of Land Consolidation, School of Land Engineering, Chang’an University, Xi’an 710054, China
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Remote Sens. 2022, 14(20), 5239; https://doi.org/10.3390/rs14205239
Submission received: 14 September 2022 / Revised: 13 October 2022 / Accepted: 15 October 2022 / Published: 20 October 2022
Browse Figures
Versions Notes

Abstract

:
Fine particulate matter (PM2.5) is a major pollutant in Guanzhong Urban Agglomeration (GUA) during the winter, and GUA is one of China’s regions with the highest concentrations of PM2.5. Daily surface PM2.5 maps with a spatial resolution of 1 km × 1 km can aid in the control of PM2.5 pollution. Thus, the Random Forest and eXtreme Gradient Boosting (RF-XGBoost) model was proposed to fill the missing aerosol optical depth (AOD) at the station scale before accurately estimating ground-level PM2.5 using the recently released MODIS AOD product derived from Multi-Angle Implementation of Atmospheric Correction (MAIAC), high density meteorological and topographic conditions, land-use, population density, and air pollutions. The RF-XGBoost model was evaluated using an out-of-sample test, revealing excellent performance with a coefficient of determination (R2) of 0.93, root-mean-square error (RMSE) of 12.49 μg/m3, and mean absolution error (MAE) of 8.42 μg/m3. The result derived from the RF-XGBoost model indicates that the GUA had the most severe pollution in the winter of 2018 and 2019, owing to the burning of coal for heating and unfavorable meteorological circumstances. Over 90% of the GUA had an annual average PM2.5 concentrations decrease of 3 to 7 μg/m3 in 2019 compared to the previous year. Nevertheless, the air pollution situation remained grim in the winter of 2019, with more than 65% of the study area meeting the mean PM2.5 values higher than 35 μg/m3 and the maximum reaching 95.57 μg/m3. This research would be valuable for policymakers, environmentalists, and epidemiologists, especially in urban areas.

Graphical Abstract

1. Introduction

PM2.5, or fine particulate matter with aerodynamic diameters of 2.5 μm or less, not only exacerbates photochemical pollution and climate change but also substantially influences human health and quality of life [1]. The increase in concentration of PM2.5 is caused by cases of natural phenomenon, including dust intrusion, volcano eruptions, forest fires, and the everyday life and production activity of mankind [2,3]. China has experienced rapid economic growth in recent years that undoubtedly has contributed to the corresponding increase of PM2.5 concentrations due to intensive human activity and huge industrial emissions [4]. Since 2010, China has successively promulgated the “12th Five-Year Plan” for National Environment Protection [5], the Air Pollution Prevention and Control Action Plan [6], and the Blue Sky Protection Campaign [7] to limit the number of days with high levels of air pollution. China completed 1436 monitoring stations in 338 cities [8], and the number of days with adequate air quality grew by 5.8% countrywide by 2020 compared to 2015 [9]. Nevertheless, some areas in China, such as Beijing-Tianjin–Heibei and Guanzhong Urban Agglomeration (GUA), have still been suffering from PM2.5 pollution, especially the GUA, which was subjected to pollution for approximately 29.4% of all days in 2020 [10], showing that PM2.5 must be monitored continuously and accurately. However, the established PM2.5 observation network cannot fully capture the spatial distribution over large areas because the monitoring stations are primarily located in urban areas. As a result, various models were investigated to estimate ground-level PM2.5 concentrations based on the relationship between satellite remote sensing aerosol optical depth (AOD) and PM2.5 concentrations, frequently in conjunction with meteorological conditions and land use, etc. [11].
Machine learning and deep learning, multiple linear regression and Least Absolute Shrinkage and Selection Operator [12], decision tree [13], Random Forest ([14,15], AdaBoost [16], eXtreme Gradient Boosting (XGBoost) [17,18], Gradient Boost Regression Tree (GBRT) [19], Gradient Boosting Machines (GBM) [20], neural network (Arhami et al., 2013) convolutional neural networks [21,22,23], the Elman Neural Network (ENN) and Back Propagation Neural Network (BPNN) [19], have been increasingly used in recent years to predict PM2.5 concentrations due to their superior capabilities in data mining and excellent model performance, such as improved machine learning algorithms calculating spatial and temporal information as input variables when the models were trained to incorporate spatiotemporal heterogeneity between AOD and PM2.5 [24,25,26,27]. Comparatively, tree-based machine learning, specifically the ensemble algorithm, which includes bagging, boosting, and stacking and can accurately capture non-linear relationships and interactions between predictors, has demonstrated a significant improvement in model performance with higher R2 and lower RMSE and MAE [28]. In particular, XGBoost, as a typical ensemble algorithm, performs efficiently with far fewer resources [9].
Satellite-based AOD, with several spatial and temporal resolutions generated from various sensors using different algorithms, is an extremely useful and indicative variable to assess PM2.5 exposure. The latest AOD product derived from the MAIAC algorithm [29] was increasingly employed due to its high spatial resolution of 1 km × 1 km. The drawback of AOD, which severely restricts the further improvement of model performance, is the considerable number of missing values caused by cloud cover and high surface reflectivity [30]. The association among outputs from the GEOS-Chem model, land-use, and non-missing AOD were explored to predict the missing AOD values, which eventually improved the model performance [22]. In addition, predictions and fusions of MAIAC AOD from Terra and Aqua based on spatial and temporal smoothing [31] and linear regression approaches [15,32] also contributed to the optimization of prediction power. Previous studies have demonstrated that AOD is strongly influenced by natural emissions, meteorological conditions (e.g., temperature, humidity), and anthropogenic pollution [33,34].
In almost all surface PM2.5 exposure estimating models, the meteorological condition is another important variable affecting air pollution formation, transport, and deposition [35], especially in regards to temperature and precipitation [36,37]. However, the spatial resolution of meteorological data was much lower than that of the PM2.5 concentrations maps, which could limit the effect of modeling [20].
This research made an attempt to integrate the RF and XGBoost model to estimate PM2.5 concentrations of GUA where the atmospheric pollution is the most serious in China. The objectives of this study are as follows: (1) to forecast the missing AOD on the monitoring station scale using RF base on the relationship between the existing AOD and factors including meteorology, the Digital Elevation Model (DEM), Global Land Cover (GLC), and People Density (PD), land use (LU), CO, SO2, NO2, and PM10, and to examine the feature importance and select variables using XGBoost before modelling; (2) to generate 1 km PM2.5 concentrations maps and analyze the spatio-temporal variation of PM2.5 in GUA; (3) to investigate the possible causes of PM2.5 pollution to assist with environmental management.

2. Materials and Methods

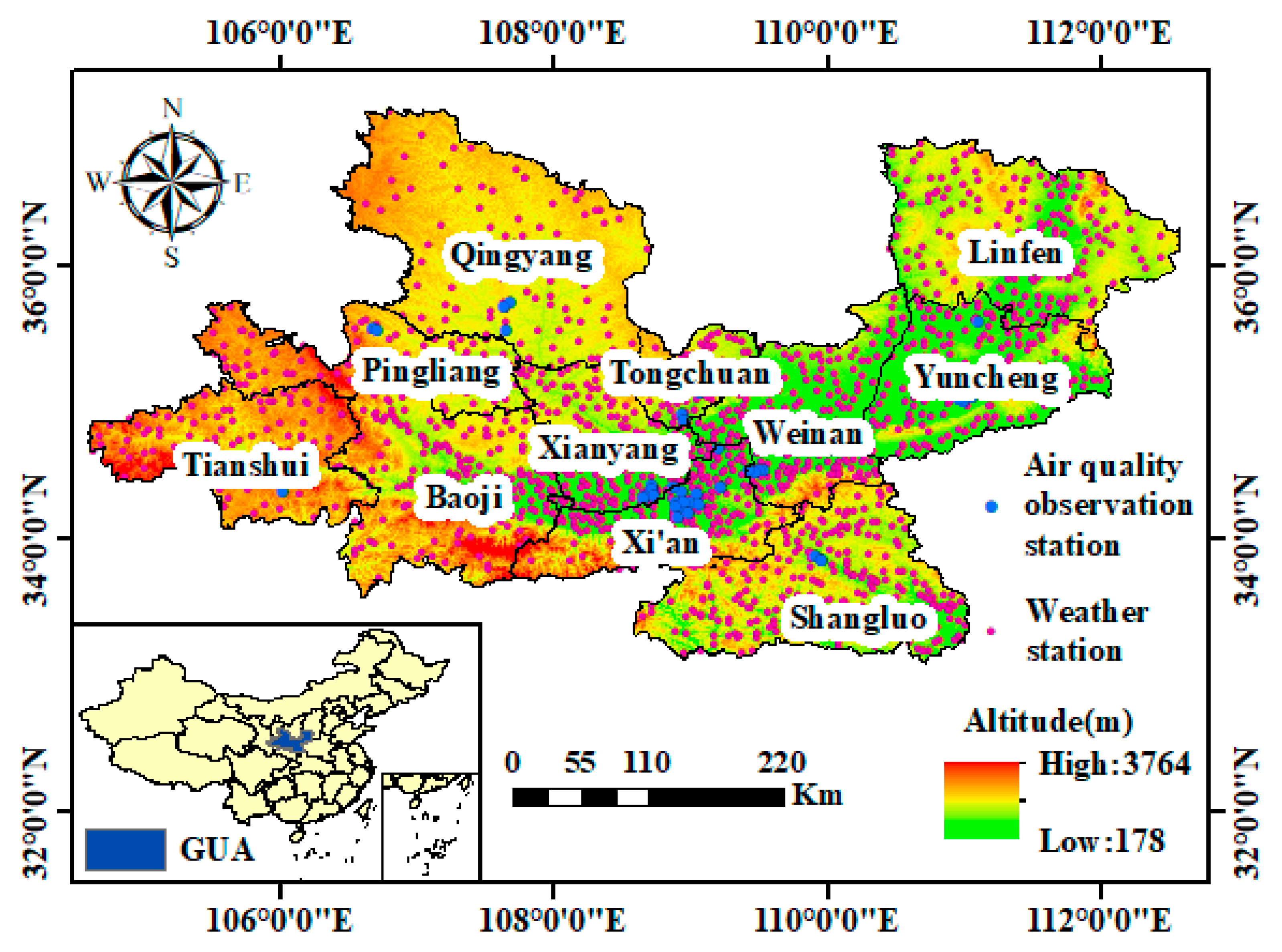
2.1. Study Area

GUA is the largest group located between 33.10° and 37.16° North and 104.58° and 112.57° East in central China, covering western Shanxi Province, the middle part of Shaanxi Province, and eastern Gansu Province (Figure 1). It is characterized by weak atmospheric dispersion [38] due to the embracing of Qinling mountain in the south and Loess Plateau in the north. According to the seventh National Census, the study area has a population of around 41 million people, with one mega-city, Xi’an, and nine medium-sized cities, including Xianyang, Baoji, Weinan, Tongchuan, Linfen, Yuncheng, Qingyang, Pingliang, and Tianshui. The yearly average PM2.5 concentrations in cities throughout GUA exceeds the standards II (35 μg/m3) set by China’s Ministry of Ecology and Environment based on the Bulletin of Ecological Environment from 2018 to 2020.

2.2. Data Source

2.2.1. Ground Measurements

Hourly data for average PM2.5, PM10, SO2, CO, and NO2 mass concentrations for the years 2018–2020 were downloaded from China National Environmental Monitoring Centre (http://www.cnemc.cn (accessed on 15 October 2021)). 56 air pollution stations were unevenly and sparsely distributed in the study area, which were mainly set in urban areas (Figure 1). The missing, abnormal, and repeated values were examined and removed before calculating monthly, seasonal, and yearly mean PM2.5 concentrations.

2.2.2. MODIS AOD

The Terra and Aqua MODIS C6 daily 1-km MCD19A2 products derived from the MAIAC algorithm were employed in this study. The AOD data from 2018 to 2020 were extracted by the PM2.5 monitoring sites from Google Earth Engine (GEE) (https://code.earthengine.google.com (accessed on 15 October 2021)), using the mean value of the three or four bands at the wavelength of 550 nm, and extreme values (above 4) were excluded [22] from modeling. Because of bright surfaces, cloud contamination and extreme values, approximately 69% of the AOD data was missing [39], which greatly impacted the model’s performance.

2.2.3. Meteorological Conditions

The meteorological data of 1677 meteorological observation stations (Figure 1) were provided by Shaanxi Meteorological Bureau (http://sn.cma.gov.cn/ (accessed on 15 October 2021)), which included coordinates, maximum temperature, minimum temperature, average temperature, total precipitation accumulation from 8 pm to 8 pm, total precipitation accumulation from 8 am to 8 am, evaporation, 2-min average wind speed, average relative humidity and sunshine hours (Table 1). Extreme weather related variables, such as 2-min average wind speed greater than 50 m/s and sunshine time greater than 14 h, were excluded from the dataset. The daily meteorological maps were interpolated by inverse distance weight (IDW) method in the python platform with a spatial resolution of 1 km × 1 km and a temporal resolution of 1 day.

2.2.4. Auxiliary Data

Auxiliary data, including DEM, GLC, and PD, were also used to improve the model performance. Both the DEM and the GLC had a spatial resolution of 30 m, obtained from the United States Geological Survey (http://usgs.gov/ (accessed on 15 October 2021)) and Big Earth Data Science Engineering Program (http://www.casearth.com/ (accessed on 15 October 2021)). PD was obtained from GEE with the spatial resolution 0.009° × 0.009°. All the auxiliary data were resampled to the spatial resolution of 1 km × 1 km to match the AOD data.

2.3. Methodology

2.3.1. Data Integration

In this study, the AOD, meteorological conditions, and auxiliary data were reprojected to a uniform projection of WGS84. The coordinates of PM2.5 monitoring sites were used to extract all independent variables across temporal-spatial domain in the python platform. Moreover, the date (day of the year (DOY)) and coordinates were included in the dataset due to the spatial and temporal heterogeneity of PM2.5. Thus, a dataset with 48,548 samples and 21 variables was constituted. However, among the samples, 33,415 samples had no AOD values due to the high reflectance surfaces and clouds.

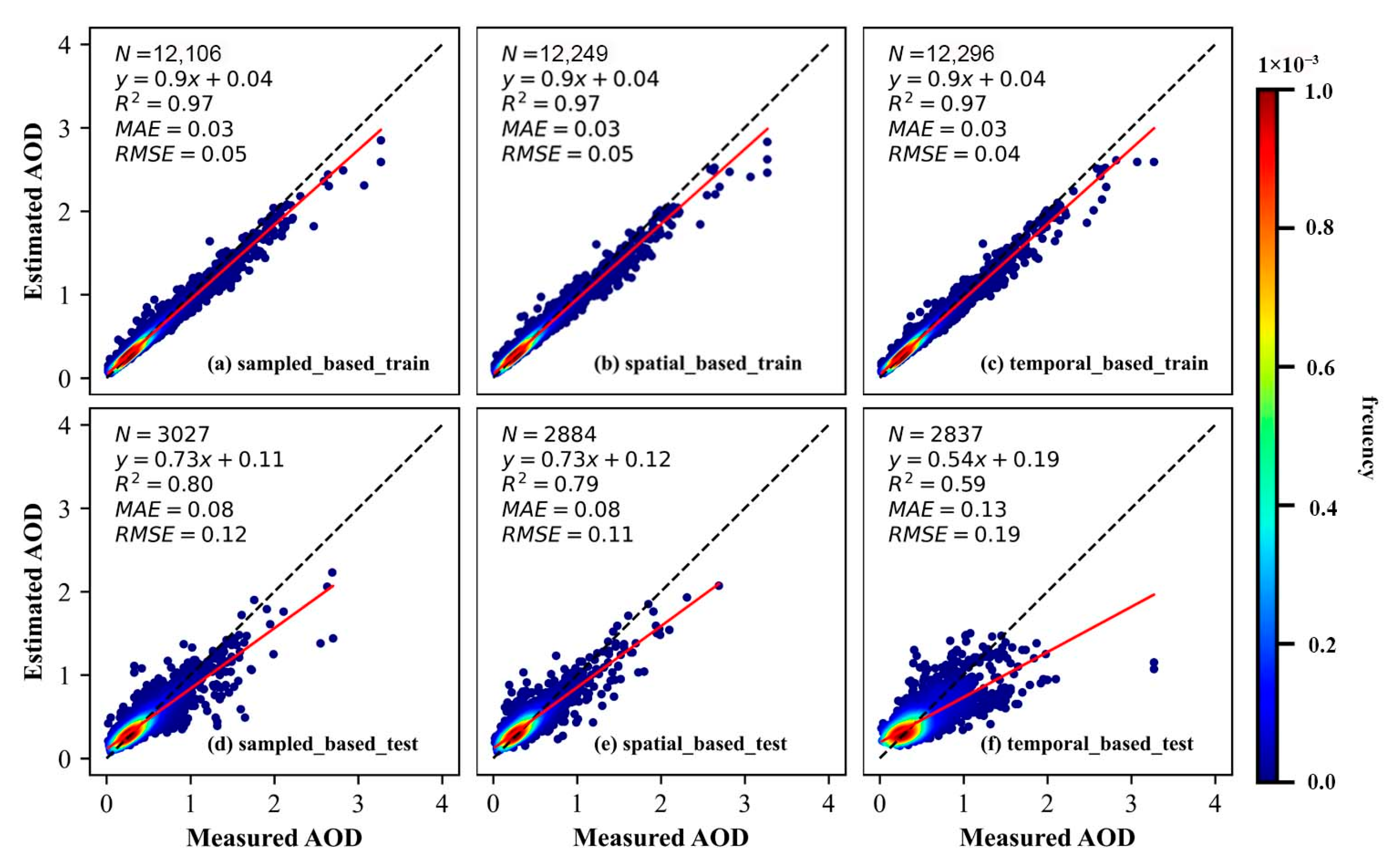
2.3.2. Fill Missing AOD with RF

AOD was influenced by meteorology and land use, according to a prior study [30]. RF, as a machine learning method with randomly sampling and independently building trees, is more robust to noise [40]; thus, it was used to investigate the relationship between AOD and other variables (meteorology, GLC, DEM, and PD).
The dataset was divided into two distinct groups; a group with AOD (GWA) and a group of missing AOD (GMA). The former had 15,133 samples and was used to build an optimal model using RF to estimate AOD values, while the latter applied the optimal model to predict and assign AOD values for the 33,415 samples. The meteorological data, GLC, DEM, PD and air pollution variables (except for PM2.5) were used in both model building and estimation stages for the two groups. Firstly, GWA was randomly split into the training and testing datasets with proportions of 80% and 20%, respectively. Secondly, an initial model was trained using RF with default hyper parameters for the training dataset, in which the AOD was the label (dependent variable) and meteorology, DEM, GLC, LU, PD, CO, SO2, NO2, and PM10 were the features (independent variables). The grid search based on the 10-fold cross-validation approach was then utilized to modify the hyper parameters by comparing the coefficient of determination (R2) of the model. The optimal RF model was obtained when the value of R2 was high and stable. Thirdly, all the data of the testing dataset was input into the optimal RF model to estimate AOD values, which were compared with the measured AOD values by R2, root-mean-square error (RMSE), and intercept and slope of the regression line to evaluate the accuracy of the model. To obtain a model with better generalization, methods such as reducing the number and depth of the trees were adopted to simplify the model when the model was over-fitting. On the contrary, the complexity of the model was increased when the model was under-fitting. Finally, all the data of GMA, including the meteorology, DEM, GLC, LU, PD, CO, SO2, NO2, and PM10 were put into the optimal RF model, and all the missing AOD values were estimated.

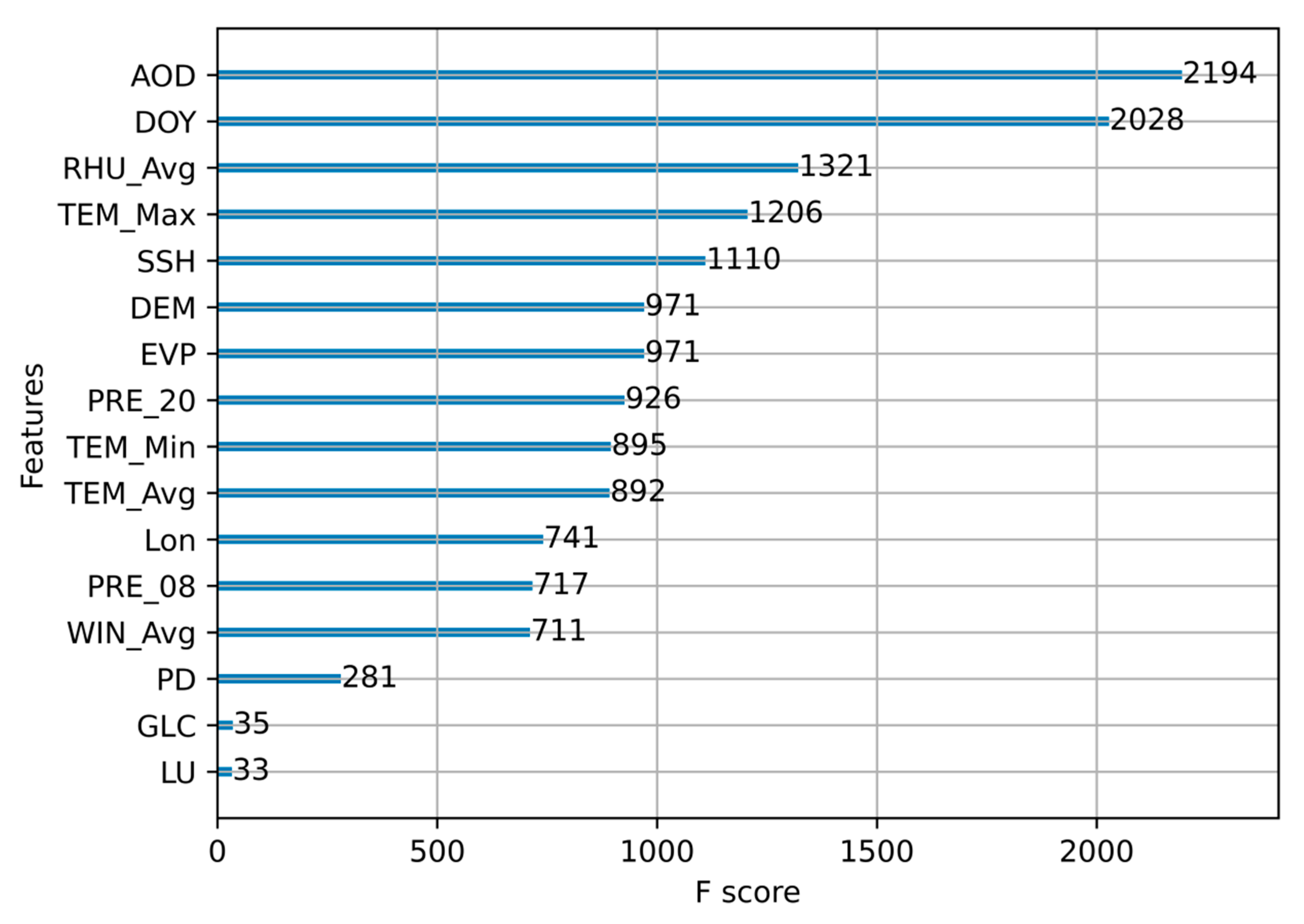
2.3.3. XGBoost Model and Feature Selection

XGBoost, a tree boosting machine learning system, has been widely used by researchers in a wide range of fields with satisfactory results [9]. In particular, during recent years, several studies have applied the XGBoost algorithm for air quality purposes [41,42,43,44]. XGBoost could efficiently prevent over-fitting via three methods—regularized objective, shrinkage, and column subsampling—resulting in more accurate prediction. A regularized objective aids in penalizing complexity and selecting a basic and effective model. Shrinkage reduces the influence of each particular tree and leaves room for future trees to enhance the model. Column subsampling, which is less memory consuming when training a model, is more efficient than row subsampling to avoid over-fitting [40]. For computation efficiency, the exact greedy algorithm combined with a weighted quantile sketch algorithm and a novel sparsity-aware algorithm based on the block structure aids in reducing computation time and memory consumption when developing a model [45]. Nevertheless, the XGBoost model performs well in existing literature compared to other ensemble algorithms, such as RF, GBDT, highly randomized trees (ERT), and GBM.
For all the 48,548 samples, the Pearson correlation coefficients (r) and p_values between the 17 selected variables (AOD, meteorology, DEM, GLC, LU and PD) and PM2.5 concentrations were calculated and analyzed (Table 2). The air quality variables (CO, SO2, NO2, and PM10) were not considered in this step due to the sparsely distributed station. The correlation coefficients between PM2.5 and five variables are positive, most of which are very low particularly for GLC (0.09), LU (0.07), and PD (0.02). The r of satellite-derived AOD was significantly higher than other variables, which is important in estimating PM2.5 (Figure 2). In contrast, the remaining twelve variables show negative correlation coefficients, especially for TEM_AVG, TEM_Min, TEM_Max, and EVP, with r of −0.48, −0.47, −0.47, and −0.35, respectively. The latitude (Lat) variable, with r and p_values of −0.00 and 0.26, was removed from the dataset due to the extremely low correlation between Lat and surface PM2.5 concentrations.
Four steps were implemented to obtain an optimum model for estimating ground-level PM2.5 concentrations. First, the XGBoost model was used to calculate feature importance using all variables with potential influence on surface PM2.5 to preliminarily fit the model and calculate the contribution of each variable, and the feature scores were then re-arranged in descending order (Figure 3). Second, the RMSE and R2 were employed to examine the accuracy of XGBoost model when the features were recursively eliminated as described by previous research [17]. When GLC, PD and LU were removed from the dataset, the model’s performance remained almost constant with only a minor decrease in R2 and RMSE; thus, these three variables were excluded from the XGBoost model and the remaining variables were used to train the model. Third, the dataset was divided into two groups—the first group, with the years 2018–2019, was prepared as the dataset for modeling (DFM), and the second group in 2020 was used as the dataset for predicting (DFP). Fourth, the DFM was split into a sample-based training set and a sample-based testing set with proportions of 80% and 20%, respectively. The training set was used to train and validate the model, while the testing set was used to verify the model. The built-in functions, KFold and CV from the scikit-learn and XGBoost library packages, were used to tune the hyperparameters, which considerably impacted the model’s performance and resilience.

2.3.4. Model Evaluation

In this study, the performance of the RF and XGBoost models was evaluated using the statistical metrics R2, RMSE, and MAE in conjunction with three universally accepted and independent validation approaches, namely sample, spatial, and temporal-based testing. The dataset was randomly split into the sample, spatial, and temporal-based training and testing datasets taking the index, site index, and DOY as basic factors, with the proportions of training and testing sets as 80% and 20%, respectively. The dataset was GWA when verifying the ability of the RF model to estimate AOD, whereas the dataset was DFM when verifying the ability of the XGBoost model to estimate PM2.5 concentrations. The sample, spatial, and temporal-based training datasets were used to train the RF and XGBoost model with the tuned hyper-parameters. In contrast, the testing dataset was used to evaluate the model’s performance, which may lead to a comprehensive understanding of the RF and XGBoost model’s performance. After that, the measured AOD and PM2.5 values were compared with the predicted values by the above metrics and scatter plot with a linear regression line.
The assessment of the XGBoost model is composed of two sections. The first section involves XGBoost model training and testing on the sample, temporal and spatial-based scales. The second phase includes forecasting daily PM2.5 concentrations for 2020 using the XGBoost model and then quantitatively evaluating the algorithm’s predictive power.
The trained RF-XGBoost model was then used to predict PM2.5 concentrations for each grid cell with a spatial resolution of 1 km × 1 km for each day. In addition, the monthly, seasonal, and annual PM2.5 maps were generated by averaging each variable and then inputting the average values into the model.

3. Results

3.1. Model Performance of RF

GWA containing 15,133 samples was used to build an optimal model with RF to estimate AOD values. The best hyper parameters (n_estimators = 300) of RF were obtained by parameter tuning. The amounts of samples among the sample, spatial, and temporal-based training datasets were approximately equal. According to the RF model fitting results, the R2 between measured and estimated AOD is consistent (0.97) for the three datasets, with MAE equal to 0.03 and RMSE values less than 0.05, respectively (Figure 4a–c). Compared to the measured AOD, the estimated AOD has a high regression slope of 0.90 and a small intercept of 0.04. Regarding the RF model testing results, the sample and spatial-based testing datasets also performed well with R2 greater than 0.79, MAE equal to 0.08, and RMSE less than 0.12, respectively (Figure 4d–e). However, the temporal-based testing dataset had lower R2 (0.59) and higher MAE (0.13) and RMSE (0.19), respectively (Figure 4f). Therefore, the RF model can estimate the missing AOD at the station scale using GWA.

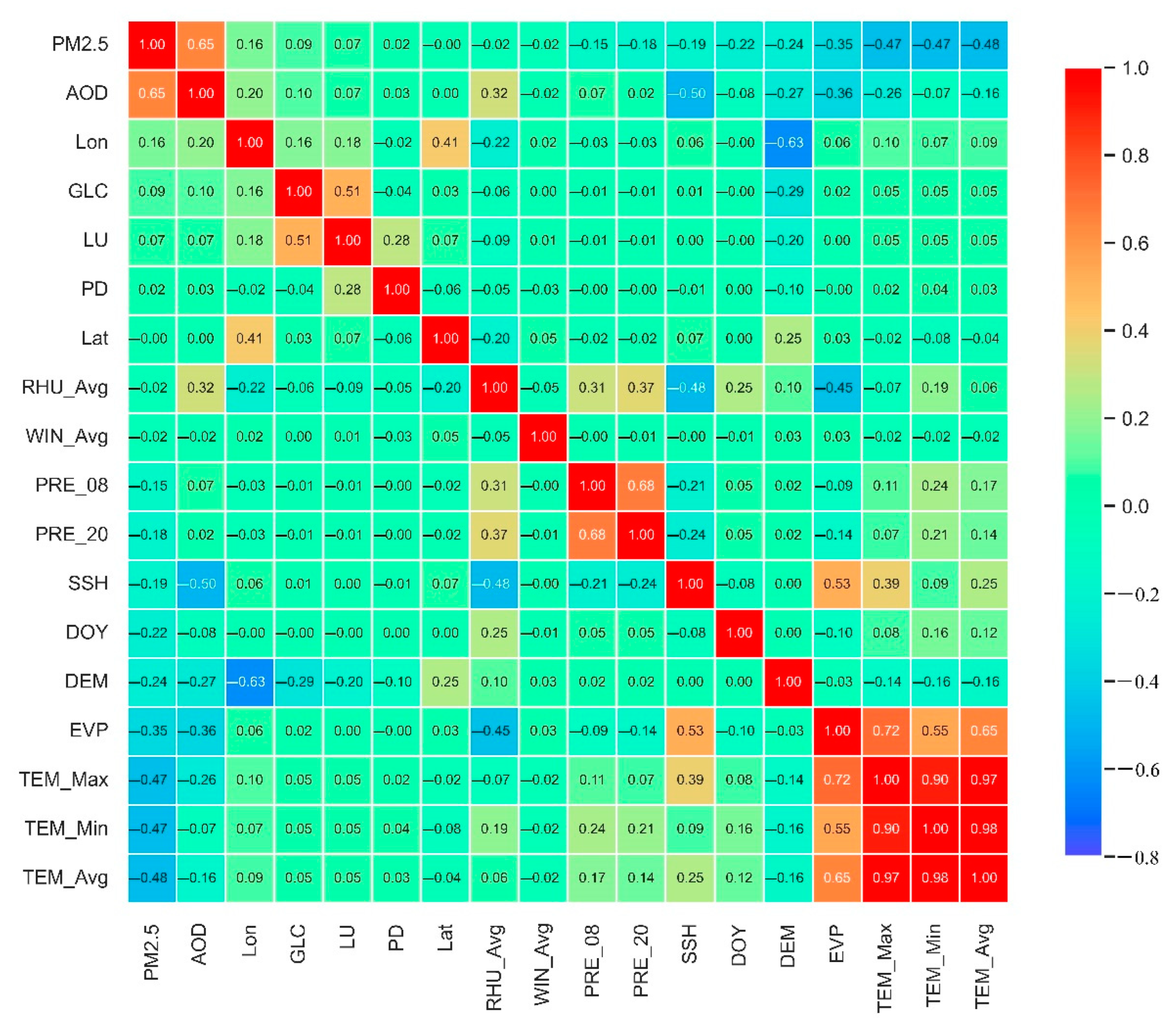
3.2. Statistics of Variables

All the data with 48,548 matched samples for the years 2018–2020 in GUA were plotted in the histograms along with the basic statistics including minimum, maximum, mean, and standard deviation for each variable (Figure 5). The pattern of the daily PM2.5 concentrations were similar to that of the AOD (Wei et al. 2019a), which was consistent with the result of correlation analysis. The annual mean measured PM2.5 concentration was 52.55 ± 45.22 μg/m3 by averaging all ground-based stations in GUA, where the lowest PM2.5 concentration was 26.01 ± 12.86 μg/m3 in summer, and the highest was 91.88 ± 60.31 μg/m3 in winter. The annual AOD after filling the missing values was 0.60. The seasonal mean AODs were 0.54, 0.55, 0.61, and 0.70 in spring, summer, autumn, and winter, respectively (Figure 5), with similar values in spring and summer.

3.3. Model Performance of XGBoost

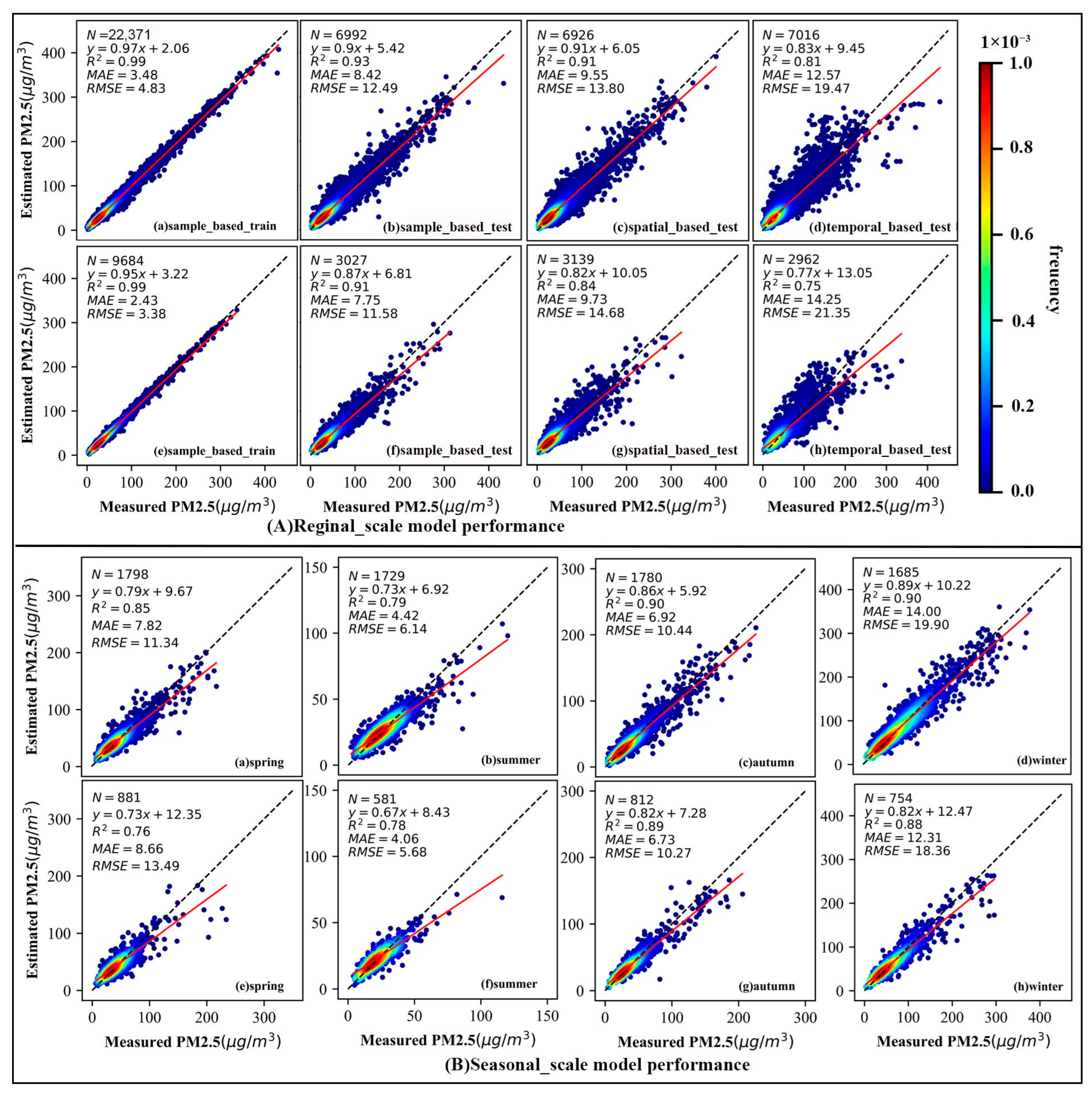
3.3.1. Reginal-Scale Model Performance

The specific values of hyper parameters (num_round = 300, objective = reg:linear, booster = btree, eta = 0.1, max_depth = 9, gamma = 3, colsample_bytree = 0.8, colsample_bylevel = 0.8, alpha = 60, lambda = 2) of the XGBoost model were used in this study by parameter tuning. As shown in Figure 6A, the sample-based training accuracies of the XGBoost model-fitting results have R2 of 0.99 in both DFM and GWA. Figure 6A depicts the density scatterplots of model performance for DFM (Figure 6A (a–d)) and GWA (Figure 6A (e–h)) for 2018–2019 in GUA, using sample-based train, sample, spatial, and temporal-based tests. Because of the spatial and temporal heterogeneity of PM2.5 concentrations, the sample-based test outperformed the temporal-based and spatial-based tests in DFM and GWA, with better R2 and lower MAE and RMSE. On the sample scale, the DFM model showed better performance with higher R2 of 0.93 but lower performance with higher MAE (8.42 μg/m3) and RMSE (12.49 μg/m3) than GWA with R2, MAE, and RMSE of 0.91, 7.75 μg/m3, and 11.58 μg/m3, respectively. On both temporal and spatial scales, DFM performed better with greater R2 and lower MAE and RMSE (Figure 6A). In general, spatial-based model accuracies for both DFM and GWA are significantly higher than temporal-based model accuracies. On the spatial-based scale, the DFM model has an improvement over the GWA model with better R2, MAE, and RMSE of 0.91, 9.55 μg/m3, and 13.80 μg/m3, respectively. The overall R2, MAE, and RMSE values for the DFM model for the temporal-based test were 0.81, 12.57 μg/m3, and 19.47 μg/m3, which are better than the values for the GWA model (R2 = 0.75, MAE = 14.25 μg/m3, RMSE = 21.35 μg/m3), suggesting that DFM with filling the missing AOD has enhanced the model performance (Figure 6A (d, h)). However, according to the researches using machine learning algorithms [26,40], the DFM model tends to slightly underestimate PM2.5 values on extremely polluted days (slope = 0.90, intercept = 5.42).

3.3.2. Seasonal Model Performance

DFM and GWA were split by season for 2018–2019 to test model performance on the sample-based scale in GUA (Figure 6B). For each of the four seasons (spring, summer, autumn, and winter), DFM was separated into 8989, 8643, 8899, and 8425 samples, whereas GWA was divided into 4405, 2903, 4057, and 3768 samples, respectively. Next, we divided each season’s samples into training and testing samples with a 0.2 testing size for each. The test accuracies of the DFM model had higher R2 values (Figure 6B (a–d)) than that of the GWA model for all the four seasons (Figure 6B (e–h)). The models of autumn and winter performed equally well in DFM and GWA, with R2 more than or equal to 0.88, which was higher than models of spring and summer. Because of the heavy pollution of PM2.5 concentrations in winter, the MAE and RMSE values of DFM (14.00 μg/m3 and 19.90 μg/m3) and GWA (14.25 μg/m3 and 21.35 μg/m3,) were significantly higher than the other three seasons. In contrast, the DFM and DFC models had the lowest model performance in summer due to less PM2.5 concentrations, mainly caused by frequent precipitation and high relative humidity. In general, the DFM model performed better than the GWA model for all the four seasons, especially in spring when there is an obvious gap in overall R2, MAE, and RMSE.

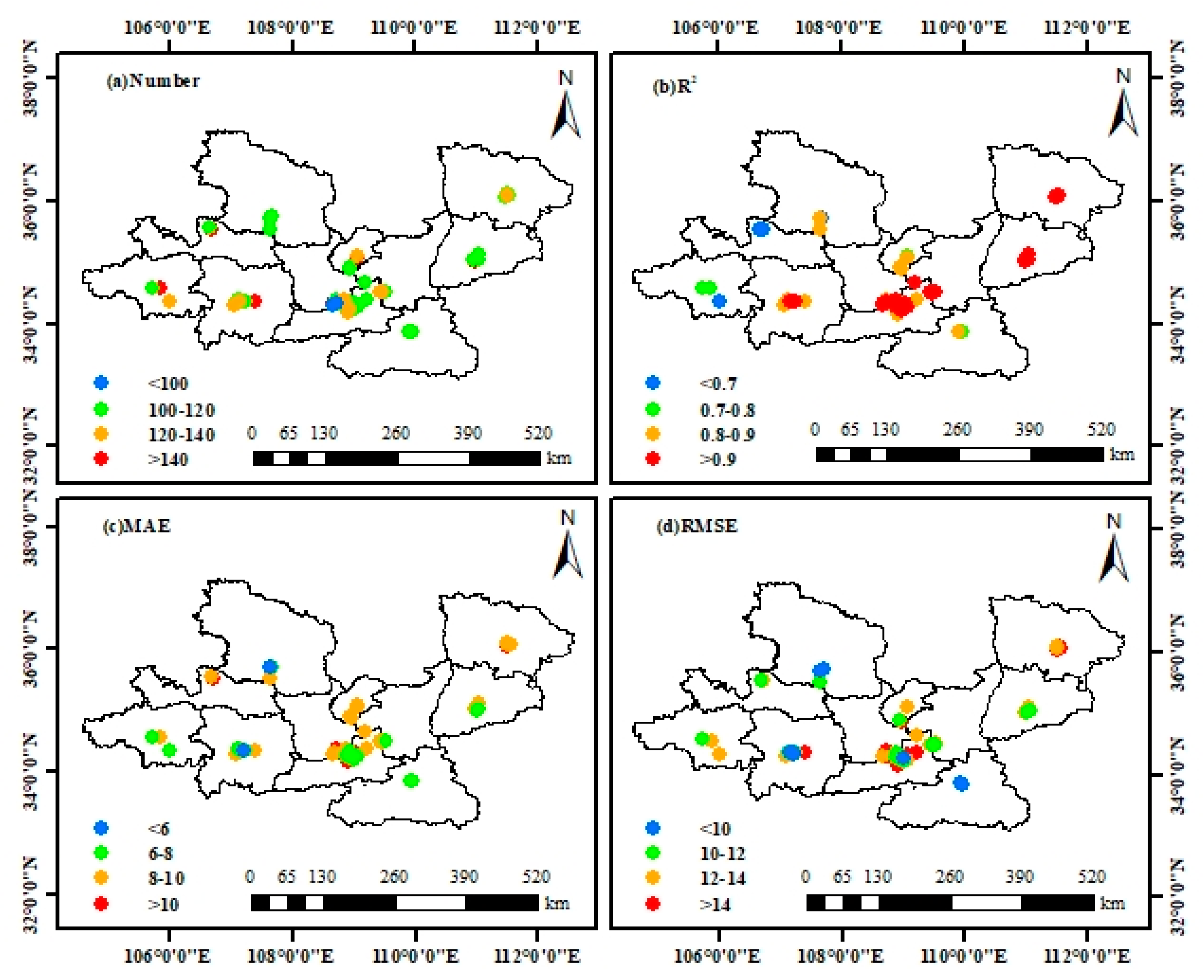
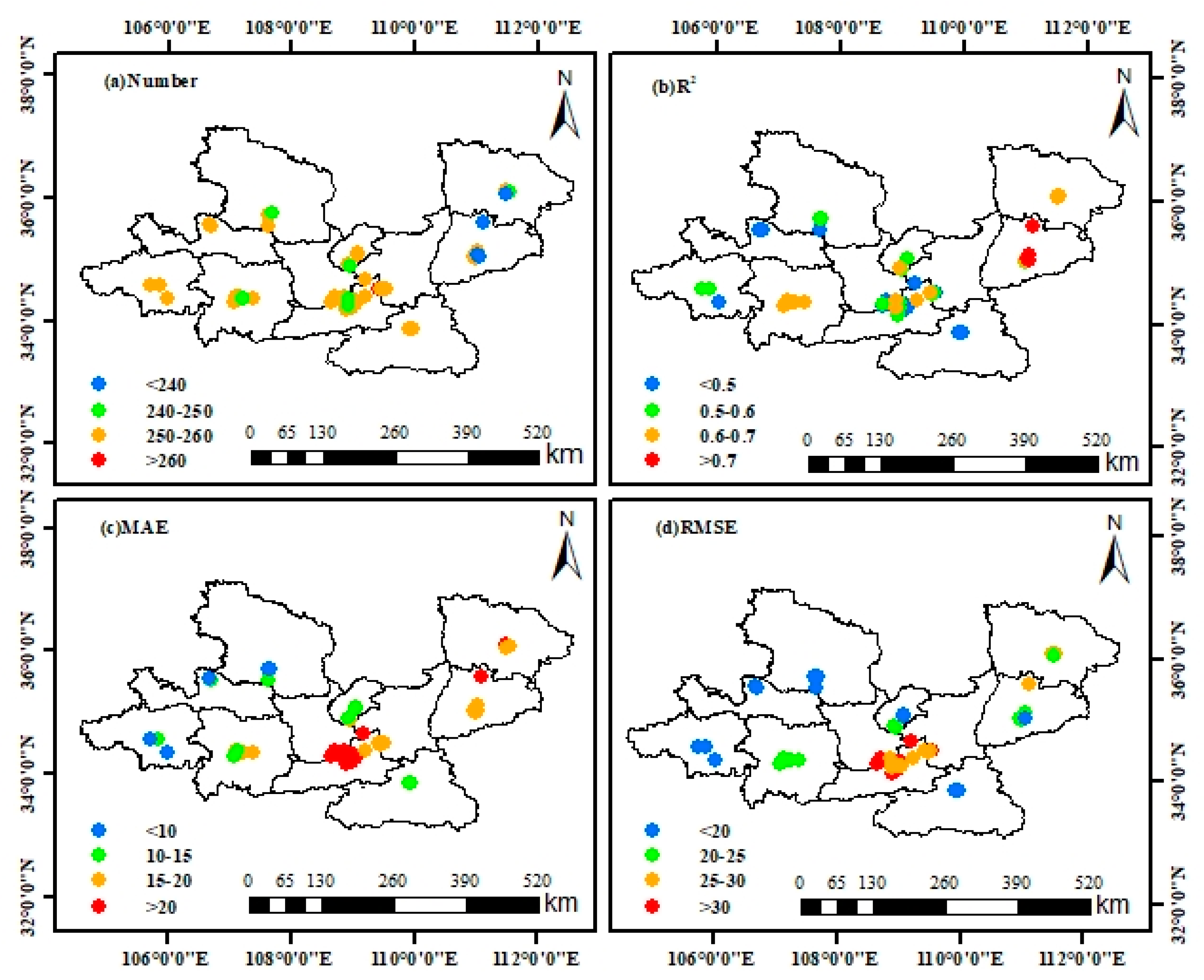
3.3.3. Site-Scale Model Performance

We evaluated the test accuracies of the DFM model at each monitoring station using the sample-based test. The spatial patterns showed that the samples of individual station ranged from 91 to 151, except for a station in Xi’an, which yielded only 31 samples, possibly due to random splitting (Figure 7a). The stations with samples between 100 and 140 were almost 82% of the total stations, indicating that the samples’ distribution was relatively homogeneous. The mean R2 was 0.88, and more than 85% of the stations had a R2 higher than 0.82, particularly in the densely populated hinterland of the Guanzhong basin (GZB). In contrast, R2 was quite low in a few stations located at higher altitudes around the GZB (Figure 7b), likely due to reduced environmental impact from human activities. The distribution of MAE and RMSE were similar (Figure 7c,d), and the average MAE and RMSE in GUA were 8.47 μg/m3 and 12.37 μg/m3, respectively. More than 85% of the monitoring stations had a low prediction error with MAE of less than 10.00 μg/m3 and RMSE less than 15.00 μg/m3. A few stations in Xi’an, Xianyang, and Linfen reported higher prediction errors due to more intensive human activities and considerable pollution emissions. The results revealed that the PM2.5-AOD relationship could be efficiently enhanced by the DFM-trained XGBoost model.

3.4. Model Prediction of XGBoost

The XGBoost model’s predictability in GUA was evaluated using DFM from 2018 to 2019 and DFP in 2020 for model training and prediction. The daily PM2.5 concentrations predicted by the XGBoost model and measured by air pollution stations were compared by analyzing the statistical metrics and the R2, MAE, and RMSE were 0.61, 17.66 μg/m3 and 26.02 μg/m3, respectively. There were a total of 13,493 samples from 56 monitoring stations in DFP, and most of the stations (91%) had more than 240 samples (Figure 8a). More than 42% of the stations had R2 larger than 0.61 (Figure 8b), which were mostly distributed across Linfen, Yuncheng, Weinan, Xianyang, Baoji, and parts of Xi’an. However, the XGBoost model underestimates the high PM2.5 values [19,46,47] and slightly overrates the low PM2.5 concentrations for the stations with R2 less than 0.61. Therefore, the MAE and RMSE were higher in highly polluted areas, such as Xi’an, and the lower MAE and RMSE were correlated with the minute pollution sites of PM2.5.

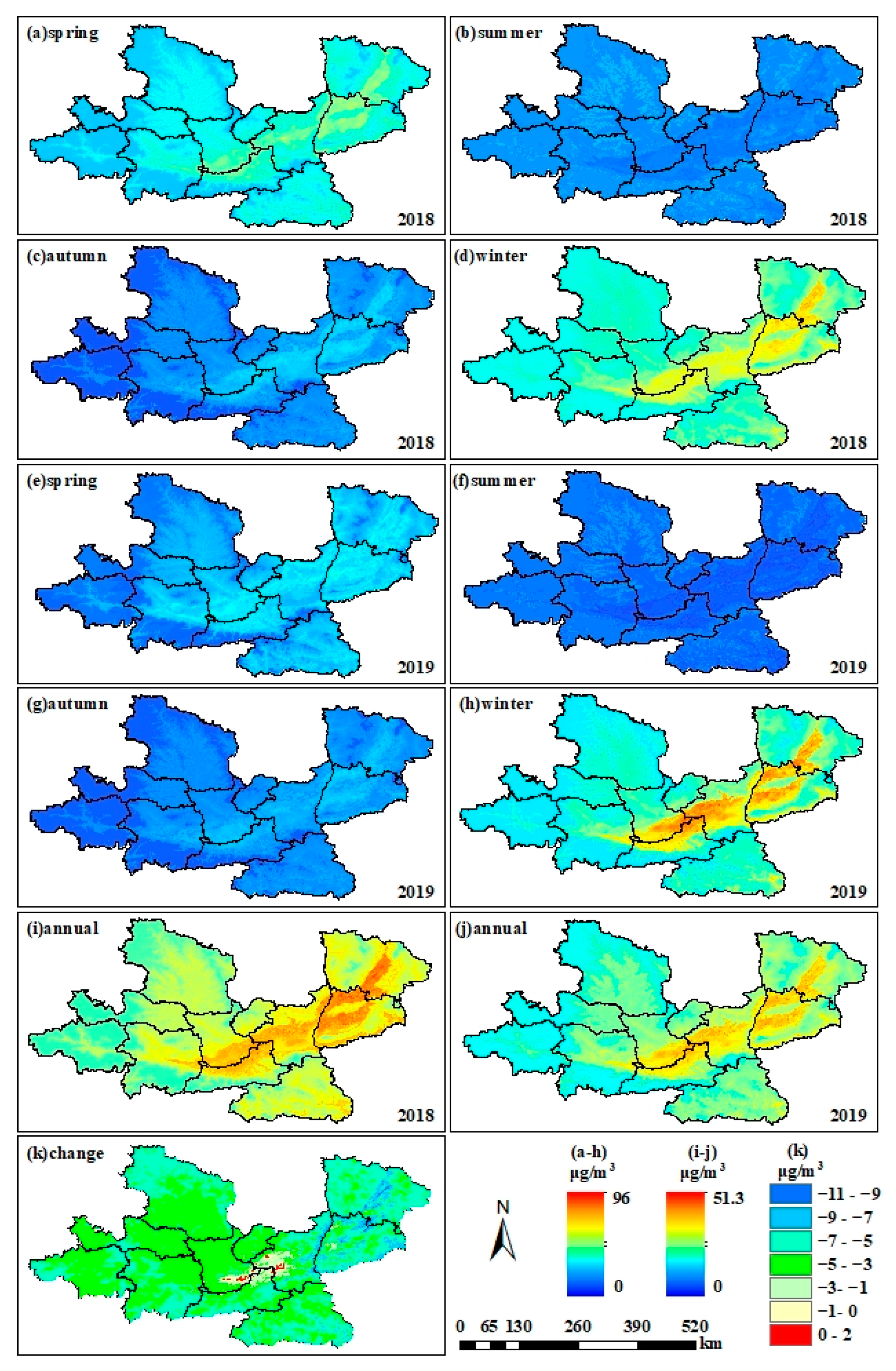
3.5. Seasonal and Annual Distribution of PM2.5

Figure 9 shows the seasonal and annual PM2.5 concentrations distribution with a spatial resolution of 1 km × 1 km, derived from the RF-XGBoost model, demonstrating the temporal and spatial heterogeneity and aggregation. The predicted annual PM2.5 concentrations were spatially consistent with in situ measurements and previous studies [42]. Figure 9a–h depict the spatial distribution of the seasonal mean PM2.5 concentrations calculated by the RF-XGBoost model, illustrating the spatial difference in PM2.5 pollution. Winter always experienced the most serious pollution, with an average PM2.5 value of 42.77 μg/m3 and 42.08 μg/m3 in 2018 and 2019, respectively, followed by spring with PM2.5 values of 32.95 ± 6.62 μg/m3 and 22.03 ± 5.97 μg/m3. Comparatively, the temporal variations of PM2.5 concentrations in summer (17.66 ± 2.41 μg/m3 and 12.85 ± 2.47 μg/m3) and autumn (17.14 ± 5.16 μg/m3 and 16.79 ± 4.28 μg/m3) were relatively low. Compared to 2018, the seasonal average PM2.5 concentrations decreased significantly in 2019, especially in spring, with a reduction of 10.92 μg/m3. However, the air pollution situation was still grim in the winter of 2019, with more than 65% of the study area meeting the mean PM2.5 values > 35 μg/m3 and the maximum reaching 95.57 μg/m3.
The spatial distribution patterns were similar in 2018 and 2019, as shown in Figure 9i–j, with the annual mean PM2.5 concentrations being 29.62 ± 5.97 μg/m3 and 24.63 ± 6.01 μg/m3, respectively. The highest values were consistently found in the plain area of GUA, where Linfen and Yuncheng in the east were subjected to the most severe pollution, followed by the cities of Weinan, Xianyang, and Xi’an when analyzed spatially.
Figure 9k shows the rate of change in annual PM2.5 concentrations from 2018 to 2019 in GUA. Over 99% of the study region showed a decrease in PM2.5 values, with significant reductions (>7 μg/m3) occurring primarily in the east and the greatest decrease being 10.74 μg/m3. Meanwhile, almost 93% of the study area exhibited approximately 3~7 μg/m3 reductions. On the contrary, increasing only occurred in the local areas of Weinan and Xianyang with a growth of less than 2 μg/m3.

4. Discussion

4.1. RF-XGBoost Model Performances

The RF-XGBoost model filled in missing AOD by employing many variables and produced a high sample-based R2 (0.93) in GUA. Furthermore, we investigated the prediction power of the model based on data from 2020 on a daily scale and obtained an R2 of 0.61.
Since the MAIAC AOD was released, a series of models have been proposed to explore the relationship between PM2.5 and MAIAC AOD, along with meteorological conditions and other auxiliary data in China [24,25,27,48,49,50,51], the Middle East [14,52,53], South Africa [15], and USA [54,55,56,57,58,59], mainly due to the high spatial resolution 1 km × 1 km. The predictive power of the model is essentially important for the usability of the model in the future; however, only a few studies have evaluated the predictive power using the dataset acquired before or after the modeling and testing datasets [25].
There are a series of novelties and advantages of the adopted RF-XGBoost model compared to previous studies (Table 3) that used MAIAC AOD as an explanatory factor for ground-level PM2.5 concentrations. First, the tentative fill of missing AOD by RF could effectively increase the sample size, and removing the variables having a negligible correlation to PM2.5 concentrations by XGBoost can simplify the dataset. This approach proposed in our study is versatile and has significantly improved the model performance. In terms of R2, the adopted RF-XGBoost model not only surpassed the statistical regression models [57] including the GAM model [60], the GWR model [25], and Multiple Linear Regression (MLR) [54,55], but also performed slightly better than machine and deep learning approaches, e.g., RF models [52], improved random forest [27], space-time random forest [26], GBM [56], Gradient Boosting Descent Tree [48], XGBoost models [53,59], space-time extremely randomized trees [25], Deep Belief Network [53], and some ensemble models [50,58].
Second, the high-density meteorological measurements used for modeling contributed to the high model performance. The atmospheric environment is very complex [24], and PM2.5 concentrations usually change along with weather conditions. In this research, there are 1677 meteorological stations for the area of 161,526 km2. According to research based on statistics between PM2.5 and each meteorological variable in the study area, pollution decreased sharply when cumulative precipitation values reached 0.30 mm. TEM_Avg between −5~15 °C and RHU_Avg between 50%~80% may lead to high pollution. EVP greater than 5 mm and WIN_Avg larger than 2 m/s contributed to the dispersion of PM2.5. Therefore, informative meteorology promoted our RF-XGBoost model to predict the ground-level PM2.5 concentrations accurately.
Third, the selected RF-XGBoost model was applied to daily PM2.5 concentrations in 2020 based on 13,493 data samples for model prediction with an R2 of 0.61, which is superior to the existing models [25]. The predicted R2 of all models was lower than the validation R2 mainly because the change in meteorological conditions was exceedingly complicated. The models trained based on meteorological conditions could not capture all weather conditions during the study period. Therefore, it’s more appropriate to train the model based on meteorological conditions simultaneously to estimate PM2.5 concentrations. Another contributory factor was the COVID-19 restrictions which greatly reduced the emission of PM2.5 from the sources of industry, traffic, etc. [61,62,63]. The COVID-19, especially the lockdown of the whole country in February 2020, had significantly reduced the primary emissions from the sources, including industrial operations, motor vehicle exhaust, construction operations, and smoke from restaurants, which were the major emission sources that cause air pollution [61]. As the petrochemical industry, construction industry, and facility manufacturing were strongly affected and hampered by both the upstream and downstream chains, all other industries were almost brought to a standstill, which led to lowered PM2.5 emission [62]. The large reductions in vehicular emissions due to the sharp decline in vehicle and public transport can effectively mitigate air pollution in megacities [63]. Therefore, the PM2.5 concentrations during COVID-19 restrictions were much lower than previous years in the same time period, which made it difficult to predict.
A comparison between the results from RF-XGBoost and the dataset from the methodology developed by Donkelaar in 2021 [64] showed that the changing tendency of spatial and temporal distribution of PM2.5 concentrations was consistent. The benefits of the RF-XGBoost model are that (1) the spatial resolution is 1 km × 1 km which showed more detail information of spatial distribution of PM2.5 concentrations; (2) the values of PM2.5 concentrations are more accurate compared with observations from ground stations averaged by monthly and annual means. On the contrary, the limitations are that (1) the RF-XGBoost model did not consider the representation of physics, chemistry, and transport within the atmosphere; (2) the RF-XGBoost model did not evaluate the uncertainty of PM2.5 concentrations. Another limitation of the RF-XGBoost model is underestimating PM2.5 in high pollution days and overestimating for low values, similar to most of the PM2.5 estimation models based on machine learning [15,25,27,65,66]. Several theories have been presented [25] to explain why the limitation of PM2.5 models occurred, in which the small number of high-pollution samples was the main factor, limiting the model’s learning capacity. For example, only 735 samples, less than 2% of all samples of DFM, have PM2.5 concentrations greater than 200 μg/m3.

4.2. Comparision with Other Ensemble Models

As demonstrated in Section 2.3, the combination of RF and XGBoost was used to fill the missing AOD at the station scale and then accurately estimate ground-level PM2.5. Moreover, the RF-XGBoost model was compared with other ensemble models after the datasets and hyper parameters were pre-processed for RF-XGBoost and other ensemble models. Firstly, some features of GWA were removed and the remaining features were AOD, SSH, TEM_Avg, TEM_Max, TEM_Min, RHU_Avg, PRE_20, PRE_08, WIN_Avg, EVP, DOY, Lon, and DEM, which were consistent with the features of DFM and DFP that were used to evaluate the model performance of RF-XGBoost. Secondly, GWA was divided into two groups; the first group with the years 2018–2019 was prepared as the dataset for training and testing ensemble models with 12,368 samples, and the second group of 2020 with 2765 samples was used as the dataset for predicting. Third, DFM and DFP obtained by filling missing AOD with RF model were used to evaluate RF-XGBoost, where DFM with the years 2018–2019 with 34,956 samples was used to train and test, and DFP with the year 2020 with 13,493 samples was used to validate the model prediction. Finally, we tuned hyper parameter n_estimators = 300, the number of estimator being 300, for models used to compare and evaluate the model performance.
The RF, ETR, and GBDT were imported from the scikit-learn package, while the XGBoost and LightGBM were imported from independent packages, respectively. Among the five ensemble models, RF and ERT models are derived from “Bagging” that each tree in the ensemble is built from a sample drawn with replacement from the training set, which works best with strong and complex models. On the contrary, GBDT, XGBoost and LightGBM are derived from “Boosting” that synthesizes multiple interdependent and related weak estimators into a strong estimator [67], which usually work best in weak models. Table 4 shows the accuracies and efficiencies of five ensemble models used for estimating ground-level PM2.5 in GUA with the same dataset and estimators. In terms of time consumption, the training speed of XGBoost and LightGBM is much faster than other models, especially the LightGBM which just took less than 0.005 s. From a memory consumption perspective, models based on the Boosting algorithm are less memory-consuming because they work in serial, which does not consume much memory. The RF-XGBoost model was the most time and memory-consuming because of the filling of missing AOD in the first step and then estimating PM2.5. Models in Table 4 performed well due to the combining of 300 weak estimators. Among them, ERT and LightGBM showed high estimation accuracy, whereas RF and ERT showed high prediction accuracy. The RF-XGBoost model showed the highest R2 for the out-of-sample test and the second highest R2 for predicting PM2.5 in 2020, along with RMSE and MAE that were lower than other approaches considered.

4.3. Reasons for PM2.5 Pollution in the GZB

PM2.5 distribution from the RF-XGBoost model demonstrated that the areas exceeding the secondary national air quality standard (35 μg/m3) significantly decreased from ~18% in 2018 to ~9% in 2019 (Figure 9i,j). The values for the entire yearly PM2.5 concentrations in Shaanxi province in 2015 were greater than 35 μg/m3 [51]; thus, the air quality has been dramatically improved due to the significant factors, especially the Three-Year Blue-Sky Action Plan initiated in 2018 and the air pollution control implemented by various levels of government in recent years. However, the GZB in GUA consistently had the highest levels of PM2.5 pollution.
As mentioned above, winter always experienced serious pollution mainly due to burning coal for heating, which has been listed as one of the primary causes of air pollution. While the transport of PM2.5 was from the neighboring provinces of Shanxi and Henan [68], even the North China Plain [69] was another contributor to air pollution caused by easterly winds in winter. Generally, convergence between southeast winds from a subtropical anticyclone and northwest winds from Siberian high forms a stable warm high at the surface layer and further forms an apparent low wind speed area over the GBZ, making it difficult for the pollutants to be evacuated from GBZ. GBZ, on the other hand, always had a lengthy high-pressure system in the winter [70], which readily led to temperature inversion layers and stable temperature stratification, which is not favorable for the diffusion and diluting of pollutants [71]. In addition, the inversion limits the planetary boundary layer’s diurnal evolution, reducing the vertical transmission of pollutants [72]. The descending mountain breeze from the Loess Plateau and Qinling Mountains not only carried pollutants into the basin but also created a convergence zone that accumulated air pollution due to the cooling of mountainous areas at night [73]. The frequent and varied degree of dusty weather in spring may have polluted the air in GBZ, which could explain the average PM2.5 value of 32.95 μg/m3 in 2018.
The meteorological conditions between summer and winter showed a significant difference that affected the PM2.5 concentrations, especially temperature, relative humidity, and precipitation [74,75,76]. Among them, rainfall was the main factor, with more than 3.2 mm daily in summer and less than 0.15 mm in winter, efficiently scavenging PM2.5. Meanwhile, high temperatures in summer (daily mean temperature of 24.95 °C) brought a series of intense thermal activities in the atmosphere, promoting the dispersion of PM2.5 [73]. Moreover, high relative humidity in summer (daily mean relative humidity of 68.6%) affected both the particle diameter [77] and optical properties [76], which led to the aggregation of PM2.5 particles. PM2.5 concentrations in particles decreased through dry and wet depositions [78] when aggregation grew with a certain weight.

5. Conclusions

The MAIAC AOD, with a spatial resolution of 1 km ×1 km, was extensively used to estimate ground-level PM2.5 concentrations; however, the missing AOD caused by cloud cover and high surface reflectivity severely restricted the further improvement of model performance. Therefore, the RF-XGBoost pipeline is proposed, which employs an RF regression to boost the number of samples by filling the missing AOD on the station scale, improving training capacity. The built-in function of XGBoost regression is used to analyze feature importance, select variables, and then non-linearly investigate the link between PM2.5 and AOD after filling, together with high-density meteorological fields, spatiotemporal information, and auxiliary variables. The sample-, spatial-, and temporal-based test approaches are applied to examine the model performance. The relevant statistics, machine learning, and deep learning models are also collected for comparison.
The RF-XGBoost model significantly improved the estimation of ground-level PM2.5 concentrations in GUA with test R2, RMSE, and MAE of 0.93, 12.49 μg/m3, and 8.42 μg/m3, respectively, which surpasses all of the statistics and deep learning models and outperforms most of the machine learning models presented in existing studies. Meanwhile, The RF-XGBoost model has an advanced level of prediction with an R2 of 0.61. The seasonal and annual PM2.5 concentrations distribution from the RF-XGBoost model reveal that winter always experiences the most serious pollution, followed by spring, and PM2.5 concentrations in 2019 significantly decreased compared to 2018. The daily ground-level PM2.5 concentrations product with a spatial resolution of 1 km × 1 km in GUA can be accurately generated using the RF-XGBoost model, which can assist researchers working in environmental protection and epidemiological domains, particularly in urban areas.

Author Contributions

L.L. (Lujun Lin): Investigation, Writing—Original draft preparation, Methodology, Formal analysis, Validation, Data Curation. Y.L.: Investigation, Writing—Original draft preparation. L.L. (Lei Liu): Conceptualization, Resources, Writing—Review & Editing, Supervision, Project administration. Y.Z.: Investigation, Supervision. D.X.: Supervision, Writing—Review & Editing, Funding acquisition. F.Y.: Conceptualization, Supervision, Funding acquisition. T.A.: Writing—Review & Editing. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Open Research Fund of TPESER [grant number TPESER202208]; the National Natural Science Foundation of China [grant number 42071258]; the Natural Science basic Research Program of Shaanxi Province [grant numbers 2022JQ-240].

Data Availability Statement

The dataset is available on reasonable request from the corresponding author.

Acknowledgments

We thank the participants of this study for their valuable contributions.

Conflicts of Interest

There are no conflicts of interest in submitting this manuscript, and it has been approved for publication by all of the authors.

References

  1. Lelieveld, J.; Evans, J.S.; Fnais, M.; Giannadaki, D.; Pozzer, A. The contribution of outdoor air pollution sources to premature mortality on a global scale. Nature 2015, 525, 367–371. [Google Scholar] [CrossRef] [PubMed]
  2. Lu, D.; Xu, J.; Yue, W.; Mao, W.; Yang, D.; Wang, J. Response of PM2.5 pollution to land use in China. J. Clean. Prod. 2019, 244, 118741. [Google Scholar] [CrossRef]
  3. Rushingabigwi, G.; Nsengiyumva, P.; Sibomana, L.; Twizere, C.; Kalisa, W. Analysis of the atmospheric dust in Africa: The breathable dust’s fine particulate matter PM2.5 in correlation with carbon monoxide. Atmos. Environ. 2020, 224, 117319. [Google Scholar] [CrossRef]
  4. Li, G.; Fang, C.; Wang, S.; Sun, S. The Effect of Economic Growth, Urbanization, and Industrialization on Fine Particulate Matter (PM2.5) Concentrations in China. Environ. Sci. Technol. 2016, 50, 11452–11459. [Google Scholar] [CrossRef] [PubMed]
  5. China National Environmental Monitoring Centre. Notice About Monitoring According to National Air Monitoring Net “12th Five-Year Plan”. 2012. Available online: http://www.cnemc.cn/gzdt/wjtz/201204/t20120419_648459.shtml (accessed on 15 March 2022). (In Chinese).
  6. Chinese State Council. National Environment Protection “12th Five-Year Plan”. 2011. Available online: http://www.gov.cn/zwgk/2011-12/20/content_2024895.htm (accessed on 15 March 2022). (In Chinese)
  7. Chinese State Council. Action Plan on Air Pollution Prevention and Control. 2013. Available online: http://www.gov.cn/zwgk/2013-09/12/content_2486773.htm (accessed on 15 March 2022). (In Chinese)
  8. Chinese State Council. Three-Year Action Plan on Defending the Blue Sky. 2018. Available online: http://www.gov.cn/zhengce/content/2018-07/03/content_5303158.htm (accessed on 15 March 2022). (In Chinese)
  9. Chen, T.; Guestrin, C. XGBoost. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining—KDD’16, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
  10. Ministry of Ecology and Environment the People’s Republic of China. 2020 Bulletin of China’s Ecological Environment. 2021. Available online: https://www.mee.gov.cn/hjzl/sthjzk/zghjzkgb/202105/P020210526572756184785.pdf (accessed on 15 March 2022). (In Chinese)
  11. Sorek-Hamer, M.; Chatfield, R.; Liu, Y. Review: Strategies for using satellite-based products in modeling PM2.5 and short-term pollution episodes. Environ. Int. 2020, 144, 106057. [Google Scholar] [CrossRef] [PubMed]
  12. Xu, Y.; Ho, H.C.; Wong, M.S.; Deng, C.; Shi, Y.; Chan, T.C.; Knudby, A. Evaluation of machine learning techniques with multiple remote sensing datasets in estimating monthly concentrations of ground-level PM2.5. Environ. Pollut. 2018, 242 Pt B, 1417–1426. [Google Scholar] [CrossRef]
  13. Zuo, X.; Guo, H.; Shi, S.; Zhang, X. Comparison of Six Machine Learning Methods for Estimating PM2.5 Concentration Using the Himawari-8 Aerosol Optical Depth. J. Indian Soc. Remote Sens. 2020, 48, 1277–1287. [Google Scholar] [CrossRef]
  14. Li, J.; Garshick, E.; Hart, J.E.; Li, L.; Shi, L.; Al-Hemoud, A.; Huang, S.; Koutrakis, P. Estimation of ambient PM2.5 in Iraq and Kuwait from 2001 to 2018 using machine learning and remote sensing. Environ. Int. 2021, 151, 106445. [Google Scholar] [CrossRef]
  15. Zhang, D.; Du, L.; Wang, W.; Zhu, Q.; Bi, J.; Scovronick, N.; Naidoo, M.; Garland, R.M.; Liu, Y. A machine learning model to estimate ambient PM2.5 concentrations in industrialized highveld region of South Africa. Remote Sens. Environ. 2021, 266, 112713. [Google Scholar] [CrossRef]
  16. Chen, J.; Yin, J.; Zang, L.; Zhang, T.; Zhao, M. Stacking machine learning model for estimating hourly PM2.5 in China based on Himawari 8 aerosol optical depth data. Sci. Total Environ. 2019, 697, 134021. [Google Scholar] [CrossRef]
  17. Joharestani, M.Z.; Cao, C.; Ni, X.; Bashir, B.; Talebiesfandarani, S. PM2.5 Prediction Based on Random Forest, XGBoost, and Deep Learning Using Multisource Remote Sensing Data. Atmosphere 2019, 10, 373. [Google Scholar] [CrossRef] [Green Version]
  18. Just, A.C.; De Carli, M.M.; Shtein, A.; Dorman, M.; Lyapustin, A.; Kloog, I. Correcting Measurement Error in Satellite Aerosol Optical Depth with Machine Learning for Modeling PM2.5 in the Northeastern USA. Remote Sens. 2018, 10, 803. [Google Scholar] [CrossRef] [Green Version]
  19. Tian, H.; Zhao, Y.; Luo, M.; He, Q.; Han, Y.; Zeng, Z. Estimating PM2.5 from multisource data: A comparison of different machine learning models in the Pearl River Delta of China. Urban Clim. 2020, 35, 100740. [Google Scholar] [CrossRef]
  20. Zeng, Z.; Gui, K.; Wang, Z.; Luo, M.; Geng, H.; Ge, E.; An, J.; Song, X.; Ning, G.; Zhai, S.; et al. Estimating hourly surface PM2.5 concentrations across China from high-density meteorological observations by machine learning. Atmospheric Res. 2021, 254, 105516. [Google Scholar] [CrossRef]
  21. Zheng, T.; Bergin, M.H.; Hu, S.; Miller, J.; Carlson, D.E. Estimating ground-level PM2.5 using micro-satellite images by a convolutional neural network and random forest approach. Atmos. Environ. 2020, 230, 117451. [Google Scholar] [CrossRef]
  22. Di, Q.; Kloog, I.; Koutrakis, P.; Lyapustin, A.; Wang, Y.; Schwartz, J. Assessing PM2.5 Exposures with High Spatiotemporal Resolution across the Continental United States. Environ. Sci. Technol. 2016, 50, 4712–4721. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  23. Sun, K.; Tang, L.; Qian, J.; Wang, G.; Lou, C. A deep learning-based PM2.5 concentration estimator. Displays 2021, 69, 102072. [Google Scholar] [CrossRef]
  24. Li, X.; Zhang, X. Predicting ground-level PM2.5 concentrations in the Beijing-Tianjin-Hebei region: A hybrid remote sensing and machine learning approach. Environ. Pollut. 2019, 249, 735–749. [Google Scholar] [CrossRef] [Green Version]
  25. Wei, J.; Li, Z.; Cribb, M.; Huang, W.; Xue, W.; Sun, L.; Guo, J.; Peng, Y.; Li, J.; Lyapustin, A.; et al. Improved 1 km resolution PM2.5 estimates across China using enhanced space–time extremely randomized trees. Atmos. Chem. Phys. 2020, 20, 3273–3289. [Google Scholar] [CrossRef] [Green Version]
  26. Wei, J.; Huang, W.; Li, Z.; Xue, W.; Peng, Y.; Sun, L.; Cribb, M. Estimating 1-km-resolution PM2.5 concentrations across China using the space-time random forest approach. Remote Sens. Environ. 2019, 231, 111221. [Google Scholar] [CrossRef]
  27. Chen, W.; Ran, H.; Cao, X.; Wang, J.; Teng, D.; Chen, J.; Zheng, X. Estimating PM2.5 with high-resolution 1-km AOD data and an improved machine learning model over Shenzhen, China. Sci. Total Environ. 2020, 746, 141093. [Google Scholar] [CrossRef] [PubMed]
  28. Chen, B.; Song, Z.; Pan, F.; Huang, Y. Obtaining vertical distribution of PM2.5 from CALIOP data and machine learning algorithms. Sci. Total Environ. 2021, 805, 150338. [Google Scholar] [CrossRef] [PubMed]
  29. Lyapustin, A.; Wang, Y.; Korkin, S.; Huang, D. MODIS Collection 6 MAIAC algorithm. Atmospheric Meas. Tech. 2018, 11, 5741–5765. [Google Scholar]
  30. Paciorek, C.J.; Liu, Y. Limitations of remotely sensed aerosol as a spatial proxy for fine particulate matter. Environ. Health Perspect. 2009, 117, 904–909. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  31. Just, A.C.; Wright, R.O.; Schwartz, J.; Coull, B.A.; Baccarelli, A.A.; Tellez-Rojo, M.M.; Moody, E.; Wang, Y.; Lyapustin, A.; Kloog, I. Using High-Resolution Satellite Aerosol Optical Depth To Estimate Daily PM2.5 Geographical Distribution in Mexico City. Environ. Sci. Technol. 2015, 49, 8576–8584. [Google Scholar] [CrossRef] [Green Version]
  32. Wei, J.; Li, Z.; Guo, J.; Sun, L.; Huang, W.; Xue, W.; Fan, T.; Cribb, M. Satellite-Derived 1-km-Resolution PM1 Concentrations from 2014 to 2018 across China. Environ. Sci. Technol. 2019, 53, 13265–13274. [Google Scholar] [CrossRef]
  33. Chew, B.N.; Campbell, J.R.; Salinas, S.V.; Chang, C.W.; Reid, J.S.; Welton, E.J.; Holben, B.N.; Liew, S.C. Aerosol particle vertical distributions and optical properties over Singapore. Atmospheric Environ. 2013, 79, 599–613. [Google Scholar] [CrossRef]
  34. Madhavan, B.L.; Niranjan, K.; Sreekanth, V.; Sarin, M.M.; Sudheer, A.K. Aerosol characterization during the summer monsoon period over a tropical coastal Indian station, Visakhapatnam. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef] [Green Version]
  35. Zhang, H.; Wang, Y.; Hu, J.; Ying, Q.; Hu, X.M. Relationships between meteorological parameters and criteria air pollutants in three megacities in China. Environ. Res. 2015, 140, 242–254. [Google Scholar] [CrossRef]
  36. Monforte, P.; Ragusa, M.A. Temperature Trend Analysis and Investigation on a Case of Variability Climate. Mathematics 2022, 10, 2202. [Google Scholar] [CrossRef]
  37. Fan, Y.; van den Dool, H. A global monthly land surface air temperature analysis for 1948–present. J. Geophys. Res. Atmos. 2008, 113, D01103. [Google Scholar] [CrossRef]
  38. Han, Y.; Xu, H.; Zheng, C.; Liu, P. Particulate matters emitted from maize straw burning for winter heating in rural areas in Guanzhong Plain, China: Current emission and future reduction. Atmospheric Res. 2017, 184, 66–76. [Google Scholar]
  39. Liu, Y.; Paciorek, C.J.; Koutrakis, P. Estimating regional spatial and temporal variability of PM(2.5) concentrations using satellite data, meteorology, and land use information. Environ. Health Perspect 2009, 117, 886–892. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  40. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
  41. Akritidis, D.; Zanis, P.; Georgoulias, A.K.; Papakosta, E.; Tzoumaka, P.; Kelessis, A. Implications of COVID-19 Restriction Measures in Urban Air Quality of Thessaloniki, Greece: A Machine Learning Approach. Atmosphere 2021, 12, 1500. [Google Scholar] [CrossRef]
  42. Aljanabi, M.; Shkoukani, M.; Hijjawi, M. Ground-level Ozone Prediction Using Machine Learning Techniques: A Case Study in Amman, Jordan. Int. J. Autom. Comput. 2020, 17, 667–677. [Google Scholar] [CrossRef]
  43. Keller, C.A.; Evans, M.J.; Knowland, K.E.; Hasenkopf, C.A.; Modekurty, S.; Lucchesi, R.A.; Oda, T.; Franca, B.B.; Mandarino, F.C.; Díaz Suárez, M.V.; et al. Global impact of COVID-19 restrictions on the surface concentrations of nitrogen dioxide and ozone. Atmos. Chem. Phys. 2021, 21, 3555–3592. [Google Scholar] [CrossRef]
  44. Sun, Y.; Yin, H.; Lu, X.; Notholt, J.; Palm, M.; Liu, C.; Tian, Y.; Zheng, B. The drivers and health risks of unexpected surface ozone enhancements over the Sichuan Basin, China, in 2020. Atmos. Chem. Phys. 2021, 21, 18589–18608. [Google Scholar] [CrossRef]
  45. Wang, J.; He, L.; Lu, X.; Zhou, L.; Tang, H.; Yan, Y.; Ma, W. A full-coverage estimation of PM2.5 concentrations using a hybrid XGBoost-WD model and WRF-simulated meteorological fields in the Yangtze River Delta Urban Agglomeration, China. Environ. Res. 2022, 203, 111799. [Google Scholar] [CrossRef]
  46. Gui, K.; Che, H.; Zeng, Z.; Wang, Y.; Zhai, S.; Wang, Z.; Luo, M.; Zhang, L.; Liao, T.; Zhao, H.; et al. Construction of a virtual PM2.5 observation network in China based on high-density surface meteorological observations using the Extreme Gradient Boosting model. Environ. Int. 2020, 141, 105801. [Google Scholar] [CrossRef]
  47. Fu, D.; Song, Z.; Zhang, X.; Xia, X.; Wang, J.; Che, H.; Wu, H.; Tang, X.; Zhang, J.; Duan, M. Mitigating MODIS AOD non-random sampling error on surface PM2.5 estimates by a combined use of Bayesian Maximum Entropy method and linear mixed-effects model. Atmos. Pollut. Res. 2020, 11, 482–490. [Google Scholar] [CrossRef]
  48. He, W.; Meng, H.; Han, J.; Zhou, G.; Zheng, H.; Zhang, S. Spatiotemporal PM2.5 estimations in China from 2015 to 2020 using an improved gradient boosting decision tree. Chemosphere 2022, 296, 134003. [Google Scholar] [CrossRef] [PubMed]
  49. He, Q.; Gu, Y.; Zhang, M. Spatiotemporal trends of PM2.5 concentrations in central China from 2003 to 2018 based on MAIAC-derived high-resolution data. Environ. Int. 2020, 137, 105536. [Google Scholar] [CrossRef] [PubMed]
  50. Chen, G.; Li, Y.; Zhou, Y.; Shi, C.; Guo, Y.; Liu, Y. The comparison of AOD-based and non-AOD prediction models for daily PM2.5 estimation in Guangdong province, China with poor AOD coverage. Environ. Res. 2021, 195, 110735. [Google Scholar] [CrossRef] [PubMed]
  51. Zhang, P.; Ma, W.; Wen, F.; Liu, L.; Yang, L.; Song, J.; Wang, N.; Liu, Q. Estimating PM2.5 concentration using the machine learning GA-SVM method to improve the land use regression model in Shaanxi, China. Ecotoxicol. Environ. Saf. 2021, 225, 112772. [Google Scholar] [CrossRef] [PubMed]
  52. Nabavi, S.O.; Haimberger, L.; Abbasi, E. Assessing PM2.5 concentrations in Tehran, Iran, from space using MAIAC, deep blue, and dark target AOD and machine learning algorithms. Atmos. Pollut. Res. 2018, 10, 889–903. [Google Scholar] [CrossRef]
  53. Bagheri, H. A machine learning-based framework for high resolution mapping of PM2.5 in Tehran, Iran, using MAIAC AOD data. Adv. Space Res. 2022, 69, 3333–3349. [Google Scholar] [CrossRef]
  54. Ghahremanloo, M.; Choi, Y.; Sayeed, A.; Salman, A.K.; Pan, S.; Amani, M. Estimating daily high-resolution PM2.5 concentrations over Texas: Machine Learning approach. Atmospheric Environ. 2021, 247, 118209. [Google Scholar] [CrossRef]
  55. Goldberg, D.L.; Gupta, P.; Wang, K.; Jena, C.; Zhang, Y.; Lu, Z.; Streets, D.G. Using gap-filled MAIAC AOD and WRF-Chem to estimate daily PM2.5 concentrations at 1 km resolution in the Eastern United States. Atmos. Environ. 2019, 199, 443–452. [Google Scholar] [CrossRef]
  56. Pu, Q.; Yoo, E.-H. Ground PM2.5 prediction using imputed MAIAC AOD with uncertainty quantification. Environ. Pollut. 2021, 274, 116574. [Google Scholar] [CrossRef]
  57. Kloog, I.; Chudnovsky, A.A.; Just, A.C.; Nordio, F.; Koutrakis, P.; Coull, B.A.; Lyapustin, A.; Wang, Y.; Schwartz, J. A New Hybrid Spatio-Temporal Model For Estimating Daily Multi-Year PM2.5 Concentrations Across Northeastern USA Using High Resolution Aerosol Optical Depth Data. Atmos. Environ. 2014, 95, 581–590. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  58. Di, Q.; Amini, H.; Shi, L.; Kloog, I.; Silvern, R.; Kelly, J.; Sabath, M.B.; Choirat, C.; Koutrakis, P.; Lyapustin, A. An ensemble-based model of PM2.5 concentration across the contiguous United States with high spatiotemporal resolution. Environ. Int. 2019, 130, 104909. [Google Scholar] [CrossRef] [PubMed]
  59. Just, A.C.; Arfer, K.B.; Rush, J.; Dorman, M.; Shtein, A.; Lyapustin, A.; Kloog, I. Advancing methodologies for applying machine learning and evaluating spatiotemporal models of fine particulate matter (PM2.5) using satellite data over large regions. Atmos. Environ. 2020, 239, 117649. [Google Scholar] [CrossRef] [PubMed]
  60. Li, L.; Zhang, J.; Meng, X.; Fang, Y.; Ge, Y.; Wang, J.; Wang, C.; Wu, J.; Kan, H. Estimation of PM2.5 concentrations at a high spatiotemporal resolution using constrained mixed-effect bagging models with MAIAC aerosol optical depth. Remote Sens. Environ. 2018, 217, 573–586. [Google Scholar] [CrossRef]
  61. Nie, D.; Shen, F.; Wang, J.; Ma, X.; Li, Z.; Ge, P.; Ou, Y.; Jiang, Y.; Chen, M.; Chen, M.; et al. Changes of air quality and its associated health and economic burden in 31 provincial capital cities in China during COVID-19 pandemic. Atmos. Res. 2020, 249, 105328. [Google Scholar] [CrossRef]
  62. Li, L.; Li, Q.; Huang, L.; Wang, Q.; Zhu, A.; Xu, J.; Liu, Z.; Li, H.; Shi, L.; Li, R.; et al. Air quality changes during the COVID-19 lockdown over the Yangtze River Delta Region: An insight into the impact of human activity pattern changes on air pollution variation. Sci. Total Environ. 2020, 732, 139282. [Google Scholar] [CrossRef]
  63. Zhang, X.; Song, C.; Liu, B.; Lu, G.; Shi, Z.; Li, W. Chemistry of Atmospheric Fine Particles During the COVID-19 Pandemic in a Megacity of Eastern China. Geophys. Res. Lett. 2021, 48, 2020GL091611. [Google Scholar]
  64. Van Donkelaar, A.; Hammer, M.S.; Bindle, L.; Brauer, M.; Brook, J.R.; Garay, M.J.; Hsu, N.C.; Kalashnikova, O.V.; Kahn, R.A.; Lee, C.; et al. Monthly Global Estimates of Fine Particulate Matter and Their Uncertainty. Environ. Sci. Technol. 2021, 55, 15287–15300. [Google Scholar] [CrossRef]
  65. Xiao, Q.; Chang, H.H.; Geng, G.; Liu, Y. An Ensemble Machine-Learning Model To Predict Historical PM2.5 Concentrations in China from Satellite Data. Environ. Sci. Technol. 2018, 52, 13260–13269. [Google Scholar] [CrossRef]
  66. Yang, N.; Shi, H.; Tang, H.; Yang, X. Geographical and temporal encoding for improving the estimation of PM2.5 concentrations in China using end-to-end gradient boosting. Remote Sens. Environ. 2021, 269, 112828. [Google Scholar] [CrossRef]
  67. Wei, J.; Li, Z.; Pinker, R.T.; Wang, J.; Sun, L.; Xue, W.; Li, R.; Cribb, M. Himawari-8-derived diurnal variations in ground-level PM2.5 pollution across China using the fast space-time Light Gradient Boosting Machine (LightGBM). Atmos. Chem. Phys. 2021, 21, 7863–7880. [Google Scholar] [CrossRef]
  68. Li, X.; Bei, N.; Tie, X.; Wu, J.; Liu, S.; Wang, Q.; Liu, L.; Wang, R.; Li, G. Local and transboundary transport contributions to the wintertime particulate pollution in the Guanzhong Basin (GZB), China: A case study. Sci. Total Environ. 2021, 797, 148876. [Google Scholar] [CrossRef] [PubMed]
  69. Wu, J.; Bei, N.; Li, X.; Cao, J.; Feng, T.; Wang, Y.; Tie, X.; Li, G. Widespread air pollutants of the North China Plain during the Asian summer monsoon season: A case study. Atmos. Chem. Phys. 2018, 18, 8491–8504. [Google Scholar] [CrossRef]
  70. Watson, J.G.; Cao, J.; Watson, J.G.; Wang, X.; Chow, J.C. PM2.5 pollution in China’s Guanzhong Basin and the USA’s San Joaquin Valley mega-regions. Faraday Discuss 2021, 226, 255–289. [Google Scholar] [PubMed]
  71. Wang, J.; Lu, X.; Yan, Y.; Zhou, L.; Ma, W. Spatiotemporal characteristics of PM2.5 concentration in the Yangtze River Delta urban agglomeration, China on the application of big data and wavelet analysis. Sci. Total Environ. 2020, 724, 138134. [Google Scholar] [CrossRef] [PubMed]
  72. Bei, N.; Zhao, L.; Xiao, B.; Meng, N.; Feng, T. Impacts of local circulations on the wintertime air pollution in the Guanzhong Basin, China. Sci. Total Environ. 2017, 592, 373–390. [Google Scholar] [CrossRef] [PubMed]
  73. Wei, N.; Wang, N.; Huang, X.; Liu, P.; Chen, L. The effects of terrain and atmospheric dynamics on cold season heavy haze in the Guanzhong Basin of China. Atmos. Pollut. Res. 2020, 11, 1805–1819. [Google Scholar] [CrossRef]
  74. Zhang, X.; Xu, H.; Liang, D. Spatiotemporal variations and connections of single and multiple meteorological factors on PM2.5 concentrations in Xi’an, China. Atmos. Environ. 2022, 275, 119015. [Google Scholar] [CrossRef]
  75. Gong, S.; Zhang, L.; Liu, C.; Lu, S.; Pan, W.; Zhang, Y. Multi-scale analysis of the impacts of meteorology and emissions on PM2.5 and O3 trends at various regions in China from 2013 to 2020 2. Key weather elements and emissions. Sci. Total Environ. 2022, 824, 153847. [Google Scholar] [CrossRef] [PubMed]
  76. Gupta, P.; Christopher, S.A. Particulate matter air quality assessment using integrated surface, satellite, and meteorological products: Multiple regression approach. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
  77. Wang, J.; Martin, S.T. Satellite characterization of urban aerosols: Importance of including hygroscopicity and mixing state in the retrieval algorithms. J. Geophys. Res. Earth Surf. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
  78. Li, J.; Chen, H.; Li, Z.; Wang, P.; Cribb, M.; Fan, X. Low-level temperature inversions and their effect on aerosol condensation nuclei concentrations under different large-scale synoptic circulations. Adv. Atmos. Sci. 2015, 32, 898–908. [Google Scholar] [CrossRef]
Remotesensing 14 05239 g001 550
Figure 1. The study area and locations of the air quality observation stations and weather stations.
Figure 1. The study area and locations of the air quality observation stations and weather stations.
Remotesensing 14 05239 g001
Remotesensing 14 05239 g002 550
Figure 2. The correlation coefficient matrix between PM2.5 Observation and each variable in GUA.
Figure 2. The correlation coefficient matrix between PM2.5 Observation and each variable in GUA.
Remotesensing 14 05239 g002
Remotesensing 14 05239 g003 550
Figure 3. Feature importance for the XGBoost model.
Figure 3. Feature importance for the XGBoost model.
Remotesensing 14 05239 g003
Remotesensing 14 05239 g004 550
Figure 4. Density scatterplots of the RF model with sample, spatial, and temporal-based train examination results (a–c) and test evaluation results (d–f) for GWA. The black dash and solid red lines represent the 1:1 and linear regression lines, respectively.
Figure 4. Density scatterplots of the RF model with sample, spatial, and temporal-based train examination results (a–c) and test evaluation results (d–f) for GWA. The black dash and solid red lines represent the 1:1 and linear regression lines, respectively.
Remotesensing 14 05239 g004
Remotesensing 14 05239 g005 550
Figure 5. Histograms and descriptive statistics (minimum, maximum, mean, and standard deviation) for PM2.5 and the independent variables used for modeling. Data are from 2018–2020 over GUA. The number of samples is 48,449.
Figure 5. Histograms and descriptive statistics (minimum, maximum, mean, and standard deviation) for PM2.5 and the independent variables used for modeling. Data are from 2018–2020 over GUA. The number of samples is 48,449.
Remotesensing 14 05239 g005
Remotesensing 14 05239 g006 550
Figure 6. Density scatterplots of regional-scale model (A) with sample_based train, sample_based test, spatial_based test and temporal_based test examination results for DFM (a–c) and DFC (d–f) at daily scale, and seasonal scale (B) with DFM (top row) and DFC (bottom row) based sample_based test for sprint (a,e), summer (b,f), autumn (c,g) and winter (d,h) in GUA. The black dash and solid red lines represent the 1:1 and linear regression lines, respectively.
Figure 6. Density scatterplots of regional-scale model (A) with sample_based train, sample_based test, spatial_based test and temporal_based test examination results for DFM (a–c) and DFC (d–f) at daily scale, and seasonal scale (B) with DFM (top row) and DFC (bottom row) based sample_based test for sprint (a,e), summer (b,f), autumn (c,g) and winter (d,h) in GUA. The black dash and solid red lines represent the 1:1 and linear regression lines, respectively.
Remotesensing 14 05239 g006
Remotesensing 14 05239 g007 550
Figure 7. Spatial distributions of (a) the number of examined samples (N) at each monitoring station, (b) R2, (c) MAE (μg/m3), and (d) RMSE (μg/m3) between PM2.5 estimations and measurements from DFM for the years of 2018–2019 in GUA.
Figure 7. Spatial distributions of (a) the number of examined samples (N) at each monitoring station, (b) R2, (c) MAE (μg/m3), and (d) RMSE (μg/m3) between PM2.5 estimations and measurements from DFM for the years of 2018–2019 in GUA.
Remotesensing 14 05239 g007
Remotesensing 14 05239 g008 550
Figure 8. Spatial distributions of (a) the number of examined samples (N) at each monitoring station, (b) R2, (c) MAE (μg/m3), and (d) RMSE (μg/m3) between PM2.5 predictions and measurements from DFP in 2020 in GUA.
Figure 8. Spatial distributions of (a) the number of examined samples (N) at each monitoring station, (b) R2, (c) MAE (μg/m3), and (d) RMSE (μg/m3) between PM2.5 predictions and measurements from DFP in 2020 in GUA.
Remotesensing 14 05239 g008
Remotesensing 14 05239 g009 550
Figure 9. The mean predicted seasonal (a–h) and annual (i–j) PM2.5 concentrations distribution based on the XGBoost model and the rate of change of annual PM2.5 concentrations from 2018 to 2019 (k).
Figure 9. The mean predicted seasonal (a–h) and annual (i–j) PM2.5 concentrations distribution based on the XGBoost model and the rate of change of annual PM2.5 concentrations from 2018 to 2019 (k).
Remotesensing 14 05239 g009
Table
Table 1. Variables used in the model development and validation.
Table 1. Variables used in the model development and validation.
VariablesShort NameUnitSpatial ResolutionTemporal
Resolution		Description
AODAOD 1 kmDaily
Geographical featuresLon° longitude
Lat° latitude
Temporal featureDOYday Day of year
Air pollutionsSO2μg/m3 24 h average
COμg/m3 24 h average
NO2μg/m3 24 h average
PM10μg/m3 24 h average
Meteorological featuresTEM_Avg°C Dailyaverage temperature
TEM_Max°C Dailymaximum temperature
TEM_Min°C Dailyminimum temperature
RHU_Avg% Dailyaverage relative humidity
PRE_2020mm Dailyprecipitation from 20:00 to 20:00
PRE_0808mm Dailyprecipitation from 08:00 to 08:00
WINm/s Daily2-min average wind speed
EVPmm Dailyevaporation
SSHhour Dailysunshine hours
Topographic featureDEMm30 m Digital Elevation Model
GLC 30 mAnnualGlobal Land Cover
LU 30 mAnnualLand use
PopulationPD 0.09°AnnualPeople Density
Estimated featurePM2.5μg/m3 Daily
Table
Table 2. Pearson correlation coefficients and p_values of each variable on PM2.5 concentrations from the monitoring stations in GUA from 2018–2020.
Table 2. Pearson correlation coefficients and p_values of each variable on PM2.5 concentrations from the monitoring stations in GUA from 2018–2020.
Positive VariablesNegative Variables
NO.Variablerp_ValueNO.Variablerp_Value
1AOD0.650.001TEM_Avg−0.480.00
2Lon0.160.002TEM_Min−0.470.00
3GLC0.090.003TEM_Max−0.470.00
4LU0.070.004EVP−0.350.00
5PD0.020.005DEM−0.240.00
6DOY−0.220.00
7SSH−0.190.00
8PRE_20−0.180.00
9PRE_08−0.150.00
10WIN_Avg−0.020.00
11RHU_Avg−0.020.00
12Lat−0.000.26
Table
Table 3. A comparison of model performance between RF-XGBoost and other models.
Table 3. A comparison of model performance between RF-XGBoost and other models.
ModelStudy AreaModel ValidationPredictive PowerReferences Origin
R2RMSEMAEMPESlopeInterceptDaily R2
RFTexas0.69–0.81------[54]
MEMTexas0.62–0.74------[54]
MLRTexas0.45–0.59------[54]
MLREastern United States0.75---0.89--[55]
STRHenan-Hubei-Hunan0.5929.43-19.880.6225.55-[49]
GAMBeijing-Tianjin-Hebei0.823--0.925.8-[60]
GWRBeijing-Tianjin-Hebei0.8122--0.998.18-[60]
Mixed modelBeijing-Tianjin-Hebei0.8719--0.97-[60]
RFTehran0.6817.52-----[52]
DNNNew York State0.662.18-1.58---[56]
RFNew York State0.811.63-1.15---[56]
GBMNew York State0.851.44-1.02---[56]
Ensemble modelNew York State0.861.43-1---[56]
Statics modelNortheastern USA0.882.32--1.01--[57]
Ensemble modelUnited States 0.862.79--0.96--[58]
RFIraq and Kuwait0.71------[14]
GA-SVMShaanxi0.8412.110.07----[51]
XGBoostNew England states0.64–0.802.91–4.42-----[59]
RFSouth Africa0.89.4--1.13−3.66-[15]
XGBoostTehran0.748.976.88----[53]
Extra TreesTehran0.689.637.66----[53]
Random ForestTehran0.699.517.5----[53]
SVRTehran0.6310.367.98----[53]
DBNTehran0.669.997.67----[53]
DAE + SVRTehran0.689.757.32----[53]
MLRChina0.4120.0430.03-0.4130.030.38[25]
GWRChina0.5323.2819.26-0.6120.930.44[25]
Two-stageChina0.7118.5914.54-0.7115.10.35[25]
RFChina0.8117.9111.5-0.7712.560.53[25]
STRFChina0.8515.579.77-0.829.640.55[25]
STEMChina0.8910.356.71-0.866.160.65[25]
GBDTChina0.9210.146.02-0.923.73-[48]
RFGuangdong0.80–0.838.20–9.20--0.76–0.78--[50]
RFShenzhen0.884.34--0.778.43-[27]
IRFShenzhen0.923.66--0.826.6-[27]
XGBoostGUA0.9111.587.75-0.876.81-Our study
RF-XGBoostGUA0.9312.498.42-0.95.420.61Our study
Table
Table 4. A comparison of the model performances of different ensemble models and the RF-XGBoost model. TC and MC refer to the time and memory of computer consumption during the model training.
Table 4. A comparison of the model performances of different ensemble models and the RF-XGBoost model. TC and MC refer to the time and memory of computer consumption during the model training.
ModelOut-of-Sample TestTCMCModel-Prediction
SamplesR2RMSEMAE(s)(MB)SamplesR2RMSEMAE
RF12,3680.8813.368.2816.00354.7127650.5225.5019.17
ERT0.9011.937.546.00489.780.5724.1418.03
GBDT0.8415.2710.106.00152.410.4826.6719.33
XGBoost0.8912.567.941.00169.020.4028.6319.72
LightGBM0.9012.237.810.00169.640.4028.6019.92
RF-XGBoost34,9560.9212.858.7340.002281.5313,4930.5424.7618.64
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Lin, L.; Liang, Y.; Liu, L.; Zhang, Y.; Xie, D.; Yin, F.; Ashraf, T. Estimating PM2.5 Concentrations Using the Machine Learning RF-XGBoost Model in Guanzhong Urban Agglomeration, China. Remote Sens. 2022, 14, 5239. https://doi.org/10.3390/rs14205239

AMA Style

Lin L, Liang Y, Liu L, Zhang Y, Xie D, Yin F, Ashraf T. Estimating PM2.5 Concentrations Using the Machine Learning RF-XGBoost Model in Guanzhong Urban Agglomeration, China. Remote Sensing. 2022; 14(20):5239. https://doi.org/10.3390/rs14205239

Chicago/Turabian Style

Lin, Lujun, Yongchun Liang, Lei Liu, Yang Zhang, Danni Xie, Fang Yin, and Tariq Ashraf. 2022. "Estimating PM2.5 Concentrations Using the Machine Learning RF-XGBoost Model in Guanzhong Urban Agglomeration, China" Remote Sensing 14, no. 20: 5239. https://doi.org/10.3390/rs14205239

APA Style

Lin, L., Liang, Y., Liu, L., Zhang, Y., Xie, D., Yin, F., & Ashraf, T. (2022). Estimating PM2.5 Concentrations Using the Machine Learning RF-XGBoost Model in Guanzhong Urban Agglomeration, China. Remote Sensing, 14(20), 5239. https://doi.org/10.3390/rs14205239

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop