Biases Analysis and Calibration of ICESat-2/ATLAS Data Based on Crossover Adjustment Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of Study Area and Data
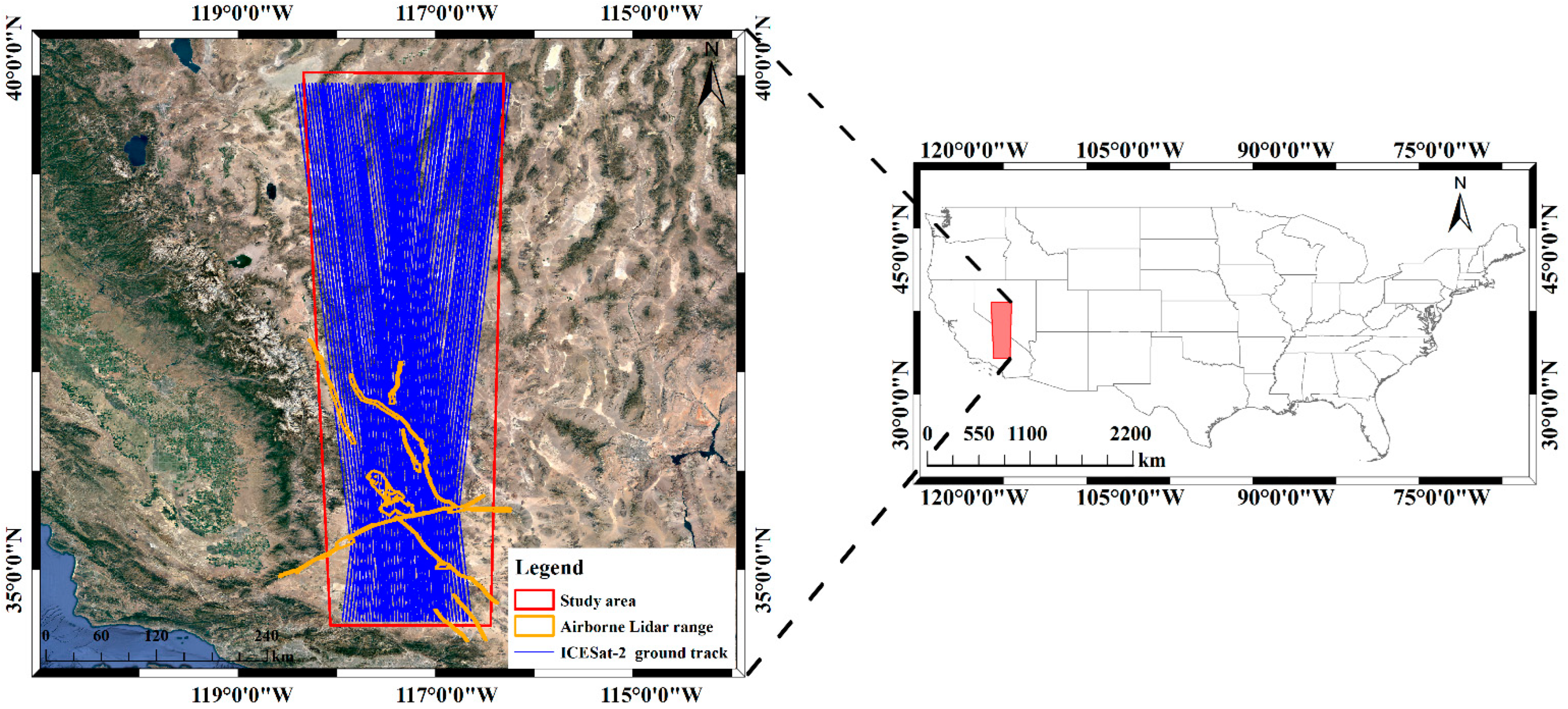
2.1.1. Study Area
2.1.2. ICESat-2 Data
2.1.3. Airborne Lidar Data
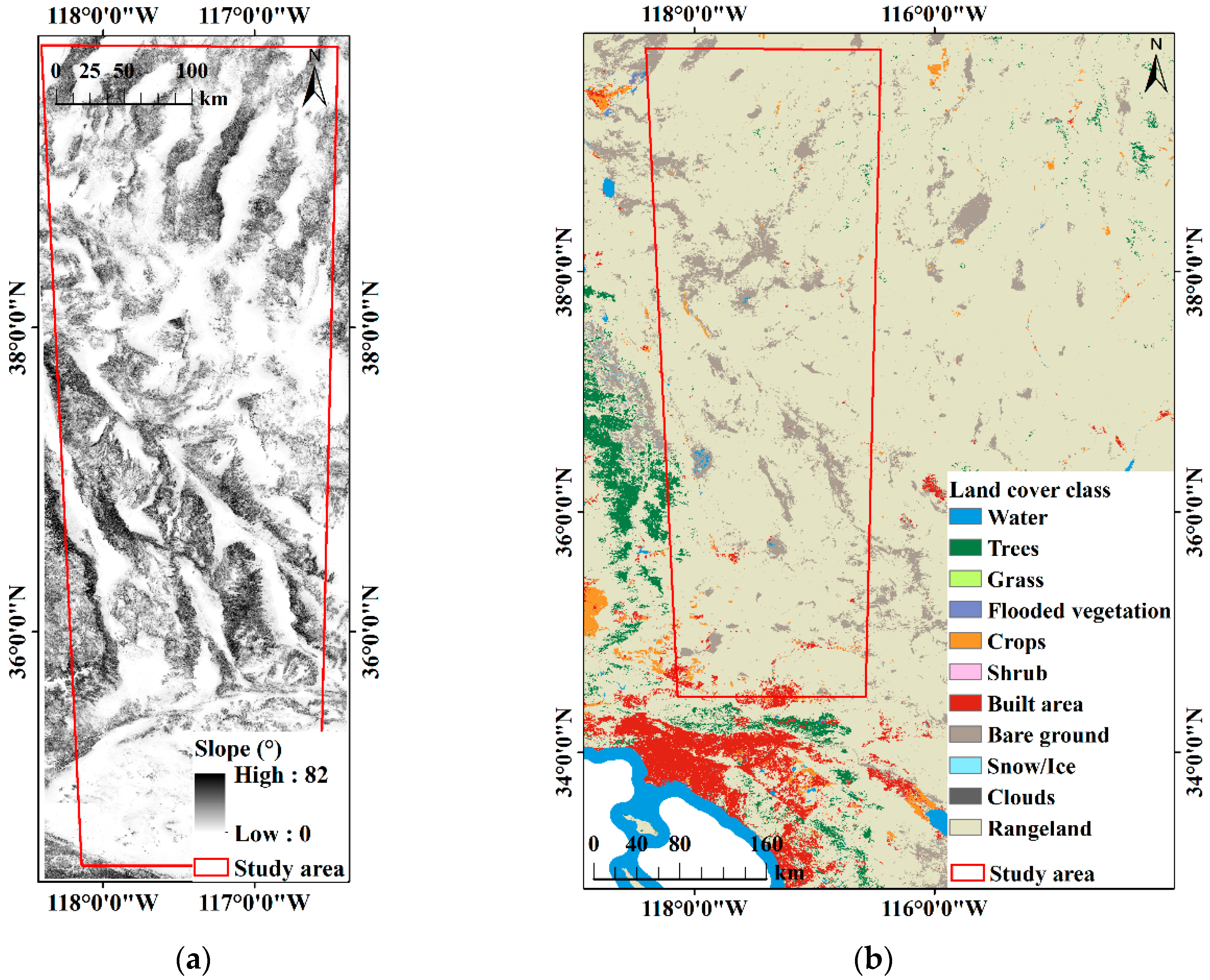
2.1.4. Ancillary Data
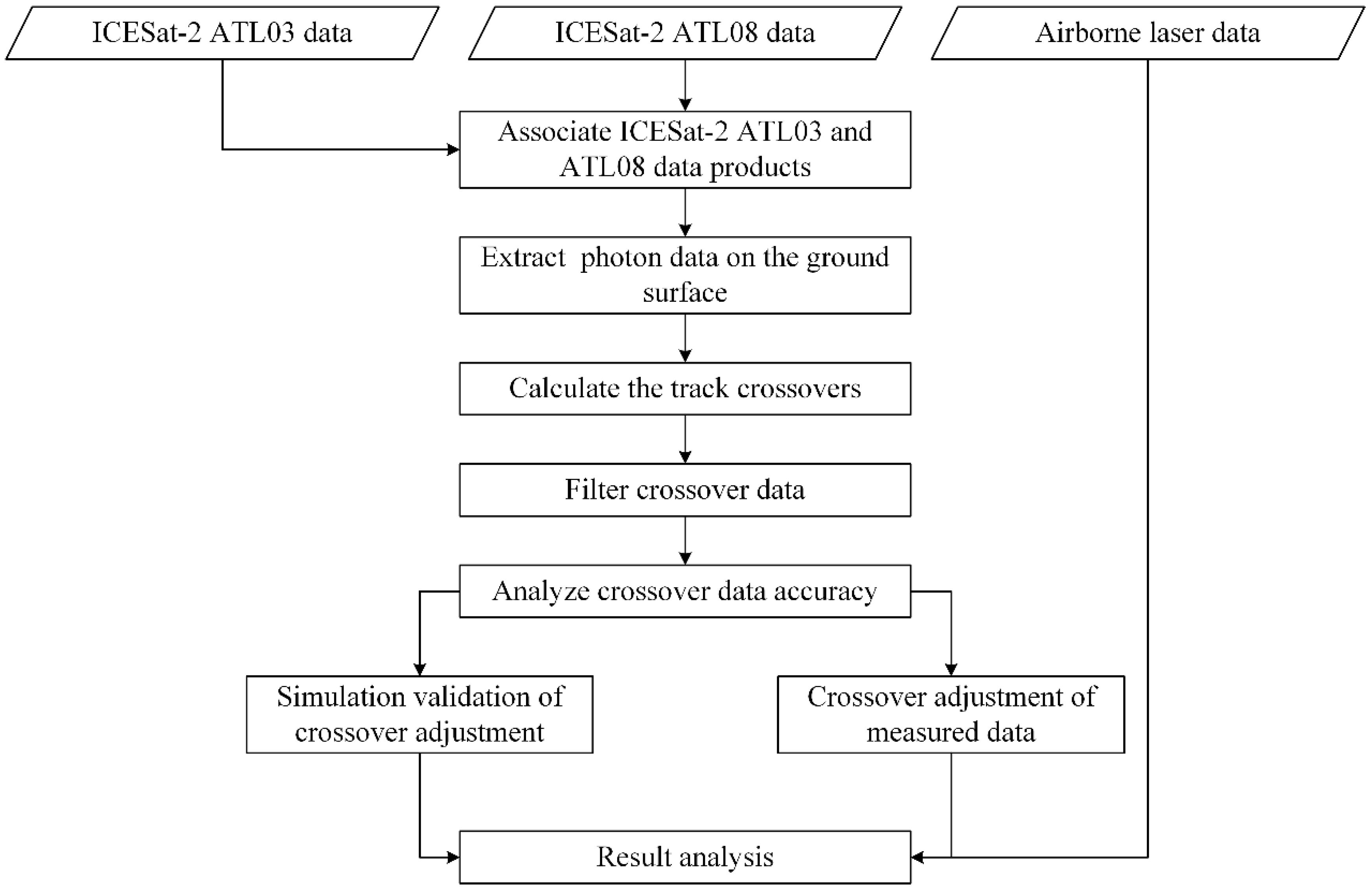
2.2. Crossover and Crossover Adjustment
- Determine whether there is a crossover between any two beams. According to the following conditions: (a) the minimum longitude of the ascending arc should be less than the maximum longitude of the descending arc; (b) the maximum longitude of the ascending arc should be greater than the minimum longitude of the descending arc. Thus, we can preliminarily determine whether there is a crossover between any two beams.
- Locate the area where the crossover exists. Calculate the latitude difference corresponding to the laser point at the same longitude position of the two beams. The location where the difference changes from positive to negative or from negative to positive is the area where the crossover exists, and the potential crossover is located among the four laser points (two laser points per beam) in the area.
- Obtain the crossover. Calculate the distance between any two laser points between different beams, and the two points with the smallest distance (must be less than 0.7 m) are the final crossover.
2.3. Accuracy Validation
3. Results
3.1. Crossovers Accuracy Analysis
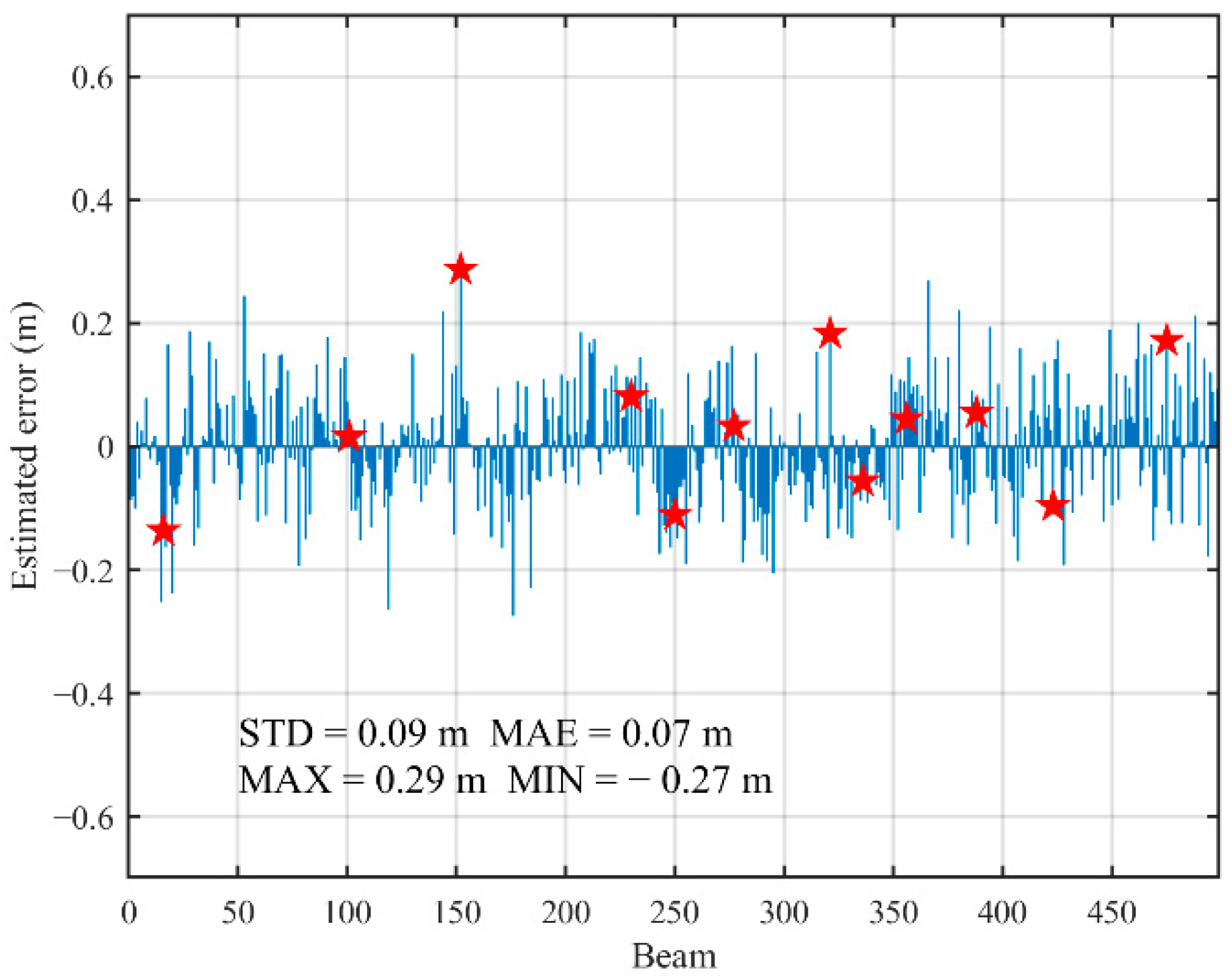
3.2. Simulation Validation of Crossover Adjustment
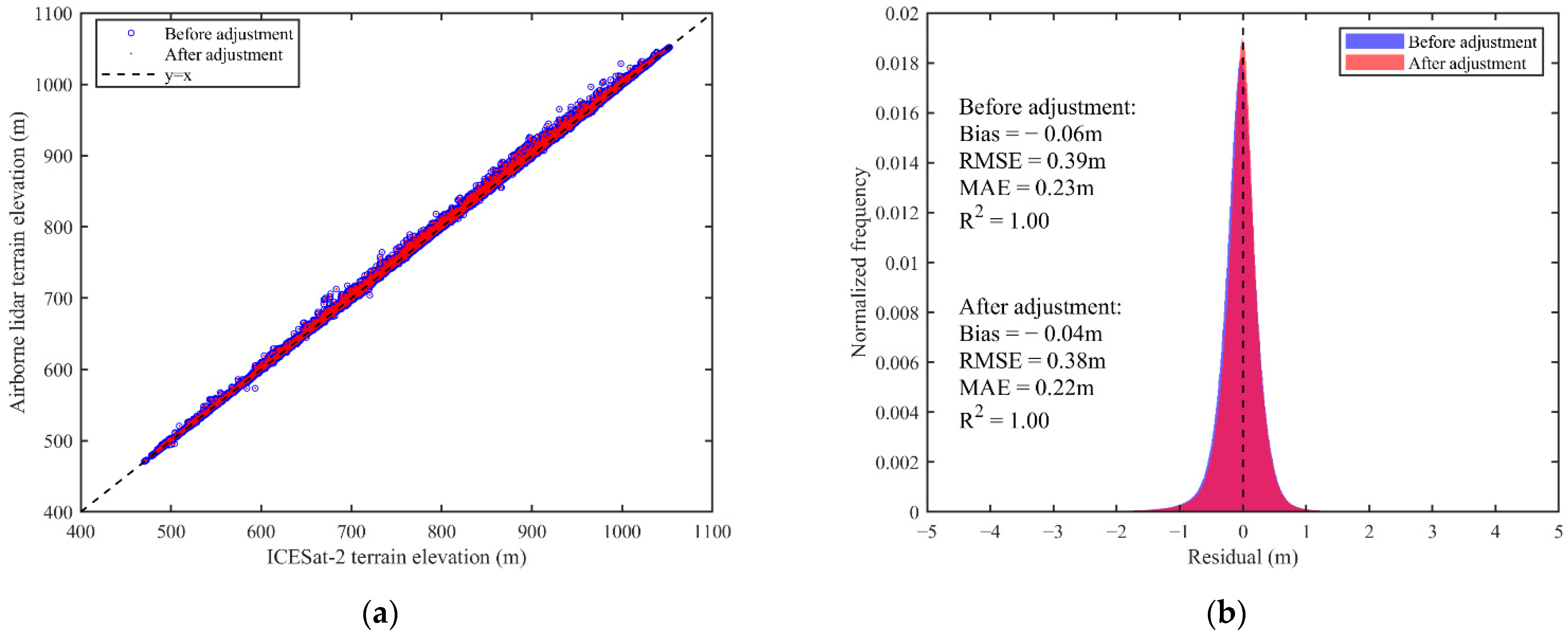
3.3. Validation and Analysis of ICESat-2 Measured Data
4. Discussion
4.1. Influencing Factors of Crossover Differences
4.1.1. Effect of Terrain Slope on Crossover Differences
4.1.2. Effect of Land Cover Types on Crossover Differences
4.2. Adjustment Model Analysis
4.3. Innovations, Applications, and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cao, B.; Fang, Y.; Gao, L.; Hu, H.; Jiang, Z.; Sun, B.; Lou, L. An active-passive fusion strategy and accuracy evaluation for shallow water bathymetry based on ICESat-2 ATLAS laser point cloud and satellite remote sensing imagery. Int. J. Remote Sens. 2021, 42, 2783–2806. [Google Scholar] [CrossRef]
- Geng, T.; Zhang, S.; Xiao, F.; Li, J.; Xuan, Y.; Li, X.; Li, F. DEM Generation with ICESat-2 Altimetry Data for the Three Antarctic Ice Shelves: Ross, Filchner-Ronne and Amery. Remote Sens. 2021, 13, 5137. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Pitts, K. The ATL08 land and vegetation product for the ICESat-2 Mission. Remote Sens. Environ. 2019, 221, 247–259. [Google Scholar] [CrossRef]
- Smith, B.; Fricker, H.A.; Holschuh, N.; Gardner, A.S.; Adusumilli, S.; Brunt, K.M.; Csatho, B.; Harbeck, K.; Huth, A.; Neumann, T.; et al. Land ice height-retrieval algorithm for NASA’s ICESat-2 photon-counting laser altimeter. Remote Sens. Environ. 2019, 233, 111352. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Chen, W.F.; Xie, H.J. Tibetan Plateau’s Lake Level and Volume Changes From NASA’s ICESat/ICESat-2 and Landsat Missions. Geophys. Res. Lett. 2019, 46, 13107–13118. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, X.X.; Nie, S.; Xi, X.H.; Li, D.; Zheng, W.W.; Chen, S.C. Ground elevation accuracy verification of ICESat-2 data: A case study in Alaska, USA. Opt. Express 2019, 27, 38168–38179. [Google Scholar] [CrossRef] [PubMed]
- Fernandez-Diaz, J.C.; Velikova, M.; Glennie, C.L. Validation of ICESat-2 ATL08 Terrain and Canopy Height Retrievals in Tropical Mesoamerican Forests. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2022, 15, 2956–2970. [Google Scholar] [CrossRef]
- Malambo, L.; Popescu, S.C. Assessing the agreement of ICESat-2 terrain and canopy height with airborne lidar over US ecozones. Remote Sens. Environ. 2021, 266, 112711. [Google Scholar] [CrossRef]
- Li, B.B.; Xie, H.; Liu, S.J.; Tong, X.H.; Tang, H.; Wang, X. A Method of Extracting High-Accuracy Elevation Control Points from ICESat-2 Altimetry Data. Photogramm. Eng. Remote Sens. 2021, 87, 821–830. [Google Scholar] [CrossRef]
- Li, B.B.; Xie, H.; Tong, X.H.; Tang, H.; Liu, S.J.; Jin, Y.N.; Wang, C.; Ye, Z. High-Accuracy Laser Altimetry Global Elevation Control Point Dataset for Satellite Topographic Mapping. IEEE Trans. Geosci. Remote Sens. 2022, 60, 3177026. [Google Scholar] [CrossRef]
- Magruder, L.; Neuenschwander, A.; Klotz, B. Digital terrain model elevation corrections using space-based imagery and ICESat-2 laser altimetry. Remote Sens. Environ. 2021, 264, 112621. [Google Scholar] [CrossRef]
- Rowlands, D.; Carabajal, C.; Luthcke, S.; Harding, D.; Sauber, J.; Bufton, J. Satellite Laser Altimetry. On-Orbit Calibration Techniques for Precise Geolocation. Rev. Laser Eng. 2000, 28, 796–803. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Rowlands, D.D.; Mccarthy, J.J.; Pavlis, D.E.; Stoneking, E. Spaceborne Laser-Altimeter-Pointing Bias Calibration from Range Residual Analysis. J. Spacecr. Rocket. 2000, 37, 374–384. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Carabajal, C.C.; Rowlands, D.D. Enhanced geolocation of spaceborne laser altimeter surface returns: Parameter calibration from the simultaneous reduction of altimeter range and navigation tracking data. J. Geodyn. 2002, 34, 447–475. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Rowlands, D.D.; Williams, T.A.; Sirota, M. Reduction of ICESat systematic geolocation errors and the impact on ice sheet elevation change detection. Geophys. Res. Lett. 2005, 32, 312–321. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Thomas, T.C.; Pennington, T.A.; Rebold, T.W.; Nicholas, J.B.; Rowlands, D.D.; Gardner, A.S.; Bae, S. ICESat-2 Pointing Calibration and Geolocation Performance. Earth Space Sci. 2021, 8, e2020EA001494. [Google Scholar] [CrossRef]
- Magruder, L.A.; Schutz, B.E.; Silverberg, E.C. Laser pointing angle and time of measurement verification of the ICESat laser altimeter using a ground-based electro-optical detection system. J. Geod. 2003, 77, 148–154. [Google Scholar] [CrossRef]
- Xie, J.; Tang, X.; Mo, F.; Tang, H.; Wang, Z.; Wang, X.; Liu, Y.; Tian, S.; Liu, R.; Xia, X. In-orbit geometric calibration and experimental verification of the ZY3-02 laser altimeter. Photogramm. Rec. 2018, 33, 341–362. [Google Scholar] [CrossRef]
- Martin, C.; Thomas, R.H.; Krabill, W.B.; Manizade, S.S. ICESat range and mounting bias estimation over precisely-surveyed terrain. Geophys. Res. Lett. 2005, 32, 242–257. [Google Scholar] [CrossRef]
- Filin, S. Calibration of spaceborne laser Altimeters-an algorithm and the site selection problem. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1484–1492. [Google Scholar] [CrossRef]
- Nan, Y.; Feng, Z.; Liu, E.; Li, B. Iterative Pointing Angle Calibration Method for the Spaceborne Photon-Counting Laser Altimeter Based on Small-Range Terrain Matching. Remote Sens. 2019, 11, 2158. [Google Scholar] [CrossRef]
- Zhao, P.; Li, S.; Ma, Y.; Liu, X.; Yang, J.; Yu, D. A new terrain matching method for estimating laser pointing and ranging systematic biases for spaceborne photon-counting laser altimeters. ISPRS J. Photogramm. Remote Sens. 2022, 188, 220–236. [Google Scholar] [CrossRef]
- Rowlands, D.; Pavlis, D.; Lemoine, F.; Neumann, G.A.; Luthcke, S. The use of laser altimetry in the orbit and attitude determination of Mars Global Surveyor. Geophys. Res. Lett. 1999, 26, 1191–1194. [Google Scholar] [CrossRef]
- Neumann, G.A.; Rowlands, D.D.; Lemoine, F.G.; Smith, D.E.; Zuber, M.T. Crossover analysis of Mars Orbiter Laser Altimeter data. J. Geophys. Res. 2001, 106, 23753–23768. [Google Scholar] [CrossRef]
- Mazarico, E.; Neumann, G.; Rowlands, D.; Smith, D. Geodetic constraints from multi-beam laser altimeter crossovers. J. Geod. 2010, 84, 343–354. [Google Scholar] [CrossRef]
- Hu, W.; Di, K.; Liu, Z.; Ping, J. A new lunar global DEM derived from Chang’E-1 Laser Altimeter data based on crossover adjustment with local topographic constraint. Planet Space Sci. 2013, 87, 173–182. [Google Scholar] [CrossRef]
- Mazarico, E.; Barker, M.K.; Neumann, G.A.; Zuber, M.T.; Smith, D.E. Detection of the lunar body tide by the Lunar Orbiter Laser Altimeter. Geophys. Res. Lett. 2014, 41, 2282–2288. [Google Scholar] [CrossRef]
- Li, F.; Zhu, C.; Hao, W.; Yan, J.; Ye, M.; Barriot, J.-P.; Cheng, Q.; Sun, T. An Improved Digital Elevation Model of the Lunar Mons Rümker Region Based on Multisource Altimeter Data. Remote Sens. 2018, 10, 1442. [Google Scholar] [CrossRef]
- Hao, W.; Zhu, C.; Li, F.; Yan, J.; Ye, M.; Barriot, J.-P. Illumination and communication conditions at the Mons Rümker region based on the improved Lunar Orbiter Laser Altimeter data. Planet Space Sci. 2019, 168, 73–82. [Google Scholar] [CrossRef]
- Harpold, R.; Urban, T.; Schutz, B. An initial crossover and along-track analysis of ice sheets using ICESat altimeter data. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 11–15 December 2006; p. C41A-0316. [Google Scholar]
- Brunt, K.; Neumann, T.; Larsen, C. Assessment of altimetry using ground-based GPS data from the 88S Traverse, Antarctica, in support of ICESat-2. Cryosphere 2019, 13, 579–590. [Google Scholar] [CrossRef]
- Brunt, K.M.; Neumann, T.A.; Smith, B.E. Assessment of ICESat-2 Ice Sheet Surface Heights, Based on Comparisons over the Interior of the Antarctic Ice Sheet. Geophys. Res. Lett. 2019, 46, 13072–13078. [Google Scholar] [CrossRef]
- Brunt, K.M.; Smith, B.E.; Sutterley, T.C.; Kurtz, N.T.; Neumann, T.A. Comparisons of Satellite and Airborne Altimetry with Ground-Based Data from the Interior of the Antarctic Ice Sheet. Geophys. Res. Lett. 2021, 48, e2020GL090572. [Google Scholar] [CrossRef]
- Li, R.; Li, H.; Hao, T.; Qiao, G.; Cui, H.; He, Y.; Hai, G.; Xie, H.; Cheng, Y.; Li, B. Assessment of ICESat-2 ice surface elevations over the Chinese Antarctic Research Expedition (CHINARE) route, East Antarctica, based on coordinated multi-sensor observations. Cryosphere 2021, 15, 3083–3099. [Google Scholar] [CrossRef]
- Magruder, L.A.; Brunt, K.M.; Alonzo, M. Early ICESat-2 on-orbit Geolocation Validation Using Ground-Based Corner Cube Retro-Reflectors. Remote Sens. 2020, 12, 3653. [Google Scholar] [CrossRef]
- Magruder, L.; Brunt, K.; Neumann, T.; Klotz, B.; Alonzo, M. Passive ground-based optical techniques for monitoring the on-orbit ICESat-2 altimeter geolocation and footprint diameter. Earth Space Sci. 2021, 8, e2020EA001414. [Google Scholar] [CrossRef]
- Harpold, R.; Urban, T.; Webb, C.; Schutz, B. Assessment of ICESat repeat track estimation techniques for polar elevation change detection. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 10–14 December 2007; p. C23A-0943. [Google Scholar]
- Harpold, R.; Urban, T.; Schutz, B. Sensitivity Analysis of Repeat Track Estimation Techniques for Detection of Elevation Change in Polar Ice Sheets. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 15–19 December 2008; p. C31A-0472. [Google Scholar]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The Ice, Cloud, and land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Neumann, T.A.; Martino, A.J.; Markus, T.; Bae, S.; Bock, M.R.; Brenner, A.C.; Brunt, K.M.; Cavanaugh, J.; Fernandes, S.T.; Hancock, D.W.; et al. The Ice, Cloud, and Land Elevation Satellite—2 mission: A global geolocated photon product derived from the Advanced Topographic Laser Altimeter System. Remote Sens. Environ. 2019, 233, 111325. [Google Scholar] [CrossRef]
- Neumann, T.; Brenner, A.; Hancock, D.; Robbins, J.; Saba, J.; Harbeck, K.; Gibbons, A.; Lee, J.; Luthcke, S.B.; Rebold, T. ICESat-2 Algorithm Theoretical Basis Document for Global Geolocated Photons (ATL03). 2021. Available online: https://icesat-2.gsfc.nasa.gov/sites/default/files/page_files/ICESat2_ATL03_ATBD_r004.pdf (accessed on 11 April 2022).
- Neuenschwander, A.L.; Pitts, K.L.; Jelley, B.P.; Robbins, J.; Klotz, B.; Popescu, S.C.; Nelson, R.F.; Harding, D.; Pederson, D.; Klotz, B.; et al. ICESat-2 Algorithm Theoretical Basis Document for Land-Vegetation Along-Track Products (ATL08). 2021. Available online: https://icesat-2.gsfc.nasa.gov/sites/default/files/page_files/ICESat2_ATL08_ATBD_r004.pdf (accessed on 11 April 2022).
- Xing, Y.Q.; Huang, J.P.; Gruen, A.; Qin, L. Assessing the Performance of ICESat-2/ATLAS Multi-Channel Photon Data for Estimating Ground Topography in Forested Terrain. Remote Sens. 2020, 12, 2084. [Google Scholar] [CrossRef]
- Hudnut, K.W.; Brooks, B.; Scharer, K.; Hernandez, J.L.; Dawson, T.E.; Oskin, M.E.; Arrowsmith, R.; Goulet, C.A.; Blake, K.; Boggs, M.L.; et al. 2019 Ridgecrest, CA Post-Earthquake Lidar Collection; National Center for Airborne Laser Mapping (NCALM); OpenTopography: San Diego, CA, USA, 2020. [Google Scholar] [CrossRef]
- Karra, K.; Kontgis, C.; Statman-Weil, Z.; Mazzariello, J.C.; Mathis, M.; Brumby, S.P. Global land use/land cover with Sentinel 2 and deep learning. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 4704–4707. [Google Scholar]
- Wessel, P. XOVER: A cross-over error detector for track data. Comput. Geosci. 1989, 15, 333–346. [Google Scholar] [CrossRef]
- Bae, S.; Helgeson, B.; James, M.; Magruder, L.; Sipps, J.; Luthcke, S.; Thomas, T. Performance of ICESat-2 Precision Pointing Determination. Earth Space Sci. 2021, 8, e2020EA001478. [Google Scholar] [CrossRef]
- Thomas, T.C.; Luthcke, S.B.; Pennington, T.A.; Nicholas, J.B.; Rowlands, D. ICESat-2 Precision Orbit Determination. Earth Space Sci. 2021, 8, e2020EA001496. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Pennington, T.; Rebold, T.; Thomas, T. Algorithm Theoretical Basis Document (ATBD) for ATL03g ICESat-2 Receive Photon Geolocation. 2019. Available online: https://icesat-2.gsfc.nasa.gov/sites/default/files/page_files/ICESat2_ATL03g_ATBD_r002.pdf (accessed on 11 April 2022).
- Liu, A.; Cheng, X.; Chen, Z. Performance evaluation of GEDI and ICESat-2 laser altimeter data for terrain and canopy height retrievals. Remote Sens. Environ. 2021, 264, 112571. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Guenther, E.; White, J.C.; Duncanson, L.; Montesano, P. Validation of ICESat-2 terrain and canopy heights in boreal forests. Remote Sens. Environ. 2020, 251, 112110. [Google Scholar] [CrossRef]
- Pirooznia, M.; Naeeni, M.R. The application of least-square collocation and variance component estimation in crossover analysis of satellite altimetry observations and altimeter calibration J. Oper. Oceanogr. 2020, 13, 100–120. [Google Scholar] [CrossRef]

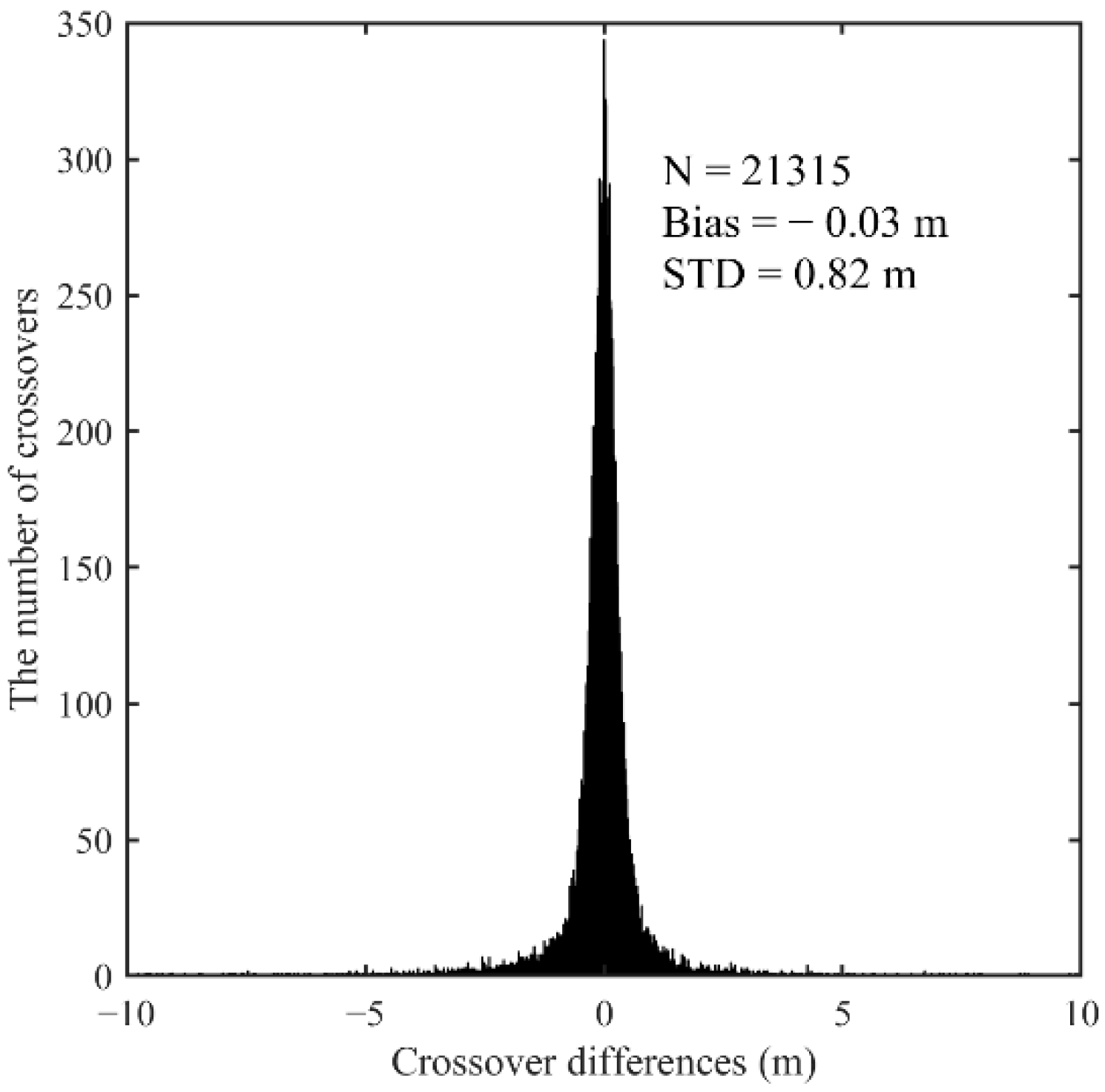
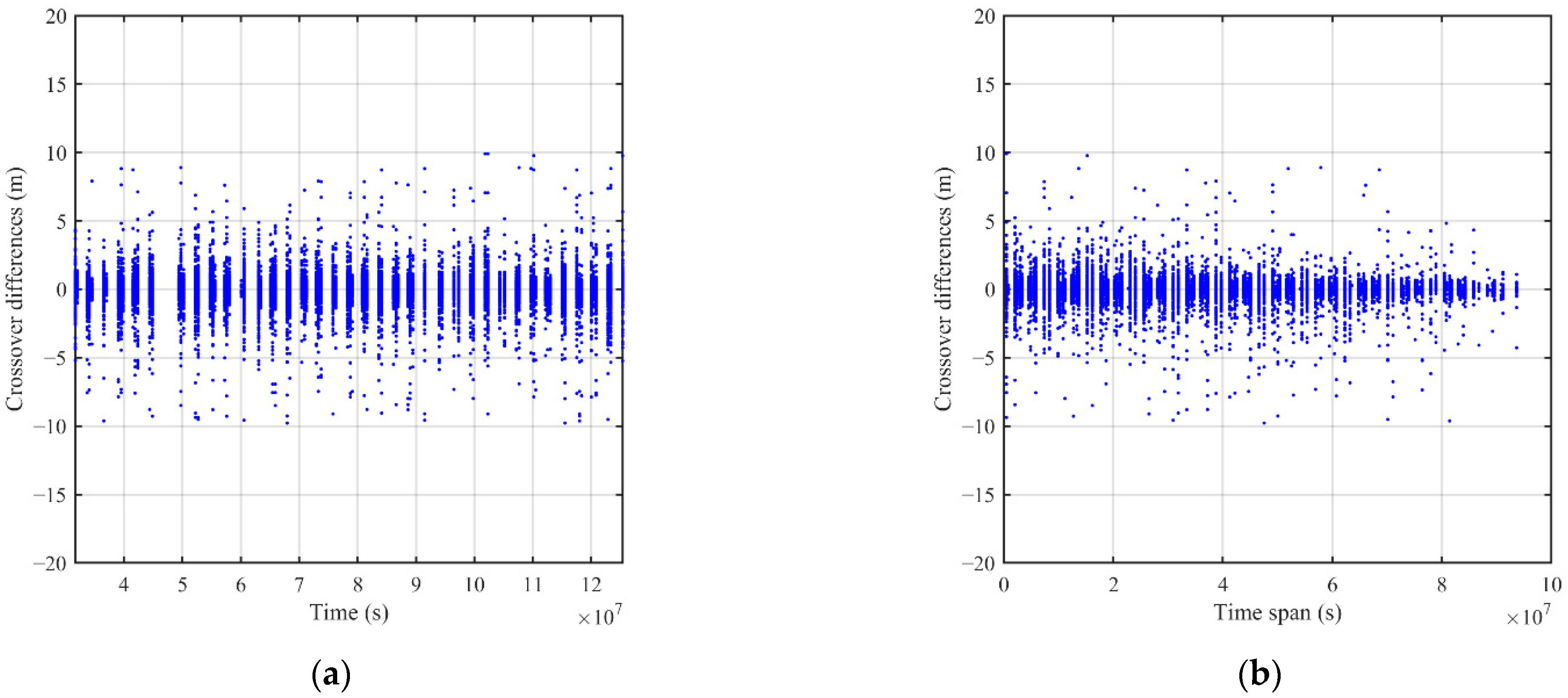
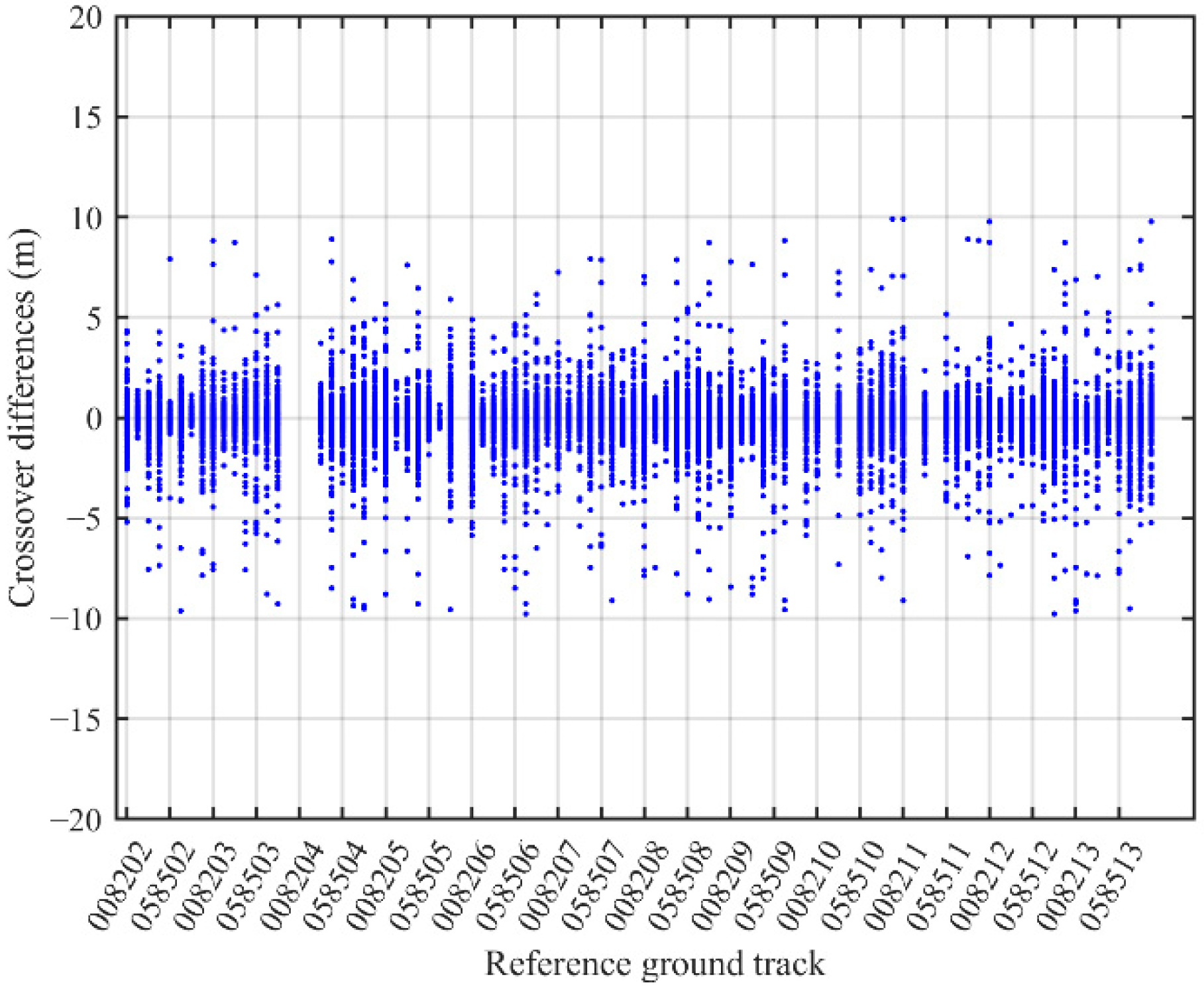

| Crossover Differences (m) | 0–5 | 5–10 | 10–15 | 15–20 | >20 |
| Number | 21,292 | 103 | 31 | 8 | 5 |
| STD (m) | 0.66 | 6.78 | 12.43 | 18.56 | 31.17 |
| Percentage (%) | 99.31% | 0.48% | 0.15% | 0.04% | 0.02% |
| Date | RGT | Cycle | Strong/Weak | Beam |
|---|---|---|---|---|
| 20190130 | 0501 | 02 | strong | gt1l |
| 20190604 | 1027 | 03 | strong | gt1l |
| 20190730 | 0501 | 04 | strong | gt1l |
| 20191002 | 0082 | 05 | strong | gt2r |
| 20200203 | 0585 | 06 | strong | gt1r |
| 20200428 | 0501 | 07 | weak | gt1l |
| 20200826 | 0943 | 08 | strong | gt2l |
| 20201223 | 1385 | 09 | strong | gt3l |
| 20200223 | 0943 | 10 | weak | gt3l |
| 20210422 | 0440 | 11 | strong | gt1r |
| 20210922 | 1385 | 12 | strong | gt3r |
| 20211001 | 0143 | 13 | weak | gt3l |
| STD (m) | Bias (m) | MAX (m) | MIN (m) | |
|---|---|---|---|---|
| Before adjustment | 0.82 | −0.02 | 9.91 | −9.78 |
| After adjustment | 0.80 | 0.00 | 9.47 | −9.83 |
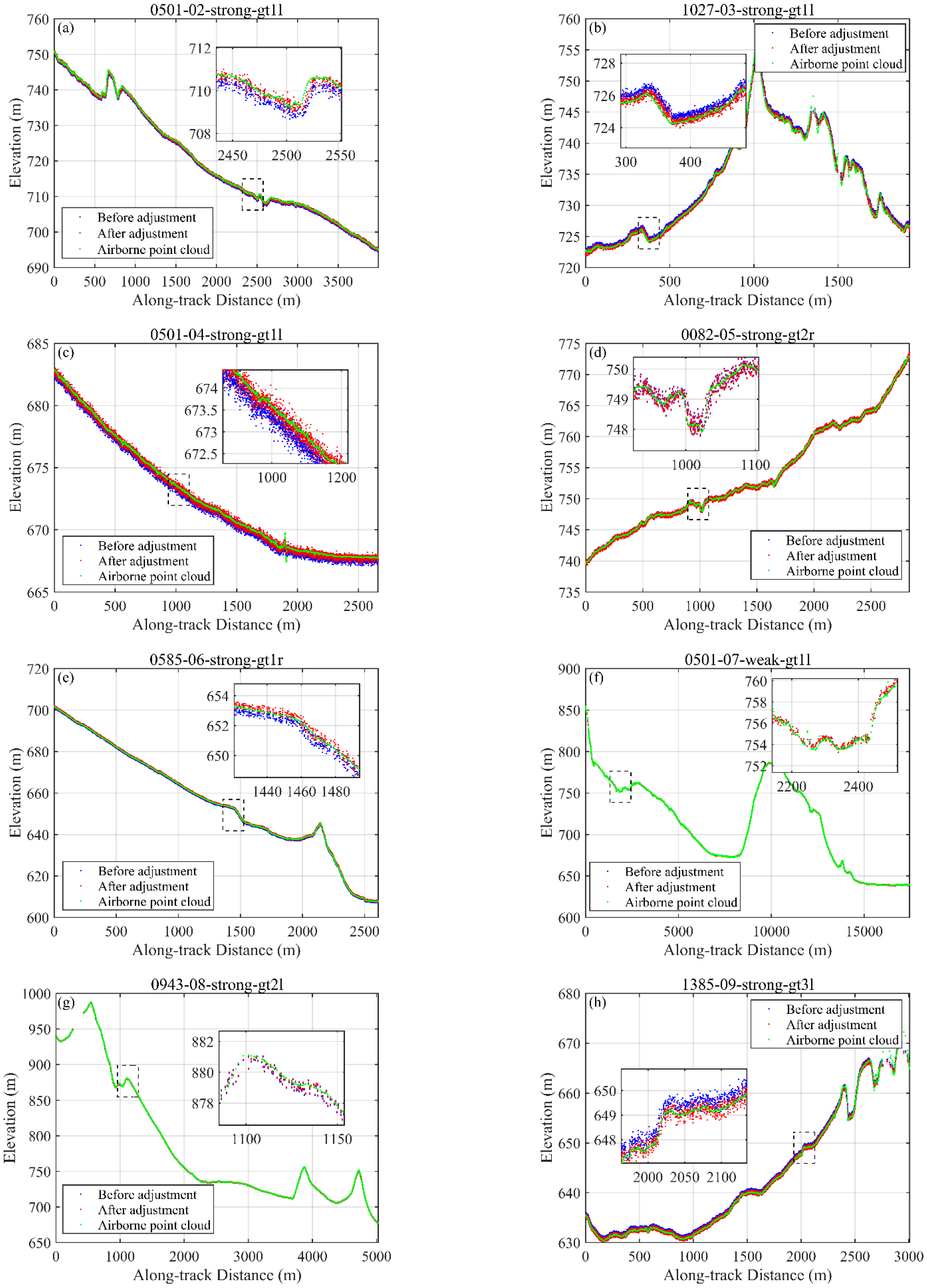
| Beam | Number | Added Error (m) | Estimated Error (m) | Difference (m) | Before Adjustment | After Adjustment |
|---|---|---|---|---|---|---|
| RMSE (m) | ||||||
| 0501-02-strong-gt1l | 13,320 | −0.41 | 0.30 | −0.11 | 0.43 | 0.23 |
| 1027-03-strong-gt1l | 6140 | 0.34 | −0.33 | 0.01 | 0.47 | 0.34 |
| 0501-04-strong-gt1l | 12,862 | −0.19 | 0.22 | 0.03 | 0.30 | 0.15 |
| 0082-05-strong-gt2r | 10,144 | −0.12 | −0.02 | −0.14 | 0.20 | 0.20 |
| 0585-06-strong-gt1r | 9939 | −0.32 | 0.40 | 0.08 | 0.31 | 0.26 |
| 0501-07-weak-gt1l | 17,254 | 0.19 | −0.01 | 0.18 | 0.25 | 0.25 |
| 0943-08-strong-gt2l | 10,811 | −0.11 | 0.05 | −0.06 | 0.35 | 0.33 |
| 1385-09-strong-gt3l | 10,159 | 0.36 | −0.32 | 0.04 | 0.41 | 0.24 |
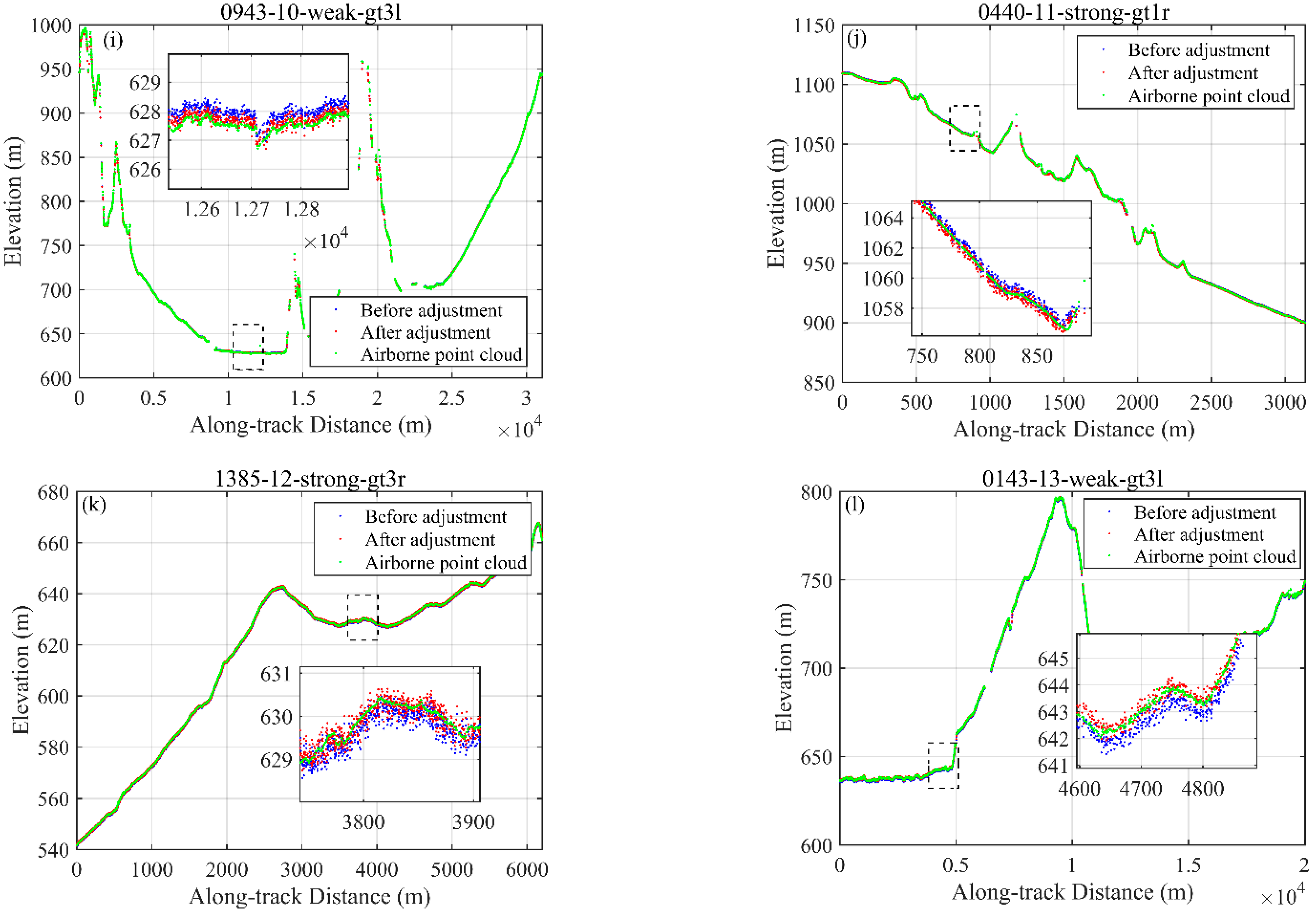
| 0943-10-weak-gt3l | 22,065 | 0.44 | −0.27 | 0.17 | 0.72 | 0.66 |
| 0440-11-strong-gt1r | 6675 | 0.22 | −0.31 | −0.09 | 0.54 | 0.58 |
| 1385-12-strong-gt3r | 23,960 | −0.12 | 0.17 | 0.05 | 0.30 | 0.23 |
| 0143-13-weak-gt3l | 15,757 | −0.22 | 0.51 | 0.29 | 0.50 | 0.31 |
| Beam | Number | Estimated Error (m) | Before Adjustment | After Adjustment |
|---|---|---|---|---|
| RMSE (m) | ||||
| 0501-02-strong-gt1l | 13,320 | −0.11 | 0.21 | 0.22 |
| 1027-03-strong-gt1l | 6140 | 0.02 | 0.34 | 0.34 |
| 0501-04-strong-gt1l | 12,862 | 0.03 | 0.16 | 0.14 |
| 0082-05-strong-gt2r | 10,144 | −0.14 | 0.22 | 0.20 |
| 0585-06-strong-gt1r | 9939 | 0.08 | 0.21 | 0.25 |
| 0501-07-weak-gt1l | 17,254 | 0.18 | 0.30 | 0.26 |
| 0943-08-strong-gt2l | 10,811 | −0.06 | 0.32 | 0.33 |
| 1385-09-strong-gt3l | 10,159 | 0.04 | 0.25 | 0.24 |
| 0943-10-weak-gt3l | 22,065 | 0.17 | 0.68 | 0.66 |
| 0440-11-strong-gt1r | 6675 | −0.10 | 0.56 | 0.59 |
| 1385-12-strong-gt3r | 23,960 | 0.06 | 0.25 | 0.23 |
| 0143-13-weak-gt3l | 15,757 | 0.29 | 0.35 | 0.31 |
| Terrain Slope (°) | 0–5 | 5–10 | 10–15 | 15–20 | 20–25 | 25–30 | >30 | |
|---|---|---|---|---|---|---|---|---|
| All crossovers | Number | 11,035 | 2937 | 2319 | 2020 | 1447 | 909 | 772 |
| STD (m) | 1.16 | 1.14 | 0.90 | 1.08 | 0.82 | 0.95 | 0.93 | |
| Crossovers (difference < 10 m) | Number | 11,009 | 2930 | 2316 | 2015 | 1446 | 908 | 771 |
| STD (m) | 0.82 | 0.86 | 0.78 | 0.80 | 0.76 | 0.86 | 0.80 |
| Terrain Slope (°) | 0–5 | 5–10 | 10–15 | 15–20 | 20–25 | 25–30 | >30 | |
|---|---|---|---|---|---|---|---|---|
| Number | 6,158,823 | 655,499 | 165,507 | 60,282 | 30,516 | 14,155 | 8320 | |
| Before adjustment | Bias (m) | −0.04 | −0.09 | −0.20 | −0.45 | −0.70 | −1.04 | −1.38 |
| RMSE (m) | 0.28 | 0.50 | 0.83 | 1.27 | 1.69 | 2.26 | 2.69 | |
| After adjustment | Bias (m) | −0.02 | −0.08 | −0.19 | −0.43 | −0.68 | −1.02 | −1.36 |
| RMSE (m) | 0.27 | 0.50 | 0.82 | 1.27 | 1.69 | 2.25 | 2.68 |
| Land Types | Water | Trees | Crops | Built Area | Bare Land | Rangeland | |
|---|---|---|---|---|---|---|---|
| All crossovers | Number | 1 | 17 | 62 | 144 | 2082 | 19,133 |
| STD (m) | - | 0.60 | 0.56 | 1.26 | 1.11 | 1.09 | |
| Crossovers (difference < 10 m) | Number | 1 | 17 | 62 | 143 | 2074 | 19,098 |
| STD (m) | - | 0.60 | 0.56 | 0.85 | 0.82 | 0.82 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Fang, Y.; Zhang, S.; Cao, B.; Wang, Z. Biases Analysis and Calibration of ICESat-2/ATLAS Data Based on Crossover Adjustment Method. Remote Sens. 2022, 14, 5125. https://doi.org/10.3390/rs14205125
Wang T, Fang Y, Zhang S, Cao B, Wang Z. Biases Analysis and Calibration of ICESat-2/ATLAS Data Based on Crossover Adjustment Method. Remote Sensing. 2022; 14(20):5125. https://doi.org/10.3390/rs14205125
Chicago/Turabian StyleWang, Tao, Yong Fang, Shuangcheng Zhang, Bincai Cao, and Zhenlei Wang. 2022. "Biases Analysis and Calibration of ICESat-2/ATLAS Data Based on Crossover Adjustment Method" Remote Sensing 14, no. 20: 5125. https://doi.org/10.3390/rs14205125
APA StyleWang, T., Fang, Y., Zhang, S., Cao, B., & Wang, Z. (2022). Biases Analysis and Calibration of ICESat-2/ATLAS Data Based on Crossover Adjustment Method. Remote Sensing, 14(20), 5125. https://doi.org/10.3390/rs14205125






