Abstract
This paper suggests a new algorithm for automatic building point cloud filtering based on the Z coordinate histogram. This operation aims to select the roof class points from the building point cloud, and the suggested algorithm considers the general case where high trees are associated with the building roof. The Z coordinate histogram is analyzed in order to divide the building point cloud into three zones: the surrounding terrain and low vegetation, the facades, and the tree crowns and/or the roof points. This operation allows the elimination of the first two classes which represent an obstacle toward distinguishing between the roof and the tree points. The analysis of the normal vectors, in addition to the change of curvature factor of the roof class leads to recognizing the high tree crown points. The suggested approach was tested on five datasets with different point densities and urban typology. Regarding the results’ accuracy quantification, the average values of the correctness, the completeness, and the quality indices are used. Their values are, respectively, equal to 97.9%, 97.6%, and 95.6%. These results confirm the high efficacy of the suggested approach.
1. Introduction
Light Detection and Ranging (LiDAR) data provide considerable advantages over other photogrammetric and remote sensing data sources. The data can be acquired at high speed and density during the day or night, and have automated processing potential and the possibility of simultaneous georeferenced detection of other supplementary data: laser intensity, RGB, and infrared images [1]. In addition, the laser scanning technique differs from other 3D data acquisition sensors such as optical cameras. The heavy demand for LiDAR data necessitates an increased need for automatic processing tools. Of these tools, the two main operations are the automatic classification and the automatic modelling of LiDAR data. In urban areas, a point cloud consists of several classes such as terrain, roads, buildings, vegetation, and other manmade objects. As each class has its own modelling demands, it is necessary to separate the city classes before starting the modelling step. In urban zones, the building class is of particular importance. Once this class is extracted, two families of modelling approaches are available: model-driven and data-driven [2]. In this context, the input data of any selected modelling algorithm is a building point cloud consisting of a set of points mainly covering the roof surfaces, as the scanning is usually achieved using an airborne vehicle. The building facades will be partially covered with low point density depending on the building location in comparison to the scanning trajectory and the orientation of the facade’s planes. In any case, the roof points will be distributed into scanning lines formed according to the quality of the employed scanning system [3]. Moreover, the building point cloud may contain points covering the surrounded terrain in addition to the low and high vegetation that is associated with the building. Other inconsequential points may be present in the building point cloud such as those that are due to the objects located near the building and the decoration of the facade. However, the modelling approaches used for constructing the building model use the hypothesis that the building point cloud consists of only the roof surfaces (except for the vertical surfaces) [4], which is why the building cloud points need to be classified into two classes: the roof points and the nonroof (undesirable) points. In fact, the undesirable points sometimes represent an obstacle in the modelling algorithms, especially when their percentage exceeds certain limits. Sometimes they are considered as the main reason for automatic modelling failure or the source for some deformations in the obtained building model [5].
Automatic filtering of LiDAR building point cloud has become a very hot research topic. Shao et al. [6] develop a top-down strategy that starts by seed point sets’ detection with semantic information. Then, the region-growing algorithm is applied to detect the building roof point cloud. Moreover, for filtering the LiDAR data and extracting the building class, Wen et al. [7] use Graph Attention Convolution Neural Network (GACNN). This technique is directly applied to the city point cloud. In another way, Varlik and Uray [8] prefer to project the LiDAR point cloud firstly onto a 2D plane before employing a U-net architecture deep-learning network. Alternatively, after detecting the building class, Hui et al. [9] apply multiscale progressive growth to optimize the obtained result.
Tarsha Kurdi et al. [10] suggested an algorithm for automatic extraction of the roof point cloud from the building point cloud by analysis of the Z histogram of the building point cloud. Unfortunately, this algorithm did not consider an important case, which is the case of high trees associated with the building roof. The importance of this case arises when the building mask is automatically extracted from the city point cloud by automatic classification. In this case, a considerable number of buildings will be extracted with their attached trees [11]. This paper suggests an extension of the filtering approach suggested by Tarsha Kurdi et al. [10] for considering the case of high trees that occlude the building roof. The suggested approach starts with the application of the algorithm suggested by Tarsha Kurdi et al. [10] that detects the combined roof and tree crown point cloud. To extract the building roof, three criteria are calculated and analyzed: the normal vector, the standard deviation, and the change of curvature factor. At this stage, the employed threshold values are automatically determined for each building point cloud independently (smart thresholds). This procedure increases the filtering success percentage because it considers the particularity of the point cloud of each building. Finally, the misclassified points are correctly reclassified by using an image-processing operation.
This paper consists of eight sections. The first section introduces the problem of the presence of high trees associated with the building roof which may be considered as a real obstacle in the automatic building-modelling algorithm. Second, similar and related approaches in the literature are discussed. Third, the approach suggested by Tarsha Kurdi et al. [10] is summarized. Fourth, the limitation of the previous approach is highlighted in the case of high trees associated with building roofs. Fifth, the suggested approach is detailed step by step. Section 6 and Section 7 discuss the accuracy and the limitations of the suggested algorithm. Finally, the conclusion draws a panoramic budget and exposes future work.
2. Related Work
In LiDAR data, the aim of the building-extraction algorithm is the extraction of building class from the city point cloud [12]. Unfortunately, the majority of the classification approaches suggested in the literature cannot perfectly achieve the classification task because some misclassified points will be present in the classification result, e.g., the recognition of trees associated with building roofs still represents a challenge, as it is possible to detect a misclassified vegetation segment within the building class when the distribution of the vegetation segment points is similar to that of the building roof. That is why the detected building point cloud needs to be filtered before starting the modelling step.
In the case of building extraction by separating the off-terrain from the terrain classes, Demir [13] studied the case of low terrain slopes and detected the off-terrain objects via an elevation threshold. Thereafter, the nonbuilding objects were cancelled because they have no planar features. In the same context, modern approaches can use the machine-learning paradigm as suggested by Maltezos et al. [11]. This algorithm employed a deep-learning paradigm based on a convolutional neural network model for building detection from the city point cloud. The successful extraction percentage was about 80%. Moreover, the classification approach developed by Liu et al. [12] combined the Point Cloud Library (PCL) region growth segmentation and the histogram. For this purpose, they employed a PCL region growth algorithm to segment the point cloud and then calculated the normal vector for each cluster. The histograms of normal vector components were calculated to separate the building point cloud from the nonbuilding. Despite the classification result in this approach being better than the former ones, the obtained results still need improvement and filtering before starting the modelling step.
It is now understood why most of the modelling algorithms include a point cloud filtering step. Tarsha Kurdi et al. [14] calculated the building Digital Surface Model (DSM) by eliminating the undesirable points associated with vertical elements such as the building facade. In fact, DSM is a 2D matrix where the pixel value is equal to the interpolated Z coordinate of LiDAR points located in this pixel. This procedure cannot always eliminate all these points, which is why Park et al. [15] eliminate the unnecessary objects by realizing the cube operator to segment the building point cloud into roof surface patches, including superstructures, removing the unnecessary objects, detecting the boundaries of buildings and defining the model key points for building modelling. Zhang et al. [16] and Li et al. [17] used a region-growing algorithm based on the Triangulated Irregular Network (TIN) or grid data structures to detect the building roof point clouds.
In order to identify the roof points, some authors used additional data such as the ground plan [18] or the aerial images [19,20,21], while many others (Jung and Sohn [22] and Awrangjeb et al. [23]) considered only the extracted roof point cloud instead of the whole building point cloud to construct 3D building roof models.
Hu et al. [19] filter the building point cloud through projecting back the building points on imagery using the Normalized Difference Vegetation Index (NDVI). Then, the Euclidean clustering is applied to remove vegetation clusters with small areas. In another approach, the building point cloud is divided into two classes by using machine-learning techniques [24]. These classes are the roof and the façade classes. For achieving this goal, the TensorFlow neural network for deep learning is employed. Unfortunately, the result is not so promising where the classification percentages of the semantic classes are less than 85%. In the context of façade point class recognition, another technique is suggested by Martin-Jimenez et al. [25]. It suggests the calculation of the normal vector of the building point cloud. For this purpose, the covariance matrix is calculated for each point and its eight neighboring points. Then, the calculated normal vector is assigned to the tested point. This method does not consider the presence of decorative elements in the building facades in addition to the surrounding terrain point and small vegetation.
At this stage, it is important to note that the building point cloud may be divided into two main classes, which are roof and nonroof classes. The roof class involves a point set that is employed by the building construction algorithms, whereas the nonroof class is a point set of undesirable and useless points for the building modelling algorithms. The undesirable points represent the surrounding terrain, façade, vegetation, and noise. For the purposes of this paper, we will use the term undesirable points to describe the nonroof class, and the procedure of roof points extraction from the building point cloud will be referred to as filtering.
3. Filtering of Building Point Cloud Which Does Not Contain High Trees
This section summarizes the filtering approach suggested by Tarsha Kurdi et al. [10] because the suggested algorithm in this paper represents an extension of the previous one. Building point clouds can be extracted through the manual or automatic classification of the city LiDAR point cloud. The approach suggested by Tarsha Kurdi et al. [10] detects the roof points from the building point cloud based on the analysis of the Z coordinate histogram. This algorithm supposes that the input building point cloud does not contain high trees (the same height or higher than the roof). The basic hypothesis adopted is that the point density of the roof surfaces is considerably greater than the building’s facades. This algorithm starts by calculating the histogram of the Z coordinate of the building point cloud (see Figure 1b,e and Figure 2b,e). This histogram consists of a set of consecutive 1m bins, each bar value representing the number of points within an altitude interval. The ideal histogram step value is dependent on the altimetry accuracy of the point cloud, the roof-texture thickness and the inclination of roof surfaces. For more details about the step value assignment in addition to all technical characteristics and analysis please see Tarsha Kurdi et al. [10].
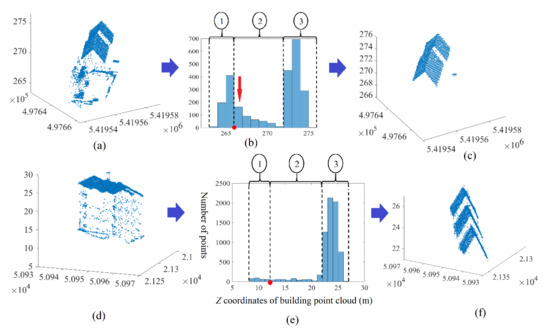
Figure 1.
(a,d) Building point clouds in Vaihingen and Hermanni datasets; (b,e) histograms of Z coordinate of building point clouds consecutively of the last two buildings; (c,f) final results of building point clouds’ filtering; The red dot in (b,e) is the PSTF; “1,2,3” in circles in (b,e) are building section numbers.
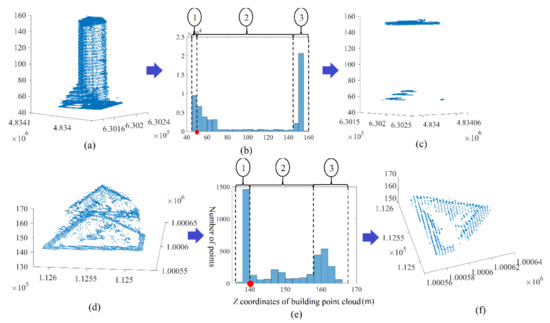
Figure 2.
(a,d) Building point clouds, respectively, in Toronto and Strasbourg datasets; (b,e) histograms of Z coordinate of building point clouds consecutively of the last two buildings; (c,f) final results of building point clouds’ filtering; The red dots in (b,e) are the PSTF; “1,2,3” in circles in (b,e) are building section numbers.
From Figure 1 and Figure 2, the histogram of the Z coordinate of the building point cloud consists of three sections. Section 1 represents the terrain surrounding the building, low vegetation, noise, and the lower parts of the façade. Section 2 represents the points spread on the building façades, and Section 3 represents the roof point cloud. In order to determine the limits between these three sections, eight rules are adopted as follows:
Rule 1: The leftmost bar of the histogram belongs to the terrain section.
Rule 2: The rightmost bar of the histogram belongs to the building roof section.
Rule 3: Location of PSTF (point separating terrain and façade) (the red dot in Figure 1b). This point must be located within the four leftmost bars in the histogram. If the number of terrain points is not negligible (case of a flat terrain), the PSTF will be located after the bin with a significant population within the first four bars. If there is not a substantial number of terrain points within the building point cloud (case of significant terrain slope), the PSTF will be situated beside the fourth bar. In this case, the number of terrain bins will increase but their populations will drop down. Moreover, the first four bins will be considered as terrain bins whereas the other terrain bins will appear in the façade section. This misclassification is tolerated because it will not affect the final result, which is the detection of the roof point cloud.
Rule 4: Each bin with a considerable population (given the threshold) after the PSTF belongs to the roof surface section.
Rule 5: The roof points are presented in the histogram by one- or multi-bins situated after the PSTF. All bins to the right of the previous roof surface bin belong to the roof.
Rule 6: The bar of the façade section that is immediately located before the roof surface section may represent roof and façade points together. Therefore, the points belonging to the upper half of this bar must be added to the roof section.
Rule 7: All undesirable point bars situated after the PSTF have small values (given the threshold) in comparison to the values of roof surface bars.
Rule 8: In the histogram and after the PSTF, there are some bars with smaller values than the roof surface bars and greater values than the undesirable point bars (red arrows in Figure 1b). As these bars do not belong to the undesirable point or to the roof class, they are described as fuzzy bars. This is why it is necessary to check the presence of small roof planes amongst the points represented in the fuzzy bars.
In fact, the idea of fuzzy bars solves the problem of the sensitivity of threshold value selection. Indeed, the point sets represented by fuzzy bars will be checked for the presence of roof planes within them. This approach is well-known in remote sensing as applying fuzzy logic [26]. For more details about this algorithm and the employed threshold values, see Tarsha Kurdi et al. [10].
This rule list could be written as a pseudocode which clarifies all employed equations, as follows:
Where n is the number of bars in the histogram; PSTF: point separating terrain and façade; hrb: roof bars; hfb: façade bars; hfuz: fuzzy bars.
4. Results of Filtering Algorithm Application
The experiments illustrated in this section not only prove the necessity of improving the previous filtering algorithm but also underline the differences between the extended and nonextended filtering algorithms. The algorithm described in the last section was tested with two sorts of building point cloud samples. The first ones represent building clouds that do not contain high trees that occlude the roof, whereas the second samples represent building clouds that contain high trees that occlude the roof. Figure 1 and Figure 2 present the results of the last algorithm application on building clouds without associated trees and Figure 3 shows the results with attached trees adjacent to the roofs.
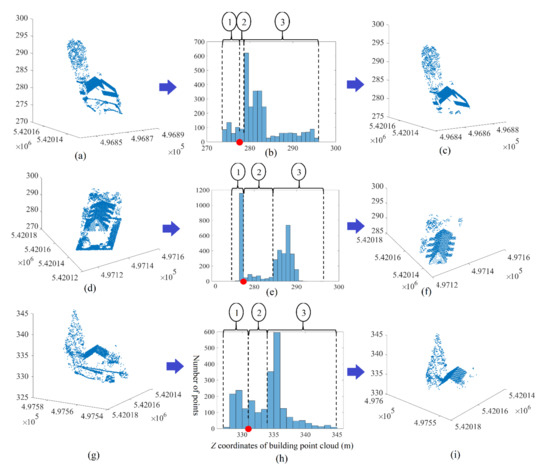
Figure 3.
Results of filtering algorithm application in case of buildings which contain high trees that occlude the roof. (a,d,g) The original building point clouds; (b,e,h) histograms of building point clouds; (c,f,i) noisy roof point clouds; (a–c) building number 4; (d–f) building number 5; (g–i) building number 6; The red dots in (b,e,h) are the PSTF; “1,2,3” in circles in (b,e,h) are building section numbers.
In Figure 1 and Figure 2 where the building clouds do not contain trees that occlude the roof, the algorithm successfully eliminated all undesirable points and saved only the roof points (see Figure 1c,e and Figure 2c,e). By contrast, in Figure 3 where the building clouds contain trees that occlude the roof, the algorithm eliminated all undesirable points except for the tree crowns, and saved the tree crowns in addition to the roof points (see Figure 3c,e,f).
Although the tree crowns are not excluded in the filtering results, the façade points which represent an obstacle in the building cloud filtering procedure are eliminated. This shows, in the case of the presence of trees that occlude the roof, a path towards cancelling the tree points based on the elimination of the vertical element points. At this stage, before improving the filtering algorithm, two remarks have to be considered:
- The analysis of fuzzy bars in the building point cloud histogram has to be postponed to the end of the tree point elimination. This choice is supported by the fact that the roof planes, perhaps presented by fuzzy bars, are low in comparison to the building roof level and have smaller areas. If these planes were to be extracted before eliminating the tree points, they may be eliminated during the tree point recognition step.
- The application of the first seven rules on the building point cloud creates a new point cloud that represents the building roof (without the planes of fuzzy bars) in addition to the tree crown. This cloud will be named the noisy roof cloud.
At this stage, it is useful to state that the results of extended filtering approach of the same samples mentioned in Figure 3 will be later illustrated in Figure 10, where the tree crowns are successfully distinguished thanks to the extended algorithm. The next section explains the suggested extension of the filtering algorithm.
5. Extended Filtering Algorithm
This paper suggests an extension of the filtering approach suggested by Tarsha Kurdi et al. [10] to consider the case of building point cloud containing high trees that occlude the roof. Figure 4 shows the workflow of the extended algorithm.
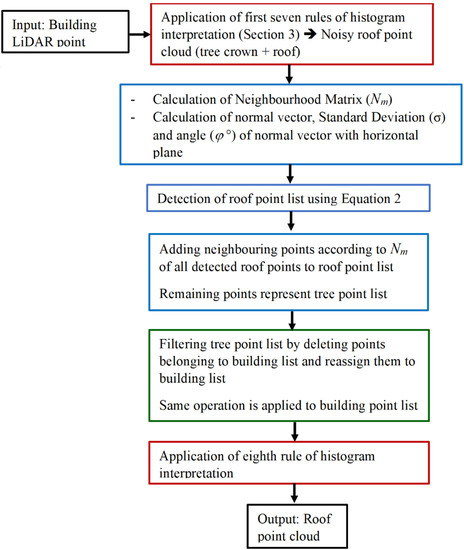
Figure 4.
Workflow of the extended filtering algorithm where σ is the standard deviation of the fitted plane, φ° is the angle of the normal vector with the horizontal plane, Ccf is the change of curvature factor, and Thσ, Thφ and Thccf are their respective thresholds.
The extended algorithm starts by applying the first seven rules of histogram interpretation to the building point cloud (see Section 3). This operation allows the elimination of the majority of noisy points under the roof level except for the roof planes linked to the fuzzy bars. The eliminated noisy points represent the façade points, the surrounding terrain points, the low vegetation points, the high tree stem, and low branch points, and all other noisy points such as objects located near the building. The obtained point cloud represents the roof in addition to the associated tree crowns, which is why it is named the noisy roof point cloud. The next section exposes the calculation of the Neighborhood Matrix (Nm) of the noisy roof point cloud.
5.1. Selection of Neighbouring Points
To calculate the normal vectors and roof features of the noisy point cloud, the approach suggested by Dey et al. [27] was adopted. This selection used the dynamic method for selecting the neighborhood of each point. Consequently, only the necessary minimum number of neighboring points were considered for each roof point. This leads to minimizing the error during the estimation of the normal vectors and the roof features values.
The approach suggested by Dey et al. [27] starts by selecting the initial minimum number of neighboring points by considering the case of a regular distribution of points where each point has eight neighboring points. To reliably calculate a normal vector to a plane, the point selection needs an evenly distributed sample of points from the plane. To ensure the neighborhood is not limited to a single scanning line, the considered point and its neighborhood are fitted to a 3D line where the standard deviation value represents an indicator factor reflecting the number of scanning lines that are included in the neighboring points. If the considered point and its neighborhood belong to more than one scanning line, the estimated values of the normal vector and the roof features will correctly describe the point’s geometric position regarding the roof facets. Alternatively, if the considered point and its neighborhood belong to only one scanning line, the estimated values of the normal vector and the roof features may be inaccurate. In this context, an iteration loop is employed to increase the number of neighboring points in each iteration until the selected neighboring points are located on more than one scanning line. For more details about this algorithm, please see Kumar Dey et al. [27].
The neighborhood is selected using only X and Y coordinates instead of X, Y and Z. This choice is adopted because the 3D neighborhood selection leads to the detection of all points situated within a sphere around the considered point, whereas in 2D, the neighborhood selection allows the detection of all points situated within a vertical cylinder around the considered point. In the case of a point located on a roof plane, the two selection options provide almost the same result, but in the case of a point located on a tree, where the LiDAR points are distributed on the branches and leaves, the neighborhoods differ. Consequently, this choice helps to increase the difference between the roof and the tree points when the normal vector and roof features are calculated, as shown in the next section.
The operation described in this section allows us to define a new matrix named the Neighborhood Matrix (Nm). This matrix is determined from the neighboring points for each cloud point. This matrix consists of n rows (n is the number of points of noisy roof cloud) and N columns. The number N represents the maximum possible number of neighboring points (please see Dey et al. [27]). Furthermore, In the point cloud list, the order of each point is the point number, e.g., if the point number i has 45 neighboring points, then the first 45 entries of the row number i will contain the neighboring point numbers, and the rest of cells of this row will contain zeros. This matrix will be employed for calculating the normal vector in addition to the roof feature values. Moreover, it will be used later (see Section 5.4) to recognize the roof points.
Once the Nm is calculated, the normal vectors of the noisy roof cloud can be calculated.
5.2. Calculation of Normal Vectors and Change of Curvature Factor
Once the neighboring points are determined for each LiDAR point through the matrix Nm, the best plane passing through each point can be fitted and the normal vector then can be calculated. To achieve this objective, the plane equation will be fitted using the eigenvectors of the covariance matrix which was employed by Sanchez et al. [28]. In this paper, three criteria are employed for distinguishing the roof points from the tree ones. These criteria are the standard deviation (σ) of the fitted plane (in meters), the angle (φ°) of the normal vector with the horizontal plane and the change of curvature factor (Ccf) (unitless) which is calculated based on the eigenvalues according to Equation (1) [29].
where are the eigenvalues in descending order.
Once the target criteria are calculated for all cloud points, the next step is the filtering of the noisy roof points from the tree ones.
5.3. Filtering of Noisy Roof Point Cloud
In order to recognize the roof points in the noisy roof cloud, the three criteria calculated in the last section will be implemented. In this context, all points conforming to Equation (2) are selected.
where σi, φi and Ccf i are, respectively, the standard deviation, the angle (φ°) and the change of curvature factor of the point number i. Furthermore, Thσ, Thφ and Thccf are the assigned thresholds that are used for detecting the roof points. In this context, the employed threshold values change from one building to other, and a stochastic method is adopted for calculating the smart threshold values. This method relies on the histogram analysis as shown in the next section.
5.4. Calculation of Smart Threshold Values
For noisy roof cloud, Figure 5a,b and Figure 6 represent examples of the histograms of σ, φ° and Ccf, respectively. The step values in these histograms are, respectively, equal to 0.2 m, 10° and 0.01 (unitless). These values are selected empirically depending on the range of each parameter and the sensitivity of the parameter variation to the filtering results, e.g., in Figure 5 and Figure 6, the variation of φ° values has less influence on the filtering result than the variation of Ccf parameter, which is why the number of bins of φ° histogram is fewer than the number of bins of Ccf histogram. Though the high-quality results shown in Section 6 demonstrate that the selected values of the three histogram steps are successful, more investigations are needed to prove their optimal values, which can be applied to different point densities and urban typologies.
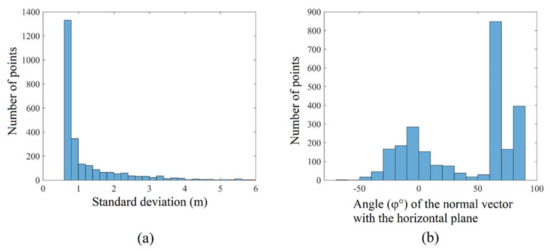
Figure 5.
(a,b) Histograms of standard deviation (σ) and the angle (φ°) of normal vector with horizontal plane of noisy point cloud.
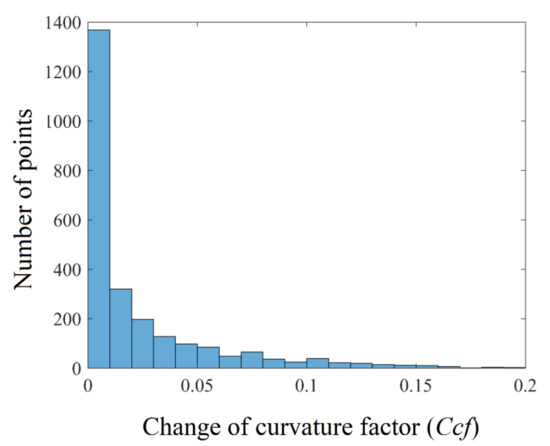
Figure 6.
Histogram of change of curvature factor (Ccf) of noisy point cloud.
In Figure 5a, the longest bar, which is the leftmost bar, represents most of the points that belong to the roof. Indeed, the majority of roof point neighborhoods (except for the roof plane boundary points) have similar standard deviations. Moreover, seen in Figure 5a, the value of roof standard deviation is at a minimum in comparison to the plane boundaries, tree, and noisy points. In fact, the typical roof points’ neighborhood standard deviation value is dependent on factors such as cloud altimetry accuracy and roof-texture thickness. At this stage, it is important to note that some of the points represented by the roof section of the histogram do not belong to the roof. This is because among the tree points it is possible to find some points that fit a plane with their neighborhood with minimal standard deviation. Moreover, some of the roof points such as the roof plane boundary points, the points of roof details such as chimneys and windows, and roof noise points, may be present in the other histogram bins. Despite the majority of roof points being represented by the roof section bins in the histogram, the percentage in these bins differs from one building to another. Indeed, the variation in texture thickness, the point density, and the roof complexity play an essential role in determining this percentage. Notwithstanding this, in all buildings, the majority of roof points will be represented by the roof section of the standard deviation histogram. Nevertheless, the use of only the standard deviation criterion is not enough to detect the roof points. Finally, the same analysis can be applied to the histogram of Ccf presented in Figure 6.
In Figure 5b, knowing that the histogram is oriented from the left to the right, all bars starting from the longest one to the right end of the histogram represent the majority of roof points. All remarks in the last paragraph can also be applied to this histogram.
At this stage, there are three remarks that must be made. First, each one of the three histograms illustrated in Figure 5 and Figure 6 can be divided into two sections: a roof point section that represents the majority of roof points and a noise section that represents the majority of noise points. Second, in the roof point sections of the three histograms, the percentage of roof points is different from one histogram to another. Third, the number of points presented in the roof sections in the three histograms is not the same.
In order to smartly (automatically) determine the three threshold values employed in Equation (2), four rules are empirically adopted. Figure 7 illustrates the used algorithm for automatic calculation of the employed thresholds. The applied rule list could be summarized as follows:
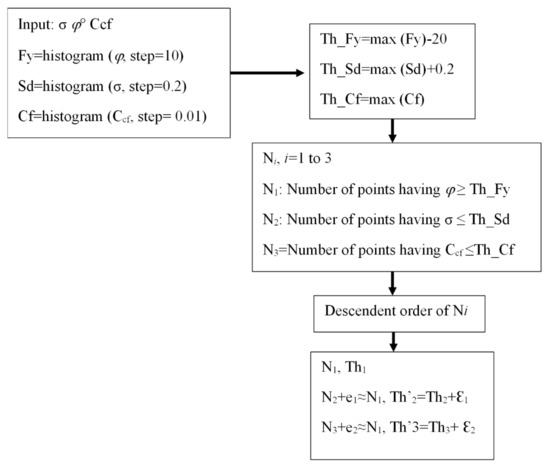
Figure 7.
Algorithm flowchart for smart calculation of employed thresholds; Thi (Th_Fy, Th_Sd, Th_Cf) are the used thresholds; εi are last shifts applied on thresholds; ei: are difference of number of points detected by thresholds before applying the shifts εi.
Rule 1: In the case of the building represented by Figure 5, the most frequent value of the angle (φ°) according to Figure 5b is 70°. This value is very big with respect to the other values in the interval of angle value [−60°, 90°]. This is why a tolerance value has to be added in order to consider the small uncertainties of fitted plane orientations. These uncertainties normally occur due to the use of a minimum number of neighboring points for fitting the best plane. Consequently, the threshold Thφ is shifted to two bins to the left of the most frequent angle bin.
Rule 2: Rule 1 is applied for the Thσ threshold, except the threshold Thσ is shifted to only one bar to the right of the most frequent standard deviation bar.
Rule 3: The threshold Thccf is considered to be the most frequent value in the histogram (Figure 6) without shifting.
Rule 4: The threshold (among the last three) that allows the selection of the maximum number of points is chosen, and the other two threshold values, are shifted so as to select a similar number of points using each threshold individually.
The application of this strategy allows the value of thresholds to change from one building to other (Table 1).

Table 1.
Values of calculated thresholds for the three buildings represented in Figure 3 in addition to five other buildings from Vaihingen point cloud.
From Table 1, it can be noted that the threshold Thσ value is constant in eight buildings (Thσ = 0.8 m). In fact, the nine buildings belong to the same point cloud (Vaihingen city) and have the same urban typology and similar texture. On the other hand, the values of the thresholds Thφ and Thccf are related to the architecture complexity level of the roof, e.g., Building 2 has the most architecturally complex roof. This is why the Thφ value is the smallest (30°) and Thccf value is the largest (0.04).
Once the thresholds values are assigned, Equation (2) is applied for detecting the roof points. Figure 8a shows the results of the application of this procedure. It may be observed that all roof points are detected, except for the boundary points and the roof detail points. To complete the recognition of roof points, the Nm matrix is employed. For each detected point in Figure 8a, all its neighboring points have to be added to the roof class according to the matrix Nm. Figure 8b illustrates the result of adding the neighboring points. At this stage, all remaining points in the noisy point cloud will represent the tree class (red color in Figure 8c). Inside the black circles in Figure 8c, some roof points that were misclassified as vegetation points can be seen. The process for improving this result is detailed in the next section.
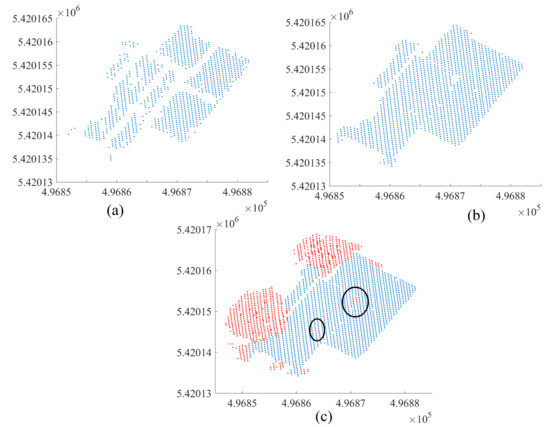
Figure 8.
Separation roof points from high tree points. (a) Employment threshold result; (b) adding neighboring points to the result; (c) building points are in blue and tree points are in red; black circles refer to misclassified points.
5.5. Improvement of Filtering Results
The filtering algorithm presented previously separates the noisy roof cloud into two classes, which are the roof class and the noise or vegetation class. In the obtained result (see Figure 8c), there are some building points classified as noise and vice versa. In this section, an additional operation will be added to the filtering algorithm for improving the result. In this context, two normalized Digital Surface Models (nDSM) are calculated [30]. The first one is of the roof class (Figure 9b), whereas the second one is of the noise class (Figure 9a). The two nDSM models have the same dimensions which correspond to the dimensions of the whole noisy point cloud nDSM. At this stage, a new matrix is defined that is named Noisy Cloud 2D Matrix (NC2DM). To calculate this matrix, the noisy point cloud is superimposed over an empty matrix with the same dimensions as the last nDSM. Each cell in this matrix will contain a set of points that are located within the cell borders [30]. In fact, NC2DM has special importance because it serves as a link between the nDSM and the noisy point cloud, e.g., one nonzero pixel in nDSM corresponds to a list of points (belonging to the noisy point cloud) that are located in this pixel. Consequently, if any pixel of the roof nDSM is reassigned to the noise class, the list of points located in this pixel will be extracted from the roof cloud and reassigned to the noise cloud. In this context, the matrix NC2DM offers the possibility of directly recognizing the set of points that is moved from one class to another.
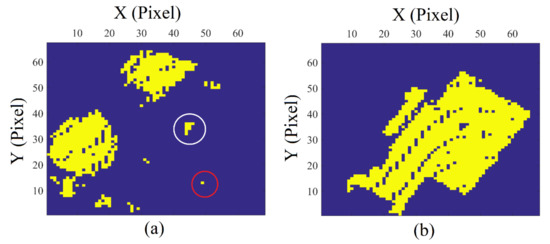
Figure 9.
Visualization of normalized Digital Surface Models (nDSM) before improvement; (a) vegetation class; (b) roof class.
Starting with the noise nDSM, a region-growing algorithm is applied for segmenting the noise nDSM. For each segment, if it is entirely located within the roof perimeter then it is considered as part of the roof, e.g., the segment situated within the white circle in Figure 9a is located inside the roof perimeter, so it is reassigned to the roof class. Moreover, a segment with an area smaller than 5 pixels and tangent to the roof is considered as part of the roof, e.g., the segment within the red circle in Figure 9a is tangent to the roof perimeter and its area is equal to 1 pixel, so it is reassigned to the roof class. The last two types of pixels are cancelled from the noise class and reassigned to the roof class. Inversely, the same operation is applied to the roof class.
Once the improved filtering algorithm is completed, rule 8 (Section 3) is applied to add the result of fuzzy bars analysis. Figure 10 shows the final results of filtering the three building point clouds illustrated in Figure 3. In this figure, all trees (in green color) are recognized, and the building roof (in red color) is detected accurately.
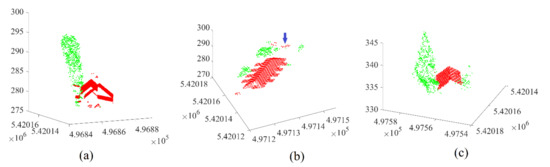
Figure 10.
Final filtering results of three building point clouds illustrated in Figure 3; (a) Building 1; (b) Building 2; (c) Building 3. Green color represents vegetation and red color represents roof.
At this stage, it is important to note that the extended filtering algorithm can be applied in the case of existing high trees associated with the building as well as in the case of nonexistent high trees in the building point cloud. The difference between the two cases is the processing time. Of course, if there are no high trees occluding the roof, the application of the original filtering algorithm will be faster because the processing time consumed by the extended algorithm is greater than the original algorithm. In the next section, the accuracy of the suggested filtering algorithm will be estimated using the five point clouds exposed in Section 6.1.
6. Results
Before presenting the results of the suggested approach, it is unavoidable to detail the used dataset samples. The next section introduces the employed point clouds.
6.1. Datasets
To evaluate the efficiency of the suggested approach, five datasets were used (Hermanni, Strasbourg, Toronto, Vaihingen and Aitkenvale) (See Figure 11 and Table 2). These five test sites contain 12, 56, 72, 68 and 28 buildings, respectively. The selected sites represent different urban typologies, and their point clouds have different point densities. While some of them contain high trees associated with the building, others are vegetation-free. This choice is adopted for estimating the reliability of the filtering approach in these two cases. Table 2 shows the characteristics of the selected point cloud samples such as their acquisition dates and height, the employed sensor and the point density.

Figure 11.
Locations of the study areas: (a) Hermanni; (b) Toronto; (c) Aitkenvale; (d) Vaihingen; (e) Strasbourg.

Table 2.
Tested datasets.
The Hermanni dataset represents a housing area in Helsinki city, where multistorey buildings are enclosed by trees. This data belongs to the building extraction project of EuroSDR [31].
The Strasbourg point cloud in France represents Victory boulevard. This sample has special importance because it has a low point density and it represents several urban typologies. Toronto point cloud [32] in Canada, contains both low and high-storey buildings with significant architectural variety.
The fourth dataset is selected in Germany, in Vaihingen city [32]. The scanned area covers small detached houses within a zone rich in vegetation. The trees associated with buildings represent a high variation of quality and volume. The last dataset is of Aitkenvale in Queensland, Australia [33]. It contains 28 buildings with a high point density (29–40 point/m2). It covers an area of 214 m × 159 m and it contains residential buildings and tree coverage that partially covers buildings. In terms of topography, it is a flat area.
6.2. Accuracy Estimation
To estimate the accuracy of the extended filtering algorithm, the roof point clouds of the chosen building samples were manually extracted (point per point), since manual extraction is supposed to be more accurate than automatic extraction [1], and then considered as the reference.
Figure 12 compares the number of points between the building point clouds, the reference roof clouds, and the filtered roof clouds of the Vaihingen dataset. The first 51 buildings have trees associated with the roofs and the last 17 buildings are high-vegetation-free. It can be seen that the filtering algorithm performs the task of recognizing high trees associated with the roofs well. Consequently, the results in the case of high-tree-occluded buildings are comparable to the case of high-tree-free buildings. Indeed, the number of points of the filtered roof clouds is similar to that of the reference models.
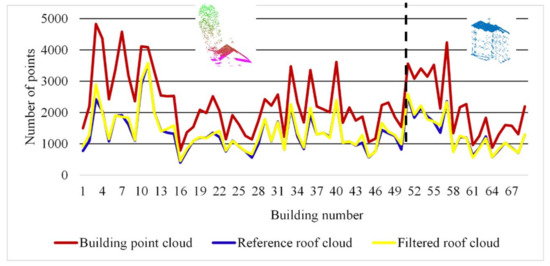
Figure 12.
Comparison between number of points of building point clouds, reference roof clouds and filtered roof clouds of Vaihingen dataset; the first 51 buildings have trees associated with roofs and the last 17 buildings have no trees associated with roofs.
In the context of error estimation, the confusion matrix is used for calculating the correctness (Corr), the completeness (Comp), and the quality indices (Q) (Equations (3)–(5) [1]):
where TP (true positive) means the common points of both reference and detected roof, FN (false negative) means the points of the reference not found in the detected roof and FP (false positive) means the points of the detected roof not found in the reference.
Table 3 shows the correctness, completeness and quality indices for the five datasets used. It can be noted that the undesirable point proportion in the building point cloud is considerable (average = 26.7%). The high accuracy of the suggested filtering algorithm can be observed from the values of the correctness and completeness indices that were almost always greater than 95%.

Table 3.
Average values of three datasets’ filtering accuracy elements.
The quality value for the Toronto data (94.23%) is smaller in comparison to the Hermanni data (99.45%). In fact, as mentioned in Section 6.1, the Toronto data represents tall buildings with a wide variety of rooftop and façade structures and textures, e.g., in the building illustrated in Figure 13a–c, a set of high-density points are detected inside the building (see the red arrow in Figure 13a). These points are perhaps due to the quality of the façade texture on that level. On one hand, as these points fit a plane and have a high density, they are detected by the filtering algorithm. On the other hand, these points were confusing for the operator who achieved the filtering manually because it is unusual to find this quantity of points inside a building. To summarize, the cascading flat roof property and texture variety in the data for Toronto play a major role in this result, and it is possible that the quality value may be underestimated in this case.
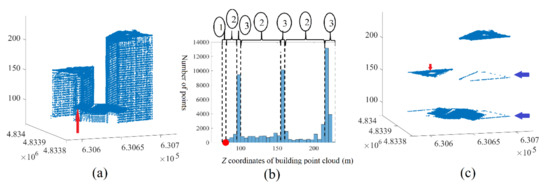
Figure 13.
(a) Building point cloud in Toronto dataset; (b) histogram of Z coordinate of building point cloud; (c) final result of building point cloud filtering; the red dot in (b) is PSTF; the blue arrow in (c) façade points that are saved; the red arrow in (c) the missed small and low plane; “1,2,3” in circles in (b) are building section numbers.
From another viewpoint, the quality evaluation of Vaihingen, Toronto, Strasbourg, and Aitkenvale filtering results are all smaller also than that of Hermanni dataset. Indeed, the developed algorithm suffers from three limitations that decrease the accuracy of the final filtering results. These limitations are:
- In the case of high buildings with a high point density, the small roof planes that are not located in the main roof level may not be detected.
- In the case of buildings that consist of several masses with different heights, the portions of façade points with the same altitudes of the low roof planes will not be cancelled.
- Some of high tree points will not be eliminated.
On one hand, these limitations may adequately explain why the FN values are slightly greater than zero. On the other hand, the higher FN values may be due to the accuracy of the manual extraction of the reference roof clouds. Indeed, in the manual extraction, the presence of confusing points attached to the transparent surfaces of buildings sometimes makes the operator unsure of the proper classification. Regarding the importance of the last three points, they will be detailed in Section 7.
However, despite the difference in the typology, the point density and the undesirable point percentage in these five point-clouds, the excellent results show the capacity of the suggested filtering algorithm to process the majority of building and point cloud qualities.
7. Discussion
In this section, four ideas are discussed which are the accuracy discussion, accuracy comparison between the suggested approach and similar ones, comparison with deep-learning-based methods and the ablation study applied on a building point cloud containing high trees.
7.1. Filtering Accuracy Discussion
Concerning the algorithm limitations, if the roof area is large and the point density is high, the threshold of the number of the façade points according to Rule 6 (Section 3) will have a considerable relative size (10% of the greatest roof bar), e.g., if a flat roof area = 500 m2 and the mean point density = 6 points/m2, the threshold of the number of the façade points according to Rule 6 =300 points. Consequently, the detection probability of a small and low roof plane (for example: area = 5 m2 and the number of points = 30 points) will be low because the number of the plane points in addition to the façade points belonging to the same bar may be smaller than the selected threshold. In the same context, when the building is high, this probability will decrease more because the point density of the roof surface will be greater than the mean point density. Figure 13c shows that one low and small roof plane is missed by the filtering algorithm (the red arrow points to a missed roof plane).
The second case of probable filtering error is when the building consists of several masses of differing heights. The portions of façade points that have the same altitudes of the lower roof planes will not be cancelled (blue arrows in Figure 13c). Indeed, the saved façade points in this case may belong to the same bins of the lower roof planes.
In the case of trees associated with roofs, despite the suggested algorithm’s ability to recognize the majority of tree points, some tree points with the same characteristics of roof points (σ, φ and Ccf) may not be eliminated (see blue arrow in Figure 10b). In fact, the percentage of these points in all tested buildings, in comparison to the number of the tree points, was negligible (less than 1%), which is why their influence on the modelling step was neglected.
Another limitation of the suggested algorithm is that it was tested only on the Lidar point clouds. Therefore, more tests are required in the future for other point cloud types such as the photogrammetric point clouds from oblique areal imaging, oblique scanners or from Unmanned Aerial Vehicle (UAV) imagery.
In conclusion, despite the last limitations not being common, the algorithm could be improved by considering them. Although the suggested filtering algorithm has the previous limitations, it always conserves the main roof planes and eliminates the majority of undesirable points (Q = 95.6%). The testing results on a great number of buildings, illustrated in Figure 12, shows the proficiency of the suggested approach, where the successful filtering rate is equal to 98% despite the variation in typology and point density of selected samples.
7.2. Accuracy Comparison
In the literature, the building point cloud filtering procedure is applied in two contexts. First, in the context of automatic classification of a point cloud when the classification approach aims to detect the building point clouds, the filtering operation is applied on the building mask to improve its quality [9,11]. Second, in the building modelling algorithm, the filtering operation is applied to the building point cloud before starting the construction of the building model. Hence, the filtering algorithm aims to eliminate the undesirable points before starting the modelling step [34,35,36]. In the two last cases, the filtering algorithm is merged with the classification or modelling approaches. This is why it is rare to find independent accuracy estimations of a filtering algorithm in the literature. Despite this, the influence of the employed filtering operation will appear in the quality of the final product (building mask or building model). This is why the accuracy of the suggested approach is compared with the accuracy of the approaches [7,9,11,34,35,36] in the context of comparing the efficacity of the suggested approach with other similar approaches suggested in the literature
To clarify how this comparison can be achieved, let us take this example. First, the result of an urban point cloud classification is a building mask named m1. According to the classification accuracy, a certain amount of nonbuilding points and noisy points may be present in this mask. Second, a region-growing algorithm is applied to this mask to detect each building independently and is then filtered by the suggested algorithm in this paper. This procedure allows for generating a filtered building mask named m2. Third, a 2D outlines modelling algorithm is applied to m1, which produces a new model named m3. Finally, the three calculated masks can be compared with a reference model to estimate their accuracy through the confusion matrix. If the deformations generated by the modelling algorithm in m3 are neglected, a comparison between the last three models’ accuracies can be achieved, to judge which model is more faithful to the reference model.
According to Griffiths and Boehm [37], the high trees associated with the building roof are considered the main source of incorrect results among the several LiDAR data procedures such as automatic building extraction using convolutional neural networks [7,11] and building outlines’ modelling [34,35,36]. In this context, it is useful to compare the accuracy of the suggested approach with the accuracy of six previous studies (Table 4).

Table 4.
Accuracy comparison of suggested approach with previous studies.
At this stage, it is more appropriate to compare algorithms as they perform on common datasets. This is why all selected approaches in Table 4 employ the Vaihingen dataset (Table 2) provided by the ISPRS (International Society for Photogrammetry and Remote Sensing).
From Table 4, it can be noticed that correctness and the quality factors in the suggested approach (97.9% and 95.6%) are considerably greater than the other six approaches, where the maximum values are equal to 96.8% and 93.2% in Zhao et al. [36]. These two measures consider the FP value (the points of the detected roof not found in the reference) which represent, in this case, the high trees occluding to the roofs. The completeness factor does not consider the FP value, which is why the values of completeness of the previous approaches (99.4% in Widyaningrum et al. [35]) are sometimes greater than the same measure in the suggested approach (97.6%). From this comparison, the importance of elimination of the high trees associated with the roofs can be deduced.
It is important to note that the accuracy of the classification approaches which use the convolutional neural networks [7,11] is lower than the accuracy of the suggested approach (Table 4) when applied to the same Vaihingen dataset. This fact emphasizes the necessity of recognition and elimination of the high trees associated with building roofs which sometimes play the main role of accuracy dropping in the classification algorithms.
Finally, it is important to remember that the approach suggested by Tarsha Kurdi et al. [10] did not consider the case of tree presence that is associated with the building roof, which is why it gives the erroneous result shown in Figure 3, when there are trees attached to the building roof.
7.3. Comparison with Deep-Learning-Based Methods
At this stage, a specific comparison with deep-learning-based methods can clarify the importance of the suggested approach, which is a rule-based approach. One deep-learning-based approach consists of three main steps: training, validation, and testing [11]. The training operation permits calculating the architecture deep-learning network parameters that allow for classifying the labelled input point cloud. For this purpose, the employed labelled point cloud is divided into training and validation data. The same network with the calculated parameters will be applied to the validation point cloud. Once the learning parameters are validated, they can be used for testing other datasets. Otherwise, the rule-based filtering method is based on the physical behavior of the point cloud [38], and consists of a list of operations connected through a suggested workflow network. On one hand, the application of the deep-learning-based approach to LiDAR data envisages three issues, which are the input feature selection, the training- and validation-data labelling, and overfitting. On the other hand, its advantages regarding rule-based approaches are the possibility of simultaneous application in different types of land, no need for parameter adjustment, and fast performance for high-volume data [38]. In fact, the suggested rule-based approach does not suffer from the issues presented in deep-learning-based approaches. Furthermore, the parameter adjustment problem is minimized by using the idea of fuzzy bars among the Z-coordinate histogram analysis (see Section 3) and the employment of smart thresholds (see Section 5.4). Finally, in order to be fair, the deep-learning-based approaches for LiDAR data filtering nowadays represent a hot research topic that can profit from all available rule-based approaches to recognize the efficient input features.
7.4. Ablation Study
To show the contributions of the improved modules, an ablation study is applied to the building point cloud shown in Figure 10a. As shown in Table 5, the total building point cloud contains 2936 points and consists of three classes: roof, tree and undesirable points. The filtering algorithm before the extension eliminates only the undesirable points (433 points). Thereafter, for removing the high tree crown points, the employment of three features together (φ°, σ and ccf) with the smart thresholds enable recognizing the roof points accurately. Consequently, the results illustrated in Figure 5 underline the necessity of the extension achieved on the original filtering algorithm.

Table 5.
Number of points detected in each step of suggested algorithm.
8. Conclusions and Perspective
This paper suggested a new approach to automatic building point cloud filtering for detecting the roof point cloud. This algorithm is important as the majority of building-modelling algorithms try to construct the building models by focusing on the building roof point cloud. Indeed, eliminating the undesirable points from the building point cloud helps to improve the quality of the constructed building model and increases the probability of success of the modelling algorithm, especially when the quantity of the undesirable points is considerable. In this context, the suggested approach considers the general case when there are trees occluding the building roof. Although the suggested algorithm suffers from some limitations that may slightly reduce the accuracy of some results, the expounded filtering algorithm conserves the building’s main roof cloud and eliminates most of the undesirable points. Nevertheless, more investigations are envisaged in the future to make allowance for the limitation cases. Although this algorithm was tested using five datasets with different typologies and point densities, it still needs to be tested and extended in future research to include other point cloud types, such as photogrammetric point clouds from oblique areal imaging or from Unmanned Aerial Vehicle (UAV) imagery.
Author Contributions
Conceptualization: F.T.K.; Methodology: F.T.K.; Software: F.T.K.; Validation: F.T.K., M.A., Z.G., G.C., E.K.D.; Formal analysis: F.T.K.; Investigation: F.T.K., E.K.D., M.A., Z.G., G.C; Resources: F.T.K., M.A., Z.G., G.C., E.K.D.; Data curation: F.T.K., E.K.D., M.A., Z.G., G.C.; Writing—original draft preparation: F.T.K.; Writing—review and editing: F.T.K., M.A., E.K.D., Z.G., G.C.; Visualization: F.T.K., M.A., Z.G., G.C., E.K.D.; Supervision: F.T.K., M.A., Z.G., G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
ISPRS datasets was provided by the German Society for Photogrammetry, Remote Sensing and Geoinformation (DGPF) [32]. Hermanni dataset was provided by EuroSDR [31]. Dataset of Aitkenvale in Queensland, Australia is provided by Awrangjeb et al. [33]. Strasbourg dataset is provided by Tarsha Kurdi et al. [2].
Acknowledgments
We would like to thank the German Society for Photogrammetry, Remote Sensing and Geoinformation (DGPF) for providing Vaihingen and Toronto datasets [32].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shan, J.; Yan, J.; Jiang, W. Global Solutions to Building Segmentation and Reconstruction. Topographic Laser Ranging and Scanning: Principles and Processing, 2nd ed.; Shan, J., Toth, C.K., Eds.; CRC Press: Boca Raton, FL, USA, 2018; pp. 459–484. [Google Scholar]
- Tarsha Kurdi, F.; Landes, T.; Grussenmeyer, P.; Koehl, M. Model-driven and data-driven approaches using Lidar data: Analysis and comparison. In Proceedings of the ISPRS Workshop, Photogrammetric Image Analysis (PIA07), International Archives of Photogrammetry, Remote Sensing and Spatial Information Systems. Munich, Germany, 19–21 September 2007; 2007; Volume XXXVI, pp. 87–92, Part3 W49A. [Google Scholar]
- Wehr, A.; Lohr, U. Airborne laser scanning—An introduction and overview. ISPRS J. Photogramm. Remote Sens. 1999, 54, 68–82. [Google Scholar] [CrossRef]
- He, Y. Automated 3D Building Modelling from Airborne Lidar Data. Ph.D. Thesis, University of Melbourne, Melbourne, Australia, 2015. [Google Scholar]
- Tarsha Kurdi, F.; Awrangjeb, M. Comparison of Lidar building point cloud with reference model for deep comprehension of cloud structure. Can. J. Remote Sens. 2020, 46, 603–621. [Google Scholar] [CrossRef]
- Shao, J.; Zhang, W.; Shen, A.; Mellado, N.; Cai, S.; Luo, L.; Wang, N.; Yan, G.; Zhou, G. Seed point set-based building roof extraction from airborne LiDAR point clouds using a top-down strategy. Autom. Constr. 2021, 126, 103660. [Google Scholar] [CrossRef]
- Wen, C.; Li, X.; Yao, X.; Peng, L.; Chi, T. Airborne LiDAR point cloud classification with global-local graph attention convolution neural network. ISPRS J. Photogramm. Remote Sens. 2021, 173, 181–194. [Google Scholar] [CrossRef]
- Varlik, A.; Uray, F. Filtering airborne LIDAR data by using fully convolutional networks. Surv. Rev. 2021, 1–11. [Google Scholar] [CrossRef]
- Hui, Z.; Li, Z.; Cheng, P.; Ziggah, Y.Y.; Fan, J. Building extraction from airborne LiDAR data based on multi-constraints graph segmentation. Remote Sens. 2021, 13, 3766. [Google Scholar] [CrossRef]
- Tarsha Kurdi, F.; Awrangjeb, M.; Munir, N. Automatic filtering and 2D modelling of Lidar building point cloud. Trans. GIS J. 2021, 25, 164–188. [Google Scholar] [CrossRef]
- Maltezos, E.; Doulamis, A.; Doulamis, N.; Ioannidis, C. Building extraction from LiDAR data applying deep convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2019, 16, 155–159. [Google Scholar] [CrossRef]
- Liu, M.; Shao, Y.; Li, R.; Wang, Y.; Sun, X.; Wang, J.; You, Y. Method for extraction of airborne LiDAR point cloud buildings based on segmentation. PLoS ONE 2020, 15, e0232778. [Google Scholar] [CrossRef]
- Demir, N. Automated detection of 3D roof planes from Lidar data. J. Indian Soc. Remote Sens. 2018, 46, 1265–1272. [Google Scholar] [CrossRef]
- Tarsha Kurdi, F.; Awrangjeb, M.; Munir, N. Automatic 2D modelling of inner roof planes boundaries starting from Lidar data. In Proceedings of the 14th 3D GeoInfo 2019, Singapore, 26–27 September 2019; pp. 107–114. [Google Scholar] [CrossRef] [Green Version]
- Park, S.Y.; Lee, D.G.; Yoo, E.J.; Lee, D.C. Segmentation of Lidar data using multilevel cube code. J. Sens. 2019, 2019, 4098413. [Google Scholar] [CrossRef]
- Zhang, K.; Yan, J.; Chen, S.C. A framework for automated construction of building models from airborne Lidar measurements. In Topographic Laser Ranging and Scanning: Principles and Processing, 2nd ed.; Shan, J., Toth, C.K., Eds.; CRC Press: Boca Raton, FL, USA, 2018; pp. 563–586. [Google Scholar]
- Li, M.; Rottensteiner, F.; Heipke, C. Modelling of buildings from aerial Lidar point clouds using TINs and label maps. ISPRS J. Photogramm. Remote Sens. 2019, 154, 127–138. [Google Scholar] [CrossRef]
- Vosselman, G.; Dijkman, S. 3D building model reconstruction from point clouds and ground plans. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2001, 34, 37–44. [Google Scholar]
- Hu, P.; Miao, Y.; Hou, M. Reconstruction of Complex Roof Semantic Structures from 3D Point Clouds Using Local Convexity and Consistency. Remote Sens. 2021, 13, 1946. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Daniel, S.; Guériot, D.; Sintès, C.; Le Caillec, J.-M. Super-Resolution-Based Snake Model—An Unsupervised Method for Large-Scale Building Extraction Using Airborne LiDAR Data and Optical Image. Remote Sens. 2020, 12, 1702. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, H.; Chen, Y.; Yan, K.; Chen, M. 3D building roof modelling by optimizing primitive’s parameters using constraints from Lidar data and aerial imagery. Remote Sens. 2014, 6, 8107–8133. [Google Scholar] [CrossRef] [Green Version]
- Jung, J.; Sohn, G. Progressive modelling of 3D building rooftops from airborne Lidar and imagery. In Topographic Laser Ranging and Scanning: Principles and Processing, 2nd ed.; Shan, J., Toth, C.K., Eds.; CRC Press: Boca Raton, FL, USA, 2018; pp. 523–562. [Google Scholar]
- Awrangjeb, M.; Gilani, S.A.N.; Siddiqui, F.U. An effective data-driven method for 3D building roof reconstruction and robust change detection. Remote Sens. 2018, 10, 1512. [Google Scholar] [CrossRef] [Green Version]
- Pirotti, F.; Zanchetta, C.; Previtali, M.; Della Torre, S. Detection of building roofs and façade from aerial laser scanning data using deep learning. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 4211, 975–980. [Google Scholar] [CrossRef] [Green Version]
- Martin-Jimenez, J.; Del Pozo, S.; Sanchez-Aparicio, M.; Laguela, S. Multi-scale roof characterization from Lidar data and aerial orthoimagery: Automatic computation of building photovoltaic capacity. J. Autom. Constr. 2020, 109, 102965. [Google Scholar] [CrossRef]
- Sibiya, M.; Sumbwanyambe, M. An algorithm for severity estimation of plant leaf diseases by the use of colour threshold image segmentation and fuzzy logic inference: A proposed algorithm to update a “Leaf Doctor” application. AgriEngineering 2019, 1, 205–219. [Google Scholar] [CrossRef] [Green Version]
- Dey, K.E.; Tarsha Kurdi, F.; Awrangjeb, M.; Stantic, B. Effective Selection of Variable Point Neighbourhood for Feature Point Extraction from Aerial Building Point Cloud Data. Remote Sens. 2021, 13, 1520. [Google Scholar] [CrossRef]
- Sanchez, J.; Denis, F.; Coeurjolly, D.; Dupont, F.; Trassoudaine, L.; Checchin, P. Robust normal vector estimation in 3D point clouds through iterative principal component analysis. ISPRS J. Photogramm. Remote Sens. 2020, 163, 18–35. [Google Scholar] [CrossRef] [Green Version]
- Thomas, H.; Goulette, F.; Deschaud, J.; Marcotegui, B.; LeGall, Y. Semantic Classification of 3D Point Clouds with Multiscale Spherical Neighborhoods. In Proceedings of the International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 390–398. [Google Scholar] [CrossRef] [Green Version]
- Tarsha Kurdi, F.; Landes, T.; Grussenmeyer, P. Joint combination of point cloud and DSM for 3D building reconstruction using airborne laser scanner data. In Proceedings of the 4th IEEE GRSS / WG III/2+5, VIII/1, VII/4 Joint Workshop on Remote Sensing & Data Fusion over Urban Areas and 6th International Symposium on Remote Sensing of Urban Areas, Télécom, Paris, France, 11–13 April 2007; p. 7. [Google Scholar]
- Eurosdr. Available online: www.eurosdr.net (accessed on 23 November 2021).
- Cramer, M. The DGPF test on digital aerial camera evaluation—Overview and test design. Photogramm.-Fernerkund.-Geoinf. 2010, 2, 73–82. [Google Scholar] [CrossRef]
- Awrangjeb, M.; Zhang, C.; Fraser, C.S. Automatic extraction of building roofs using LiDAR data and multispectral imagery. ISPRS J. Photogramm. Remote Sens. 2013, 83, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Huang, R.; Yang, B.; Liang, F.; Dai, W.; Li, J.; Tian, M.; Xu, W. A top-down strategy for buildings extraction from complex urban scenes using airborne LiDAR point clouds. Infrared Phys. Technol. 2018, 92, 203–218. [Google Scholar] [CrossRef]
- Widyaningrum, E.; Gorte, B.; Lindenbergh, R. Automatic Building Outline Extraction from ALS Point Clouds by Ordered Points Aided Hough Transform. Remote Sens. 2019, 11, 1727. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Duan, Y.; Zhang, Y.; Cao, R. Extracting buildings from and regularizing boundaries in airborne LiDAR data using connected operators. Int. J. Remote Sens. 2016, 37, 889–912. [Google Scholar] [CrossRef]
- Griffiths, D.; Boehm, J. Improving public data for building segmentation from Convolutional Neural Networks (CNNs) for fused airborne lidar and image data using active contours. ISPRS J. Photogramm. Remote Sens. 2019, 154, 70–83. [Google Scholar] [CrossRef]
- Ayazi, S.M.; Saadat Seresht, M. Comparison of traditional and machine learning base methods for ground point cloud labeling. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2019, XLII-4/W18, 141–145. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).