Two Simulated Spectral Databases of Lunar Regolith: Method, Validation, and Application
Abstract
:1. Introduction
2. Methods
2.1. Hapke Radiative Transfer Model
2.2. The Optical Constants of Minerals
2.3. Simulation Method
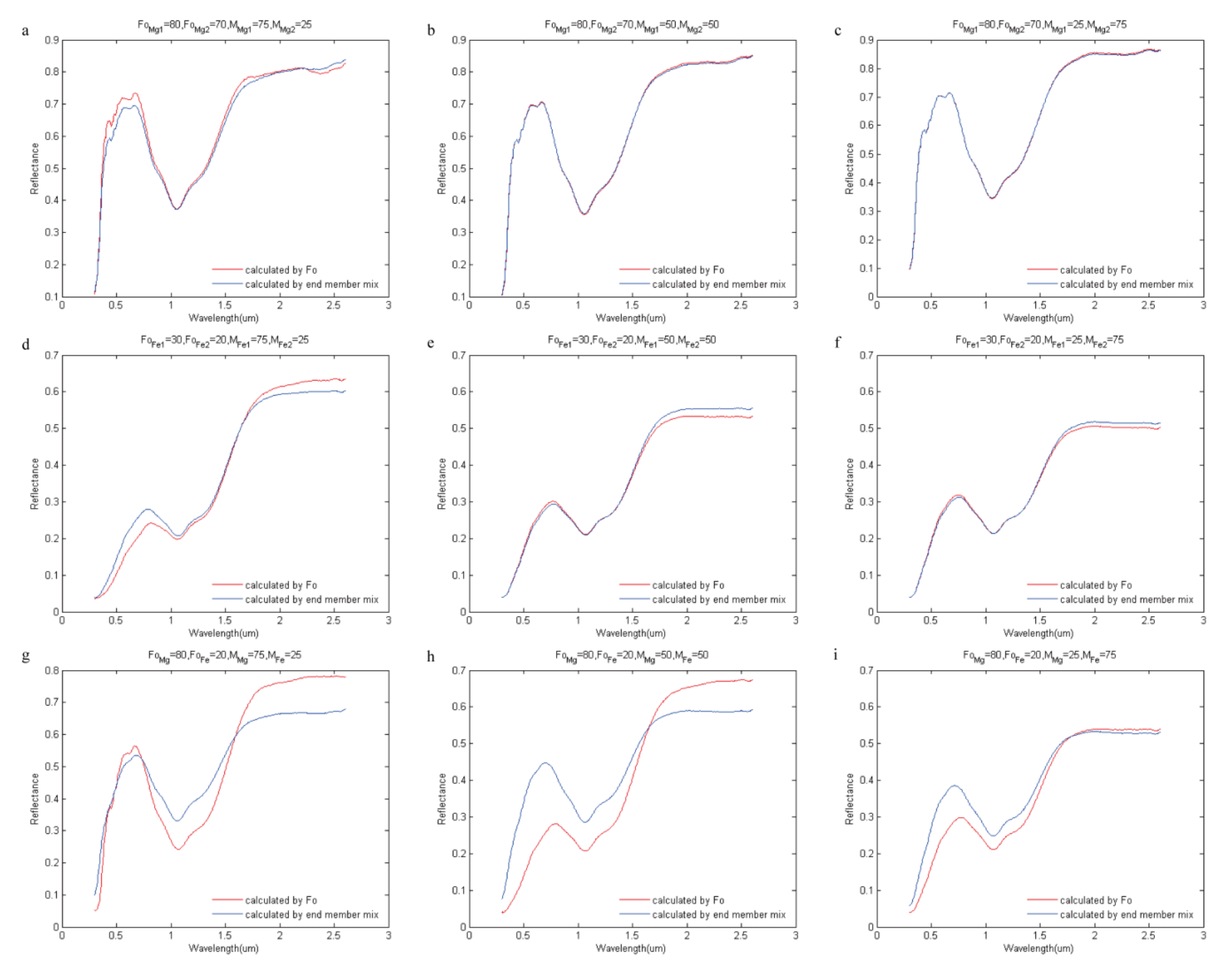
3. Multiple Solutions and Application of the Model
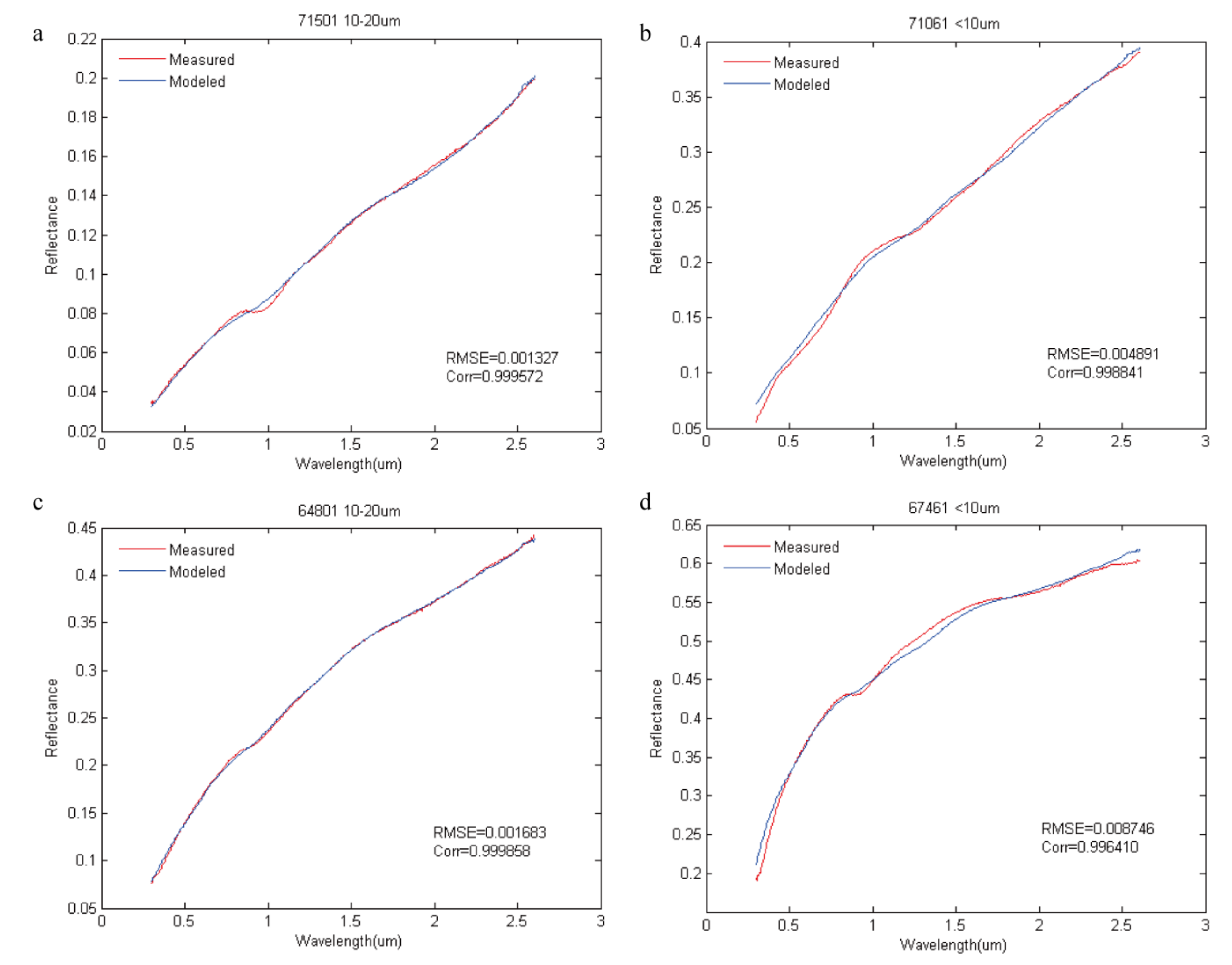
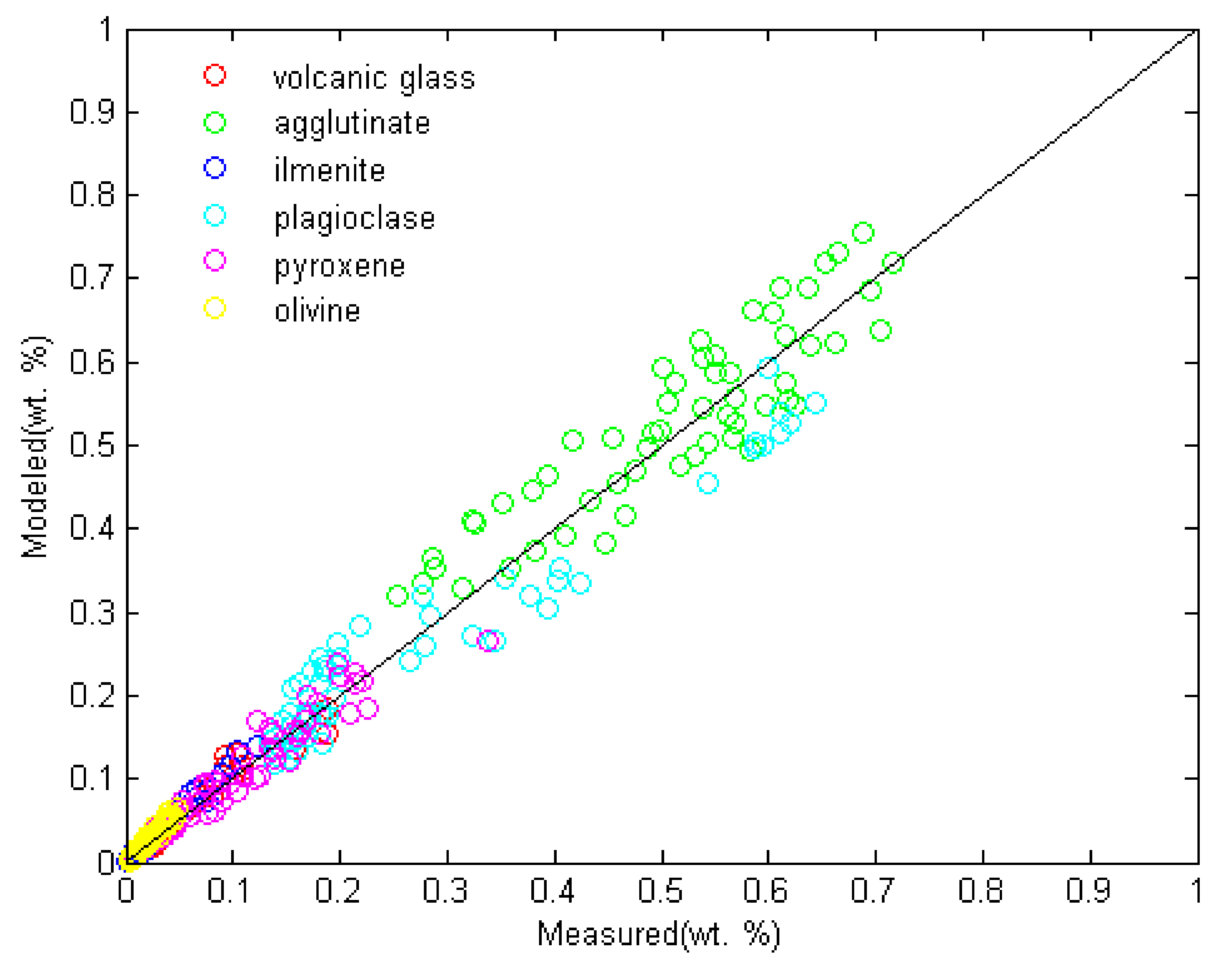
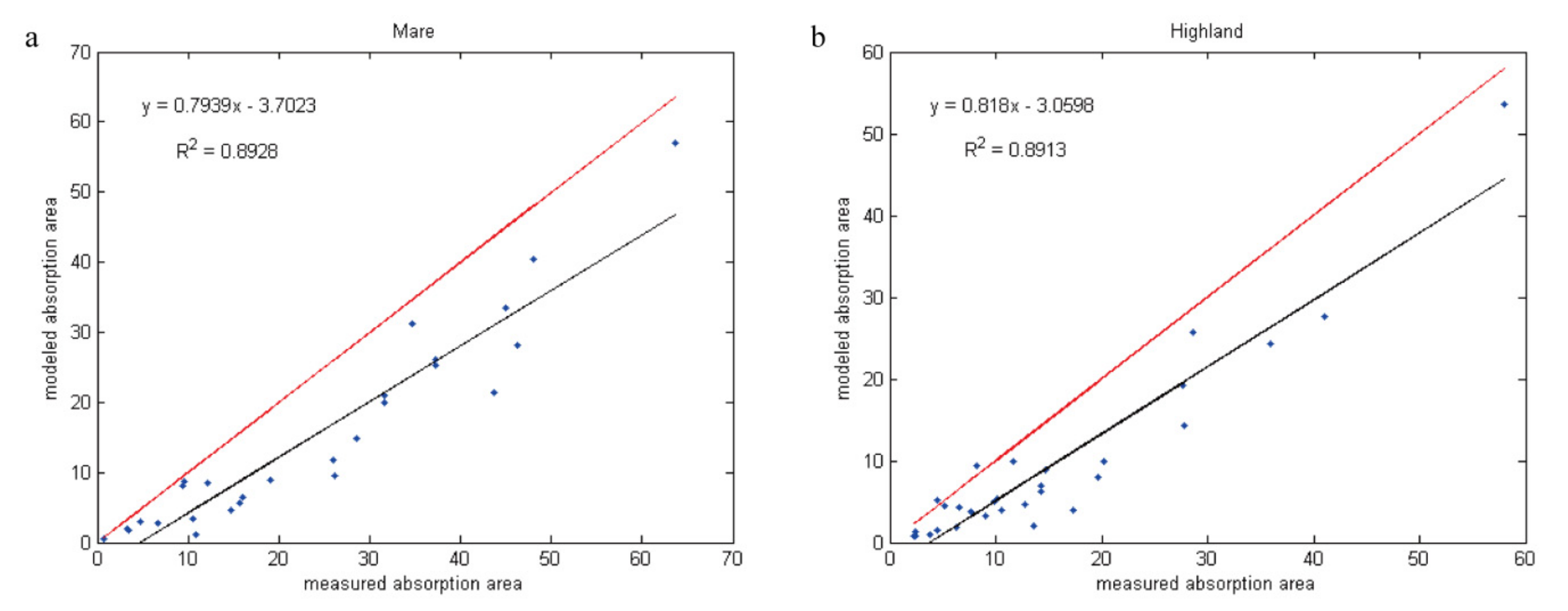
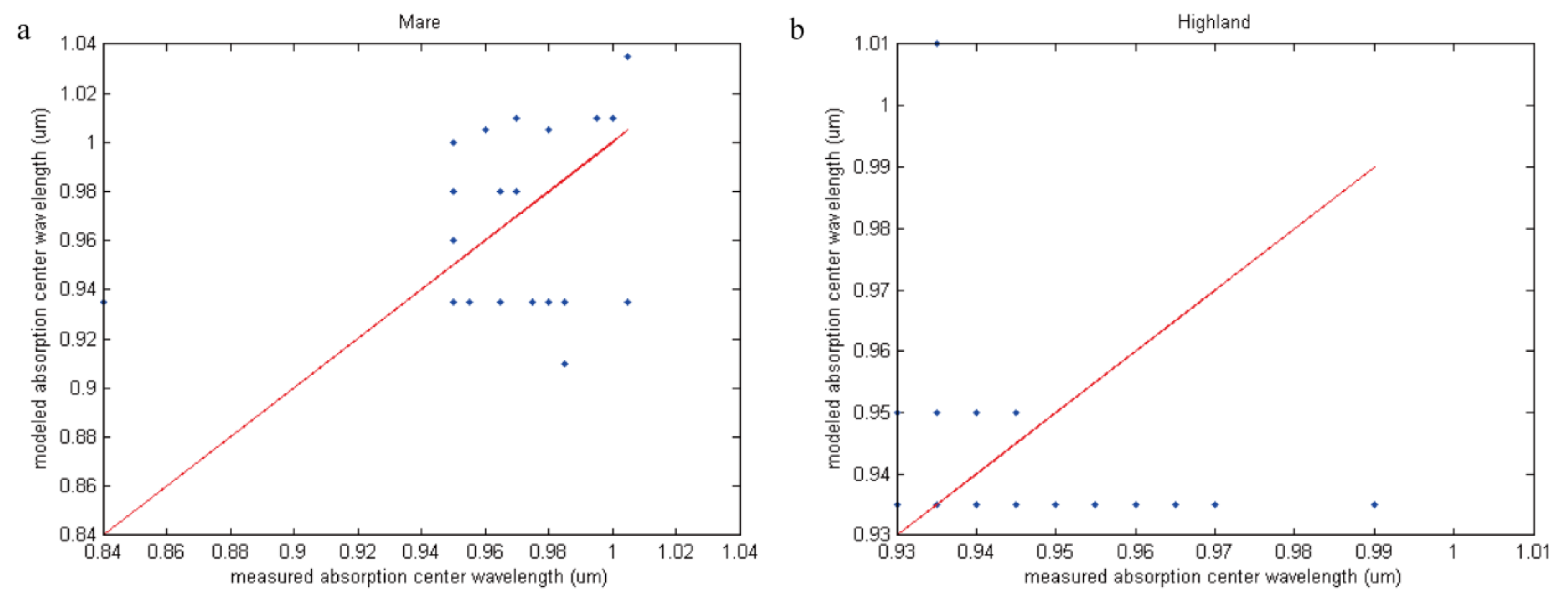
4. The Validation of Spectral Simulation
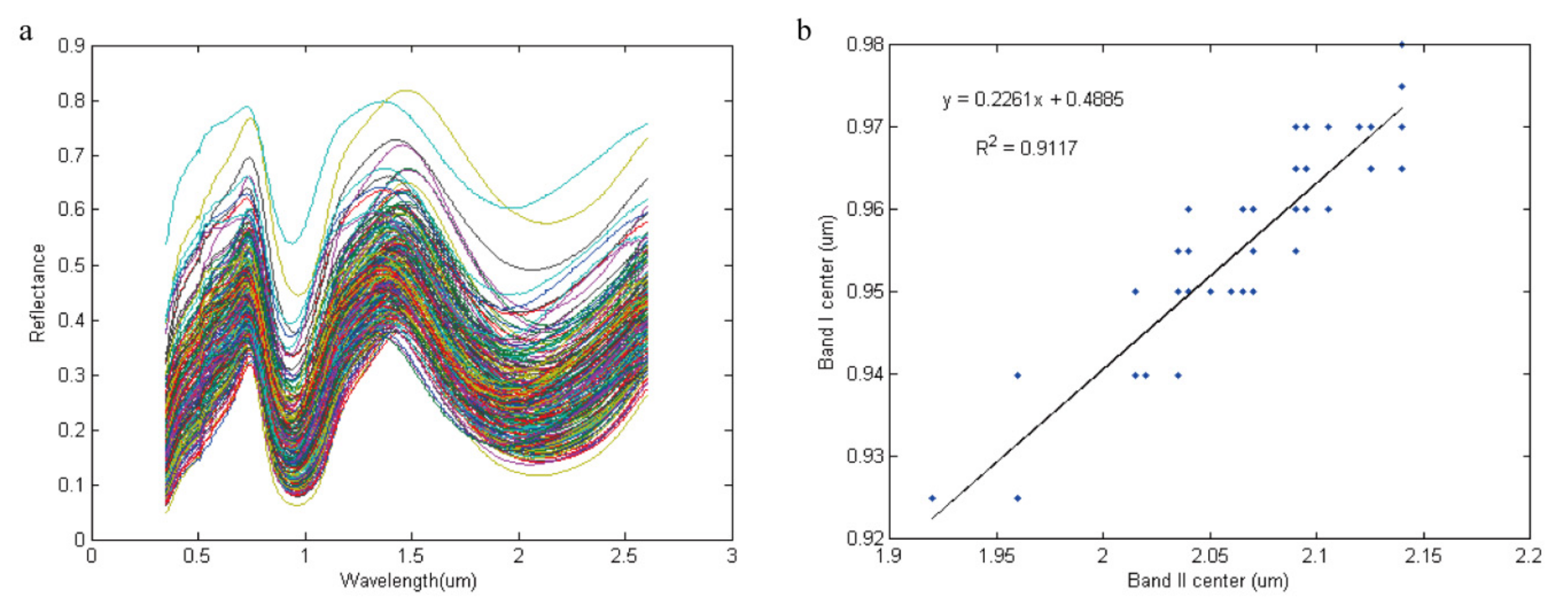
5. Simulated Spectral Datasets
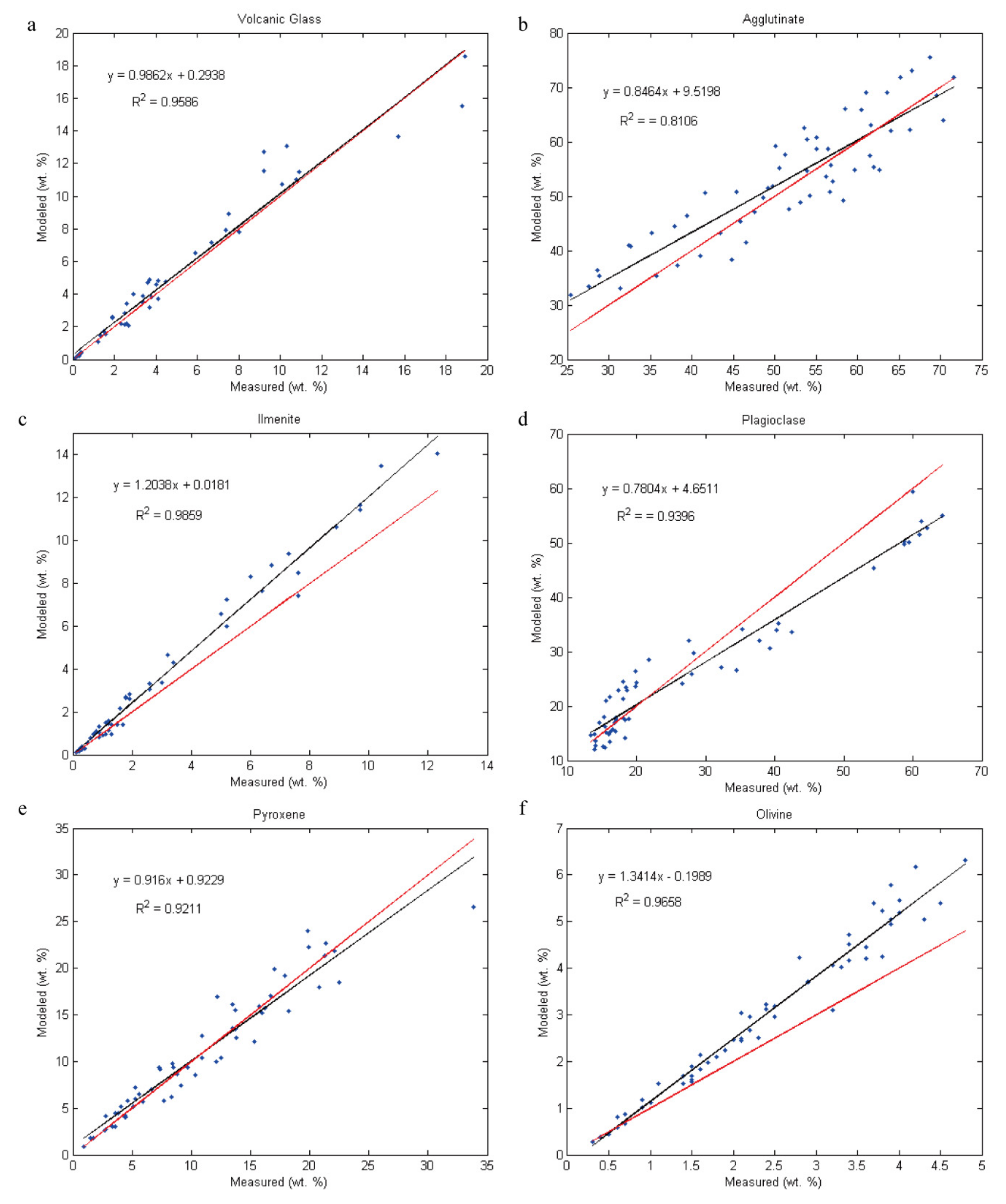
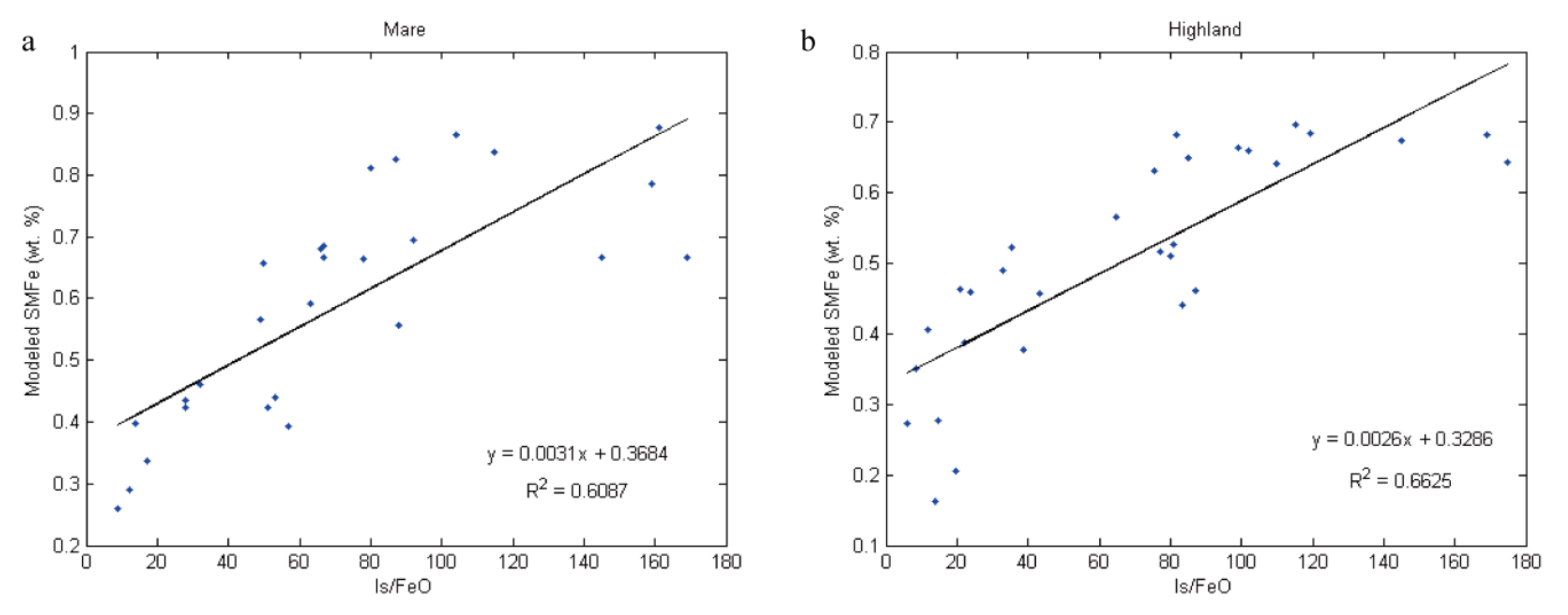
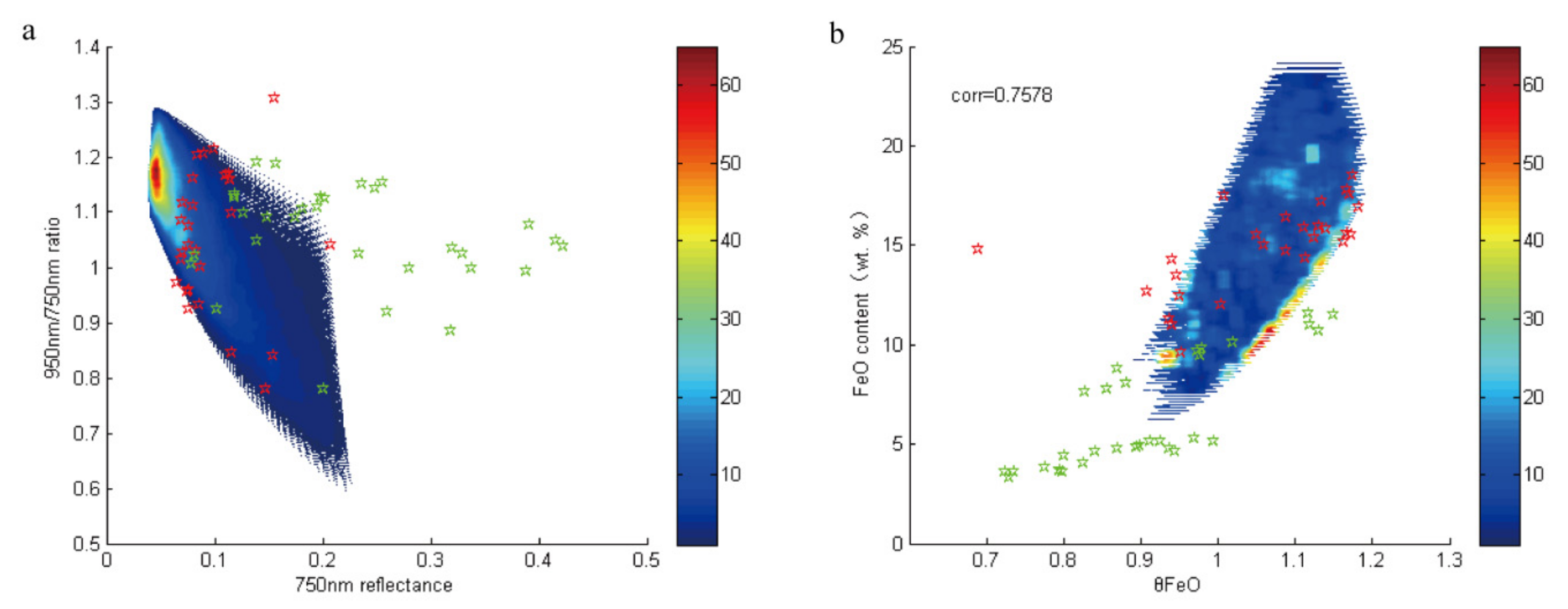
6. Application of Simulated Spectra
7. Discussion
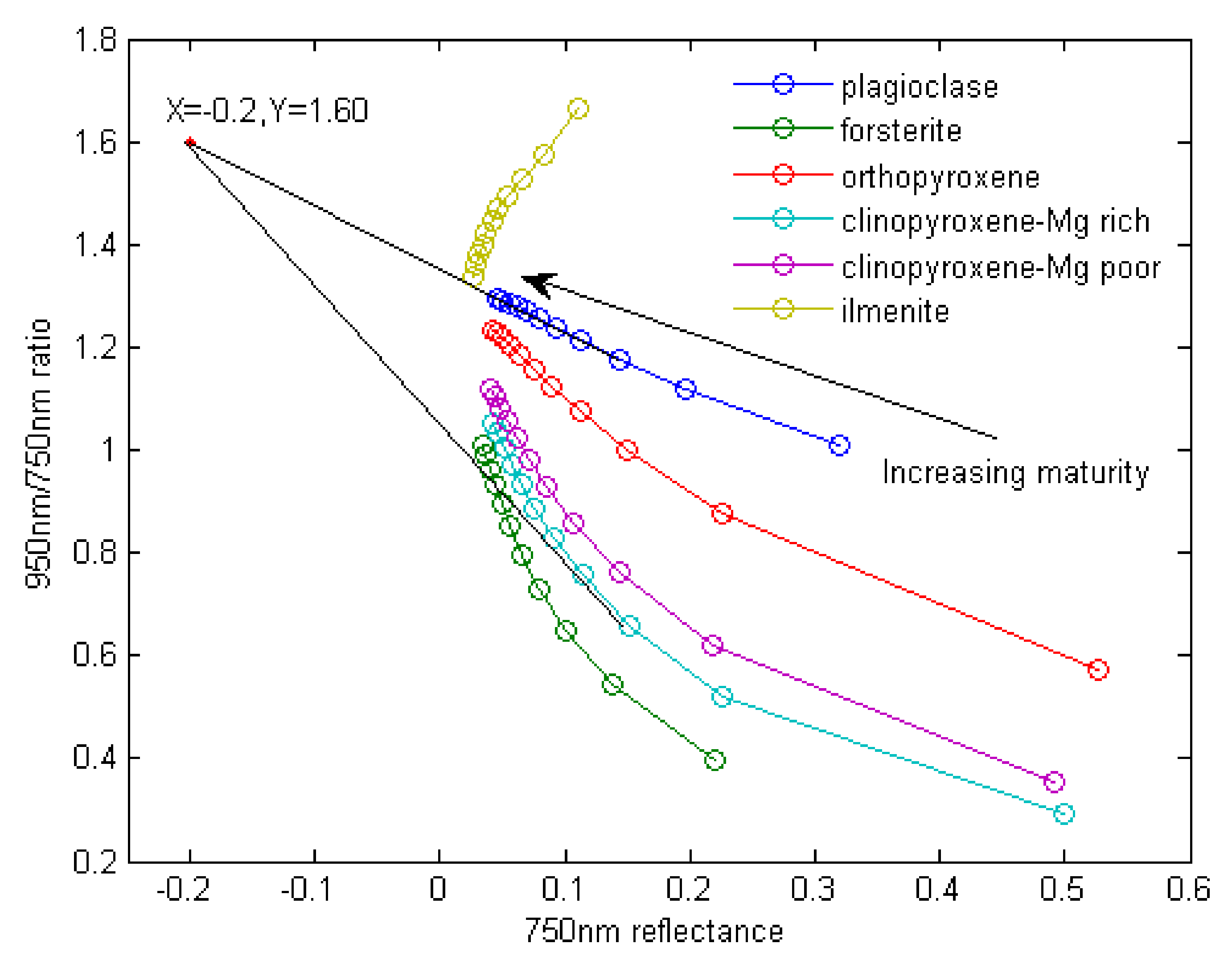
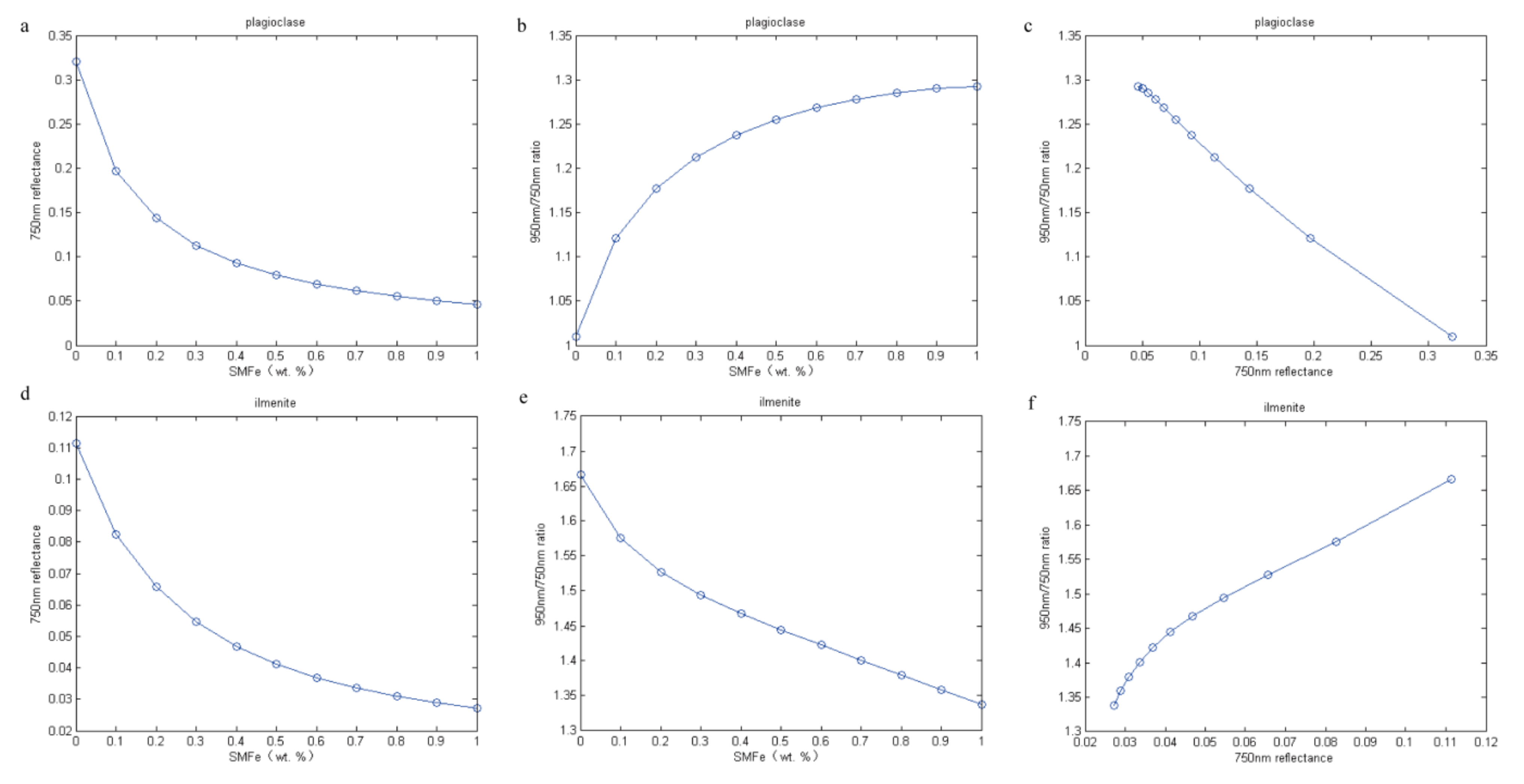
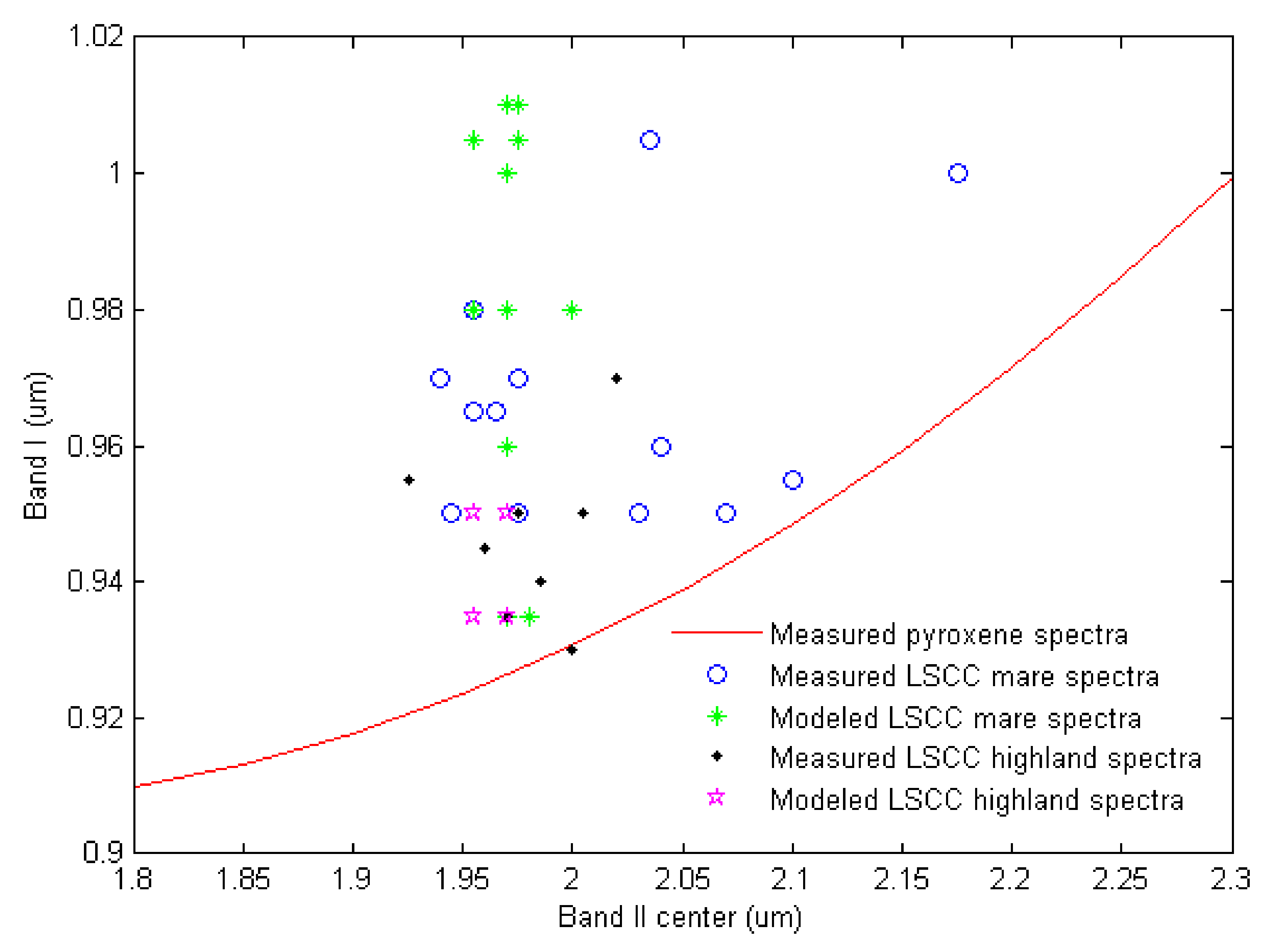
7.1. Simulation of Spectral Parameters
7.2. The Isomorphism of Olivine
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lucey, P.G.; Taylor, G.J.; Malaret, E. Abundance and Distribution of Iron on the Moon. Science 1995, 268, 1150–1153. [Google Scholar] [CrossRef] [PubMed]
- Ohtake, M.; Matsunaga, T.; Haruyama, J.; Yokota, Y.; Morota, T.; Honda, C.; Ogawa, Y.; Torii, M.; Miyamoto, H.; Arai, T.; et al. The global distribution of pure anorthosite on the Moon. Nature 2009, 461, 236–240. [Google Scholar] [CrossRef] [PubMed]
- Ohtake, M.; Takeda, H.; Matsunaga, T.; Yokota, Y.; Haruyama, J.; Morota, T.; Yamamoto, S.; Ogawa, Y.; Hiroi, T.; Karouji, Y.; et al. Asymmetric crustal growth on the Moon indicated by primitive farside highland materials. Nat. Geosci. 2012, 5, 384–388. [Google Scholar] [CrossRef]
- Wu, Y. Major elements and Mg# of the Moon: Results from Chang’E-1 Interference Imaging Spectrometer (IIM) data. Geochim. Cosmochim. Acta 2012, 93, 214–234. [Google Scholar]
- Yamamoto, S.; Nakamura, R.; Matsunaga, T.; Ogawa, Y.; Ishihara, Y.; Morota, T.; Hirata, N.; Ohtake, M.; Hiroi, T.; Yokota, Y.; et al. Possible mantle origin of olivine around lunar impact basins detected by SELENE. Nat. Geosci. 2010, 3, 533–536. [Google Scholar] [CrossRef]
- Yamamoto, S.; Nakamura, R.; Matsunaga, T.; Ogawa, Y.; Ishihara, Y.; Morota, T.; Hirata, N.; Ohtake, M.; Hiroi, T.; Yokota, Y.; et al. Massive layer of pure anorthosite on the Moon. Geophys. Res. Lett. 2012, 39, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Yamamoto, S.; Nakamura, R.; Matsunaga, T.; Ogawa, Y.; Ishihara, Y.; Morota, T.; Hirata, N.; Ohtake, M.; Hiroi, T.; Yokota, Y.; et al. Olivine-rich exposures in the South Pole-Aitken Basin. Icarus 2011, 218, 331–344. [Google Scholar] [CrossRef]
- Yamamoto, S.; Nakamura, R.; Matsunaga, T.; Ogawa, Y.; Ishihara, Y.; Morota, T.; Hirata, N.; Ohtake, M.; Hiroi, T.; Yokota, Y.; et al. Global occurrence trend of high-Ca pyroxene on lunar highlands and its implications. J. Geophys. Res. Planets 2015, 120, 831–848. [Google Scholar] [CrossRef] [Green Version]
- Lucey, P.G.; Norman, J.A.; Crites, S.T.; Taylor, J.G.; Hawke, B.R.; Lemelin, M.; Melosh, H.J. A large spectral survey of small lunar craters: Implications for the composition of the lunar mantle. Am. Mineral. 2014, 99, 2251–2257. [Google Scholar] [CrossRef]
- Vinckier, Q.; Hardy, L.; Gibson, M.; Smith, C.; Putman, P.; Hayne, P.O.; Sellar, R.G. Design and Characterization of the Multi-Band SWIR Receiver for the Lunar Flashlight CubeSat Mission. Remote Sens. 2019, 11, 440. [Google Scholar] [CrossRef] [Green Version]
- Zhou, P.; Zhao, Z.; Huo, H.-Y.; Liu, Z. Retrieval of Photometric Parameters of Minerals Using a Self-Made Multi-Angle Spectrometer Based on the Hapke Radiative Transfer Model. Remote Sens. 2021, 13, 3022. [Google Scholar] [CrossRef]
- Peng, M.; Di, K.; Wang, Y.; Wan, W.; Liu, Z.; Wang, J.; Li, L. A Photogrammetric-Photometric Stereo Method for High-Resolution Lunar Topographic Mapping Using Yutu-2 Rover Images. Remote Sens. 2021, 13, 2975. [Google Scholar] [CrossRef]
- Lucey, P.G. Model near-infrared optical constants of olivine and pyroxene as a function of iron content. J. Geophys. Res. Earth Surf. 1998, 103, 1703–1713. [Google Scholar] [CrossRef]
- Lucey, P.G.; Blewett, D.; Taylor, G.J.; Hawke, B.R. Imaging of lunar surface maturity. J. Geophys. Res. Earth Surf. 2000, 105, 20377–20386. [Google Scholar] [CrossRef]
- Blewett, D.; Lucey, P.G.; Hawke, B.R.; Jolliff, B.L. Clementine images of the lunar sample-return stations: Refinement of FeO and TiO2 mapping techniques. J. Geophys. Res. Earth Surf. 1997, 102, 16319–16325. [Google Scholar] [CrossRef]
- Shkuratov, Y.; Starukhina, L.; Hoffmann, H.; Arnold, G. A Model of Spectral Albedo of Particulate Surfaces: Implications for Optical Properties of the Moon. Icarus 1999, 137, 235–246. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 1. Theory. J. Geophys. Res. Earth Surf. 1981, 86, 3039–3054. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 3. Correction for macroscopic roughness. Icarus 1984, 59, 41–59. [Google Scholar] [CrossRef] [Green Version]
- Hapke, B. Bidirectional reflectance spectroscopy: 4. The extinction coefficient and the opposition effect. Icarus 1986, 67, 264–280. [Google Scholar] [CrossRef] [Green Version]
- Hapke, B. Theory of Reflectance and Emittance Spectroscopy; Cambridge Univ. Press: Cambridge, UK, 1993; p. 455. [Google Scholar]
- Hapke, B. Bidirectional reflectance spectroscopy: 5. The coherent backscatter opposition effect and anisotropic scattering. Icarus 2002, 157, 523–534. [Google Scholar] [CrossRef] [Green Version]
- Hapke, B. Theory of Reflectance and Emittance Spectroscopy; Cambridge University Press: Cambridge, UK, 2005; 472p. [Google Scholar]
- Hapke, B. Bidirectional reflectance spectroscopy: 6. Effects of porosity. Icarus 2008, 195, 918–926. [Google Scholar] [CrossRef] [Green Version]
- Denevi, B.W.; Lucey, P.G.; Sherman, S.B. Radiative transfer modeling of near-infrared spectra of lunar mare soils: Theory and measurement. J. Geophys. Res. Space Phys. 2008, 113, E02003. [Google Scholar] [CrossRef]
- Liu, D.; Li, L.; Sun, Y. An improved radiative transfer model for estimating mineral abundance of immature and mature lunar soils. Icarus 2015, 253, 40–50. [Google Scholar] [CrossRef]
- Lucey, P.G. Mineral maps of the Moon. Geophys. Res. Lett. 2004, 31, L08701. [Google Scholar] [CrossRef]
- Yan, B.; Wang, R.; Gan, F.; Wang, Z. Minerals mapping of the lunar surface with Clementine UVVIS/NIR data based on spectra unmixing method and Hapke model. Icarus 2010, 208, 11–19. [Google Scholar] [CrossRef]
- Li, S.; Li, L. Radiative transfer modeling for quantifying lunar surface minerals, particle size, and submicroscopic metallic Fe. J. Geophys. Res. Space Phys. 2011, 116, E09001. [Google Scholar] [CrossRef]
- Lemelin, M.; Morisset, C.-E.; Germain, M.; Hipkin, V.; Goïta, K.; Lucey, P.G. Ilmenite mapping of the lunar regolith over Mare Australe and Mare Ingenii regions: An optimized multisource approach based on Hapke radiative transfer theory. J. Geophys. Res. Planets 2013, 118, 2582–2593. [Google Scholar] [CrossRef]
- Heiken, G.H.; Vaniman, T.; French, B.M. Lunar Sourcebook: A User’s Guide to the Moon; Cambridge Univ. Press: New York, NY, USA, 1991. [Google Scholar]
- Taylor, L.A.; Pieters, C.M.; Patchen, A.; Taylor, D.S.; Morris, R.V.; Keller, L.P.; McKay, D.S. Mineralogical characterization of lunar highland soils. Lunar Planet. Sci. 2003, XXXIV, 1774. [Google Scholar]
- Taylor, L.A.; Pieters, C.; Patchen, A.; Taylor, D.H.S.; Morris, R.V.; Keller, L.P.; McKay, D.S. Mineralogical and chemical characterization of lunar highland soils: Insights into the space weathering of soils on airless bodies. J. Geophys. Res. Planets 2010, 115, E02002. [Google Scholar] [CrossRef]
- Warell, J.; Davidsson, B. A Hapke model implementation for compositional analysis of VNIR spectra of Mercury. Icarus 2010, 209, 164–178. [Google Scholar] [CrossRef]
- Trang, D.; Lucey, P.G.; Gillis-Davis, J.J.; Cahill, J.T.S.; Klima, R.L.; Isaacson, P.J. Near-infrared optical constants of naturally occurring olivine and synthetic pyroxene as a function of mineral composition. J. Geophys. Res. Planets 2013, 118, 708–732. [Google Scholar] [CrossRef]
- Mustard, J.F.; Pieters, C.M. Photometric phase functions of common geologic minerals and applications to quantitative analysis of mineral mixture reflectance spectra. J. Geophys. Res.–Solid Earth 1989, 94, 13619–13634. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Radiative Transfer; Dover Publications Inc.: Mineola, NY, USA, 2013. [Google Scholar]
- Yolken, H.T.; Kruger, J. Optical constants of iron in the visible region. J. Opt. Soc. Am. 1965, 55, 842–844. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical constants of transition metals: Ti, V, Cr, Mn, Fe, Co, Ni, and Pd. Phys. Rev. 1974, B9, 5056–5070. [Google Scholar] [CrossRef]
- Bell, P.M.; Mao, H.K.; Weeks, R.A. Optical spectra and electron paramagnetic resonance of lunar and synthetic glasses: A study of the effects of controlled atmosphere, composition, and temperature. In Proceedings of the Lunar Science: Conference Proceedings: 7th, Houston, TX, USA, 15–19 March 1976; pp. 2543–2559. [Google Scholar]
- Masson, C.R.; Smith, I.B.; Jamieson, W.D.; McLachlan, J.L.; Volborth, A. Chromatographic and mineralogical study of Apollo 14 fines. In Proceedings of the Lunar Science: Conference Proceedings: 3rd, Houston, TX, USA, 10–13 January 1972; pp. 1029–1036. [Google Scholar]
- Egan, W.G.; Hilgeman, T. The interstellar medium: UV complex index of refraction of several candidate materials. Astron. J. 1975, 80, 587–594. [Google Scholar] [CrossRef]
- Heiken, G.; McKay, D.S. Petrography of Apollo 17 soils. In Proceedings of the Lunar Science: Conference Proceedings: 5th, Houston, TX, USA, 18–22 March 1974; pp. 843–860. [Google Scholar]
- Starukhina, L.V.; Shkuratov, Y.G. A theoretical model of lunar optical maturation: Effects of submicroscopic reduced iron and particle size variations. Icarus 2001, 152, 275–281. [Google Scholar] [CrossRef]
- Noble, S.K.; Pieters, C.M.; Taylor, L.A.; Morris, R.V.; Allen, C.C.; McKAY, D.S.; Keller, L.P. The optical properties of the finest fraction of lunar soil: Implications for space weathering. Meteorit. Planet. Sci. 2001, 36, 31–34. [Google Scholar] [CrossRef]
- Hapke, B. Space weathering from Mercury to the asteroid belt. J. Geophys. Res. Space Phys. 2001, 106, 10039–10073. [Google Scholar] [CrossRef]
- Lucey, P.G.; Riner, M.A. The optical effects of small iron particles that darken but do not redden: Evidence of intense space weathering on Mercury. Icarus 2011, 212, 451–462. [Google Scholar] [CrossRef]
- Taylor, L.A.; Pieters, C.M.; Morris, R.V.; Keller, L.P.; McKay, D.S.; Parchen, A.; Wentworth, S.J. Integration of the chemical and mineralogical characteristics of lunar soils with reflectance spectroscopy. Lunar Planet. Sci. Conf. 1999, XXX, 1859. [Google Scholar]
- Wu, Y.Z. Reflectance spectroscopy of the Moon and its application. Earth Sci. Front. 2014, 21, 074–087. [Google Scholar]
- Taylor, L.A.; Pieters, C.M.; Keller, L.P.; Morris, R.V.; McKay, D. S Lunar mare soils: Space weathering and the major effects of surface-correlated nanophase Fe. J. Geophys. Res. 2001, 106, 27985–27999. [Google Scholar] [CrossRef]
- Morris, R.V. The surface exposure (maturity) of lunar soils: Some concepts and Is/FeO complication. In Proceedings of the Lunar Science: Conference Proceedings: 9th, Houston, TX, USA, 13–17 March 1978; pp. 2287–2297. [Google Scholar]
- Pieters, C.M.; Fischer, E.M.; Rode, O.; Basu, A. Optical effects of space weathering: The role of the finest fraction. J. Geophys. Res. Earth Surf. 1993, 98, 20817–20824. [Google Scholar] [CrossRef] [Green Version]
- Morris, R.V. Origins and size distribution of metallic iron particles in the lunar regolith. In Proceedings of the Lunar Science: Conference Proceedings: 11th, Houston, TX, USA, 17–21 March 1980; pp. 1697–1712. [Google Scholar]
- Gillis, J.J.; Jolliff, B.L.; Elphic, R.C. A revised algorithm for calculating TiO2 from Clementine UVVIS data: A synthesis of rock, soil and remotely sensed TiO2 concentrations. J. Geophys. Res. 2003, 108, 5009. [Google Scholar]
- Adams, J.B. Visible and near-infrared diffuse reflectance spectra of pyroxenes as applied to remote sensing of solid objects in the solar system. J. Geophys. Res. Earth Surf. 1974, 79, 4829–4836. [Google Scholar] [CrossRef]
- Cloutis, E.A.; Gaffey, M.J. Pyroxene spectroscopy revisited: Spectral-compositional correlations and relationship to geothermometry. J. Geophys. Res. Space Phys. 1991, 96, 22809–22826. [Google Scholar] [CrossRef]
- Lucey, P.G.; Steutel, D. Global mineral maps of the Moon. Lunar Plant. Sci. 2003, XXXIV, 1051. [Google Scholar]
- Pieters, C.M.; Besse, S.; Boardman, J.; Buratti, B.; Cheek, L.; Clark, R.N.; Combe, J.P.; Dhingra, D.; Goswami, J.N.; Green, R.O.; et al. Mg-spinel lithology: A new rock type on the lunar farside. J. Geophys. Res. Space Phys. 2011, 116, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Dhingra, D.; Pieters, C.M.; Boardman, J.W.; Head, J.W.; Isaacson, P.J.; Taylor, L.A. Compositional diversity at Theophillus Crater: Understanding the geological context of Mg-spinel bearing central peaks. Geophys. Res. Lett. 2011, 38, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Yamamoto, S.; Nakamura, R.; Matsunaga, T.; Ogawa, Y.; Ishihara, Y.; Morota, T.; Hirata, N.; Ohtake, M.; Hiroi, T.; Yokota, Y.; et al. A new type of pyroclastic deposit on the Moon containing Fe-spinel and chromite. Geophys. Res. Lett. 2013, 40, 4549–4554. [Google Scholar] [CrossRef]
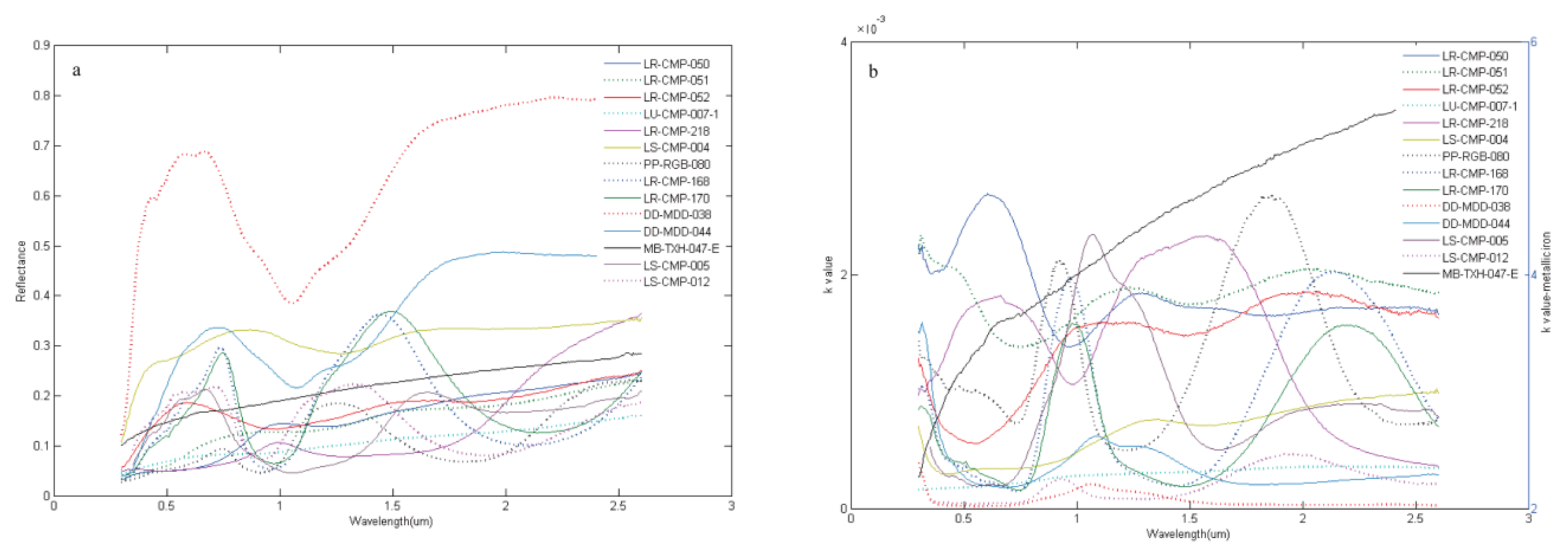
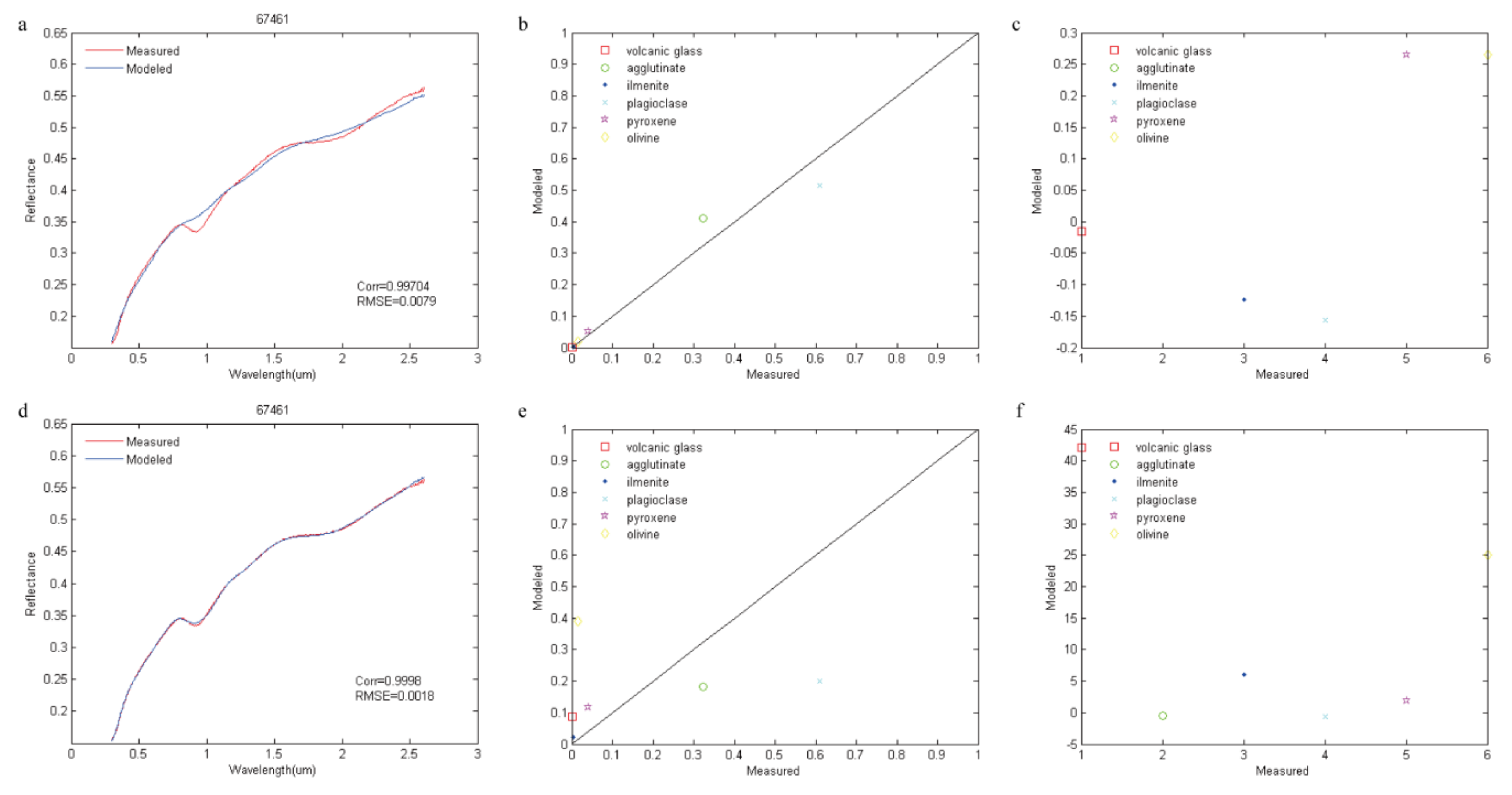


| Mineral | Real Index (n) | Reference |
|---|---|---|
| agglutinate | 1.49 | Bell et al. (1976) [39] |
| volcanic glass | 1.64 | Masson et al. (1972) [40] |
| plagioclase | 1.56 | Egan and Hilgeman (1975) [41] |
| olivine | 1.83 | Lucey (1998) [13] |
| orthopyroxene | 1.77 | Lucey (1998) [13] |
| clinopyroxene | 1.73 | Lucey (1998) [13] |
| ilmenite | 2.13 | Johnson and Christy (1974) [38] |
| metallic iron | 2.25–3.36 | Johnson and Christy (1974) [38] |
| Mineral | Sample ID | |
|---|---|---|
| Volcanic glass | black glass | LR-CMP-050 |
| orange glass | LR-CMP-051 | |
| green glass | LR-CMP-052 | |
| Agglutinate | LU-CMP-007-1 | |
| Olivine | Forsterite | DD-MDD-038 |
| Fayalite | DD-MDD-044 | |
| Ilmenite | LR-CMP-218 | |
| Clinopyroxene | Mg rich | LR-CMP-168 |
| Mg poor | LR-CMP-170 | |
| Orthopyroxene | PP-RGB-080 | |
| Plagioclase | LS-CMP-004 | |
| Metallic iron | MB-TXH-047-E |
| Mineral Sample ID | Plagioclase | Forsterite | Orthopyroxene | Clinopyroxene | Clinopyroxene | Ilmenite | |
|---|---|---|---|---|---|---|---|
| Oxide (wt. %) | LS-CMP-004 | LS-CMP-005 | LS-CMP-012 | (Mg Rich) | (Mg Poor) | LR-CMP-218 | |
| FeO | 4.99 | 11.34 | 11.16 | 20.30 | 25.40 | 41.40 | |
| MgO | 19.09 | 43.61 | 27.52 | 18.30 | 11.00 | 3.06 | |
| TiO2 | 0.05 | 0.03 | 0.32 | 0.61 | 1.15 | 53.70 | |
| SiO2 | 42.88 | 39.93 | 53.90 | 51.00 | 48.30 | 0.03 | |
| Al2O3 | 20.73 | 1.53 | 3.44 | 1.35 | 1.52 | 0.21 | |
| Cr2O3 | 0.11 | 0.34 | 0.52 | 0.55 | 0.29 | 1.04 | |
| Fe2O3 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| MnO | 0.07 | 0.13 | 0.20 | 0.35 | 0.38 | 0.36 | |
| CaO | 11.41 | 1.14 | 3.26 | 6.80 | 10.80 | 0.03 | |
| Na2O | 0.23 | 0.02 | 0.05 | 0.03 | 0.03 | 0.00 | |
| K2O | 0.03 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | |
| P2O5 | 0.03 | 0.04 | 0.04 | 0.00 | 0.00 | 0.00 | |
| Simulated Variables | Volcanic Glass (wt. %) | Agglutinate (wt. %) | Ilmenite (wt. %) | Plagioclase (wt. %) | Pyroxene (wt. %) | Olivine (wt. %) | SMFe Content (wt. %) | Particle Size (μm) |
|---|---|---|---|---|---|---|---|---|
| Upper limits | 18.9 | 71.6 | 12.3 | 64.3 | 33.8 | 4.8 | 0 | 0 |
| Lower limits | 0.1 | 25.4 | 0.1 | 13.4 | 0.9 | 0.3 | 1 | 45 |
| Relative Error (%) | Volcanic Glass | Agglutinate | Ilmenite | Plagioclase | Pyroxene | Olivine |
|---|---|---|---|---|---|---|
| Strict (Simulation) | −0.015800 | 0.265300 | −0.122900 | −0.156400 | 0.265300 | 0.265200 |
| Wide (Inversion) | 42.114200 | −0.435300 | 6.062300 | −0.670600 | 1.894200 | 25.003000 |
| Samples | 20–45 μm | 10–20 μm | <10 μm | |||
|---|---|---|---|---|---|---|
| RMSE | Corr | RMSE | Corr | RMSE | Corr | |
| 10084 | 0.001776 | 0.998469 | 0.002787 | 0.999062 | 0.002318 | 0.998898 |
| 12001 | 0.003292 | 0.996986 | 0.002108 | 0.999331 | 0.00384 | 0.998635 |
| 12030 | 0.003955 | 0.996376 | 0.003831 | 0.997865 | 0.00307 | 0.999263 |
| 15041 | 0.002437 | 0.998561 | 0.002202 | 0.999135 | 0.003484 | 0.999034 |
| 15071 | 0.003669 | 0.997447 | 0.001773 | 0.999551 | 0.002437 | 0.999466 |
| 70181 | 0.002453 | 0.998141 | 0.002396 | 0.999036 | 0.002811 | 0.999340 |
| 71061 | 0.003969 | 0.996196 | 0.004799 | 0.997808 | 0.004891 | 0.998841 |
| 71501 | 0.001433 | 0.999221 | 0.001327 | 0.999572 | 0.002189 | 0.999154 |
| 79221 | 0.001942 | 0.998744 | 0.002661 | 0.998692 | 0.00195 | 0.999503 |
| 10084 | 0.001776 | 0.998469 | 0.002787 | 0.999062 | 0.002318 | 0.998898 |
| Samples | 20–45 μm | 10–20 μm | <10 μm | |||
|---|---|---|---|---|---|---|
| RMSE | Corr | RMSE | Corr | RMSE | Corr | |
| 14141 | 0.004348 | 0.997865 | 0.004495 | 0.998654 | 0.004745 | 0.998499 |
| 14163 | 0.005338 | 0.995430 | 0.003370 | 0.999038 | 0.002957 | 0.999457 |
| 14259 | 0.003444 | 0.997875 | 0.003513 | 0.999490 | 0.00489 | 0.998793 |
| 14260 | 0.004792 | 0.996195 | 0.003494 | 0.999382 | 0.004797 | 0.998883 |
| 61141 | 0.005253 | 0.997511 | 0.003536 | 0.999367 | 0.006009 | 0.998613 |
| 61221 | 0.008383 | 0.99267 | 0.003194 | 0.999038 | 0.003748 | 0.998928 |
| 62231 | 0.005750 | 0.996993 | 0.004372 | 0.999071 | 0.004615 | 0.999118 |
| 64801 | 0.004529 | 0.99863 | 0.001683 | 0.999858 | 0.006572 | 0.998465 |
| 67461 | 0.00840 | 0.996475 | 0.007905 | 0.997042 | 0.008746 | 0.996410 |
| 67481 | 0.004386 | 0.998596 | 0.00851 | 0.998472 | 0.006989 | 0.998281 |
| Samples | 20–45 μm | 10–20 μm | <10 μm | |||
|---|---|---|---|---|---|---|
| 10084 | 29.357330 | Y | 19.090910 | Y | 15.791520 | N |
| 12001 | 24.869890 | Y | 14.424440 | Y | 9.875270 | Y |
| 12030 | 23.022140 | Y | 12.520270 | Y | 7.269090 | Y |
| 15041 | 23.079240 | Y | 14.659100 | Y | 9.988960 | Y |
| 15071 | 20.153500 | Y | 12.690960 | Y | 9.999870 | Y |
| 70181 | 25.662460 | Y | 14.788270 | Y | 9.793450 | Y |
| 71061 | 21.518310 | Y | 12.042240 | Y | 6.879350 | Y |
| 71501 | 25.987210 | Y | 15.509300 | Y | 18.572280 | N |
| 79221 | 24.609920 | Y | 16.360630 | Y | 5.111250 | Y |
| 10084 | 29.357330 | Y | 19.090910 | Y | 15.791520 | N |
| Samples | 20–45 μm | 10–20 μm | <10 μm | |||
|---|---|---|---|---|---|---|
| 14141 | 35.071200 | Y | 18.91996 | Y | 4.344820 | Y |
| 14163 | 24.593370 | Y | 11.55559 | Y | 7.464690 | Y |
| 14259 | 25.062550 | Y | 11.04594 | Y | 7.625370 | Y |
| 14260 | 27.741030 | Y | 11.17127 | Y | 7.393020 | Y |
| 61141 | 44.990720 | Y | 7.62445 | N | 5.062500 | Y |
| 61221 | 44.340120 | Y | 13.58927 | Y | 3.844930 | Y |
| 62231 | 12.251470 | N | 6.60201 | N | 4.633810 | Y |
| 64801 | 45.000000 | Y | 19.97687 | Y | 4.621100 | Y |
| 67461 | 6.027510 | N | 10.45335 | Y | 3.272480 | Y |
| 67481 | 7.768130 | N | 3.77796 | N | 2.349130 | Y |
| Mare | 20–45 μm | 10–20 μm | <10 μm | Highland | 20–45 μm | 10–20 μm | <10 μm |
|---|---|---|---|---|---|---|---|
| 10084 | 1.00 | 1.51 | 2.99 | 14141 | 2.15 | 1.60 | 2.15 |
| 12001 | 4.69 | 4.12 | 5.08 | 14163 | 2.09 | 0.53 | 1.58 |
| 12030 | 3.16 | 1.05 | 1.58 | 14259 | 3.61 | 1.58 | 3.11 |
| 15041 | 5.26 | 2.09 | 4.10 | 14260 | 1.58 | 0.53 | 1.58 |
| 15071 | 3.11 | 1.58 | 4.10 | 61141 | 0.00 | 1.06 | 0.00 |
| 70181 | 6.97 | 6.97 | 6.97 | 61221 | 0.53 | 1.06 | 8.02 |
| 71061 | 1.55 | 7.61 | 11.31 | 62231 | 5.56 | 2.09 | 2.60 |
| 71501 | 1.03 | 4.10 | 4.59 | 64801 | 0.00 | 0.00 | 0.54 |
| 79221 | 2.55 | 6.97 | 6.97 | 67461 | 1.58 | 0.00 | 0.53 |
| 67481 | 2.09 | 0.53 | 1.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, P.; Zhao, Z.; Wei, G.; Huo, H.-Y. Two Simulated Spectral Databases of Lunar Regolith: Method, Validation, and Application. Remote Sens. 2022, 14, 277. https://doi.org/10.3390/rs14020277
Zhou P, Zhao Z, Wei G, Huo H-Y. Two Simulated Spectral Databases of Lunar Regolith: Method, Validation, and Application. Remote Sensing. 2022; 14(2):277. https://doi.org/10.3390/rs14020277
Chicago/Turabian StyleZhou, Ping, Zhe Zhao, Guangyuan Wei, and Hong-Yuan Huo. 2022. "Two Simulated Spectral Databases of Lunar Regolith: Method, Validation, and Application" Remote Sensing 14, no. 2: 277. https://doi.org/10.3390/rs14020277
APA StyleZhou, P., Zhao, Z., Wei, G., & Huo, H.-Y. (2022). Two Simulated Spectral Databases of Lunar Regolith: Method, Validation, and Application. Remote Sensing, 14(2), 277. https://doi.org/10.3390/rs14020277






