Abstract
The aim of this work is to study the influence of errors on the accuracy of estimation of absorbed solar energy in the visible spectral range in the water column of the Barents Sea occurring due to the use of various satellite ocean color chlorophyll-retrieval algorithms. The estimates of absorbed energy are based on data obtained during field experiments conducted in various parts of the Barents Sea in June-August 2021, as well as on modeling results. A new regional algorithm for evaluation of chlorophyll concentration in the Barents Sea (B22) is presented as a data source. This algorithm provides more accurate estimates compared to the standard MODIS algorithm under conditions of coccolithophore bloom. Comparing of the results of hydro-optical modeling to the data of shipboard hydro-optical measurements made it possible to validate the obtained data and confirmed the correctness of the selected models. Furthermore, we calculate the parameters of underwater light fields and the absorbed thermal energy in the visible spectral range in the seawater column, showing that differences in the chlorophyll concentration due to the accuracy of satellite bio-optical algorithms (30–50%) have little effect on the vertical distribution of solar energy absorbed in the seawater column.
1. Introduction
The absorption of solar radiation by seawater and by its optically active constituents (OAC) is a main component of the thermal budget [] and a significant stratification mechanism of the upper ocean layer []. These are also one of the main processes modulating heat flow in the Arctic. Not only absorption but also a horizontal transfer of heat by water masses is significant. From this point of view, the Barents Sea is an important area to study because the Norwegian Atlantic Current passes through it, which carries relatively warm waters to the north and northeast [].
To fully describe and model the absorption of visible solar radiation processes, it is necessary to determine the set of inherent and apparent optical properties of seawater, the measurement of which is a difficult and time-consuming task, especially in marine expeditions. Therefore, hydro-optical models used to solve forward [] and inverse [] problems of radiative transfer in seawater are important. They should minimize the parameters necessary for measurement, provide additional validation, and allow for numerical calculation of light propagation, its absorption, and conversion into heat, depending on the optical characteristics of seawater.
Usually, when calculating heating in the visible range of the spectrum, simplified models are used [] for waters of the first optical case, where the optical characteristics are determined by the presence of phytoplankton and parameterized according to the concentration of chlorophyll-a (Chl) [].
Chl is a standard satellite bio-optical product and is a good marker of phytoplankton biomass, which enables tracking of the state of the marine ecosystem. The standard procedure for calculating Chl from MODIS spectroradiometer data (chlor_a product, https://oceancolor.gsfc.nasa.gov/atbd/chlor_a, USA, accessed on 7 July 2022) consists of using the color index (CI) algorithm [] for oligotrophic waters with Chl < 0.15 mg m−3 and using the OC3M algorithm for more productive waters with Chl > 0.2 mg m−3. The latter is a member of the OCx regression family of algorithms developed by NASA for various ocean color scanners, starting with SeaWiFS []. In between these values, the CI and OC3M algorithms are blended using a weighted approach. In addition to regression algorithms, quasi-analytical algorithms can be used, such as GIOP [] and QAA [], with the help of which spectral characteristics of light absorption by phytoplankton are determined, making it possible to estimate Chl and its contribution to the absorption of light energy by seawater.
Because standard global bio-optical algorithms do not take into account the regional specifics of different seas, such as, coccolithophore blooming in the Barents Sea or the influence of river runoff in the Kara Sea, they can lead to significant errors in some water areas [,]. Therefore, a large number of regional algorithms have been developed [,,,], making it possible to achieve more accurate estimates of Chl.
It is essential to carry out regular in situ measurements of Chl, as is undertaken in the Barents Sea by various research groups, both using shipboard measurements [,,,,] and using automated platforms, such as gliders [] and bio-Argo buoys (https://maps.biogeochemical-argo.com/bgcargo, accessed on 7 July 2022). This makes it possible to take into account various regional factors that lead to errors in global bio-optical algorithms, such as coccolithophore blooms, the significant influence of colored dissolved organic matter (CDOM) absorption on the formation of sea color, and the influx of terrigenous dissolved and suspended substances. According to [,,], not all CDOM correlates with Chl in the Barents Sea. A significant influence of terrigenous CDOM was observed in the southeastern part due to the influence of the Pechora River []. In the central part of the Barents Sea, CDOM is mainly of autochthonous origin, although its contribution to total light absorption is comparable with or exceeds that of phytoplankton []. In those expedition data, the distribution of CDOM absorption coefficients did not correlate with Chl, presumably due to a temporal mismatch between the intensive spring bloom and the subsequent degradation of phytoplankton into detritus and CDOM.
The increased content of CDOM in comparison to that in the waters of the first optical case, which is typical for Arctic seas, can lead to a significant redistribution of the light energy absorbed in seawater. At high values of CDOM, the upper layers are heated more strongly, whereas the deeper layers are less intensely heated []. In addition, most models imply that the light attenuation by various seawater components is constant with depth [].
To calculate the absorption of solar energy in seawater, various algorithms for the numerical solution of the radiation transfer equation (RTE) are used, for example, Hydrolight (https://www.sequoiasci.com/product/hydrolight, accessed on 7 July 2022) and DISORT []. Software products developed on the basis of these algorithms include various hydro-optical models. When developing and using such models, it is important to take into account that the resulting equations, corrected for large spatiotemporal samples, may not work in some regions, usually as a result of result of atypical light-scattering or absorbing characteristics or non-standard relations between OAC of seawater. Furthermore, the uncertainties between the data of hydro-optical modeling and experimental measurements are usually associated with poor determination of inherent or apparent optical properties [].
To calculate the full list of light field parameters in the sea column without taking into account polarization, it is sufficient to determine the spectra of light absorption (a(λ)) and the volume-scattering function (β(γ,λ)) (VSF). However, in practice, it is more convenient to measure a(λ) for various OACs of seawater, the spectrum of the light attenuation coefficient (c(λ)) to estimate b(λ), and the light backscattering coefficient (bb) [] to restore the volume-scattering function from the backscattering ratio bb/b. The latter does not depend much on the wavelength, which is true for spherical scattering particles and partly true for non-spherical, inhomogeneous particles. Although apparent optical properties can be calculated based on inherent properties [,], for additional validation, it is desirable to measure the underwater downwelling (Ed(λ)) and upwelling (Eu(λ)) plane irradiance and the remotely sensed reflectance (Rrs(λ)), which makes it possible to solve direct and inverse problems of radiative transfer, which is important both to validate measurements and hydro-optical models.
Thus, in many models, Chl is a key parameter that determines the entire set of inherent optical properties used to calculate the solar energy absorbed in the seawater column. In addition, satellite color scanners are the main source of data on Chl. Therefore, the aim of this work is to study the influence of errors occurring in association with the use of various satellite Chl-retrieval algorithms on the accuracy of estimation of absorbed solar energy in the visible spectral range in the water column of the Barents Sea.
2. Materials and Methods
2.1. Study Area
Shipboard measurement data were obtained in the Barents Sea during cruises 83 [] and 84 [] of the R/V ‘Akademik Mstislav Keldysh’, which were carried out in June–August 2021. We selected five stations with the corresponding weather conditions for detailed analysis to obtain satellite data (Section 2.4). The selected stations are located in different parts of the sea: 7013 in the southern part of the sea, 7044 in the central part, 7069 northwest of Svalbard, and 7090 and 7091 east of Svalbard (Table 1). For the first four stations, a full range of onboard measurements was performed (Section 2.2). At station 7090, satellite data could not be obtained due to constant dense cloudiness, so we used satellite data from nearby station 7091. The work at this station was performed at night; thus, no light field measurements were taken there. The closeness of the values of the bio-optical characteristics measured at stations 7090 and 7091 makes it possible to use the data from these stations jointly.

Table 1.
Information about the selected stations.
Despite the differences in geographical location, the Chl concentration at these stations differs insignificantly (Figure 1), and, according to the standard MODIS chlor_a algorithm [,], is 0.3–0.5 mg m−3, which corresponds to mesotrophic waters. The presence of phytoplankton blooms and the influence of river runoff were not recorded. The studied waters are close to the case 1 type: phytoplankton cells and the associated OACs make the main contribution to the absorption and scattering of light in seawater relative to other OACs []. The quasi-homogeneous spatial distribution of bio-optical parameters in the areas of the stations makes it possible to extend the measurement results to regions with similar bio-optical characteristics and to calculate the solar energy absorbed in the seawater column.
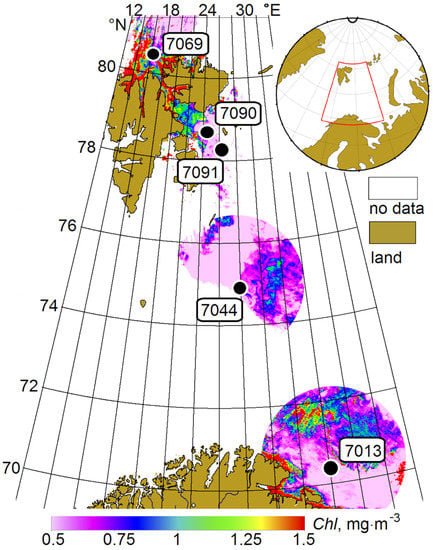
Figure 1.
Position of the stations of cruises 83 and 84 of the R/V ‘Akademik Mstislav Keldysh’ against the background of the averaged spatial distribution of chlorophyll-a concentration according to MODIS/Aqua and Terra (chlor_a) data: 7013—12 June 2021; 7044—26 July 2021; 7069—9 August 2021; 7090 and 7091—17 August 2021.
2.2. Field Measurements
The complex of hydro-optical measurements at the selected stations included vertical profiles of the spectral irradiance of the descending and ascending radiation fluxes (Ed(λ, z) and Eu(λ, z), respectively), vertical profiles of photosynthetic active radiation (PAR), vertical profiles of the beam attenuation coefficient of seawater at a wavelength of 530 nm (c(530, z)), and spectra of the light absorption coefficient of optically active constituents of samples of the seawater surface layer (ai(λ)). The fluorescence intensities of chlorophyll-a (FlChl) obtained using a flow-through measuring complex were also used in the present study.
The following devices were used:
- An instrument complex to measure surface and underwater photosynthetically active radiation []. The complex was developed and built at the Ocean Optics Laboratory of the Shirshov Institute of Oceanology of the Russian Academy of Sciences (SIO) based on LI-192 LI-COR photodiode sensors (measuring total irradiance in the range of 400–700 nm), supplemented by devices to collect and transmit information.
- A set of two Ramses submersible hyperspectral radiometers. The radiometers are designed to measure underwater irradiance spectra in the wavelength range of 320–950 nm with a spectral resolution of 3.3 nm. The simultaneous use of two sensors, making it possible to carry out synchronous measurements of Ed(λ, z) and Eu(λ, z). Thus, it is possible to directly calculate the spectral diffuse attenuation coefficients (Kd(λ, z)) from the obtained Ramses data.
- A portable spectrophotometer with an integrating sphere ICAM (integrating cavity absorption meter) []. The device was used to determine the spectra of the total light absorption coefficient of seawater (a(λ)), as well as the spectra of the light absorption coefficient of particles (ap(λ)) and CDOM (ag(λ)). The measurement data were processed according to the method described in [].
- A PUM-200 submersible transmissometer. The device was designed and assembled at the Laboratory of Ocean Optics, SIO RAS []. Its goal is to measure vertical profiles (c(530, z)), as well as seawater temperature and chlorophyll-a fluorescence intensity.
- A flow-through measuring complex [], which includes a PFD-2M two-channel flow-through fluorimeter, a laser hyperspectral fluorimeter [], a PUM-A transmissometer, and a thermosalinograph. In the present study, we used only spatial distributions of the Chl fluorescence intensity (FlChl) excited by radiation at wavelength of 532 nm and registered near 685 nm. The measurements were taken in the seawater surface layer at a depth of 2–3 m, with a spatial resolution of about 50 m. Calibration of the flow-through fluorimeter according to the data of direct determinations of the Chl concentration made it possible to obtain the distributions of this quantity (Chlfl) along the ship’s route. When calibrating the flow-through fluorimeter data, there were no significant deviations associated with non-photochemical quenching (NPQ) []. In our recent work [], based on the results of the analysis of 648 samples, we demonstrated that the effect of NPQ on the relationship between the Chl fluorescence intensity and its concentration in the studied polar region is small. It is important to note that most of the samplings were carried out under conditions of a polar day in cloudy weather, which reduces the variations in the PAR flux and, accordingly, minimizes the influence of NPQ.
The Chl and pheophytin “a” concentrations directly determined on-board the vessel using the fluorometric method with acidification and extraction in 90% acetone on a Trilogy 1.1 fluorimeter (Turner Designs, United States) in the ship laboratory according to []. The device was calibrated by means of the standard Sigma C6144-1MG chlorophyll “a” powder according to the method recommended by the manufacturer. Phytoplankton species composition analysis was performed in the laboratory after the cruise.
The light-scattering coefficient (b(530)) and the spectrum of the diffuse attenuation coefficient (Kd(λ)) were additionally calculated based on the obtained measurement data. Solving the inverse hydro-optical problem enabled determination of the backscattering index (bb(530)). The volume-scattering function and the seawater reflectance spectra (ρmodel(λ)) were also modeled.
2.3. Hydro-Optical Models and Algorithms
The propagation and absorption of solar radiation in seawater were modelled using the approach described in [,] based on the numerical solution of radiation transfer equations for the system atmosphere—rough surface—ocean, considered as a set of plane-parallel homogeneous layers with given optical properties. If the reflection and transmission operators for each layer are calculated, then using well-known recursive formulae (for example, []), the angular distributions of radiance at the boundaries of any layers can be determined as a function of the solar zenith and azimuth angles. The irradiance, PAR, and the amount of absorbed radiation in any layer can be easily determined based on known radiances.
The reflection and transmission operators for each layer were calculated with the discrete ordinate method using the DISORT code [].
For the atmosphere in the cloudless case, we used a three-layer model consisting of an upper, non-scattering absorbing ozone layer, the Rayleigh atmosphere, and an aerosol with the Gordon–Castaño model phase function []; with respect to the optical thickness, , where the Angstrom index (A) and the aerosol optical depth (τa(869)) are taken from satellite ocean color scanner data.
The measurements at station 7044 were performed under overcast conditions. In this case, we used a four-layer model: ozone layer, Rayleigh layer, cloud, and Rayleigh layer. The heights of the upper and lower cloud boundaries do not significantly affect the result []. When processing data from station 7044, it was assumed that the lower boundary of the cloud layer is located at a height of 1 km and that the boundary is located at a height of 3 km. An essential parameter is the optical thickness of the cloud (τcl). In our case, it was assumed to equal 30, corresponding to the value providing an acceptable agreement with the results of measurements of irradiance by the Ramses instrument. The C1 water cloud model [] was adopted as the cloud-scattering phase function.
The surface was treated as a separate layer. Formulae for a smooth surface can be found in []; for a rough surface, the results reported in [,] were used. The calculation performed for a rough surface (wind speed less than 4 m s−1, corresponding to the conditions of shipboard measurements) showed that the instantaneous PAR values in the upper 10-m layer differ from the calculation results for a smooth surface by no more than 1%. Thus, all calculations were performed for the windless case.
To estimate the scattering phase function of water layers, we used a two-parameter model of the light-scattering properties of seawater [], according to which the volume-scattering function can be represented as the sum of contributions from scattering by pure seawater (index w), small particles (index s), and large particles (index l).
Small particles are assumed to be mineral particles less than 1 μm in size with an index of refraction (relative to water) of n = 1.15; large particles are biological particles larger than 1 μm in size with an index of refraction of n = 1.03. The model is defined as:
where is the VSF of pure water at 550 nm, vs and vl are concentrations of small and large particles, respectively, ; functions and are tabulated in [].
To define the parameters of the model (vf and vc), we first integrated (1) over the whole sphere, then over the backward hemisphere. As a result, for each wavelength, we obtained a pair of linear equations with two variables []:
where , and .
b = bw + vs bs + vl bl;
bb = ½ bw + vf bbs + vc bbl,
bb = ½ bw + vf bbs + vc bbl,
According to (2), it follows that there is a one-to-one correspondence between the pairs ((vf, vc) and (b, bb)). In other words, within the framework of this model, the parameters b(λ) and bb(λ) for a fixed value of wavelength completely determine the scattering properties of seawater. If the solutions of Equation (2) are substituted into (1) and the normalization factor is taken into account, then we obtain the scattering phase function and, consequently, all the parameters necessary for the numerical solution of the radiative transfer equations.
Thus, for complete description of the optical properties of water, it is sufficient to determine the spectral dependence of the absorption coefficient (a(λ)), as well as the scattering coefficients (b) and backscattering (bb) for a given wavelength (λ0) (530 nm in our case).
Assuming that the absorption coefficient a(λ) is known, an algorithm can be used to calculate bb according to the subsurface radiance reflectance, ρ = π·Lu/Ed, where Lu is the subsurface upwelling radiance, and Ed is the subsurface downwelling irradiance. This algorithm is based on the well-known formulae [,,,] that enable calculation of the backscattering coefficient according to parameters ρ and a. This approximate formula can be used to express the subsurface reflectance (ρ(λ)) through the parameter u = bb/(a + bb). Solving the equation ρ = F(u) with respect to u yields parameter bb. The spectra (ρ(λ)) were calculated based on remote sensing reflectance (Rrs(λ)) using the following formula []: , where Rrs(λ) was measured by MODIS/Aqua and OLCI/Sentinel-3A. To determine the absorption coefficient (a(λ)), we used an integrating cavity absorption meter.
It is not possible to determine the value of b using remote sensing data, so to find b(λ0), we used the beam attenuation coefficient c(530) determined with the help of a PUM transparency meter, yielding b(530) = c(530) − a(530).
This result can be used as a first approximation, the accuracy of which is determined by the accuracy of the above approximate formulae. A more accurate result can be obtained by minimizing the quadratic form:
where λi is the wavelength of the spectral bands of the satellite ocean color scanner, ρ(λi) is the measured value of the subsurface reflectance, and is the values of the same reflectance depending on parameters vs and vl calculated by solving RTE. For stations 7044, 7069, and 7091, we used a limited set of spectral channels without 412, 443, and 469 nm, as the values of ρ(λi) for these wavelengths contradicted the results of shipboard measurements of the absorption coefficient. This may be the result of an erroneous atmospheric correction in the shortwave range at low solar elevations.
An attempt to use the Levenberg-Marquardt numerical method to minimize the form (3) led to a positive result only in the case of station 7013 due to the significant dependence of the function S(vs,vl) on the only parameter, i.e., bb. In this regard, in order to determine the optimal values of vs and vl, we solved the problem of the extremum of function S under the following conditions imposed on the variables (vs and vl): b(530,vs,vl) = c(530) − a(530), where c(530) and a(530) are measured values. The results of this algorithm are the profiles of apparent optical properties (AOPs) shown in Section 3.3 and Discussion.
When constructing these profiles, the stratification of seawater was not taken into account. To take it into consideration within the framework of this model, it is necessary to establish the connection between the measured profiles of optical characteristics, such as beam attenuation coefficient (c(530)), chlorophyll concentration and its fluorescence intensity, and the depth dependences of the values vs, vl and the absorption coefficient (a(λ,z)).
Satisfactory agreement between the measured and calculated profiles of downwelling irradiance Ed(z) was possible within the framework of a simpler model, ‘case 1 new’ []. According to this model, all IOPs are uniquely determined through a single parameter, the chlorophyll concentration (Chl). In particular, the absorption coefficient is modeled as the sum of three components: , where aw is absorption by pure water, ap is absorption by particulate matter, and ag is absorption by yellow matter (Gelbstoff). For the parameter ap [], was used; for the yellow matter absorption the following formula was applied []:
with default values of fg = 0.2, λ0 = 440 nm, and S = 0.014 nm−1. A comparison of ap and ag values calculated from these formulae with the ICAM measurements showed that whereas this model may be a good approximation for ap, the values of ag calculated with the default (fg) are significantly lower than the ICAM results. In calculations according to this scheme, the measured values of the Chl concentration obtained at varying depths were used. This approach allows us to study the effect of taking into account the OAC stratification on the result of calculating underwater light fields.
Hypothetical values of Chl* concentration were used to estimate the influence of Chl concentration on the result of calculation of energy absorbed by seawater (Section 3.2). In this case, the model described in [] was used in the calculations, the result of which replaced the ap(λ) values obtained using the integrating sphere.
2.4. Satellite Data
Level 2 data of ocean color satellite scanners MODIS/Aqua, MODIS/Terra, OLCI/Sentinel-3A, and OLCI/Sentinel-3B were used. The MODIS data were downloaded from the NASA Ocean Color website (https://oceancolor.gsfc.nasa.gov/, USA, accessed on 7 July 2022) and the OLCI data were obtained from the Earth Observation Portal website (https://eoportal.eumetsat.int/, Darmstadt, Germany, accessed on 7 July 2022). Satellite data were further processed using the SMCS software package developed at the SIO Ocean Optics Laboratory [].
The selection of satellite data was difficult due to frequent cloudiness during the shipboard measurements. Therefore, for stations 7013 and 7044, satellite data were selected for two days preceding field measurements. During the selection of satellite data, the time interval between field and satellite measurements did not exceed 48 h. Furthermore, the nine pixels closest to the station should not have been marked with a CLDICE flag. From the satellite data satisfying these conditions, only the best MODIS overpass for each station was selected by expert evaluation, taking into account the sun zenith angle, the scanner viewing angle, and the absence of obvious distortion of the Rrs(λ) spectrum.
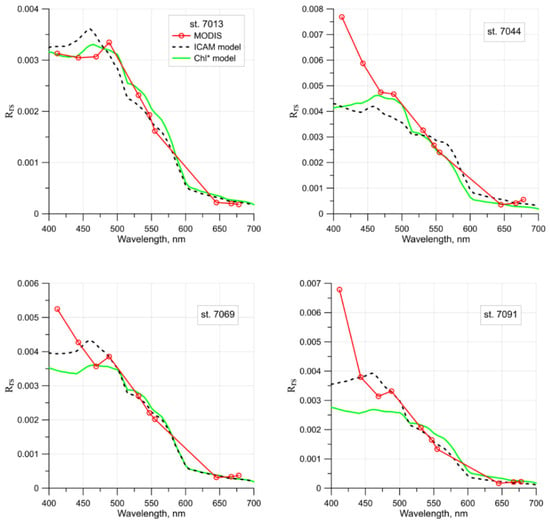
Figure 2 shows a comparison of the Rrs(λ) spectra obtained from the MODIS satellite ocean color data with modeling results. Both absorption data measured with ICAM and model values for the selected Chl* concentrations were used for modeling (Section 3.2). Good agreement was achieved between the model and satellite spectra for the entire visible range for station 7013. For the other stations, significant differences are noticeable for the 412 nm band, which is associated with atmospheric correction errors. The differences between the model and satellite spectra for station 7044 arise because this station is located at the boundary of the area of increased Chl concentration (Figure 1). In addition, the difference in the time of shipboard and satellite measurements at this station was 32 h. For the wavelength of 530 nm used in our hydro-optical model (Section 2.3), the error between the model and satellite data does not exceed 8%.
2.5. SIO RAS Regional Chl-Retrieval Alghorithm
The B98 regional algorithm for estimating chlorophyll-a concentrations from satellite data in the Barents Sea [] was created on the basis of shipboard measurements on cruises 13 and 14 of the R/V ‘Akademik Sergey Vavilov’ in August–September 1998. The B98 algorithm uses the color index for the 531 and 547 nm spectral bands, as the atmospheric correction errors are usually much smaller than for the short-wavelength channels. Most of the in situ measurements in 1998 (15 out of 21) were performed in the Pechora Sea, which is characterized by an increased content of CDOM.
Validation according to shipboard measurements in 2016–2020 [] showed that the B98 regional algorithm is not suitable for the open waters of the Barents Sea. Therefore, a modified B22 regional algorithm was developed using the same color index as B98:
Chl = 1.97 [Rrs(531)/Rrs(547)]−7.76.
Formula (5) was derived on the basis of satellite estimates of Rrs(λ) of MODIS Aqua/Terra ocean color scanners and shipboard Chl measurements (26 pairs, with a time interval between field and satellite measurements of less than 12 h). The average relative error (RE) of the B22 algorithm in this data set is 38%, the root mean square error (RMSE) is 0.21 mg m−3, the coefficient of determination is 0.32, p-value < 0.001, and the bias is −0.04 mg m−3. If the admissible time interval between satellite and field measurements is increased to 48 h (121 pairs), the RMSE will increase to 0.38 mg m−3, RE = 49%, and bias = −0.05 mg m−3 correspondingly.
3. Results
3.1. Validation of the SIO RAS Regional Chl-Retrieval Alghorithm
To validate the satellite algorithms, we used fluorimeter data of the flow-through complex obtained on cruises 83 and 68 of R/V ‘Akademik Mstislav Keldysh’ (AMK) in June 2021 and August 2017, respectively. The data of cruise 83 are interesting because these are our first Chl measurements in June for the Barents Sea (the previous measurement data were obtained in July–September), and they were carried out in the absence of phytoplankton bloom (the average values of the Chl concentration evaluated based on fluorimeter data <Chlfl> was equal to 0.44–0.50 mg m−3). In the case of AMK 68, the measurements were carried out in an area of strong coccolithophore bloom (according to direct measurements, the concentration of coccolithophores in the surface layer varied in the range of 1.4–6.3 million cells/L). The bloom can affect the accuracy of satellite algorithms with respect to estimations of Chl concentration. The Chl values there were noticeably higher (<Chlfl> = 1.27 mg m−3). To calibrate the fluorimeter data, we used Chl values measured at stations in the Barents Sea. The MODIS/Aqua data average daily composites (Figure 3A,B) were calculated, and data with the STRAYLIGHT flag were excluded to eliminate the distortion of satellite data near clouds.
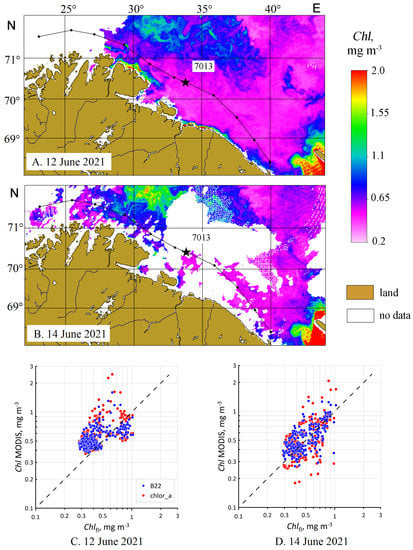
Figure 3.
The spatial distributions of Chl concentration according to MODIS/Aqua data on 12 June (A) and 14 June (B), 2021, calculated using the B22 regional algorithm. The black line shows the ship’s route. Comparison of the Chl values calculated from satellite data on 12 June (C) and 14 June (D), 2021 and measured with a fluorimeter. The dotted line is the perfect fit (1:1).
The measurements in the Barents Sea during cruise AMK 83 were performed on 13–15 June 2021, but satellite data were available only for 12 and 14 June (Figure 3A,B). Unfortunately, on 14 June, even in the daily composite, there are large gaps in data due to cloudiness. A comparison of satellite and fluorometric estimates of Chl values (Figure 3C,D, Table 2) showed that the Chl estimates of the standard chlor_a and regional B22 algorithms in the absence of phytoplankton blooms actually coincide. In 14 June, the time of satellite measurements is closer to the time of field measurements, and the errors of satellite Chl estimates (B22: RMSE = 0.15 mg m−3, RE = 23%, bias = +0.04 mg m−3) are somewhat lower than for June 12 (B22: RMSE = 0.17 mg m−3, RE = 32%, bias = +0.08 mg m−3).

Table 2.
The correspondence parameters between the values of chlorophyll concentration measured with a fluorimeter and calculated based on MODIS data by standard and regional algorithms, depending on the data set.
A comparison of satellite and fluorometric estimates of Chl values in the case of coccolithophore bloom during cruise AMK 68 (Figure 4, Table 2) showed that the presence of bloom had little effect on the accuracy of satellite algorithms. The errors of the standard and regional satellite algorithms actually coincide in magnitude. However, if the standard algorithm overestimates Chl in the entire range of values (0.5–2 mg m−3), then the regional algorithm yields estimates mainly in the range 1.5–2 mg m−3. This leads to a decrease in bias for the regional algorithm. If compared with the validation of the Chl retrieval algorithms in the absence of phytoplankton bloom, we note that in the case of coccolithophore bloom, the relative errors are approximately the same (24–28%), but the absolute errors are slightly higher (about 0.4 mg m−3). This could be the result of both errors, either in the calibration of the fluorimeter under the conditions of coccolithophore blooms, and the time difference between the fluorometric and satellite measurements (about a day).
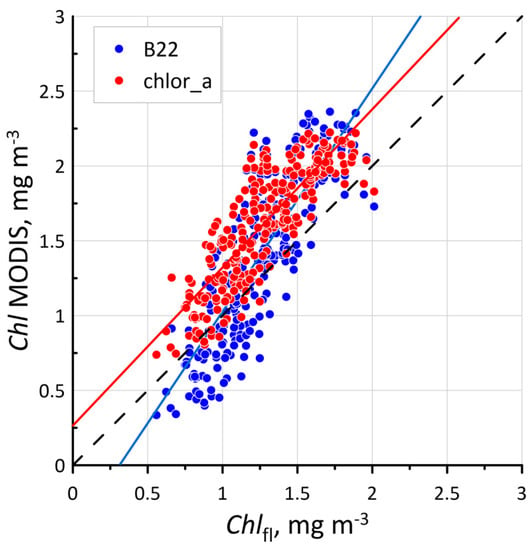
Figure 4.
Comparison of Chl values calculated based on satellite data obtained on 14–15 August 2017 and measured using a flow-through fluorimeter. The dashed line is the perfect fit (1:1), and the colored lines are linear regressions.
3.2. Chlorophyll Concentrations
MODIS/Aqua data were selected based on the criteria (Section 2.4). Further Chl concentrations were estimated using the global standard chlor_a and regional B22 algorithms (Table 3). For stations 7013 and 7069, satellite estimates actually coincide with the results of direct determinations. For stations 7044 and 7091, satellite estimates were underestimated and overestimated, respectively. This could be the result of both a large time interval between satellite and field measurements and errors of satellite algorithms. The differences between the two satellite algorithms for these stations and the selected satellite data can be considered insignificant.

Table 3.
Chlorophyll concentrations calculated based on satellite data by various algorithms (chlor_a, B22) and measured in situ.
Table 3 also contains the Chl* data selected in such a way that the estimated values differ by several fold relative to the measured values, whereas satellite estimates of Chl fall in the range between Chl in situ and Chl*. This makes it possible to use the Chl* values to assess the influence of the Chl concentration on the values of solar energy absorbed in the photic layer (Section 4.1).
3.3. Validation of Instantaneous Irradiance Calculations
Model calculations were validated on the basis of the results of the downward flux measurements of irradiance performed at the stations using the Ramses spectroradiometer. The measured vertical profiles of the seawater beam attenuation coefficient were used to take into account the OAC stratification (Figure 5). Differences were observed between these profiles: a sharp peak at a depth of about 15 m at station 7013, a decrease in values with depth at station 7044, increasing values with depth (up to 30 m) at station 7069, and quasi-homogeneous distribution at station 7091. The influence of the c(530, z) vertical profile type on the calculation results will be analyzed below.
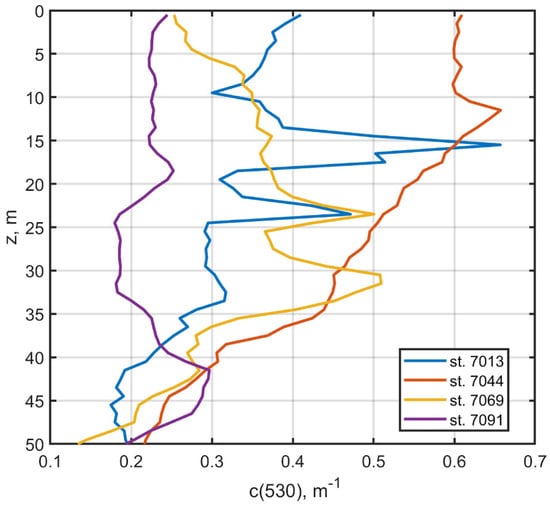
Figure 5.
Measured c(530, z) vertical profiles for the selected stations.
We compared the values of instantaneous irradiance for λ = 530 nm, which corresponds to the wavelength of measurements of the beam attenuation coefficient. The measured Ed(530, z) vertical profiles, as well as the results of simulation performed under the assumption of the homogeneity of the upper layer and for pure water, are shown in Figure 6.
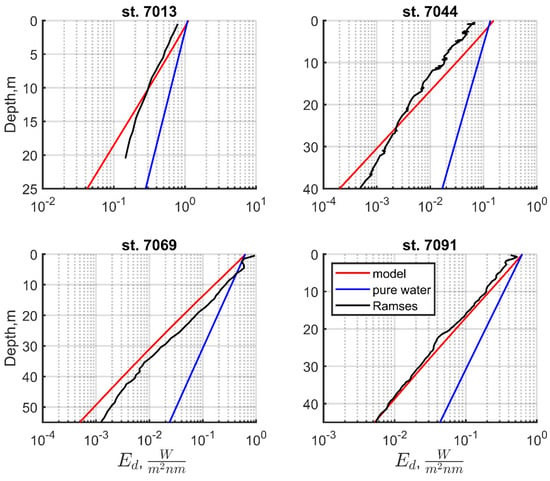
Figure 6.
Ed(530, z) vertical profiles from direct measurements of Ramses (black lines), from modeling data taking into account OAC (red lines), and for a hypothetical case of pure water (blue lines).
The measured and modeled values are in general agreement, taking into account the OAC. The small-scale variability of the data of direct measurements is mainly associated with the variability of the light conditions of observation that occurred during the measurements and caused by the presence of variable cloudiness, which is characteristic of the Arctic, as well as the ship’s rolling. Therefore, the figure does not show a part of the profile obtained at station 7013 during sharp changes in cloudiness.
In comparison to the hypothetical case of radiation propagation in pure water, it is possible to estimate the contribution of the OAC at each station. The most significant discrepancy between the modeling results for real and pure water is observed at station 7044, where the highest Chl concentration (1.07 mg m−3) was obtained as a result of direct measurements. Corresponding curves are closest at station 7091, where the minimum Chl concentration (0.17 mg m−3) was recorded.
We further compared the values of Kd_PAR(z) for the PAR range calculated based on the data of direct determinations using LI-COR and modelling to verify the quality of the spectral model (Figure 7). The agreement between the results is acceptable: RE = 53%, 51%, 27%, and 7% for the selected stations, respectively. The best agreement between the data was obtained at stations 7069 and 7091, with good weather conditions during data collection. The bend in the measured vertical profile (Kd_PAR(z)) at station 7069 in the region of 30 m, as well as the break in the corresponding profile for station 7044 near 10 m, are the result of the peculiarities of the OAC stratification, which are clearly distinguishable in the c(530, z) profiles (Figure 5). Section 4.2 is devoted to a possible approach to accounting for stratification.
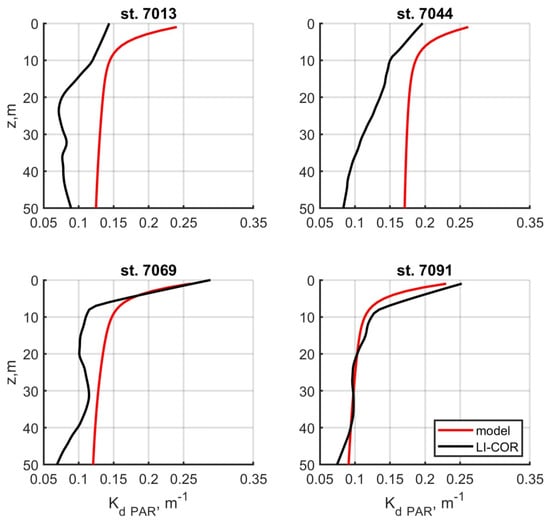
Figure 7.
Kd_PAR(z) vertical profiles in the PAR range based on data of direct determinations (black lines) and modeling (red lines).
4. Discussion
4.1. The Influence of Chl Concentration on the Accuracy of Calculating the Seawater Energy Absorbed in the PAR Range
The energy absorbed in the seawater in the PAR range (Eabs(z)) was calculated using the data interpolated in depth with a step of dz = 1 m according to the following equation:
Eabs(z) = Ed(z) + Eu(z + dz) − Ed(z + dz) − Eu(z),
Figure 8 compares the data of in situ measurements with three model calculations: data obtained as a result of direct determinations of Chl concentration values, Chl*, and a hypothetical case of pure water. The Chl* values were chosen in such a way that the results of the satellite algorithms are between the Chl in situ and Chl* values (Section 3.2). This approach makes it easier to understand the results, as the vertical distribution of the energy absorbed in seawater will be enclosed between two reference curves. The absolute values of Eabs(z) depend on the lighting conditions, which are difficult to model under partial cloudiness. To optimally fit the results of in situ measurements, the model data were consistently shifted along the horizontal axis.
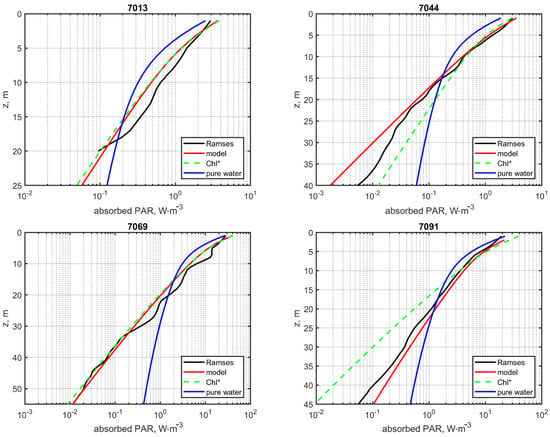
Figure 8.
Vertical distributions of solar energy absorbed in seawater in the PAR range drawn from direct measurements (black lines) and modeling based on in situ measurements (red lines), selected Chl* values (green dotted lines), and the pure water hypothesis (blue lines).
Figure 8 shows agreement between the calculation results and direct measurements. The position of the green line relative to the red line is in full agreement with the Chl in situ and Chl* values. For example, at station 7044, the latter calculation was performed with a fourfold decrease in Chl concentration in comparison to the results of the direct measurements. With lower Chl content, more light is absorbed in deeper layers, a trend similar to the case of pure water. Although the corresponding lines are in the logarithmic representation and merge in the surface layer, the difference in magnitude shows the correct relationship (not depicted here). For other stations, Chl* > Chl in situ, so the relative variability of the model results with depth is inverse.
Analysis of the results obtained at four stations differing in geographic location and type of c(530, z) profile showed that the accuracy of estimating the Chl concentration in the Barents Sea has an insignificant effect on the accuracy of estimating the solar energy absorbed in seawater. This is the result of the relatively small contribution of absorption by phytoplankton to the total absorption by seawater in the Barents Sea during the study period. It makes possible to use the data of satellite algorithms to determine the Chl concentration in such calculations: for correct estimations of the absorbed energy, an accuracy of 30–50% of such algorithms is sufficient. In the case of a discrepancy in the estimate of the Chl concentration by more than two times, the difference will be observed only in the layers located deeper than 10 m (stations 7044 and 7091).
With a small effect of the Chl concentration, the difference relative to pure water is primarily the result of CDOM absorption. This result is in agreement with the results reported in [], where it was shown that CDOM plays a major role in light and heat absorption in the Barents Sea during a large part of the year. This is because CDOM absorbs light in mainly in the short-wavelength area, where photons have higher energy []. It is important that the errors in determining ag(443) from satellite data in the Arctic exceed the errors of satellite algorithms to estimate the Chl concentration [], highlighting the primary role of CDOM in the absorption of solar energy by the seawater and making the development of methods for estimating ag(443) necessary. Such an improvement will entail a refinement of the seasonal estimates of radiance balance in the Barents Sea [,].
4.2. The Impact of Considering IOP Stratification
To investigate the effect of inherent optical property (IOP) stratification, calculations were performed using Morel’s ‘case 1 new’ model [], in which all IOPs can be calculated based on Chl concentration (Section 2.3). Figure 9 shows an example of the results of such a calculation of the downwelling irradiance Ed(530, z) in comparison to the data obtained at station 7069. The Chl concentration was measured at the depths of 1, 6, 15, 22, 38, and 52 m. To carry out the calculations, the obtained Chl values were interpolated.
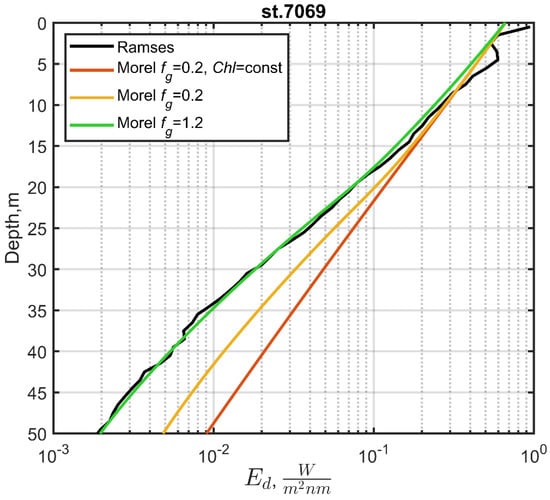
Figure 9.
Comparison of downwelling irradiance Ed(530, z) profiles measured with Ramses (black line) and calculated using the ‘case 1 new’ model for fg = 0.2 (red and yellow lines) and fg = 1.2 (green line) at station 7069. The red curve was calculated without taking into account stratification.
Figure 9 shows that the results of calculations using the parameter fg = 0.2 (see Equation (3)) differ significantly from the results of measurements at depths greater than 15 m (RE = 147%), whereas for fg = 1.2, we obtained excellent agreement between the calculation results and measurements (RE = 8%). Therefore, Morel’s ‘case 1 new’ model, with a slight modification, can take into account IOP stratification (Figure 5). Compared to calculations without stratification, this approach makes it possible to achieve improved agreement between the measured and calculated Ed(530, z) profiles. Furthermore, it is of interest to study the influence of other factors vertical distribution, such as CDOM absorption and the particle-scattering coefficients. In this case, it is possible to use a special technique to calculate the vertical profile of CDOM absorption [].
4.3. An Example of Using OLCI Data
The method used in this work to exclude short-wavelength channels of the Rrs MODIS spectra, which are affected by atmospheric correction errors, showed good agreement between the parameters of underwater light fields when compared to direct measurements. In this section, we consider the applicability of this approach in terms of using better quality satellite data. Take, for example, OLCI data of 9 August 2021, selected for station 7069. In comparison to the MODIS spectrum used in the main part of the work, the OLCI spectrum does not exhibit an unrealistic increase in Rrs in short-wavelength channels, which contradicts to the data of direct determinations of the seawater absorption coefficient (Figure 10a). The results of model calculations are close to satellite data for the entire Rrs OLCI spectrum, and for MODIS, the model spectrum of Rrs makes it possible to avoid the influence of errors in shortwave channels. Such errors typical for the Arctic region lead to underestimated values of the CDOM absorption coefficient compared to those measured on the integrating sphere, leading to low accuracy of satellite algorithms in this region [].
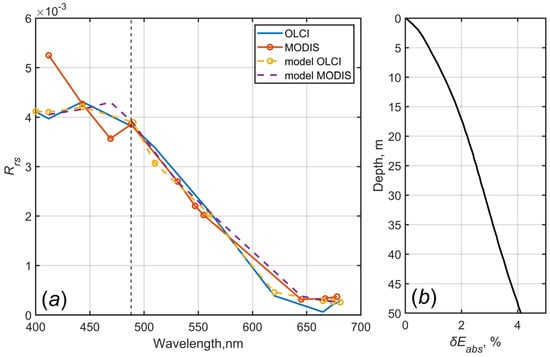
Figure 10.
Rrs spectra obtained from MODIS and OLCI data (solid lines) and as a result of modelling (dashed lines); the vertical dotted line shows the cutoff area of short-wavelength MODIS channels (a); relative deviation of absorbed energy calculated using different Rrs spectra: full OLCI and shortened MODIS (b).
Figure 10b shows the vertical dependence of the relative deviation of the energy absorbed by seawater calculated using different Rrs spectra: full OLCI and shortened MODIS (488–667 nm). A small error (0–4%) arises due to the close values of Rrs (530) used for the model setting.
5. Conclusions
Field experiments conducted in various parts of the Barents Sea in June-August 2021 showed that shipboard measurements of seawater light absorption and attenuation coefficients, as well as light field parameters, in combination with satellite reflectance data, make it possible to calculate a complete set of hydro-optical characteristics. Furthermore, the effect of errors in the atmospheric correction of MODIS data was reduced by eliminating three short-wavelength bands. A comparison of the results of hydro-optical modeling with data of shipboard hydro-optical measurements made it possible to validate the obtained data and confirmed the correctness of the settings of the selected models. This made it possible to calculate the parameters of underwater light fields and the absorbed thermal energy in the visible spectral range in the seawater column.
A regional algorithm for estimating the Chl concentration in the Barents Sea (B22), based on data of direct determinations carried out in 2016–2020 is presented in this paper. Validation according to the data of the flow-through measuring complex showed that the relative error of this algorithm is about 25%. We demonstrated that B22 provides more accurate estimates of the Chl concentration compared to the standard NASA algorithm under conditions of coccolithophore bloom.
Calculations of solar radiation absorbed in the seawater column in the PAR range were performed for various Chl concentrations, as well as for the hypothetical case of pure water. The results were in agreement with the data of onboard measurements of light field parameters. We demonstrated that differences in the Chl concentration due to the accuracy of satellite bio-optical algorithms (30–50%) have little effect on the vertical distributions of the energy absorbed in the seawater column.
To increase the accuracy of heat content calculations, it is advisable to take into account the stratification of the OAC. In this paper, we provided an example of modification of Morel’s model [] to account for this factor. Application of this approach makes it possible to achieve improved agreement between the measured and calculated downwelling irradiance vertical profiles.
The obtained results can be used in integrated climate models [] to estimate heat fluxes at the ocean–atmosphere boundary and to study the mechanisms of heat redistribution in the water column.
Author Contributions
Conceptualization, D.G.; methodology, S.S. and S.V.; software, S.S.; validation, S.V., I.S. and E.A.; formal analysis, D.G. and S.V.; investigation, D.G., S.S., A.Y., P.S., I.S. and E.A.; writing, D.G., S.V., S.S. and P.S.; visualization, A.Y., D.G., S.V. and I.S.; project administration, D.G.; funding acquisition, D.G. All authors have read and agreed to the published version of the manuscript.
Funding
Shipboard data retrieval was carried out as part of the state assignment of SIO RAS (theme No. FMWE-2021-0001) and partially validated within the state budget theme of POI FEB RAS (No. 0211-2021-0007). Satellite chlorophyll-retrieval algorithm development and its validation were funded by the Russian Science Foundation (research project 21-77-10059). Solar energy absorption calculations were performed with the financial support through a grant from the Ministry of Education and Science of Russia (No. 075-15-2021-934) (The study of anthropogenic and natural factors of changes in the composition of air and environmental objects in Siberia and the Russian sector of the Arctic in conditions of rapid climate change using the Tu-134 Optik flying laboratory).
Data Availability Statement
Not applicable.
Acknowledgments
We are grateful to the GSFC NASA for the MODIS data. We are also grateful to V.A. Artemyev, A.V. Grigoriev, and A.N. Khrapko for help with optical measurements; M.D. Kravchishina for determining the concentration of chlorophyll-a; L.A. Pautova for determining the concentration of coccolithophores; the Honored Professor of the Department of Biophysics of the Faculty of Biology of Moscow State University S.I. Pogosyan for the possibility of using the ICAM absorption meter; and A.A. Akhmanov for priceless support in the field of linguistics.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ohlmann, J.C. Ocean radiant heating in climate models. J. Clim. 2003, 16, 1337–1351. [Google Scholar] [CrossRef]
- Mobley, C.D.; Chai, F.; Xiu, P.; Sundman, L.K. Impact of improved light calculations on predicted phytoplankton growth and heating in an idealized upwelling-downwelling channel geometry. J. Geophys. Res. 2015, 120, 875–892. [Google Scholar] [CrossRef]
- Beszczynska-Möller, A.; Fahrbach, E.; Schauer, U.; Hansen, E. Variability in Atlantic water temperature and transport at the entrance to the Arctic Ocean, 1997–2010. ICES J. Mar. Sci. 2012, 69, 852–863. [Google Scholar] [CrossRef]
- Hedley, J.D.; Mobley, C.D. HydroLight 6.0 EcoLight 6.0. Technical Documentation; Numerical Optics Ltd.: Tiverton, UK, 2021; 131p, Available online: https://www.numopt.com/doc/HE60TechDoc.pdf (accessed on 14 August 2022).
- Werdell, P.J.; Franz, B.A.; Bailey, S.W.; Feldman, G.C.; Boss, E.; Brando, V.E.; Dowell, M.; Hirata, T.; Lavender, S.J.; Lee, Z.; et al. Generalized ocean color inversion model for retrieving marine inherent optical properties. Appl. Opt. 2013, 52, 2019–2037. [Google Scholar] [CrossRef] [PubMed]
- Morel, A.; Antoine, D. Heating rate within the upper ocean in relation to its bio–optical state. J. Phys. Oceanogr. 1994, 24, 1652–1665. [Google Scholar] [CrossRef]
- Morel, A.; Prieur, L. Analysis of variations in ocean color 1. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
- Hu, C.; Lee, Z.; Franz, B. Chlorophyll a algorithms for oligotrophic oceans: A novel approach based on three-band reflectance difference. J. Geophys. Res. 2012, 117, C01011. [Google Scholar] [CrossRef]
- O’Reilly, J.E.; Maritorena, S.; Mitchell, B.G.; Siegel, D.A.; Carder, K.L.; Garver, S.A.; Kahru, M.; McClain, C. Ocean color chlorophyll algorithms for SeaWiFS. J. Geophys. Res. 1998, 103, 24937–24953. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef] [PubMed]
- Kopelevich, O.V.; Burenkov, V.I.; Ershova, S.V.; Sheberstov, S.V.; Evdoshenko, M.A. Application of SeaWiFS data for studying variability of bio-optical characteristics in the Barents, Black and Caspian Seas. Deep Sea Res. Part II Top. Stud. Oceanogr. 2004, 51, 1063–1091. [Google Scholar] [CrossRef]
- Vazyulya, S.; Khrapko, A.; Kopelevich, O.; Burenkov, V.; Eremina, T.; Isaev, A. Regional algorithms for the estimation of chlorophyll and suspended matter concentration in the Gulf of Finland from MODIS-Aqua satellite data. Oceanology 2014, 56, 737–756. [Google Scholar] [CrossRef]
- Kopelevich, O.V.; Sahling, I.V.; Vazyulya, S.V.; Glukhovets, D.I.; Sheberstov, S.V.; Burenkov, V.I.; Karalli, P.G.; Yushmanova, A.V. Bio-Optical Characteristics of the Seas, Surrounding the Western Part of Russia, from Data of the Satellite Ocean Color Scanners of 1998–2017; VASh FORMAT, OOO: Moscow, Russia, 2018. [Google Scholar]
- Suslin, V.; Churilova, T. A regional algorithm for separating light absorption by chlorophyll-a and coloured detrital matter in the Black Sea, using 480–560 nm bands from ocean colour scanners. Int. J. Remote Sens. 2016, 37, 4380–4400. [Google Scholar] [CrossRef]
- Demidov, A.B.; Kopelevich, O.V.; Mosharov, S.A.; Sheberstov, S.V.; Vazyulya, S.V. Modelling Kara Sea phytoplankton primary production: Development and skill assessment of regional algorithms. J. Sea Res. 2017, 125, 1–17. [Google Scholar] [CrossRef]
- Salyuk, P.; Bukin, O.; Alexanin, A.; Pavlov, A.; Mayor, A.; Shmirko, K.; Krikun, V. Optical properties of Peter the Great Bay waters compared with satellite ocean colour data. Int. J. Remote Sens. 2010, 31, 4651–4664. [Google Scholar] [CrossRef]
- Glukhovets, D.I.; Kopelevich, O.V.; Sahling, I.V.; Artemiev, V.A.; Pautova, L.A.; Lange, E.K.; Kravchishina, M.D. Biooptical characteristics of the surface layer of the Baltic, Norwegian, and Barents seas in summer 2014–2016 from shipboard and satellite data. Oceanology 2017, 57, 410–418. [Google Scholar] [CrossRef]
- Kravchishina, M.D.; Klyuvitkin, A.A.; Volodin, V.D.; Glukhovets, D.I.; Dubinina, E.O.; Kruglinskii, I.A.; Kudryavtseva, E.A.; Matul, A.G.; Novichkova, E.A.; Politova, N.V.; et al. Systems research of sedimentation in the European arctic in the 84th cruise of the research vessel Akademik Mstislav Keldysh. Oceanology 2022, 62, 660–663. [Google Scholar] [CrossRef]
- Glukhovets, D.I.; Salyuk, P.A.; Sheberstov, S.V.; Vazyulya, S.V.; Sahling, I.V.; Stepochkin, I.E. Retrieval of the full complex of optical characteristics for heat content assessing in the southern part of the Barents Sea in June 2021. Probl. Remote Sens. Earth Space 2021, 18, 214–225. [Google Scholar] [CrossRef]
- Asim, M.; Brekke, C.; Mahmood, A.; Eltoft, T.; Reigstad, M. Improving chlorophyll-a estimation from Sentinel-2 (MSI) in the Barents Sea using machine learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5529–5549. [Google Scholar] [CrossRef]
- Lewis, K.M.; Arrigo, K.R. Ocean color algorithms for estimating chlorophyll a, CDOM absorption, and particle backscattering in the Arctic Ocean. J. Geophys. Res. 2020, 125, e2019JC015706. [Google Scholar] [CrossRef]
- Kostakis, I.; Röttgers, R.; Orkney, A.; Bouman, H.A.; Porter, M.; Cottier, F.; Berge, J.; McKee, D. Development of a bio-optical model for the Barents Sea to quantitatively link glider and satellite observations. Philos. Trans. A Math. Phys. Eng. Sci. 2020, 378, 20190367. [Google Scholar] [CrossRef] [PubMed]
- Hancke, K.; Hovland, E.K.; Volent, Z.; Pettersen, R.; Johnsen, G.; Moline, M.; Sakshaug, E. Optical properties of CDOM across the Polar Front in the Barents Sea: Origin, distribution and significance. J. Mar. Syst. 2014, 130, 219–227. [Google Scholar] [CrossRef]
- Wernand, M.R.; van der Woerd, H.J.; Gieskes, W.W. Trends in ocean colour and chlorophyll concentration from 1889 to 2000, worldwide. PLoS ONE 2013, 8, e63766. [Google Scholar] [CrossRef] [PubMed]
- Kirk, J.T. Solar heating of water bodies as influenced by their inherent optical properties. J. Geoph. Res. 1988, 93, 10897–10908. [Google Scholar] [CrossRef]
- Stamnes, K.; Tsay, S.-C.; Wiscombe, W.; Jayaweera, K. Numerically stable algorithm for discrete-ordinate-method radiative transfer in multiple scattering and emitting layered media. Appl. Opt. 1988, 27, 2502–2509. [Google Scholar] [CrossRef] [PubMed]
- Chang, G.; Barnard, A.; Zaneveld, J.R.V. Optical closure in a complex coastal environment: Particle effects. Appl. Opt. 2007, 46, 7679–7692. [Google Scholar] [CrossRef] [PubMed]
- Lefering, I.; Bengil, F.; Trees, C.; Röttgers, R.; Bowers, D.; Nimmo-Smith, A.; McKee, D. Optical closure in marine waters from in situ inherent optical property measurements. Opt. Express 2016, 24, 14036–14052. [Google Scholar] [CrossRef] [PubMed]
- Mobley, C. The Oceanic Optics Book; International Ocean Colour Coordinating Group (IOCCG): Monterey, CA, USA, 2022. [Google Scholar] [CrossRef]
- Shifrin, K.S. Introduction to Ocean Optics; Gidrometeoizdat: Leningrad, Soviet Union, 1983. [Google Scholar]
- Grigoriev, A.V.; Khrapko, A.N. Autonomous profiling system for measurement of underwater PAR. In Proceedings of the Modern Methods and Means of Oceanological Measurements, Moscow, Russia, 15–17 May 2019; Shirshov Institute of Oceanology of the Russian Academy of Sciences (SIO RAS): Moscow, Russia, 2019; pp. 240–243. [Google Scholar]
- Pogosyan, S.I.; Durgaryan, A.M.; Konyuhov, I.V.; Chivkunova, O.B.; Merzlyak, M.N. Absorption spectroscopy of microalgae, cyanobacteria, and dissolved organic matter: Measurements in an integrating sphere cavity. Oceanology 2009, 49, 934–939. [Google Scholar] [CrossRef]
- Glukhovets, D.I.; Sheberstov, S.V.; Kopelevich, O.V.; Zajceva, A.F.; Pogosyan, S.I. Measurement of sea water absorption factor using integrating sphere. Light Eng. 2018, 26, 120–126. [Google Scholar] [CrossRef]
- Artemiev, V.A.; Taskaev, V.R.; Grigorev, A.V. Autonomous transparency meter PUM-200. In Proceedings of the Modern Methods and Means of Oceanological Measurements, Moscow, Russia, 18–20 May 2021; Shirshov Institute of Oceanology of the Russian Academy of Sciences (SIO RAS): Moscow, Russia, 2021; pp. 95–99. [Google Scholar]
- Goldin, Y.A.; Glukhovets, D.I.; Gureev, B.A.; Grigoriev, A.V.; Artemiev, V.A. Shipboard flow-through complex for measuring bio-optical and hydrological seawater characteristics. Oceanology 2020, 60, 814–822. [Google Scholar] [CrossRef]
- Glukhovets, D.I.; Goldin, Y.A. Express method for chlorophyll concentration assessment. J. Photochem. Photobiol. 2021, 8, 100083. [Google Scholar] [CrossRef]
- Roesler, C.S.; Barnard, A.H. Optical proxy for phytoplankton biomass in the absence of photophysiology: Rethinking the absorption line height. Methods Oceanogr. 2013, 7, 79–94. [Google Scholar] [CrossRef]
- Arar, E.J.; Collins, G.B. Method 445.0. In Vitro Determination of Chlorophyll “a” and Pheophytin “a” in Marine and Freshwater Algae by Fluorescence, Revision 1.2; Environmental Protection Agency: Cincinnati, OH, USA, 1997. [Google Scholar]
- Plass, G.N.; Kattawar, G.W.; Catchings, F.E. Matrix operator theory of radiative transfer. 1: Rayleigh scattering. Appl. Opt. 1973, 12, 314–329. [Google Scholar] [CrossRef]
- Kopelevich, O.; Sheberstov, S.; Vazyulya, S. Effect of a coccolithophore bloom on the underwater light field and the albedo of the water column. J. Mar. Sci. Eng. 2020, 8, 456. [Google Scholar] [CrossRef]
- Gordon, H.R.; Castaño, D.J. Aerosol analysis with coastal zone color scanner. A simple method for including multiple scattering effects. Appl. Opt. 1989, 28, 1320–1326. [Google Scholar] [CrossRef] [PubMed]
- Ershova, S.V.; Kopelevich, O.V.; Sheberstov, S.V. A method for estimating the penetration of solar radiation into the waters of the Arctic Seas using satellite data: The case of a totally overcast sky. Oceanology 2002, 42, 17–26. [Google Scholar]
- Deirmenjian, D. Electromagnetic Scattering of Spherical Polydispersions; Elsevier: New York, NY, USA, 1969. [Google Scholar]
- Gordon, H.R.; Wang, M. Surface-roughness considerations for atmospheric correction of ocean color sensors. I: The Rayleigh-scattering component. Appl. Opt. 1992, 32, 4247–4260. [Google Scholar] [CrossRef]
- Nakajima, T.; Tanaka, M. Effect of wind-generated waves on the transfer of solar radiation in the atmosphere-ocean system. J. Quant. Spectrosc. Radiat. Transf. 1983, 29, 521–537. [Google Scholar] [CrossRef]
- Kopelevich, O.V. Low-parameter model of the optical properties of seawater. In Optika Okeana; Nauka: Moscow, Russia, 1983; Volume 1, pp. 208–234. [Google Scholar]
- Burenkov, V.I.; Sheberstov, S.V.; Artemiev, V.A.; Taskaev, V.R. Estimation of the error in measuring the indicator of light attenuation by seawater in the turbid waters of the Arctic seas. Light Eng. 2019, 27, 103–111. [Google Scholar] [CrossRef]
- Morel, A.; Gentili, B. Diffuse reflectance of oceanic waters. Bidirectional aspects. Appl. Opt. 1993, 32, 6864–6879. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters. I. A semianalytical model. Appl. Opt. 1998, 37, 6329–6338. [Google Scholar] [CrossRef] [PubMed]
- Mobley, C.D.; Gentili, B.; Gordon, H.R.; Jin, Z.; Kattawar, G.W.; Morel, A.; Reinersman, P.; Stamnes, K.; Stavn, R.H. Comparison of numerical models for computing underwater light fields. Appl. Opt. 1993, 32, 7484–7504. [Google Scholar] [CrossRef]
- Gordon, H.R.; Brown, O.B.; Evans, R.H.; Smith, R.C.; Baker, K.S.; Clark, D.K. A semianalytic radiance model of ocean color. J. Geophys. Res. Space Phys. 1988, 93, 10909–10924. [Google Scholar] [CrossRef]
- Bricaud, A.; Morel, A.; Babin, M.; Allali, K.; Claustre, H. Variations in light absorption by suspended particles with chlorophyll a concentration in oceanic (case 1) waters: Analysis and implications for bio-optical models. J. Geophys. Res. 1998, 103, 31033–31044. [Google Scholar] [CrossRef]
- Sheberstov, S.V. A system for batch processing of oceanographic satellite data. Curr. Probl. Remote Sens. Earth Space 2015, 12, 154–161. [Google Scholar]
- Karalli, P.G.; Vazyulya, S.V. Modification of the regional satellite algorithm for determining the concentration of chlorophyll-a in the Barents Sea. In Proceedings of the XI Conference “Current problems in Optics of Natural Waters”, St. Petersburg, Russia, 29 September–1 October 2021; pp. 234–239. [Google Scholar]
- Glukhovets, D.; Kopelevich, O.; Yushmanova, A.; Vazyulya, S.; Sheberstov, S.; Karalli, P.; Sahling, I. Evaluation of the CDOM Absorption Coefficient in the Arctic Seas Based on Sentinel-3 OLCI Data. Remote Sens. 2020, 12, 3210. [Google Scholar] [CrossRef]
- Kopelevich, O.V.; Burenkov, V.I.; Vazyulya, S.V.; Sheberstov, S.V.; Nabiullina, M.V. An assessment of the photosynethetically active radiance balance in the Barents sea from the data of the SeaWiFS satellite color scanner. Oceanology 2003, 43, 786–796. [Google Scholar] [CrossRef]
- Kopelevich, O.V.; Sheberstov, S.V.; Burenkov, V.I.; Vazyulya, S.V.; Likhacheva, M.V. Assessment of underwater irradiance and absorption of solar radiation at water column from satellite data. In Proceedings of the Current Research on Remote Sensing, Laser Probing, and Imagery in Natural Waters, St. Petersburg, Russia, 13 April 2007; Volume 6615, pp. 56–66. [Google Scholar]
- Yushmanova, A.V.; Deryagin, D.N.; Glukhovets, D.I. Considering of bio-optical characteristics stratification for light fields calculation in type I waters. J. Oceanol. Res. 2022, 50, 38–48. [Google Scholar] [CrossRef]
- Madec, G.; Bourdallé-Badie, R.; Bouttier, P.A.; Bricaud, C.; Bruciaferri, D.; Calvert, D.; Chanut, J.; Clementi, E.; Coward, A.; Delrosso, D.; et al. NEMO Ocean Engine; Institut Pierre-Simon Laplace (IPSL): Guyancourt, France, 2017. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).