Intrinsic Calibration of Multi-Beam LiDARs for Agricultural Robots

Abstract

With the advantages of high measurement accuracy and wide detection range, LiDARs have been widely used in information perception research to develop agricultural robots. However, the internal configuration of the laser transmitter layout changes with increasing sensor working duration, which makes it difficult to obtain accurate measurement with calibration files based on factory settings. To solve this problem, we investigate the intrinsic calibration of multi-beam laser sensors. Specifically, we calibrate the five intrinsic parameters of LiDAR with a nonlinear optimization strategy based on static planar models, which include measured distance, rotation angle, pitch angle, horizontal distance, and vertical distance. Firstly, we establish a mathematical model based on the physical structure of LiDAR. Secondly, we calibrate the internal parameters according to the mathematical model and evaluate the measurement accuracy after calibration. Here, we illustrate the parameter calibration with three steps: planar model estimation, objective function construction, and nonlinear optimization. We also introduce the ranging accuracy evaluation metrics, including the standard deviation of the distance from the laser scanning points to the planar models and the 3σ criterion. Finally, the experimental results show that the ranging error of calibrated sensors can be maintained within 3 cm, which verifies the effectiveness of the laser intrinsic calibration.

1. Introduction

Light Detection and Ranging (LiDAR) sensors, cameras, and other information perception sensors are essential components in current robotics and automation systems [1,2]. The performance of such systems highly depends on the quality of intrinsic and extrinsic calibration parameters for these sensors [3,4,5,6]. Accurate intrinsic parameters can ensure that the data obtained by the sensors are meaningful and valid. Currently, the intrinsic calibration techniques of cameras are relatively mature and many open-source packages are available [7,8]. However, the intrinsic calibration of LiDAR needs further investigation due to its complex manufacturing process. Typically, LiDAR is subjected to rigorous internal calibration before leaving the factory with initial parameter values. As the service time of LiDARs increases, the initial parameters may not maintain their optimal values due to changes caused by shock in the internal mechanical parts of the sensor. Especially in the agriculture field, rough farmland will exacerbate the loosening of internal components of LiDARs mounted on ground vehicles.

At present, LiDARs have a wide range of applications in the agricultural field. Some common LiDAR-based research hotpots include 3D reconstruction [9,10], crop phenotyping [11], and yield estimation [12], etc. For these applications, the observed objects (such as crops and fruits) are characterized by small measurement targets and fine information perception. This characteristic requires LiDAR to meet centimeter-level or even millimeter-level measurement accuracy. For example, LiDAR-based crop organ-level phenotyping requires measuring fine morphological parameters such as leaf length, leaf angle, and stem diameters of crops [11]. Therefore, it is especially critical to study the intrinsic calibration of LiDARs for agricultural application scenarios.

To ensure a high measurement accuracy of LiDARs, a secondary calibration of the sensor parameters is required. In this paper, we investigate the intrinsic calibration of the multi-beam laser sensors, and the main contributions are as follows:

(1) We established a mathematical model based on the physical structure of HDL-64E_S3, determined the objective function of sensor intrinsic calibration, and solved it based on nonlinear optimization.

(2) We verified the feasibility of an intrinsic calibration strategy by field experiments in unstructured agricultural environments.

2. Related Work

2.1. LiDAR Application in Agriculture

Compared with cameras, LiDARs have the advantages of higher measurement accuracy, better robustness, and richer 3D environment information. These advantages give LiDARs great potential for applications in agriculture [13]. The relevant literature indicates that LiDARs have been widely used in research on agricultural robot navigation [14,15,16,17], target identification [18,19,20,21], and high-throughput crop phenotyping [22,23,24,25]. 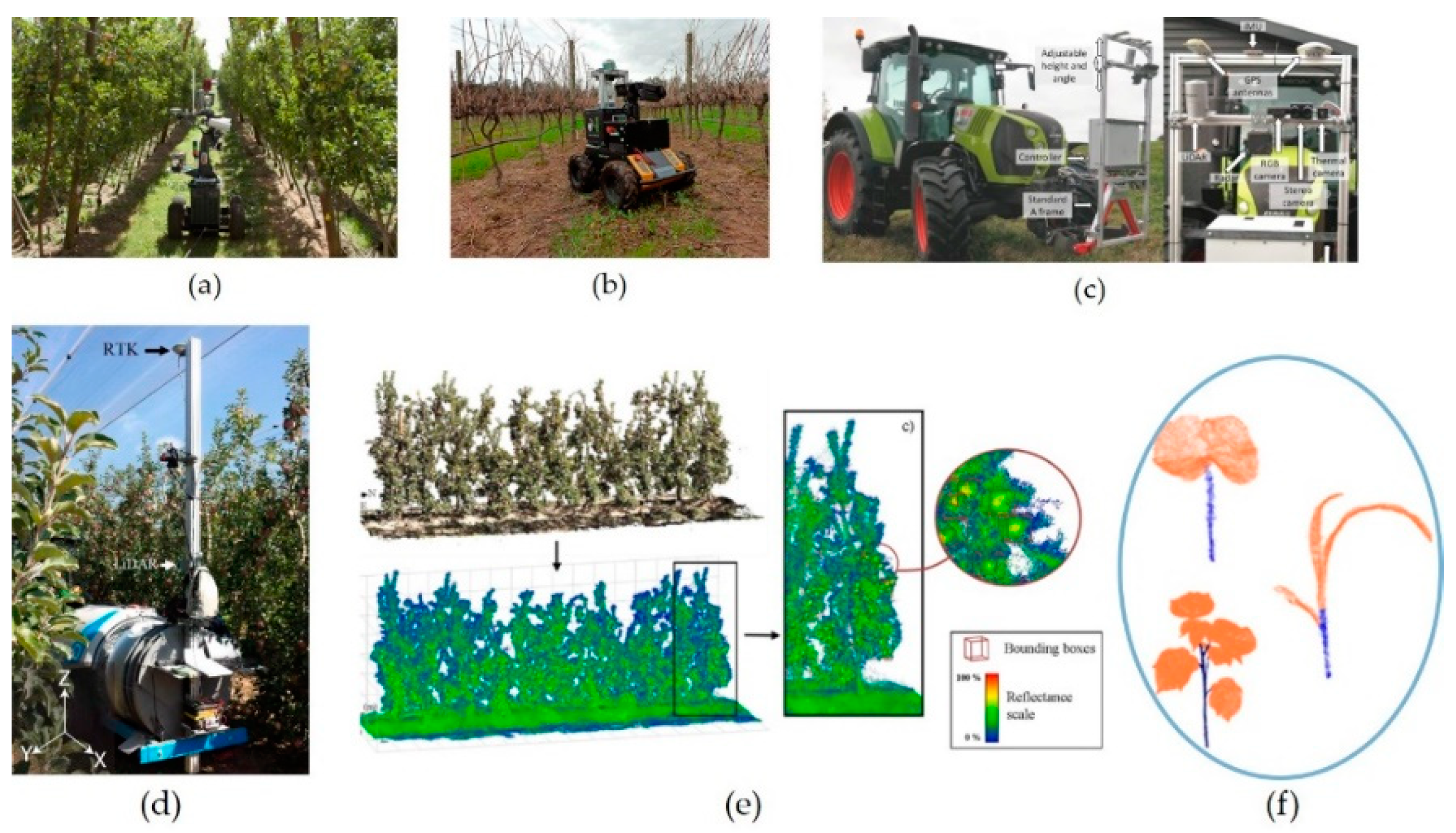Figure 1 shows some examples of LiDAR applications in agricultural environments. For example, Ref. [15] proposed an algorithm called VineSLAM suitable for localization and mapping in a woody-crop vineyard. This approach used both point- and semiplane-features extracted from 3D LiDAR data to map the environment and localize the robot using a novel particle filter that considers both feature modalities. Crop discrimination at the plant or patch level is vital for modern technology enabled agriculture. Ref. [21] used an advanced deep learning framework to improve and apply an object-level classification to three kinds of vegetable crops (cabbage, tomato, and eggplant) using high-resolution LiDAR point clouds. Ref. [11] proposed a new field sensing solution to high-throughput phenotyping. In their solution, they allowed the robot to move around the parcel to collect the point cloud and adopted an open-source library, Point Cloud Library, to acquire plant height and row space. Although LiDARs have extremely attractive applications, as mentioned earlier, their measurement accuracy may gradually decrease during long-term use. Therefore, it is necessary to investigate the intrinsic calibration of LiDARs.

2.2. Lidar Intrinsic Calibration

The intrinsic calibration of LiDAR is directly related to its type and working principle. Different types of LiDARs have different working principles, so their corresponding mathematical models are also different. At present, LiDAR can be roughly divided into two categories according to its working principles: multi-beam LiDAR and solid-state LiDAR.

Multi-beam LiDAR performs scanning through spinning a macroscopic component, either the whole sensor or an optical element such as a prism or a galvanometer mirror. Therefore, it has advantages in larger horizontal field of view. However, this mechanical construction results in the moving parts with large enclosures and poor mechanical tolerance to vibration and shock. Thus, it is necessary to calibrate the intrinsic parameters before use. Normally, the intrinsic parameters and mathematical models corresponding to different beam versions of LiDARs are also different. The 64-beam LiDAR have five intrinsic parameters, whereas the 16-beam and 32-beam LiDAR have three intrinsic parameters [3,26,27,28,29,30,31]. According to a literature search, the target models used for LiDAR intrinsic calibration include both planar and columnar models. Ref. [29] proposed a measurement calibration method based on the condition-adjustment equation and compared the calibration results with those of the original factory to prove the effectiveness of the method. Ref. [32] estimated the intrinsic parameters of a 32-beam LiDAR based on constrained point clouds of column surface features (e.g., light poles) and fitted 3D column surface models. Some studies also demonstrate intrinsic calibration methods without feature targets. Ref. [33] put forward an unsupervised calibration method, which assumes that points in space are located on adjacent surfaces. Based on this assumption, an energy function was defined to calibrate the intrinsic and extrinsic parameters of LiDARs.

Solid-state LiDAR uses electronic components such as optical phased arrays, photonic ICs, and far field radiation patterns instead of mechanical rotating components to realize the adjustment of the emitted laser angle. They can avoid large mechanical parts in their physical structure and have generated great interest because they also provide scalability, reliability and embeddedness. At present, there are few studies on the intrinsic calibration of solid-state LiDAR [3,28]. Ref. [28] introduced a geometrical model for the scanning system of a solid-state LiDAR based only on Snell’s law and its specific mechanics, but compared with multi-beam LiDAR, it is limited in the horizontal field of view. Thus, solid-state LiDAR is not capable of covering a 360° horizontal field of view.

In summary, multi-beam LiDAR is still the mainstream sensor in many application studies due to its wide-ranging horizontal view. In this paper, we select the Velodyne HDL-64E_S3 multi-beam 3D LiDAR to conduct the study of intrinsic calibration. Firstly, we introduce the data transmission format for HDL-64E_S3 and establish a mathematical model based on the physical structure and working principle to determine the relationship between the internal parameters and the point cloud data. Secondly, according to the measurement accuracy evaluation metrics of LiDARs presented in the paper, the objective function for sensor intrinsic calibration is derived. Finally, the nonlinear optimization algorithm is used to find the optimal solution for the system of overdetermined equations formed by the objective function.

3. Materials and Methods

3.1. HDL-64E_S3 LiDAR

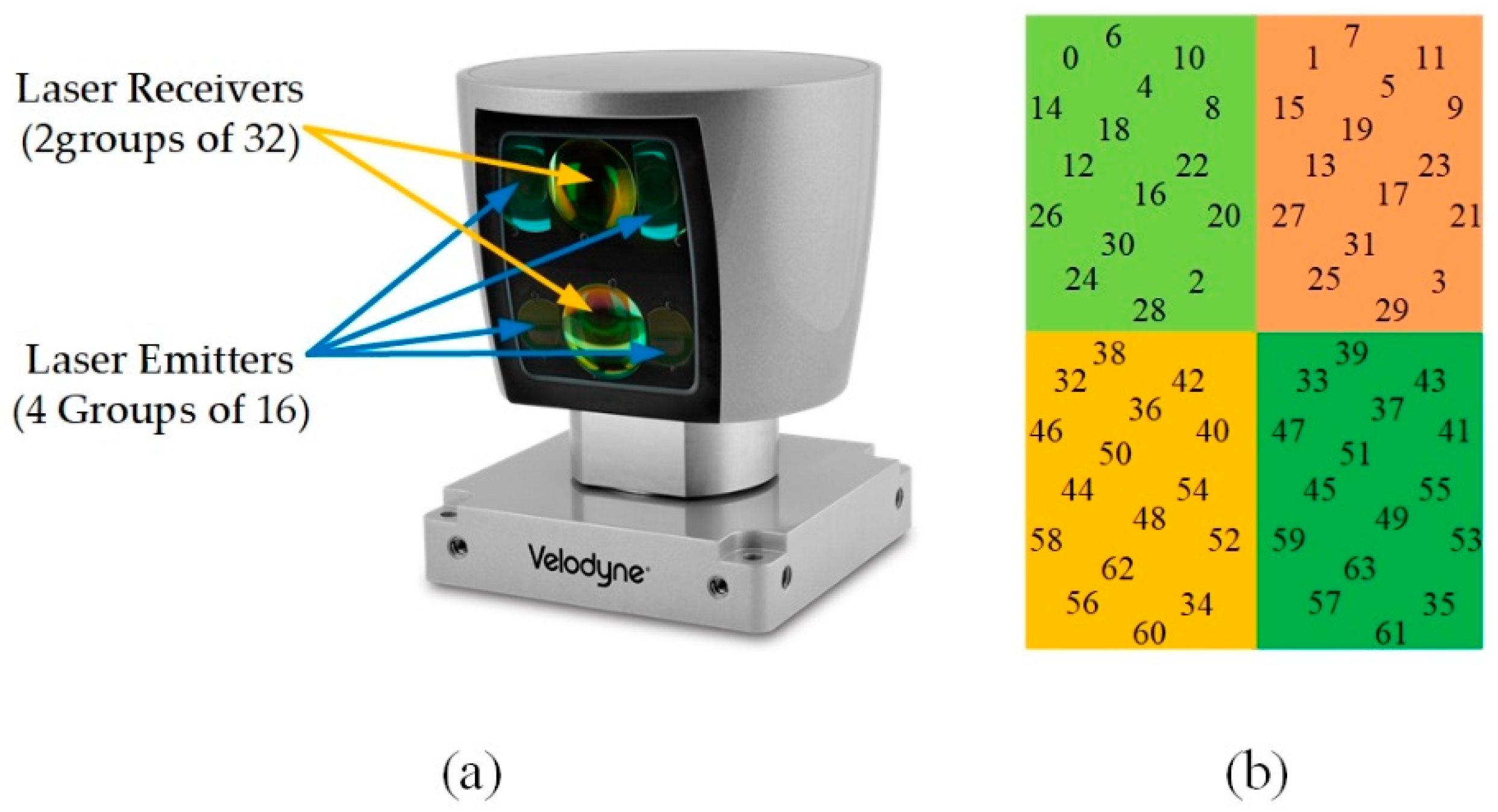
The Velodyne HDL-64E_S3 LiDAR is shown in Figure 2a. This type of LiDAR consists of 64 laser emitters that fire laser beams outward at different pitch angles. Meanwhile, these laser emitters are driven by a high-speed rotating motor to achieve a panoramic scan with a pitch-view angle-range of 30° and a horizontal-view angle-range of 360°. In addition, the sensor is equipped with 64 laser receivers for measuring the distance information returned by target reflection. The laser emitters are divided into 4 groups with 16 in each group. The serial number and arrangement position of each group are shown in Figure 2b (each group is indicated by a different color). The two groups of emitters located in the upper and lower regions are called the upper block sequences (corresponding to laser sequences from 0 to 31) and the lower block sequences (corresponding to laser sequences from 32 to 63), respectively. After the sensor is powered on, the upper block sequences and the lower block sequences fire laser beams in pairs flowing in the order of arrangement. In Figure 2b, laser emitters 0 and 32 belong to the same simultaneous light-emitting pairs, for example.

3.1.1. Data Transmission Format

Data transmission of HDL-64E_S3 is based on UPD Ethernet packets. Each packet contains a header, a data payload of firing data, and status data. Data packets are assembled with the collection of all firing data for six upper block sequences and six lower block sequences. The upper and lower block sequences are distinguished by block identification bits (the upper and lower block identification bits are /0xEEFF and /0xDDFF, respectively). The upper block laser distance and intensity data are collected first followed by the lower block laser data. The data packet is then combined with the status and header data in a UDP packet transmitted over Ethernet. The overall structure of the packets is shown in Figure 3.

As can be seen from Figure 3, each block laser data contains only one 2-byte block identification bit (namely block id) and one 2-byte rotation angle. The remaining data are 2 bytes of distance and 1 byte of intensity information, which are collected by the laser in the corresponding block sequence. Here, block id corresponds to the block sequence, that is, the upper block or the lower block. Different block sequences correspond to different laser serial numbers, as shown in Figure 2b. By identifying the block id, we could get the data (rotation angle, distance, and intensity) of the corresponding block sequence laser collected. The rotation angle represents the instantaneous rotation angle of LiDAR, not the 32 lasers in the block sequence. Since all the lasers are mounted on the same plane, the actual rotation angle of each laser consists of the instantaneous angle and the compensation angle.

As described in the previous section, a data packet has 12 group block sequences, of which 6 groups are upper block sequences and 6 groups are lower block sequences. Each block data includes a block id, rotation angle, and other information collected by the lasers, including distance and intensity. In addition, the status data always contains a GPS 4-byte timestamp. The status data also contains one type of data, which rotates through a sequence of different pieces of information. This is not the focus of this paper and will not be elaborated here.

3.1.2. Mathematical Model for Point Coordinates Calculation

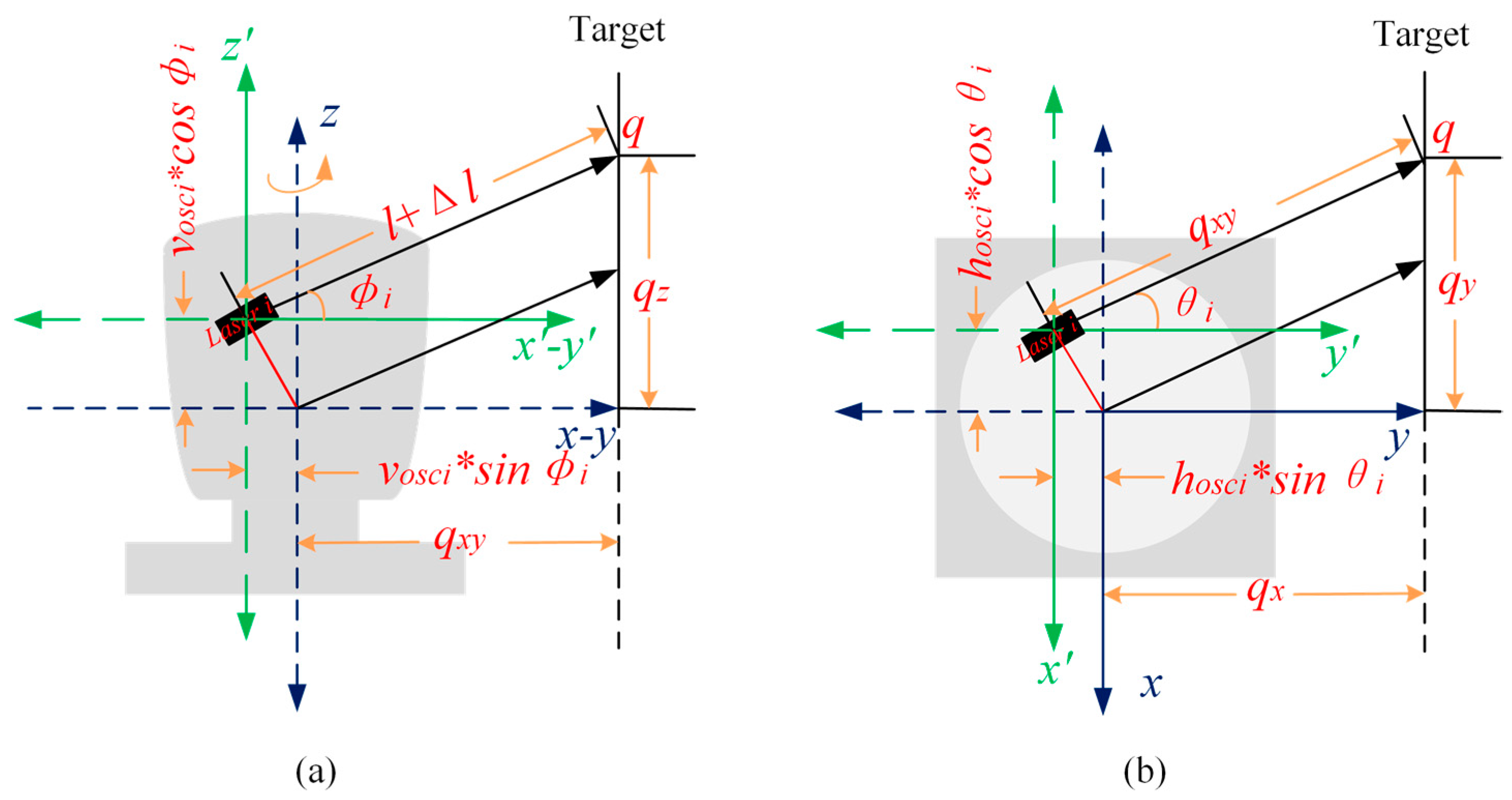
Based on the physical structure of the sensors’ eccentric rotation, we established a mathematical model of point coordinates calculation for HDL-64E_S3, as shown in Figure 4 [27,29,31]. In the model, we constructed two Cartesian coordinate systems, where the coordinate origins of blue and black coordinate systems are the center point of LiDAR and the laser emitter inside LiDAR, respectively. The point cloud output from HDL-64E_S3 LiDAR is determined by solving the mapping relationships between these two coordinate systems. The main parameters in the mathematical model are as follows:

• $l_i$: Measured distance returned by lasers;
• $\mathrm{\Delta }{l}_i$: Distance compensation value for laser-measured distance $l_i$;
• ${\theta }_i$: Rotation angle in the X-Y plane (counterclockwise rotation for positive direction);
• $\mathrm{\Delta }{\theta }_i$: Compensation angle for horizontal rotation angle ${\theta }_i$;
• ${\phi }_i$: Pitch angle in the Y-Z plane;
• $h_{osc\_}{}_i$: Horizontal compensation distance of lasers (the red line in Figure 4b);
• $v_{osc}{}_{\_i}$: Vertical compensation distance of lasers (the red line in Figure 4a).

Here, the letter i is the serial number of laser emitters; $l_i+\mathrm{\Delta }{l}_i$ and ${\theta }_i+\mathrm{\Delta }{\theta }_i$ are the actual distance and actual rotation angle collected by lasers, respectively.

Typically, long-term wear and tear on LiDAR causes slight changes in the pitch angle of laser emitters, which results in the factory-set pitch angle ${\phi }_i$ no longer maintaining the optimal parameters. Furthermore, it causes other internal parameters associated with the pitch angle to change as well. To compensate for the changes in pitch angles, we redefine the pitch angle of the laser emitters as ${\phi }_i+\mathrm{\Delta }{\phi }_i$, where the $\mathrm{\Delta }{\phi }_i$ is the change value in the pitch angle of the laser emitter with the serial number i. Therefore, the coordinate values (x, y, z) of the target measured can be expressed as:

$$\begin{array}{l}x=((l_i+\mathrm{\Delta }{l}_i)\cos ({\phi }_i+\mathrm{\Delta }{\phi }_i)-v_{osc\_i}\sin ({\phi }_i+\mathrm{\Delta }{\phi }_i))\sin ({\theta }_i+\mathrm{\Delta }{\theta }_i)-h_{osc}{}_{\_i}\cos ({\theta }_i+\mathrm{\Delta }{\theta }_i)\\ y=((l_i+\mathrm{\Delta }{l}_i)\cos ({\phi }_i+\mathrm{\Delta }{\phi }_i)-v_{osc\_i}\sin ({\phi }_i+\mathrm{\Delta }{\phi }_i))\cos ({\theta }_i+\mathrm{\Delta }{\theta }_i)+h_{osc}{}_{\_i}\sin ({\theta }_i+\mathrm{\Delta }{\theta }_i)\\ z=(l_i+\mathrm{\Delta }{l}_i)\sin ({\phi }_i+\mathrm{\Delta }{\phi }_i)+v_{osc\_}{}_i\cos ({\phi }_i+\mathrm{\Delta }{\phi }_i)\end{array}$$

(1)

Equation (1) can be simplified as:

$$f(x,y,z)=g(l,\mathrm{\Delta }l,\theta ,\mathrm{\Delta }\theta ,\phi ,\mathrm{\Delta }\phi ,h_{osc},v_{osc})$$

(2)

where $\mathrm{\Delta }l$, $\mathrm{\Delta }\theta$, $\mathrm{\Delta }\phi$, $h_{osc}$, and $v_{osc}$ are the 5 intrinsic parameters that are to be calibrated. $l$, and $\theta$ and $\phi$ are known parameters, which can be obtained from the UDP packet and factory calibration files, respectively. Thus, Equation (2) can be further expressed as:

$$f(x,y,z)=g(\mathrm{\Delta }l,\mathrm{\Delta }\theta ,\mathrm{\Delta }\phi ,h_{osc},v_{osc})$$

(3)

3.2. Parameter Calibration

An offline calibration approach based on the static plane models is used to compensate for the measurement errors of the sensors [36,37]. First, we scan the surrounding environment with planar information using a LiDAR placed at a fixed position. Then, we fit the estimation planes based on the point clouds returned by the LiDAR. Finally, we correct the internal parameters using the estimated planar models. The specific steps of the intrinsic calibration are as follows.

(i) Estimating the Plane Model. We estimate the plane models using the raw data collected by our LiDAR and calculate the parameters of the plane models.

(ii) Constructing the Objective Function. We assume that the lower the dispersion of the distance from the laser scanned points to the plane model, the higher the accuracy of the parameter calibration. Here, we substitute the mathematical model of LiDAR point coordinates into the plane model of the point cloud estimation and solve the distance function from the scanned point to the plane model. According to our assumption, it is known that the minimization equation of this distance function is the objective function of parameter calibration.

(iii) Solving the Overdetermined Equation. We construct a system of overdetermined equations based on the objective function, in which we take the tuple of sensor measurement values and the corresponding plane model parameters as the input values for the objective function. To find the optimal solution of the system of overdetermined equations, a nonlinear optimization algorithm based on the Levenberg–Marquardt (LM) algorithm is used for our parameter calibration algorithm [38].

3.2.1. Plane Model

Theoretically, the points q(x, y, z) measured onto the plane by lasers should match the plane equation of the scanned plane. Thus, we formulate the plane equation as:

$$a_{k}x+b_{k}y+c_{k}z+d_k=0$$

(4)

where the letter k is the number of scanned planes and $a_k,b_k,c_k,d_k$ are the plane model parameters, which can be calculated by the Random Sample Consensus (RANSAC) algorithm. RANSAC is a parameter estimation algorithm for mathematical models that has a good evaluation in terms of efficiency and accuracy of plane detection. We implement the detection of multiple planes by calling the SACSegmentation function from the Point Cloud Library (PCL). The distance threshold was set to 0.002 m and the maximum number of iterations was set to 10,000.

3.2.2. Objective Function

To construct the objective function, we take the number of noisy points nearby the planar point cloud as the evaluation metric of the measurement accuracy, which can visualize the dispersion of the point cloud on the plane scanned by LiDAR, as shown in Figure 5. The figure shows the plane model and related point cloud collected by LiDAR, where the points of different colors indicate the measured values scanned by lasers of different serial numbers. We can see that there are some significant noise points around the plane, which indicate the point clouds obtained by LiDAR have a large dispersion. Here, we quantify the dispersion of the point cloud by the Standard Deviation (SD) of the Point-to-Plane Distance (P2P-D). Ideally, all points should lie on the plane, i.e., P2P-D is 0. However, it is in fact difficult to satisfy the ideal condition, so we can estimate the dispersion of the points by solving the minimum of SD. The equation for solving the minimum of SD is:

$$min\left\{{\displaystyle {\sum }_{q\in Q}\sqrt{Var(dist(q,p))}|p\in P_k}\right\}$$

(5)

where k is the scanned plane number, P is the set of parameters of all fitted planes, p is a group of plane parameters within plane P, Q is a tuple of raw measured values returned by all laser beams (i.e., distance, rotation angle, and laser serial number), and q is a tuple of raw measured values returned by one of the laser beams. The $dist(q,p)$ function is used to calculate the distance from the set of parameters q to the corresponding plane p in the Cartesian coordinate system. Thus, P2P-D is:

$$dist(q,p)=\frac{a_k{x}_i+b_k{y}_i+c_k{z}_i+d_k}{\sqrt{a_k{}^2+b_k{}^2+c_k{}^2}}$$

(6)

We know that Equation (5) is a monotonic function with respect to Equation (6). Therefore, we can infer that solving for the minimum of SD is equivalent to solving for the minimum of P2P-D. The objective function used for intrinsic calibration can be expressed as:

$$min\left\{{\displaystyle {\sum }_{q\in Q}dist(q,p)|p\in P_k}\right\}$$

(7)

From the working principle of HDL-64E_S3, it is known that the sensor has 64 laser emitters and each laser emitter has 5 internal parameters. Therefore, if there are k scan planes, we need to calibrate 64 × 5 × k internal parameters according to the objective function.

3.2.3. Nonlinear Optimization

The previous section demonstrates that the objective function is a system of overdetermined equations. To obtain the optimal solution of the system of equations, we utilize the LM algorithm for the nonlinear optimization of the objective function. The LM algorithm modifies the Gaussian Newton method by adding trust regions to the increments of the function variables, which limits the range of variables that change during the iterative process. The LM algorithm specifies that the approximation of the increment within the trust region is a valid increment; otherwise, the approximation is inaccurate. The LM algorithm can effectively avoid the matrix non-singularity and pathological problems of the linear system of equations, and it also provides the advantages of both the gradient method and the Newton method by adjusting the damping coefficient.

We assume that $v$ is a column vector consisting of intrinsic parameters. From Equations (1) and (7), the least squares equation can be constructed as:

$$\arg \underset{v}{\min }G(v)=\frac{1}{2}{\displaystyle \sum _{m=1}^N{‖g(v)‖}^2}$$

(8)

where m is the index of the scanned point, N is the total number of point clouds around the scanned plane, $v={(\mathrm{\Delta }l,\mathrm{\Delta }\theta ,\mathrm{\Delta }\phi ,h_{osc},v_{osc})}^T$, and $g(v)$ is the distance from the scanned points to the plane, that is P2P-D.

According to the LM algorithm, the iteration increments $\mathrm{\Delta }{v}^{\ast }$ of the variable $v$ can be expressed as:

$$\mathrm{\Delta }{v}^{\ast }=-{(J{(v_n)}^{T}J(v_n)+\mu I)}^{-1}J{(v_n)}^{T}g(v_n)$$

(9)

where $I$ is the identity matrix, $g(v_n)$ is the two-order Taylor expansion of $g(v)$ at $v=v_n$, and $J(v_n)$ is the Jacobi matrix obtained by the derivative of $g(v)$ concerning the column vectors $v$ at $v=v_n$.

Equation (9) can be further abbreviated as:

$$\mathrm{\Delta }{v}^{*}=-{(H+\mu I)}^{-1}g$$

(10)

where $H$ is the Hessian matrix, $H=J{(v_n)}^{T}J(v_n)$; $g$ is the closure error vector, $g=J{(v_n)}^{T}g(v_n)$; and $\mu$ is the damping coefficient, which is determined by the gain ratio $\rho$. The mathematical expression for the gain ratio $\rho$ is:

$$\rho =\frac{G(v)-G(v+\mathrm{\Delta }v)}{M(0)-M(\mathrm{\Delta }v)}$$

(11)

where $M(\mathrm{\Delta }v)$ is assumed to describe the behavior of $G$ in the current iteration, which is defined as:

$$M(\mathrm{\Delta }v)\equiv G(v)+J^{T}g(v)\mathrm{\Delta }v+\frac{1}{2}{(\mathrm{\Delta }v)}^T{J}^{T}J(\mathrm{\Delta }v)$$

(12)

The grain ration $\rho$ represents the similarity between the two-order Taylor expansion $M(\mathrm{\Delta }v)$ and $G$. Its numerator and denominator represent the amount of variation of the function $G$ and the first-order Taylor expansion $M$ with the independent variable $\mathrm{\Delta }v$, respectively.

We determine the damping coefficient $\mu$ based on the value of the gain rate $\rho$. The damping coefficient $\mu$ is expressed as a segmental function:

$$\left\{\begin{array}{c}\mu =2\mu \\ \mu =\mu /3\end{array}\right.\begin{array}{cc}& \begin{array}{c}\rho <0.25\\ \rho >0.75\end{array}\end{array}$$

(13)

As a result, the iterative increment $\mathrm{\Delta }v$ can be obtained from Equations (10) and (13). The optimal solution of the intrinsic parameters can be calculated based on the iterative results of $v_n+\mathrm{\Delta }v$. It is worth mentioning that, similar to Gaussian–Newton algorithm, the LM algorithm also needs to set the initial parameter values. We set the initial values of the LM algorithm as the factory parameters of the LiDAR.

4. Results

4.1. Experimental Scheme

The experimental scheme for the intrinsic calibration of LiDAR consists of three steps: data acquisition, intrinsic calibration, and experimental validation.

(i) Data Acquisition. This step is to extract the raw data collected by lasers and parse the data. The raw data includes the rotation angle, measurement distance, and intensity collected by the corresponding serial number of laser emitters. Data parsing is a process that obtains the Cartesian coordinate representation of the raw data based on UPD Ethernet packets. The UDP data transfer format is described in the previous Section 3.1.1 and Section 3.1.2.

(ii) Intrinsic Calibration. We performed a secondary calibration of the internal parameters based on the results of the parsed data. The calibration steps include plane estimation, objective function construction, and nonlinear optimization. The details of the implementation of intrinsic calibration can be found in Section 3.2.

(iii) Experimental Verification. To verify the intrinsic calibration results of the sensors, we used the SD and 3sigma criteria (including the σ, 2σ, and 3σ criteria) of P2P-D to judge the effectiveness of the sensor intrinsic calibration. In general, the higher the calibration accuracy is, the smaller the SD and the larger the percentage of the 3sigma criterion are.

Finally, we compared the differences of the five internal parameters before and after calibration. The experimental scheme is shown in Figure 6.

4.2. Experimental Settings

To sufficiently demonstrate the feasibility of the calibration scheme, we conducted calibration experiments and verification experiments. For the calibration experiments, we determined the optimal solution for the five internal parameters of the LiDAR with help of the relationship between the planar model and the point cloud obtained by LiDAR. As a result, we could obtain the LiDAR calibration file by this experiment. For the verification experiments, we compared the range performance before and after calibration in agricultural scenarios.

4.2.1. Calibration Experiments

We selected the Velodyne HDL-64E_S3 LiDAR with 360° panoramic scanning for the intrinsic calibration. The experimental site was an underground parking lot surrounded by flat walls. The point cloud data of the walls scanned by laser emitters can be used to estimate the plane model for our calibration algorithm. To ensure accurate calibration of the entire sensor system, we selected four walls that can cover 360° panoramic information for plane estimation. Figure 7 and Figure 8 show the flat walls and corresponding point cloud data used for plane model estimation, respectively. Note that the LiDAR is mounted on a mobile platform in a tilted manner. This arrangement ensures that sufficient point cloud data is acquired and also prevents the estimated normal of the plane model from coinciding with the coordinate axes of the sensor itself. If the scanned plane normal is consistent with the direction of the sensor coordinate axis, this will lead to a lack of parameters in the objective function G. Thus, we cannot solve the optimal results of the target function G.

4.2.2. Verification Experiments

Furthermore, we performed field experiments to verify the accuracy of the calibration results for ranging effects in agricultural scenarios. Due to the lack of corresponding planes in the agricultural scene, we use two 30 × 40 cm² planar plates as verification targets. As shown in Figure 9, the LiDAR is placed at a fixed position, and the planar plates marked with rectangles are erected in both orientations of the sensor. During the experiments, the planar plates are placed at different distances from the LiDAR, such as 2.5 m, 5 m, 7.5 m, and 10m. In this way, we can verify the feasibility of the calibration scheme by calculating the standard deviation of P2P-D and 3σ criteria based on plane plates.

4.3. Experimental Results

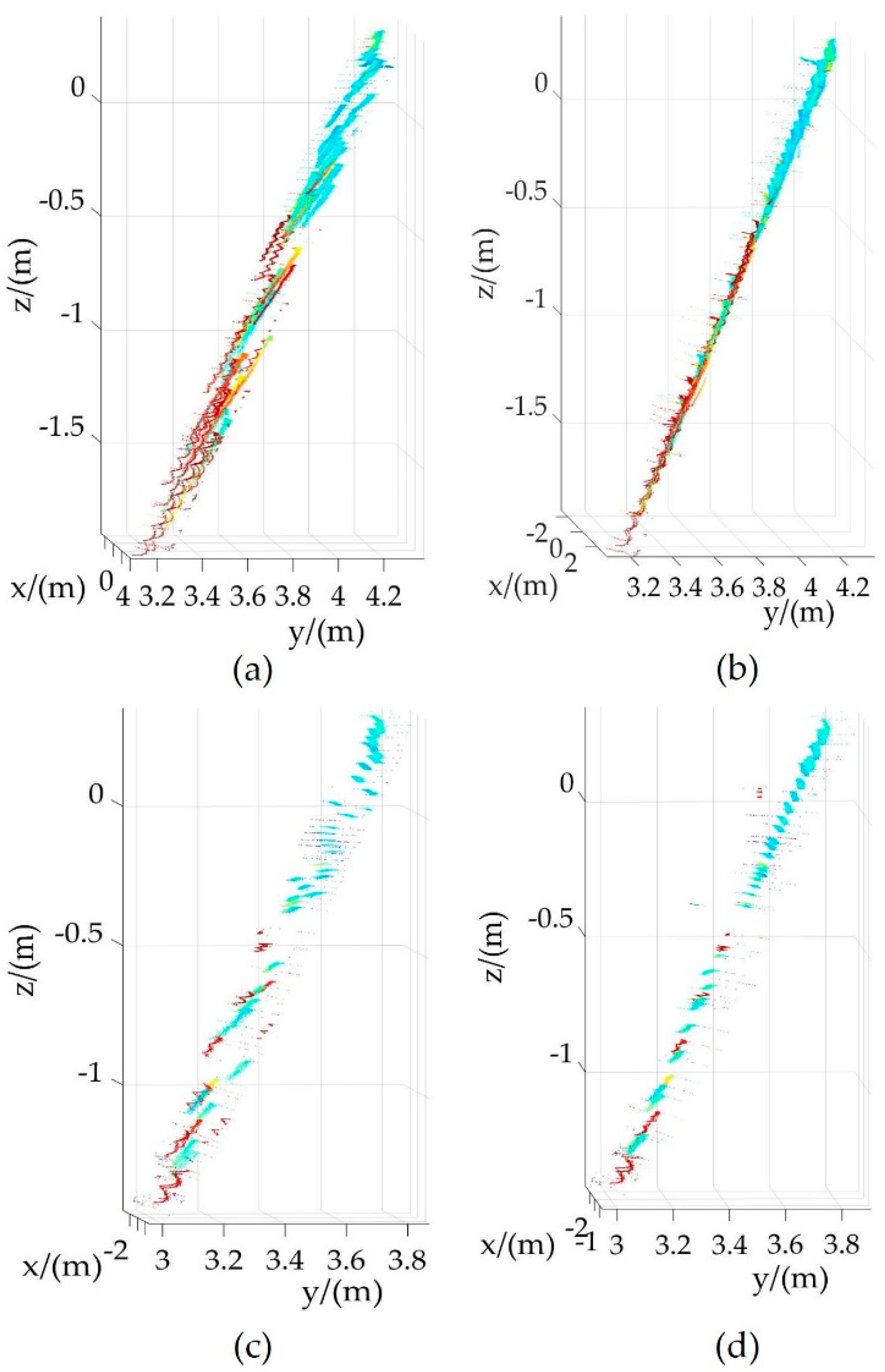
Figure 10 shows the projection results of the planar point clouds before and after the LiDAR calibration, where the internal parameters before calibration are the factory default values. The x, y, and z axes in the figure represent the position information of the laser scanning points in the Cartesian coordinate system. Here, Figure 10a,b show the point cloud projection results of the scanned wall 2 before and after calibration, respectively. Similarly, Figure 10c,d show the point cloud projection results of the scanned wall 4 before and after calibration, respectively. It is obvious from Figure 10 that the point cloud dispersion after parameter calibration is smaller than that before parameter calibration.

4.3.1. Standard Deviation Verification

According to the principle of numerical statistical analysis, we assume that the planar point clouds acquired by LiDAR are subject to a normal distribution. The SD of P2P-D can be used to judge the dispersion of the point clouds before and after the parameter calibration, as shown in Figure 11. In the figure, the horizontal and vertical axes indicate the laser beam sequence and the SD of P2P-D, respectively. The blue and orange lines indicate the SD of the P2P-D before and after intrinsic calibration, respectively. We found that the point clouds returned by the sensor before calibration have high dispersion, whereas the dispersion decreased after calibration. By calculating the mean value of SD of 64 laser beams, we can see that the mean value of SD before calibration was 2.76 cm, and the maximum SD reached 5.64 cm, whereas the mean value of SD after calibration was 1.58 cm, and the SD of most laser beams stayed within 3 cm. Therefore, the mean value of SD of the laser sensor was reduced by 1.18 cm after calibration.

4.3.2. Sigma Criterion Verification

To further quantify the effectiveness of the calibration results, we used the 3sigma criterion (σ, 2σ, and 3σ criteria) to analyze the distribution of the laser point clouds. The 3sigma criterion is often used to characterize the probability distribution of random variables in the normal distribution. Figure 12, Figure 13 and Figure 14 show the proportion of P2P-D values in a certain range for all points around the fitting plane before and after calibration. The range refers to the σ, 2σ, and 3σ confidence intervals, that is the proportion of P2P-D in the range of $(\mu \pm \sigma )$, $(\mu \pm 2\sigma )$, and $(\mu \pm 3\sigma )$, respectively. In these figures, the horizontal and vertical axes indicate the laser beam sequence and percentage of the 3sigma criterion, respectively. The blue and orange lines indicate the verification results before and after intrinsic calibration, respectively. From these three figures, it can be seen that the dispersion of the point clouds after calibration was significantly lower than that before calibration.

Table 1. The mean percentages of P2P-D for 64 laser beams according to 3σ criterion.

Mean Percentage (%)	μ ± σ	μ ± 2σ	μ ± 3σ
Before calibration	70.81	95.68	98.29
After calibration	79.87	95.93	99.09
Increase values	9.06	0.25	0.80

quantifies the mean percentage values of P2P-D for the 64 laser emitters in the three intervals of $(\mu \pm \sigma )$, $(\mu \pm 2\sigma )$, and $(\mu \pm 3\sigma )$ before and after calibration, respectively, using the data from Figure 11, Figure 12 and Figure 13. Within the σ confidence interval, the mean values of P2P-D for 64 lasers before and after calibration were 70.81% and 79.87%, respectively. Within the 2σ confidence interval, the mean values before and after calibration were 95.68% and 95.93%, respectively. Within the 3σ confidence interval, the mean values before and after calibration were 98.29% and 99.09%, respectively. As a result, the mean percentages of P2P-D for 64 lasers improved by 9.06%, 0.25%, and 0.8% after calibration in the σ, 2σ, and 3σ confidence intervals, respectively. We can see that the calibration effect was not significantly improved within 2σ confidence interval from Table 1. This is because the sensor had a high measurement accuracy before calibration.

4.3.3. Differences in Calibration Parameters

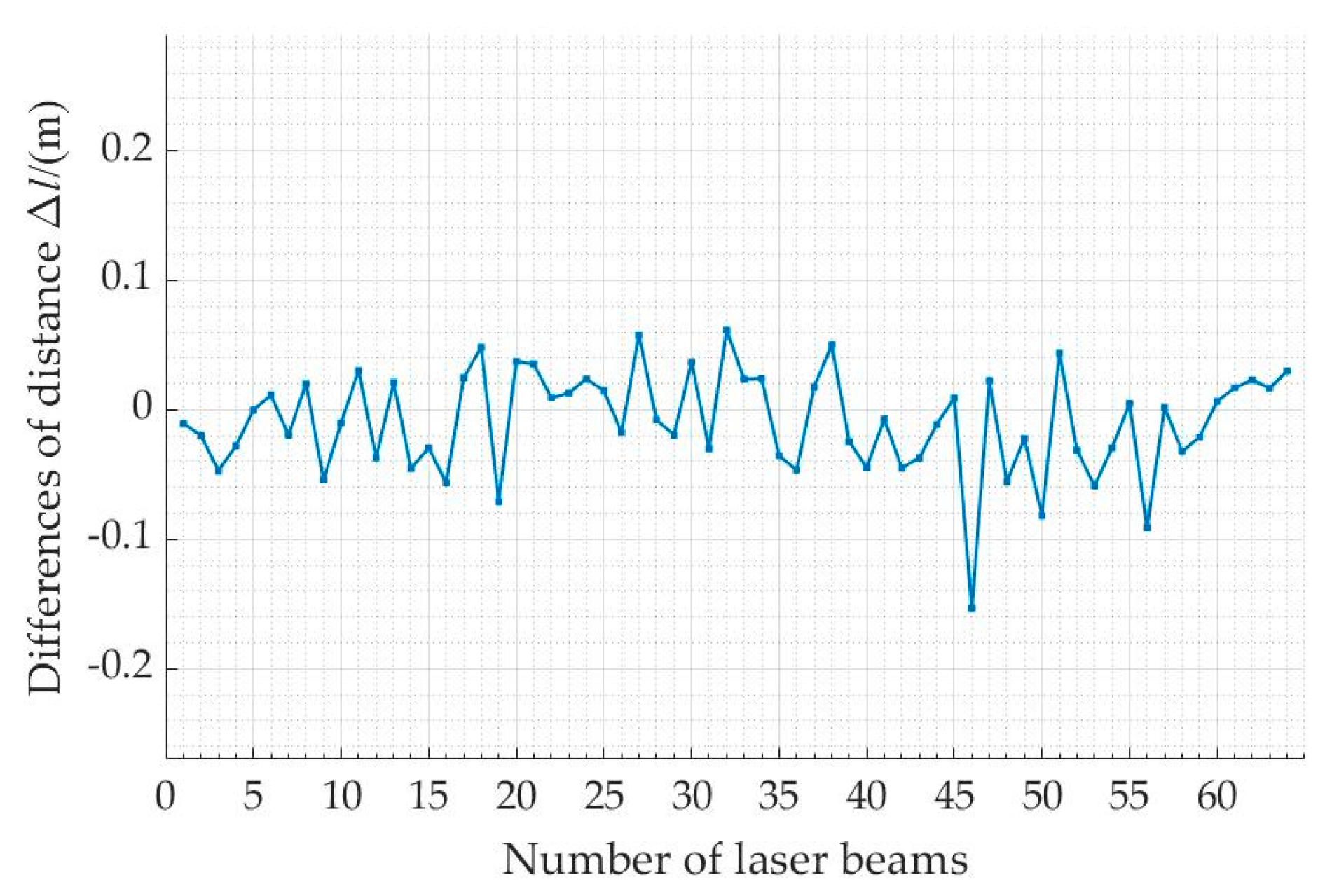
Based on the calibration results presented in the previous section, we further analyzed the differences in the five intrinsic parameters (distance, rotation angle, pitch angle, horizontal distance, and vertical distance) before and after sensor calibration, as shown in Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19. In these figures, the horizontal axis represents the laser beam sequences, and the vertical axis represents the differences between before and after calibration.

Table 2. The mean values and differences in five intrinsic parameters for the 64 laser beams.

Mean Values	Intrinsic Parameters
	Measured Distance	Rotation Angle	Vertical Angle	Horizontal Distance	Vertical Distance
	$\mathrm{\Delta }{\mathit{l}}_{\mathit{i}}$/(m)	$\mathrm{\Delta }{\mathit{\theta }}_{\mathit{i}}$/(°)	$\mathrm{\Delta }{\mathit{\phi }}_{\mathit{i}}$/(°)	${\mathit{h}}_{\mathit{o}\mathit{s}\mathit{c}}{}_{\_\mathit{i}}$/(m)	${\mathit{v}}_{\mathit{o}\mathit{s}\mathit{c}}{}_{\_\mathit{i}}$/(m)
Before calibration	1.44342	0.01089	−0.17410	0.00000	0.18180
After calibration	1.43410	0.00304	−0.16752	0.01579	0.18649
Differences	−0.00932	−0.00785	0.00658	0.01579	0.00469

shows the mean values and differences in the five intrinsic parameters for the 64 laser beams before and after calibration. The differences in the five intrinsic parameters of the LiDAR were as follows: the measured distance $\mathrm{\Delta }{l}_i$ decreased by 0.00932 m; the rotation angle $\mathrm{\Delta }{\theta }_i$ decreased by 0.00785°; the vertical angle $\mathrm{\Delta }{\phi }_i$ decreased by 0.00658°; the horizontal distance $h_{osc}$ increased by 0.01579 m; and the vertical distance $v_{osc}$ increased by 0.00469 m.

4.3.4. Verification Experiments in Agriculture Scene

We verified the feasibility of the intrinsic calibration using the standard deviation of the P2P-D and 3σ criterion in an agricultural scene, as shown in

Table 3. The standard deviation of P2P-D and the percentage within σ, 2σ, 3σ confidence intervals at different distances.

Distance (m)		2.5 (m)	5 (m)	7.5 (m)	10 (m)
Standard deviation σ (m)	Before calibration	0.0401	0.0572	0.0433	0.0427
	After calibration	0.0275	0.0427	0.0193	0.0244
Increase values (m)		−0.0126	−0.0145	−0.024	−0.0183
μ± σ (%)	Before calibration	71.12	72.12	73.91	74.24
	After calibration	75.84	78.84	76.95	75.64
Increase values (%)		4.72	6.72	3.04	1.4
μ± 2σ (%)	Before calibration	93.58	95.54	92.63	95.42
	After calibration	97.41	95.49	93.90	93.09
Increase values (%)		3.83	−0.05	1.27	−2.33
μ± 3σ (%)	Before calibration	97.95	98.79	96.83	97.36
	After calibration	97.65	99.52	96.76	98.25
Increase values (%)		−0.3	0.73	−0.07	0.89

. We found that the increase values are generally positive within the σ and 3σ confidence intervals. Nevertheless, there was a significant negative growth of 2.33% within the 2σ confidence intervals, when the distance was 10 m. The reason may be that the LM algorithm is trapped in a local optimal solution rather than global optimal solution. At the same time, we found that the standard deviation after calibration was relatively decreased, which implies less dispersion of the point cloud on the planar plates. These results demonstrate the effectiveness of the calibration strategy.

5. Discussion and Conclusions

LiDAR has the advantages of high accuracy measurement performance, large-ranging area, and an open-source information sensing algorithm, and it is therefore, increasingly used in agricultural robots. However, the looseness of the internal components of the sensor can lead to a reduction in its ranging accuracy. According to the surveyed literature, research to improve the measurement accuracy of LiDAR still does not attract sufficient attention. Researchers focus more on studying data processing algorithms based on laser point cloud information. In this paper, we conduct research on the intrinsic calibration of LiDAR from the perspective of the ranging principle for laser sensors. A nonlinear optimization strategy based on static plane models is proposed for the calibration of five intrinsic parameters (distance, rotation angle, pitch angle, horizontal distance, and vertical distance) for multi-beam LiDAR.

First, we established the mathematical model by analyzing the working principle of LiDAR with the Velodyne HDL-64E_S3 LiDAR as an example. Then, a nonlinear optimization strategy based on the planar models was used to correct the internal parameters of laser sensors. We concentrated on the three stages (planar model estimation, objective function construction, and nonlinear optimization) of parameter correction. Finally, we demonstrated the effectiveness of the intrinsic calibration by analyzing the standard deviation of the point-to-plane distance and the 3sigma criterion. The experimental results illustrate that:

(1) The dispersion of the laser point clouds after calibration was significantly lower than that before calibration, indicating that the calibrated LiDAR has a higher measurement accuracy.

(2) The maximum standard deviation of the distance from the laser scanning points to the calibration plane before calibration was 5.64 cm, whereas the standard deviation after calibration stayed within the range of 3 cm.

(3) The percentages of points within σ, 2σ, and 3σ confidence intervals to the total number of points increased by 9.06%, 0.25%, and 0.80%, respectively.

The intrinsic calibration of the multi-beam LiDAR can solve the problem of measuring accuracy degradation due to vibration of the internal components of LiDAR sensors. We are optimistic that our work can improve the detection accuracy of agricultural robots in applications such as path planning, obstacle avoidance, target recognition, and phenotype observation. It can also provide inspiration for researchers to develop agricultural intelligent equipment with higher accuracy, wider application range, and improved robustness.