Soil Moisture Estimation Based on Polarimetric Decomposition and Quantile Regression Forests
Abstract
:1. Introduction
2. Materials
2.1. Study Area
2.2. UAVSAR Data
2.3. Ground Measurements
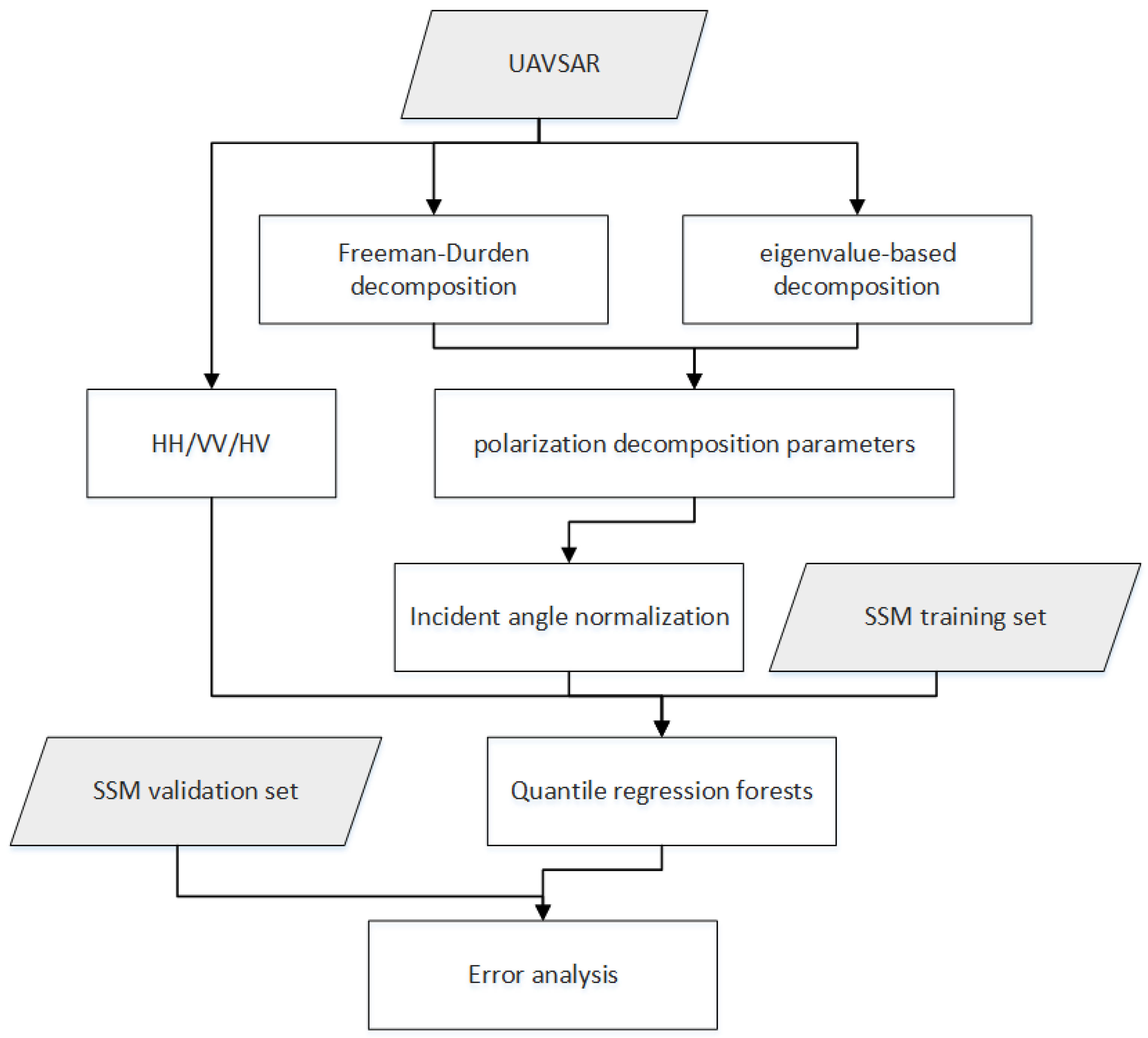
3. Methods
3.1. Polarimetric Decompositions
3.1.1. Freeman-Durden Decomposition
3.1.2. Eigenvalue-Based Decomposition
3.2. Normalization of Polarimetric Parameters
3.3. SSM Estimation
3.3.1. Quantile Regression Forests (QRF)
3.3.2. Copula Quantile Regression (CQR)
3.4. Evaluation Method
4. Results
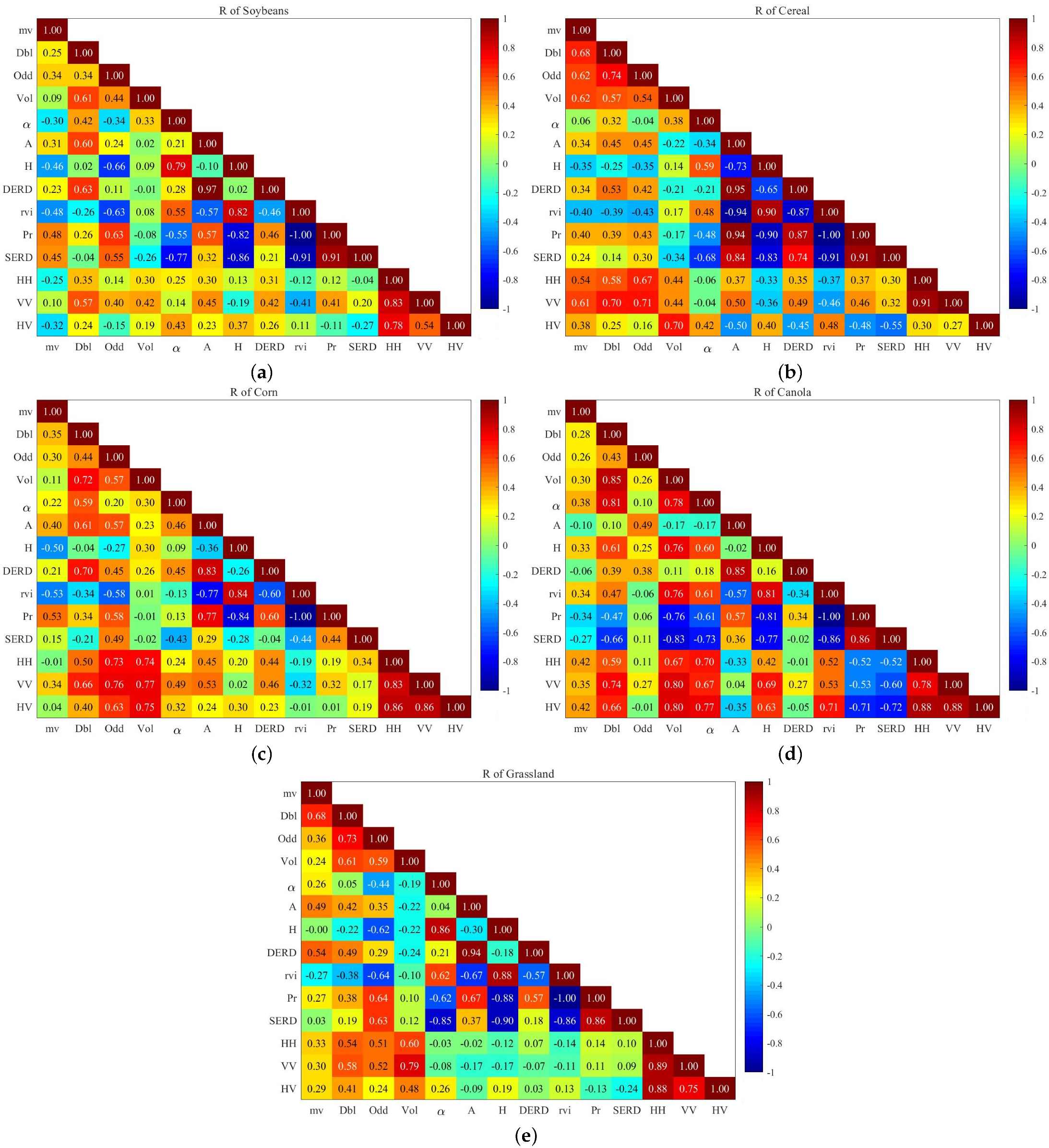
4.1. Correlation Analysis
4.2. SSM Estimation of Different Crop Coverage Areas
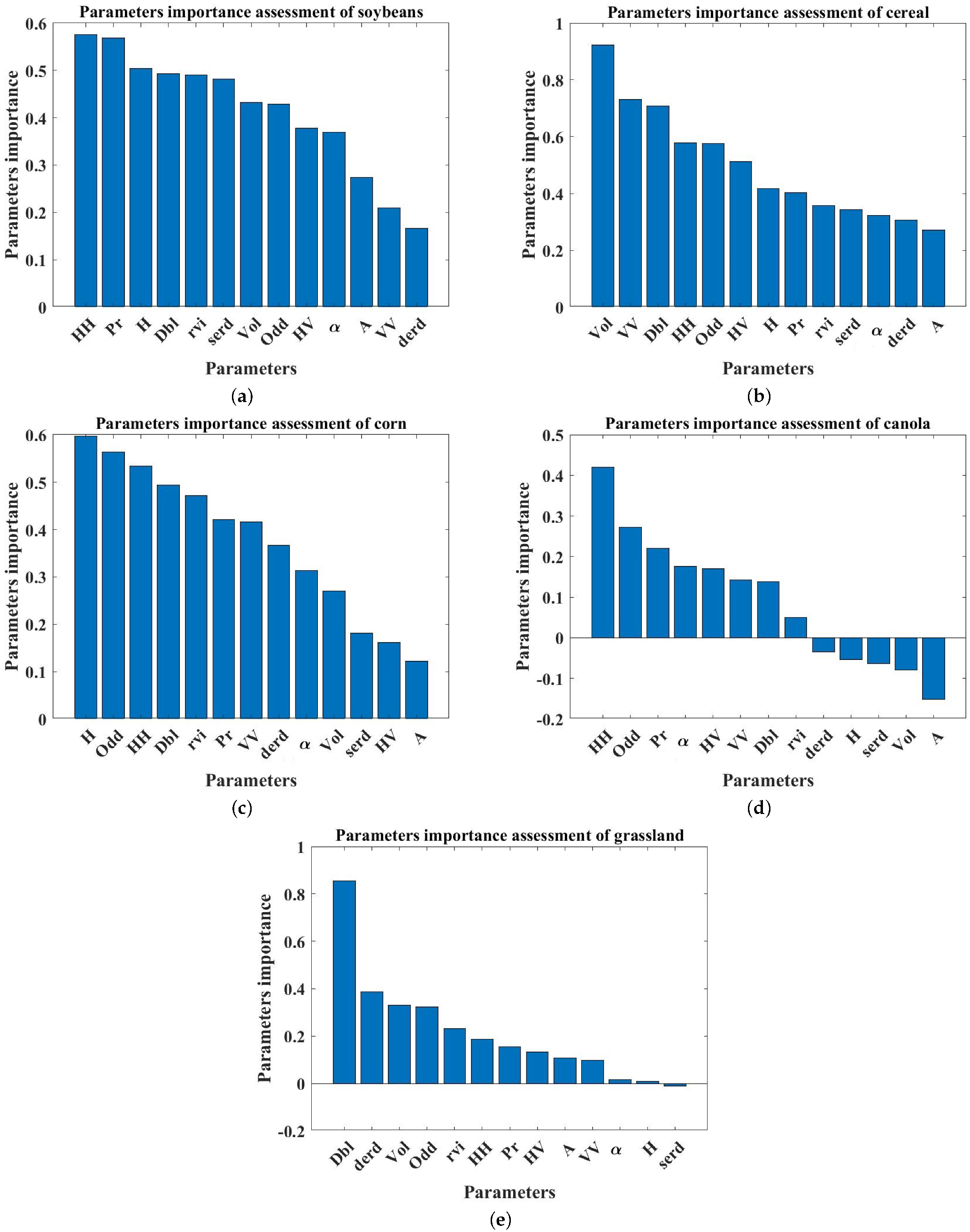
4.3. Parameter Importance Assessment
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moran, M.S.; Inoue, Y.; Barnes, E.M. Opportunities and limitations for image-based remote sensing in precision crop management. Remote Sens. Environ. 1997, 61, 319–346. [Google Scholar] [CrossRef]
- El Hajj, M.; Baghdadi, N.; Zribi, M.; Belaud, G.; Cheviron, B.; Courault, D.; Charron, F. Soil moisture retrieval over irrigated grassland using X-band SAR data. Remote Sens. Environ. 2016, 176, 202–218. [Google Scholar] [CrossRef]
- Zhao, H.; Di, L.; Sun, Z.; Hao, P.; Yu, E.; Zhang, C.; Lin, L. Impacts of Soil Moisture on Crop Health: A Remote Sensing Perspective. In Proceedings of the 2021 9th International Conference on Agro-Geoinformatics (Agro-Geoinformatics), Shenzhen, China, 26–29 July 2021; pp. 1–4. [Google Scholar]
- Norbiato, D.; Borga, M.; Degli Esposti, S.; Gaume, E.; Anquetin, S. Flash flood warning based on rainfall thresholds and soil moisture conditions: An assessment for gauged and ungauged basins. J. Hydrol. 2008, 362, 274–290. [Google Scholar] [CrossRef]
- Abowarda, A.S.; Bai, L.; Zhang, C.; Long, D.; Li, X.; Huang, Q.; Sun, Z. Generating surface soil moisture at 30 m spatial resolution using both data fusion and machine learning toward better water resources management at the field scale. Remote Sens. Environ. 2021, 255, 112301. [Google Scholar] [CrossRef]
- Peng, J.; Albergel, C.; Balenzano, A.; Brocca, L.; Cartus, O.; Cosh, M.H.; Crow, W.T.; Dabrowska-Zielinska, K.; Dadson, S.; Davidson, M.W.; et al. A roadmap for high-resolution satellite soil moisture applications–confronting product characteristics with user requirements. Remote Sens. Environ. 2021, 252, 112162. [Google Scholar] [CrossRef]
- Babaeian, E.; Sadeghi, M.; Franz, T.E.; Jones, S.; Tuller, M. Mapping soil moisture with the OPtical TRApezoid Model (OPTRAM) based on long-term MODIS observations. Remote Sens. Environ. 2018, 211, 425–440. [Google Scholar] [CrossRef]
- Peters, J.; De Baets, B.; De Clercq, E.M.; Ducheyne, E.; Verhoest, N.E. The potential of multitemporal Aqua and Terra MODIS apparent thermal inertia as a soil moisture indicator. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 934–941. [Google Scholar]
- Wang, H.; Magagi, R.; Goita, K.; Wang, K. Soil moisture retrievals using ALOS2-ScanSAR and MODIS synergy over Tibetan Plateau. Remote Sens. Environ. 2020, 251, 112100. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Shi, H.; Zhao, L.; Yang, J.; Lopez-Sanchez, J.M.; Zhao, J.; Sun, W.; Shi, L.; Li, P. Soil moisture retrieval over agricultural fields from L-band multi-incidence and multitemporal PolSAR observations using polarimetric decomposition techniques. Remote Sens. Environ. 2021, 261, 112485. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Martinuzzi, J.M.; Font, J.; Berger, M. Soil Moisture Retrieval from Space: The Soil Moisture and Ocean Salinity (SMOS) Mission. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1729–1735. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The soil moisture active passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Chen, K.S.; Wu, T.D.; Tsay, M.K.; Fung, A.K. Note on the multiple scattering in an IEM model. IEEE Trans. Geosci. Remote Sens. 2000, 38, 249–256. [Google Scholar] [CrossRef]
- Chen, K.S.; Wu, T.D.; Tsang, L.; Qin, L.; Fung, A.K. Emission of rough surfaces calculated by the integral equation method with comparison to three-dimensional moment method simulations. IEEE Trans. Geosci. Remote Sens. 2003, 41, 90–101. [Google Scholar] [CrossRef]
- Fung, A.K.; Chen, K.S. An Update on the IEM Surface Backscattering Model. IEEE Geosci. Remote Sens. Lett. 2004, 1, 75–77. [Google Scholar] [CrossRef]
- Dubois, P.C.; Van Zyl, J.; Engman, T. Measuring soil moisture with imaging radars. IEEE Trans. Geosci. Remote Sens. 2002, 33, 915–926. [Google Scholar] [CrossRef]
- Nicolas, B.; Mohammad, C.; Mehrez, Z.; Mohammad, H.; Simonetta, P.; Niko, V.; Hans, L.; Frederic, B.; Francesco, M. A new empirical model for radar scattering from bare soil surfaces. Remote Sens. 2016, 8, 920. [Google Scholar] [CrossRef]
- Shi, J.; Wang, J.; Hsu, A.Y.; O’Neill, P.E.; Engman, E.T. Estimation of bare soil moisture and surface roughness parameters using L-band SAR image data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1254–1266. [Google Scholar]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. Semi-empirical model of the ensemble-averaged differential Mueller matrix for microwave backscattering from bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1348–1355. [Google Scholar] [CrossRef]
- Zhu, L.; Walker, J.P.; Ye, N.; Rüdiger, C. Roughness and vegetation change detection: A pre-processing for soil moisture retrieval from multi-temporal SAR imagery. Remote Sens. Environ. 2019, 225, 93–106. [Google Scholar] [CrossRef]
- Attema, E.P.W.; Ulaby, F.T. Vegetation modeled as a water cloud. Radio Sci. 1978, 13, 357–364. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Sarabandi, K.; Mcdonald, K.; Whitt, M.; Dobson, M.C. Michigan microwave canopy scattering model. Int. J. Remote Sens. 1990, 11, 1223–1253. [Google Scholar] [CrossRef]
- Baghdadi, N.N.; El Hajj, M.; Zribi, M.; Fayad, I. Coupling SAR C-band and optical data for soil moisture and leaf area index retrieval over irrigated grasslands. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 9, 1229–1243. [Google Scholar] [CrossRef]
- Bai, X.; He, B.; Li, X.; Zeng, J.; Wang, X.; Wang, Z.; Zeng, Y.; Su, Z. First assessment of Sentinel-1A data for surface soil moisture estimations using a coupled water cloud model and advanced integral equation model over the Tibetan Plateau. Remote Sens. 2017, 9, 714. [Google Scholar] [CrossRef]
- Pathe, C.; Wagner, W.; Sabel, D.; Doubkova, M.; Basara, J.B. Using ENVISAT ASAR global mode data for surface soil moisture retrieval over Oklahoma, USA. IEEE Trans. Geosci. Remote Sens. 2009, 47, 468–480. [Google Scholar] [CrossRef]
- Kim, Y.; van Zyl, J.J. A time-series approach to estimate soil moisture using polarimetric radar data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2519–2527. [Google Scholar]
- Pal, M.; Maity, R.; Suman, M.; Das, S.K.; Patel, P.; Srivastava, H.S. Satellite-based probabilistic assessment of soil moisture using C-band quad-polarized RISAT1 data. IEEE Trans. Geosci. Remote Sens. 2016, 55, 1351–1362. [Google Scholar] [CrossRef]
- Ma, C.; Li, X.; Notarnicola, C.; Wang, S.; Wang, W. Uncertainty quantification of soil moisture estimations based on a Bayesian probabilistic inversion. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3194–3207. [Google Scholar] [CrossRef]
- Nguyen, H.H.; Cho, S.; Jeong, J.; Choi, M. A D-vine copula quantile regression approach for soil moisture retrieval from dual polarimetric SAR Sentinel-1 over vegetated terrains. Remote Sens. Environ. 2021, 255, 112283. [Google Scholar] [CrossRef]
- Hajnsek, I.; Jagdhuber, T.; Schon, H.; Papathanassiou, K.P. Potential of estimating soil moisture under vegetation cover by means of PolSAR. IEEE Trans. Geosci. Remote Sens. 2009, 47, 442–454. [Google Scholar] [CrossRef]
- Huang, X.; Wang, J.; Shang, J. An adaptive two-component model-based decomposition on soil moisture estimation for C-band RADARSAT-2 imagery over wheat fields at early growing stages. IEEE Geosci. Remote Sens. Lett. 2016, 13, 414–418. [Google Scholar] [CrossRef]
- Wang, H.; Magagi, R.; Goita, K. Comparison of different polarimetric decompositions for soil moisture retrieval over vegetation covered agricultural area. Remote Sens. Environ. 2017, 199, 120–136. [Google Scholar] [CrossRef]
- Wang, H.; Magagi, R.; Goïta, K. Potential of a two-component polarimetric decomposition at C-band for soil moisture retrieval over agricultural fields. Remote Sens. Environ. 2018, 217, 38–51. [Google Scholar] [CrossRef]
- Notarnicola, C.; Angiulli, M.; Posa, F. Soil moisture retrieval from remotely sensed data: Neural network approach versus Bayesian method. IEEE Trans. Geosci. Remote Sens. 2008, 46, 547–557. [Google Scholar] [CrossRef]
- Paloscia, S.; Pettinato, S.; Santi, E.; Notarnicola, C.; Pasolli, L.; Reppucci, A. Soil moisture mapping using Sentinel-1 images: Algorithm and preliminary validation. Remote Sens. Environ. 2013, 134, 234–248. [Google Scholar] [CrossRef]
- Santi, E.; Paloscia, S.; Pettinato, S.; Fontanelli, G. Application of artificial neural networks for the soil moisture retrieval from active and passive microwave spaceborne sensors. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 61–73. [Google Scholar] [CrossRef]
- Kumar, P.; Prasad, R.; Choudhary, A.; Gupta, D.; Mishra, V.; Vishwakarma, A.; Singh, A.; Srivastava, P. Comprehensive evaluation of soil moisture retrieval models under different crop cover types using C-band synthetic aperture radar data. Geocarto Int. 2019, 34, 1022–1041. [Google Scholar] [CrossRef]
- Hajnsek, I.; Pottier, E.; Cloude, S.R. Inversion of surface parameters from polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 2003, 41, 727–744. [Google Scholar] [CrossRef]
- He, L.; Panciera, R.; Tanase, M.A.; Walker, J.P.; Qin, Q. Soil moisture retrieval in agricultural fields using adaptive model-based polarimetric decomposition of SAR data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4445–4460. [Google Scholar] [CrossRef]
- Jagdhuber, T.; Hajnsek, I.; Papathanassiou, K.P. An iterative generalized hybrid decomposition for soil moisture retrieval under vegetation cover using fully polarimetric SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 8, 3911–3922. [Google Scholar] [CrossRef]
- Ponnurangam, G.G.; Jagdhuber, T.; Hajnsek, I.; Rao, Y. Soil moisture estimation using hybrid polarimetric SAR data of RISAT-1. IEEE Trans. Geosci. Remote Sens. 2015, 54, 2033–2049. [Google Scholar] [CrossRef]
- Wang, H.; Magagi, R.; Goita, K.; Jagdhuber, T. Refining a polarimetric decomposition of multi-angular UAVSAR time series for soil moisture retrieval over low and high vegetated agricultural fields. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1431–1450. [Google Scholar] [CrossRef]
- Gururaj, P.; Umesh, P.; Shetty, A. Assessment of surface soil moisture from ALOS PALSAR-2 in small-scale maize fields using polarimetric decomposition technique. Acta Geophys. 2021, 69, 579–588. [Google Scholar] [CrossRef]
- Baghdadi, N.; Cresson, R.; Pottier, E.; Aubert, M.; Mehrez, M.; Jacome, A.; Benabdallah, S. A potential use for the C-band polarimetric SAR parameters to characterize the soil surface over bare agriculture fields. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3844–3858. [Google Scholar] [CrossRef]
- Bourgeau-Chavez, L.L.; Leblon, B.; Charbonneau, F.; Buckley, J.R. Evaluation of polarimetric Radarsat-2 SAR data for development of soil moisture retrieval algorithms over a chronosequence of black spruce boreal forests. Remote Sens. Environ. 2013, 132, 71–85. [Google Scholar] [CrossRef]
- Pasolli, L.; Notarnicola, C.; Bruzzone, L.; Bertoldi, G.; Chiesa, S.D.; Niedrist, G.; Tappeiner, U.; Zebisch, M. Polarimetric RADARSAT-2 imagery for soil moisture retrieval in alpine areas. Can. J. Remote Sens. 2011, 37, 535–547. [Google Scholar] [CrossRef]
- Bai, X.; He, B.; Xu, D. Potential use of radarsat-2 polarimetric parameters for estimating soil moisture in prairie areas. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3043–3046. [Google Scholar]
- Zhang, X.; Chen, B.; Zhao, H.; Fan, H.; Zhu, D. Soil moisture retrieval over a semiarid area by means of PCA dimensionality reduction. Can. J. Remote Sens. 2016, 42, 136–144. [Google Scholar] [CrossRef]
- Hariharan, S.; Mandal, D.; Tirodkar, S.; Kumar, V.; Bhattacharya, A.; Lopez-Sanchez, J.M. A novel phenology based feature subset selection technique using random forest for multitemporal PolSAR crop classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4244–4258. [Google Scholar] [CrossRef]
- Kumar, P.; Prasad, R.; Gupta, D.; Mishra, V.; Vishwakarma, A.; Yadav, V.; Bala, R.; Choudhary, A.; Avtar, R. Estimation of winter wheat crop growth parameters using time series Sentinel-1A SAR data. Geocarto Int. 2018, 33, 942–956. [Google Scholar] [CrossRef]
- Wang, H.; Magagi, R.; Goïta, K.; Trudel, M.; McNairn, H.; Powers, J. Crop phenology retrieval via polarimetric SAR decomposition and Random Forest algorithm. Remote Sens. Environ. 2019, 231, 111234. [Google Scholar] [CrossRef]
- Yadav, V.P.; Prasad, R.; Bala, R.; Vishwakarma, A.K. An improved inversion algorithm for spatio-temporal retrieval of soil moisture through modified water cloud model using C-band Sentinel-1A SAR data. Comput. Electron. Agric. 2020, 173, 105447. [Google Scholar] [CrossRef]
- McNairn, H.; Jackson, T.J.; Wiseman, G.; Belair, S.; Berg, A.; Bullock, P.; Colliander, A.; Cosh, M.H.; Kim, S.B.; Magagi, R.; et al. The soil moisture active passive validation experiment 2012 (SMAPVEX12): Prelaunch calibration and validation of the SMAP soil moisture algorithms. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2784–2801. [Google Scholar] [CrossRef]
- McNairn, H.; Powers, J.; Wiseman, G. SMAPVEX12 Land Cover Classification Map; NASA DAAC at the National Snow and Ice Data Center: Boulder, CO, USA, 2014.
- SMAP Validation Experiment 2012. Experimental Plan. Available online: https://nsidc.org/sites/nsidc.org/files/technical-references/SMAPVEX12_Experiment_Plan.pdf (accessed on 5 May 2022).
- SMAP Validation Experiment 2012. SMAPVEX12 Database Report. Available online: https://nsidc.org/sites/nsidc.org/files/technical-references/SMAPVEX12-database-report-final.pdf (accessed on 5 May 2022).
- Dataset: UAVSAR, NASA. 2012. Retrieved from ASF DAAC 12 December 2021. Available online: https://search.asf.alaska.edu/ (accessed on 21 August 2022).
- Wiseman, G.; Bullock, P.; Berg, A. SMAPVEX12 Probe-Based In Situ Soil Moisture Data for Agricultural Area; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2014.
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Mladenova, I.E.; Jackson, T.J.; Bindlish, R.; Hensley, S. Incidence angle normalization of radar backscatter data. IEEE Trans. Geosci. Remote Sens. 2012, 51, 1791–1804. [Google Scholar] [CrossRef]
- Meinshausen, N.; Ridgeway, G. Quantile regression forests. J. Mach. Learn. Res. 2006, 7, 983–999. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Bair, E.; Hastie, T.; Paul, D.; Tibshirani, R. Prediction by supervised principal components. J. Am. Stat. Assoc. 2006, 101, 119–137. [Google Scholar] [CrossRef]
- Janitza, S.; Strobl, C.; Boulesteix, A.L. An AUC-based permutation variable importance measure for random forests. BMC Bioinform. 2013, 14, 1–11. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 1–21. [Google Scholar] [CrossRef]
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.; Kanae, S.; Kowalczyk, E.; Lawrence, D.; et al. Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef]
- Wu, W.; Geller, M.A.; Dickinson, R.E. The response of soil moisture to long-term variability of precipitation. J. Hydrometeorol. 2002, 3, 604–613. [Google Scholar] [CrossRef]
- Wagner, W.; Scipal, K.; Pathe, C.; Gerten, D.; Lucht, W.; Rudolf, B. Evaluation of the agreement between the first global remotely sensed soil moisture data with model and precipitation data. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]




| Sensitivity | Polarization | Canola | Corn | Grassland | Soybeans | Cereal |
|---|---|---|---|---|---|---|
| slope | HH | 10.27 | −0.59 | 12.17 | −6.32 | 9.90 |
| VV | 9.18 | 18.61 | 8.50 | 1.90 | 11.94 | |
| HV | 17.78 | 3.22 | 14.82 | −9.85 | 8.83 | |
| R | HH | 0.42 | -0.01 | 0.33 | −0.27 | 0.55 |
| VV | 0.35 | 0.34 | 0.30 | 0.09 | 0.59 | |
| HV | 0.42 | 0.04 | 0.29 | −0.32 | 0.38 |
| Crop | MIN cm/cm | MEAN cm/cm | MAX cm/cm | STD cm/cm | N |
|---|---|---|---|---|---|
| soybeans | 0.052 | 0.220 | 0.588 | 0.105 | 201 |
| cereal | 0.087 | 0.294 | 0.525 | 0.110 | 150 |
| corn | 0.052 | 0.137 | 0.313 | 0.057 | 102 |
| canola | 0.059 | 0.207 | 0.378 | 0.087 | 76 |
| grassland | 0.159 | 0.296 | 0.538 | 0.071 | 58 |
| Crop | MIN cm | MEAN cm | MAX cm | STD cm |
|---|---|---|---|---|
| soybeans | 7.0 | 26.6 | 75.9 | 17.5 |
| cereal | 33.7 | 74.2 | 113.6 | 17.6 |
| corn | 13.2 | 102.9 | 269.6 | 73.2 |
| canola | 6.5 | 88.2 | 148.2 | 37.4 |
| grassland | 5.9 | 30.5 | 66.1 | 15.9 |
| Crop | Method | MRE | RMSE | R | KGE | RDA |
|---|---|---|---|---|---|---|
| soybeans | QRF | 0.101 | 0.059 | 0.745 | 0.612 | 0.107 |
| CQR | 0.109 | 0.080 | 0.481 | 0.384 | 0.121 | |
| cereal | QRF | 0.002 | 0.053 | 0.905 | 0.732 | 0.012 |
| CQR | −0.003 | 0.086 | 0.710 | 0.491 | 0.004 | |
| corn | QRF | 0.120 | 0.037 | 0.802 | 0.577 | 0.140 |
| CQR | 0.197 | 0.043 | 0.715 | 0.458 | 0.222 | |
| canola | QRF | 0.227 | 0.079 | 0.763 | 0.288 | 0.155 |
| CQR | 0.202 | 0.075 | 0.738 | 0.373 | 0.190 | |
| grassland | QRF | 0.001 | 0.037 | 0.665 | 0.431 | −0.009 |
| CQR | −0.003 | 0.036 | 0.718 | 0.488 | −0.008 |
| Crop | SRP | MIN | MEAN | MAX | STD |
|---|---|---|---|---|---|
| soybeans | s | 0.34 | 0.88 | 1.89 | 0.32 |
| l | 5.50 | 11.88 | 18.5 | 3.58 | |
| cereal | s | 0.44 | 1.14 | 2.26 | 0.40 |
| l | 2.50 | 11.03 | 25.50 | 5.02 | |
| corn | s | 0.60 | 1.27 | 1.89 | 0.44 |
| l | 6.50 | 12.11 | 22.50 | 4.60 | |
| canola | s | 0.69 | 1.22 | 1.71 | 0.34 |
| l | 6.00 | 9.96 | 15.50 | 3.07 | |
| grassland | s | 0.35 | 1.07 | 1.76 | 0.42 |
| l | 6.00 | 14.00 | 22.50 | 6.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Lv, X.; Wang, R. Soil Moisture Estimation Based on Polarimetric Decomposition and Quantile Regression Forests. Remote Sens. 2022, 14, 4183. https://doi.org/10.3390/rs14174183
Zhang L, Lv X, Wang R. Soil Moisture Estimation Based on Polarimetric Decomposition and Quantile Regression Forests. Remote Sensing. 2022; 14(17):4183. https://doi.org/10.3390/rs14174183
Chicago/Turabian StyleZhang, Li, Xiaolei Lv, and Rui Wang. 2022. "Soil Moisture Estimation Based on Polarimetric Decomposition and Quantile Regression Forests" Remote Sensing 14, no. 17: 4183. https://doi.org/10.3390/rs14174183
APA StyleZhang, L., Lv, X., & Wang, R. (2022). Soil Moisture Estimation Based on Polarimetric Decomposition and Quantile Regression Forests. Remote Sensing, 14(17), 4183. https://doi.org/10.3390/rs14174183






