A Magnetic Interference Compensation Method for Airborne Electronic Equipment without Current Sensors

Abstract

With the rapid development of unmanned aerial vehicles (UAVs) technology, using UAVs for magnetic surveys is a booming branch. However, the magnetic interference generated by the UAV hinders the further application of UAV magnetic survey systems. In addition to the interference caused by the UAV maneuvering, the dynamic interference of airborne equipment has also been found and become one of the factors restricted by the detection accuracy of magnetic surveys. This paper proposes a multi-source two-channel linear time-invariant (MTLI) correlation model, considering the maneuvering magnetic interference and airborne equipment magnetic interference. The magnetic interference can be estimated and compensated by interference correlation without current sensors. Compared with the traditional aeromagnetic compensation process and other compensation methods considering the magnetic interference of airborne equipment, the proposed method can provide stable compensation effects in maneuvers and smooth flight, and the workflow is simple and fast. The actual flight experiment is conducted, and the results show that the two kinds of UAV interference fields are suppressed significantly with a root mean square error of 0.0062 and 0.0296 nT in smooth flight and maneuvering flight.

1. Introduction

In the past two decades, unmanned aerial vehicles (UAVs) have been used in many scientific research fields for various applications. Among them, the use of UAVs for magnetic surveys is a booming branch and is expected to be actively applied in the future [1]. However, the interference that is generated by the aircraft platform may significantly affect the detection performance. Aeromagnetic compensation is designed to solve the problem of magnetic interference generated by aircraft platforms.

Although nonmagnetic materials are used as much as possible in the design, some modules and structures of the UAVs still contain ferromagnetic materials (e.g., engines, motors). Magnetic fields generated by these ferromagnetic materials and the electromagnetic fields generated by the airborne electronic system during operation contribute to the main components of the interference. In fact, this problem also exists in traditional aeromagnetic surveys [2]. Most research on aeromagnetic compensation has mainly focused on the suppression of the magnetic interference generated by aircraft maneuvers [3] and the onboard electronic equipment (OBE) [4].

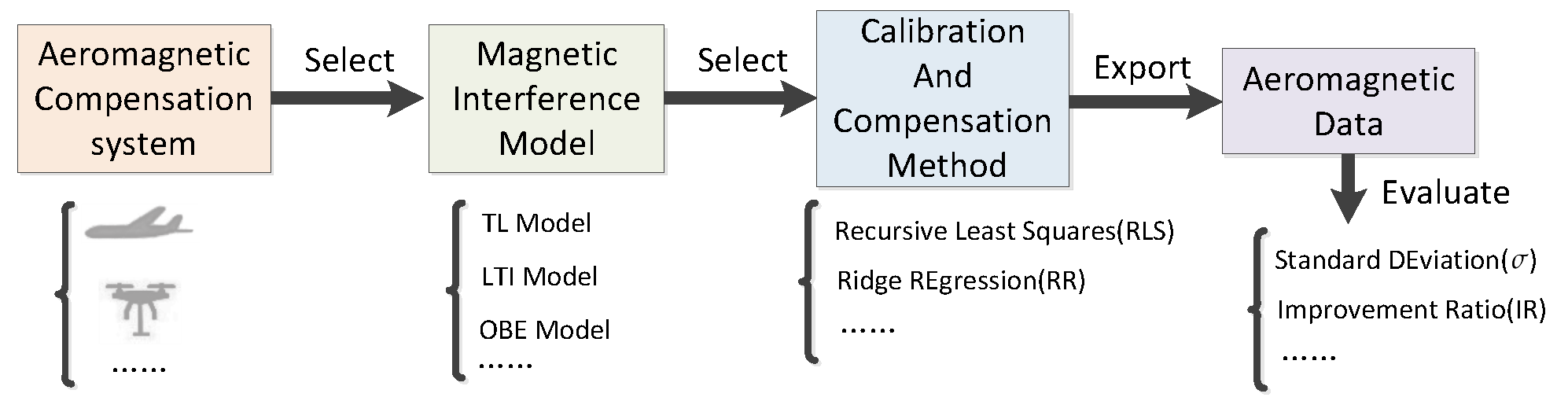
Given that the aircraft platform affects the accuracy of magnetic measurements, Tolles proposed a classical aeromagnetic compensation model in the 1940s [5] named the Tolles–Lawson (TL) model. Paul Leliak proposed sinusoidal maneuvers to improve compensation performance in 1961 [3]. In 1980, B.W. Leach proposed a ridge regression algorithm to solve the aeromagnetic compensation parameters [6]. Most of the aeromagnetic interference compensation problems can be solved by selecting an appropriate solution method for the TL model. In 2011 and 2013, Gerardo Noriega proved the viability and reliability of using the standard deviation of the signal as an assessment criterion through a large number of aeromagnetic trials [7,8]. This evaluation method is also used in this paper. By comparing the improvement ratio (IR) [7], a more suitable compensation model and calculation method can be selected. The above is a typical framework of aeromagnetic compensation technology progress, which is shown in Figure 1. Many researchers constantly propose various improvements in improving models and methods in order to obtain higher-quality aeromagnetic data.

In addition to building magnetic interference models based on the principle of interference sources, some researchers also put forward clever methods that are more suitable for engineering applications by using the characteristics of the system. For time-varying interferences with an unknown signature, Sheinker proposed an adaptive magnetic interference cancelation method by using a pair of magnetometers, which obtained good results for highly correlated interference magnetic fields [9]. Further, based on the signal correlation [10], Mu et al. established a two-channel linear time-invariant (LTI) model to remove UAV interference. This method is completely different from the traditional compensation flight, and the interference related to the UAV is regarded as a whole rather than several parts related to maneuvers. Adaptive interference cancellation is realized by a pair of magnetometers based on the assumption that the interference signal is irrelevant to the target signal.

In reference [11], an experiment was designed to add two magnetometers to the body to evaluate the dynamic noise gradient, but it was found that the main factor affecting the dynamic noise of magnetic detection came from the current in the OBE. In [12], a linear system approach for the mitigation of onboard noise sources by some reference sensors was developed. However, there is no perfect expression of the measurement in the dynamic process of the auxiliary sensor. In [4], an improved procedure for aeromagnetic compensation is presented, the interferences due to the strobe and beacon lights are modeled to be proportional to the currents flowing through the lights, and the currents are measured by the OBE sensors.

Study [13] provides a method for finding the position of the OBE switching effect through the first derivative of the magnetic field and then correcting it. This method is easy to implement in stable aeromagnetic data, but it cannot work properly when the magnetic signal changes dramatically during the large-angle maneuver of the platform.

It can be seen that the importance of magnetic interference compensation for OBE on UAVs has been gradually paid attention to. However, in previous studies and experiments, the magnetic interference model could not comprehensively consider the body interference [9,10,11], current sensors were needed to realize the simultaneous compensation of multiple interferences [4], or the proposed method could only be applied in special smooth flight [13]. It is challenging to achieve a multi-type aeromagnetic compensation method with higher applicability and accuracy without changing the installation mode of most existing magnetic detection systems.

It can be seen that the magnetic interference compensation for OBE on UAVs has the following limitations:

• Adding current sensors brings additional overhead and sensor noise.
• Magnetic interference from maneuvering (TL Model) and magnetic interference of OBE occur simultaneously during flight.

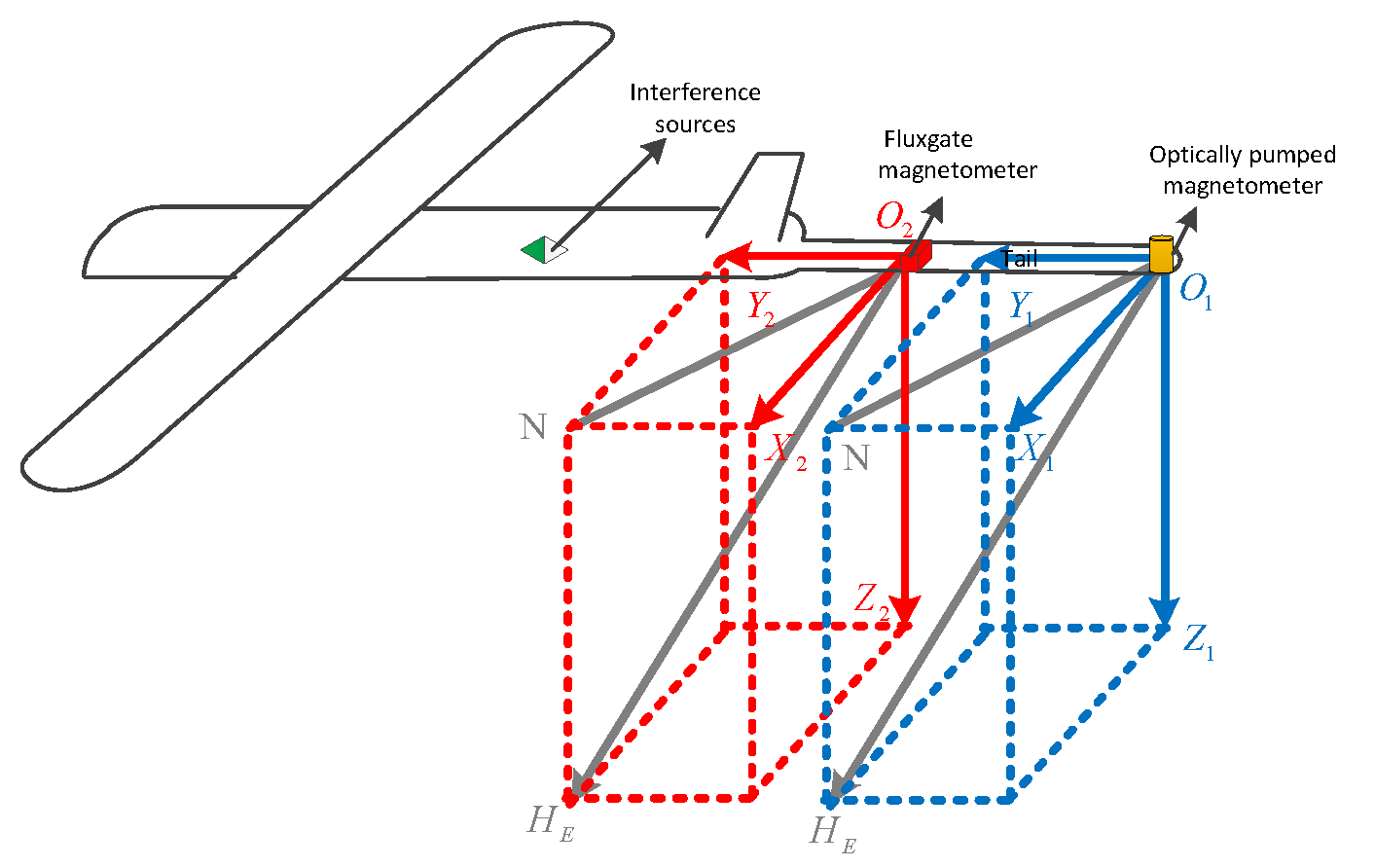
In practice, there are two different magnetometers in the magnetic detection systems. One is a scalar magnetometer, which is far from the aircraft and used to measure the scalar target magnetic signal; the other is a vector magnetometer, which is near the aircraft body and used to obtain the direction cosine of the geomagnetic field in the reference system of airborne platform. Thus, both magnetometers will collect scalar and vector magnetic fields at the same time [4]. Statistics presented in [1] show that $25\%$ of 16 Fixed-Wing UAV cases in recent years used both scalar and vector magnetometers. Each of these cases can directly apply the methods in this article to improve data quality without the need to introduce additional current sensors. It is also suitable for Manned Fixed-Wing Aircraft with similar installation schemes.

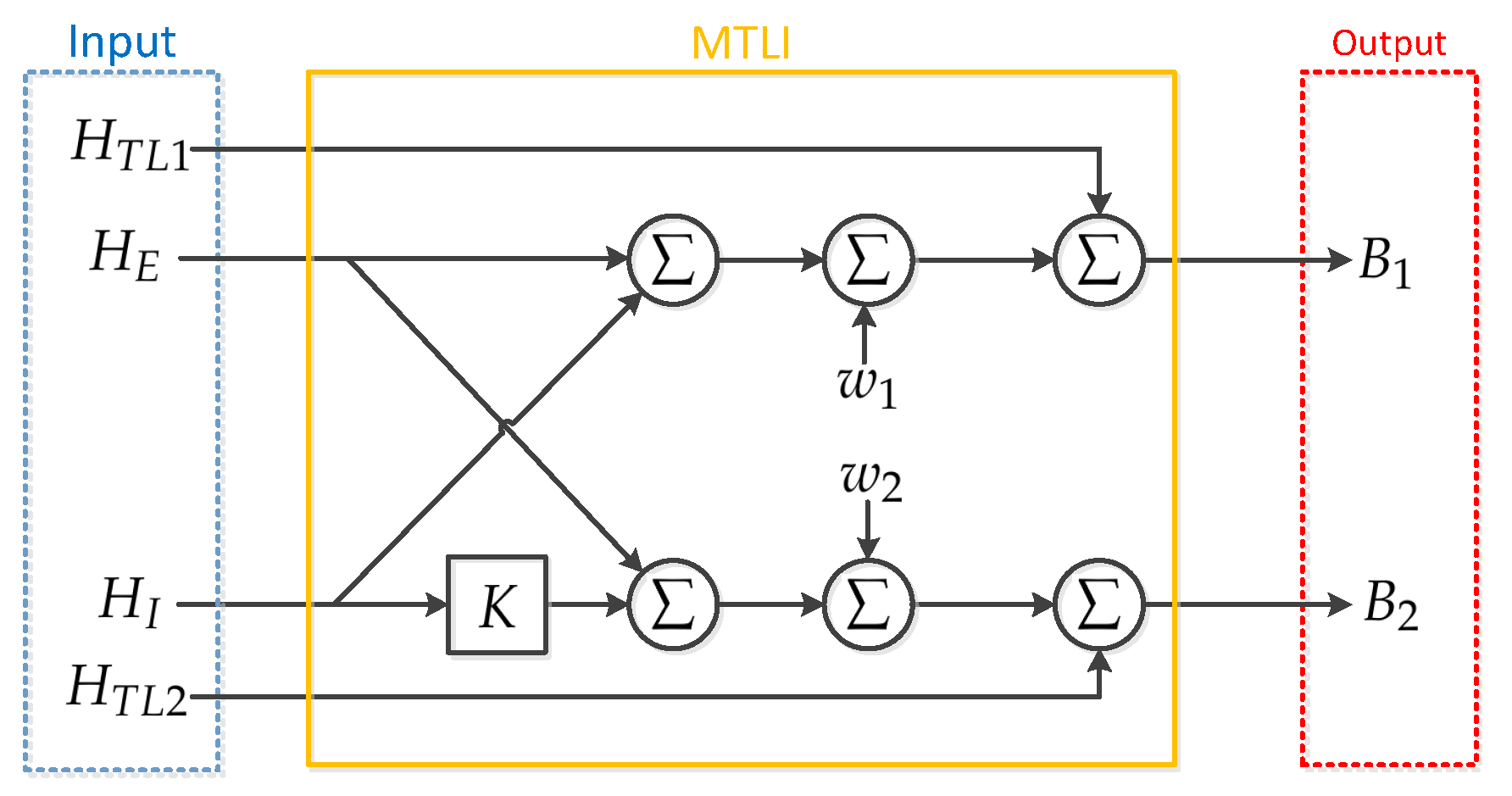
This paper presents a magnetic interference compensation method based on the multi-source two-channel linear time-invariant (MTLI) correlation model. In the proposed method, the magnetic interference can be estimated and compensated for by interference correlation without adding current sensors or changing the structure of most aeromagnetic detection systems. The method is especially effective for canceling a time-varying magnetic interference with an unknown signature, especially the interference originating from OBE that varies unexpectedly with time. In this study, we lay out the theoretical analysis and demonstrate the method using computer simulations. The experiments with real magnetic signals support theoretical and simulation results. The high accuracy and the simple implementation make the proposed method attractive for magnetic surveys.

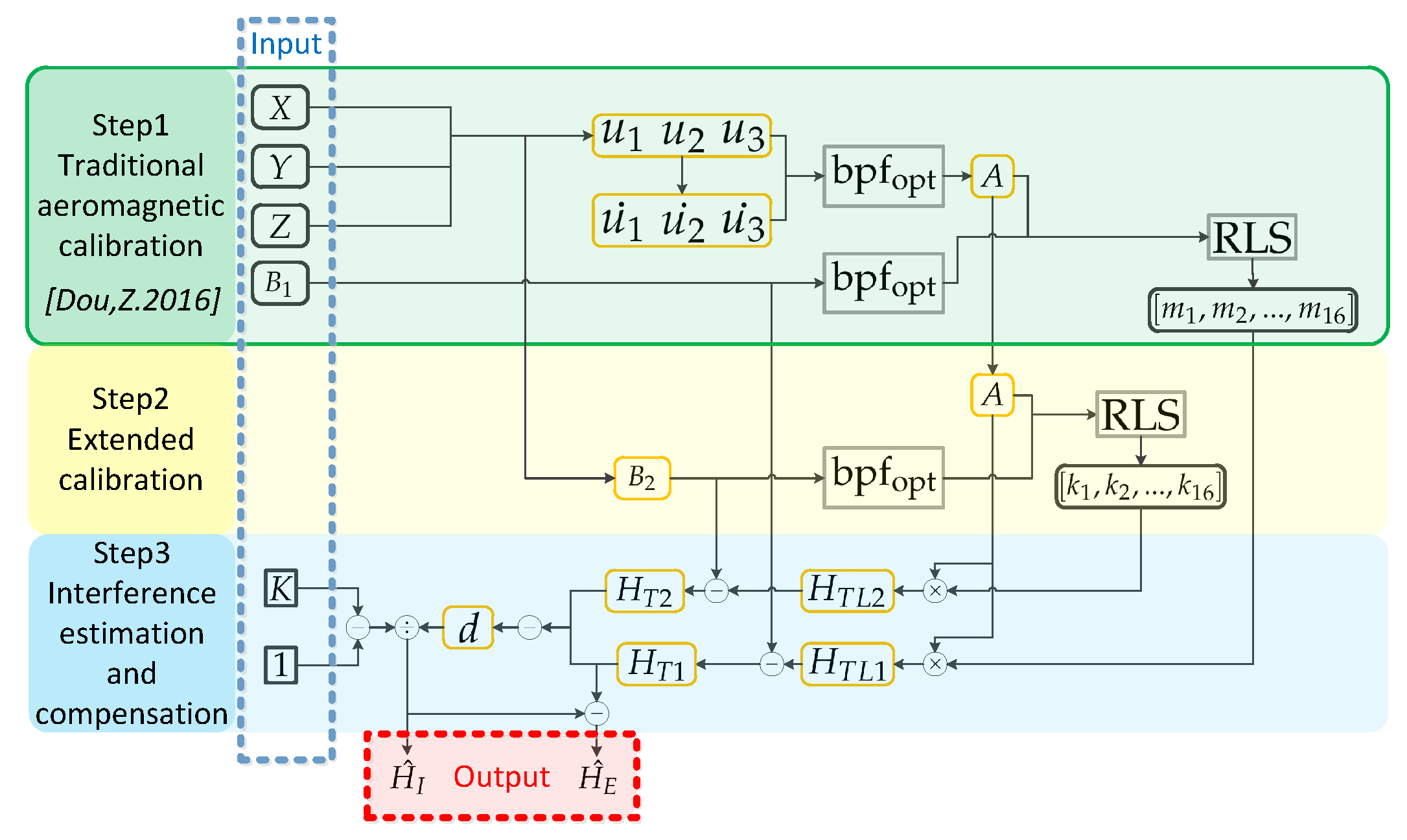
The paper is organized as follows. Section 2 presents the configuration of the UAV-magnetometer system and correlation model. The steps for estimating and compensating magnetic interference are also given in this section. Section 3 analyzes the error of magnetic interference estimation. The numerical analysis and experimental results are discussed in Section 4 and Section 5. Section 6 provides the conclusions of this research.

2. Correlation Model and Coordinate System Analysis

2.1. MTLI Correlation Model

In the aeromagnetic compensation process, common equipment installation methods are shown in Figure 2. $O_2$ is the fluxgate (vector magnetometer) installed in the middle of the tail rod, and $O_1$ is the magnetometer (scalar magnetometer) installed at the end of the tail rod. The green arrow shows an OBE with magnetic interference.

The magnetometer coordinate system $O_1$-$X_1{Y}_1{Z}_1$ is defined as: the installation position of the optically pumped magnetometer is the origin $O_1$, the front of the aircraft is the positive of the $Y_1$-axis, the left-wing of the aircraft is the positive of the $X_1$-axis, and the vertically downward direction is the positive of $Z_1$-axis. The fluxgate coordinate system $O_2$-$X_2{Y}_2{Z}_2$ is similar to $O_1$-$X_1{Y}_1{Z}_1$.

The corresponding maneuver action is: the rotation around the $X_1$-axis and $X_2$-axis is pitch, the rotation around the $Y_1$-axis and $Y_2$-axis is roll, and the rotation around the $Z_1$-axis and $Z_2$-axis is yaw.

The multi-source two-channel linear time-invariant (MTLI) correlation model is established based on the configuration of a UAV-magnetometer system, as shown in Figure 3. Where $B_1$ and $B_2$ represent the origional output of the magnetometer and fluxgate and the output of MTLI. $H_{TL1}$ and $H_{TL2}$ represent the interference produced by the platform at $O_1$ and $O_2$. $H_E$ represents the same ambient magnetic field sensed by the magnetometer and fluxgate. The interference of OBE, $H_I$, is sensed differently at $O_1$ and $O_2$, where it is stronger by a factor of K at $O_2$, which is closer to the OBE. Since the mounting scheme of the body is constant, K is a constant. $w_1$ represents the intrinsic noise of the magnetometer, and $w_2$ represents the intrinsic noise of the fluxgate. We assume that $H_E$, $H_I$, $w_1$, and $w_2$ are all zero means.

We express the correlation model as an equation set using Formula (1).

$$\begin{array}{c}\hfill B_1=H_{TL1}+H_E+H_I+w_1\\ \hfill B_2=H_{TL2}+H_E+K{H}_I+w_2\end{array}$$

(1)

2.2. Magnetic Interference at Position $O_1$ and $O_2$

In real applications, the directional vector is measured by a fluxgate. The three axes of the fluxgate are aligned with the axes as $O_2$-$X_2{Y}_2{Z}_2$, respectively. Therefore, the direction cosine computed in $O_2$-$X_2{Y}_2{Z}_2$ can be used to represent the direction cosine in $O_1$-$X_1{Y}_1{Z}_1$. The calculation method of the direction cosine by the fluxgate was mentioned in the 1980s [6] and has been used up to now. Suppose that the output of the three fluxgate axes is $\overrightarrow{X},\overrightarrow{Y},\overrightarrow{Z}$, then

$$\begin{array}{c}\hfill u_1=Cos{X}_1=Cos{X}_2=\frac{|\overrightarrow{X}|}{\sqrt{{\overrightarrow{X}}^2+{\overrightarrow{Y}}^2+{\overrightarrow{Z}}^2}}\\ \hfill u_2=Cos{Y}_1=Cos{Y}_2=\frac{|\overrightarrow{Y}|}{\sqrt{{\overrightarrow{X}}^2+{\overrightarrow{Y}}^2+{\overrightarrow{Z}}^2}}\\ \hfill u_3=Cos{Z}_1=Cos{Z}_2=\frac{|\overrightarrow{Z}|}{\sqrt{{\overrightarrow{X}}^2+{\overrightarrow{Y}}^2+{\overrightarrow{Z}}^2}}\end{array}$$

(2)

The issue of minimizing the interference for traditional aeromagnetic surveys has been addressed thoroughly by developing compensation strategies both in the hardware and software [7,14,15]. Post-compensation is usually necessary in addition to keeping the magnetometer as far away from the drones as possible. An equation with 16 terms is established by linking interference with a maneuver to calculate the compensation coefficients:

$$\overrightarrow{H_{TL1}}=\sum _{i=1}^3{a}_i{u}_i+\sum _{i=1}^3\sum _{j=1}^3{b}_{ij}{u}_i{u}_j+\sum _{i=1}^3\sum _{j=1}^3{c}_{ij}{u}_i\dot{u_j}$$

(3)

where $u_i,i=1,2,3$ are the direction cosines to $O_1$-$X_1{Y}_1{Z}_1$ separately, $\dot{u_j},j=1,2,3$ is the derivation of $u_j$, and $a_i,b_{ij},c_{ij}$ are the coefficients of the model to estimate in the calibration process. As the direction cosines satisfy

$$\sum _{i=1}^3{u}_i^2=1,\sum _{i=1}^3{u}_i\dot{u_i}=0$$

(4)

Formula (3) can be simplified as

$$\overrightarrow{H_{TL1}}=\sum _{i=1}^{16}{m}_i{g}_i$$

(5)

where $g_i$ includes $u_i,u_i{u}_j,u_i\dot{u_j}$, and $m_i$ are coefficients to estimate that consist of $a_i,b_{ij},c_{ij}$.

The output of the fluxgate can also be used to calculate the scalar magnetic field, so the platform interference can also be described by the TL model at fluxgate. It should be noted that the coefficients $k_i$ used to describe the interference at $O_2$ are different from $m_i$.

$$\overrightarrow{H_{TL2}}=\sqrt{{\overrightarrow{X}}^2+{\overrightarrow{Y}}^2+{\overrightarrow{Z}}^2},\overrightarrow{H_{TL2}}=\sum _{i=1}^{16}{k}_i{g}_i$$

(6)

The coefficients $k_i$ and $m_i$ could be solved by the recursive least squares (RLS) method with an adaptive filter (${\mathrm{bpf}}_{\mathrm{opt}}$) in [14]. In the calculation process of coefficients $k_i$ and $m_i$, $H_{TL1}$ and $H_{TL2}$ can be replaced by $B_1$ and $B_2$ since the ${\mathrm{bpf}}_{\mathrm{opt}}\left(H_I\right)$ is small.

$$\begin{array}{cc}\hfill & [m_1,m_2,...,m_{16}]={\left(A^{T}A\right)}^{-1}{A}^T{\mathrm{bpf}}_{\mathrm{opt}}\left(B_1\right)\hfill \\ \hfill & [k_1,k_2,...,k_{16}]={\left(A^{T}A\right)}^{-1}{A}^T{\mathrm{bpf}}_{\mathrm{opt}}\left(B_2\right)\hfill \\ & A={\mathrm{bpf}}_{\mathrm{opt}}\left([g_1,g_2,...,g_{16}]\right)\hfill \end{array}$$

(7)

After calculating the coefficients $k_i$ and $m_i$, $\overrightarrow{H_{TL1}}$,$\overrightarrow{H_{TL2}}$ can be calculated in real-time in practical applications according to Formulas (5) and (6).

2.3. Derivation of K in MTLI Correlation Model

During flight, the magnetic interference of OBE measured at $O_2$ is $K{H}_I$, and measured at $O_1$ is $H_I$. The distance between $O_1$ and the OBE is $L_1$. The distance between $O_2$ and the OBE is $L_2$. Assuming that the fluxgate is far enough away from the OBE, it can be regarded as a magnetic dipole. Similarly, since $L_1$ is larger than $L_2$, the OBE can also be regarded as a magnetic dipole at $O_1$. The magnetic field generated by the magnetic dipole can be expressed as

$$\overrightarrow{K{H}_I}={\displaystyle \frac{3\overrightarrow{L_1}\left(\overrightarrow{M}•\overrightarrow{L_1}\right)-{\left|\overrightarrow{L_1}\right|}^2\overrightarrow{M}}{4\pi {\left|\overrightarrow{L_1}\right|}^5}},\overrightarrow{H_I}={\displaystyle \frac{3\overrightarrow{L_2}\left(\overrightarrow{M}•\overrightarrow{L_2}\right)-{\left|\overrightarrow{L_2}\right|}^2\overrightarrow{M}}{4\pi {\left|\overrightarrow{L_2}\right|}^5}}$$

(8)

M is the magnetic moment of the interference source. Therefore, there are:

$$\begin{array}{cc}\hfill K& =\frac{K{H}_I}{H_I}=\frac{4\pi {\left|\overrightarrow{L_2}\right|}^5}{4\pi {\left|\overrightarrow{L_1}\right|}^5}\frac{3\overrightarrow{L_1}\overrightarrow{M}•\overrightarrow{L_1}-{\left|\overrightarrow{L_1}\right|}^2\overrightarrow{M}}{3\overrightarrow{L_2}\overrightarrow{M}•\overrightarrow{L_2}-{\left|\overrightarrow{L_2}\right|}^2\overrightarrow{M}}\hfill \end{array}$$

(9)

Since $L_1$ and $L_2$ are along the tail rod, so $\overrightarrow{L_1}=n\overrightarrow{L_2}$, n is a constant. Substitute $\overrightarrow{L_1}=n\overrightarrow{L_2}$ into Formula (9). The value of K can be calculated by measuring the values of $L_1$ and $L_2$.

$$\begin{array}{ccc}\hfill K& =\frac{{\left|\overrightarrow{L_2}\right|}^5}{n^5{\left|\overrightarrow{L_2}\right|}^5}\frac{n^2\left(3\overrightarrow{L_2}\overrightarrow{M}•\overrightarrow{L_2}-{\left|\overrightarrow{L_2}\right|}^2\overrightarrow{M}\right)}{3\overrightarrow{L_2}\overrightarrow{M}•\overrightarrow{L_2}-{\left|\overrightarrow{L_2}\right|}^2\overrightarrow{M}}\hfill & \hfill =\frac{1}{n^3}=\frac{{\left|\overrightarrow{L_2}\right|}^3}{{\left|\overrightarrow{L_1}\right|}^3}\end{array}$$

(10)

2.4. Estimation and Compensation of OBE’s Magnetic Interference

The estimation method of the geomagnetic field to be measured based on the MTLI correlation model is presented. First, we define the magnetic field after the compensation of the magnetometer and fluxgate as $H_{T1}$ and $H_{T2}$. $H_{TL1}$ and $H_{TL2}$ are computed using the method described in Section 2.2.

$$H_{T1}=B_1-H_{TL1},H_{T2}=B_2-H_{TL2}$$

(11)

Then, we calculate the difference, d, using

$$d=H_{T1}-H_{T2}=(K-1)H_I+w_1-w_2$$

(12)

Notice that d is independent of $H_E$ and is a function of $H_I$ and noises $w_1$ and $w_2$ only. The calculation method of K is given in Section 2.3. Here, given K, we can estimate the interference $H_I$ from Formula (12) using

$$\widehat{H_I}=\frac{d}{K-1}=\frac{H_{T1}-H_{T2}}{K-1}$$

(13)

Finally, $H_E$ can be estimated from Formulas (1) and (13) using

$$\widehat{H_E}=H_{T1}-\widehat{H_I}=\frac{K{H}_{T1}-H_{T2}}{K-1}$$

(14)

The steps for estimating $H_I$ and $H_E$ are shown in Figure 4. The green part is the aeromagnetic calibration process required by most aeromagnetic compensation systems [1], and the $m_i$ coefficients can be solved by the method in [14]. The estimation and compensation process of magnetic interference is only one more constant K than the input of the traditional magnetic anomaly detection system, which can be easily measured.

Therefore, magnetic interference estimation and compensation based on the MTLI correlation model are easy to implement and do not need current sensors to be added to the system. See the next section for the error analysis of the proposed method.

3. The Error Propagation

The above estimator of $\widehat{H_I}$ in Formula (13) is not free from noise, and, in fact, substituting Formula (1) into (13) yields

$$\widehat{H_I}=H_I+\frac{w_2-w_1}{K-1}$$

(15)

For $K\gg 1$, the noise influence is attenuated. Large values of K can be obtained by deploying the fluxgate much closer to the OBE than the magnetometer. Substituting Formula (1) into (14) means we can get the expression for the above estimator’s noise:

$$\widehat{H_E}=H_E+H_I+w_1-\widehat{H_I}$$

(16)

Now substituting Formula (15) into (16) yields:

$$\widehat{H_E}=H_E+\frac{K}{K-1}{w}_1-\frac{1}{K-1}{w}_2$$

(17)

Formula (17) no longer contains the residue of $H_I$ in the estimated signal $\widehat{H_E}$. However, $\widehat{H_E}$ has been recovered at the expense of an additional noise component from fluxgate. Again, larger values of K can reduce noise influence.

Now, let us assume zero mean processes, the powers of the signals and noises are expressed by Formula (18). Here, $E\{·\}$ is the expectation operator.

$$\begin{array}{c}\hfill {\sigma }_E^2=E\left\{H_E^2\right\}=\sum H_E^2,{\sigma }_I^2=E\left\{H_I^2\right\}=\sum H_I^2,\\ \hfill {\sigma }_1^2=E\left\{w_1^2\right\}=\sum w_1^2,{\sigma }_2^2=E\left\{w_2^2\right\}=\sum w_2^2\end{array}$$

(18)

3.1. The Error Propagation of $H_I$

Now we will focus on calculating the error for the interference estimator. Using Formula (15), the error in estimating $H_I$ is expressed by

$$▵H_I=\widehat{H_I}-H_I=\frac{1}{K-1}{w}_2-\frac{1}{K-1}{w}_1$$

(19)

Using the definitions in Formula (18) and the assumptions that the noise and signals are uncorrelated, we obtain the expression for the estimator’s variance:

$$E\left\{{[▵H_I]}^2\right\}={\left(\frac{1}{K-1}\right)}^2({\sigma }_1^2+{\sigma }_2^2)$$

(20)

We use the ratio of the estimated interference power and the actual interference power to describe the deviation of the estimate.

$$e_I=\frac{E\left\{{[▵H_I]}^2\right\}}{E\left\{H_I^2\right\}}=\frac{1}{{\sigma }_I^2}\sum {\widehat{H_I}}^2={\left(\frac{1}{K-1}\right)}^2\frac{({\sigma }_1^2+{\sigma }_2^2)}{\left({\sigma }_I^2\right)}$$

(21)

Here, we define the interference-to-noise ratio $\left(INR\right)$ and the noise-to-noise ratio $\left(NNR\right)$ by

$$INR=\frac{{\sigma }_I^2}{{\sigma }_1^2},NNR=\frac{{\sigma }_2^2}{{\sigma }_1^2}$$

(22)

The relative error in estimating $H_I$ can be expressed as

$$e_I=\frac{1+NNR}{{(K-1)}^{2}INR}$$

(23)

3.2. The Error Propagation of $H_E$

Then error analysis is performed on $H_E$. The error in estimating the signal in Formula (14) is expressed using Formula (17):

$$▵H_E=\widehat{H_E}-H_E=\frac{K}{K-1}{w}_1-\frac{1}{K-1}{w}_2$$

(24)

Now, calculate the variance of the estimator using

$$E\left\{{[▵H_E]}^2\right\}={\left(\frac{K}{K-1}\right)}^2{\sigma }_1^2+{\left(\frac{1}{K-1}\right)}^2{\sigma }_2^2$$

(25)

From Formula (25), the error in estimating $H_E$ is a function connection with not only the noise at the magnetometer, ${\sigma }_1^2$, but also the noise at the fluxgate, ${\sigma }_2^2$. Though the influence of ${\sigma }_2^2$ is $K^2$ times weaker than ${\sigma }_1^2$, the interference has been canceled at the expense of additional noise from the fluxgate.

The same as $e_I$, we calculate $e_E$ as follows:

$$e_E=\frac{E\left\{{[▵H_E]}^2\right\}}{E\left\{H_E^2\right\}}=\frac{K^2}{{(K-1)}^2}\frac{{\sigma }_1^2}{{\sigma }_E^2}+\frac{1}{{(K-1)}^2}\frac{{\sigma }_2^2}{{\sigma }_E^2}$$

(26)

Formula (22) is used for substitution Formula (26), and defining the signal-to-noise ratio $SNR=\frac{{\sigma }_E^2}{{\sigma }_1^2}$:

$$e_E=\frac{K^2}{{(K-1)}^2}\frac{1}{SNR}+\frac{NNR}{{(K-1)}^{2}SNR}=\frac{K^2+NNR}{{(K-1)}^{2}SNR}$$

(27)

In the derivation of $e_I$ and $e_E$, $e_I$ is related to the values of $K,NNR$ and $INR$, $e_E$ also is related to the values of $K,NNR$, and what is more, $e_E$ is related to $SNR$. Both $e_I$ and $e_E$ are decreased indefinitely with K, but $e_E$ is ultimately bounded by $1/SNR$. From Formula (27), the error $e_E$ is not influenced by the $INR$ value; this conclusion can be applied to an aeromagnetic compensation process.

In the aeromagnetic compensation process, in order to obtain a more accurate $\widehat{H_E}$, a high-precision magnetometer is used. Therefore, ${\sigma }_1^2$ is usually very small, and the $SNR$ value will be relatively large. In this case, we only need to select a high-precision fluxgate to get a smaller $NNR$, and we need to appropriately place the fluxgate closer to the interference source to get a bigger K. Then, we can get a smaller $e_E$. Since $e_E$ is independent of $INR$, even if the $INR$ is small, that is, it is difficult to distinguish the OBE’s interference from the magnetic field to be measured in the magnetometer’s output, the OBE’s interference can be well compensated. The application of this conclusion perfectly avoids the extra monitoring of OBE’s interference and compensates dynamic noise with the lowest cost only by modifying the calculation process.

4. Numerical Analysis

In order to test the proposed method, we have developed a computer simulation implementing the model in Formula (1) and the estimators in Formulas (13) and (14). We use synthesized signals, interference, and noise for the testing, where the signal $H_E$ and the interference $H_I$ are generated using monochromatic sinusoidal signals with frequencies of 0.1 and 0.12 Hz, respectively. Frequency signals with very similar frequencies are also used to increase the authenticity of the simulation process. The noise is produced by a random number generator seed using a Gaussian distribution.

We have chosen here to use a window of N = 60,000 samples, which is about 100 min for a sampling rate of 10 samples/s. From a practical point of view, using a long window does not pose a problem since the processing may be performed offline. The longer window is used here to facilitate statistical analysis of the performance of this method. In practical application, this method can also be calculated quickly, point by point. During the simulation, we set ${\sigma }_E=30$ and ${\sigma }_I=35$ to simulate the real application of magnetic interference that is difficult to peel off the situation.

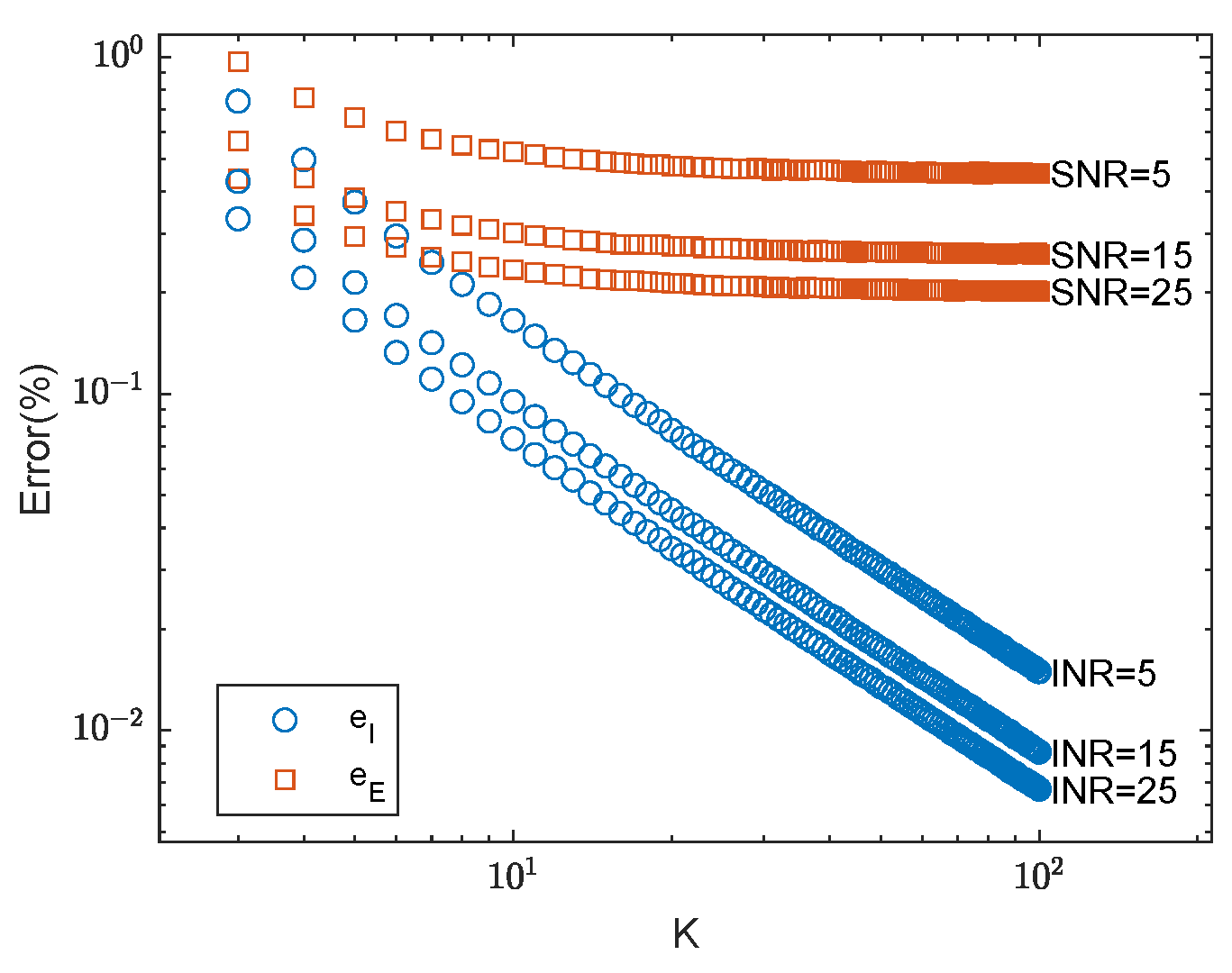
Figure 5 depicts the errors as a function of K, and, as expected, the errors decrease as a function of K. Here, we set $NNR=10$ to mimic the common fluxgate noise and magnetometer noise. The influence of K, $INR$, and $SNR$ on the estimation error was analyzed. Figure 5 clearly shows that large values of K enable a better estimation of the interference, which is important for estimating the signal $H_E$. Thus, in the case of a known source of interference (such as the steering gear and radio of an aircraft), it is better to place the fluxgate as close as possible to the source of the interference and the magnetometer as far away as possible, provided that the magnetic interference can be regarded as a magnetic dipole. 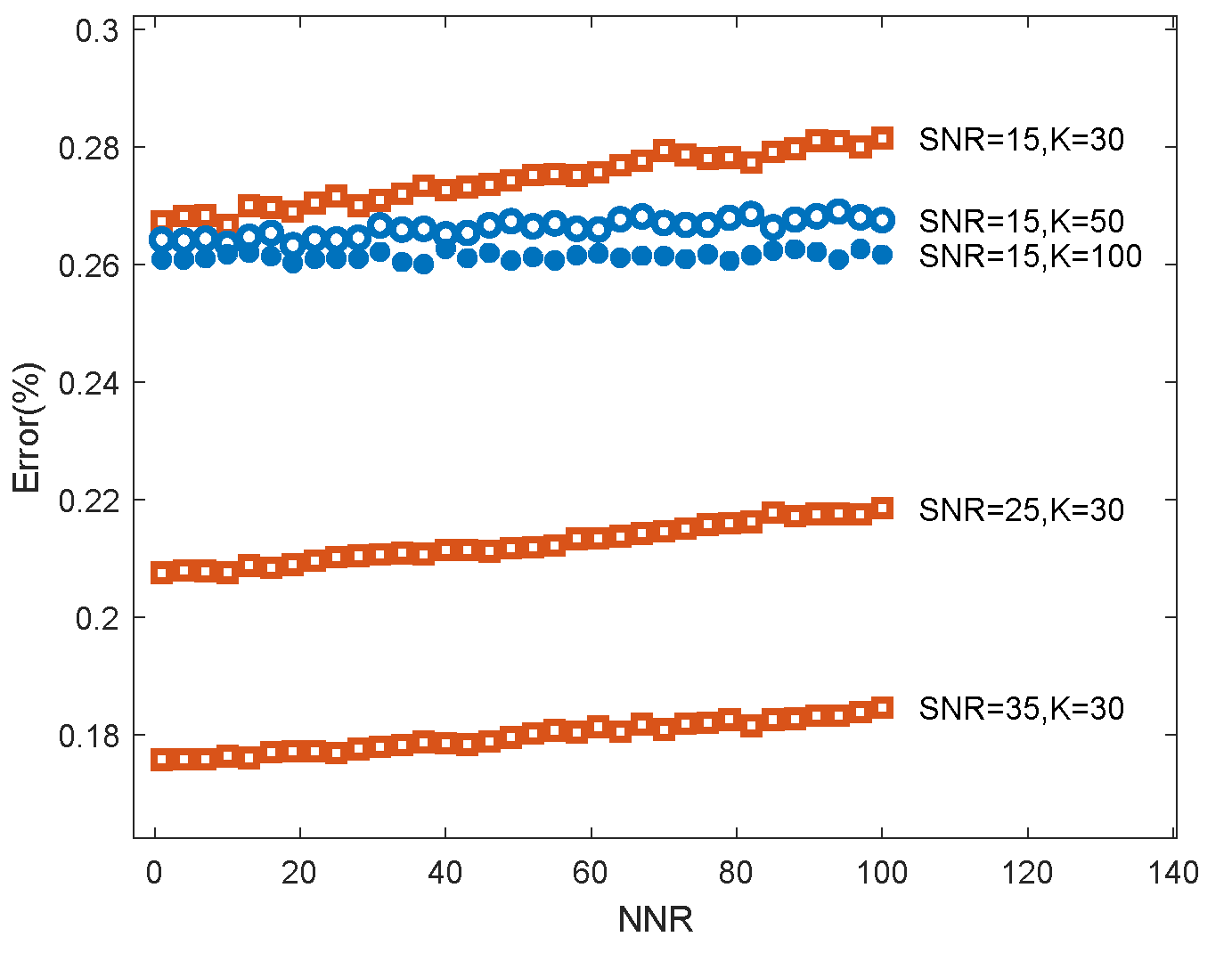Again, we see in Figure 6 that the larger K, the smaller the estimation error $e_E$; here we set $INR=25$. Figure 6 also shows that when the magnetic field to be measured changes more dramatically; that is, when the $SNR$ is larger, the estimation of this method will be more accurate.

5. Experiment

5.1. Experiment Design and Sensors

Real flight experiments are carried out in Gansu Province, China, where the geomagnetic background field is magnetically quiet. The experiment was carried out at the end of April 2020 with the purpose of evaluating the performance of the proposed method. The site was prepared by marking off a 20 × 20 km area. The UAV used for this study was a fixed-wing aircraft fitted with a Differential Real-Time Kinematic (D-RTK) system. The RTK approach was used to measure fluctuations in the computed positioning estimates, obtained through the use of Global Navigational Satellite Systems (GNSS), and relaying these to the UAV in real-time to compensate accordingly. Mission planning and autonomous flight control was handled through Universal ground Control Software (UgCS). A GSM19M magnetometer bases tation from Gemsystems was placed near the take-off location of the survey area and used for sampling the geomagnetic diurnal variation.

The UAV has a wingspan of 18 m, and a magnetometer is mounted at the end of the wing. The optically pumped magnetometer with ⁴He atoms is used for measuring the scalar magnetic field, which is well suited for measuring the geomagnetic field, and its principle can be seen in [16]. Select sensor specifications of the magnetometer and fluxgate are provided in

Table 1. Specifications of the magnetometer and fluxgate.

	Parameter	Value	Notes
Magnetometer	Sensitivity	0.0006 nT/$\sqrt{(}Hz)$
	Dynamic	15,000∼105,000 nT	The scalar magnetic field
	Deadzone	-
	Heading error	<1 nT	When uncompensated
	Atomic family	4He [16]
Fluxgate	Sensitivity	1 nT
	Dynamic	−100∼100 µT	The vector magnetic field
	Deadzone	-

. The OBE-producing magnetic interference is installed in the fuselage, so $L_1=9$. A fluxgate is installed 2.7 m away from the fuselage, which means $L_2=2.7$, $K=37$. All data are synchronized by the pulse per second signal with a sampling frequency of 10 Hz.

The experiments were carried out according to aeromagnetic compensation standards; we let the platform perform roll, pitch, and yaw maneuvers in the four directions of east, south, west, and north in a fixed period of about 8–12 s. The flying altitude was more than 3000 m, which was high enough to avoid the magnetic interference caused by the local geology. Flight tracks are shown in Figure 7a, in which the maneuvering flight and smooth flight tracks are basically the same.

5.2. Data Processing

Standard processing steps were applied to the magnetic dataset: (i) Timestamping and positioning; (ii) Despiking of erroneous GNSS; (iii) Removal of diurnal variation as monitored by a base station. Figure 7b,c show the original magnetic field and the compensated magnetic field measured in the maneuvering flight and smooth flight. The aeromagnetic data are well compensated by the method proposed in this paper.

5.3. Experiment Results on Fluxgate

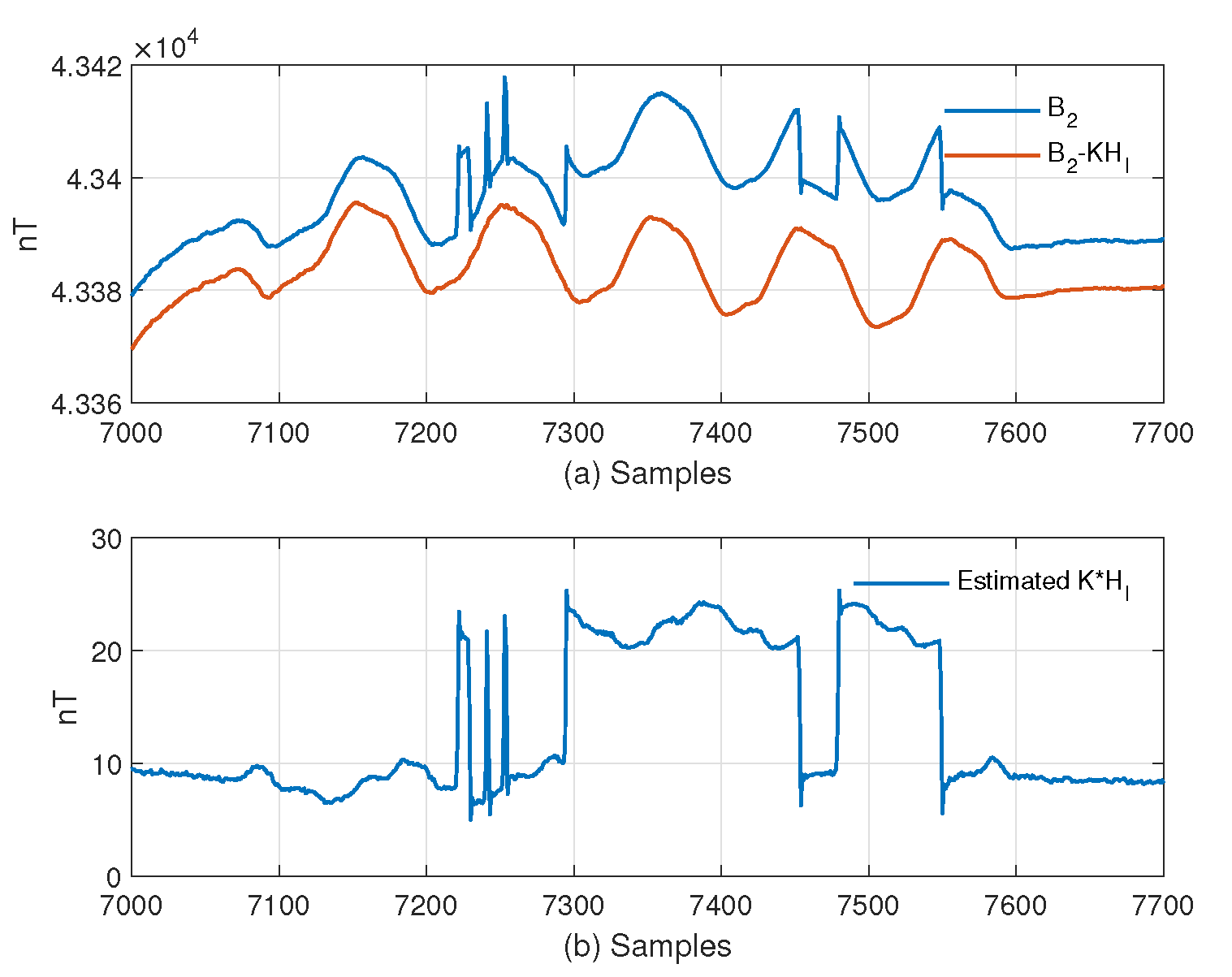
Since the OBE is closer to the fluxgate ($L_2<L_1$), the effect of compensation for the OBE’s interference can be observed more intuitively and significantly on the fluxgate. We show the results of the fluxgate’s magnetic field value $B_2$ before and after compensation during a period of roll maneuvering.

The blue line in Figure 8a is the magnetic field synthesized by the fluxgate. It can be seen that since the fluxgate is close to the aircraft, the dynamic magnetic interference caused by the switch of electrical equipment can be obviously observed in a “gate” shape with a size of about 15–20 nT, and its occurrence time is irregular. Figure 8b shows the OBE’s magnetic interference at the fluxgate position estimated from Formula (13). When the OBE’s magnetic interference is removed from $B_2$, the result is the red line in Figure 8a. The fluxgate output is obviously smooth after removing the OBE’s magnetic interference, and the magnetic interference caused by maneuvering action is retained.

5.4. Experiment Results on Magnetometer

The ultimate goal of removing the OBE’s magnetic interference is to make the magnetometer’s output cleaner. Therefore, this section shows the compensation effect of the magnetometer output.

We compared this method with those in [10,14]. It should be noted that the formula used to calculate k in [10] is based on the input of similar precision sensors, while the accuracy of $B_1$ in the widely used aeromagnetic compensation system involved in this paper is much higher than that of $B_2$. Therefore, the calculation of its k in [10] is calculated by Formula (10) in this paper, and the method is cited as Mu,Y. 2020-M. In addition to directly observing the signal, the standard deviation($\sigma$) in reference [7] is used to evaluate the system noise. The smaller the $\sigma$ is, the smaller the dynamic noise of the system is.

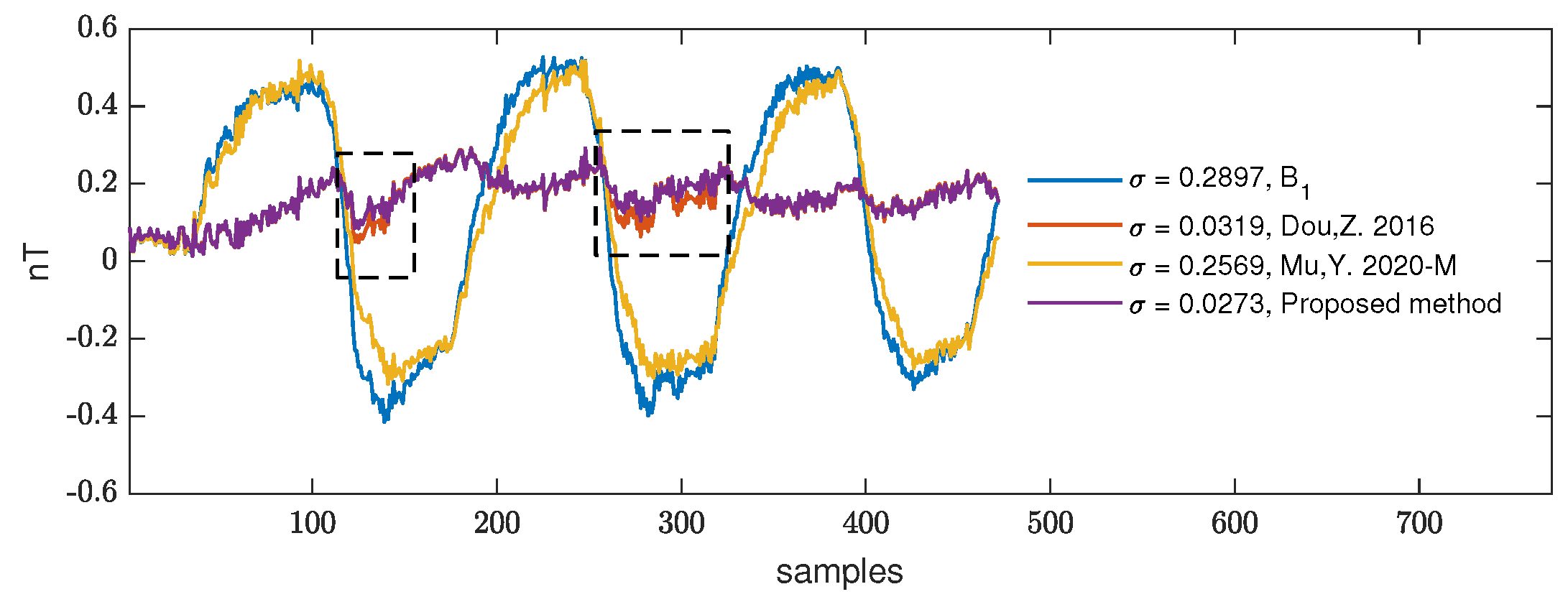
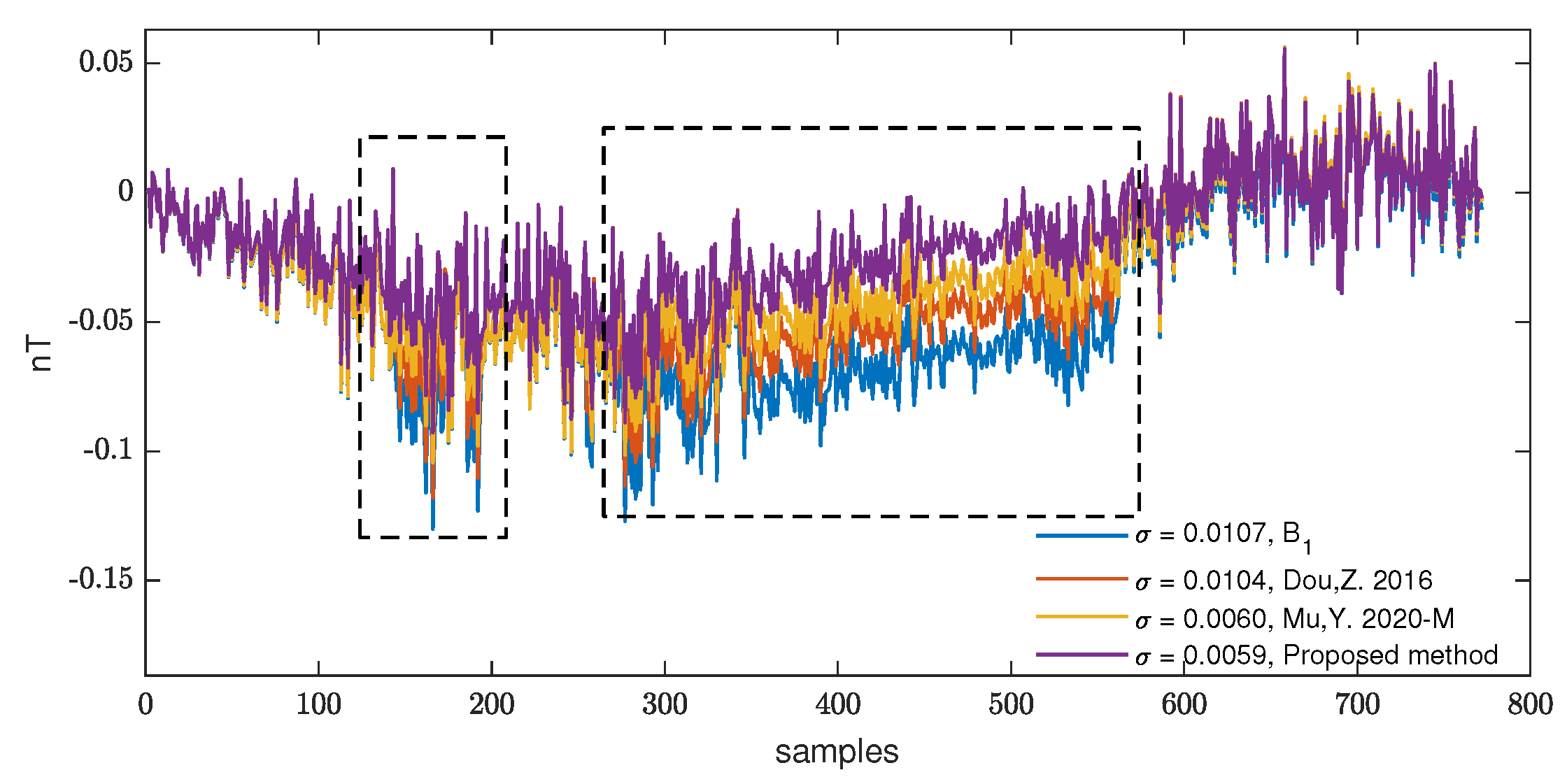
First, we compare the performance of the three methods in the maneuvering process. In Figure 9, the blue line represents the original signal, which is $\sigma =0.2897$, the red line is the calibration and compensation method mentioned in reference [14], and the yellow line represents the compensation result of Mu,Y. 2020-M. The purple line is the result of the method in this paper. The dotted-box part is the obvious repair process of this kind of magnetic interference. The method Mu,Y. 2020-M cannot provide good results in maneuvering because it does not consider the interference of the body itself in its system. However, the results are close to the method proposed in this paper in smooth flight. The method in this paper can accurately compensate for the OBE’s magnetic interference in addition to the magnetic interference caused by maneuvering. The purple line in Figure 9 and Figure 10 are part of the data in Figure 7, which have been aligned and detrended to facilitate the observation of the compensation effect of magnetic interference.

The results combined with the standard deviation $\sigma$ of the three methods in smooth flight data are shown in Figure 10. The method proposed in this paper can accurately compensate the OBE’s magnetic interference in the maneuver and also performs well in the smooth flight.

The above results show the effect of the local data when the OBE’s magnetic interference occurs. Since the occurrence is random, in order to evaluate the performance of the proposed method in the long-duration flight data, we used the same evaluation method to evaluate the flight data in different directions. The flight duration in each direction is not less than 5 min.

Table 2. The comparison of standard deviations $\sigma$ (the lower, the better) by the three methods.

	Maneuvering Flight				Smooth Flight
Direction	East	South	West	North	East	South	West	North
Raw	0.1480	0.0841	0.2492	0.2532	0.0119	0.0090	0.0166	0.0157
Dou,Z. 2016 [14]	0.0300	0.0217	0.0269	0.0263	0.0117	0.0086	0.0123	0.0085
Mu,Y. 2020-M [10]	0.1439	0.1115	0.2247	0.2287	0.0100	0.0069	0.0145	0.0146
Proposed Method	0.0296	0.0185	0.0250	0.0241	0.0100	0.0066	0.0091	0.0062

shows the effect of the proposed method on maneuvering flight and smooth flight. The values in the table are the standard deviations $\sigma$ of data in a certain direction, where the lower, the better. Columns 1–4 represent the maneuvering flight of the aircraft in different directions. Columns 5–8 represent the smooth flight of the aircraft in different directions. The proposed method can perform well under different flight conditions. The $\sigma$ of maneuver data in different directions is obviously larger than that of smooth flight data. This is because maneuvering involves rolling, pitching, and yawing. In Method Mu,Y. 2020-M, the $\sigma$ after compensation is close to or even greater than the raw data because the magnetic influence brought by aircraft maneuvers is not considered.

More importantly, this method does not introduce other noises in the process of OBE’s interference without switch, can accurately compensate for all noises caused by this type, and does not need an additional recognition algorithm to avoid the robustness problem caused by recognition accuracy.

6. Conclusions

In this work, the multi-source two-channel linear time-invariant (MTLI) correlation model is presented, which takes into account both the OBE’s magnetic interference and body interference described by the TL model. The most important feature of the MTLI model is that it can compensate for both types of magnetic interference without introducing current sensors. For different types of flight (maneuvering flight and smooth flight), the results are better than those considering only one of the magnetic interferences. The calibration and compensation method based on the MTLI model is also very convenient for engineering implementation; we only need to introduce the distance from the OBE to the fluxgate and magnetometer. The rationality of this method is given by error analysis and simulation. The actual flight experiment is conductedm and the results show that the two kinds of magnetic interference fields are suppressed significantly with a root mean square error of 0.0062 and 0.0296 nT in smooth and maneuvering flights.