Inverse Synthetic Aperture LiDAR Imaging of Rough Targets under Small Rotation Angles
Abstract
:1. Introduction
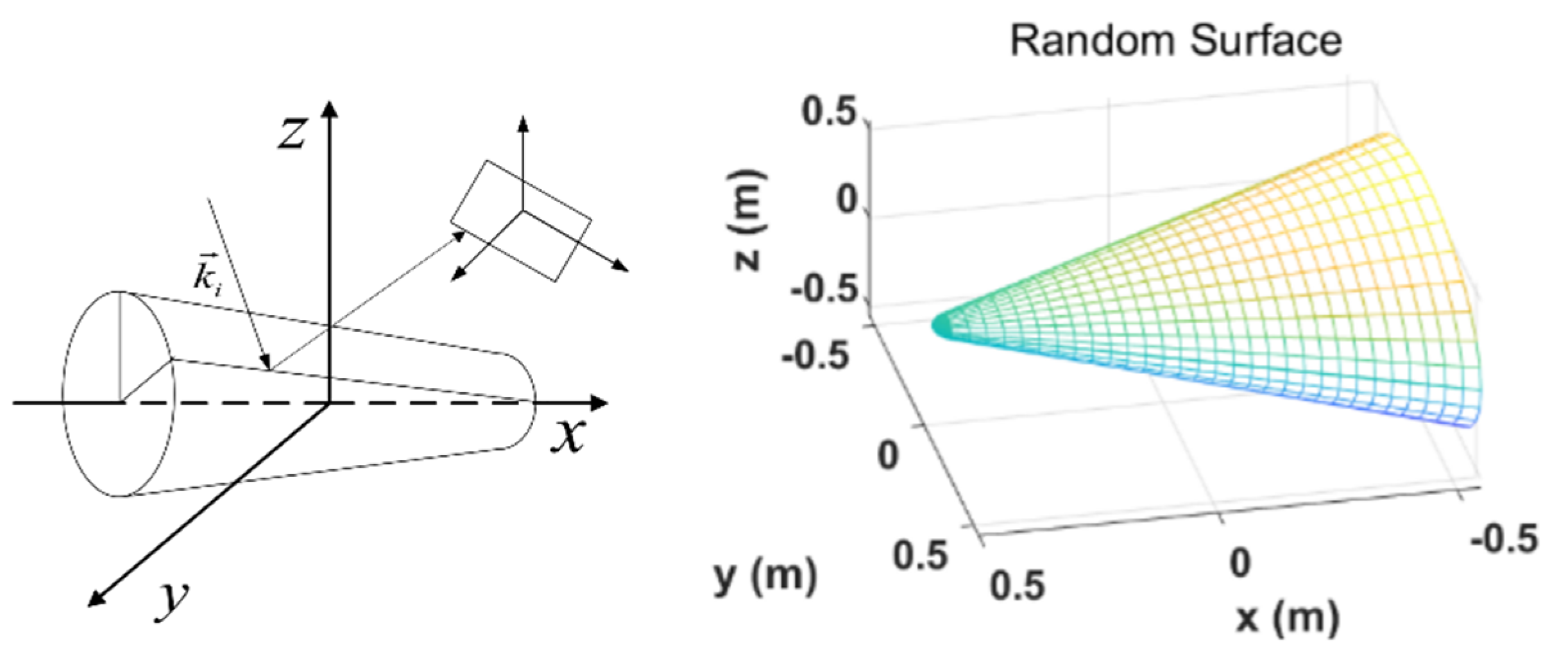
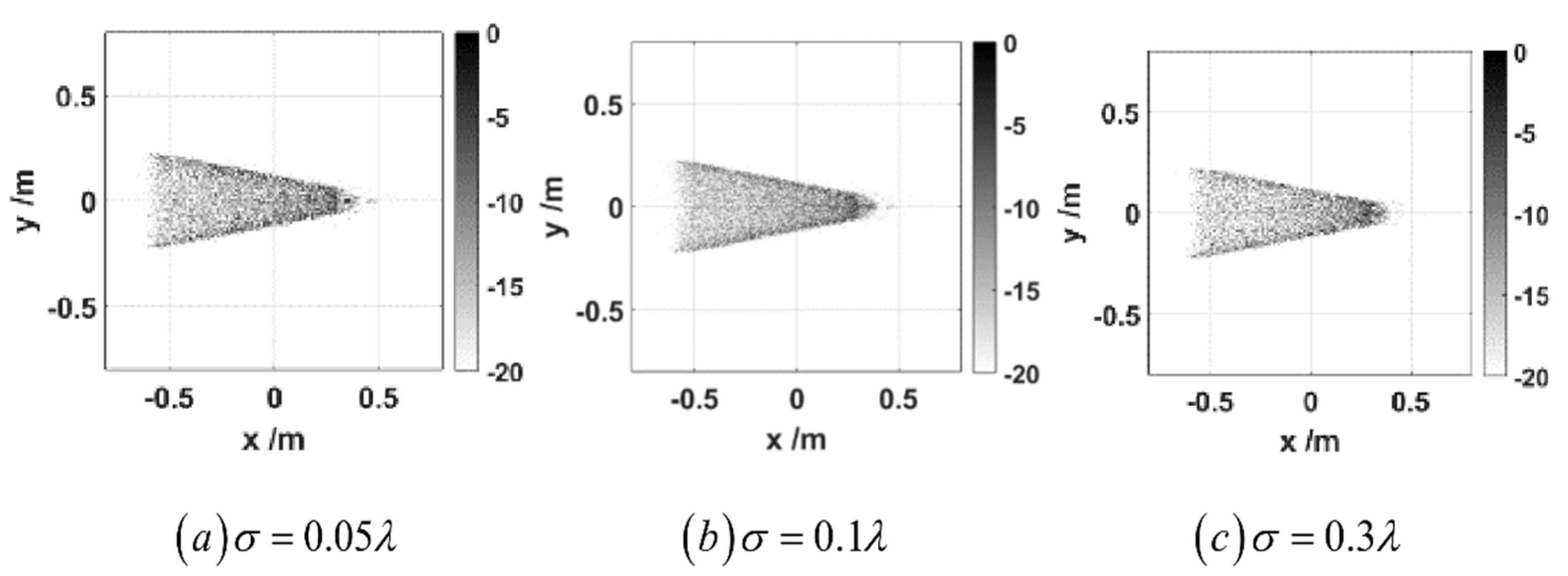
2. Geometric Modeling and Theoretical Formula Derivation
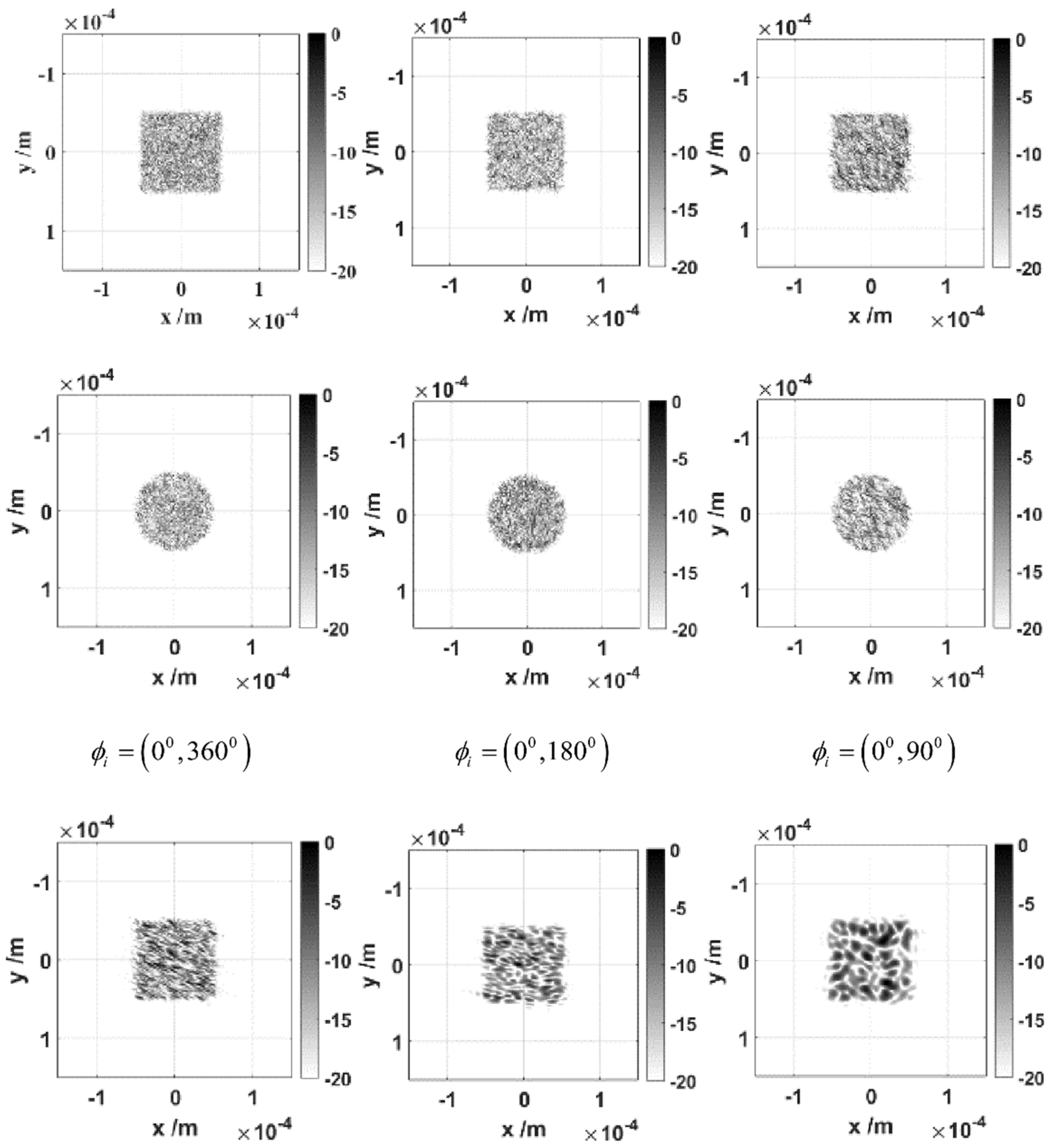
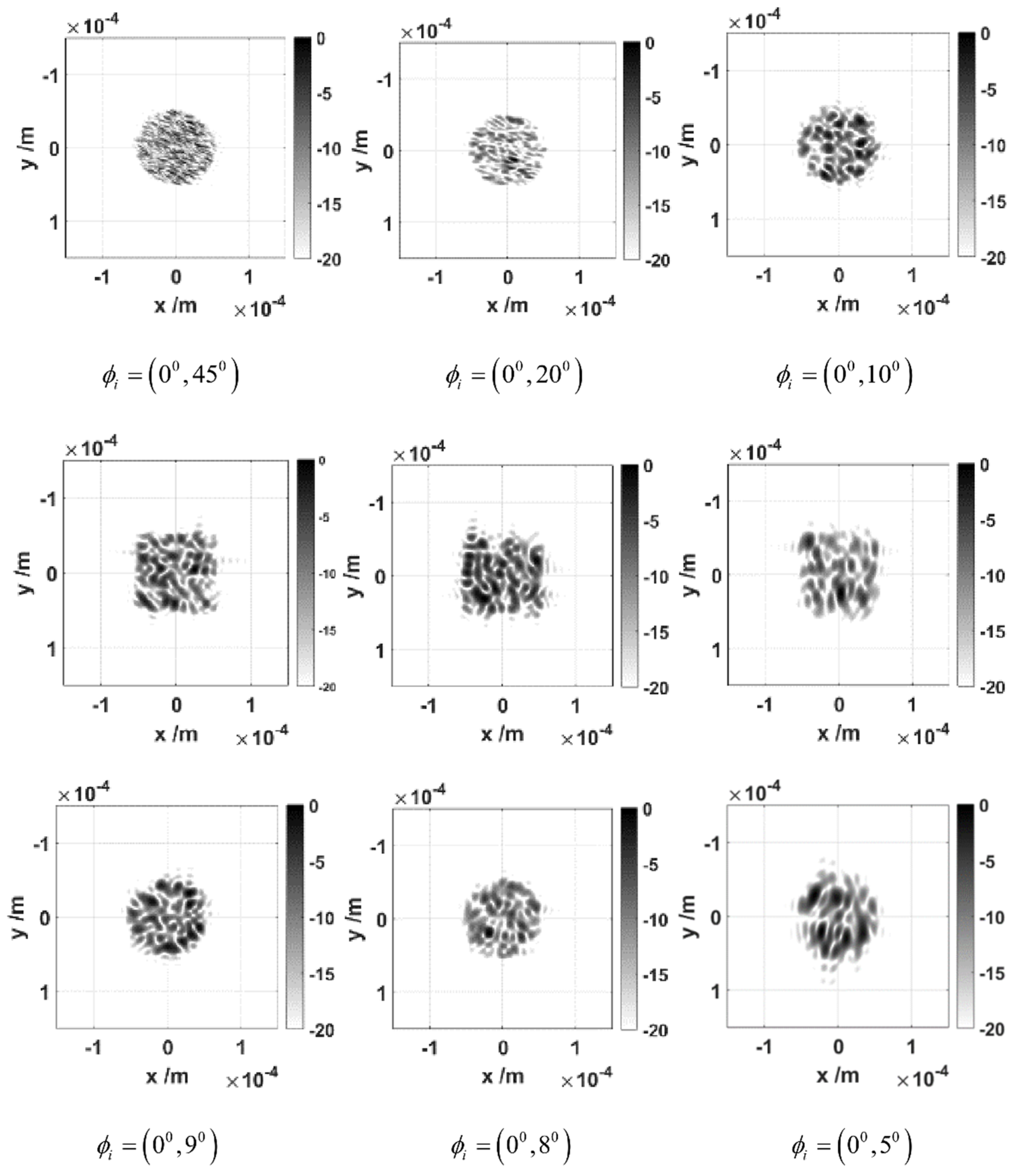
3. Rotation Angle Imaging of Rough Plane and Targets
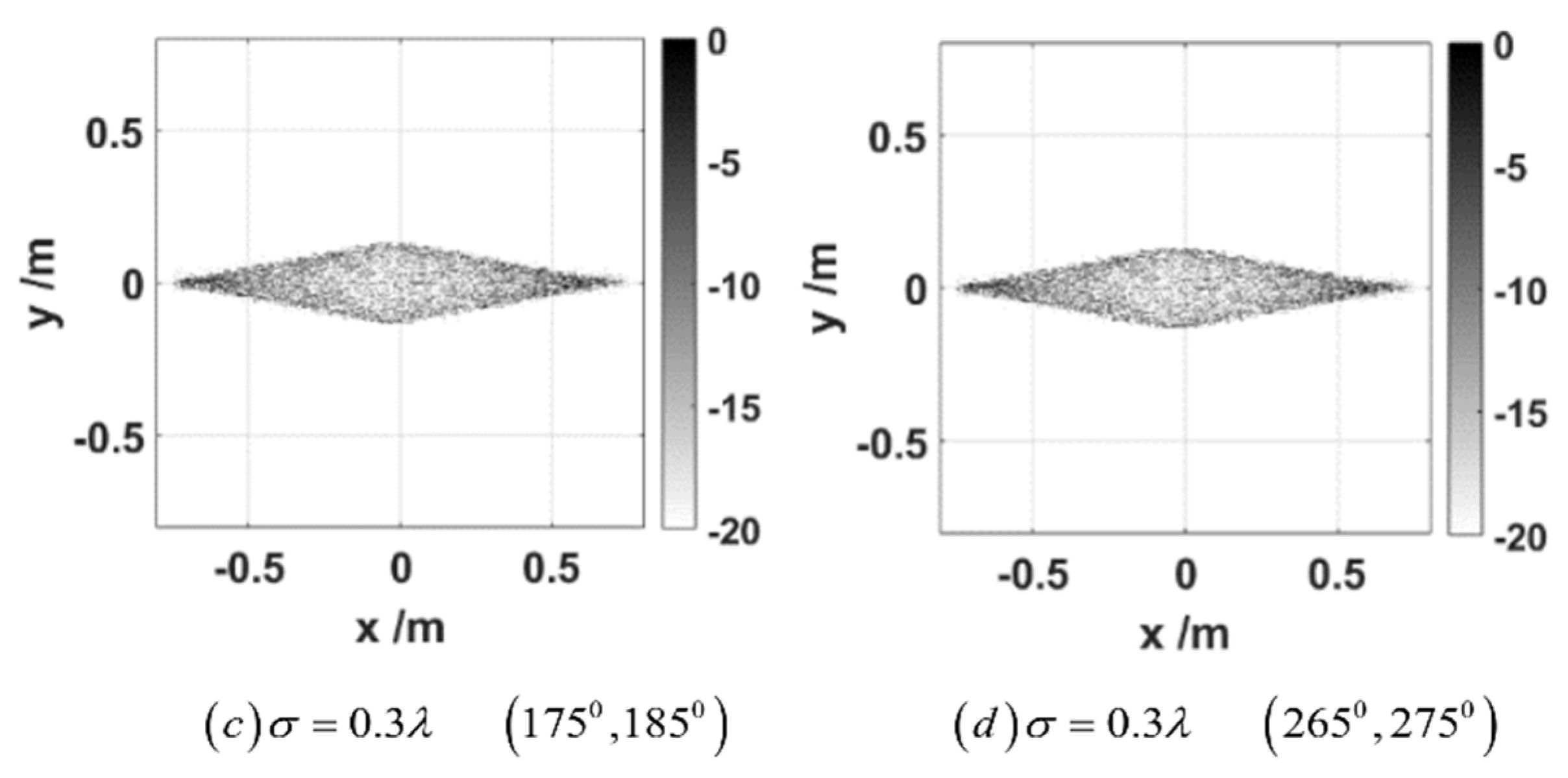
4. ISAL Image of Blunt-Nosed Cones and Double Cones under a Small Rotation Angle
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hang, R.U.A.N.; Wu, Y.H.; Xin, J.I.A.; Wei, Y.E. Inverse synthetic aperture lidar imaging algorithm for spin targets. Acta Photonica Sin. 2013, 42, 1238–1243. [Google Scholar] [CrossRef]
- Han, Z.; Wang, C.; Zheng, W. Research progress of synthetic aperture lidar imaging error compensation. Fly. Missile 2019, 5, 84–89. [Google Scholar]
- Wang, Q.; Pepin, M.; Wright, A.; Dunkel, R.; Atwood, T.; Santhanam, B.; Gerstle, W.; Doerry, A.W.; Hayat, M.M. Reduction of vibration-induced artifacts in synthetic aperture radar imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3063–3073. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Pepin, M.; Beach, R.J.; Dunkel, R.; Atwood, T.; Santhanam, B.; Gerstle, W.; Doerry, A.W.; Hayat, M.M. SAR-Based Vibration Estimation Using the Discrete Fractional Fourier Transform. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4145–4156. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Sun, J.; Lei, P.; Hong, W. SAR-based paired echo focusing and suppression of vibrating targets. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7593–7605. [Google Scholar] [CrossRef]
- Wu, J. Research on synthetic aperture lidar imaging. J. Radars 2012, 1, 353–360. [Google Scholar] [CrossRef]
- Liang, G.; Mengdao, X.; Xiaodong, Z.; Yu, T. Inverse synthetic aperture lidar imaging of indoor measured data. Infrared Laser Eng. 2011, 40, 637–642. [Google Scholar]
- Liu, L.; Zhou, Y.; Zhi, Y.; Sun, J.; Wu, Y.; Luan, Z.; Yan, A.; Wang, L.; Dai, E.; Lu, W. Large-aperture synthetic aperture laser imaging radar demonstration prototype and its laboratory verification. Acta Opt. 2011, 31, 1–5. [Google Scholar]
- Wlqn, R. Maximum entropy regularization in inverse synthetic aperture radar imagery. IEEE Trans. Signal. Process. 1992, 40, 969–973. [Google Scholar]
- Ozdemir, C. Inverse Synthetic Aperture Radar Imaging with MATLAB Algorithms; Wiley: New York, NY, USA, 2012. [Google Scholar]
- Victor, C.; Chen, M.M. Inverse Synthetic Aperture Radar Imaging: Principle, Algorithm, and Applications; SciTech USA: Reston, VA, USA, 2014. [Google Scholar]
- Wang, Y.; Wang, Z.; Zhao, B.; Xu, L. Compensation for High-Frequency Vibration of Platform in SAR Imaging Based on Adaptive Chirplet Decomposition. IEEE Geosci. Remote Sens. Lett. 2016, 13, 792–795. [Google Scholar] [CrossRef]
- Ya-Kun, L.; Wu, Y.H.; Xue, J.S.; Wang, H.Y. Inverse synthetic aperture lidar imaging algorithm for maneuvering targets. Acta Photonica Sin. 2018, 47, 68–78. [Google Scholar]
- Shengjie, L.; Hanchu, F.; Kai, W.; Yudong, Z. Inverse synthetic aperture lidar joint compensation imaging algorithm based on Nelder-Mead simplex method. Acta Opt. 2018, 38, 0711002. [Google Scholar] [CrossRef]
- Kang, M.S.; Kim, K.T. Compressive Sensing based SAR Imaging and Autofocus using Improved Tikhonov Regularization. IEEE Sens. J. 2019, 19, 5529–5540. [Google Scholar] [CrossRef]
- Chen, H.; Hu, H.; Xu, W. High-sensitivity receiving technology of space-based inverse synthetic aperture lidar. Shanghai Aerosp. 2019, 36, 6. [Google Scholar]
- Zeng, C.; Han, Y.; Liu, B.; Sun, P.; Li, X.; Chen, P. Sparse imaging of airborne inverse synthetic aperture lidar micro-moving targets. Opt. Lasers Eng. 2021, 140, 106547. [Google Scholar] [CrossRef]
- Jian, L.; Kunpeng, W.; Kai, J.; Chen, X.; Hanchu, F.; Kai, W. Inverse synthetic aperture lidar motion-compensated imaging algorithm for maneuvering targets. J. Opt. 2021, 41, 10. [Google Scholar]
- Yang, S.Y.; Chi, L.; He, J. An inverse synthetic aperture lidar imaging algorithm. Laser Infrared 2010, 40, 904–909. [Google Scholar] [CrossRef]
- Yin, H.; Guo, L.; Li, Y.; Han, L.; Xing, M.; Zeng, X. Varying Amplitude Vibration Phase Suppression Algorithm in ISAL Imaging. Remote Sens. 2022, 14, 1122. [Google Scholar] [CrossRef]
- Urabi. Microwave Remote Sensing; Science Press: Beijing, China, 1988. [Google Scholar]
- Xue, J.; Cao, Y.; Wu, Z.; Li, Y.; Zhang, G.; Yang, K.; Gao, R. Simulating the Scattering Echo and Inverse Synthetic Aperture Lidar Imaging of Rough Targets. Ann. Der Phys. 2022, 534, 2100491. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Book-Review—Microwave Remote Sensing—Active and Passive. Space Sci. Rev. 1983, 35, 295. [Google Scholar]
- Tsang, L.; Kong, J.A.; Ding, K.H. Scattering of Electromagnetic Waves: Theories and Applications||Fundamentals of Random Scattering; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- RefractiveIndex.INFO Website: © 2008–2020 Mikhail Polyanskiy. (Refractive Index Database) Website: 20082020 Mikhail Polyanskiy. Available online: https://refractiveindex.info (accessed on 9 July 2021).



| Rotation Angle Range (0) | |||||||
|---|---|---|---|---|---|---|---|
| Classification of Rough Target Computation Time (s) | |||||||
| Calculation time for rough square plate (s) | 82.891 | 40.128 | 21.214 | 10.169 | 4.180 | 1.896 | |
| Calculation time for rough circular plate (s) | 83.038 | 41.502 | 20.897 | 10.582 | 4.305 | 1.954 | |
| Calculation time for rough cone (s) | 1254.488 | 604.422 | 299.206 | 144.274 | 60.251 | 29.762 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, J.; Cao, Y.; Qu, T.; Wu, Z.; Li, Y.; Zhang, G.; Yang, K. Inverse Synthetic Aperture LiDAR Imaging of Rough Targets under Small Rotation Angles. Remote Sens. 2022, 14, 2694. https://doi.org/10.3390/rs14112694
Xue J, Cao Y, Qu T, Wu Z, Li Y, Zhang G, Yang K. Inverse Synthetic Aperture LiDAR Imaging of Rough Targets under Small Rotation Angles. Remote Sensing. 2022; 14(11):2694. https://doi.org/10.3390/rs14112694
Chicago/Turabian StyleXue, Jiyu, Yunhua Cao, Tan Qu, Zhensen Wu, Yanhui Li, Geng Zhang, and Kai Yang. 2022. "Inverse Synthetic Aperture LiDAR Imaging of Rough Targets under Small Rotation Angles" Remote Sensing 14, no. 11: 2694. https://doi.org/10.3390/rs14112694
APA StyleXue, J., Cao, Y., Qu, T., Wu, Z., Li, Y., Zhang, G., & Yang, K. (2022). Inverse Synthetic Aperture LiDAR Imaging of Rough Targets under Small Rotation Angles. Remote Sensing, 14(11), 2694. https://doi.org/10.3390/rs14112694








