Abstract
Ocean observation is essential for studying ocean dynamics, climate change, and carbon cycles. Due to the difficulty and high cost of in situ observations, existing ocean observations are inadequate, and satellite observations are mostly surface observations. Previous work has not adequately considered the spatio-temporal correlation within the ocean itself. This paper proposes a new method—convolutional long short-term memory network (ConvLSTM)—for the inversion of the ocean subsurface temperature and salinity fields with the sea surface satellite observations (sea surface temperature, sea surface salinity, sea surface height, and sea surface wind) and subsurface Argo reanalyze data. Given the time dependence and spatial correlation of the ocean dynamic parameters, the ConvLSTM model can improve inversion models’ robustness and generalizability by considering ocean variability’s significant spatial and temporal correlation characteristics. Taking the 2018 results as an example, our average inversion results in an overall normalized root mean square error (NRMSE) of 0.0568 °C/0.0027 PSS and a correlation coefficient (R) of 0.9819/0.9997 for subsurface temperature (ST)/subsurface salinity (SS). The results show that SSTA, SSSA SSHA, and SSWA together are valuable parameters for obtaining accurate ST/SS estimates, and the use of multiple channels in shallow seas is effective. This study demonstrates that ConvLSTM is superior in modeling the subsurface temperature and salinity fields, fully taking global ocean data’s spatial and temporal correlation into account, and outperforms the classic random forest and LSTM approaches in predicting subsurface temperature and salinity fields.
1. Introduction
The ocean performs a decisive role in regulating and stabilizing the climate system through material transport and energy exchange. The assessment and monitoring of the marine environment have received increasing attention due to ongoing natural variability and the effects of human activities on ecosystems. As a result of global warming, most of the additional heat in the Earth’s climate system has entered the oceans in recent decade [1], resulting in a significant boost in ocean temperatures [2,3]. From 1993 to 2008, the global upper ocean warmed substantially [4]. The heating of the ocean interior has become an essential factor in slowing global warming [5,6,7,8].
On the other hand, ocean salinity is momentous for ocean warming research. Previous studies have proposed a salinity mechanism to explain how the seawater warming signal propagates from the upper to the middle ocean, which illustrates the significance of the distribution of salinity in the evolution of ocean warming [6]. In addition, ocean salinity is also involved in regulating the global water cycle [9]. Temperature and salinity are associated with thermal salt expansion, contributing significantly to rising sea levels [10]. Therefore, inversion and prediction of subsurface temperature and salinity fields are essential to enhancing the understanding of subsurface ocean variability [11].
With the progress of satellite remote sensing technology, it is possible to construct large-area and high-frequency ocean observation datasets. The current state of distribution of ocean elements can be quickly captured through satellite observations’ timely return. However, due to the attenuation of electromagnetic waves in seawater, observational information targeting the ocean interior has become less available. Due to the lack of in situ data, the study of mechanisms and processes within the ocean is minimal, leading to uncertainties in the analysis and estimation of ocean warming [6,12,13]. Although projects such as the Argo have effectively improved deep-sea observations [14], the available data still do not meet the need for scientific research on the ocean interior. Researchers urgently need more information on the ocean interior to understand its internal characteristics and global changes.
Deep-sea remote sensing, combined with buoys’ observation data, has excellent potential for inversion of ocean interior information from satellite observations [15,16]. The methods are mainly classified into dynamic, statistical, or both. Traditional dynamic methods mainly include kinetic-based numerical simulations and physical models. However, these methods are highly complex and only work effectively in specific regions and conditions while requiring vast computational resources, with all models run on supercomputers [17,18,19,20,21,22]. In contrast, statistical methods are relatively more practical and flexible and can be implemented in more general situations in the era of big marine data [23,24,25,26]. Data-driven statistical methods have demonstrated good accuracy and timely speed in relevant applications, including incredibly advanced models based on machine learning. Empirical statistical models are well established, including linear regression models [17,27,28,29,30], methods based on empirical orthogonal functions [31,32], geographically weighted regression models [16] and nonlinear machine learning models such as artificial neural networks [33,34], self-organizing mappings [35,36,37], support vector machines, random forest [38], clustering neural networks [11], and XGBoost [39]. Although classical machine learning algorithms have contributed significantly to the study of deep-sea remote sensing, they cannot consider ocean data’s spatio-temporal characteristics.
Compared to the above-mentioned methods, deep learning networks have deeper hidden layers and larger architectures, which can capture more complex features [40,41,42]. It has now made world-renowned achievements in computer vision, natural language processing, and various applications in marine and atmospheric sciences [43,44,45,46,47,48,49].
Ocean data have typical spatial nonlinearity and time dependence [36,50,51]. As a specific deep learning algorithm, the LSTM [52] algorithm can effectively take into account the temporal dependence of ocean data, but it has not yet been able to learn effectively at the spatial scale.
The convolutional long short-term memory network (ConvLSTM) algorithm proposed by [53] further takes into account the spatial information in the time series and can combine the temporal and spatial characteristics of the data. The authors of [44] applied this method to atmospheric wind field forecasting and obtained accurate, large-scale predictions. This method can also invert the subsurface parameters of other ocean variables (e.g., currents, eddies) by combining multiple sea surface factors.
In this paper, a new deep learning method (ConvLSTM) is applied to invert the ocean subsurface temperature and salinity fields using satellite observations of SST (sea surface temperate), SSS (sea surface salinity), SSH (sea surface height), and SSW (sea surface wind). The accuracy of the results is evaluated by comparing the inverted variable fields with the observed fields. The feasibility and effectiveness of the target method are verified by comparing it with other machine learning algorithms (random forest, LSTM).
2. Study Area and Data
The oceans cover about 71% of the Earth’s surface area and account for about 97% of the total water on Earth. The Pacific Ocean is the largest and deepest ocean globally, with the most marginal seas and islands. It is located between Asia, Oceania, Antarctica, and North and South America. With 181.3 million km2, it stretches from the Arctic Ocean to the Southern Ocean, covering about 46% of the Earth’s water surface and about 32% of its total area, which is larger than the total area of all landmasses on Earth.
In order to validate the inversion method proposed in this study, the region shown in Figure 1 was chosen as the study area, which is located in the central Pacific Ocean (30°S–30°N, 160°E–120°W) and has a vast sea area with a significant temperature difference. There are several oceanic current zones, such as warm equatorial current and the equatorial countercurrent, with the typical sea-air interaction phenomenon ENSO (El Niño-Southern Oscillation). The study of this region could effectively verify the proposed inversion method of oceanic elements.
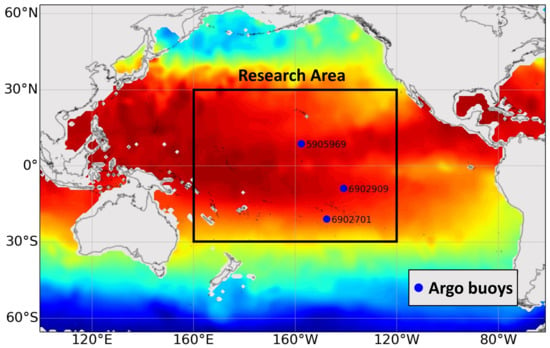
Figure 1.
Schematic map of the study area and its zoning, a research area in this study is in the central Pacific (160°E–120°W and 30°S–30°N); the Argo buoys No. 5905969, 6902701, and 6902909 are used for vertical profiles verification.
Advances in modern ocean remote sensing observations have provided multi-source data for this study. The Argo program has accumulated over 2.5 million temperature and salinity profiles in the global ocean and will add an average of 140,000 profiles per year. The BOA_Argo dataset obtained from the China Argo Real-time Data Center (CARDC, http://www.argo.org.cn/, accessed on 10 April 2022) is a monthly global gridded dataset that has been quality-reconditioned [54]. The Argo data with 1° × 1° spatial resolution have global coverage at 58 standard depth levels in the upper 2000 m. The SST is determined from Optimum Interpolation Sea-Surface Temperature (OISST, https://www.ncdc.noaa.gov/oisst, accessed on 10 April 2022) data with a spatial resolution of 0.25° × 0.25° since 1981 [55]. The SSS is obtained from the Soil Moisture and Ocean Salinity (SMOS, http://eopi.esa.int, accessed on 10 April 2022) of the European Space Agency with a spatial resolution of 0.25° × 0.25° from 2009 [56]. To ensure as many experimental data as possible, we used the Argo SSS data from 2004 to 2008 spliced with the SMOS data. The SSH data were obtained from (AVISO, http://www.aviso.altimetry.fr, accessed on 10 April 2022) altimetry with spatial resolution 0.25° × 0.25°, covering the period from January 1993 to the present [57]. The SSW was obtained from Cross-Calibrated Multi-Platform (CCMP, https://rda.ucar.edu/datasets/ds745.1/ accessed on 10 April 2022), with a spatial resolution of 0.25° × 0.25° since 1987 [58].
From all the above remote sensing variables (SST, SSS, SSH, USSW, and VSSW) and Argo gridded data, their climatology (averaged from 2004 to 2018) needs to be subtracted in order to obtain their anomaly values and remove the climatological seasonal variation signal. ST and SS serve as the corresponding labels for model training and testing and are the main elements for assessing the quality of this model. This study downsamples the spatial resolutions of different data separately. The spatial resolution is uniform to 1° × 1°, ensuring that the input data have the exact spatial and temporal resolution to facilitate the learning and discovery data rules at the same spatial scale. Since the training data belong to different scalars, all the data are normalized to [0,1] before inputting the network.
In addition, to compare the inversion effects at different spatial and temporal resolutions, we also additionally used 0.04° × 0.08° daily hindcast data from the HYbrid Coordinate Ocean Model (HYCOM, https://www.hycom.org/data/glby0pt08/expt-93pt0, accessed on 5 May 2022) [59], which contains ST/SS and SSH from the surface to 2000 m in the deep ocean. The Argo buoy data from CARDC were used as labels for the daily true values.
3. Methods
3.1. Random Forests
Ref. [60] combined the classification trees into a random forest, randomizing the use of variables (columns), and the use of data (rows) in the results of the classification trees was then aggregated to improve the prediction accuracy without a significant increase in computing power. Random forests are touted as one of the best current algorithms, which are more robust to missing data and unbalanced data and can predict up to several thousand explanatory variables very well.
The random forest algorithm has been widely used in ocean subsurface temperature inversion [38]. In this study, the random forest method was chosen to perform the inversion of STA/SSA. Referring to the experimental configuration of [38], the mtry is set to 2, ntree is set to 500, for achieving the best experimental results.
3.2. LSTM
Long short-term memory (LSTM) is a special kind of neural network, which is a more complex deep neural network model than traditional machine learning methods. It is stable and robust for modeling long-range correlations in various previous studies [61]. The main innovation of LSTM is its storage unit, which essentially acts as an accumulator of state information. The unit is accessed, written, and cleared by several self-parameterizing control gates. Whenever a new input comes, its information is accumulated in the cell if the input gate is activated. In addition, if the forgetting gate is opened, the past cell state may be “forgotten” in the process. The output gate controls whether the latest cell output is propagated to the final state. In this paper, we follow the formulation of FC-LSTM as in [62]. The key equations are shown in below, where ⊙ denotes the Hadamard product:
Based on the experience of previous studies [61], a three-layer LSTM model was constructed as a comparison experiment in this study. The input size of the LSTM model is (n_samples, n_time_steps, n_channels), where n_samples are the input sample size, the n_time_ steps are the historical timestep required for one inversion, and n_channels are the number of features of the input data. The hidden layer of the LSTM model was set to 120, and the dropout between each layer was set to 0.3.
3.3. ConvLSTM
Ref. [53] proposed the ConvLSTM algorithm, a recurrent neural network for spatio-temporal prediction. Compared with the traditional LSTM model, it has a convolutional structure in both the input-to-state and state-to-state transitions, a feature that allows it to take into account the spatial information of the input data to the maximum extent while retaining the good temporal correlation of the original LSTM model. This feature is mainly achieved by using convolution operators. Compared to the fully connected layer of the LSTM, the convolution operator allows the input information to be a two-dimensional matrix and performs further extraction of the spatial information in the matrix. The critical equations of the ConvLSTM are shown below, where ∗ denotes the convolution operator, ⊙ denotes the Hadamard product, and is a sigmoid function used as the activation function applied to the weighted sum of the inputs of each gate.
This study used a grid search approach to determine the model’s hyperparameters. Based on previous research experience, we tried 1-layer, 2-layer, and 3-layer ConvLSTM networks and finally settled on using a 3-layer ConvLSTM with additional normalization between each layer. Based on the experience of previous studies, the batch size was set to 32, which can improve the training speed and ensure the fast convergence of the model. The detailed model parameters are listed in Table 1. The network models and weights are trained separately for the temperature and salinity tasks, which can improve the efficiency of model tuning.

Table 1.
Parameters of the ConvLSTM model and optimal values after tuning for ST/SS inversion.
The changes in ocean elements have typical periodic characteristics, and different time steps have different effects on the inversion effect. We set up four comparison experiments for the timesteps for ST Monthly, SS Monthly, ST Daily, and SS Daily, respectively. Among them, the monthly experiments used the whole training set and test set, and the daily experiments used the 1-year (April 2019–April 2020) training set and the whole test set (to speed up the training). As shown in Tables S1–S4 in the Supplementary Materials, we chose the minimum NRMSE for each depth as the optimal timesteps for the model. The experimental results show a significant difference in the optimal timesteps for different depths in different experiments. It is worth noting that the spatial and temporal correlations between the ocean interior elements and the surface elements are changing with depth, so the best timesteps will be set separately for each layer of depth in the subsequent experiments.
3.4. Experimental Setup
Figure 2 illustrates the model architecture for using ConvLSTM to invert the ocean subsurface temperature and salinity fields. Multi-channel ocean surface data are input to the ConvLSTM model, and the model subsequently outputs STA/SSA for the target month; the entire ST/SS fields data can be obtained from STA/SSA plus their climatology. Data from January 2004 to December 2017 (180 months) are used as the training set, and data in 2018 (12 months) are retained to serve as the test set. In addition, we set up a set of comparison experiments using daily high-resolution data. The experiments used numerical model data from HYCOM, including ST SS and SSH data from 5 December 2018 to 4 May 2022. The data from March 2019 to May 2022 were used as the training set and those from December 2018 to March 2019 were retained as the test set. The data required for the model are continuous in space and time. However, empty values exist in the dataset because of islands and land, so we used a mask to deal with missing values in the training and evaluation of the model.
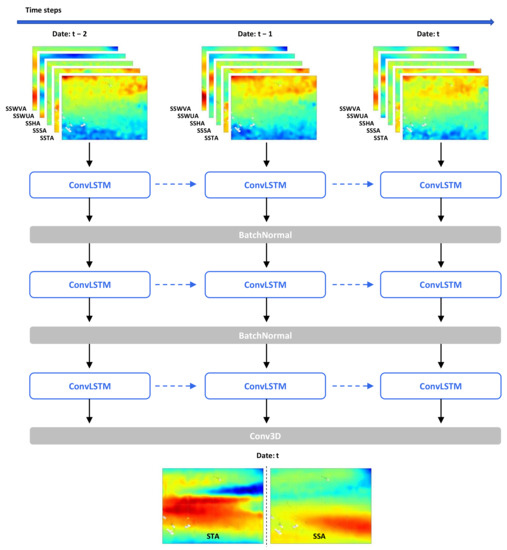
Figure 2.
Flowchart for STA/SSA inversion in the Pacific Ocean using remote sensing data based on the ConvLSTM model.
In data preprocessing, the input of a ConvLSTM is a set of images over time as a 5D tensor with shape (n_samples, n_time_steps, rows, cols, n_channels), and the output needs to be reshaped as a 4D tensor of (n_samples, filters, rows, cols), where n_samples are the input sample size, the n_time_steps are the historical timestep required for one inversion, rows and cols are the length and width of the input data, and n_channels are the number of features of the input data.
NRMSE and the R correlation coefficient are used as the evaluation metrics to make a quantifiable assessment of the effect of the study.
Here, is the actual observed value of time i, is the predicted value at the same time, m is the number of data, is the average value of the actual observed values, and is the average value of the predicted values.
In order to figure out the effects of different parameter combinations for the reconstruction of ST/SS fields and compare the performance of ConvLSTM, RFs, and LSTM, 12 experiment cases to optimize the feature combination were designed for the prediction of 2018 (Table 2). Our data experiments were operated on a PC with a simulation environment as follows.

Table 2.
Design of experiments.
- -
- Hardware: Intel I9-11900K CPU, NVIDIA RTX 3090 GPU.
- -
- System environment: Ubuntu 18.04 system, Python 3.8.2, Tensorflow 2.4.0, Keras 2.4.3.
4. Results and Discussion
4.1. Comparison of Multiple Channels
In this study, a series of ConvLSTM-based inversion models were designed to predict ST and SS using different inputs to compare the effects of different parameter combinations on ST/SS inversion. Figure 3 shows the performance analysis for all combinations. Overall, the ConvLSTM model shows excellent performance for both ST and SS tasks and can invert the temperature and salinity distributions of the ocean subsurface well. The comparison shows that multi-channel data have a significant impact on such tasks.
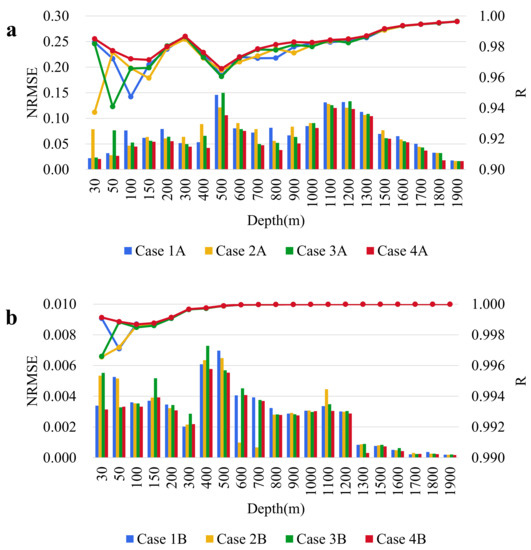
Figure 3.
The NRMSE (left, bar) and R (right line) of inversion results at different depths by ConvLSTM models in different cases: (a) ST, (b) SS.
For the inversion of the ocean subsurface temperature in Figure 3a, it is shown that the multi-channel input gives a significant change in the model’s performance, with R rising, then falling, and finally rising again. NRMSE first rises from 0 to 200 m and then has a significant rise from200 to 500 m, then falls from 500 m onwards, followed by another rise and fall. The average NRMSE and R for different cases at all depths are 0.0732/0.0746/0.0702/0.0682 and 0.9802/0.9788/0.9799/0.9819, respectively. Therefore, Case 4A has the best performance on ST construction, which indicates that SSH/SSW can show a significant positive impact in the ST inversion task. The difference between multiple channels is evident in the more upper ocean of 30–200 m, and then it decreases with increasing depth. This indicates that the surface ocean features, influenced by strong sea–air interactions, have a significant effect on the inversion of the subsurface ocean temperature fields.
For the comparison of SS inversions, the comparison results of different experiments are shown in Figure 3b. Overall, R continues to rise after a brief decline, and NRMSE shows an increasing trend from 0 to 150 m, followed by a brief decline, reaching a maximum error at 400 m. NRMSE also gradually decreases with increasing depth. The averages of NRMSE and R for salinity inversion at all depths are 0.0028/0.0026/0.0029/0.0025 and 0.9996/0.9995/0.9996/0.9997. Unlike the previous ST experiments, the effect of each channel during the salinity inversion experiment is not apparent. The smallest average NRMSE is Case 4B, only 0.0004 less than the largest Case 3B. The above results indicate that the application of multiple channels in the salinity inversion task has played a specific effect. All the comparison results have more obvious differences within 100 m. The data of Case 4B almost achieve the best case in 0–100 m, which indicates that the multi-channel data still have a more significant impact in shallow waters.
The above experiments demonstrate that it is effective to use multi-channel data to enhance the ConvLSTM model for the inversion of temperature and salinity fields, especially in shallow waters, where the results of multi-channel datasets are often the best. Case 4A and Case 4B are set as the default configurations in subsequent experiments.
4.2. Spatial Error Analysis
Figure 4 and Figure 5 present a comparison of ST and SS for different depths (50, 100, 300, 500, and 1000 m) of the ConvLSTM model inversion (i) and Argo labels (ii) for one particular time snapshot (March 2018). The error (iii) is the absolute error of the Argo data subtracted from the inversion data. From the perspective of spatial distribution, model inversion results are consistent with the distribution of the Argo grid. As the depth increases, the absolute error of the model decreases, but the similarity between the inversion results and the truth data decreases. This may be due to the spatial and temporal correlation information of the ocean surface being gradually confounded by complex internal ocean processes, but the model lacks sufficient data to learn such processes. As shown in Figure 4, the retrieval R values of the five different depth ranges were 0.9860, 0.9777, 0.98624, 0.9582, and 0.9781, respectively. The corresponding NRMSE values were 0.0198, 0.0711, 0.0478, 0.1315 and 0.0993, respectively. At 50 m, the inversion results are almost consistent with the truth data. The overall temperature of the Western Pacific is higher than that of the Eastern Pacific. The seawater temperature gradually decreases from the equator to the poles. The main error is in the equatorial Eastern Pacific, presumably due to the effect of the La Niña phenomenon. At a 100 m depth, the details of the inversion results gradually disappear at the edges, and the contours start to become rounded. However, the trend of the overall temperature distribution is the same. At 300 m, in contrast to the shallow sea, the seawater temperature in the equatorial region is significantly lower than on both sides. The error distribution is gradually not regular. At 500 m and 1000 m depth, the temperature variation in the sea gradually decreases, and the model can still maintain the overall distribution pattern similar to the actual value.
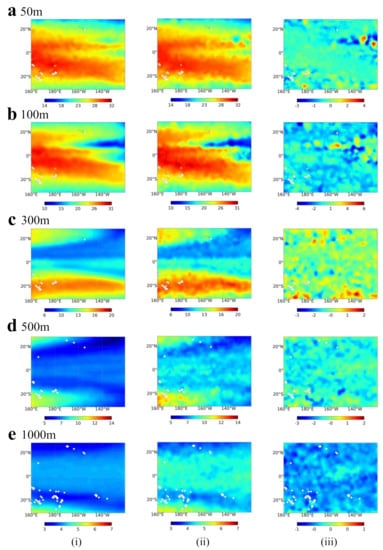
Figure 4.
Spatial distribution of ConvLSTM-reconstructed ST in (i) Case 4A and (ii) Argo ST, and (iii) the absolute error of ConvLSTM-predicted ST at depth levels of (a) 50 m, (b) 100 m, (c) 300 m, (d) 500 m, and (e) 1000 m in March 2018.
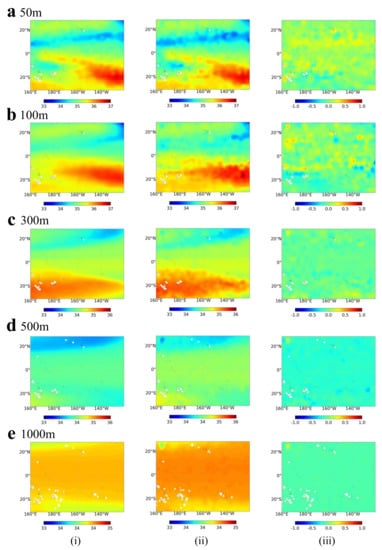
Figure 5.
Spatial distribution of ConvLSTM-reconstructed SS in (i) Case 4B and (ii) Argo SS, and (iii) the absolute error of ConvLSTM-reconstructed SS at depth levels of (a) 50 m, (b) 100 m, (c) 300 m, (d) 500 m, and (e) 1000 m in March 2018.
At shallower depths (50–300 m), the salinity inversion results are very similar to the Argo label values, as shown in Figure 5, with an overall error in the range of (−1,1), which proves the usability of the model. The retrieval R values of the five different depth ranges were 0.9991, 0.9985, 0.9996, 0.9999, and 0.9999, respectively. The corresponding NRMSE values were 0.0033, 0.0035, 0.0022, 0.0058, and 0.0032, respectively. The absolute error is still in the smaller range in the deeper salinity inversions from 500 m to 1000 m.
In a comprehensive view, the temperature and salinity field inversion model based on ConcLSTM can effectively invert the temperature and salinity distributions at different ocean depths, and the overall error is within acceptable limits. The errors are significant in parts of the equatorial region within the Eastern and Western Pacific due to the influence of the La Niña phenomenon. The effectiveness still needs to be improved for deeper inversions, and we believe that more data analysis may help solve this problem.
4.3. Temporal Error Analysis
The temperature and salinity for different months of 2018 using the ConvLSTM inversion model are shown in Figure 6 and Figure 7. The metrics include NRMSE and Pearson’s correlation coefficient R, with each grid point representing the average metric between the predicted and actual values for the month, and all performance results are obtained based on the testing set. In general, the mean NRMSE of ST is less than 0.15, the correlation coefficient is over 0.9 for all months, the mean NRMSE of SS is less than 0.007, and the correlation coefficient is more significant than 0.99 for the whole year. In the temperature inversion experiment, March to May and September to November were the months with relatively large errors that the ENSO phenomenon may have influence that year. The correlation coefficient becomes higher with depth, reaching 0.9964 at 1900 m. This result is mainly because the magnitude of change in the deep layer is much less than in the shallow layer. The NRMSE first increases and decreases in the salinity inversion experiment, while the R correlation coefficient increases with depth. At 1900 m, the average NRMSE is 0.00019, and the average R is 0.9997. The results demonstrate that the experimental accuracy of salinity is higher than that of temperature. This is mainly due to the stability of the salinity distribution itself and the vital learning ability of the model. The difference between months is not significant, mainly due to the stability of the salinity distribution itself and the model’s ability to learn this temporal pattern. Overall, our model could accurately estimate the distribution of the temperature and salinity fields below the sea surface, and its performance was very stable at different depths and times.
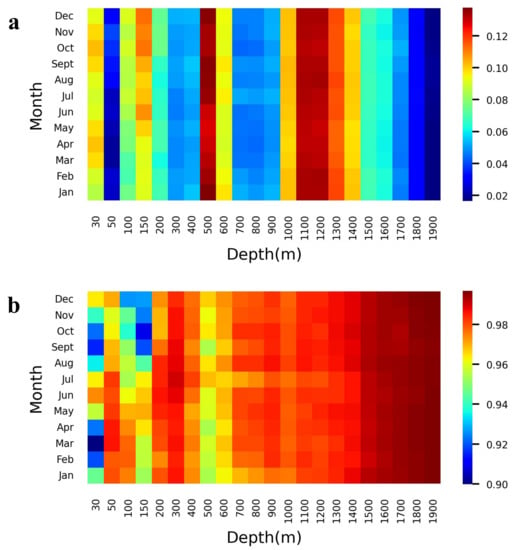
Figure 6.
Model performance for ST estimation. (a) Normalized root mean square error (NRMSE), (b) coefficient of correlation (R) of the ST estimation at each depth level and in each month of 2018.
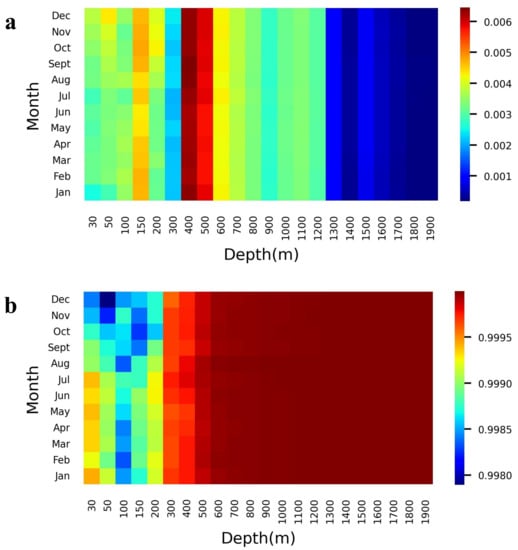
Figure 7.
Model performance for SS estimation. (a) Normalized root mean square error (NRMSE), (b) coefficient of correlation (R) of the SS estimation at each depth level and in each month of 2018.
4.4. Longitude Profile Validation
To further analyze the subsurface thermohaline field distribution in the Pacific Ocean and estimate the inversion performance of the ConvLSTM model from a vertical perspective, we selected a profile in the meridional direction to analyze the vertical variation of ST/SS. Figure 8 shows the vertical profiles along the longitude of 188.5°. Figure 8a shows a wide range of warm zones in the Central and Western equatorial Pacific due to the weak La Niña phenomenon, and the seawater in the south is warmer than in the north. The surface seawater in the Eastern Pacific is pushed to the central Western Pacific, resulting in a distinct warm band within 200 m of the surface layer. With increasing depth, the La Niña effect gradually decays, and the seawater temperature distribution tends to level off after 300 m. However, in the Pacific region at 5–10°N, there is a distinct low-temperature zone extending from 50 m to about 400 m, which may be caused by the accelerated flow of the North Equatorial Warm Current during La Niña. Figure 8c shows the vertical profile at the longitude of 188.5° (171.5°W) for ConvLSTM-inversed ST. The model’s inversion is very similar to the Argo grid values, with 95.86% of the prediction errors within ±2 °C and 85.5% within ±1 °C. Figure 8b is the vertical profile at the longitude of 188.5° for Argo SS. The salinity distribution is similar to the temperature, with salinity values that are higher in the south than in the north and decrease with increasing depth. There is a high concentration of brine mass between 100 and 250 m, which is not present in the temperature profile. Figure 8d shows the salinity profile at the longitude of 188.5° for ConvLSTM-inversed SS. As mentioned in the previous results, 99.49% of the profile points have an overall error within ±0.3 PSS, and more than 91.59% are within ±0.2 PSS. It can be concluded that the inversion performance of ConvLSTM is excellent. The overall prediction results of the temperature and salinity profiles show similar trends to the true values, indicating our ConvLSTM model’s promising performance.
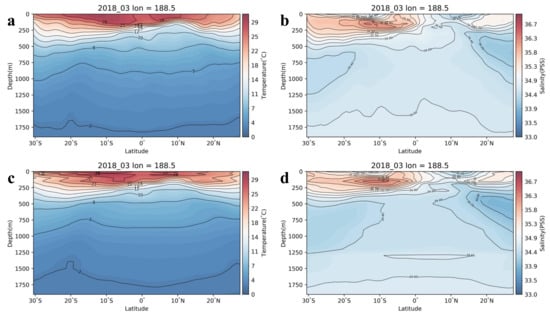
Figure 8.
The meridianal vertical profiles of the ocean subsurface thermohaline in March 2018 at the longitude of 188.5° for (a) Argo ST, (b) Argo SS, (c) ConvLSTM-inversed ST, and (d) ConvLSTM-inversed SS.
4.5. Comparison of Different Models
In addition to the ConvLSTM model, we also used the classical machine learning model RFs and the deep learning model LSTM with the same dataset for the same temperature and salinity fields inversion experiments.
The bar graphs of temperature and salinity inversions using different models are shown in Figure 9. Overall, RFs, LSTM, and ConvLSTM all have good performance, and the gap between the models gradually decreases with increasing depth and has the same trend of variation. The NRMSE of the temperature inversion models are all less than 0.15, and the R correlation coefficients are all over 0.94. The average NRMSE and R of each model are 0.063/0.0671/0.0568 and 0.9806/0.9747/0.9819, respectively. In the shallow waters of 0–300 m, the errors among the models are more pronounced, and the LSTM model performs the worst, followed by the RFs. The best is ConvLSTM, which confirms the previous experiments that the ConvLSTM model can mor thoroughly learn the spatio-temporal correlation properties within the data than the direct machine learning model and the temporal correlation-based LSTM. The error between the models gradually decreases in the middle and deep-sea from 300 m to 1900 m. The R correlation coefficient increases with depth, reaching the highest value at 1900 depth, which is not much different from the experimental results in the previous section.
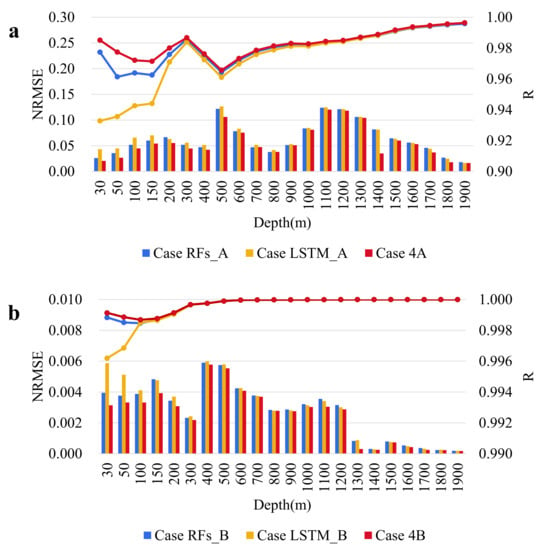
Figure 9.
The inversion accuracy of (a) ST and (b) SS at different depths using RFs, LSTM, and ConvLSTM models.
The average NRMSE and R of salinity inversion models are 0.0028/0.0029/0.0027 and 0.9997/0.9995/0.9997, respectively. The LSTM model is the least effective, followed by RFs, and the best is ConvLSTM; the error between the models gradually decreases with increasing depth, and they are nearly equal by th end. The error of the salinity inversion model is much smaller than that of the temperature. The results of the experiments also show that there is a sharp change in salinity under the influence of oceanic thermocline leapfrog.
The temperature and salinity inversion results of different models are shown in Figure 10 and Figure 11, which illustrate the inversion of RFs, LSTM, and ConvLSTM and ground truth, respectively. At 50 m depth, both RFs and ConvLSTM can invert the temperature distribution well, while the edges of LSTM seem too smooth, which makes many details become lost. At 100 m depth, the difference in seawater temperature due to La Niña is observed. The overall inversion of the ConvLSTM model is closest to the label value, the RFs overestimate the temperature value at the southern equator (0°,180°), and the edges are more apparent and not over-smoothed compared to the LSTM. At depths of 300 m and below, the overall estimates of all three models are smaller than the actual values, but the distribution pattern is consistent with the truth values, with the equator being cold and the north and south sides hot.
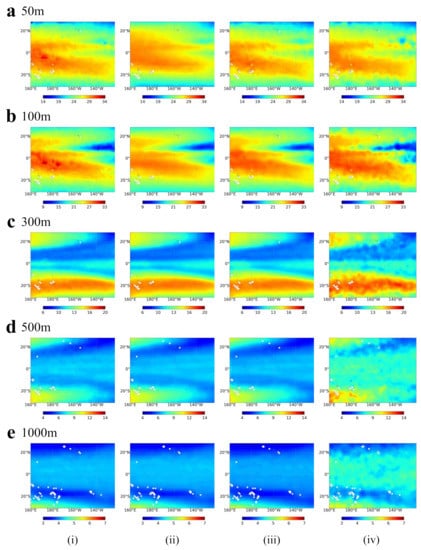
Figure 10.
ST spatial distribution of (i) RFs, (ii) LSTM, (iii) ConvLSTM, and (iv) Argo gridded at (a) 50 m, (b) 100 m, (c) 300 m, (d) 500 m, and (e) 1000 m in March 2018.
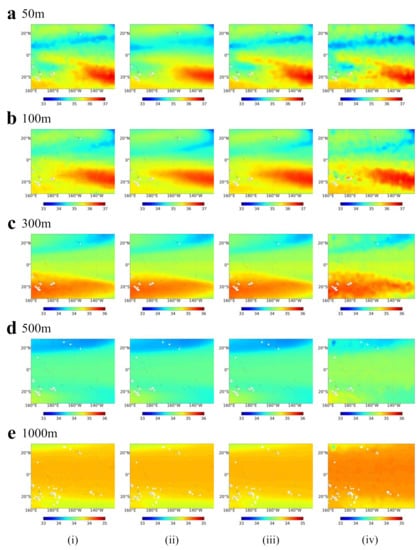
Figure 11.
SS spatial distribution of (i) RFs, (ii) LSTM, (iii) ConvLSTM, and (iv) Argo gridded at (a) 50 m, (b) 100 m, (c) 300 m, (d) 500 m, and (e) 1000 m in March 2018.
For salinity, at 50 m depth, the ConvLSTM model can perform a complete inverse performance of the low salinity zone located at 10°N, which is not continuous in the other two models. At a 100 m depth, the ConvLSTM model can still invert the best results. At 20°S, 180° near the Fiji Islands, the RFs predictions are too fragmented, and the edges show jaggedness. The LSTM model is still over-smoothed and loses much detail, while the ConvLSTM model still maintains the advantage in detail and overall. From 300 m depth downward, the error between the models gradually decreases, which agrees with the conclusion of the previous experiments.
4.6. Comparison of Different Temporal and Spatial Scales
The above experiments fully demonstrate the superiority of the model for the monthly 1° × 1° temperature and salinity fields’ inversion tasks. To further test the applicability of the model at different spatial and temporal scales, we set up an additional set of experiments using daily high-resolution (0.24° × 0.24°) data for the inversion of the temperature and salinity fields. The experimental results of the inversion using HYCOM daily numerical model data are shown in Figure 12. The experimental results show that the model can still maintain good results for the inversion of daily data. With the change in depth, both showed a similar trend of change.
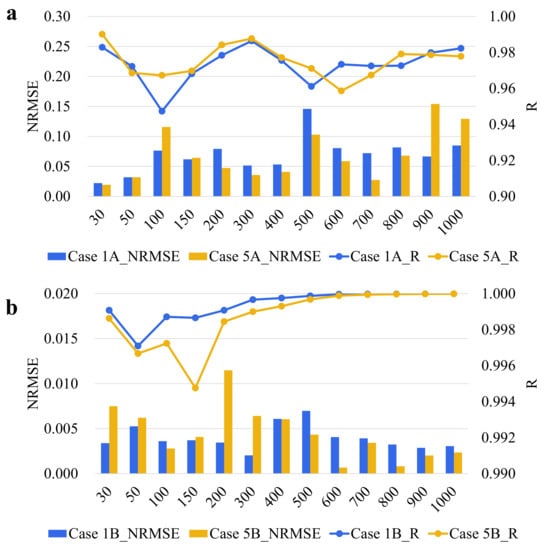
Figure 12.
The inversion accuracy of (a) ST and (b) SS for monthly and daily data at different depths using the ConvLSTM model.
In the temperature-inversion experiments, the average NRMSE and R of the monthly and daily models are 0.0699/0.0689, and 0.9733/0.9752, respectively. The NRMSE of the daily model is significantly higher than that of the monthly model at 100 m, 900 m, and 1000 m depths. The maximum error between the two occurs at 900 m depth, where the NRMSE difference reaches 0.0874, and the minimum error occurs at 50 m (0.0001). In the correlation coefficient curves, the trends of daily inversion results are consistent with the monthly ones. It is noteworthy that at some depths, the model with a higher correlation coefficient has a higher NRMSE. We think this may be caused by the different numbers of data between them. The test set for monthly data has only 12 months (40 × 60 grid points), while the set for the daily data has 117 days (250 × 333 grid points).
For the salinity inversion, the mean NRMSE and R of the monthly and daily models are 0.0040/0.0045 and 0.9993/0.9987, respectively. The NRMSE of the daily experiments is significantly higher than the monthly ones at the 30 m, 50 m, 150 m, and 200 m depths. This may be since shallow waters are susceptible to surface winds and waves and since the daily salinity variability is higher than the monthly one. In the correlation coefficient curve, the difference between the two sets of experiments gradually decreases with increasing depth. This may be due to the relatively stable variation in salinity itself in deeper seas.
To study the vertical profiles in the region, we randomly selected some Argo buoys to compare with the model effects. Figure 13 shows the vertical profiles of Argo ST/SS (black line) and the ST/SS profiles predicted by ConvLSTM (red line), as well as the labeled values of the HYCOM product (blue line). It can be seen that the predicted values of ConvLSTM are closest to the HYCOM-labeled values in the temperature experiments because the model is trained with the HYCOM labels. The model inversion results are also very similar to the Argo buoy values, which demonstrates the inversion potential of the ConvLSTM model. In the salinity comparison experiments, the model inversions appear significantly different from the Argo and HYCOM true values from 0 to 300 m, but the overall trend is similar below 300 m. The actual error is only about 0.5 PSU because of the high resolution of the coordinate axes of the salinity map. In the temperature and salinity experiments, the label value of HYCOM is relatively consistent with the data of Argo buoys, which also proves the correctness of our data selection for the daily degree experiments. Although there is some error between HYCOM data and Argo buoys, the ConvLSTM model can learn the spatio-temporal correlation between the ocean surface and subsurface fields and achieve inversions similar to the hindcast data and the actual observations.
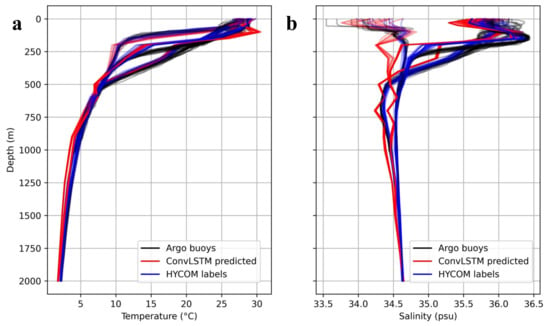
Figure 13.
The vertical profiles of some grid points in the study area for (a) ST, (b) SS.
Overall, our proposed ConvLSTM inversion model is still able to perform well in the high-resolution daily inversion task. It is worth noting that although the daily experiment uses more data, its results do not improve significantly but rather are inferior to the monthly experiment in the salinity experiment. This illustrates the sensitivity of ocean processes to specific temporal and spatial scales; the higher the spatial and temporal resolution, the more difficult it is to perform inversions. This is also in line with the law of data science itself.
5. Conclusions
This paper proposes a new approach based on a deep learning ConvLSTM algorithm to reconstruct the subsurface temperature and salinity fields within 2000 m. The sea surface elements (sea surface temperature, sea surface salinity, sea surface height, and sea surface wind) were used to invert the temperature and salinity fields at different depths inside the ocean, using Argo gridded product and buoys profiles as the label and validation set for the experiments.
The results show that the ConvLSTM model can successfully reconstruct the thermohaline field in the ocean interior at different depths and times. Compared with the three-channel results, the NRMSE of the five-channel results decreased by 22.4% (ST) and 12% (SS), respectively. Compared with other models, the average NRMSE of our method decreased by 12.32% (ST) and 12% (SS), respectively. The inversion experiments at different depths and months demonstrate that the model has better generalization ability and robustness. The ConvLSTM can better capture the spatio-temporal correlation of sea surface elements and has excellent potential in the task of inversion of the ocean interior through the surface. The model can still guarantee good performance in high-resolution daily inversion tasks, which demonstrates the robustness of the model at different spatial and temporal scales.
Overall, for the ocean subsurface’s temperature and salinity inversion task, our model can capture the spatial and temporal correlations in the ocean interior with a superior architecture to RFs and LSTM. Our study still has some limitations. The available Argo data are too sparse for deep learning, and the algorithm of matrix convolution has limited performance for ocean data with irregular edges. We will try to apply more data and more novel algorithms in the next step, and using the combination of the physical dynamics model and AI is also the direction of our future research. This study extends the application of satellite data and provides some new insights into ocean dynamics from a data-driven perspective. Moreover, it provides methodological support for remote sensing, artificial intelligence, and oceanography.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs14112584/s1, Table S1: Results of NRMSE inversion at different depths of monthly ST at different timesteps. Table S2: Results of NRMSE inversion at different depths of monthly SS at different timesteps. Table S3: Results of NRMSE inversion at different depths of daily ST at different timesteps. Table S4: Results of NRMSE inversion at different depths of daily S at different timesteps.
Author Contributions
Conceptualization, T.S. and D.X.; methodology, W.W., F.M.; validation, W.W.; formal analysis, T.S., W.W., F.M., J.W., R.H.; investigation, W.W.; data curation, W.W.; writing—original draft preparation, W.W.; writing—review and editing, T.S., D.X., F.M.; visualization, W.W., J.W., R.H.; supervision, T.S.; project administration, T.S.; funding acquisition, D.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China U1811464, U21A6001, and the CAS Key Laboratory of Science and Technology on Operational Oceanography Open Project Funding No OOST2021-03.
Data Availability Statement
The SST data were obtained from the OISST (https://www.ncei.noaa.gov/data/sea-surface-temperature-optimum-interpolation/v2.1/access/avhrr/, accessed on 10 April 2022), the SSS data were obtained from SMOS (https://earth.esa.int/eogateway/catalog/smos-science-products, accessed on 10 April 2022). The SSW vector analysis products were obtained from (https://rda.ucar.edu/datasets/ds745.1/, accessed on 10 April 2022). Archiving, Validation, and Interpretation of Satellite Oceanographic data (AVISO) for sea level data were obtained from (https://www.aviso.altimetry.fr/en/data.html, accessed on 10 April 2022), the daily ST/SS/SSH were obtained from HYCOM (https://www.hycom.org/data/glby0pt08/expt-93pt0, accessed on 5 May 2022), and the BOA_Argo for Argo gridded data and Argo profiles were obtained from (http://www.argo.org.cn, accessed on 10 April 2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bindoff, N.L.; Willebrand, J.; Artale, V.; Cazenave, A.; Gregory, J.M.; Gulev, S.; Hanawa, K.; Le Quere, C.; Levitus, S.; Nojiri, Y.; et al. Observations: Oceanic climate change and sea level. In Climate Change 2007: The Physical Science Basis; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Meyssignac, B.; Boyer, T.; Zhao, Z.; Hakuba, M.Z.; Landerer, F.; Stammer, D.; Köhl, A.; Kato, S.; L’Ecuyer, T.; Ablain, M. Measuring Global Ocean Heat Content: To Estimate Earth’s Energy Imbalance. Front. Mar. Sci. 2019, 6, 437. [Google Scholar] [CrossRef]
- Johnson, G.C.; Lyman, J.M. Warming trends increasingly dominate global ocean. Nat. Clim. Chang. 2020, 10, 757–761. [Google Scholar] [CrossRef]
- Boyer, T.; Domingues, C.M.; Good, S.A.; Johnson, G.C.; Lyman, J.M.; Ishii, M.; Gouretski, V.; Willis, J.K.; Antonov, J.; Wijffels, S.; et al. Sensitivity of global upper-ocean heat content estimates to mapping methods, XBT bias corrections, and baseline climatologies. J. Clim. 2016, 29, 4817–4842. [Google Scholar] [CrossRef]
- Balmaseda, M.A.; Trenberth, K.E.; Källén, E. Distinctive climate signals in reanalysis of global ocean heat content. Geophys. Res. Lett. 2013, 40, 1754–1759. [Google Scholar] [CrossRef]
- Chen, X.; Tung, K.K. Varying planetary heat sink led to global-warming slowdown and acceleration. Science 2014, 345, 897–903. [Google Scholar] [CrossRef]
- Drijfhout, S.S.; Blaker, A.T.; Josey, S.A.; Nurser, A.J.; Sinha, B.; Balmaseda, M.A. Surface warming hiatus caused by increased heat uptake across multiple ocean basins. Geophys. Res. Lett. 2014, 41, 7868–7874. [Google Scholar] [CrossRef]
- Song, Y.T.; Colberg, F. Deep ocean warming assessed from altimeters, Gravity Recovery and Climate Experiment, in situ measurements, and a non-Boussinesq ocean general circulation model. J. Geophys. Res. Ocean. 2011, 116, C0202. [Google Scholar] [CrossRef]
- Bao, S.; Zhang, R.; Wang, H.; Yan, H.; Yu, Y.; Chen, J. Salinity profile estimation in the Pacific Ocean from satellite surface salinity observations. J. Atmos. Ocean. Technol. 2019, 36, 53–68. [Google Scholar] [CrossRef]
- Cazenave, A.; Meyssignac, B.; Ablain, M.; Balmaseda, M.; Bamber, J.; Barletta, V.; Beckley, B.; Benveniste, J.; Berthier, E.; Blazquez, A.; et al. Global sea-level budget 1993-present. Earth Syst. Sci. Data 2018, 10, 1551–1590. [Google Scholar]
- Lu, W.; Su, H.; Yang, X.; Yan, X.H. Subsurface temperature estimation from remote sensing data using a clustering-neural network method. Remote Sens. Environ. 2019, 229, 213–222. [Google Scholar] [CrossRef]
- Su, H.; Wu, X.; Lu, W.; Zhang, W.; Yan, X.H. Inconsistent Subsurface and Deeper Ocean Warming Signals During Recent Global Warming and Hiatus. J. Geophys. Res. Ocean. 2017, 122, 8182–8195. [Google Scholar] [CrossRef]
- Wang, G.; Cheng, L.; Abraham, J.; Li, C. Consensuses and discrepancies of basin-scale ocean heat content changes in different ocean analyses. Clim. Dyn. 2018, 50, 2471–2487. [Google Scholar] [CrossRef]
- Jayne, S.R.; Roemmich, D.; Zilberman, N.; Riser, S.C.; Johnson, K.S.; Johnson, G.C.; Piotrowicz, S.R. The argo program: Present and future. Oceanography 2017, 30, 18–28. [Google Scholar] [CrossRef]
- Su, H.; Wu, X.; Yan, X.H.; Kidwell, A. Estimation of subsurface temperature anomaly in the Indian Ocean during recent global surface warming hiatus from satellite measurements: A support vector machine approach. Remote Sens. Environ. 2015, 160, 63–71. [Google Scholar] [CrossRef]
- Su, H.; Huang, L.; Li, W.; Yang, X.; Yan, X.H. Retrieving Ocean Subsurface Temperature Using a Satellite-Based Geographically Weighted Regression Model. J. Geophys. Res. Ocean. 2018, 123, 5180–5193. [Google Scholar] [CrossRef]
- Guinehut, S.; Dhomps, A.L.; Larnicol, G.; Le Traon, P.Y. High resolution 3-D temperature and salinity fields derived from in situ and satellite observations. Ocean. Sci. 2012, 8, 845–857. [Google Scholar] [CrossRef]
- Liu, L.; Peng, S.; Wang, J.; Huang, R.X. Retrieving density and velocity fields of the ocean’s interior from surface data. J. Geophys. Res. Ocean. 2014, 119, 8512–8529. [Google Scholar] [CrossRef]
- Liu, L.E.; Xue, H.; Sasaki, H. Reconstructing the Ocean Interior from High-Resolution Sea Surface Information. J. Phys. Oceanogr. 2019, 49, 3245–3262. [Google Scholar] [CrossRef]
- Wang, J.; Flierl, G.R.; Lacasce, J.H.; Mcclean, J.L.; Mahadevan, A. Reconstructing the Ocean’s Interior from Surface Data. J. Phys. Oceanogr. 2013, 43, 1611–1626. [Google Scholar] [CrossRef]
- Yan, X.H.; Jo, Y.H.; Liu, W.T.; He, M.X. A New Study of the Mediterranean Outflow, Air–Sea Interactions, and Meddies Using Multisensor Data. J. Phys. Oceanogr. 2006, 36, 691–710. [Google Scholar] [CrossRef][Green Version]
- Yan, X.-H.; Okubo, A. Three-dimensional analytical model for the mixed layer depth. J. Geophys. Res. Ocean. 1992, 97, 20201–20226. [Google Scholar] [CrossRef]
- Akbari, E.; Alavipanah, S.K.; Jeihouni, M.; Hajeb, M.; Haase, D.; Alavipanah, S. A Review of Ocean/Sea Subsurface Water Temperature Studies from Remote Sensing and Non-Remote Sensing Methods. Water 2017, 9, 936. [Google Scholar] [CrossRef]
- Holloway, J.; Mengersen, K. Statistical Machine Learning Methods and Remote Sensing for Sustainable Development Goals: A Review. Remote Sens. 2018, 10, 1365. [Google Scholar] [CrossRef]
- Klemas, V.; Yan, X.H. Subsurface and deeper ocean remote sensing from satellites: An overview and new results. Prog. Oceanogr. 2014, 122, 1–9. [Google Scholar] [CrossRef]
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine learning in geosciences and remote sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef]
- Carnes, M.R.; Teague, W.J.; Mitchell, J. Inference of subsurface thermohaline structure from fields measurable by satellite. J. Atmos. Ocean. Technol. 1994, 11, 2. [Google Scholar] [CrossRef]
- Fox, D.; Teague, W.; Barron, C.; Carnes, M.; Lee, C. The modular ocean data assimilation system (MODAS). J. Atmos. Ocean. Technol. 2002, 19, 240–252. [Google Scholar] [CrossRef]
- Nardelli, B.; Santoleri, R. Reconstructing synthetic profiles from surface data. J. Atmos. Ocean. Technol. 2004, 21, 693–703. [Google Scholar] [CrossRef]
- Jeong, Y.; Hwang, J.; Park, J.; Jang, C.J.; Jo, Y.H. Reconstructed 3-D Ocean Temperature Derived from Remotely Sensed Sea Surface Measurements for Mixed Layer Depth Analysis. Remote Sens. 2019, 11, 3018. [Google Scholar] [CrossRef]
- Maes, C.; Behringer, D.; Reynolds, R.W.; Ming, J. Retrospective analysis of the salinity variability in the western tropical Pacific Ocean using an indirect minimization approach. J. Atmos. Ocean. Technol. 2000, 17, 512–524. [Google Scholar] [CrossRef]
- Nardelli, B.B.; Santoleri, R. Methods for the Reconstruction of Vertical Profiles from Surface Data: Multivariate Analyses, Residual GEM, and Variable Temporal Signals in the North Pacific Ocean. J. Atmos. Ocean. Technol. 2005, 22, 1762–1781. [Google Scholar] [CrossRef]
- Ali, M.; Swain, D.; Weller, R. Estimation of ocean subsurface thermal structure from surface parameters: A neural network approach. Geophys. Res. Lett. 2004, 31, L20308. [Google Scholar] [CrossRef]
- Su, H.; Zhang, H.; Geng, X.; Qin, T.; Lu, W.; Yan, X.H. OPEN: A new estimation of global ocean heat content for upper 2000 meters from remote sensing data. Remote Sens. 2020, 12, 2294. [Google Scholar] [CrossRef]
- Wu, X.; Yan, X.H.; Jo, Y.H.; Liu, W.T. Estimation of Subsurface Temperature Anomaly in the North Atlantic Using a Self-Organizing Map Neural Network. J. Atmos. Ocean. Technol. 2012, 29, 1675–1688. [Google Scholar] [CrossRef]
- Chapman, C.; Charantonis, A.A. Reconstruction of Subsurface Velocities from Satellite Observations Using Iterative Self-Organizing Maps. IEEE Geosci. Remote Sens. Lett. 2017, 14, 617–620. [Google Scholar] [CrossRef]
- Chen, C.; Yang, K.; Ma, Y.; Wang, Y. Reconstructing the Subsurface Temperature Field by Using Sea Surface Data Through Self-Organizing Map Method. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1812–1816. [Google Scholar] [CrossRef]
- Su, H.; Li, W.; Yan, X.H. Retrieving Temperature Anomaly in the Global Subsurface and Deeper Ocean from Satellite Observations. J. Geophys. Res. Ocean. 2018, 123, 399–410. [Google Scholar] [CrossRef]
- Su, H.; Yang, X.; Lu, W.; Yan, X.H. Estimating subsurface thermohaline structure of the global ocean using surface remote sensing observations. Remote Sens. 2019, 11, 1598. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Bolton, T.; Zanna, L. Applications of Deep Learning to Ocean Data Inference and Subgrid Parameterization. J. Adv. Model. Earth Syst. 2019, 11, 376–399. [Google Scholar] [CrossRef]
- Ham, Y.G.; Kim, J.H.; Luo, J.J. Deep learning for multi-year ENSO forecasts. Nature 2019, 573, 568–572. [Google Scholar] [CrossRef]
- Song, T.; Jiang, J.; Li, W.; Xu, D. A Deep Learning Method with Merged LSTM Neural Networks for SSHA Prediction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2853–2860. [Google Scholar] [CrossRef]
- Song, T.; Li, Y.; Meng, F.; Xie, P.; Xu, D. A Novel Deep Learning Model by BiGRU with Attention Mechanism for Tropical Cyclone Track Prediction in Northwest Pacific. J. Appl. Meteorol. Climatol. 2021, 61, 3–12. [Google Scholar] [CrossRef]
- Song, T.; Wang, J.; Xu, D.; Wei, W.; Han, R.; Meng, F.; Li, Y. Unsupervised Machine Learning for Improved Delaunay Triangulation. J. Mar. Sci. Eng. 2021, 9, 1398. [Google Scholar] [CrossRef]
- Song, T.; Han, N.; Zhu, Y.; Li, Z.; Li, Y.; Li, S.; Peng, S. Application of deep learning technique to the sea surface height prediction in the South China Sea. Acta Oceanol. Sin. 2021, 40, 68–76. [Google Scholar] [CrossRef]
- Meng, F.; Song, T.; Xu, D.; Xie, P.; Li, Y. Forecasting tropical cyclones wave height using bidirectional gated recurrent unit. Ocean. Eng. 2021, 234, 108795. [Google Scholar] [CrossRef]
- Meng, F.; Xu, D.; Song, T. ATDNNS: An adaptive time–frequency decomposition neural network-based system for tropical cyclone wave height real-time forecasting. Future Gener. Comput. Syst. 2022, 133, 297–306. [Google Scholar] [CrossRef]
- Meng, F.; Song, T.; Xu, D. Simulating Tropical Cyclone Passive Microwave Rainfall Imagery Using Infrared Imagery via Generative Adversarial Networks. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Uitz, J.; Claustre, H.; Morel, A.; Hooker, S.B. Vertical distribution of phytoplankton communities in open ocean: An assessment based on surface chlorophyll. J. Geophys. Res. Ocean. 2006, 111, C08005. [Google Scholar] [CrossRef]
- Charantonis, A.A.; Badran, F.; Thiria, S. Retrieving the evolution of vertical profiles of Chlorophyll-a from satellite observations using Hidden Markov Models and Self-Organizing Topological Maps. Remote Sens. Environ. 2015, 163, 229–239. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the 29th Annual Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Li, H.; Xu, F.; Zhou, W.; Wang, D.; Wright, J.S.; Liu, Z.; Lin, Y. Development of a global gridded A rgo data set with B arnes successive corrections. J. Geophys. Res. Ocean. 2017, 122, 866–889. [Google Scholar] [CrossRef]
- Huang, B.; Liu, C.; Banzon, V.; Freeman, E.; Graham, G.; Hankins, B.; Smith, T.; Zhang, H.M. Improvements of the daily optimum interpolation sea surface temperature (DOISST) version 2.1. J. Clim. 2021, 34, 2923–2939. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements ofthe global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Hauser, D.; Tourain, C.; Hermozo, L.; Alraddawi, D.; Aouf, L.; Chapron, B.; Dalphinet, A.; Delaye, L.; Dalila, M.; Dormy, E.; et al. New observations from the SWIM radar on-board CFOSAT: Instrument validation and ocean wave measurement assessment. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5–26. [Google Scholar] [CrossRef]
- Atlas, R.; Hoffman, R.N.; Ardizzone, J.; Leidner, S.M.; Jusem, J.C.; Smith, D.K.; Gombos, D. A cross-calibrated, multiplatform ocean surface wind velocity product for meteorological and oceanographic applications. Bull. Am. Meteorol. Soc. 2011, 92, 157–174. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Hurlburt, H.E.; Smedstad, O.M.; Halliwell, G.R.; Hogan, P.J.; Wallcraft, A.J.; Baraille, R.; Bleck, R. The HYCOM (hybrid coordinate ocean model) data assimilative system. J. Mar. Syst. 2007, 65, 60–83. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Su, H.; Qin, T.; Wang, A.; Lu, W. Reconstructing ocean heat content for revisiting global ocean warming from remote sensing perspectives. Remote Sens. 2021, 13, 3799. [Google Scholar] [CrossRef]
- Graves, A. Generating sequences with recurrent neural networks. arXiv 2013, arXiv:1308.0850. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).